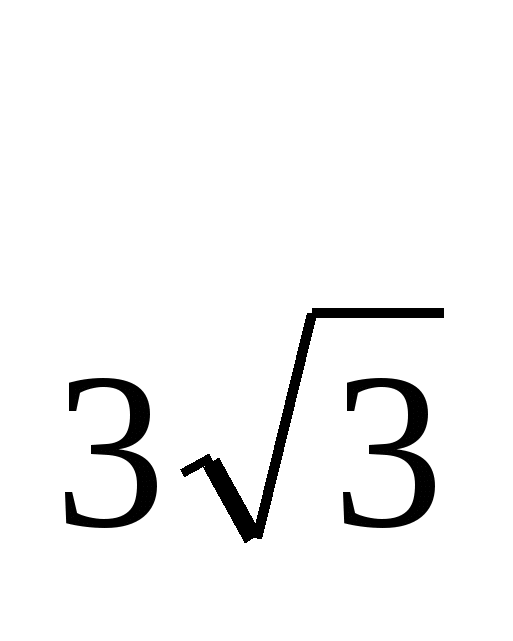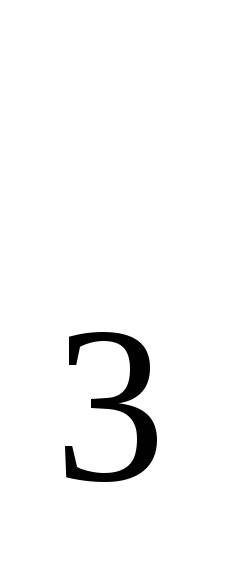Программа
итогового экзамена по математике
Раменское,
2013 г.
Пояснительная записка
Программа итогового экзамена по математике предназначена для студентов СПО.
Тест является основной формой проверки знаний за курс математики.
Объем теста – 20 заданий.
Продолжительность проведения экзамена – 5 часов.
Программа итогового экзамена по математике
Для успешной подготовки к итоговому экзамену по математике году студентам следует обратить особое внимание на повторение тем, согласно стандарта.
-
Тригонометрия:
Основные формулы тригонометрии. Функции и их графики. Решение тригонометрических уравнений и неравенств.
-
Производная:
Правила вычисления производных. Производная сложной функции. Производная показательной функции. Метод интервалов. Применение производной к исследованию функции.
-
Первообразная:
Основное свойство первообразной. Правила нахождения первообразных.
-
Понятие степени:
Корень n-ой степени и его свойства. Степень с рациональным показателем. Решение иррациональных уравнений.
5. Показательная и логарифмическая функции:
Показательная функция. Решение показательных уравнений и неравенств. Логарифмы и их свойства. Логарифмическая функция. Решение логарифмических уравнений и неравенств. Свойства функций.
6. Стереометрия:
Многогранники. Тела вращения.
Критерии оценки контрольной работы
1 задание:
Степень с рациональным показателем – 1 балл
2 задание:
Степень с рациональным показателем – 1 балл
3 задание:
Свойства логарифмической функции – 1 балл
4 задание:
Основные тригонометрические формулы – 2 балла
5 задание:
Основные тригонометрические формулы–2 балла
6 задание:
Решение тригонометрических уравнений– 1 балл
7 задание:
Решение иррациональных уравнений – 2 балла
8 задание:
Решение показательных уравнений – 2 балла
9 задание:
Метод интервалов — Решение иррациональных уравнений – 1 балл
10 задание:
Свойства тригонометрических функций – 1 балл
11 задание:
Вычисление производных — 1 балл
12 задание:
Нахождение первообразной функции – 1 балл
13 задание:
Решение логарифмических уравнений – 1 балл
14 задание:
Нахождение максимального и минимального значений функции – 2 балла
15 задание:
Свойства тел в стереометрии – 1 балл
16 задание:
Площадь криволинейной трапеции – 3 балла
17 задание:
Построение графика логарифмической функции – 3 балла
18 задание:
Решение показательных неравенств — 3 балла
19 задание:
Многогранники — 3 балла
20 задание:
Тела вращения — 3 балла
Рекомендации для проверки (проведения) экзаменационного теста.
Тест состоит из 20 заданий.
Задания содержат по 4 варианта ответов, причем каждый вопрос имеет только один вариант правильного ответа. Выберите нужный вариант и отметьте соответствующую ячейку в таблицу ответов.
Максимальный балл за тест – 35.
0 – 14 баллов — «2» («неудовлетворительно»)
15 – 19 баллов — «3» («удовлетворительно»)
21 – 29 баллов — «4» («хорошо»)
30 – 35 баллов — «5» («отлично» )
Ответы
Вариант 1
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
|
1 |
|
|
|
|
|
|
|
|
||||||||||||
|
2 |
|
|
|
|
|
|
||||||||||||||
|
3 |
|
|
||||||||||||||||||
|
4 |
|
|
|
|
Вариант 2
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
|
1 |
|
|
|
|
||||||||||||||||
|
2 |
|
|
|
|
||||||||||||||||
|
3 |
|
|
|
|
|
|
|
|||||||||||||
|
4 |
|
|
|
|
|
Вариант 3
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
|
1 |
|
|
|
|
||||||||||||||||
|
2 |
|
|
|
|
|
|
||||||||||||||
|
3 |
|
|
|
|
||||||||||||||||
|
4 |
|
|
|
|
|
|
Бланк ответов
экзаменационного теста
по математике
Ф.И.О.___________________________________________________
Группа № ________________________
Специальность ____________________
___ вариант.
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
|
1 |
||||||||||||||||||||
|
2 |
||||||||||||||||||||
|
3 |
||||||||||||||||||||
|
4 |
Вариант 1
-
Вычислите 29
– 15.
-
2) 43 3) 73 4) 101.
-
Упростите выражение
.
-
5 2) 1 3) 10 4) 0.
3) Упростите выражение – 2
.
1) 2) 1 3) 8
4) 20.
4) Найдите значение , если
= -0,8 и
.
1) -0,6 2) 0,6 3) 0,2 4) 0,36
5) Упростите выражение 7cos2α – 5 + 7sin2α.
1) 1 + cos2α 2) 2 3) -12 4) 12.
6) Решите уравнение = 1.
1)2n, n
2)
3)
+2
n, n
4)
n, n
7) Укажите промежуток, которому принадлежит корень уравнения = -х.
1) 2) (35;37) 3) (-2;
4)
.

1) [-4;0) 2) [0;1) 3) [-∞;-4) 4) [4;6).
9) Решите неравенство ≤0.
1) (-∞;-2) [
) 2) [-2;
)
( 1;+∞) 3) (-∞;-2) 4) (-∞;-5)
(-2;
.
10) Найдите множество значений функции у =– 2.
1) [3;1] 2) (-∞;+∞) 3) [-1;1] 4) [-3;-1].
11) Найдите производную функции f(x) = .
1) -4 2) -8
3) 8
4)
.
12) Укажите первообразную функции f(x) = 2х + 4х3 – 1.
1) х2 + х4 – х 2) 2х2 + 4х4 3) 2 + 12х2 4) х2+х4.
13) Решите равнение +
=
.
1) 0 2) 4 3) 9 4) 15.
14) Найдите точки максимума функции у = х3 – 3х2 .
1) 0 2) 2 3) -2 4) 3.
15) Найдите диагонали прямоугольного параллелепипеда по трем его измерениям: 2; 2; 1.
1) 5 2) 10 3) 3 4) 31.
16) Вычислите площадь фигуры (S), ограниченной линиями у = 4 – х2, у = 0, х = 0, х = 2.
1) 8 2) 2 3) 5
4) 6
.
17) Укажите область определения функции у =.
1) (-∞;0)(2;+∞) 2) (-2;+∞) 3) (2;+∞) 4) (0;2).
18) Найдите наибольшее целое решение неравенства – 1
0.
1) 0 2) -1 3) 1 4) 2.
19) Площади двух граней прямоугольного параллелепипеда равны 56дм2 и 192дм2, а длина их общего ребра 8дм. Найдите объем параллелепипеда.
1) 840 2) 1029 3) 1344 4) 1210.
20) Образующая конуса равна 12см и составляет с плоскостью основания угол 300. Найдите объем конуса, считая = 3.
1) 384 2) 192 3) 24 4) 648.
Вариант 2
-
Вычислите 7 — 3∙
.
-
2) 8 3) -5 4) -17.
-
Упростите выражение
.
1) 1,2 2) 5 3) 4)
.
3) Упростите выражение +
—
.
1) 2 +2 2) 7 3) 3 — 6
4) 2.
4) Найдите значение, если
=
и 0
.
1) — 2)
3)
4)
.
5) Упростите выражение -3sin2α — 6 – 3cos2α.
1) 1 2) 2cosα 3) cosα + 4) -9 .
6) Укажите промежуток, которому принадлежит корень уравнения = -х.
1) 2) (-
;-10) 3)
4)
.
7) Решите уравнение = 1.
1) n, n
2)
3)
+2
n, n
4)
n,n
.

1) [-4;0) 2) [0;1) 3) [1;4) 4) [4;6).
9) Решите неравенство ≤ 0.
1) (-2;) 2) [-2;2)
(
;+∞) 3) (-∞;3) 4) (-∞;-2)
(
].
10) Найдите множество значений функции у = + 4.
1) [3;5] 2) (-∞;+∞) 3) [-1;1] 4) [-5;-3].
11) Найдите производную функции f(x) = .
1) 3 2)
3) -3
4) —
.
12) Укажите первообразную функции f(x) = 3х2 + 2х -4.
1) х3+ х2 — 4х 2) 6х + 2 3) х3+ х2 4) х2+ х – 4х.
13) Решите равнение +
=
1) 0 2) 11 3) 3 4) 12.
14) Найдите точку минимума функции у = х2 — 1.
1) -1 2) 1 3) -2 4) 0.
15) Найдите диагонали прямоугольного параллелепипеда по трем его измерениям: 2; 3; 6.
1) 55 2) 7 3) 49 4) 11.
16) Вычислите площадь фигуры (S), ограниченной линиями у = х3 + 1, у = 0, х = 0, х = 2.
1) 8 2) 5 3) 6 4) 4.
17) Укажите область определения функции у =.
1) (-∞;0)(4;+∞) 2) (-4;+∞) 3) (4;+∞) 4) (0;4).
18) Найдите наименьшее целое решение неравенства – 1
0.
1) 0 2) 1 3) -1 4) 2.
19) Площади двух граней прямоугольного параллелепипеда равны 35см2 и 42см2, а длина их общего ребра 7см. Найдите объем параллелепипеда.
1) 840 2) 10290 3) 770 4) 210.
20) Образующая конуса равна 24см и составляет с плоскостью основания угол 300. Найдите объем конуса, считая = 3.
1) 3840 2) 1092 3) 5184 4) 648.
Вариант 3
1) Вычислите 2∙ – 0,90
1)10,9 2) 11 3) 9,1 4) 9.
2) Упростите выражение
-
2) 2 3) 0,7 4) 36.
3) Упростите выражение —
+
1) -1 + 2) -2 3) 0 4)
.
4) Найдите значение , если
= —
и
1) 2)
3)
4)
5) Упростите выражение -4sin2α +5 – 4cos2α
1) 1 2) 1 + 8sin2α 3) 1 + 8cos2α 4) 9.
6) Укажите промежуток, которому принадлежит корень уравнения = -х
1) 2) (-∞;-2) 3)
4)
.
7) Решите уравнение = -1
1) 2)0 3)
+2
n, n
4)
n, n

= 16
1) [-4;0) 2) [0;1) 3) [1;4) 4) [4;6).
9) Решите неравенство ≥0
1) (-∞;-8] (
; 2) 2) [-8;
)
( 2;+∞) 3) (-∞; 2) 4) (-∞;-8)
(2; +∞

10) Найдите множество значений функции у = – 1
1) [-1;1] 2) (-∞;+∞) 3) [-2;0] 4) [0;2].
11) Найдите производную функции f(x) =
1) -18 2) 6
3) 18
4)
.
12) Укажите первообразную функции f(x) = 5х4 – 2х + 1
1) 5х5 – 2х2 + 1 2) 20х3 – х 3) х4 – 2х + х 4) х5 – х2 + х.
13) Решите равнение +
=
1) 15 2) 5 3) 4 4) 10.
14) Найдите точку максимума функции у = 4х – х4
1) 4 2) 2 3) -4 4) 0.
15) Найдите диагонали прямоугольного параллелепипеда по трем его измерениям: 6; 6; 7
1) 19 2) 11 3) 121 4) 36.
16) Вычислите площадь фигуры (S), ограниченной линиями у = 1 – х3, у = 0, х = 0, х = 1.
1) 1 2) 3)
4) 1
.
17) Укажите область определения функции у =.
1) (-3;+∞) 2) (-∞;0)(3;+∞) 3) (3;+∞) 4) (0;3).
18) Найдите наибольшее целое решение неравенства – 1
0.
1) 1 2) -1 3) 2 4) 0.
19) Площади двух граней прямоугольного параллелепипеда равны 20см2 и 45см2, а длина их общего ребра 5см. Найдите объем параллелепипеда.
1) 240 2) 120 3) 180 4) 4500.
20) Образующая конуса равна 18дм и составляет с плоскостью основания угол 300. Найдите объем конуса, считая = 3.
1) 3804 2) 2192 3) 2187 4) 6408.
10-12. Чтение графика функции
Используя график функции у = f(x) (см. рис. ниже), определите и запишите ответ
10.1. Промежутки возрастания и убывания функции.
11.1. При каких значениях x
12.1. Наибольшее и наименьшее значения функции.
10.2. Промежутки возрастания и убывания функции.
11.2. Наибольшее и наименьшее значения функции.
12.2. При каких значениях x
10.3. Промежутки, на которых
11.3. Точки экстремума функции.
12.3. Наибольшее и наименьшее значения функции.
10.4. Нули функции.
11.4. Промежутки возрастания и убывания функции.
12.4. Наибольшее и наименьшее значения функции.
10.5. При каких значениях x функция y не имеет производной.
11.5. При каких значениях x выполняется
12.5. Наибольшее и наименьшее значения функции.
10.6. При каких значениях x выполняется
11.6. Промежутки возрастания и убывания функции.
12.6. При каких значениях x выполняется
10.7. При каких значениях x выполняется
11.7. Промежутки возрастания и убывания функции.
12.7. При каких значениях x выполняется
10.8. Область определения функции.
11.8. При каких значениях x выполняется
12.8. При каких значениях x выполняется
10.9. Область определения функции.
11.9. При каких значениях x выполняется
12.9. При каких значениях x выполняется
10.10. Область определения функции.
11.10. При каких значениях x выполняется 
12.10. Промежутки возрастания и убывания функции.
10.11. Область определения функции.
11.11. При каких значениях x выполняется
12.11. Промежутки возрастания и убывания функции.
10.12. Область определения функции.
11.12. При каких значениях x выполняется
12.12. Промежутки возрастания и убывания функции
.
10.13. Область определения функции.
11.13. При каких значениях x выполняется
12.13. При каких значениях x выполняется
10.14. При каких значениях x выполняется
11.14. При каких значениях x выполняется
12.14. Наибольшее и наименьшее значения функции.
10.15. Область определения функции.
11.15. При каких значениях x выполняется 
12.15. При каких значениях x выполняется
10.16. При каких значениях x выполняется
11.16. Промежутки возрастания и убывания функции.
12.16. Наибольшее и наименьшее значения функции.
10.17. При каких значениях x выполняется
11.17. Точки экстремума функции.
12.17. Промежутки возрастания и убывания функции.
10.18. При каких значениях x выполняется
11.18. Промежутки возрастания и убывания функции.
12.18. Наибольшее и наименьшее значения функции.
10.19. Область определения функции.
11.19. При каких значениях x выполняется
12.19. Точки экстремума функции.
10.20. При каких значениях x выполняется
11.20. При каких значениях x выполняется
12.20. Наибольшее и наименьшее значения функции.
II. ЗАДАНИЕ ДЛЯ ЭКЗАМЕНУЮЩЕГОСЯ. Вариант №1
-
Вычислите значение выражения
-
Решите уравнение
-
Вычислите значение выражения
-
Решите уравнение:
-
Решите уравнение
-
Вычислите
+
-
Найти угол между векторами
-
В футбольной команде 11 человек. Необходимо выбрать капитана и его заместителя. Сколькими способами это можно сделать?
-
. Решите уравнение
-
Решите неравенство:
II. ЗАДАНИЕ ДЛЯ ЭКЗАМЕНУЮЩЕГОСЯ. Вариант №2
1. Вычислите значение выражения
2. Решите уравнение
3.Вычислите значение выражения: lg100-lg10+lg1
4. Решить уравнение
5.Решите уравнение
6. Вычислить
7. Даны координаты точек А(3;-2;1), В(5;1;-4),С(2;0;1),Д(5;-1;3). Найти угол между векторами АВ и СД.
8. На соревнованиях по лёгкой атлетике наш техникум представляла команда из 10 спортсменов. Сколькими способами тренер может определить, кто из них побежит в эстафете на первом, втором, третьем и четвёртом этапах?
9.Решить уравнение:5x+1+5x + 5x-1
10. Решить неравенство:
II. ЗАДАНИЕ ДЛЯ ЭКЗАМЕНУЮЩЕГОСЯ. Вариант №3
1. Вычислите значение выражения: 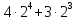
2. Решите уравнение : =11.
3.Вычислите значение выражения
4.Решите уравнения:
5. Вычислить:
6. Решить уравнение:
7.Найти скалярное произведение векторов:
8. В теннисном турнире участвуют 10 спортсменов. Сколькими способами теннисисты могут завоевать золото, серебро и бронзу?
9.Решить уравнение: 7x -7x-1 = 6
10. Решить неравенство:
II. ЗАДАНИЕ ДЛЯ ЭКЗАМЕНУЮЩЕГОСЯ. Вариант №4
1. Вычислите значение выражения.
2. Решите уравнение
3. Вычислите значение выражения.
4.Решите уравнение
5. Вычислить:
6. Решить уравнение: 0,5x+7*0,51-2x = 2
7.Найти скалярное произведение векторов:
8. Сколькими способами из 15 учеников класса можно выбрать трёх для участия в праздничном концерте?
9.Решить уравнение: 3x+2 +3x = 10
10. Решить неравенство:
II. ЗАДАНИЕ ДЛЯ ЭКЗАМЕНУЮЩЕГОСЯ. Вариант № 5
1. Вычислите значение выражения. 2*53+3*52
2. Решите уравнение = 7
3. Вычислите значение выражения.
4.Решите уравнение
5. Вычислить:
6. Решить уравнение:
7. Вычислите длину вектора:
8. Имеются помидоры, огурцы, лук. Сколько различных салатов можно приготовить, если в каждый салат должно входить 2 различных вида овощей?
9.Решить уравнение: 4x – 2x+1 = 48
10. Решить неравенство:
II. ЗАДАНИЕ ДЛЯ ЭКЗАМЕНУЮЩЕГОСЯ. Вариант № 6
1. Вычислите значение выражения. + log
8+ log
2
2. Решите уравнение =4.
3. Вычислите значение выражения.
4.Решите уравнение
5. Вычислить: log8+ log
2
6. Решить уравнение: 112Х+5=1
7. Вычислите длину векторов:
8. Сколько существует различных двузначных чисел, в записи которых можно использовать цифры 1, 2, 3, 4, 5, 6, если цифры в числе должны быть различными?.
9.Решить уравнение: 32x – 2*32x-1 – 2*32x-2 = 1
10. Решить неравенство:
II. ЗАДАНИЕ ДЛЯ ЭКЗАМЕНУЮЩЕГОСЯ. Вариант № 7
1. Вычислите значение выражения:
2. Решите уравнение =0
3. Вычислите значение выражения.
4.Решите уравнение
5 Найти ,
.
6. Решить уравнение: 17Х+2=Х
7. Вычислите длину вектора
8. На 1 курсе 12 учащихся, имеющих по математике оценки «4-5». Сколькими способами можно сформировать команду из 4 человек для участия в математической олимпиаде?
9.Решить уравнение:2x + 2x-3 = 18
10. Решить неравенство:
.
II. ЗАДАНИЕ ДЛЯ ЭКЗАМЕНУЮЩЕГОСЯ. Вариант № 8
1. Вычислите значение выражения:
2.
3. Вычислите значение выражения.
4.Решите уравнение
5. Вычислить:
6. Решить уравнение: 11х-10=121
7. Вычислите длину вектора
8. Из города А в город В ведут две дороги, из города В в С – три дороги, из города С до пристани – две дороги. Туристы хотят проехать из города А через города В и С к пристани. Сколькими способами они могут выбрать маршрут?
9.Решить уравнение: 3x +4*3x+1 = 13
10. Решить неравенство:
II. ЗАДАНИЕ ДЛЯ ЭКЗАМЕНУЮЩЕГОСЯ. Вариант № 9
1. Вычислите значение выражения:
2. Решите уравнение =0
3. Вычислите значение выражения.
4.Решите уравнение
5. Вычислить:
6. Решить уравнение: 11х-10=121
7 Найти скалярное произведение а ( 4; — 7; — 3) в ( 3; -2; 1)
8. Сколько двузначных чисел можно составить из чисел 1,2,3,4?
9.Решить уравнение: 5x+1 +3*5x-1 -6*5x +10 = 0
10. Решить неравенство:42x -5*4x + 4
II. ЗАДАНИЕ ДЛЯ ЭКЗАМЕНУЮЩЕГОСЯ. Вариант № 10
1. Вычислите значение выражения:
2. Решить уравнение =
3. Вычислите значение выражения.
4.Решите уравнение
5. Вычислить:
6. Решить уравнение: 2х+1=64
7 Найти угол между векторами, а = 6i + 4k в =2 i -12 k
8. Сколько существует различных двузначных чисел, в записи которых можно использовать цифры 1, 2, 3, 4, 5, 6, если цифры в числе должны быть различными?
9.Решить уравнение: 2x+3— 2x+1 = 12
10. Решить неравенство:2x+2x+2≤ 20
II. ЗАДАНИЕ ДЛЯ ЭКЗАМЕНУЮЩЕГОСЯ. Вариант № 11
1. Вычислите значение выражения:
2. Решить уравнение
= 5
3. Вычислите значение выражения.
—
4.Решите уравнение
5. Вычислить: 27log32
6. Решить уравнение: 4х+1=8
7 Найти скалярное произведение векторов а ( 4; — 7; — 3), в ( 3; -2; 1)
8. Сколькими способами могут быть расставлены 5 участниц финального забега на 5-ти беговых дорожках?
9.Решить уравнение: 2x+1 +2x-1 +2x =28
10. Решить неравенство:
II. ЗАДАНИЕ ДЛЯ ЭКЗАМЕНУЮЩЕГОСЯ. Вариант № 12
1. Вычислите значение выражения: 27log32+
2. Решить уравнение
3. Вычислите значение выражения.
4.Решите уравнение
5. Вычислить: log8+ log
2
6. Решить уравнение: 4х+1=8
7 Найти скалярное произведение векторов а ( 4; — 7; — 3), в ( 3; -2; 1)
8. Сколькими способами из 7 человек можно выбрать комиссию, состоящую из 3 человек?
9.Решить уравнение: 3x-1 -3x +3x+1 = 63
10. Решить неравенство:
II. ЗАДАНИЕ ДЛЯ ЭКЗАМЕНУЮЩЕГОСЯ. Вариант № 13
1. Вычислите значение выражения:
2. Решить уравнение
8
3. Вычислите значение выражения. 27log32
4.Решите уравнение
5. Вычислить:
6. Решить уравнение:
7 Найти угол между векторами: а = 3i + 4k , в =5 i+ 12 k
8. Восемь студентов обменялись рукопожатиями. Сколько было рукопожатий?
9.Решить уравнение: 23x+2 -23x-2 = 30
10. Решить неравенство: 16x 0,125
II. ЗАДАНИЕ ДЛЯ ЭКЗАМЕНУЮЩЕГОСЯ. Вариант № 14
1. Вычислите значение выражения:
2. Решить уравнение
3. Вычислите значение выражения.
4.Решите уравнение
5. Вычислить:
6. Решить уравнение: 2х+1=64
7 Найти угол между векторами: а = 2i + j + 2k в = 3i + 2j -2k
8 Сколькими способами можно разложить 7 разных монет в три кармана?
9.Решить уравнение: 2*4x =64
10. Решить неравенство 2x -2x-415
II. ЗАДАНИЕ ДЛЯ ЭКЗАМЕНУЮЩЕГОСЯ. Вариант № 15
1. Вычислите значение выражения: при
.
2. Решить уравнение: 7
3. Вычислите значение выражения.
4.Решите уравнение
5. Вычислить: log8+ log
2
6. Решить уравнение: 17х-16=1
7 Найти угол между векторами: а = 2i + j + 2k в = 3i + 2j -2k
8 Семь девушек водят хоровод. Сколькими различны ми способами они могут встать в круг?
9.Решить уравнение: 64x -8x -56 = 0
10. Решить неравенство: .
II. ЗАДАНИЕ ДЛЯ ЭКЗАМЕНУЮЩЕГОСЯ. Вариант № 16
1. Найдите значение выражения при
.
2. Решить уравнение: 7
3. Вычислите значение выражения. log327-lg0,01+log0,6 0,36+log71.
4.Решите уравнение
5. Вычислить:
6. Решить уравнение: 4x-1 =1
7 Найти угол между векторами: а = 2i + j + 2k в = 3i + 2j -2k
8 У мамы 2 яблока и 3 груши. Каждый день в течение 5 дней подряд она выдает по одному фрукту. Сколькими способами это может быть сделано?
9.Решить уравнение: 16x -17*4x +16=0
10. Решить неравенство: 1002х+1
II. ЗАДАНИЕ ДЛЯ ЭКЗАМЕНУЮЩЕГОСЯ. Вариант № 17
1. Вычислите значение выражения:
2. Решить уравнение
3. Вычислите значение выражения. log
8+ log
2
4.Решите уравнение
5. Вычислить:
6. Решить уравнение:
7 Найти угол между векторами: а = 2i + j + 2k в = 3i + 2j -2k
8 В пассажирском поезде 9 вагонов. Сколькими способами можно рассадить в поезде 4 человека, при условии, что все они должны ехать в различных вагонах?
10. Решить неравенство: .
II. ЗАДАНИЕ ДЛЯ ЭКЗАМЕНУЮЩЕГОСЯ. Вариант № 18
1. Вычислите значение выражения:
2. Решить уравнение
3. Вычислите значение выражения.
4.Решите уравнение
5. Вычислить:
6. Решить уравнение:
7 Найти угол между векторами: а = 4i + j -2k в = 3i + 4j -2k
8 Для участия в команде тренер отбирает 5 мальчиков из 10. Сколькими
способами он может сформировать команду, если 2 определенных мальчика
должны войти в команду?
9.Решить уравнение: 3x+9x-1 – 810 = 0
10. Решить неравенство: 7x-2 49
II. ЗАДАНИЕ ДЛЯ ЭКЗАМЕНУЮЩЕГОСЯ. Вариант № 19
1. Вычислите значение выражения:
2. Решить уравнение
3. Вычислите значение выражения. log5250 – log52
4.Решите уравнение
5. Вычислить:
6. Решить уравнение:
7 Найти угол между векторами: а = -2i + 5j + 2k в = 7i + 6j -2k
8 В шахматном турнире принимали участие 15 шахматистов, причем
каждый из них сыграл только одну партию с каждым из остальных.
Сколько всего партий было сыграно в этом турнире?
9.Решить уравнение: 9x -3x – 6 = 0
10. Решить неравенство: 3x-2 9
II. ЗАДАНИЕ ДЛЯ ЭКЗАМЕНУЮЩЕГОСЯ. Вариант № 20
1. Вычислите значение выражения: 60,5 3 0,5(0,25) 0,25 .
2. Решить уравнение = 5.
3. Вычислите значение выражения.
4.Решите уравнение
5. Вычислить
6. Решить уравнение:
7 Найти угол между векторами: а = 2i + j + 2k в = 3i + 2j -2k
8 Сколькими способами можно расставить 8 ладей на шахматной доске так, чтобы они не били друг друга?
9.Решить уравнение: 52x -5x – 600 = 0
10. Решить неравенство log5 (4х+1) -1.
Государственное бюджетное профессиональное образовательное учреждение
Иркутской области
«Черемховский техникум промышленной индустрии и сервиса»
|
Рассмотрены и одобрены на заседании методической комиссии преподавателей общеобразовательных дисциплин «_____»___сентября____2015 г. Протокол № ____1______ Председатель МК ___________________ Богданова В.А. |
Утверждаю Зам. директора ГБПОУ ИО ЧТПиС _______________С.Н. Дроботенко «_____»_____________2015 г |
.
КОНТРОЛЬНО-ОЦЕНОЧНЫЕ МАТЕРИАЛЫ
для проведения промежуточной и итоговой аттестации
по УД «Математика»
за период 2015-2016 учебного года
в группах 1 курса
профиля:
Разработчик:
Стефанцева Наталья Геннадьевна, преподаватель общественных дисциплин
ГБПОУ ИО ЧТПиС
Черемхово
2015
Содержание
I. Общие положения.
II. Паспорт комплекта контрольно-оценочных средств
III. Контрольно-измерительные материалы для проведения письменного экзамена в виде набора контрольных заданий
I. Общие положения
1. Пояснительная записка
1.1 Нормативная база
Комплект контрольно-оценочных средств для проведения промежуточной аттестации в форме экзамена по УД «Математика» разработан на основании нормативных документов:
-
ФГОС среднего (полного) общего образования в пределах ОПОП НПО/СПО с учетом профиля получаемого профессионального образования в соответствии с федеральными базисными учебными планами и примерными учебными планами для образовательных учреждений РФ, реализующих программы общего образования (приказ Минобразования России от 09.03.2004 г. № 1 312)
-
Рабочая программа учебной дисциплины Математика
-
Положение о текущем контроле знаний и промежуточной аттестации студентов НПО/СПО ГБПОУ ИО «Черемховский техникум промышленной индустрии и сервиса»
1.2 Общие положения
Экзамен по математике проводится за счет времени, выделяемого ФГОС НПО/СПО на промежуточную аттестацию.
Содержание экзаменационных материалов отвечает требованиям к уровню подготовки выпускников, предусмотренным государственным образовательным стандартом среднего (полного) общего образования и зафиксированным в примерной программе учебной дисциплины «Математика» для профессий НПО и специальностей СПО.
Экзамен по математике проводится с использованием экзаменационных материалов в виде набора контрольных заданий.
II. Паспорт комплекта контрольно-оценочных средств
2.1 Область применения
Комплект контрольно-оценочных средств предназначен для контроля и оценки образовательных достижений обучающихся, освоивших программу учебной дисциплины ОУД 03 Математика в рамках реализации федерального государственного образовательного стандарта по программам подготовки квалифицированных рабочих (служащих)
Профессия: Электро-газосварщик
Машинист локомотива
Технология продукции общественного питания
2.2. 2.Сводные данные об объектах оценивания, основных показателях оценки
Таблица№1
|
Результаты освоения учебных достижений (объекты оценивания) |
Основные показатели оценки результата |
|
У1. Решать рациональные, показательные, логарифмические, тригонометрические уравнения, сводящиеся к линейным и квадратным, а также аналогичные неравенства и системы; |
Выполнение:
выбор правильного ответа на числовой прямой использование свойств логарифмических функций; преобразование тригонометрических выражений |
|
У2. Умение находить производные элементарных функций; находить первообразную функции; вычислять в простейших случаях площади и объемы с использованием определенного интеграла; находить производные элементарных функций; использовать производную для изучения свойств функций и построения графиков; |
Применение
|
|
У3. Решать планиметрические и простейшие стереометрические задачи на нахождение геометрических величин (длин, углов, площадей, объемов); проводить доказательные рассуждения в ходе решения задач; описывать взаимное расположение прямых и плоскостей в пространстве. |
Выполнение правильного построения чертежа;
|
|
У4. Находить наименьшее и наибольшее значения функций; умение находить производную функции |
|
|
У5. Уметь решать иррациональные уравнения и логарифмические неравенства |
|
|
У6. Уметь выполнять арифметические действия над числами; находить значения корня, степени, логарифма, тригонометрических функций; находить число по проценту |
|
|
У7. Уметь выполнять преобразования выражений, применяя формулы, связанные со свойствами степеней, логарифмов, тригонометрических функций; |
|
|
У8. Уметь вычислять значение функции по заданному значению аргумента при различных способах задания функции; определять основные свойства числовых функций, строить графики функций, иллюстрировать по графику свойства элементарных функций; |
|
|
У9. Уметь описывать взаимное расположение прямых и плоскостей в пространстве, изображать основные многогранники и круглые тела; выполнять чертежи по условиям задач; |
|
|
У10. Уметь находить вероятности событий и элементы комбинаторики |
|
|
З 1.Знание свойства показательной и логарифмической функции |
— применение свойств степени, показательной функции, равносильности уравнений |
|
З 2.Знание теоретических основ начал математического анализа |
|
|
З 3. Знание формулировок аксиом и основных теорем и их следствий; понятия тела вращения: цилиндр, конус и шар; свойств перпендикуляра и наклонной; основных теорем планиметрии и стереометрии понятия объема тела |
|
|
З4. Знание понятия о числовых функциях и их основных свойствах, графиках функций. свойств и графиков степенной, показательной, логарифмической функций; |
|
|
З 5. Знание свойств иррациональных. показательных, логарифмических, тригонометрических уравнений и неравенств; Основных приемов решения уравнений и неравенств с одной и двумя переменными; |
|
|
З6. Знание обобщенного понятия о степени числа, корня n-степени из числа; преобразований степенных выражений; преобразований выражений, содержащих логарифмы; |
|
|
З7. Знание о производной функции, ее геометрическом и физическом смысле. правила вычисления производные элементарных функций;. уравнение касательной к графику функции исследования функций с помощью производной |
|
|
З8. Знание первообразной функции и определенного интеграла, формулы Ньютона — Лейбница; |
|
|
З8. Знание основ комбинаторики и теории вероятностей |
|
2.3 Содержание и структура экзаменационной работы
Письменная экзаменационная работа по учебной дисциплине ОУД 03. Математика состоит из 2-х частей: обязательной и дополнительной.
В обязательную часть включаются задания минимально обязательного уровня, в дополнительную часть – более сложные.
В обязательную часть работы включены задания базового уровня по всем основным разделам требований ФГОС – геометрия (планиметрия и стереометрия), алгебра, начала математического анализа, теория вероятностей, комбинаторика .
При выполнении заданий обязательной части обучающиеся должны продемонстрировать базовую математическую компетентность. Задания этой группы проверяют базовые вычислительные и логические умения и навыки, умение анализировать информацию, представленную в графиках и таблицах, использовать простейшие вероятностные и статистические модели, ориентироваться в простейших геометрических конструкциях, владение основными алгоритмами, знание и понимание ключевых элементов содержания (математических понятий, их свойств, приемов решения задач и пр.), умение пользоваться математической записью, а также применять математические знания в простейших практических ситуациях.
Обязательная часть содержит 19 заданий.
К каждому типу заданий прилагается инструкция по форме представления ответа.
Дополнительная часть направлена на проверку владения материалом на повышенном уровне и умение решать математические задачи, не сводящиеся к прямому применению алгоритма. Эта часть должна содержать не менее 4 заданий повышенного уровня сложности из различных разделов курса математики .
При выполнении всех заданий дополнительной части необходимо представить описание хода решения задачи и полученный ответ. Возможны различные способы решения в записи развернутого ответа. Главное требование – решение должно быть математически грамотным, из него должен быть понятен ход рассуждений автора работы. При этом оценивается продвижение обучающегося в решении задачи, а не недочеты по сравнению с «эталонным» решением. При решении задачи можно использовать любые математические факты без доказательств и ссылок, содержащиеся в учебниках и учебных пособиях, допущенных или рекомендованных Министерством образования и науки РФ.
Распределение заданий по частям экзаменационной работы с указанием первичных баллов представлено в таблице 2.
Таблица 2
|
Части работы |
Число заданий |
Максимальный первичный балл |
Тип заданий |
|
Часть 1 (обязательная) |
8 |
8 |
С выбором ответа С кратким ответом |
|
11 |
11 |
||
|
Часть 2 (дополнительная) |
7 |
14 |
С развёрнутым ответом |
|
Итого |
26 |
33 |
При подборе контрольных заданий для проведения экзамена использован перечень элементов содержания по математике.
Предлагаемый перечень элементов содержания и требований к уровню подготовки обучающихся составлен на основе Федерального компонента государственных стандартов основного общего и среднего (полного) общего образования по математике базового/профильного уровня (Приказ Минобразования России от 05.03.2004 г. № 1089 «Об утверждении федерального компонента государственных образовательных стандартов начального общего, основного общего и среднего (полного) общего образования» (в ред. Приказов Минобрнауки РФ от 03.06.2008 № 164 от 31.08.2009 № 320, от 19.10.2009 № 427).
Проверяемые элементы содержания
Таблица 3
|
Введение |
Математика в науке, технике, экономике, информационных технологиях и практической деятельности. |
|
Развитие понятия о числе |
Целые и рациональные числа. Действительные числа. |
|
Корни, степени и логарифмы |
Корни и степени. Корни натуральной степени из числа и их свойства. Степени с рациональными показателями, их свойства. Степени с действительными показателями. Логарифм. Логарифм числа. Основное логарифмическое тождество. Десятичные и натуральные логарифмы. Правила действий с логарифмами. Преобразование алгебраических, рациональных, иррациональных степенных, показательных и логарифмических выражений. |
|
Прямые и плоскости в пространстве |
Взаимное расположение двух прямых в пространстве. Параллельность прямой и плоскости. Параллельность плоскостей. Перпендикулярность прямой и плоскости. Перпендикуляр и наклонная. Угол между прямой и плоскостью. Двугранный угол. Угол между плоскостями. Перпендикулярность двух плоскостей. |
|
Элементы комбинаторики |
Основные понятия комбинаторики. Задачи на подсчет числа размещений, перестановок, сочетаний. Решение задач на перебор вариантов. Формула бинома Ньютона. Свойства биноминальных коэффициентов. Треугольник Паскаля. |
|
Координаты и векторы |
Прямоугольная (декартова) система координат в пространстве. Формула расстояния между двумя точками. Векторы. Модуль вектора. Равенство векторов. Сложение векторов. Умножение вектора на число. Разложение вектора по направлениям. Угол между двумя векторами. Проекция вектора на ось. Координаты вектора. Скалярное произведение векторов. |
|
Основы тригонометрии |
Радианная мера угла. Синус, косинус, тангенс и котангенс числа. Основные тригонометрические тождества, формулы приведения. Синус, косинус и тангенс суммы и разности двух углов. Синус и косинус двойного угла. Преобразования простейших тригонометрических выражений. Простейшие тригонометрические уравнения. Решение тригонометрических уравнений. |
|
Функции, их свойства и графики. Степенные, показательные, логарифмические и тригонометрические функции |
Функции. Область определения и множество значений; график функции, построение графиков функций, заданных различными способами. Свойства функции: монотонность, четность, нечетность, ограниченность, периодичность. Промежутки возрастания и убывания, наибольшее и наименьшее значения, точки экстремума. Графики |
|
Многогранники |
Вершины, ребра, грани многогранника. Призма. Прямая и наклонная призма. Правильная призма. Параллелепипед. Куб. Пирамида. Правильная пирамида. Тетраэдр. Симметрии в кубе, в параллелепипеде. Сечения куба, призмы и пирамиды. Представление о правильных многогранниках. |
|
Тела и поверхности вращения |
Цилиндр и конус. Основание, высота, боковая поверхность, образующая, развертка. Осевые сечения и сечения, параллельные основанию. Шар и сфера, их сечения. |
|
Начала математического анализа |
Последовательности. Способы задания и свойства числовых последовательностей. Понятие о производной функции, её геометрический и физический смысл. Уравнение касательной к графику функции. Производные суммы, разности, произведения, частного. Производные основных элементарных функций. Применение производной к исследованию функций и построению графиков. Примеры использования производной для нахождения наилучшего решения в прикладных задачах. Применение производной к исследованию функций и построению графиков. Нахождение скорости для процесса, заданного формулой и графиком. Первообразная и интеграл. Применение определенного интеграла для нахождения площади криволинейной трапеции. Формула Ньютона—Лейбница. Примеры применения интеграла в физике и геометрии. |
|
Измерения в геометрии |
Объем и его измерение. Формулы объема куба, прямоугольного параллелепипеда, призмы, цилиндра. Формулы объема пирамиды и конуса. Формулы площади поверхностей цилиндра и конуса. Формулы объема шара и площади сферы. Подобие тел. Отношения площадей поверхностей и объемов подобных тел. |
|
Элементы теории вероятностей. Элементы математической статистики |
Событие, вероятность события, сложение и умножение вероятностей. Представление данных (таблицы, диаграммы, графики), генеральная совокупность, выборка, среднее арифметическое, медиана. |
|
Уравнения и неравенства |
Равносильность уравнений, неравенств, систем. Рациональные, иррациональные, показательные и тригонометрические уравнения, неравенства и их системы. Основные приемы их решения. Использование свойств и графиков функций при решении уравнений и неравенств. Метод интервалов. |
2.3.Процедура проведения экзамена.
На выполнение письменной экзаменационной работы отводится 240 минут.
Для проведения экзамена по математике с использованием экзаменационных материалов в виде набора контрольных заданий каждому обучающемуся выдаётся:
— текст с одним из четырех вариантов письменной экзаменационной работы;
— инструкция по выполнению экзаменационной работы;
— лист для черновика.
Все задания обучающийся выполняет на листах с печатной основой
Перед началом выполнения письменной экзаменационной работы (время не входит в 4 астрономических часа) преподаватель контролирует заполнение личных данных обучающихся, знакомит обучающихся со структурой экзаменационной работы, с критериями оценивания еѐ результатов.
Обучающимся поясняется, что экзаменационная работа состоит из двух частей: обязательной и дополнительной. В обязательную часть включены задания минимально обязательного уровня, а в дополнительную часть – более сложные. Выполнение каждого из заданий оценивается в баллах. Количество баллов, которое можно получить за правильное выполнение того или иного задания, проставлено в скобках рядом с его номером. Баллы, полученные за все выполненные задания, суммируются.
Шкала перевода баллов в отметки по пятибалльной системе показывает, сколько баллов необходимо набрать, чтобы получить отметку «3», «4» или «5». Шкала остаётся открытой для обучающихся в течение всего экзамена, они могут ориентироваться на неё в ходе выполнения экзаменационной работы. Обучающиеся могут просчитать при помощи шкалы, сколько и какие задания необходимо выполнить правильно, чтобы получить определённую отметку.
Обучающиеся должны начинать выполнение экзаменационной работы с заданий обязательной части. Для получения удовлетворительной отметки необязательно выполнять минимум 15 заданий обязательной части, но только после выполнения достаточного для получения удовлетворительной отметки количества заданий обязательной части обучающийся может переходить к заданиям дополнительной части, чтобы повысить оценку до «4» или «5». Обучающийся может начинать выполнение работы с любого задания с нужным количеством баллов, учитывая при этом степень своей уверенности в ответе.
Шкала перевода баллов в отметки по пятибалльной системе
|
Отметка |
Число баллов, необходимое для получения отметки |
|
«2» (неудовлетворительно) |
Менее 15 |
|
«3» (удовлетворительно) |
15-19 |
|
«4» (хорошо) |
20-23 |
|
«5» (отлично) |
Более 23 |
III. Контрольно-измерительные материалы для проведения письменного экзамена в виде набора контрольных заданий
3.1 Краткая инструкция для обучающихся по выполнению экзаменационной работы
На письменный экзамен учащиеся приходят за 20 мин до начала экзамена. При себе иметь шариковую, гелиевую или капиллярную ручку с черными чернилами;
К экзамену по математике при себе также иметь чертежные инструменты и справочные материалы, которые можно использовать.
Во время проведения экзаменов запрещается иметь при себе и использовать средства связи и электронно-вычислительную технику, за исключением случаев, установленных нормативно-правовыми актами РФ.
Получить от преподавателя и ассистента черновики и экзаменационный комплект с вложенными в них контрольно-измерительными материалами (КИМ), бланками ответов № 1 и № 2.
Внимательно прослушать инструктаж, проводимый преподавателем, информирующий экзаменующих о порядке проведения экзамена,
правилах заполнения бланков, продолжительности экзамена
Заполнить регистрационные части бланков: бланка регистрации, бланков ответов № 1 и 2.
На выполнение экзаменационной работы дается 4 часа (240 минут).
Работа состоит из двух частей и содержит 26 заданий.
Часть 1 содержит 19 заданий с выбором ответа и с кратким ответом. Задания части 1 считаются выполненными, если экзаменующий выбрал верные ответы.
Часть 2 содержит 7 более сложных заданий ( А20-А26) по материалу курса математики. При их выполнении надо записать полное решение и ответ.
Совет: для экономии времени пропускать задание, которое не удается выполнить сразу и переходить к следующему. К выполнению пропущенных заданий можно вернуться, если у Вас останется время.
– начинать работу всем следует с выполнения заданий обязательной части;
– для получения удовлетворительной оценки не обязательно выполнять все задания обязательной части;
– правильное выполнение определенной части заданий обязательной части, во-первых, гарантирует получение отметки «3», а во-вторых, дает основу для повышения отметки до «4» или «5» при правильном выполнении нескольких заданий дополнительной части;
– при выполнении заданий дополнительной части следует проследить по шкале перевода баллов в отметки — сколько заданий достаточно правильно выполнить, чтобы получить 4 или 5; После объявления о времени начала экзамена, которое фиксируется на доске, приступить к выполнению экзаменационной работы.
Во время экзамена учащиеся должны соблюдать установленный порядок проведения экзамена и следовать указаниям организаторов.
Во время экзамена учащиеся не вправе общаться друг с другом, свободно перемещаться по кабинету, пользоваться справочными материалами, иметь при себе и использовать средства связи и электронно-вычислительной техники.
Учащиеся могут выходить из кабинета в случае необходимости (в туалет, в медицинскую комнату), предварительно сдав бланки.
По окончании экзамена необходимо:
сдать экзаменационный материал КИМ, черновики, бланки ответов № 1 и № 2;
Допускается досрочная сдача экзаменационных материалов, которая прекращается за пятнадцать минут до окончания экзамена.
Желаем успеха!
3.2. Контрольная работа по математике
По профессиям: электрогазосварщик,
машинист локомотива
ВАРИАНТ № 1
Часть 1.
1. Найдите значение выражения
2. Одна из точек, отмеченных на координатной прямой, соответствует числу
Какая это точка?
1) точка M
2) точка N
3) точка P
4) точка Q
3. Сравните числа и 10.
В ответе укажите номер правильного варианта.
1)
2)
3)
4. Решите уравнение .
Если корней несколько, запишите их через точку с запятой в порядке возрастания.
5. Установите соответствие между функциями и их графиками.
Графики
Функции
|
А) |
Б) |
В) |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
|
А |
Б |
В |
6. Выписаны первые несколько членов арифметической прогрессии: 3; 6; 9; 12;… Какое из следующих чисел есть среди членов этой прогрессии?
|
1) 83 |
2) 95 |
3) 100 |
4) 102 |
7. Найдите значение выражения при
8. На каком рисунке изображено множество решений неравенства
В ответе укажите номер правильного варианта.
-
В выпуклом четырехугольнике ABCD
,
,
,
. Найдите угол A. Ответ дайте в градусах.
-
Найдите градусную меру ∠MON, если известно, NP — диаметр, а градусная мера ∠MNP равна 18°.
11. В прямоугольнике одна сторона равна 96, а диагональ равна 100. Найдите площадь прямоугольника.
12. На клетчатой бумаге с размером клетки 1см x 1см отмечены точки А, В и С. Найдите расстояние от точки А до прямой ВС. Ответ выразите в сантиметрах.
13. Укажите номера верных утверждений.
1) Любые три прямые имеют не более одной общей точки.
2) Если угол равен 120°, то смежный с ним равен 120°.
3) Если расстояние от точки до прямой больше 3, то и длина любой наклонной, проведённой из данной точки к прямой, больше 3.
Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.
14. Куриные яйца в зависимости от их массы подразделяют на пять категорий: высшая, отборная, первая, вторая и третья. Используя данные, представленные в таблице, определите, к какой категории относится яйцо, массой 35,5 г.
|
Категория |
Масса одного яйца, г |
|
Высшая |
75,0 и выше |
|
Отборная |
65,0 − 74,9 |
|
Первая |
55,0 − 64,9 |
|
Вторая |
45,0 — 54,9 |
|
Третья |
35,0 — 44,9 |
В ответе укажите номер правильного варианта.
1) отборная
2) первая
3) вторая
4) третья
15. На рисунке показано, как изменялась температура воздуха на протяжении одних суток. По горизонтали указано время суток, по вертикали — значение температуры в градусах Цельсия. Найдите наибольшее значение температуры. Ответ дайте в градусах Цельсия.
16. Расстояние от Солнца до Нептуна свет проходит примерно за 252,95 минуты. Найдите приблизительно расстояние от Солнца до Нептуна, ответ округлите до миллионов км. Скорость света равна 300 000 км/с.
17. На сколько градусов повернется Земля вокруг своей оси за 7 часов?
18. На диаграмме показано содержание питательных веществ в какао, молочном шоколаде, фасоли и сушёных белых грибах. Определите по диаграмме, в каком продукте содержание жиров находится в пределах от 15% до 25%.
*К прочему относятся вода, витамины и минеральные вещества.
1) какао
2) шоколад
3) фасоль
4) грибы
19. Родительский комитет закупил 25 пазлов для подарков детям на окончание года, из них 15 с машинами и 10 с видами городов. Подарки распределяются случайным образом. Найдите вероятность того, что Толе достанется пазл с машиной.
Часть 2.
20. Центростремительное ускорение при движении по окружности (в м/c2) можно вычислить по формуле где
— угловая скорость (в с−1), а R — радиус окружности. Пользуясь этой формулой, найдите расстояние R (в метрах), если угловая скорость равна 3 с−1, а центростремительное ускорение равно 45 м/c2.
21. Решите уравнение
22. Первую половину трассы автомобиль проехал со скоростью 55 км/ч, а вторую — со скоростью 70 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
23. Постройте график функции
и определите, при каких значениях m прямая y = m имеет с графиком ровно две общие точки.
24. Основания трапеции равны 9 и 15. Найдите отрезок, соединяющий середины диагоналей трапеции.
25. Известно, что около четырёхугольника ABCD можно описать окружность и что продолжения сторон AB и CD четырёхугольника пересекаются в точке M. Докажите, что треугольники MBC и MDA подобны.
26. В трапеции ABCD боковая сторона AB перпендикулярна основаниюBC. Окружность проходит через точки C и D и касается прямой AB в точке E. Найдите расстояние от точки E до прямой CD, если AD = 6, BC = 5.
ВАРИАНТ № 2.
ЧАСТЬ 1.
1. Найдите значение выражения
2. На координатной прямой отмечено число
В ответе укажите номер правильного варианта.
Какое из утверждений относительно этого числа является верным?
1)
2)
3)
4)
3. Найдите значение выражения (1,7 · 10− 5)(2 · 10− 2).
В ответе укажите номер правильного варианта.
1) 0,0000034
2) 34000000000
3) 0,000000034
4) 0,00000034
4. Решите уравнение (x − 9)2 = (x − 3)2.
5. На рисунке изображены графики функций вида y = kx + b. Установите соответствие между знаками коэффициентов k и b и графиками функций.
Графики
Коэффициенты
|
А) k 0, b 0 |
Б) k 0, b |
В) k 0 |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
|
А |
Б |
В |
6. Выписаны первые несколько членов геометрической прогрессии: 1; −5; 25; … Найдите сумму первых 5 её членов.
7. Упростите выражение и найдите его значение при
.
В ответе запишите найденное значение.
8. Решение какого из данных неравенств изображено на рисунке?
В ответе укажите номер правильного варианта.
1)
2)
3)
4)
9. В треугольнике ABC проведены медиана BM и высота BH . Известно, что AC = 15 и BC = BM. Найдите AH.
10. В окружности с центром в точке О проведены диаметры AD и BC, угол OCD равен 30°. Найдите величину угла OAB.
11. Периметр ромба равен 40, а один из углов равен 60°. Найдите площадь ромба, делённую на .
12. Найдите площадь трапеции, изображённой на рисунке.
13. Укажите номера верных утверждений.
1) В любую равнобедренную трапецию можно вписать окружность.
2) Диагональ параллелограмма делит его углы пополам.
3) Площадь прямоугольного треугольника равна половине произведения его катетов.
Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.
14. В таблице приведены расстояния от Солнца до четырёх планет Солнечной системы. Какая из этих планет ближе всех к Солнцу?
|
Планета |
Нептун |
Юпитер |
Уран |
Венера |
|
Расстояние (в км) |
4,497 · 109 |
7,781 · 108 |
2,871 · 109 |
1,082 · 108 |
В ответе укажите номер правильного варианта.
1) Нептун
2) Юпитер
3) Уран
4) Венера
15. На рисунке изображён график изменения атмосферного давления в городе Энске за три дня. По горизонтали указаны дни недели, по вертикали — значения атмосферного давления в миллиметрах ртутного столба. Укажите наименьшее значение атмосферного давления во вторник.
16. В начале 2010 г. в поселке было 730 жителей, а в начале 2011 г. их стало 803. На сколько процентов увеличилось число жителей поселка за год?
17. На каком расстоянии (в метрах) от фонаря стоит человек ростом 2 м, если длина его тени равна 1 м, высота фонаря 9 м?
18. На диаграмме представлены семь крупнейших по площади территории (в млн км2) стран мира. Какое из следующих утверждений неверно?
.
1) По площади территории второе место в мире занимает Канада.
2) Площадь территории Австралии составляет 7,7 млн км2.
3) Площадь Китая больше площади Канады.
4) Площадь США больше площади Бразилии на 1 млн км2.
19. В магазине канцтоваров продаётся 200 ручек, из них 31 красная, 25 зелёных, 38 фиолетовых, ещё есть синие и чёрные, их поровну. Найдите вероятность того, что при случайном выборе одной ручки будет выбрана красная или чёрная ручка.
ЧАСТЬ 2.
20. Зная длину своего шага, человек может приближённо подсчитать пройденное им расстояние s по формуле s = nl, где n — число шагов, l — длина шага. Какое расстояние прошёл человек, если l = 70 см, n =1400 ? Ответ выразите в километрах.
21. Решите неравенство
22. Из пункта А в пункт В, расстояние между которыми 13 км, вышел пешеход. Одновременно с ним из В в А выехал велосипедист. Велосипедист ехал со скоростью, на 11 км/ч большей скорости пешехода, и сделал в пути получасовую остановку. Найдите скорость пешехода, если известно, что они встретились в 8 км от пункта В.
23.. Постройте график функции и определите, при каких значениях прямая
имеет с графиком не менее одной, но не более трёх общих точек.
24. Прямая AD, перпендикулярная медиане ВМ треугольника АВС, делит её пополам. Найдите сторону АС, если сторона АВ равна 4.
25. В параллелограмме ABCD диагонали AC и BD пересекаются в точке O. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника AOB.
26. Основание AC равнобедренного треугольника ABC равно 8. Окружность радиуса 5 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
ВАРИАНТ № 3.
ЧАСТЬ 1.
1. Вычислите:
2. Какому из данных промежутков принадлежит число
В ответе укажите номер правильного варианта.
1) [0,5;0,6]
2) [0,6;0,7]
3) [0,7;0,8]
4) [0,8;0,9]
3. Укажите наибольшее из следующих чисел.
В ответе укажите номер правильного варианта.
1)
2)
3)
4)
4. Решите уравнение
Если корней несколько, запишите их через точку с запятой в порядке возрастания.
5. Найдите значение по графику функции , изображенному на рисунке.
|
1) |
2) |
3) |
4) |
6. Геометрическая прогрессия задана условием b1 = −7, bn + 1 = 3bn. Найдите сумму первых 5 её членов.
7. Упростите выражение и найдите его значение при . В ответ запишите полученное число.
8. На каком рисунке изображено множество решений неравенства
В ответе укажите номер правильного варианта.
1) 1
2) 2
3) 3
4) 4
9. Найдите угол АDС равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной АВ углы, равные 30° и 50° соответственно.
10. Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 8.
11. Высота BH ромба ABCD делит его сторону AD на отрезки AH = 5 и HD = 8. Найдите площадь ромба.
.
12. Из квадрата вырезали прямоугольник (см. рисунок). Найдите площадь получившейся фигуры.
13. Какие из следующих утверждений верны?
1) Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы составляют в сумме 90°, то эти две прямые параллельны.
2) Если угол равен 60°, то смежный с ним равен 120°.
3) Если при пересечении двух прямых третьей прямой внутренние односторонние углы равны 70° и 110°, то эти две прямые параллельны.
4) Через любые три точки проходит не более одной прямой.
Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.
14. В таблице приведены размеры штрафов за превышение максимальной разрешённой скорости, зафиксированное с помощью средств автоматической фиксации, установленных на территории России на 1 января 2013 года.
|
Превышение скорости, км/ч |
11 − 20 |
21 − 40 |
41 − 60 |
61 и более |
|
Размер штрафа, руб. |
100 |
300 |
1000 |
2500 |
Какой штраф должен заплатить владелец автомобиля, зафиксированная скорость которого составила 175 км/ч на участке дороги с максимальной разрешённой скоростью 110 км/ч?
В ответе укажите номер правильного варианта.
1) 100 рублей
2) 300 рублей
3) 1000 рублей
4) 2500 рублей
15.. В таблице даны рекомендуемые суточные нормы потребления (в г/сутки) жиров, белков и углеводов детьми от 1 года до 14 лет и взрослыми.
|
Вещество |
Дети от 1 года до 14 лет |
Мужчины |
Женщины |
|
Жиры |
40—97 |
70—154 |
60—102 |
|
Белки |
36—87 |
65—117 |
58—87 |
|
Углеводы |
170—420 |
257—586 |
Какой вывод о суточном потреблении жиров, белков и углеводов 13-летним мальчиком можно сделать, если по подсчётам диетолога в среднем за сутки он потребляет 90 г жиров, 90 г белков и 359 г углеводов? В ответе укажите номера верных утверждений.
1) Потребление жиров в норме.
2) Потребление белков в норме.
3) Потребление углеводов в норме.
16. Государству принадлежит 60% акций предприятия, остальные акции принадлежат частным лицам. Общая прибыль предприятия после уплаты налогов за год составила 40 млн. р. Какая сумма из этой прибыли должна пойти на выплату частным акционерам?
17. Пол комнаты, имеющей форму прямоугольника со сторонами 4 м и 9 м, требуется покрыть паркетом из прямоугольных дощечек со сторонами 10 см и 25 см. Сколько потребуется таких дощечек?
18. а диаграмме показано содержание питательных веществ в какао, молочном шоколаде, фасоли и сушёных белых грибах. Определите по диаграмме, в каком продукте содержание белков превышает 30%.
*К прочему относятся вода, витамины и минеральные вещества.
1) какао 2) шоколад 3) фасоль 4) грибы
19. Стрелок 4 раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,5. Найдите вероятность того, что стрелок первые 3 раза попал в мишени, а последний раз промахнулся.
ЧАСТЬ 2.
20. В фирме «Родник» стоимость (в рублях) колодца из железобетонных колец рассчитывается по формуле , где n — число колец, установленных при рытье колодца. Пользуясь этой формулой, рассчитайте стоимость колодца из 5 колец.
21. Решите уравнение:
22. Из пункта А в пункт В, расстояние между которыми 13 км, вышел пешеход. Через полчаса навстречу ему из В в А выехал велосипедист, который ехал со скоростью, на 11 км/ч большей скорости пешехода. Найдите скорость велосипедиста, если известно, что они встретились в 5 км от пункта А.
23. Постройте график функции и определите, при каких значениях построенный график не будет иметь общих точек с прямой
.
24. Точка H является основанием высоты BH, проведённой из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите PK, если BH = 16.
25. Окружности с центрами в точках I и J пересекаются в точках A и B, причём точки I и J лежат по одну сторону от прямой AB. Докажите, что отрезки AB и IJ перпендикулярны.
26. В равнобедренной трапеции ABCD боковые стороны равны меньшему основанию BC. К диагоналям трапеции провели перпендикуляры BH и CE. Найдите площадь четырёхугольника BCEH, если площадь трапеции ABCD равна 36 .
ВАРИАНТ № 4.
ЧАСТЬ 1.
1. Вычислите:
2. На координатной прямой отмечено число Расположите в порядке возрастания числа
и
В ответе укажите номер правильного варианта.
1)
2)
3)
4)
3. Расстояние от Земли до Солнца равно 147,1 млн км. В каком случае записана эта же величина?
В ответе укажите номер правильного варианта.
1) 1,471⋅1010 км
2) 1,471⋅108 км
3) 1,471⋅107 км
4) 1,471⋅106 км
4. Найдите корни уравнения
Если корней несколько, запишите их через точку с запятой в порядке возрастания.
5. Задание 5 № 193101. Найдите значение по графику функции изображенному на рисунке.
6. Дана геометрическая прогрессия (bn), знаменатель которой равен 2, аb1 = 16. Найдите b4.
7. Сократите дробь
8. На каком рисунке изображено множество решений неравенства ?
В ответе укажите номер правильного варианта.
1) 1
2) 2
3) 3
4) 4
9. В треугольнике угол равен 90°, . Найдите
.
10. Центральный угол AOB опирается на хорду ABдлиной 6. При этом угол OAB равен 60°. Найдите радиус окружности.
-
Найдите площадь трапеции, изображённой на рисунке.
-
Из квадрата вырезали прямоугольник (см. рисунок). Найдите площадь получившейся фигуры.
13. Укажите номера верных утверждений.
1) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.
2) Треугольник со сторонами 1, 2, 4 существует.
3) Если в ромбе один из углов равен 90°, то такой ромб — квадрат.
4) В любом параллелограмме диагонали равны.
14. Для квартиры площадью 135 м2 заказан натяжной потолок белого цвета. Стоимость работ по установке натяжных потолков приведена в таблице.
|
Цвет потолка |
Цена в рублях за 1 м2 (в зависмости от площали помещения) |
|||
|
до 10 м2 |
от 11 до 30 м2 |
от 31 до 60 м2 |
свыше 60 м2 |
|
|
белый |
1200 |
1000 |
800 |
600 |
|
цветной |
1350 |
1150 |
950 |
750 |
Какова стоимость заказа, если действует сезонная скидка в 20%?
В ответе укажите номер правильного варианта.
1) 81 000 рублей
2) 64 800 рублей
3) 6480 рублей
4) 80 980 рублей
15. На графиках показано, как во время телевизионных дебатов между кандидатами А и Б телезрители голосовали за каждого из них. Сколько всего телезрителей проголосовало к 40-й минуте дебатов?
.
16. Площадь земель крестьянского хозяйства, отведённая под посадку сельскохозяйственных культур, составляет 24 га и распределена между зерновыми и овощными культурами в отношении 5:3. Сколько гектаров занимают овощные культуры?
17. крепостного рва равна 8 м, ширина 5 м, а высота крепостной стены от ее основания 20 м. Длина лестницы, по которой можно взобраться на стену, на 2 м больше, чем расстояние от края рва до верхней точки стены (см. рис.). Найдите длину лестницы.
18. На диаграмме показаны религиозные составы населения Германии, США, Австрии и Великобритании. Определите по диаграмме, в какой стране доля католиков превышает 50%.
1) Германия
2) США
3) Австрия
4) Великобритания
19. Стрелок 4 раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,5. Найдите вероятность того, что стрелок первые 3 раза попал в мишени, а последний раз промахнулся.
ЧАСТЬ 2.
20. В фирме «Родник» стоимость (в рублях) колодца из железобетонных колец рассчитывается по формуле C = 6000 + 4100 · n , где n — число колец, установленных при рытье колодца. Пользуясь этой формулой, рассчитайте стоимость колодца из 20 колец.
21. Решите систему уравнений
22. Расстояние между городами А и В равно 490 км. Из города А в город В со скоростью 55 км/ч выехал первый автомобиль, а через час после этого навстречу ему из города В выехал со скоростью 90 км/ч второй автомобиль. На каком расстоянии от города А автомобили встретятся?
23. Постройте график функции и определите, при каких значениях параметра прямая
имеет с графиком три общие точки.
24. Окружность, вписанная в треугольник ABC, касается его сторон в точках M, K и P. Найдите углы треугольника ABC, если углы треугольника MKP равны 39°, 78° и 63°.
25. Основания BC и AD трапеции ABCD равны соответственно 5 и 20,BD = 10. Докажите, что треугольники CBD и ADB подобны.
26. В трапеции ABCD боковая сторона AB перпендикулярна основаниюBC. Окружность проходит через точки C и D и касается прямой AB в точке E. Найдите расстояние от точки E до прямой CD, если AD = 6, BC = 5.
3.3 Критерии оценки экзаменационной работы в виде набора контрольных заданий
Оценка 5 (отлично) ставится за работу, выполненную полностью без ошибок и недочётов; в логических рассуждениях и обосновании решения нет пробелов и ошибок; в решении нет математических ошибок (возможна одна неточность, описка, не являющаяся следствием незнания или непонимания учебного материала).
Оценка 4 (хорошо) работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки); допущена одна ошибка или два-три недочета в выкладках, рисунках, чертежах или графиках (если эти виды работы не являлись специальным объектом проверки).
Оценка 3 (удовлетворительно) ставится, если обучающийся правильно выполнил не менее 2/3 всей работы или допустил не более одной грубой ошибки и двух недочётов, не более одной грубой и одной не грубой ошибки, не более трёх негрубых ошибок, одной негрубой ошибки и трёх недочётов, при наличии четырёх-пяти недочётов.
Оценка 2 (неудовлетворительно) ставится, если число ошибок и недочётов превысило норму для оценки 3 или правильно выполнено не менее 2/3 всей работы; допущены существенные ошибки, показавшие, что учащийся не владеет обязательными умениями по данной теме в полной мере
КЛЮЧ
|
№ |
1 вариант |
2 вариант |
3 вариант |
4 вариант |
|
|
-3786,7 |
20 |
1,03 |
1,55 |
|
|
1 |
1 |
1 |
2 |
|
|
1 |
4 |
2 |
2 |
|
|
-5;3 |
6 |
0,5;1 |
3;6 |
|
|
412 |
132 |
4 |
1 |
|
|
4 |
521 |
-847 |
128 |
|
|
31 |
1,5 |
0,4 |
84 |
|
|
4 |
3 |
1 |
2 |
|
|
95 |
11,25 |
80 |
33 |
|
|
144 |
30 |
4 |
6 |
|
|
2688 |
50 |
156 |
270 |
|
|
2 |
28 |
52 |
58 |
|
|
1;3 |
3 |
2;3;4 |
13|31|1;3|1,3 |
|
|
4 |
4 |
4 |
2 |
|
|
16 |
756 |
1;3|13|1; 3 |
50000 |
|
|
4553000000 |
10 |
16000000 |
9 |
|
|
105 |
3,5 |
1440 |
15 |
|
|
1 |
3 |
4 |
3 |
|
|
0,6 |
0,42 |
0,0625 |
0,0625 |
|
|
5 |
0,98 |
26500 |
88000 |
|
|
-8:-5 |
-1;0;5 |
(3; −4) |
|
|
|
61,6 |
5 |
16 км/ч |
220 |
|
|
2,6 |
2/3;1;2 |
(0;5) |
|
|
|
3 |
8 |
16 |
102°, 24°, 54° |
|
|
||||
|
|
3,2 |
9 |
25. 1 вариант.
Известно, что около четырёхугольника ABCD можно описать окружность и что продолжения сторон AB и CD четырёхугольника пересекаются в точке M. Докажите, что треугольники MBC и MDA подобны.
Решение.
Поскольку четырёхугольник ABCD вписанный, сумма углов BAD и BCD равна 180°.
Следовательно,
∠MCB = 180° − ∠BCD = ∠BAD.
Получаем, что в треугольниках MBC и MDA углы MCB и MAD равны, угол M общий, следовательно, эти треугольники подобны.
25. 2 вариант.
В параллелограмме ABCD диагонали AC и BD пересекаются в точке O. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника AOB.
Решение.
Проведём высоту так, чтобы она проходила через точку
Углы и равны друг другу как вертикальные. Вспомним также, что диагонали делятся точкой пересечения пополам, следовательно, Рассмотрим треугольники и , они прямоугольные, имеют равные углы и равные гипотенузы, следовательно эти треугольники равны, а значит равны отрезки
и
. Таким образом,
Площадь параллелограмм равна а площадь треугольника
25. 3 вариант.
Окружности с центрами в точках I и J пересекаются в точках A и B, причём точки I и J лежат по одну сторону от прямой AB. Докажите, что отрезки AB и IJ перпендикулярны.
Решение.
Точка I равноудалена от A и B, поэтому она лежит на серединном перпендикуляре к отрезку AB. То же можно сказать и о J . Значит IJ — серединный перпендикуляр к AB.
25. 4 вариант.
Основания BC и AD трапеции ABCD равны соответственно 5 и 20,BD = 10. Докажите, что треугольники CBD и ADB подобны.
Решение.
Углы CBD и BDA равны, как накрест лежащие при параллельных прямых. В треугольниках и следовательно, эти треугольники подобны по двум парам подобных сторон и углу между ними.
Контрольная работа по математике
по профессии среднего профессионального образования
Технология продукции общественного питания
-
Вычислить предел:
1). Ответ:
2). Ответ:
3) Ответ
4). Ответ
5). Ответ :
6) Ответ:
7). Ответ:
8). Ответ:
9). Ответ:
10). Ответ:
11). Ответ:
12). Ответ:
13). Ответ:
2. Пользуясь определением производной, найти производную функции у, если:
-
,
-
,
-
у = 5 − 6x ,
-
у= 4 − 7x,
-
,
-
,
-
у = 2х2 — 13х +3,
-
у=-3x2-13x,
-
у=7x2+3x,
-
у =4 – 5х + 2х2,
-
у = 3х2 — 2х – 8,
-
у=х3— 9х – 4,
-
у=3х3 — 4х2 — 8х – 4,
-
у =-2х3 -4х2 -4х
-
Решить задачи по теории вероятностей.
№ 1. В кармане у Миши 4 конфеты – «Грильяж», «Маска», «Белочка», «Красная шапочка», а так же ключи от квартиры. Вынимая ключи, Миша случайно выронил из кармана одну конфету. Найдите вероятность того, что потерялась конфета «Маска»
№ 2. Оля, Денис, Витя, Артур и Рита бросали жребий – кому начать игру. Найдите
вероятность того, что начинать игру будет Рита?
№ 3. Катя, Настя, Игорь, Даша и Андрей бросали жребий – кому начать игру.
Найдите вероятность того, что начинать игру будет мальчик?
№ 4. Игральную кость бросают один раз. Найдите вероятность того, что выпало
число очков не меньше, чем 3?
№ 5. Бабушка решила дать внуку Илье на дорогу какой-нибудь случайно
выбранный фрукт. У неё было 3 зелёных яблока, 3 зеленых груши и 2 желтых
банана. Найдите вероятность того, что Илья получит фрукт зеленого цвета?
№ 6. Игральную кость бросают два раза. Найдите вероятность того, что оба раза
выпало число большее 3?
№ 7. Игральную кость бросают два раза. Найдите вероятность того, что один раз
выпало число большее 3, а другой раз — меньшее 3?
№ 8. В случайном эксперименте симметричную монету бросают дважды. Найдите
вероятность того, что орёл выпадет ровно один раз?
№ 9. В случайном эксперименте симметричную монету бросают три раза. Найдите
вероятность того, что решка выпадет ровно два раза?
№ 10. В случайном эксперименте бросают две игральные кости. Найдите
вероятность того, что в сумме выпадет 7 очков?
№ 11. В соревнованиях по керлингу выступают 20 команд из 5 стран: Швеция,
Норвегия, Финляндия, Канада, Дания. Причем каждая страна выставила по 4
команды. Порядок выступления команд определяется жеребьевкой. Найдите
вероятность того, что 17-ой по счету будет выступать одна из команд Канады?
№ 12. В соревнованиях по керлингу выступают 20 команд из 5 стран: Швеция,
Норвегия, Финляндия, Канада, Дания. Причем каждая страна выставила по 4
команды. Порядок выступления команд определяется жеребьевкой. Найдите
вероятность того, что 17-ойп по счету будет выступать одна из команд
Швеции, Норвегии или Дании?
№ 13. В коробке находятся 7 красных шаров, 13 белых шаров и 6 голубых шаров.
Определите вероятность того, что наудачу взятый из коробки шар окажется
белым.
№ 14. В копилке находятся монеты достоинством 2 рубля – 14 штук, 5 рублей – 10
штук и 10 рублей – 6 штук. Какова вероятность того, что первая монета,
выпавшая из копилки, будет достоинством 10 рублей?
№ 15. В корзине лежат 7 помидоров, 6 огурцов, 12 перцев. Найдите вероятность того,
что первый наугад взятый овощ из корзины будет перцем.
КЛЮЧ
|
№ |
№ |
ответ |
|
1 |
1 |
(-1/3) – неопределённость -раскрывать путём разложения на множители |
|
2 |
(-1/3) — неопределённость -раскрывать путём домножения на сопряжённое выражение |
|
|
3 |
:(-1/2) — неопределённость -раскрывать путём вынесения за скобки x с наибольшим показателем |
|
|
4 |
:(0) — неопределённость -раскрывать путём вынесения за скобки x с наибольшим показателем |
|
|
5 |
— неопределённость -раскрывать путём вынесения за скобки x с наибольшим показателем |
|
|
6 |
— –неопределённость — раскрывать с помощью метода приведения ко второму замечательному пределу — сначала преобразовать скобку следующим образом |
|
|
7 |
-–неопределённость — раскрывать с помощью метода приведения ко второму замечательному пределу — сначала преобразовать скобку следующим образом |
|
|
8 |
— неопределённость — раскрывать с помощью метода приведения ко второму замечательному пределу — сначала преобразовать скобку следующим образом |
|
|
9 |
– неопределённость — раскрывать с помощью метода приведения к первому замечательному пределу |
|
|
10 |
– неопределённость — раскрывать с помощью метода приведения к первому замечательному пределу=1 |
|
|
11 |
-–неопределённость — раскрывать с помощью метода приведения к первому замечательному пределу=1 |
|
|
12 |
(6). –воспользоваться свойством вычисления предела непрерывной функции |
|
|
13 |
). –воспользоваться свойством вычисления предела непрерывной функции |
|
|
2 |
1 |
-2 |
|
2 |
8 |
|
|
3 |
-6 |
|
|
4 |
-7 |
|
|
5 |
2х-1 |
|
|
6 |
2а+в |
|
|
7 |
4х-13 |
|
|
8 |
6х-13 |
|
|
9 |
14х+3 |
|
|
10 |
-5+4х |
|
|
11 |
6х-2 |
|
|
12 |
3х2-9 |
|
|
13 |
9х2-8х-8 |
|
|
14 |
-6х2-8х-4 |
|
|
3 |
1 |
0,25 |
|
2 |
0,2 |
|
|
3 |
0,4 |
|
|
4 |
2/3 |
|
|
5 |
0,75 |
|
|
6 |
0,25 |
|
|
7 |
1/3 |
|
|
8 |
0,5 |
|
|
9 |
3/8 |
|
|
10 |
1/6 |
|
|
11 |
0,2 |
|
|
12 |
0,6 |
|
|
13 |
0,5 |
|
|
14 |
0,2 |
|
|
15 |
0,48 |
Критерии оценивания заданий
|
Оценка в пятибалльной шкале |
Критерии оценки |
Количество правильно данных вопросов |
|
«2» |
Выполнено менее 50% заданий |
Даны верные ответы менее, чем на 21 вопросов |
|
«3» |
Выполнено 51-74 % заданий |
Даны верные ответы на 21-30 вопроса |
|
«4» |
Выполнено 75-89% заданий |
Даны верные ответы на 31-37 вопросов |
|
«5» |
Выполнено более 90% заданий |
Данные верные ответы на 38-42 вопросов |
Критерии оценивания заданий:
За каждое правильно выполненное тестовое задание (верный ответ) ставится 1 балл, за
Критерии оценивания выполнения практического задания
Своевременность выполнения практической работы.
Выполнение работы в полном объеме с соблюдением необходимой последовательности
вычислений.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД
ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА
|
ОДОБРЕНО предметной общегуманитарных общеобразовательных Протокол№4 Председатель П(Ц)К _____________ |
УТВЕРЖДАЮ зам. директора по учебной работе __________ Квиралашвили Н.У 8 апреля 2019 г. |
Дисциплина«Математика»
Билет №1
1.
Корни
натуральной степени из числа и их свойства.
2.
Перпендикуляр
и наклонная.
3.
Событие,
вероятность события.
4.
Примеры:
1)
Решить уравнения
2)Найти
предел
5.
Задача:
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД
ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА
|
ОДОБРЕНО предметной общегуманитарных общеобразовательных Протокол№4 Председатель П(Ц)К _____________Гаджиева |
УТВЕРЖДАЮ заместитель директора по учебной работе __________ Квиралашвили Н.У 8 апреля 2019 г. |
Дисциплина«Математика»
Билет
№2
1.
Степени
с рациональными показателями, их свойства.
2.
Параллелепипед.
Куб.
3.
Понятие
о пределе последовательности.
4.
Примеры:
1)Упростите выражение
cos2x-6+sin2x
2) Найти производную
5. Задача:
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД
ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА
|
ОДОБРЕНО предметной общегуманитарных общеобразовательных Протокол№4 Председатель П(Ц)К _____________ |
УТВЕРЖДАЮ заместитель директора по учебной работе __________ Квиралашвили Н.У 8 апреля 2019 г. |
Дисциплина«Математика»
Билет
№3
1.
Логарифми
его свойства
2. Двугранный угол.
3. Понятие о
производной функции, её геометрический смысл.
4. Примеры:
1) Найти значение производной функции
f1(x)
при x=0—1
2) Найти предел
5.
Задача:
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД
ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА
|
ОДОБРЕНО предметной общегуманитарных общеобразовательных Протокол Председатель П(Ц)К _____________ |
УТВЕРЖДАЮ заместитель директора по учебной работе __________ Квиралашвили Н.У 8 апреля 2019 г. |
Дисциплина«Математика»
Билет
№4
1. Радианная
мера угла
2. Раскрытие
неопределенностей 0/0 и ∞/∞.
3. Цилиндр.
4. Примеры:
1)Вычислите
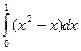
2) Упростите выражение
cos4x—sin4x
5. Задача:
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД
ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА
|
ОДОБРЕНО предметной общегуманитарных общеобразовательных Протокол Председатель П(Ц)К _____________ |
УТВЕРЖДАЮ заместитель директора по учебной работе __________ Квиралашвили Н.У 8 апреля 2019 г. |
Дисциплина«Математика»
Билет
№5
1.
Основные
тригонометрические тождества
2.
Геометрические преобразования пространства:
параллельный перенос
3.
Понятие о производной функции
4.
Примеры
1)Необходимо
выбрать в подарок 4 из 10 имеющихся книг. Сколькими способами можно это
сделать?
2)
Найти значение производной функции
f1(x) при x=1
5.
Задача:
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД
ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА
|
ОДОБРЕНО предметной общегуманитарных общеобразовательных Протокол№4 Председатель П(Ц)К _____________ |
УТВЕРЖДАЮ заместитель директора по учебной работе __________ Квиралашвили Н.У 8 апреля 2019 г. |
Дисциплина«Математика»
Билет
№6
1. Геометрический
смысл производной функции
2. Геометрические
преобразования пространства: симметрия относительно плоскости
3. Шар и сфера, их
сечения.
4. Примеры:
1)
Из 30 участников собрание надо
выбрать председателя и секретаря. Сколькими способами это можно сделать?
2) Найти
производную
f(x)=xcosx
5.
Задача:
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД
ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА
|
ОДОБРЕНО предметной общегуманитарных общеобразовательных Протокол Председатель П(Ц)К _____________ |
УТВЕРЖДАЮ заместитель директора по учебной работе __________ Квиралашвили Н.У 8 апреля 2019 г. |
Дисциплина«Математика»
Билет
№7
1. Физический смысл
производной функции
2.
Арксинус, арккосинус, арктангенс
числа
3.
Формулы
объема куба, прямоугольного параллелепипеда
4.
Примеры:
1) Сколько шестизначных чисел (без повторения цифр) можно
составить из цифр 0, 3, 5, 6, 7, 8?
2) Решите уравнения
5.
Задача:
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД
ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА
|
ОДОБРЕНО предметной общегуманитарных общеобразовательных Протокол Председатель П(Ц)К _____________ |
УТВЕРЖДАЮ заместитель директора по учебной работе __________ Квиралашвили Н.У 8 апреля 2019 г. |
Дисциплина«Математика»
Билет
№8
1.
Функции.Область
определения и множество значений; график функции.
2. Производные суммы,
разности, произведения, частного.
3.
Формулы
объема цилиндра
4. Примеры:
1)
Сколькими способами 8 человек
могут встать в очередь в театральную кассу?
2) Вычислить:1)
; 2)
5. Задача:
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД
ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА
|
ОДОБРЕНО предметной общегуманитарных общеобразовательных Протокол Председатель П(Ц)К _____________ |
УТВЕРЖДАЮ заместитель директора по учебной работе __________ Квиралашвили Н.У 8 апреля 2019 г. |
Дисциплина«Математика»
Билет
№9
1. Исследование
функции по схеме.
2. Производные
основных элементарных функций.
3. Формулы
объема куба.
4. Примеры:
1)
Вычислить
2)
3)
2) Решить
уравнения
5. Задача:
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД
ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА
|
ОДОБРЕНО предметной общегуманитарных общеобразовательных Протокол Председатель П(Ц)К _____________ |
УТВЕРЖДАЮ заместитель директора по учебной работе __________ Квиралашвили Н.У 8 апреля 2019 г. |
Дисциплина«Математика»
Билет
№10
1. Действия над
векторами в пространстве
2. Производные
основных элементарных функций.
3. Параллелепипед.
Куб.
4. Примеры:
1)
Упростить:
(sin2x+tx2xsin2x)ctgx
2)
Найти
значение выражения
5.
Задача:
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД
ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА
|
ОДОБРЕНО предметной общегуманитарных общеобразовательных Протокол Председатель П(Ц)К _____________ |
УТВЕРЖДАЮ заместитель директора по учебной работе __________ Квиралашвили Н.У 8 апреля 2019 г. |
Дисциплина«Математика»
Билет
№11
1. Перпендикуляр и
наклонная.
2. Понятие о пределе последовательности.
3.
Логарифми
его свойства.
4.
Примеры
1)Вычислите
5-4 *
56; 3) 710 : 712;
5) (3-4)-1;
2)Написать
уравнение касательной к графику функции в точке с абсциссой x0
5.
Задача:
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД
ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА
|
ОДОБРЕНО предметной общегуманитарных общеобразовательных Протокол Председатель П(Ц)К _____________ |
УТВЕРЖДАЮ заместитель директора по учебной работе __________ Квиралашвили Н.У 8 апреля 2019 г. |
Дисциплина«Математика»
Билет
№12
1. Корни
натуральной степени из числа и их свойства
2. Производные суммы,
разности, произведения, частного.
3. Аксиомы
стереометрии
4. Примеры:
1) Вычислите
44 *4-3;
65-3 : 65-3; (82)-2
* 83
2) В группе 30 студентов. Необходимо выбрать старосту,
заместителя старосты и профорга. Сколько существует способов это сделать?
5.
Задача :
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД
ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА
|
ОДОБРЕНО предметной общегуманитарных общеобразовательных Протокол Председатель П(Ц)К _____________ |
УТВЕРЖДАЮ заместитель директора по учебной работе __________ Квиралашвили Н.У 8 апреля 2019 г. |
Дисциплина«Математика»
Билет
№13
1. Пирамида.
Правильная пирамида.
2. Показательная
функция, свойства и график.
3.
Арксинус, арккосинус, арктангенс
числа
4.
Примеры:
1)
Вычислить:
81* 3-4;
2) 9-6 * 95; 3) (3-1)5
*272;
2)
Порядок выступления 7 участников конкурса
определяется жребием. Сколько различных вариантов жеребьевки при этом возможно?
5.
Задача
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД
ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА
|
ОДОБРЕНО предметной общегуманитарных общеобразовательных Протокол Председатель П(Ц)К _____________ |
УТВЕРЖДАЮ заместитель директора по учебной работе __________ Квиралашвили Н.У 8 апреля 2019 г. |
Дисциплина«Математика»
Билет
№14
1. Шар
и сфера, их сечения
2. Основные
понятия комбинаторики
3. Действия над
векторами в пространстве
4. Примеры
1)
Вычислить:
60
: 6-3 5) 9-2 : 3-6; 6)
125-4 : 25-5
2) Вычислите
5.
Задача:
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД
ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА
|
ОДОБРЕНО предметной общегуманитарных общеобразовательных Протокол Председатель П(Ц)К _____________ |
УТВЕРЖДАЮ заместитель директора по учебной работе __________ Квиралашвили Н.У 8 апреля 2019 г. |
Дисциплина«Математика»
Билет
№15
1.
Формулы
объема цилиндра
2.
Степени
с рациональными показателями, их свойства.
3. Основные
тригонометрические тождества
4. Примеры:
1)
Решите уравнение
sin2x = cosx—
cos2x
2)
Найти производную
f 1(x) при x=0 —1
5. Задача
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД
ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА
|
ОДОБРЕНО предметной общегуманитарных общеобразовательных Протокол Председатель П(Ц)К _____________ |
УТВЕРЖДАЮ заместитель директора по учебной работе __________ Квиралашвили Н.У 8 апреля 2019 г. |
Дисциплина«Математика»
Билет
№16
1. Формулы
объема цилиндра, конуса
2. Исследование
функции по схеме.
3. Раскрытие
неопределенностей 0/0
4. Примеры:
1)
Вычислите
2) В шахматном турнире участвуют 16 человек. Сколько
партий должно быть сыграно в турнире, если между любыми двумя участниками
должна быть сыграна одна партия?
5. Задача:
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД
ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА
|
ОДОБРЕНО предметной общегуманитарных общеобразовательных Протокол Председатель П(Ц)К _____________ |
УТВЕРЖДАЮ заместитель директора по учебной работе __________ Квиралашвили Н.У 8 апреля 2019 г. |
Дисциплина«Математика»
Билет
№17
1. Формулы
объема шара
2. Раскрытие
неопределенностей ∞/∞.
3. Параллельный
перенос
4. Примеры:
1) Решите
графически
2) На борту самолёта 12 мест рядом с
запасными выходами и 18 мест за перегородками, разделяющими салоны. Остальные
места неудобны для пассажира высокого роста. Пассажир В. высокого роста.
Найдите вероятность того, что на регистрации при случайном выбореместа пассажиру
В. достанется удобное место, если всего в самолёте 300 мест
5. Задача:
МИНИСТЕРСТВО
ОБРАЗОВАНИЯ И НАУКИ РД
ГБПОУ
КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА
|
ОДОБРЕНО предметной общегуманитарных общеобразовательных протокол ______________ |
УТВЕРЖДАЮ зам. _______________ |
Дисциплина«Математика»
Билет
№18
1.
Формулы
объема куба, прямоугольного параллелепипеда
2. Радианная мера
угла.
3.
Логарифмическая
функция, свойства и график
4.
Примеры:
1)
Вычислите
2)
Из множества натуральных чисел от 10 до 19 наудачу
выбирают одно число. Какова вероятность того, что оно делится на 3?
5. Задача
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД
ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА
|
ОДОБРЕНО предметной общегуманитарных общеобразовательных Протокол Председатель П(Ц)К _____________ |
УТВЕРЖДАЮ заместитель директора по учебной работе __________ Квиралашвили Н.У 8 апреля 2019 г. |
Дисциплина«Математика»
Билет
№19
1.
Формулы
объема призмы
2.
Физический
смысл производной
3.
Событие,
вероятность события
4.
Примеры:
1) Напишите
первые пять членов последовательности.
аn=2n+1/2n
2)Решите
уравнение
5.
Задача:
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД
ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА
|
ОДОБРЕНО предметной общегуманитарных общеобразовательных Протокол Председатель П(Ц)К _____________ |
УТВЕРЖДАЮ заместитель директора по учебной работе __________ Квиралашвили Н.У 8 апреля 2019 г. |
Дисциплина«Математика»
Билет
№20
1.
Формулы
объема пирамиды, усеченной пирамиды
2.
Геометрический
смысл производной
3. Степенная
функция, свойства и график.
4. Примеры:
1) Решить уравнения
2) В
сборнике билетов по биологии всего 55 билетов, в 11 из них встречается вопрос
по ботанике. Найдите вероятность того, что в случайно выбранном на экзамене
билете школьнику
достанетсявопрос
по ботанике.
5. Задача:
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД
ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА
|
ОДОБРЕНО предметной общегуманитарных общеобразовательных Протокол Председатель П(Ц)К _____________ |
УТВЕРЖДАЮ заместитель директора по учебной работе __________ Квиралашвили Н.У 8 апреля 2019г. |
Дисциплина«Математика»
Билет
№21
1. Площади
поверхностей тел вращения.
2. Понятие о
производной функции
3. Функции.Область
определения и множество значений; график функции
4. Примеры:
1) Решите уравнения
2) В
сборнике билетов по математике всего 25 билетов, в 10 из них встречается вопрос
по неравенствам. Найдите вероятность того, что в случайно выбранном на экзамене
билете школьнику
не достанетсявопроса по неравенствам.
5. Задача:
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД
ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА
|
ОДОБРЕНО предметной общегуманитарных общеобразовательных Протокол Председатель П(Ц)К _____________ |
УТВЕРЖДАЮ заместитель директора по учебной работе __________ Квиралашвили Н.У 8 апреля 2019 г. |
Дисциплина«Математика»
Билет
№22
1.
Векторы
в пространстве.
2. Основные
тригонометрические тождества.
3.
Раскрытие
неопределенностей 0/0.
4.
Примеры:
1)
Решить
уравнение
3(x-2)-5=4-(5x-1)
2)
Исследуйте
функцию и постройте график
f(x)=3x-1
5.
Задача:
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД
ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА
|
ОДОБРЕНО предметной общегуманитарных общеобразовательных Протокол Председатель П(Ц)К _____________ |
УТВЕРЖДАЮ заместитель директора по учебной работе __________ Квиралашвили Н.У 8 апреля 2019 г. |
Дисциплина«Математика»
Билет
№23
1. Площади
поверхностей тел вращения.
2. Логарифми его
свойства
3. Радианная мера
угла.
4. Примеры:
1) Решить уравнения
.
2)Исследуйте
функцию и постройте график
f(x)=x2+2
5.
Задача:
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД
ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА
|
ОДОБРЕНО предметной общегуманитарных общеобразовательных Протокол Председатель П(Ц)К _____________ |
УТВЕРЖДАЮ заместитель директора по учебной работе __________ Квиралашвили Н.У 8 апреля 2019 г. |
Дисциплина«Математика»
Билет
№24
1. Конус. Усеченный
конус.
2.
Корни
натуральной степени из числа и их свойства.
3.
Арксинус, арккосинус, арктангенс
числа
4.
Примеры:
1) Вычислите
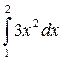
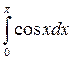
2)
Первести из градусной меры в радианную
450,600,360
5.
Задача
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА
ОДОБРЕНО предметной (цикловой) комиссией общегуманитарных и общеобразовательных дисциплин
ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА
ОДОБРЕНО предметной (цикловой) комиссией общегуманитарных и общеобразовательных дисциплин
ОДОБРЕНО предметной (цикловой) комиссией общегуманитарных и общеобразовательных дисциплин
ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА
ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА
ОДОБРЕНО предметной (цикловой) комиссией общегуманитарных и общеобразовательных дисциплин
ОДОБРЕНО предметной (цикловой) комиссией общегуманитарных и общеобразовательных дисциплин
ОДОБРЕНО предметной (цикловой) комиссией общегуманитарных и общеобразовательных дисциплин протокол №4 от 8 апреля 2019 г
ОДОБРЕНО предметной (цикловой) комиссией общегуманитарных и общеобразовательных дисциплин
ОДОБРЕНО предметной (цикловой) комиссией общегуманитарных и общеобразовательных дисциплин
ОДОБРЕНО предметной (цикловой) комиссией общегуманитарных и общеобразовательных дисциплин
ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА
Поделитесь с коллегами:
Управление образования и науки Тамбовской области
МБОУ «Жердевская средняя общеобразовательная школа»
Утверждаю
Зам.директора по учебно-воспитательной
работе МБОУ «Жердевская СОШ» ___________________Н.С.Лесникова
Утверждаю
Зам.директора по учебной работе
ТОГБОУ СПО «Жердевский
колледж сахарной промышленности» ____________________Н.В.Зингер
Комплект контрольно-измерительных материалов
по учебной дисциплине
МАТЕМАТИКА
для специальности 15.02.01 Монтаж и техническая эксплуатация промышленного оборудования (по отраслям)
Жердевка
2015
Комплект контрольно-измерительных материалов разработан на основе программы учебной дисциплины «Математика» для специальности 15.02.01 Монтаж и техническая эксплуатация промышленного оборудования (по отраслям).
Разработчик(и):
Муниципальное бюджетное общеобразовательное учреждение «Жердевская средняя общеобразовательная школа»
Учитель математики Розман Б.Г.
Одобрено на заседании предметно-цикловой комиссии математических и общих естественнонаучных дисциплин
Протокол №_______ от «_____» _________ 20____г.
Председатель _______________Л.В. Бредищева
СОДЕРЖАНИЕ
1
Паспорт комплекта контрольно-оценочных средств
4
2
Результаты освоения учебной дисциплины, подлежащие проверке
7
3
Оценка освоения учебной дисциплины
11
3.1
Формы и методы оценивания
11
3.2
Типовые задания для оценки освоения учебной дисциплины
17
3.2.1
Тестовые задания
17
3.2.2
Проверочные работы
37
3.2.3
Примеры заданий для устных опросов
46
3.2.4
Контрольные работы
53
3.2.5
Экзаменационные вопросы
61
3.2.6
Экзаменационные задачи
63
3.2.7
Примеры экзаменационных билетов
65
4
Критерии оценивания по результатам текущего, рубежного и итогового контроля
67
4.1
Пояснительная записка
67
4.2
Критерии оценок
67
5
Перечень материалов, оборудования и информационных источников, используемых в аттестации
68
6
Основная учебная, справочная и методическая литература
69
1 Паспорт комплекта контрольно-оценочных средств
В результате освоения учебной дисциплины «Математика» обучающийся должен обладать следующими предусмотренными программой по специальности 15.02.01 «Монтаж и техническая эксплуатация промышленного оборудования (по отраслям)» умениями и знаниями:
Умения:
-
У1. Выполнять арифметические действия над числами, сочетая устные и письменные приемы; находить приближенные значения величин и погрешности вычислений (абсолютная и относительная); сравнивать числовые выражения.
-
У2. Находить значения корня, степени, логарифма, тригонометрических выражений на основе определения, используя при необходимости инструментальные средства; пользоваться приближенной оценкой при практических расчетах.
-
У3. Выполнять преобразования выражений, применяя формулы, связанные со свойствами степеней, логарифмов, тригонометрических функций.
-
У4. Вычислять значение функции по заданному значению аргумента при различных способах задания функции.
-
У5. Определять основные свойства числовых функций, иллюстрировать их на графиках.
-
У6. Строить графики изученных функций, иллюстрировать по графику свойства элементарных функций.
-
У7. Использовать понятие функции для описания и анализа зависимостей величин.
-
У8. Находить производные элементарных функций.
-
У9. Использовать производную для изучения свойств функций и построения графиков.
-
У10. Применять производную для проведения приближенных вычислений, решать задачи прикладного характера на нахождение наибольшего и наименьшего значения.
-
У11. Вычислять в простейших случаях площади и объемы с использованием определенного интеграла.
-
У12. Решать рациональные, показательные, логарифмические, тригонометрические уравнения, сводящиеся к линейным и квадратным, а также аналогичные неравенства и системы.
-
У13. Использовать графический метод решения уравнений и неравенств.
-
У14. Изображать на координатной плоскости решения уравнений, неравенств и систем с двумя неизвестными.
-
У15. Составлять и решать уравнения и неравенства, связывающие неизвестные величины в текстовых (в том числе прикладных) задачах.
-
У16. Решать простейшие комбинаторные задачи методом перебора, а также с использованием известных формул.
-
У17. Вычислять в простейших случаях вероятности событий на основе подсчета числа исходов.
-
У18. Распознавать на чертежах и моделях пространственные формы; соотносить трехмерные объекты с их описаниями, изображениями.
-
У19. Описывать взаимное расположение прямых и плоскостей в пространстве, аргументировать свои суждения об этом расположении.
-
У20 Анализировать в простейших случаях взаимное расположение объектов в пространстве.
-
У21. Изображать основные многогранники и круглые тела; выполнять чертежи по условиям задач.
-
У22. Строить простейшие сечения куба, призмы, пирамиды.
-
У23. Решать планиметрические и простейшие стереометрические задачи на нахождение геометрических величин (длин, углов, площадей, объемов);
-
У24. Использовать при решении стереометрических задач планиметрические факты и методы.
-
У25. Производить действия над векторами в координатной и некоординатной форме.
-
У26. Составлять уравнения прямой на плоскости и в пространстве.
-
У27. Проводить доказательные рассуждения в ходе решения задач.
Знания:
-
З1. Формулы сокращенного умножения, бином Ньютона, абсолютную и относительную погрешности, правила округления, правила действий с приближенными числами.
-
З2. Определение степени с действительным показателем, правила действий со степенями и корнями.
-
З3. Определение логарифма, правила действий с логарифмами, основное логарифмическое тождество.
-
З4. Способы задания функций, понятия области определения и области значения функций.
-
З5. Свойства элементарных функций (степенной, показательной, логарифмической, тригонометрических).
-
З6. Критерии определения четности, периодичности, знакопостоянства, монотонности функций.
-
З7. Понятие производной функции, производные основных элементарных функций, правила нахождения производных.
-
З8. Геометрический и механический смысл производной, уравнений касательной к графику функции.
-
З9. Понятие производной сложной функции.
-
З10. Понятие дифференциала, формулу нахождения приближенного значения функции с помощью производной.
-
З11. Понятие точек экстремума и экстремумов функции, необходимое и достаточное условия экстремума функции одной переменной.
-
З12. Формулу Ньютона — Лейбница вычисления определенных интегралов.
-
З13. Способы решения уравнений и неравенств (линейных, квадратных, показательных, логарифмических, иррациональных).
-
З14. Способы решения систем уравнений и неравенств.
-
З15. Понятие о перестановках, размещениях, сочетаниях.
-
З16. Классическую формулу вероятности события.
-
З17. Аксиомы стереометрии.
-
З18. Основные теоремы о взаимном расположении прямых и плоскостей в пространстве (признаки параллельности и перпендикулярности прямых и плоскостей, теорему о трех перпендикулярах).
-
З19. Определение вектора, модуля вектора, правила действий с векторами в координатной и в некоординатной форме.
-
З20. Способы задания прямой на плоскости и в пространстве, смысл углового коэффициента в уравнении прямой.
-
З21. Формулы определения площадей поверхностей и объемов геометрических тел (многогранников и тел вращения).
Формой аттестации по учебной дисциплине является:
экзамен.
2 Результаты освоения учебной дисциплины, подлежащие проверке
В результате аттестации по учебной дисциплине осуществляется комплексная проверка следующих умений и знаний согласно таблице 1.
Таблица 1
Результаты обучения:
умения, знания
Показатели оценки результата
Форма контроля и оценивания
Уметь:
-
У1. Выполнять арифметические действия над числами, сочетая устные и письменные приемы; находить приближенные значения величин и погрешности вычислений (абсолютная и относительная); сравнивать числовые выражения.
-
У2. Находить значения корня, степени, логарифма, тригонометрических выражений на основе определения, используя при необходимости инструментальные средства; пользоваться приближенной оценкой при практических расчетах.
-
У3. Выполнять преобразования выражений, применяя формулы, связанные со свойствами степеней, логарифмов, тригонометрических функций.
-
У4. Вычислять значение функции по заданному значению аргумента при различных способах задания функции.
-
У5. Определять основные свойства числовых функций, иллюстрировать их на графиках.
-
У6. Строить графики изученных функций, иллюстрировать по графику свойства элементарных функций.
-
У7. Использовать понятие функции для описания и анализа зависимостей величин.
-
У8. Находить производные элементарных функций.
-
У9. Использовать производную для изучения свойств функций и построения графиков.
-
У10. Применять производную для проведения приближенных вычислений, решать задачи прикладного характера на нахождение наибольшего и наименьшего значения.
-
У11. Вычислять в простейших случаях площади и объемы с использованием определенного интеграла.
-
У12. Решать рациональные, показательные, логарифмические, тригонометрические уравнения, сводящиеся к линейным и квадратным, а также аналогичные неравенства и системы.
-
У13. Использовать графический метод решения уравнений и неравенств.
-
У14. Изображать на координатной плоскости решения уравнений, неравенств и систем с двумя неизвестными.
-
У15. Составлять и решать уравнения и неравенства, связывающие неизвестные величины в текстовых (в том числе прикладных) задачах.
-
У16. Решать простейшие комбинаторные задачи методом перебора, а также с использованием известных формул.
-
У17. Вычислять в простейших случаях вероятности событий на основе подсчета числа исходов.
-
У18. Распознавать на чертежах и моделях пространственные формы; соотносить трехмерные объекты с их описаниями, изображениями.
-
У19. Описывать взаимное расположение прямых и плоскостей в пространстве, аргументировать свои суждения об этом расположении.
-
У20 Анализировать в простейших случаях взаимное расположение объектов в пространстве.
-
У21. Изображать основные многогранники и круглые тела; выполнять чертежи по условиям задач.
-
У22. Строить простейшие сечения куба, призмы, пирамиды.
-
У23. Решать планиметрические и простейшие стереометрические задачи на нахождение геометрических величин (длин, углов, площадей, объемов);
-
У24. Использовать при решении стереометрических задач планиметрические факты и методы.
-
У25. Производить действия над векторами в координатной и некоординатной форме.
-
У26. Составлять уравнения прямой на плоскости и в пространстве.
-
У27. Проводить доказательные рассуждения в ходе решения задач.
Правильное выполнение практических заданий (задач), правильные ответы на тестовые и устные вопросы
Правильное выполнение практических заданий (задач), правильные ответы на тестовые и устные вопросы,
Правильные ответы на устные вопросы и тесты, правильное решение задач
Правильные ответы на устные вопросы и тесты, правильное решение задач
Правильные ответы на устные вопросы и тесты, правильное решение задач
Правильные ответы на устные вопросы и тесты, правильное решение задач
Правильные ответы на устные вопросы и тесты.
Правильные ответы на устные вопросы и тесты, правильное решение задач
Правильные ответы на устные вопросы и тесты, правильное решение задач
Правильное выполнение практических заданий (задач), правильные ответы на тестовые и устные вопросы
Правильные ответы на устные вопросы и тесты, правильное решение задач
Правильные ответы на устные вопросы и тесты, правильное решение задач
Правильное решение задач
Правильные ответы на устные вопросы и тесты, правильное решение задач
Правильные ответы на устные вопросы и тесты, правильное решение задач
Правильные ответы на устные вопросы и тесты, правильное решение задач
Правильные ответы на устные вопросы и тесты, правильное решение задач
Правильные ответы на устные вопросы и тесты, правильное решение задач
Правильные ответы на устные вопросы и тесты
Правильные ответы на устные вопросы и тесты
Правильные ответы на устные вопросы и тесты, правильное решение задач
Правильное решение задач
Правильные ответы на устные вопросы и тесты, правильное решение задач
Правильные ответы на устные вопросы и тесты, правильное решение задач
Правильные ответы на устные вопросы и тесты, правильное решение задач
Правильные ответы на устные вопросы и тесты, правильное решение задач
Правильные ответы на устные вопросы и тесты, правильное решение задач
Практическое задание (задача), тест, устный вопрос, экспертная оценка
Практическое задание (задача), тест, устный вопрос, экспертная оценка
Практическое задание (задача), тест, устный вопрос, экспертная оценка
Практическое задание (задача), тест, устный вопрос, экспертная оценка
Практическое задание (задача), тест, устный вопрос, экспертная оценка
Практическое задание (задача), тест, устный вопрос, экспертная оценка
Устный вопрос, экспертная оценка
Практическое задание (задача), тест, устный вопрос, экспертная оценка
Практическое задание (задача), тест, устный вопрос, экспертная оценка
Практическое задание (задача), тест, устный вопрос, экспертная оценка
Практическое задание (задача), тест, устный вопрос, экспертная оценка
Практическое задание (задача), тест, устный вопрос, экспертная оценка
Практическое задание (задача), тест, устный вопрос, экспертная оценка
Практическое задание (задача), тест, устный вопрос, экспертная оценка
Практическое задание (задача), тест, устный вопрос, экспертная оценка
Практическое задание (задача), тест, устный вопрос, экспертная оценка
Практическое задание (задача), тест, устный вопрос, экспертная оценка
Практическое задание (задача), тест, устный вопрос, экспертная оценка
Тест, устный вопрос, экспертная оценка
Тест, устный вопрос, экспертная оценка
Практическое задание (задача), тест, устный вопрос, экспертная оценка
Практическое задание (задача), тест, устный вопрос, экспертная оценка
Практическое задание (задача), тест, устный вопрос, экспертная оценка
Практическое задание (задача), тест, устный вопрос, экспертная оценка
Практическое задание (задача), тест, устный вопрос, экспертная оценка
Практическое задание (задача), тест, устный вопрос, экспертная оценка
Практическое задание (задача), тест, устный вопрос, экспертная оценка
Знать:
-
З1. Формулы сокращенного умножения, бином Ньютона, абсолютную и относительную погрешности, правила округления, правила действий с приближенными числами.
-
З2. Определение степени с действительным показателем, правила действий со степенями и корнями.
-
З3. Определение логарифма, правила действий с логарифмами, основное логарифмическое тождество.
-
З4. Способы задания функций, понятия области определения и области значения функций.
-
З5. Свойства элементарных функций (степенной, показательной, логарифмической, тригонометрических).
-
З6. Критерии определения четности, периодичности, знакопостоянства, монотонности функций.
-
З7. Понятие производной функции, производные основных элементарных функций, правила нахождения производных.
-
З8. Геометрический и механический смысл производной, уравнений касательной к графику функции.
-
З9. Понятие производной сложной функции.
-
З10. Понятие дифференциала, формулу нахождения приближенного значения функции с помощью производной.
-
З11. Понятие точек экстремума и экстремумов функции, необходимое и достаточное условия экстремума функции одной переменной.
-
З12. Формулу Ньютона — Лейбница вычисления определенных интегралов.
-
З13. Способы решения уравнений и неравенств (линейных, квадратных, показательных, логарифмических, иррациональных).
-
З14. Способы решения систем уравнений и неравенств.
-
З15. Понятие о перестановках, размещениях, сочетаниях.
-
З16. Классическую формулу вероятности события.
-
З17. Аксиомы стереометрии.
-
З18. Основные теоремы о взаимном расположении прямых и плоскостей в пространстве (признаки параллельности и перпендикулярности прямых и плоскостей, теорему о трех перпендикулярах).
-
З19. Определение вектора, модуля вектора, правила действий с векторами в координатной и в некоординатной форме.
-
З20. Способы задания прямой на плоскости и в пространстве, смысл углового коэффициента в уравнении прямой.
-
З21. Формулы определения площадей поверхностей и объемов геометрических тел (многогранников и тел вращения).
Правильные ответы на устные вопросы и тесты, правильное решение задач
Правильные ответы на устные вопросы и тесты, правильное решение задач
Правильные ответы на устные вопросы и тесты, правильное решение задач
Правильные ответы на устные вопросы и тесты, правильное решение задач
Правильные ответы на устные вопросы и тесты, правильное решение задач
Правильные ответы на устные вопросы и тесты, правильное решение задач
Правильные ответы на устные вопросы и тесты, правильное решение задач
Правильные ответы на устные вопросы и тесты, правильное решение задач
Правильное решение задач
Использование ПК, Интернета и печатных изданий при поиске информации
Правильные ответы на устные вопросы и тесты, правильное решение задач
Правильное решение задач
Правильное решение задач
Правильное решение задач
Использование ПК, Интернета и печатных изданий при поиске информации
Использование ПК, Интернета и печатных изданий при поиске информации
Правильные ответы на устные вопросы и тесты
Правильные ответы на устные вопросы и тесты
Правильные ответы на устные вопросы и тесты, правильное решение задач
Правильные ответы на устные вопросы и тесты, правильное решение задач
Правильные ответы на устные вопросы и тесты, правильное решение задач
Практическое задание (задача), тест, устный вопрос, экспертная оценка
Практическое задание (задача), тест, устный вопрос, экспертная оценка
Практическое задание (задача), тест, устный вопрос, экспертная оценка
Практическое задание (задача), тест, устный вопрос, экспертная оценка
Практическое задание (задача), тест, устный вопрос, экспертная оценка
Практическое задание (задача), тест, устный вопрос, экспертная оценка
Практическое задание (задача), тест, устный вопрос, экспертная оценка
Практическое задание (задача), тест, устный вопрос, экспертная оценка
Экспертная оценка
Практическое задание (задача), тест, устный вопрос, экспертная оценка
Практическое задание (задача), тест
Практическое задание (задача), тест
Практическое задание (задача), тест, устный вопрос, экспертная оценка
Экспертная оценка
Экспертная оценка
Устный вопрос, тест, экспертная оценка
Устный вопрос, тест, экспертная оценка
Практическое задание (задача), тест, устный вопрос, экспертная оценка
Практическое задание (задача), тест, устный вопрос, экспертная оценка
Практическое задание (задача), тест, устный вопрос, экспертная оценка
3 Оценка освоения учебной дисциплины
3.1 Формы и методы оценивания
Контроль и оценка освоения учебной дисциплины «Математика» по темам (разделам) представлены в Таблице 2.
Элемент учебной дисциплины
Формы и методы контроля
Текущий контроль
Рубежный контроль
Итоговый контроль
Форма контроля
Проверяемые У, З
Форма контроля
Проверяемые У, З
Форма контроля
Проверяемые У, З
Раздел 1. Алгебра
Тема 1.1 Развитие понятия о числе
Устный опрос, решение задач, тестирование
У1,З1
Тема 1.2 Корни, степени и логарифмы
Устный опрос, решение задач, тестирование
У2,У3,З2,З3
Тема 1.3 Основы тригонометрии
Устный опрос, решение задач, тестирование
У2,У3
Контрольная работа №1
У2,У3
Тема 1.4 Степенные, показательные, логарифмические и тригонометрические функции
Устный опрос, решение задач, тестирование
У4-У7, З4-З6
Тема 1.5 Уравнения и неравенства
Устный опрос, решение задач, тестирование
У12-У15, З13,З14
Контрольная работа №2
У12-У15, З13,З14
Раздел 2. Начала математического анализа
Таблица 2
Тема 2.1 Элементы теории пределов
Устный опрос, решение задач, тестирование
У7
Тема 2.2 Дифференциальное исчисление функций одной переменной
Устный опрос, решение задач, тестирование
У8-У10,З7-З11
Тема 2.3 Интегральное исчисление функций одной переменной
Устный опрос, решение задач, тестирование
У11,З12
Контрольная работа №3
У7-У11,З7-З12
Раздел 3. Комбинаторика и теория вероятностей
Тема 3.1 Элементы комбинаторики
Устный опрос, решение задач, тестирование
У16,З15
Тема 3.2 Элементы теории вероятностей
Устный опрос, решение задач, тестирование
У17,З16
Раздел 4. Геометрия
Тема 4.1 Координаты и векторы
Устный опрос, решение задач, тестирование
У25, У26,З19,З20
Тема 4.2 Прямые и плоскости в пространстве
Устный опрос, решение задач, тестирование
У18-У20, З17,З18
Тема 4.3 Многогранники
Устный опрос, решение задач, тестирование
У21-У24, З21
Тема 4.4 Тела и поверхности вращения
Устный опрос, решение задач, тестирование
У21-У24, З21
Тема 4.5 Измерения в геометрии
Устный опрос, решение задач, тестирование
У21-У24, З21
Контрольная работа №4
У18-У26, З17-З21
Экзамен
У1-У27, З1-21
3.2 Типовые задания для оценки освоения учебной дисциплины
Для текущего, рубежного и итогового контроля преподавателем созданы фонды оценочных средств (ФОС). ФОС включают в себя педагогические контрольно-измерительные материалы, предназначенные для определения соответствия (или несоответствия) индивидуальных образовательных достижений основным показателям результатов подготовки: контрольных работ (тесты), перечень тем мультимедийных презентаций и критерии их оценки; вопросы для проведения экзамена по дисциплине.
3.2.1 Тестовые задания
Тесты (контрольно-оценочные средства) обеспечивают возможность объективной оценки знаний и умений, обучающихся в баллах по единым для всех критериям.
При разработке тестов используются задания закрытого типа: после текста вопроса предлагается перечень закрытий, т.е. возможные варианты ответа, а так же открытые.
При разработке дисциплинарных и других тестов используются задания: — на классификацию предметов, явлений по указанному признаку («Укажите…, относящуюся к …», «На какие группы подразделяют …», «Что относится к …»;
— на установление значения того или иного явления, процесса (Какое влияние оказывает…);
— на объяснение, обоснование («Чем объяснить …», «Увеличение … при сокращении … объясняется…»);
— на определение цели действия процесса («Какую цель преследует…», «Каково назначение …», «Для чего выполняется …») и т.п.;
При ответе на вопрос может быть несколько правильных вариантов ответов или только один.
Примеры тестовых заданий
Тест по теме «Развитие понятия о числе»
Технологическая карта контрольно-измерительных материалов
Курс
1
Предмет
Математика
Учебник, по которому ведется преподавание
-
Алгебра и начала математического анализа: учебник для 10-11 кл.общеобразоват.учреждений / [А.Н.Колмогоров, А.М.Абрамов, Ю.П.Дудницын и др.]; под ред.А.Н.Колмогорова. — М.: Просвещение, 2008.
-
Богомолов, Н.В. Практические занятия по математике: Учеб. пособие для средних спец. учебных заведений/Н.В.Богомолов. — М.: Высшая школа, 2003.
Тема контроля
Преобразование алгебраических выражений. Степени и корни.
Вид контроля
текущий
Форма и методы контроля
1) по степени индивидуализации — индивидуальный;
2) по манере исполнения — письменный;
3) по способу подачи контролирующих заданий — тест.
Тип контроля
внешний
Время контроля
45 минут
Цель контроля
Проверить уровень усвоения обучающимися понятия степени с рациональным показателем, формул сокращенного умножения, умения применять свойства степени и корня в процессе преобразования числовых и алгебраических выражений.
Содержание контроля
Тест включает в себя 8 заданий, из которых одно — на преобразование рациональных числовых выражений, одно — на преобразование иррациональных числовых выражений, два — на преобразование степенных выражений, четыре — на преобразование буквенных алгебраических выражений и работу с формулами.
Критерии оценивания
Отметка «5» выставляется, если выполнено 8 заданий
Отметка «4» выставляется, если выполнено 6-7 заданий
Отметка «3» выставляется, если выполнено 4-5 заданий
Отметка «2» выставляется, если выполнено менее 4 заданий
Вариант 1
Ответами к заданиям теста являются целые числа или числа, записанные в виде десятичной дроби
1. Найдите значение выражения 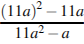
2. Найдите 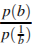
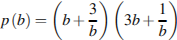
.
3. Найдите значение выражения 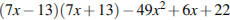
.
4. Найдите значение выражения: 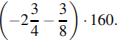
5. Найдите значение выражения 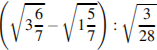
6. Найдите значение выражения 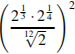
7. Найдите значение выражения 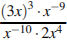
8. Среднее геометрическое трёх чисел и
вычисляется по формуле
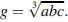
Вариант 2
Ответами к заданиям теста являются целые числа или числа, записанные в виде десятичной дроби
1. Найдите значение выражения 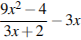
2. Найдите 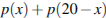
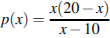
.
3. Найдите значение выражения 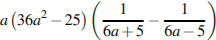
.
4. Найдите значение выражения 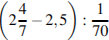
5. Найдите значение выражения 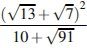
6. Найдите значение выражения 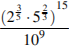
7. Найдите значение выражения 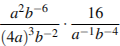
8. Площадь ромба 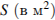
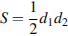
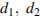
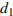
равна 30 м, а площадь ромба 120 м2.
Тест по теме «Корни, степени и логарифмы»
Технологическая карта контрольно-измерительных материалов
Курс
1
Предмет
Математика
Учебник, по которому ведется преподавание
-
Алгебра и начала математического анализа: учебник для 10-11 кл.общеобразоват.учреждений / [А.Н.Колмогоров, А.М.Абрамов, Ю.П.Дудницын и др.]; под ред.А.Н.Колмогорова. — М.: Просвещение, 2008.
-
Богомолов, Н.В. Практические занятия по математике: Учеб. пособие для средних спец. учебных заведений/Н.В.Богомолов. — М.: Высшая школа, 2003.
Тема контроля
Логарифмы. Свойства Логарифмов
Вид контроля
текущий
Форма и методы контроля
1) по степени индивидуализации — индивидуальный;
2) по манере исполнения — письменный;
3) по способу подачи контролирующих заданий — тест.
Тип контроля
внешний
Время контроля
45 минут
Цель контроля
Проверить уровень усвоения обучающимися понятия логарифма, свойств логарифмов, формулы перехода логарифма к другому основанию и умения применять свои знания в предложенной ситуации.
Содержание контроля
Тест включает в себя 10 заданий, 8 из которых на вычисление логарифмов с применением всех свойств и 2 на решение несложных логарифмических уравнений, требующих преобразования выражения с помощью свойств логарифма и проверки корней уравнения.
Критерии оценивания
Отметка «5» выставляется, если выполнено 9-10 заданий
Отметка «4» выставляется, если выполнено7-8 заданий
Отметка «3» выставляется, если выполнено 5-6 заданий
Отметка «2» выставляется, если выполнено менее 5 заданий
Вариант 1
Ответами к заданиям теста являются целые числа или числа, записанные в виде десятичной дроби
В1. Вычислить 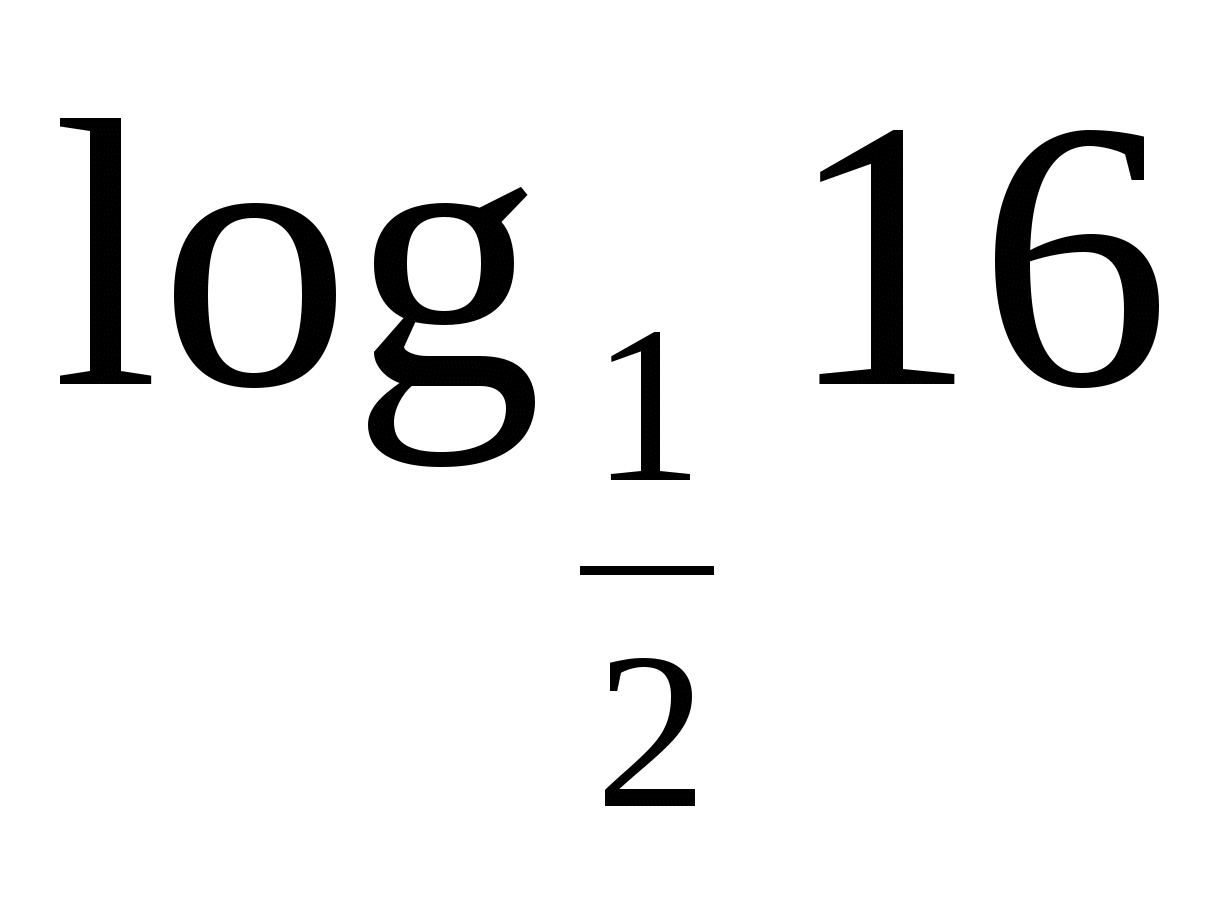
В2. Вычислить 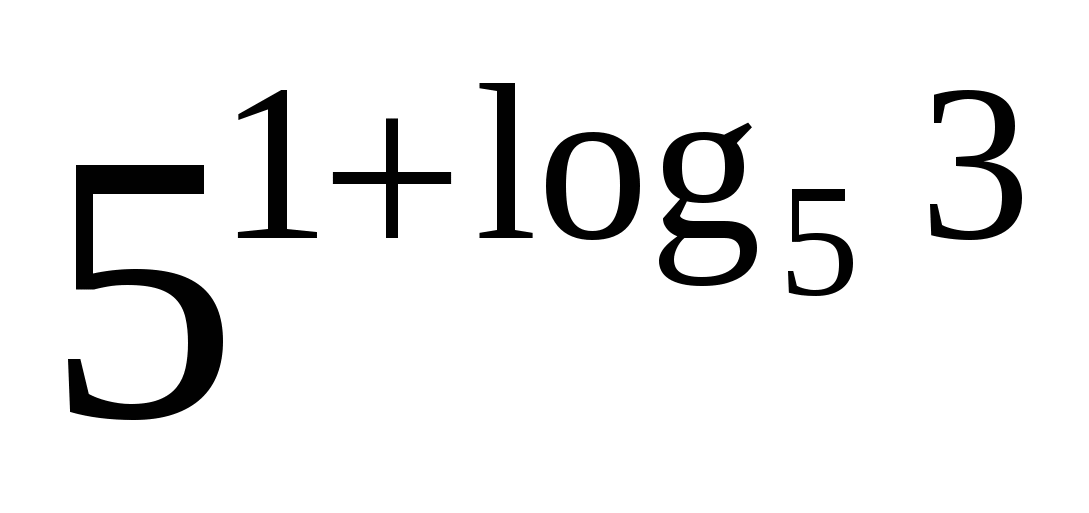
В3. Вычислить 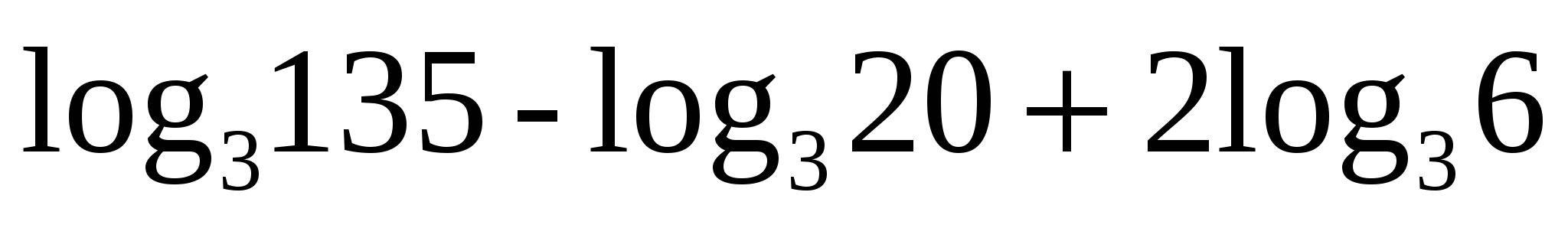
В4. Вычислить 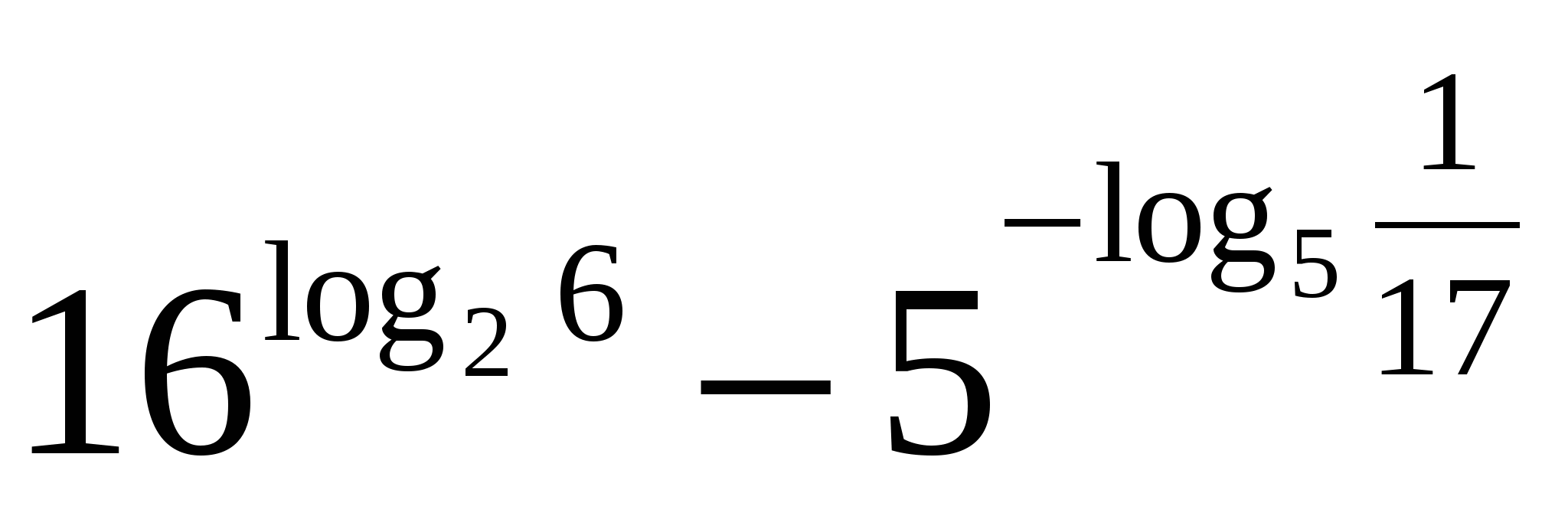
В5. Вычислить 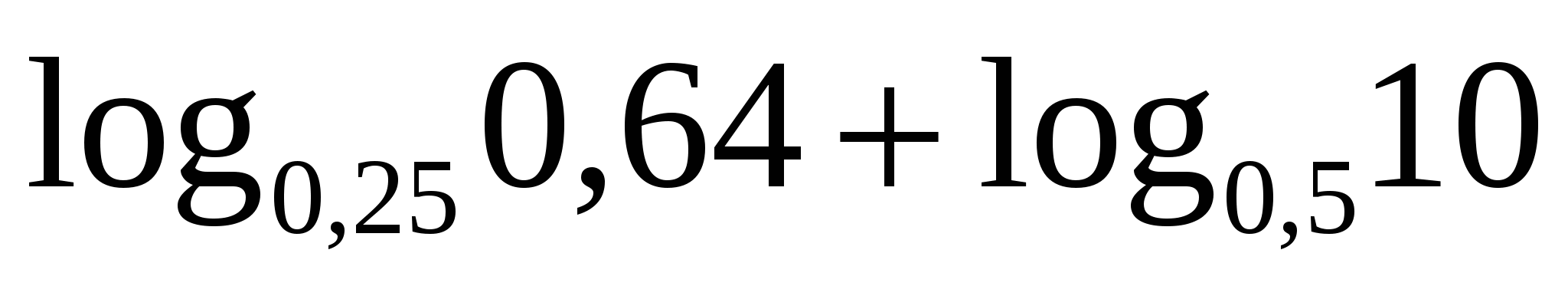
В6. Вычислить 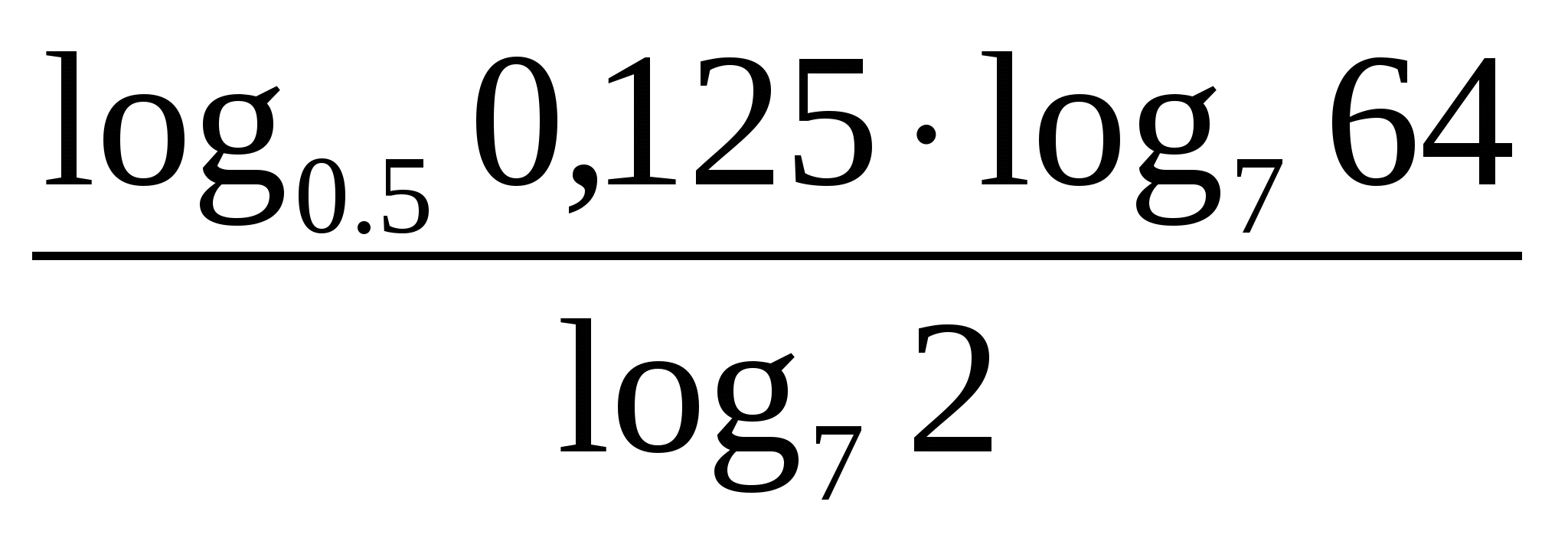
В7. Найти значение выражения 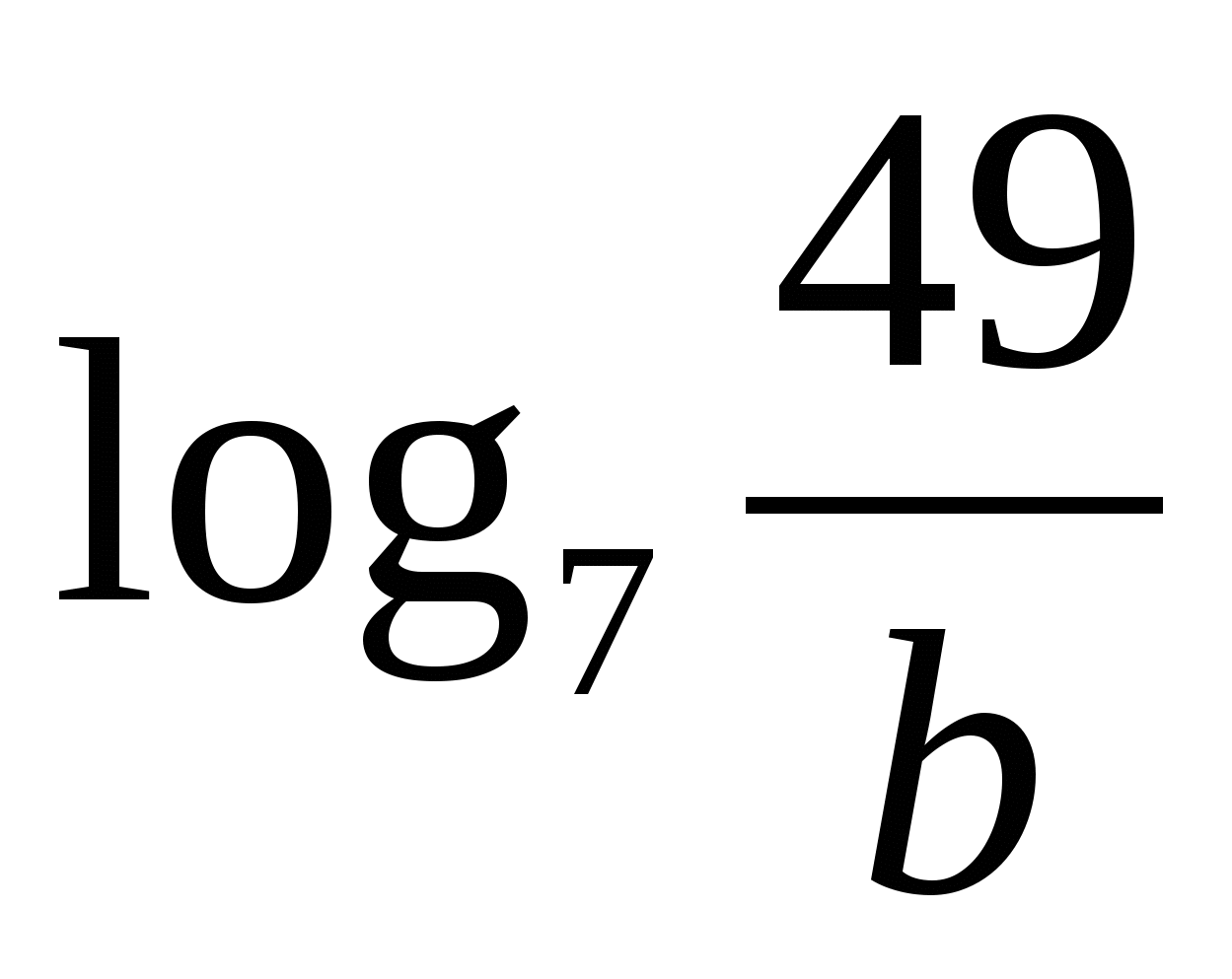
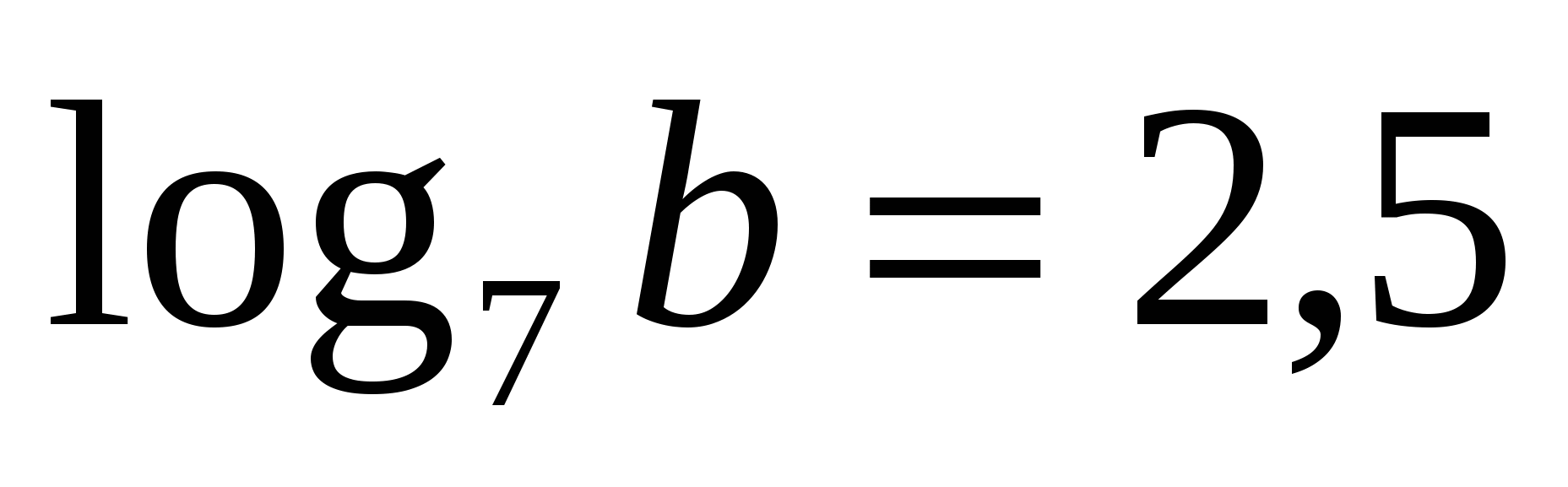
В8. Найти значение выражения 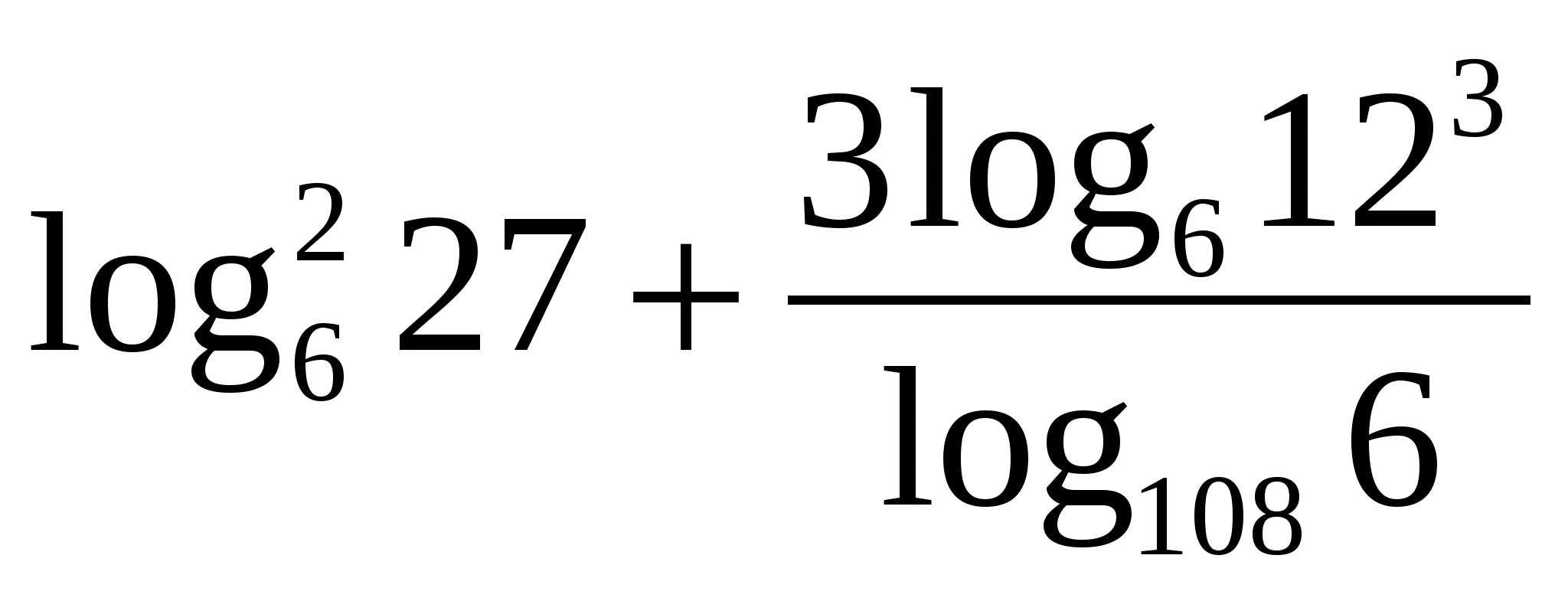
В9. Решить уравнение 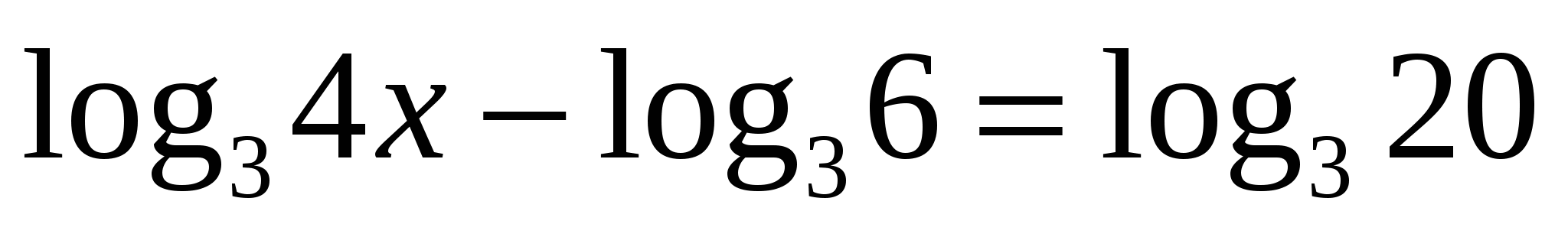
В10. Найдите корень или сумму корней уравнения, если их несколько 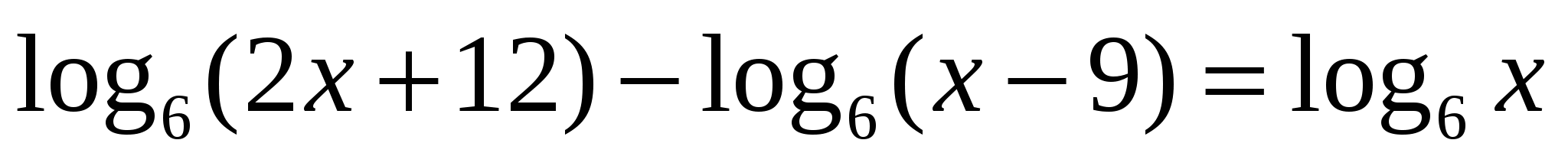
Вариант 2
Ответами к заданиям теста являются целые числа или числа, записанные в виде десятичной дроби
В1. Вычислить 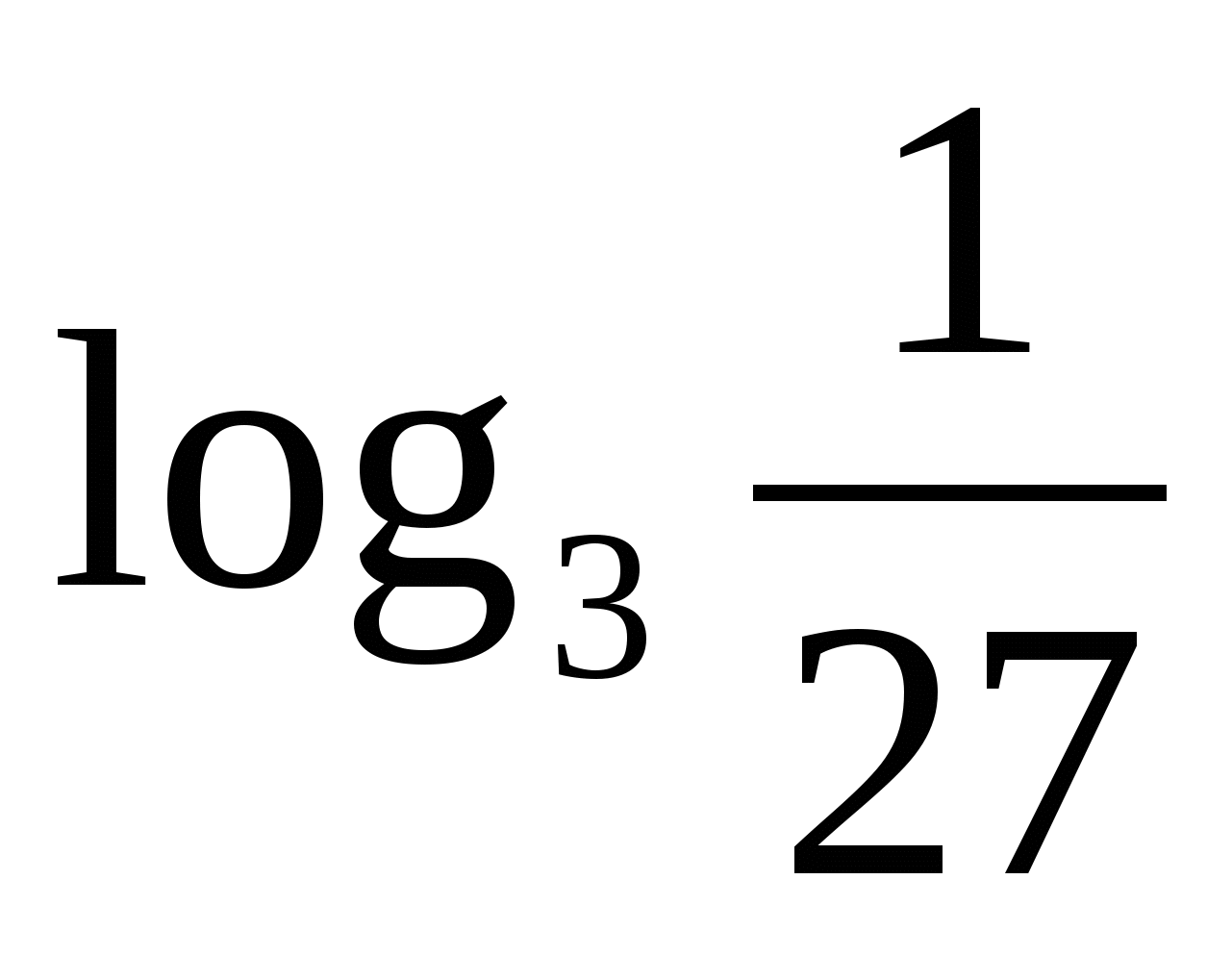
В2. Вычислить 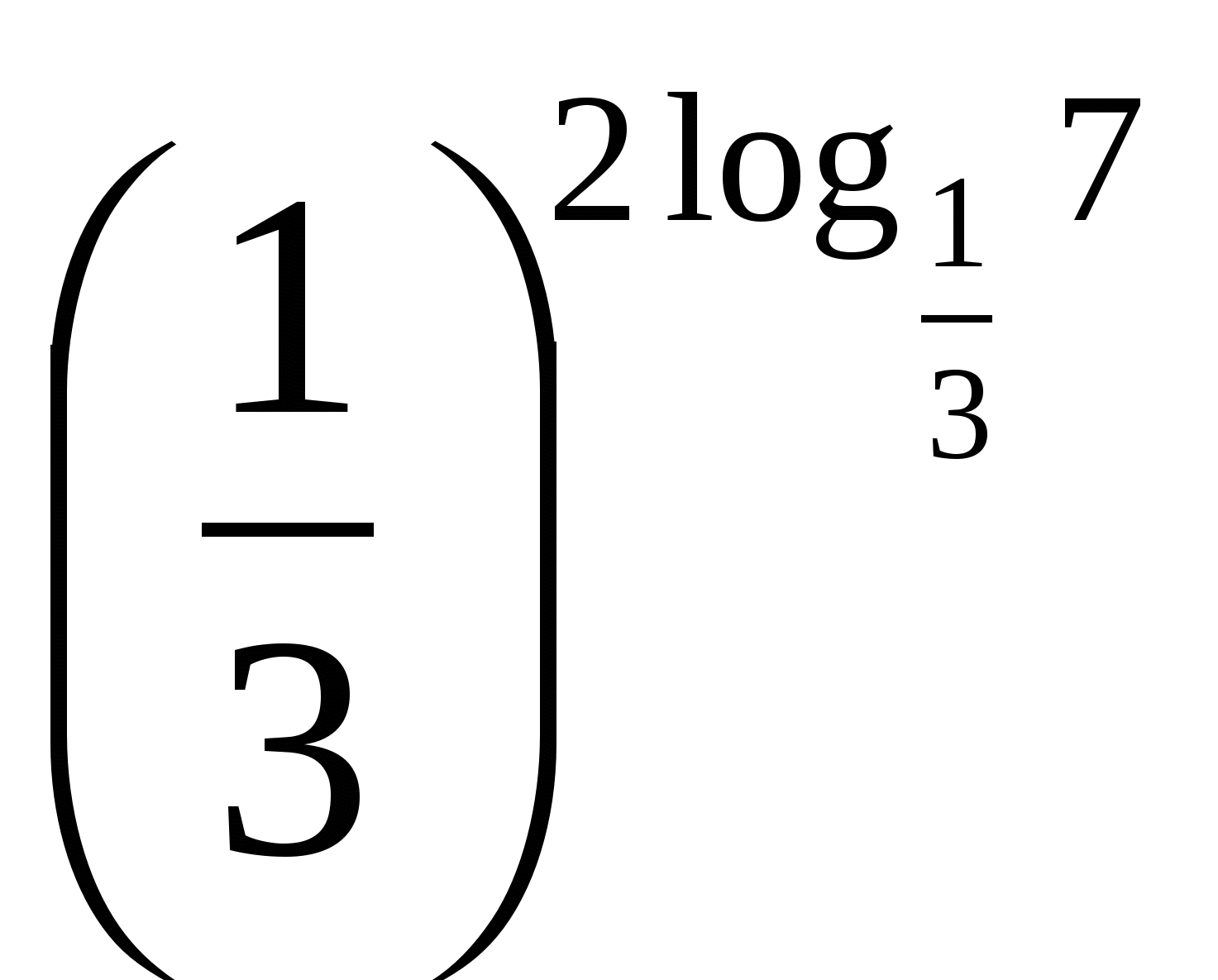
В3. Вычислить 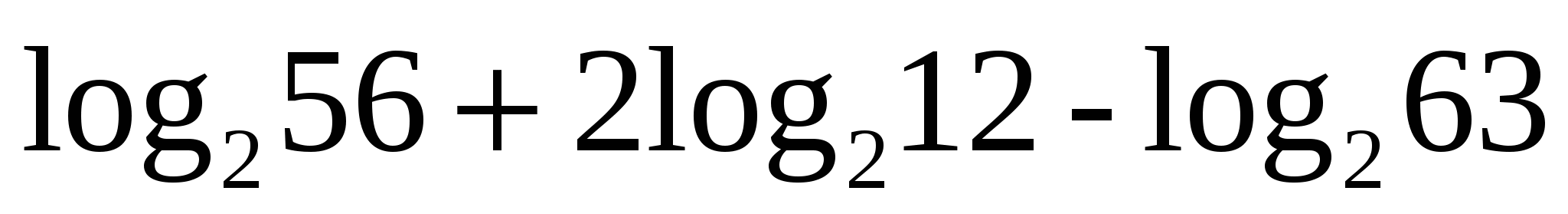
В4. Вычислить 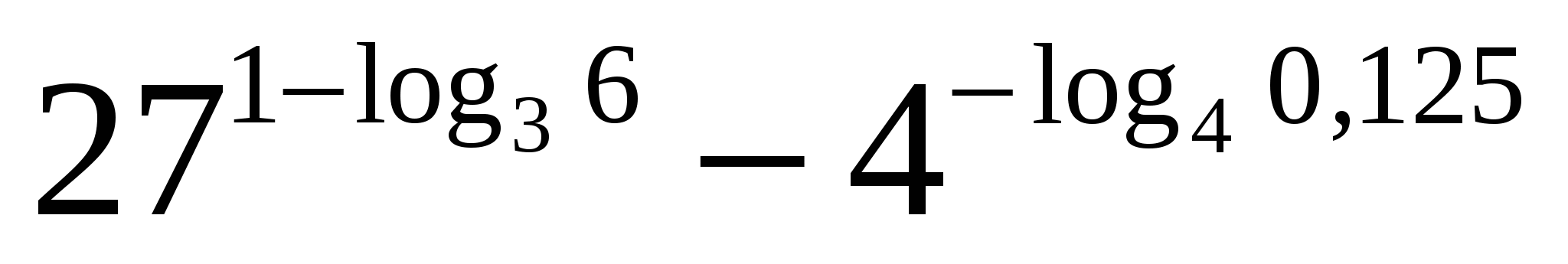
В5. Вычислить 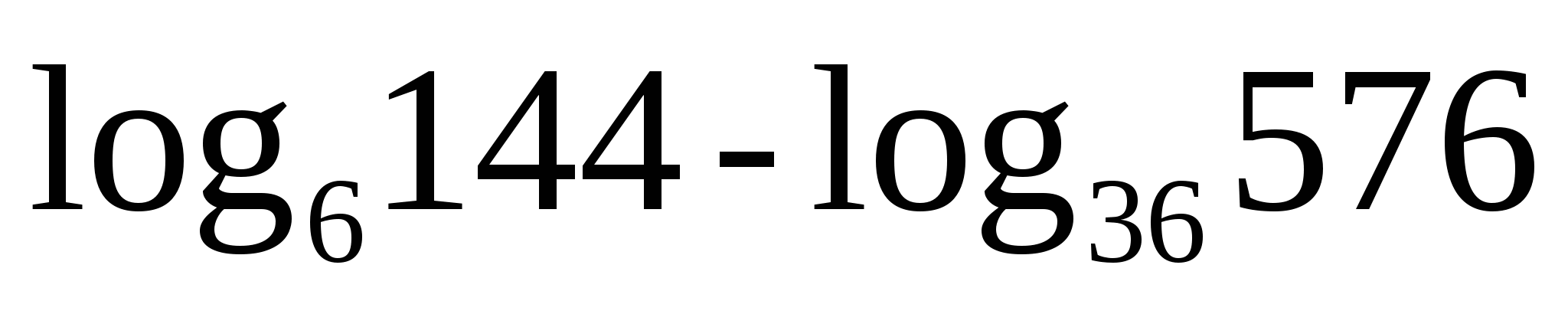
В6. Вычислить 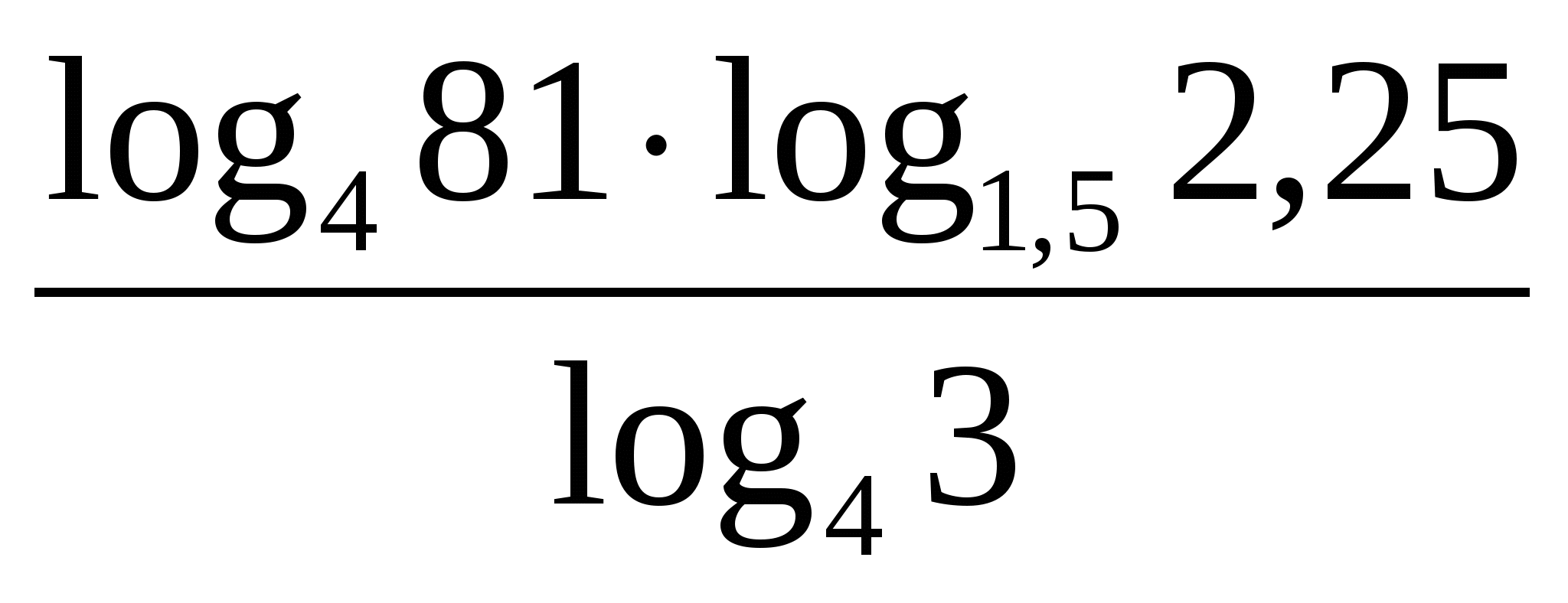
В7. Найти значение выражения 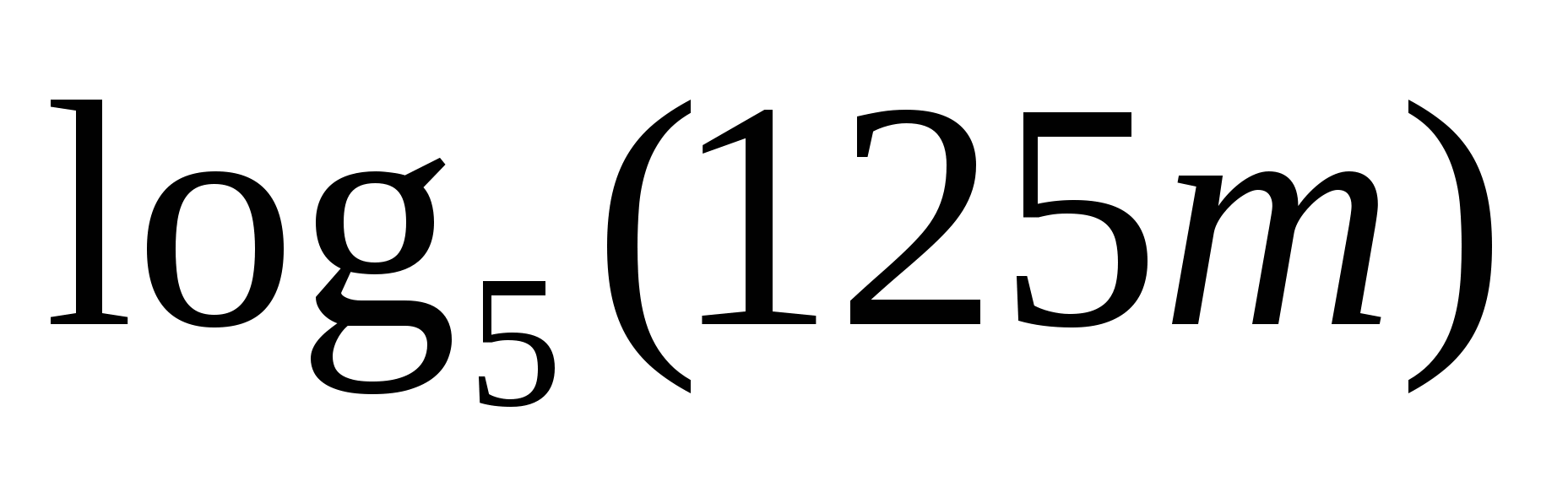
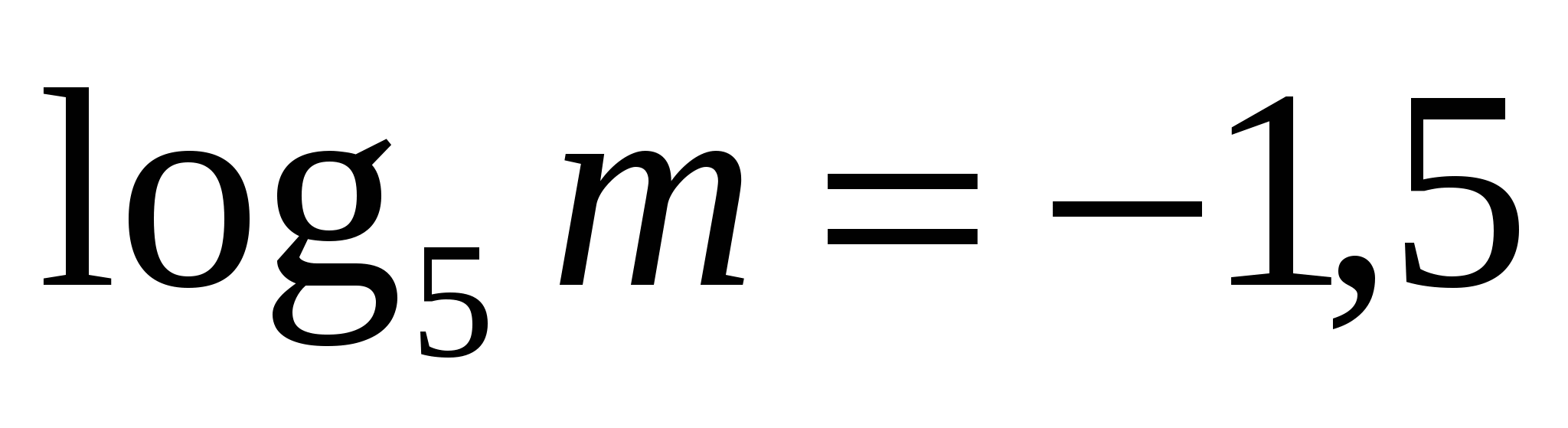
В8. Найти значение выражения 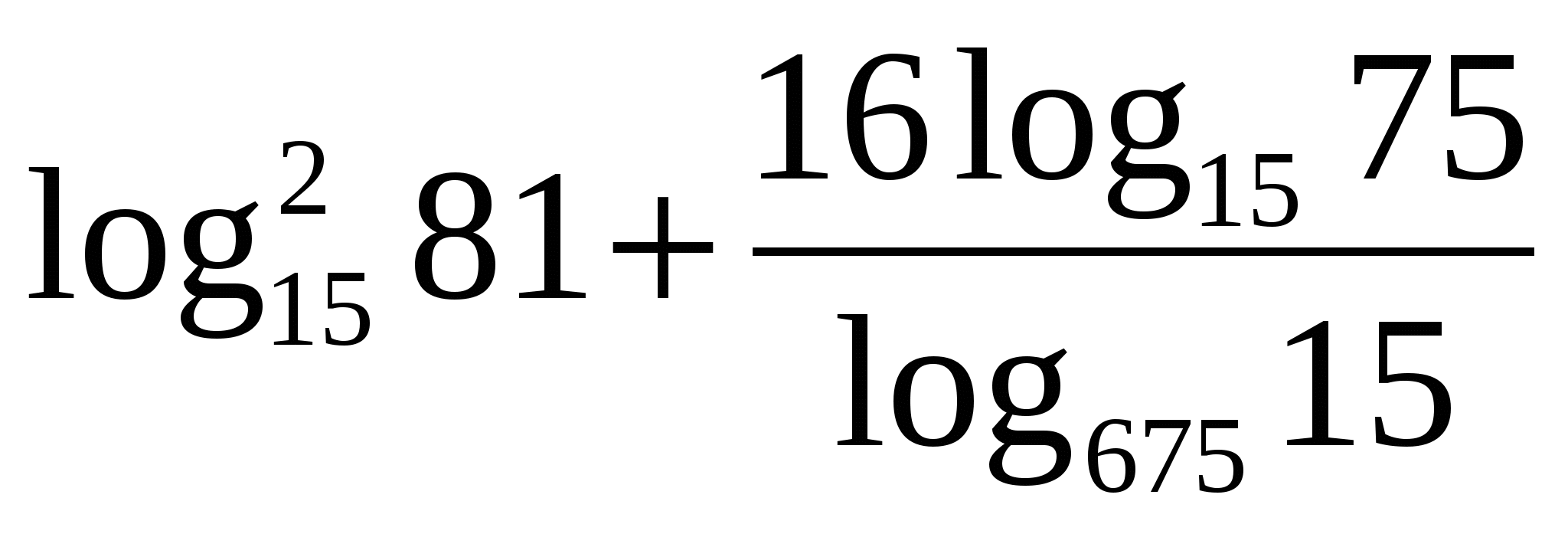
В9. Решить уравнение 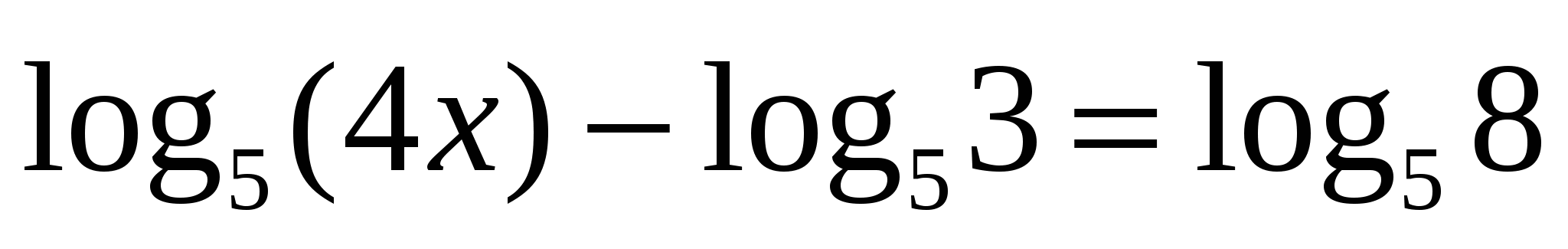
В10. Найдите корень или сумму корней уравнения, если их несколько 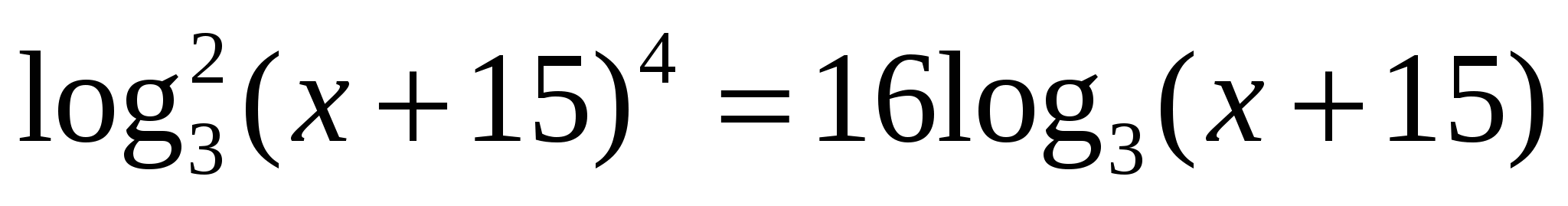
Тест по теме «Уравнения и неравенства»
Технологическая карта контрольно-измерительных материалов
Курс
1
Предмет
Математика
Учебник, по которому ведется преподавание
-
Алгебра и начала математического анализа: учебник для 10-11 кл.общеобразоват.учреждений / [А.Н.Колмогоров, А.М.Абрамов, Ю.П.Дудницын и др.]; под ред.А.Н.Колмогорова. — М.: Просвещение, 2008.
-
Богомолов, Н.В. Практические занятия по математике: Учеб. пособие для средних спец. учебных заведений/Н.В.Богомолов. — М.: Высшая школа, 2003.
Тема контроля
Текстовые задачи на составление уравнений и их систем
Вид контроля
текущий
Форма и методы контроля
1) по степени индивидуализации — индивидуальный;
2) по манере исполнения — письменный;
3) по способу подачи контролирующих заданий — тест.
Тип контроля
внешний
Время контроля
45 минут
Цель контроля
Проверить уровень усвоения обучающимися знаний о решении уравнений и их систем и умения применять свои знания в предложенной ситуации.
Содержание контроля
Тест включает в себя 5 задач, из которых две на проценты и смеси, две на движение и одна на совместную работу.
Критерии оценивания
Отметка «5» выставляется, если выполнено 9-10 заданий
Отметка «4» выставляется, если выполнено7-8 заданий
Отметка «3» выставляется, если выполнено 5-6 заданий
Отметка «2» выставляется, если выполнено менее 5 заданий
Вариант 1
Ответами к заданиям теста являются целые числа или числа, записанные в виде десятичной дроби
-
В понедельник акции компании подорожали на некоторое количество процентов, а во вторник подешевели на то же самое количество процентов. В результате они стали стоить на
дешевле, чем при открытии торгов в понедельник. На сколько процентов подорожали акции компании в понедельник?
-
Имеются два сосуда. Первый содержит 30 кг, а второй — 20 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 68% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 70% кислоты. Сколько килограммов кислоты содержится в первом сосуде?
-
Теплоход проходит по течению реки до пункта назначения 200 км и после стоянки возвращается в пункт отправления. Найдите скорость течения, если скорость теплохода в неподвижной воде равна 15 км/ч, стоянка длится 10 часов, а в пункт отправления теплоход возвращается через 40 часов после отплытия из него. Ответ дайте в км/ч.
-
На изготовление 475 деталей первый рабочий тратит на 6 часов меньше, чем второй рабочий на изготовление 550 таких же деталей. Известно, что первый рабочий за час делает на 3 детали больше, чем второй. Сколько деталей в час делает первый рабочий?
-
Из пункта A в пункт B одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью, меньшей скорости первого на 13 км/ч, а вторую половину пути — со скоростью 78 км/ч, в результате чего прибыл в пункт В одновременно с первым автомобилем. Найдите скорость первого автомобиля, если известно, что она больше 48 км/ч. Ответ дайте в км/ч.
Вариант 2
Ответами к заданиям теста являются целые числа или числа, записанные в виде десятичной дроби
-
Цена холодильника в магазине ежегодно уменьшается на одно и то же число процентов от предыдущей цены. Определите, на сколько процентов каждый год уменьшалась цена холодильника, если, выставленный на продажу за 20 000 рублей, через два года был продан за 15 842 рублей.
-
Смешав 30-процентный и 60-процентный растворы кислоты и добавив 10 кг чистой воды, получили 36-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 41-процентный раствор кислоты. Сколько килограммов 30-процентного раствора использовали для получения смеси?
-
Теплоход проходит по течению реки до пункта назначения 255 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 1 км/ч, стоянка длится 2 часа, а в пункт отправления теплоход возвращается через 34 часа после отплытия из него. Ответ дайте в км/ч.
-
На изготовление 99 деталей первый рабочий тратит на 2 часа меньше, чем второй рабочий на изготовление 110 таких же деталей. Известно, что первый рабочий за час делает на 1 деталь больше, чем второй. Сколько деталей в час делает второй рабочий?
-
Из пункта A в пункт B одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью 24 км/ч, а вторую половину пути — со скоростью, на 16 км/ч большей скорости первого, в результате чего прибыл в пункт B одновременно с первым автомобилем. Найдите скорость первого автомобиля. Ответ дайте в км/ч.
Тест по теме «Элементы комбинаторики»
Условие задачи
Варианты ответов
1
2
3
4
5
1
Вычислить 4!
18
12
24
72
Нет нужного ответа
2
Вычислить 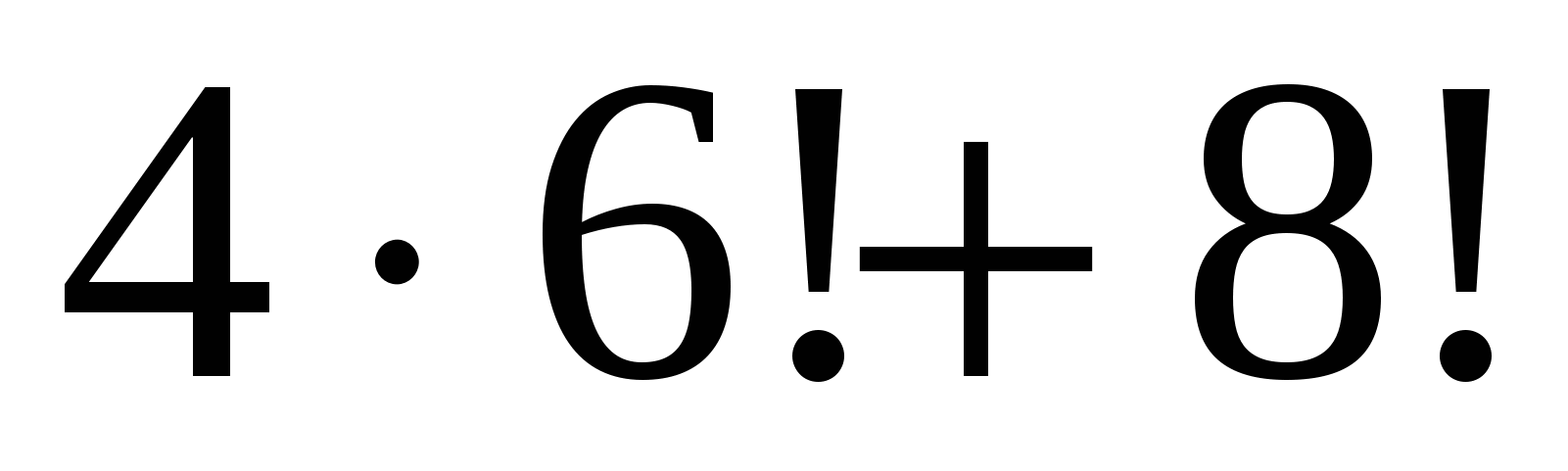
192
43200
3600
8640
Нет нужного ответа
3
Вычислить 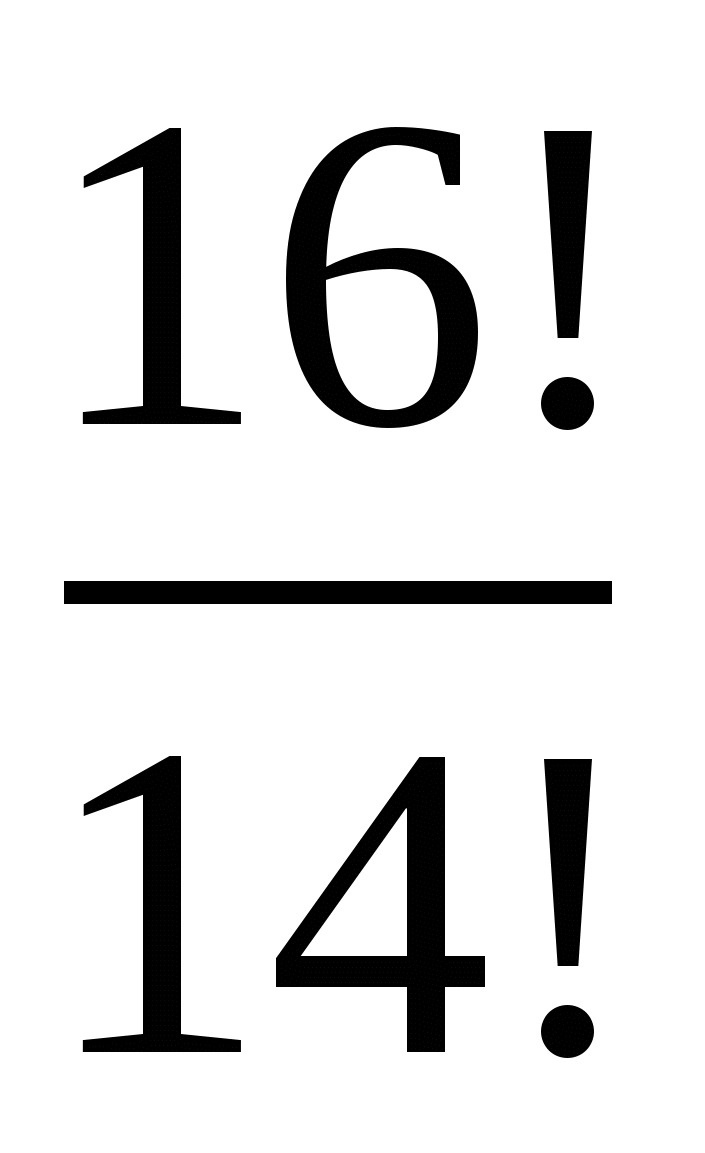
156
16
240
Нет нужного ответа
4
Решить уравнение 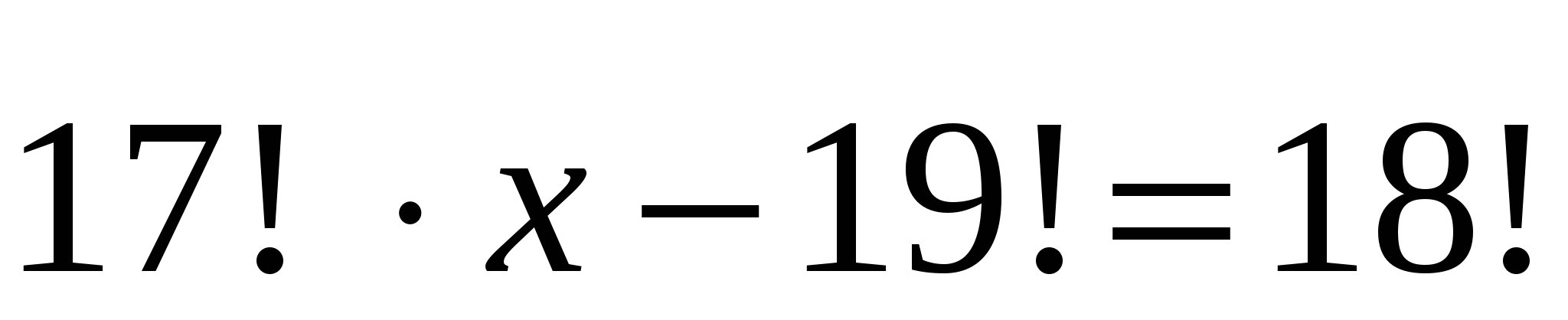
360
37/17
1/17
342
Нет нужного ответа
5
При каком значении n справедливо равенство? 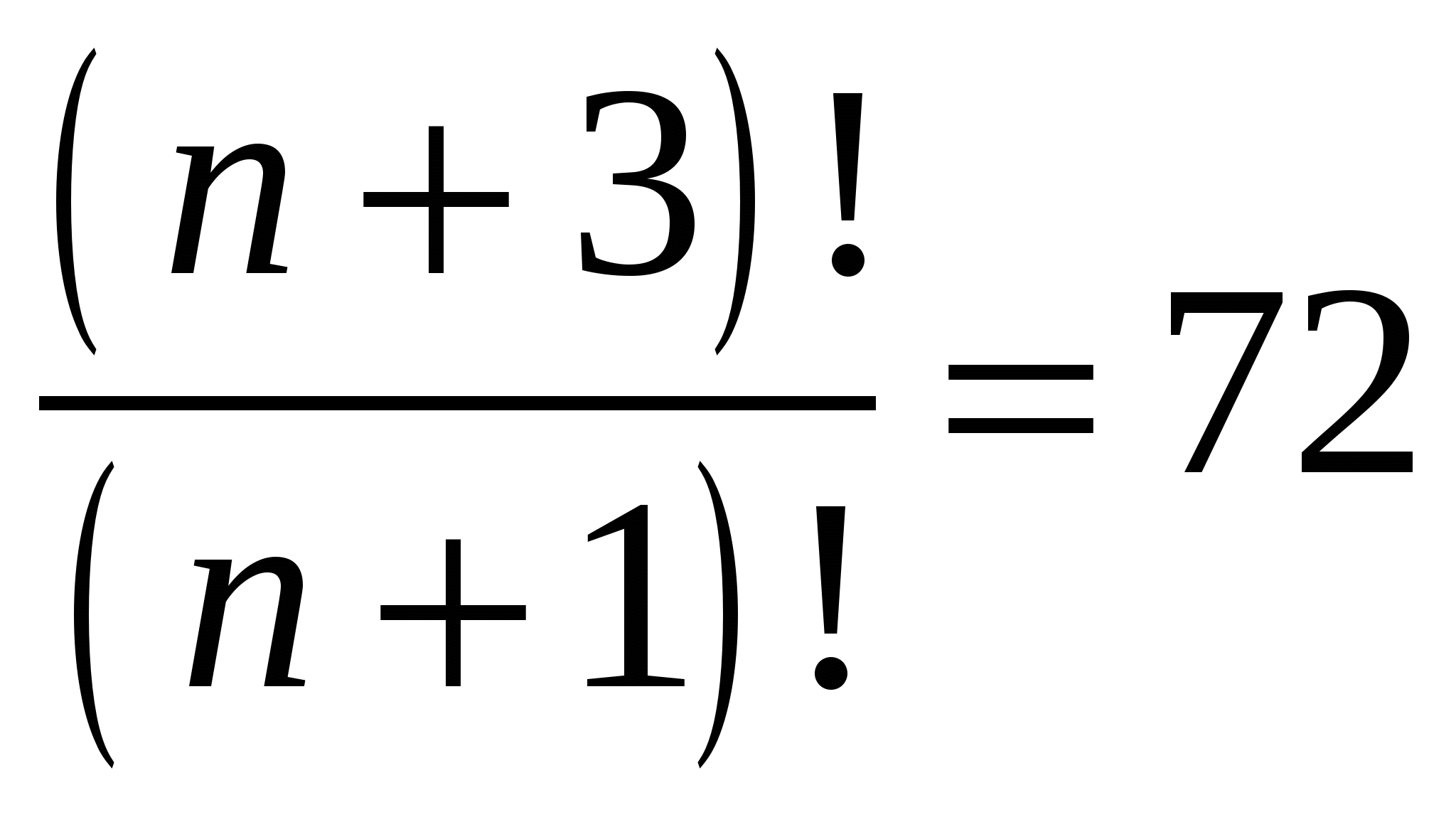
5
4
7
6
Нет нужного ответа
6
У повара имеется 9 видов овощей. Сколько разных салатов можно приготовить, если каждый салат состоит 4 разных овощей.
256
36
81
126
Нет нужного ответа
7
Сколькими способами можно покрасить пять елок в серебристый, зеленый и синий цвета, если количество краски не ограничено, а каждую елку красим только в один цвет?
243
15
6
120
Нет нужного ответаВремя выполнения 30 минут
Тест по теме «Координаты и векторы»
Время выполнения 45 минут
Вариант 1
Ответами к заданиям теста являются целые числа или числа, записанные в виде десятичной дроби
1. Вектор 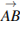
(5; 3) имеет координаты (3; 1). Найдите абсциссу точки
2. Найдите сумму координат вектора +
.
3. Из точки А(6; 
4. Найдите угловой коэффициент прямой, проходящей через точки с координатами (−2; 0) и (0; 2).
5. Прямая a проходит через точки с координатами (0; 4) и (−6; 0). Прямая b проходит через точку с координатами (0; −6) и параллельна прямой a. Найдите абсциссу точки пересечения прямой b с осью Ox.
6. Точки O(0; 0), A(6; 8), B(8; 2) являются вершинами треугольника. Найдите длину его средней линии CD, параллельной OA.
Вариант 2
Ответами к заданиям теста являются целые числа или числа, записанные в виде десятичной дроби
1. Вектор 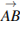
(3; 6) имеет координаты (9; 3). Найдите сумму координат точки
2. Найдите сумму координат вектора .
3. Через точку А(6; 
4. Найдите угловой коэффициент прямой, проходящей через точки с координатами (2; 0) и (0; 2).
5. Прямая a проходит через точки с координатами (0; 4) и (6; 0). Прямая b проходит через точку с координатами (0; 
6. Точки O(0; 0), A(10; 0), B(8; 6), C(2; 6) являются вершинами трапеции. Найдите длину ее средней линии DE.
Тест по теме «Прямые и плоскости в пространстве»
Время выполнения 30 минут
Вариант 1
1. К плоскости проведены две равные наклонные. Равны ли их проекции?
2. Какое из следующих утверждений верно?
а) Две прямые перпендикулярные третьей перпендикулярны между собой;
б) прямая называется перпендикулярной плоскости, если она перпендикулярна хотя бы одной прямой, лежащей в этой плоскости;
в) две прямые, перпендикулярные к плоскости, перпендикулярны между собой;
г) прямая называется перпендикулярной плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости.
3. Прямая m перпендикулярна к прямым a и b, лежащим в плоскости α, но m не перпендикулярна к плоскости α. Выясните взаимное расположение прямых a и b.
а) параллельны; б) пересекаются; в) скрещиваются; г) определить нельзя.
4. Прямая а перпендикулярна к прямым с и b, лежащим в плоскости α, прямая а перпендикулярна к плоскости α. Выясните взаимное расположение прямых с и b.
а) только параллельны; б) только пересекаются; в) параллельны или пересекаются; г) определить нельзя.
5. В треугольнике АВС , АН — высота треугольника. Вне плоскости АВС выбрана точка Д, причем ДВ ⊥ ВС, ДВ ⊥ АВ . Плоскости ДВС перпендикулярна прямая
а) АД; б) АВ; в) АН; г) АС.
6. Прямая а, параллельная прямой b, пересекает плоскость α. Прямая с параллельна прямой b, тогда:
а) прямые а и с пересекаются; б) прямая с лежит в плоскости α;
в) прямые а ис скрещиваются; г) прямые а и с параллельны.
7. Каким может быть взаимное расположение прямых а и b, если через прямую а можно провести плоскость, параллельную прямой b?
а) скрещиваются или пересекаются;
б) скрещиваются или параллельны;
в) только скрещиваются;
г) только параллельны.
8. Прямые а и в лежат в параллельных плоскостях, следовательно эти прямые
а) скрещиваются или пересекаются; б) скрещиваются или параллельны;
в) только скрещиваются; г) только параллельны.
9. Каким может быть взаимное расположение двух прямых, если обе они параллельны одной плоскости?
а) только параллельны; б) все случаи взаимного расположения;
в) только скрещиваются; г) только пересекаются.
10. Прямая а параллельна плоскости α. Какое из следующих утверждений верно?
а) Прямая а параллельна любой прямой, лежащей в плоскости α;
б) прямая а не пересекает ни одну прямую, лежащую в плоскости α;
в) прямая а скрещивается со всеми прямыми плоскости α;
г) прямая а имеет общую точку с плоскостью .
Вариант 2
1. Какое из следующих утверждений неверно?
а) Если прямая перпендикулярна к двум прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости;
б) если прямая перпендикулярна к плоскости, то она ее пересекает;
в) если две плоскости перпендикулярны к прямой, то они параллельны;
г) если две прямые перпендикулярны к плоскости ,то они параллельны.
2. Две наклонные, проведенные к плоскости, имеют равные проекции. Равны ли сами наклонные?
3. Если одна из двух скрещивающихся прямых перпендикулярна к плоскости, то будет ли перпендикулярна к этой плоскости вторая прямая?
а) Да; б) да, но при определенных условиях; в) определить нельзя; г) нет.
4. Точка E не принадлежит плоскости прямоугольника ABCD. BE⊥ AB, BE⊥ BC. Тогда прямая CD и плоскость BCE:
а) параллельны; б) перпендикулярны; в) определить их взаимное расположение нельзя ; г) прямая лежит в плоскости.
5. АВСД — квадрат. Вне его плоскости выбрана точка К, причем КА ⊥ АВ. Плоскости АКД перпендикулярна прямая
а) ДС; б) КС; в) ВК; г) ВС.
6. Прямая с, параллельная прямой а, пересекает плоскость β. Прямая b параллельна прямой а, тогда:
а) прямые b и с пересекаются; б) прямая b лежит в плоскости β;
в) прямые b и с скрещиваются; г) прямые b и с параллельны.
7. Каким может быть взаимное расположение прямых а и b, если любая плоскость, проходящая через а, не параллельна b?
а) скрещиваются; б) параллельны; в) пересекаются; г) определить нельзя.
8. Прямые а и в лежат в параллельных плоскостях, следовательно эти прямые
а)скрещиваются или пересекаются; б) скрещиваются или параллельны; в) только скрещиваются; г) только параллельны.
9. Прямая а параллельна плоскости α. Какое из следующих утверждений верно?
а) Прямая а параллельна любой прямой, лежащей в плоскости α;
б) прямая а не пересекает ни одну прямую, лежащую в плоскости α;
в) прямая а скрещивается со всеми прямыми плоскости α;
г) прямая а имеет общую точку с плоскостью .
10. Каким может быть взаимное расположение прямых а и b, если прямая а лежит в плоскости α, а прямая b параллельна этой плоскости?
а) Параллельны или пересекаются;
б) скрещиваются или пересекаются;
в) параллельны или скрещиваются;
г) определить нельзя.
Итоговый тест по дисциплине «Математика»
Курс
1
Предмет
Математика
Учебник, по которому ведется преподавание
-
Алгебра и начала математического анализа: учебник для 10-11 кл.общеобразоват.учреждений / [А.Н.Колмогоров, А.М.Абрамов, Ю.П.Дудницын и др.]; под ред.А.Н.Колмогорова. — М.: Просвещение, 2008.
-
Богомолов, Н.В. Практические занятия по математике: Учеб. пособие для средних спец. учебных заведений/Н.В.Богомолов. — М.: Высшая школа, 2003.
-
Погорелов, А.В. Геометрия. 10-11 кл.: учеб. для общеобразоват. учреждений: базовый и профильный уровни/А.В.Погорелов. — М.: Просвещение, 2010.
Тема контроля
Итоговый тест по курсу математики
Вид контроля
рубежный
Форма и методы контроля
1) по степени индивидуализации — индивидуальный;
2) по манере исполнения — письменный;
3) по способу подачи контролирующих заданий — тест.
Тип контроля
внешний
Время контроля
60 минут
Цель контроля
Проверить уровень усвоения обучающимися умений и знаний У1-У27, З1-З21 по курсу математики.
Содержание контроля
Тест включает в себя 12 заданий по основным темам курса математики в соответствии с программой учебной дисциплины.
Критерии оценивания
Отметка «5» выставляется, если выполнено 11-12 заданий
Отметка «4» выставляется, если выполнено 9-10 заданий
Отметка «3» выставляется, если выполнено 7-8 заданий
Отметка «2» выставляется, если выполнено менее 7 заданий
Инструкция по выполнению итогового теста:
1. Проверка готовности учащихся к занятиям.
2. Запрещается пользоваться какими-либо техническими средствами (телефоном с интернетом и т.п.).
3. Каждому присутствующему учащемуся раздаётся вариант итогового теста и двойной тетрадный лист со штампом учебного заведения в верхнем левом углу.
4. На первой странице двойного тетрадного листка внизу под штампом пишется: итоговое тестировании по дисциплине «Математика», группа и курс, фамилия и имя в родительном падеже, номер варианта, внизу страницы дата проведения тестирования.
5. На второй странице в столбик пишутся номера вопросов.
6. Варианты ответов отделяются от номеров вопросов тире.
7. После данного варианта ответа в виде цифры больше ничего не пишется (расшифровка ответа), там, где требуется слово в ответе написать, пишется только слово-ответ.
8. Что исправить уже данный вариант ответа, его необходимо аккуратно одной косой линией зачеркнуть и рядом разборчиво написать новый вариант ответа (в противном случае все исправления будут оцениваться как ошибочные).
9. После проверки тестовых ответов до студентов доводятся оценки.
Вариант 1
Ответами к заданиям теста являются целые числа или числа, записанные в виде десятичной дроби
Задание 1 . В сентябре 1 кг винограда стоил 60 рублей, в октябре виноград подорожал на 25%, а в ноябре еще на 20%. Сколько рублей стоил 1 кг винограда после подорожания в ноябре?
Задание 2 . На рисунке жирными точками показано суточное количество осадков, выпадавших в Мурманске с 7 по 22 ноября 1995 года. По горизонтали указываются числа месяца, по вертикали — количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, сколько дней из данного периода выпадало менее 3 миллиметров осадков.
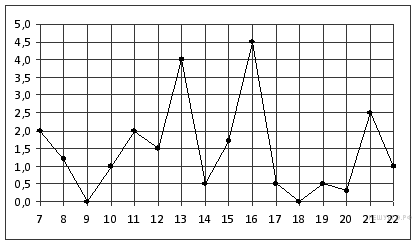
Задание 3. Найдите корень уравнения 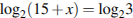
Задание 4. В треугольнике 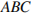
равен 90°,
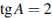
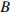
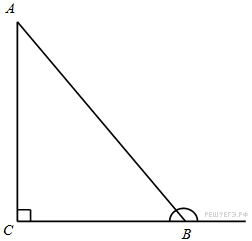
Задание 5. Для транспортировки 45 тонн груза на 1300 км можно воспользоваться услугами одной из трех фирм-перевозчиков. Стоимость перевозки и грузоподъемность автомобилей для каждого перевозчика указана в таблице. Сколько рублей придется заплатить за самую дешевую перевозку?
Перевозчик
Стоимость перевозки одним автомобилем
(руб. на 100 км)
Грузоподъемность автомобилей
(тонн)
А
3200
3,5
Б
4100
5
В
9500
12
Задание 6. Найдите сумму координат вектора 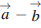
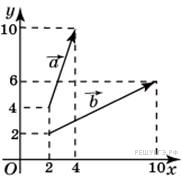
Задание 7. Найдите значение выражения .
Задание 8. На рисунке изображен график производной функции f(x), определенной на интервале (−7; 4). Найдите промежутки возрастания функции f(x). В ответе укажите сумму целых точек, входящих в эти промежутки.
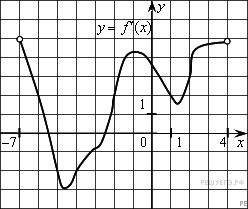
Задание 9. Найдите объем 
.
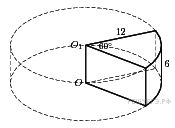
Задание 10. Для определения эффективной температуры звeзды используют закон Стефана-Больцмана, согласно которому мощность излучения нагретого тела 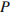
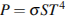
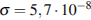
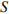
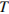
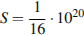

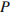
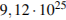
Задание 11. Даша и Маша пропалывают грядку за 12 минут, а одна Маша — за 20 минут. За сколько минут пропалывает грядку одна Даша?
Задание 12. Найдите наименьшее значение функции 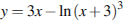
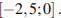
Вариант 2
Ответами к заданиям теста являются целые числа или числа, записанные в виде десятичной дроби
Задание 1. Цена на электрический чайник была повышена на 16% и составила 3480 рублей. Сколько рублей стоил чайник до повышения цены?
Задание 2. На графике показан процесс разогрева двигателя легкового автомобиля. На оси абсцисс откладывается время в минутах, прошедшее от запуска двигателя, на оси ординат — температура двигателя в градусах Цельсия. Определите по графику, сколько минут двигатель нагревался от температуры 60 °C до температуры 90 °C.
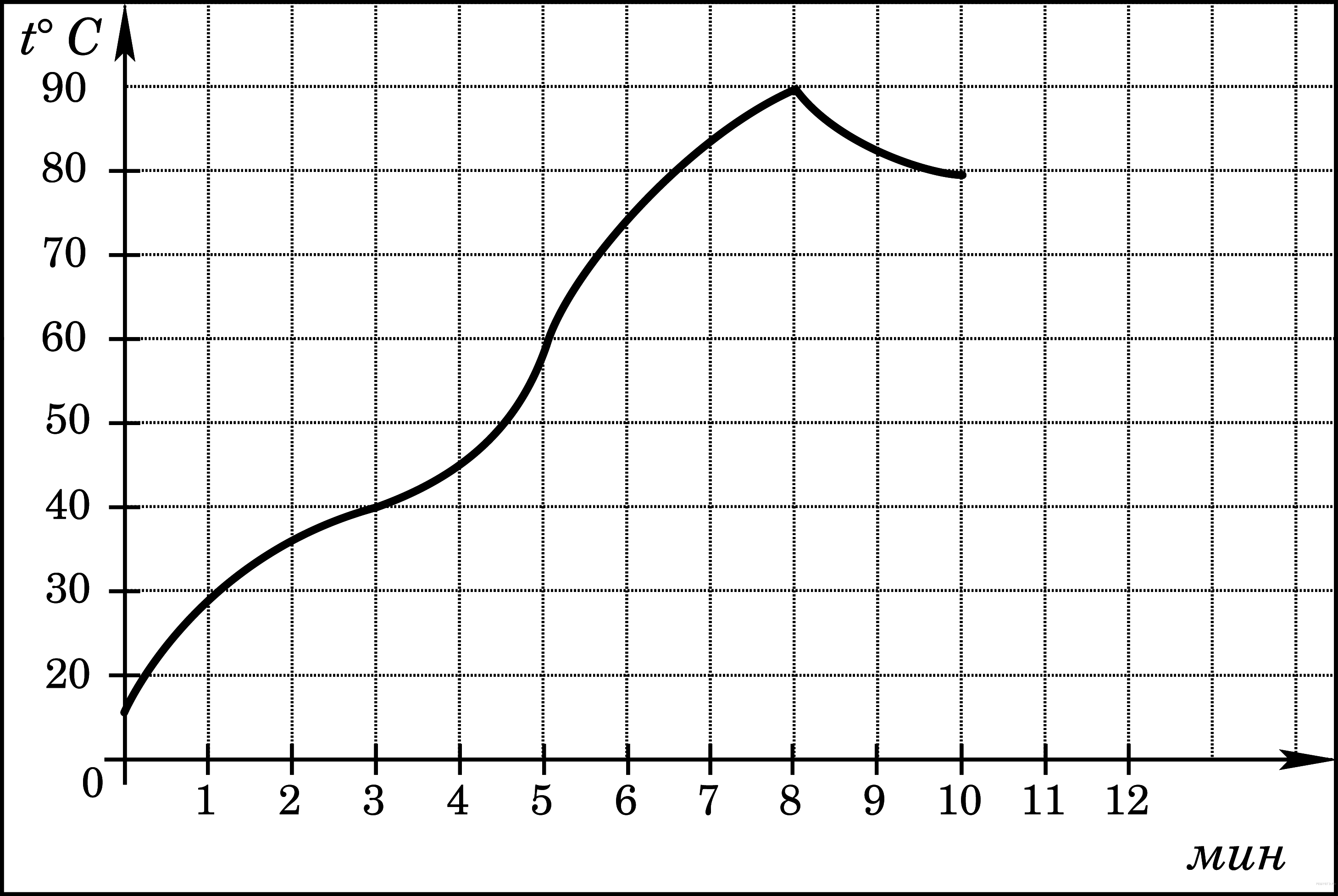
Задание 3. Найдите корень уравнения 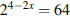
Задание 4. Найдите косинус угла . В ответе укажите значение косинуса, умноженное на
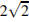
.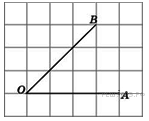
Задание 5. Интернет-провайдер (компания, оказывающая услуги по подключению к сети Интернет) предлагает три тарифных плана.
Тарифный план
Абонентская плата
Плата за трафик
План «0»
Нет
2,5 руб. за 1 Мб
План «500»
550 руб. за 500 Мб трафика в месяц
2 руб. за 1 Мб сверх 500 Мб
План «800»
700 руб. за 800 Мб трафика в месяц
1,5 руб. за 1 Мб сверх 800 Мб
Пользователь предполагает, что его трафик составит 600 Мб в месяц и, исходя из этого, выбирает наиболее дешевый тарифный план. Сколько рублей заплатит пользователь за месяц, если его трафик действительно будет равен 600 Мб?
Задание 6. Найдите площадь треугольника, вершины которого имеют координаты (2; 2), (8; 10), (8; 8).
Задание 7. Найдите значение выражения 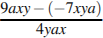
Задание 8. Материальная точка движется прямолинейно по закону 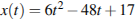
Задание 9. Длина окружности основания цилиндра равна 3, высота равна 2. Найдите площадь боковой поверхности цилиндра.
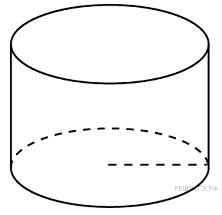
Задание 10. При адиабатическом процессе для идеального газа выполняется закон 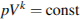
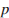
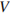
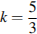
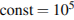

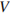
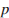
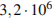
Задание 11. Первая труба пропускает на 1 литр воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает первая труба, если резервуар объемом 110 литров она заполняет на 2 минуты дольше, чем вторая труба заполняет резервуар объемом 99 литров?
Задание 12. Найдите наибольшее значение функции 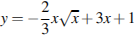
3.2.2 Проверочные работы
Проверочная работа по теме «Развитие понятия о числе»
Комплексные числа
Время выполнения 45 минут
Вариант 1
1. Найдите действительную часть комплексного числа, если:
z=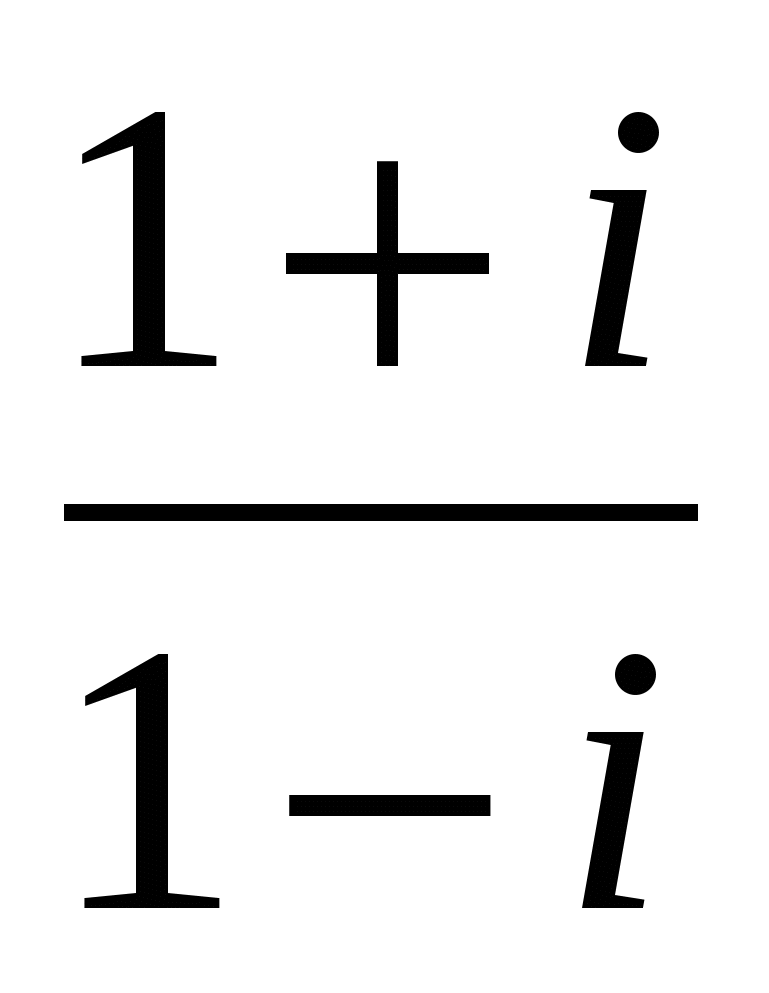
2. Найдите сумму 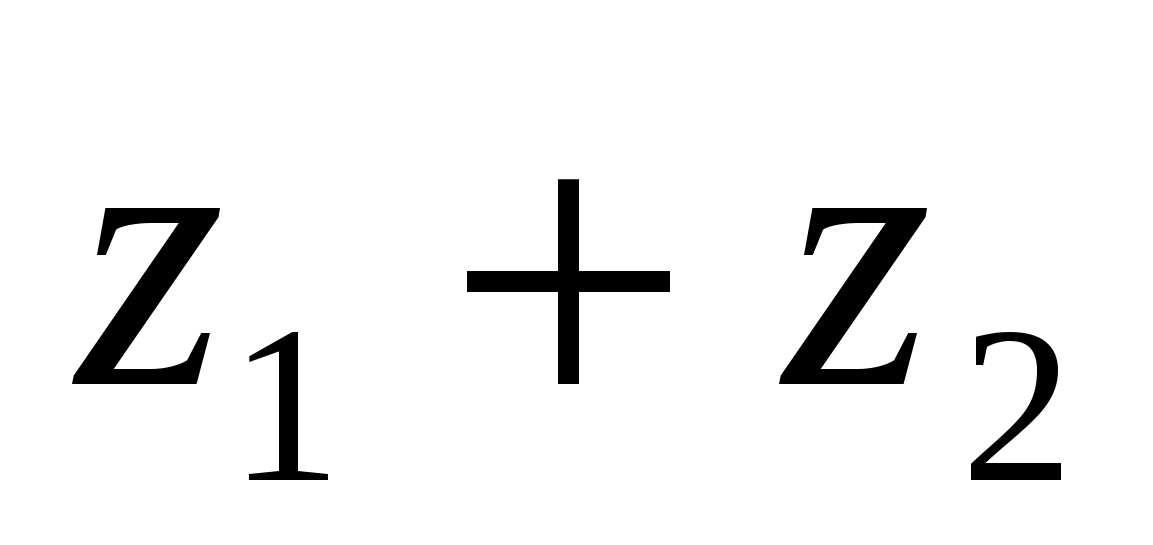
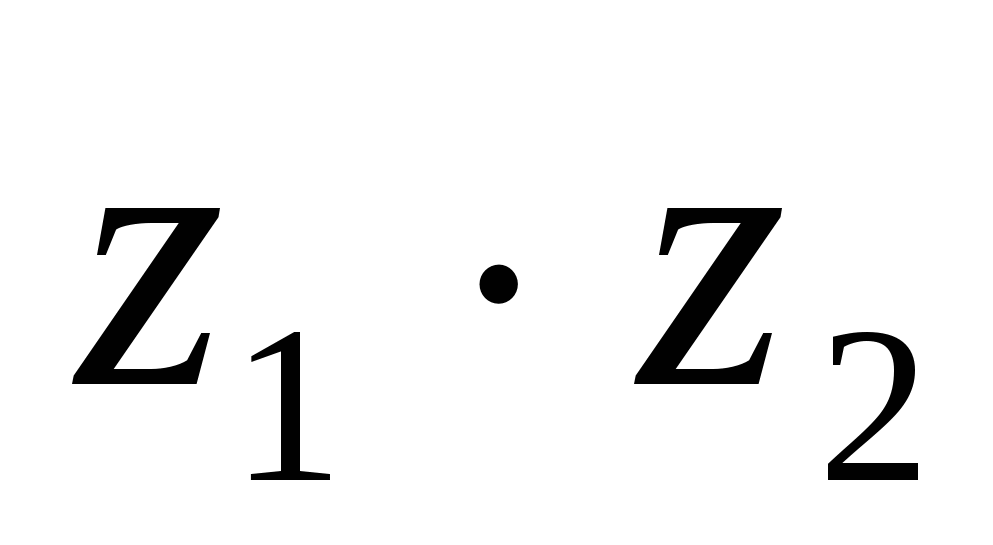
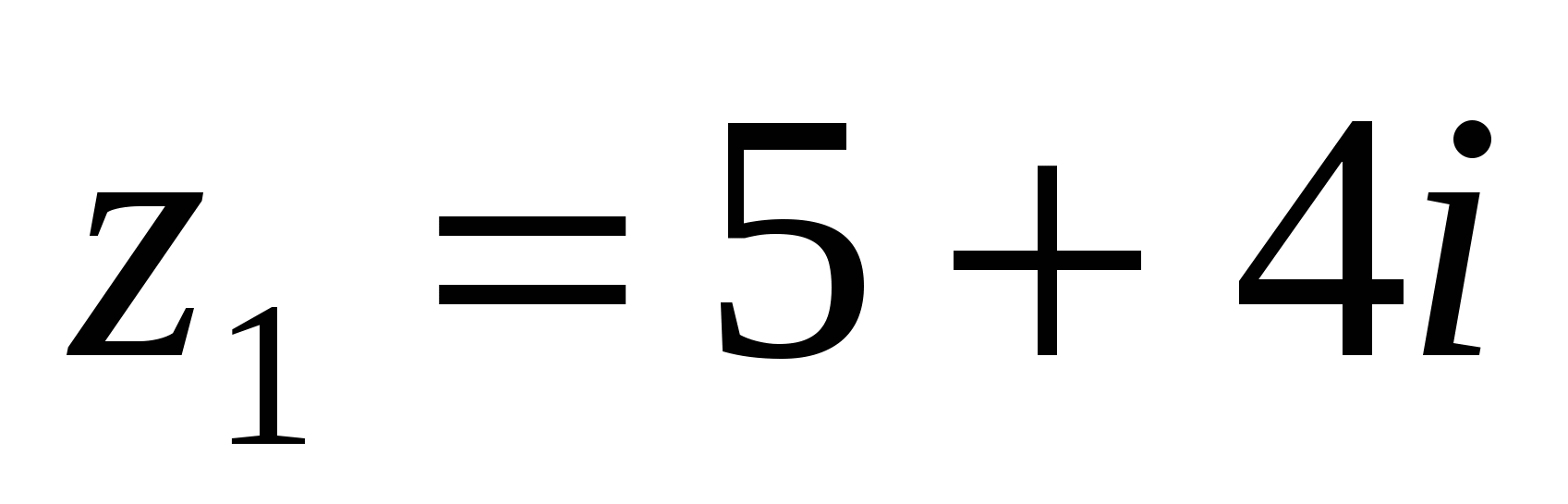
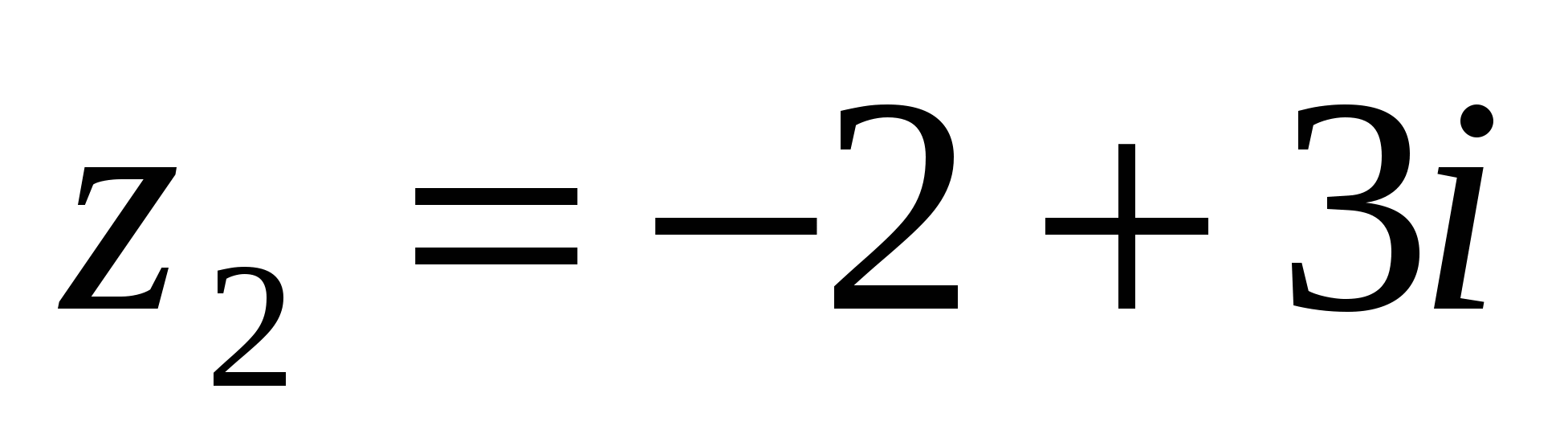
3. Степень мнимой единицы. Вычислите: 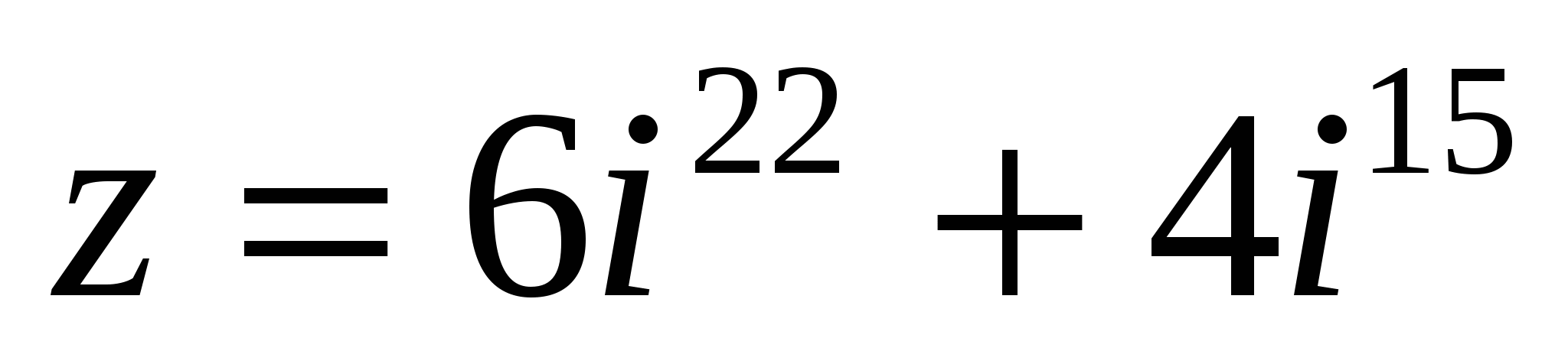
4. Найдите модуль комплексного числа 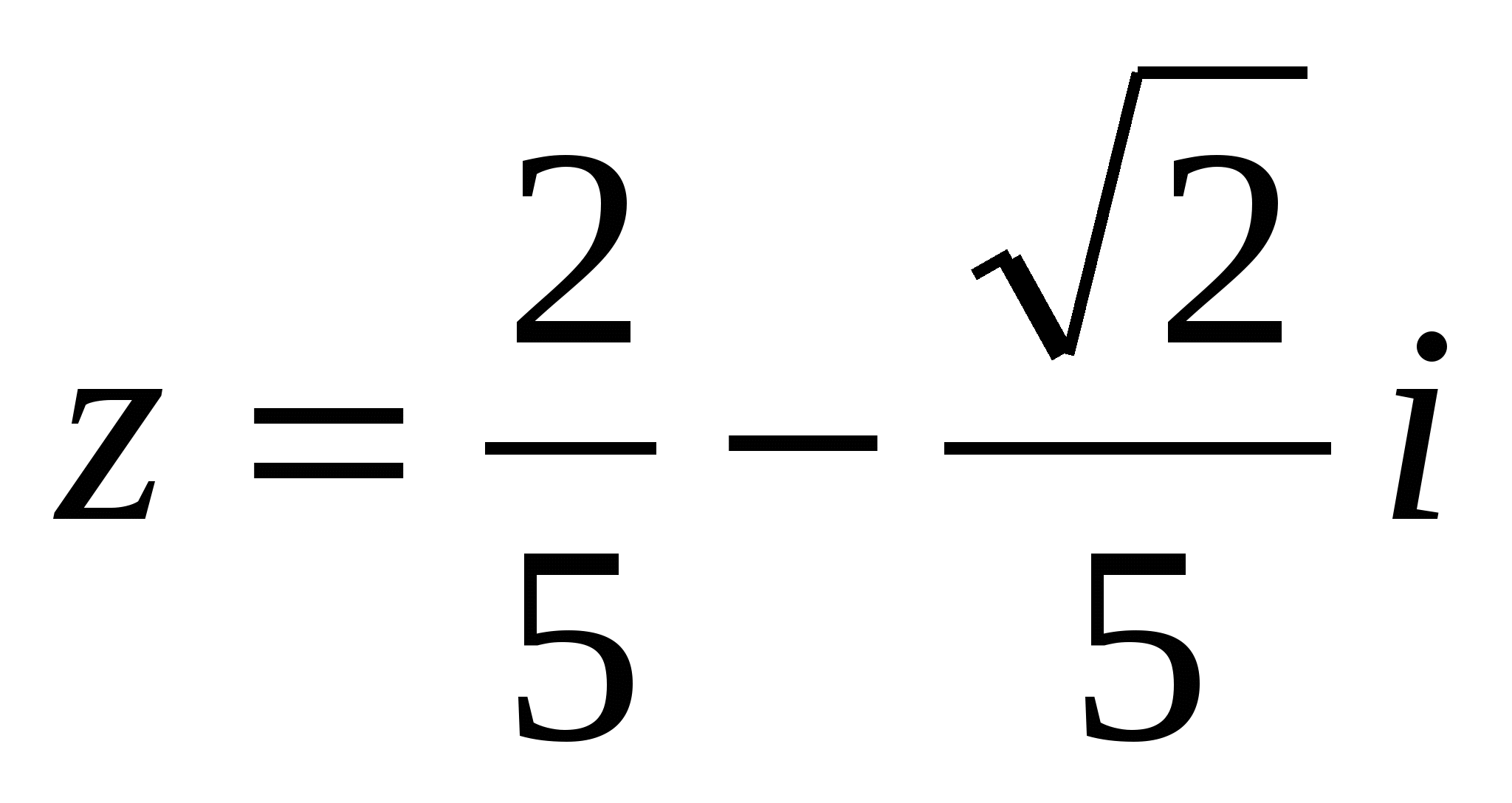
5. Представьте в алгебраической форме комплексное число
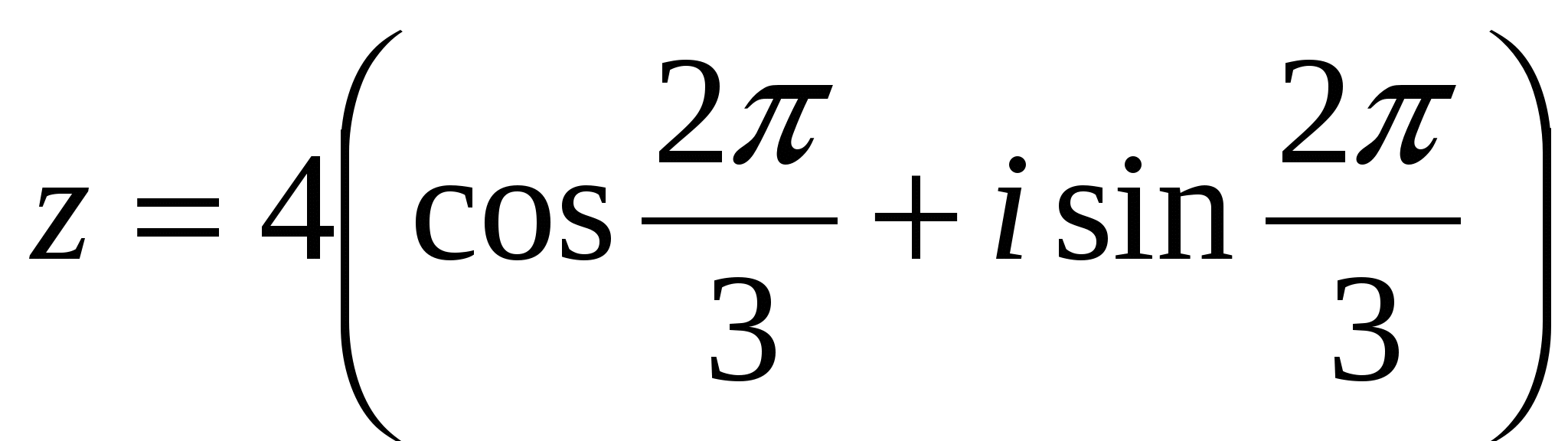
Вариант 2
1. Найдите действительную часть комплексного числа, если: z=(5+9·i)·(1+i)- 9 -3∙i.
2. Найдите разность 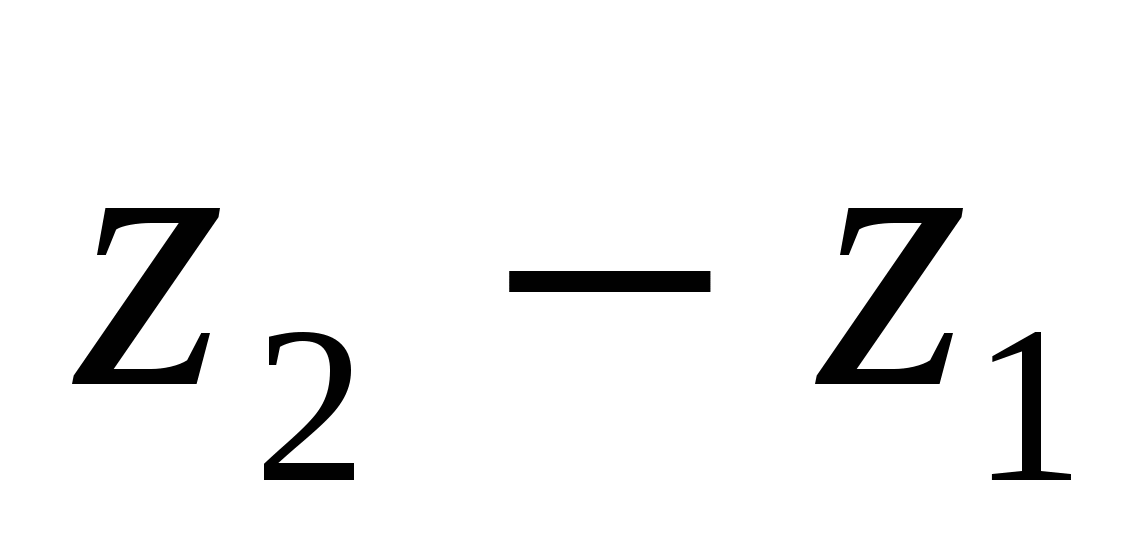
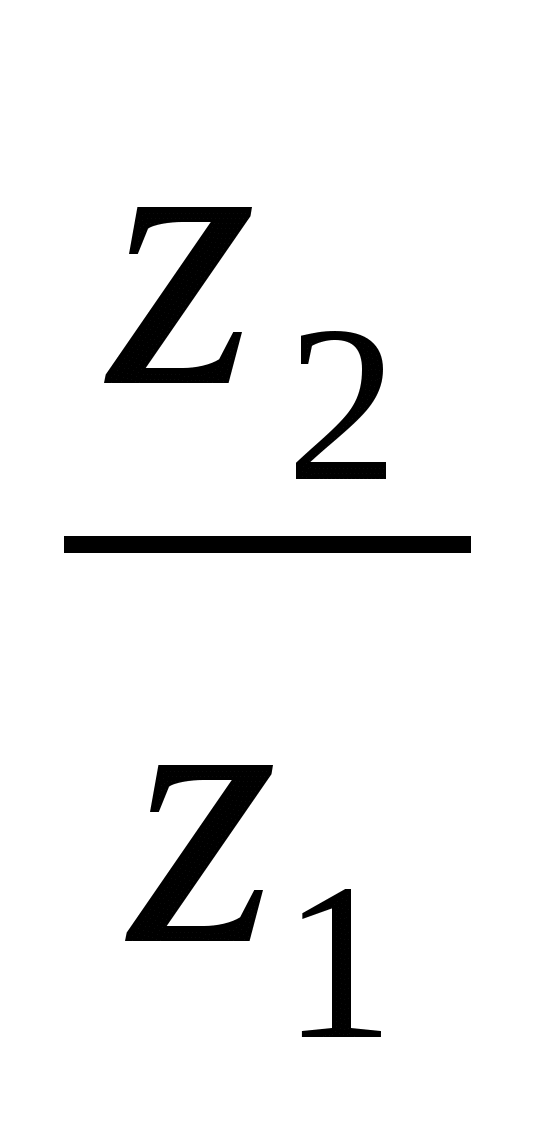
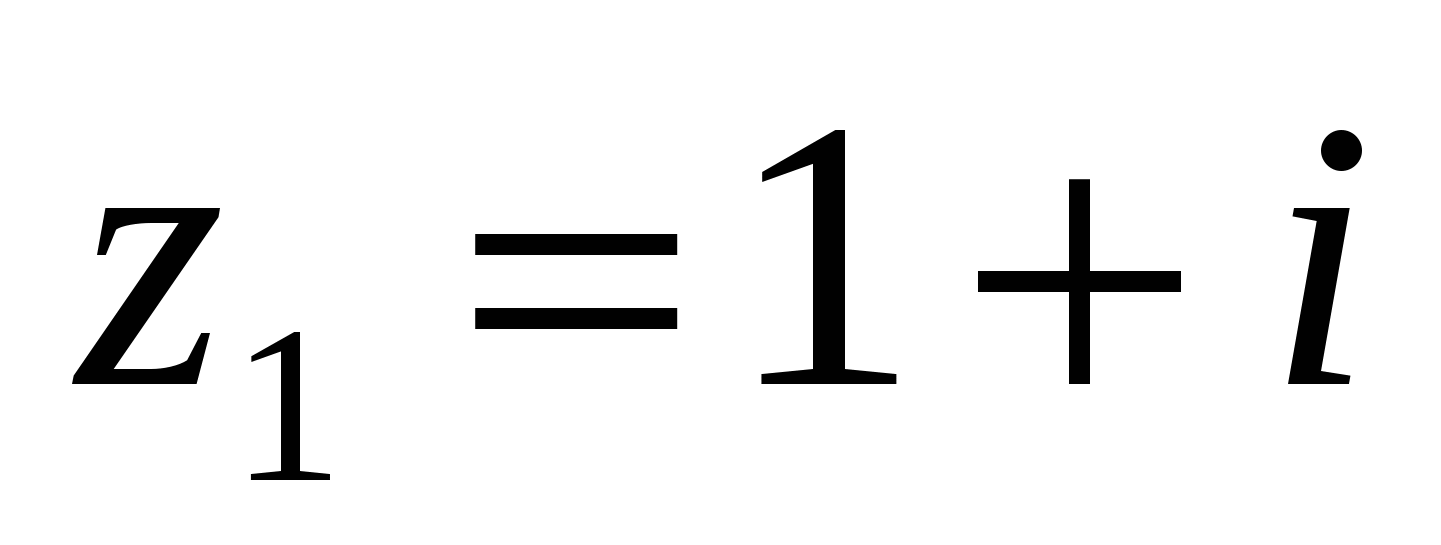
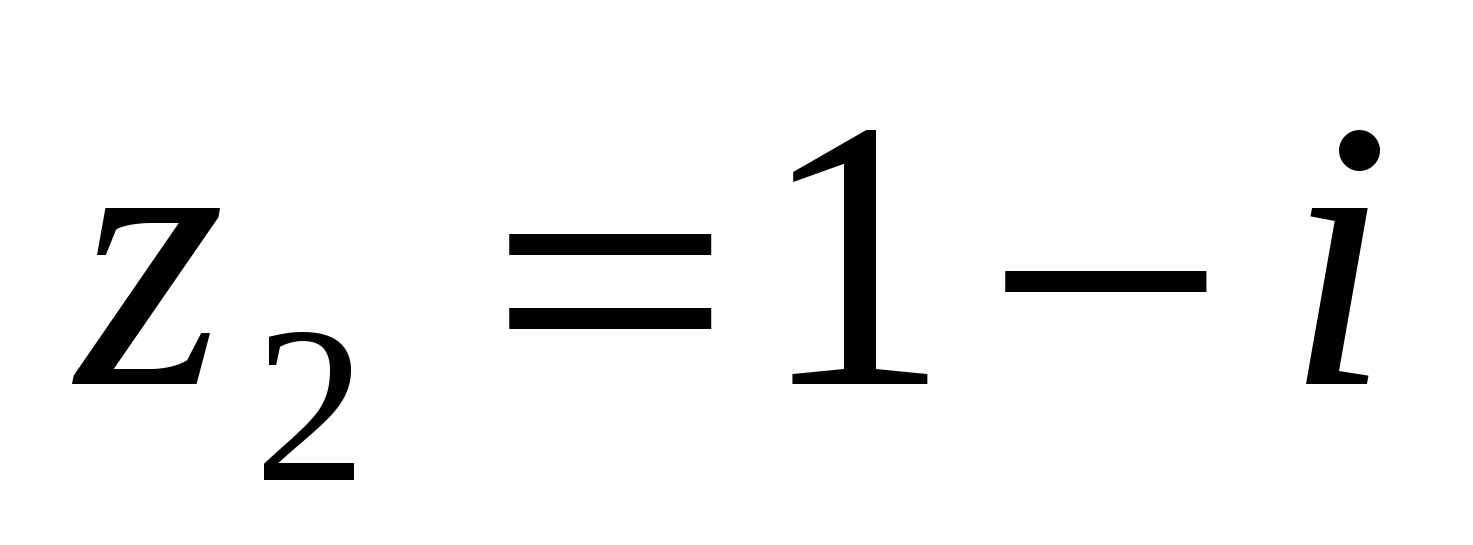
3. Постройте комплексное число в виде вектора 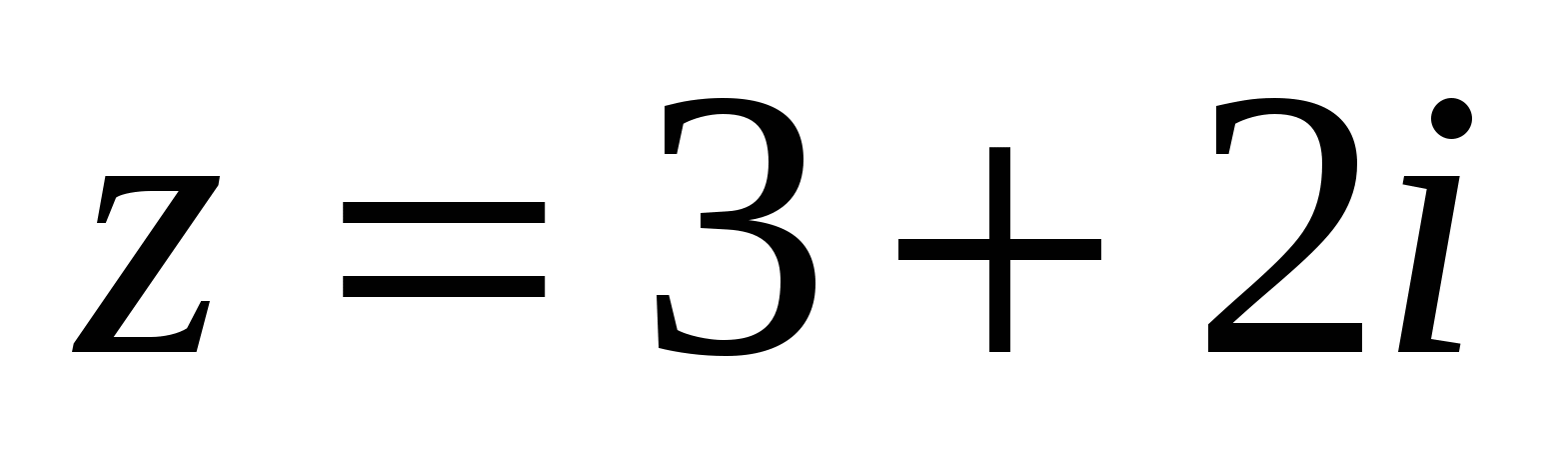
4. Представьте в тригонометрической форме комплексное число 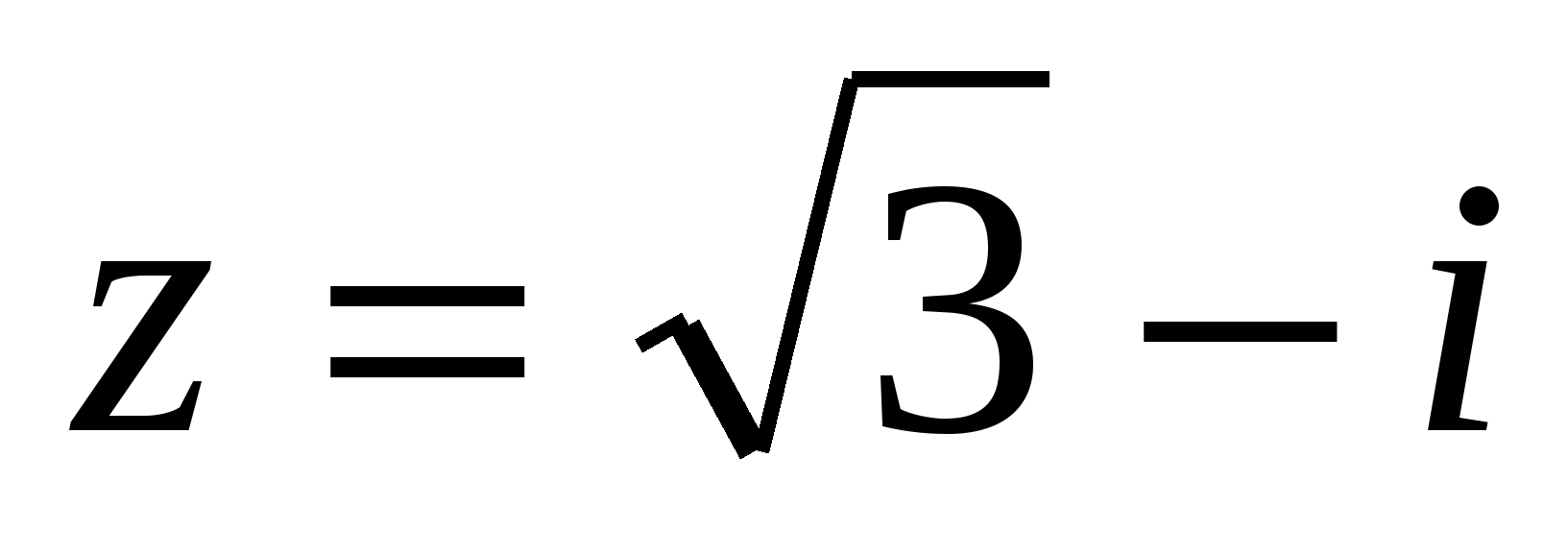
5. Представьте в алгебраической форме комплексное число
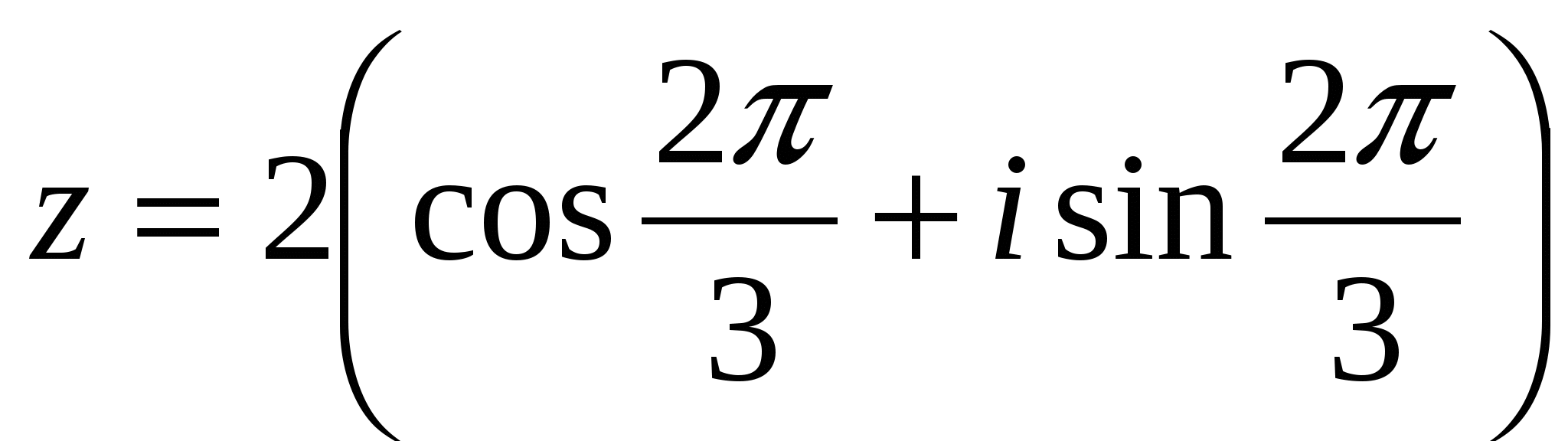
Проверочная работа по теме «Элементы теории пределов»
Время выполнения 45 минут
Вариант 1
-
Вычислить предел функции:

-
Вычислить предел функции:
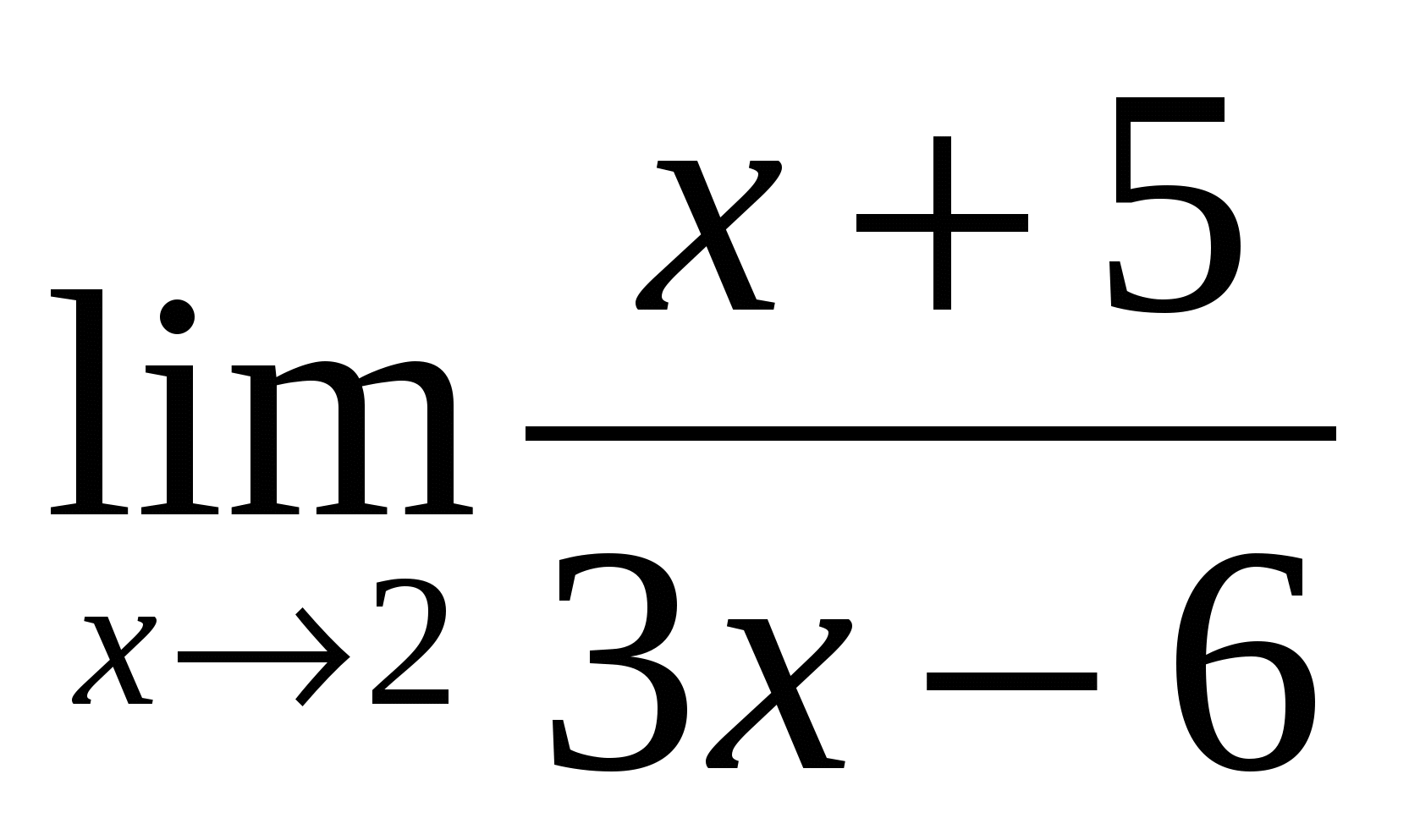
-
Вычислить предел функции:
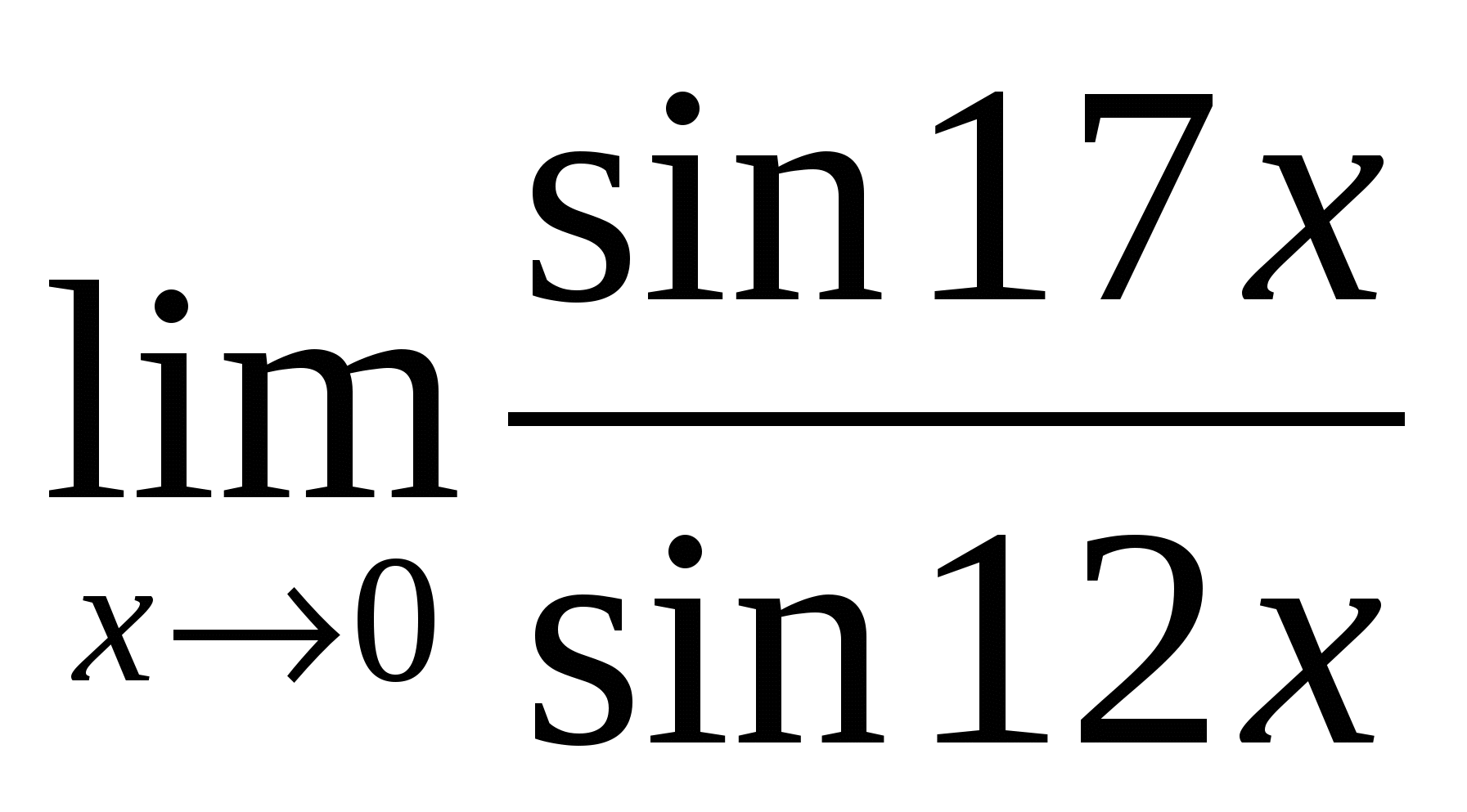
-
Вычислить предел функции:
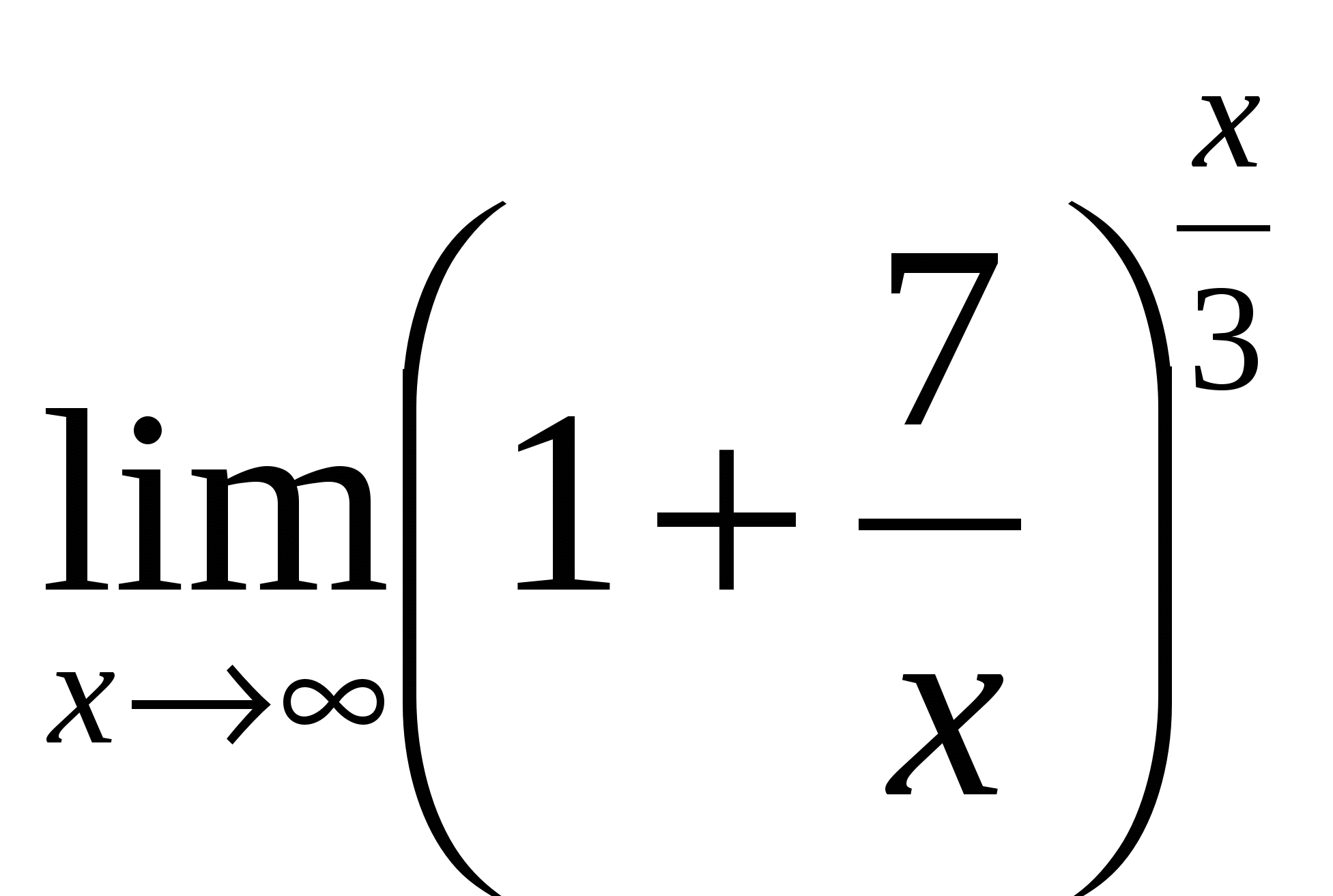
Вариант 2
-
Вычислить предел функции:
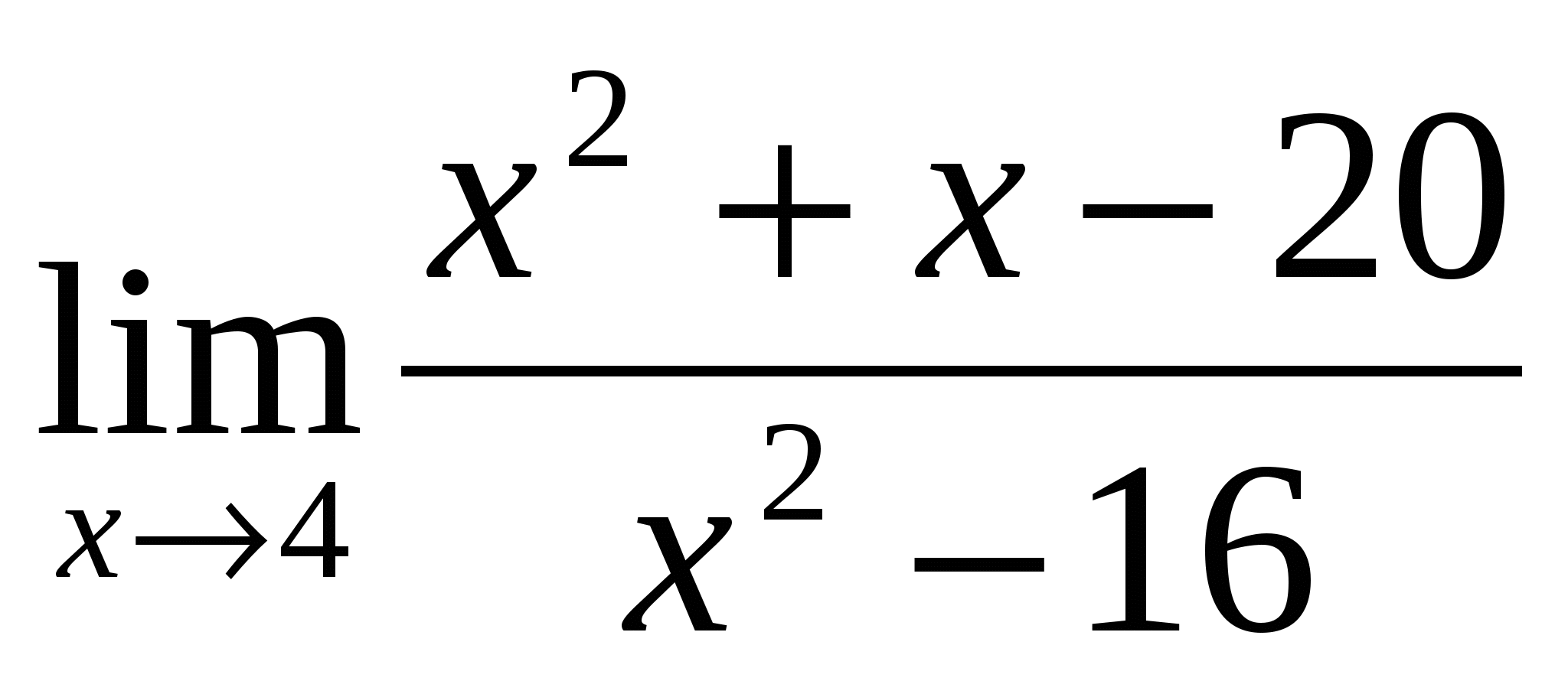
-
Вычислить предел функции:
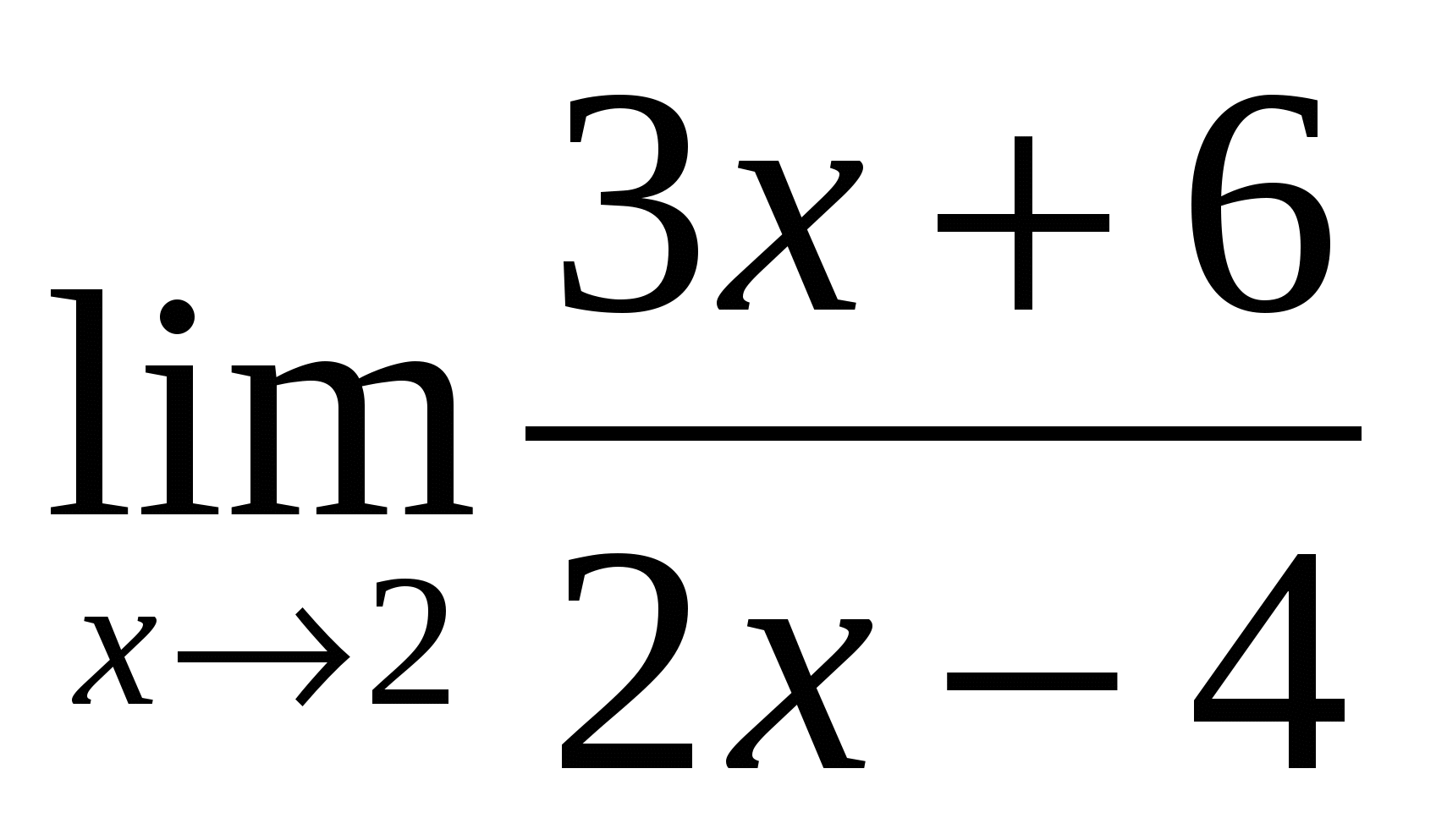
-
Вычислить предел функции:
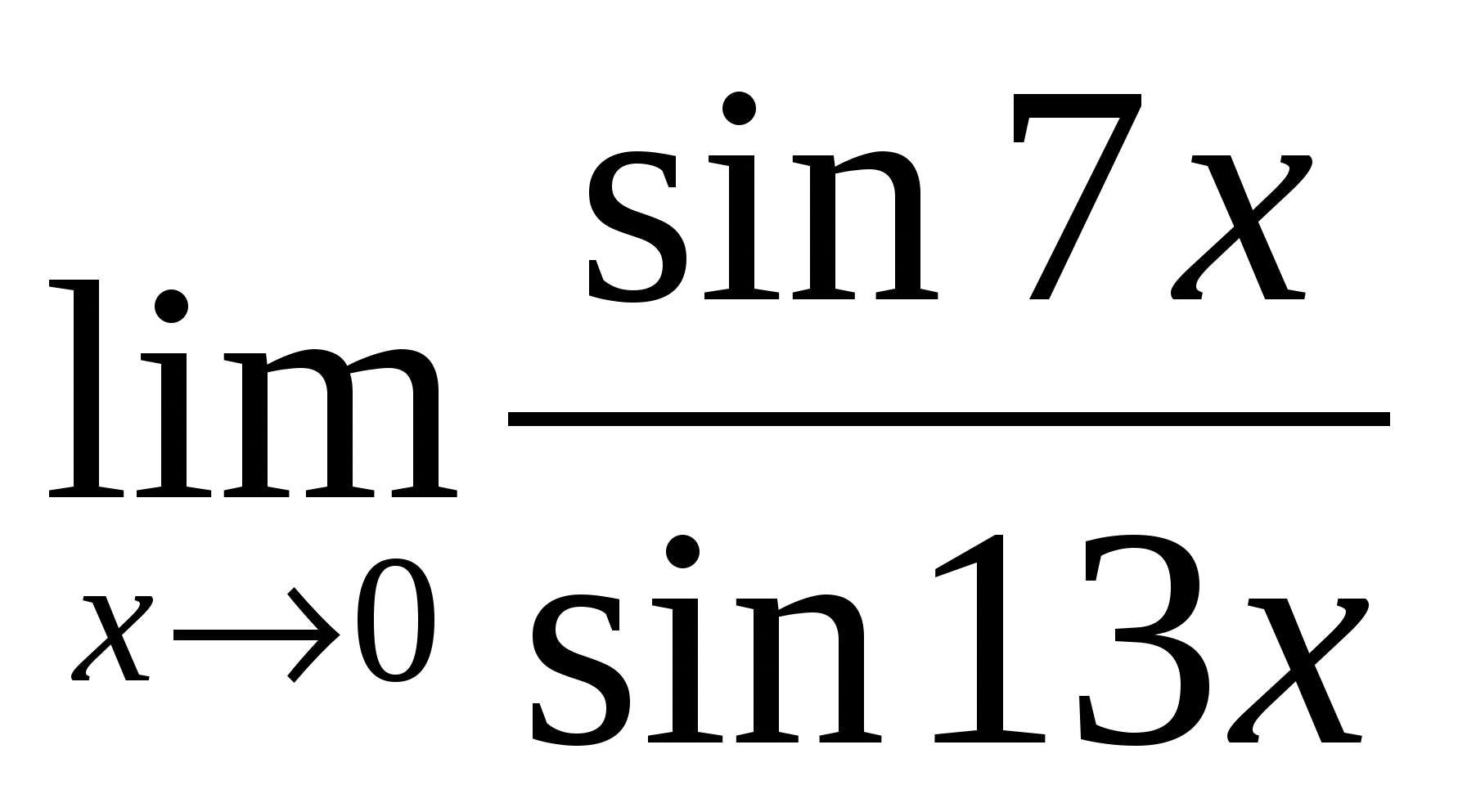
-
Вычислить предел функции:
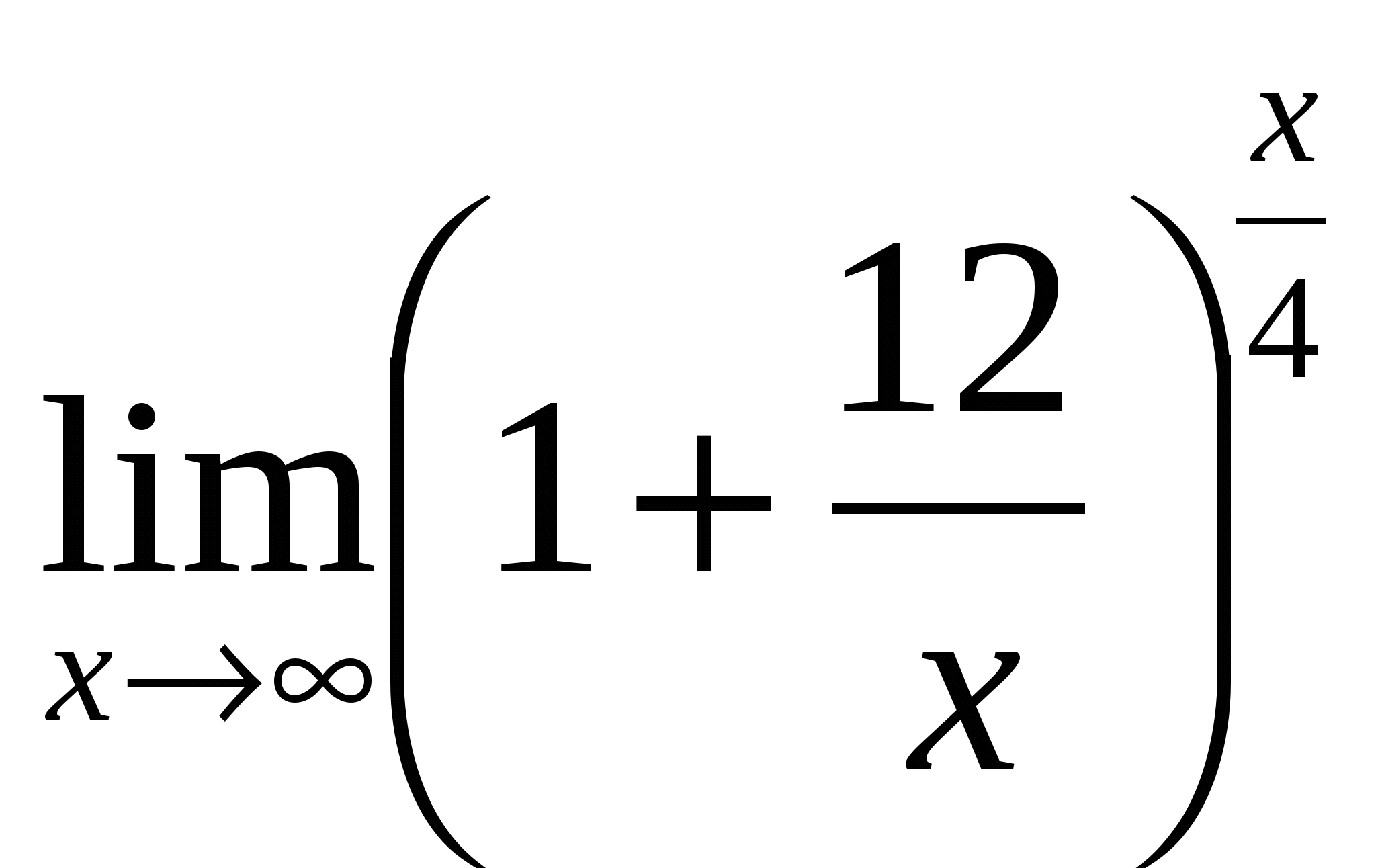
Вариант 3
-
Вычислить предел функции:
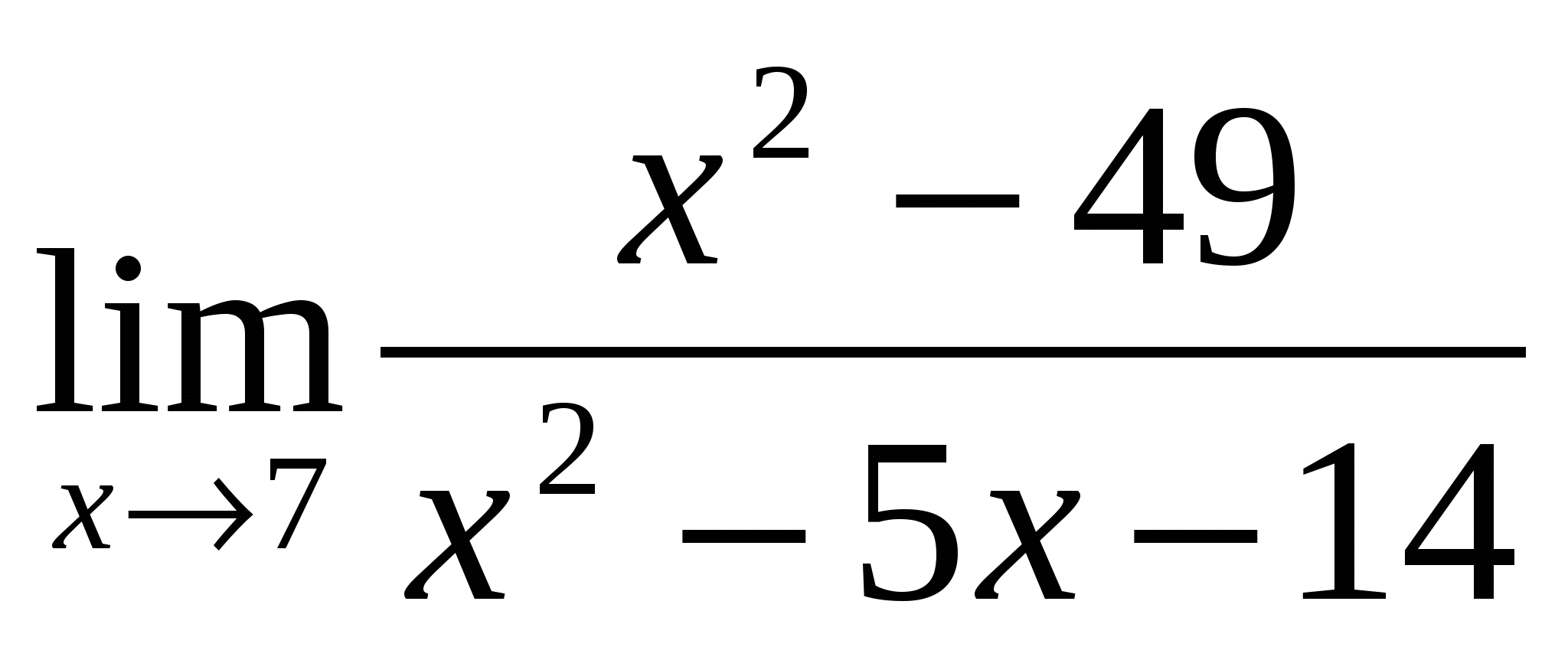
-
Вычислить предел функции:
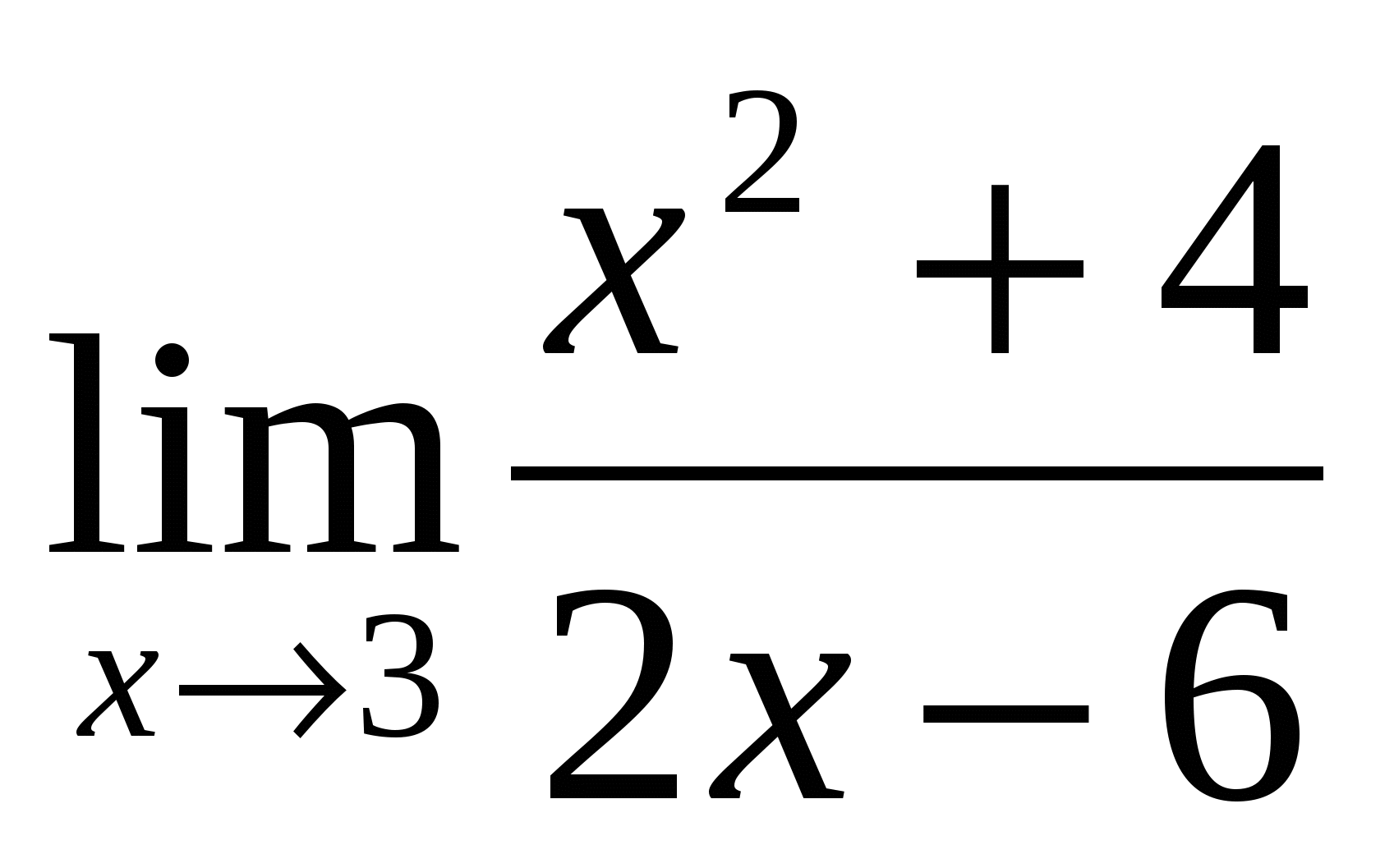
-
Вычислить предел функции:
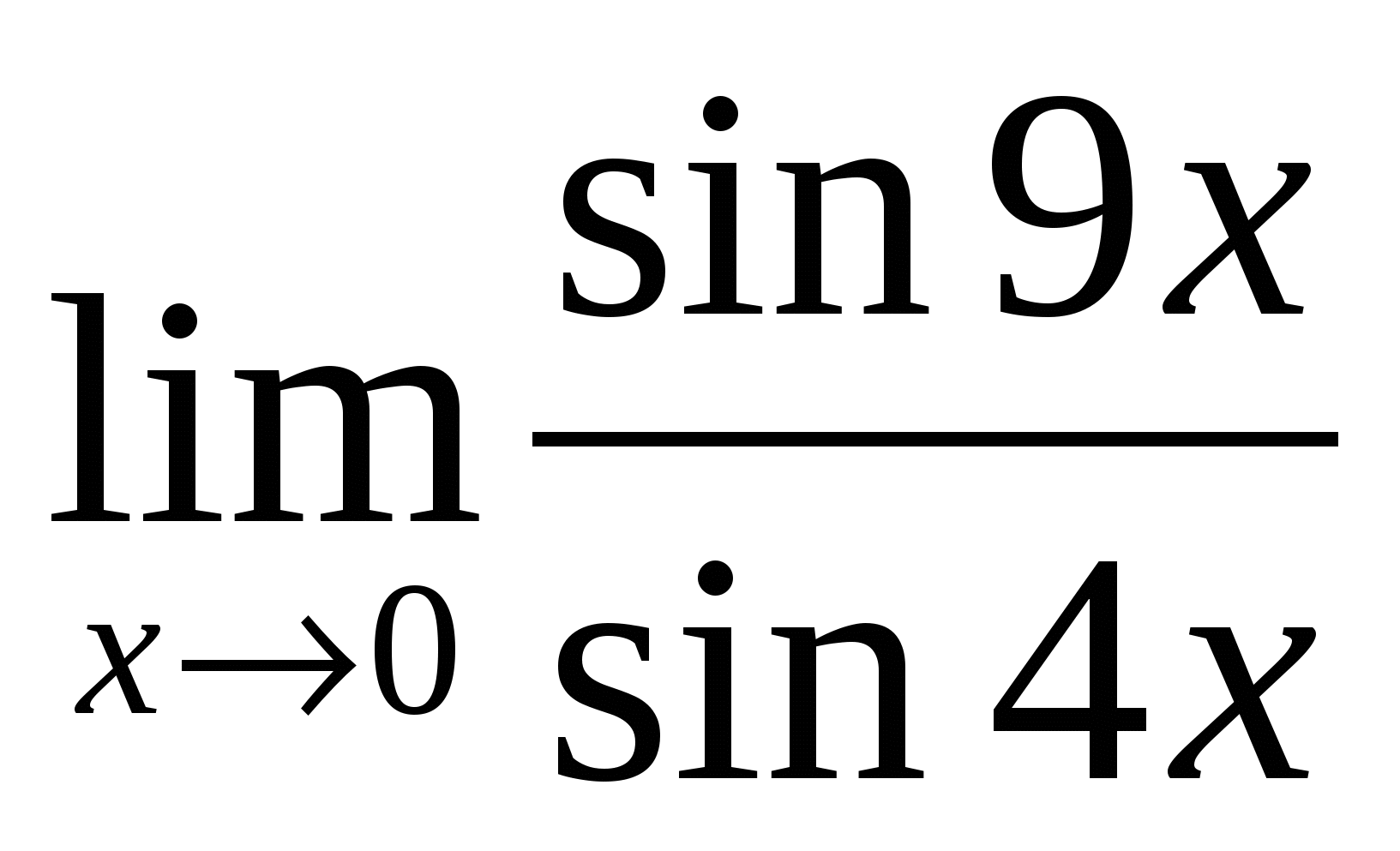
-
Вычислить предел функции:
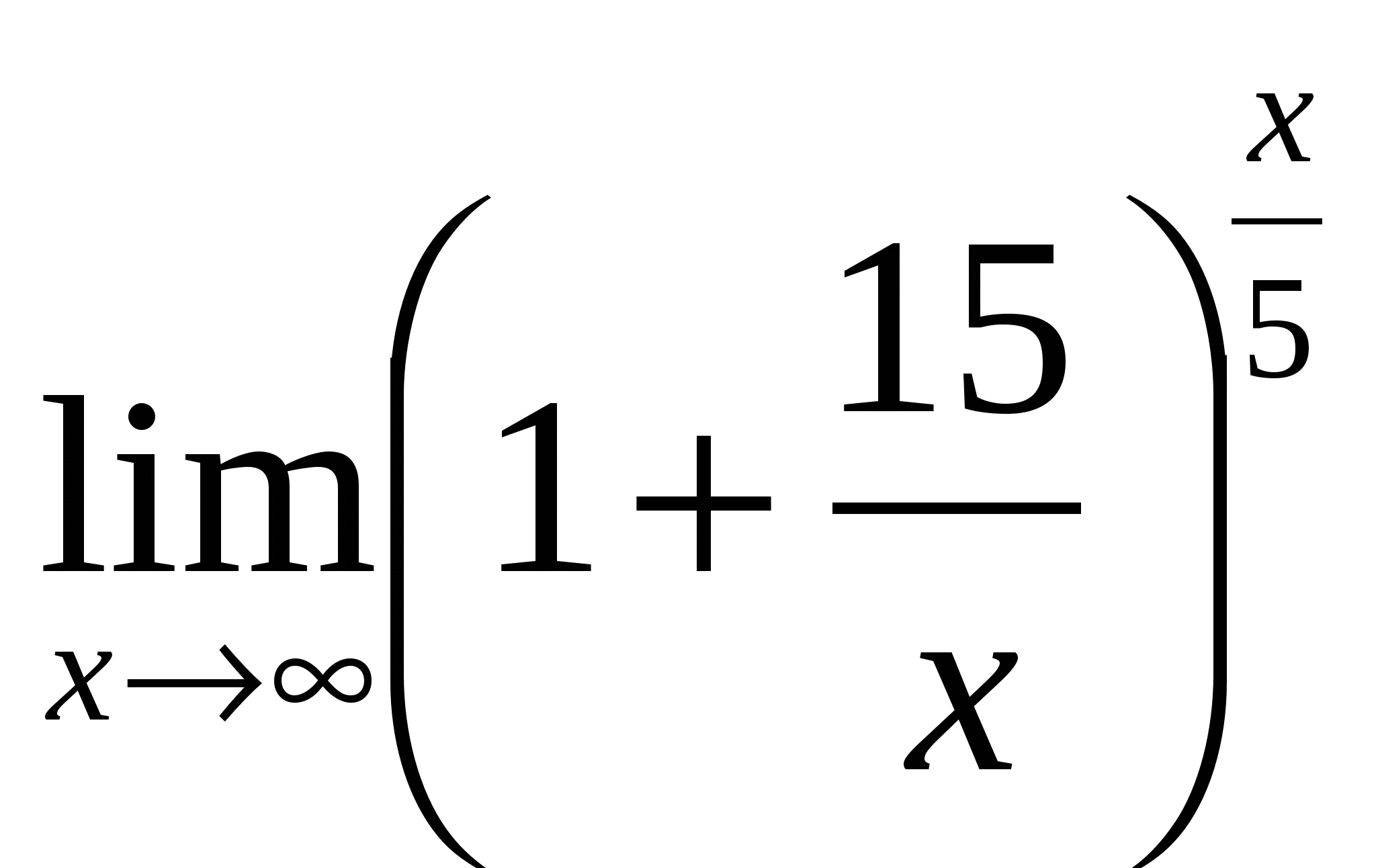
Вариант 4
-
Вычислить предел функции:
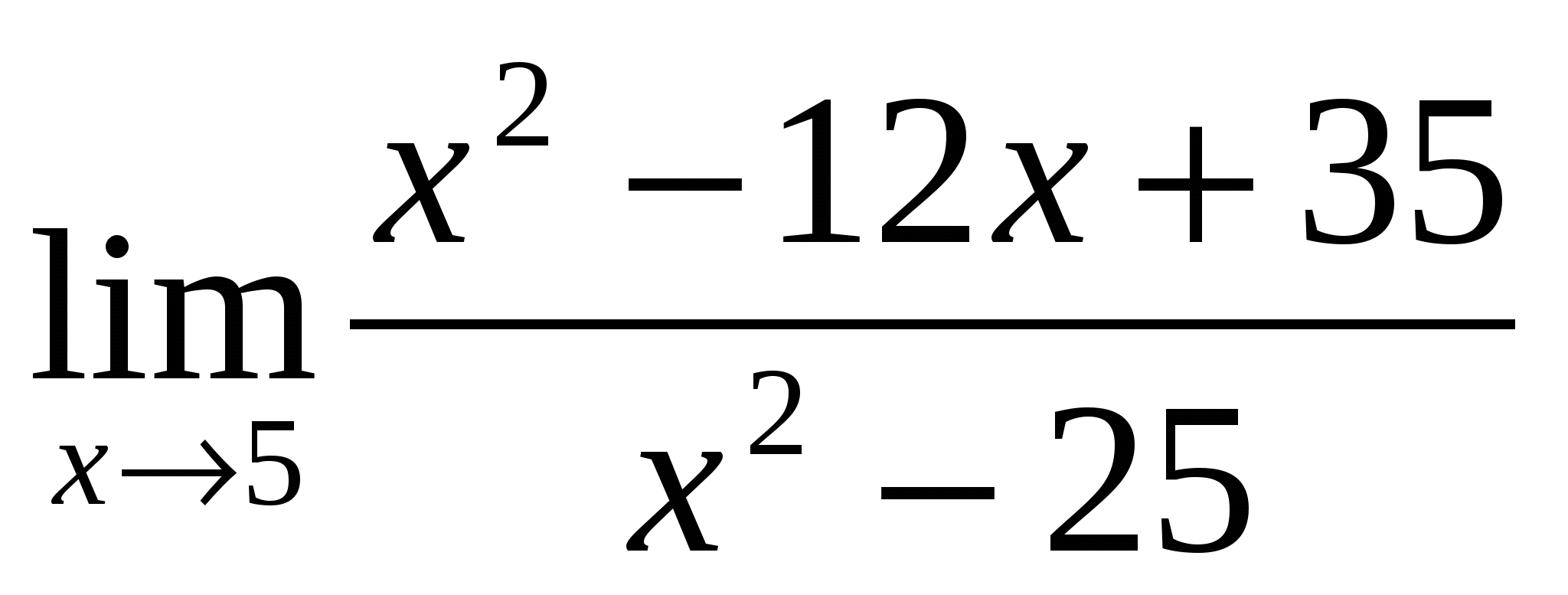
-
Вычислить предел функции:
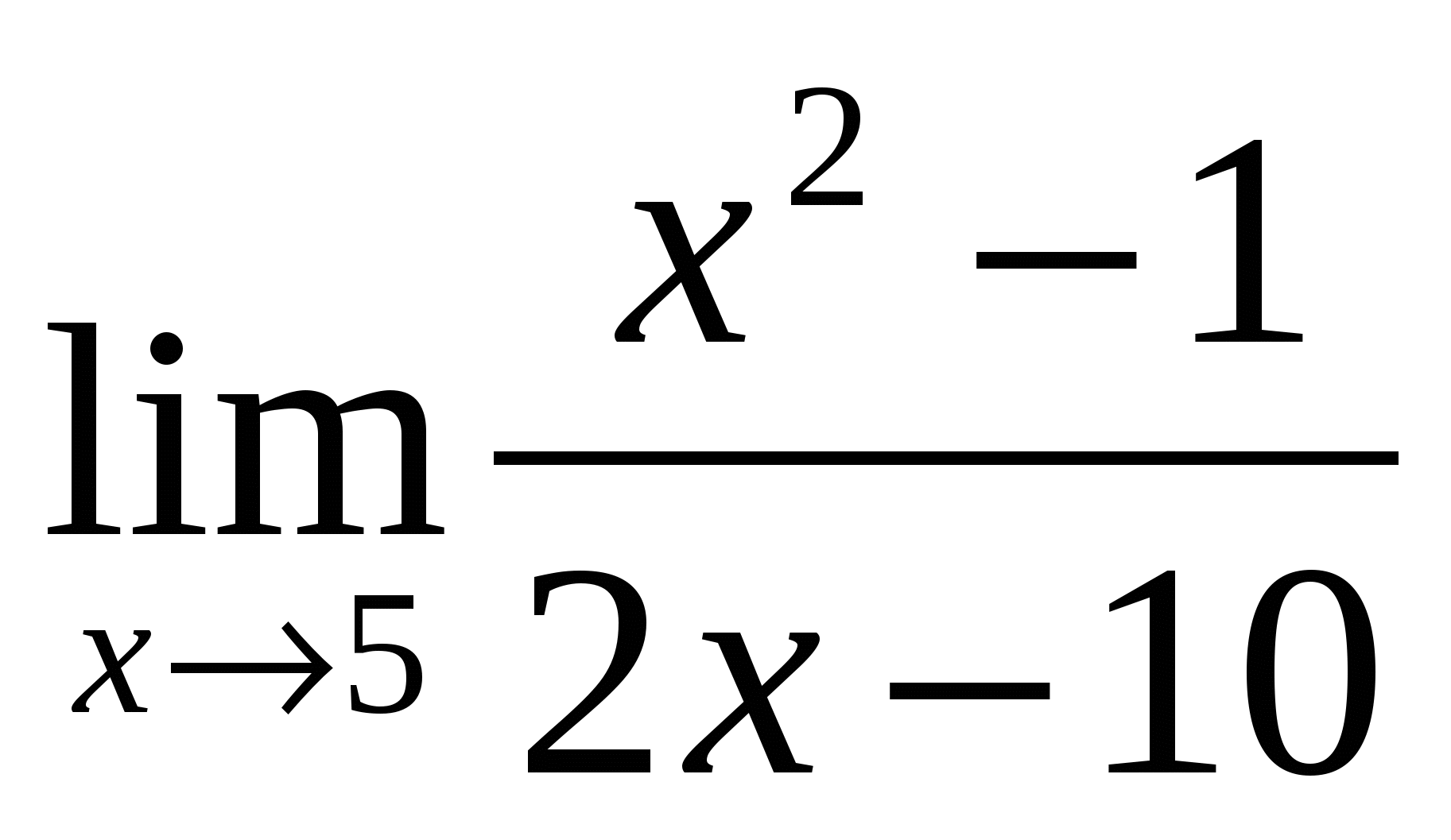
-
Вычислить предел функции:
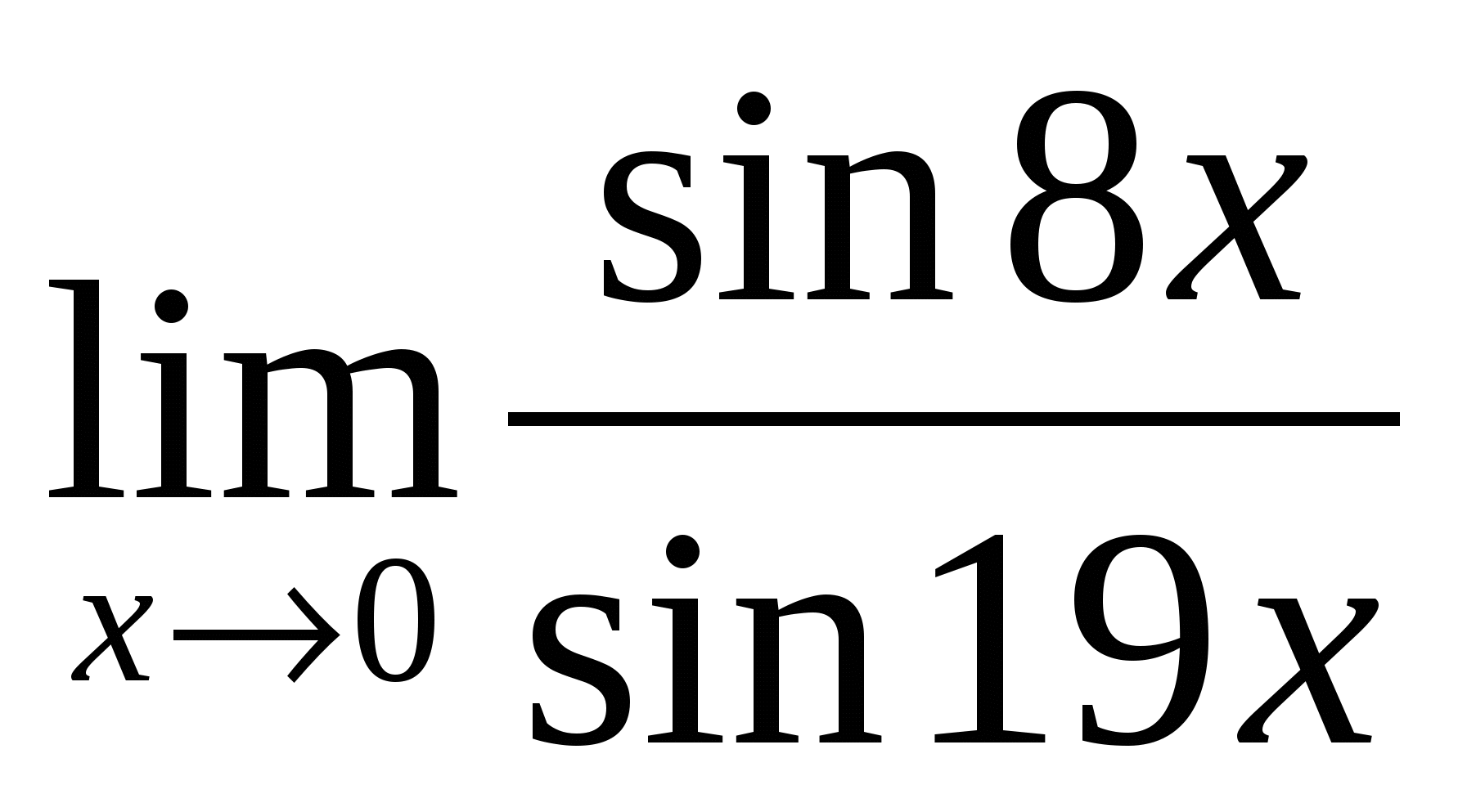
-
Вычислить предел функции:
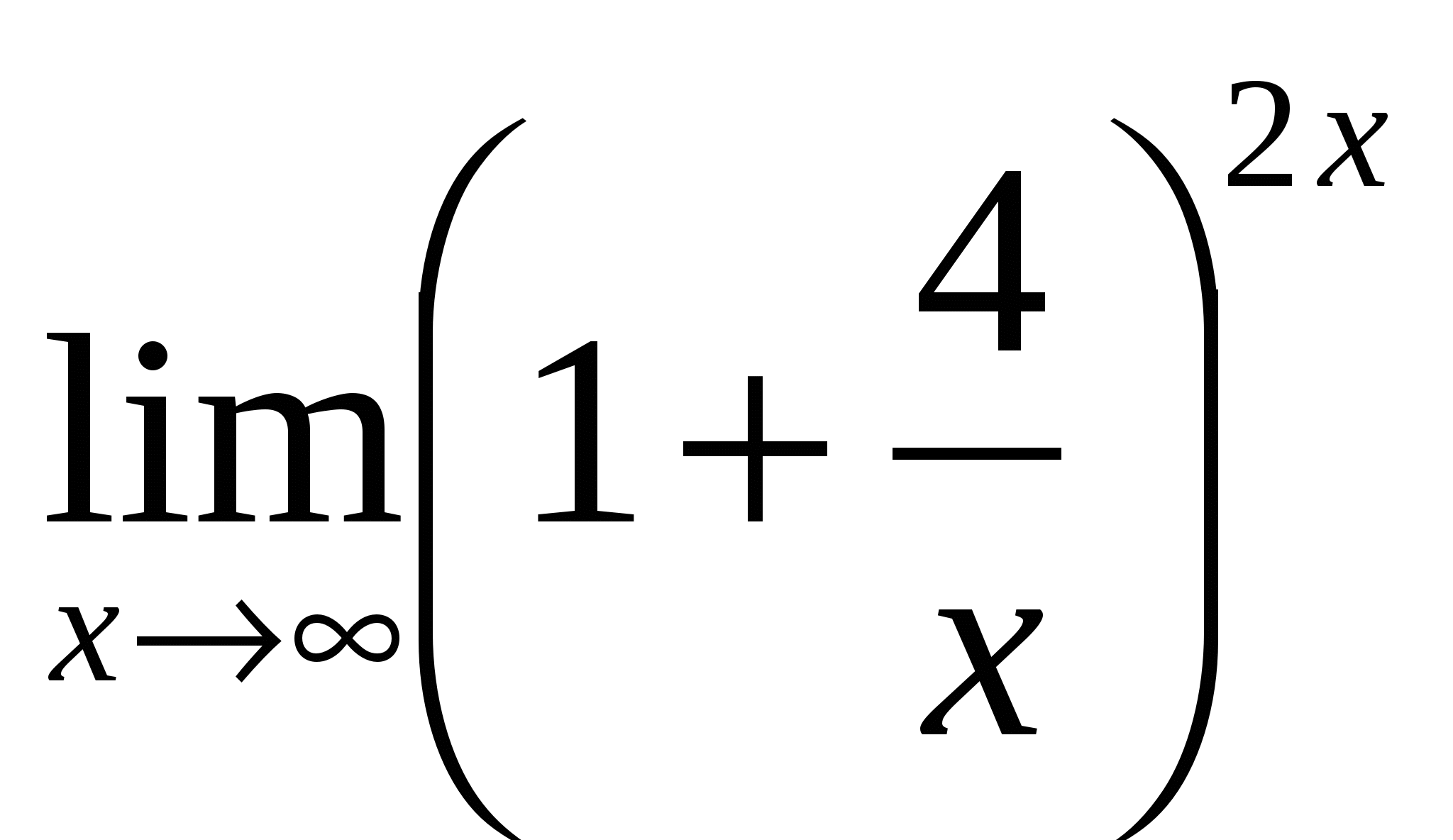
Вариант 5
-
Вычислить предел функции:
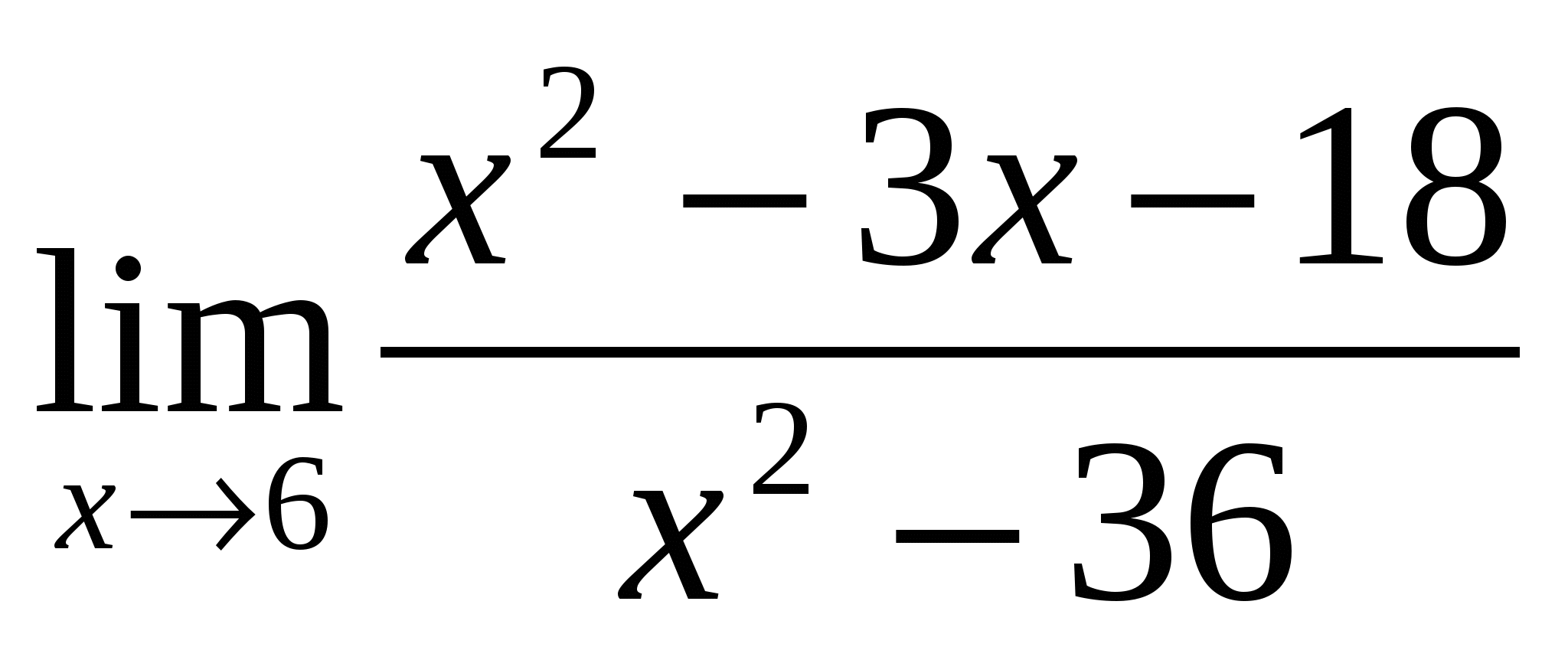
-
Вычислить предел функции:
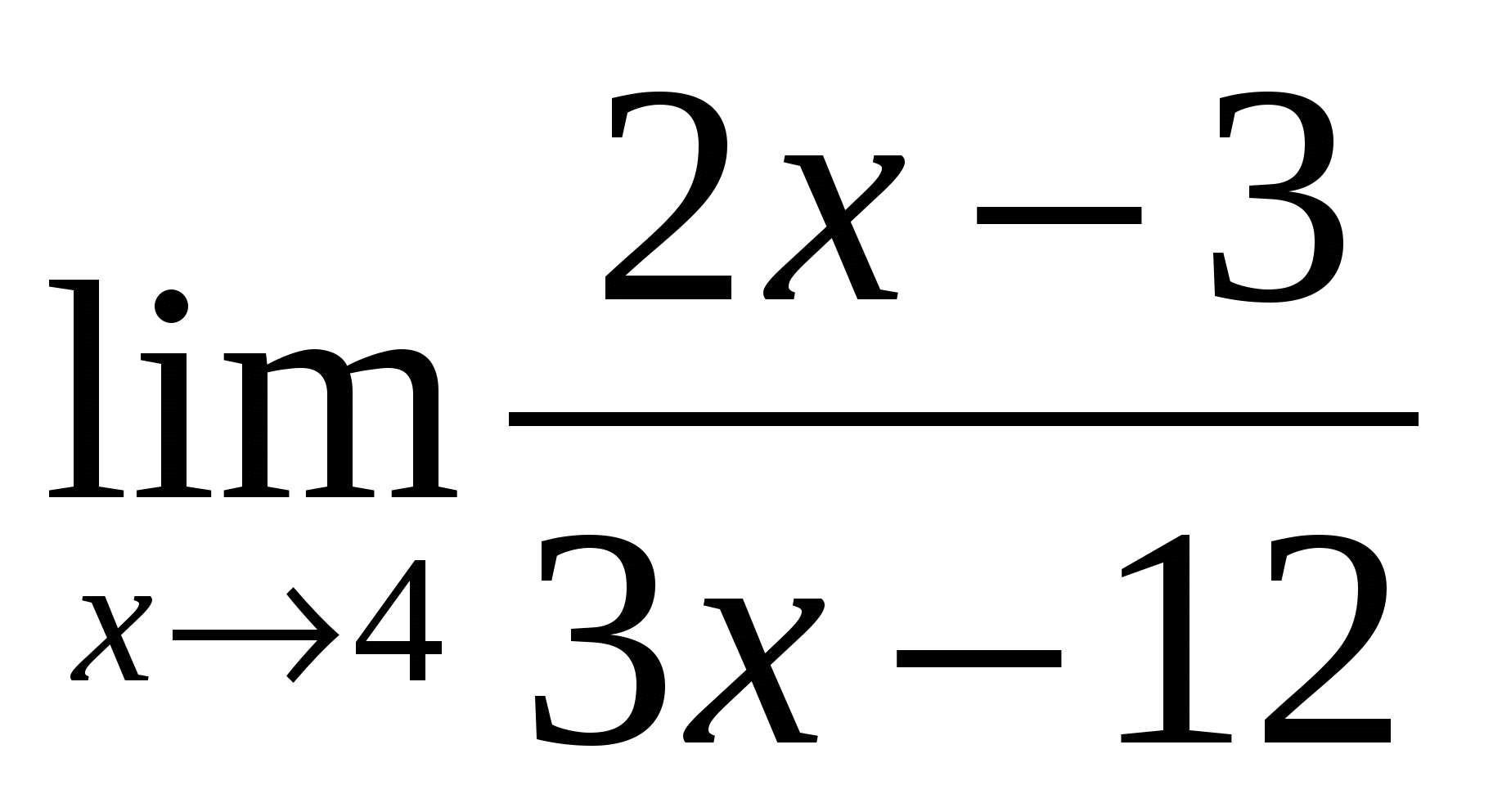
-
Вычислить предел функции:
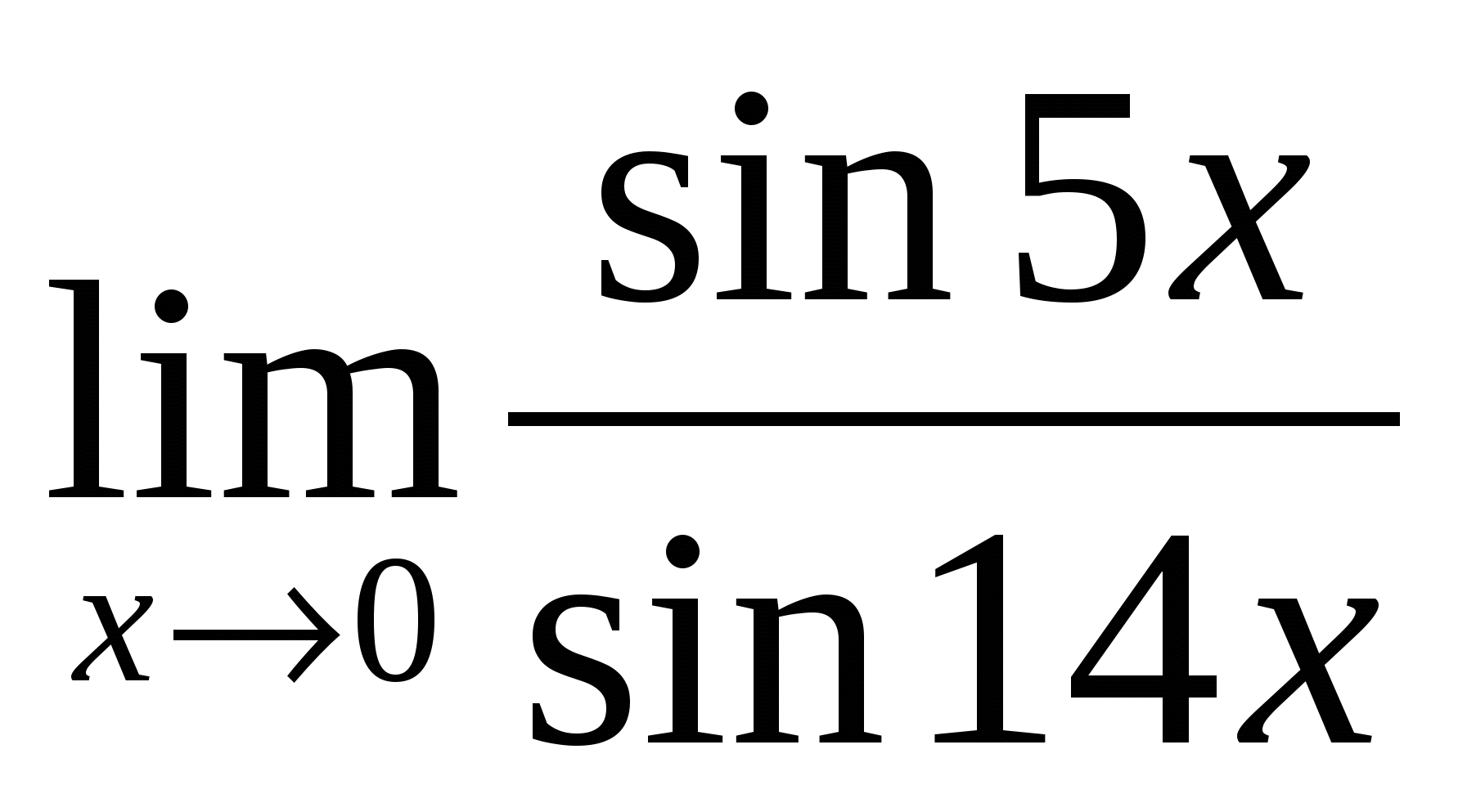
-
Вычислить предел функции:
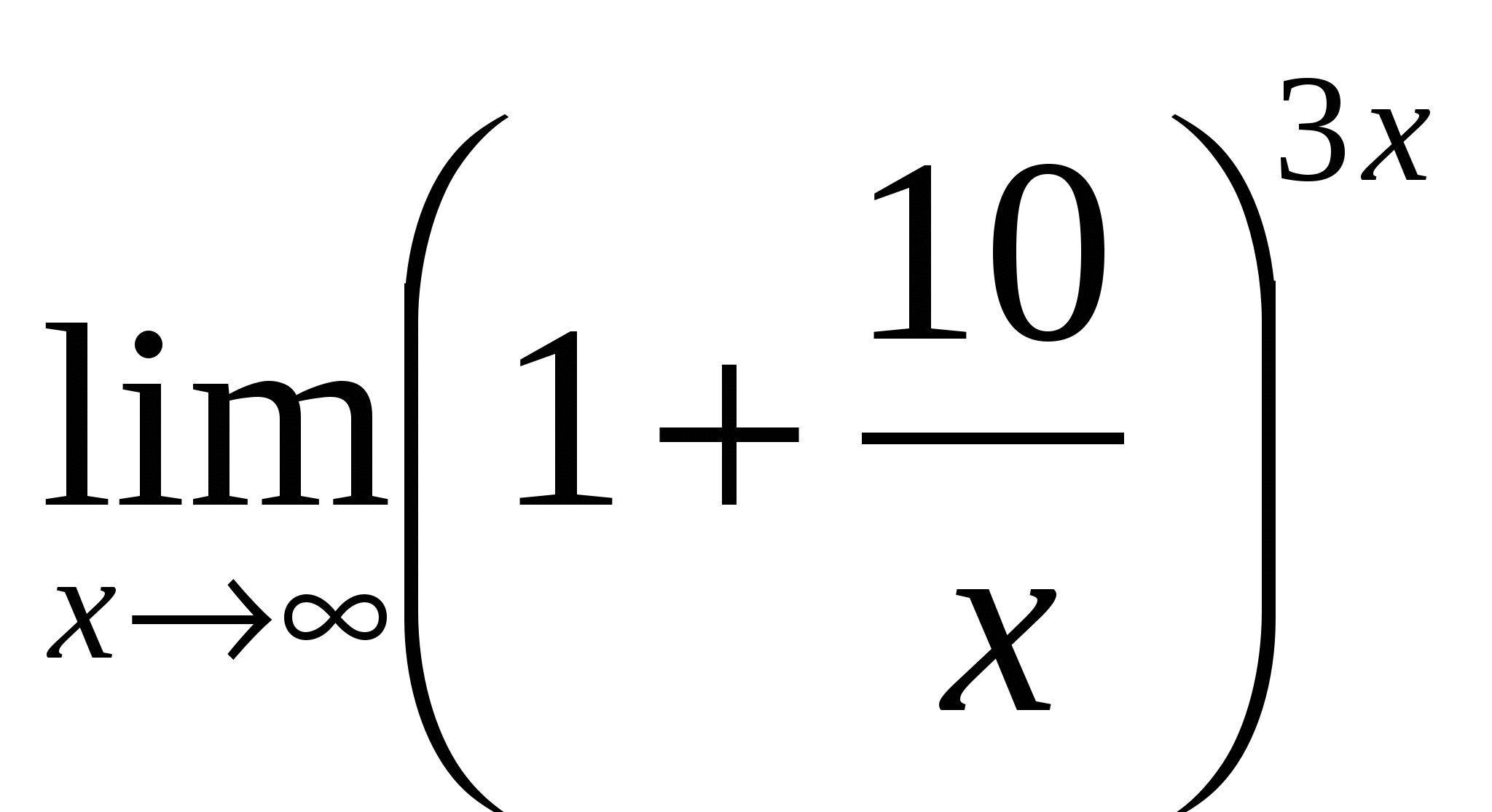
Вариант 6
-
Вычислить предел функции:
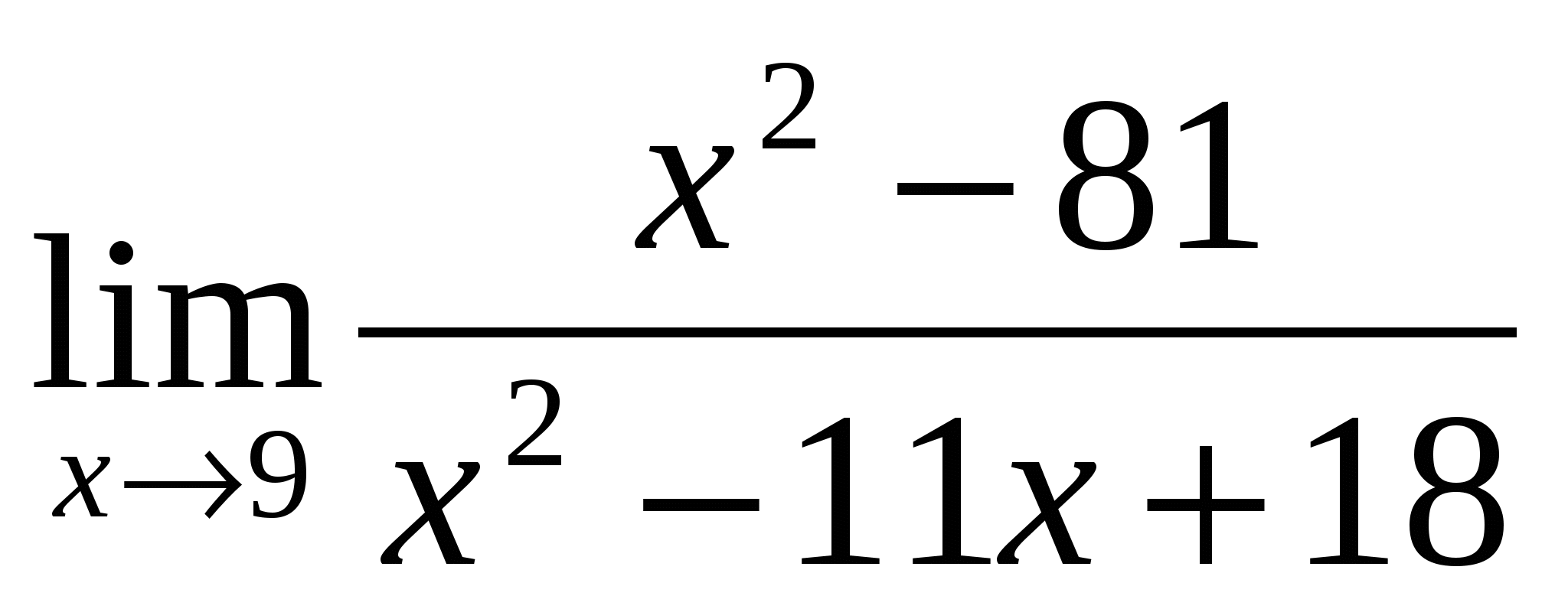
-
Вычислить предел функции:
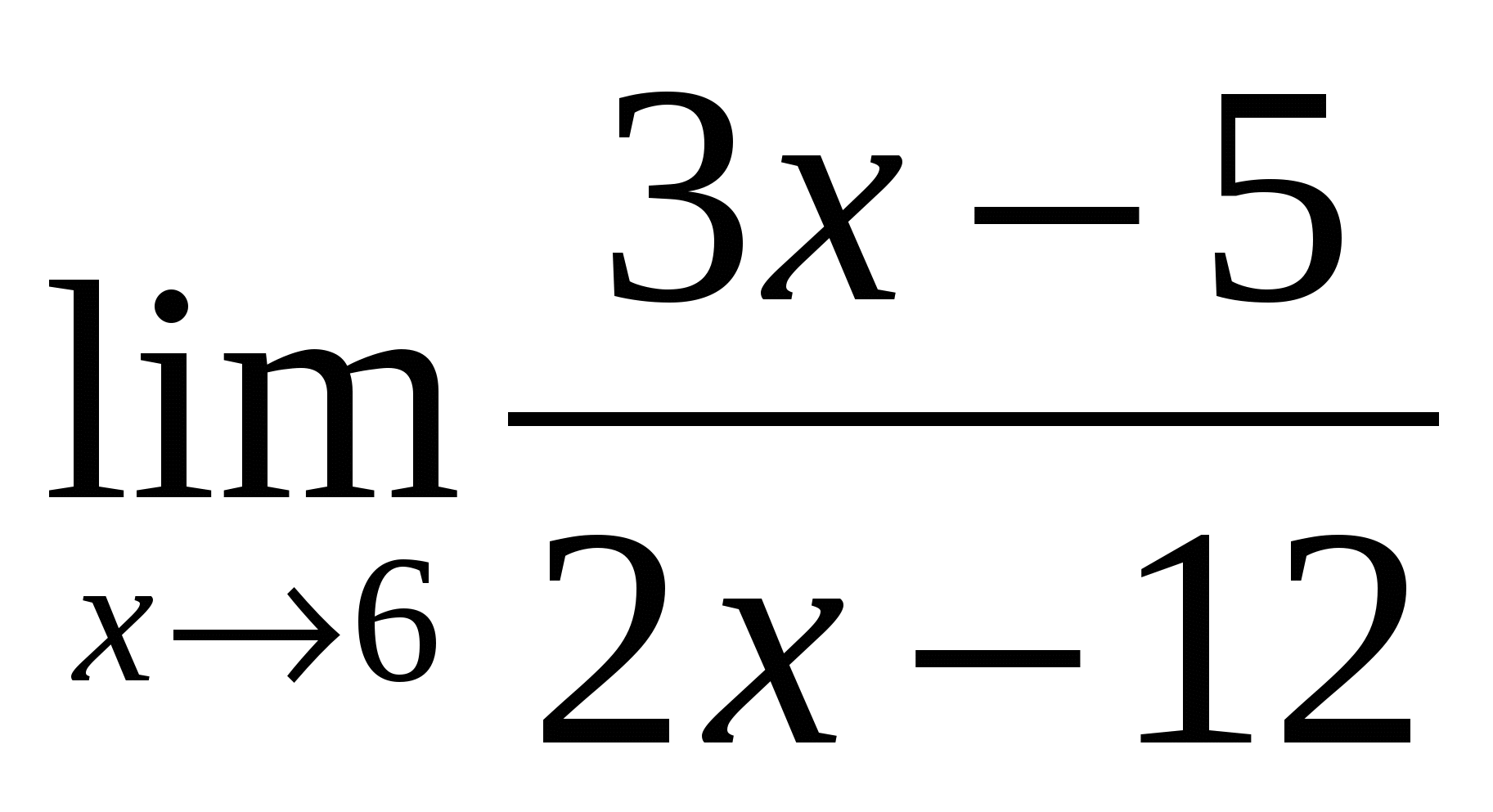
-
Вычислить предел функции:
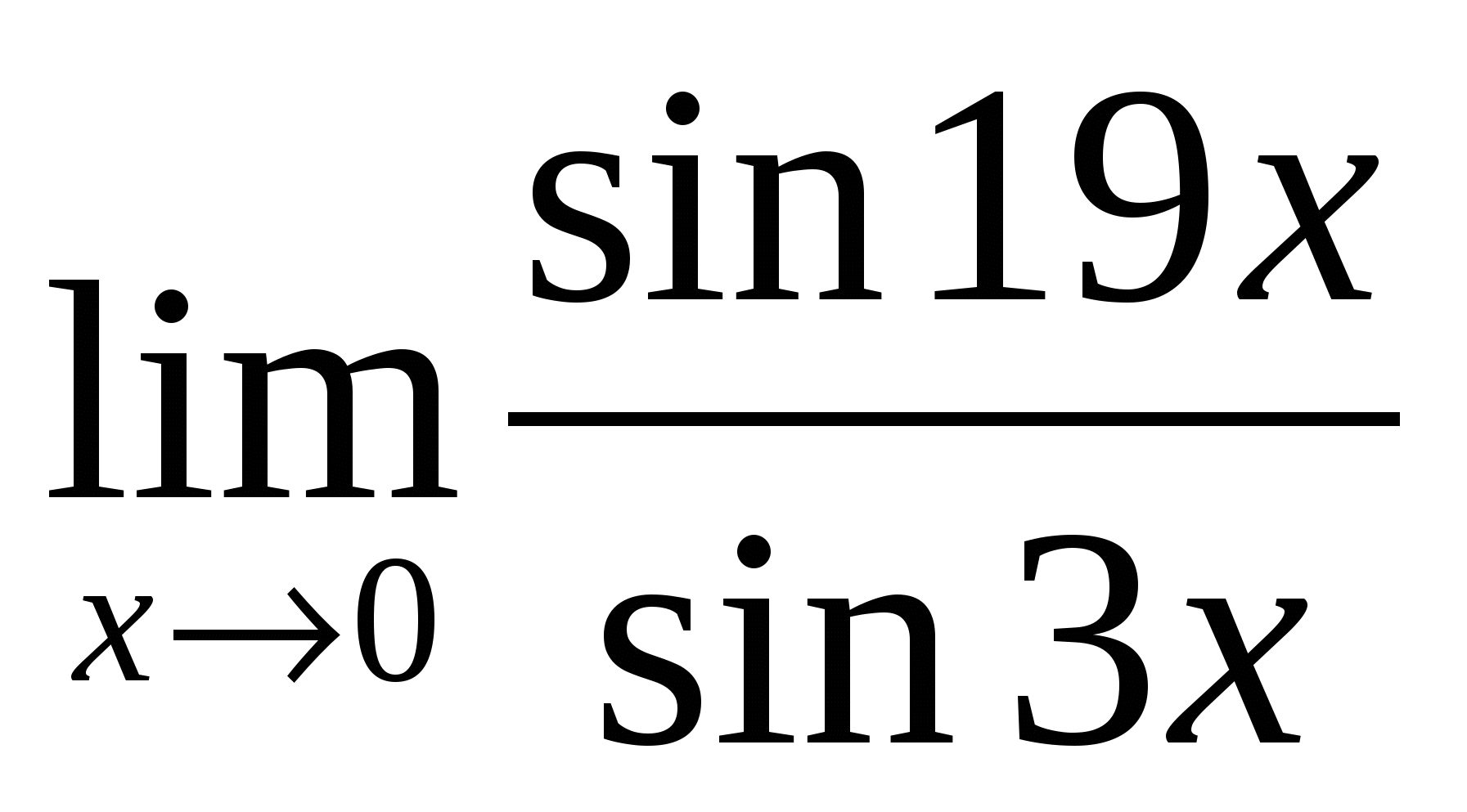
-
Вычислить предел функции:
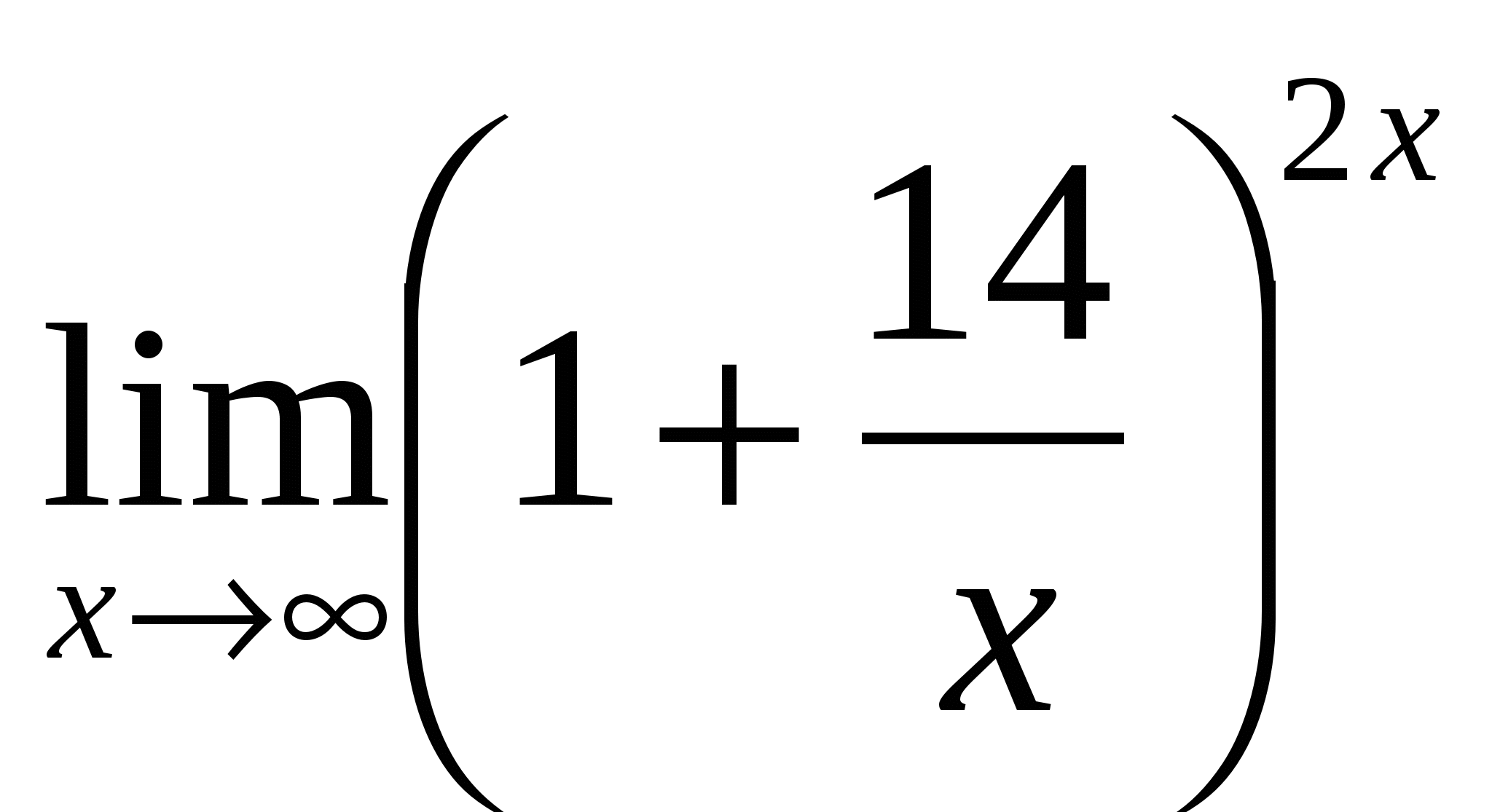
Проверочная работа 1 по теме « Дифференциальное исчисление функций одной переменной «
Правила вычисления производных. Производная сложной функции. Геометрический и физический смысл производной.
Время выполнения 45 минут
Вариант 1
-
Найти производную функции
.
-
Найти производную третьего порядка функции
.
-
Написать уравнение касательной к графику функции
в точке с абсциссой
,
.
-
Материальная точка движется по закону
. Найти скорость и ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.)
Вариант 2
-
Найти производную функции
.
-
Найти производную третьего порядка функции
.
-
Написать уравнение касательной к графику функции
в точке с абсциссой
,
.
-
Материальная точка движется по закону
. Найти скорость и ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.)
Вариант 3
-
Найти производную функции
.
-
Найти производную третьего порядка функции
.
-
Написать уравнение касательной к графику функции
в точке с абсциссой
,
.
-
Материальная точка движется по закону
. Найти скорость и ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.)
Вариант 4
-
Найти производную функции
.
-
Найти производную третьего порядка функции
.
-
Написать уравнение касательной к графику функции
в точке с абсциссой
,
.
-
Материальная точка движется по закону
. Найти скорость и ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.)
Вариант 5
-
Найти производную функции
.
-
Найти производную третьего порядка функции
.
-
Написать уравнение касательной к графику функции
в точке с абсциссой
,
.
-
Материальная точка движется по закону
. Найти скорость и ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.)
Вариант 6
-
Найти производную функции
.
-
Найти производную третьего порядка функции
.
-
Написать уравнение касательной к графику функции
в точке с абсциссой
,
.
-
Материальная точка движется по закону
. Найти скорость и ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.)
Проверочная работа 2 по теме « Дифференциальное исчисление функций одной переменной»
Исследование функций с помощью производной
Время выполнения 45 минут
Исследовать функцию с помощью первой производной и построить ее график.
Вариант 1
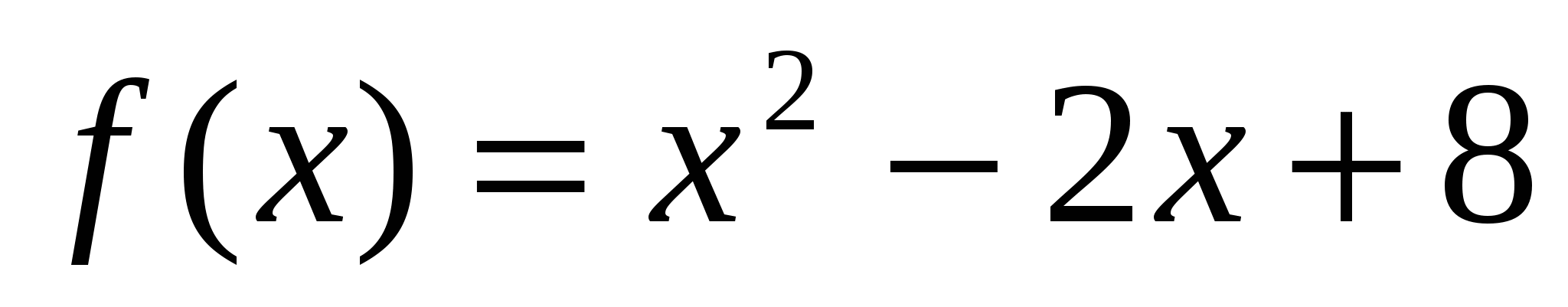
Вариант 2
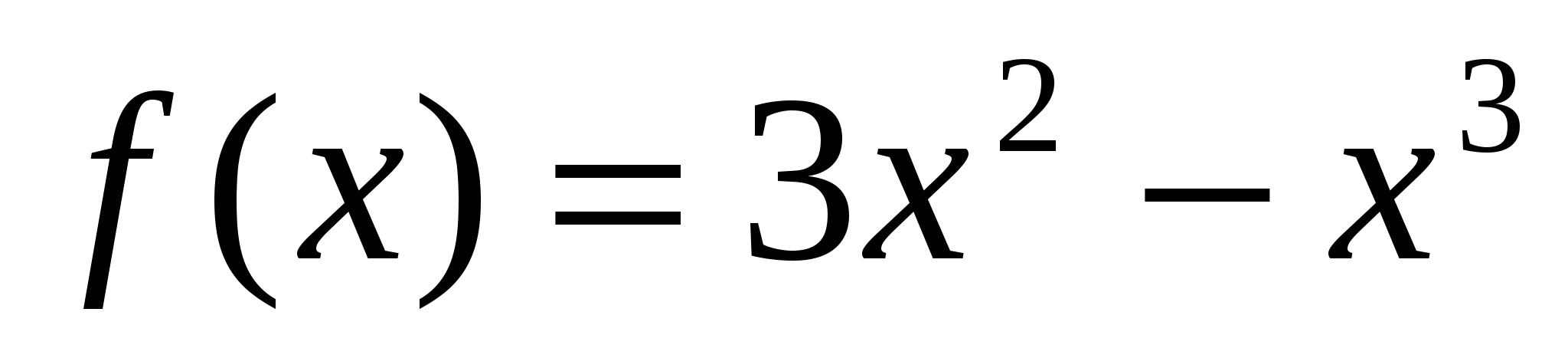
Вариант 3
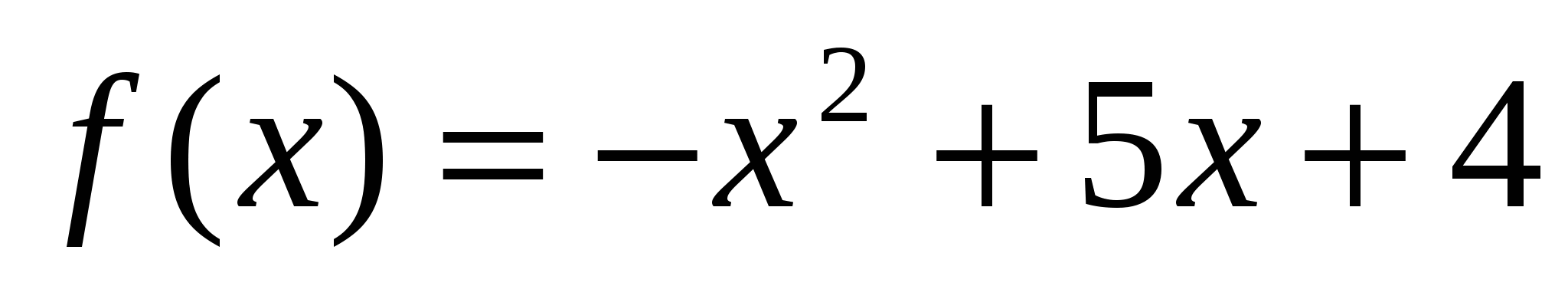
Вариант 4
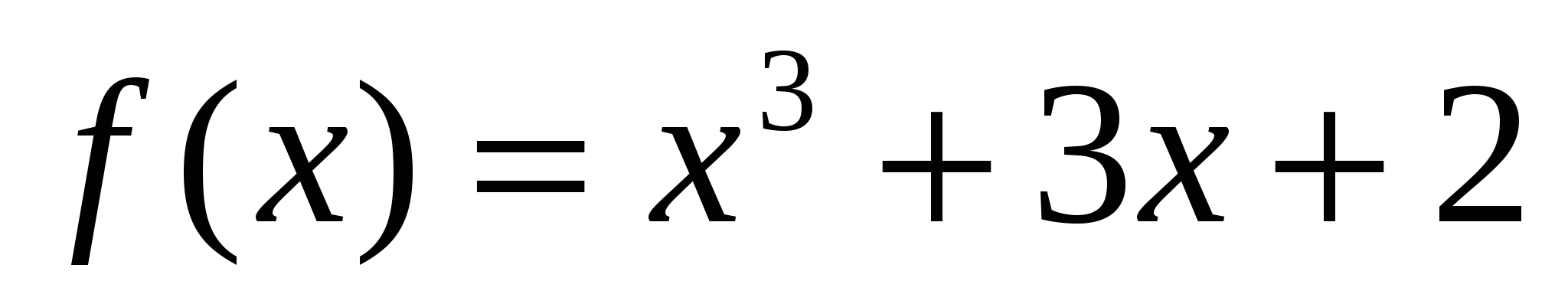
Вариант 5
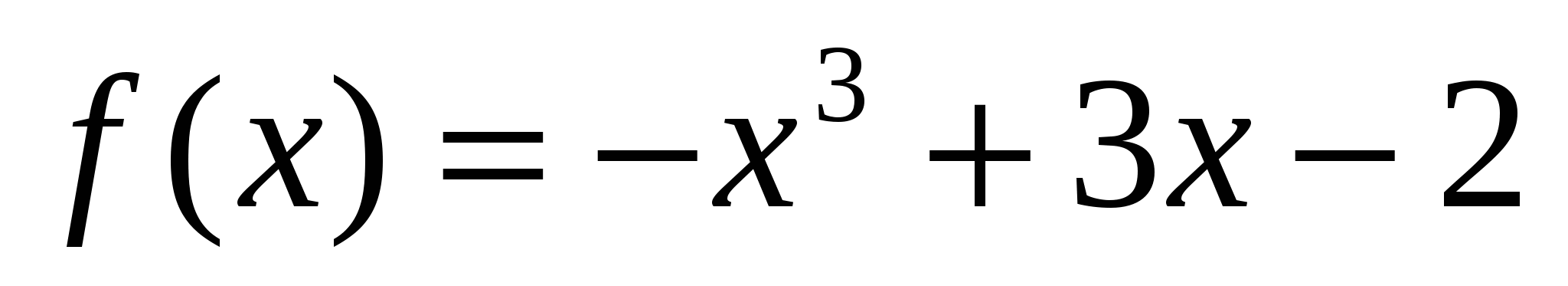
Вариант 6
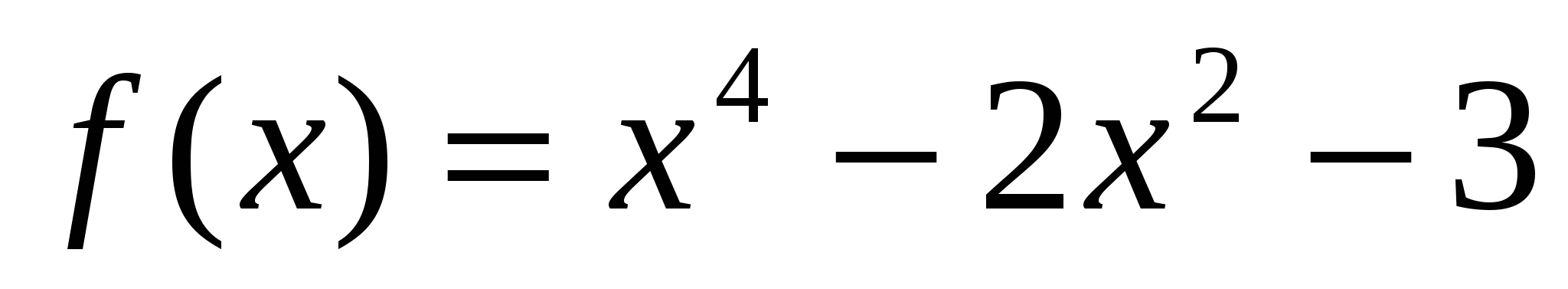
Проверочная работа по теме «Интегральное исчисление функций одной переменной»
Время выполнения 45 минут
Вариант 1
-
Вычислить определенный интеграл:
.
-
Вычислить определенный интеграл:
.
-
Вычислить, предварительно сделав рисунок, площадь фигуры, ограниченной линиями:
.
-
Найти объем тела, полученного при вращении вокруг оси абсцисс криволинейной трапеции, ограниченной линиями:
.
-
Скорость движения точки изменяется по закону
(м/с). Найти путь S, пройденный точкой за 10 с от начала движения.
Вариант 2
-
Вычислить определенный интеграл:
.
-
Вычислить определенный интеграл:
.
-
Вычислить, предварительно сделав рисунок, площадь фигуры, ограниченной линиями:
.
-
Найти объем тела, полученного при вращении вокруг оси абсцисс криволинейной трапеции, ограниченной линиями:
.
-
Скорость движения точки изменяется по закону
(м/с). Найти путь S, пройденный точкой за четвертую секунду.
Проверочная работа по теме «Элементы теории вероятностей»
Время выполнения 45 минут
Вариант 1
-
Из корзины, в которой находятся 4 белых и 7 черных шара, вынимают один шар. Найти вероятность того, что шар окажется черным.
-
Вероятность того, что батарейка бракованная, равна 0,06. Покупатель в магазине выбирает случайную упаковку, в которой две таких батарейки. Найдите вероятность того, что обе батарейки окажутся исправными.
-
Вероятность того, что в случайный момент времени температура тела здорового человека окажется ниже чем 36,8 °С, равна 0,81. Найдите вероятность того, что в случайный момент времени у здорового человека температура окажется 36,8 °С или выше.
-
Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 45% этих стекол, вторая — 55%. Первая фабрика выпускает 3% бракованных стекол, а вторая — 1%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.
-
торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.
Вариант 2
1. В корзине 20 шаров: 5 синих, 4 красных, остальные черные. Выбирают наудачу один шар. Определить, с какой вероятностью он будет цветным.
2. Какова вероятность того, что случайно выбранный телефонный номер оканчивается двумя чётными цифрами?
3. При изготовлении подшипников диаметром 67 мм вероятность того, что диаметр будет отличаться от заданного не больше, чем на 0,01 мм, равна 0,965. Найдите вероятность того, что случайный подшипник будет иметь диаметр меньше чем 66,99 мм или больше чем 67,01 мм.
4. Ковбой Джон попадает в муху на стене с вероятностью 0,9, если стреляет из пристрелянного револьвера. Если Джон стреляет из не пристрелянного револьвера, то он попадает в муху с вероятностью 0,2. На столе лежит 10 револьверов, из них только 4 пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнётся.
5. В магазине стоят два платёжных автомата. Каждый из них может быть неисправен с вероятностью 0,05 независимо от другого автомата. Найдите вероятность того, что хотя бы один автомат исправен.
Проверочная работа по теме «Координаты и векторы»
Время выполнения 45 минут
Вариант 1
Даны векторы 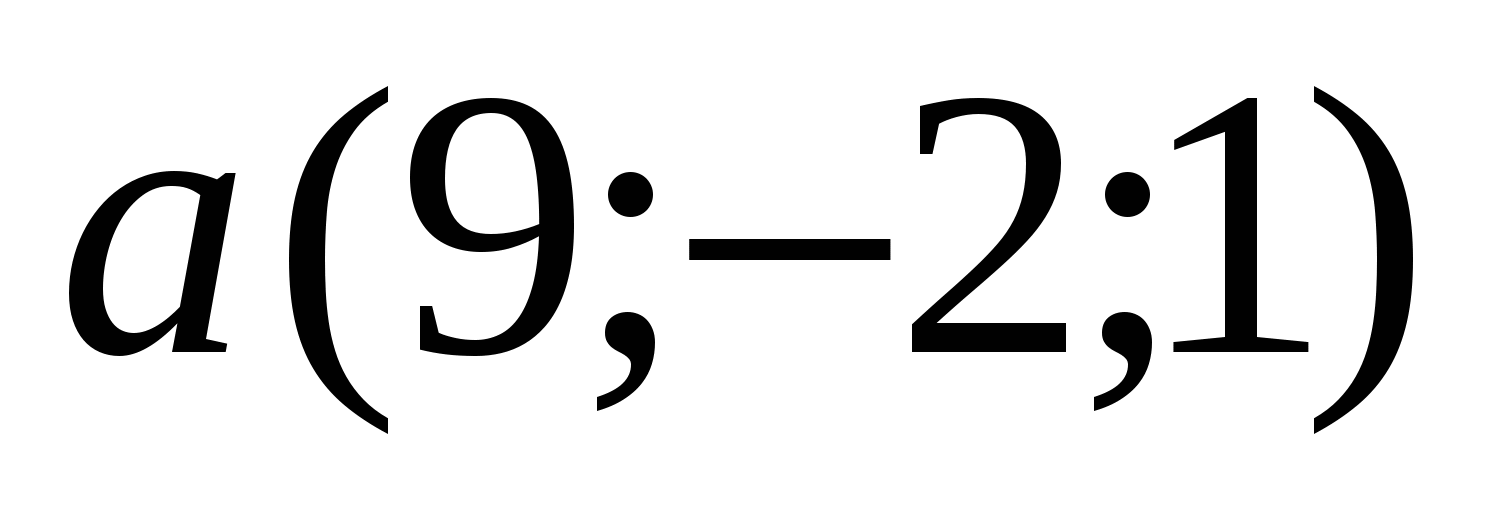
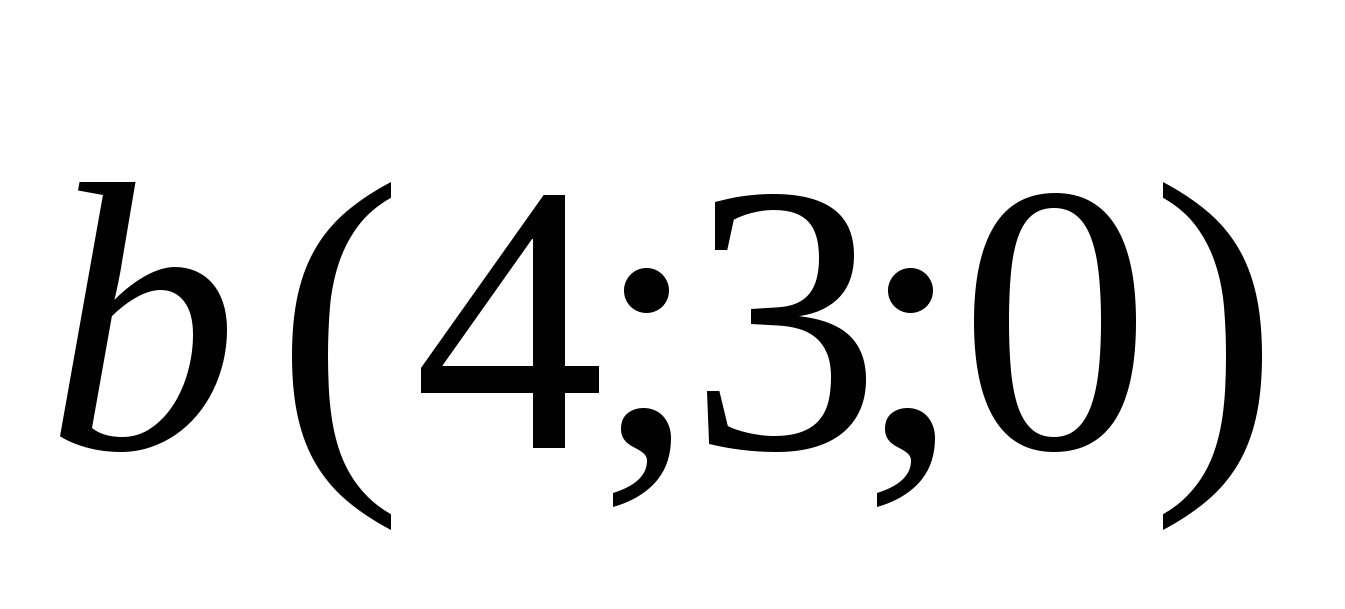
-
Найти
.
-
Найти
.
-
Найти
.
-
Найти
.
-
Найти координаты векторов
,
,
.
-
В прямоугольной декартовой системе координат построить точки A (0; 0),
B (3; -4), C (-3; 4). Определить расстояние между точками A и B, B и C, A и C.
Вариант 2
Даны векторы 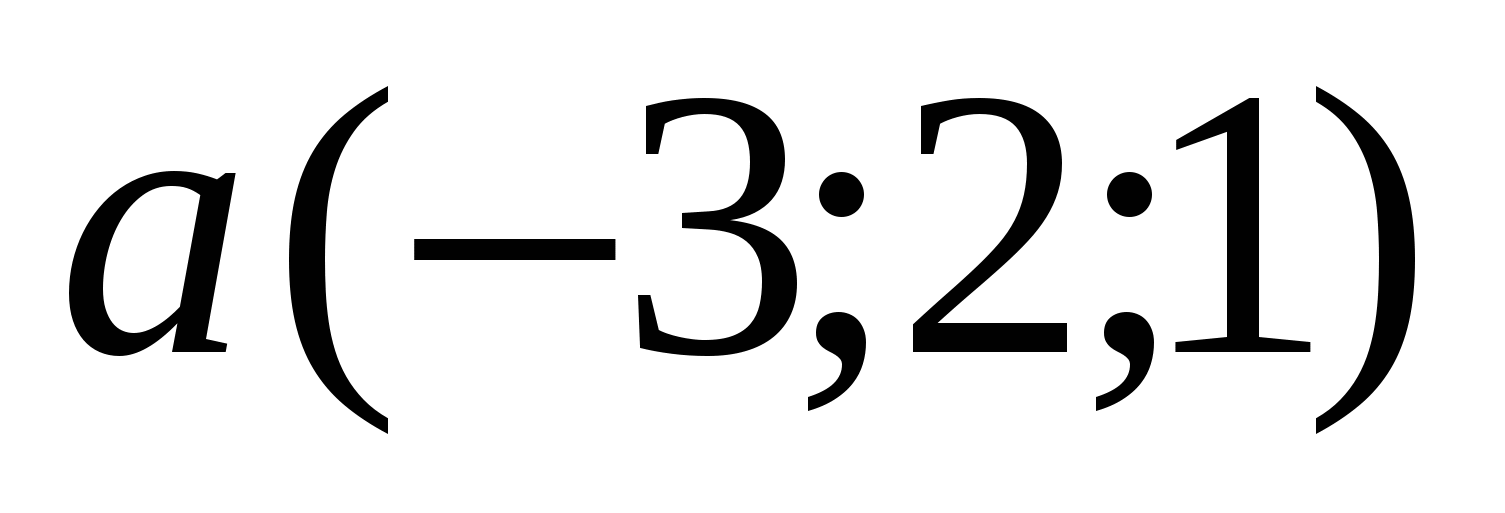
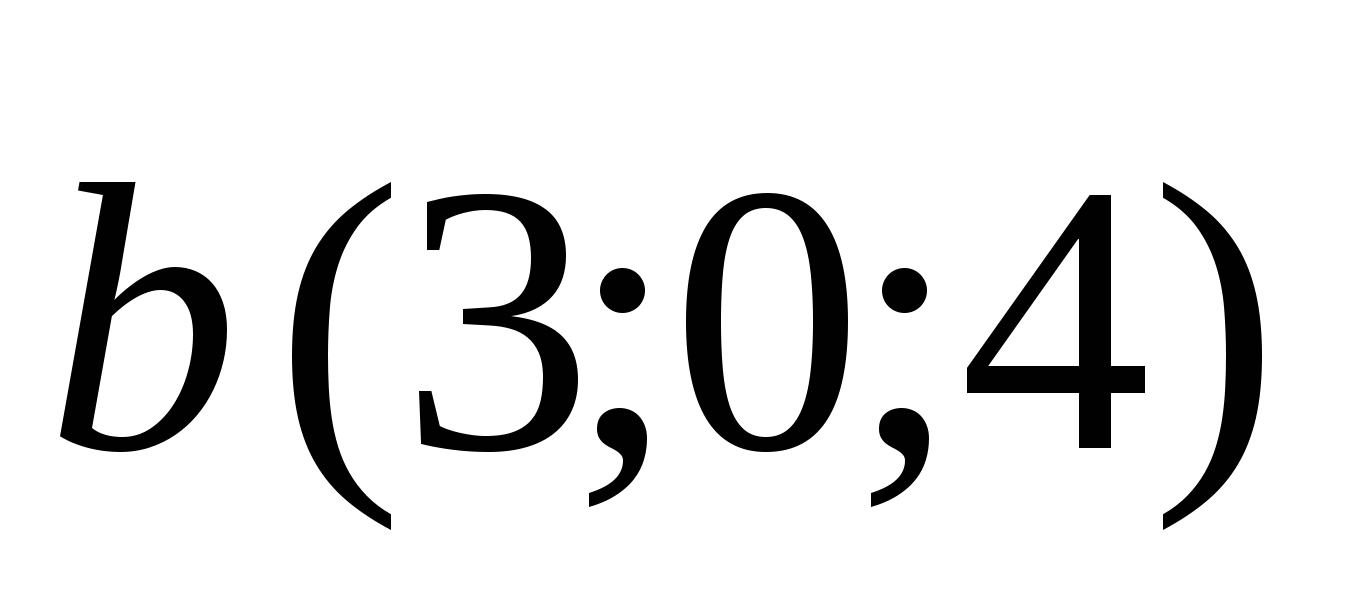
-
Найти
.
-
Найти
.
-
Найти
.
-
Найти
.
-
Найти координаты векторов
,
,
.
-
В прямоугольной декартовой системе координат построить точки A (0; 0),
C (-3; 4), D (-2; 2) E (10; -3). Определить расстояние между точками C и D, A и D, D и E.
Проверочная работа по темам «Многогранники», «Тела и поверхности вращения»
Уровень С
Время выполнения 60 минут
Вариант 1
1. В правильной треугольной призме боковое ребро равно
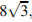
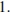
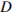
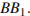
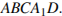
2. В правильную шестиугольную пирамиду, боковое ребро которой равно 10, а высота равна 6, вписана сфера. (Сфера касается всех граней пирамиды.) Найдите площадь этой сферы.
3. Радиус основания конуса равен 6, а его высота равна 8. Плоскость сечения содержит вершину конуса и хорду основания, длина которой равна 4. Найдите расстояние от центра основания конуса до плоскости сечения.
Вариант 2
1. В правильной треугольной призме боковое ребро равно
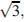
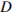
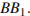
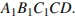
2. В правильную шестиугольную пирамиду, боковое ребро которой равно 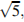
вписана сфера. (Сфера касается всех граней пирамиды.) Найдите площадь этой сферы.
3. Радиус основания конуса равен 5, а его высота равна 12. Плоскость сечения содержит вершину конуса и хорду основания, длина которой равна 6. Найдите расстояние от центра основания конуса до плоскости сечения.
3.2.3 Примеры заданий для устных опросов
Устный опрос 1 по теме «Основы тригонометрии»
Карточка — задание №1
«Тригонометрические формулы»
Заполните пропуски:
-
300 = ___ рад;
-
3π/2 рад = ___0;
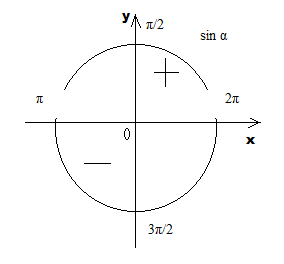
-
сos α — ____четная функция;
-
1 + ctg2 α = _______.
Карточка — задание №2
«Тригонометрические формулы»
Заполните пропуски:
-
600 = ___ рад;
-
π/2 рад = ___0;
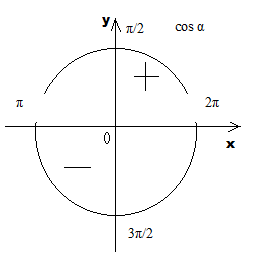
-
ctg α — ____четная функция;
-
1 + tg2 α = _______.
Карточка — задание №3
«Тригонометрические формулы»
Заполните пропуски:
-
450 = ___ рад;
-
π рад = ___0;
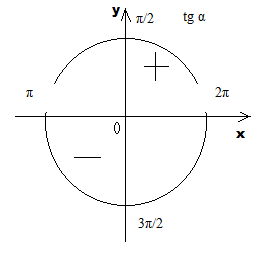
-
sin α — ____четная функция;
-
sin2 α + _____ = 1.
Карточка — задание №4
«Тригонометрические формулы»
Заполните пропуски:
-
600 = ___ рад;
-
2π рад = ___0;
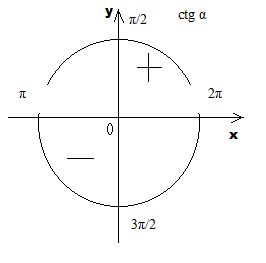
-
tg α — ____четная функция;
-
____ + cos2α = 1.
Устный опрос 2 по теме «Основы тригонометрии»
1) 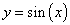
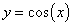
; 4)
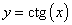
Соотнесите тригонометрические функции и их графики:
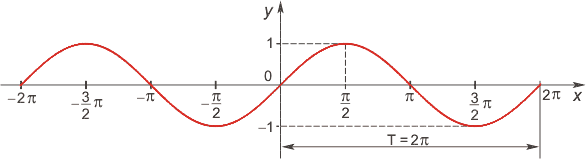
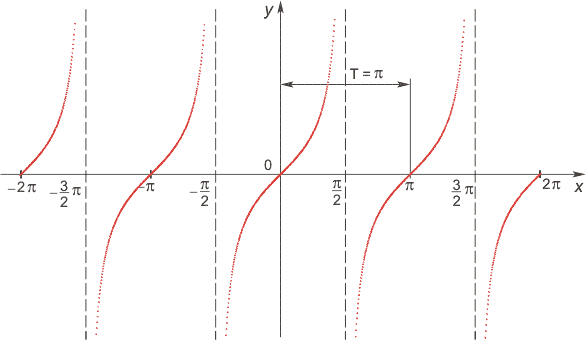
Б)
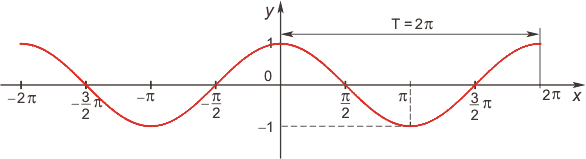
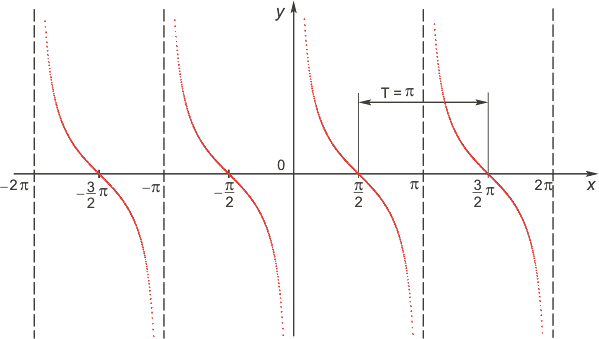
Устный опрос по теме » Степенные, показательные, логарифмические и тригонометрические функции »
Опрос проводится перед изучением темы для закрепления умений работы с графиками и диаграммами
1. На графике изображена зависимость крутящего момента двигателя от числа его оборотов в минуту. На оси абсцисс откладывается число оборотов в минуту, на оси ординат — крутящий момент в Н 

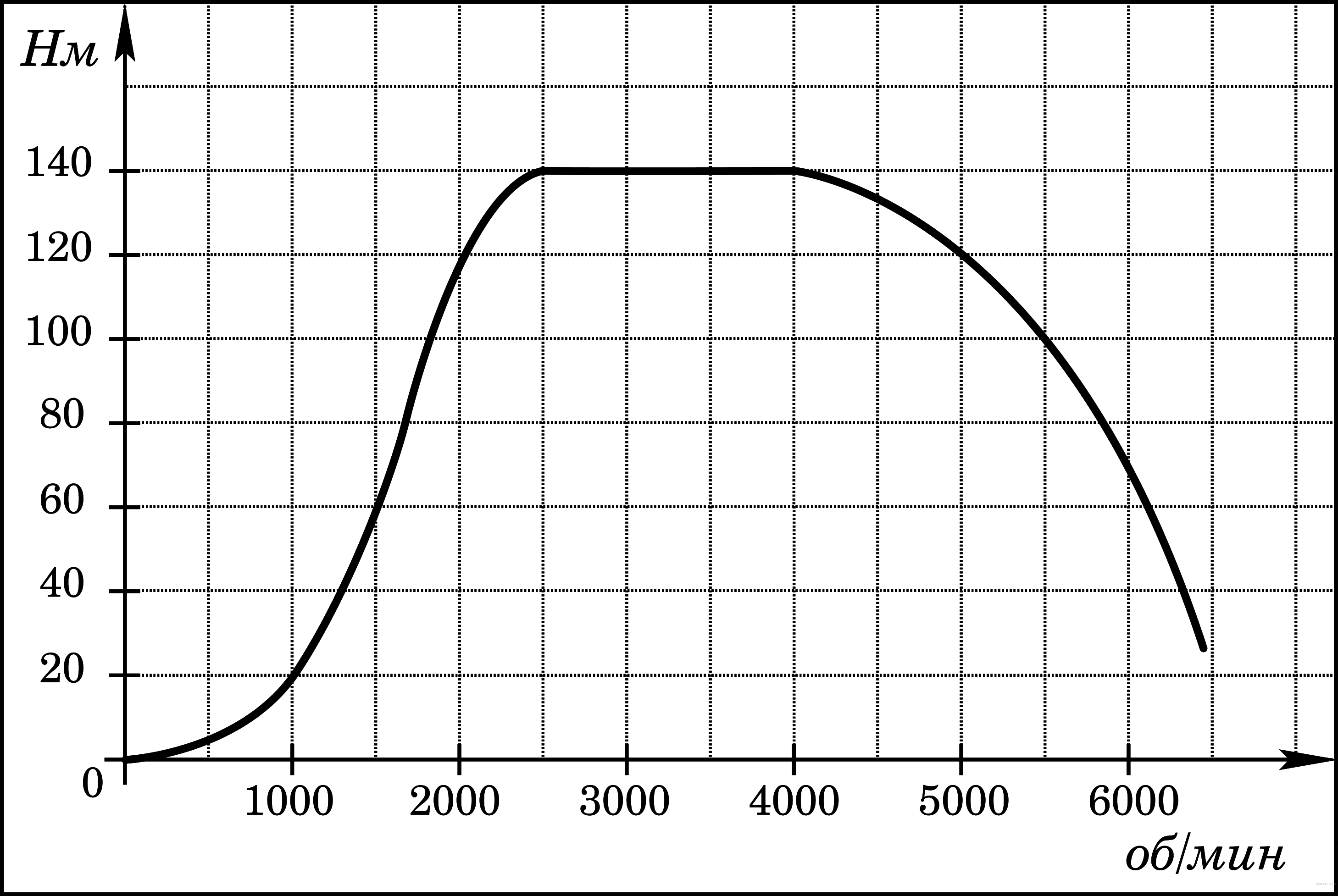
2. В ходе химической реакции количество исходного вещества (реагента), которое еще не вступило в реакцию, со временем постепенно уменьшается. На рисунке эта зависимость представлена графиком. На оси абсцисс откладывается время в минутах, прошедшее с момента начала реакции, на оси ординат — масса оставшегося реагента, который еще не вступил в реакцию (в граммах). Определите по графику, сколько граммов реагента вступило в реакцию за три минуты?
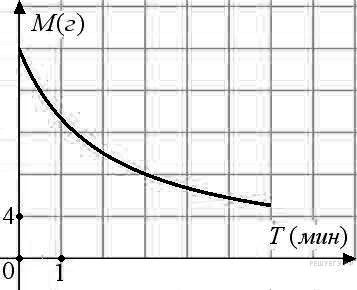
3. На рисунке точками показана аудитория поискового сайта Ya.ru во все месяцы с декабря 2008 по октябрь 2009 года. По горизонтали указываются месяцы, по вертикали − количество посетителей сайта хотя бы раз в данном месяце. Для наглядности точки на рисунке соединены линией. Определите по рисунку разность между наибольшей и наименьшей аудиторией сайта Ya.ru в указанный период.
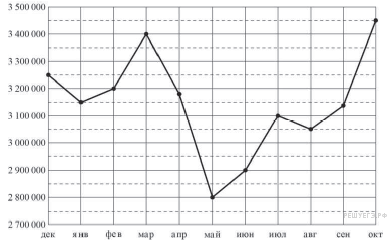
4. На рисунке показано изменение биржевой стоимости акций целлюлозно-бумажного завода в первой половине апреля. 2 апреля бизнесмен приобрёл 250 акций этого завода. 6 апреля он продал 150 акций, а оставшиеся акции продал 11 апреля. Сколько рублей потерял бизнесмен в результате этих операций?
Устный опрос по теме » Дифференциальное исчисление функций одной переменной »
Сформулировать правила дифференцирования и записать производные основных элементарных функций:
1о.
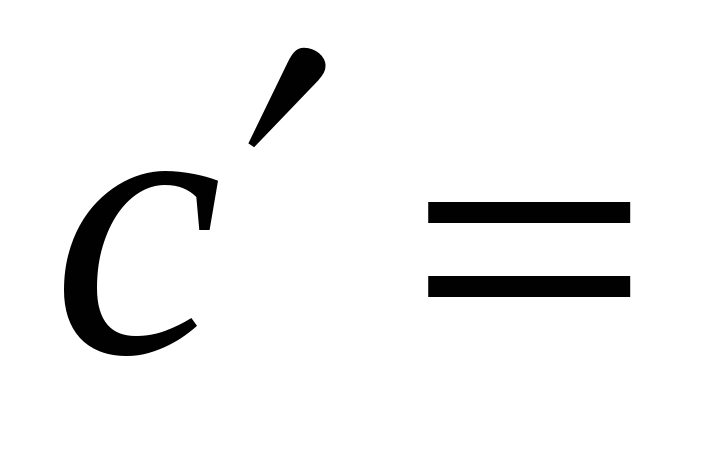
8о.
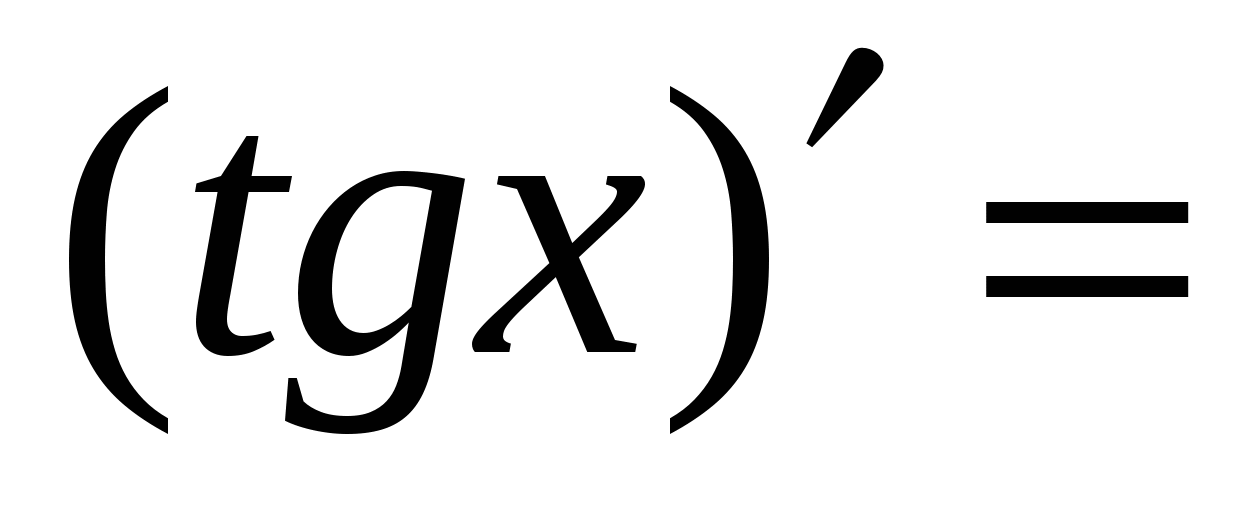
2о.
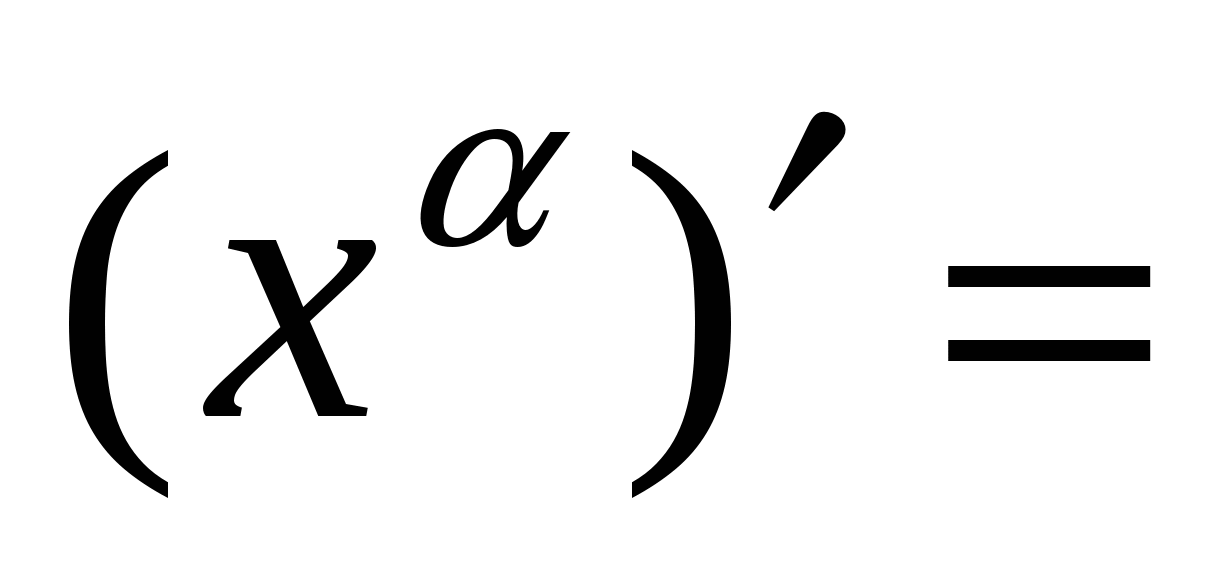
В частности, 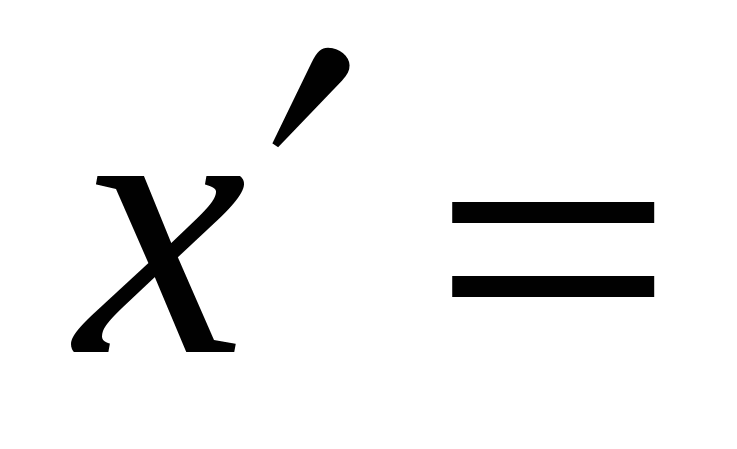
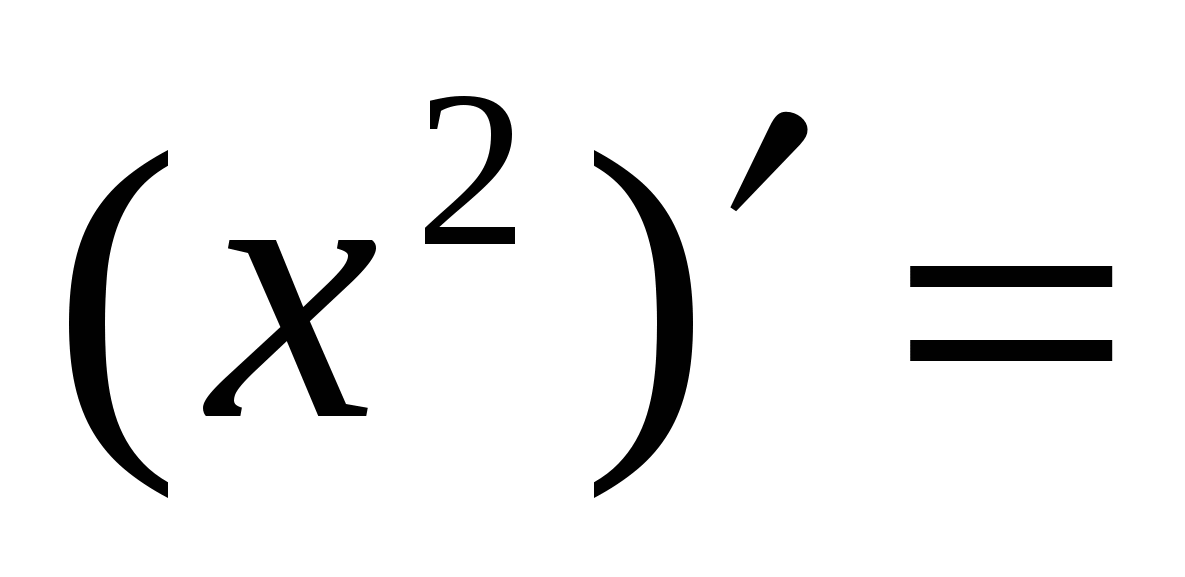
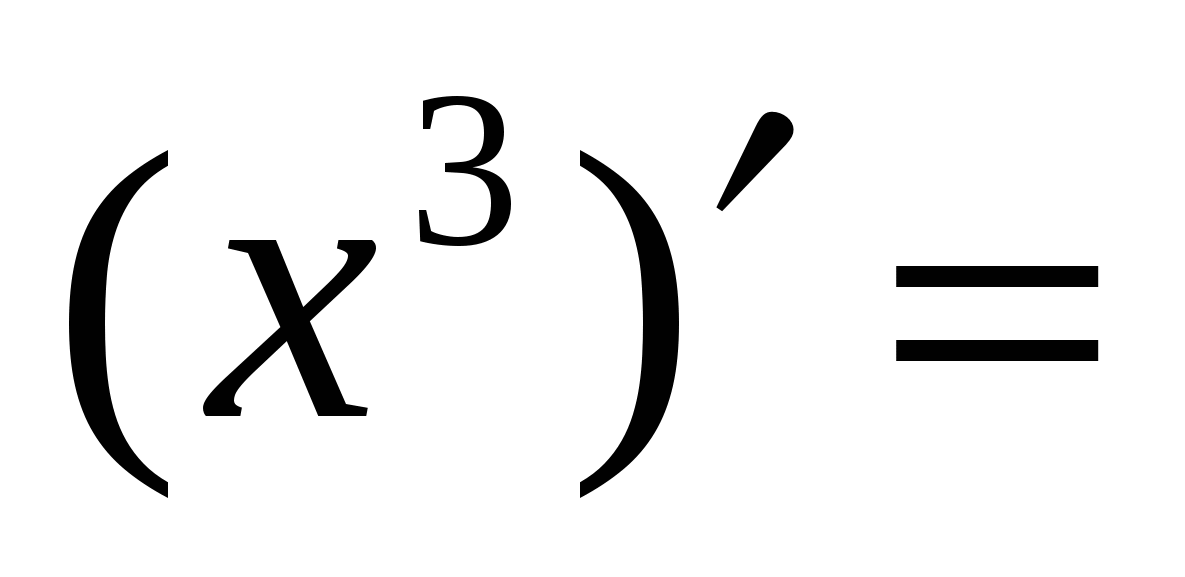
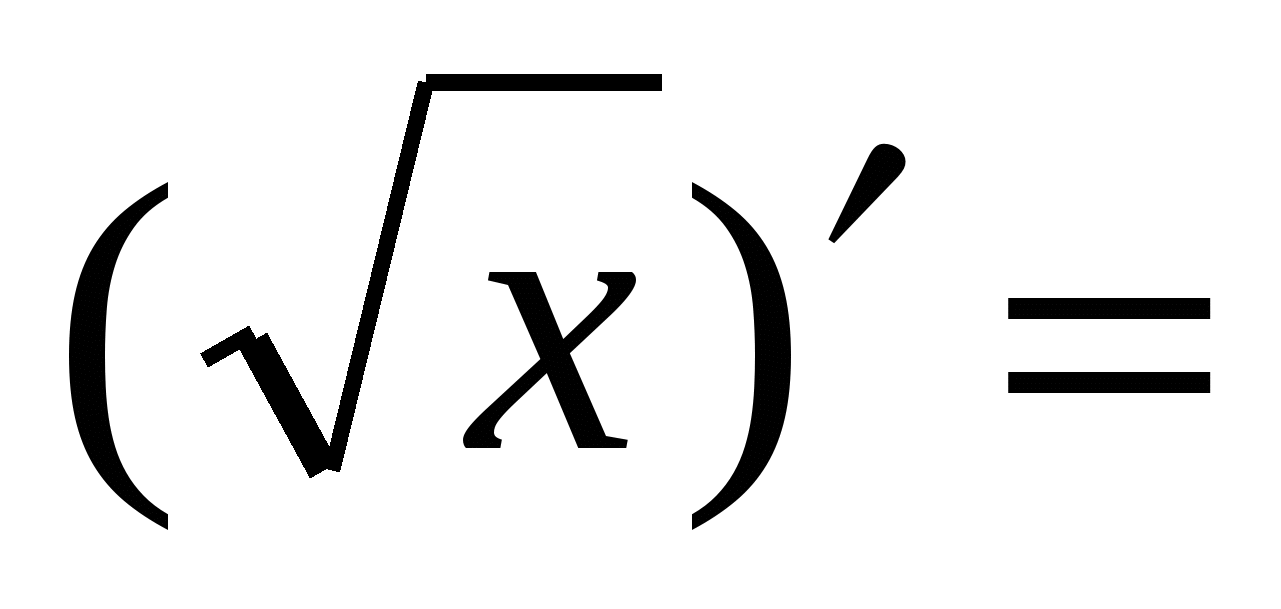
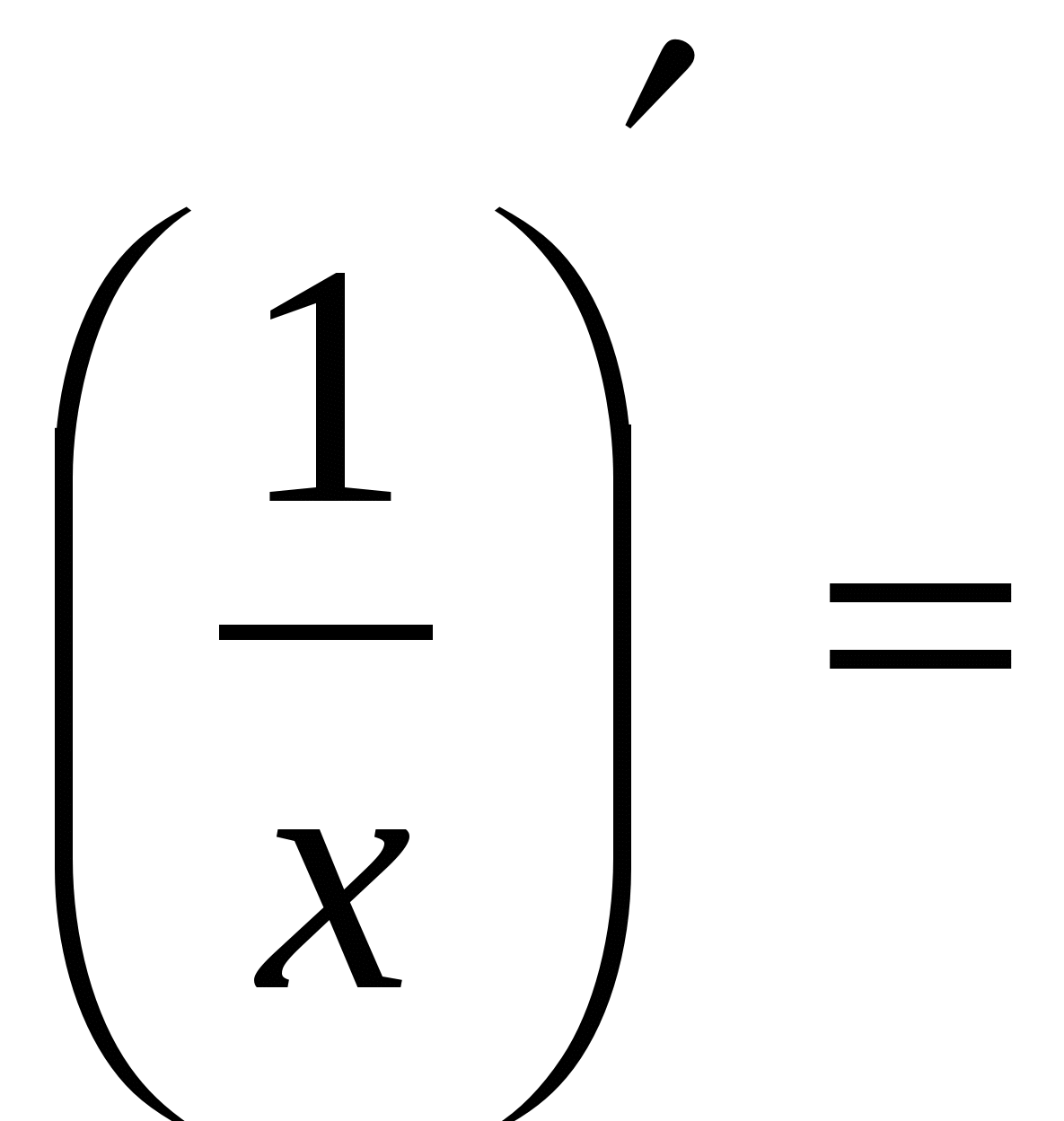
9о.
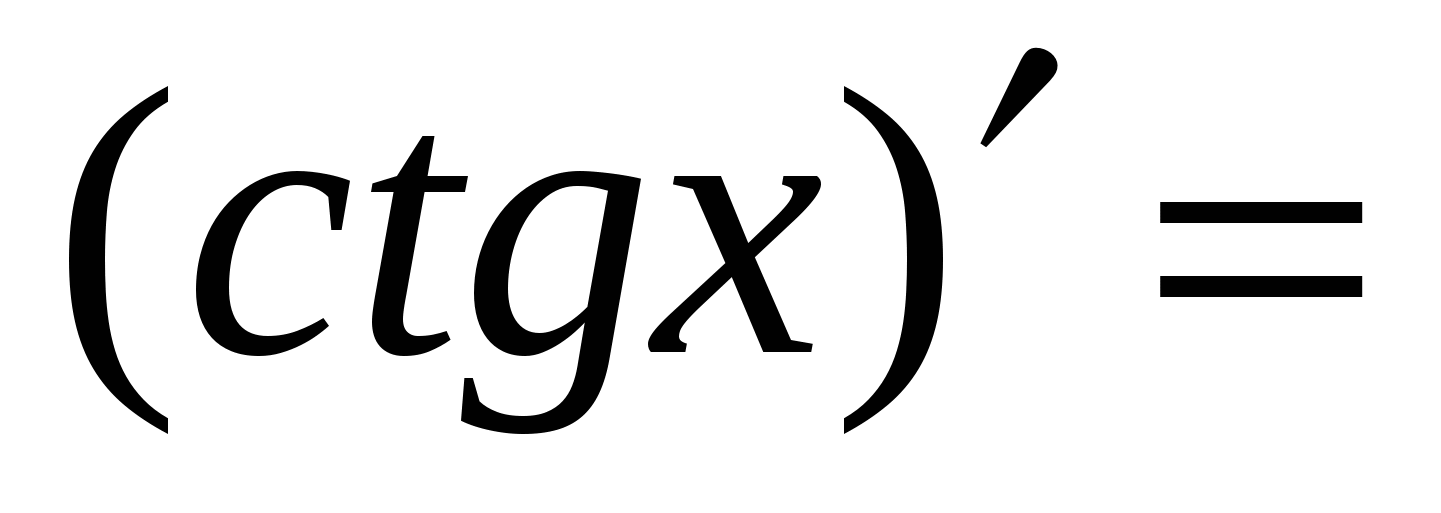
10о.
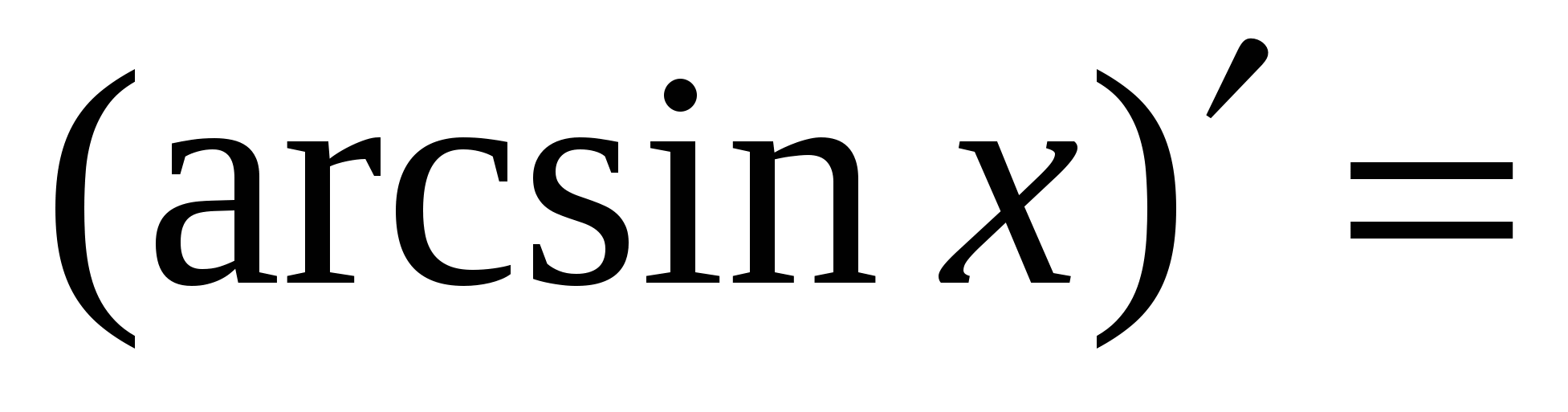
11о.
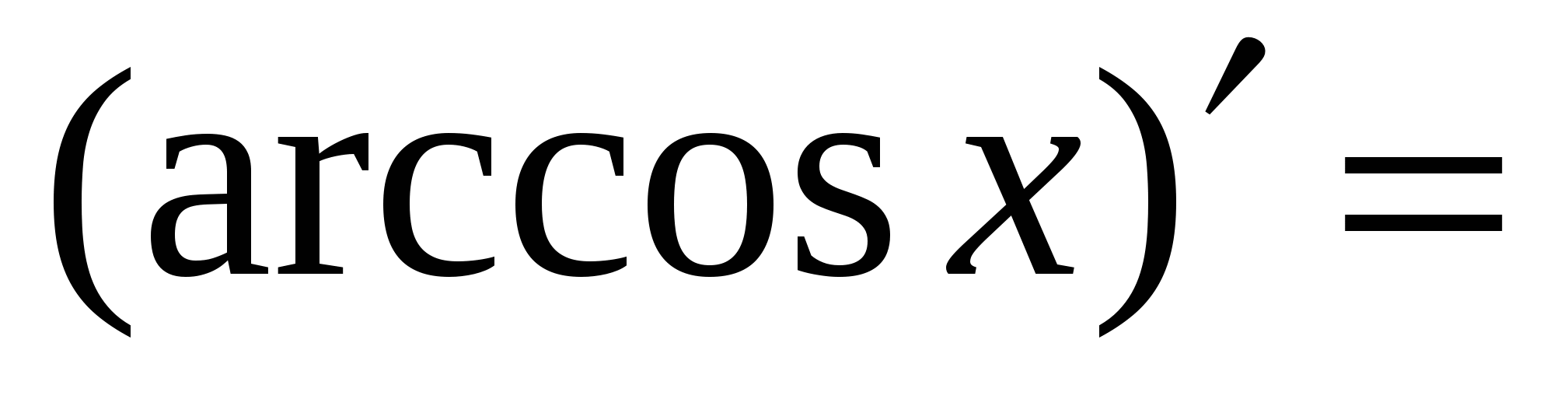
12о.
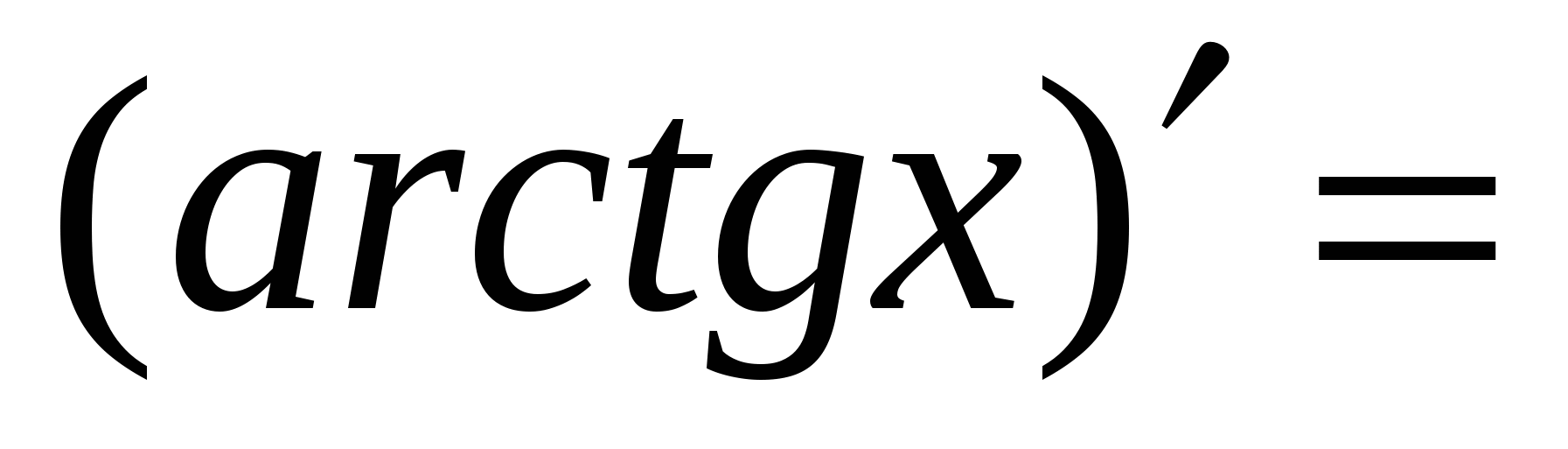
13о.
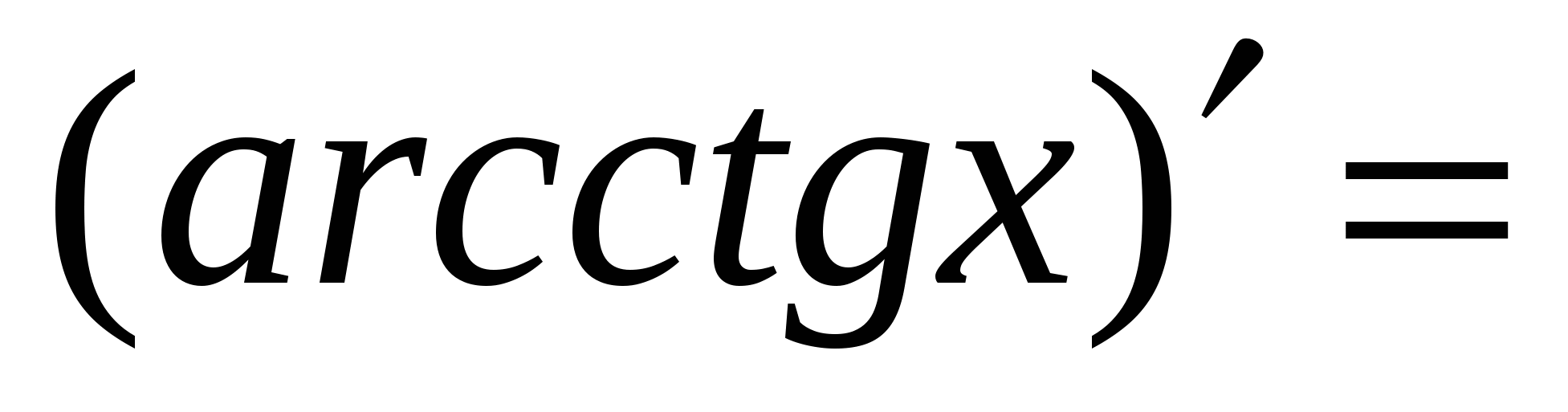
ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ
14о.
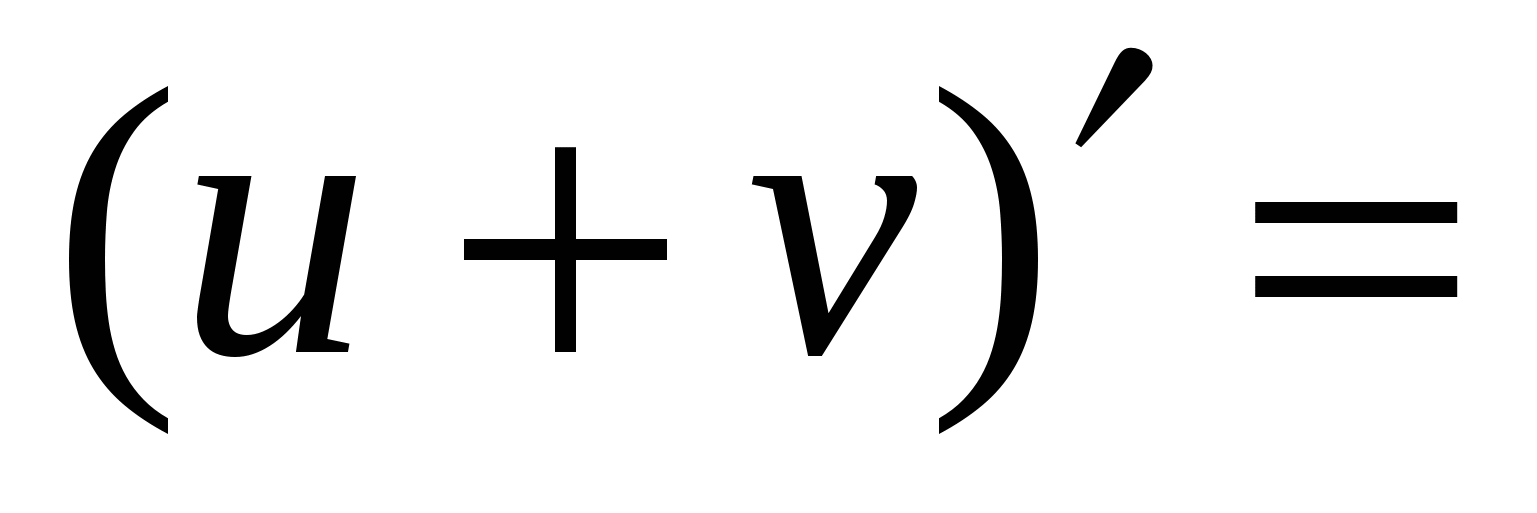
3о.
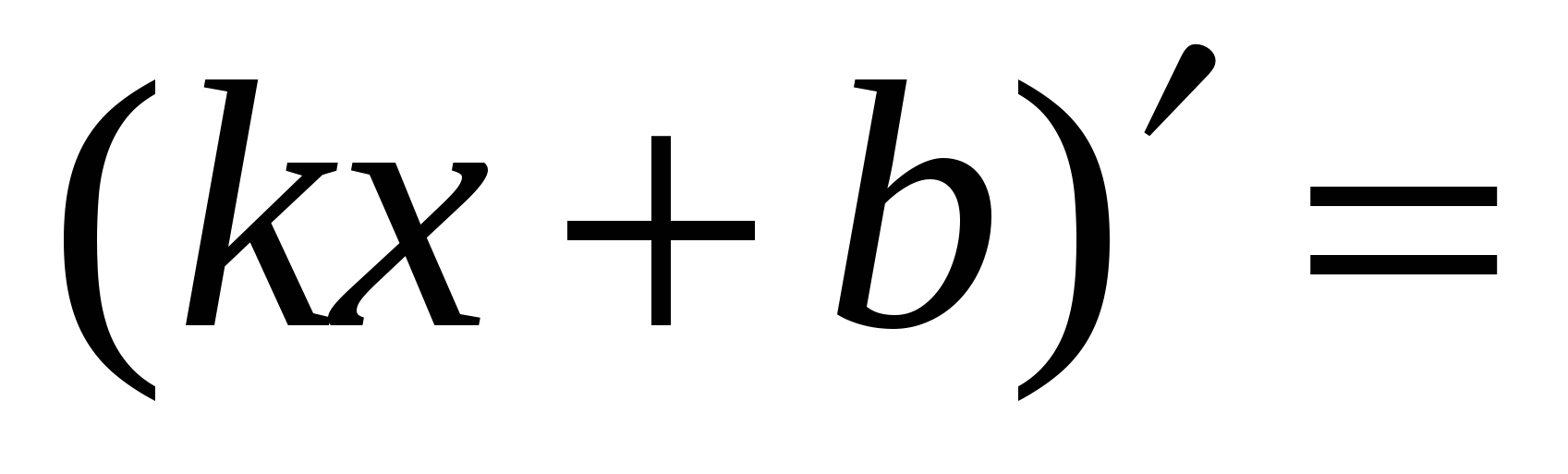
15о.
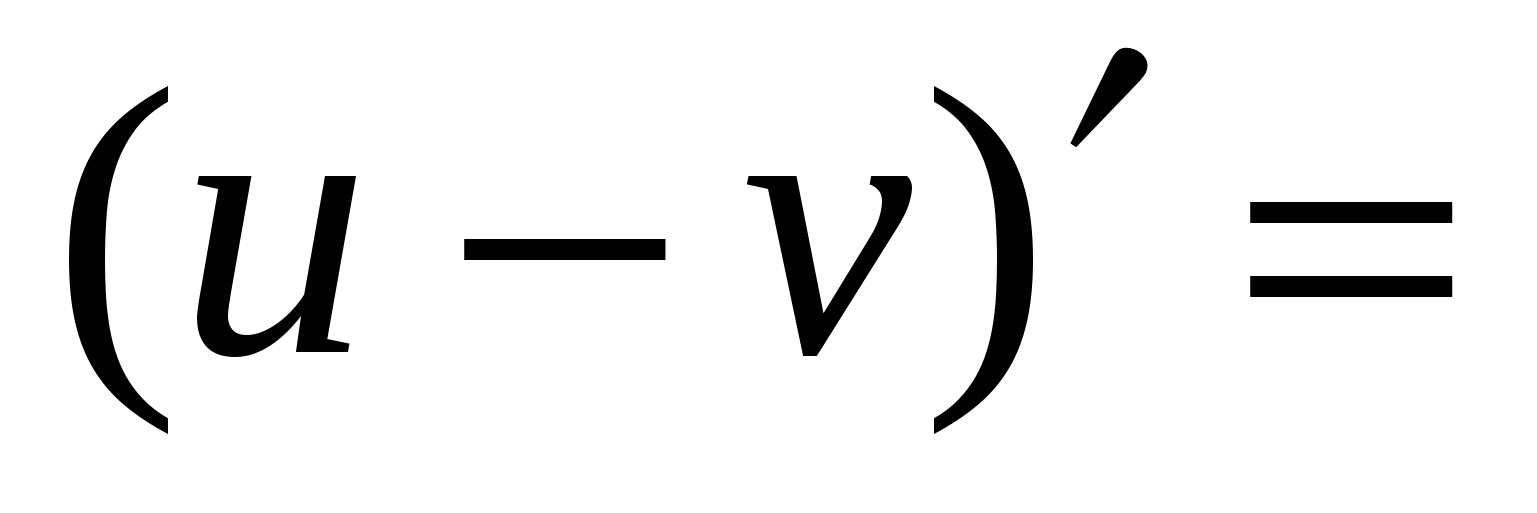
4о.
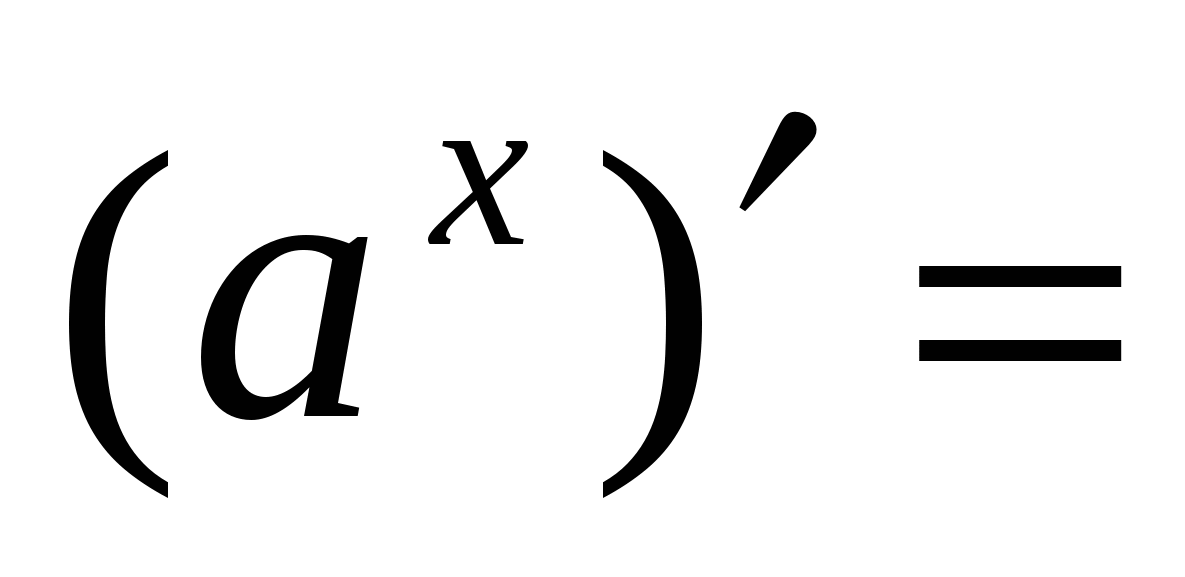
В частности, 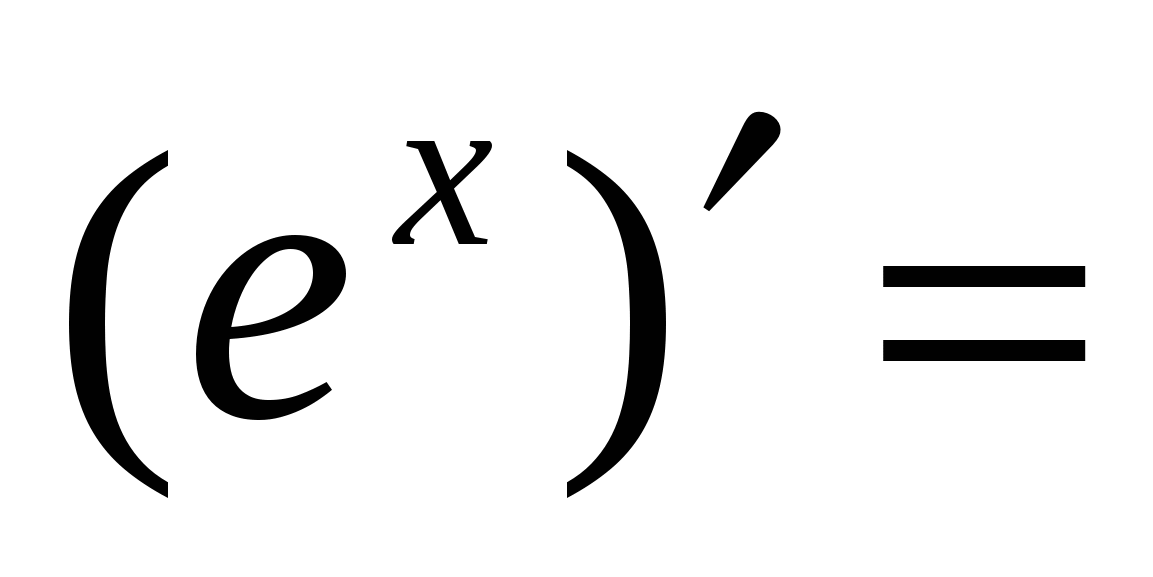
16о.
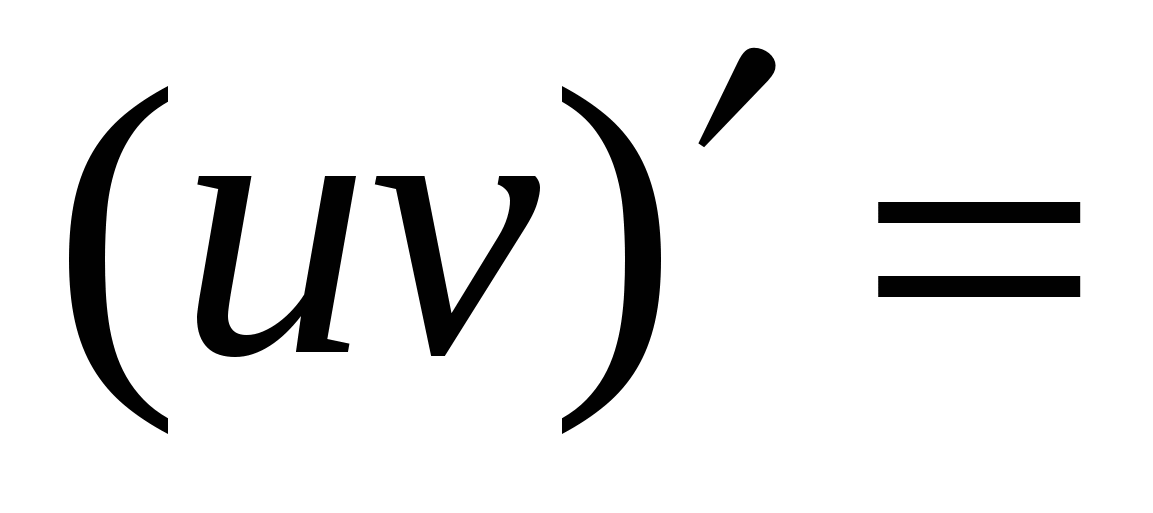
17о.
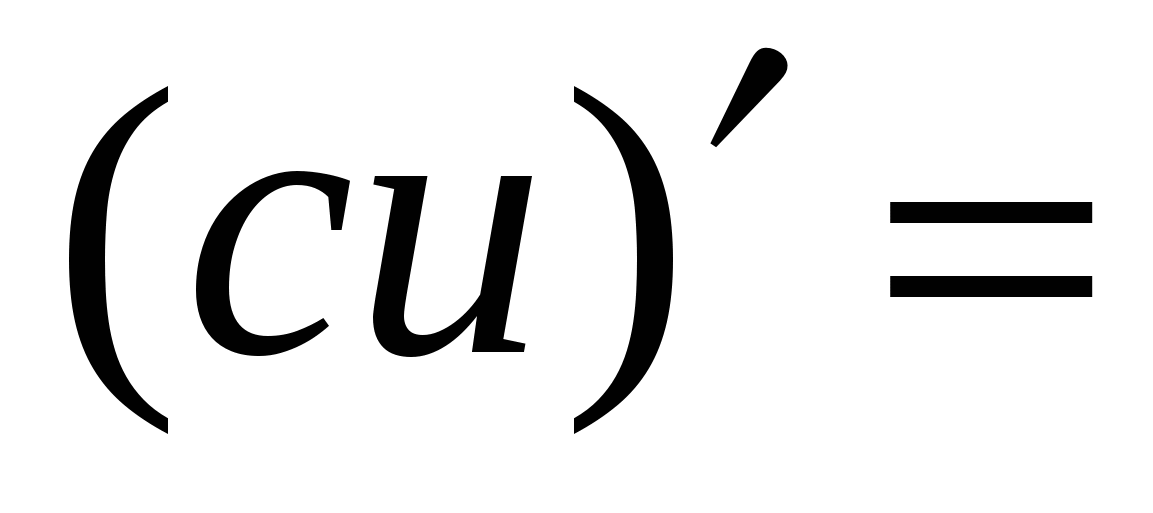
5о.
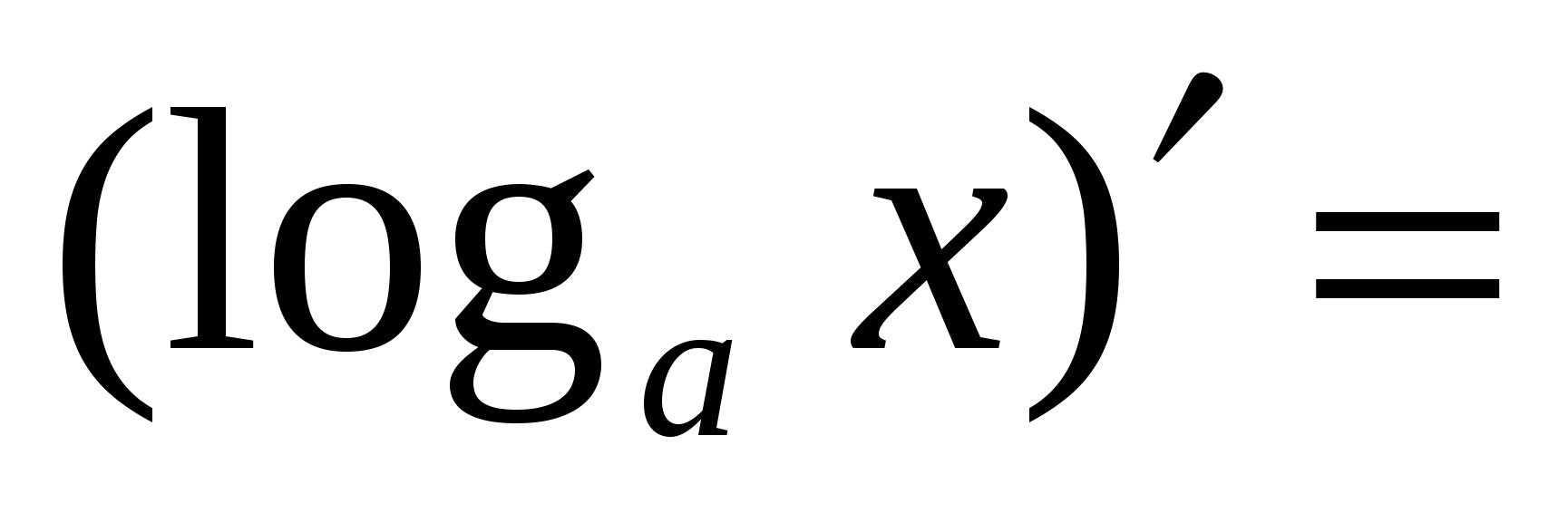
В частности, 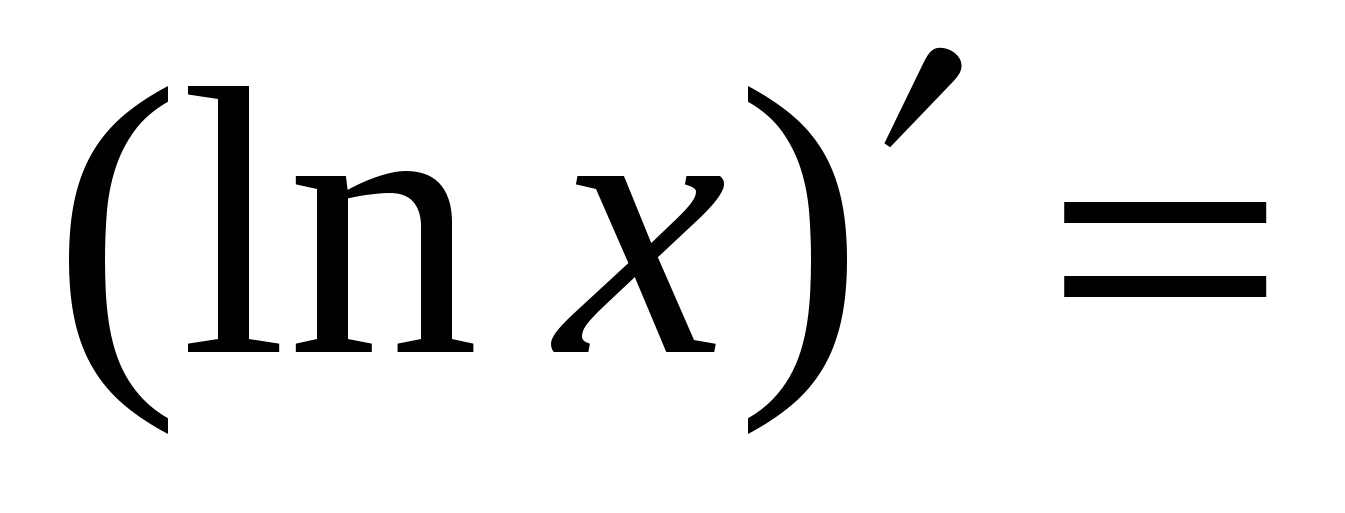
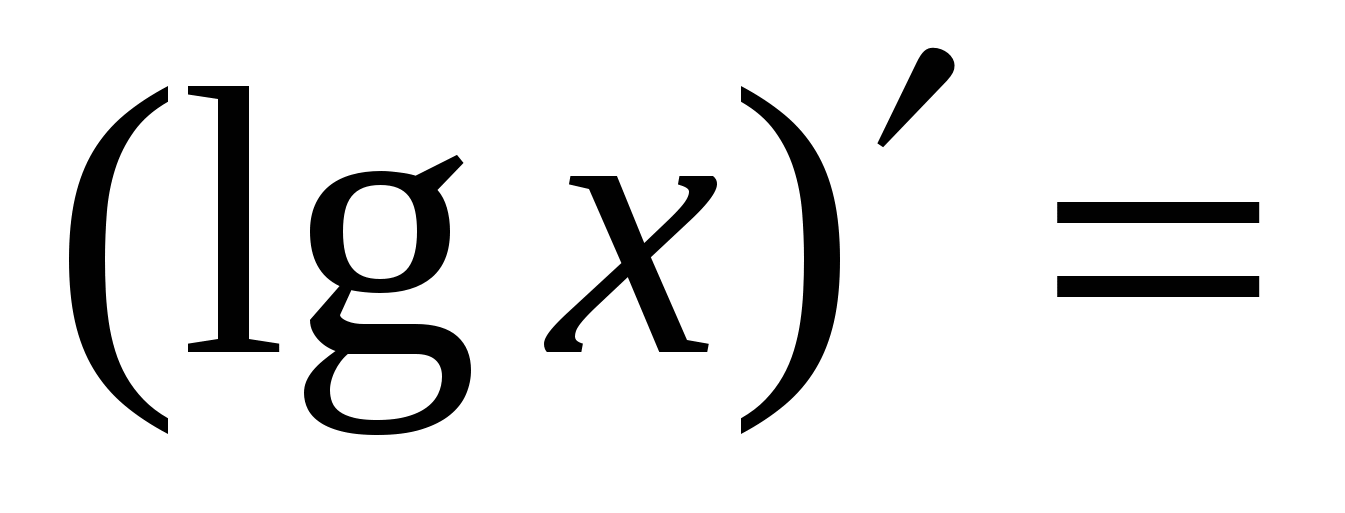
18о.
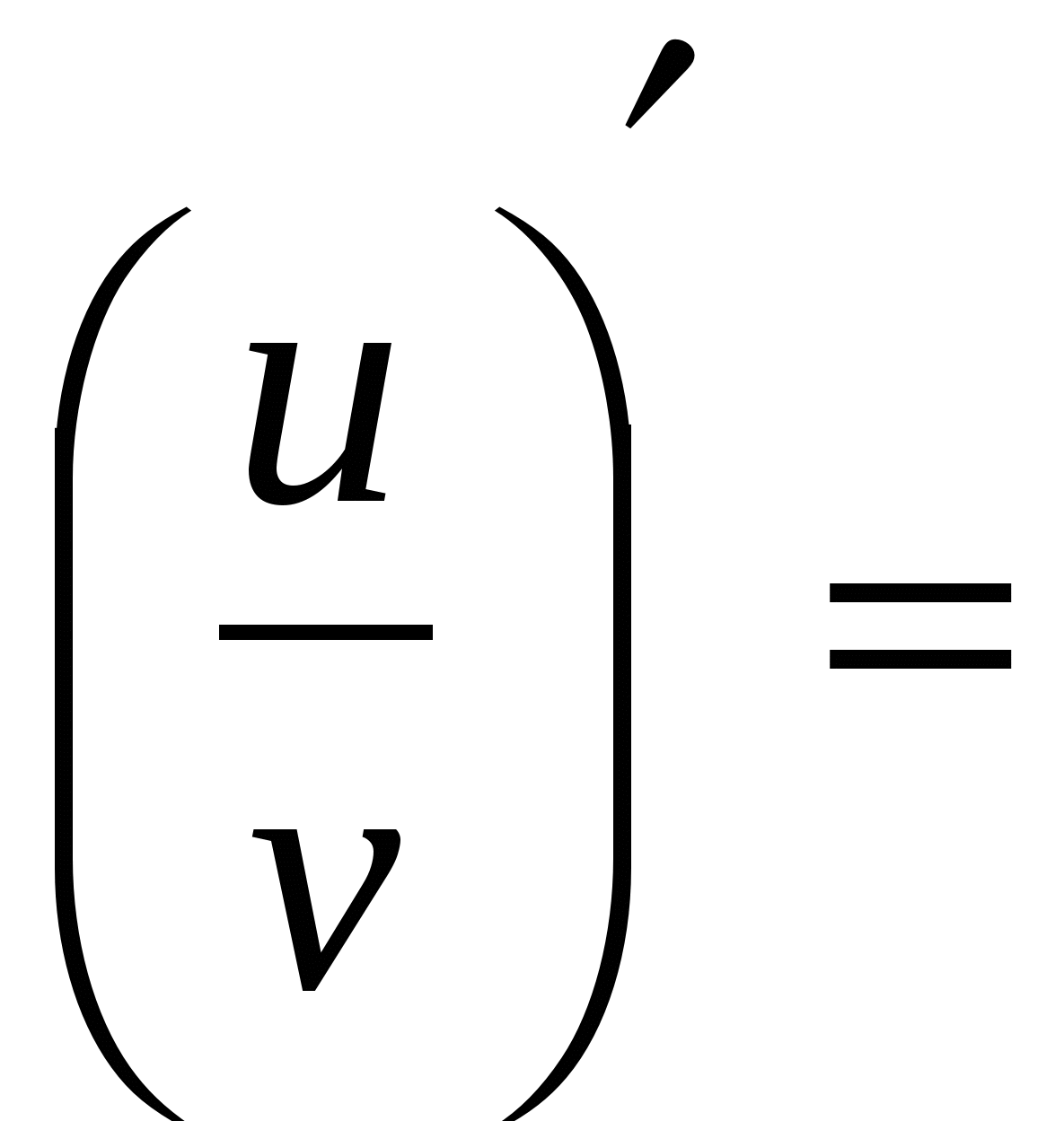
В частности, 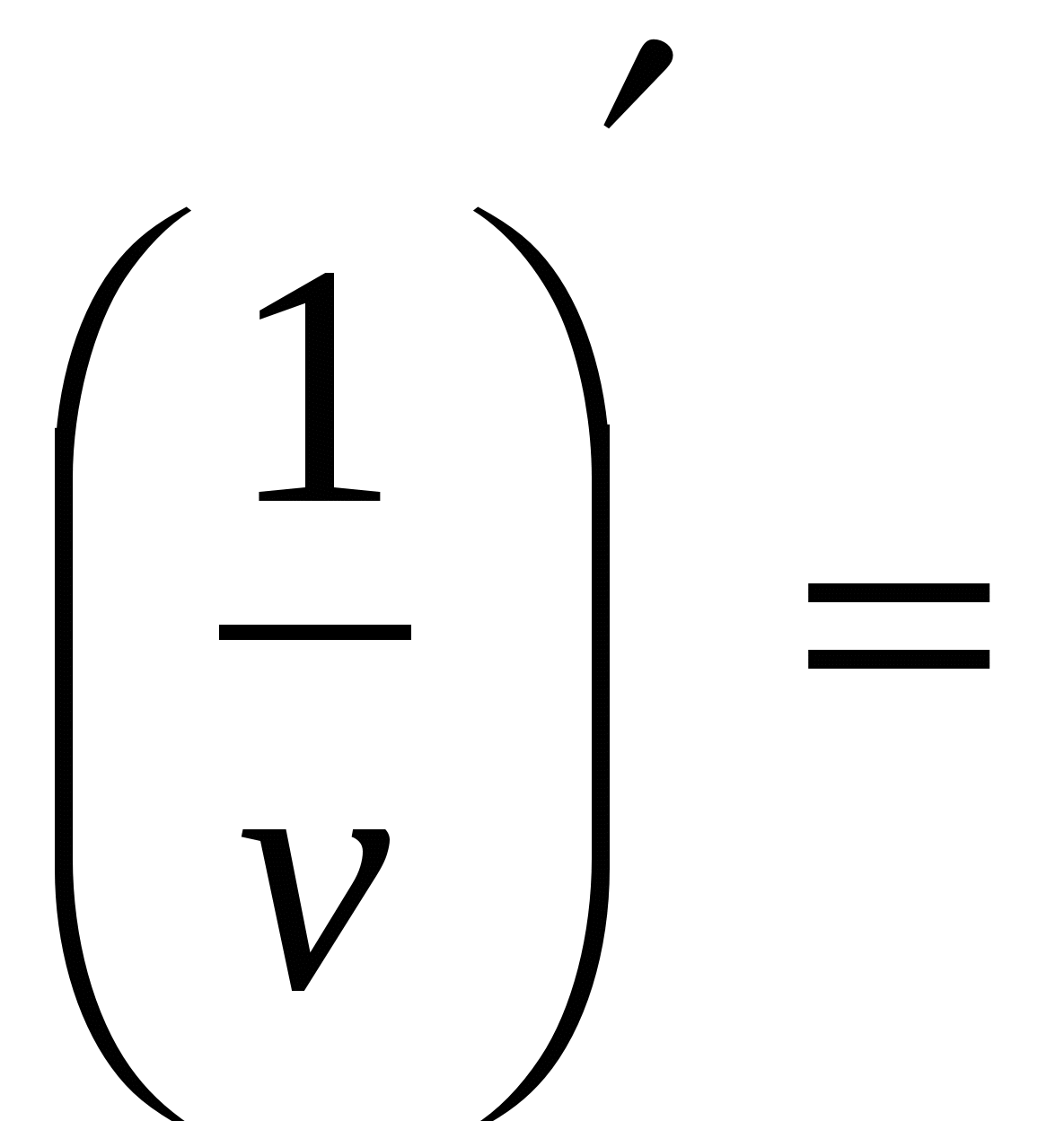
6о.
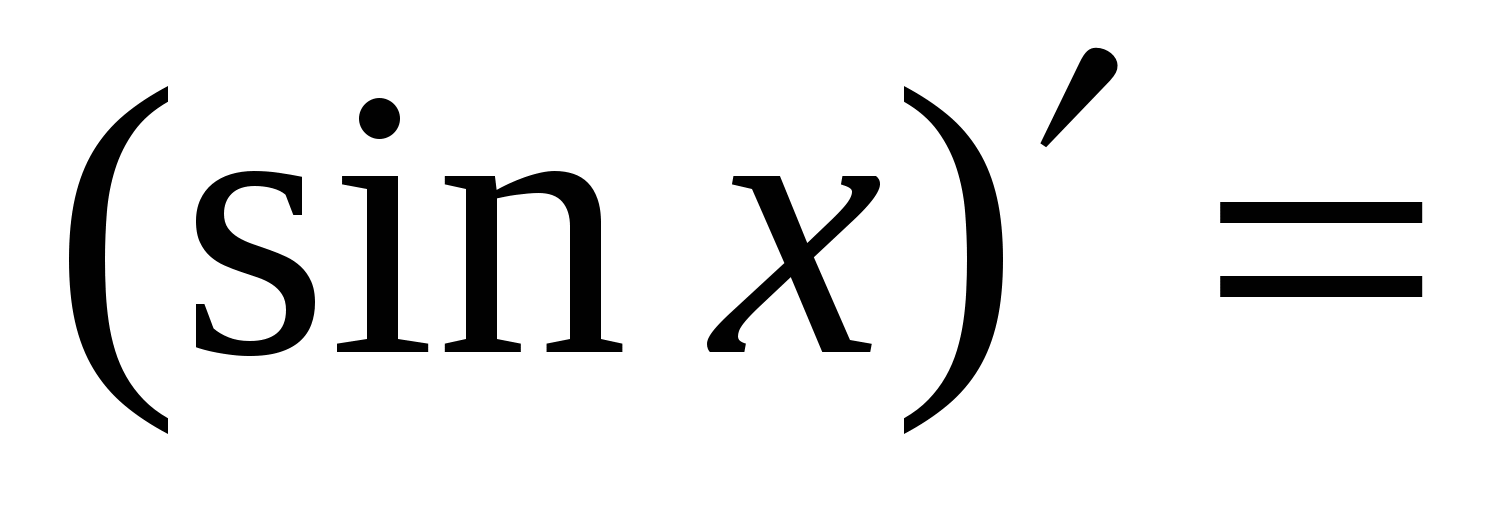
ПРОИЗВОДНАЯ СЛОЖНОЙ ФУНКЦИИ
7о.
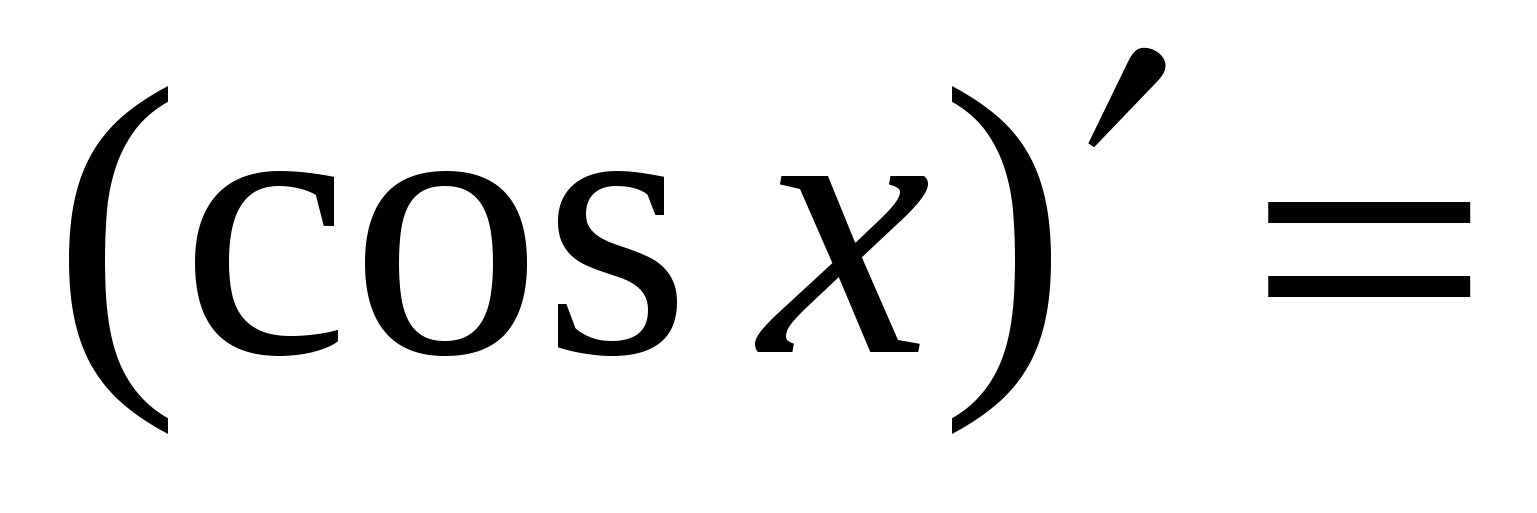
19о.
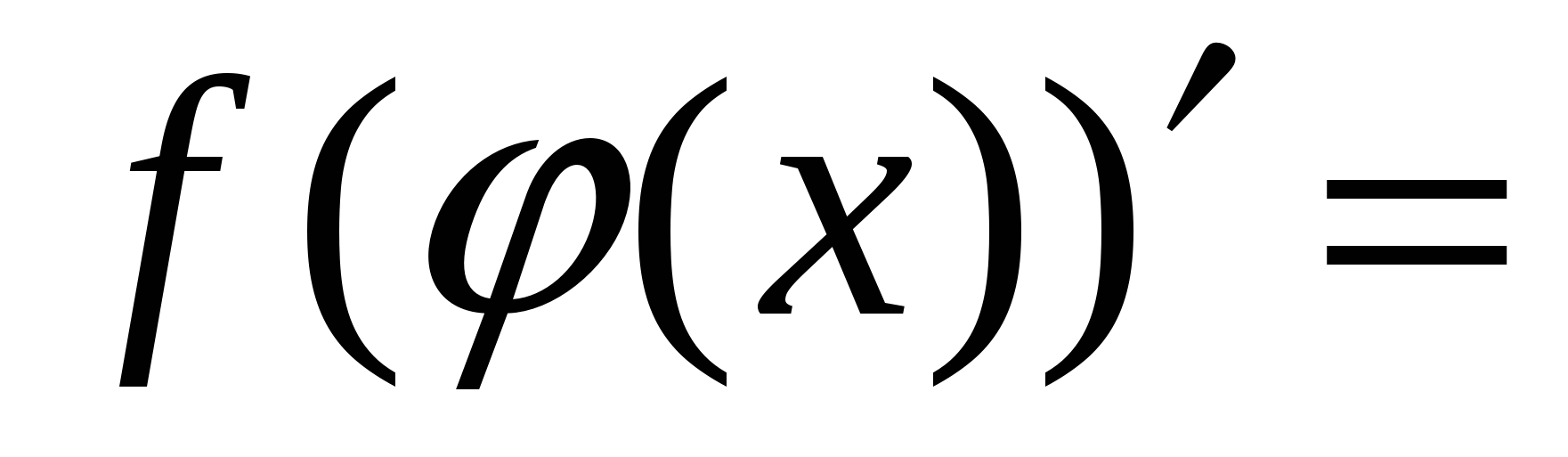
Устный опрос по теме «Интегральное исчисление функций одной переменной»
Записать табличные интегралы:
1о.
2о. 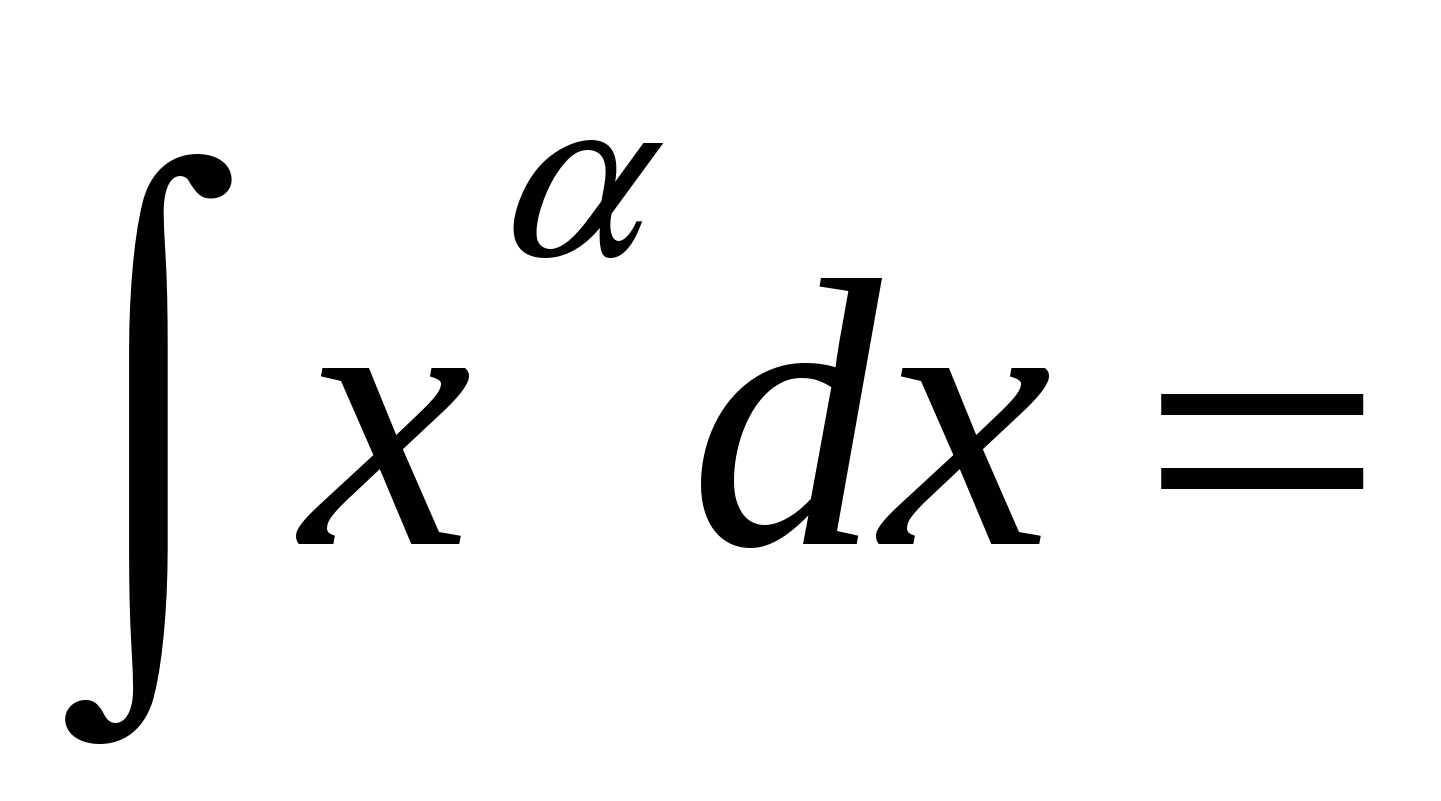
В частности, 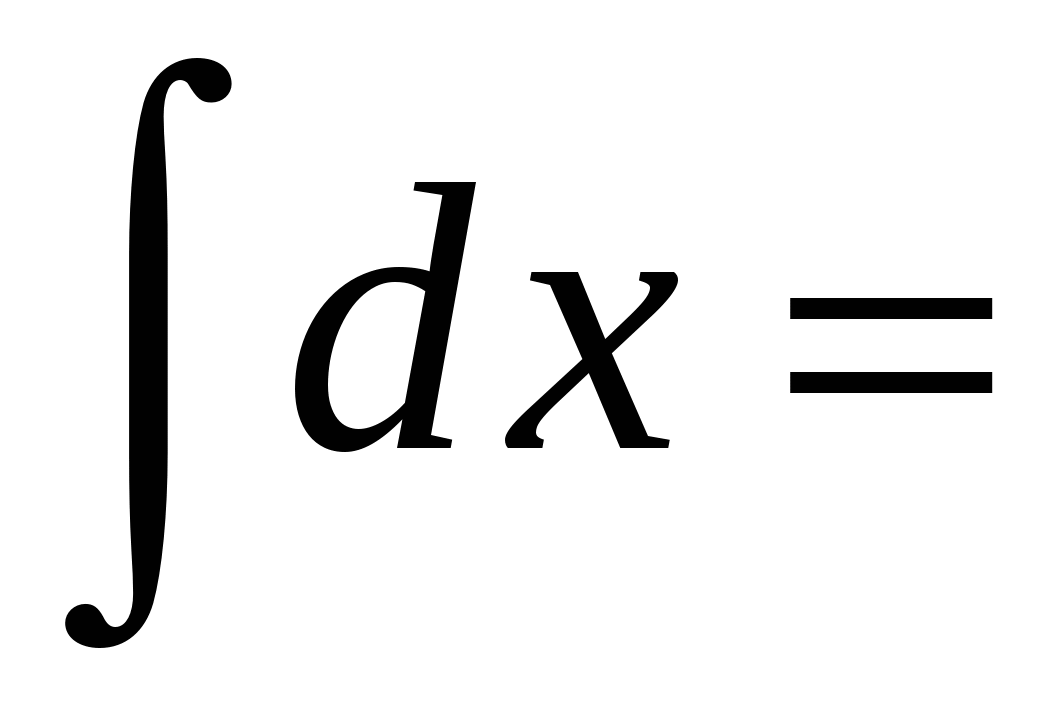
3о.
4о. 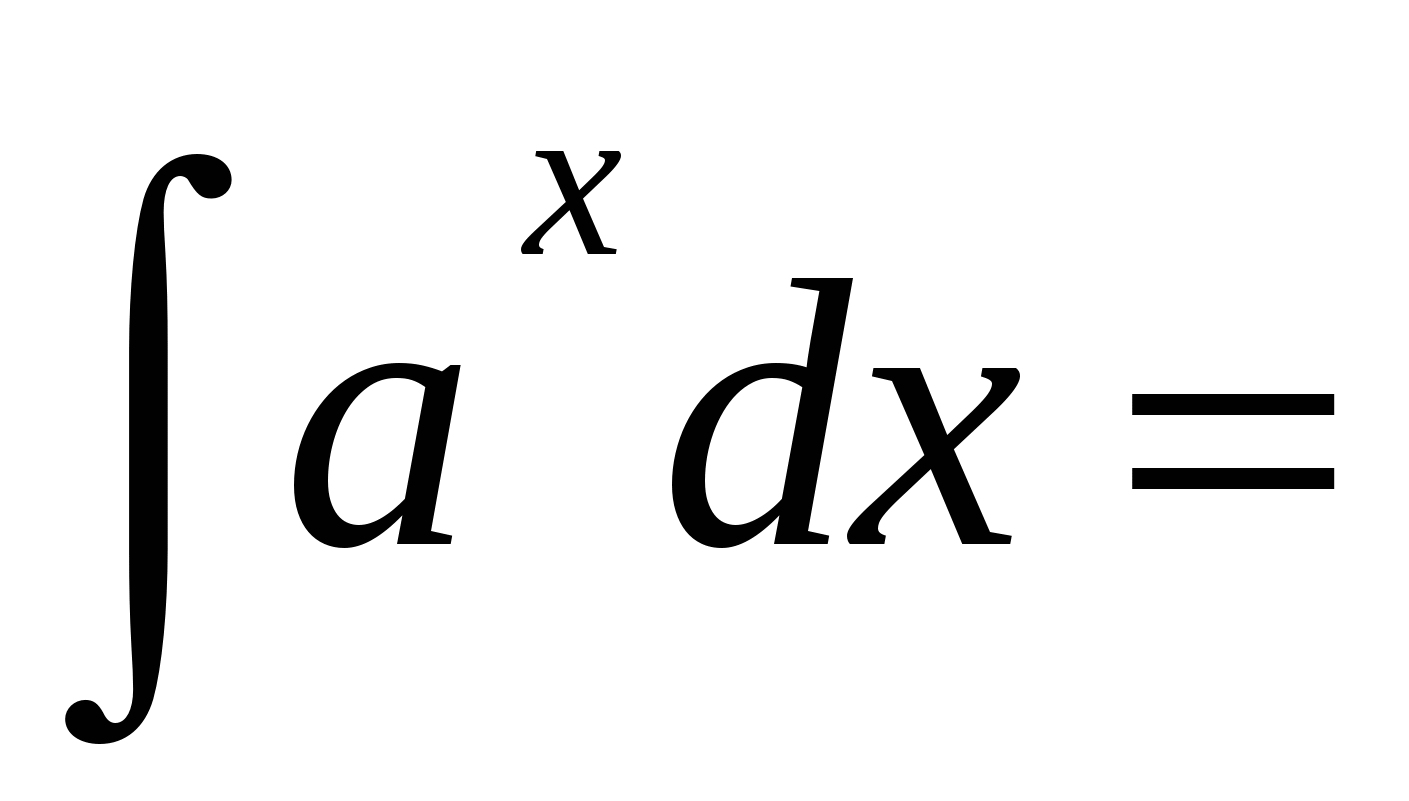
В частности, 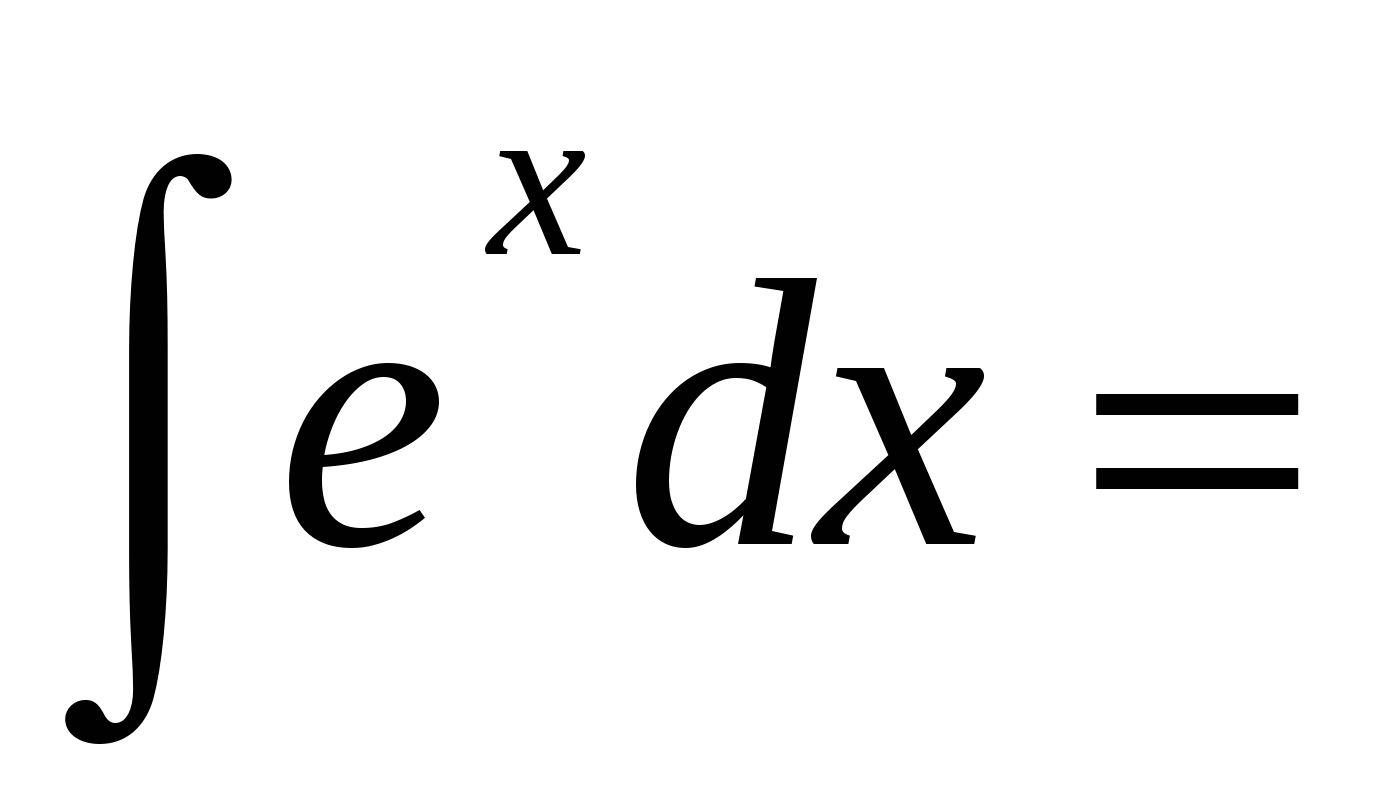
5о. 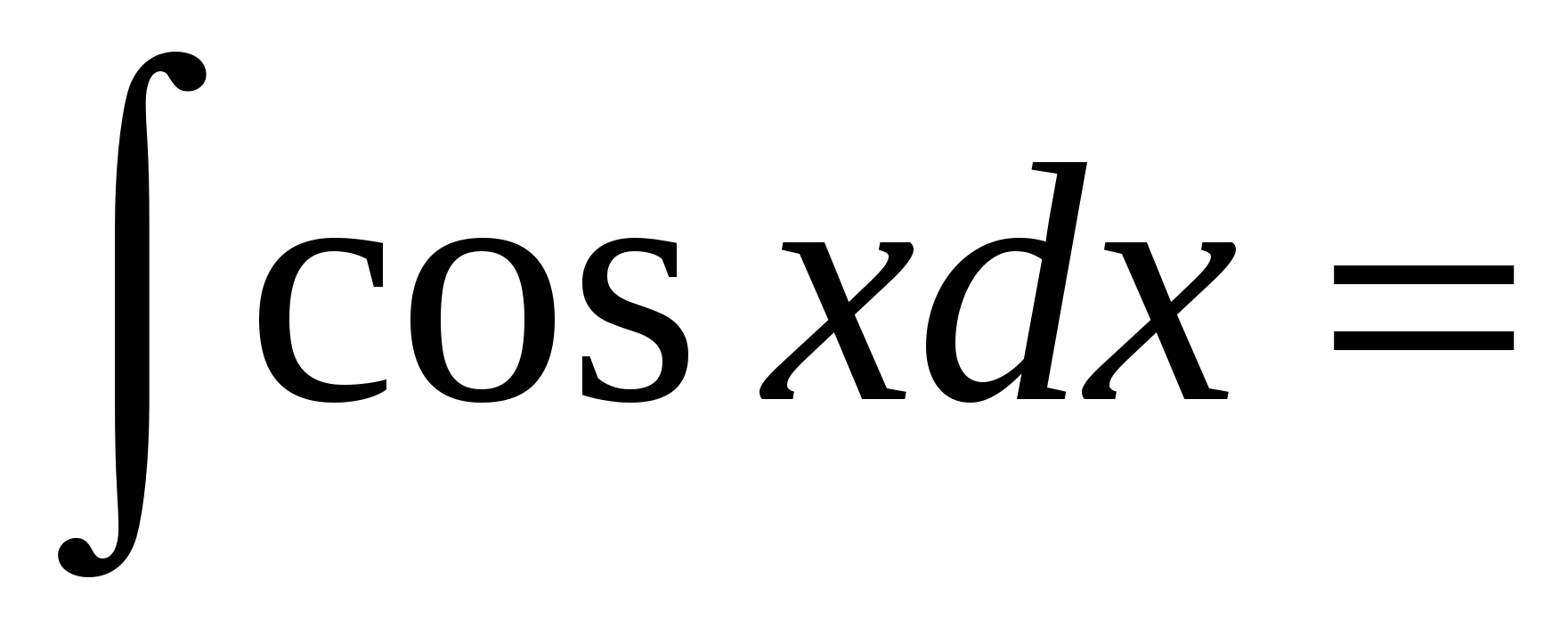
6о.
7о.
8о. 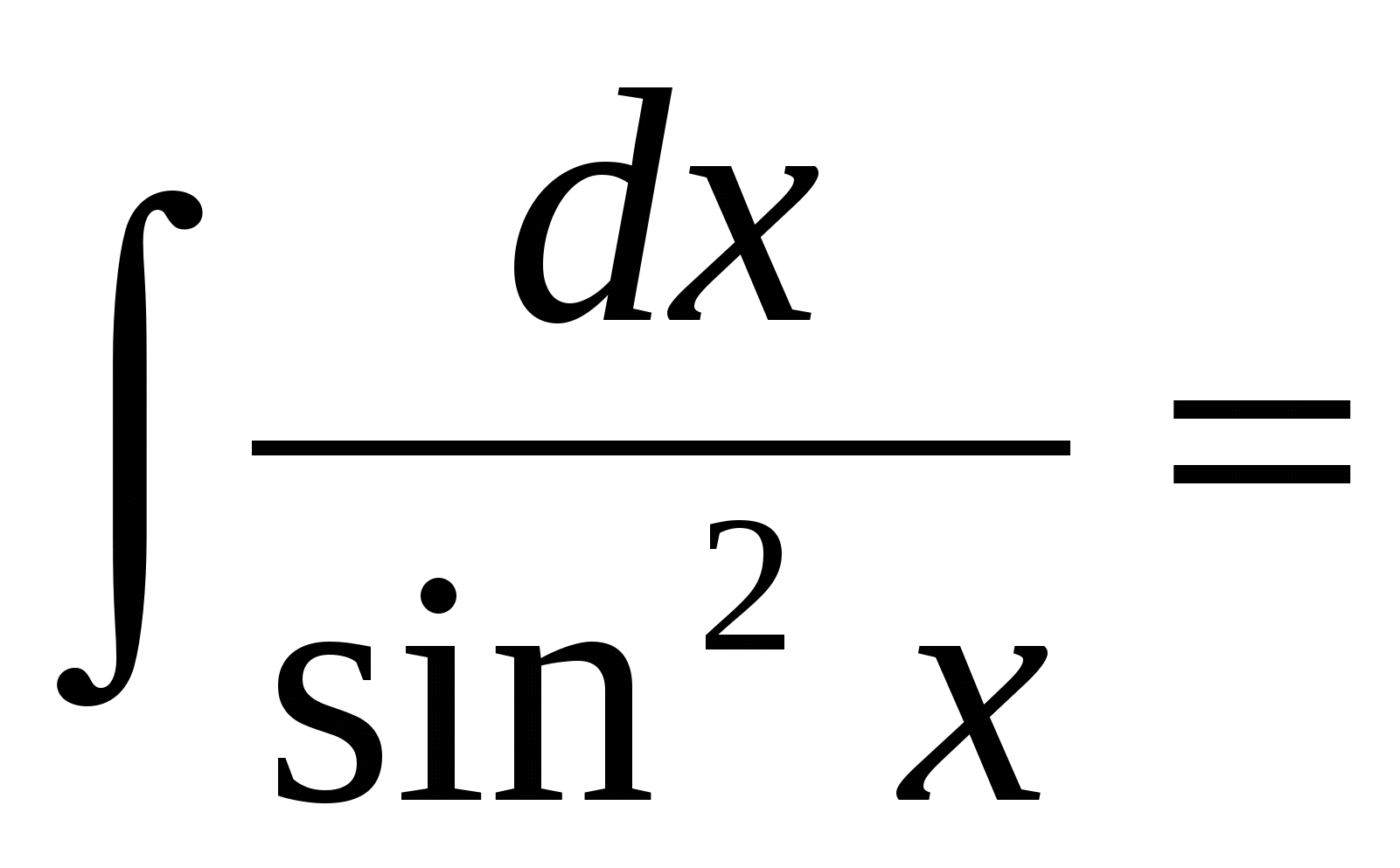
9о. 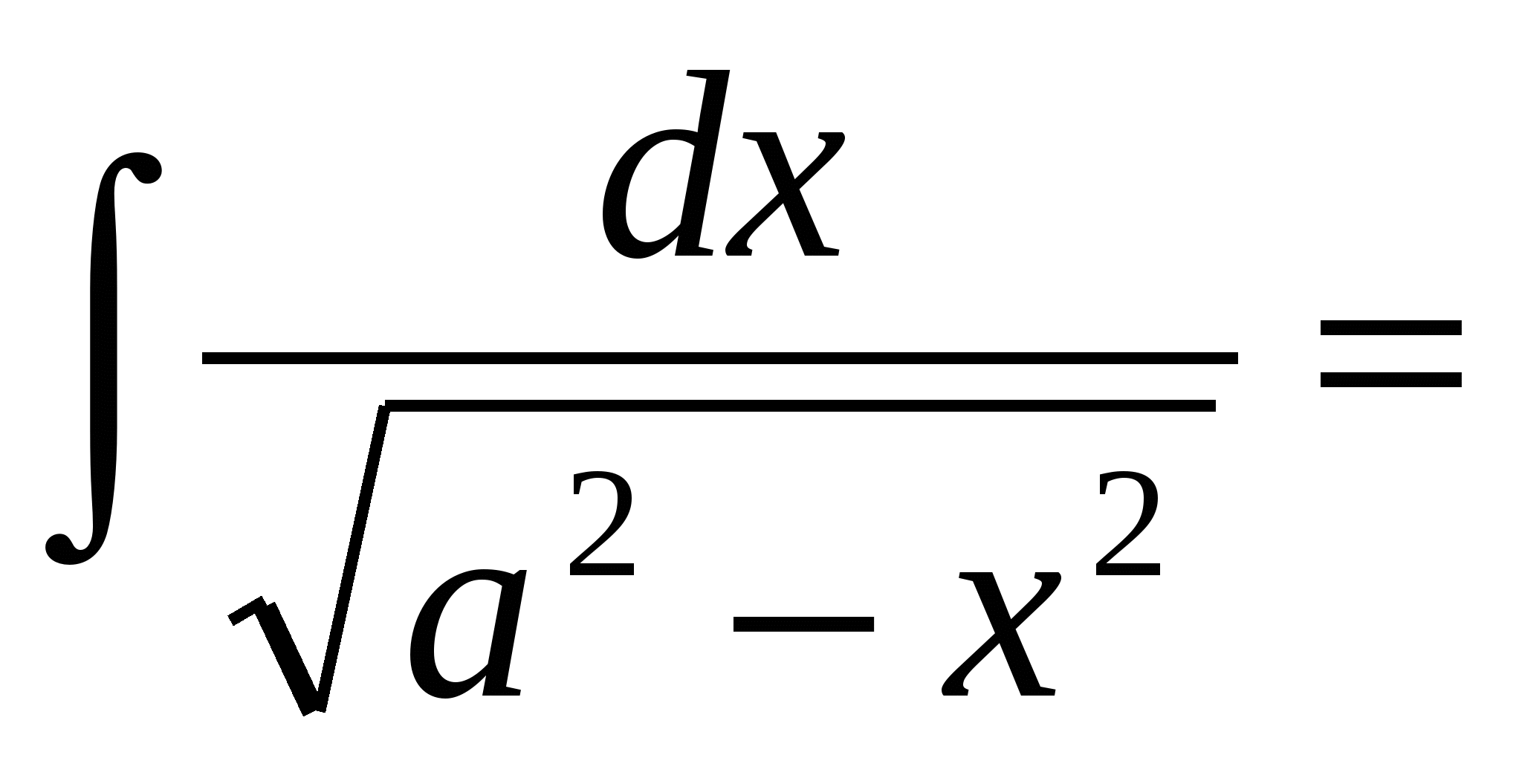
В частности, 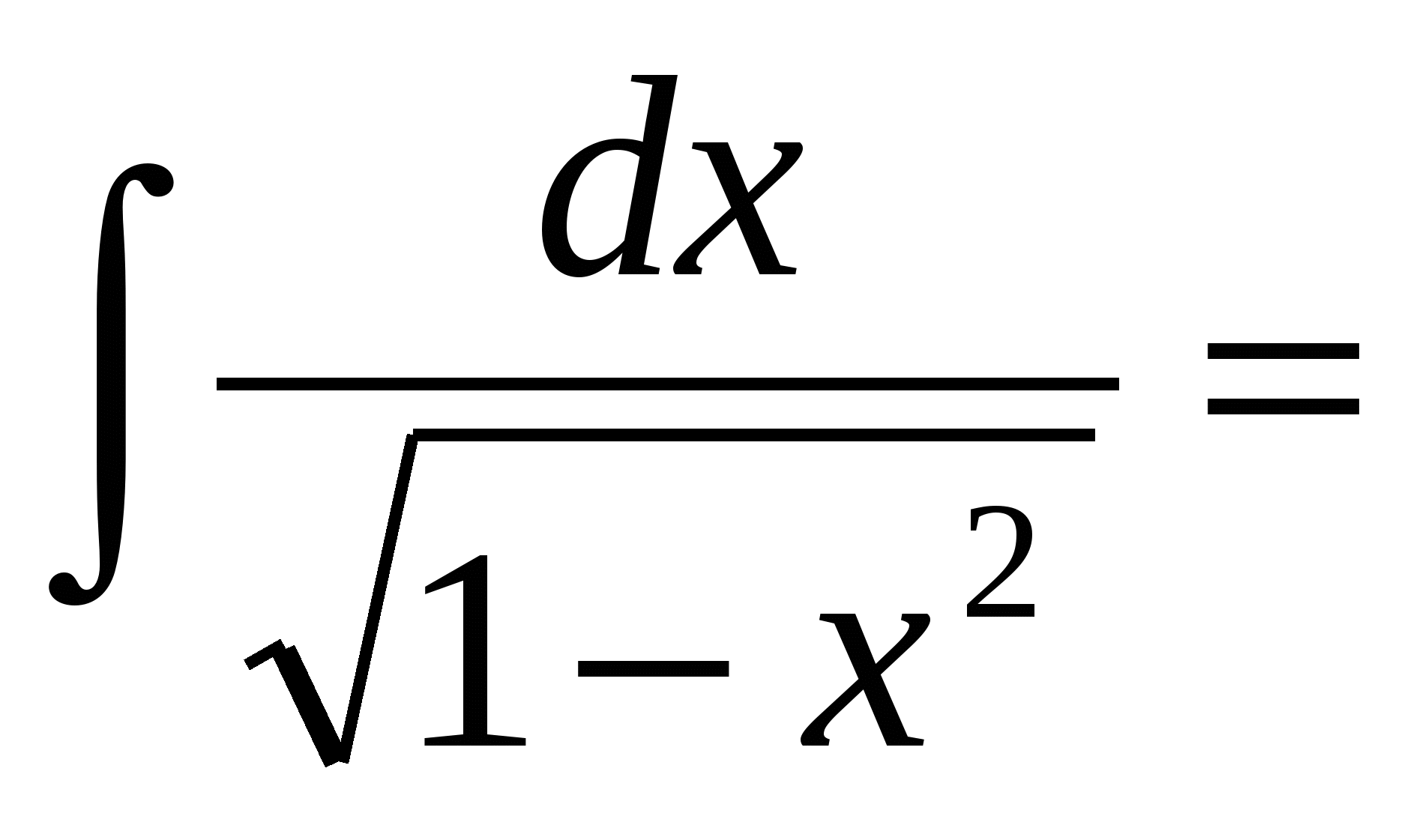
10о. 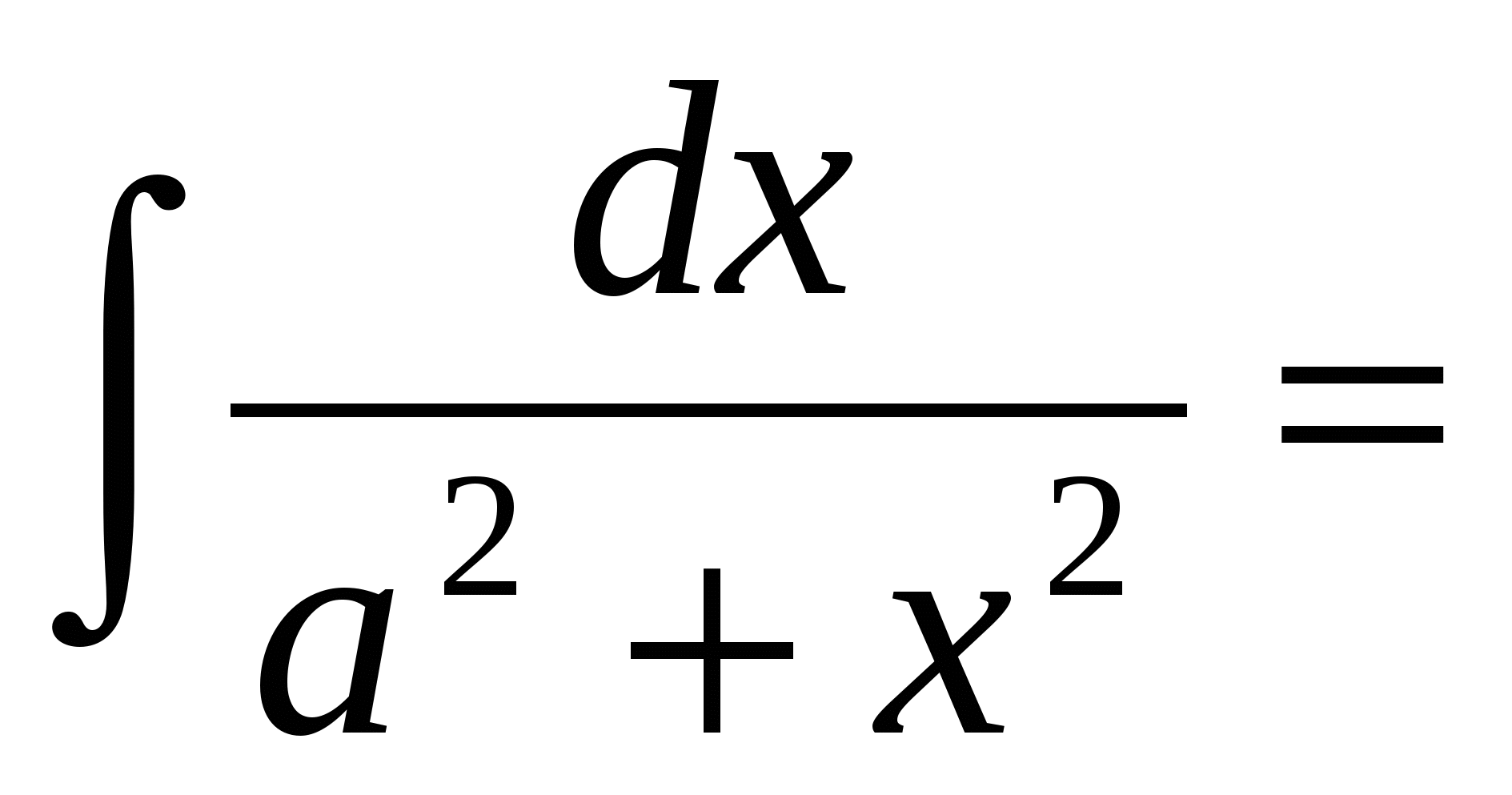
В частности, 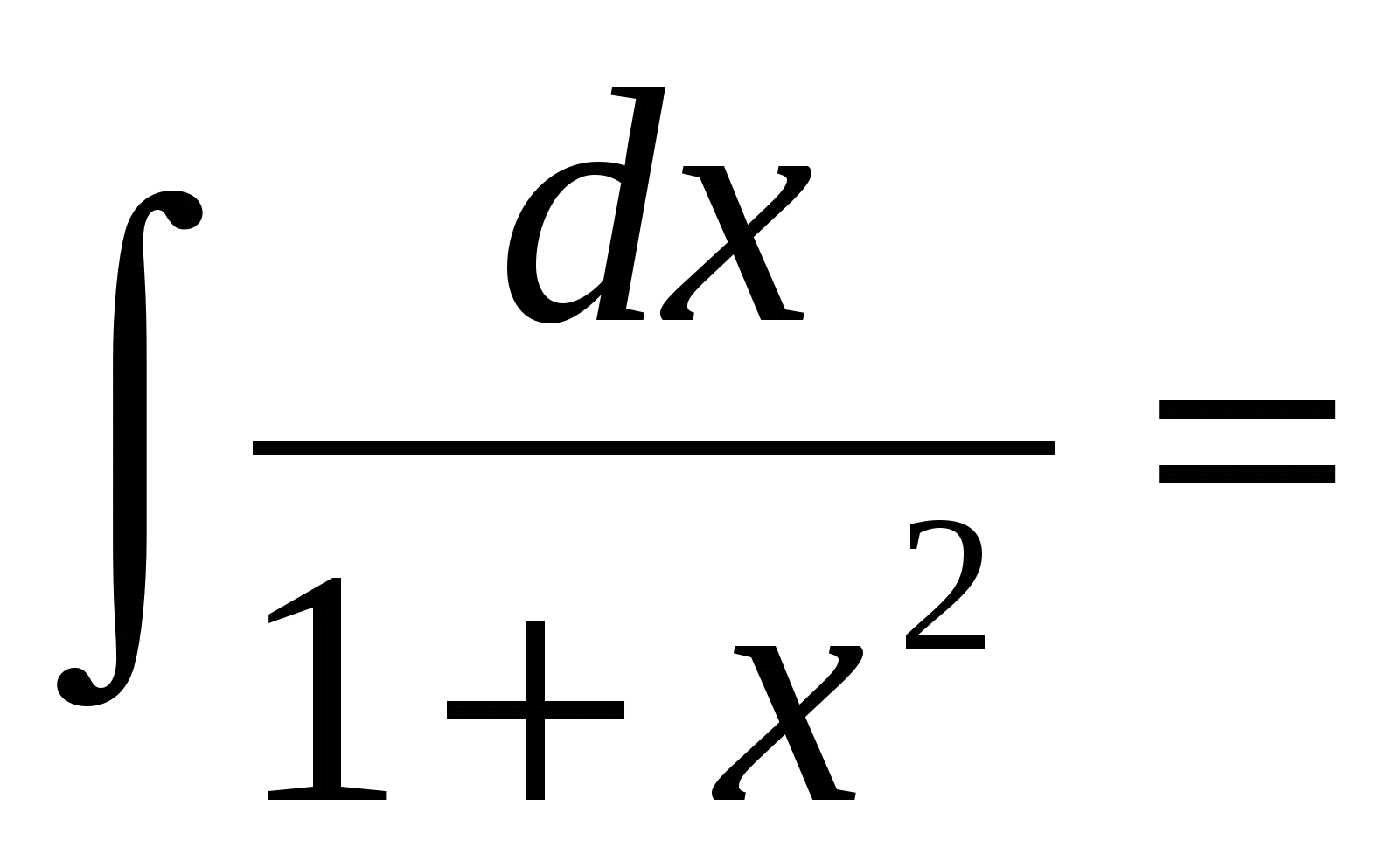
3.2.4 Контрольные работы
Контрольная работа №1 по теме «Основы тригонометрии»
Время выполнения 90 минут
Вариант 1
1. Найдите 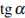
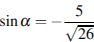
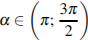
2. Найдите 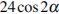
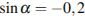
3. Найдите значение выражения 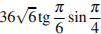
4. Найдите значение выражения 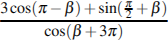
5. Решите уравнение 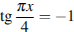
6. Решите уравнение 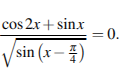
7. Деталью некоторого прибора является квадратная рамка с намотанным на неe проводом, через который пропущен постоянный ток. Рамка помещена в однородное магнитное поле так, что она может вращаться. Момент силы Ампера, стремящейся повернуть рамку, (в Н
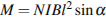
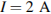
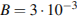
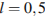
— число витков провода в рамке,
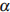
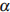

Вариант 2
1. Найдите 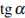
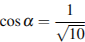
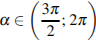
2. Найдите 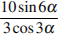
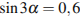
3. Найдите значение выражения 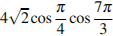
4. Найдите значение выражения 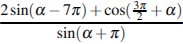
5. Решите уравнение 
6. Решите уравнение 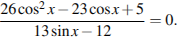
7. Очень лeгкий заряженный металлический шарик зарядом 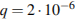
м/с, на него начинает действовать постоянное магнитное поле, вектор индукции
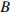
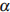
Тл. При этом на шарик действует сила Лоренца, равная
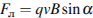
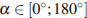
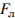
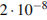
Контрольная работа №2 по теме «Уравнения и неравенства»
Время выполнения 90 минут
Вариант 1
Уровень В
-
Найдите корень уравнения:
.
-
Решите уравнение
.
-
Решите уравнение
. Если уравнение имеет более одного корня, в ответе запишите больший из корней.
-
Решите уравнение
.
-
Найдите корень уравнения:
.
-
Найдите корень уравнения
.
-
Имеется два сплава. Первый сплав содержит 10% никеля, второй — 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава меньше массы второго?
Уровень С
а) Решите уравнение 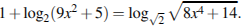
б) Найдите все корни этого уравнения, принадлежащие отрезку 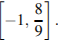
Вариант 2
Уровень В
-
Найдите корень уравнения:
.
-
Найдите корень уравнения
-
Решите уравнение
. Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
-
Решите уравнение
.
-
Найдите корень уравнения:
-
Решите уравнение
.
-
Первый сплав содержит 10% меди, второй — 40% меди. Масса второго сплава больше массы первого на 3 кг. Из этих двух сплавов получили третий сплав, содержащий 30% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
Уровень С
а) Решите уравнение 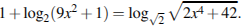
б) Найдите все корни этого уравнения, принадлежащие отрезку 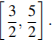
Контрольная работа №3 по теме «Интегральное исчисление функций одной переменной»
Время выполнения 90 минут
Уровень А
Вариант №1
Вариант №2
1. Докажите, 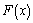
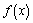
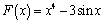
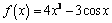
,
.
2. Вычислите интегралы:
1) 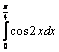
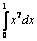
1) 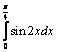
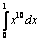
3. Для функции
Найдите какую-нибудь первообразную, значение которой в точке
— отрицательное число.
3. Для функции
Найдите какую-нибудь первообразную, значение которой в точке
— положительное число.
Уровень В
Вариант №1
Вариант №2
1.Вычислите интегралы:
1) 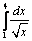
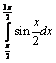
1) 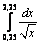
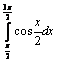
2. Вычислите площадь фигуры, ограниченной линиями:
1)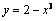
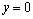
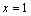
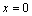
2) ,
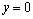
1)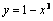
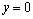
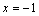
2) ,
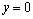
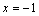
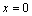
Уровень С
Вариант №1
Вариант №2
1.Вычислите площадь фигуры, ограниченной графиком функции , касательной к этому графику в точке с абсциссой
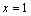
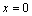
1. Вычислите площадь фигуры, ограниченной графиком функции 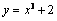
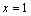
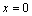
2. Вычислите площадь фигуры, ограниченной графиками функций 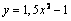

2. Вычислите площадь фигуры, ограниченной графиками функций 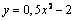
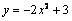
3. Дана функция
. Известно, что график некоторой ее первообразной проходит через точку
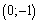
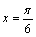
3. Дана функция
. Известно, что график некоторой ее первообразной проходит через точку
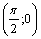
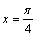
Контрольная работа №4 по теме «Измерения в геометрии»
Время выполнения 90 минут
Вариант 1
Уровень В
-
Найдите объем многогранника, вершинами которого являются точки
,
,
,
,
,
прямоугольного параллелепипеда
, у которого
,
,
.
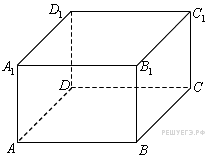
-
В
правильной треугольной пирамиде
медианы основания
пересекаются в точке
. Площадь треугольника
равна 9; объем пирамиды равен 6. Найдите длину отрезка
.
-
Около шара описан цилиндр, площадь поверхности которого равна 18. Найдите площадь поверхности шара.
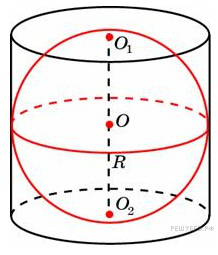
-
В сосуд, имеющий форму правильной треугольной призмы, налили 2300
воды и погрузили в воду деталь. При этом уровень воды поднялся с отметки 25 см до отметки 27 см. Найдите объем детали. Ответ выразите в
.
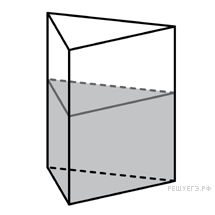
-
Объем конуса равен 16. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.
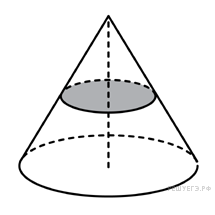
Уровень С
Площадь боковой поверхности правильной четырёхугольной пирамиды SABCD равна 108, а площадь полной поверхности этой пирамиды равна 144. Найдите площадь сечения, проходящего через вершину S этой пирамиды и через диагональ её основания.
Вариант 2
Уровень В
-
Объем параллелепипеда
равен 4,5. Найдите объем треугольной пирамиды
.
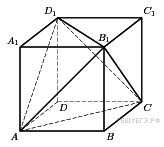
-
В
правильной треугольной пирамиде
медианы основания
пересекаются в точке
. Площадь треугольника
равна 2; объем пирамиды равен 5. Найдите длину отрезка
.
-
Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 25.
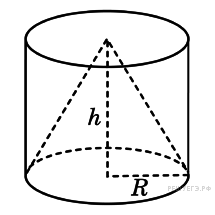
-
В
сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 80 см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в 4 раза больше, чем у первого? Ответ выразите в см.
-
Площадь большого круга шара равна 3. Найдите площадь поверхности шара.
Уровень С
В правильной четырёхугольной пирамиде SABCD с основанием ABCD проведено сечение через середины рёбер AB и BC и вершину S. Найдите площадь этого сечения, если боковое ребро пирамиды равно 5, а сторона основания равна 4.
3.2.5 Экзаменационные вопросы
-
Аксиомы стереометрии.
-
Векторы и скалярные величины.
-
Взаимное расположение двух плоскостей в пространстве.
-
Взаимное расположение двух прямых в пространстве.
-
Взаимное расположение прямой и плоскости.
-
Возрастание и убывание функций.
-
Геометрический смысл производной.
-
График логарифмической функции.
-
График степенной функции.
-
Графики тригонометрических функций.
-
Действия над векторами, заданными в координатной форме. Угол между векторами.
-
Действия над комплексными числами.
-
Замечательные пределы.
-
Иррациональные уравнения.
-
Квадратные уравнения, их решение.
-
Классическая формула вероятности.
-
Комплексные числа. Алгебраическая форма комплексного числа.
-
Конус, площадь поверхности и объем конуса.
-
Координаты вектора.
-
Линейные уравнения, их решение, свойства
-
Логарифмическая функция, ее свойства и график.
-
Логарифмы с произвольным основанием. Основное логарифмическое тождество.
-
Механический смысл производной.
-
Механический смысл производной. Вторая производная.
-
Модуль вектора. Действия над векторами.
-
Непрерывность функции в точке и на промежутке. Асимптоты.
-
Обратные тригонометрические функции.
-
Определенный интеграл. Формула Ньютона-Лейбница.
-
Определитель 2-го порядка
-
Основные тригонометрические тождества.
-
Перестановки, размещения, сочетания.
-
Перпендикуляр и наклонная.
-
Пирамида. Площадь поверхности и объем пирамиды.
-
Площадь ортогональной проекции.
-
Показательная функция, ее свойства и график.
-
Понятие первообразной.
-
Правила нахождения производных.
-
Предел последовательности.
-
Призма, ее площадь поверхности и объем.
-
Производная сложной функции.
-
Решение дробно-рациональных неравенств методом интервалов.
-
Решение системы из 2-х линейных уравнений методом Крамера.
-
Свойства функций: четность, нечетность, периодичность, область определения, область значений, монотонность.
-
Скалярное произведение векторов.
-
Соотношения между градусной и радианной мерами дуг.
-
Таблица первообразных.
-
Таблица производных.
-
Теорема о трех перпендикулярах.
-
Точки экстремума и экстремумы функций.
-
Тригонометрическая форма комплексного числа.
-
Тригонометрические уравнения.
-
Тригонометрические функции двойного аргумента.
-
Уравнение сферы.
-
Уравнения плоскости в пространстве.
-
Уравнения прямой на плоскости.
-
Функция. Способы задания функции.
-
Цилиндр. Площадь поверхности и объем цилиндра.
-
Числовая последовательность.
-
Числовые множества: натуральные, целые, рациональные, действительные числа.
-
Шар и сфера.
3.2.6 Экзаменационные задачи
1) Решите систему неравенств:

х — 3 > -3x + 1.
2) Решите уравнение:
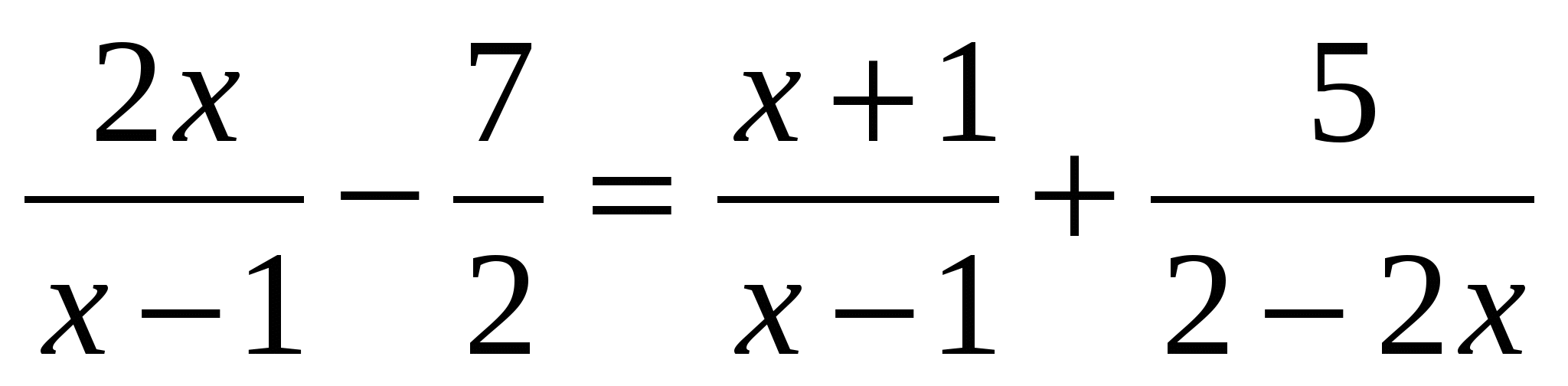
3) Вычислите х: log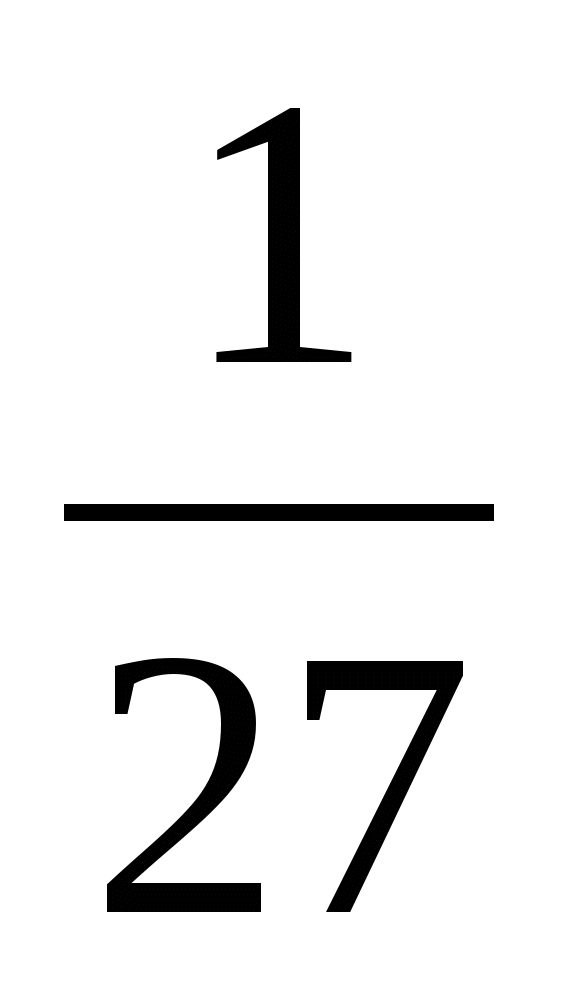
4) Решите биквадратное уравнение:
х4 — 5х2 + 4 = 0.
5) Решите систему методом Крамера:

4х + 3у =- 27.
6) Найдите область определения функции:
у = 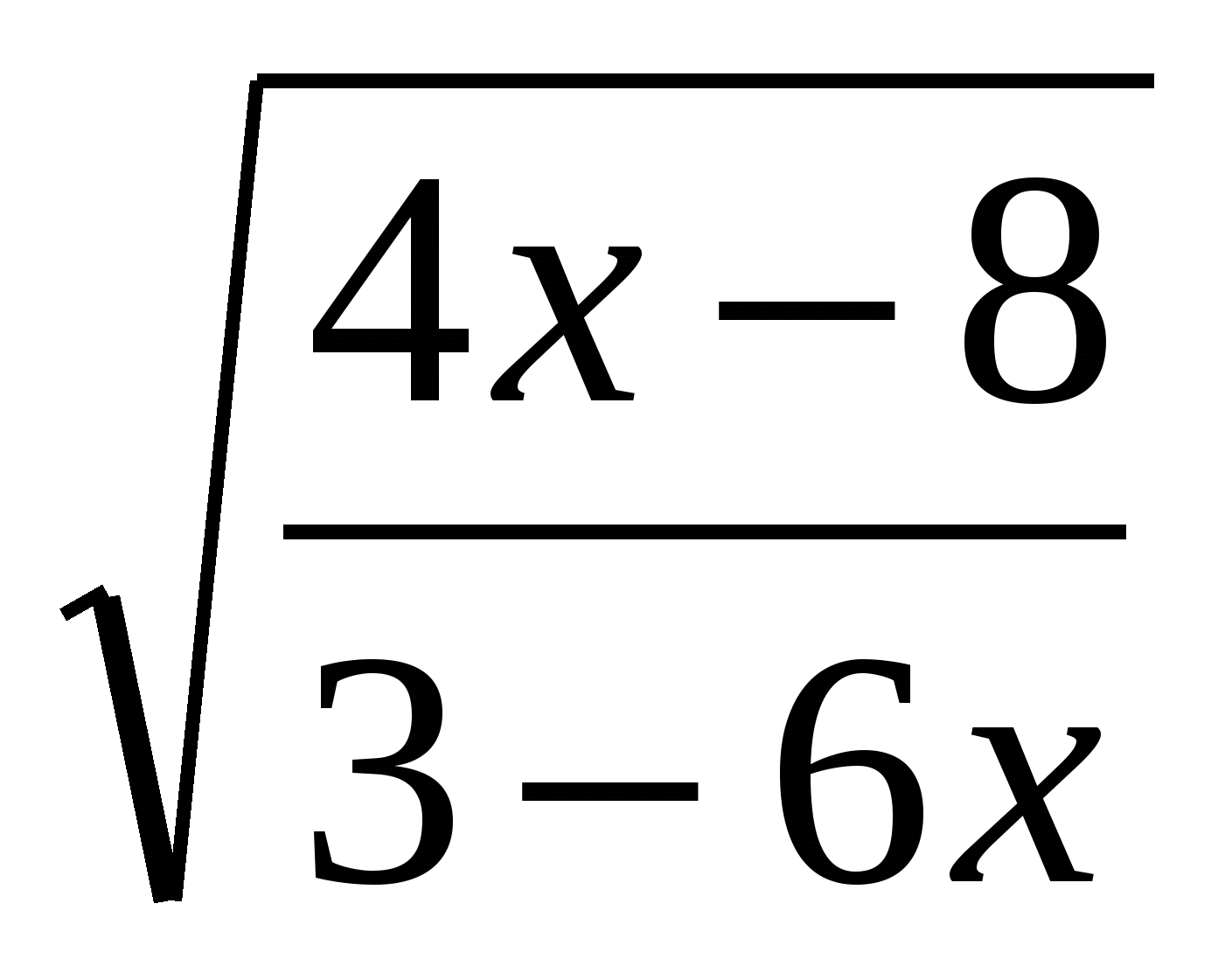
7) Решите квадратное уравнение:
(х — 3)2 + (х — 4)2 — (х — 5)2 — х = 24.

x2 — 5х + 6 < 0.
9) Найдите значение производной функции в точке М(1;1): у = 3 х — 1.
10) Постройте график функции: у = log2(х — 2).
11) Решите показательное уравнение:
9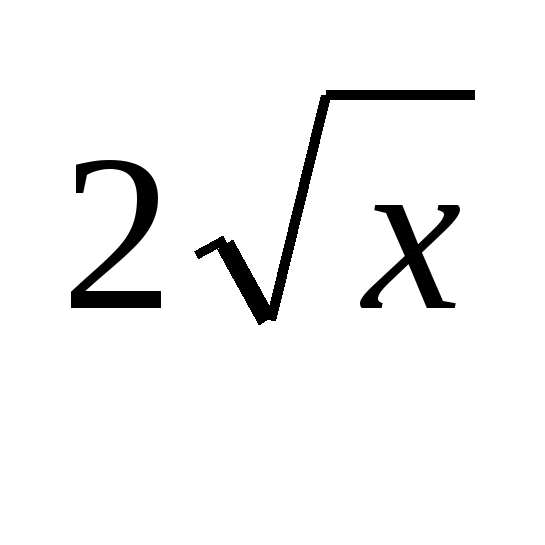
12) Решите показательное неравенство:
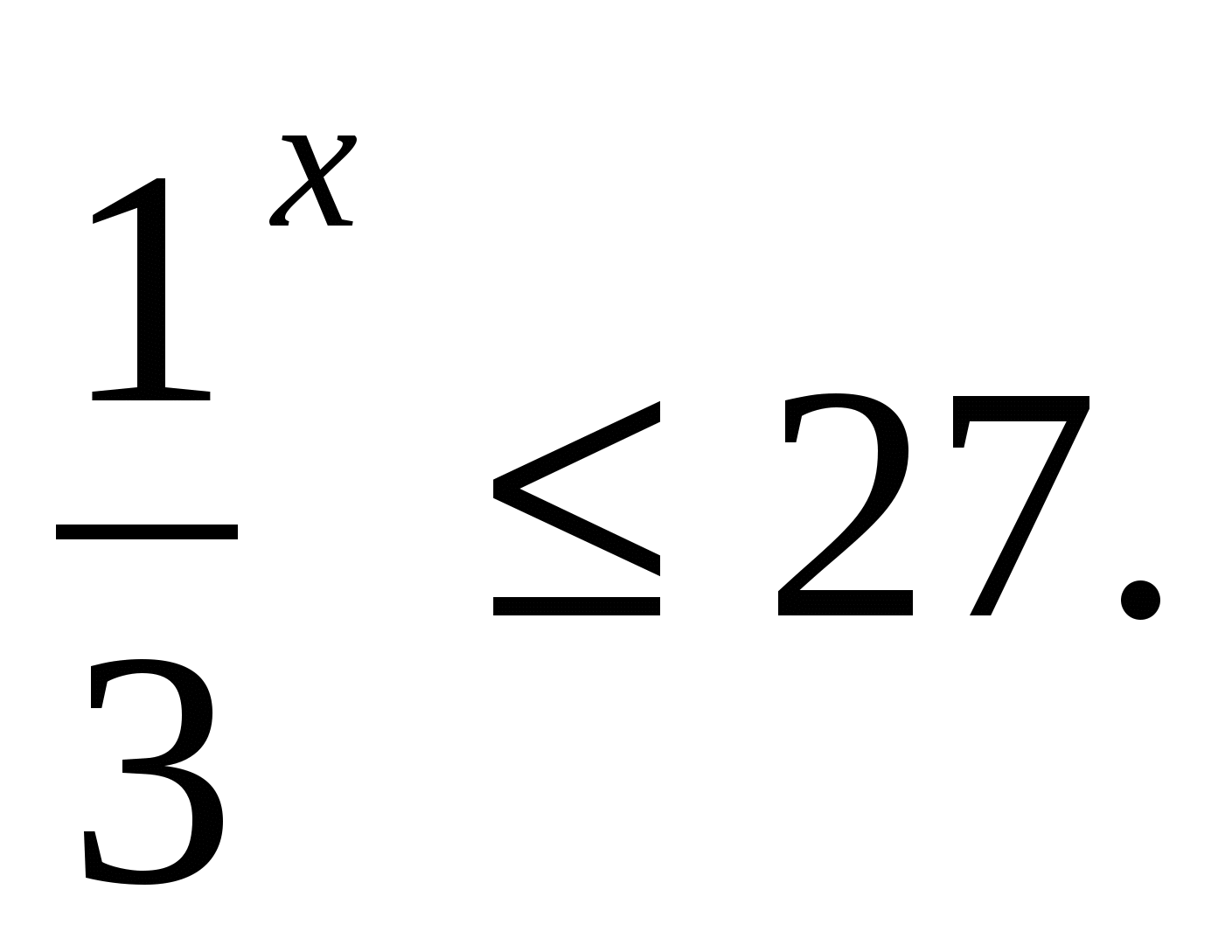
13) Найдите первообразную функции у = sin x + 2, проходящую через точку М(0;1).
14) Найдите угловой коэффициент касательной, проведенной к графику функции
y = x2-2x+4 в точке х0 = -1.
15) Решите иррациональное уравнение:
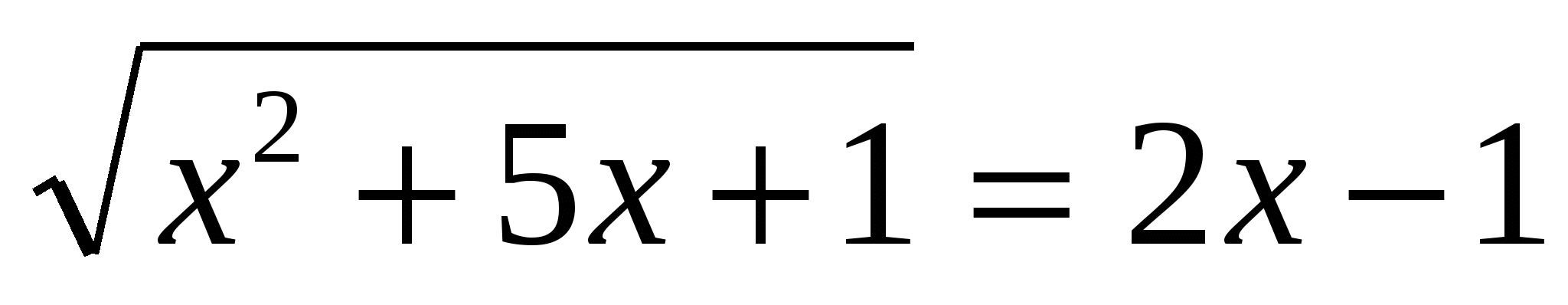
16) Найдите градусную меру угла 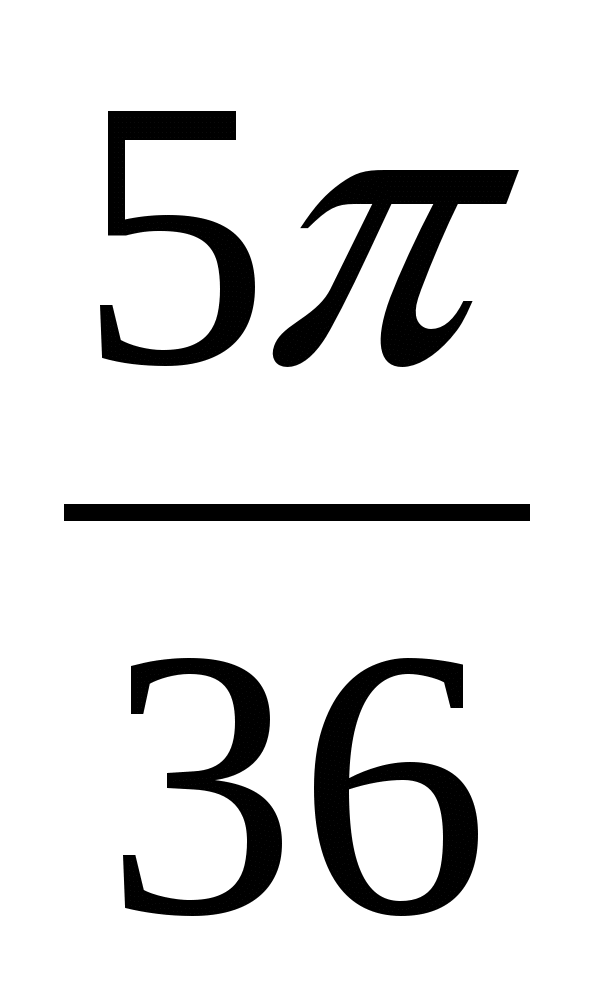
17) Решите тригонометрическое уравнение:
tg (3x + 1) = 1.
18) Найдите площадь ортогональной проекции фигуры на плоскость, если площадь фигуры равна 20 см2, а угол между плоскостью фигуры и плоскостью проекции составляет 450.
19) Найти производную функции: у = (2х+3)8.
20) Найдите площадь фигуры, ограниченной линиями: y = 4-x2, y=0.
21) Из точки А на плоскость α проведены перпендикуляр АВ и наклонная АС. Длина перпендикуляра АВ равна 12 см, длина проекции наклонной ВС равна 5 см. Найдите длину наклонной АС.
22) Найдите координаты и длину вектора 
23) Найдите область определения функции:
У = log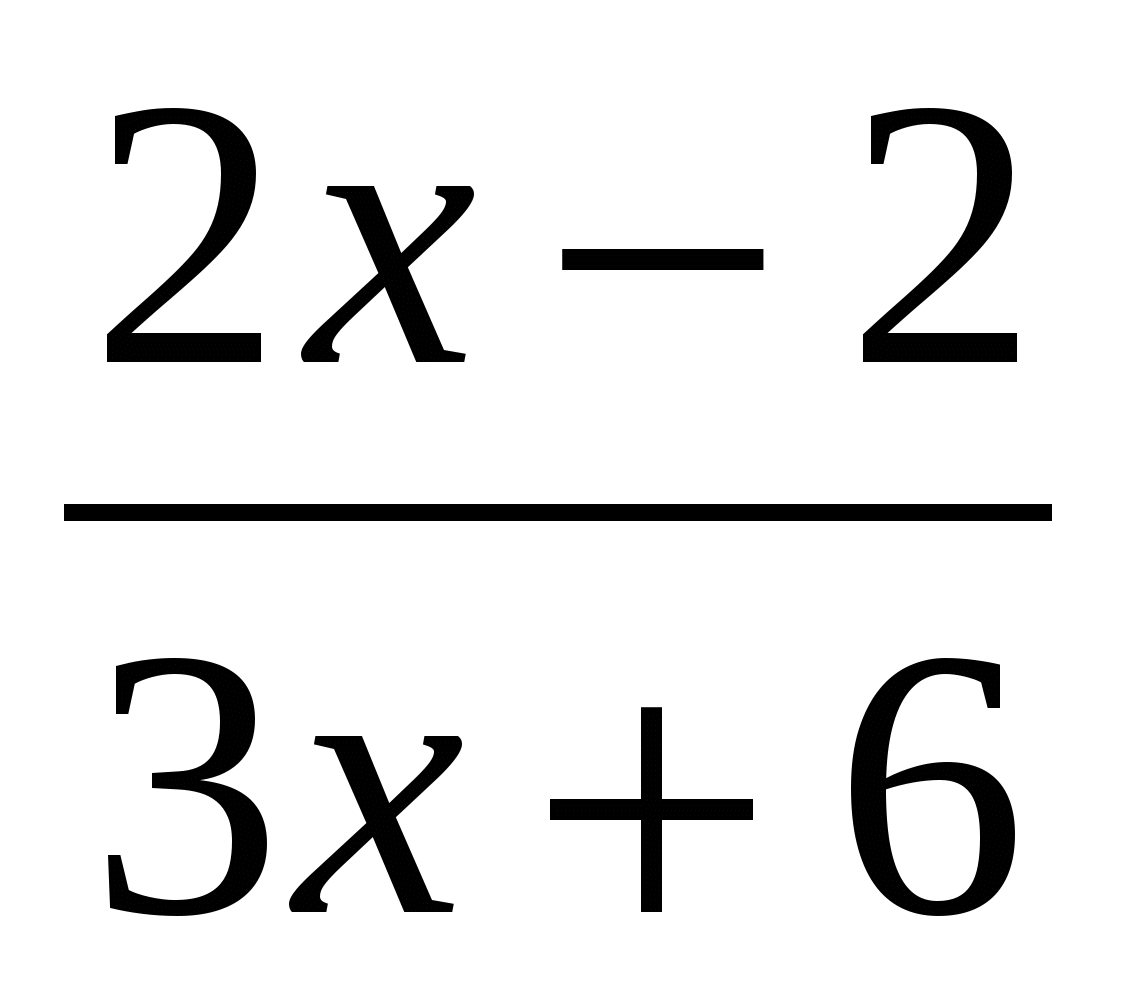
24) Проверьте, коллинеарны ли векторы а = (2;6) и с = (-6;2).
25) Бросают игральную кость. Какова вероятность, что выпадет больше 4 очков?
26) Найдите cos x, если sin x = 0.6 и x — угол 2 четверти.
27) Найдите скорость тела в момент времени t=3 с, если его координата
изменяется по закону: x = t3 — 2t2 + 3.
28) Проверьте, ортогональны ли векторы а = (2;6) и с = (-6;2).
29) Вычислите координаты точки М, которая делит отрезок АВ в
отношении 1: 4, если А (1;-2), В(-4; 12).
30) Постройте прямую, заданную общим уравнением 4х — 2у + 6 = 0.
3.2.7 Примеры экзаменационных билетов
Билет №1
1. Числовые множества: натуральные, целые, рациональные, действительные числа.
2. Тригонометрические функции двойного аргумента.
3. Решите систему неравенств:

х — 3 > -3x + 1.
Билет №2
-
Линейные уравнения, их решение, свойства.
-
Тригонометрические уравнения.
-
Вычислите х: log
=x.
Билет №3
-
Определитель 2-го порядка.
-
Обратные тригонометрические функции.
3. Решите уравнение:
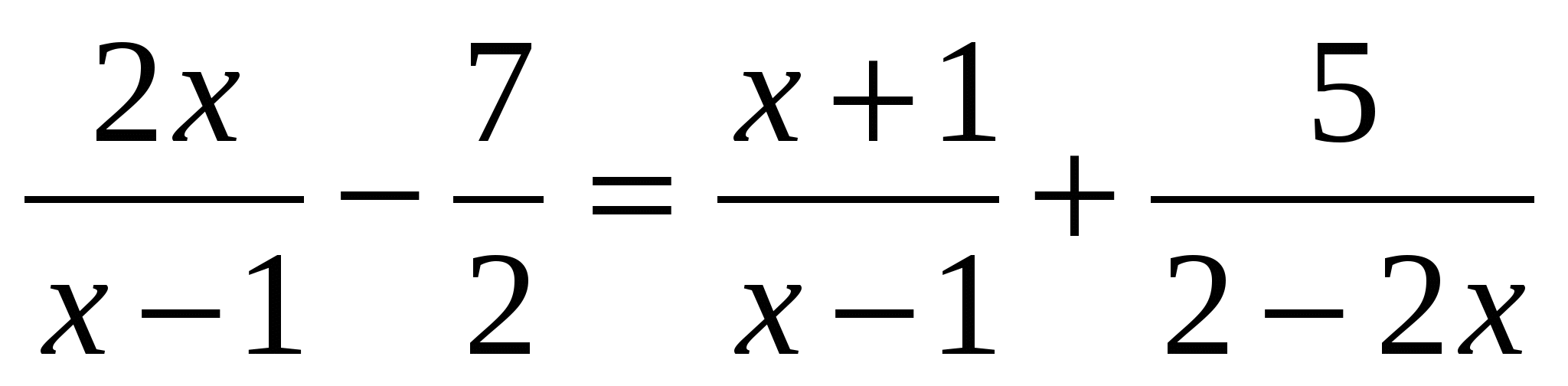
Билет №4
-
Решение системы из 2-х линейных уравнений методом Крамера.
-
Графики тригонометрических функций.
3. Решите биквадратное уравнение:
х4 — 5х2 + 4 = 0.
Билет №5
1. Производная сложной функции.
2. График логарифмической функции.
-
Решите систему методом Крамера:
2
4х + 3у =- 27.
Билет №6
-
Решение дробно-рациональных неравенств методом интервалов.
-
График степенной функции.
-
Решите квадратное уравнение:
(х — 3)2 + (х — 4)2 — (х — 5)2 — х = 24.
Билет №7
-
Квадратные уравнения, их решение.
-
Механический смысл производной.
3. Найдите область определения функции:
у = 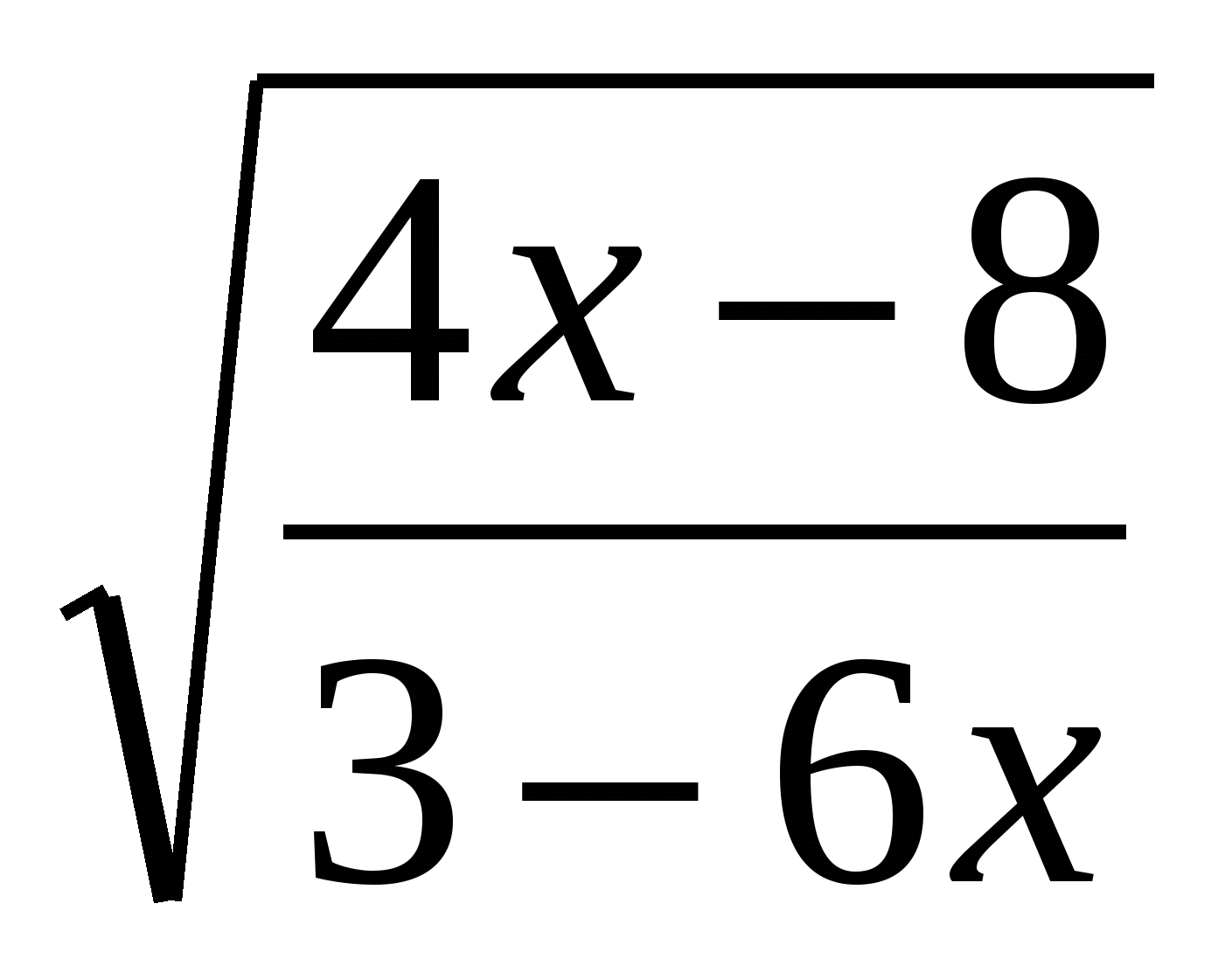
Билет №8
-
Таблица производных.
-
Призма, ее площадь поверхности и объем.
3. Решите квадратное неравенство методом интервалов:
x2 — 5х + 6 < 0.
Билет №9
-
Иррациональные уравнения.
-
Точки экстремума и экстремумы функций.
3. Найдите значение производной функции в точке М(1;1): у = 3 х — 1.
Билет №10
-
Правила нахождения производных.
-
Взаимное расположение двух плоскостей в пространстве.
3. Решите показательное уравнение:
9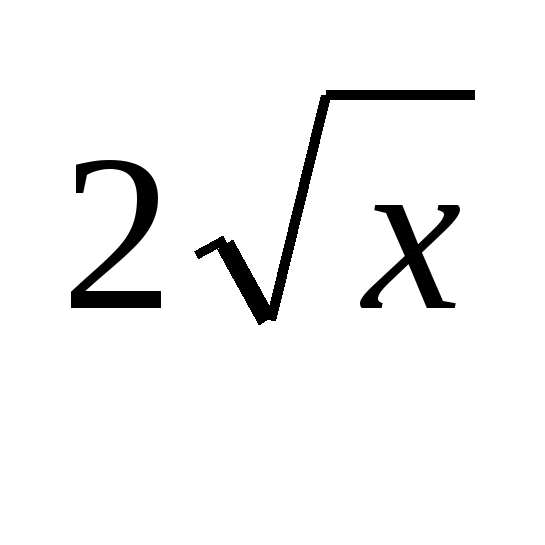
4 Критерии оценивания по результатам текущего, рубежного и итогового контроля
4.1 Пояснительная записка
Оценка умений и знаний студентов по математике происходит в ходе текущего, рубежного и итогового контроля. Предметом оценки служат умения и знания, предусмотренные программой по дисциплине «Математика». Текущий контроль проводится преподавателем в процессе проведения теоретических занятий — устный опрос, тестирование, проверочная работа. Рубежный контроль осуществляется после изучения ключевых тем курса математики в форме контрольной работы. Обучение учебной дисциплине завершается итоговым контролем в форме экзамена.
Формы и методы текущего, рубежного и итогового контроля по учебной дисциплине доводятся до сведения обучающихся не позднее двух месяцев от начала обучения по основной профессиональной образовательной программе.
Обязательные пункты при осуществлении текущего, рубежного и итогового контроля по дисциплине «Математика»:
-
Текущий контроль проводится ежеурочно в форме: устного ответа, оценки выполнения практического задания (решения задачи), докладов, сообщений, тестовых заданий.
-
Рубежный контроль проводится в форме контрольной работы по изученной теме. Контрольная работа включает стандартные ключевые задачи по контролируемой теме и задание повышенной сложности.
-
Итоговый контроль (аттестация) обучающихся по дисциплине «Математика» проводится в форме экзамена.
Экзаменационный билет содержит два теоретических вопроса и задачу по изученному предмету. К экзамену допускаются обучающиеся, имеющие положительные оценки по всем контрольным работам, включенным в рубежный контроль.
4.2 Критерии оценок
При оценивании письменных и устных ответов обучающихся преподаватель придерживается следующих критериев.
-
Оценка «5» — ответы на вопросы даны в полном объеме, все задачи решены верно.
-
Оценка «4» — ответы на вопросы даны в полном объеме, все задачи решены верно, но допущены неточности или несущественные ошибки при оформлении документов.
-
Оценка «3» — ответы на вопросы даны, все задачи решены, но допущены существенные ошибки и неточности.
-
Оценка «2» — ответы на вопросы не даны, задачи не решены.
Оценка индивидуальных образовательных достижений по результатам текущего контроля и промежуточной аттестации производится в соответствии с универсальной шкалой (таблица 3).
Таблица 3
-
Процент результативности (правильных ответов)
Качественная оценка индивидуальных образовательных достижений
балл (отметка)
вербальный аналог
90 ÷ 100
5
отлично
80 ÷ 89
4
хорошо
70 ÷ 79
3
удовлетворительно
менее 70
2
не удовлетворительно
5 Перечень материалов, оборудования и информационных источников, используемых в аттестации
-
Дидактический материал по всем изучаемым темам (планы и конспекты уроков, презентации, видеоуроки);
-
комплект материалов для текущего и рубежного контроля (тесты, проверочные и контрольные работы)
-
комплект материалов для итогового контроля (экзаменационные билеты);
-
интерактивная доска, компьютер, проектор;
-
набор макетов многогранников и тел вращения.
6 Основная учебная, справочная и методическая литература
Перечень рекомендуемых учебных изданий, Интернет-ресурсов, дополнительной литературы:
Основные источники:
1. Алгебра и начала математического анализа: учебник для 10-11 кл.общеобразоват.учреждений / [А.Н.Колмогоров, А.М.Абрамов, Ю.П.Дудницын и др.]; под ред.А.Н.Колмогорова. — М.: Просвещение, 2008.
2. Богомолов, Н.В. Практические занятия по математике: Учеб. пособие для средних спец. учебных заведений/Н.В.Богомолов. — М.: Высшя школа, 2003.
3. Вентцель, Е.С. Теория вероятностей: Учебник для вузов. — М.: Высшая школа, 2008.
4. Григорьев, С.Г. Математика: учебник для студентов средних проф. учреждений/С.Г.Григорьев, С.В.Задулина; под ред. В.А.Гусева. — М.: Изд. центр «Академия», 2009.
5. Математика. Подготовка к ЕГЭ-2016: учеб.-метод. пособие/Под ред. Ф.Ф.Лысенко, С.Ю.Кулабухова. — Ростов-на-Дону: Легион-М, 2015.
6. Погорелов, А.В. Геометрия 10-11 кл.: учеб. для общеобразоват. учреждений: базовый и профильный уровни/А.В.Погорелов. — М.: Просвещение, 2010.
Дополнительные источники:
-
Брадис, В.М. Четырехзначные математические таблицы: Для средней школы. — М.: Просвещение, 2010.
-
Геометрия: Учебник для студентов средних проф. учебных заведений/Под ред.Г.Н.Яковлева. — М.:Наука, 2010.
-
Глейзер, Г.Д., Саакян С.М., Алексеев А.С., Вяльцева И.Г. Алгебра и начала анализа: Учеб. пособие для 9-11 кл. вечерней школы. — М.: Просвещение, 2009.
-
Гмурман, В.Е. Теория вероятностей и математическая статистика. Учебное пособие для вузов. — М.: Высшая школа, 2007.
-
Григорьев, В.Г. Элементы высшей математики: учебник для студентов учреждений среднего проф. образования/В.П.Григорьев, Ю.А.Дубинский. — М.: Изд. центр «Академия», 2007.
-
Гусев, В.А., Мордович, А.Г. Математика: Справочные материалы: Кн.для учащихся. — М.: Просвещение, 2003.
-
Зайцев, И.А. Высшая математика: Учебник для с/х вузов. — М.: Высшая школа, 2008.
-
problems.ru/.
-
fipi.ru/.
-
school-collection.edu.ru/catalog/rubr/696f5fc4-7f5c-b610-713f-014b7f9c0bc8.
-
myefe.ru/mybook/product/matematika-spo.html.
-
math.sch878.edusite.ru/p16aa1.html.
-
reshuege.ru/.














































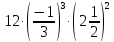
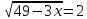
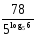
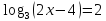
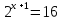
 +
+ 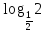
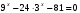
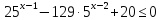
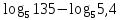
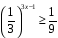
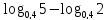
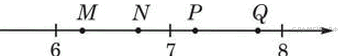
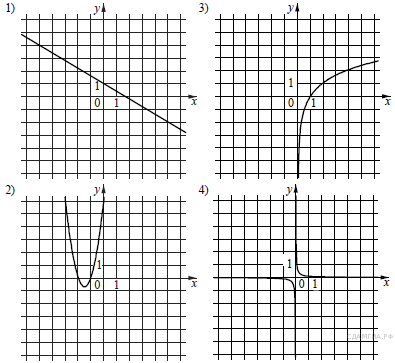
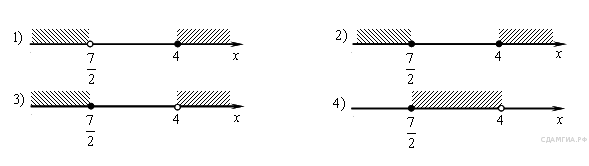
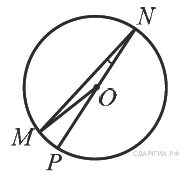
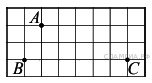
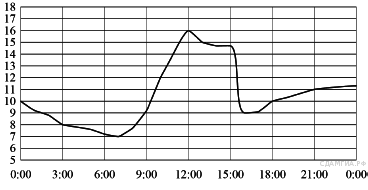
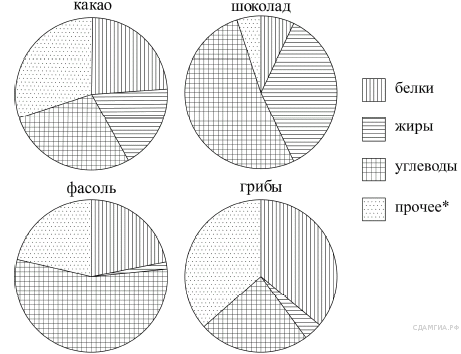
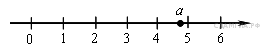
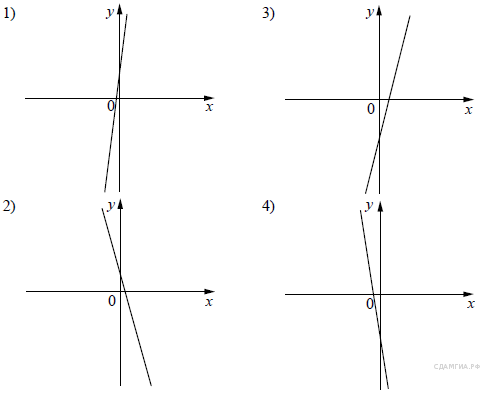
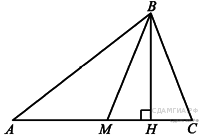
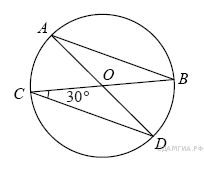
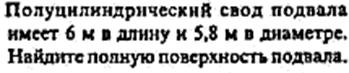
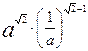

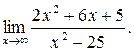
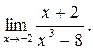

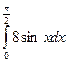




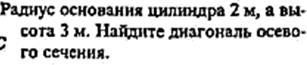
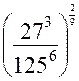


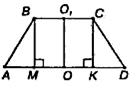


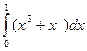

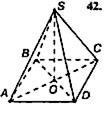

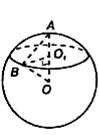

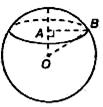
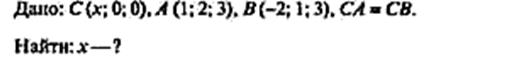
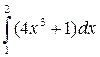

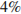 дешевле, чем при открытии торгов в понедельник. На сколько процентов подорожали акции компании в понедельник?
дешевле, чем при открытии торгов в понедельник. На сколько процентов подорожали акции компании в понедельник? 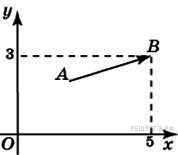
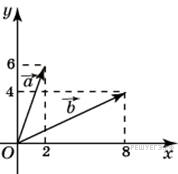
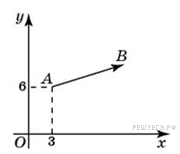
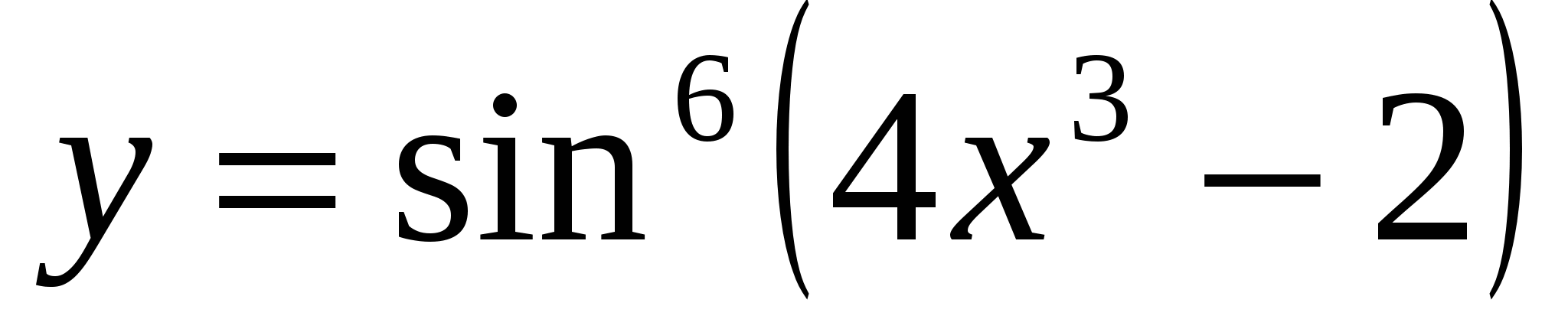 .
. 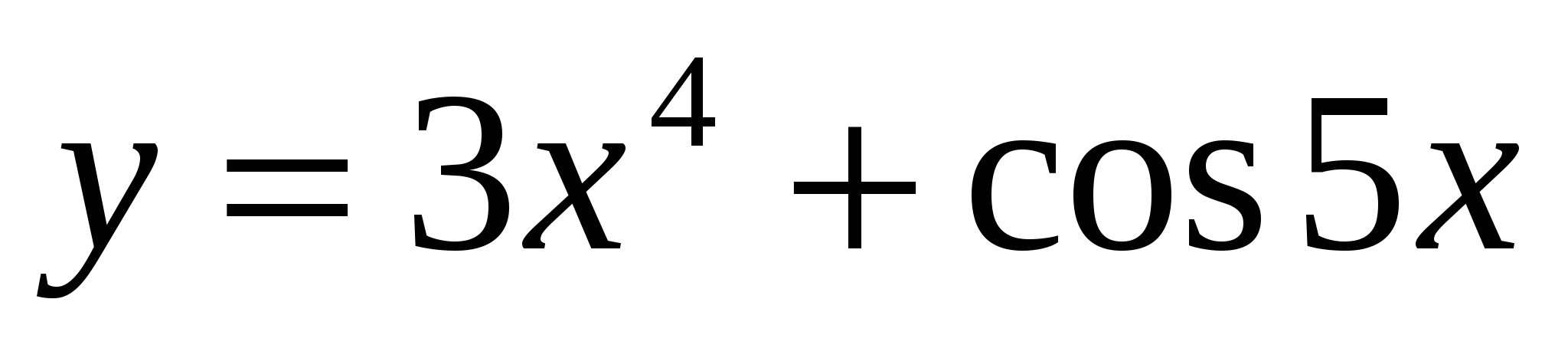 .
. 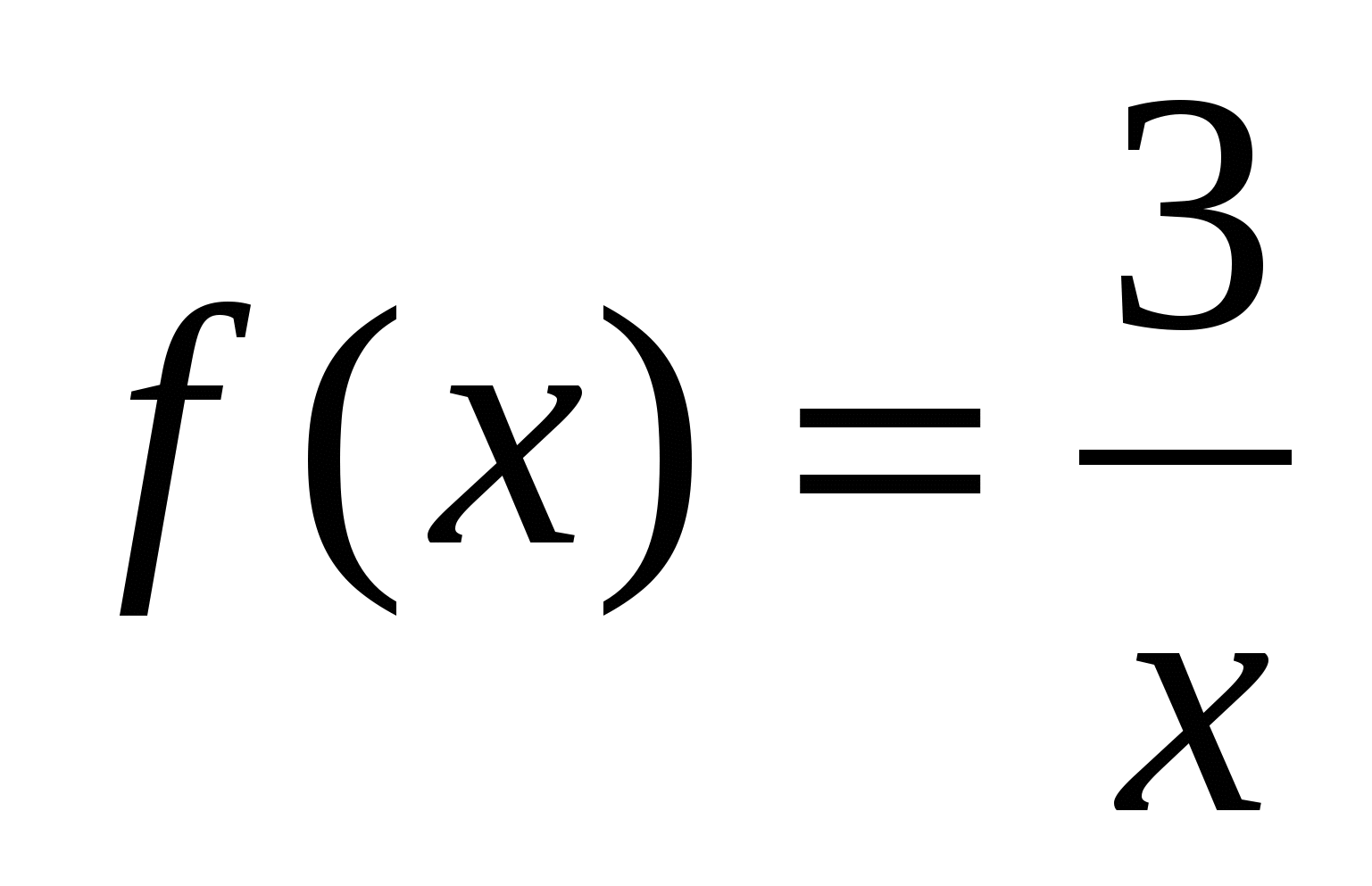 в точке с абсциссой
в точке с абсциссой 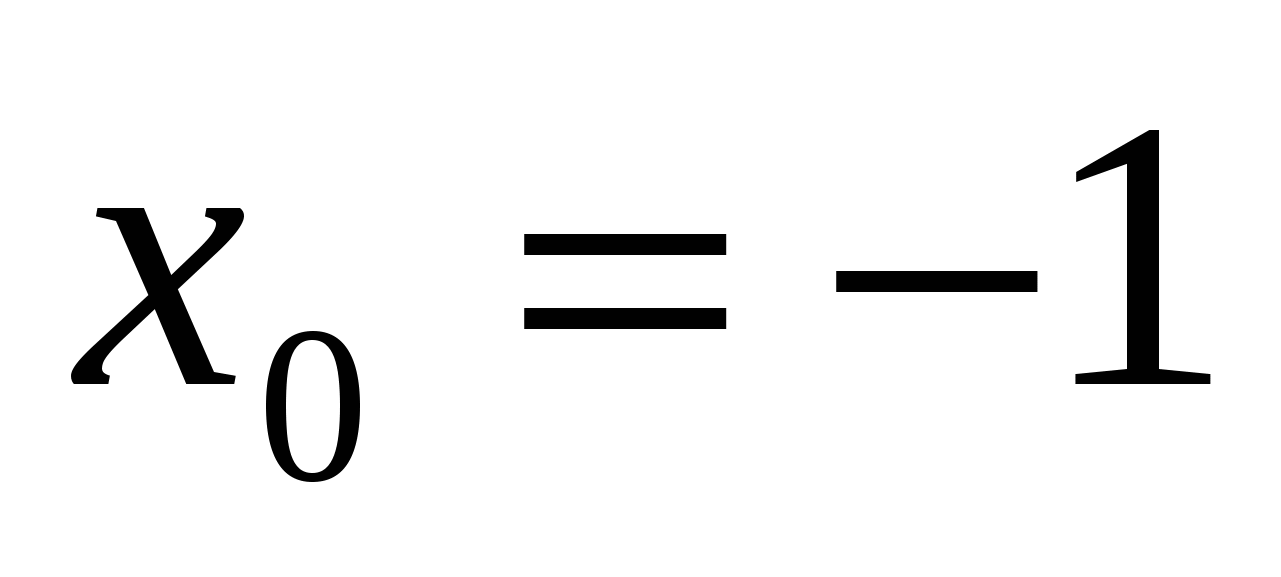 ,
, 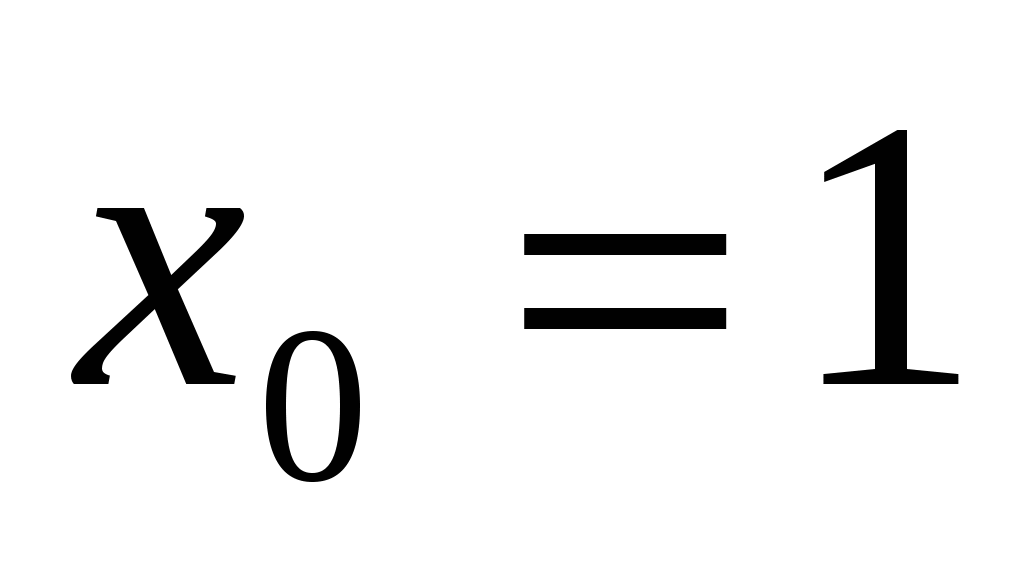 .
. 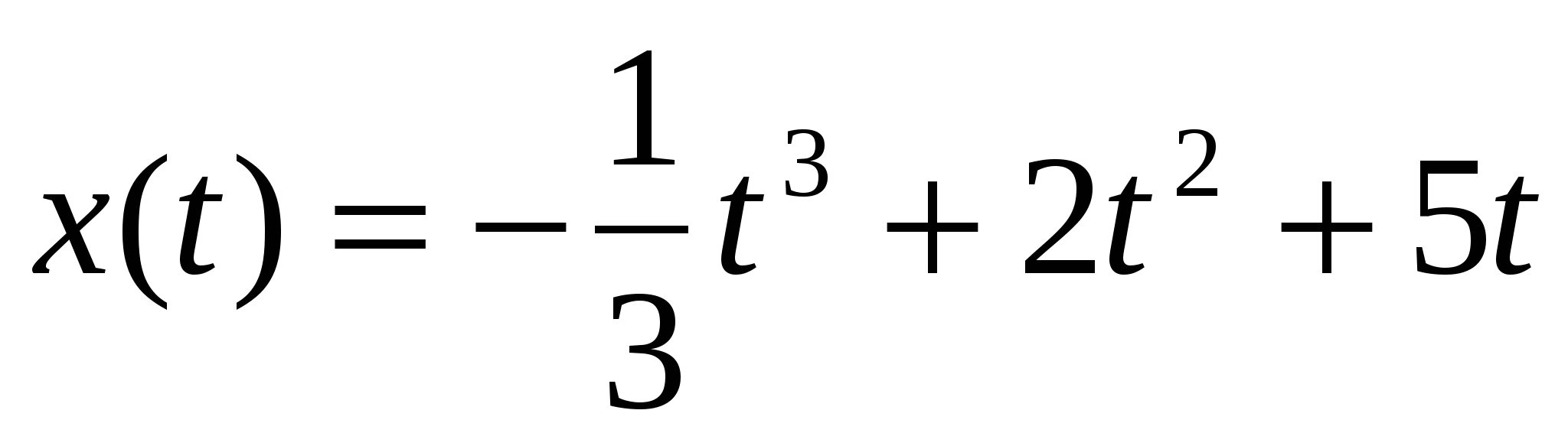 . Найти скорость и ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.)
. Найти скорость и ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.) 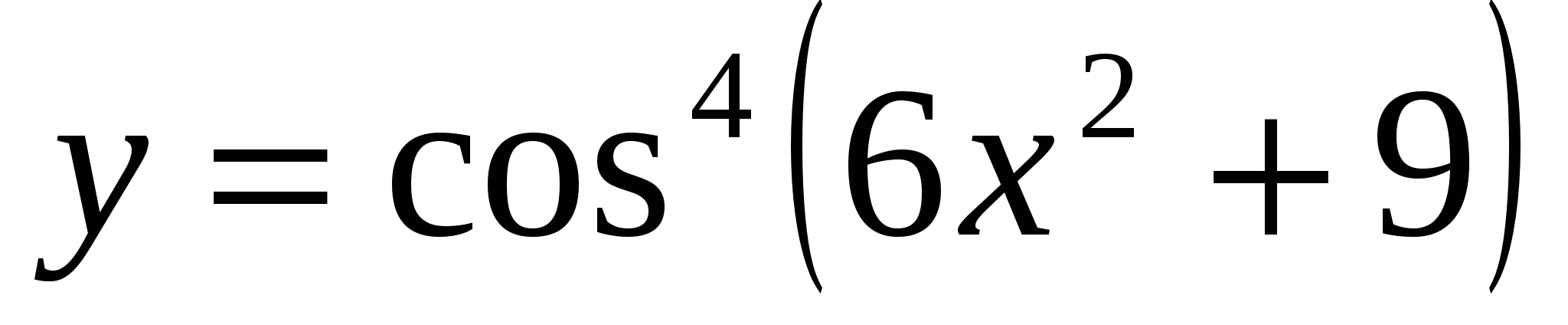 .
. 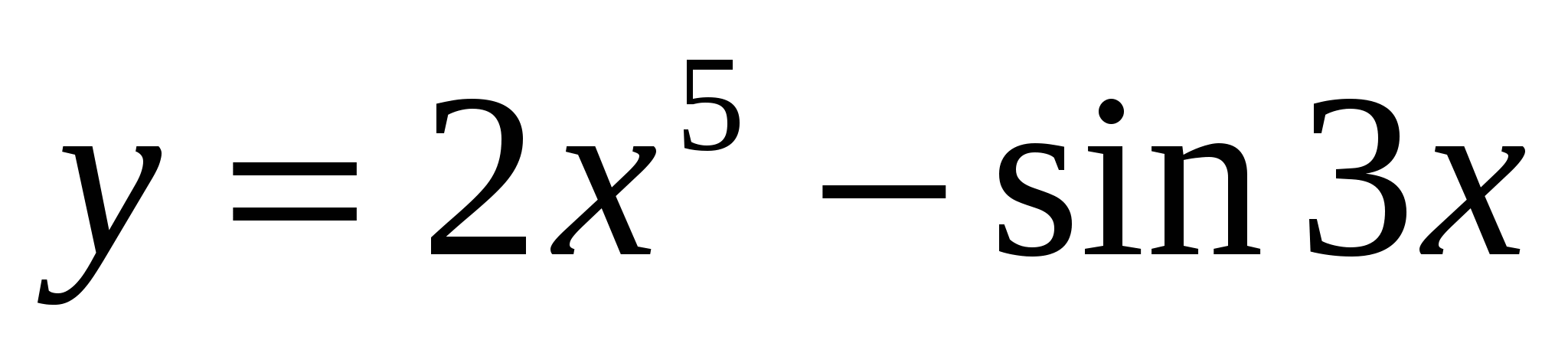 .
. 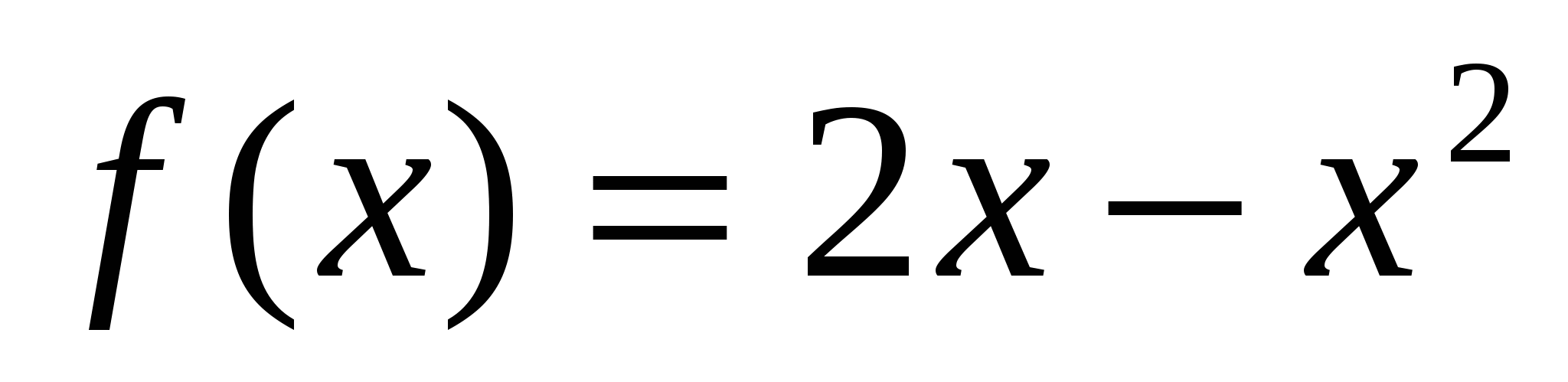 в точке с абсциссой
в точке с абсциссой 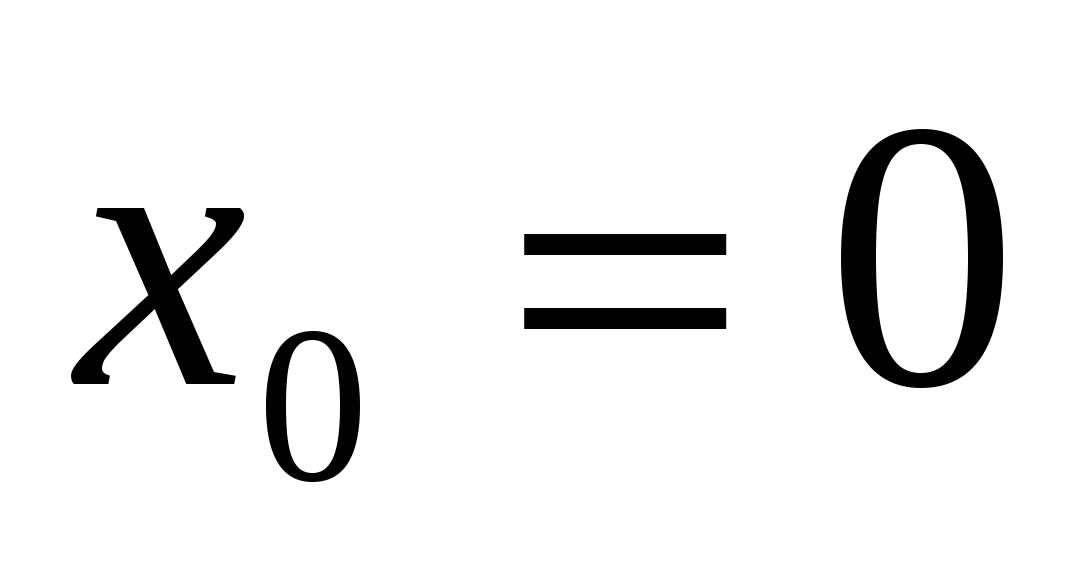 ,
, 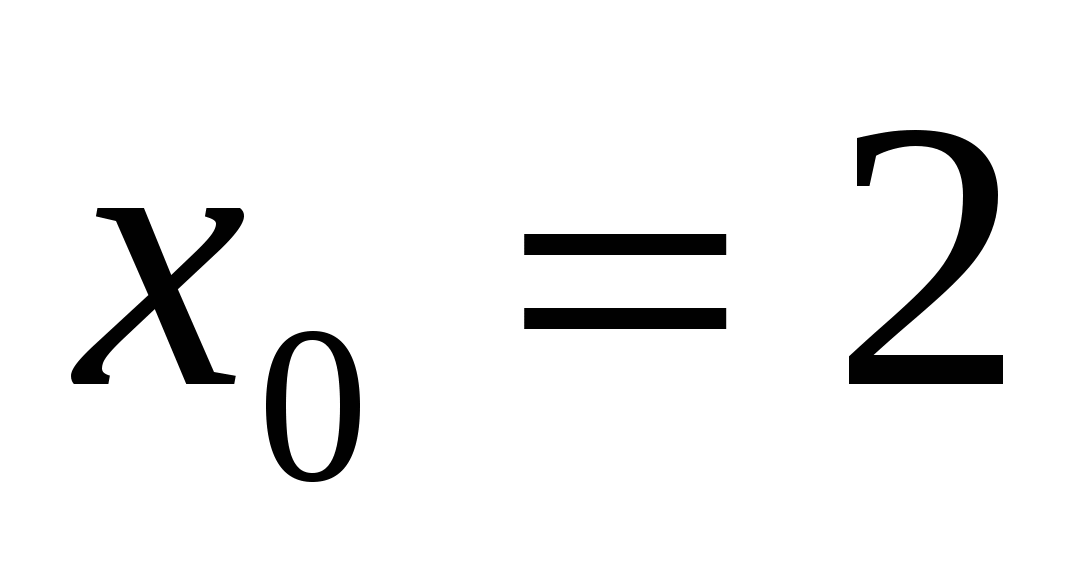 .
. 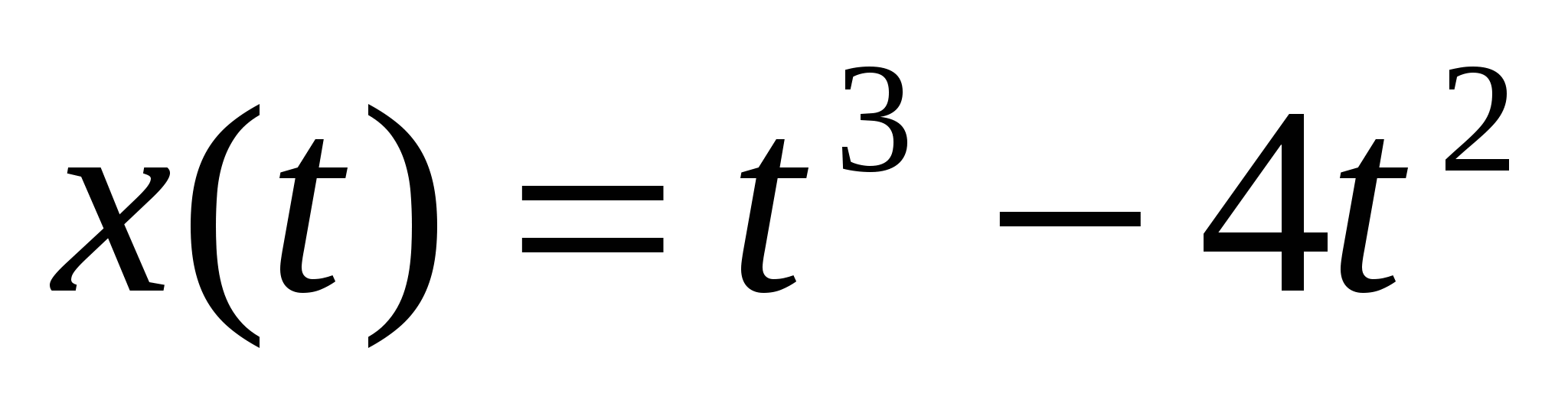 . Найти скорость и ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.)
. Найти скорость и ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.) 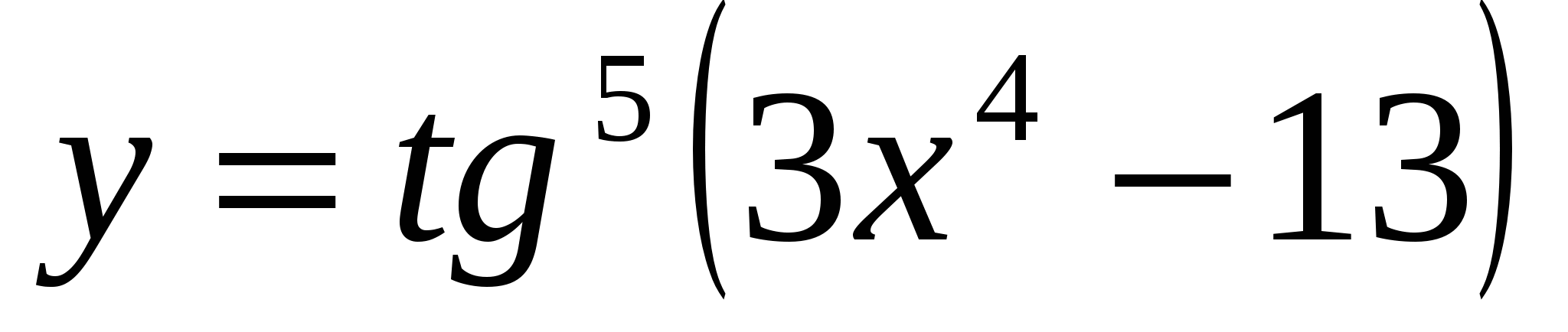 .
. 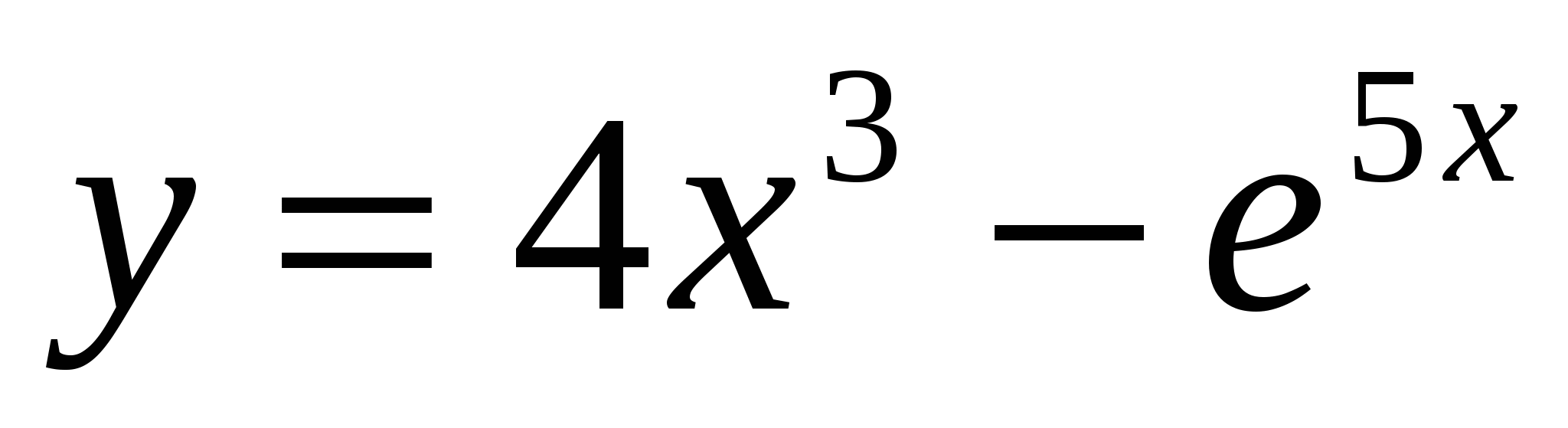 .
. 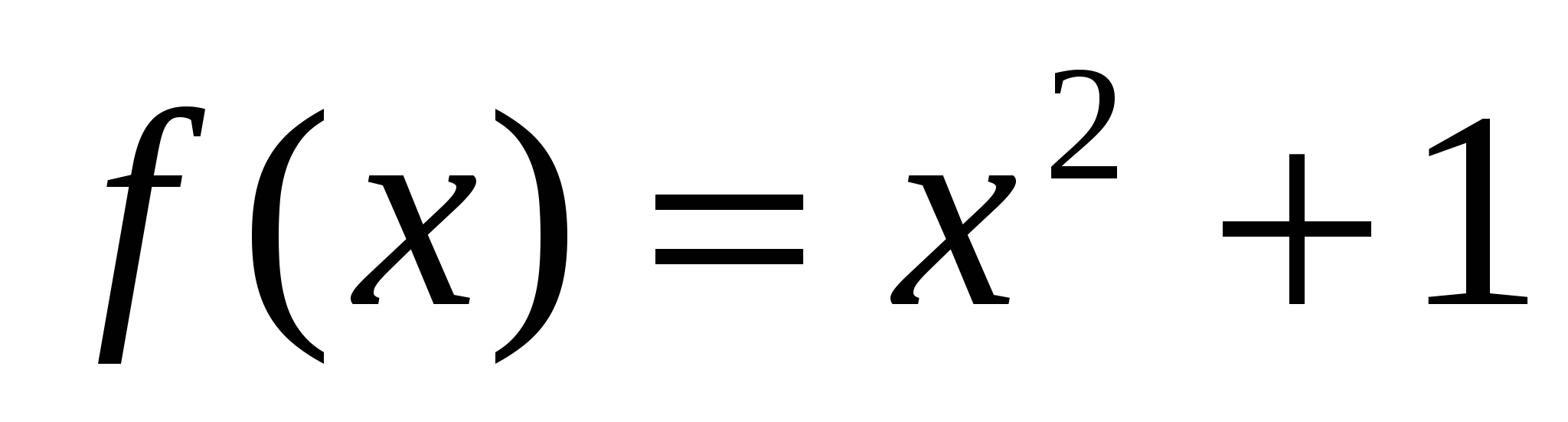 в точке с абсциссой
в точке с абсциссой 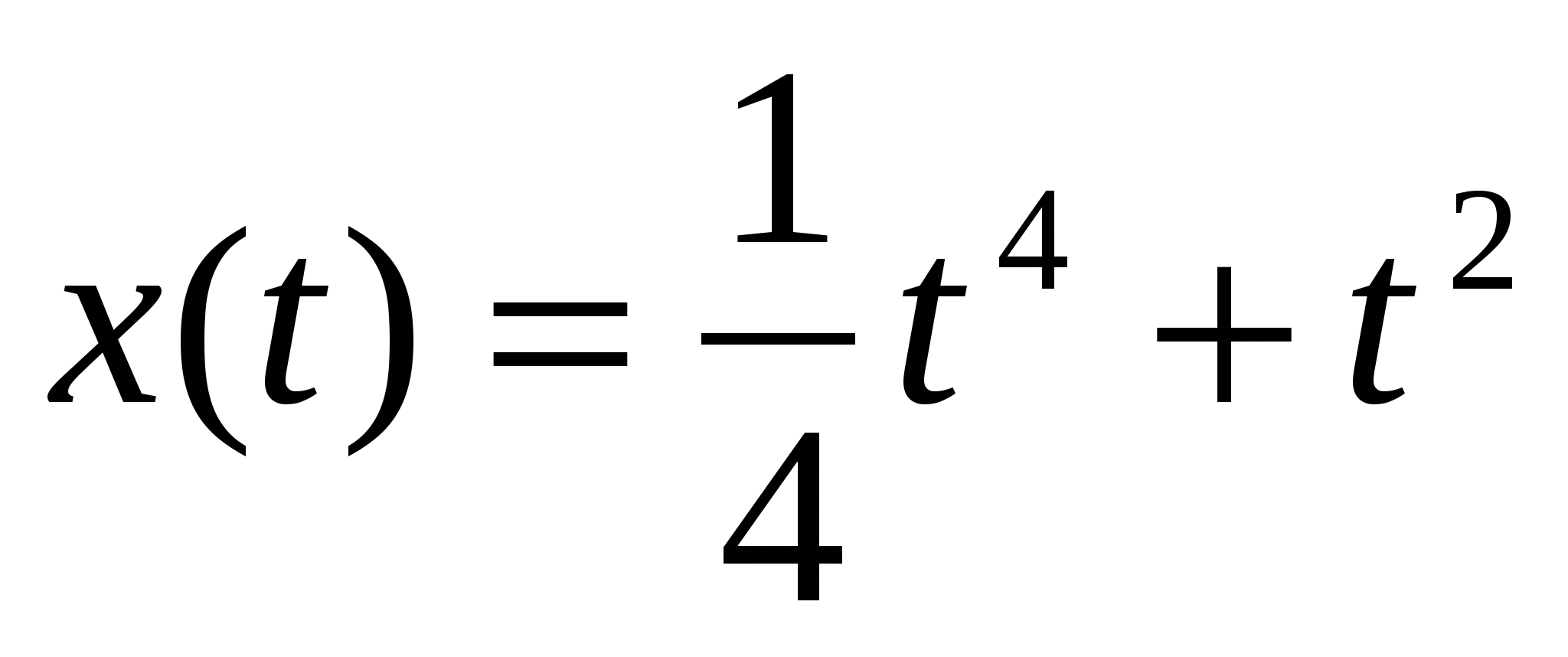 . Найти скорость и ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.)
. Найти скорость и ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.) 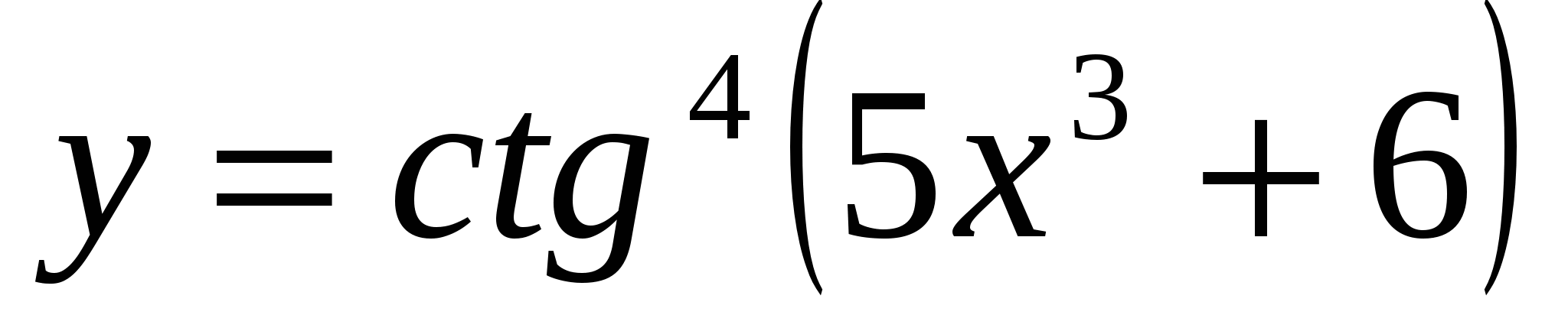 .
. 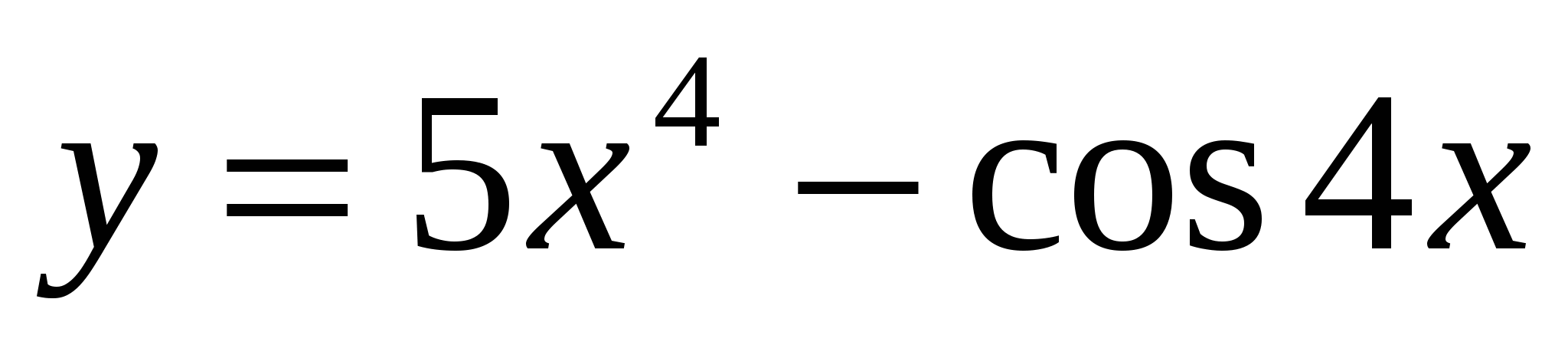 .
. 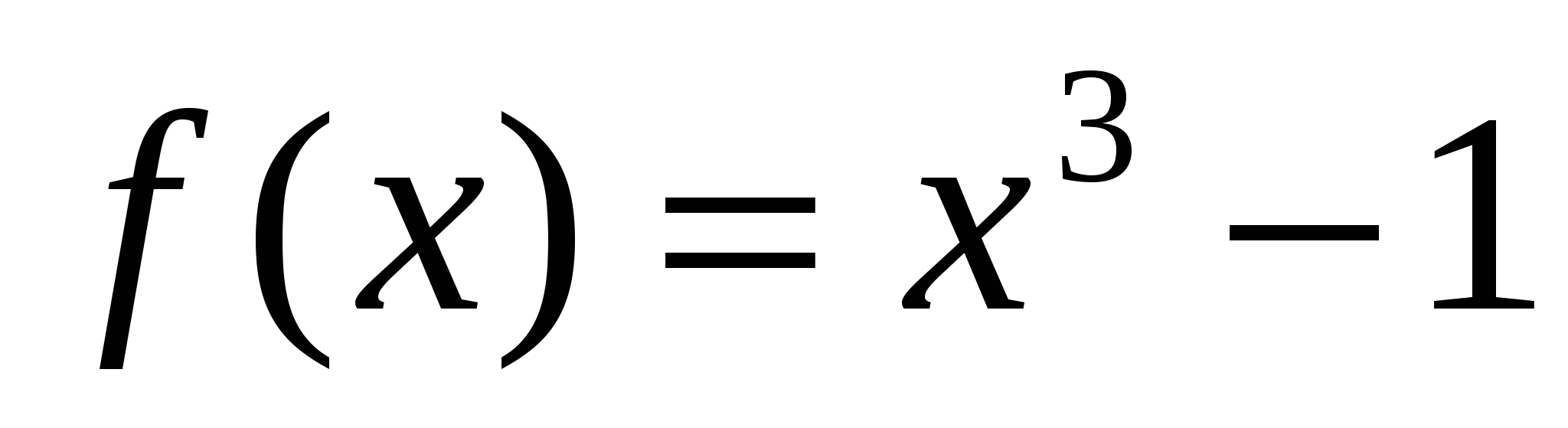 в точке с абсциссой
в точке с абсциссой 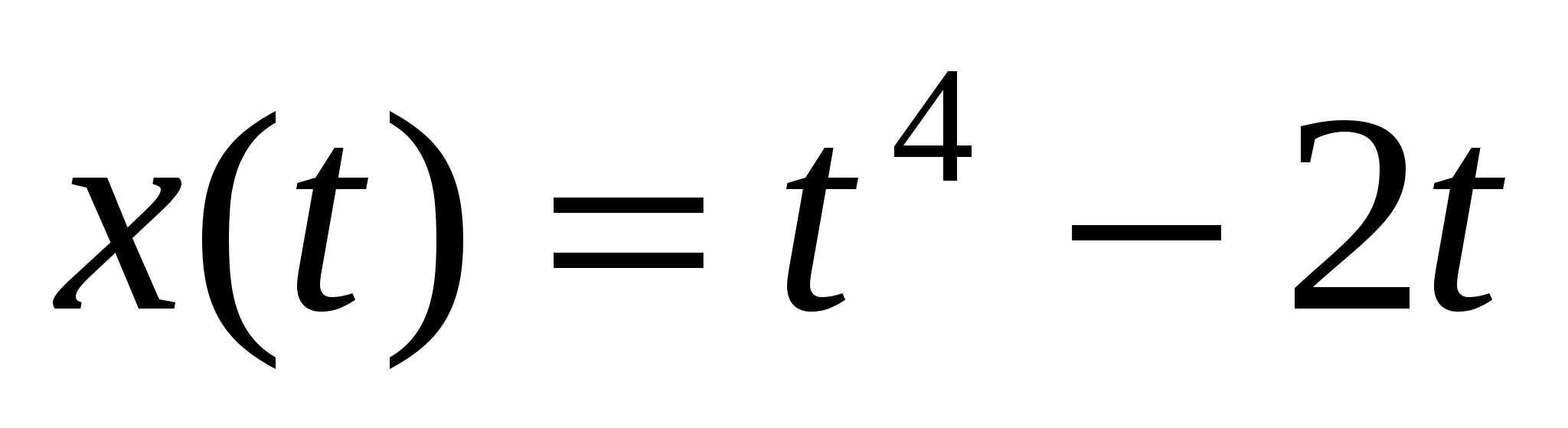 . Найти скорость и ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.)
. Найти скорость и ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.) 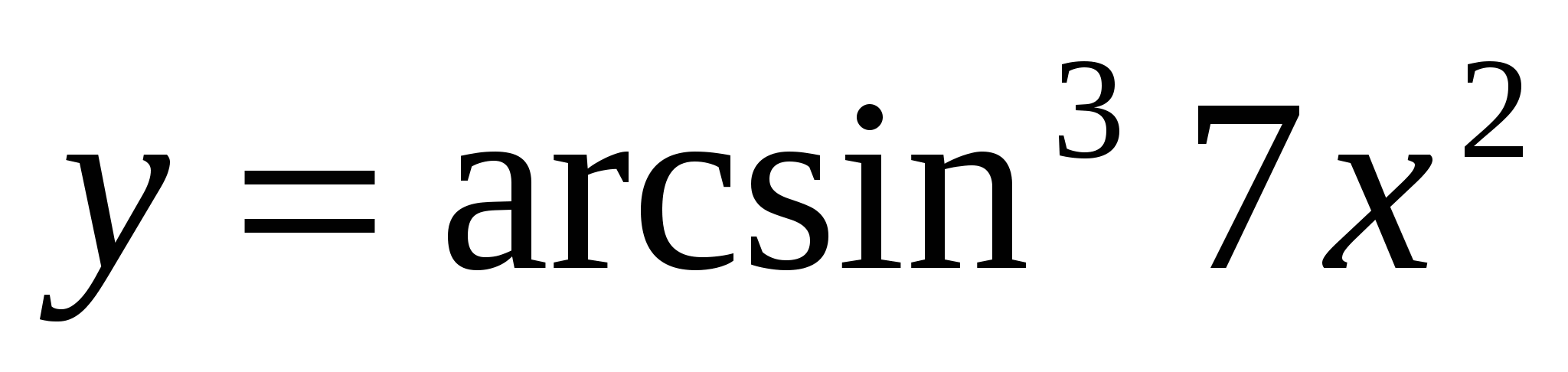 .
. 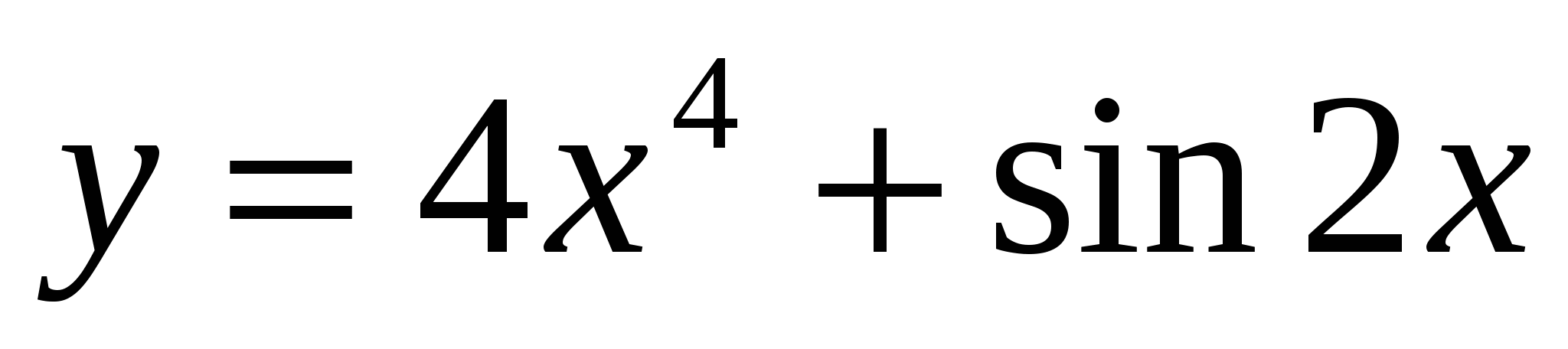 .
. 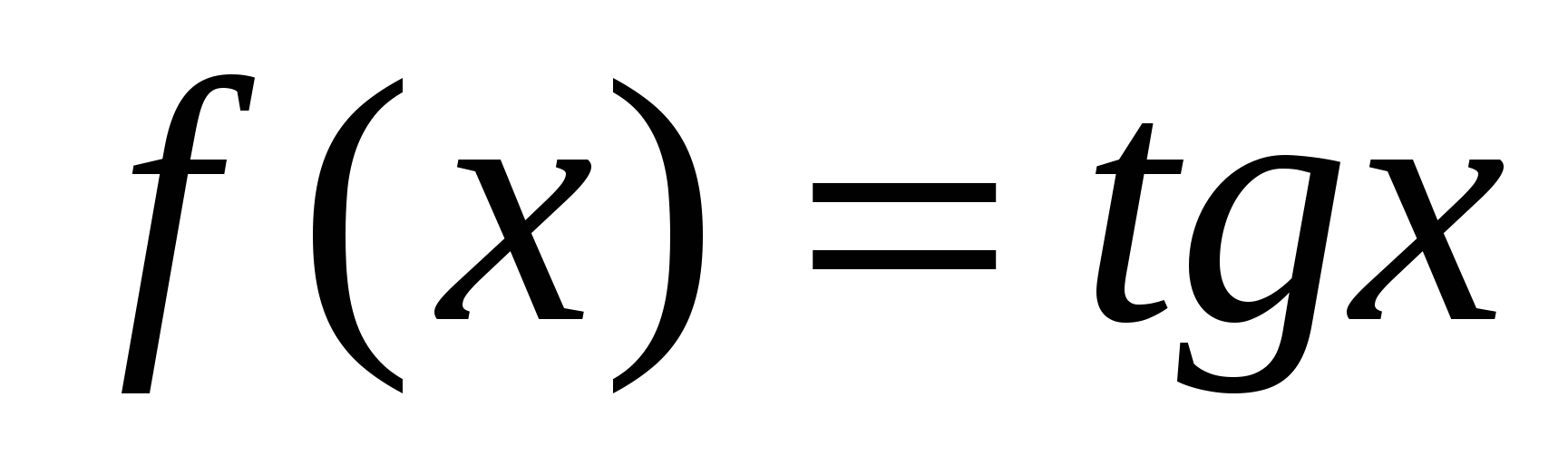 в точке с абсциссой
в точке с абсциссой 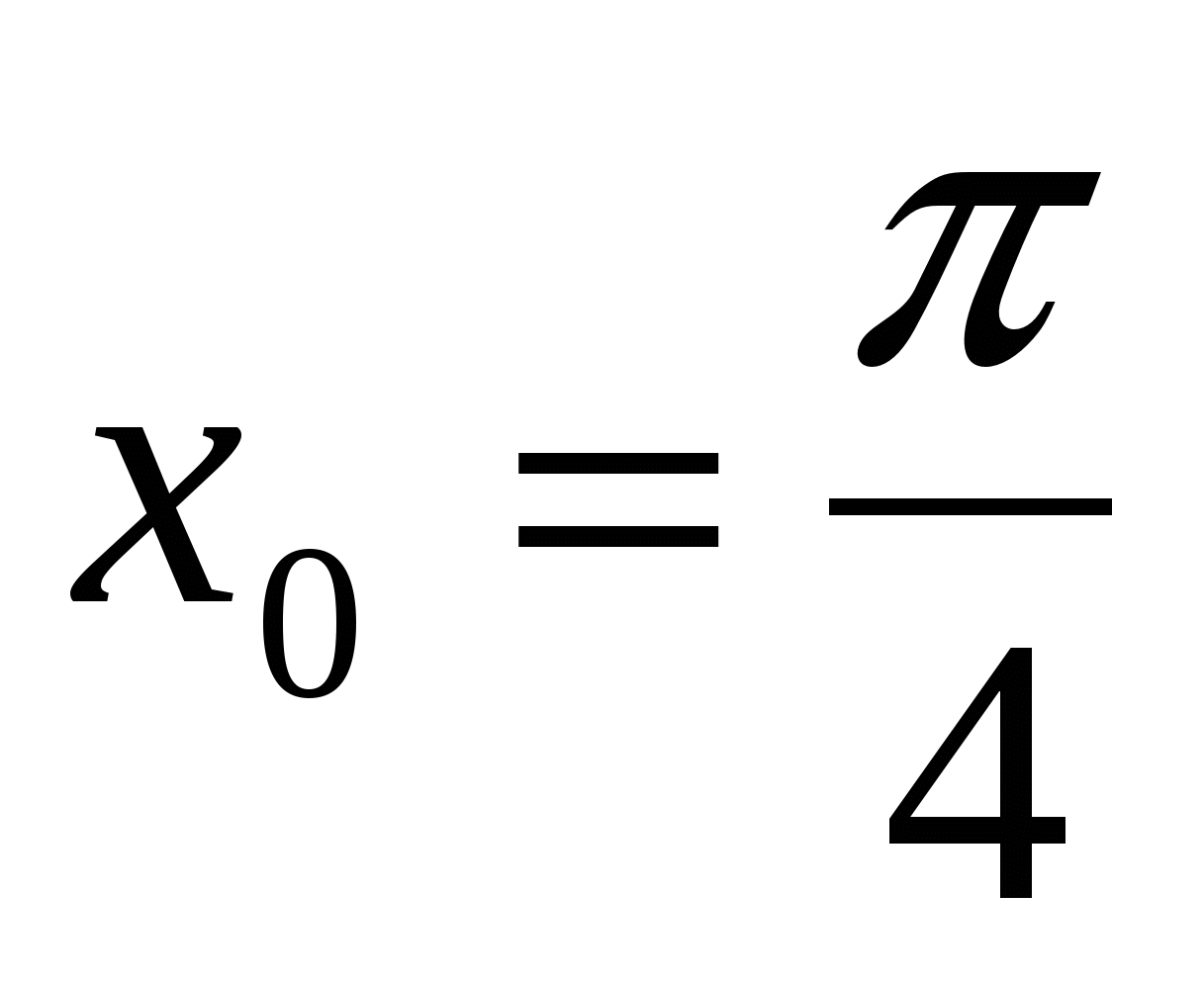 ,
, 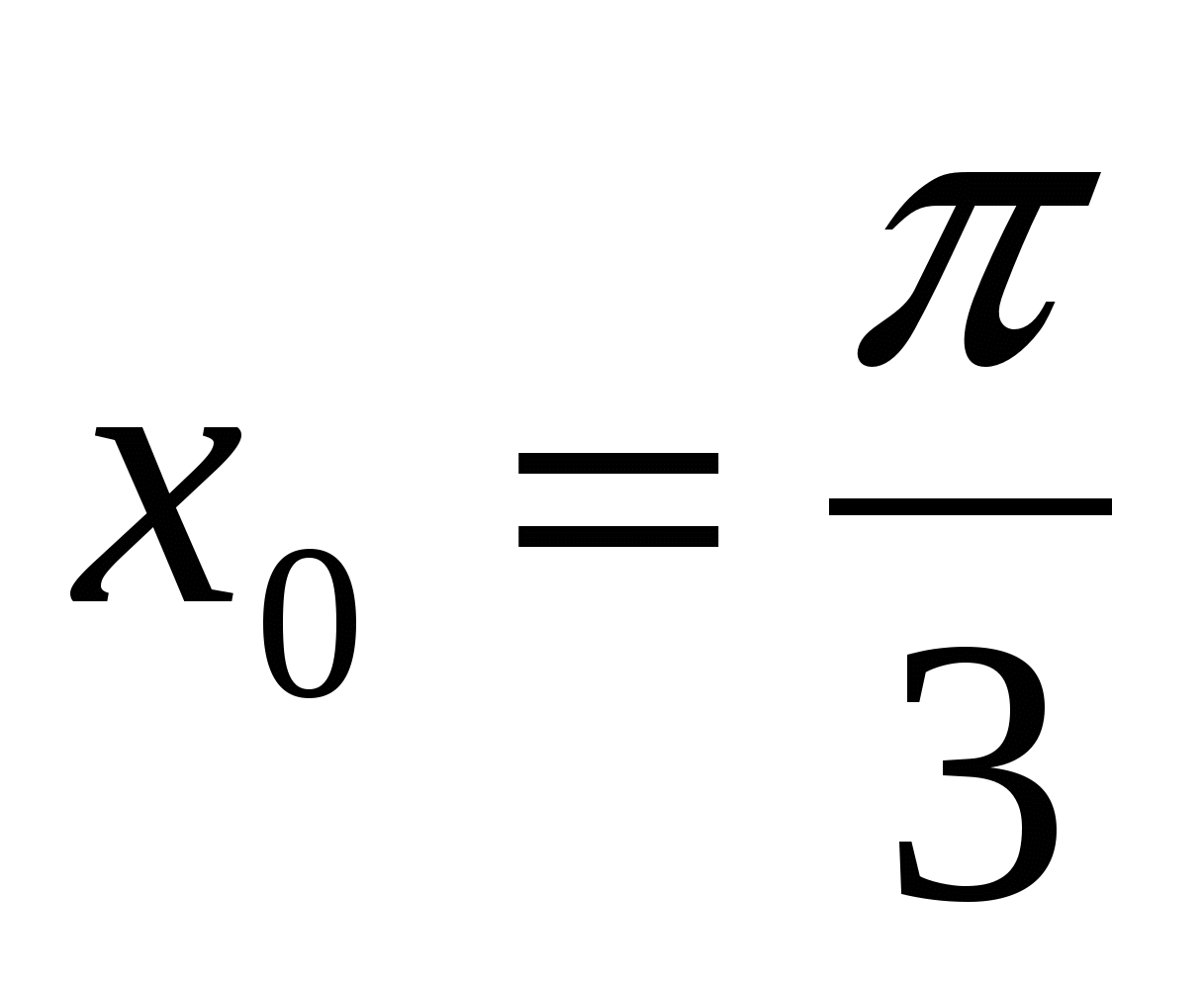 .
. 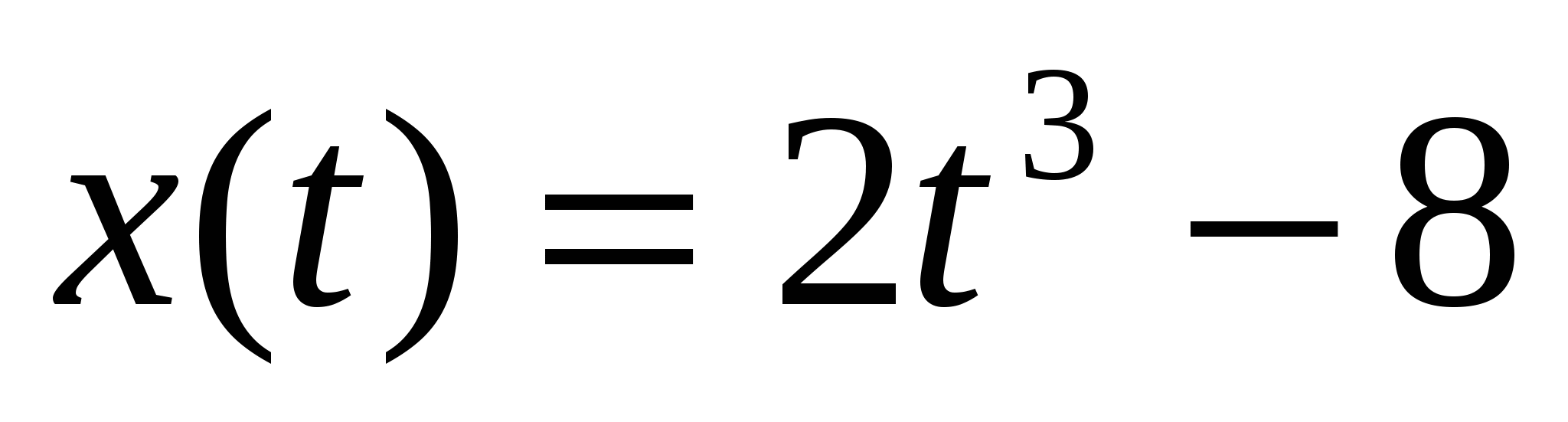 . Найти скорость и ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.)
. Найти скорость и ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.) 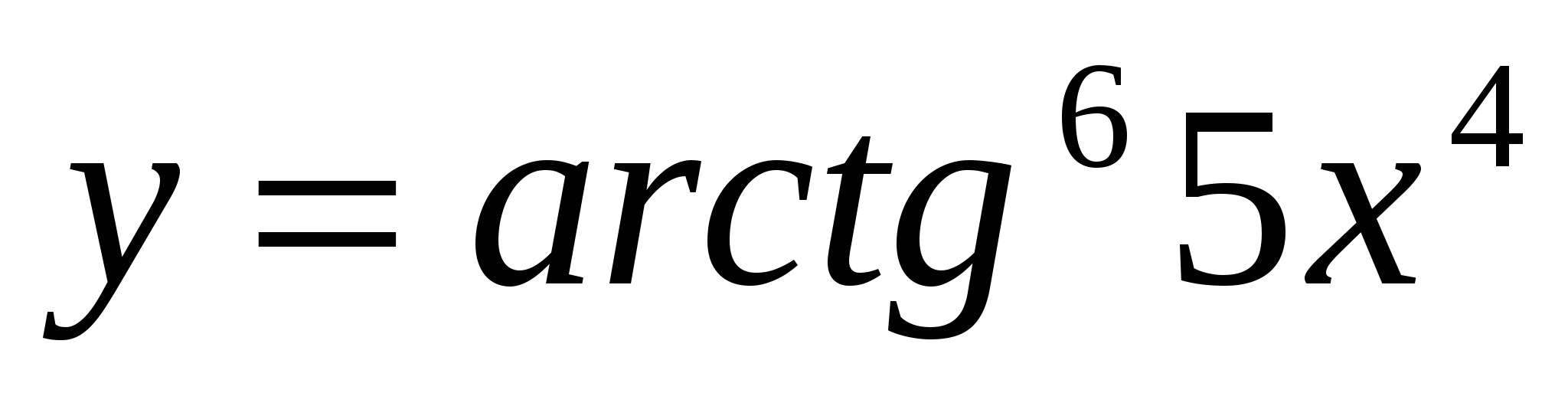 .
. 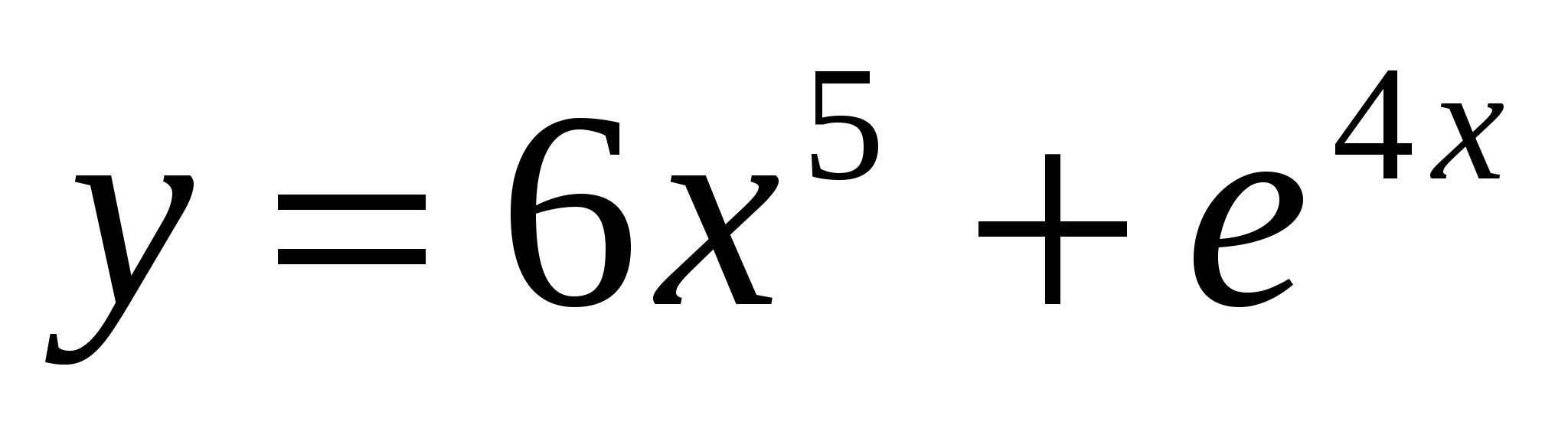 .
. 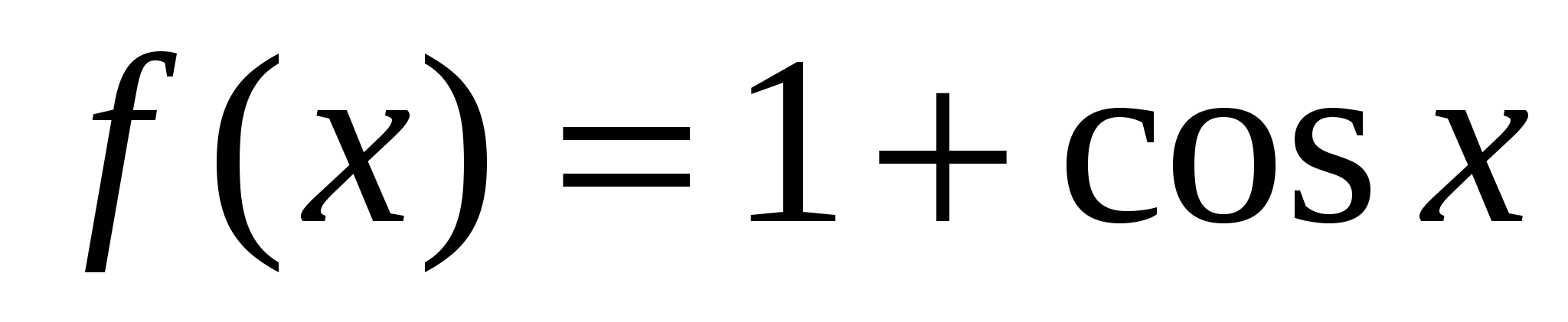 в точке с абсциссой
в точке с абсциссой 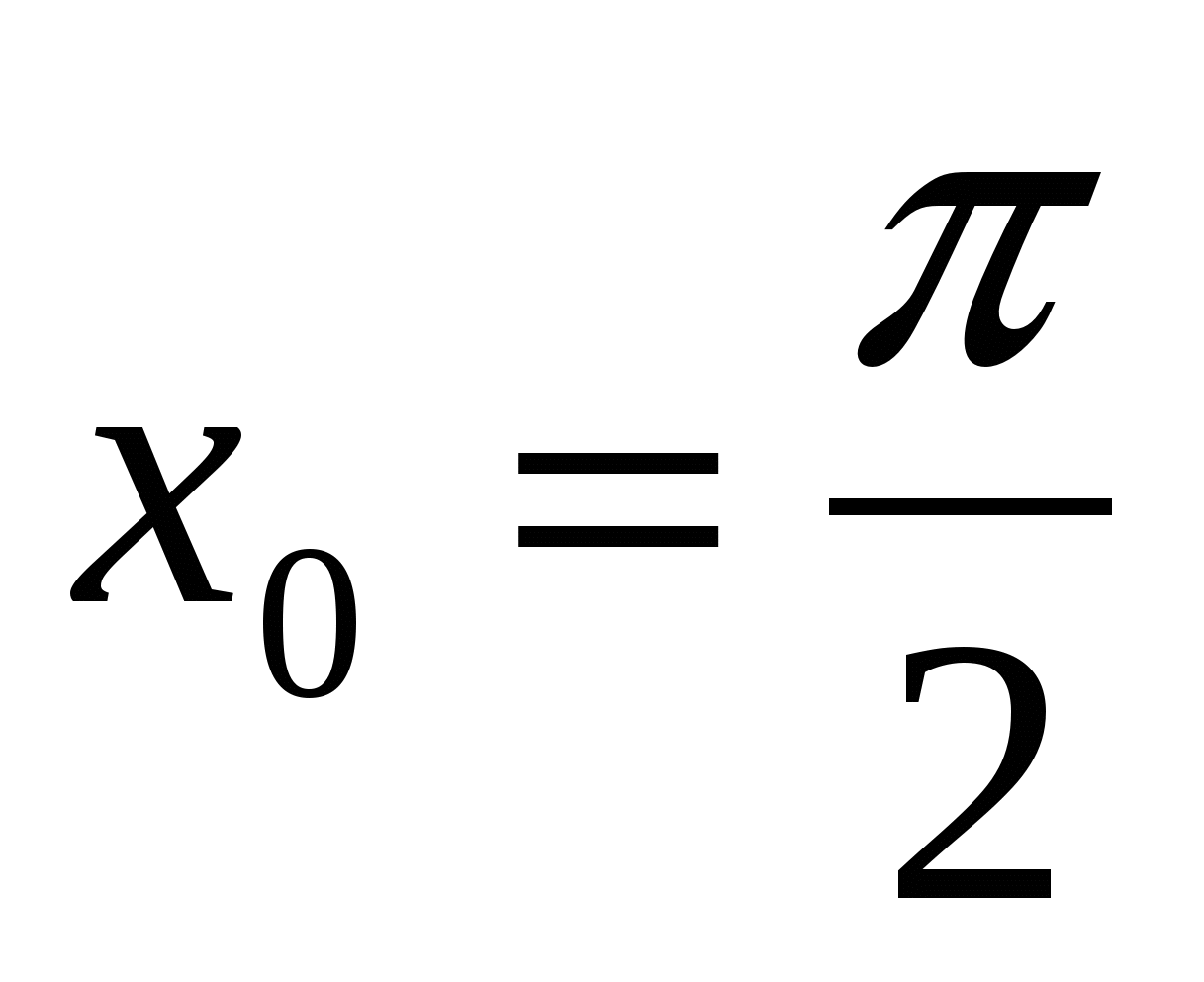 .
. 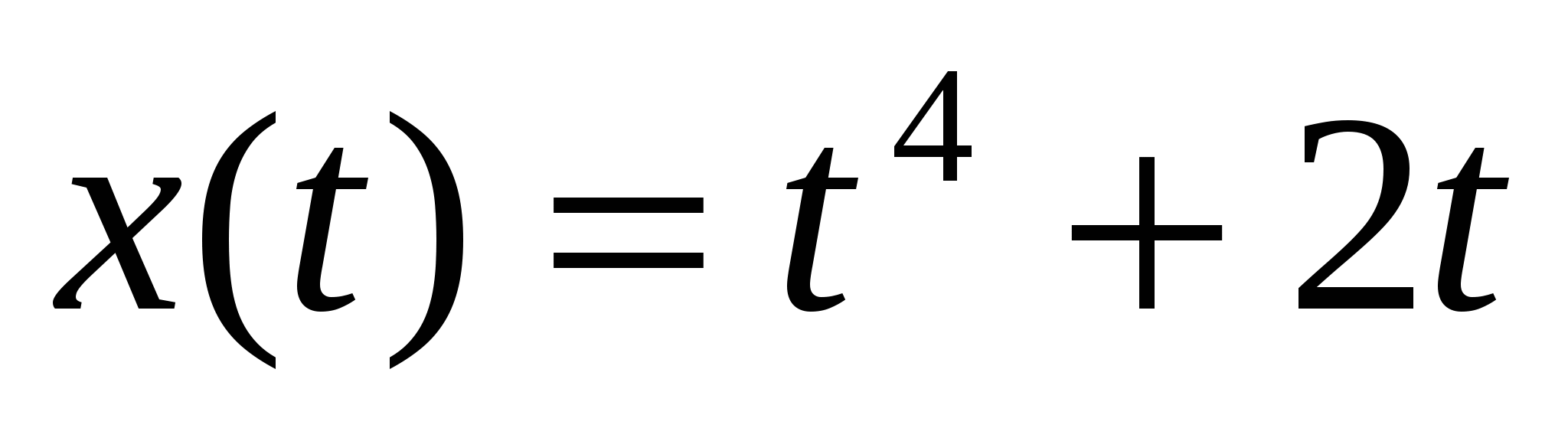 . Найти скорость и ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.)
. Найти скорость и ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.) 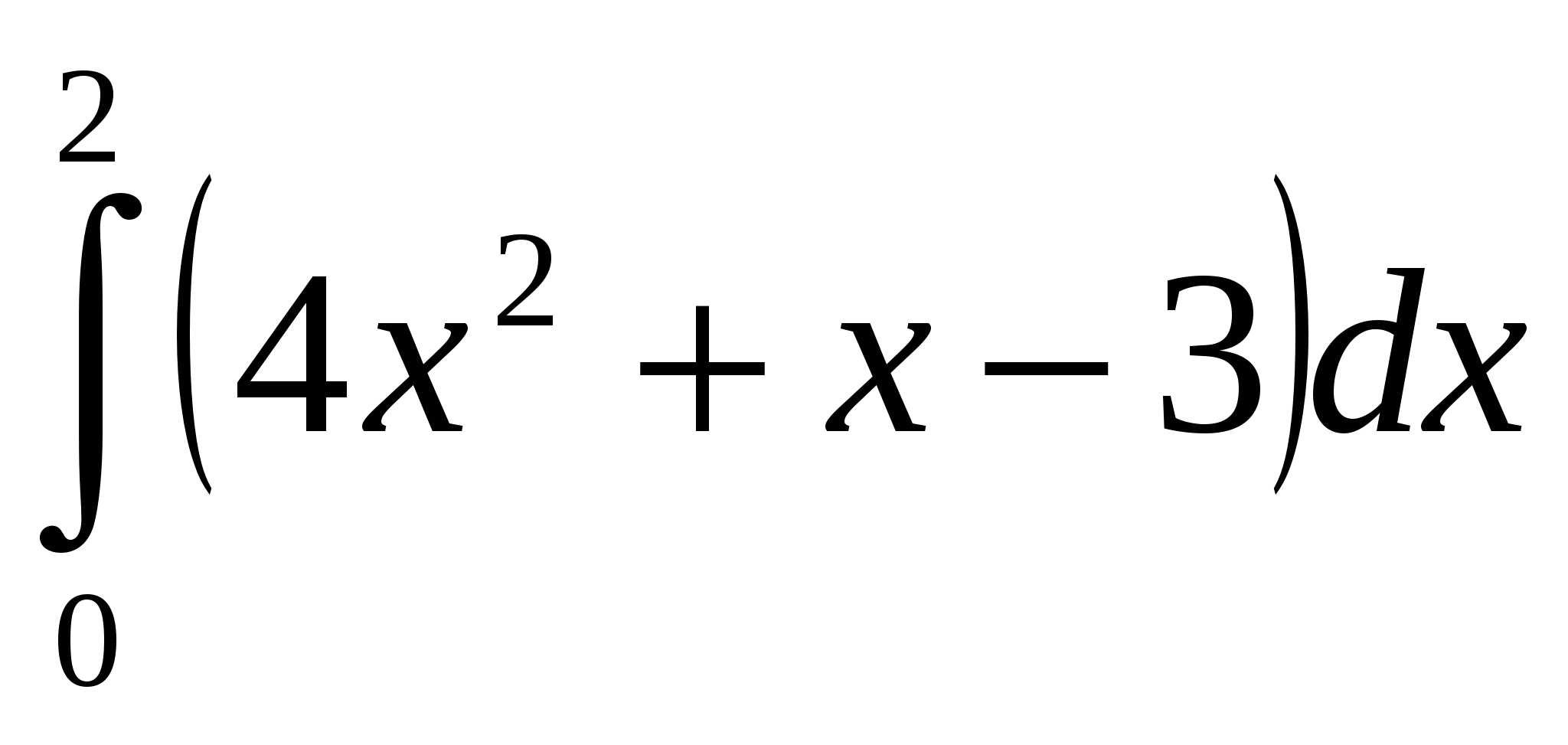 .
. 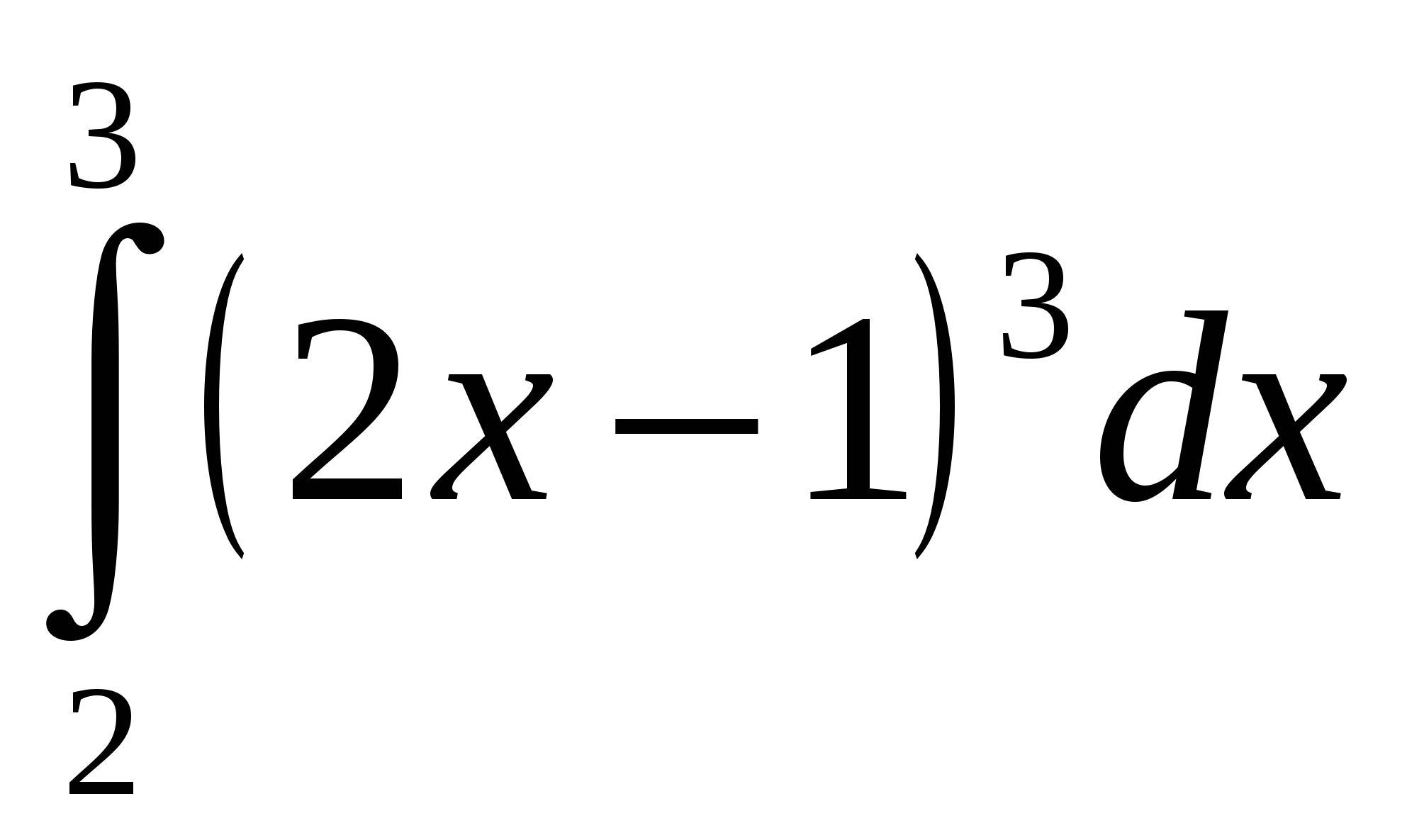 .
. 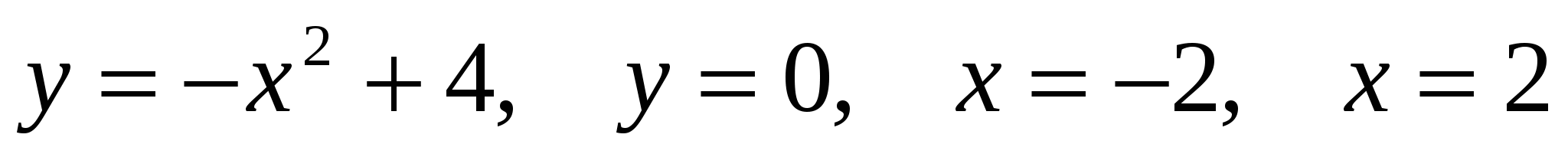 .
. 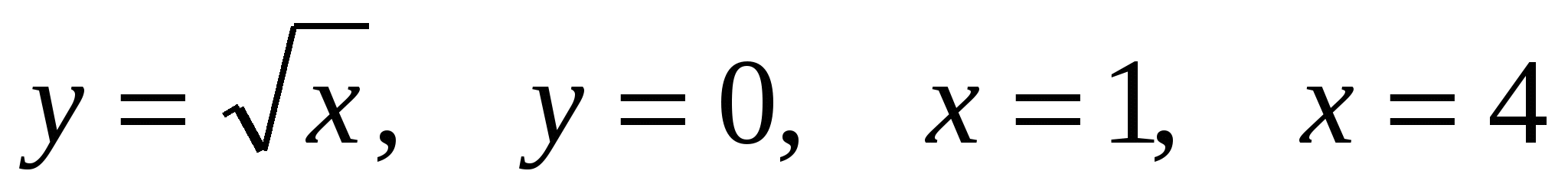 .
. 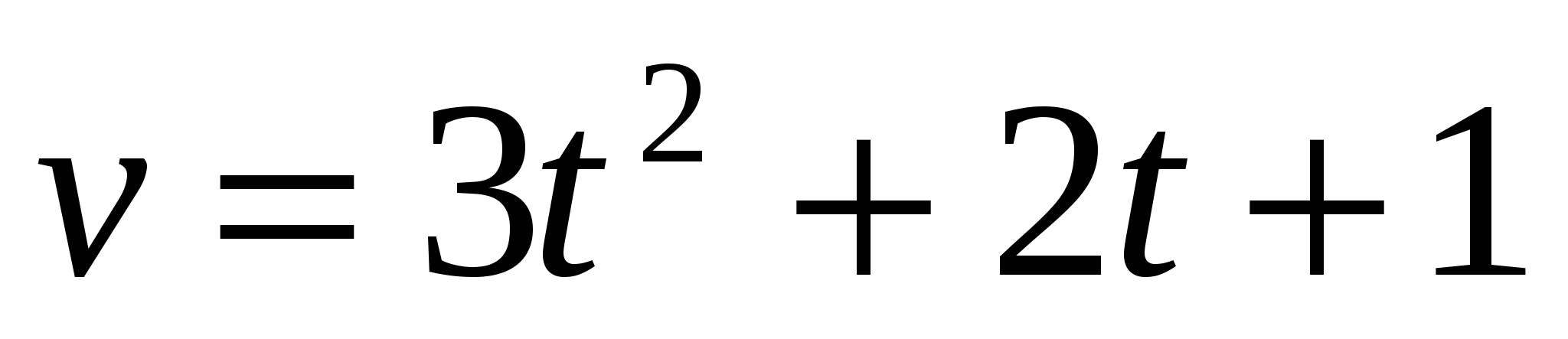 (м/с). Найти путь S, пройденный точкой за 10 с от начала движения.
(м/с). Найти путь S, пройденный точкой за 10 с от начала движения. 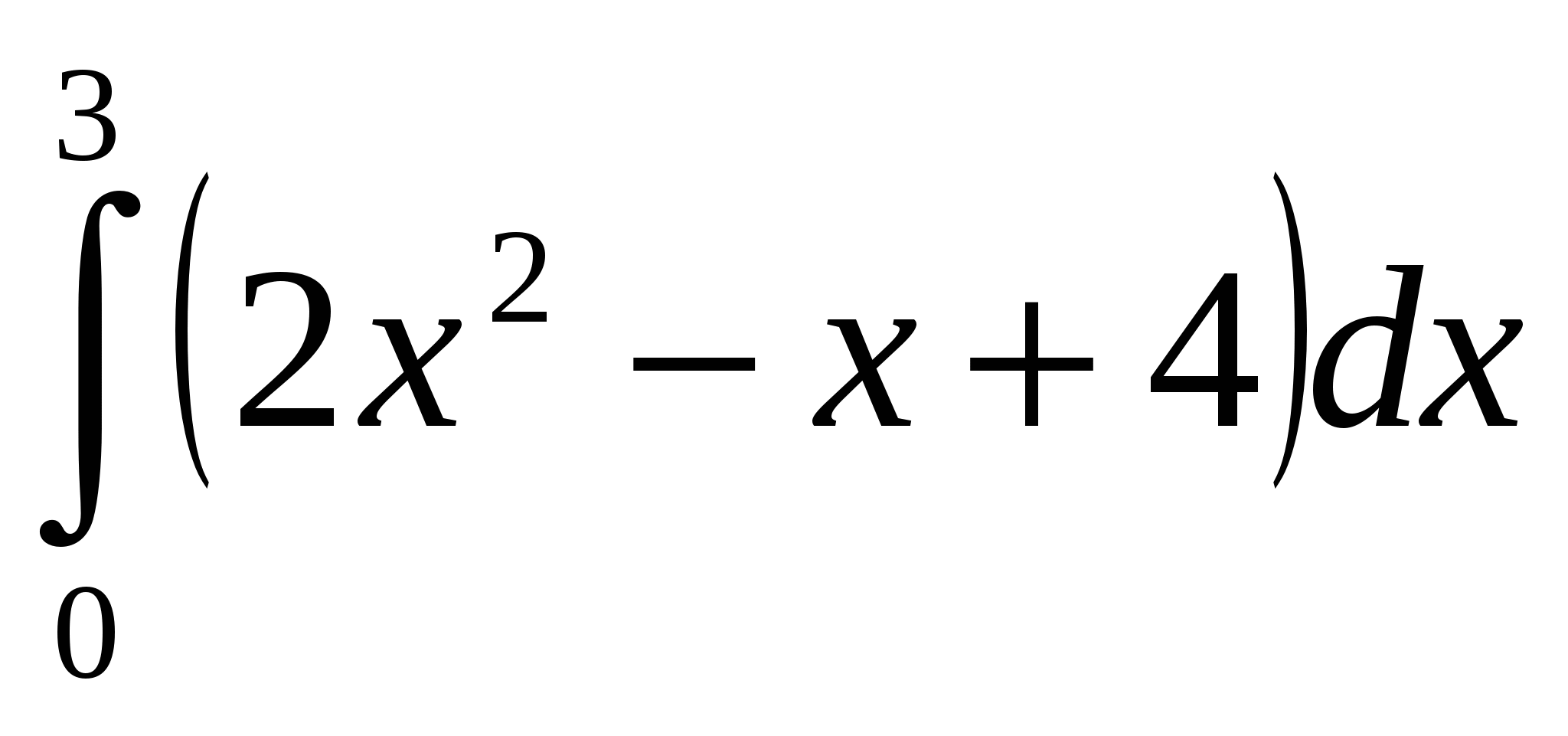 .
. 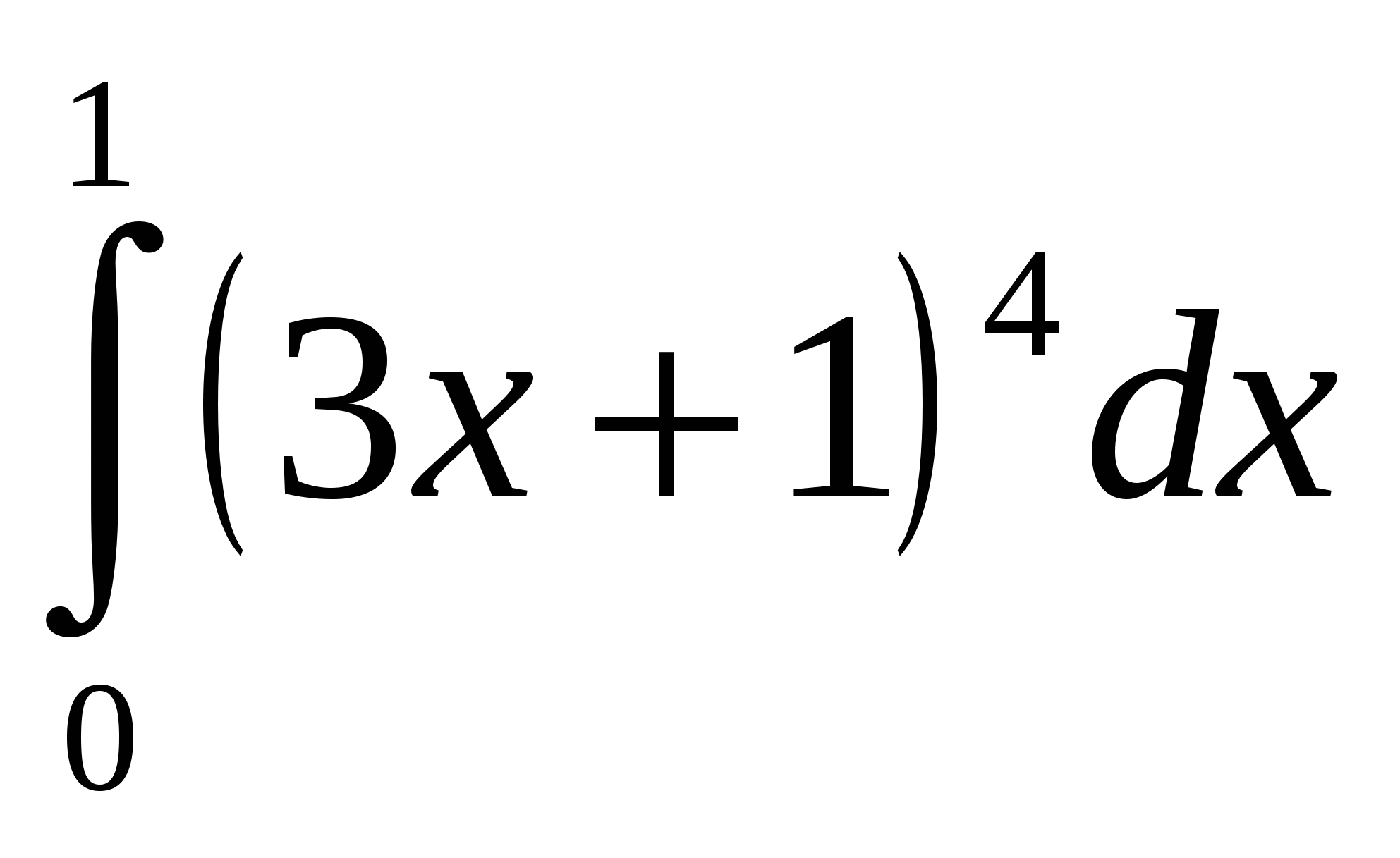 .
. 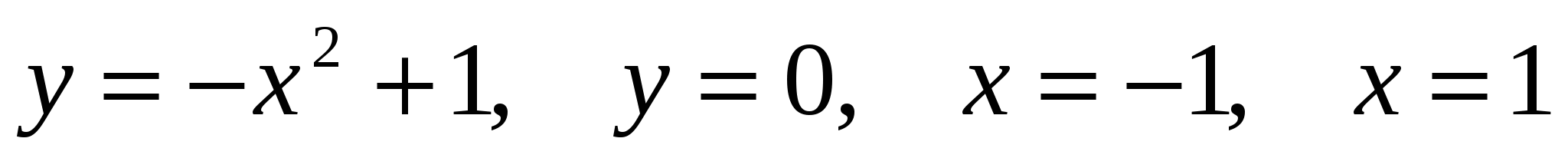 .
. 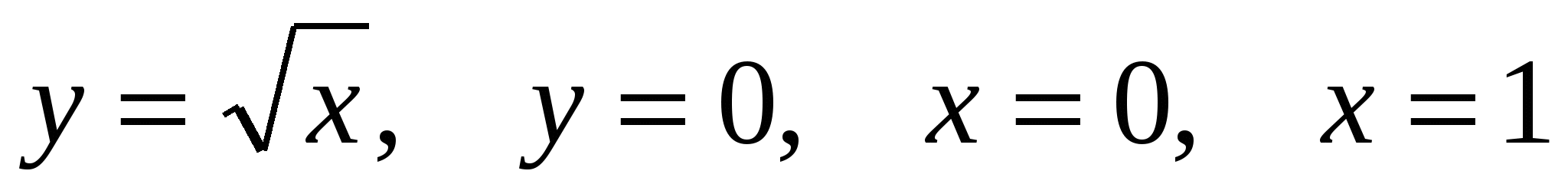 .
. 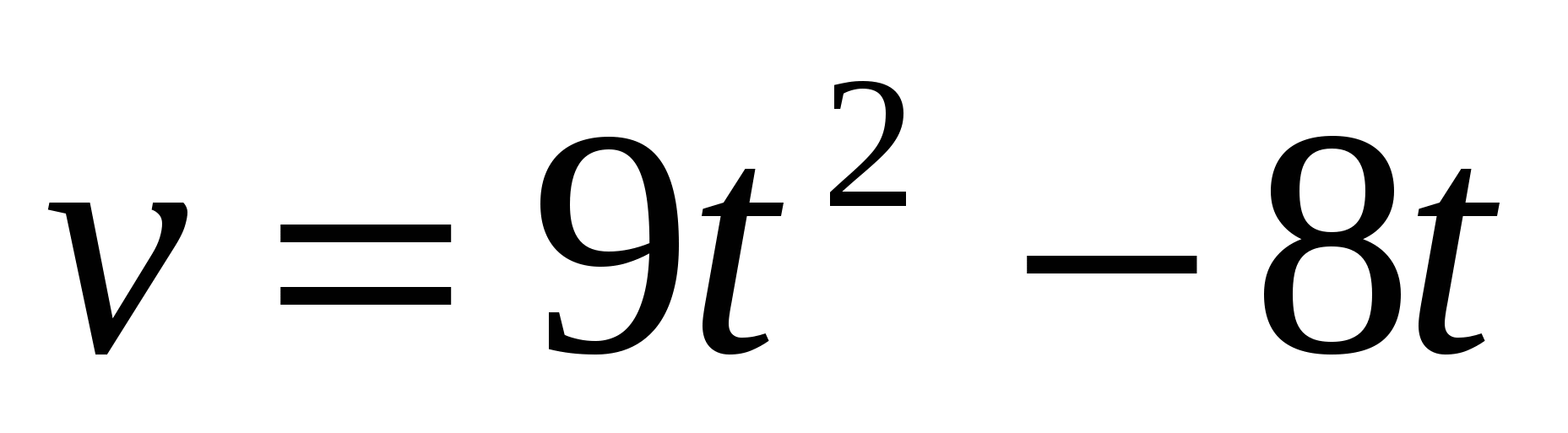 (м/с). Найти путь S, пройденный точкой за четвертую секунду.
(м/с). Найти путь S, пройденный точкой за четвертую секунду. 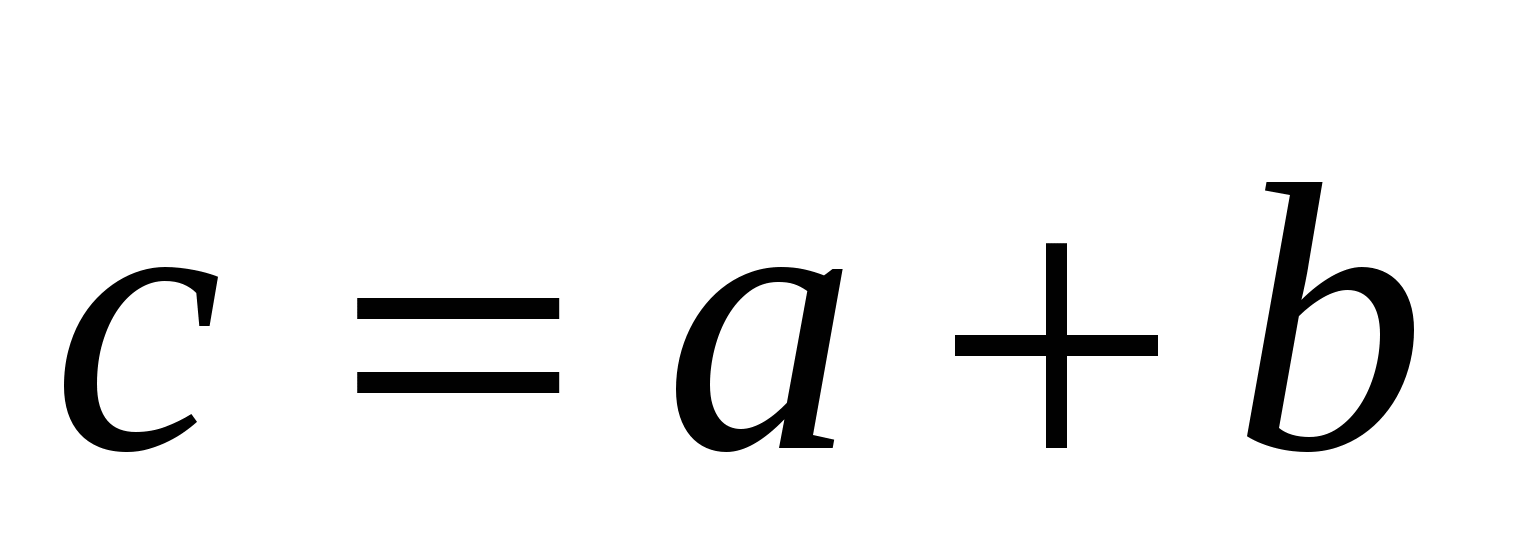 ,
, 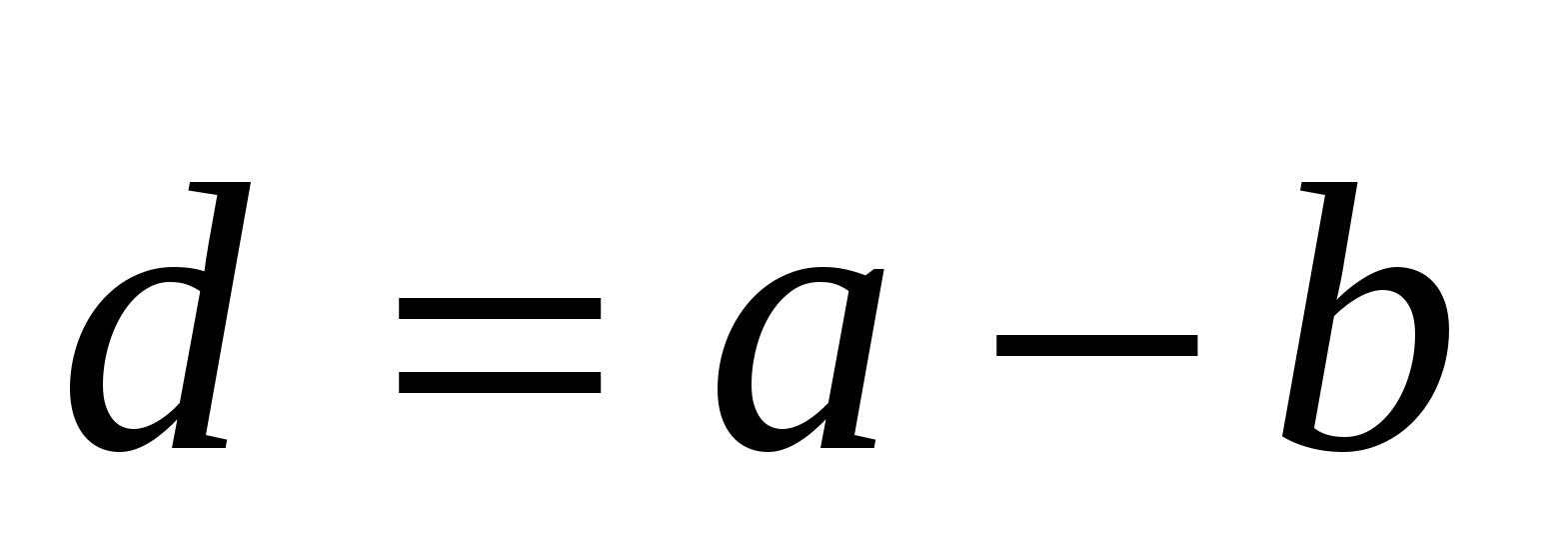 ,
, 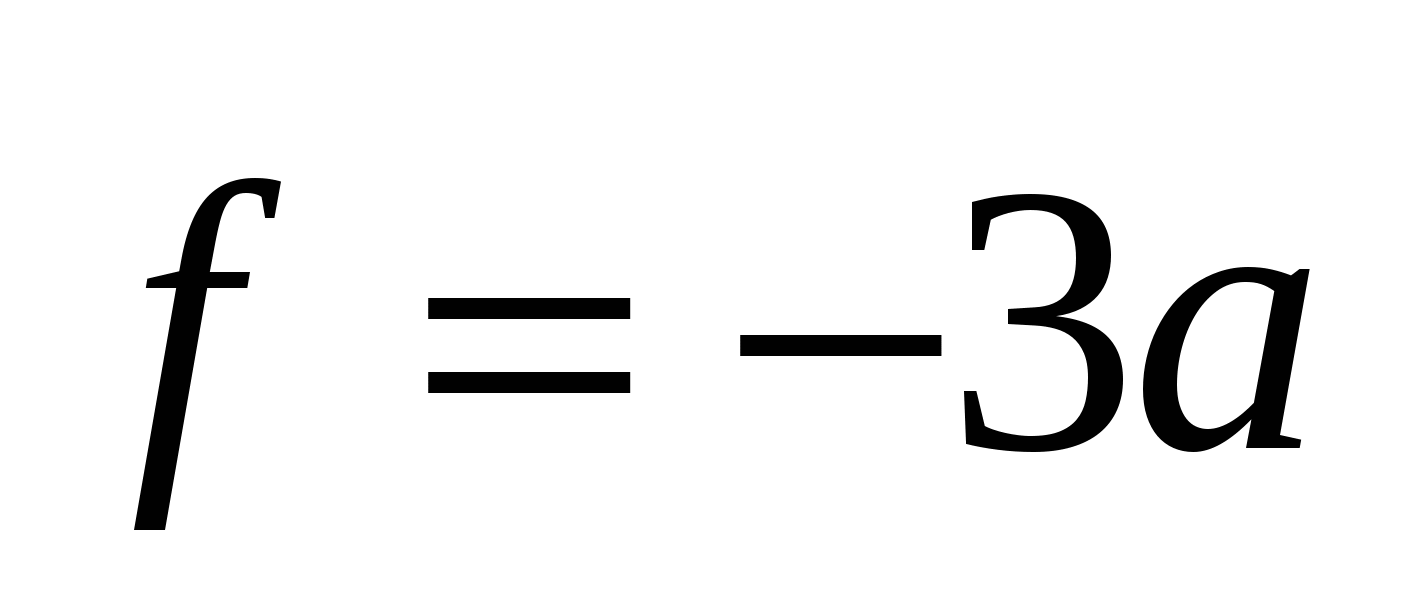 .
. 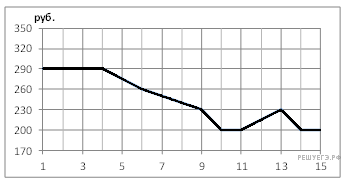
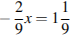 .
. 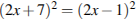 .
. 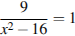 . Если уравнение имеет более одного корня, в ответе запишите больший из корней.
. Если уравнение имеет более одного корня, в ответе запишите больший из корней. 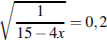 .
. 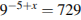 .
. 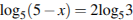 .
. 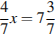 .
. 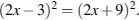
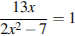 . Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
. Если уравнение имеет более одного корня, в ответе запишите меньший из корней. 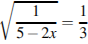 .
. 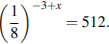
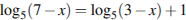 .
. 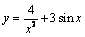
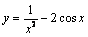
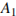 ,
,  ,
, 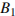 прямоугольного параллелепипеда
прямоугольного параллелепипеда 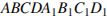 , у которого
, у которого 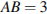 ,
, 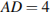 ,
, 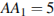 .
. 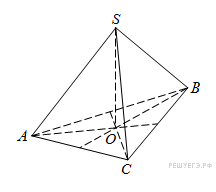 правильной треугольной пирамиде
правильной треугольной пирамиде 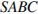 медианы основания
медианы основания  .
.  воды и погрузили в воду деталь. При этом уровень воды поднялся с отметки 25 см до отметки 27 см. Найдите объем детали. Ответ выразите в
воды и погрузили в воду деталь. При этом уровень воды поднялся с отметки 25 см до отметки 27 см. Найдите объем детали. Ответ выразите в  .
. 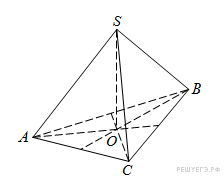 правильной треугольной пирамиде
правильной треугольной пирамиде  сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 80 см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в 4 раза больше, чем у первого? Ответ выразите в см.
сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 80 см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в 4 раза больше, чем у первого? Ответ выразите в см.