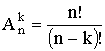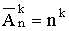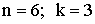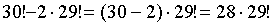Экзамен сдают 30 студентов группы сколькими способами можно составить список очередности

Задачи по комбинаторики для 11 класса

Подборка задач по комбинаторике (с ответами) для 11 класса.

Просмотр содержимого документа
«Задачи по комбинаторики для 11 класса»

Задачи по комбинаторики

Задача 1: Сколькими способами можно составить список из 5 учеников?

Ответ: перестановки, 5! = 120.

Задача 2: В футбольной команде (11 человек) нужно выбрать капитана и его заместителя. Сколькими способами это можно сделать?

Ответ: размещения из 11 по 2, А 2 ₁₁= 110.

Задача 3: Расписание на день содержит 5 уроков. Определить количество возможных расписаний при выборе из 14 предметов, при условии, что ни один предмет не стоит дважды.

Ответ: размещения из 14 по 5, 1320.

Задача 4: Сколько различных трехцветных флагов можно сделать, комбинируя синий, красный и белый цвета?

Ответ: перестановки, 6 способов.

Задача 5: В классе 24 ученика. Сколькими способами можно сформировать команду из 4 человек для участия в математической олимпиаде?

Ответ: сочетания из 24 по 4,

Задача 6: Сколько трехзначных чисел можно составить из цифр 1, 2, 3, если каждая цифра входит в изображение числа только 1 раз?

Ответ: перестановки, 6 способов.

Задача 7: Сколькими различными способами можно избрать из 15 человек делегацию в составе 3 человек?

Ответ: сочетания, 455 способами.

Задача 8: Из ящика, где находится 15 шаров, нумерованных последовательно от 1 до 15, требуется вынуть 3 шара. Определить число возможных комбинаций при этом?

Ответ: размещения, 2830 способами.

Задача 9: Сколько четырехзначных чисел можно составить из цифр 0, 1, 2, 3, если каждая цифра входит в изображение числа только 1 раз?

Ответ: перестановки, 4! – 3! =18.

Задача 10: Сколькими способами можно разместить 6 пассажиров в четырехместной каюте?

Ответ: размещения из 6 элементов по 4, 360 способами.

Задача 11: Сколькими способами можно выбрать 2 детали из ящика, содержащего 10 деталей?

Ответ: сочетания из 10 элементов по 2, 45 способами.

Задача 12: Бригадир должен отправить на работу бригаду из 4 человек. Сколько бригад по 4 человека в каждой можно составить из 13 человек?

Ответ: сочетания из 13 по 4, 715 бригад.

Задача 13: При встрече 16 человек обменялись рукопожатиями. Сколько всего было сделано рукопожатий?

Ответ: сочетания из 16 по 2, 120 рукопожатий.

Задача 14: Группа учащихся в 30 человек пожелала обменяться своими фотокарточками. Сколько всего фотокарточек потребовалось для этого?

Ответ: сочетание из 30 по 2, 435 фотокарточек.

Задача 15: Сколько различных плоскостей можно провести через 10 точек, если никакие три из них не лежат на одной прямой и никакие четыре точки не лежат в одной плоскости?

Ответ: сочетание из 10 по 3; 120 точек

Задача 16: Сколько существует различных семизначных телефонных номеров?

Задача 17: Сколько существует различных семизначных телефонных номеров, если в каждом номере нет повторяющихся цифр?

Ответ: размещение из 10 по 7.

Задача 18: Сколько существует таких перестановок 7 учеников, при которых 3 определенных ученика находятся рядом друг с другом? Ответ: 720 = 3! · 5!

Задача 19: На книжной полке стоит собрание сочинений в 30 томах. Сколькими различными способами их можно переставить, чтобы: а) тома 1 и 2 стояли рядом; б) тома 3 и 4 рядом не стояли?

Задача 20: Сколько существует трёхзначных чисел, все цифры которых нечётные и различные?

Ответ: размещение из 5 по 3, 60.

Задача 21: У одного мальчика имеется 10 марок для обмена, а у другого – 8. Сколькими способами они могут обменять 2 марки одного на 2 марки другого?

Ответ: сочетания, С 2 ₁₀·С 2 ₈ = 1260.

Источник

Математика — онлайн помощь

Рассмотрим множество, состоящее из n различных элементов. Требуется выбрать из них какие-нибудь k элементов и расположить эти k элементов в каком-либо порядке. Такие упорядоченные последовательности называются размещениями из n элементов по k элементов (упорядоченные – следовательно, последовательности <1,2>и <2,1>— различные размещения).

Если в последовательности нет одинаковых элементов, то говорят о размещении без повторений. Их количество

Если в последовательности допускается наличие одинаковых элементов, то говорят о размещении с повторениями. Их количество

Любое подмножество (неупорядоченное), состоящее из k элементов, называется сочетанием из n элементов по k элементов.

Различные сочетания отличаются друг от друга только самими входящими в них элементами, порядок их следования безразличен, т.е. по условию задачи подмножества <1,2>и <2,1>не различны (соединены).

Число сочетаний без повторений

.

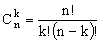
Число сочетаний с повторениями

.

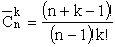
Количество способов переставить элементов в заданном множестве (количество перестановок) вычисляется по формуле

.

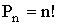
При решении простейших комбинаторных задач можно использовать следующую таблицу, определяющую число множеств, состоящих из k элементов, отбираемых из множества, содержащего n элементов

Рассмотрим разницу между сочетаниями, размещениями с повторениями, без повторений на следующих примерах.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

ПРИМЕР 13.2.1 В коробке 6 шаров, пронумерованных от 1 до 6. Из коробки вынимаются друг за другом 3 шара и в этом же порядке записывают полученные цифры. Сколько трехзначных чисел можно таким образом записать?

Решение: По условию задачи подмножества <1;2;3>и <3;1;2>– различные. Повторов в подмножестве быть не может, так как шары не возвращаются в коробку.

.

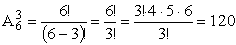
ПРИМЕР 13.2.2. В коробке 6 шаров пронумерованных от 1 до 6. Из коробки вынимаются 3 шара и записывают число в порядке возрастания цифр. Сколько трехзначных чисел можно таким образом записать?

Решение: По условию задачи подмножества <1;2;3>и <3;2;1>дают число 123, т.е. не являются различными.

.

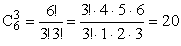
ПРИМЕР 13.2.3. Условие задачи 2.1 (шары возвращаются в коробку)

Решение: .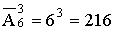

ПРИМЕР 13.2.4. Условие задачи 2.2 (шары возвращаются в коробку)

Решение: .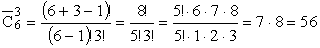

ПРИМЕР 13.2.5. Сколько различных перестановок можно составить из букв слова «комар»?

Решение: .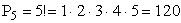

ПРИМЕР 13.2.6. Сколько различных перестановок можно составить из букв слова «задача»?

Решение: Если бы все шесть букв слова были различны, то число перестановок было бы 6! Но буква «а» встречается в данном слове три раза, и перестановки только этих трех букв «а» не дают новых способов расположения букв. Поэтому число перестановок букв слова «задача» будет не 6!, а в 3! раза меньше, то есть .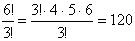

ПРИМЕР 13.2.7. В мастерской имеется материал 5 цветов. Поступил заказ на пошив флагов, состоящих из трех горизонтальных полос разного цвета каждый. Сколько таких различных флагов может сшить мастерская?

.

Решение: Флаги отличаются друг от друга как цветом полос, так и их порядком, поэтому разных флагов можно сделать 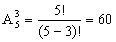штук.

ПРИМЕР 13.2.8. Сколькими способами можно распределить 5 учеников по 3 параллельным классам?

Решение: Составим вспомогательную таблицу

Таким образом, видно, что если для одного ученика существует 3 варианта выбора класса, то для всех 5 учеников существует 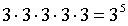способов распределения по классам.

ПРИМЕР 13.2.9. На книжной полке помещается 30 томов. Сколькими способами их можно расставить, чтобы при этом первый и второй том не стояли рядом?

Решение: Произведем рассуждения “от обратного”. Тридцать томов на одной полке можно разместить 30! способами.

.

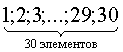
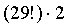
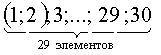
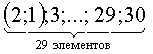
Если 1 и 2 тома должны стоять рядом, то число вариантов расстановки сокращается до , т.к. комбинацию из 1 и 2 тома можно считать за один том, но при этом они могут стоять как (1;2) или (2;1), т.е.

, .

Тогда искомое число способов расстановки есть

ПРИМЕР 13.2.10. Чемпионат, в котором участвуют 16 команд, проводится в два круга, т.е. каждая команда дважды встречается с любой другой. Определить, какое количество встреч следует провести.

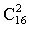
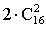
Решение: По условию задачи из 16 команд для каждой встречи требуется отобрать 2 команды. В данном случае отбор производится без повтора и порядок отбора не важен, т.е. число вариантов — . Так как команды должны играть дважды число вариантов удваивается, т.е. .

ПРИМЕР 13.2.11. Автомобильная мастерская имеет для окраски 10 основных цветов. Сколькими способами можно окрасить автомобиль, если смешивать от 3 до 7 основных цветов?

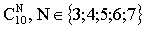
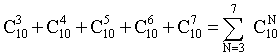
Решение: По условию задачи отбор цветов для окраски производится без повтора и порядок отбора не важен, т.е. число вариантов зависит лишь от числа отбираемых для окраски цветов — . Поэтому общее число вариантов есть

.

ПРИМЕР 13.2.12. Турист прошел маршрут из пункта A в пункт B, из B в C и вернулся обратно. Сколько вариантов маршрута существует, если из пункта A в пункт B ведут 3 дороги, а из B в C — 4 и нельзя возвращаться той дорогой, по которой уже прошел?

Решение: Составим схему.

Из рисунка видно, что вариантов маршрута из А в B существует 3, и из B в C – 4, т.е. всего маршрутов .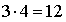

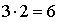
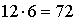
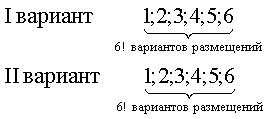
На обратном пути вариантов маршрута из С в B существует 3 (один уже пройден), и из B в А – 2, т.е. всего возможных обратных маршрутов осталось . Тогда всего вариантов маршрута .

ПРИМЕР 13.2.13. Двенадцати ученикам выданы два варианта контрольной работы. Сколькими способами можно посадить учеников в два ряда по 6 человек, чтобы у сидящих рядом не было одинаковых вариантов, а у сидящих друг за другом был один и тот же вариант?

Решение: Рассуждения произведем несколькими способами

I способ) Первоначально 12 учеников разбивают на 2 группы по 6 человек. Это можно сделать 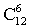способами.

Затем они могут распределиться по своим рядам согласно схеме

.

Поэтому всего способов распределения учеников будет .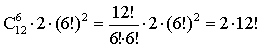

II способ) Первоначально 12 учеников запускают в класс, указывая место, где каждый должен сидеть, например “второй ряд, третье место”. Так как посадочных мест также 12, то всего вариантов распределения 12!
Варианты контрольной работы могут распределиться

“I вариант – I ряд, II вариант – II ряд”

“II вариант – I ряд, I вариант – II ряд”,

Таким образом, всего способов распределения учеников будет .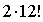

По приведенным решениям видно, что результаты решений совпадают.

ПРИМЕР 13.2.14. Сколько существует вариантов расположения шести гостей за круглым шестиместным столом?

Решение: Эта задача имеет разные решения и, соответственно разные ответы – в зависимости от того, что понимать под различным расположением гостей за столом. Поэтому исследуем возможные варианты.

Если считать, что нам важно, кто сидит на каком стуле, то это простая задача на перестановки и, следовательно, всего вариантов .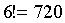

Если же важно не то, кто какой стул занял, а то, кто рядом с кем сидит, то требуется рассмотреть варианты взаимного расположения гостей. В таком случае, расположения гостей, получаемые одно из другого при повороте гостей вокруг стола, фактически являются одинаковыми (смотри рисунок).

Очевидно, что для любого расположения гостей таких одинаковых вариантов, получаемых друг из друга поворотом, — шесть. Тогда общее число вариантов уменьшается в шесть раз и их остается .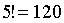
В случае же, когда нас интересует только взаимное расположение гостей, то одинаковыми можно считать и такие симметричные расположения, при которых у каждого гостя остаются те же соседи за столом, только левый и правый меняются местами (смотри рисунок).

В такой постановке вопроса общее число различных вариантов расположений гостей уменьшается вдвое и составляет 60.

Отметим, что каждое решение будет считаться правильным при соответствующей постановке задачи.

ПРИМЕР 13.2.15. Семнадцать студентов сдали экзамены по 4 предметам только на “хорошо” и “отлично”. Верно ли утверждение, что хотя бы у двух из них оценки по экзаменационным предметам совпадают?

Решение: Очевидно, что в данном случае речь идет о возможных вариантах вида

Предмет	1	2	3	4
Студент 1	4	4	5	5
Студент 2	5	4	4	5
Студент 3	5	5	5	5
…	…	…	…	…
Студент 17	4	4	5	4

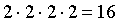
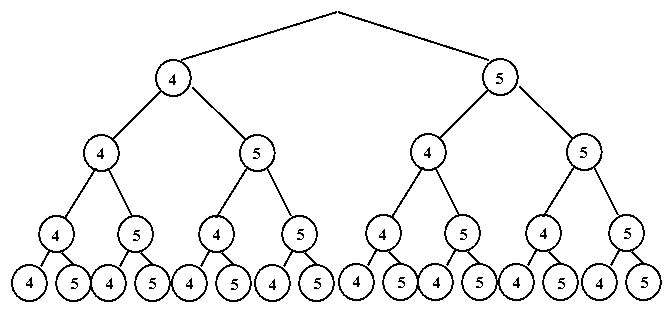
Данный пример можно решить способом, изложенным в примере 13.1.8., и получить количество вариантов . Приведем другой наглядный способ решения, использующий так называемое “дерево решений”,который представляет все варианты (16 штук) получения экзаменационных оценок.

.

По “дереву решений” видно, что 16 студентов могут сдать экзамены только на “хорошо” и “отлично” так, что их результаты будут отличаться, но если студентов 17, хотя бы одно повторение обязательно будет.

При решении задач комбинаторики используются следующие правила.

Если некоторый объект A может быть выбран из совокупности объектов m способами, а другой объект B может быть выбран nспособами, то:

Правило суммы: выбрать либо A, либо B можно m+n способами.

Правило произведения. Пара объектов (A,B) в указанном порядке может быть выбрана 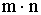способами.

Примеры и задачи для самостоятельного решения

Решить комбинаторную задачу.

13.2.1.1. В группе 25 студентов. Сколькими способами можно выбрать старосту, заместителя старосты и профорга?

13.2.1.2. В группе 25 студентов. Сколькими способами можно выбрать актив группы, состоящий из старосты, заместителя старосты и профорга?

13.2.1.3. Сколькими способами можно составить список из 10 человек?

13.2.1.4. Сколькими способами из 15 рабочих можно создать бригады по 5 человек в каждой?

13.2.1.5. Буквы азбуки Морзе образуются как последовательности точек и тире. Сколько букв можно составить, используя для кодировки каждой из букв: а) ровно 5 символов? б) не более пяти символов?

13.2.1.6. Кости для игры в домино метятся двумя цифрами. Кости симметричны, и поэтому порядок чисел не существенен. Сколько различных костей можно образовать, используя числа 0,1,2,3,4,5,6?

13.2.1.7. Сколько различных звукосочетаний можно взять на десяти выбранных клавишах рояля, если каждое звукосочетание может содержать от трех до десяти различных звуков?

13.2.1.8. В вазе стоят 10 красных и 5 розовых гвоздик. Сколькими способами можно выбрать из вазы пять гвоздик одного цвета?

13.2.1.9. В некоторых странах номера трамвайных маршрутов обозначаются двумя цветными фонарями. Какое количество различных маршрутов можно обозначить, если использовать фонари восьми цветов?

13.2.1.10. Команда компьютера записывается в виде набора из восьми цифровых знаков – нулей и единиц. Каково максимальное количество различных команд?

13.2.1.11. Десять групп занимаются в десяти расположенных подряд аудиториях. Сколько существует вариантов расписания, при которых группы 1 и 2 находились бы в соседних аудиториях?

13.2.1.12. Два почтальона должны разнести 10 писем по 10 адресам. Сколькими способами они могут распределить работу?

13.2.1.13. Замок открывается только в том случае, если набран определенный трехзначный номер. Попытка состоит в том, что набирают наугад три цифры из заданных пяти. Угадать номер удалось только на последней из всех возможных попыток. Сколько попыток предшествовало удачной?

13.2.1.14. Номер автомобильного прицепа состоит из двух букв и четырех цифр. Сколько различных номеров можно составить, используя 30 букв и 10 цифр?

13.2.1.15. У одного студента есть 7 DVD дисков, а у другого – 9 дисков. Сколькими способами они могут обменять 3 диска одного на 3 диска другого?

13.2.1.16. На вершину горы ведут 7 дорог. Сколькими способами турист может два раза подняться на гору и спуститься с нее, если по одной и той же дороге нельзя проходить дважды?

13.2.1.17. У ювелира было 9 разных драгоценных камней: сапфир, рубин, топаз и т.д. Ювелир планировал изготовить браслет для часов, однако три камня было украдено. Насколько меньше вариантов браслета он может изготовить по сравнению с первоначальными планами?

13.2.1.18. В поезд метро на начальной станции вошли 10 пассажиров. Сколькими способами могут выйти все пассажиры на последующих 6 станциях?

13.2.1.19. За одним столом надо рассадить 5 мальчиков и 5 девочек так, чтобы не было двух рядом сидящих мальчиков и двух рядом сидящих девочек. Сколькими способами это можно сделать?

13.2.1.20. В классе 25 учеников. Верно ли утверждение, что, по крайней мере, у трех из них день рождения в один и тот же месяц?

13.2.1.21. На участке железной дороги расположено 25 станций с билетной кассой в каждой. Касса каждой станции продает билеты до любой другой станции, притом в обоих направлениях. Сколько различных вариантов билетов можно выдать на этом участке?

13.2.1.22. На официальном приеме 50 человек обменялись рукопожатиями. Сколько было сделано рукопожатий?

13.2.1.23. Сколько диагоналей у выпуклого двадцатиугольника?

Уважаемые студенты
На нашем сайте можно получить помощь по всем разделам математики и другим предметам:
✔ Решение задач
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

• 
  
  

В группе 30 студентов сколькими способами можно выделить двух человек для дежурства, причем из них старший?

---

С этим файлом связано 1 файл(ов). Среди них: Типовые задачи часть 4.pdf.
Показать все связанные файлы

---

Подборка по базе: статистика учебное пособие .doc, Учебное пособие для ПИ_2022.pdf, Учебное пособие, Царев.pdf, ОПОРНЫЙ КОНСПЕКТ ЛЕКЦИЙ по МДК 05.01 Технология работ по професс, Методическое пособие расчет.doc, Учебное пособие по теме реклама.doc, Алгебра 7 Методическое пособие.pdf, Уч пособие лог_испр_все.doc, Учебное пособие Электротехника.pdf, Метод пособие по ворд.docx

---

РАЗДЕЛ ВТОРОЙ. ВВЕДЕНИЕ В ТЕОРИЮ ВЕРОЯТНОСТЕЙ

2.1. Элементы комбинаторики

Пример 2.1.1. Вычислить .

Решение. Т.к. при , то .

Пример 2.1.2. Вычислить число перестановок из 4 элементов.

Решение. Т.к. , то .

Пример 2.1.3. Вычислить число размещений из 7 элементов по 2.

Решение. .

Пример 2.1. 4. Вычислить число сочетаний из 5 элементов по 32.

Решение. .

Пример 2.1.5. В ящике 300 деталей. Известно, что 150 из них – 1-го сорта, 120 – 2-го, а остальные – 3-го. Сколько существует способов извлечения из ящика одной детали 1-го или 3-го сорта?

Решение. Деталь 1-го сорта может быть извлечена способами, 3-го сорта – способами. По правилу суммы существует способов извлечения одной детали 1-го или 3-го сорта.

Пример 2.1.6. Из 30 участников собрания надо выбрать председателя и секретаря. Сколькими способами это можно сделать?

Решение. Председателем может быть выбран любой из участников, секретарём – любой из оставшихся . По правилу произведения число способов выбора председателя и секретаря равно .

Пример 2.1.7. Порядок выступления 7 участников конкурса определяется жребием. Сколько различных вариантов жеребьёвки при этом возможно?

Решение. Каждый вариант жеребьёвки отличается только порядком участников конкурса, т.е. является перестановкой из 7 элементов. Поэтому число различных вариантов жеребьёвки равно .

Пример 2.1.8. Расписание одного дня состоит из 4 уроков различных дисциплин. Определить число вариантов расписания при выборе из 8 дисциплин.

Решение. Вариант расписания представляет набор 4 различных дисциплин из 8, отличающийся от других вариантов как составом дисциплин, так и порядком их следования, т.е. является размещением из 8 элементов по 4.

Поэтому число вариантов равно .

Пример 2.1.9. На тренировке занимаются 12 баскетболистов. Сколько может быть образовано стартовых пятёрок?

Решение. При составлении стартовой пятёрки играет роль только её состав. Поэтому количество стартовых пятёрок равно числу сочетаний из 12 элементов по 5: .

Пример 2.1.10. В вазе стоят 10 белых и 5 красных роз. Сколькими способами можно выбрать 7 роз, чтобы среди них было 3 красные розы?

Решение. По условию задачи среди выбранных 7 цветов 4 белых и 3 красные розы. 4 белые розы можно выбрать способами, 3 красные – способами. Согласно правилу произведения извлечь 7 роз, среди которых 4 белых и 3 красные розы можно способами.

Задачи для самостоятельного решения

1. Вычислите: 1) ; 2) ; 3) ; 4) ; 5) ; 6) ;
7) ; ; 9) ; 10) .

2. На блюде лежат 4 яблока и 3 груши. Сколькими способами можно выбрать один плод?

3. В группе 15 человек. Необходимо выбрать старосту, его заместителя и профорга. Сколько существует способов это сделать?

4. Из города в город ведут 4 дороги, а из города в город — 3 дороги. Туристы хотят проехать из города в город через город . Сколькими способами они могут выбрать маршрут?

5. Сколькими способами можно расставить 8 участников финального забега на восьми беговых дорожках?

6. Экзамен сдают 20 студентов. Сколько существует возможных вариантов их очерёдности?

7. Семь юношей, в число которых входят Петя и Игорь, становятся в ряд. Найдите число возможных комбинаций, если: а) Петя должен находиться в конце ряда; б) Петя должен находиться в конце ряда, а Игорь –

в начале ряда; в) Петя и Игорь должны стоять рядом?

8. Сколько можно составить шестизначных номеров телефона из 9 цифр: 1, 2, 3, 4, 5, 6, 7, 8, 9, если в каждом номере все цифры различны?

9. Необходимо выбрать в подарок 4 из 10 имеющихся различных книг. Сколькими способами это можно сделать?

10. В вазе стоят 9 белых и 4 розовых тюльпана. Сколькими способами можно выбрать из вазы 5 цветов?

11. Бригада, занимающаяся ремонтом здания, состоит из 12 маляров и 5 плотников. Из них для ремонта цокольного этажа надо выделить 4 маляра и 2 плотников. Сколькими способами это можно сделать?

12. Из 12 солдат, в число которых входят Иванов и Петров, надо отправить в наряд 4 человек. Сколькими способами это можно сделать, если: а) Иванов и Петров должны пойти в наряд; б) Иванов и Петров должны остаться; в) Иванов должен пойти в наряд, а Петров – остаться?

2.2. Классическое определение вероятности

Пример 2.2.1. Игральный кубик бросили один раз. Какова вероятность того, что выпало число очков больше, чем 4?

Решение. Случайный эксперимент – бросание кубика. Элементарный исход – число на выпавшей грани. Граней всего шесть. Перечислим все элементарные исходы: 1, 2, 3, 4, 5, 6. Значит общее число элементарных исходов . Событию – выпало больше, чем 4 – благоприятствуют два элементарных исхода: 5 и 6. Следовательно, . Согласно классическому определению вероятности .

Пример 2.2.2. Бросают два игральных кубика. Найдите вероятность того, что в сумме выпадет 9 очков.

Решение. Элементарный исход в данном опыте – упорядоченная пара чисел. Множество элементарных исходов представим в виде таблицы 1. Строки соответствуют результату первого броска, столбцы – результату второго броска. Всего элементарных исходов .

Таблица 1

	1	2	3	4	5	6
1	2	3	4	5	6	7
2	3	4	5	6	7	8
3	4	5	6	7	8	9
4	5	6	7	8	9	10
5	6	7	8	9	10	11
6	7	8	9	10	11	12

В каждой клетке таблицы запишем сумму выпавших очков. Событию – сумма выпавших очков равна 9 – благоприятствуют 4 исхода. Следовательно, . Поэтому .Пример 2.2.3. В среднем из 1000 аккумуляторов, поступивших в продажу, 6 неисправны. Найдите вероятность того, что один купленный аккумулятор окажется исправным.

Решение. Элементарный исход – случайно выбранный аккумулятор. Поэтому . Событию – аккумулятор исправен – благоприятствует 1000–6=994 исхода: . Тогда .

Пример 2.2.4. Найти вероятность того, что при вынимании одной случайной карты из колоды 36 карт, получим карту «Туз» или карту масти черви.

Решение. Элементарный исход – случайно выбранная карта. Поэтому . Событию – карта туз или карта масти черви – благоприятствует исходов (9 карт масти черви и 3 туза оставшихся мастей): . Тогда .

Пример 2.2.5. Буквы Т, Е, И, Я, Р, О написаны на отдельных карточках. Ребёнок берёт карточки в случайном порядке и кладёт одну за другой.

Какова вероятность того, что получится слово «ТЕОРИЯ»?

Решение. Пусть событие – получение слова «ТЕОРИЯ». Различные комбинации шести букв из имеющихся различных шести представляют собой перестановки, так как отличаются только порядком следования букв. Поэтому общее количество элементарных исходов . Событию благоприятствует 1 исход. Поэтому .

Пример 2.2.6. Буквы Т, Е, И, Я, Р, О написаны на отдельных карточках. Ребёнок выбирает произвольно 3 карточки и кладёт одну за другой. Какова вероятность того, что получится слово «ТОР»?

Решение. Пусть событие – получение слова «ТОР». Комбинации 3-х букв из имеющихся шести представляют размещения из 6 элементов по 3, так как могут отличаться как составом входящих букв, так и порядком их следования. Поэтому общее количество элементарных исходов , из которых событию благоприятствует . Следовательно, .

Пример 2.2.7. По условиям «Спортлото 6 из 45» участник лотереи, угадавший 4,5 или 6 видов спорта из отобранных при случайном розыгрыше 6-ти видов спорта из 45, получает денежный приз. Найти вероятность того, что будут угаданы: а) все 6 номеров; б) 4 номера.

Решение. а) Пусть событие – угаданы все 6 видов спорта из 45. Количество элементарных исходов (всех вариантов заполнения карточек спортлото) , т.к. каждый вариант заполнения отличается лишь составом видов спорта (порядок роли не играет). Число исходов, благоприятствующих событию , есть . Поэтому,

.

б) Пусть событие – угаданы 4 вида спорта из 6 выигравших. Количество элементарных исходов (см. (а)). Число способов выбора четырёх видов спорта из шести выигравших равно , а двух невыигрышных – . Число исходов, благоприятствующих событию В, равно . Поэтому,

.

Задачи для самостоятельного решения

1. Бросают два игральных кубика. Найдите вероятность того, что в сумме выпадет а) 5 очков; б) 11 очков; в) 13 очков.

2. Бросают два игральных кубика. Найдите вероятности следующих событий: а) сумма выпавших очков равна восьми, а модуль разности – четырём; б) сумма выпавших очков равна пяти, а произведение – четырём.

3. Заполните таблицу 2, в которой – число всех элементарных равновозможных исходов испытания; число исходов, благоприятствующих событию ; вероятность наступления события .

Таблица 2

№	Испытание (эксперимент)		Событие
1	Подбрасывание игрального кубика		Выпавшее число очков нечетно
2	Подбрасывание игрального кубика		Выпавшее число очков кратно 3
3	Подбрасывание игрального кубика		Выпавшее число очков не менее 4
4	Подбрасывание игрального кубика		Выпавшее число очков больше 6
5	Подбрасывание игрального кубика		Выпавшее число очков является целым числом
6	Раскручивание стрелки рулетки, разделенной на 8 равных секторов, занумерованных числами от 1 до 8		Остановка стрелки на секторе с номером кратным 3
7	Раскручивание стрелки рулетки, разделенной на 8 равных секторов, занумерованных числами от 1 до 8		Остановка стрелки на секторе, номер которого не больше 5

4. Маша дважды бросает игральный кубик. В сумме у нее выпало 7 очков. Найдите вероятность того, что при одном из бросков выпало 5 очков.

5. Набирая номер телефона, абонент забыл последние 3 цифры. Зная то, что они различны, набрал их наудачу. Найдите вероятность того, что набраны нужные цифры.

6. В среднем из 1100 садовых насосов, поступивших в продажу, 11 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает.

7. Найти вероятность того, что при вынимании одной случайной карты из колоды 36 карт, получим карту «Дама» или карту масти треф.

8. В ящике 12 белых, 7 чёрных и 11 синих шаров. Наудачу вынимают один шар. Какова вероятность, что вынутый шар – не белый?

9. Какова вероятность того, что случайно выбранной двузначное число

кратно: а) 10; б) 5; в) 14.

10. В коробке имеется 4 одинаковых занумерованных шара. Наудачу по одному извлекают все шары. Найдите вероятность того, что номера извлечённых шаров появятся в возрастающем порядке.

11. На пяти карточках написаны буквы Н, Е, Ф, Т, Ь. После тщательного перемешивания берут по одной карточке и кладут последовательно рядом. Какова вероятность, что получится слово «НЕФТЬ»?

12. Слово «МОЛНИЯ» разрезали на буквы. Взяли наудачу 4 буквы и выложили в ряд. Какова вероятность, что получится слово «МИЛЯ»?

13. Комиссия по качеству раз в месяц проверяет качество продуктов в двух из 30-ти магазинов, среди которых находятся и два известных вам магазина. Какова вероятность того, что в течение месяца они оба будут проверены?

14. Из 30 студентов 10 имеют спортивные разряды. Какова вероятность того, что выбранные наудачу 3 студента – разрядники?

15. Из 20 акционерных обществ (АО) 4 являются банкротами. Гражданин приобрёл по одной акции шести АО. Какова вероятность того, что среди купленных акций две окажутся акциями банкротов?

16. Среди 25 студентов, из которых 15 девушек, разыгрываются 4 билета, причём каждый может выиграть только один билет. Какова вероятность того, что среди обладателей билета окажутся: а) 4 девушки;
б) 4 юноши; в) 3 юноши и 1 девушка.

© Преподаватель Анна Евкова

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Правовые документы

Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Задачи по комбинаторики

Задача 1: Сколькими способами можно составить список из 5 учеников?

Ответ: перестановки, 5! = 120.

Задача 2: В футбольной команде (11 человек) нужно выбрать капитана и его заместителя. Сколькими способами это можно сделать?

Ответ: размещения из 11 по 2, А²₁₁= 110.

Задача 3: Расписание на день содержит 5 уроков. Определить количество возможных расписаний при выборе из 14 предметов, при условии, что ни один предмет не стоит дважды.

Ответ: размещения из 14 по 5, 1320.

Задача 4: Сколько различных трехцветных флагов можно сделать, комбинируя синий, красный и белый цвета?

Ответ: перестановки, 6 способов.

Задача 5: В классе 24 ученика. Сколькими способами можно сформировать команду из 4 человек для участия в математической олимпиаде?

Ответ: сочетания из 24 по 4,

Задача 6: Сколько трехзначных чисел можно составить из цифр 1, 2, 3, если каждая цифра входит в изображение числа только 1 раз?

Ответ: перестановки, 6 способов.

Задача 7: Сколькими различными способами можно избрать из 15 человек делегацию в составе 3 человек?

Ответ: сочетания, 455 способами.

Задача 8: Из ящика, где находится 15 шаров, нумерованных последовательно от 1 до 15, требуется вынуть 3 шара. Определить число возможных комбинаций при этом?

Ответ: размещения, 2830 способами.

Задача 9: Сколько четырехзначных чисел можно составить из цифр 0, 1, 2, 3, если каждая цифра входит в изображение числа только 1 раз?

Ответ: перестановки, 4! – 3! =18.

Задача 10: Сколькими способами можно разместить 6 пассажиров в четырехместной каюте?

Ответ: размещения из 6 элементов по 4, 360 способами.

Задача 11: Сколькими способами можно выбрать 2 детали из ящика, содержащего 10 деталей?

Ответ: сочетания из 10 элементов по 2, 45 способами.

Задача 12: Бригадир должен отправить на работу бригаду из 4 человек. Сколько бригад по 4 человека в каждой можно составить из 13 человек?

Ответ: сочетания из 13 по 4, 715 бригад.

Задача 13: При встрече 16 человек обменялись рукопожатиями. Сколько всего было сделано рукопожатий?

Ответ: сочетания из 16 по 2, 120 рукопожатий.

Задача 14: Группа учащихся в 30 человек пожелала обменяться своими фотокарточками. Сколько всего фотокарточек потребовалось для этого?

Ответ: сочетание из 30 по 2, 435 фотокарточек.

Задача 15: Сколько различных плоскостей можно провести через 10 точек, если никакие три из них не лежат на одной прямой и никакие четыре точки не лежат в одной плоскости?

Ответ: сочетание из 10 по 3; 120 точек

Задача 16: Сколько существует различных семизначных телефонных номеров?

Ответ: 10⁷.

Задача 17: Сколько существует различных семизначных телефонных номеров, если в каждом номере нет повторяющихся цифр?

Ответ: размещение из 10 по 7.

Задача 18: Сколько существует таких перестановок 7 учеников, при которых 3 определенных ученика находятся рядом друг с другом? Ответ: 720 = 3! · 5!

Задача 19: На книжной полке стоит собрание сочинений в 30 томах. Сколькими различными способами их можно переставить, чтобы: а) тома 1 и 2 стояли рядом; б) тома 3 и 4 рядом не стояли?

Ответ: а)2∙29!; б)28∙29!

Задача 20: Сколько существует трёхзначных чисел, все цифры которых нечётные и различные?

Ответ: размещение из 5 по 3, 60.

Задача 21: У одного мальчика имеется 10 марок для обмена, а у другого – 8. Сколькими способами они могут обменять 2 марки одного на 2 марки другого?

Ответ: сочетания, С²₁₀·С²₈ = 1260.