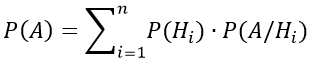Экзамен сдают студенты трех групп - Помощь в подготовке к экзаменам и поступлению

Закажите у меня новую работу, просто написав мне в чат!

Экзамен сдавали студенты трех групп, причем в i -й группе учатся mi % студентов i  1, 2,3 . Вероятность сдать экзамен на положительную оценку для студента i -й группы i n %. Наудачу выбранный студент экзамен не сдал. Определить вероятность того, что этот студент из j-й группы?

Основное событие А − выбранный наудачу студент экзамен не сдал. Гипотезы: 𝐻1 − этот студент из первой группы; 𝐻2 − этот студент из второй группы; 𝐻3 − этот студент из третьей группы. Вероятности гипотез (по классическому определению вероятности): Условные вероятности: Вероятность того, что не сдавший экзамен студент – это студент из первой группы, по формуле Байеса: Ответ: 𝑃(𝐻1|𝐴) = 0,65

Источник

Пусть совокупность событий H₁,H₂,…,H_n — образуют полную группу событий, а также их объединение даёт достоверное событие и они попарно несовместные. В случае наступления каждого из событий H_i, событие А может настать с некоторой условной вероятностью P_Hi·(A)

События H_i называют гипотезами.

Запишем формулу полной вероятности:

P(A)=P(H₁)·P_H₁(A)+P(H₂)·P_H2(A)+…+P(H_n)

или эту формулу можно представить в следующем виде:

Пример 1

В пирамиде пять винтовок, три из которых снабжены оптическим прицелом. Вероятность того, что стрелок поразит мишень при выстреле из винтовки с оптическим прицелом, равна 0,95; для винтовки без оптического прицела эта вероятность равна 0,7. Найти вероятность того, что мишень будет поражена, если стрелок произведет один выстрел из наудачу взятой винтовки.

Решение

А — «мишень поражена»

H₁: «выстрел из винтовки с оптическим прицелом»

H₂: «выстрел из винтовки без оптического прицела»

Находим вероятности

Р(H₁)=3/5=0.6, Р(H₂) =2/5=0.4

Р_H1(А)=0.95, Р_H2(А)=0.7

Итак, по формуле полной вероятности находим вероятность

Р(А)=P(H₁)·P_H₁(A)+P(H₂)·P_H2(A)=0,57·0,92+0,43·0,8=0,524+0,344=0,868

Пример 2

В вычислительной лаборатории имеются шесть клавишных автоматов и четыре полуавтомата. Вероятность того, что за время выполнения некоторого расчета автомат не выйдет из строя, равна 0,95; для полуавтомата эта вероятность равна 0,8. Студент производит расчет на наудачу выбранной машине. Найти вероятность того, что до окончания расчета машина не выйдет из строя.

Решение

А — «до конца расчета машина не выйдет из строя»

H₁ — «клавишный автомат не выйдет из строя»

H₂ — «полуавтомат не выйдет из строя»

Из условия задачи получаем

Р(H₁)=6/10=0,6 Р(H₂)=4/10=0,4

Условные вероятности равны

Р_H1(А)=0.95, Р_H2(А)=0.8

Воспользуемся формулу полной вероятности, имеем:

Р(А)=P(H₁)·P_H₁(A)+P(H₂)·P_H2(A)=

=0,6·0,95+0,4·0,8=0,89

Пример 3

Экзамен сдают студенты трех групп. В первой группе 7, во второй 6 и в третьей 8 студентов. Студент из первой группы сдаст экзамен с вероятностью 0.9, из второй группы с вероятностью 0.8 и из третьей группы с вероятностью 0.7. С какой вероятностью сдаст экзамен случайно вызванный студент?

Решение

Cобитые А — «случайно вызванный студент сдаст экзамен»

Н₁: студент из 1-ой группы

Р(H₁)=7/21; Р(A|H₁)=0.9

Н₂: студент из 2-ой группы

Р(H₂)=6/21; Р(A|H₂)=0.8

Н₃: студент из 3-ей группы

Р(H₃)=8/21; Р(A|H₃)=0.7

По формуле полной вероятности получаем:

Р(А)=P(H₁)·Р(A|H₁)+P(H₂)·Р(A|H₂)+P(H₃)·P(A|H₃)=

=7/21·0.9+6/21·0.8+8/21·0.7=0.795

Пример 4

В первой урне содержится 10 шаров, из них 8 белых; во второй урне 20 шаров, из них 4 белых. Из каждой урны наудачу извлекли по одному шару, а затем из этих двух шаров наудачу взят один шар. Найти вероятность того, что взят белый шар.

Решение

A— «наудачу извлечённый из двух выбранных шаров — белый шар»

H₁: «шар извлечен из первой урны»

H₂: «шар извлечен из второй урны»

По условию задачи, следует, что из каждой урны извлекается одинаковое количество шаров, тогда получаем вероятности

Р(H₁)=Р(H₂)=1/2

Найдем условные вероятности того, что из первой урны

Р_H1(A)=8/10=3/10

и второй урны извлечен белый шар

Р_H2(A)=4/20=1/5

Применяя формулу полной вероятности, найдем вероятность того, что взят белый шар

Р(А)=P(H₁)·P_H₁(A)+P(H₂)·P_H2(A)=

=1/2·4/5+1/2·1/5=1/2

Источник

Известно, что в среднем с первой попытки сдают зачет в первой группе 75% студентов, во второй и третьей – 65% и 40%, соответственно. Какова вероятность того, что наудачу взятая работа будет зачтенной?

махня

29.05.18

Учеба и наука / Математика

1 ответ

Источник

Экзамен сдавали студенты трех групп, причем в i -й группе учатся mi% студентов (i = 1, 2, 3). Вероятность сдать экзамен на положительную оценку для студента i-й группы ni%. Наудачу выбранный студент экзамен не сдал. Определить вероятность того, что этот студент из i -й группы?

m1 = 50, m2 = 30, m3=20, n1=70, n2=80, n3=90, i=2

Мозг / Ответ

Сомневаешься в ответе?
Смотреть другие ответы

УЗНАВАЙ
БОЛЬШЕ НА
школьникам!

У тебя проблема с домашними заданиями? Попроси о помощи!

80% ответов приходят в течение 10 минут;
Мы не только ответим, но и объясним;
Качество гарантируется нашими экспертами.

Хочу завести аккаунт!

Что ты хочешь узнать?

Самые новые вопросы

СРОЧНО !!! 80 БАЛЛОВ Из центра окружности О

1 Просмотров

Источник

1

§ 3. Условные вероятности. Полная вероятность. Формула Байеса. Пример. Бросают игральную кость, у которой грани с числом очков 1, 2 и 3 покрашены красным цветом, а грани с числом очков 4, 5 и 6 – черным цветом. Найти вероятность, что выпало четное число очков, з ная, что в результате броска выпала черная грань ? Решение. То, что выпала чрная грань, сужает пространство элементарных событий Ω до трех-элементного: Ω B = выпала черная грань, где n B = 3. Для события A = число очков четное сопутствующие элементарные события будем искать среди элементов множестваB. Т.к. среди числа очков 4, 5 и 6 четных чисел два, то получаем: P(A | B)

3

Теорема умножения вероятностей в общем случае: Замечание: доказывается методом математической индукции. Если n = 3, то формула имеет вид: Задача. В урне 4 белых, 3 синих и 2 черных шара. Из урны случайным образом вынимают один за другим 3 шара без возвращения назад. Найти вероятность того, что шары выбраны в порядке: белый, синий, черный. Решение. P(Белый,Синий,Черный)= = P( Белый )*P( Синий | Белый )*P( Черный | Белый, Синий )= = 4/9*3/8*2/7=1/21.

4

Следствие: если A B, то P(A|B) = P(A) и по теореме умножения вероятностей P(AB) = P(A)*P(B). Пример. При бросании игральной кости каждое следующее выпавшее число очков не зависит от предыдущего. Независимые события. С другой стороны сумма выпавших очков, например при двух бросаниях, зависит от числа очков, выпавших при первом броске. Зависимые события.

5

В общем случае: События A 1,A 2,…,A n независимые (в совокупности), если каждое из событий не зависит от произведения любого числа остальных событий и от каждого из остальных событий в отдельности. В этом случае верно равенство: Замечание: из попарной независимости событий не следует их независимость в совокупности.

6

Пример 1. Монету подбрасывают 2 раза, броски между собой независимы. Найти вероятность, что a)выпадут 2 герба, b)выпадет хотя бы 1 герб. Решение. Т.к.броски между собой независимые, то события Г 1 = герб выпадет при 1-ом броске, Г 2 = герб выпадет при 2-ом броске, Р 1 = при 1-ом броске выпадет решетка, Р 2 = при 2-ом броске выпадет решетка — независимые. Т.к. вероятность выпадения герба/решетки при каждом броске ½, то a)Вероятность, что выпадут 2 герба: P(Г 1 Г 2 )=P(Г 1 )P(Г 2 )= ½*½ = ¼. b)Выпадения хотя бы 1 герба соответствует событию, что герб выпедет при 1-ом, при 2-ом или при обоих бросках, вероятность которого: P(Г 1 Р 2 +Р 1 Г 2 +Г 1 Г 2 ) = P(Г 1 )P(Р 2 )+ P(Р 1 )P(Г 2 )+ P(Г 1 )P(Г 2 ) = 1/2*1/2+1/2*1/2+1/2*1/2=3/4. Или через обратное событие, означающее, что герб не выпал ни разу: P(Г 1 Р 2 +Р 1 Г 2 +Г 1 Г 2 ) =1- P(Р 1 Р 2 )=1-1/2=3/4.

7

Пример 2. Два студента выполняют по очереди свободные броски в корзину. У каждого 2 броска. Премию получает тот, кто попадет первым. Вероятность попадания бросающего первым при каждом броске 0,4, бросающего вторым 0,7. Найти вероятность получения премии каждым из бросающих. Решение. Пусть результаты бросков независимы. Обозначим события: П 1 =Первый студент бросает и попадает и П 2 =Второй студент бросает и попадает. Соответствующие противоположные события: П 1 = Первый студент бросает мимо и П 2 = Второй студент бросает мимо. Бросающий первым получит премию в результате следущей серии бросков: попадает и получает премию или бросает мимо, тогда второй также бросает мимо, затем первый попадает и получает премию. Вероятность серии: Вероятность получения премии бросающим вторым:

8

Пример 3. надежность элемента p. Для повышения надежности элемент дублируется параллельно двумя элементами с такой же надежности. Найти надежность полученной системы. Решение. Т.к. элемент дублируется параллельно, то полученная система будет работать, если работает хотя бы один элемент. p p p Надежность элемента означает вероятность его безотказной работы за данный промежуток времени. E1 E2 E3 Обозначим события: E 1 =1-ый элемент работает в течение заданного времени, E 2 =2-ой элемент работает в течение заданного времени, E 3 =3-ий элемент работает в течение заданного времени. Надежность всей системы равна вероятности: Или через обратное событие, зная, что элемент выходит из строя с вероятностью 1- p :

9

Пусть события H 1,…, H n (гипотезы) образуют полную систему несовместимых событий и имеют вероятности P(H 1 ),…, P(H n ). Пусть событие A может произойти только с одним из событий H i, и известна условная вероятность события A при условии H i : P(A | H i ), i=1,…, n. Тогда формула полной вероятности события A : Формула полной вероятности. Доказательство: т.к. A может произойти только с одним из H i : Т.к. гипотезы образуют полную систему несовместимых событий: AHi AHj =, i, j = 1,…,n, i j. По формуле сложения вероятностей: и по формуле умножения: Заменяем в формуле (1) отдельные слагаемые правой частью последнего равенства. Получаем формулу полной вероятности: (1)

10

Событие A может произойти только с одним из событий H 1, H 2, H 3 (студенты могут быть только из указанных групп). Тогда по формуле полной вероятности: Пример. Экзамен сдают студенты трех групп. В первой группе 7, во второй 6 и в третьей 8 студентов. Студент из первой группы сдаст экзамен с вероятностью 0.9, из второй группы с вероятностью 0.8 и из третьей группы с вероятностью С какой вероятностью сдаст экзамен случайно вызванный студент? Решение:Обозначим события: A: случайно вызванный студент сдаст экзамен; H 1 : студент из 1-ой группы; H 2 : студент из 2-ой группы; H 3 : студент из 3-ей группы. P(H 1 )=7/21; P(H 2 )=6/21; P(H 3 )=8/21. P(A|H 1 )=0.9; P(A|H 2 )=0.8; P(A|H 3 )=0.95. =7/21*0.9+6/21*0.8+8/21*0.95=(7*0.9+6*0.8+8*0.95)/

11

Пусть события H 1,…, H n (гипотезы) образуют полную систему несовместимых событий и имеют вероятности P(H 1 ),…, P(H n ). Пусть событие A может произойти только с одним из событий H i, и известна условная вероятность события A при условии H i : P(A|H i ), i=1,…, n. Тогда условная вероятность гипотезы H i при условии, что произошло событие A находится по формуле Байеса: Доказательство : по коммутативности умножения событий: откуда что и требовалось доказать. Формула полной вероятности по формуле умножения вероятностей: Формула Байеса. Thomas Bayes

12

Пример. В ящике 5 красных, 6 зеленых и 7 синих коробок. В каждой красной коробке 6 черных и 4 белых шара, в каждой зеленой 7 черных и 5 белых шара и в каждой синей 5 черных и 9 белых шара. Из ящика в темноте выбирают коробку и из нее шар, который оказался черным. Найти вероятности, что шар был выбран из первой, второй или третьей коробки? Вероятность выбора шара из красной коробки при условии, что шар черный: P(черный шар из зеленой коробки): P(черный шар из синей коробки): Решение: Обозначим события: A: выбранный шар черный; H 1 : выбрана красная коробка; H 2 : выбрана зеленая коробка; H 3 : выбрана синяя коробка. P(H 1 )=5/18; P(H 2 )=6/18; P(H 3 )=7/18. P(A|H 1 )=6/10; P(A|H 2 )=7/12; P(A|H 3 )=5/14.

Источник

Три
группы студентов сдавали экзамен по
математике. В первой группе успешно
сдали 80% студентов, во второй – 75%,
третьей – 90%. Найти вероятность того,
что наудачу выбранный студент из этих
групп сдал успешно экзамен, если
численность первой группы в 2 раза
больше численности второй и в 3 раза
больше численности третьей группы.
В
магазин поступают плащи с трех фабрик
в соотношении 2:5:3. Комбинированные
плащи среди продукции составляют в
среднем 97, 96, 98% соответственно. Наудачу
выбранный плащ оказался комбинированным.
С какой фабрики вероятнее всего он
поступил?
На
первом станке изготовлено 20 деталей,
из них 7 с дефектом, на втором 30 деталей,
из них 4 с дефектом, на третьем – 50
деталей, из них 10 с дефектом. С общего
конвейера взята наудачу деталь,
оказавшаяся без дефекта. Найти вероятность
того, что она изготовлена на третьем
станке.
По
результатам проверки контрольных работ
оказалось, что в первой группе получили
положительные оценки 20 из 30 студентов,
во второй группе 15 из 25. Найти вероятность
того, что наудачу выбранная работа,
имеющая положительную оценку, написана
студентом первой группы.
На
склад поступила продукция трех цехов
в соотношении 2:5:3. Средний процент
второсортных изделий для продукции
первого цеха 3%, для второго – 2%, третьего
– 1%. Найти вероятность того, что наудачу
взятое изделие, оказавшееся второсортным,
произведено первым цехом.
В
магазин поступили часы с трех заводов:
с первого 40%, со второго – 45% и остальные
с третьего. В продукции первого завода
спешат 20% часов, второго – 30% и третьего
– 10%. Найти вероятность того, что
купленные в этом магазине часы спешат.
На
радиолокатор с вероятностью 0,8 поступает
смесь полезного сигнала с помехой, с
вероятностью 0,2 – одна помеха. Полезный
сигнал с помехой приемное устройство
регистрирует с вероятностью 0,7, помеху
– с вероятностью 0,3. Устройство
зарегистрировало наличие какого-то
сигнала. Найти вероятность того, что в
его составе есть полезный сигнал.
Нормальный
режим функционирования робота
зарегистрирован в 60% случаях работы,
форсированный в 30% и недогруженный –
в 10%. Его надежность при нормальном
режиме 0,8, при форсированном 0,6, при
недогруженном – 0,9. Найти полную
надежность робота.
В
продажу поступили телевизоры от трех
фирм. Продукция первой фирмы содержит
20% телевизоров со скрытым дефектом,
второй – 10% и третьей – 5%. Найти
вероятность приобретения исправного
телевизора, если в магазин поступило
30% телевизоров от первой фирмы, 20% от
второй и 50% от третьей.
Система
обнаружения самолета из-за помех может
давать ложные показания с вероятностью
0,05, а при наличии цели система обнаруживает
ее с вероятностью 0,9. Вероятность
появления цели в зоне обнаружения 0,25.
Найти вероятность ложной тревоги.
По
летящей цели производится три выстрела.
Вероятность попадания в нее при первом
выстреле 0,5, при втором – 0,6, при третьем
– 0,8. При одном попадании цель будет
сбита с вероятностью 0,3, при двух – 0,6,
при трех – цель будет сбита наверняка.
Найти вероятность того, что цель будет
сбита.
На
склад поступают детали с трех станков.
Вероятность выпуска брака на первом
станке 0,03, на втором 0,02, на третьем 0,01.
Производительность первого станка в
три раза больше производительности
второго, а третьего в два раза больше
второго. Найти вероятность того, что:
наудачу взятая со склада деталь будет
бракованной.
При
отклонении от нормального режима работы
автомата срабатывает сигнализатор С-1
с вероятностью 0,8, а сигнализатор С-2
срабатывает с вероятностью 1. Вероятность
того, что автомат снабжен сигнализатором
С-1 или С-2, соответственно, 0,6 и 0,4. Получен
сигнал о разладке автомата. Найти
вероятность того, что он снабжен
сигнализатором С-1.
Вступительные
экзамены сдают 50 абитуриентов
агрономического факультета и 30
биологического. Вероятность успешной
сдачи экзаменов на агрономический
факультет – 0,6, на биологический – 0,7.
Наудачу выбранный абитуриент успешно
сдал экзамен. Какова вероятность того,
что он с агрономического факультета.
Три
токаря обрабатывают однотипные детали.
Первый обрабатывает за смену 40 деталей,
второй – 45, третий – 50. Вероятность
получения брака при изготовлении одной
детали для первого токаря 0,03, для второго
– 0,05, для третьего – 0,02, Из общей
выработки за смену наудачу выбрана
деталь, оказавшаяся бракованной. Найти
вероятность того, что она изготовлена
первым токарем.
Из
45 однотипных деталей 10 изготовлены на
первом станке-автомате, из них 2
нестандартные, 15 – на втором, из них
одна нестандартная, 20 – на третьем, из
них три нестандартные. Все детали
поступают на общий конвейер. Взятая
наудачу с него деталь оказалась
нестандартной. Найти вероятность того,
что она изготовлена на втором станке.
Имеются
три партии компьютеров в количестве
25, 35 и 40 штук. Вероятность того, что
компьютеры, поставляемые разными
фирмами-производителями, проработают
без ремонта заданное время, равны для
этих партий, соответственно, 0,75, 0,82 и
0,9. Найти вероятность того, что наудачу
выбранный компьютер проработает без
ремонта заданное время.
В
сборочный цех попадают детали с трех
станков-автоматов, первый из которых
дает 0,3% брака, второй 0,1% и третьего
0,2%. Найти вероятность попадания на
сборку небракованной детали, если с
автоматов поступило, соответственно,
500, 200 и 300 деталей.
По
результатам проверки контрольных работ
оказалось, что в первой группе
положительную оценку получили 15 из 20
студентов, во второй 20 из 25 и в третьей
18 из 20. Найти вероятность того, что
наудачу выбранная работа с положительной
оценкой написана студентом третьей
группы.
Изделие
проверяется одним из двух контролеров.
Вероятность того, что изделие попадет
к первому контролеру, равна 0,55, ко
второму – 0,45. Вероятность того, что
изделие признано стандартным первым
контролером, равна 0,9, а вторым – 0,98.
Изделие признано стандартным. Найти
вероятность того, что изделие проверял
второй контролер.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник