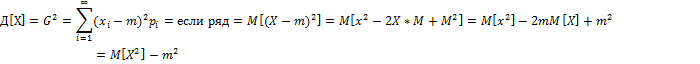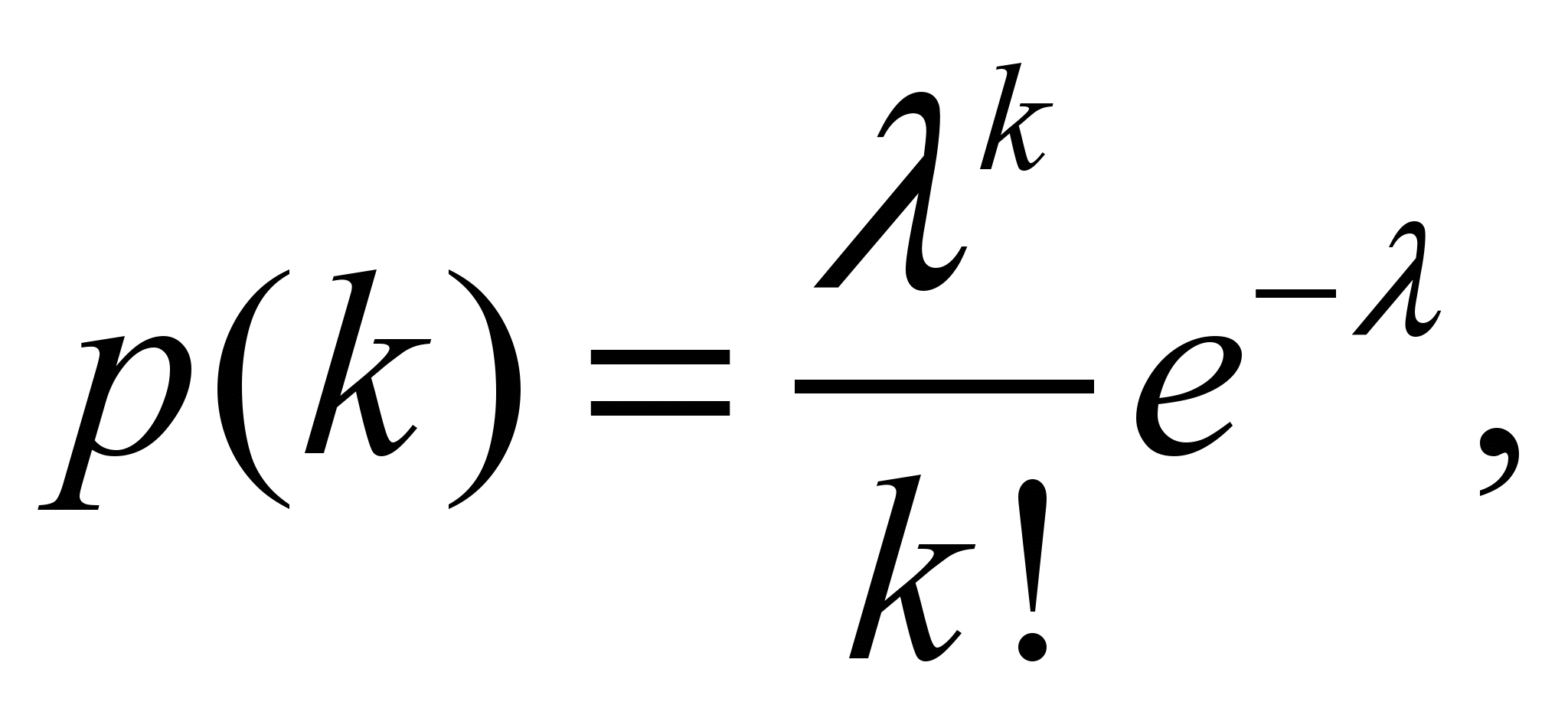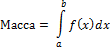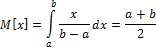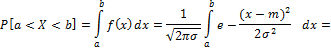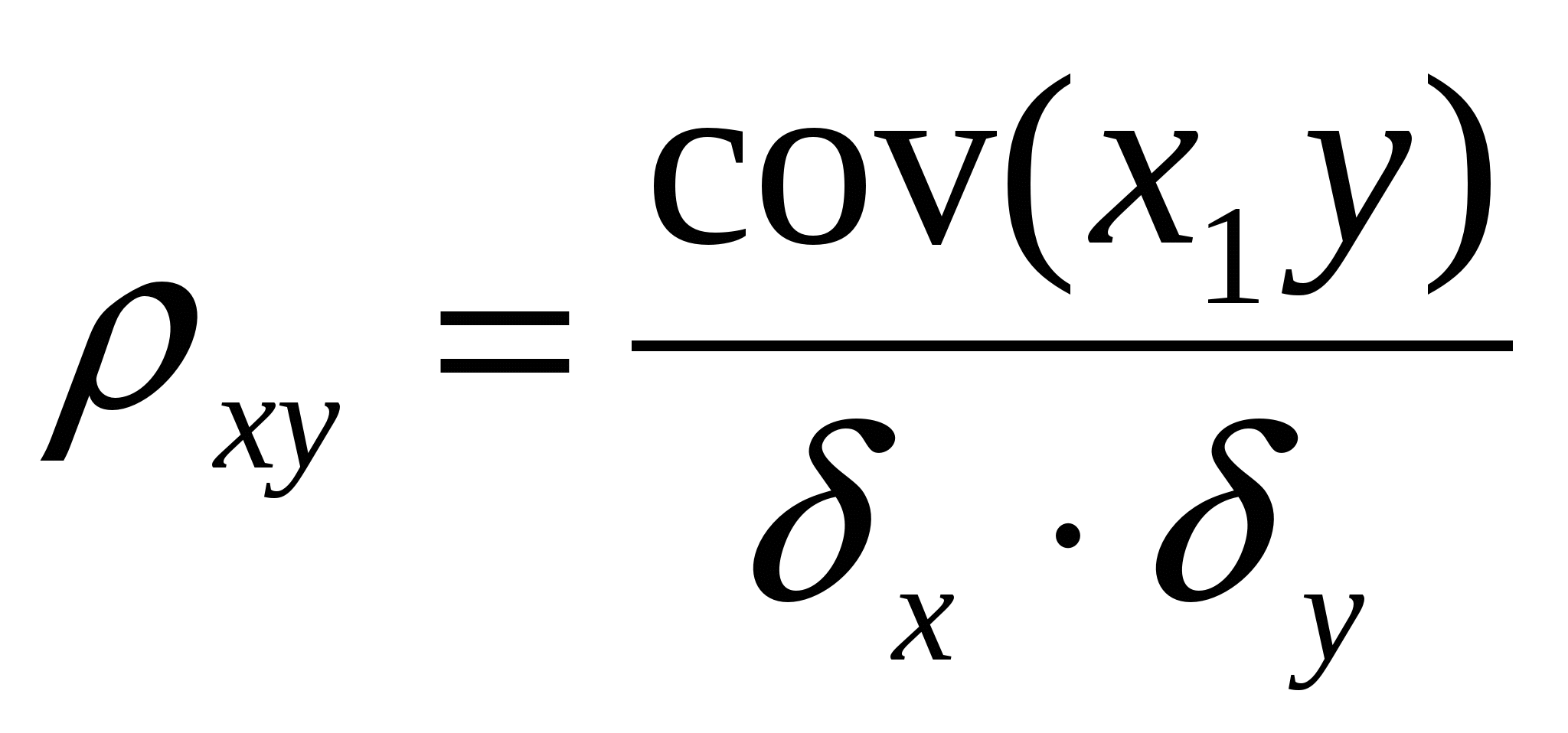Экзамен теория вероятностей шпоры

1

Теория вероятностей

Случайные события.
Пространство элементарных событий.
Алгебра событий.

Событие
– любой исход эксперимента (всякий
факт, который в результате опыта может
произойти или не произойти).

Случайные – не
можем предвидеть (подбрасывание монеты).

А – появление герба
при бросании монеты;

В – попадание в
цель при выстреле;

С – появление туза
при вынимании карты из колоды.

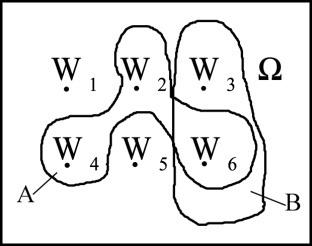
Пространство
элементарных событий.

I эксперемент
эл.исходы: W₁
– вып. «1»

W₂
– вып. «2»

W₆
– вып. «6»

Сложн.событ.
(выпис.четное): А=

Выпадение очков
кратное 3: В=

Пространство
эл-ных событий
– множество всех элемент.исходов данного
эксперемента.

II эксперимент –
подбрас.2 игр.кости

(1,1) (1,2) … (1,6) Ω

(2,1) (2,2) … (2,6)

. . . . . . . .

(6,1) (6,2) … (6,6)

Сложное соб.А –
подмн-во Ω

Алгебра событий
– совокупность событий, на кот.опр-ны
операции:

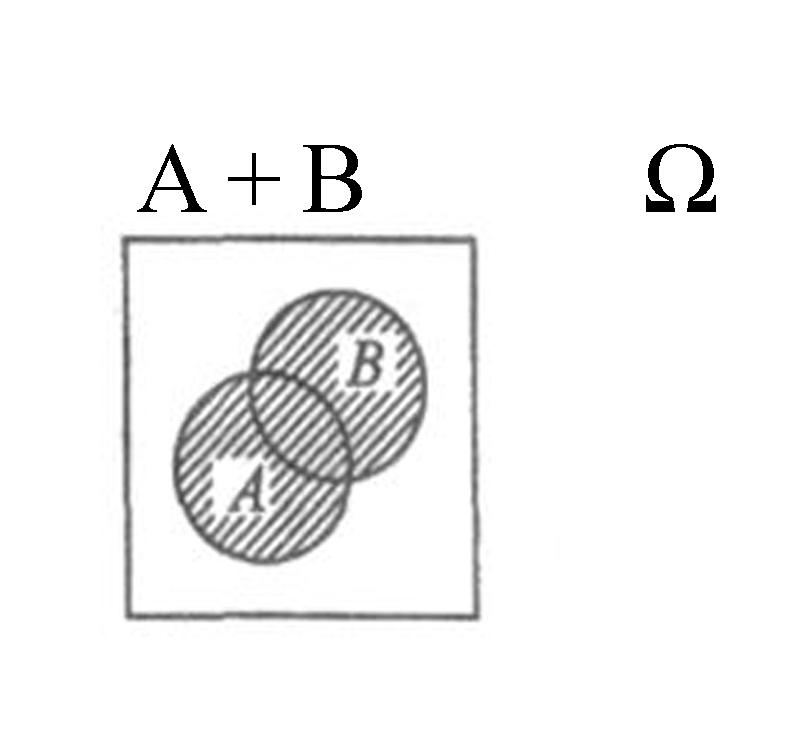
А+В – событие,
состоящее в том, что либо
происходит А, либо В, либо А и В.

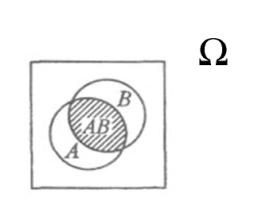
АВ – событие,
состоящее в том, что А и В происходят
вместе.

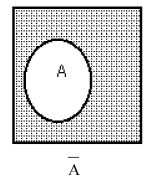
Ā – (отрицание) –
событие, состоящее в том, что А не
происходит.

Пример:

А+В=

AB=

Ā=

Ω — достовер.соб.,
кот.происходит всегда

Ø = ᾯ (напр. Выпадение
«7» на кубике)

2

Вероятность соб.
–численная мера степени объективной
возможности этого события. (связано с
понятием частоты
соб-я)

Более вероятные –
кот. происходят чаще;

Мало вероятные –
кот. почти никогда не происходят.

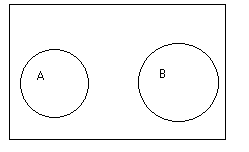
Два события А и В
назыв. несовместимыми
если они не
могут одновременно произойти.

Вероятность
– некот.число, кот.лежит от 0 до 1,
показывает насколько
часто
происходит событие в серии экспериментов.

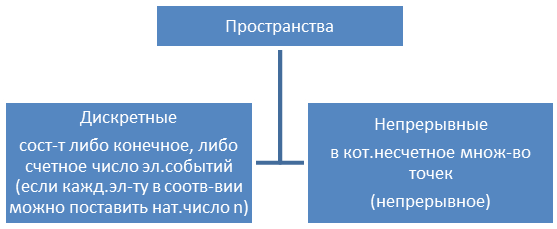
Вероятность в
дискретных и непрерывных пространствах
элем.событий.

Пр.: монета
подбрасываемая до появления герба

Ω=

Р(А) – вероятность
соб.А

(числ.мера степени
объективной возможности того события
– частота)

Аксиоматически:

экспер→дискр.пр.эл.соб.→

Свойства:

P(

Свойства вероятности:

Р(Ø)

Р(Ω)=1

n

P(A+B) =
P(A) + P(B) – P(AB)

AB=Ø P(A+B) = P(A) + P(B)

P(Ā) = 1 – P(A)

Классическая
схема равновероятных событий

Равновероятные
события

Если W_i
новероятны или равновозможные (ни одно
из этих событий не явл.объективно более
возможным, чем другое)

=N
– число эл.иск. в Ω

i=1,2,…N

P(A)==

← Формула
классической вероятности

Р(А)=

0

Благопр.случай –
появление этого случая влечет за собой
появление данного соб.

Комбинаторика

Выборки:
Упорядоченные:

С
возвращением (с
повторением)

Без
возвращения

Неупорядоченные

С
возвращением (с
повторением)

Без
возвращения

3

Теоремы сложения
и умножения вероятности.

Р(А+В) = Р(А) + Р(В) –
вероятность суммы 2-ух несовместных
событий равна сумме вероятностей этих
событий.

;

Нет случаев,
кот.благопр. и А, и В вместе →

P(A+B+C) = P(A) + P(B) + P(C)

)

Следствие 1.
Если соб.
образуют полную группу несовместимых
событий, то сумма их вер-тей равна 1.

Следствие 2. Сумма
вероятностей противоположных событий
равна 1;

Р(А) + Р(Ā) = 1

Р(А+В) = Р(А)+Р(В)-Р(АВ)
– для совместимых

Р(А+В+С)=
Р(А)+Р(В)+Р(С)–Р(АВ)–Р(АС)–Р(ВС)+Р(АВС)

Р(АВ)=Р(А)+Р(В)+Р(С)-Р(А+В)-Р(А+С)-р(В+С)+Р(А+В+С)

2)Соб.А назыв.
независимым
от соб.В, если
вер-сть соб.А не зависит от того, произошло
соб.В или нет.

Подбррас.2 монеты:

А – появление герба
на 1ой монете.

В – появление герба
на 2ой монете.

Условная вероятность
– вер-сть соб.А при условии, что соб.В
произошло. Р(А∕В)

Р(А∕В)=Р(А) – условия
независимости.

Теорема умножения

Р(АВ)=Р(А)Р(В∕А)
вероятность произведения 2ух событий
равна произведению вер-сти одного из
них на условную вер-сть другого, вычисл.при
условии, что первое имело место. (для
зависимых соб.)

Р(АВС)=Р(А) Р(В∕А)Р(С∕АВ)

Док-во:

Р(АВ)=Р(А)*Р(В) необх.
и дост.усл.независ-ти.

Следствие 1. Если,
соб.А не зависит от соб.В, то и соб.В не
зависит от соб.А.

Следствие 2.
Вероятность произведения 2ух независимых
событий равна произведению вер-тей этих
событий.

4

Формула полной
вероятности и формула Байеса.

Формула полной
вер-сти явл.следствием обеих основных
теорем.

(гипотезы)

Н_1,
Н_2,
…Н_к
– полная
группа событий или разбиение Ω, если:

Н₁+
Н_2,+
_…+Н_к=Ω

Не пересекаются
между собой

H_i*H_j=Ø
i≠j I,j=1,2,…k

A=AH₁+AH₂+AH₃+…+AH_k
(все слагаемые
АН_i несовместны)

Р(А)=Р(АН₁+АН₂+…+АН_к)=Р(АН₁)+Р(АН₂)+…+Р(РН_к)=Р(Н₁)Р(А∕Н₂)+…+Р(Н_к)Р(А∕Н_к)

– формула полной вероятности.

Формула Бейеса
(теорема гипотез) явл.следствием теоремы
умножения и формулы полной вер-сти.
(необх-мо найти усл.вер-сть Р(Н_i∕A)
для каждой гипотезы.

Пр. Из какой урны
более вероятно вытащить бел.шар? (Н₁
или Н₂)?

Р(Н₁∕A)
V Р(Н₂∕A)

Р(Н_i∕A)=
вычисл.по формуле полн.вер-сти

5

Дискретные сл.в.
Ряд распределения. Числовые характеристики.

Ω=

Случайная величина

X=X(W_i)числ.ф-ция,
определенная на каждом элементарном
исходе. (пространстве элем.соб.)

X₁=X(W₁)

X₂=X(W₂)

Случайная величина
– величина, которая в результате опыта
может принять то или иное значение,
причем неизвестно заранее, какое именно.

Пр.

1. число
   попаданий при 3х выстрелах (0;1;2;3)

2. число
   вызовов, поступивших на телефон.станцию
   за сутки (1;2;3;4….)

3. частота
   попаданий при 10 выстрелах (0;0,1;0,2;….10)

дискретные
– можно заранее перечислить

непрерывные
– непрерывно заполняют некоторый
промежуток.

Пр.

1. абсцисса
   точки попадания при выстреле;

2. ошибка
   взвешивания тела на аналитич.весах;

3. скорость
   летат.аппарата в момент выходп на
   заданную высоту;

4. все
   наугад взятого зерна пшеницы.

(границы неопределенные,
расплывчатые)

Производится опыт
соб.А – может появиться, а может и нет.

Вместо соб.А
расмотр.сл.вел.Х, кот.=1

Если соб.А не
происходит Х=0

Х – характеристическая
сл.вел.соб.А

Х – сл.вел.

Х₁,Х₂….Х_n
– возможные значения сл.вел.Х

Ряд распределения

Закон распределения
– всякое соотношение, устанавливающее
связь между возможными значениями
сл.вел-ны и соответствующими им
вероятностями.

Простейшей формой
задания закона распределения дисер.сл.вел.Х
явл. таблица,
в кто.перечислены возможные значения
сл.вел. и соответствующие им вероятности.

1)
ряд распределения сл.вел.Х

2)

многоугольник
распределения (один из форм закона
распределения)

3)иногда удобной
оказывается «механическая»
интерпретация
ряда распред-я (система матер.точек с
какими-то массами, расп.на оси абсцисс)

Числовые
характеристики дискр.сл.величины

Числ.хар-ки
– хар-ки, кот.характер-ют различн.св-ва
случ-ной вел.

Характеристики
положения

(мат.ожид-е, мода,
медиана)

Указывают некоторые
среднее ориентировочное значение, около
которого группируются все возможные
значения случ.вел.

1. Мат.ожидание
   — сумма произведений всех возможных
   значений сл.вел. на вероятности этих
   значений.
   

при большом числе
опытов среднее арифмет.наблюденных
значений сл.вел.приближается (сходится
по вероятности) к ее матем.ожиданию.

М(Х) – абсцисса
центра тяжести системы матер.точек.

Свойства М(х):

1)М(Х+а)=М(х)+а, а
=const

2)М(аХ)=аМ(х)

3)М(Х+Y)=M(X)+M(Y)

4)h(X) – ф-ция Х, тогда

5) M(a)=a

2)Мода – наиболее
вероятное значение (М)

3)Медиана : Р(Х

Моменты. Дисперсия.
Среднее квадратическое отклонение.

— определяет разброс отн-но
(хар-ка рассеивания)

Дисперсия –
мат.ожидание квадрата соответствующей
центрированной величины.

Среднее
квадратич.отклонение G=

(для наглядной
характеристики рассеивания)

Размерность
совпадает с размеренностью сл.вел.

Свойства :

1. Неотрицательная
   =0

2. С-константа,
   

3. 

4. 

Моменты (опис.св-ва
распр-я):

Начальные

d_k

k=0,1,2….

d=1

=m

=
хар-ка формы распределения

Центральные

М_к

M₀
= 1

M₁
= M=0

M₂
= M=Д

M₃
— хар-ка
формы распред-я

Хар-ка формы
распределения:

Асимметрия

A_s(X)

A_s(X)=

Эксцесс

Е_х(Х)

Центрированная
сл.вел. –
отклонение сл.вел.Х от ее мат.ожид-я
Х=Х-М_х

6

Повторение
испытаний. Схема Бернулли. Биномиальное
распределение. Формула Пуассона.

Один и тот же опыт
повторяется соб.А может появиться или
нет.

Нас интересует не
результат каждого отдельного опыта, а
общее число появлений соб.А в резте
серии опытов.

Пр.число попаданий
среди группы выстрелов.

Х~В(n₁,p)
– случ.вел.Х имеет биноминал.распр-е с
параметрами n и p.

Схема Бернулли:
(идеализир.ситуация) (если n=1)

Исходы эксперемента:
«успех» (А)

«неуспех» (Ā)

К- число успехов в
n исп-нии.

Р(А)=р

Р(Ā)=1-р=q

Эксперимент
повторяется n раз, р и q не изменяются.

Рассм.случ.вел.Х
– число успехов в n
испытаний по схеме Бернулли.

Х=0,1,2,…n
(целочисл.дискр.знач-я)

M(X)=n*p

Д(Х)=n*p*q

P(AA….A
ĀĀ….Ā)=
(для
конкр.посл-сти)

Если n
большое, то в силу ЦПТ В(n,p)N(np;npq)

Если n
большое, а
— фикс.число, то

Приближенная
формула Пуассона

n
– велико

p
– мало

0,1 n*p10

где
=n*p

Док-во формулы

7

Распределение
Пуассона. Геометрическое распределение.

Распределение
Пуассона (Закон редких событий)

Дискр.сл.вел.Х=0,1,2,…
имеет распр-е Пуассона с параметром
,
если вероят-сть того, что она примет
определение значения к, выражается
формулой.

К=0,1,2,…

=n*p

Редкое событие:
стоим на перекрестке и подсчит.число
столкновений.

Физич.модель,
приводящ.к распределению Пуассона.

Поток событий
– посл-сть некот.случ.соб-тий во времени.

Постулаты:

1. Поток
   явл.стационарным

2. Отсутствует
   последствие (т.е.без
   памяти)

3. Поток
   явл.ординарным

Вероятность того,
что на интервале t
произойдет к событий =

Поток явл.стационарным,
если данная вер-сть произойдет независимо
от времени.

Ординарность: можно
найти столь малый интервал ,
для которого вер-сть того, что на
произойдет 1 соб-е
произойдет 2 и более событий
при

Распр-е Пуассона
играет ключ.роль в теории массового
обслуживания.

Пр.

1. Поток
   входящих телефон.звонков;

2. Поломки
   оборудования;

3. Длит-сть
   исполнения ремонтных работ стабильно
   работающим сотрудником;

4. Ошибка
   печати;

5. Дефекты
   в длинной ленте или цепи.

Геометрическое
распределение

p-
вер-сть успеха

q-
вер-сть неуспеха

p
и q
неизмен. Испытания независима дгур от
друга.

Х – число
эксперементов, кот. необх-мо произвести
до появ-я 1-го успеха.

Х=1,2…..

K=1,2,3….

M

8

Непрерывные
сл.вел. Функция распределения и плотность
распределения и их свойства. Равномерное
и экспоненц.распр-я.

Непрер.случ.вел. –
числ.ф-ция, кот.задана на пространстве
эл.событий.

Пример: время
работы, время работы прибора.

Плотность
распределения.

Берем еденич.массу
и распределяем по мн-ву случ.вел.

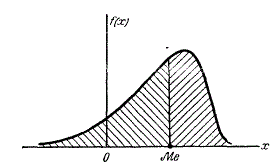
F(x)
– плотность распр-ния массы (вероятностей)

Свойства f(x):

1)ф-ция неотриц.
f(x)0

2)

3)

Функция
распределения.

Свойства f(x):

1. 

2. 

3. Механич.
   интерпретация f(x)

4. 

Равномерное
распределение.

— интервал. (вероятность любого интервала
зависит только от его длины)

F(x)=

Д(X)=M(

Применяется:
ошибка округления.

Экспоненциальное
распределение.

(моделирующее время между 2-мя
последовательными свершениями одного
и того же события)

Пр.

1)время отказа
аппаратуры;

2)время между 2ух
последовательных покупателей;

3)время ожидания
автобуса на остановке

(отсутствие памяти
– кол-во времени, затрач.на ожидание
автобуса, не влияет на время, кот.ему
придется прождать)

Д(Х)=

Ех(
— частный случай распр-ния хи-квадрат

9

Свойства
мат.ожидания и дисперсии. Квантили.
Мода, медиана, асимметрия и эксцесс.

1. 

2. 

3. 

4. h(x)
   – ф-ция Х

5. 

1. Неотриц.
   Д(х)

2. Д

3. Д

4. Д

Квантиль

Пусть сл.вел.Х имеет
f(x),
F(x)

Квантилью порядка
р(0р1)
Хр назыв.абсцисса, кот.определяет от
себя слева на графике плотности площадь
= р.

Способы определения
квантили

1. 

2. 

h_x
— квантиль
порядка 0,5 (медиана)

Мода
– значение, в котором плотность
вероятности max.

Полимодальное
распр.- более 1 max.

Антимодальное —
посредине min.

Медиана
– значение, для которого одинаково
вероятно, окажется ли сл.вел.меньше или
больше h_x.

Геом.медиана –
абсцисса точки, в кот.площадь, огранич.кривой
распределения делится пополам.

Хар-ка формы
распределения.

Асимметрия

Хар-ка «скошенности»
распределения

Экцесс

Хар-ет форму распр-я
в окр-сти вершин (хар-ка «крутости»)

Если m,r)

10

Нормальное
распределение (Гаусса)

Вероятность
попадания в интервал симметричный
относительно М(х).

Ассиметрия и эксцесс
распределения. Стандартизированное
норм.распр-е и его свойство. Правило 3
сигм.

Явл.предельным
законом, к котор.приближаются другие
законы распр-я при весьма часто
встречающихся типичных условиях.

Замена:

— центр
рассеивания.(особенно
в задачах стрельбы).

Вероятность
попадания в интервал.

Замена:

X=

dx=

=

Свойства:

1)

2)

3)

4)

;

m=h=d

Стандартизованное
нормальное распределение.

Стандартизация:

1 этап (центрированный):
X-m

– стандартиз.сл.вел.

x)
– плотность
распр-я.

x)=

Функция распр-я:
x)=

Правило 3 сигм:

P

11

Системы дискретных
сл.вел.

Таблица распределения.
Независимость. Ковариация. Условные
распределения. Системы непрерыв.сл.вел.

Рез-т опыта
описывается не 1 сл.вел., а 2умя или
>сл.вел-нами, образующими комплекс
или систему.

(напр.: точка
попадания снаряда опр-тся абсциссой и
ординатой)

При рассмотрении
вопросов, связан.с сист.сл.вел.удобно
пользоваться геом.интепретацией
системы.

(напр.(X,Y)
можно изобразить случайной точкой на
плоскости с коорд-ми X
и Y.

Часто вместо образа
случ.точки
пользуются образом случайного
вектора.

(X,Y)
– случ.вектор с коорд-ми

Х=Х_1,Х₂,
…Х_к

Y=Y₁,Y₂,…Y_k
— дискр.сл.вел.

— закон распр-я для (X,Y)

Ф-ция распр-я.

Y X	X1	X2	…	XK	Σ
Y1	P11	P21	…	PK1	PY1
Y2	P12	P22	…	PK2	PY2
…	…	…	…	…	…
yn	P1n	P2n	…	Pkn	Pyn
Σ	Px1	Px2	…	Pxk

Крайние маргинальные
распределения.

Р_у1*Р_х1=Р₁₁

X
и Y
независимы.

(если хотя бы 1
невыполн., то зависимы)

Условные
распределения.

Независимость
случ.вел-н.

(не завис.от того,
какое значение приняла др.величина)

X
и Y
независ.сл.вел., если:

,
т.е.усл.вер-сть совпадает с безусловной.

Если X
и Y
независимы, то
необх.и дост.усл-е независ-сти величин.

Ковариация.

Мат.ожидание
произведения центрированных случ.величин.

Cov(X,Y)=M

Cov(X,Y)=

Свойство: если X
и Y
независимы,
то

(однако обратное
неверно, т.е. если ,
то не обязат.независ.)

—
ковариац.мтр

=

Системы
непр.сл.вел.

Распр.системы
непр.вел.обычно хар-ют не ф-цией распр-,
а плотностью
распр-я.

F(X,Y)
– плотность распр-я

1. F(X,Y)

2. 

12

Мат.ожидание и
дисперсия суммы сл.в. Мат.ожидание
произв-я сл.в.

Если зависимы

Если независ.

13

Коэф-т корреляции
как хар-ка статистич.связи. Некоррелир-сть
и независимость сл.вел.

Если X
и Y
независимы, то

Свойства:

1.

2. если ,
то между X
и Y
имеется лин.зависимость Х=a+b*Y

3. Показыв.степень
лин.завис-ти, когда
Чем ближе к 1, тем
коэфф.корреляции. (мера (индикатор)
лин.зав-сти между X
и Y)

14

Законы больших
чисел и предельные теоремы. Теорема
Бернулли. Теорема Чебышева.

При очень большом
числе сл.явлений средний их рез-т
практически перестает быть случайным
и может предсказан с большой степенью
определенности.

1. Сходимость по вер-сти

Х₁,Х₂,…Х_n

Посл-сть сходится
по вер-сти к сл.в.А при

при большом числе опытов частота
соб.приближается в вер-сти этого соб.

Если сущ.
то и ,
что

1. Неравенство Чебышева

Пусть Х – любая
сл.вел.

t0
– люб.число

=1

Каково бы ни было
положит.число ,
вер-сть того, что вел.Х отклонится от
своего мат.ожидания не меньше, чем на
огранич.сверху.

Предельные теоремы
дают возможность не только осущ-ть
научн.прогнозы, в обл-сти сл.явл-ний, но
и оценивать
точность
этих прогнозов.

(Закон больших
чисел)

Предельные теоремы
дают возможность
не только осущ-ть научн.прогнозы, в
обл-сти сл.явл-ний, но и
оценивать точность
этих прогнозов.

(Закон больших
чисел)

Теорема Чебышева.

Пуст ь Х₁,
Х₂,
…Х_n
– незав.сл.вел. имеют одно и тоже расрп-е.

Тогда

При достаточно
большом числе независ.опытов со.ариф-ое
наблюденных значений сл.вел.сходятся
по вер-сти к ее мат.ожид-ю.

Док-ство:
воспольз.нер-вом Чебышева.

Сл.в.Х

,
t=const

Сколь угодна
сход.по
вер-сти близка к 1

Теорема Бернулли.
(следствие т.Чебышева)

(устанавл.связь
между астотой соб.и его вер-стью).

Пусть проводится
(n)
экспериментов. В каждом эксперименте
появл.соб.А (успех) с вер-стью (р).

И появл.(Ā) (неуспех)
с вер-тью q=1-p

Рез-ты экспер-тов
не влияют друг на друга.

При неогранич.увеличении
числа опытов h
частота соб.А сходится по вер-сти к его
вер-сти р.

k
– число успехов в n
испытаний; n
–число экспер-тов.

15

Центральная
предельная теорема. Теорема Муавра-Лапласа.

(колич-ная форма
закона больших чисел)

Все формы ЦПТ
посвящены установлению условий, при
кот.возникает норм.закон распр.

N(m,

В теории стрельбы
N(m,
играет особо важную роль, т.к в боль-ве
случаев практики корд-ты точек попадания
и точек разрыва снарядов распределяются
по норм. Закону.

Х₁,
Х₂,
…Х_n
– незав.сл.вел.с одним и тем же распр-ем

X=
Х₁+
…+Х_n
– сумма
случ.вел.

Рассм.нормир-ную
случ.вел. (

Ф-ция растр-я
равномерно по х.

Ф-ция распр-я
норм.зак.с пар-ми N(0;1)

Следствие ( ЦПТ)

1. Х=

)

1. 

1. 

1. Теорема Муавра-Лапласа.

Х=

Напр.число успехов
лежит в интервале (a,b)

16

Распределение
сред.ариф-го независ. с.в. и отн-ной
частоты при большом числе наблюдений
n.

Среднее ариф.сл.вел.

Х₁,
Х₂,
…Х_n
– незав.сл.вел., имеющ.одно и тоже распр-е

Среднее
арифм.(выборочное среднее)

Относит.частота
и свойства.

n
– объем выборки

к – число эл-тов
выборки, кот.облад.св-вом А относит.частота
появления св-ва А

	0	1
	q	p

Статистика.

17

Предмет
мат.статистики. Осн.понятия: выборка,
генер.сов-сть статистики. Распр-е выборки,
выборочные моменты. Выборочный вектор.

Мат.статистика
позволяет получать обоснован.выводы о
параметрах, видах распр-й и др.св-вах
сл.вел.по конечной совокупности наблюдений
над ними – выборке. (предмет: описание
и анализ данных наблюдений).

Выборка –
мн-во случаев, с помощью определен.процедуры
выбран.из ген.сов-сти для участия в
исследовании.

Ген.сов-сть
– сов-сть всех объектов (единиц), отн-но
которых ученый намерен делать выводы
при изучении конкр.проблемы.

Мн-во всех обследуемых
объектов.

Статистика
– измеримая
числовая ф-ция от выборки, не зависящих
от неизвестных пар-ров распр-я.

-осн.хар-ки ген.сов-сти
(среднее дисперсия, т.д.)

Выборка должна
быть репрезентативной. (давать правильное
представл-е о ген.сов-сти)

Простой случ.выбор
– все эл-ты ген.сов-сти должны иметь
равные шансы попасть в выборку.

Закон распр-я
сл.вел.Х назыв. распределением
ген.сов-сти,
а случ.вектор (Х₁,Х₂,…Х_n)
– выборочным
вектором.

Часто требуется
охарак-ть ген.сов-сть некоторыми
колич.показателями, кот.определяют
положение центра распр-я, рассеяние
(разброс) и асимметрию, что дает возможность
сравнить одну сов-сть данных с другой.

По выборке можно
определить приближенные значения
(оценки)
этих числ.хар-к,
кот.называются выборочными
характеристиками.

Оценки моментов:

+

Распр-е выборки
– распр-е
дискр.сл.вел., приним.значения Х₁,Х₂,….Х_n
с вероятностями 1∕n.

18

Задача
стат.оценивания. Несмещенность и
состоятельность оценок, эффективность
оценок.

Задача
– нахождение
приближенных значений – оценок параметров
распределения по выборке.

Статистика
– некоторая ф-ция эл-тов выборки.

Вид распр-я известен

Критерии для
выбора наилучшей оценки.

Ответы на популярные вопросы

Отзывы студентов

Добавляйте материалы
и зарабатывайте!

Продажи идут автоматически

Обучение Подробнее

Случайности не случайны… Всё решает вероятность событий!

В ЕГЭ по математике целых два задания на теорию вероятностей, поэтому стоит уделить ей в два раза больше внимания! Первое решается по основной формуле вероятности, а вот над вторым придётся подумать и вспомнить, какие бывают события.

Мы структурировали типы задач, которые могут попасться на экзамене, и сделали эту полезную шпаргалку с формулами и теорией — сохраняйте карточки, чтобы подготовка к ЕГЭ по математике была ещё продуктивнее.

Тема: Шпаргалка по теории вероятностей и математической статистике

Раздел: Бесплатные рефераты по теории вероятностей и математической статистике

Тип: Шпаргалка | Размер: 434.63K | Скачано: 1742 | Добавлен 04.10.08 в 15:24 | Рейтинг: +126 | Еще Шпаргалки

Вопросы к экзаменационному зачету:

1. Классификация случайных событий. Классическое определение вероятности. Свойства вероятности события, непосредственный подсчет вероятности. Примеры.

2. Статистическое определение вероятности события и условия его применимости. Пример.

3. Несовместимые и совместимые события. Сумма событий. Теорема сложения вероятностей с доказательством. Пример.

4. Полная группа событий. Противоположные события. Соотношения между вероятностями

противоположных событий (с выводом). Пример.

5. Зависимые и независимые события. Произведение событий. Понятие условной вер-ти. Теорема умножения вер-тей с док-вом. Пример.

6. Формулы полной вер-ти и Байеса с док-вом. Примеры.

7. Повторные независимые испытания. Формула Бернулли с выводом. Примеры.

8. Локальная теорема Муавра-Лапласа, условия её применимости. Св-ва ф-ии f(x). Пример.

9. Асимптотическая ф-ла Пуассона и условия её применимости. Пример.

10. Интегральная теорема Муавра-Лапласа и условия её применимости. Функция Лапласа f(x) и её свойства. Пример.

11. Следствия из интегральной теоремы Муавра-Лапласа с выводом. Примеры.

12. Понятие случайной величины и её описание. Дискретная слв и её закон (ряд) распределения. Независимые слв. Примеры.

13. Математ. операции над дискретными слвелечинами. Приведите пример построения закона распределения слвел Z=X+Y или Z=XY по заданным распределениям X и Y.

14. Математическое ожидание дискретной случвел и его свойства с выводом. Примеры.

15. Дисперсия дискретной случвел и её свойства с выводом. Примеры.

16. Математическое ожидание и дисперсия числа m и частности mn наступлений события в n-повторных независимых испытаниях, с выводом.

17. Случайная величина, распределённая по биномиальному закону, её математическое ожидание и дисперсия. Закон распределения Пуассона.

18. Функция и распределения случайной величины, её определение, свойства и график.

19. Непрерывная случайная величина (НСВ). Вероятность отдельного взятого значения НСВ. Математическое ожидание и дисперсия НСВ. (+Функция распределения НСВ.)

20. Плотность вероятности Непрерывных СВ, её определение, свойства. Кривая распределения. Связь между функцией распределения и плотностью вероятности НСВ. Математическое ожидание и дисперсия НСВ.

21. Определение нормального закона распределения. Теорико-вероятный смысл его параметров. Нормальная кривая и зависимость её положения и формы от параметров.

22. Функция распределения нормальной распределённой слвеличины и её выражение через функцию Лапласа.

23. Формулы для определения вероятности: а)попадания нормально распределённой слвел в заданный интервал; б) её отклонения от математического ожидания. Правило «трёх сигм».

24. Центральная предельная теорема. Понятия о теореме Ляпунова и её значение. Пример.

25. Понятие двумерной (n-мерной) слвел. Примеры. Таблица её распределения. Условные распределения и их нахождение по таблице распределения.

26. Ковариация и коэффициент корреляции (КК) слвеличин. Связь между некоррелированностью и независимостью слвеличин.

27. Понятие о двумерном нормальном законе распределения. Условные математические ожидания и дисперсии.

28. Неравенство Маркова (лемма Чебышева) с док-вом для дискретной слвеличины. Пример.

29. Неравенство Чебышева для средней арифметической слвеличин. Теорема Чебышева с док-м и её значение и пример.

30. Теорема Чебышева с выводом и его частные случаи для слв, распределённой по биномиальному закону, и для частности события.

31. Закон больших чисел. Теорема Бернулли с док-м и её значение. Пример.

32. Вариационный ряд, его разновидности. Средняя арифметическая и дисперсия ряда. Упрощённый способ их расчёта.

33. Генеральная и выборочные совокупности. Принцип образования выборки. Собственно-случайная выборка с повторным и бесповторным отбором членов. Репрезентативная выборка. Основная задача выборочного метода.

34. Понятие об оценке параметров генеральной совокупности. Свойства оценок: несмещенность, состоятельность, эффективность.

35. Оценка генеральной доли по собственно – случайной выборке. Несмещённость и состоятельность выборочной доли.

36. Оценка генеральной средней по собственно – случайной выборке. Несмещённость и состоятельность выборочной средней.

37. Оценка генеральной дисперсии по собственно – случайной выборке. Смещённость выборочной дисперсии (без вывода).

38. Понятие об интервальном оценивании. Доверительная вероятность и доверительный интервал. Предельная ошибка выборки. Ошибки репрезентативности выборки (случайные и систематические).

39. Формула доверительной вер-ти при оценке генеральной доли признака. Средняя квадратическая ошибка повторной и бесповторной выборок и построение доверительного интервала для генеральной доли признака.

40. Формула доверительной вер-ти при оценке генеральной средней. Средняя квадратическая ошибка повторной и бесповторной выборок и построение доверительного интервала для генеральной средней.

41. Определение необходимого объёма повторной и бесповторной выборок при оценке генеральной средней и доли.

42. Статистическая гипотеза и статистический критерий. Ошибки 1 и 2 ряда. Уровень значимости и мощности критерия. Принцип практической уверенности.

43. Построение теоретического закона распределения по опытным данным. Понятие о критериях согласия.

44. Критерий согласия x – Пирсона и схема его применения.

45. Функциональная, статистическая и корреляционная зависимости. Различия между ними. Основные задачи теории корреляции.

46. Линейная парная регрессия. Система нормальных уравнений для определения параметров прямых регрессии. Выборочная ковариация. Формулы для расчета коэффициентов регрессии.

47. Оценка тесноты связи. Коэффициент корреляции (выборочный), его свойства и оценка достоверности.

+126

04.10.08 в 15:24
Автор:nastyav

---

Понравилось? Нажмите на кнопочку ниже. Вам не сложно, а нам приятно).

---

Чтобы скачать бесплатно Шпаргалки на максимальной скорости, зарегистрируйтесь или авторизуйтесь на сайте.

Важно! Все представленные Шпаргалки для бесплатного скачивания предназначены для составления плана или основы собственных научных трудов.

---

Друзья! У вас есть уникальная возможность помочь таким же студентам как и вы! Если наш сайт помог вам найти нужную работу, то вы, безусловно, понимаете как добавленная вами работа может облегчить труд другим.

Добавить работу

---

Если Шпаргалка, по Вашему мнению, плохого качества, или эту работу Вы уже встречали, сообщите об этом нам.

---

Добавление отзыва к работе

Добавить отзыв могут только зарегистрированные пользователи.

---

Похожие работы

• Шпоры по теории вероятностей и математической статистике
• Шпаргалка по теории вероятностей и математической статистике
• Шпаргалки по теории вероятностей и математической статистике
• Ответы на вопросы по теории вероятностей к экзамену

Основные понятия теории вероятности.

Теория вероятности есть наука, изучающая закономерности случайных явлений.

Случайное явление – это такое явление, которое при неоднократном воспроизведении одного и того же опыта протекает каждый раз по-разному.

В природе нет ни одного физического явления, в котором бы не присутствовали элементы случайностей. Факторы, влияющие на случайности, являются случайными и второстепенными.

Под событием в теории вероятности понимается всякий факт, который в результате опыта может произойти или не произойти. Если количественно сравнивать между собой события по степени их возможности, нужно с каждым событием связать число, которое тем больше, чем более возможно событие. Такое число называется вероятностью Р.

Для достоверного события Р=1, для невозможного события Р=0. Несколько событий в данном опыте называются равновозможными, если появление одного из них не более возможно, чем другого Непосредственный подсчет вероятности.

Для того, чтобы определить в опыте вероятность непосредственно из условий самого опыта, необходимо, чтобы различные исходы опыта обладали симметрией, и в силу этого были объективно одинаково возможны.

Несколько событий в одном опыте образуют полную группу событий, если в результате опыта непременно должно появиться хотя бы одно из них.

Несколько событий называются несовместными в данном опыте, если никакие 2 из них не могут появляться вместе.

Несколько событий в данном опыте называются равновозможными, если по условию симметрии есть основания считать, что ни одно из этих событий не является объективно более возможным, чем другие.

Существуют группы событий, обладающих всеми 3мя свойствами. Такие события называются случаями, и решение такой задачи называется схемой случаев или схемой урн. Классическая формула вероятности решает задачи, попадающие под схему урн.

Случайной величиной называется величина, которая в результате опыта может принимать то или иное значение, причем неизвестно заранее, какое именно.

Случайные величины, которые принимают только отдельные друг от друга значения, называются дискретными.

Случайные величины, всевозможные значения которых заполняют собой некоторый промежуток, называются непрерывными.

Суммой 2х событий А и В называют событие С, состоящее в выполнении или события А, или события В, или 2х одновременно.

Произведением 2х событий А и В называется событие С, состоящее в совместном появлении событий А и В.

Классическое определение вероятности.

Если n-общее число элементарных событий и все они равновозможные, то вероятность события А:

,

 где m_A— число исходов, благоприятствующих появлению события А.

Классическая формула вероятности решает задачи, попадающие под схему урн.

Частота или статистическая вероятность.

Частота – отношение числа появлений нужного события к общему числу опытов.

р=0 – для невозможных событий и р=1 для достоверных событий.

Частоту событий называют статистической вероятностью, и про нее говорят, что при увеличении количества опытов частота сходится по вероятности увеличения Р.

Геометрическая вероятность. Задача о встрече.

Чтобы преодолеть недостаток классического определения вероятности, состоящий в том, что оно неприменимо к испытаниям с бесконечным числом исходов, вводят геометрические вероятности — вероятности попадания точки в область (отрезок, часть плоскости и т. д.).

Пусть отрезок l составляет часть отрезка L. На отрезок L наудачу поставлена точка. Это означает выполнение следующих предположений: поставленная точка может оказаться в любой точке отрезка L, вероятность попадания точки на отрезок l пропорциональна длине этого отрезка и не зависит от его расположения относительно отрезка L. В этих предположениях вероятность попадания точки на отрезок l определяется равенством

Р = Длина l / Длина L.

З а м е ч а н и е 1. Приведенные определения являются частными случаями общего определения геометрической вероятности. Если обозначить меру (длину, площадь, объем) области через mes, то вероятность попадания точки, брошенной наудачу (в указанном выше смысле) в область g — часть области G, равна

Р = mes g / mes G.

З а м е ч а н и е 2. В случае классического определения вероятность достоверного (невозможного) события равна единице (нулю): справедливы и обратные утверждения (например, если вероятность события равна нулю, то событие невозможно). В случае геометрического определения вероятности обратные утверждения не имеют места. Например, вероятность попадания брошенной точки в одну определенную точку области G равна нулю, однако это событие может произойти, и, следовательно, не является невозможным.

Задача о встрече:

Два лица и условились встретиться в определенном месте между двумя и тремя часами дня. Пришедший первым ждет другого в течении 10 минут, после чего уходит. Чему равна вероятность встречи этих лиц, если каждый из них может прийти в любое время в течение указанного часа независимо от другого?

Решение.   Будем считать интервал с 14 до 15 часов дня отрезком [0,1] длиной 1 час. Пусть («кси») и («эта»)  —  моменты прихода и (точки отрезка [0,1]). Все возможные результаты эксперимента  –  множество точек квадрата со стороной 1:  .

Можно считать, что эксперимент сводится к бросанию точки наудачу в квадрат. При этом благоприятными исходами являются точки множества (10 минут = 1/6 часа). То есть попадание в множество наудачу брошенной в квадрат точки означает, что и встретятся. Тогда вероятность встречи равна

Теоремы сложения вероятностей

Теорема: Вероятность суммы 2х несовместных событий равняется сумме их вероятностей.

Р(А+В)=Р(А)+Р(В)

Д-во:

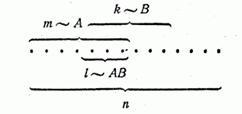
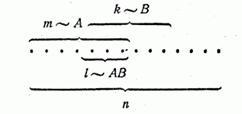
Используем схему случаев, из которых m~A, k~B, P(A)=m/n, P(B)=k/n. Поскольку А и В несовместные, то получается, что

m+k=A+B

P(A+B)= (m+k)/n=m/n+k/n=P(A)+P(B )/

1.                       Если события А1…Аn образуют полную группу несовместных событий, то сумма их вероятностей = 1. Противоположными называются 2 несовместных события, которые образуют полную группу {0;P}

A=”0” – P

A=”P” – q

2.                       Сумма вероятностей события и его противоположности равняется 1

P(A)+P(-A)=1

p+q=1

3.                       Вероятность суммы 2х совместных событий А и В равняется сумме их вероятности без учета вероятности их совместного появления.

P(A+B)=P(A)+P(B)-P(AB)

Теоремы умножения вероятностей

Событие А называется независимым от события B, если вероятность события А не зависит от того, произошло событие В или нет.

 — критерий независимости событий

События А и В называются независимыми тогда, когда Р(АВ) = Р(А)*Р(В)

Вероятность события А, вычисляемая при условии, что имело место другое событие В, называется условной вероятностью Р(А/В)=P(AB)/P(B).

Свойства условных вероятностей.

Свойства условных вероятностей аналогичны свойствам безусловных вероятностей.

1.           0 £ Р(А/В) £ 1, т.к. ; АВ Ì В, Р(АВ) £ Р(В)

2.           Р(А/А)=1

3.           ВÌА, è Р(А/В)=1

4.          

5.           Р[(A+C)/B] = Р(А/В) + Р(C/В) – Если события А и С несовместны

Р[(A+C)/B] = Р(А/В) + Р(C/В) — Р(АC/В) – Если события А и С совместны

Теорема. Вероятность произведения двух событий равна произведению вероятности одного события на условную вероятность другого.

Док—во:

P(AB)=l/n;  P(A)=m/n; P(B/A)=l/m; l/n=m/n * l/m => P(AB)=P(A)*P(B/A)

Следствия:

1.                       Если событие А не зависит от события В, то и событие В не зависит от события А

2.                       Вероятность произведения 2х независимых событий равна произведению вероятностей этих событий.

P(AB)=P(A)*P(B)

 Формула полной вероятности

Формула полной вероятности является следствием теории сложения и умножения. Пусть требуется определить вероятность некоторого события А, которое может произойти вместе с событиями H1…Hn, образующих полную группу несовместных событий. Эти события называются гипотезами.

Докажем, что вероятность события А будет вычисляться по формуле:

Доказательство: Т.к. гипотезы Hi образуют полную группу, то событие А может появиться только в комбинации с какой-нибудь из гипотез. Т.к. гипотезы несовместны, то и комбинации будут несовместны, поэтому к ним можно применить теорему сложения:

А=Н1*А+Н2*А+…+Hn*A;

Формула Бейеса

Имеется полная группа несовместных гипотез H1…Hn. Вероятность этих гипотез до опыта известна. Произведен опыт, в результате которого произошло событие А.

Условные вероятности гипотез находятся по формуле:

P(A*Hi)=P(A)*P(Hi/A)=P(Hi)*P(A/Hi);

 — Ф-ла Бейеса.

Повторение испытаний. Частная теорема о повторении опыта.

На практике часто прилагаются задачи, в которых один и тот же опыт повторяется неоднократно., причем нас интересует не отдельное, а общее число появлений события А в серии опытов. Предположим, что опыты являются независимыми величинами. Независимые опыты могут проводиться в одинаковых или разных условиях. При одинаковых условиях вероятность события А будет одинаковой и к нему относится частная теорема. Если опыты разные, то к нему относится общая теорема о повторении опытов.

Частная теорема:

Вероятность одного сложного события, состоящего в том, что в n испытаниях событие A наступит ровно k раз и не наступит n—k раз, по теореме умножения вероятностей независимых событий равна .Таких сложных событий может быть столько, сколько можно составить сочетаний из n элементов по k элементов, т.е. . Т.к. эти сложные события несовместны, то по теореме сложения вероятностей несовместных событий искомая вероятность равно сумме вероятностей всех возможных сложных событий. Поскольку вероятности всех этих сложных событий одинаковы, то искомая вероятность равна вероятности одного сложного события, умноженной на их число:

. Эта формула называется формулой Бернулли.

Определение вероятностей по формуле Бернулли усложняется при больших значениях n и при малых p или q. В этом случае удобнее использовать приближенные асимптотические формулы. Если , а , но , то в этом случае

Эта формула определяется теоремой Пуассона. Если в схеме Бернулли количество опытов n достаточно велико , а вероятность р события А в каждом опыте постоянно, то вероятность  может определяться по приближенной формуле Муавра-Лапласа:

,

где ;

 — локальная функция Лапласа, которая табулирована и приводится в справочниках. Данная формула отражает, так называемую, локальную теорему Муавра-Лапласа.

Вероятность появления события А не менее m раз при n опытах вычисляется по формуле:

                            

Вероятность появления события А хотя бы один раз при n опытах

                               

Наивероятнейшее число  наступление события А в n опытах, в каждом из которых оно может наступить с вероятностью p (и не наступить с вероятностью q=1-p), определяется из двойного неравенства

                                   

Если событие А в каждом опыте может наступить с вероятностью p, то количество n опытов, которое необходимо произвести для того, чтобы с заданной вероятностью Рзад. можно было утверждать, что данное событие А произойдет по крайней мере один раз, находится по формуле:

                           

Частная теорема о повторении опытов касается того случая, когда вероятность события А во всех опытах одна и та же.

Общая теорема о повторении опытов. Производящая функция.

Если производятся n независимых опытов в различных условиях, причем вероятность появления события А в i-м опыте равна  то вероятность Р того, что событие А в n опытах появится m раз, равна коэффициенту при Z в разложении по степеням Z производящей функции  где

Функция распределения случайной величины.

Рассмотрим дискретную случайную величину Х со своими значениями, каждое из которых является возможным, но не равновозможным: p(x1)=p1 … p(xn)=pn. Сумма pi=1- критерий сходимости.

Законом распределения случайной величины называется всякое соотношение, которое связывает между собой значения всякой величины и ее вероятности.

Функция распределения:

Для непрерывной случайной величины невозможно составить закон распределения, поэтому для количественной характеристики удобно пользоваться не вероятностью отдельного события Х, а вероятностью события Х<x, где х – некоторая текущая переменная. Эти вероятности образуют некоторую функцию оси X.

F(x)=F(X<x)- интегральный закон распределения.

Свойства:

1.                       Функция F(x)-неубывающая функция.

Любой x2>x1 => F(x2)≥F(x1).

Д-во: Пусть х2>х1. Событие, состоящее в том, что Х примет значение, меньшее х2, можно подразделить на 2 несовместных события:

1)      Х примет значение, меньшее х1, с вероятностью Р(Х<x1)

2)      Х примет значение, удовлетворяющее неравенству x1≤X<x2, с вероятностью Р(x1≤X<x2).

По теореме сложения имеем

P(X<x2)=P(X<x1)+P( x1≤X<x2). Отсюда: P(X<x2)-P(X<x1)= P( x1≤X<x2) или F(x2)-F(x1)=P(x1≤X<x2). Так как любая вероятность есть число неотрицательное, то F(x2)-F(x1)≥0, или F(x2)≥F(x1), чтд.

2.                       F(-∞)=0

3.                       F(∞)=1

4.                       Значения функции распределения принадлежат отрезку [0;1]

0≤F(x)≤1

Д-во: Свойство вытекает из определения функции распределения как вероятности: вероятность всегда есть неотрицательное число, не превышающее 1.

Функция распределения есть вероятность того, что случайная величина X, в результате нашего опыта попадает левее т. х.

Для дискретных случайных величин также можно составить функцию распределения:

F(x)=P(X<x)=.

Вероятность попадания случайной величины на заданный участок.

P(α≤x≤β)=F(β)-F(α).

Вероятность попадания для непрерывной случайной величины в любое отдельное значение =0.

Плотность распределения

Плотность распределения — производная абсолютно непрерывной функции распределения.

P(x<X<x+∆x)=F(x+∆x)-F(x)

P(α<x<β)=

F(x)=P(X<x)=P(-∞<X<x)

F(x)=

Основные свойства плотности распределения:

1.                       f(x)≥0

Д-во: Функция распределения – неубывающая функция, следовательно, ее производная – функция неотрицательная.

2.                       =1

Несобственный интеграл  выражает вероятность события, состоящего в том, что случайная величина примет значение, принадлежащее интервалу(-∞;∞). Очевидно, такое событие достоверно, следовательно, вероятность его равна 1.

Эти 2 свойства геометрически определяют то, что кривая распределения всегда лежит выше оси Ох и площадь под кривой равна 1.

Числовые характеристики случайных величин.

Числовые характеристики случайной величины – числа, суммарно описывающие случайную величину.

Математическое ожидание:

Для дискретной случ. величины – сумма произведений всех ее возможных значений на их вероятности.

M(x)=x1p1+x2p2+…+xnpn

Если дискретная случ. величина Х принимает счетное множество возможных значений, то

причем мат ожидание существует, если ряд в правой части сходится абсолютно.

Математическое ожидание числа появлений события в одном испытании равно вероятности этого события.

Вероятностный смысл : математическое ожидание приближенно равно среднему арифметическому наблюдаемых значений случайной величины.

Математическое ожидание M(X) числа появлений события А в n  независимых испытаниях равно произведению числа испытаний на вероятность появления событий в каждом испытании: M(X)=np.

Для непрерывной случ величины:

Отклонением называют разность между случ величиной и ее мат ожиданием.

Мат ожидание отклонения равно 0: M[X—M(X)]=0, т.к. M[X—M(X)]=M(X)-M[X(X)]=M(X)-M(X)=0.

Дисперсия:

Для дискретной случ величины — мат ожидание квадрата отклонения случ величины от ее мат ожидания: D(X)=M[X—M(X)]². Для тот, чтобы найти дисперсию, достаточно вычислить сумму произведений возможных значений квадрата отклонения на их вероятности

D(X)=M(X²)-[M(X)]²

Д-во: D(X)= M[X—M(X)]²=M[X²-2XM(X)+M²(X)]=M(X²)-2M(X)M(X)+M²(X)=M(X²)-M²(X).

Дисперсия числа появлений события А в n независимых испытаниях, в каждом из которых вероятность p появления события постоянна, равна произведению числа испытаний на вероятности появления и непоявления события в одном испытании: D(X)=npq.

Для непрерывной случ величины:

Среднее квадратическое отклонение:

 – для оценки рассеяния возможных значений случ величины вокруг ее среднего значения.

Начальный момент: 

Центральный момент:

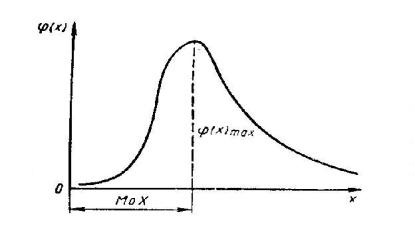
Мода случ величины – наиболее вероятное значение этой случ величины.

Медиана – это такое значение, для которого выполняется равенство p(x<Me)=P(x>Me). Геометрически это означает, что медиана является абсциссой точки, которой площадь, ограниченная кривой распределения, делится пополам.

Неравенство Чебышева

Пусть имеется случ величина Х, заданная mx и D(x). Неравенство Чебышева утверждает, что каково бы ни было положительное число α, вероятность того, что величина Х отклонится от своего мат ожидания не меньше, чем на α, ограничено сверху величиной:

Д-во:

Возьмем произвольное положительное число α>0 и вычислим вероятность того, что величина Х отклонится от своего mx не меньше чем на α.

Вероятность  , т.е. надо просуммировать вероятности значений, которые не лежат на AB.

Т.к. не все члены суммы не отрицательны, то D(x) можно уменьшить , взяв не все значения xi:

что и требовалось доказать.

Теорема Чебышева

Среднее арифметическое (, my=mx, D(y)=D(x)/n) случ величины Х есть случ величина с очень маленькой дисперсией и при достаточно большом n ведет себя как не случ.

Теорема Чебышева:

При достаточно большом числе независимых опытов, среденее арифметическое наблюдаемых значений случ величины сходится по вероятности к ее mх.

P(|xn—a|<ε)>1-δ,  ε, δ -> 0.

P(|(∑xi/n) — mx|1-δ

Д—во:

Y=∑xi/n, my=mx, Dy=Dx/n.

Применим к случ величине Y неравенство Чебышёва.

P(|y—my|≥ε)≤Dy/ε²=Dx/nε².

P(|(∑xi/n)-mx|≥ε)≤δ

P(|(∑xi/n)-mx|<ε)>1-δ

Обобщенная теорема Чебышева и теорема Маркова.

Обобщенная теорема Чебышёва:

Если х1…хn независимые случ величины, заданные своими мат ожиданиями и дисперсиями, и сами все дисперсии ограничены сверху одним и тем же числом L (D(x)<L), то при возрастании n ср. арифметическое наблюдаемых значений сходится к среднему арифметическому их мат ожиданий:

P(|(∑xi/n) – (∑mxi/n)|<ε)>1-δ;

Теорема Маркова:

Если имеются ЗАВИСИМЫЕ случ величины х1..хn и если при n->∞ выполняется условие , то среднее арифметическое наблюдаемых значений случ величины Х сходится к среднему арифметическому их мат ожидания.

Характеристические функции

Характеристической функцией случ величины Х называется функция , которая представляет собой мат ожидание некоторой комплексной величины . Если х является дискретной случ величиной, заданной своим законом распределения, то ее характеристическая функция выглядит так:

Если х — непрерывная случ величина, то ее характеристическая функция:

Преобразование,  которому надо подвергнуть f(x), чтобы получить g(x), является преобразование Фурье.

Свойства характеристических функций:

1.       y=ax, gy(t)=gx(at)

2.       y=∑Xk, gy(t)=∏gxk(t)

Центральная предельная теорема

Если x1…xn – независимые случ величины, имеющие один и тот же закон распределения, с мат ожиданием и дисперсией, то при неограниченном увеличении n, закон распределения Y неограниченно приближается к нормальному закону.

Yn=∑Xk

Д-во: согласно 2му свойству характеристической функции (все значения имеют одинаковый закон распределения, а значит и характеристическая функция у всех одинакова):

…

Следствие из теоремы Ляпунова-теоремы Лапласа.

Теорема Лапласа:

x1…xn – независимые случ величины, заданные своими мат ожиданиями и дисперсией. Предположим, что условия центральной предельной теоремы выполнены и число слагаемых достаточно для того, чтобы случ величина Y=∑Xi была распределена по нормальному закону. Тогда

Д-во: Пусть производится n независимых опытов, в каждом из которых событие А может появиться с вероятностью p. Согласно теореме Ляпунова следующие случ величины будут приближаться к нормальному закону распределения:

Локальная теорема Лапласа:

Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события А равняется pn, наступит ровно k раз приблизительно равно:

Интегральная теорема Лапласа:

Вероятность того что в n независимых испытаниях, в каждом из которых вероятность появления события А=р, событие наступит не меньше к1 раз и не больше к2 раз, равна:

Pn(k1,k2)≈Ф(Xk2)-Ф(Xk1).

Xk1=(k1-np)/;  Xk2=(k2-np)/; 

Свойства числовых характеристик(мат ожидание, дисперсия).

Мат ожидание:

1.       Математическое ожидание постоянной величины равно самой постоянной:

M(C)=C

Д-во: Будем рассматривать постоянную С как дискретную случайную величину, которая имеет одно возможное значения С и принимает его с вероятностью р=1. М(С)=С*1=С.

2.        Постоянный множитель можно выносить за знак математического ожидания: М(СХ)=СМ(Х)

 Д-во: Пусть случайная величина Х задана законом распределения вероятностей:

 или

Математическое ожидание случ. величины СХ:

 M(CX)=Cx1p1+Cx2p2+…Cxnpn=C(x1p1+x2p2+…xnpn)=CM(X) => M(CX)=CM(X).

3.       Математическое ожидание произведения двух независимых случ. величин равно произведению их мат ожиданий. M(XY)=M(X)M(Y)

Д-во: Пусть независимы случайные величины Х и Y заданы своими законами распределения вероятностей:

Составив все значения, которые может принимать случ. величина XY, напишем закон распределения XY.

Мат ожидание равно сумме произведений всех возможных значений на их вероятности:

M(XY)=x1y1*p1g1+x2y1*p2g1+x1y2*p1g2+x2y2*p2g2=y1g1(x1p1+x2p2)+y2g2(x1p1+x2p2)=

=(x1p1+x2p2)(y1g1+y2g2)=M(X)M(Y).

Следствие:

M(XYZ)=M(X)M(Z)M(Y)

4.       Мат ожидание суммы двух случ величин равно сумме мат ожиданий слагаемых:

M(X+Y)=M(X)+M(Y)

Д-во: Пусть случ величины X и Y заданы следующими законами распределения:

Составим все возможные значения величины X+Y: x1+y1; x2+y1; x1+y2; x2+y2. Обозначим их вероятности соответственно p11, p12, p21 и p22. Мат ожидание X+Y равно:

M(X+Y)=(x1+y1)p11+(x1+y2)p12+(x2+y1)p21+(x2+y2)p22=x1(p11+p12)+x2(p21+p22)+

+y1(p11+p21)+y2(p12+p22).

p11+p12=p, т.к. Событие «Х примет значение х1» влечет за собой событие «Х+Y примет значения x1+y1 или x1+y2», вероятность которого равно p11+p12. Следовательно, p11+p12=p1.

Аналогично: p21+p22=p2; p11+p21=g1 и p12+p22=g2. Получим:

M(X+Y)=(x1p1+x2p2)+(y1g1+y2g2)=M(X)+M(Y)

Следствие:M(X+Y+Z)=M(X)+M(Y)+M(Z)

Дисперсия:

1.       D(C)=0;

Д-во: D(C)=M{[C—M(C)]²}=M[(C—C)²]=M(0)=0.

2.       D(CX)=C²D(X)

Д—во: D(CX)=M{[CX-M(CX)]²}= M{[CX-CM(X)]²}=M{C²[X-M(X)]²}=C²M{[X-M(X)]²}=C²D(X).

3.       D(X+Y) =D(X)+D(Y).

Д—во: D(X+Y) = M[(X+Y)²]-[M(X+Y)]²= M[X²+2XY++Y²]-[M(X)+M(Y)]²=M(X²)+2M(X)M(Y)+

+M(Y²)-M²(X)-2M(X)M(Y)-M²(Y)={ M(X²)-[M(X)]²}+{ M(Y²)-[M(Y)]²}=D(X)+D(Y).

Следствие 1: D(X+Y+Z)=D(X)+D(Y)+D(Z)

Следствие 2: D(C+X)=D(X)+D(C)=D(X)

4.       D(X-Y)=D(X)+D(Y)

Д-во: D(X—Y)=D(X)+D(-Y)=D(X)+(-1)²D(Y)=D(X)+D(Y)

Нормальное распределение

Нормальным называют распределение вероятностей непрерывной случ величины, которое описывается плотностью:

где a-мат ожидание, а σ – среднее квадратическое отклонение Х.

1.       D(f)=R

2.      

3.      

4.      

Вероятность того, что Х примет значение, принадлежащее интервалу (α,β)

P(α<X<β)=Ф((β—a)/σ)-Ф((α—a)/σ), где  – функция Лапласа.

1.       Ф(-∞)=0

2.       Ф(+∞)=1

3.       Ф(-х)=1-Ф(х)

P(mx—l<x<mx+l)=Ф(l/σ)-Ф(-l/σ)=2Ф(l/σ)-1

Асимметрия, эксцесс, мода и медиана нормального распределения соответственно равны:

As=0, Ek=0, M0=a, Me=a, где a=M(x).

Правило «трех сигма».

Если случайная величина распределена нормально, то абсолютная величина ее отклонения от мат ожидания не превосходит утроенного среднего квадратического отклонения.

Запишем вероятность того, что отклонение нормально распределенной случайной величины от математического ожидания меньше заданной величины D:

 

            Если принять D = 3s, то получаем с использованием таблиц значений функции Лапласа:

 

            Т.е. вероятность того, что случайная величина отклонится от своего математического ожидание на величину, большую чем утроенное среднее квадратичное отклонение, практически равна нулю.

            Это правило называется правилом трех сигм.

Равномерное распределение

На практике очень часто встречаются случ числа, про которые заранее известно, чтоих значения лежат в пределах некоторого интервала, и все значения случ величины одинаково вероятны.

О таких случ числах говорят, что они распределены равномерно. Плотность такого распределения сохраняет постоянное значение, а именно f(x)=1/(b—a). Вне этого интервала f(x)=0.

Вероятность попадания значения случ числа в заданный интервал (a;b), можно вычислить по формуле:  .

График плотности равомерного распределения симметричен относительно прямой x=(a+b)/2, поэтому M(x)=(a+b)/2. Этот же результат можно получить по формуле .

. Подставив формулы, полученные выше, получим D(x)=(b—a)²/12. В таком случае среднее квадратическое отклонение случ числа равно .

Закон Пуассона

Рассмотрим дискретную случ величину Х, которая может принимать целые неотрицательные значения. Говорят, что случ величина распределена по закону Пуассона, если вероятность того, что она примет значение m, выражена формулой:  , где a – параметр Пуассона.

Доказательство:

                                          

                                                                      x      

           

/

/

.

Равенство мат ожидания и дисперсии параметру а используется на практике для решения вопроса правдоподобия гипотезы о том, что случ величина Х распределяется по закону Пуассона.

Пусть на оси абсцисс случ образом распределены точки. Допустим, что случ образом распределенные точки удовлетворяют следующим условиям:

1.    Вероятность попадания того или иного числа точек на отрезок l зависит от их положения на оси абсцисс.

2.    Точки распределяются по оси абсцисс независимо друг от друга.

3.    Вероятность попадания на малый участок ∆х 2х и более точек пренебрежимо мала по сравнению с вероятностью попадания одной точки.

Выделим отрезок длины l и рассмотрим дискретную случ величину Х числа точек, попадающих на этот отрезок.

Докажем, что случ величина Х подчиняется закону Пуассона и посчитаем вероятность того, что на этот отрезок попадет ровно m точек. Рассмотрим маленький участок этой прямой ∆х и вычислим вероятность того, что на этот участок попадет хотя бы одна точка.

Согласно 3му условию вероятность попадания на участок ∆х 2 и более точек ≈0, поэтому мат ожидание будет = вероятности попадания хотя бы одной точки на ∆х.

            Для вычисления вероятности попадания на отрезок l ровно m точек, разделим этот участок на n частей: ∆х = l/n, p=λ∆x=λl/n, q=1-(λl/n).

По условию 2 вероятности попадания точек являются независимыми можно использовать частную теорему повторения опыта:

Параметр a определяется как ср. число точек, попадающих на нужный отрезок.

Функция одного случайного аргумента

Если каждому возможному значению случайной величины Х соответствует одно возможное значение случайной величины Y, то Y называют функцией случайного аргумента X: Y=φ(X).

Рассмотрим случай, когда X— дискретная случ величина с возможными значениями x1…xn, вероятности которых p1…pn. Тогда Yтоже является дискретной случ величиной со всевозможными случ событиями: y=f(x1)…y=f(xn).

Т.к. событие «величина X примет значение xi» влечет за собой событие «величина Y примет значение f(xi)», то вероятности всевозможных значений Y соответственно равны p1…pn.

Мат ожидание случ величины будет рассчитываться: M(y)=M(f(x))=∑f(xi)pi.

При записи закона распределения вероятности y руководствуются следующими правилами:

1.    Если различным возможным значениям X соответствуют различные возможные значения Y, то вероятности соответствующих значений X и Y равны между собой: P(X=xi)=P(y=f(xi))=pi.

2.    Если различным возможным значениям Х соответствуют значения Y, среди которых есть равные между собой, то следует складывать вероятности повторяющихся значений Y.

Рассмотрим непрерывную случ величину Х, которая задана своей плотностью, если у=f(x) дифференцируемая монотонная функция, обратная функция которой x=φ(y), то плотность распределения случ величины y определяется след функцией: g(y)=f[φ(y)|φ’(y)].

Соответствующее мат ожидание:

Если отыскание ф-ии g(y) является затрудненным, то можно исп. след формулу:

.

.

Функция двух случайных аргументов

Если каждой паре возможных значений случ величин X и Y соответствует одно возможное значение случайной величины Z, то Z называют функцией двух случ аргументов X и Y: Z=φ(X, Y).

1.       Пусть X и Y – дискретные независимые случ величины. Для того, чтобы составить закон распределения функции Z=X+Y, надо найти все возможные значения Z и их вероятности. Т.к. X и Y независимые случ величины, то zi=xi+yi, pz=px*py. Если zi=zj, то их вероятности складываются.

2.       Пусть X и Y – непрерывные случ величины. Доказано: если X и Y независимы, то плотность распределения g(z) суммы Z=X+Y (при условии, что плотность хотя бы одного из аргументов задана на интервале(-∞;∞) одной формулой) может быть найдена с помощью формулы:

, где f1, f2 – плотности распределения аргументов.

Если возможные значения аргументов неотрицательны, то g(z) находят по формуле:

Плотность распределения суммы независимых случ величин называют композицией, а закон распределения вероятностей называют устойчивым, если композиция таких законов есть тот же закон. M(z)=M(x)+M(y); D(z)=D(x)+D(y).

Закон распределения двумерной случайной величины

Законом распределения дискретной двумерной случ величины называют перечень возможных значений этой величины, т.е. пар чисел (xi, yj) и их вероятностей P(xi, yj).

Зная закон распределения двумерной дискретной случ величины, можно найти законы распределения каждой из составляющих. Например: События (X=x1, Y=y1)…(X=x1, Y=Ym) – несовместны, поэтому вероятность P(x1) того, что Х примет значение х1, по теореме сложения такова: P(x1)=p(x1, y1)+…+p(x1, ym). Т.о. вероятность того, что Х примет значение xi, равна сумме вероятностей «столбца хi». Аналогично, сложив «строки Yj», получим вероятность P(Y=yj).

Статистическое распределение выборки.  Эмпирическая функция распределения. Полигон и гистограмма.

Пусть для изучения количественного признака Х из генеральной совокупности извлечена выборка x1…xk объема n. Наблюдавшиеся значения xi признака X называют вариантами, а последовательность вариант, записанных в возрастающем порядке, — вариационным рядом.

Статистическим распределением выборки называют перечень вариант xi вариационного ряда и соответствующих им частот ni (сумма всех частот равна n) или относительных частот wi(сумма = 1).

Статистическое распределение выборки можно задать также в виде последовательности интервалов и соответствующих им частот.

Эмпирической функцией распределения – называют функцию F*(x), определяющую для каждого значения х относительную частоту события X<x: F*(x)=nx/n, где nx – число вариант, меньших х, n—  объем выборки. Эмпирическая функция обладает следующими свойствами:

1.       Значения эмпирической функции принадлежат отрезку [0;1].

2.       F*(x) – неубывающая функция.

3.       Если x1 – наименьшая варианта, а xk – наибольшая, то F*(x)=0 при x≤x1 и F*(x)=1 при x≥xk.

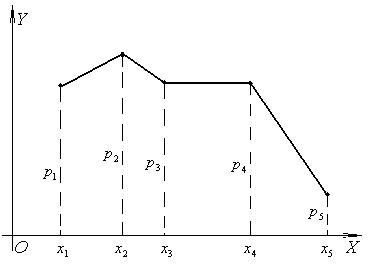
А. Дискретное распределение признака X. Полигоном частот называют ломанную, отрезки которой соединяют точки (x1,n1)…(xk,nk), где xi – варианты выборки и ni – соответствующие им частоты.

Полигоном относительных частот называют ломанную, отрезки которой соединяют точки (xk,wk), где xk – варианты выборки, а wk— соответствующие им относительные частоты.

Б. Непрерывное распределение признака X. При непрерывном распределении признака весь интервал, в котором заключены все наблюдаемые значения признака, разбивают на ряд частичных интервалов длины h, и находят ni – сумму частот вариант, попавших в i-тый интервал. Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длины h, а высоты равны соотношению ni/h. Площадь прямоугольника равна h(ni/h)=ni – сумме частот вариант, попавших в интервал. Площадь гистограммы частот равна сумме всех частот, т.е. объему выборки.

Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длины h, а высоты равны соотношению wi/h. Площадь прямоугольника равна соответствующей относительной частоте, а площадь гистограммы = 1.

Числовые характеристики статистического распределения

Критерии согласия(критерии Пирсона).

Допустим, что данное статистическое распределение выровнено с помощью некоторой теоретической кривой. Как бы хорошо ни была подобрана теоретическая кривая, между ней и мтатистич. распределением неизбежны некоторые расхождения. Критерий согласия отвечает на вопрос, объясняются ли эти  расхождения ошибками измерения или расхождение явл. существенным и подобранная нами кривая плохо выравнивает статистическое распределение.

Выдвигается гипотеза Н, состоящая в том, что случ величина X подчиняется данному закону распределения. Для того, чтобы принять или опровергнуть гипотезу Н, рассматривают некоторую величину Н, характеризующую степень расхождения теоретического и статистического распределений.

В зависимости от выбора величины Н существует несколько критериев согласия. Используем для доказательства критерий χ² или критерий Пирсона.

Предположим, что произведено m независимых опытов, в каждом из которых случ величина Х приняла некоторое значение. Результаты записываются в виде статистического ряда. Для теоретического значения распределения можно найти теоретическую вероятность попадания случ величины в каждый интервал. Проверим согласованность теоретического и статистического распределений: выберем в качестве меры расхождения сумму квадратов отклонения, взятых с некоторым коэффициентом Сi.

Коэффициент Сi вводится, потому что в общем случае отклонения, относящиеся к различным разрядам нельзя считать равноправными.

Пирсон полагает, что если в качестве веса взятьCi=n/pi, то при больших значениях n распределение величины U обладает следующими свойствами: оно практически не зависит от ф-ии распределения, а зависит только от числа разрядов.

Распределение χ² зависит от параметра r, называемым числом степеней свободы, с увеличением которого распределение медленно приближается к нормальному.

После расчета χ² для статистического распределения по расчетным таблицам находим значение χ-критическое. Если χ² -критическое > χ² -наблюдаемого – нет оснований опровергать гипотезуH.

Функция распределения системы двух случайных величин

Систему случ чисел величин X и Y изображают случ точкой на плоскости с координатами (X,Y), тогда вместо т. используется понятие случ вектора. Функция распределения системы 2х случ величин называется вероятностью совместного выполнения двух неравенств:

P(x,y)=P(X<x)P(Y<y).  Геометрически это означает, что функция распределения есть вероятность попадания случ точки в бесконечный квадрат с вершиной в точке (X,Y), лежащий ниже и левее этой точки.

Свойства функции распределения:

1.       x2>x1, F(x2,y)≥F(x1,y)

y2>y1, F(x,y2)≥F(x, y1)

2.       F(x,-∞)=F(-∞,y)=F(-∞,-∞)=0

3.       F(∞,∞)=1

4.       F(x, ∞)=F(x); F(∞,y)=F(y);

 Плотность распределения системы двух случайных величин.

Плотностью распределения системы 2х случ величин называется вторая смешанная частная производная от функции распределения:

P((x,y)cP∆)=F(x+∆x, y+∆y)-F(x+∆x, y)-F(x, y+∆y)+F(x,y)

Плотность распределения системы случ величин представляет собой плотность распределения массы в точке с координатами x,y.

f(x,y)dxdy

Элем. вероятность f(x,y)dxdy есть вероятность попадания в элемент. прямоугольник со сторонами dx, dy. Эта вероятность равна объему параллелепипеда, ограниченного сверху поверхностью f(x,y) и отражающегося на элементарный участок dxdy.

Свойства плотности:

1.       f(x,y)≥0

2.        — полный объем тела, ограниченного поверхностью распределения с плоскостью xOy = 1.

 Условные законы распределения.

Зная совместный закон распределения можно легко найти законы распределения каждой случайной величины, входящей в систему. Однако, на практике чаще стоит обратная задача – по известным законам распределения случайных величин найти их совместный закон распределения. В общем случае эта задача является неразрешимой, т.к. закон распределения случайной величины ничего не говорит о связи этой величины с другими случайными величинами. Кроме того, если случайные величины зависимы между собой, то закон распределения не может быть выражен через законы распределения составляющих, т.к. должен устанавливать связь между составляющими. Все это приводит к необходимости рассмотрения условных законов распределения.

             Определение. Распределение одной случайной величины, входящей в систему, найденное при условии, что другая случайная величина приняла определенное значение, называется условным законом распределения. Условный закон распределения можно задавать как функцией распределения, так и плотностью распределения.

            Условная плотность распределения вычисляется по формулам:

            Условная плотность распределения обладает всеми свойствами плотности распределения одной случайной величины.

Зависимые и независимые случайные величины.

2 случ величины называются независимыми, если закон распределения одной из них не зависит от того, какие возможные значения приняла другая величина.

Следовательно, условные распределения независимых величин равны их безусловным распределениям.

Теорема: Для того, чтобы случайные величины X и Y были независимыми, необходимо и достаточно, чтобы функция распределения системы (X, Y) была равна произведению функций распределения составляющих:

F(x, y)=F1(x)F2(y)

Доказательство: а) необходимость. Пусть X, Y –независимы, тогда X<x, Y<y тоже независимы и P(X<x, Y<y)=P(X<x)P(Y<y); F(x,y)=F1(x)F2(y).

б) Достаточность: Пусть F(x, y)=F1(x)F2(y) => P(X<x, Y<y)=P(X<x)P(Y<y) => X, Y— независимы.

Следствие: Для того, чтобы непрерывные случайные величины X и Y были независимыми, необходимо и достаточно, чтобы плотность совместного распределения системы (X, Y) была равна произведению плотностей распределения составляющих:

f(x, y)=f1(x)f2(y)

Доказательство: а) необходимость. Пусть X и Y – независимые непрерывные случайные величины. Тогда F(x,y)=F1(x)F2(y). Дифференцируя это равенство по x, затем по y, имеем:

 или f(x, y)=f1(x)f2(y).

б) достаточность: Пусть f(x, y)=f1(x)f2(y). Интегрируя по х, затем по у, получим

 или F(x,y)=F1(x)F2(y). => X, Y – независимы.

Метод наименьших квадратов.

Метод наименьших квадратов (МНК) — метод оценки параметров модели на основании экспериментальных данных, содержащих случайные ошибки. В основе метода лежат следующие рассуждения: при замене точного (неизвестного) параметра модели приблизительным значением необходимо минимизировать разницу между экспериментальными данными и теоретическими (вычисленными при помощи предложенной модели). Это позволяет рассчитать параметры модели с помощью МНК с минимальной погрешностью.

Мерой разницы в методе наименьших квадратов служит сумма квадратов отклонений действительных (экспериментальных) значений от теоретических. Выбираются такие значения параметров модели, при которых сумма квадратов разностей будет наименьшей – отсюда название метода:

  = min

где Y – теоретическое значение измеряемой величины, y – экспериментальное.

При этом полученные с помощью МНК параметры модели являются наиболее вероятными.

Метод наименьших квадратов, а также его различные модификации (нелинейный МНК, взвешенный МНК и т.д.) широко используется в аналитической химии, в частности, при построении градуировочной модели. Как правило, предполагается линейная зависимость (параметры которой требуется установить) между аналитическим сигналом и содержанием определяемого вещества. В этом случае метод наименьших квадратов позволяет оптимизировать параметры градуировки (и получить наименьшую погрешность анализа), а сумма квадратов разностей теоретического и экспериментального значения аналитического сигнала является мерой погрешности градуировки и линейно связана с так называемой остаточной дисперсией (дисперсией адекватности модели)

Предложите, как улучшить StudyLib

(Для жалоб на нарушения авторских прав, используйте

другую форму
)

1 Сформулируйте три аксиомы вероятности и на их основе докажите

теорему сложения вероятностей для двух событий.

2 Какие события A и B называются независимыми? Докажите, что

если события A и B независимы, то независимы события А и B.

3 События A и B независимы; события A и C также независимы. При

этом события B и C несовместны.

Докажите, что отсюда вытекает независимость событий A и B  C.

Предварительно определите понятия: «независимость»,

«несовместность».

4 Определите понятия: «условная вероятность», «полная группа

событий». Сформулируйте и докажите теорему, утверждающую при

выполнении ряда условий справедливость формулы Байеса.

5 Выведите формулу для вероятности Pnk наступления k успехов

в серии n испытаний по схеме Бернулли.

6 В каких случаях применяется интегральная приближенная формула

Лапласа? Используя эту формулу, получите оценку вероятности

отклонения относительной частоты события A в n независимых

испытаниях от вероятности p наступления A в 1 опыте.

7 Докажите, что если X и Y – независимые случайные величины,

принимающие конечное множество значений, то E(XY)= E(X)*E(Y).

8 Докажите, что если X и Y – дискретные случайные величины,

принимающие конечное множество значений, то E(X+Y)= E(X)+E(Y).

9 Пусть X – дискретная случайная величина, распределенная по

биномиальному закону с параметрами n и p. Докажите, что EX  

np,DX  np1 − p.

Пусть X – дискретная случайная величина, распределенная по

закону Пуассона с параметром . Докажите, что EX   .

11 Пусть X – дискретная случайная величина, распределенная по

геометрическому закону с параметром p. Докажите, что EX  1p

12 Перечислите основные свойства коэффициента корреляции.

Докажите, что коэффициент корреляции

ρX,Y случайных величин X и Y удовлетворяет условию |ρX,Y| 1.

13 Сформулируйте определение ковариации и перечислите ее

основные свойства. Используя эти свойства, вычислите коэффициент

корреляции a  bX,X, если a и b – константы b ≠0

14 Выведите формулы для математического ожидания и дисперсии

случайной величины, равномерно распределенной на отрезке [a,b].

15 Докажите, что для нормальной случайной величины X с функцией

плотности распределения f(x)=… математическое ожидание E(X)=μ.

16 Докажите, что для нормальной случайной величины X с функцией

плотности распределения f(x)=… дисперсия D(X)=2.