Итоговая аттестация по математике в форме ОГЭ 8 класс
Просмотр содержимого документа
«Вариант 3»
Итоговая аттестация
учащихся 8 класса по МАТЕМАТИКЕ
Вариант № 1303
Часть 1
• Для заданий с выбором ответа (2, 3, 8, 14) из четырёх предложенных вариантов выберите один верный.
В бланке ответов № 1 поставьте знак «×» в клеточку, номер которой соответствует номеру выбранного вами ответа.
• Для заданий с кратким ответом полученный результат сначала запишите на листе с текстом работы после слова «Ответ». Если получена обыкновенная дробь, обратите её в десятичную.
Перенесите ответ в бланк ответов № 1 справа от номера соответствующего задания, начиная с первой клеточки. Каждый символ (цифру, знак минус, запятую или точку с запятой) пишите в отдельной клеточке в соответствии с приведёнными в бланке образцами. Единицы измерений указывать не нужно.
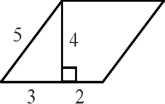
-
Если при решении задания 4 найдено несколько корней, запишите их (в любом порядке) в бланк ответов № 1, разделив точкой с запятой (;).
Ответом к заданиям 5 и 13 является последовательность цифр. Перенесите цифры в бланк № 1 без пробелов, запятых и других символов.
Модуль «Алгебра»
-
Найдите значение выражения: 2,4 / (2,9 – 1,4).
Ответ: ___________
-
На координатной прямой отмечены числа а и с.
а с
• •
-1 0 1

-
с – а 0;
-
–а 0;
3) 0 с + 1
4) ас 0.
Ответ: _______________
-
В каком случае числа 2
, 5
и 6 расположены в порядке возрастания?
-
6; 2
; 5
;
-
2
; 6; 5
;
-
5
; 6; 2
;
-
2
; 5
; 6.
Ответ: _____________
4. Решите уравнение: х2 +3х – 18 = 0.
Ответ: _____________________
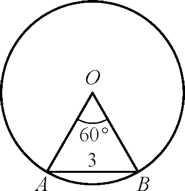
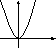
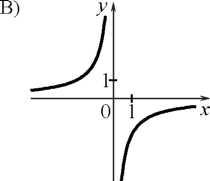
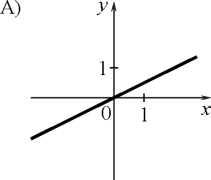
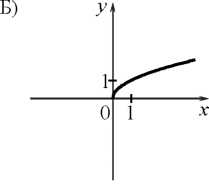
5. Установите соответствие между графиками функций и формулами, которые их задают.
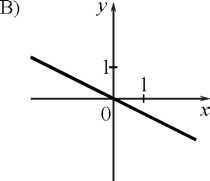
-
у = —
х; 2) у = —
; 3) у = — х2; 4) у =
Ответ:
|
А |
Б |
В |
6. Найдите наименьшее целое решение неравенства: 4(х — 1) – 8х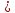
Ответ: ______________
7. Упростите выражение (а +2)2-а(4 -7а) и найдите его значение при а = — 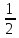
Ответ: _____________
8. Было засеяно 24 га земли, что составило 15% площади всего поля. Какова площадь поля?
1) 360; 2) 160; 3) 310; 4) 180.
Ответ: ________
Модуль «Геометрия»
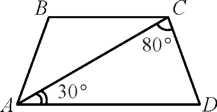
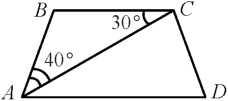
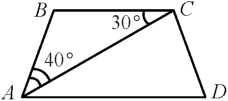
9. Найдите угол ADC равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной АВ углы, равные 30° и 50° соответственно.
Ответ: _____________
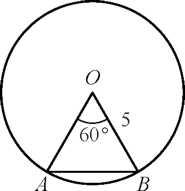
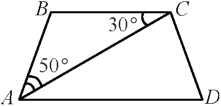
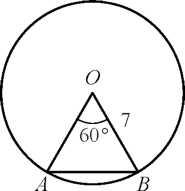
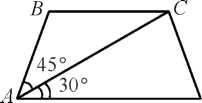
10. Центральный угол АОВ, равный 60°, опирается на хорду АВ длиной 3. Найдите радиус окружности.
Ответ: ____________
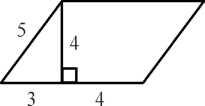
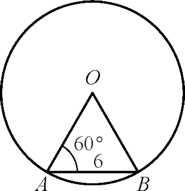
11. Найдите площадь параллелограмма, изображённого на рисунке
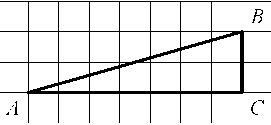
12. Найдите тангенс угла С треугольника ABC , изображённого на рисунке.
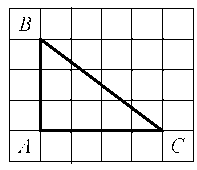
Ответ: ____________
13. Укажите номера верных утверждений.
1) Если три стороны одного треугольника пропорциональны трём сторонам другого треугольника, то такие треугольники подобны.
2) Сумма смежных углов равна 1800.
3) Любая высота равнобедренного треугольника является его биссектрисой.
Ответ: _____________
Модуль «Реальная математика»
14. Учёный Комаров выезжает из Москвы на конференцию в Санкт- Петербургский университет. Работа конференции начинается в 8:30. В таблице дано расписание ночных поездов Москва – Санкт-Петербург.
|
Номер поезда |
Отправление из Москвы |
Прибытие в Санкт-Петербург |
|
032АВ |
22:50 |
05:48 |
|
026А |
23:00 |
06:30 |
|
002А |
23:55 |
07:55 |
|
004А |
23:59 |
08:00 |
Путь от вокзала до университета занимает полтора часа. Укажите номер самого позднего (по времени отправления) из московских поездов, которые подходят учёному Иванову.
-
032АВ 2) 026А 3) 002А 4) 004А.
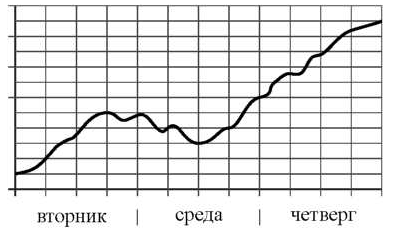
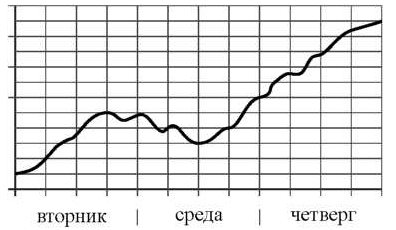
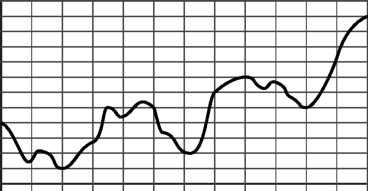
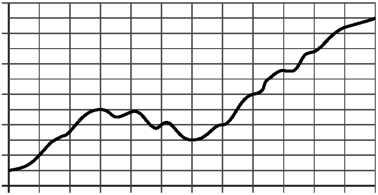
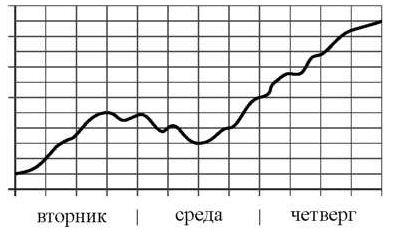
15. На рисунке изображён график изменения атмосферного давления в городе Энске за три дня. По горизонтали указаны дни недели, по вертикали — значения атмосферного давления в миллиметрах ртутного столба. Укажите наибольшее значение атмосферного давления во вторник.
762
760
758
756
754
752
750
Ответ: _________
16. Блюдце, которое стоил 40 рублей, продаётся с 10% — ой скидкой. При покупке 10 таких блюдец покупатель отдал кассиру 500 рублей. Сколько рублей сдачи он должен получить?
Ответ: ___________________
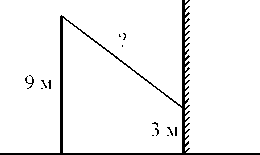
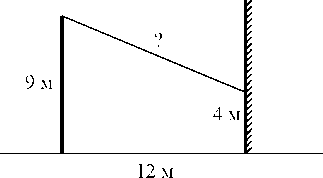
17. От столба высотой 12 м к дому натянут провод, который крепится на высоте
3м от земли (см. рисунок). Расстояние от дома до столба 12 м. Вычислите длину провода.
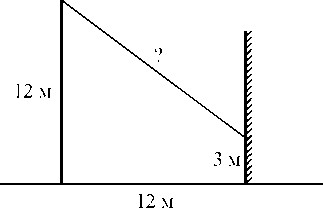
Ответ: ____________
18. На диаграмме представлено распределение количества пользователей некоторой социальной сети по странам мира. Всего в этой социальной сети 9 млн. пользователей.
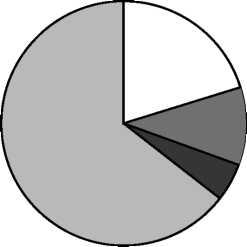




Какое из следующих утверждений неверно?
-
Пользователей из Беларуси меньше, чем пользователей из Украины.
-
Пользователей из России больше 4 миллионов.
-
Пользователей из Украины больше четверти общего числа пользователей.
-
Пользователей из Беларуси больше, чем пользователей из Финляндии.
В ответе запишите номер выбранного утверждения.
Ответ: _________________
19. Найдите медиану ряда чисел 1, 12, 5, 17, 2, 8, 11, 7.
Ответ6 ____________
20. Найдите среднее арифметическое ряда чисел -8,2; -5,6; — 0,4; 3,9; 12,8.
Ответ: ___________
Часть 2
При выполнении заданий 21-26 используйте бланк ответов № 2. Сначала укажите номер задания, а затем запишите его решение и ответ. Пишите чётко и разборчиво. Обращаем Ваше внимание на то, что записи в черновике не будут учитываться при оценивании работы.
21. Найдите наименьшее значение выражения (х + 5у — 7)2 + (3х + 2у + 5)2 и значения х и у, при которых оно достигается.
Ответ: ___________
22. Найдите все значения параметра а, при которых уравнение ах2 – (2а + 6)х + 3а + 3 = 0 имеет единственный корень.
Ответ: __________
23. Решите уравнение: 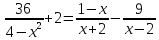
Ответ: ____________
24. Упростите выражение: 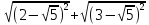
Ответ: ____________
25. Центральный угол АОВ на 30о больше вписанного угла, опирающегося на дугу АВ. Найдите этот вписанный угол.
26. Диагональ параллелограмма, равная 6,5 см, перпендикулярна к стороне параллелограмма, равной 3,4 см. Найдите площадь параллелограмма.
Просмотр содержимого документа
«Демонстрационный вариант»
Итоговая аттестация
учащихся 8 класса по МАТЕМАТИКЕ
Демонстрационный вариант
Часть 1
• Для заданий с выбором ответа (2, 3, 8, 14) из четырёх предложенных вариантов выберите один верный.
В бланке ответов № 1 поставьте знак «×» в клеточку, номер которой соответствует номеру выбранного вами ответа.
• Для заданий с кратким ответом полученный результат сначала запишите на листе с текстом работы после слова «Ответ». Если получена обыкновенная дробь, обратите её в десятичную.
Перенесите ответ в бланк ответов № 1 справа от номера соответствующего задания, начиная с первой клеточки. Каждый символ (цифру, знак минус, запятую или точку с запятой) пишите в отдельной клеточке в соответствии с приведёнными в бланке образцами. Единицы измерений указывать не нужно.
-
Если при решении задания 4 найдено несколько корней, запишите их (в любом порядке) в бланк ответов № 1, разделив точкой с запятой (;).
Ответом к заданиям 5 и 13 является последовательность цифр. Перенесите цифры в бланк № 1 без пробелов, запятых и других символов.
Модуль «Алгебра»
-
Найдите значение выражения: (6,96– 1,5) / 2,4.
Ответ: ___________________
-
На координатной прямой отмечены числа а и с.

• •
-1 0 1
Какое из следующих утверждений неверно?
1) а – с 0;
2) -3 а + 1
3) –с -1;
4) 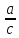
Ответ: __________
-
В каком случае числа 2
, 5
и 6 расположены в порядке возрастания?
-
6; 2
; 5
;
-
2
; 6; 5
;
-
5
; 6; 2
;
-
2
; 5
; 6.
Ответ: _____________
4. Решите уравнение: х2 — 5х – 14 = 0.
Ответ: _____________________
-
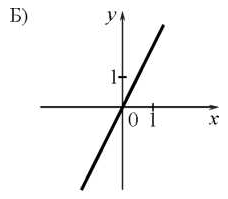
Установите соответствие между графиками функций и формулами, которые их задают.
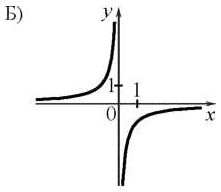
В)
-
у = —
; 2) у=х2; 3) у = 2х + 4; 4) у=
..
|
А |
Б |
В |
6. Решите неравенство: 3х – 1 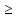
Ответ: ___________________
7. Упростите выражение (а — 4)2-2а(5а -4) и найдите его значение при а =- 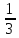
Ответ: _______________
8. Было засеяно 48 га земли, что составило 30% площади всего поля. Какова площадь поля?
1) 360; 2) 160; 3) 310; 4) 180.
Ответ: ________
Модуль «Геометрия»
9. Найдите угол ADC равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной АВ углы, равные 30° и 40° соответственно.
Ответ: ____________
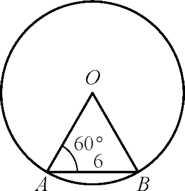
10. Центральный угол АОВ опирается на хорду АВ длиной 6. При этом угол ОАВ равен 60°. Найдите радиус окружности.
Ответ: _________
11. Найдите площадь параллелограмма, изображённого на рисунке.

5 4
3 7
Ответ: _________
12. Найдите тангенс угла А треугольника ABC , изображённого на рисунке
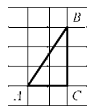
Ответ:__________
13. Укажите номера верных утверждений.
1) Если три стороны одного треугольника пропорциональны трём сторонам другого треугольника, то такие треугольники подобны.
2) Сумма смежных углов равна 1800.
3) Любая высота равнобедренного треугольника является его биссектрисой.
Ответ: _____________
Модуль «Реальная математика»
14. Бизнесмен Соловьёв выезжает из Москвы в Санкт- Петербург на деловую встречу, которая назначена на 10:00. В таблице дано расписание ночных поездов Москва – Санкт-Петербург.
|
Номер поезда |
Отправление из Москвы |
Прибытие в Санкт-Петербург |
|
038А |
00:43 |
08:45 |
|
020У |
00:54 |
09:00 |
|
016А |
01:00 |
08:38 |
|
030А |
01:10 |
09:37 |
Путь от вокзала до места встречи занимает полчаса. Укажите номер самого позднего (по времени отправления) из московских поездов, которые подходят учёному Иванову.
1)038А; 2) 020У; 3) 016А; 4) 030А.
Ответ: _
15. На рисунке изображён график изменения атмосферного давления в городе Энске за три дня. По горизонтали указаны дни недели, по вертикали — значения атмосферного давления в миллиметрах ртутного столба. Укажите наибольшее значение атмосферного давления во вторник.
762
758
754

вторник среда четверг
Ответ: __________
16. Чашка, которая стоила 90 рублей, продаётся с 10%-й скидкой. При покупке 10 таких чашек покупатель отдал кассиру 1000 рублей. Сколько рублей сдачи он должен получить?
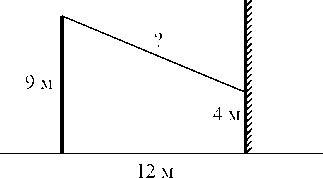
17. От столба высотой 9 м к дому натянут провод, который крепится на высоте
4м от земли (см. рисунок). Расстояние от дома до столба 12 м. Вычислите длину провода.
Ответ: ________________
18. На диаграмме представлено распределение количества пользователей некоторой социальной сети по странам мира. Всего в этой социальной сети 9 млн. пользователей.
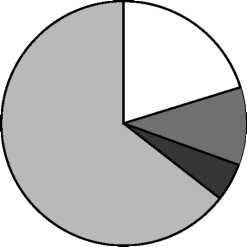



— Другие страны
Какое из следующих утверждений неверно?
-
Пользователей из Беларуси меньше, чем пользователей из Украины.
-
Пользователей из России больше 4 миллионов.
-
Пользователей из Украины больше четверти общего числа пользователей.
-
Пользователей из Беларуси больше, чем пользователей из Финляндии.
В ответе запишите номер выбранного утверждения.
Ответ: _________________
19. Найдите размах ряда чисел 21, 18, 35, 4, 16, 39, 11
Ответ: _____________
20. Найдите медиану ряда чисел 1, 12, 5, 17, 2, 8, 11, 7.
Ответ: ______________
Часть 2
При выполнении заданий 21-26 используйте бланк ответов № 2. Сначала укажите номер задания, а затем запишите его решение и ответ. Пишите чётко и разборчиво. Обращаем Ваше внимание на то, что записи в черновике не будут учитываться при оценивании работы.
21. Найдите наименьшее значение выражения (2х + у + 3)2 + (3х – 2у + 
Ответ:__________
22. При каких значениях параметра в уравнение (в + 1)х2 + вх – 1 = 0 имеет единственный корень?
Ответ: ______________
23. Решите уравнение: .
Ответ: ____________
24. Упростите выражение:
Ответ: ___________
25. Прямая MN касается окружности с центром в точке О, М – точка касания, ےMNO=30о, а радиус окружности равен 5см. Найдите NO.
Ответ: __________
26. Найдите площадь равнобедренного треугольника, боковая сторона которого равна 13 см, а основание 10 см.
Просмотр содержимого документа
«ОТВЕТЫ»
ОТВЕТЫ
|
№ |
Вар 1 |
Вар 2 |
Вар 3 |
Вар 4 |
Вар 5 |
|
1 |
2,25 |
1,5 |
1,6 |
1,75 |
6,625 |
|
2 |
2 |
1 |
1 |
2 |
2 |
|
3 |
1 |
4 |
2 |
4 |
4 |
|
4 |
-9; 2 |
-5; 3 |
-6; 3 |
-2; 7 |
1; 3 |
|
5 |
2 4 3 |
1 3 2 |
4 3 1 |
3 4 2 |
3 1 2 |
|
6 |
-11 |
-1 |
-2 |
10 |
1 |
|
7 |
8 |
15 |
6 |
10 |
48,5 |
|
8 |
2 |
2 |
2 |
1 |
4 |
|
9 |
110 |
120 |
80 |
70 |
105 |
|
10 |
5 |
7 |
3 |
4 |
6 |
|
11 |
40 |
28 |
20 |
44 |
75 |
|
12 |
0,4 |
1,5 |
0,75 |
2,5 |
3,5 |
|
13 |
1 2 |
2 |
1 2 |
1 3 |
2 3 |
|
14 |
2 |
1 |
2 |
2 |
3 |
|
15 |
751 |
753 |
755 |
761 |
755 |
|
16 |
190 |
280 |
140 |
230 |
50 |
|
17 |
10 |
13 |
15 |
17 |
9 |
|
18 |
3 |
1 |
3 |
4 |
4 |
|
19 |
14 |
68 |
7,5 |
35 |
23 |
|
20 |
41 |
13 |
0,5 |
41 |
7,5 |
|
21 |
0, х= — 2, у= 1 |
0, х= 2, у= 1 |
0, х= — 3, у= 2 |
0, х= -1, у= -1 |
0, х= 4, у= -3 |
|
22 |
-6;-3 |
-2;-1 |
-1,5; 0; 3 |
-3; 0; 3 |
-1 |
|
23 |
2 |
2 |
-4 |
-2 |
1 |
|
24 |
|
-4 |
1 |
1 |
2 |
|
25 |
15 |
16 |
30 |
10 |
10 |
|
26 |
60 |
32 |
22,1 |
60 |
72 |
Просмотр содержимого документа
«вариант 2»
Итоговая аттестация
учащихся 8 класса по МАТЕМАТИКЕ
Вариант № 1302
Часть 1
• Для заданий с выбором ответа (2, 3, 8, 14) из четырёх предложенных вариантов выберите один верный.
В бланке ответов № 1 поставьте знак «×» в клеточку, номер которой соответствует номеру выбранного вами ответа.
• Для заданий с кратким ответом полученный результат сначала запишите на листе с текстом работы после слова «Ответ». Если получена обыкновенная дробь, обратите её в десятичную.
Перенесите ответ в бланк ответов № 1 справа от номера соответствующего задания, начиная с первой клеточки. Каждый символ (цифру, знак минус, запятую или точку с запятой) пишите в отдельной клеточке в соответствии с приведёнными в бланке образцами. Единицы измерений указывать не нужно.
-
Если при решении задания 4 найдено несколько корней, запишите их (в любом порядке) в бланк ответов № 1, разделив точкой с запятой (;).
Ответом к заданиям 5 и 13 является последовательность цифр. Перенесите цифры в бланк № 1 без пробелов, запятых и других символов.
Модуль «Алгебра»
-
Найдите значение выражения:
.
Ответ: __________________
-
На координатной прямой отмечены числа а и с.
а с
• •
-1 0 1

1) а – с 0;
2) -3 а + 1
3) –с -1;
4) 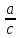
Ответ: __________
3. В каком случае числа 4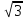
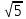
1) 7; 4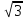
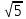
2) 4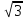
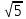
3) 3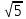
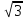
4) 3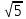
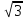
Ответ: _____________
4. Решите уравнение: х2 +2х – 15 = 0.
Ответ: _____________________
5. Установите соответствие между графиками функций и формулами, которые их задают.
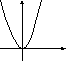
А)
-
у = х2; 2) у = —
; 3) у = 2х; 4) у=
..
Ответ:
|
А |
Б |
В |
6. Найдите наибольшее целое решение неравенства: 4у – 9 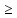
Ответ: _____________
7. Упростите выражение (а — 4)2-2а(5а -4) и найдите его значение при а =- 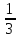
Ответ: _______________
8. В цехе работают 50 человек, 40 человек из них составляет молодёжь. Сколько процентов составляет молодёжь?
1) 92; 2) 80; 3) 0,8; 4) 60.
Модуль «Геометрия»
9. Найдите угол ABC равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной CD углы, равные 20° и 100° соответственно.
Ответ; __________________
10. Центральный угол АОВ равен 60°. Найдите длину хорды АВ, на которую он опирается, если радиус окружности равен 7.
Ответ: ___________
11. Найдите площадь параллелограмма, изображённого на рисунке
Ответ: ________________
12. Найдите тангенс угла А треугольника ABC , изображённого на рисунке
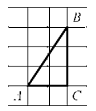
Ответ: _______________
13. Укажите номера верных утверждений.
-
Если три угла одного треугольника равны трем углам другого треугольника, то такие треугольники подобны.
-
Сумма смежных углов равна 180° .
-
Любая медиана равнобедренного треугольника является его биссектрисой.
Ответ: _______________
Модуль «Реальная математика»
14. Бизнесмен Петров выезжает из Москвы в Санкт- Петербург на деловую встречу, которая назначена на 9:30. В таблице дано расписание ночных поездов Москва – Санкт-Петербург.
|
Номер поезда |
Отправление из Москвы |
Прибытие в Санкт-Петербург |
|
038А |
00:43 |
08:45 |
|
020У |
00:54 |
09:02 |
|
016А |
01:00 |
08:38 |
|
116С |
01:00 |
09:06 |
Путь от вокзала до места встречи занимает полчаса. Укажите номер самого позднего (по времени отправления) из московских поездов, которые подходят учёному Иванову.
1)038А; 2) 020У; 3) 016А; 4) 116С.
Ответ: _________
15. На рисунке изображён график изменения атмосферного давления в городе Энске за три дня. По горизонтали указаны дни недели, по вертикали — значения атмосферного давления в миллиметрах ртутного столба. Укажите наименьшее значение атмосферного давления в среду.
762



750 вторник среда четверг
Ответ: _______________________
16. Тарелка, которая стоила 80 рублей, продаётся с 10% — ой скидкой. При покупке 10 таких тарелок покупатель отдал кассиру 1000 рублей. Сколько рублей сдачи он должен получить?
Ответ: ___________________
17. От столба высотой 9 м к дому натянут провод, который крепится на высоте
4м от земли (см. рисунок). Расстояние от дома до столба 12 м. Вычислите длину провода.
Ответ: ________________
18. На диаграмме представлено распределение количества пользователей некоторой социальной сети по странам мира. Всего в этой социальной сети 9 млн. пользователей.
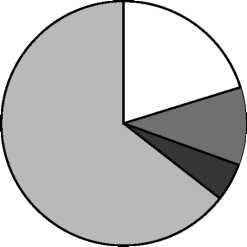




Какое из следующих утверждений неверно?
-
Пользователей из России меньше 4 миллионов.
-
Пользователей из Украины меньше трети общего числа пользователей.
-
Пользователей из Беларуси больше, чем пользователей из Дании.
-
Пользователей из России больше, чем пользователей из Беларуси.
В ответе запишите номер выбранного утверждения.
Ответ: _________________
19. Найдите размах ряда чисел 3, 17, 24, 9, 15, 71, 56.
Ответ: ______________
20. . Найдите моду ряда чисел 18, 23, 13, 14, 13, 15, 13, 72.
Ответ: ______________
Часть 2
При выполнении заданий 21-26 используйте бланк ответов № 2. Сначала укажите номер задания, а затем запишите его решение и ответ. Пишите чётко и разборчиво. Обращаем Ваше внимание на то, что записи в черновике не будут учитываться при оценивании работы.
21. Найдите наименьшее значение выражения (2х — 3у — 1)2 + (3х + у — 7)2 и значения х и у, при которых оно достигается.
Ответ: _______________
22. При каких значениях параметра в уравнение (в + 1)х2 + вх – 1 = 0 имеет единственный корень?
Ответ: ______________
23. Решите уравнение: 
Ответ: ______________
24. Упростите выражение: 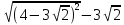
Ответ: ____________
25. Хорды MN и KP пересекаются в точке Т. Найдите MN, если КТ=6см, РТ=8см, а длина МТ в три раза меньше длины NT.
Ответ: ______________
26. Сторона ромба равна 8 см, а один из углов равен 150о Найдите площадь ромба.
Ответ: _______________
Просмотр содержимого документа
«вариант 4»
Итоговая аттестация
учащихся 8 класса по МАТЕМАТИКЕ
Вариант № 1304
Часть 1
• Для заданий с выбором ответа (2, 3, 8, 14) из четырёх предложенных вариантов выберите один верный.
В бланке ответов № 1 поставьте знак «×» в клеточку, номер которой соответствует номеру выбранного вами ответа.
• Для заданий с кратким ответом полученный результат сначала запишите на листе с текстом работы после слова «Ответ». Если получена обыкновенная дробь, обратите её в десятичную.
Перенесите ответ в бланк ответов № 1 справа от номера соответствующего задания, начиная с первой клеточки. Каждый символ (цифру, знак минус, запятую или точку с запятой) пишите в отдельной клеточке в соответствии с приведёнными в бланке образцами. Единицы измерений указывать не нужно.
-
Если при решении задания 4 найдено несколько корней, запишите их (в любом порядке) в бланк ответов № 1, разделив точкой с запятой (;).
Ответом к заданиям 5 и 13 является последовательность цифр. Перенесите цифры в бланк № 1 без пробелов, запятых и других символов.
Модуль «Алгебра»
-
Найдите значение выражения:
.
Ответ: __________________
2. На координатной прямой отмечены числа а и в
а в

-1 0 1
Какое из следующих утверждений неверно?
1) -4 а – 1
2) –в
3) а + в
4) а2в
Ответ: _____________
3. В каком случае числа 2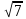

1) 2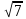

2) 4
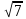
3) 4
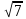
4) 5; 2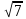

Ответ? ____________
4. Решите уравнение: х2 — 5х – 14 = 0.
Ответ: _____________________
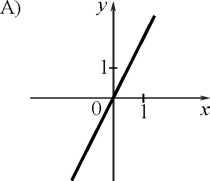
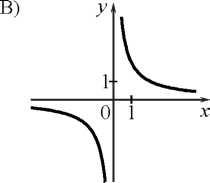
5. Установите соответствие между графиками функций и формулами, которые их задают.
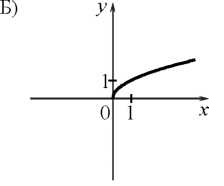
-
у=х2: 2) у =
; 3) у = 2х: 4) у=
.
Ответ:
|
А |
Б |
В |
6. Найдите наибольшее целое решение неравенства: 5(х + 2) – х 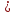
Ответ: ___________
7. Упростите выражение (а + 3)2-2а(3 -4а) и найдите его значение при а =- 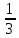
Ответ: _____________
8. В сплаве меди и цинка меди содержится 12%. Масса сплава 1200 г. Сколько в смеси цинка?
1) 1056; 2) 956; 3) 144; 4) 1000.
Ответ: ______________
Модуль «Геометрия»
9. Найдите угол ADC равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной АВ углы, равные 30° и 40° соответственно.
Ответ: ____________
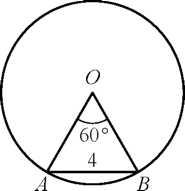
10. Центральный угол АОВ, равный 60°, опирается на хорду АВ длиной 4. Найдите радиус окружности.
Ответ: ____________
11. Найдите площадь параллелограмма, изображённого на рисунке

5 4
3 8
Ответ: __________
12. Найдите тангенс угла В треугольника ABC , изображённого на рисунке.
Ответ: _____________
13. Укажите номера верных утверждений.
1) Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то треугольники подобны.
2) Смежные углы равны.
3) Медиана равнобедренного треугольника, проведённая к его основанию, является его высотой
Ответ: ____________
Модуль «Реальная математика»
14. Бизнесмен Соловьёв выезжает из Москвы в Санкт- Петербург на деловую встречу, которая назначена на 10:00. В таблице дано расписание ночных поездов Москва – Санкт-Петербург.
|
Номер поезда |
Отправление из Москвы |
Прибытие в Санкт-Петербург |
|
038А |
00:43 |
08:45 |
|
020У |
00:54 |
09:00 |
|
016А |
01:00 |
08:38 |
|
030А |
01:10 |
09:37 |
Путь от вокзала до места встречи занимает полчаса. Укажите номер самого позднего (по времени отправления) из московских поездов, которые подходят учёному Иванову.
1)038А; 2) 020У; 3) 016А; 4) 030А.
Ответ: _
15. На рисунке изображён график изменения атмосферного давления в городе Энске за три дня. По горизонтали указаны дни недели, по вертикали — значения атмосферного давления в миллиметрах ртутного столба. Укажите наибольшее значение атмосферного давления за данные три дня.
762
760
758
756
754
752
750
Ответ: _
16. Ложка, которая стоила 30 рублей, продаётся с 10% — ой скидкой. При покупке 10 таких ложек покупатель отдал кассиру 500 рублей. Сколько рублей сдачи он должен получить?
Ответ: ___________________
________
17. От столба высотой 12 м к дому натянут провод, который крепится на высоте
4м от земли (см. рисунок). Расстояние от дома до столба 15 м. Вычислите длину провода.
15 м
18. На диаграмме представлено распределение количества пользователей некоторой социальной сети по странам мира. Всего в этой социальной сети 9 млн. пользователей.
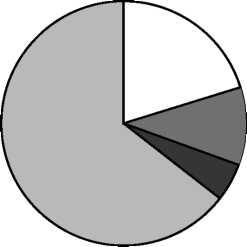




Какое из следующих утверждений неверно?
-
Пользователей из Украины больше, чем пользователей из Беларуси.
-
Пользователей из Украины меньше четверти общего числа пользователей.
-
Пользователей из Беларуси больше, чем пользователей из Эстонии.
-
Пользователей из России больше 8 миллионов.
В ответе запишите номер выбранного утверждения.
Ответ: _________________
19. Найдите размах ряда чисел 21, 18, 35, 4, 16, 39, 11
Ответ: _____________
20. Найдите медиану ряда чисел 32, 41, 49, 30, 37, 42, 40, 45, 52.
Ответ: ______________
Часть 2
При выполнении заданий 21-26 используйте бланк ответов № 2. Сначала укажите номер задания, а затем запишите его решение и ответ. Пишите чётко и разборчиво. Обращаем Ваше внимание на то, что записи в черновике не будут учитываться при оценивании работы.
___
21. Найдите наименьшее значение выражения (4х — 3у + 1)2 + (х – 5у — 4)2 и значения х и у, при которых оно достигается.
Ответ: _________
22. При каких значениях параметра к уравнение кх2 – 6х + к = 0 имеет единственный корень?
Ответ: __________
23. Решите уравнение: 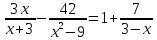
Ответ: _________
24. Упростите выражение: 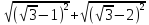
Ответ: ___________
25. Прямая КЕ касается окружности с центром в точке О, К – точка касания. Найдите ОЕ, если КЕ=8см, а радиус окружности равен 6см.
Ответ: ___________
26. Диагональ прямоугольника равна 13 см, а одна из сторон равна 5 см. Найдите площадь прямоугольника.
Просмотр содержимого документа
«вариант 5»
Итоговая аттестация
учащихся 8 класса по МАТЕМАТИКЕ
Вариант № 1305
Часть 1
• Для заданий с выбором ответа (2, 3, 8, 14) из четырёх предложенных вариантов выберите один верный.
В бланке ответов № 1 поставьте знак «×» в клеточку, номер которой соответствует номеру выбранного вами ответа.
• Для заданий с кратким ответом полученный результат сначала запишите на листе с текстом работы после слова «Ответ». Если получена обыкновенная дробь, обратите её в десятичную.
Перенесите ответ в бланк ответов № 1 справа от номера соответствующего задания, начиная с первой клеточки. Каждый символ (цифру, знак минус, запятую или точку с запятой) пишите в отдельной клеточке в соответствии с приведёнными в бланке образцами. Единицы измерений указывать не нужно.
-
Если при решении задания 4 найдено несколько корней, запишите их (в любом порядке) в бланк ответов № 1, разделив точкой с запятой (;).
Ответом к заданиям 5 и 13 является последовательность цифр. Перенесите цифры в бланк № 1 без пробелов, запятых и других символов.
Модуль «Алгебра»
-
Найдите значение выражения:
.
Ответ: __________________
-
На координатной прямой отмечены числа х и у.

х 0 у
Какое из приведённых утверждений неверно?
1) ху
2) у – х
3) х2у 0;
4) х + у 0.
Ответ: __________
-
Значение какого из данных выражений является наибольшим?
-
; 2)
/
; 3)
•
; 4) 2
.
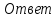
-
Решите уравнение: х2 — 4х + 3 = 0.
Ответ: _________
-
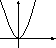
Установите соответствие между графиками функций и формулами, которые их задают.
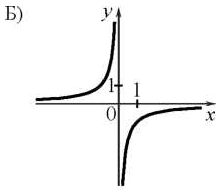
В)
-
у = —
; 2) у=х2; 3) у = 2х + 4; 4) у=
..
Ответ
|
А |
Б |
В |
6. Найдите наименьшее целое решение неравенства: 3х + 1 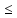
Ответ: __________
7. Упростите выражение (а — 7)2-а(3а — 14) и найдите его значение при а = — 0,5. В ответ запишите найденное значение.
Ответ: ______
8. Юннаты собрали 180 кг семян акации и клёна. Семена акации составили 20% всех собранных семян. Сколько семян клёна собрали юннаты?
1) 160; 2) 36; 3) 154; 4) 144.
Ответ: ________
Модуль «Геометрия»
9. Найдите больший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной АВ углы, равные 30° и 45° соответственно.
Ответ: __________
10. Центральный угол АОВ опирается на хорду АВ длиной 6. При этом угол ОАВ равен 60°. Найдите радиус окружности.
Ответ: _________
11. Найдите площадь параллелограмма, изображённого на рисунке.
Ответ: __________
12. Найдите тангенс угла В треугольника ABC , изображённого на рисунке.
Ответ: _____________
13. Укажите номера верных утверждений.
1) Существует квадрат, который не является прямоугольником.
2) Если два угла треугольника равны, то равны и противолежащие им стороны.
3) Внутренние накрест лежащие углы, образованные двумя параллельными прямыми и секущей, равны.
Ответ: _____________
14. Студентка Цветкова выезжает из Наро-Фоминска в Москву на занятия в университет. Занятия начинаются в 9:00. В таблице приведено расписание утренних электропоездов от станции Нара до Киевского вокзала в Москве.
|
Отправление от ст. Нара |
Прибытие на Киевский вокзал |
|
6:17 |
7:13 |
|
6:29 |
7:50 |
|
6:35 |
7:59 |
|
7:05 |
8:23 |
Путь от вокзала до университета занимает 45 минут. Укажите время отправления от станции Нара самого позднего из электропоездов, которые подходят студентке.
1) 6:17 2) 6:29 3) 6:35 4) 7:05
Ответ: _____
15. На рисунке изображён график изменения атмосферного давления в городе Энске за три дня. По горизонтали указаны дни недели, по вертикали — значения атмосферного давления в миллиметрах ртутного столба. Укажите наибольшее значение атмосферного давления во вторник.
762
758
754

вторник среда четверг
Ответ: __________
16. Альбом, который стоил 120 рублей, продаётся с 25% — ой скидкой. При покупке 5 таких альбомов покупатель отдал кассиру 500 рублей. Сколько рублей сдачи он должен получить?
Ответ: ___________________
17. От столба к дому натянут провод длиной 10 м, который закреплён на стене дома на высоте 3 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 8 м.
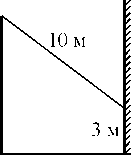
?
8м
Ответ: _______________
18. На диаграмме представлено распределение количества пользователей некоторой социальной сети по странам мира. Всего в этой социальной сети 12 млн. пользователей.
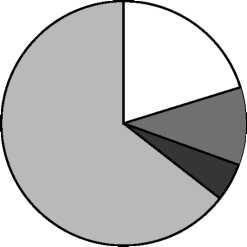




Какое из следующих утверждений неверно?
-
Пользователей из России больше, чем пользователей из Украины и Беларуси вместе.
-
Пользователей из Украины больше, чем пользователей из Латвии.
-
Примерно две трети общего числа пользователей – из России.
-
Пользователей из Украины больше 3 миллионов.
В ответе запишите номер выбранного утверждения.
Ответ: _________________
19. Найдите моду ряда чисел 58, 23, 25, 28, 23, 15, 14, 75.
Ответ: _____________
20. Найдите медиану ряда чисел 1, 12, 5, 17, 2, 8, 11, 7.
Ответ: ______________
Часть 2
При выполнении заданий 21-26 используйте бланк ответов № 2. Сначала укажите номер задания, а затем запишите его решение и ответ. Пишите чётко и разборчиво. Обращаем Ваше внимание на то, что записи в черновике не будут учитываться при оценивании работы.
21. Найдите наименьшее значение выражения (2х + 5у + 7)2 + (3х – у — 15)2 и значения х и у, при которых оно достигается.
Ответ: ________
22. При каком значении параметра в уравнение (в + 5)х2 + (2в + 10)х + 4 = 0 имеет только один корень?
Ответ: _______
23. Решите уравнение: 
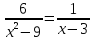
Ответ: _________
24. Упростите выражение: 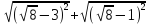
Ответ: ________
25. Прямая MN касается окружности с центром в точке О, М – точка касания, ےMNO=30о, а радиус окружности равен 5см. Найдите NO.
Ответ: __________
26. Сторона ромба равна 12 см, а один из углов равен 120о Найдите площадь ромба.
Просмотр содержимого документа
«вариант1»
Итоговая аттестация
учащихся 8 класса по МАТЕМАТИКЕ
Вариант № 1301
Часть 1
• Для заданий с выбором ответа (2, 3, 8, 14) из четырёх предложенных вариантов выберите один верный.
В бланке ответов № 1 поставьте знак «×» в клеточку, номер которой соответствует номеру выбранного вами ответа.
• Для заданий с кратким ответом полученный результат сначала запишите на листе с текстом работы после слова «Ответ». Если получена обыкновенная дробь, обратите её в десятичную.
Перенесите ответ в бланк ответов № 1 справа от номера соответствующего задания, начиная с первой клеточки. Каждый символ (цифру, знак минус, запятую или точку с запятой) пишите в отдельной клеточке в соответствии с приведёнными в бланке образцами. Единицы измерений указывать не нужно.
-
Если при решении задания 4 найдено несколько корней, запишите их (в любом порядке) в бланк ответов № 1, разделив точкой с запятой (;).
Ответом к заданиям 5 и 13 является последовательность цифр. Перенесите цифры в бланк № 1 без пробелов, запятых и других символов.
Модуль «Алгебра»
-
Найдите значение выражения: (6,9 – 1,5) / 2,4.
Ответ: ___________________
-
На координатной прямой отмечены числа а и в
а в

-1 0 1
Какое из следующих утверждений неверно?
1) -2 в – 1
2) –а
3) а + в
4) а2в
Ответ: ______________
3. В каком случае числа 2
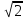
1) 2
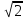
2) 2
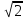
3) 3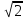

4) 4; 2
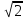
Ответ? ____________
4. Решите уравнение: х2 +7х – 18 = 0.
Ответ: _____________________
5. Установите соответствие между графиками функций и формулами, которые их задают.
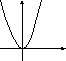
В)
-
1) У=
; 2) У=
; 3) у=х2; 4) у=
.
|
А |
Б |
В |
6. Найдите наибольшее целое решение неравенства: 3х – 1 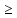
Ответ: ___________________
7. Упростите выражение (а — 3)2-а(5а -6) и найдите его значение при а = — 0,5. В ответ запишите найденное значение.
8. В классе обучается 30 человек. С контрольной работой справились 90% учащихся. Сколько человек не справились с контрольной работой?
27; 2) 3; 3) 9; 4) 5.
Модуль «Геометрия»
9. Найдите угол ABC равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной CD углы, равные 30° и 80° соответственно.
Ответ: ____________________
10. Центральный угол АОВ равен 60°. Найдите длину хорды АВ, на которую он опирается, если радиус окружности равен 5.
Ответ: _____________________
11. Найдите площадь параллелограмма, изображённого на рисунке.

5 4
3 7
Ответ: __
12. Найдите тангенс угла А треугольника ABC , изображённого на рисунке.
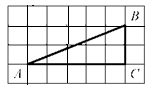

13. Укажите номера верных утверждений.
1) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
-
Вертикальные углы равны.
-
Любая биссектриса равнобедренного треугольника является его медианой.
Модуль «Реальная математика»
14. Учёный Иванов выезжает из Москвы на конференцию в Санкт- Петербургский университет. Работа конференции начинается в 10:00. В таблице дано расписание ночных поездов Москва – Санкт-Петербург.
|
Номер поезда |
Отправление из Москвы |
Прибытие в Санкт-Петербург |
|
026А |
23:00 |
06:30 |
|
002А |
23:55 |
07:55 |
|
038А |
00:44 |
08:48 |
|
016А |
01:00 |
08:38 |
Путь от вокзала до университета занимает полтора часа. Укажите номер самого позднего (по времени отправления) из московских поездов, которые подходят учёному Иванову.
-
026А 2) 002А 3) 038А 4) 016А.
15. На рисунке изображён график изменения атмосферного давления в городе Энске за три дня. По горизонтали указаны дни недели, по вертикали — значения атмосферного давления в миллиметрах ртутного столба. Укажите наименьшее значение атмосферного давления во вторник.
762
760
758
756
754
752
750
16. Чашка, которая стоила 90 рублей, продаётся с 10%-й скидкой. При покупке 10 таких чашек покупатель отдал кассиру 1000 рублей. Сколько рублей сдачи он должен получить?
17. От столба высотой 9 м к дому натянут провод, который крепится на высоте 3м от земли (см. рисунок). Расстояние от дома до столба 8 м. Вычислите длину провода.
8м
18. На диаграмме представлено распределение количества пользователей некоторой социальной сети по странам мира. Всего в этой социальной сети 8млн пользователей.
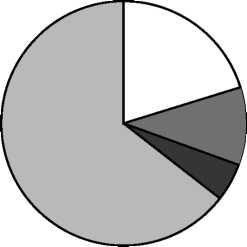



— Беларусь

Какое из следующих утверждений неверно?
-
Пользователей из России больше, чем пользователей из Украины.
-
Пользователей из Беларуси больше, чем пользователей из Швеции.
-
Больше трети пользователей сети — из Украины.
-
Пользователей из России больше 4 миллионов.
В ответе запишите номер выбранного утверждения.
Ответ:__________
19. Найдите моду ряда чисел 8, 23, 25, 14, 13, 15, 14, 71.
Ответ: _______
20. Найдите медиану ряда чисел 32, 41, 49, 30, 37, 42, 40, 45, 52.
Ответ: ____
ЧАСТЬ 2 на следующей странице
Часть 2
При выполнении заданий 21-26 используйте бланк ответов № 2. Сначала укажите номер задания, а затем запишите его решение и ответ. Пишите чётко и разборчиво. Обращаем Ваше внимание на то, что записи в черновике не будут учитываться при оценивании работы.
21. Найдите наименьшее значение выражения (2х + у + 3)2 + (3х – 2у + 
Ответ:__________
22. При каких значениях параметра а уравнение (3а + 9)х2 + ах – 1 = 0 имеет единственный корень?
Ответ: __________
23. Решите уравнение:
Ответ: _________
24. Упростите выражение: .
Ответ: _____________
25. Хорды АВ и CD пересекаются в точке Е. Найдите CD, если АЕ=4см, ВЕ=9см, а длина СЕ в четыре раза больше длины DE.
Ответ: ____________
26. Найдите площадь равнобедренного треугольника, боковая сторона которого равна 13 см, а основание 10 см.
Ответ: ____________
Промежуточная аттестация по математике за курс 8 класса
Ф.И._______________________________________________
ВАРИАНТ 1.
Модуль «Алгебра».
1. Найдите значение выражения 
2. Найдите значение выражения
1) 2

3.Найдите корни уравнения 
|
4. На рисунках изображены графики функций вида y=kx+b. Установите соответствие между графиками функций и знаками коэффициентов k и b. |
|
А Б В .
5. Найдите значение выражения 

Модуль «Геометрия».
6. Найдите больший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной АВ углы, равные 30° и 45° соответственно. Ответ дайте в градусах

7. Найдите тангенс угла С треугольника ABC, изображённого на рисунке.

|
8. Какие из данных утверждений верны? Запишите их номера. |
|||||||||
|
Модуль «Реальная математика»
9. На графике изображена зависимость атмосферного давления от высоты
над уровнем моря. По горизонтали указана высота над уровнем моря
в километрах, по вертикали — атмосферное давление в миллиметрах ртутного столба. На какой высоте (в км) летит воздушный шар, если барометр, находящийся в корзине шара, показывает давление 220 миллиметров ртутного столба?
|
10. На диаграмме показано содержание питательных веществ в фасоли. Определите по диаграмме, содержание каких веществ превосходит 50%.
*к прочему относятся вода, витамины и минеральные вещества |
|
|
|
11.Куриные яйца в зависимости от их массы подразделяют на пять категорий: высшая, отборная, первая, вторая и третья. Используя данные, представленные в таблице, определите, к какой категории относится яйцо массой 62,2 г.
Ответ:____________ |
Промежуточная аттестация по математике за курс 8 класса
Ф.И._______________________________________________
ВАРИАНТ 2.
1.Найдите значение выражения 
2. .Найдите значение выражения
1) 5

3.Решите уравнение 
|
4.На рисунках изображены графики функций вида y=kx + b. Установите соответствие между графиками функций и знаками коэффициентов k и b. |
|
.А Б В
5. Найдите значение выражения 

Модуль «Геометрия».
6.Найдите больший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной АВ углы, равные 25° и 40° соответственно. Ответ дайте в градусах.

7.Найдите тангенс угла А треугольника ABC, изображённого на рисунке.
Ответ:__________
|
8.Укажите номера верных утверждений. |
|||||||||
|
Модуль «Реальная математика»
9.На графике изображена зависимость атмосферного давления от высоты
над уровнем моря. По горизонтали указана высота над уровнем моря
в километрах, по вертикали — атмосферное давление в миллиметрах ртутного столба. На какой высоте (в км) летит воздушный шар, если барометр, находящийся в корзине шара, показывает давление 720 миллиметров ртутного столба?
10. На диаграмме показан возрастной состав населения Индонезии. Определите по диаграмме, население какого возраста преобладает.
1. 0-14 лет 2. 15-50 лет 3. 51-64 лет 4. 65 лет и более
11. Куриные яйца в зависимости от их массы подразделяют на пять категорий: высшая, отборная, первая, вторая и третья. Используя данные, представленные в таблице, определите, к какой категории относится яйцо массой 72,5 г.
|
Категория |
Масса одного яйца, не менее, г |
|
Высшая |
75,0 |
|
Отборная |
65,0 |
|
Первая |
55,0 |
|
Вторая |
45,0 |
|
Третья |
35,0 |
Ответ:___________
12 сентября 2020
В закладки
Обсудить
Жалоба
Четыре варианта по математике для проведения пробного ОГЭ для учеников 8 класса.
Тесты содержат 20 задач в первой части и 3 задачи во второй части, все задания соответствуют изученному курсу 5-8 класса. Для составления тестов были использован открытый банк заданий ФИПИ.
Без ответов.
8m-oge.pdf
Автор: Ибрагимова Сония Равиловна, учитель математики.
И т о г о в а я р а б о т а п о м а т е м а т и к е ( п р о м е ж у т о ч н а я а т т ест аци я в ф ор ме О Г Э ), 8 к ласс .
Вариант 1 Часть 1
1. Найти значение выражения
+0,09
2. Выберите неверное равенство: 1)
( )
.44)4;10166)3;9,081,0)2;39
2
−=−=+==
3. Установите соответствие между графиками функций и формулами, которые их задают.
1) у=2х 2) у=—2х 3) у=х+2 4) у=2 5) у = х
2
4. Упростите выражение
; 4)2.
5. Решите уравнение х
2
+3х—4=0.Найдите среднее арифметическое корней. 1)1. 2) -1,5. 3) —3. 4) нет корней.
6. Решите систему уравнений:
1) (- 3; 1); 2) (3; 1); 3) (1; — 3); 4) (- 1; — 3).
7. Решить неравенство и выбрать, на каком рисунке изображено множество его решений.
8. Решите систему неравенств:
Часть 2 модуль
«Геометрия»
9.
Найдите площадь
ромба, если его
диагонали равны
315 и 2.
10. На какое расстояние
следует отодвинуть от
стены дома нижний конец
лестницы, длина которой 13
м, чтобы верхний ее конец
оказался на высоте 12 м?
11. Найдите площадь трапеции,
изображенной на рисунке.
12. Найдите тангенс
угла А треугольника ABC,
изображенного на рисунке.
Модуль «Реальная
математика».
13. В фирме такси в данный момент
свободно 20 машин: 9 черных, 4 желтых
и 7 зеленых. По вызову выехала
одна из машин, случайно оказавшаяся
ближе всего к заказчику. Найдите
вероятность того, что к нему приедет
желтое такси.
14. Куриные яйца в зависимости от их массы подразделяют на 5
категорий. Используя данные, представленные в таблице,
определите, к какой категории относится яйцо, массой 65,8 г.
1) Высшая. 2) Отборная. 3) Первая. 4) Вторая.
Часть 2. Модуль «Алгебра» (запишите полное решение и ответ)
15. Найдите отрицательный корень уравнения 2х
2
+72=0
16. Решите уравнение:
.
17. Найти значения а, при которых уравнение
не имеет корней
18. Решите систему уравнений:
2
2 3,
2 2.
y x x
yx
= + −
=−
19. Два лесоруба, работая вместе, выполнили норму вырубки за 4 дня. Сколько дней нужно на выполнение
этой работы каждому лесорубу отдельно, если первому для вырубки нормы нужно на 6 дней меньше, чем
другому?
И т о г о в а я р або та по а л г е б р е . 8 к л а сс. Вариант 2. Часть 1.
1. Найти значение выражения 0,08+
2. Выберите неверное равенство: 1)
( )
.1515)4;2257)3;2,04,0)2;416
2
=−=−==
3.Установите соответствие между графиками функций и формулами, которые их
задают
1) у =
2) у = | х | 3) у=х+2 4) у=2 5) у = х
2
4. Упростите выражение
; 4)2.
5. Решите уравнение х
2
—7х+10=0. Найдите среднее арифметическое корней. 1) -3,5 2) 2 3) 3,5 4)
нет корней
6. Решите систему уравнений:
1) ( 2; 1); 2) (2; 0); 3) (1; 2) ; 4) (1; 2).
7. Решить неравенство 1) (− ∞; 
8. Решите систему неравенств:
Модуль
«Геометрия»
9. Найти
площадь
прямоугольного
треугольника,
если его катеты
равны 5 и 12
см.
10. Лестницу длиной 3 м
прислонили к дереву. На какой
высоте (в метрах) находится
верхний её конец, если нижний
конец отстоит от ствола дерева на
1,8 м?
11. Найдите площадь
трапеции, изображенной на
рисунке.
12. Найдите тангенс
угла AOB, изображенного на
рисунке.
Модуль «Реальная математика». 13. У бабушки 20 одинаковых по форме пирогов: 10 с
капустой, остальные с вареньем. Бабушка достает случайно выбранный пирог. Найдите вероятность того,
что это будет пирог с вареньем.
14. В таблице приведены нормативы по бегу на 30 метров для учащихся 9—х классов. Какую отметку
получит девочка, пробежавшая эту дистанцию за 5,36 секунды? 1) «5». 2) «4». 3) «3». 4) Норматив не
выполнен.
Часть 2. 15. Найдите отрицательный корень уравнения 2х
2
+50=0
16. Решите уравнение:
.
17. Найти значения а, при которых уравнение
имеет два различных корня.
18. Решите систему уравнений:
2
3 8 2,
25 8 .
y x x
yx
= − −
=−
19. Один кран наполняет бассейн на 6 часов быстрее другого. Два крана, работая вместе, наполняют
бассейн за 4 часа. За сколько часов может наполнить бассейн каждый кран, работая отдельно.
Ответы
Модуль «Реальная математика»
№ 19. 1 вариант. Пусть – первый лесоруб выполняет норму за х дней.
Участники
совместной работы
Совместная работа 4 дня. Уравнение
.
Одно решение х=-4 не соответствует физической сути задачи. Время второго лесоруба
х+6=6+6=12 (дней). Ответ. Первый лесоруб выполнит работу за 6 дней, а второй за 12 дней.
№ 19. 2 вариант. Один кран наполняет бассейн на 6 часов быстрее другого. Два крана, работая вместе,
наполняют бассейн за 4 часа. За сколько часов может наполнить бассейн каждый кран, работая отдельно.
Уравнение.
, х
2
—2х—24=0, Д=100, х=6 и х=—4 (не подходит). Ответ: 1 кран –за 6 часов, 2 кран—
за 6+6=12 (ч.)
ИТОГОВАЯ КОНТРОЛЬНАЯ РАБОТА ЗА КУРС 8 КЛАССА В ФОРМАТЕ ОГЭ
Спецификация и текст итоговой работы.
- Назначение тестовой работы
Назначение итоговой работы – выявить и оценить степень соответствия подготовки учащихся
8 классов образовательных учреждений требованиям государственного образовательного стандарта основного общего образования по математике.
- Нормативно-правовая база
Документы, определяющие нормативно-правовую базу аттестационной работы:
- Федеральный компонент государственного стандарта общего образования (приказ Минобразования России «Об утверждении федерального компонента государственных стандартов начального общего, основного общего и среднего (полного) общего образования» от 5 марта 2004 года № 1089),
- Закон Российской Федерации «Об образовании».
- Характеристика структуры и содержания работы
Общее количество заданий в работе – 22
Характеристика структуры работы
Всего в работе 22 задания, из которых 18 заданий базового уровня (часть 1), 4 задания повышенного уровня. Работа состоит из двух модулей «Алгебра» и «Геометрия». Модуль «Алгебра» содержит 14 заданий: в части 1 – двенадцать заданий, в части 2 – два задания. Модуль «Геометрия» содержит 8 заданий: в части 1 – шесть заданий, в части 2 – два задания.
Часть 1 предусматривает две формы ответа:
с выбором ответа из четырех предложенных, с кратким ответом.
В части 2 нужно оформить развернутый ответ с записью решения.
Распределение заданий по частям работы
|
Части работы |
Число заданий |
Максимальный первичный балл |
Типы заданий |
|
Часть 1 |
18 |
18 |
с выбором ответа с кратким ответом |
|
Часть 2 |
4 |
8 |
с развернутым ответом |
|
Итого: |
22 |
26 |
- Проверяемые элементы содержания
Содержание и структура теста дают возможность достаточно полно проверить необходимый комплекс знаний и умений по предмету. Большинство заданий содержат элементы содержания, изучаемые в 8 классе.
Перечень элементов предметного содержания, проверяемых на итоговой работе.
|
№ вопроса |
Проверяемое содержание |
|
1.1 |
Арифметические действия с десятичными дробями |
|
1. 2 |
Представление данных в виде таблиц, диаграмм, графиков |
|
1.3 |
Изображение чисел точками координатной прямой. Определение квадратного корня |
|
1.4 |
Свойства квадратных корней и их применение в вычислениях |
|
1. 5 |
Представление данных в виде таблиц, диаграмм, графиков |
|
1.6 |
Квадратное уравнение, формула корней квадратного уравнения |
|
1.7 |
Проценты. Решение задач на проценты. |
|
1.8 |
Представление данных в виде таблиц, диаграмм, графиков |
|
1.9 |
Алгебраическая дробь. Сокращение дробей. Действия с алгебраическими дробями. Рациональные выражения и их преобразования |
|
1.10 |
Буквенные выражения. Числовое значение буквенного выражения |
|
1.11 |
Линейные неравенства с одной переменной |
|
1.12 |
Свойства степени с целым показателем |
|
1.13 |
Прямоугольный треугольник. Теорема Пифагора |
|
1.14 |
Трапеция, средняя линия трапеции; равнобедренная трапеция. Сумма углов треугольника. Сумма углов выпуклого многоугольника |
|
1.15 |
Центральный, вписанный угол; величина вписанного угла |
|
1.16 |
Площадь параллелограмма |
|
1.17 |
Площадь треугольника |
|
1.18 |
Смежные углы. Равнобедренный треугольник. Свойства равнобедренного треугольника. Признаки подобия треугольников |
|
1.19 |
Решение рациональных уравнений |
|
1.20 |
Решение текстовых задач алгебраическим способом |
|
1.21 |
Прямоугольник, квадрат, ромб, их свойства и признаки |
|
1.22 |
Высота, медиана, биссектриса, средняя линия треугольника; точки пересечения серединных перпендикуляров, биссектрис, медиан, высот или их продолжений Сумма углов треугольника. Внешние углы треугольника |
- Проверяемые умения
Перечень требований к уровню подготовки обучающихся, освоивших обязательный минимум содержания образовательной программы по математике за курс 8 класса
|
Код требования |
Требования к уровню подготовки учащихся, достижение которого проверяется на итоговой работе. Уметь: |
|
2. 1 |
Выполнять вычисления и преобразования |
|
2.2 |
Уметь извлекать статистическую информацию, представленную в таблицах |
|
2.3 |
Уметь определять координаты точки плоскости, строить точки с заданными координатами |
|
2. 4 |
Применять свойства арифметических квадратных коней для вычисления значений и преобразования числовых выражений, содержащих квадратные корни |
|
2. 5 |
Интерпретировать графики реальных зависимостей |
|
2. 6 |
Решать квадратное уравнение с помощью формул |
|
2.7 |
Решать задачи на проценты. |
|
2. 8 |
Анализировать реальные числовые данные, представленные на диаграммах |
|
2. 9 |
Выполнять преобразования с алгебраическими дробями |
|
2.10 |
Находить значения буквенных выражений, осуществляя необходимые подстановки и преобразования |
|
2.11 |
Решать линейные неравенства с одной переменной |
|
2.12 |
Выполнять основные действия со степенями с целыми показателями, |
|
2.13 |
Описывать реальные ситуации на языке геометрии, решать практические задачи, связанные с нахождением геометрических величин |
|
2.14 |
Решать планиметрические задачи на нахождение градусных мер углов |
|
2.15 |
Находить градусную меру центральных и вписанных угол |
|
2.16 |
Применять формулу для нахождения площади параллелограмма |
|
2.17 |
Применять формулу для нахождения площади треугольника |
|
2.18 |
Решать рациональные уравнения |
|
2.19 |
Решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений, исходя из формулировки задачи |
|
2.20 |
Применять свойства и признаки ромба для решения задач |
|
2.21 |
Распознавать геометрические фигуры на плоскости, различать их взаимное расположение, изображать геометрические фигуры; выполнять чертежи по условию задачи |
- Необходимое количество вариантов КИМ
Итоговая работа будет представлена в двух вариантах.
- Время выполнения и условия проведения работы
Время выполнения работы – 90 минут (2 урока).
Дополнительное оборудование не требуется.
- Система оценивания отдельных заданий и работы в целом
За верное выполнение каждого задания 1 части работы (1-18) выставляется 1 балл. За неверный ответ или его отсутствие выставляется 0 баллов. Максимальное количество баллов, которое может набрать обучающийся, правильно выполнивший 18 тестовых заданий первой части работы, – 18 баллов.
За верное выполнение заданий 2 части экзаменационной работы (19-22) обучающийся получает по 2 балла за каждое задание. За неверный ответ или его отсутствие выставляется 0 баллов.
Если задание выполнено частично, порядок выполнения построения правильный или задание выполнено правильно, допускаются неточности в оформлении или негрубые ошибки обучающий получает 1 балл.
Максимальное количество баллов, которое может набрать обучающийся, правильно выполнивший 4 задания второй части работы, – 8 балла.
Максимальное количество баллов, которое может получить обучающийся за выполнение всей итоговой работы, – 26 баллов.
Критерии оценивания
«5» — 21-26 баллов
«4» — 14 — 20 баллов
«3» — 8 – 13 баллов
«2» — 0 – 7 баллов
Для получения за работу отметки «удовлетворительно», необходимо набрать минимум 8 тестовых баллов (но не менее 3 тестовых баллов по алгебре и 2 баллов по геометрии).
Шкала оценивания работы Шкала оценивания уровня
сформированности УУД
|
Количество баллов |
Оценка |
|
21 – 26 |
5 |
|
14- 20 |
4 |
|
8 — 13 |
3 |
|
0 — 7 |
2 |
|
Баллы |
Уровень УУД |
|
14 -26 |
повышенный |
|
8 — 13 |
базовый |
Итоговая работа по математике в 8 классе в форме ОГЭ.
Вариант 1
Часть 1
Ответами к заданиям 1–18 являются цифра, число.
При выполнении заданий 2, 3, 4, 8, 11, 12, 18 обведите кружком номер правильного ответа.
Для остальных заданий части 1 ответом является число. Ответ запишите в поле ответа в тексте работы. Если получилась обыкновенная дробь, ответ запишите в виде десятичной.
- Найдите значение выражения: 2,4 + 0,24⋅1,2 Ответ:____________________
- В таблице приведены нормативы по бегу на 30 метров для учащихся 9-х классов.
|
Мальчики |
Девочки |
|||||
|
Отметка |
«5» |
«4» |
«3» |
«5» |
«4» |
«3» |
|
Время, секунды |
4,6 |
4,9 |
5,3 |
5,0 |
5,5 |
5,9 |
Какую отметку получит девочка, пробежавшая эту дистанцию за 5,36 секунды?
1) Отметка «5».
2) Отметка «4».
3) Отметка «3».
4) Норматив не выполнен.
- На координатной прямой отмечены точки A, B, C, D. Одна из них соответствует числу
.
Какая это точка?
1) точка A
2) точка B
3) точка C
4) точка D
- Найдите значение выражения
.
1) 360
2)
3)
4)
- На графике изображена зависимость атмосферного давления (в миллиметрах ртутного столба) от высоты над уровнем моря (в километрах). На какой высоте (в км) летит воздушный шар, если барометр, находящийся в корзине шара, показывает давление 540 миллиметров ртутного столба?
Ответ:____________________
- Решите уравнение
.
Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.
Ответ:____________________
- Кисть, которая стоила 240 рублей, продаётся с 25%-й скидкой. При покупке двух таких кистей покупатель отдал кассиру 500 рублей. Сколько рублей сдачи он должен получить?
Ответ:____________________
- На диаграмме показано содержание питательных веществ в молочном шоколаде. Определите по диаграмме, содержание каких веществ преобладает.
*-к прочему относятся вода, витамины и минеральные вещества.
1) жиры 2) белки 3) углеводы 4) прочее.
- Упростите выражение
и найдите его значение при
. В ответ запишите полученное число.
Ответ:____________________
- В фирме «Эх, прокачу!» стоимость поездки на такси (в рублях) рассчитывается по формуле C = 150 + 11 · (t − 5), где t — длительность поездки, выраженная в минутах (t > 5). Пользуясь этой формулой, рассчитайте стоимость 14-минутной поездки.
Ответ:____________________
- Решите неравенство .
.
1) ;
2) ;
3) ;
4) .
- Вычислите:
- 49;
2) 49;
3) ;
4) .
- Пожарную лестницу длиной 13 м приставили к окну пятого этажа дома. Нижний конец лестницы отстоит от стены на 5 м.
На какой высоте расположено окно? Ответ дайте в метрах
Ответ:____________________
- Найдите больший угол равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной AB углы,
равные 30° и 45° соответственно.
Ответ:____________________
- AC и BD — диаметры окружности с центром O. Угол ACB равен 79°. Найдите угол AOD. Ответ дайте в градусах.
Ответ:____________________
- Найдите площадь параллелограмма, изображённого на рисунке.
Ответ:____________________
- На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.
Ответ:____________________
- Укажите номера верных утверждений.
1) Если три стороны одного треугольника пропорциональны трём сторонам другого треугольника, то треугольники подобны.
2) Сумма смежных углов равна 180°.
3) Любая высота равнобедренного треугольника является его биссектрисой.
Если утверждений несколько, запишите их номера в порядке возрастания.
Часть 2
|
При выполнении заданий 19–22 запишите решение и ответ. |
|
Модуль «Алгебра» |
- Решите уравнение:
.
- Теплоход проходит по течению реки до пункта назначения 176 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 3 км/ч, стоянка длится 1 час, а в пункт отправления теплоход возвращается через 20 часов после отплытия из него.
- Высота AH ромба ABCD делит сторону CD на отрезки DH = 12 и CH = 3. Найдите высоту ромба.
- В треугольнике АВС углы А и С равны 30° и 50° соответственно. Найдите угол между высотой ВН и биссектрисой BD.
ВАРИАНТ 2
Часть 1
Ответами к заданиям 1–18 являются цифра, число.
При выполнении заданий 2, 3, 4, 8, 11, 12, 18 обведите кружком номер правильного ответа.
Для остальных заданий части 1 ответом является число. Ответ запишите в поле ответа в тексте работы. Если получилась обыкновенная дробь, ответ запишите в виде десятичной.
1. Найдите значение выражения: Ответ:____________________
2. В таблице приведены размеры штрафов за превышение максимальной разрешённой скорости, зафиксированное с помощью средств автоматической фиксации, установленных на территории России на 1 января 2013 года.
|
Превышение скорости, км/ч |
11 − 20 |
21 − 40 |
41 − 60 |
61 и более |
|
Размер штрафа, руб. |
100 |
300 |
1000 |
2500 |
Какой штраф должен заплатить владелец автомобиля, зафиксированная скорость которого составила 175 км/ч на участке дороги с максимальной разрешённой скоростью 110 км/ч?
В ответе укажите номер правильного варианта.
1) 100 рублей 2) 300 рублей 3) 1000 рублей 4) 2500 рублей
3. Одна из точек, отмеченных на координатной прямой, соответствует числу . Какая это точка?
1) точка M 2) точка N 3) точка P 4) точка Q
4. Найдите значение выражения: .
1)
2)
3)
4) 90
5. На рисунке показано, как изменялась температура воздуха на протяжении одних суток. По горизонтали указано время суток, по вертикали — значение температуры в градусах Цельсия. Найдите наименьшее значение температуры. Ответ дайте в градусах Цельсия.
Ответ:____________________
6. Решите уравнение: -21.
Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.
Ответ:____________________
7. Чайник, который стоил 800 рублей, продаётся с 5%-й скидкой. При покупке этого чайника покупатель отдал кассиру 1000 рублей. Сколько рублей сдачи он должен получить?
Ответ:____________________
8. На диаграмме показано содержание питательных веществ в какао-порошке. Определите по диаграмме, содержание каких веществ наименьшее.
*-к прочему относятся вода, витамины и минеральные вещества.
1) жиры 2) белки 3) углеводы 4) прочее
9. Упростите выражение и найдите его значение при
.
Ответ:____________________
10. В фирме «Чистая вода» стоимость (в рублях) колодца из железобетонных колец рассчитывается по формуле , где
— число колец, установленных при рытье колодца. Пользуясь этой формулой, рассчитайте стоимость колодца из 11 колец.
Ответ:____________________
11.Решите неравенство:
и определите, на каком рисунке изображено множество его решений.
12. Вычислите:
Варианты ответа:
1) 2) -8 3) 8 4)
13. Точка крепления троса, удерживающего флагшток в вертикальном положении, находится на высоте 15 м от земли. Расстояние от основания флагштока до места крепления троса на земле равно 8 м. Найдите длину троса.
Ответ:____________________
14. Сумма двух углов равнобедренной трапеции равна 140°. Найдите больший угол трапеции. Ответ дайте в градусах.
Ответ:____________________
15. В окружности с центром O AC и BD — диаметры. Угол ACB равен 26°. Найдите угол AOD. Ответ дайте в градусах.
Ответ:____________________
16. Найдите площадь треугольника, изображённого на рисунке.
17.На клетчатой бумаге с размером клетки 1см x 1см отмечены точки А, В и С. Найдите расстояние от точки А до прямой ВС. Ответ выразите в сантиметрах.
18. Какие из данных утверждений верны? Запишите их номера.
1) Каждая из биссектрис равнобедренного треугольника является его медианой.
2) Диагонали прямоугольника равны.
3) У любой трапеции боковые стороны равны.
Часть 2
19. Решите уравнение
20. Теплоход проходит по течению реки до пункта назначения 140 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 5 км/ч, стоянка длится 11 часов, а в пункт отправления теплоход возвращается через 32 часа после отплытия из него.
21. Высота AH ромба ABCD делит сторону CD на отрезки DH = 12 и CH = 1. Найдите высоту ромба.
22. В треугольнике АВС углы А и С равны 40° и 60° соответственно. Найдите угол между высотой ВН и биссектрисой BD.
Итоговая работа по математике (промежуточная аттестация в форме ОГЭ), 8 класс. Вариант 1 Часть 1
1. Найти значение выражения +0,09
2. Выберите неверное равенство: 1)
3. Установите соответствие между графиками функций и формулами, которые их задают.
1) у=2х 2) у=-2х 3) у=х+2 4) у=2 5) у = х2
4. Упростите выражение 1)
; 2)10; 3)
; 4)2.
5. Решите уравнение х2+3х-4=0.Найдите среднее арифметическое корней. 1)1. 2) -1,5. 3) -3. 4) нет корней.
6. Решите систему уравнений: 
7. Решить неравенство и выбрать, на каком рисунке изображено множество его решений.
8. Решите систему неравенств: 
|
Часть 2 модуль «Геометрия» 9. Найдите площадь ромба, если его диагонали равны 315 и 2. |
10. На какое расстояние следует отодвинуть от стены дома нижний конец лестницы, длина которой 13 м, чтобы верхний ее конец оказался на высоте 12 м? |
11. Найдите площадь трапеции, изображенной на рисунке. |
12. Найдите тангенс угла А треугольника ABC, изображенного на рисунке. |
|
Модуль «Реальная математика». 13. В фирме такси в данный момент свободно 20 машин: 9 черных, 4 желтых и 7 зеленых. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того, что к нему приедет желтое такси. |
14. Куриные яйца в зависимости от их массы подразделяют на 5 категорий. Используя данные, представленные в таблице, определите, к какой категории относится яйцо, массой 65,8 г. 1) Высшая. 2) Отборная. 3) Первая. 4) Вторая.
|
Часть 2. Модуль «Алгебра» (запишите полное решение и ответ)
15. Найдите отрицательный корень уравнения 2х2—72=0
16. Решите уравнение: 
17. Найти значения а, при которых уравнение не имеет корней
18. Решите систему уравнений: 
19. Два лесоруба, работая вместе, выполнили норму вырубки за 4 дня. Сколько дней нужно на выполнение этой работы каждому лесорубу отдельно, если первому для вырубки нормы нужно на 6 дней меньше, чем другому?
Итоговая работа по алгебре. 8 класс. Вариант 2. Часть 1.
1. Найти значение выражения 0,08+
2. Выберите неверное равенство: 1)
3.Установите соответствие между графиками функций и формулами, которые их задают
1) у = 
4. Упростите выражение 1)1; 2)
; 3)
; 4)2.
5. Решите уравнение х2-7х+10=0. Найдите среднее арифметическое корней. 1) -3,5 2) 2 3) 3,5 4) нет корней
6. Решите систему уравнений: 1) ( 2; 1); 2) (2; 0); 3) (1; 2) ; 4) (1; 2).
7. Решить неравенство 1) (− ∞;

8. Решите систему неравенств:
|
Модуль «Геометрия» 9. Найти площадь прямоугольного треугольника, если его катеты равны 5 и 12 см. |
10. Лестницу длиной 3 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 1,8 м? |
11. Найдите площадь трапеции, изображенной на рисунке. |
12. Найдите тангенс угла AOB, изображенного на рисунке. |
Модуль «Реальная математика». 13. У бабушки 20 одинаковых по форме пирогов: 10 с капустой, остальные с вареньем. Бабушка достает случайно выбранный пирог. Найдите вероятность того, что это будет пирог с вареньем.
14. В таблице приведены нормативы по бегу на 30 метров для учащихся 9-х классов. Какую отметку получит девочка, пробежавшая эту дистанцию за 5,36 секунды? 1) «5». 2) «4». 3) «3». 4) Норматив не выполнен.
|
Мальчики |
Девочки |
|||||
|
Отметка |
«5» |
«4» |
«3» |
«5» |
«4» |
«3» |
|
Время, секунды |
4,6 |
4,9 |
5,3 |
5,0 |
5,5 |
5,9 |
Часть 2. 15. Найдите отрицательный корень уравнения 2х2 -50=0
16. Решите уравнение: .
17. Найти значения а, при которых уравнение имеет два различных корня.
18. Решите систему уравнений:
19. Один кран наполняет бассейн на 6 часов быстрее другого. Два крана, работая вместе, наполняют бассейн за 4 часа. За сколько часов может наполнить бассейн каждый кран, работая отдельно.
Ответы
|
№ |
Вариант 1 |
Вариант 2 |
|
Модуль «Алгебра» |
||
|
1 |
1,34 |
1,83 |
|
2 |
4 |
2 |
|
3 |
4135 |
3214 |
|
4 |
2 |
1 |
|
5 |
2 |
3 |
|
6 |
3 |
2 |
|
7 |
2 |
4 |
|
8 |
3 |
3 |
|
Модуль «Геометрия» |
||
|
9 |
315 |
30 |
|
10 |
5 |
2,4 |
|
11 |
28 |
168 |
|
12 |
0,4 |
2 |
|
Модуль «Реальная математика» |
||
|
13 |
0,2 |
0,5 |
|
14 |
2 |
2 |
|
Часть 2 |
||
|
15 |
-6 |
-5 |
|
16 |
2 |
2 |
|
17 |
(1, 125; +∞) |
(-1/3; +∞) |
|
18 |
(1; 0) (- 1; — 4) |
(3; 1) (- 3; 49) |
|
19 |
№ 19. 1 вариант. Пусть – первый лесоруб выполняет норму за х дней.
|
Компоненты работы |
А |
t |
|
|
Участники совместной работы |
|||
|
1 лесоруб |
1 |
х |
|
|
2 лесоруб |
1 |
х+6 |
|
Совместная работа 4 дня. Уравнение +

.
Одно решение х=-4 не соответствует физической сути задачи. Время второго лесоруба
х+6=6+6=12 (дней). Ответ. Первый лесоруб выполнит работу за 6 дней, а второй за 12 дней.
№ 19. 2 вариант. Один кран наполняет бассейн на 6 часов быстрее другого. Два крана, работая вместе, наполняют бассейн за 4 часа. За сколько часов может наполнить бассейн каждый кран, работая отдельно. Уравнение. 
Дата публикации:
13.10.2019
Описание:
Автор: Таболина Ирина Анатольевна
Тесты в формате ОГЭ можно использовать как тренировочные или переводной экзамен по математике за 8 класс.
Переводной экзамен по математике за курс 8 класса
На выполнение контрольной работы отводится 60 минут.
Чтобы получить удовлетворительную оценку, нужно обязательно выполнить 6 заданий. Краткое решение заданий обязательно.
МОУ СОШ №66, г. Магнитогорск
1 вариант
Часть 1
Модуль Алгебра
4. Решите систему неравенств:
6. Найти значение выражения:
7. Решите неравенство: 2х-3(х+1) > 2+х.
8. По формуле F = ma найдите F , если m= 20 кг и a= 500000 м/с2 , где m-масса тела, a- ускорение.
1) 105
2) 106
3) 108
4) 107
Модуль Геометрия
9. Найти
Скачать работу


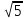 , 5
, 5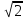 и 6 расположены в порядке возрастания?
и 6 расположены в порядке возрастания?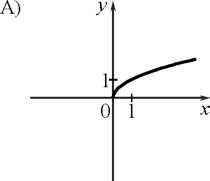

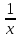 ; 3) у = — х2; 4) у =
; 3) у = — х2; 4) у = 
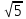 , 5
, 5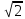 и 6 расположены в порядке возрастания?
и 6 расположены в порядке возрастания?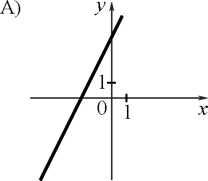
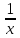 ; 2) у=х2; 3) у = 2х + 4; 4) у=
; 2) у=х2; 3) у = 2х + 4; 4) у=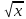 ..
..
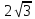
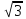
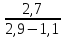 .
.
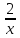 ; 3) у = 2х; 4) у=
; 3) у = 2х; 4) у=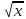 ..
..
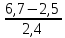 .
.
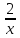 ; 3) у = 2х: 4) у=
; 3) у = 2х: 4) у=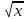 .
.

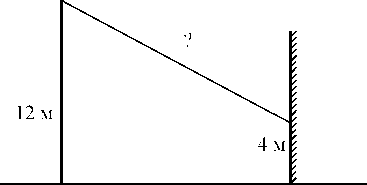
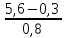 .
.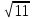
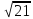
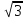 ; 3)
; 3)  •
•  ; 4) 2
; 4) 2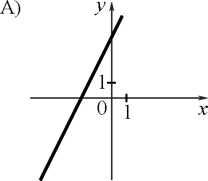
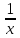 ; 2) у=х2; 3) у = 2х + 4; 4) у=
; 2) у=х2; 3) у = 2х + 4; 4) у=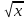 ..
..
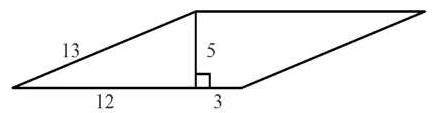

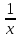 ; 2) У=
; 2) У=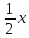 ; 3) у=х2; 4) у=
; 3) у=х2; 4) у=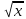 .
.