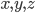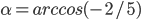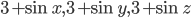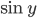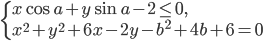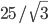Вступительные испытания
Приём в бакалавриат и специалитет осуществляется по результатам единого государственного экзамена (ЕГЭ) и по результатам вступительных испытаний МФТИ для отдельных категорий поступающих. Победители и призёры олимпиад школьников обладают особыми правами в соответствии с пп. 2.10 – 2.12 Правил приёма в МФТИ.
Начало экзаменов: 10:00; место проведения: главный корпус МФТИ. С собой необходимо иметь ручку (синего или черного цвета), бумага выдается на месте.
Во время проведения вступительных испытаний участникам запрещается иметь при себе и использовать средства связи, справочные материалы и электронно-вычислительную технику, за исключением выданных экзаменатором. При нарушении поступающим во время проведения вступительных испытаний Правил приёма в МФТИ, экзаменационная комиссия вправе удалить его с места проведения вступительного испытания с составлением акта об удалении.
Конкурсные группы с указанием перечня вступительных испытаний и их приоритета, соответствие профилям олимпиад, дающих особое право поступления без вступительных испытаний
Программы вступительных испытаний
- Программа вступительного испытания по физике
- Пример вступительного испытания по физике
- Программа вступительного испытания по математике
- Пример вступительного испытания по математике
- Программа вступительного испытания по информатике
- Пример вступительного испытания по информатике
- Программа вступительного испытания по химии
- Пример вступительного испытания по химии
- Программа вступительного испытания по русскому языку
- Пример вступительного испытания по русскому языку
- Видео «Подготовка к экзамену по русскому языку»
Вступительные испытания МФТИ могут сдавать:
- дети-инвалиды, инвалиды;
- иностранные граждане;
- лица, имеющие среднее профессиональное или высшее образование;
- лица, которые получили документ о среднем общем образовании после 26 июля 2017 года, прошли государственную итоговую аттестацию (ГИА) по образовательным программам среднего общего образования не в форме ЕГЭ (либо прошли итоговую аттестацию в иностранных образовательных организациях и не сдавали ЕГЭ в указанный период);
- лица, получившие в 2018 году аттестат о среднем общем образовании по результатам государственной итоговой аттестации в образовательных организациях, расположенных на территориях Республики Крым и города федерального значения Севастополя;
- по отдельным общеобразовательным предметам – лица, которые прошли ГИА по этим общеобразовательным предметам в форме государственного выпускного экзамена, при условии, что они получили документ о среднем общем образовании после 26 июля 2017 года и в этот период не сдавали ЕГЭ по соответствующим общеобразовательным предметам.
Расписание летней сессии
- 04.05.2017
- Новости
- Кирилл Чумачков
Публикуем окончательную версию расписания экзаменов летней сессии на 2016-2017 учебный год с официального сайта МФТИ.
Удачи на сессии!
- 1 курс зачёты, экзамены
- 2 курс зачёты, экзамены
- 3 курс зачёты, экзамены
- 4 курс зачёты, экзамены
- 5 курс зачёты, экзамены
Поделиться
Твитнуть
Поделиться
- — МЕНЮ —
- ЯГУБОВ.РФ
- ЕГЭ (ПРОФИЛЬ)
- ЕГЭ (БАЗА)
- ОГЭ (ГИА)
- ГЕНЕРАТОР
- ОЛИМПИАДЫ
- ЭКЗАМЕНЫ [МФТИ…]
- ЛИТ-РА
- ДВИ (МГУ)
- От Ягубова Р. Б.
- ЗАДАНИЯ
- ТЕМАТИКА
- РАСПИСАНИЕ
- ЗАНЯТИЯ
- ПРОГУЛЫ
- ПЛАТЕЖИ
- ФОРМУЛЫ
- ТЕТРАДЬ
- ЗАГАДКИ
- СОБЫТИЯ
- ИНВЕСТИЦИИ
- ГРУППА «ВК»
- МЫ В «YOUTUBE»
- ЯНДЕКС.КАРТЫ
- ПОИСК
- ОТЗЫВЫ
- — ВХОД —
Поступательные олимпиады МФТИ
Список поступательных олимпиад МФТИ в текущем учебном году.
- Онлайн-этапе олимпиад «Физтех» 2017 года по физике и математике
К участию в онлайн-этапе приглашаются школьники 5-11 классов, олимпиада проходит по математике и физике отдельно. Победители олимпиады «Физтех» 2017 года по физике в 11 классе могут поступить в МФТИ без экзаменов, призеры – засчитать 100 баллов ЕГЭ по предмету при поступлении.
Даты проведения: 01 октября 2016 г.– 05 февраля 2017 г.
Даты проведения заключительного этапа олимпиад «Физтех»: 25–26 февраля 2017 г. - Столичной физико-математической олимпиаде 2016 года
К участию в олимпиаде приглашаются школьники 5-11 классов, олимпиада проходит по математике и физике отдельно. Олимпиада является отборочным этапом олимпиад школьников «Физтех» по математике и физике. Победители олимпиады «Физтех» 2017 года по физике могут поступить в МФТИ без экзаменов, призеры – засчитать 100 баллов ЕГЭ по предмету при поступлении.
Дата проведения: 03 декабря 2016 г.
Даты проведения заключительного этапа олимпиад «Физтех»: 25–26 февраля 2017 г. - Открытой химической олимпиаде 2016/17 года
К участию в олимпиаде приглашаются учащиеся 9-11 классов. По итогам олимпиады абитуриентам, которые стали победителями и призерами в 11 классе, будут предоставлены льготы при поступлении в МФТИ в виде 100 баллов ЕГЭ по химии.
Даты проведения онлайн-этапа: 01 октября 2016 г. – 11 января 2017 г.
Дата проведения заключительного этапа: 12 февраля 2017 г.
Документы ЗФТШ Задания прошлых лет
Категория: Документы
Добавил: Сущенко А. А.
- 13 апреля 2022 г.
- 3 файла
- 0 комментариев
- 60944 просмотра
-
Вступительные 2019-20г
- 13.04.22
- 575 kB
- 4319 просмотров
- 4108 скачано
- Изменено 13.04.22
-
Вступительные 2020-21г
- 13.04.22
- 555 kB
- 2636 просмотров
- 3320 скачано
- Изменено 13.04.22
-
Вступительные 2021-22г
- 13.04.22
- 454 kB
- 11746 просмотров
- 9188 скачано
- Изменено 13.04.22
14 сентября 2017
В закладки
Обсудить
Жалоба
Онлайн этап пройдёт с 30 сентября 2017 года по 4 февраля 2018 года.
Участие в олимпиаде «Физтех» позволяет получить льготы при поступлении в МФТИ и другие престижные вузы России. Победители и призёры заключительного этапа олимпиады по физике и/или по математике смогут зачесть 100 баллов ЕГЭ по соответствующему их диплому предмету, победители по физике получат право поступить в МФТИ без экзаменов.
Официальный сайт: olymp.mipt.ru
Задачи онлайн этапа прошлого года
→ Математика: online17-m.pdf
→ Физика: online-17f.pdf
Задачи финального тура прошлого учебного года с решениями
→ Математика: math.rar
→ Физика: fiz.rar
Разбор задач по математике
Разбор задач по физике
Билет 1
- Когда к квадратному трехчлену
прибавили 2, его наименьшее значение увеличилось на 1, а когда из него вычли
, его наименьшее значение уменьшилось на 3. А как изменится наименьшее значение
, если к нему прибавить
?
- Решите неравенство
- Известно, что числа
образуют в указанном порядке арифметическую прогрессию с разностью
, а числа
образуют в указанном порядке непостоянную геометрическую прогрессию. Найдите
.
- В треугольнике ABC угол при вершине A в два раза больше угла при вершине C. Через вершину B проведена касательная ℓ к окружности Ω, описанной около треугольника ABC.
Расстояния от точек A и C до этой касательной равны соответственно 4 и 9.
а) Найдите расстояние от точки A до прямой BC.
б) Найдите радиус окружности Ω и длину стороны AB. - На координатной плоскости рассматриваются квадраты, все вершины которых имеют целые неотрицательные координаты, а центр находится в точке (60;45). Найдите количество таких квадратов.
- Найдите все значения параметра
такие, что система
имеет хотя бы одно решение при любом значении параметра
.
- Основание треугольной пирамиды ABCD — правильный треугольник ABC. Объем пирамиды равен
, а ее высота, проведенная из вершины D, равна 3. Точка M — середина ребра CD. Известно, что радиусы сфер, вписанных в пирамиды ABCM и ABDM, равны между собой. а) Найдите все возможные значения угла между гранями пирамиды при ребре AB; б) Найдите все возможные значения длины ребра CD, если дополнительно известно, что грани BCD и ABC взаимно перпендикулярны.
Варианты вступительных экзаменов



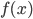
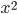
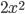
![x^{log_3x}-2le(sqrt[3]{3})^{log_{sqrt{3}}^2x}-2x^{log_3sqrt[3]{x}}](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_b190017c8da46c7cf9a1f1f6b8e2672d.gif)