-
Абитуриентам
Одним из главных принципов уникальной «системы Физтеха», заложенной в основу образования в МФТИ, является тщательный отбор одаренных и склонных к творческой работе представителей молодежи. Абитуриентами Физтеха становятся самые талантливые и высокообразованные выпускники школ всей России и десятков стран мира.
- Приемная комиссия
- Физтех-центр
- ЗФТШ
- Школы
- Олимпиады и конференции
- Студентам
- Аспирантам
- Выпускникам

- О Физтехе
- Образование
- Наука и инновации
- Новости науки
- МФТИ
- ФАЛТ
- Кафедры факультета
- Секция кафедры высшей математики
- Письменные экзаменационные работы прошлых лет
- Мат.Ан.
- ТФКП
- Ур.Мат.Физ.
- Дифуры
Письменные экзаменационные работы прошлых лет
- Мат.Ан.
- ТФКП
- Ур.Мат.Физ.
- Дифуры
Если вы заметили в тексте ошибку, выделите её и нажмите Ctrl+Enter.
Помогите рассортировать файлы. К какому предмету относится данный файл?
Ненужные и мусорные файлы можно перемещать в предмет [НА УДАЛЕНИЕ].
Помогите дать файлам осмысленные названия
Примеры:
lab1 => Лабораторная работа №1. Фотоэффект.
Savelev_molekulyarnaya_fizika => Савельев. Молекулярная физика
Ставлю 10/10
Все нравится, очень удобный сайт, помогает в учебе. Кроме этого, можно заработать самому, выставляя готовые учебные материалы на продажу здесь. Рейтинги и отзывы на преподавателей очень помогают сориентироваться в начале нового семестра. Спасибо за такую функцию. Ставлю максимальную оценку.
Отлично
Лучшая платформа для успешной сдачи сессии
Познакомился со СтудИзбой благодаря своему другу, очень нравится интерфейс, количество доступных файлов, цена, в общем, все прекрасно. Даже сам продаю какие-то свои работы.
Отлично
Студизба ван лав ❤
Очень офигенный сайт для студентов. Много полезных учебных материалов. Пользуюсь студизбой с октября 2021 года. Серьёзных нареканий нет. Хотелось бы, что бы ввели подписочную модель и сделали материалы дешевле 300 рублей в рамках подписки бесплатными.
Отлично
Отличный сайт
Лично меня всё устраивает — и покупка, и продажа; и цены, и возможность предпросмотра куска файла, и обилие бесплатных файлов (в подборках по авторам, читай, ВУЗам и факультетам). Есть определённые баги, но всё решаемо, да и администраторы реагируют в течение суток.
Отлично
Маленький отзыв о большом помощнике!
Студизба спасает в те моменты, когда сроки горят, а работ накопилось достаточно. Довольно удобный сайт с простой навигацией и огромным количеством материалов.
Хорошо
Студ. Изба как крупнейший сборник работ для студентов
Тут дофига бывает всего полезного. Печально, что бывают предметы по которым даже одного бесплатного решения нет, но это скорее вопрос к студентам. В остальном всё здорово.
Отлично
Спасательный островок
Если уже не успеваешь разобраться или застрял на каком-то задание поможет тебе быстро и недорого решить твою проблему.
Отлично
Всё и так отлично
Всё очень удобно. Особенно круто, что есть система бонусов и можно выводить остатки денег. Очень много качественных бесплатных файлов.
Отлично
Отзыв о системе «Студизба»
Отличная платформа для распространения работ, востребованных студентами. Хорошо налаженная и качественная работа сайта, огромная база заданий и аудитория.
Хорошо
Отличный помощник
Отличный сайт с кучей полезных файлов, позволяющий найти много методичек / учебников / отзывов о вузах и преподователях.
Отлично
Отлично помогает студентам в любой момент для решения трудных и незамедлительных задач
Хотелось бы больше конкретной информации о преподавателях. А так в принципе хороший сайт, всегда им пользуюсь и ни разу не было желания прекратить. Хороший сайт для помощи студентам, удобный и приятный интерфейс. Из недостатков можно выделить только отсутствия небольшого количества файлов.
Отлично
Спасибо за шикарный сайт
Великолепный сайт на котором студент за не большие деньги может найти помощь с дз, проектами курсовыми, лабораторными, а также узнать отзывы на преподавателей и бесплатно скачать пособия.
Отлично
- — МЕНЮ —
- ЯГУБОВ.РФ
- ЕГЭ (ПРОФИЛЬ)
- ЕГЭ (БАЗА)
- ОГЭ (ГИА)
- ГЕНЕРАТОР
- ОЛИМПИАДЫ
- ЭКЗАМЕНЫ [МФТИ…]
- ЛИТ-РА
- ДВИ (МГУ)
- От Ягубова Р. Б.
- ЗАДАНИЯ
- ТЕМАТИКА
- РАСПИСАНИЕ
- ЗАНЯТИЯ
- ПРОГУЛЫ
- ПЛАТЕЖИ
- ФОРМУЛЫ
- ТЕТРАДЬ
- ЗАГАДКИ
- СОБЫТИЯ
- ИНВЕСТИЦИИ
- ГРУППА «ВК»
- МЫ В «YOUTUBE»
- ЯНДЕКС.КАРТЫ
- ПОИСК
- ОТЗЫВЫ
- — ВХОД —
Олимпиада «Физтех»
Олимпиада «Физтех» — это главная олимпиада для всех желающих поступать в МФТИ, а также одна из основных олимпиад для абитуриентов Высшей школы экономики и МГУ. Успешно выступить на «Физтехе» вполне реально, только готовиться нужно начинать как минимум за год.
Олимпиада «Физтех» — это две отдельные олимпиады по математике и физике. Можно участвовать как в одной из этих олимпиад, так и в обеих сразу.
Для участия в олимпиаде «Физтех» необходимо иметь личный кабинет на портале abitu.net, через который вы получите также доступ и к другим физтеховским олимпиадам (Столичная, Выездная, Phystech.International и т. д.). Там же будут копиться ваши бонусные баллы в Кадастре абитуриентов МФТИ, начисленные за успешное выступление на указанных олимпиадах.
Олимпиада «Физтех» проходит в два этапа — отборочный и заключительный. На сегодняшний день заключительный этап предусмотрен только для учеников 9–11 классов. Тем не менее, школьникам 5–8 классов нужно непременно участвовать в олимпиадах отборочного этапа, чтобы постепенно привыкать к уровню и специфике физтеховских задач.
Отборочный этап «Физтеха» является совокупностью трёх независимых друг от друга олимпиад:
- Онлайн-этап олимпиады «Физтех»
- Физико-математическая олимпиада МИЭТ
- Отборочный тур ЛЭТИ
Чтобы пройти на заключительный этап «Физтеха», достаточно получить диплом хотя бы на одной олимпиаде отборочного этапа. Разумеется, на заключительный этап приглашаются победители и призёры предыдущего заключительного этапа.
Как готовиться к олимпиаде «Физтех»
Заключительный этап «Физтеха» сильно напоминает старые добрые письменные экзамены в МФТИ по математике и физике. Олимпиада «Физтех» унаследовала дух и традиции прежних экзаменов. Поэтому необходимое условие успеха на «Физтехе» — прорешать как можно больше задач прошлых лет. Источников много:
- Две таблицы ниже, в которых собраны варианты олимпиады «Физтех» по математике и физике начиная с 2007 года.
- Варианты вступительных экзаменов в МФТИ 1974—2008 годов. Задачи в этих брошюрах сгруппированы именно по вариантам. Это удобно для финальной шлифовки всех накопленных знаний.
- Шабунин М.И., Агаханов Н.Х. и др. Методическое пособие по математике для старшеклассников и абитуриентов. Книга содержит задачи по математике, предлагавшиеся на вступительных экзаменах в МФТИ и олимпиаде «Физтех» с 1991 года. Задачи сгруппированы по нескольким крупным тематическим разделам: «Алгебраические уравнения, системы и неравенства», «Тригонометрические уравнения, системы и неравенства» и т. д., а внутри этих разделов — просто в хронологическом порядке по годам (уже без дальнейшей классификации, что не всегда удобно).
- Чешев Ю.В. Методическое пособие по физике для старшеклассников и абитуриентов. Книга содержит задачи по физике, предлагавшиеся на вступительных экзаменах в МФТИ и олимпиаде «Физтех» с 1991 года. Задачи сгруппированы по разделам физики: механика, термодинамика, электродинамика, оптика, атомная и ядерная физика, а внутри каждого раздела они идут просто в хронологическом порядке по годам без дальнейшей классификации. Это не всегда удобно: например, если хочется порешать задачи конкретно на КПД циклов или самоиндукцию, то придётся их специально выискивать в общем потоке.
- Олимпиадные листки по математике (с более детальной тематической классификацией задач, чем в вышеупомянутой книге Шабунина) и в частности, листки по комбинаторике. Также — моя бумажная книжка Комбинаторика для олимпиадников (МЦНМО, 2019, третье издание) или её электронная версия.
- Олимпиадные листки по физике (с более детальной тематической классификацией задач, чем в книге Чешева).
Олимпиада «Физтех» по математике
Поначалу олимпиада «Физтех» по математике была стопроцентной копией письменного экзамена по математике в МФТИ: олимпиадный вариант содержал те же шесть задач, вполне аналогичные экзаменационным. Однако в 2012 году произошли изменения — задач стало восемь. К шести традиционным «абитуриентским» задачам повышенной сложности добавились две задачи по комбинаторике и целым числам (сравните, например, вариант 2011 года с вариантами 2012 и 2013 годов). Комбинаторные задачи обязательно присутствуют и на отборочных этапах (не только «Физтеха», кстати). Так что имейте это в виду и изучайте комбинаторику!
Впоследствии одну задачу убрали: в вариантах заключительного этапа
2014,
2015,
2016,
2017,
2018,
2019,
2020,
2022
годов было семь задач (шесть традиционных и одна комбинаторная). Вариант 2021 года содержал шесть задач, но он проходил онлайн из-за ковида.
Каждая задача варианта оценивается определённым количеством баллов (скажем, 7). По критериям баллы даются за различные продвижения в решении, то есть при неполном решении можно тем не менее что-то получить за эту задачу (скажем, 2 или 4 балла). Поэтому все свои полезные соображения пишите обязательно!
В таблице представлены границы дипломов первой/второй/третьей степени за последние годы. В квадратных скобках указана максимальная сумма баллов варианта олимпиады.
| Год | 9 класс | 10 класс | 11 класс |
|---|---|---|---|
| 2022 | 20/15/12 [31] | 21/17/14 [30] | 16/13/10 [33] |
| 2021 | 26/23/20 [32] | 26/23/19 [34] | 21/17/13 [34] |
| 2020 | 20/17/14 [33] | 23/20/17 [35] | 21/17/13 [35] |
| 2019 | 22/18/15 [32] | 25/21/17 [36] | 19/16/13 [40] |
| 2018 | 29/25/21 [35] | 27/24/20 [39] | 28/25/21 [39] |
| 2017 | 30/24/18 [40] | 33/27/21 [40] | 32/24/18 [46] |
| 2016 | 30/26/20 [32] | 30/24/18 [35] | 40/31/24 [48] |
Хорошо видно, что нет никакого смысла ориентироваться на баллы прошлых лет: всё зависит только от того, как наряду с вами написали остальные. Если вариант оказался лёгким, границы дипломов будут высокими; если трудным — низкими. Яркий пример — 11 класс: победитель 2019 года со своими 19 баллами не стал бы в 2018 году даже призёром.
В Перечне РСОШ олимпиада «Физтех» по математике имеет первый уровень. Диплом победителя даёт БВИ при поступлении в МФТИ на большинство направлений.
Задачи олимпиады «Физтех» по математике последних лет
| Онлайн | Финал | |
|---|---|---|
| 5 класс |
18, 17, 16 |
— |
| 6 класс |
18, 17, 16 |
— |
| 7 класс |
18, 17 16, 15, 14 |
— |
| 8 класс |
18, 17, 16 15, 14, 13 |
— |
| 9 класс |
18, 17, 16, 15 14, 13, 12, 11 |
22.1, 22.2; 21 20.1, 20.2; 19.1, 19.2 18.1, 18.2; 17.1, 17.2 16.1, 16.2, 16.3 |
| 10 класс |
18, 17, 16, 15 14, 13, 12, 11 |
22.1, 22.2; 21 20.1, 20.2; 19.1, 19.2 18.1, 18.2; 17.1, 17.2 16.1, 16.2, 16.3 15.1, 15.2, 15.3 |
| 11 класс |
18, 17, 16, 15 14, 13, 12, 11 |
22.1, 22.2; 21 20.1, 20.2; 19.1, 19.2 18.1, 18.2; 17.1, 17.2 16.1, 16.2, 16.3 15.1, 15.2, 15.3 14.1, 14.2; 13.1, 13.2 12.1, 12.2; 11.1, 11.2 10.1, 10.2; 09.1, 09.2; 08, 07 |
| Экзамен 1994 — 2008 |
08.1, 08.2, 08.3, 08.4 07.1, 07.2, 07.3, 07.4 06.1, 06.2, 06.3, 06.4 05.1, 05.2, 05.3 04.1, 04.2, 04.3 03.1, 03.2, 03.3 02.1, 02.2, 02.3 01.1, 01.2, 01.3 |
00.1, 00.2 99.1, 99.2 98.1, 98.2 97.1, 97.2, 97.3 96.1, 96.2, 96.3 95.1, 95.2, 95.3 94.1, 94.2, 94.3 |
Примечания.
- В 2016/17 и 2017/18 годах на онлайн-этапе для 5 и 6 классов давалось задание 7 класса.
- Заключительный этап для десятиклассников впервые состоялся в 2015 году, а для девятиклассников — в 2016 году.
Олимпиада «Физтех» по физике
Традиционно предлагается пять задач, каждая стоимостью 10 баллов. Таким образом, максимальная сумма баллов варианта всегда равна 50.
В таблице вы можете видеть границы дипломов первой/второй/третьей степени за последние годы.
| Год | 9 класс | 10 класс | 11 класс |
|---|---|---|---|
| 2022 | 44/38/32 | 37/31/26 | 39/36/32 |
| 2021 | 38/32/26 | 44/39/34 | 38/30/22 |
| 2020 | 45/41/35 | 43/38/33 | 40/34/27 |
| 2019 | 41/34/26 | 39/31/24 | 35/28/21 |
| 2018 | 48/43/37 | 44/37/30 | 44/38/32 |
| 2017 | 42/36/30 | 40/33/26 | 43/31/22 |
| 2016 | 49/43/37 | 49/43/37 | 49/43/37 |
Олимпиада «Физтех» по физике в Перечне РСОШ имеет первый уровень.
Задачи олимпиады «Физтех» по физике последних лет
| Онлайн | Финал | |
|---|---|---|
| 7 класс |
18, 17 16, 15, 14 |
— |
| 8 класс |
18, 17 16, 15, 14 |
— |
| 9 класс |
18, 17, 16 15, 14, 12 |
22.1, 22.2; 21.1, 21.2 20.1, 20.2; 19.1, 19.2 18.1, 18.2; 17.1, 17.2 16.1, 16.2, 16.3 |
| 10 класс |
18, 17, 16 15, 14, 12, 11 |
22.1, 22.2; 21.1, 21.2 20.1, 20.2; 19.1, 19.2 18.1, 18.2; 17.1, 17.2 16.1, 16.2, 16.3 15.1, 15.2, 15.3 |
| 11 класс |
18, 17, 16 15, 14, 12, 11 |
22.1, 22.2; 21.1, 21.2 20.1, 20.2; 19.1, 19.2 18.1, 18.2, 18.3, 18.4 17.1, 17.2 16.1, 16.2, 16.3 15.1, 15.2, 15.3 14.1, 14.2; 13.1, 13.2 12.1, 12.2; 11.1, 11.2 10; 09.1, 09.2; 08, 07 |
Примечания.
- В 2016/17 и 2017/18 годах на онлайн-этапе для 7 класса давалось задание 8 класса.
- Задания онлайн-этапа 2012/13 года найти не удалось.
- Заключительный этап для десятиклассников впервые состоялся в 2015 году, а для девятиклассников — в 2016 году.
Столичная физико-математическая олимпиада МФТИ
Столичная физико-математическая олимпиада МФТИ проводится в конце ноября—начале декабря в нескольких школах Москвы для учеников 5–11 классов.
Пятиклассникам и шестиклассникам предлагаются задачи только по математике, так как физику они пока не проходили. Школьники 7–11 классов получают задачи как по математике, так по физике.
Итоги подводятся отдельно по математике и физике. Диплом по математике даёт пропуск пропуск на заключительный этап «Физтеха» по математике; аналогично — по физике.
Составить представление о задачах Столичной олимпиады вам помогут следующие варианты:
- 2010 →
математика,
физика; - 2009 →
математика — решения,
физика — решения.
Открытая интернет-олимпиада Физтех-лицея
Открытая олимпиада Физтех-лицея появилась в 2014/15 учебном году. Олимпиада по математике проводилась для учеников 5–11 классов, олимпиада по физике — для учеников 7–11 классов.
Одиннадцатиклассники, ставшие победителями или призёрами олимпиады Физтех-лицея по математике или физике, получали приглашение на соответствующий заключительный этап олимпиады «Физтех».
Впоследствии олимпиада Физтех-лицея не проводилась (и, по всей видимости, больше её не будет). Однако очень интересные и полезные задания остались:
- Математика:
5 класс,
6 класс,
7 класс,
8 класс,
9 класс,
10 класс,
11 класс. - Физика:
7 класс,
8 класс,
9 класс,
10 класс,
11 класс.
Варианты вступительных экзаменов в МФТИ 2008 г. по математике
Вариант 1
- Решите неравенство
.
- Решите уравнение
.
- Найдите действительные решения системы уравнений
- Параллелограмм ABCD имеет площадь 4. Окружность с центром в точке О, расположенной на отрезке AD, касается отрезков AB, BC и прямой CD в точках M, N и K соответственно. Найти радиус этой окружности и стороны параллелограмма ABCD, если CK:BM=3:1.
- Найти все пары действительных чисел
, удовлетворяющие неравенству
.
- На основании ABCD четырехугольной пирамиды SABCD расположена точка O. Сфера с центром в точке О касается прямых SA, SB, SC, SD в точках A, B, K, L соответственно. Известно, что AB = KL =
, AL = 2, BK = 6, а отрезок SO составляет с плоскостью ABCD угол arccos
. Найти длины отрезков AK, OS и SD.
Вариант 5
- Решите неравенство
.
- Решите уравнение
.
- Решите систему уравнений
- В треугольнике ABC медиана BM равна 2, угол ABM равен
, угол CBM равен
. Найти стороны AB, BC и биссектрису BE треугольника ABC.
- Решите систему уравнений
- В основании пирамиды SABCD лежит параллелограмм ABCD. Сфера
радиуса
с центром O касается ребер AS, BS, AD, BC пирамиды SABCD соответственно в точках K, L, M, N, пересекает ребро AB в точках P и Q и касается грани CDS. Известно, что прямая SO перпендикулярна плоскости ABCD и пересекает ее в точке H, AB:PQ = 4:
, AS:LS=3:2. Найти угол SAB, угол SBH, высоту пирамиды и ее объем.
Ответы:
Вариант 1
или
Вариант 5
- (1;-1)
- arccos(4/9), arccos(5/9), h=2, V=64/21
В данной статье разобран пример вступительного экзамена по математике в МФТИ (бакалавриат). Если вас интересует разбор вступительного экзамена по физике, вы можете найти его на этой странице. Все решения выполнены профессиональным репетитором по математике и физике, осуществляющим подготовку абитуриентов к вступительным экзаменам в МФТИ (ФизТех).
Разбор вступительного экзамена по математике в МФТИ
Используем формулу «синус двойного угла»:
Переносим слагаемые, находящиеся справа от знака равенства, в левую сторону, меняя при этом их знак на противоположный, и выносим за скобки:
Преобразуем теперь выражение, стоящее в скобках, используя формулу «косинус двойного угла»:
Произведение равно нулю, если хотя бы один из множителей равен нулю. То есть возможны два случая:
1) .
2)
Умножим обе части последнего уравнения на и введём замену
:
Примечание. Последнее уравнение является квадратным и решается по стандартному алгоритму с помощью дискриминанта.
Возвращаемся к исходной переменной. Получаем, что либо (это уравнение не имеет решений в действительных числах, так как
), либо
. Из последнего уравнения получаем
.
Ответ: .
Преобразуем выражение с суммой кубов:
В скобках заменим член на разность
. От этого равенство не нарушится. В результате получим:
Итак, исходную систему можно представить в следующем виде:
Теперь используем замену: и
. Тогда система принимает вид:
Теперь складываем почленно оба уравнения и приходим к следующему уравнению:
Корень этого уравнения угадывается автоматически: . Других корней не будет, так как справа стоит возрастающая функция, поскольку она является суммой возрастающих функций, поэтому нулевое значение она может принимать только при каком-то одном значении
.
Итак, , значит
. Возвращаясь к исходным переменным, получаем следующую систему:
В результате приходим к окончательному ответу: и
.
В общем виде уравнение прямой может быть записано следующим образом: . Известно, что эта прямая проходит через точку
, то есть имеет место равенство:
(1)
Кроме того, прямая касается графика функции . Значит уравнение
должно иметь ровно один корень. Введём замену . Тогда последнее условие эквивалентно тому, что дискриминант квадратного уравнения
(2)
равен нулю, и корень при этом неотрицателен. То есть получаем:
Таким образом с учётом уравнения (1) приходим к следующей системе:
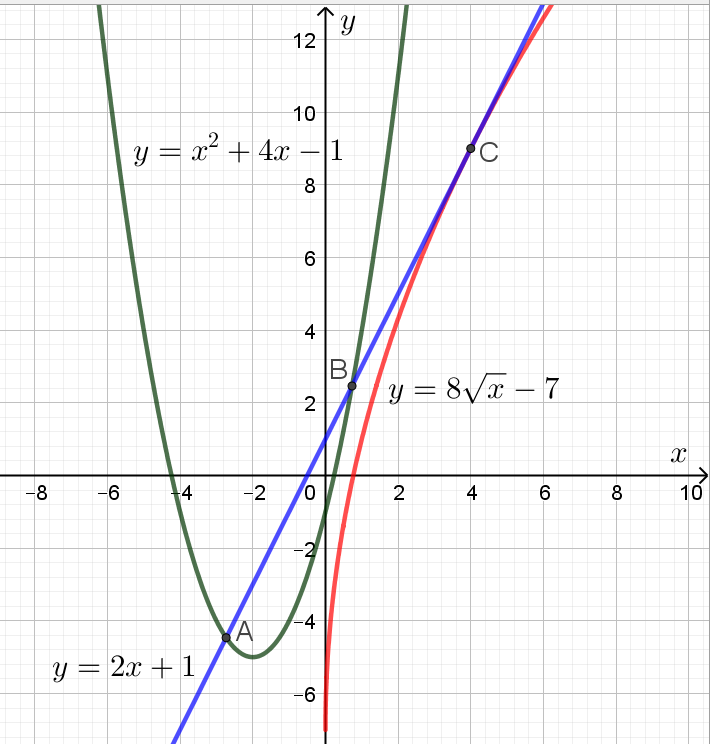
Решая эту систему методом подстановки, получаем следующие результаты: ( и
) или (
и
). При
и
уравнение (2) имеет один неотрицательный корень
. При
и
уравнение (2) имеет один неотрицательный корень
.
То есть из двух прямых и
нужно выбрать такую, которая пересекает график функции
в двух различных точках.
- Решаем сперва уравнение:
Дискриминант последнего уравнения положителен. Значит, оно имеет два различных корня. Этот случай нам подходит.
- Решаем теперь уравнение:
Дискриминант этого уравнения равен нулю. Значит, решение в этом случае будет одно. Этот случай нам не подходит.
Ответ: .
Примечание. Для наглядности изобразим ситуацию на графике, хотя делать это необязательно, поскольку в задании этого не требуют:
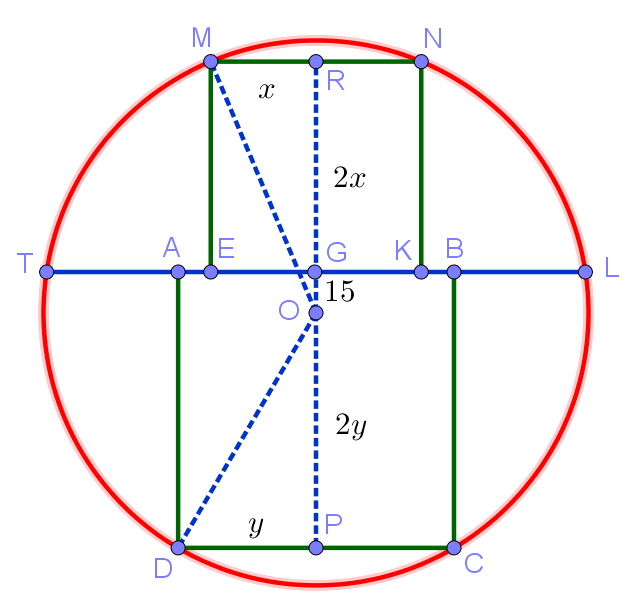
4. Хорда окружности, удалённая от центра на расстояние 15, разбивает окружность на два сегмента, в каждый из которых вписан квадрат. Найдите разность сторон этих квадратов.
Пусть радиус окружности равен . Рассмотрим прямоугольные треугольники OMR и ODP. С учётом введённых на рисунке обозначений распишем теорему Пифагора для этих треугольников:
Вычтем почленно второе уравнение из первого:
Преобразуем полученное выражение, используя формулу «разность квадратов»:
Поделим обе части этого уравнения на и обозначит разность
за
. В результате приходим к следующему уравнению:
Искомая разность сторон квадратов в наших обозначениях будет равна .
Ответ: 24.
Введём замену: . Тогда неравенство принимает вид:
Теперь, используя стандартные свойства логарифмов, представим логарифмическое выражение слева от знака неравенства следующим образом:
Введём ещё одну замену: . Тогда после умножения обеих частей неравенства на положительное число
неравенство принимает вид:
Последовательно возвращаемся к исходной переменной :
Окончательно получаем следующий ответ:
Пусть в первую бочку долили кг воды, а во вторую —
кг. Пусть в первой бочке находится
кг, а во второй
кг соли.
Тогда изначально в первой бочке процентное содержание соли составляло:
а после доливания воды оно стало равно:
Аналогично, во второй бочке изначально процентное содержание соли составляло:
а после доливания воды оно стало равно:
Тогда справедливы равенства:
(3)
(4)
Из уравнения (3) выражаем , из уравнения (4) выражаем
, а из уравнения
выражаем
. Мы ищем минимальное значение суммы
. Проще всего найти его, используя неравенство Коши:
Итак, наименьшее количество воды, которое могло быть долито в обе бочки вместе равно 80 кг.
Этот случай реализуется при , когда неравенство Коши преобразуется в равенство. То есть при
. Подставляя это в выражение
, получаем после преобразований, что
. Отрицательный корень мы в расчёт не берём.
Ответ: 80 кг.
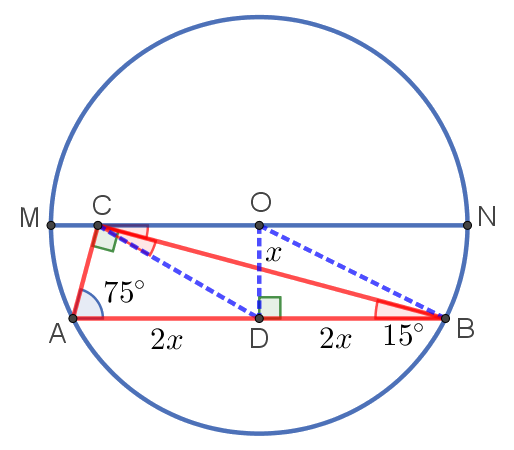
7. Вершина прямого угла C прямоугольного треугольника ABC расположена на диаметре окружности, параллельном хорде AB. Найдите площадь треугольника ABC, если ∠BAC = 75°, а радиус окружности равен 10.
Выполним следующие дополнительные построения:
- проведём высоту OD к хорде AB. Тогда D — середина AB, так как OD — высота и медиана, проведённая к основанию равнобедренного треугольника AOB;
- проведём отрезок CD. Он является медианой прямоугольного треугольника ACB, проведённой из вершины прямого угла. Значит, CD = AD = BD.
Переходим к решению:
- сумма углов в любом треугольнике равна 180°. Значит, ∠CBA = 15°;
- так как CD = BD, то треугольник CDB — равнобедренный и ∠CBD = ∠DCB = 15°;
- ∠CBD = ∠BCO = 15°, поскольку они являются накрест лежащими при параллельных прямых и секущей. Значит, ∠DСO = 30°;
- значит, в прямоугольном треугольнике COD против угла в 30° лежит катет OD, который равен половине гипотенузы CD. Пусть DO = x, а CD = AD = DB = 2x;
- из теоремы Пифагора для треугольника ODB получаем, что
, то есть
;
- тогда искомая площадь треугольника ABC равна половине произведения его высоты, проведённой к стороне AB, которая по длине равна x, на основание AB, которое по длине равно 4x. То есть искомая площадь равна
.
Ответ: 40.
выполняется для всех значений .
Преобразуем данное неравенство, раскрыв в нём скобки и использовав основное тригонометрическое тождество. В результате после всех преобразований получаем следующее неравенство:
Ведём замену , причём
. Тогда получим следующее неравенство:
Задача свелась к тому, чтобы найти все значения параметра , при котором последнее неравенство выполняется при всех
.
Для решения этой задачи представим последнее неравенство в виде:
Легко видеть, что при любых значениях
, так как дискриминант соответствующего квадратного уравнения отрицателен, и ветви соответствующей параболы направлены вверх. Поэтому мы можем разделить обе части последнего неравенства на положительное выражение
, при этом знак неравенства не поменяется:
(5)
Исследуем функцию на возрастание. Для этого определим при каких значениях
её производная положительна:
Так как , а
, то на промежутке
данная функция возрастает. Поэтому неравенство (5) будет выполняться при любом
при условии, что
, то есть
.
Ответ: .
Подготовка к вступительному экзамену по математике в МФТИ
Если вам требуется подготовка к вступительному экзамену по математике в МФТИ, обращайтесь к опытному профессиональному репетитору в Москве Сергею Валерьевичу. Возможны как очные, так и удаленный занятия через интернет с использованием интерактивной доски. Как показывает практика, в условиях ограниченности во времени именно занятия с репетитором обеспечивают наиболее эффективную подготовку к вступительным экзаменам. Подробную информацию о занятиях с репетитором вы можете найти на этой странице. Успехов вам в подготовке к экзаменам!


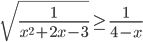
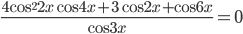
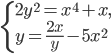
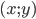
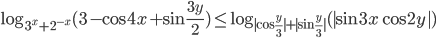
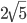
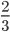
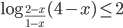
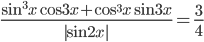
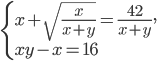
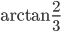
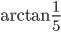
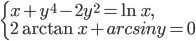
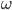
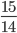
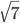
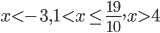
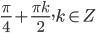
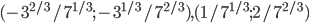
![R=sqrt[4]{3},AB=2/sqrt[4]{3},AD=4/sqrt[4]{3}](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_7115f99dd4e1ef69aaa4de6b780ebda9.gif)
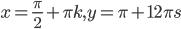
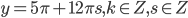
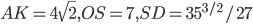
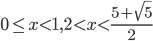
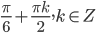
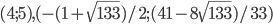
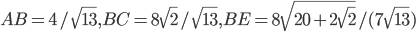
![Rendered by QuickLaTeX.com [ 4t^2-2sqrt{3}t-6=0Leftrightarrowleft[ begin{array}{l} t_1 = -frac{sqrt{3}}{2} \ t_2=sqrt{3}. end{array} ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-8e85e67c476157c1f85c10a768fe9a26_l3.png)
![Rendered by QuickLaTeX.com [ begin{cases} x^3+y^3=19 \ (xy+8)(x+y)=2. end{cases} ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-e7bc49f8e253669ff9ba49d9426f85af_l3.png)
![Rendered by QuickLaTeX.com [ begin{cases} (x+y)((x+y)^2-3xy)=19 \ (xy+8)(x+y)=2. end{cases} ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-178655bc3fda7ef894fc3bbd7840314d_l3.png)
![Rendered by QuickLaTeX.com [ begin{cases} a(a^2-3b)=19 \ a(b+8)=2 end{cases}Leftrightarrow begin{cases} a^3-3ab = 19 \ 3ab+24a=6. end{cases} ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-5c997b7d3fe4081ba0adee4f624d29fa_l3.png)
![Rendered by QuickLaTeX.com [ begin{cases} x+y = 1 \ xy=-6. end{cases} ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-4a755b8f09270e84f7dc7d2a2b347511_l3.png)
![Rendered by QuickLaTeX.com [ begin{cases} k+b = 3 \ 16-7k-kb=0. end{cases} ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-f6bc14d85bd685587ec8be4ccf4a0b59_l3.png)
![Rendered by QuickLaTeX.com [ begin{cases} x^2 = R^2-(2x+15)^2 \ y^2 = R^2 - (2y-15)^2. end{cases} ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-4d914f9a98f6f9b06171fc2db0fd713e_l3.png)
![Rendered by QuickLaTeX.com [ =40sqrt{left(frac{m+3}{m-1}-1right)(m-1)}= ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-f3a93b14138c23455fa41a3e86698c39_l3.png)
![Rendered by QuickLaTeX.com [ y'=-frac{t^2+6t-29}{(t^2-6t+11)^2}>0Leftrightarrow ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-8059bcd31ba16c4f55ea4f68984b4b4a_l3.png)