Обновлено: 12.03.2023
Теория электромагнетизма в ее классическом понимании сформировалась в XIX веке. Это фундаментальное учение о том, как устроен наш мир.
Значение электромагнетизма заключается в том, что:
- Философское и мировоззренческое значение данной теории придает описание электромагнитного поля, как особой формы существования материи.
- Электромагнетизм играл значимую роль в появлении и развитии теории относительности.
- Данный раздел физики играет большую роль в научно – техническом прогрессе.
Электромагнетизмом называют раздел физики, который посвящен изучению законов и явлений, связанных с электрическими и магнитными полями, их связью и взаимозависимостью.
Фундаментальными понятиями теории электромагнетизма являются:
- заряд;
- электрическое поле;
- потенциал;
- энергия поля;
- электромагнитное взаимодействие;
- магнитное поле;
- магнитная индукция;
- электромагнитное поле и др.
К основным законам электромагнетизма можно отнести следующие:
- закон Кулона;
- закон Ампера;
- закон Био-Савара-Лапласа;
- закон Ома;
- закон индукции Фарадея;
- уравнения Максвелла.
Закон Кулона
Обобщая результаты экспериментов с крутильными весами, Кулон предложил закон, в соответствии с которым пара точечных зарядов (рис.1) $q_1$ и $q_2$, находящихся в вакууме действуют друг на друга с силами равными $F$, направленными вдоль прямой, которая соединяет рассматриваемые заряды, при этом:
где $ epsilon_0=8,85bullet 10^$ Ф/м – электрическая постоянная; $vec F_$ — сила, действующая на заряд $q_2$ со стороны заряда $q_1$.
Рисунок 1. Закон Кулона. Автор24 — интернет-биржа студенческих работ
Готовые работы на аналогичную тему
Одноименные заряды отталкиваются, противоположные притягиваются.
Закон Кулона – это основной закон электростатики.
Для вычисления сил взаимодействия заряженных тел произвольных форм и размеров используют принцип суперпозиции, который можно сформулировать следующим образом:
Взаимодействие пары точечных зарядов не изменяется, если внести третий заряд. Он будет взаимодействовать с первыми двумя зарядами.
Закон Ампера
Датский физик Г. Эрстед обнаружил, что магнитная стрелка, при нахождении рядом с проводом с током может поворачиваться. Данное открытие стало основанием для вывода о связи магнитных и электрических явлений. Основным в открытии Эрстеда было то, что магнит реагировал на перемещающийся электрический заряд. Появилось понимание того, что магнитное поле создается перемещающимся зарядом.
Проводя анализ экспериментов Эрстеда, А. Ампер выдвинул гипотезу о том, что земной магнетизм порождается токами, которые обтекают нашу планету в направлении с запада на восток.
Вывод был сделан следующий:
Магнитные свойства каждого тела определены замкнутыми электрическими токами в нем.
Ампер установил, что два проводника с токами взаимодействуют. Если токи в параллельных проводниках однонаправленные, то эти проводники притягиваются.
Результатом экспериментов Ампера стал закон, который назвали его именем.
Сила взаимодействия пары контуров с током зависит от силы тока в каждом контуре и уменьшается при увеличении расстояния между рассматриваемыми контурами:
где $mu_0=4pibullet 10^$ Н/$A^2$ — магнитная постоянная; $ dvec F_$ – сила, с которой первый элемент с током действует на второй. Выражение (2) содержит двойное векторное произведение; $I_1; I_2$ — силы токов, которые текут в проводниках; $I_1dvec l_1$; $I_2dvec l_2$ — элементы токов (рис.2).
Рисунок 2. Закон Ампера. Автор24 — интернет-биржа студенческих работ
Закон Био – Савара – Лапласа
Проводники с током воздействуют друг на друга, посредством магнитных полей, которые их окружают.
Введем векторную величину $vec B$, которая будет характеристикой магнитного поля. Для этого параметра поля был установлен экспериментально закон, который получил название по именам его первооткрывателей, закон Био – Савара- Лапласа:
где $Idl$ — элемент с током, который создает магнитное поле; $r$ — расстояние до точки в которой поле рассматривается поле; $alpha$ — угол между векторами $dvec l$ и $vec r$.
Полученный вектор индукции нормален к векторам $dvec l$ и $vec r$, его направление определяют при помощи правила буравчика:
Если правый винт поворачивать по направлению тока, то вектор индукции в каждой точке параллелен направлению бесконечно малого перемещения конца рукоятки буравчика.
Закон Био – Савара- Лапласа играет такую же роль в магнитостатике, как закон Кулона в электростатике.
Закон Ома
В начале XIX века Г. Ом рассматривая процессы течения электрического тока в цепи, имеющей источник установил, что:
где $I$ — сила тока в цепи; $Ɛ$ — электродвижущая сила источника тока; $r$ — внутреннее сопротивление источника; $R$ — сопротивление цепи (внешнее). Выражение (4) описывает ситуацию в замкнутой цепи.
Если рассматривать участок цепи, по которому течет ток, то закон Ома представляется в виде:
где $U$ — напряжение участка; $R$ — сопротивление участка.
Если участок цепи содержит источник, то закон Ома предстанет в виде:
Выражение (6) означает, что напряжение на нагрузке меньше ЭДС на величину, равную падению напряжения ($Ir$) на внутреннем сопротивлении источника.
Закон Ома в виде (4-6) называют законом в интегральной форме.
Закон Ома в дифференциальной форме можно записать как:
где $vec j$ — вектор плотности тока; ρ – удельное сопротивление проводника; $vec E$ — вектор напряженности электрического поля.
Закон индукции Фарадея
Электромагнитная индукция была открыта Фарадеем в 1881 году.
Фарадей понимал электромагнитную индукцию как возбуждение токов в проводниках под воздействием магнитного поля.
Экспериментально доказано, что электродвижущая сила (ЭДС) ($Ɛ $) индукции в контуре пропорциональна скорости изменения магнитного потока сквозь рассматриваемый контур. В Международной системе единиц (СИ) данный результат выражен формулой:
где $Ф$ -переменный магнитный поток через замкнутый контур или его часть.
В общем случае изменение магнитного потока сквозь плоский контур вызвано:
- переменным во времени магнитным полем;
- движением контура в поле и переменой его ориентации.
Уравнения Максвелла
Максвелл доказал, что сущностью электромагнитной индукции стало создание магнитным полем вихревого электрического поля. Индукционный ток является вторичным эффектом, который появляется в проводящих веществах. Трактовка электромагнитной индукции, которую дал Максвелл стала более общей.
Уравнения Максвелла стали математическим основанием классического электромагнетизма.
Запишем их в виде системы:
$div, vec=rho left( 11 right)$,
$div, vec=0left( 12 right)$.
В выражениях (9)- (12) мы имеем: $vec E$ и $vec D$ — напряженность и индукция электрического поля;
$vec H$ и $vec B$ — напряженность и магнитная индукции;
$rho$ — объемная плотность электрического заряда;
$vec j$ — плотность тока.
Уравнения Максвелла у нас представлены в дифференциальной форме. Для однозначного описания электромагнитных полей уравнения Максвелла дополняют материальными уравнениями среды. В общем виде они записываются в виде функций:
$vec D=vec D(vec E)$; $vec B=vec B(vec H)$; $vec j=vec j(vec E)$.
Если эта схема вам прекрасно знакома и не вызывает рефлекса кое-что пояснить и дополнить, чтобы не ввела других в заблуждение, то прошу под кат. Если она вам прекрасно знакома, и вы поняли, что там требуется допояснять, то гуляйте дальше) Пост не для вас.
Если схема не очень знакома или понятна, можете заглянуть.
Возьмем один из них, один из полезнейших на мой взгляд:
Эту динамику мы можем записать в форме самой простой системы дифф. уравнений в мире (не считая экспоненты)
Обычно дифф. ур. записывают, чтобы продемонстрировать дифференциал, в данном случае производную по времени, поэтому типичная запись:
Итак, к чему все это.
Итак, мы видели, что круговая динамика это две связанные величины, которые на одном графике от времени, представляют собой две волны со сдвигом пи/2.
Таким же образом из начального возмущения распространяется электромагнитная волна, через зацикленность интенсивностей и их изменений. Изменение электрического поля порождает магнитное поле, которое, увеличиваясь (=изменяясь), порождает обратное электрическое поле, которое… и т.д. Это классическое (и верное) объяснение, известное наверное каждому.
Но… посмотрим на схему с которой все началось:
From my understanding Vern is correct. Your citation of Maxwell’s equation is a good idea, but you are incomplete. In free space you have no currents and no charges so Maxwell’s 4 equations simplify down to 2 equations (considering a single spatial dimension):
dE/dx = -dB/dt
dE/dt = -c 2 dB/dx
So when the temporal derivative of one is maximal the spatial derivative of the other is minimal (maximally negative). If you consider a simple single-frequency sinusoidal plane wave you find that this happens for E and B in phase. In the above equations:
E = Emax cos(kx-wt)
B = Bmax cos(kx-wt)
Вот, вышло, что должны быть в фазе. И еще в разных местах в интернете другие вариации на эту тему.
Правильно ли? Нет, неправильно.
Почему неправильно? Потому что ротор поля это не его производная по пространству!
dE/dx — так нельзя.
Поэтому ротор поля это не дифференциал, это специальный способ выразить его значение (наподобие смены системы координат), иначе говоря, ротор — это и есть значение поля.
Как в итоге выглядит каскадная зацикленная волна таких закрученностей?
Довольно сложно описать…
Совсем упрощенная схема выглядит так
Но это большое упрощение, такой картинки с колечками вообще не возникает, т.к. все находится во вращении и это скорее спирали, вращающиеся вокруг друг друга. Но при этом и не спирали, т.к. расходятся в пространстве, и взаимосложение даст еще более дивную картину.
Однако в любом случае… сдвиг на пи/2 есть.
Что же насчет классического рисунка? Классический рисунок представляет собой пример однонаправленной волны линейной поляризации… Что-то похожее на лазер. Такую поляризованную волну можно получить, прибавляя к электро- волне круговой поляризации ее зеркальное отражение (стереоизомер). Получится ли после такого сложения волна с колебаниями электропотенциала и магнитной интенсивности в одной фазе?
Следует помнить, что стереоизомеры вращательно-поляризованных волн не симметричны, т.к. векторы сопуствующего магнитного поля всегда повернуты под прямым углом в одну и ту же сторону.
Часто бывает, что задачу не удается решить из-за того, что под рукой нет нужной формулы. Выводить формулу с самого начала – дело не самое быстрое, а у нас на счету каждая минута.
Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.
Магнетизм: определение
Магнетизм – это взаимодействие движущихся электрических зарядов, происходящее посредством магнитного поля.
Поле – особая форма материи. В рамках стандартной модели существует электрическое, магнитное, электромагнитные поля, поле ядерных сил, гравитационное поле и поле Хиггса. Возможно, есть и другие гипотетические поля, о которых мы пока что можем только догадываться или не догадываться вовсе. Сегодня нас интересует магнитное поле.
Магнитная индукция
Так же, как заряженные тела создают вокруг себя электрическое поле, движущиеся заряженные тела порождают магнитное поле. Магнитное поле не только создается движущимися зарядами (электрическим током), но еще и действует на них. По сути магнитное поле можно обнаружить только по действию на движущиеся заряды. А действует оно на них с силой, называемой силой Ампера, о которой речь пойдет позже.
Изображение магнитного поля при помощи силовых линий
Прежде чем мы начнем приводить конкретные формулы, нужно рассказать про магнитную индукцию.
Магнитная индукция – это силовая векторная характеристика магнитного поля.
Она обозначается буквой B и измеряется в Тесла (Тл). По аналогии с напряженностью для электрического поля Е магнитная индукция показывает, с какой силой магнитное поле действует на заряд.
Кстати, вы найдете много интересных фактов на эту тему в нашей статье про теорию магнитного поля и интересные факты о магнитном поле Земли.
Как определять направление вектора магнитной индукции? Здесь нас интересует практическая сторона вопроса. Самый частый случай в задачах – это магнитное поле, создаваемое проводником с током, который может быть либо прямым, либо в форме окружности или витка.
Для определения направления вектора магнитной индукции существует правило правой руки. Приготовьтесь задействовать абстрактное и пространственное мышление!
Если взять проводник в правую руку так, что большой палец будет указывать на направление тока, то загнутые вокруг проводника пальцы покажут направление силовых линий магнитного поля вокруг проводника. Вектор магнитной индукции в каждой точке будет направлен по касательной к силовым линиям.
Сила Ампера
Представим, что есть магнитное поле с индукцией B. Если мы поместим в него проводник длиной l, по которому течет ток силой I, то поле будет действовать на проводник с силой:
Это и есть сила Ампера. Угол альфа – угол между направлением вектора магнитной индукции и направлением тока в проводнике.
Направление силы Ампера определяется по правилу левой руки: если расположить левую руку так, чтобы в ладонь входили линии магнитной индукции, а вытянутые пальцы указывали бы направление тока, отставленный большой палец укажет направление силы Ампера.
Сила Лоренца
Итак, частица с зарядом q движется в магнитном поле с индукцией В со скоростью v, а альфа – это угол между вектором скорости частицы и вектором магнитной индукции. Тогда сила, которая действует на частицу:
Как определить направление силы Лоренца? По правилу левой руки. Если вектор индукции входит в ладонь, а пальцы указывают на направление скорости, то отогнутый большой палец покажет направление силы Лоренца. Отметим, что так направление определяется для положительно заряженных частиц. Для отрицательных зарядов полученное направление нужно поменять на противоположное.
Если частица массы m влетает в поле перпендикулярно линиям индукции, то она будет двигаться по окружности, а сила Лоренца будет играть роль центростремительной силы. Радиус окружности и период обращения частицы в однородном магнитном поле можно найти по формулам:
Взаимодействие токов
Рассмотрим два случая. Первый – ток течет по прямому проводу. Второй – по круговому витку. Как мы знаем, ток создает магнитное поле.
В первом случае магнитная индукция провода с током I на расстоянии R от него считается по формуле:
Мю – магнитная проницаемость вещества, мю с индексом ноль – магнитная постоянная.
Во втором случае магнитная индукция в центре кругового витка с током равна:
Также при решении задач может пригодиться формула для магнитного поля внутри соленоида. Соленоид – это катушка, то есть множество круговых витков с током.
Пусть их количество – N, а длина самого соленоилда – l. Тогда поле внутри соленоида вычисляется по формуле:
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Магнитный поток и ЭДС
Если магнитная индукция – векторная характеристика магнитного поля, то магнитный поток – скалярная величина, которая также является одной из самых важных характеристик поля. Представим, что у нас есть какая-то рамка или контур, имеющий определенную площадь. Магнитный поток показывает, какое количество силовых линий проходит через единицу площади, то есть характеризует интенсивность поля. Измеряется в Веберах (Вб) и обозначается Ф.
S – площадь контура, альфа – угол между нормалью (перпендикуляром) к плоскости контура и вектором В.
При изменении магнитного потока через контур в контуре индуцируется ЭДС, равная скорости изменения магнитного потока через контур. Кстати, подробнее о том, что такое электродвижущая сила, вы можете почитать в еще одной нашей статье.
По сути формула выше – это формула для закона электромагнитной индукции Фарадея. Напоминаем, что скорость изменения какой-либо величины есть не что иное, как ее производная по времени.
Для магнитного потока и ЭДС индукции также справедливо обратное. Изменение тока в контуре приводит к изменению магнитного поля и, соответственно, к изменению магнитного потока. При этом возникает ЭДС самоиндукции, которая препятствует изменению тока в контуре. Магнитный поток, который пронизывает контур с током, называется собственным магнитным потоком, пропорционален силе тока в контуре и вычисляется по формуле:
L – коэффициент пропорциональности, называемый индуктивностью, который измеряется в Генри (Гн). На индуктивность влияют форма контура и свойства среды. Для катушки с длиной l и с числом витков N индуктивность рассчитывается по формуле:
Формула для ЭДС самоиндукции:
Энергия магнитного поля
Электроэнергия, ядерная энергия, кинетическая энергия. Магнитная энергия – одна из форм энергии. В физических задачах чаще всего нужно рассчитывать энергию магнитного поля катушки. Магнитная энергия катушки с током I и индуктивностью L равна:
Объемная плотность энергии поля:
На уроке Физика для чайников. Урок 18. Электрическое поле мы узнали, что такое электрическое поле. Но электрическое взаимодействие – это частный случай электромагнитного взаимодействия. Вообще, магнитное поле является порождением электрического тока. В 1820 году Х. Эрстед провел опыт, доказывающий, что электрический ток создает магнитное поле. Его опыт заключался в помещении над магнитной стрелкой прямолинейного металлического проводник а, направленного параллельно стрелке. При пропускании через проводник электрического тока стрелка поворачивалась почти перпендикулярно проводнику. При изменении направления тока стрелка разворачивалась на 180 градусов. Аналогичный разворот наблюдался, если провод переносился на другую сторону, располагаясь не над, а под стрелкой:
Вокруг неподвижного заряда создается исключительно электрическое поле. Но если этот заряд движется, то он порождает еще и магнитное поле. Если магнит лежит на столе, вокруг него есть только магнитное поле. Но если двигаться относительно магнита, то такой вот движущийся наблюдатель зафиксирует и электрическое поле. Таким образом утверждение о существовании электрического или магнитного полей в заданной точке имеет смысл только при указании системы отсчёта, относительно которой они рассматриваются. Оба поля являются проявлением единого электромагнитного поля.
Итак, движущиеся заряды создают магнитное поле. С другой стороны, если заряд поместить в магнитное поле, то он будет двигаться. Таким образом, магнитное поле, может создавать электрический ток. Это явление используется для генерации электричества, которое имеет у все у нас в розетках. Генератор представляет собой вращающийся магнит и катушку с намотанным на нем проводником. Магнит вращается, например, за счет падающей на лопасти огромного колеса воды (гидроэлектростанция).
Направление силовых линий магнитного поля и движения зарядов определяются так называемым правилом буравчика:
Если говорить по русский, то представьте себе вкручиваемый куда-либо винт. Направление вкручивания – это электрический ток. Направление вращения – это магнитное поле.
где $E↖$ — напряженность поля; $F↖$ — сила, действующая на помещенный в данную точку поля заряд $q$. Направление вектора $E↖$ совпадает с направлением силы, действующей на положительный заряд, и противоположно направлению силы, действующей на отрицательный заряд.
Единицей напряженности в СИ является вольт на метр (В/м).
Напряженность поля точечного заряда. Согласно закону Кулона, точечный заряд $q_0$ действует на другой заряд $q$ с силой, равной
Модуль напряженности поля точечного заряда $q_0$ на расстоянии $r$ от него равен
Вектор напряженности в любой точке электрического поля направлен вдоль прямой, соединяющей эту точку и заряд.
Силовые линии электрического поля
Электрическое поле в пространстве принято представлять силовыми линиями. Понятие о силовых линиях ввел М. Фарадей при исследовании магнетизма. Затем это понятие было развито Дж. Максвеллом в исследованиях по электромагнетизму.
Силовая линия, или линия напряженности электрического поля, — это линия, касательная к которой в каждой ее точке совпадает с направлением силы, действующей на положительный точечный заряд, находящийся в этой точке поля.
Линии напряженности положительно заряженного шарика;
Линии напряженности двух разноименно заряженных шариков;
Линии напряженности двух одноименно заряженных шариков
Линии напряженности двух пластин, заряженных разными по знаку, но одинаковыми по абсолютной величине зарядами.
Линии напряженности на последнем рисунке почти параллельны в пространстве между пластинами, и плотность их одинакова. Это говорит о том, что поле в этой области пространства однородно. Однородным называется электрическое поле, напряженность которого одинакова во всех точках пространства.
В электростатическом поле силовые линии не замкнуты, они всегда начинаются на положительных зарядах и заканчиваются на отрицательных зарядах. Они нигде не пересекаются, пересечение силовых линий говорило бы о неопределенности направления напряженности поля в точке пересечения. Плотность силовых линий больше вблизи заряженных тел, где напряженность поля больше.
Поле заряженного шара. Напряженность поля заряженного проводящего шара на расстоянии от центра шара, превышающем его радиус $r≥R$, определяется по той же формуле, что и поля точечного заряда. Об этом свидетельствует распределение силовых линий, аналогичное распределению линий напряженности точечного заряда.
Заряд шара распределен равномерно по его поверхности. Внутри проводящего шара напряженность поля равна нулю.
Магнитное поле. Взаимодействие магнитов
Природные (естественные) магниты
Природные магниты представляют собой куски магнитного железняка (магнетита), состоящего из $FeO$ (31 %) и $Fe_2O$ (69 %). Если такой кусок минерала поднести к мелким железным предметам — гвоздям, опилкам, тонкому лезвию и т. д., они к нему притянутся.
Искусственные постоянные магниты
Постоянный магнит — это изделие из материала, являющегося автономным (самостоятельным, изолированным) источником постоянного магнитного поля.
Искусственные постоянные магниты изготавливают из специальных сплавов, в которые входят железо, никель, кобальт и др. Эти металлы приобретают магнитные свойства (намагничиваются), если их поднести к постоянным магнитам. Поэтому, чтобы изготовить из них постоянные магниты, их специально держат в сильных магнитных полях, после чего они сами становятся источниками постоянного магнитного поля и способны длительное время сохранять магнитные свойства.
На рисунке изображены дугообразный и полосовой магниты.
На рис. даны картины магнитных полей этих магнитов, полученных методом, который впервые применил в своих исследованиях М. Фарадей: с помощью железных опилок, рассыпанных на листе бумаги, на котором лежит магнит. У каждого магнита есть два полюса — это места наибольшего сгущения магнитных силовых линий (их называют также линиями магнитного поля, или линиями магнитной индукции поля). Это места, к которым сильнее всего притягиваются железные опилки. Один из полюсов принято называть северным (($N$), другой — южным ($S$). Если поднести два магнита друг к другу одноименными полюсами, можно увидеть, что они отталкиваются, а если разноименными — притягиваются.
На рис. наглядно видно, что магнитные линии магнита — замкнутые линии. Показаны силовые линии магнитного поля двух магнитов, обращенных друг к другу одноименными и разноименными полюсами. Центральная часть этих картин напоминает картины электрических полей двух зарядов (разноименных и одноименных). Однако существенным различием электрического и магнитного полей является то, что линии электрического поля начинаются на зарядах и заканчиваются на них. Магнитных же зарядов в природе не существует. Линии магнитного поля выходят из северного полюса магнита и входят в южный, они продолжаются и в теле магнита, т. е., как было сказано выше, являются замкнутыми линиями. Поля, силовые линии которых замкнуты, называются вихревыми. Магнитное поле — это вихревое поле (в этом его отличие от электрического).
Применение магнитов
Самым древним магнитным прибором является всем хорошо известный компас. В современной технике магниты используются очень широко: в электродвигателях, в радиотехнике, в электроизмерительной аппаратуре и т. д.
Магнитное поле Земли
Земной шар является магнитом. Как у всякого магнита, у него есть свое магнитное поле и свои магнитные полюсы. Именно поэтому стрелка компаса ориентируется в определенном направлении. Понятно, куда именно должен указывать северный полюс магнитной стрелки, ведь притягиваются разноименные полюсы. Поэтому северный полюс магнитной стрелки указывает на южный магнитный полюс Земли. Этот полюс находится на севере земного шара, несколько в стороне от северного географического полюса (на острове Принца Уэльского — около $75°$ северной широты и $99°$ западной долготы, на расстоянии примерно $2100$ км от северного географического полюса).
При приближении к северному географическому полюсу силовые линии магнитного поля Земли все под большим углом наклоняются к горизонту, и в области южного магнитного полюса становятся вертикальными.
Северный магнитный полюс Земли находится вблизи южного географического полюса, а именно на $66.5°$ южной широты и $140°$ восточной долготы. Здесь силовые линии магнитного поля выходят из Земли.
Другими словами, магнитные полюсы Земли не совпадают с ее географическими полюсами. Поэтому направление магнитной стрелки не совпадает с направлением географического меридиана, и магнитная стрелка компаса лишь приблизительно показывает направление на север.
На стрелку компаса могут влиять также некоторые природные явления, например, магнитные бури, которые являются временными изменениями магнитного поля Земли, связанными с солнечной активностью. Солнечная активность сопровождается выбросом с поверхности Солнца потоков заряженных частиц, в частности, электронов и протонов. Эти потоки, движущиеся с большой скоростью, создают свое магнитное поле, взаимодействующее с магнитным полем Земли.
На земном шаре (кроме кратковременных изменений магнитного поля) встречаются области, в которых наблюдается постоянное отклонение направления магнитной стрелки от направления магнитной линии Земли. Это области магнитной аномалии (от греч. anomalia — отклонение, ненормальность). Одной из самых больших таких областей является Курская магнитная аномалия. Причиной аномалий являются огромные залежи железной руды на сравнительно небольшой глубине.
Земное магнитное поле надежно защищает поверхность Земли от космического излучения, действие которого на живые организмы разрушительно.
Полеты межпланетных космических станций и кораблей позволили установить, что у Луны и планеты Венера отсутствует магнитное поле, а у планеты Марс оно очень слабое.
Опыты Эрстедаи Ампера. Индукция магнитного поля
В 1820 г. датский ученый Г. X. Эрстед обнаружил, что магнитная стрелка, помещенная вблизи проводника, по которому течет ток, поворачивается, стремясь расположиться перпендикулярно к проводнику.
Схема опыта Г. X. Эрстеда изображена на рисунке. Проводник, включенный в цепь источника тока, расположен над магнитной стрелкой параллельно ее оси. При замыкании цепи магнитная стрелка отклоняется от своего первоначального положения. При размыкании цепи магнитная стрелка возвращается в свое первоначальное положение. Отсюда следует, что проводник с током и магнитная стрелка взаимодействуют друг с другом. На основании этого опыта можно сделать вывод о существовании магнитного поля, связанного с протеканием тока в проводнике и о вихревом характере этого поля. Описанный опыт и его результаты явились важнейшей научной заслугой Эрстеда.
В том же году французский физик Ампер, которого заинтересовали опыты Эрстеда, обнаружил взаимодействие двух прямолинейных проводников с током. Оказалось, что если токи в проводниках текут в одну сторону, т. е. параллельны, то проводники притягиваются, если в противоположные стороны (т. е. антипараллельны), то отталкиваются.
Взаимодействия между проводниками с током, т. е. взаимодействия между движущимися электрическими зарядами, называют магнитными, а силы, с которыми проводники с током действуют друг на друга, — магнитными силами.
Согласно теории близкодействия, которой придерживался М. Фарадей, ток в одном из проводников не может непосредственно влиять на ток в другом проводнике. Аналогично случаю с неподвижными электрическими зарядами, вокруг которых существует электрическое поле, был сделан вывод, что в пространстве, окружающем токи, существует магнитное поле, которое действует с некоторой силой на другой проводник с током, помещенный в это поле, либо на постоянный магнит. В свою очередь, магнитное поле, создаваемое вторым проводником с током, действует на ток в первом проводнике.
Подобно тому как электрическое поле обнаруживается по его воздействию на пробный заряд, внесенный в это поле, магнитное поле можно обнаружить по ориентирующему действию магнитного поля на рамку с током малых (по сравнению с расстояниями, на которых магнитное поле заметно меняется) размеров.
Провода, подводящие ток к рамке, следует сплести (или расположить близко друг к другу), тогда результирующая сила, действующая со стороны магнитного поля на эти провода, будет равна нулю. Силы же, действующие на такую рамку с током, будут ее поворачивать, так что ее плоскость установится перпендикулярно линиям индукции магнитного поля. В примере, рамка повернется так, чтобы проводник с током оказался в плоскости рамки. При изменении направления тока в проводнике рамка повернется на $180°$. В поле между полюсами постоянного магнита рамка повернется плоскостью перпендикулярно магнитным силовым линиям магнита.
Магнитная индукция
Магнитная индукция ($В↖$) — это векторная физическая величина, характеризующая магнитное поле.
За направление вектора магнитной индукции $В↖$ принимается:
1) направление от южного полюса $S$ к северному полюсу $N$ магнитной стрелки, свободно устанавливающейся в магнитном поле, или
2) направление положительной нормали к замкнутому контуру с током на гибком подвесе, свободно устанавливающемся в магнитном поле. Положительной считается нормаль, направленная в сторону перемещения острия буравчика (с правой нарезкой), рукоятку которого вращают по направлению тока в рамке.
Ясно, что направления 1) и 2) совпадают, что было установлено еще опытами Ампера.
Что касается величины магнитной индукции (т. е. ее модуля) $В$, которая могла бы характеризовать силу действия поля, то экспериментами было установлено, что максимальная сила $F$, с которой поле действует на проводник с током (помещенный перпендикулярно линиям индукции магнитного поля), зависит от силы тока $I$ в проводнике и от его длины $∆l$ (пропорциональна им). Однако сила, действующая на элемент тока (единичной длины и силы тока), зависит только от самого поля, т. е. отношение $/$ для данного поля является величиной постоянной (аналогично отношению силы к заряду для электрического поля). Эту величину и определяют как магнитную индукцию.
Индукция магнитного поля в данной точке равна отношению максимальной силы, действующей на проводник с током, к длине проводника и силе тока в проводнике, помещенном в эту точку.
Чем больше магнитная индукция в данной точке поля, тем с большей силой будет действовать поле в этой точке на магнитную стрелку или движущийся электрический заряд.
Единицей магнитной индукции в СИ является тесла (Тл), названная в честь сербского электротехника Николы Теслы. Как видно из формулы, $1$ Тл $=l/$
Если имеется несколько различных источников магнитного поля, векторы индукции которых в данной точке пространства равны $↖, ↖, ↖. $, то, согласно принципу суперпозиции полей, индукция магнитного поля в этой точке равна сумме векторов индукции магнитных полей, создаваемых каждым источником.
Линии магнитной индукции
Для наглядного представления магнитного поля М. Фарадей ввел понятие магнитных силовых линий, которые он неоднократно демонстрировал в своих опытах. Картина силовых линий легко может быть получена с помощью железных стружек, насыпанных на картон. На рисунке представлены: линии магнитной индукции прямого тока, соленоида, кругового тока, прямого магнита.
Линиями магнитной индукции, или магнитными силовыми линиями, или просто магнитными линиями называют линии, касательные к которым в любой точке совпадают с направлением вектора магнитной индукции $В↖$ в этой точке поля.
Если вместо железных опилок вокруг длинного прямолинейного проводника с током поместить маленькие магнитные стрелки, то можно увидеть не только конфигурацию силовых линий (концентрические окружности), но и направление силовых линий (северный полюс магнитной стрелки указывает направление вектора индукции в данной точке).
Направление магнитного поля прямого тока можно определить по правилу правого буравчика.
Если вращать рукоятку буравчика так, чтобы поступательное движение острия буравчика указывало направление тока, то направление вращения рукоятки буравчика укажет направление силовых линий магнитного поля тока.
Направление магнитного поля прямого тока можно определять также и с помощью первого правила правой руки.
Если охватить проводник правой рукой, направив отогнутый большой палец по направлению тока, то кончики остальных пальцев в каждой точке покажут направление вектора индукции в этой точке.
Вихревое поле
Линии магнитной индукции являются замкнутыми, это свидетельствует о том, что в природе нет магнитных зарядов. Поля, силовые линии которых замкнуты, называют вихревыми полями. То есть магнитное поле — это вихревое поле. Этим оно отличается от электрического поля, создаваемого зарядами.
Соленоид
Соленоид — это проволочная спираль с током.
Диамагнетики отталкиваются от магнита, парамагнетики — притягиваются. По этим признакам их можно отличить друг от друга. У большинства веществ магнитная проницаемость практически не отличается от единицы, только у ферромагнетиков намного превосходит ее, достигая нескольких десятков тысяч единиц.
Ферромагнетики. Наиболее сильные магнитные свойства проявляют ферромагнетики. Магнитные поля, создаваемые ферромагнетиками, намного сильнее внешнего намагничивающего поля. Правда, магнитные поля ферромагнетиков создаются не вследствие обращения электронов вокруг ядер — орбитального магнитного момента, а вследствие собственного вращения электрона — собственного магнитного момента, называемого спином.
Температура Кюри ($Т_с$) — это температура, выше которой ферромагнитные материалы теряют свои магнитные свойства. Для каждого ферромагнетика она своя. Например, для железа $Т_с = 753°$С, для никеля $Т_с = 365°$С, для кобальта $Т_с = 1000°$ С. Существуют ферромагнитные сплавы, у которых $Т_с 0$), или уменьшается ($∆Ф 0$,и иметь одинаковое с ними направление, если $∆Ф
Читайте также:
- Речевая культура делового разговора кратко
- История склеивания кратко и понятно
- Религиозные войны в европе 16 17 кратко
- Выделение среди соседних стран союзных враждебных и нейтральных государств россии кратко
- Раздача лекарственных средств на посту алгоритм кратко
3.1. Электромагнетизм
3.2. Взаимодействие токов
3.3. Принцип суперпозиции
3.4. Закон Био-Савара-Лапласа
3.4.1. Магнитное поле проводника с током
3.4.2. Применение закона Био-Савара-Лапласа для анализа магнитных полей проводников с током различной конфигурации. Конечный и бесконечный прямолинейный проводник с током
3.4.3. Магнитное поле кругового проводника с током
3.4.4. Магнитное поле вдали от центра контура с током
3.4.5. Магнитное поле соленоида
3.5. Магнитный поток
3.6. Напряженность магнитного поля
3.7. Силы, действующие в магнитном поле
3.7.1. Сравнение электрической и магнитной сил
3.8. Взаимодействие параллельных проводников с током
3.9. Закон Ампера
3.10. Работа по перемещению проводника стоком в магнитном поле
3.11. Действие магнитного поля на контур с током
3.12. Магнитный момент контура с током
3.13. Явление электромагнитной индукции. ЭДС электромагнитной индукции
3.14. Явление взаимоиндукции
3.15. Явление самоиндукции
3.16. Вихревые токи. Токи Фуко
3.17. Энергия магнитного поля
3.18. Плотность энергии магнитного поля
3.19. Единицы измерения магнитных величин
3.20. Магнетики. Вещества в магнитном поле
3.21. Движение зарядов в магнитном поле
3.22. Уравнения Максвелла. Обобщение теории магнитного поля
3.23. Анализ массово-зарядового состояния элементарных частиц
3.24. Приложение к теореме Остроградского-Гаусса
3.25. Первое уравнение Максвелла
3.26. Второе уравнение Максвелла
3.27. Третье уравнение Максвелла
3.28. Четвертое уравнение Максвелла
3.29. Анализ III и IV уравнений
3.1. Электромагнетизм
Электромагнетизм — это раздел электричества, рассматривающий воздействие движущихся зарядов на движущиеся заряды.
Движение заряда может быть равномерным (I закон Ньютона). Если к такому заряду привязать систему отсчета, то в этой системе заряд не движется. Таким образом, если другая заряженная частица движется параллельно первой с той же скоростью и в том же направлении, то между ними не будет магнитного взаимодействия, а только кулоновское взаимодействие. Итак, чтобы магнитное взаимодействие проявилось, частицы должны двигаться или с разной скоростью или в разном направлении.
Связь характеристик магнитного поля:
B = µ0*H; где B — индукция магнитного поля; H — напряженность магнитного поля; µ0 = 1,16 * 10-6
Для того, чтобы заряды направленно двигались в пространстве, необходимо наличие проводящей среды, специально ориентированной в пространстве.
3.2. Взаимодействие параллельных токов
Закон Фарадея:
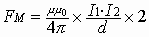
Направление токов влияет на силу взаимодействия.
По аналогии с электростатикой, где сила определяет напряженность, а напряженность — индукцию, в магнетизме напряженность и индукция — силовые характеристики. Принято в электростатике основной силовой характеристикой считать напряженность, а в магнетизме — индукцию.
Правило буравчика:
Если ток направлен по закрутке буравчика, то шляпка вращается по силовой линии. В каждой точке пространства направление силовых линий совпадает с направление касательной. Таким образом, силовые линии магнитного поля являются замкнутыми.
Примем на рисунке направление токов перпендикулярно плоскости рисунка. Тогда в точках:
A:Bрез = B1 + B2 D:Bрез = B1 — B2 C:Bрез=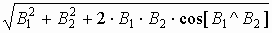

3.4. Закон Био-Савара–Лапласа
3.4.1. Магнитное поле проводника с током
В общем случае для определения магнитного поля от произвольного проводника с произвольным знаком протекания тока проводим дифференцирование. Определяем полную индукцию, как сумму элементарных индукций от элементов тока dl, содержащих dq движущегося заряда.
Согласно последнему утверждению, совпадает с перпендикуляром к плоскости, образованной векторами cкорости
и радиус- вектора
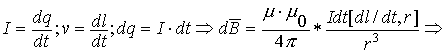
Последняя формула и есть закон Био-Савара-Лапласа для определения магнитной индукции для проводника с током.
3.4.2. Применение закона Био-Савара-Лапласа для анализа магнитных полей проводников с током различной конфигурации. Конечный и бесконечный прямолинейный проводник с током
Примем условиями: 
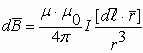
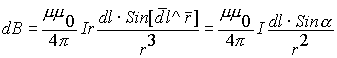
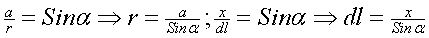
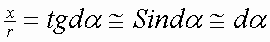
Подставляя полученное в формулу для dB, получаем:
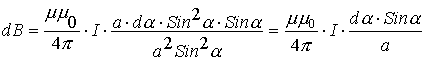
Это выражение для составляющей магнитного поля в точке p элемента проводника с током dl. Тогда полное магнитное поле проводника с током в искомой точке принимает вид:
Назовем предельные углы α1 и α2 как углы, под которыми из искомой точки видны концы проводника, создающего магнитное поле. Тогда для конечного проводника с током это будет выглядеть так:
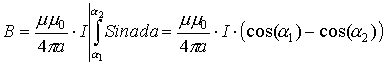
, то:
;
. Тогда
.
3.4.3. Магнитное поле кругового проводника с током
Направление магнитного поля (B) внутри кругового проводника с током также подчиняется правилу буравчика (шляпка как ток, буравчик как индукция). Магнитное поле элемента dl кругового проводника с током:
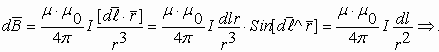
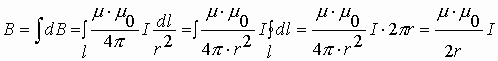
— Магнитная индукция кругового проводника (контура) с током в центре контура.
3.4.4. Магнитное поле вдали от центра контура с током
Элементы контура с током dl создают в точке А элементарные индукции dB, являющиеся трехмерным образованием в виде конуса, который дает результирующую B, равную:
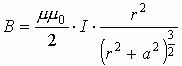
:
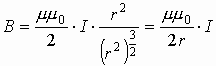
3.4.5. Магнитное поле соленоида
Если контура с током последовательно соединить в одном месте пространства, то такое образование называется соленоидом.
В таком соленоиде магнитные потоки от последовательно соединенных контуров суммируются. Так как магнитные силовые линии замкнутые, то внутри соленоида число силовых линий равно числу силовых линий всего соленоида.
А раз объем внутри соленоида ограничен, то можно сказать, что магнитное поле сконцентрировано внутри соленоида, снаружи рассеяно, и магнитные силовые линии внутри соленоида параллельны между собой и поле внутри соленоида считается однородным, вне соленоида — неоднородным. Величина магнитной индукции внутри соленоида записывается так:
, где μ — среда внутри соленоида, N — число витков соленоида, l — длина соленоида. Если обозначить
— удельное число витков
3.5. Магнитный поток
По теореме Остроградского-Гаусса в общем случае поток любого вектора через поверхность S численно равен
Индукция — вектор в пространстве, поэтому можно применить понятие потока индукции
. Если площадь фигуры, пересекающей силовые линии магнитного поля — площадь контура, по которому протекает ток, тогда
— магнитный поток контура с током. Если имеется множество последовательно соединенных контуров, то есть соленоид, то общее количество магнитных силовых линий равно сумме силовых линий, образованных каждым контуром.
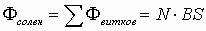
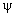
.
3.6. Напряженность магнитного поля
Зная, что , а магнитная индукция для бесконечного прямолинейного проводника с током равна
. Аналогично: Для конечного проводника:
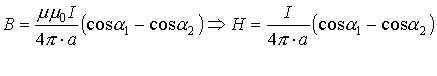
. На оси кругового витка:
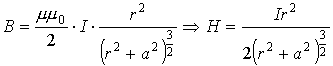
3.7. Силы, действующие в магнитном поле
Сила Лоренца — сила, действующая со стороны магнитного поля на движущийся заряд. Эмпирически получаем F В векторной форме F
, а в скалярной форме
.
Принято правило левой руки (для “+” заряда для нахождения направления силы Лоренца): если вектор входит в ладонь, вектор
направлен по отогнутым пальцам, то
направлена, как показывает большой палец. Правило правой руки для отрицательного заряда аналогично. Если на заряд действуют и электрическая и магнитная силы, то в этом случае сила Лоренца равна в векторной форме:
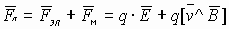
3.7.1. Сравнение электрической и магнитной сил
Сравним взаимодействие зарядов (сила Кулона) и токов, образованных этими зарядами (сила ампера) в параллельных проводниках.
Магнитное поле, действующее на заряд, создается другим зарядом, движущимся относительно первого. Предположим, что ν1=ν2, заряды находятся на расстоянии r друг от друга. Возьмем перпендикулярно
, то есть
, тогда по закону Био-Савара-Лапласа выражаем
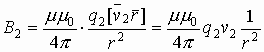
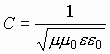
Получим 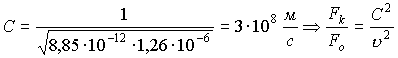
Следствия:
- Электрическая сила больше магнитной
- Магнитная сила принимает существенные значения, когда скорости зарядов близки к скорости света. Если бы С
- Поскольку скорость света конечна, магнитная сила релятивистская, то есть проявляет себя при скоростях, близких к скорости света.
3.8. Взаимодействие параллельных проводников с током
Вблизи каждого проводника с током формируется магнитное поле (сила, действующая на проводник с током, определяется по правилу левой руки: магнитные силовые линии входят в ладонь, ток по вытянутым пальцам, тогда сила направлена по отогнутому большому пальцу)
Два близко расположенных проводника с током притягиваются, с противоположным направлением токов — отталкиваются. Силы магнитного и электрического взаимодействия между движущимися зарядами противоположны.
3.9. Закон Ампера
Касается действия силы на проводник с током со стороны магнитного поля. Ориентируем проводник в соответствии с направлением тока.
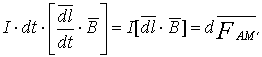
— закон Ампера в интегральной форме.
— закон Ампера в скалярной форме.
Сила Ампера указывает величину и направление силы, действующей на проводник с током I, длиной l помещенный в однородное магнитное поле. Направление задается правилом левой руки (
— в ладонь,
— вдоль пальцев,
— вдоль большого пальца).
3.10. Работа по перемещению проводника с током в магнитном поле
Длина проводника l, и перемещается он слева направо. Тогда работа по перемещению элемента проводника с током на расстояние dr равна:
.
Условия перемещения:
- магнитное поле и проводник в пространстве взаимно перпендикулярны,
.
- Направление перемещения проводника параллельно силе, вдоль которой мы совершаем работу по перемещению. То есть
— площадочка, заметаемая элементом проводника с током dl при его перемещении на dr. Тогда поток векторов B, проходящих через эту площадку:
Работа по перемещению проводника с током в магнитном поле определяется величиной тока, величиной магнитной индукции и площадью закрываемой (заметаемой) проводником при движении. Она также определяется величиной тока и магнитным потоком, проходящим через площадь, закрываемую проводником при движении.
3.11. Действие магнитного поля на контур с током
Для удобства предположим, что контур имеет прямоугольную форму.
1) Пусть dl перпендикулярен B, т. е. любой элемент контура перпендикулярен силовым линиям. Cилы Ампера, действующие на каждый прямолинейный участок контура, указаны на рисунке.
Если контур с током расположен перпендикулярно силовым линиям, то действие поля выражается в сжимании и разжимании контура. Если же контур состоит из упругого проводника, то внешнего изменения положения в пространстве не будет.
2) площадь контура с током параллельна силовым линиям. То есть нормаль плоскости контура перпендикулярна вектору магнитной индукции.
Тогда силы Ампера на каждом участке:
I. Sin=1, FA≠0, сила направлена от нас.
II, IV. Sin=0, FA=0, То есть на элемент контура с током лежащим вдоль силовых линий FA не действует.
III Sin=1, FA≠0, сила направлена к нам. Тогда если контур с током закрепить в точках A и B ,то при таком расположении его в магнитном поле он будет вращаться, то есть на него действует момент силы.
3.12. Магнитный момент контура с током
Пусть r — плечо силы. (См. предыдущий рисунок) .
. Если FA перпендикулярна r, тогда Sin=1. Это момент силы, действующий на I или III участок контура. Площадь S — между линией A B и участком тока I или III.
Поскольку в каждой из противоположных сторон контура действует самостоятельная сила Ампера, то за площадь для суммарного момента сил принимается не половина, а вся площадь контура. Тогда вводится понятие магнитного момента контура с током как собственной характеристики контура, которая численно равна произведению P=IS, где S это вся площадь контура. Направление магнитного момента задается нормалью контура с током
Тогда полный момент силы, действующий на контур с током в магнитном поле, численно равен: .
3.13. Явление электромагнитной индукции. ЭДС электромагнитной индукции
Проводник, по которому не пропускают ток, помещаем в магнитное поле. Будем перемещать проводник перпендикулярно вектору магнитного поля. По закону Лоренца так как
. Мы получили, что свободные заряды, которые, по определению, имеются в проводнике, будут перемещаться вдоль проводника. В результате перераспределения зарядов в проводнике при их движении на концах проводника возникает разность потенциалов, которая создает электрическое поле в проводнике:
. Тогда напряженность электрического поля в проводнике
Если подключим гальванометр, то можно выразить напряженность через напряжение . В равновесии Fл=Fк. То есть:
. Если закон перемещения проводника в магнитном поле произволен, то разбиваем все перемещение на отрезки dr:
, где dS=drℓ — площадь, заметаемая проводником при перемещении. Правило Фарадея: величина разности потенциалов, возникающих на концах проводника при его перемещении в магнитном поле прямо пропорциональна скорости изменения магнитного потока.
Если концы проводника замкнуты между собой, то в цепи протекает ток так, если бы проводник являлся источником тока. Тогда по закону Ампера сила, действующая на проводник с током в магнитном поле (правило левой руки) направлена в сторону, противоположную перемещению проводника в магнитном поле, то есть эта сила препятствует перемещению. Тогда:
- разность потенциалов, возникающих на концах проводника, называют ЭДС магнитной индукции.
- поскольку ЭДС вызывает силы, препятствующие движению проводника, то в законе Фарадея ставят знак “минус” (правило Ленца):
3.14. Явление электромагнитной индукции (взаимоиндукции)
В 1831 году Фарадей установил, что если изменять магнитный поток, проходящий через контур, то в этом контуре возникает ЭДС, препятствующая изменению внешнего магнитного поля. Пусть есть контур I, к которому подключен гальванометр, и контур II, к которому подключен резистор, и источник ЭДС.
- силовые линии II проводника пересекают первый контур. Если менять величину тока во II контуре, то меняется B2 , то есть магнитный поток, создаваемый вторым контуром также меняется. И по закону Фарадея в первом контуре возникает ЭДС.
- Удаление или приближение второго контура также вызывает ЭДС в первом.
- Можно поворачивать контура относительно друг друга, чтобы вызвать ЭДС в I контуре.
- Вызвать ЭДС можно также изменением магнитной среды, которая находится между контурами.
Приложение:
- Контуры с током, близко расположенные друг с другом называют связанными.
- Влияние одного контура на другой возможно только, если ток в контурах переменный (принцип трансформатора). Для усиления взаимодействия используют последовательно соединенные контура – соленоиды.
Пусть:
Соленоид 1 содержит N витков, а соленоид, II: N2 витков. S — поперечное сечение соленоида.
Если в соленоиде I изменить величину тока, то в соленоиде II возникает ЭДС, равная:
Если в каждом из контуров соленоида возникает ЭДС, то результирующая ЭДС соленоида будет равна произведению числа витков соленоида на ЭДС одного витка:
то есть: , где L12 — коэффициент взаимной индукции первого соленоида относительно второго.
Если источник неэлектрических сил подключить ко второму соленоиду, а гальванометр к первому, то ЭДС, возникающую в первом соленоиде можно будет рассчитать аналогично:
, где
— коэффициент взаимоиндукции II-ого соленоида относительно первого. Таким образом L21=L12
3.15. Явление самоиндукции
Возьмем один соленоид. Если в таком соленоиде изменять величину тока, то в контуре соленоида возникает ЭДС, стимулирующая магнитное поле, и препятствующая изменению тока в соленоиде.
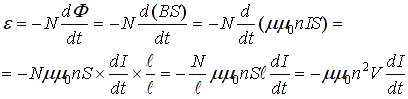
— коэффициент самоиндукции, связывающий ЭДС электромагнитной индукции и ток. Его называют индуктивностью соленоида.
Индуктивность — характеристика соленоида, связывающая скорость изменения тока в соленоиде с препятствующей ей ЭДС и определяемая только геометрическим устройством соленоида.
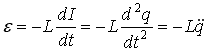
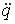
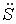
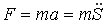
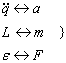
3.16. Вихревые токи или токи Фуко
В связанных контурах для передачи энергии переменного электрического тока из одного участка цепи в другой, часто используются магнитопроводящие среды.
При подаче переменного напряжения (тока) на первый 1 соленоид со второго 2 можно снять переменное напряжение (ток) противоположного направления (закон Фарадея-Ленца) Так как магнитное поле замкнутое, то сердечники делаются сплошными, чтобы избежать потери магнитного поля. Тогда сам сердечник создает замкнутый контур, по которому может протекать электрический ток. Если сопротивление сердечника мало, то по закону Джоуля-Ленца количество теплоты, выделившейся на этом сердечнике, будет велико. То есть . Эта теплота отбирается от энергии переменного электрического тока, подаваемого на соленоид. Для того, чтобы избежать паразитных тепловых потерь, магнитнопроводящие сердечники делаются из специального металла, обладающего большим сопротивлением (углеродистая сталь — пермаллой, ферритовые сплавы).
Если в связанных между собой механических частях какой- либо установки присутствуют электрические цепи с переменным током, то для предотвращения перемещения одной механической части относительно другой( когда их невозможно закрепить жестко) подвижные части делают в виде электрической цепи. ЭДС препятствует изменению магнитного поля, вызываемого движением. Возникающая ЭДС создает собственное магнитное поле, препятствующее движению механической детали. Таким образом, её движение ограничено. Это явление называют током Фуко.
Индуцирование переменного тока и напряжения используется для создания переменных токов и напряжений в местах, недоступных человеку (в вакуумных устройствах, где требуется разогреть какую-либо деталь).
Пропуская переменный ток по наружному соленоиду мы индуцируем электрический ток внутри вакуумного объема и так как соленоид внутри замкнут сам на себя, то энергия тока второго соленоида переходит в тепловую энергию. Такие устройства называют индукционными печами (температура достигает в них ≈1000С).
3.17. Энергия магнитного поля
Как любое поле, магнитное поле обладает энергией. Легче всего исследуется однородное магнитное поле, которое находится в соленоиде.
При замкнутом ключе внутри соленоида накапливается магнитная энергия. Если величину тока не менять в стационарных условиях, то часть тока идет через нагрузку, например, лампочку Л, другая часть через соленоид L.
При выключении ЭДС батареи в момент времени ток, протекающий в соленоиде, уменьшается и вызывает ЭДС электромагнитной индукции, препятствующую этому уменьшению. Эта ЭДС стремиться поддержать ток на нагрузке.
Поэтому величина тока на приборе плавно уменьшиться. Это происходит за счет энергии магнитного поля, накопленной в соленоиде.
Можно записать работу по переносу заряда для поддержания тока в цепи при выключении ключа, которая происходит за счет энергии магнитного поля, запасенной в соленоиде.
а так, как
(Закон Фарадея-Ленца) и dq=Idt,
то — закон сохранения энергии.
Тогда полная энергия магнитного поля:
— полная магнитная энергия, запасенная в соленоиде с индуктивностью L. Аналогична ситуация с включением.
Схема включения цепи с соленоидом. Время релаксации τ — время, необходимое для установления в рабочих цепях режима равновесной (стационарной) работы.
3.18. Плотность энергии магнитного поля
Плотность энергии магнитного поля – количество магнитной энергии в единице объема соленоида: 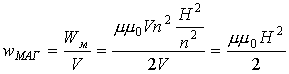
Итак:
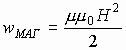
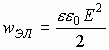
3.19. Единицы измерения магнитных величин
-
- Магнитный момент:
, где
— единичный вектор, нормаль к площади контура, определяющий ее ориентацию в пространстве.
- Магнитная индукция: так как
(см. § 12), то
— тесла.
- Магнитный поток Ф:
.
- Потокосцепление
- Индуктивность — коэффициент, зависящий от геометрических размеров соленоида.
- Магнитный момент:
- Напряженность магнитного поля для витка с током
или для соленоида
.
- Магнитная проницаемость m — показывает, во сколько раз магнитное поле в среде отличается от магнитного поля в вакууме.
— для среды.
— безразмерная.
- Магнитная постоянная
Аналогия: магнитное поле ↔ механика
Аналогия между силой и ЭДС заключается в том, что сила есть вектор и направление его действия в пространстве легко установить, а ЭДС — скаляр, и направление его действия на изменение тока в цепи указывается знаком “-”
3.20. Магнетики. Вещества в магнитном поле
Вещества, способные намагничиваться и влиять на направление вектора магнитной индукции внешнего поля B, называются магнетиками.
Способность намагничиваться — создание собственного магнитного поля в веществе, которое или усиливает, или уменьшает внешнее магнитное поле.
Собственные магнитные свойства вещества определяются электронами, связанными с атомами. Строение атома подразумевает наличие электрона e, вращающегося вокруг ядра. Магнитный момент электрона , то есть каждая орбита электрона в атоме обладает собственным магнитным моментом и создает собственное магнитное поле. В целом в веществе суммарные магнитные моменты электронов в атоме расположены хаотично и их сумма зачастую равна нулю.
Под действием внешнего магнитного поля собственные магнитные поля, созданные электронами, упорядочиваются. Это и есть явление намагниченности. Оно может сохраняться после снятия магнитного поля, а может и исчезать. У ферромагнетиков оно сохраняется, а у диа и парамагнетиков исчезает.
В результате поле равно:
, где каппа
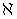
и
— магнитные моменты электронных орбит.
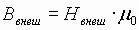
— магнитная проницаемость.
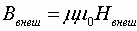
Для разных веществ значение может принимать как положительные, так и отрицательные значения. В большинстве веществ собственные магнитные моменты атомов (молекул) не зависят друг от друга и хаотично расположены в пространстве. Если к такому веществу приложить внешнее поле, то собственный магнитный момент каждого атома стремится, как волчок, выровнять положение оси вращения вдоль силовых линий внешнего поля.
Bвне — индукция внешнего магнитного поля, Pm- собственный магнитный момент атома.
Изменение собственной оси вращения (собственного магнитного момента) относительно вектора магнитной индукции (внешнего поля) называется прецессией.
Собственный механический момент или количество движения Ls (спин)
Механические моменты электронов в атоме могут отличаться только направлением движения по орбите (вдоль и против часовой стрелки).
- Если внешнее магнитное поле затрачивает энергию на прецессию, то её результирующее магнитное поле ослабляется. Такие вещества называют диа–магнетиками:
.
- В некоторых веществах внешнее магнитное поле не затрачивает энергию на прецессию, а разворачивает весь атом так, чтобы его собственное магнитное поле совпадало с внешним магнитным полем. Эти вещества -парамагнетики. Для них
.
Парамагнетики
Стрелками укажем магнитные моменты отдельных атомов.
Ферромагнетики.
Для объяснения ферромагнетизма вводим понятие доменов. Домен — совокупность атомов с одинаковым направлением собственных магнитных полей. Подобные совокупности атомов требуют меньше энергии для образования доменов, т.е. энергетически более выгодны по сравнению с разрозненными атомами. В целом собственное магнитное поле вещества равно нулю. Под действием внешнего магнитного поля домены могут увеличиваться за счет других доменов вплоть до поглощения неориентированных доменов, то есть все пространство вещества заполняется доменами, ориентированными вдоль поля. При снятии внешнего поля обратной переориентации не происходит, так как это энергетически не выгодно. В этом случае магнитная восприимчивость составляет тысячи и десятки тысяч единиц. Оказывается, реакция вещества на воздействие внешнего магнитного поля носит нелинейный характер. Это определяется способностью собственных магнитных моментов переориентироваться во внешнем магнитном поле. Сначала идёт резкое изменение ориентации во внешнем магнитном поле, магнитные моменты ориентируются вдоль силовых линий магнитного поля. Дальнейшее увеличение магнитного поля не изменяет намагниченность, так как все магнитные моменты уже ориентированы вдоль поля. Зависимость результирующего магнитного поля в веществе в целом в зависимости от внешнего поля носит характер гистерезиса.
B1 — остаточная индукция. H1 — коэрцетивная сила.
B1 — в веществе остается собственное магнитное поле без внешнего магнитного поля H1 = 0, (так создаются постоянные магниты).
H1 — внешнее поле, необходимое для снятия собственной намагниченности, B1=0. Эта величина называется коэрцетивная сила.
Анализ петли гистерезиса см. в разделе “Сегнетоэлектрики”. Если коэрцетивная сила велика, то говорят, что ферромагнетик жёсткий, если мала — то мягкий.
3.21. Движение зарядов в магнитном поле
1) Вектор скорости перпендикулярен силовым линиям.
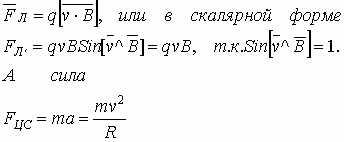
Скорость изменяется только по направлению, но не по величине. Сила Лоренца, действующая на движущуюся частицу в магнитном поле, закручивает траекторию движения в окружность, то есть появляется центростремительное ускорение: значит v изменяется только по направлению, но не по величине. Тогда приравняем
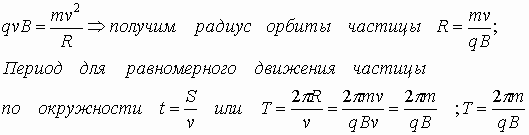
где Т – период обращения заряда по орбите
2) угол между направлением скорости и силовыми линиями не равен 90 градусам.
, 0<α<90
Дальнейший анализ траектории движения частицы относительно вектора скорости аналогичен пункту 1).
Здесь сила Лоренца
. Новой характеристикой здесь является l — шаг спирали.
Приложение:
- если частица движется вдоль силовых линий магнитного поля, то сила Лоренца равна нулю.
- Если частица неподвижна в магнитном поле, то сила Лоренца также равна нулю.
3.22. Уравнение Максвелла. Обобщение теории магнитного поля (обобщение электродинамики)
Имеется замкнутый контур и внешнее магнитное поле, меняющееся во времени. Если внешнее магнитное поле создается соленоидом с током, то изменение магнитного поля через контур произойдет, если
- в соленоид вносим сердечник,
- меняем ток в этом соленоиде,
- изменяем положение соленоида относительно контура.
Тогда в контуре появляется ЭДС по закону Фарадея-Ленца, препятствующая изменению внешнего магнитного поля, то есть стрелка прибора, который можно подключить к контуру, отклоняется, в контуре идет движении зарядов, то есть появляется электрический ток. Так как до включения магнитного поля заряды в проводнике находились в неподвижности, значит после включения поля сила Лоренца не должно действовать на заряды. Откуда же берется ЭДС? Единственным объяснением появления ЭДС в контуре, то есть движения зарядов, является появление электрического поля, сила Кулона которого заставляет заряды двигаться. Напряженность такого поля
Не зная источника внешнего магнитного поля можно записать для ЭДС в контуре
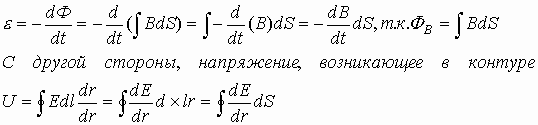
— оператор дифференцирования по координатам (декартовым или полярным). Аналогично
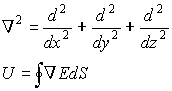
Напряжение, выраженное через законы электростатики, и ЭДС, возникшее в контуре, есть одно и то же. Тогда интегралы равны между собой, а, следовательно, и подинтегральные выражения равны.
. Здесь отображена связь между неоднородным электрическим полем и переменным магнитным.
3.23. Анализ массово-зарядового состояния (q/m) элементарных частиц
С поверхности вещества испаряют часть атомов или молекул. Как правило, при этом такие атомы обладают зарядовыми свойствами. Далее эти атомы ускоряются в электрическом поле E, и движущийся поток атомов пропускают через магнитное поле B. По закону Лоренца эти заряды в магнитном поле отклоняются. Тогда на экране за магнитным полем в разных местах оседают атомы разных зарядов. По степени отклонения атомов от прямолинейного распространения можно судить о заряде атома.
Частицы в магнитном поле отклоняются. Тогда на экране за магнитным полем в разных местах, например:
Заряд q= 1e – в точке 2 на экране.
Заряд q=2e – в точке 1 на экране.
Процесс разделения частиц по зарядам называется сепарированием, а прибор, анализирующий состав этих пучков — масспектрограф.
3.24. Приложение к теореме Остроградского-Гаусса
Для любого вектора a можно записать его поток:
Так как интегрирование и дифференцирование по сути своей противоположные операции, то можно записать, например:
Интегрирование и дифференцирование по одному и тому же параметру по сути взаимно компенсирующие операции. Тогда можно записать для вектора а:
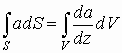
А так же:
Таким образом, можно связать линейный, поверхностный и объемный интегралы, т.е. можно переходить от линейного к поверхностному, и от поверхностного к объёмному интегралу.
Приложение к теореме Остроградского-Гаусса мы используем при рассмотрении уравнений Максвелла.
3.25. I-ое уравнение Максвелла
Итак, мы из предыдущих параграфов (§ 22, 24) получаем закон Фарадея-Ленца:
ЭДС, возникающая в контуре при изменении магнитного поля, регистрируется гальванометром как напряжение на концах проводника контура. Тогда приравняем подинтегральные выражения.
.
Переменное магнитное поле породило неоднородное электрическое поле, которое создало электрический ток, создающий собственное поле, препятствующее (знак “-“) изменению внешнего магнитного поля (закон сохранения энергии). Это и есть I-ое уравнение Максвелла.
3.26. II-ое уравнение Максвелла
Используем соленоид для создания магнитного поля. r- радиус соленоида, l — его длина, N — число витков, n — удельное число витков соленоида. Запишем напряженность соленоида
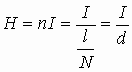
Если предположим, что соленоид намотан в один слой и витки плотно прилегают друг к другу, то — толщина одного витка. Тогда можно считать d, как элемент l, или d=dl.
Продифференцируем левую и правую часть по координатам.
— площадь сечения проводника, из которого сделан соленоид. По определению
, плотность тока
Если внутри соленоида находится среда с μ>1, то магнитное поле в соленоиде усиливается за счет электрического поля, обусловленного протекающим по проводнику током. Так как среда в соленоиде непроводящая, то электрическое поле вызывает в этой среде только смещение зарядов (смотри раздел “диэлектрики”). Тогда плотность тока зарядов проводимости и смещенных зарядов в самом общем случае, когда есть и свободные и связанные заряды
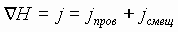
Как и в диэлектриках смещение зарядов вызывается электрической индукцией, а именно . Тогда имеем
— второе уравнение Максвелла, которое говорит, что электрическое поле, которое вызывало в проводнике электрический ток проиндуцировало в среде усиление магнитного поля, то есть сформировало его.
В I уравнении знак “-” означает, что переменное магнитное поле вызывает электрический ток, который генерирует магнитное поле, препятствующее изменению внешнего магнитного поля. Это связанно с законом сохранения энергии. Во II уравнении минус не ставится, так как за направление электрического тока принято движение положительных зарядов, а реально движутся отрицательные.
3.27. III-e уравнение Максвелла
В системе зарядов поток векторов напряженности по теореме Остроградского-Гаусса равен Если заряды распределены произвольно в пространстве, то введем понятие объемная плотность заряда:
Тогда по теореме Гаусса
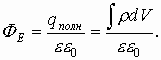
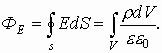
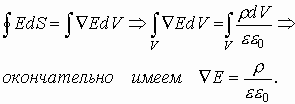
3.28. IV уравнение Максвелла
Если есть соленоид, по которому течет ток, то соленоид формирует магнитное поле. Принцип силовых линий магнитного поля B — замкнутость. Найдем поток векторов B, который по теореме Остроградского есть . Полный поток векторов найдем, замкнув соленоид поверхностью S.
Чтобы посчитать этот поток, мы должны учесть как входящие, так и выходящие через поверхность S силовые линии B магнитного поля. Результатом является компенсация этих линий, то есть общий поток равен нулю, т.к. количество входящих и выходящих линий B через поверхность S одинаково из-за замкнутости линий. Используя приложение к теореме перейдем от поверхностного интеграла к объемному
Отсюда следует, что в объеме, в котором находится соленоид, как источник магнитного поля, нет зарядов. Это IV уравнение Максвелла.
3.29. Анализ III и IV уравнений
Из III уравнения Максвелла следует, что в объеме, из которого исходят силовые линии электрического поля, находятся электрические заряды, а из IV следует, что объем, из которого исходят силовые линии магнитного поля не содержит зарядов магнитного поля.
Это доказательство того, что в природе не существует магнитных зарядов, соответственно, нет потенциала магнитного поля.
Итак, рассмотренные 4 уравнения Максвелла считаются основными, но есть еще три дополнительных.
Эти уравнения соединяют свойства электрических и магнитных полей в вакууме и средах.
Первые два уравнения Максвелла получены из поверхностных интегралов, для которых важно задать направление силовых линий, значит, в уравнениях обязательно отмечается векторность полей.
(I).
(II)
А III и IV уравнения – количественные, то есть скалярные уравнения.
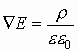
получим
(III).
И наконец (IV).
Система уравнений Максвелла отображает единую теорию электромагнитного поля и показывает, что оно есть единое поле, то есть электрического поля не существует без магнитного, а магнитное поле не существует без электрического. Можно ещё сказать, что переменное магнитное поле порождает неоднородное электрическое, а переменное электрическое поле порождает неоднородное магнитное поле.
Учебник, который она назвала лучшим (Алешкевич)
Основные законы:⚓︎
Весь раздел можно разбить на 3 части: электростатика, электродинамика (электрический ток) и электромагнетизм.
Электростатика⚓︎
- Закон сохранения заряда
- Закон Кулона (1785)
Электродинамика⚓︎
- Закон Ома (1826)
- Закон Джоуля-Ленца (1841-1842)
Электромагнетизм⚓︎
- Закон Био-Савара-Лапласа (1820)
- Закон Ампера (1820)
- Закон Фарадея-Максвела (Закон электромагнитной индукции) (1831-1861)
Закон сохранения заряда⚓︎
Заряд существует в двух видах: условно положительный и отрицательный
-
В законах
электростатики, не имея образца для сравнения, мы никогда не сможем сказать какой заряд положительный, а какой отрицательный- Если заряды разные по знаку — они притягиваются
-
Если одноименные — отталкиваются
-
Электрический заряд квантуется, т.е. существует в природе в виде заряженных частиц, которые мы считаем элементарными.Для нас это:
Единица измерения
[q] = Кл = А * с -
Закон сохранения заряда:
Для изолированной системы алгебраическая сумма зарядов в остается постоянной.
Изолированная система— система, которая не обменивается зарядом с другими системами., где
i— кол-во зарядовПример разложения по сумме:
В изначальной формулировке был бы возможен следующий процесс: заряд исчезает в одной точке пространства и мгновенно возникает в другой.
-
Электрический заряд релятивистски инвариантен, т.е. не зависит от скорости координат (а, следовательно, от того движется он или покоится). Заряд присущ частице на протяжении всего времени ее жизни.
Закон Кулона⚓︎
-
Закон Кулонарегламентирует количественное взаимодействие, силу взаимодействия точечных зарядов:Точечный заряд— это заряд тела, геометрическими размерам которого в условиях данной задачи можно пренебречь.- Если мы рассматриваем взаимодействие двух таких зарядов, то сила их взаимодействия:
- Направлена вдоль линии соединяющей оба заряда
- Прямо пропорциональна величине каждого из зарядов
- Обратно пропорциональна квадрату расстояния между зарядами
-
В векторном виде:
F - сила, с которой заряд1действует на заряд2q1иq2— величина зарядовr— радиус-вектор (вектор, направленный от заряда1к заряду2, и равный, по модулю, расстоянию между зарядами)k— коэффициент пропорциональности (зависит от системы единиц, у нас —, где
— электрическая постоянная
-
Одноименные заряды отталкиваются
Сила их взаимодействия прямо пропорциональна модулю произведения зарядов.
-
Закон Кулона справедлив в таком виде только для двух случаев:
- Первый случай для точечных зарядов, рассмотрен выше.
-
Второй случай, когда заряженные тела имеют шарообразную или сферическую форму и при этом обязательно, чтобы заряд был распределен равномерно по поверхности или равномерно по объему.
Пример:2 проводящих тела, по которым заряды могут как-то перераспределяться, то в таком виде закон уже не справедлив и приходится придумывать различные методы расчета силы взаимодействия или полей, которые создает одно или другой тело. -
В силе Кулона можно условно правую часть разделить и сказать, что все, что обведено относится например к первому заряду, тогда мы говорим о некоторой точке наблюдения, находящейся на расстоянии r от первого заряда, и все это вместе характеризует поле первого заряда.
-
Напряженность этого заряда:
То же самое можно выполнить наоборот, взяв за точку наблюдения заряд
q1и расстояние r до зарядаq2.
Напряженность электростатического поля.⚓︎
- Всякое заряженное тело создает вокруг себя поле, чтобы это поле обнаружить используется пробный заряд (
точечный,маленькийиположительный) -
В данной точке поля пробный заряд отталкивается от поля.
-
Чем ближе одноименный заряд, тем сильнее он будет отталкиваться.
-
Отношение действующей силы к величине пробного заряда характеризует конкретную точку поля и называется напряженностью. Напряженность определяется как сила, действующая на пробный заряд, помещенный в данную точку поля к величине пробного заряда.
Напряженность— силовая характеристика поля. -
Размерность
В/м(Вольт на метр) -
Расчет напряженности. Есть 2 глобальных метода:
метод суперпозицииитеорема Гаусса.-
Метод суперпозиции.
Если поле создается одним точечным зарядом
Q, то на любой пробный заряд действует сила:Тогда
напряженность:— модуль (нет знака)
Силу
Fделим на пробный зарядq, получаемнапряженность поля точечного заряда.Эту же формулу можно использовать для расчета проекции напряженности на направление от точечного заряда.
— проекция (есть знак
-или+)Если у нас есть заряд, мы проводим ось от него и такую ось традиционно называем радиальной.
Напряженность, если заряд положительный направлена от зарядаQи будет проецироваться на эту ось. Если зарядотрицательный, тонаправление силы будет противоположным.
-
-
Поле создается
системой точечных зарядов. Если на тело действует несколько сил, их надо складывать векторно, тогда согласно определению напряженности:Если результирующая сила определяется как векторная сумма то, при делении на заряд получаем сложение векторов напряженности. Это называетсяпринцип суперпозиции. В случае дискретно распределенного заряда он записывается как векторная сумма:Электрический заряд дискретен— заряд любого тела составляет целое кратное от элементарного электрического зарядае=1,6×10^-19 Кл. -
Поле создается заряженным телом.
-
Прежде чем рассчитывать напряженность, мы разбиваем тело на точечные заряды
сводим задачу к предыдущей, обозначаем какой-нибудь точечный заряд
-
Каждый точечный заряд создает поле, независимо от существования другого. Поместив в некоторую точку поля пробный заряд, находим напряженность от этого точечного, поэтому и обозначаем ее не
E, аdE(некоторая часть всего поля) -
Для расчета воспользуемся первой формулой:
-
Результирующее поле определяется по принципу
суперпозиции(для распределения заряда) через интеграл:
-

Графическое изображение поля. Силовые линии.⚓︎
Для графического изображения электростатических полей используют силовые линии — воображаемые линии.
Правила построения силовых линий:
- Касательные к этим линиям в каждой точке совпадают с вектором напряженности.
- Силовой линии приписывают направление по вектору напряженности.
-
Линии рисуют выборочно, число линий пропорционально напряженности поля. (Чем больше густота, тем больше напряженность).
где
N - число линий, пересекающих площадку,S - площадь
Густота пропорционально напряженности.
Изображаем напряженность в ряде точек 
Изобразим 2 площадки, они имеют разную площадь, но одинаковое число силовых линий. Для второй площадки (S2) густота силовых линий меньше.
Силовые линии начинаются на зарядах (если они положительные)и заканчиваются на зарядах (если они отрицательные).
Силовые линии никогда не пересекаются, потому что в каждой точке напряженность может быть определена 1 раз.
Однородное поле — напряженность во всех точках одинаково. Используем параллельные силовые линии, находящиеся на равном расстоянии друг от друга.
Потенциал Электростатического поля.⚓︎
Электростатический потенциал — скалярная энергетическая характеристика электростатического поля, характеризующая потенциальную энергию, которой обладает единичный положительный пробный заряд, помещенный в данную точку поля.
Если мы в поле помещаем какой-нибудь заряд (точечный), то на заряд начинает действовать сила и если его отпустить он куда-то полетит — исходя из этого у зарядки есть потенциальная энергия. Поделим эту потенциальную энергию на величину нашего пробного заряда — определяем характеристику данной точки поля, которая называется потенциал.
Потенциал можно определить с точностью до константы (не меньше самой константы), чтобы от константы избавиться удобно пользоваться не потенциалом, а разностью потенциалов, тогда можно воспользоваться разностью энергии:
Ни одно явление в природе или технике не определяется значением самой потенциальной энергии. Важна лишь разность значений потенциальной энергии в конечном и начальном состояниях системы тел.
Вспомним из механики — изменение энергии, это минус работа консервативной силы. (Сила Кулона — сила консервативная). Поэтому разность потенциалов между двумя точками равняется работе сил поля по перемещению пробного заряда из одной точки в другую, деленную на величину этого заряда.
С точки зрения системы СИ заряд единичный (1 Кулон) — не подходит, так как он очень большой.
Расчет потенциала — это расчет энергии. Энергия — скалярная величина. Если поле создает 1 точечный заряд, то поместив в это поле пробный заряд, мы получим энергию взаимодействия.

Константа k — обращается в ноль если мы считаем, что нулевой уровень потенциальной энергии или ноль потенциала выбран на бесконечном удалении от заряда Q
Если заряд Q создает поле, то чем дальше мы отходим от заряда, тем потенциал меньше.
Если есть система точечных зарядов — каждый из них создает поле, а значит результирующий потенциал как сумма потенциалов.
Поле заряженного тела 
Df
Связываем между собой напряженность и потенциал.⚓︎
Напряженность характеризует силу, потенциал характеризует энергию.
-
Интегральная связь:
Напряженность— это сила, действующая на точечный заряд, отнесенная к этому заряду.Потенциал—Работа (А)— мера действия силы на тело.По формуле работа это — интеграл от скалярного произведения.
Для того чтобы посмотреть переменность сил добавляем интеграл.
Для того чтобы учесть, что не всякая сила вообще совершает работу, а еще работа может быть отрицательной, добавляем скалярное произведение (именно скалярное произведение учитывает косинус угла между силой и перемещением.
Из трех формул получаем интегральную связь.
Записываем разность потенциалов, вместо работы подставляем интеграл.
, затем вносим заряд под знак интеграла, делим силу на заряд и получаем напряженность:
Скалярное произведение — это произведение двух векторов, модуля первого на модуль второго и на косинус угла между ними.
Изобразим 2 вектора:
перемещениеинапряженность.Запишем в скалярное произведение:
где альфа — угол между векторами.
АдомножимEнаcos(a)получу проекцию напряженности на направление перемещения (на направлениеdr).Er - проекция перемещенияУбираем скалярное произведение и оставляем проекцию напряженности на некоторое направление умножить на приращение этой координаты.
Выше формула так называемой интегральной связи, она используется если нам нужно найти потенциал или разность потенциалов по известной напряженности.
Второй вид связи — дифференциальная.
Чтобы перейти от дифференциальной связи, нужно избавиться от интеграла.
Рассмотрим две бесконечно близкие точки 1 и 2 (верхний и нижний пределы)
Работа подразумевает собой перемещение и точки 1 в точку 2 (суммируя все маленькие перемещения) умножив их на силу всего нашего пути.
Разность потенциалов двух бесконечно близких точек:
Начальное — конечное:
Отсюда выражаем проекцию напряженности на направление
rЭто взятое с обратным знаком производная от потенциала по этому направлению и по этой координате.
В декартовой системе координат это соотношение справедливо для любой оси.
— скорость изменения вдоль координаты
Y— это взятое с обратным знаком производная от потенциала по этому направлению и по этой координате.
В декартовой системе координат это соотношение справедливо для любой оси.
— скорость изменения вдоль координаты
Y— для
ZЛюбой вектор в трехмерной системе координат имеет 3 проекции.
Чтобы собрать вектор, нужно воспользоваться единичным ортогональным базисом. Каждую ось умножаем на ее единичный вектор.
Используя данные проекции получаем:
Получаем соотношение, которое в векторном дает нам дифференциальную запись связи.
У математиков есть формула проще, которая выводится продифференцировав по трем координатам, потом умножить на 3 единичных вектора и сложить.
Градиент:
Дифференциальную связь используем когда известно распределение потенциала, нужно найти напряженность.
Используя интегральную связь можно записать условие потенциальности поля.
Поле потенциально если действующая сила потенциальна.
Если мы и начальной точки дошли до конца и вернулись = 0
Эквипотенциальные поверхности.⚓︎
Поверхность, во всех точках которой потенциал электрического поля имеет одинаковые значения, называется эквипотенциальной поверхностью.
Между двумя любыми точками на эквипотенциальной поверхности разность потенциалов равна нулю, поэтому работа сил электрического поля при любом перемещении заряда по эквипотенциальной поверхности равна нулю.
Это означает, что вектор силы в любой точке траектории при движении заряда по эквипотенциальной поверхности перпендикулярен вектору перемещения. Следовательно, линии напряженности электростатического поля перпендикулярны эквипотенциальной поверхности
Эквипотенциальными поверхностями поля точечного заряда являются сферы, в центре которых расположен заряд.
Эквипотенциальные поверхности однородного электрического поля представляют собой плоскости, перпендикулярные линиям напряженности.
Два способа изображения электростатических полей – силовыми линиями и эквипотенциальными поверхностями – эквивалентны: имея одну из этих картин, легко построить другую
Найдем в пространстве геометрическое место точек, удовлетворяющих условию.
Если потенциал const, то изменение потенциала равняется 0
Мы хотим чтобы изменение потенциала равнялось 0
Единственная переменная, которая может равняться 0 это cos угла между напряженностью и перемещением.
Cos = 0, если угол 90 градусов или 90 + π
Эквипотенциальные поверхности всегда перпендикулярны силовым линиям
Самая большая напряженность поля на поверхности φ1
Все точки на данной поверхности обладают равным потенциалом.
Чтобы узнать у какой поверхности потенциала больше, нам понадобиться интегральная связь.
Интеграл получится положительным, а значит потенциал первой точки больше, чем второй.
Силовая линия показывает всегда направление максимального быстрого уменьшения потенциала.
Эквипотенциальные поверхности при точечном заряде:
Вблизи заряда при эквипотенциальной поверхности напряженность поля становится больше, а значит расстояние между плоскостями должно уменьшиться.
Характеристики распределения заряда.⚓︎
-
Заряд может быть распределен по стержню, и если заряд распределен равномерно вводится линейная плотность заряда.
, где
dl— интересующая нас длина,dq— заряд на этой длинеВо всех наших задачах плотность будет константа.
(Кулон/метр) -
Заряд может быть распределен по поверхности.
— поверхностная плотность
, заряд/площадь поверхности, на которую он распределен.
-
Объемная плотность заряда, если заряд распределен равномерно, то
-
Формулы, по которым можно рассчитать заряд, зная его плотность:
Последнее обновление: 2021-06-17
Созданный: 2021-06-13
Содержание
- Что такое электромагнетизм?
- Применение электромагнетизма
- Эксперименты по электромагнетизму
- Для чего нужен электромагнетизм?
- Магнетизм и электромагнетизм
- Примеры электромагнетизма
- История электромагнетизма
- Рекомендации:
Мы объясняем, что такое электромагнетизм и каковы некоторые из его приложений. А также его история и примеры.
Что такое электромагнетизм?
Электромагнетизм — это раздел физики, изучает взаимосвязь между электрическими и магнитными явлениями, то есть взаимодействия заряженных частиц с электрическим и магнитным полями.
В 1821 году были известны основы электромагнетизма. с научной работой британца Майкла Фарадея, положившей начало этой дисциплине. В 1865 году шотландец Джеймс Клерк Максвелл сформулировал четыре «уравнения Максвелла», полностью описывающие электромагнитные явления.
Смотрите также: Электростатика
Применение электромагнетизма
Электромагнитные явления имеют очень важное применение в таких дисциплинах, как машиностроение, электроника, здравоохранение, аэронавтика или гражданское строительство. Они появляются в повседневной жизни, почти не осознавая этого, в компасах, динамиках, дверных звонках, магнитных картах, жестких дисках.
Основные области применения электромагнетизма:
- Электричество.
- Магнетизм.
- Электропроводность и сверхпроводимость.
- Гамма-лучи и рентгеновские лучи.
- Электромагнитные волны.
- Инфракрасное, видимое и ультрафиолетовое излучение.
- Радиоволны и микроволны.
Эксперименты по электромагнетизму
С помощью простых экспериментов можно понять некоторые электромагнитные явления, такие как:
Электродвигатель. Чтобы провести эксперимент, демонстрирующий базовые представления о том, как работает электродвигатель, нам понадобятся:
-
- Магнит
- Одна батарейка AAA
- Винт
- Отрезок электрического кабеля длиной 20 см.
- Первый шаг. Положите кончик винта на отрицательный полюс батареи, а магнит — на головку винта. Вы можете увидеть, как элементы притягиваются друг к другу за счет магнетизма.
- Второй шаг. Соедините концы кабеля с положительным полюсом батареи и магнитом (который вместе с винтом находится на отрицательном полюсе батареи).
- Исход. Получается цепь аккумулятор-винт-магнит-кабель, через которую электрический ток течет через магнитное поле, создаваемое магнитом, и он вращается с высокой скоростью из-за постоянной тангенциальной силы, называемой «силой Лоренца». Напротив, если вы попытаетесь соединить части, меняя полюса батареи, элементы отталкиваются друг от друга.
Клетка Фарадея. Ниже приведен эксперимент, который позволяет нам понять, как электромагнитные волны текут в электронных устройствах. Для этого потребуются следующие предметы:
-
- Портативное радио или мобильный телефон на батарейках.
- Металлическая сетка с отверстиями не более 1 см.
- Плоскогубцы или ножницы, чтобы разрезать сетку
- Небольшие кусочки проволоки для прикрепления проволочной сетки
- Алюминиевая фольга (может не понадобиться)
- Первый шаг. Вырежьте прямоугольный кусок проволочной сетки высотой 20 см и длиной 80 см, чтобы можно было собрать цилиндр.
- Второй шаг. Вырежьте еще один круглый кусок металлической сетки диаметром 25 см (он должен быть достаточного диаметра, чтобы покрыть цилиндр).
- Шаг третий. Соедините концы прямоугольника металлической сетки так, чтобы он образовал цилиндр, и скрепите концы кусочками проволоки.
- Шаг четвертый. Поместите включенную магнитолу в металлический цилиндр и накройте цилиндр кругом из металлической сетки.
- Исход. Радио перестанет играть, потому что электромагнитные волны извне не могут проходить через металл.
Если вместо включенного радио вставить сотовый телефон и вызвать этот номер, чтобы он зазвонил, может случиться так, что он не будет звонить. Если он звонит, используйте более толстую металлическую решетку и отверстия меньшего размера или оберните сотовый телефон алюминиевой фольгой. Нечто подобное происходит при разговоре по мобильному телефону и входе в лифт, что приводит к отключению сигнала — это эффект «клетки Фарадея».
Для чего нужен электромагнетизм?
Электромагнетизм очень полезен для людей, поскольку существует бесчисленное множество приложений, которые позволяют им удовлетворять свои потребности. Многие инструменты, которые используются в повседневной жизни, работают из-за электромагнитных воздействий.. Электрический ток, который проходит через все разъемы в доме, например, обеспечивает множество применений (микроволновая печь, вентилятор, блендер, телевизор, компьютер), которые работают за счет электромагнетизма.
Магнетизм и электромагнетизм
Магнетизм — это явление, которое объясняет силу притяжения или отталкивания между магнитными материалами и движущимися зарядами.
Электромагнетизм включает в себя физические явления, вызываемые электрическими зарядами в состоянии покоя или в движении, которые вызывают электрические, магнитные или электромагнитные поля и влияют на материю, которая может находиться в газообразном, жидком и твердом состоянии.
Примеры электромагнетизма
Существует множество примеров электромагнетизма, среди которых наиболее распространены:
- Звонок. Это устройство, способное генерировать звуковой сигнал при нажатии переключателя. Он работает через электромагнит, который получает электрический заряд, который генерирует магнитное поле (эффект магнита), притягивающий небольшой молоток, ударяющийся о поверхность металла и издающий звук.
- Поезд на магнитной подушке. В отличие от поезда, приводимого в движение электровозом, который едет по рельсам, это транспортное средство, которое поддерживается и приводится в движение силой магнетизма и мощными электромагнитами, расположенными в его нижней части.
- Электрический трансформатор. Это электрическое устройство, позволяющее увеличивать или уменьшать напряжение (или напряжение) переменного тока.
- Электродвигатель. Это устройство, которое преобразует электрическую энергию в механическую, создавая движение под действием магнитных полей, которые генерируются внутри.
- Динамо. Это электрический генератор, который использует механическую энергию вращающегося движения и преобразует ее в электрическую энергию.
- Микроволновка. Это электрическая духовка, которая генерирует электромагнитное излучение с частотой микроволн. Это излучение заставляет молекулы воды в пище вибрировать, что приводит к быстрому выделению тепла для приготовления пищи.
- Магнитно-резонансная томография. Это медицинский тест, с помощью которого получают изображения структуры и состава организма. Он состоит из взаимодействия магнитного поля, создаваемого машиной, магнитного резонатора (который работает как магнит) и атомов водорода, содержащихся в теле человека. Эти атомы притягиваются «магнитным эффектом» устройства и создают электромагнитное поле, которое фиксируется и отображается на изображениях.
- Микрофон. Это устройство, которое улавливает акустическую энергию (звук) и преобразует ее в электрическую. Это происходит через мембрану (или диафрагму), которая притягивается магнитом в магнитном поле и производит электрический ток, пропорциональный полученному звуку.
- Планета земля. Наша планета работает как гигантский магнит из-за магнитного поля, которое создается в ее ядре (состоящем из металлов, таких как железо, никель). Вращательное движение Земли порождает поток заряженных частиц (электронов атомов ядра Земли). Этот ток создает магнитное поле, которое простирается на несколько километров над поверхностью планеты и отталкивает вредное солнечное излучение.
История электромагнетизма
- 600 г. до н.э. С. Грек Фалес из Милета заметил, что когда он натирает кусок янтаря, он заряжается и может притягивать куски соломы или перьев.
- 1820. Датчанин Ганс Кристиан Эрстед провел эксперимент, впервые объединивший явления электричества и магнетизма. Он заключался в поднесении намагниченной иглы к проводнику, по которому циркулировал электрический ток. Стрелка двигалась таким образом, что свидетельствовала о наличии магнитного поля в проводнике.
- 1826. Француз Андре-Мари Ампер разработал теорию, объясняющую взаимодействие между электричеством и магнетизмом, названную «электродинамикой». Кроме того, он первым назвал электрический ток как таковой и измерил интенсивность его протекания.
- 1831. Британский физик и химик Майкл Фарадей открыл законы электролиза и электромагнитной индукции.
- 1865. Шотландец Джеймс Клерк Максвелл представил основы электромагнетизма, сформулировав четыре «уравнения Максвелла», которые описывают электромагнитные явления.
Следуйте: Закон Фарадея
Рекомендации:
- «Что такое гистология?» в Ivy Roses.
- «Гистология» в Википедии.
- «Гистология» в Википедии.
- «Классификация тканей» в биологических науках.
- «Электромагнетизм» в Википедии.
- «Для чего нужен электромагнетизм?» в Карен Линда.
- «Что делает микрофон?» в Audio Technica.
- «Электромагнетизм» в Мадриоде.
- «Клетка Фарадея» (видео) на Educacciontv.
- «Краткая история электромагнетизма» в Nusgrem.
Учебные вопросы
1. Основы
электромагнетизма.
2. Переменный
электрический ток.
3. Электромагнитные
волны.
1. Основы электромагнетизма.
Магнитное
поле тока.
Магнитное
поле – силовое поле, действующее на
движущиеся электрические заряды и на
тела, обладающие магнитным моментом,
независимо от состояния их движения;
магнитная составляющая электромагнитного
поля. Магнитное поле было открыто в 1820
г. датским ученым Эрстедом.
Основная
силовая характеристика магнитного
поля.
Основной силовой характеристикой
магнитного поля является вектор магнитной
индукции В (вектор индукции магнитного
поля).
Демонстрация
силовых линий магнитного поля.
Значение
магнитного поля для жизни на Земле.
Магнитное поле для Земли имеет
жизненно-важное значение. Демонстрация
защиты Земли магнитным полем от солнечной
радиации. Намагниченная стрелка под
проводником без тока ориентирована на
маг-нитные полюса Земли. Демонстрация
опыта Ханса Эрстеда.
Закон
взаимодействия электрических токов —
Закон Ампера.
Андре — Мари Ампер, исследуя магнетизм,
сформулировал закон взаимодействия
электрических токов — Закон Ампера:
Параллельные проводники с электрическими
токами, текущими в одном направлении,
притягиваются, в противоположных –
отталкиваются.
Демонстрация
опытов с магнитным полем Анри Ампера.
Электродвигатель.
Опыты Ампера привели к идее использования
электричества и магнетизма для нужд
человека. Появилась идея электродвигателя.
Демонстрация устройства и работы
электродвигателя.
2. Переменный электрический ток.
Явление
электромагнитной индукции.
Явлением электромагнитной индукции
называется явление возникновения
электрического тока в проводнике под
действием переменного магнитного поля.
Открытие
Фарадеем электромагнитной индукции.
Явлением электромагнитной индукции
обнаружил Майкл Фарадей. В результате
его опытов было зафиксировано наличие
электрического тока в цепи в результате
изменения магнитного потока, который
проходит сквозь катушку. Демонстрация
опыта Фарадея переменным магнитным
полем.
Выводы
Фарадея о существовании индукционного
электрического тока.
1. Изменяющееся магнитное поле создает
электрический ток; 2. Направление
электрического тока зависит от того,
какой полюс магнита проходит в данный
момент через катушку, в каком направлении
движется магнит; 3. На значение
электрического тока влияет количество
витков в катушке. Чем больше витков, тем
и значение тока будет больше.
Индукционный
электрический ток.
Индукционный электрический ток появляется
в замкнутой цепи только тогда, когда
существует переменное магнитное поле.
Причем это магнитное поле должно
изменяться. Демонстрация опыта Фарадея
с индукционным током.
Теоретические
выводы М. Фарадея об электромагнитной
индукции.
Фарадей обосновал явление электромагнитной
индукции и сделал следующие выводы: 1.
Если изменения магнитного поля не
происходит, то не будет никакого
электрического тока; 2. Первый вывод
справедлив, даже в том случае, когда
магнитное поле существует; 3. Сила
индукционного электрического тока
прямо пропорциональна числу витков и
скорости магнитного поля, с которой
изменяется это магнитное поле относительно
витков катушки.
Электромагнитная
индукция.
Электромагнитная индукция — явление
возникновения электрического тока в
замкнутом контуре при изменении
магнитного потока, проходящего через
него.
Генератор
переменного электрического тока.
Если закрепить магнит и относительно
него двигать катушку с большим числом
витков (или наоборот, двигать магнит
относительно неподвижной катушки) будет
создаваться индукционный электрический
ток и получится простейший генератор
переменного электрического тока.
Демонстрация устройства и работы
генератора Фарадея.
Электрогенератор.
Определение и основные элементы.
Большинство существующих генераторов
переменного тока – это т.н. электромеханические
генераторы. В них за счет механического
движения подвижной части и создается
переменный электрический ток.
Использование
электрогенераторов в промышленных
целях.
Для промышленного производства
электроэнергии необходимо объединить
законы теплопроводности и электромагнитной
индукции. Если паровую турбину соединить
с генератором, получится электростанция.
Передача
электроэнергии на дальние расстояния.
Передача переменного электрического
тока на большие расстояния связана с
электромагнитной индукцией. Чтобы
передать переменный электрический ток,
используются приборы, которые называются
трансформаторами.
Трансформатор.
Определение и история создания.
Трансформатор – прибор для преобразования
электрического тока и напряжения. Первая
индукционная катушка — прообраз
трансформатора была изобретена в 1848 г.
французским механиком Г. Румкорфом. В
1876 г. Павел Яблочков (создатель дуговой
лампочки) разработал первый трансформатор
с разомкнутым магнитным сердечником.
Трансформаторы с замкнутыми сердечниками
были созданы в Англии в 1884 году братьями
Джоном и Эдуардом Гопкинсонами.
Демонстрация
устройства и работы трансформатора.
Демонстрация
кипячения воды трансформатором.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
From Wikipedia, the free encyclopedia
«Electromagnetic» redirects here. Electromagnetic may also refer to the use of an electromagnet.
«Electromagnetic force» redirects here. For the force exerted on particles by electromagnetic fields, see Lorentz force.
Electromagnetic interactions are responsible for the glowing filaments in this plasma globe
In physics, electromagnetism is an interaction that occurs between particles with electric charge via electromagnetic fields. The electromagnetic force is one of the four fundamental forces of nature. It is the dominant force in the interactions of atoms and molecules. Electromagnetism can be thought of as a combination of electrostatics and magnetism, two distinct but closely intertwined phenomena. Electromagnetic forces occur between any two charged particles, causing an attraction between particles with opposite charges and repulsion between particles with the same charge, while magnetism is an interaction that occurs exclusively between charged particles in relative motion. These two effects combine to create electromagnetic fields in the vicinity of charge particles, which can accelerate other charged particles via the Lorentz force. At high energy, the weak force and electromagnetic force are unified as a single electroweak force.
The electromagnetic force is responsible for many of the chemical and physical phenomena observed in daily life. The electrostatic attraction between atomic nuclei and their electrons holds atoms together. Electric forces also allow different atoms to combine into molecules, including the macromolecules such as proteins that form the basis of life. Meanwhile, magnetic interactions between the spin and angular momentum magnetic moments of electrons also play a role in chemical reactivity; such relationships are studied in spin chemistry. Electromagnetism also plays a crucial role in modern technology: electrical energy production, transformation and distribution, light, heat, and sound production and detection, fiber optic and wireless communication, sensors, computation, electrolysis, electroplating and mechanical motors and actuators.
Electromagnetism has been studied since ancient times. Many ancient civilizations, including the Greeks and the Mayans created wide-ranging theories to explain lightning, static electricity, and the attraction between magnetized pieces of iron ore. However, it wasn’t until the late 18th century that scientists began to develop a mathematical basis for understanding the nature of electromagnetic interactions. In the 18th and 19th centuries, prominent scientists and mathematicians such as Coulomb, Gauss and Faraday developed namesake laws which helped to explain the formation and interaction of electromagnetic fields. This process culminated in the 1860s with the discovery of Maxwell’s equations, a set of four partial differential equations which provide a complete description of classical electromagnetic fields. Besides providing a sound mathematical basis for the relationships between electricity and magnetism that scientists had been exploring for centuries, Maxwell’s equations also predicted the existence of self-sustaining electromagnetic waves. Maxwell postulated that such waves make up visible light, which was later shown to be true. Indeed, gamma-rays, x-rays, ultraviolet, visible, infrared radiation, microwaves and radio waves were all determined to be electromagnetic radiation differing only in their range of frequencies.
In the modern era, scientists have continued to refine the theorem of electromagnetism to take into account the effects of modern physics, including quantum mechanics and relativity. Indeed, the theoretical implications of electromagnetism, particularly the establishment of the speed of light based on properties of the «medium» of propagation (permeability and permittivity), helped inspire Einstein’s theory of special relativity in 1905. Meanwhile, the field of quantum electrodynamics (QED) has modified Maxwell’s equations to be consistent with the quantized nature of matter. In QED, the electromagnetic field is expressed in terms of discrete particles known as photons, which are also the physical quanta of light. Today, there exist many problems in electromagnetism that remain unsolved, such as the existence of magnetic monopoles and the mechanism by which some organisms can sense electric and magnetic fields.
History of the theory
Cover of A Treatise on Electricity and Magnetism
Originally, electricity and magnetism were considered to be two separate forces. This view changed with the publication of James Clerk Maxwell’s 1873 A Treatise on Electricity and Magnetism[1] in which the interactions of positive and negative charges were shown to be mediated by one force. There are four main effects resulting from these interactions, all of which have been clearly demonstrated by experiments:
- Electric charges attract or repel one another with a force inversely proportional to the square of the distance between them: unlike charges attract, like ones repel.[2]
- Magnetic poles (or states of polarization at individual points) attract or repel one another in a manner similar to positive and negative charges and always exist as pairs: every north pole is yoked to a south pole.[3]
- An electric current inside a wire creates a corresponding circumferential magnetic field outside the wire. Its direction (clockwise or counter-clockwise) depends on the direction of the current in the wire.[4]
- A current is induced in a loop of wire when it is moved toward or away from a magnetic field, or a magnet is moved towards or away from it; the direction of current depends on that of the movement.[4]
In April 1820, Hans Christian Ørsted observed that an electrical current in a wire caused a nearby compass needle to move. At the time of discovery, Ørsted did not suggest any satisfactory explanation of the phenomenon, nor did he try to represent the phenomenon in a mathematical framework. However, three months later he began more intensive investigations.[5][6] Soon thereafter he published his findings, proving that an electric current produces a magnetic field as it flows through a wire. The CGS unit of magnetic induction (oersted) is named in honor of his contributions to the field of electromagnetism.[7]
His findings resulted in intensive research throughout the scientific community in electrodynamics. They influenced French physicist André-Marie Ampère’s developments of a single mathematical form to represent the magnetic forces between current-carrying conductors. Ørsted’s discovery also represented a major step toward a unified concept of energy.
This unification, which was observed by Michael Faraday, extended by James Clerk Maxwell, and partially reformulated by Oliver Heaviside and Heinrich Hertz, is one of the key accomplishments of 19th-century mathematical physics.[8] It has had far-reaching consequences, one of which was the understanding of the nature of light. Unlike what was proposed by the electromagnetic theory of that time, light and other electromagnetic waves are at present seen as taking the form of quantized, self-propagating oscillatory electromagnetic field disturbances called photons. Different frequencies of oscillation give rise to the different forms of electromagnetic radiation, from radio waves at the lowest frequencies, to visible light at intermediate frequencies, to gamma rays at the highest frequencies.
Ørsted was not the only person to examine the relationship between electricity and magnetism. In 1802, Gian Domenico Romagnosi, an Italian legal scholar, deflected a magnetic needle using a Voltaic pile. The factual setup of the experiment is not completely clear, nor if current flowed across the needle or not. An account of the discovery was published in 1802 in an Italian newspaper, but it was largely overlooked by the contemporary scientific community, because Romagnosi seemingly did not belong to this community.[9]
An earlier (1735), and often neglected, connection between electricity and magnetism was reported by a Dr. Cookson.[10] The account stated:
A tradesman at Wakefield in Yorkshire, having put up a great number of knives and forks in a large box … and having placed the box in the corner of a large room, there happened a sudden storm of thunder, lightning, &c. … The owner emptying the box on a counter where some nails lay, the persons who took up the knives, that lay on the nails, observed that the knives took up the nails. On this the whole number was tried, and found to do the same, and that, to such a degree as to take up large nails, packing needles, and other iron things of considerable weight …
E. T. Whittaker suggested in 1910 that this particular event was responsible for lightning to be «credited with the power of magnetizing steel; and it was doubtless this which led Franklin in 1751 to attempt to magnetize a sewing-needle by means of the discharge of Leyden jars.»[11]
Fundamental forces
Representation of the electric field vector of a wave of circularly polarized electromagnetic radiation.
The electromagnetic force is one of the four known fundamental forces and the second strongest (after the strong nuclear force), operating with infinite range;[12] The other fundamental forces are:
- the strong nuclear force, which binds quarks to form nucleons, and binds nucleons to form nuclei; it is the strongest of the four known fundamental forces, but operates only at short range;[12]
- the weak nuclear force, which binds to all known particles in the Standard Model, and causes certain forms of radioactive decay; it is the second weakest of the four fundamental forces and, like the strong nuclear force, operates only at short range (note that in particle physics, the electroweak interaction is the unified description of two of the four known fundamental interactions of nature: electromagnetism and the weak interaction);[12]
- the gravitational force is the only one of the four fundamental forces that is not part of the Standard Model of particle physics; while by far the weakest of the four fundamental forces, the gravitational force, along with the electromagnetic force, operates at infinite range.[12]
All other forces (e.g., friction, contact forces) are derived from these four fundamental forces and they are known as non-fundamental forces.[13]
Roughly speaking, all the forces involved in interactions between atoms can be explained by the electromagnetic force acting between the electrically charged atomic nuclei and electrons of the atoms. Electromagnetic forces also explain how these particles carry momentum by their movement. This includes the forces we experience in «pushing» or «pulling» ordinary material objects, which result from the intermolecular forces that act between the individual molecules in our bodies and those in the objects. The electromagnetic force is also involved in all forms of chemical phenomena.
A necessary part of understanding the intra-atomic and intermolecular forces is the effective force generated by the momentum of the electrons’ movement, such that as electrons move between interacting atoms they carry momentum with them. As a collection of electrons becomes more confined, their minimum momentum necessarily increases due to the Pauli exclusion principle. The behaviour of matter at the molecular scale including its density is determined by the balance between the electromagnetic force and the force generated by the exchange of momentum carried by the electrons themselves.[14]
Classical electrodynamics
In 1600, William Gilbert proposed, in his De Magnete, that electricity and magnetism, while both capable of causing attraction and repulsion of objects, were distinct effects.[15] Mariners had noticed that lightning strikes had the ability to disturb a compass needle. The link between lightning and electricity was not confirmed until Benjamin Franklin’s proposed experiments in 1752 were conducted on 10 May 1752 by Thomas-François Dalibard of France using a 40-foot-tall (12 m) iron rod instead of a kite and he successfully extracted electrical sparks from a cloud.[16][17]
One of the first to discover and publish a link between man-made electric current and magnetism was Gian Romagnosi, who in 1802 noticed that connecting a wire across a voltaic pile deflected a nearby compass needle. However, the effect did not become widely known until 1820, when Ørsted performed a similar experiment.[18] Ørsted’s work influenced Ampère to produce a theory of electromagnetism that set the subject on a mathematical foundation.[19]
A theory of electromagnetism, known as classical electromagnetism, was developed by various physicists during the period between 1820 and 1873 when it culminated in the publication of a treatise by James Clerk Maxwell, which unified the preceding developments into a single theory and discovered the electromagnetic nature of light.[20] In classical electromagnetism, the behavior of the electromagnetic field is described by a set of equations known as Maxwell’s equations, and the electromagnetic force is given by the Lorentz force law.[21]
One of the peculiarities of classical electromagnetism is that it is difficult to reconcile with classical mechanics, but it is compatible with special relativity. According to Maxwell’s equations, the speed of light in vacuum is a universal constant that is dependent only on the electrical permittivity and magnetic permeability of free space. This violates Galilean invariance, a long-standing cornerstone of classical mechanics. One way to reconcile the two theories (electromagnetism and classical mechanics) is to assume the existence of a luminiferous aether through which the light propagates. However, subsequent experimental efforts failed to detect the presence of the aether. After important contributions of Hendrik Lorentz and Henri Poincaré, in 1905, Albert Einstein solved the problem with the introduction of special relativity, which replaced classical kinematics with a new theory of kinematics compatible with classical electromagnetism. (For more information, see History of special relativity.)
In addition, relativity theory implies that in moving frames of reference, a magnetic field transforms to a field with a nonzero electric component and conversely, a moving electric field transforms to a nonzero magnetic component, thus firmly showing that the phenomena are two sides of the same coin. Hence the term «electromagnetism». (For more information, see Classical electromagnetism and special relativity and Covariant formulation of classical electromagnetism.)
Extension to nonlinear phenomena
The Maxwell equations are linear, in that a change in the sources (the charges and currents) results in a proportional change of the fields. Nonlinear dynamics can occur when electromagnetic fields couple to matter that follows nonlinear dynamical laws.[22] This is studied, for example, in the subject of magnetohydrodynamics, which combines Maxwell theory with the Navier–Stokes equations.[23]
Quantities and units
Here is a list of common units related to electromagnetism:[24]
- ampere (electric current)
- coulomb (electric charge)
- farad (capacitance)
- henry (inductance)
- ohm (resistance)
- siemens (conductance)
- tesla (magnetic flux density)
- volt (electric potential)
- watt (power)
- weber (magnetic flux)
In the electromagnetic CGS system, electric current is a fundamental quantity defined via Ampère’s law and takes the permeability as a dimensionless quantity (relative permeability) whose value in vacuum is unity.[25] As a consequence, the square of the speed of light appears explicitly in some of the equations interrelating quantities in this system.
|
SI electromagnetism units
|
||||
|---|---|---|---|---|
| Symbol[26] | Name of quantity | Unit name | Symbol | Base units |
| E | energy | joule | J = C⋅V | kg⋅m2⋅s−2 |
| Q | electric charge | coulomb | C | A⋅s |
| I | electric current | ampere | A = C/s = W/V | A |
| J | electric current density | ampere per square metre | A/m2 | A⋅m−2 |
| ΔV; Δφ; ε | potential difference; voltage; electromotive force | volt | V = J/C | kg⋅m2⋅s−3⋅A−1 |
| R; Z; X | electric resistance; impedance; reactance | ohm | Ω = V/A | kg⋅m2⋅s−3⋅A−2 |
| ρ | resistivity | ohm metre | Ω⋅m | kg⋅m3⋅s−3⋅A−2 |
| P | electric power | watt | W = V⋅A | kg⋅m2⋅s−3 |
| C | capacitance | farad | F = C/V | kg−1⋅m−2⋅A2⋅s4 |
| ΦE | electric flux | volt metre | V⋅m | kg⋅m3⋅s−3⋅A−1 |
| E | electric field strength | volt per metre | V/m = N/C | kg⋅m⋅A−1⋅s−3 |
| D | electric displacement field | coulomb per square metre | C/m2 | A⋅s⋅m−2 |
| ε | permittivity | farad per metre | F/m | kg−1⋅m−3⋅A2⋅s4 |
| χe | electric susceptibility | (dimensionless) | 1 | 1 |
| G; Y; B | conductance; admittance; susceptance | siemens | S = Ω−1 | kg−1⋅m−2⋅s3⋅A2 |
| κ, γ, σ | conductivity | siemens per metre | S/m | kg−1⋅m−3⋅s3⋅A2 |
| B | magnetic flux density, magnetic induction | tesla | T = Wb/m2 = N⋅A−1⋅m−1 | kg⋅s−2⋅A−1 |
| Φ, ΦM, ΦB | magnetic flux | weber | Wb = V⋅s | kg⋅m2⋅s−2⋅A−1 |
| H | magnetic field strength | ampere per metre | A/m | A⋅m−1 |
| L, M | inductance | henry | H = Wb/A = V⋅s/A | kg⋅m2⋅s−2⋅A−2 |
| μ | permeability | henry per metre | H/m | kg⋅m⋅s−2⋅A−2 |
| χ | magnetic susceptibility | (dimensionless) | 1 | 1 |
| µ | magnetic dipole moment | ampere square meter | A⋅m2 = J⋅T−1 | A⋅m2 |
| σ | mass magnetization | ampere square meter per kilogram | A⋅m2/kg | A⋅m2⋅kg−1 |
Formulas for physical laws of electromagnetism (such as Maxwell’s equations) need to be adjusted depending on what system of units one uses. This is because there is no one-to-one correspondence between electromagnetic units in SI and those in CGS, as is the case for mechanical units. Furthermore, within CGS, there are several plausible choices of electromagnetic units, leading to different unit «sub-systems», including Gaussian, «ESU», «EMU», and Heaviside–Lorentz. Among these choices, Gaussian units are the most common today, and in fact the phrase «CGS units» is often used to refer specifically to CGS-Gaussian units.[27]
Applications
The study of electromagnetism informs electric circuits and semiconductor devices’ construction.
See also
- Abraham–Lorentz force
- Aeromagnetic surveys
- Computational electromagnetics
- Double-slit experiment
- Electromagnet
- Electromagnetic induction
- Electromagnetic wave equation
- Electromagnetic scattering
- Electromechanics
- Geophysics
- Introduction to electromagnetism
- Magnetostatics
- Magnetoquasistatic field
- Optics
- Relativistic electromagnetism
- Wheeler–Feynman absorber theory
References
- ^ «A Treatise on Electricity and Magnetism». Nature. 7 (182): 478–480. 24 April 1873. Bibcode:1873Natur…7..478.. doi:10.1038/007478a0. ISSN 0028-0836. S2CID 10178476.
- ^ «Why Do Like Charges Repel And Opposite Charges Attract?». Science ABC. 2019-02-06. Retrieved 2022-08-22.
- ^ «What Makes Magnets Repel?». Sciencing. Retrieved 2022-08-22.
- ^ a b Jim Lucas Contributions from Ashley Hamer (2022-02-18). «What Is Faraday’s Law of Induction?». livescience.com. Retrieved 2022-08-22.
- ^ «History of the Electric Telegraph». Scientific American. 17 (425supp): 6784–6786. 1884-02-23. doi:10.1038/scientificamerican02231884-6784supp. ISSN 0036-8733.
- ^ Volta and the history of electricity. Fabio Bevilacqua, Enrico A. Giannetto. Milano: U. Hoepli. 2003. ISBN 88-203-3284-1. OCLC 1261807533.
{{cite book}}: CS1 maint: others (link) - ^ Roche, John J. (1998). The mathematics of measurement : a critical history. London: Athlone Press. ISBN 0-485-11473-9. OCLC 40499222.
- ^ Darrigol, Olivier (2000). Electrodynamics from Ampère to Einstein. New York: Oxford University Press. ISBN 0198505949.
- ^ Martins, Roberto de Andrade. «Romagnosi and Volta’s Pile: Early Difficulties in the Interpretation of Voltaic Electricity» (PDF). In Fabio Bevilacqua; Lucio Fregonese (eds.). Nuova Voltiana: Studies on Volta and his Times. Vol. 3. Università degli Studi di Pavia. pp. 81–102. Archived from the original (PDF) on 2013-05-30. Retrieved 2010-12-02.
- ^ VIII. An account of an extraordinary effect of lightning in communicating magnetism. Communicated by Pierce Dod, M.D. F.R.S. from Dr. Cookson of Wakefield in Yorkshire.
Phil. Trans. 1735 39, 74-75, published 1 January 1735 - ^ Whittaker, E.T. (1910). A History of the Theories of Aether and Electricity from the Age of Descartes to the Close of the Nineteenth Century. Longmans, Green and Company.
- ^ a b c d Rehm, Jeremy; published, Ben Biggs (2021-12-23). «The four fundamental forces of nature». Space.com. Retrieved 2022-08-22.
- ^ Browne, «Physics for Engineering and Science,» p. 160: «Gravity is one of the fundamental forces of nature. The other forces such as friction, tension, and the normal force are derived from the electric force, another of the fundamental forces. Gravity is a rather weak force… The electric force between two protons is much stronger than the gravitational force between them.»
- ^ Purcell, «Electricity and Magnetism, 3rd Edition,» p. 546: Ch 11 Section 6, «Electron Spin and Magnetic Moment.»
- ^ Malin, Stuart; Barraclough, David (2000). «Gilbert’s De Magnete: An early study of magnetism and electricity». Eos, Transactions American Geophysical Union. 81 (21): 233. Bibcode:2000EOSTr..81..233M. doi:10.1029/00EO00163. ISSN 0096-3941.
- ^ «Lightning! | Museum of Science, Boston».
- ^ Tucker, Tom (2003). Bolt of fate : Benjamin Franklin and his electric kite hoax (1st ed.). New York: PublicAffairs. ISBN 1-891620-70-3. OCLC 51763922.
- ^ Stern, Dr. David P.; Peredo, Mauricio (2001-11-25). «Magnetic Fields – History». NASA Goddard Space Flight Center. Retrieved 2009-11-27.
- ^ «Andre-Marie Ampère». ETHW. 2016-01-13. Retrieved 2022-08-22.
- ^ Purcell, p. 436. Chapter 9.3, «Maxwell’s description of the electromagnetic field was essentially complete.»
- ^ Purcell: p. 278: Chapter 6.1, «Definition of the Magnetic Field.» Lorentz force and force equation.
- ^ Jufriansah, Adi; Hermanto, Arief; Toifur, Moh.; Prasetyo, Erwin (2020-05-18). «Theoretical study of Maxwell’s equations in nonlinear optics». AIP Conference Proceedings. 2234 (1): 040013. Bibcode:2020AIPC.2234d0013J. doi:10.1063/5.0008179. ISSN 0094-243X. S2CID 219451710.
- ^ Hunt, Julian C. R. (1967-07-27). Some aspects of magnetohydrodynamics (Thesis thesis). University of Cambridge. doi:10.17863/cam.14141.
- ^ «Essentials of the SI: Base & derived units». physics.nist.gov. Retrieved 2022-08-22.
- ^ «Tables of Physical and Chemical Constants, and some Mathematical Functions». Nature. 107 (2687): 264. April 1921. Bibcode:1921Natur.107R.264.. doi:10.1038/107264c0. ISSN 1476-4687.
- ^ International Union of Pure and Applied Chemistry (1993). Quantities, Units and Symbols in Physical Chemistry, 2nd edition, Oxford: Blackwell Science. ISBN 0-632-03583-8. pp. 14–15. Electronic version.
- ^ «Conversion of formulae and quantities between unit systems» (PDF). www.stanford.edu. Retrieved 29 January 2022.
Further reading
Web sources
- Nave, R. «Electricity and magnetism». HyperPhysics. Georgia State University. Retrieved 2013-11-12.
- Khutoryansky, E. «Electromagnetism – Maxwell’s Laws». YouTube. Retrieved 2014-12-28.
Textbooks
- G.A.G. Bennet (1974). Electricity and Modern Physics (2nd ed.). Edward Arnold (UK). ISBN 978-0-7131-2459-0.
- Browne, Michael (2008). Physics for Engineering and Science (2nd ed.). McGraw-Hill/Schaum. ISBN 978-0-07-161399-6.
- Dibner, Bern (2012). Oersted and the discovery of electromagnetism. Literary Licensing, LLC. ISBN 978-1-258-33555-7.
- Durney, Carl H.; Johnson, Curtis C. (1969). Introduction to modern electromagnetics. McGraw-Hill. ISBN 978-0-07-018388-9.
- Feynman, Richard P. (1970). The Feynman Lectures on Physics Vol II. Addison Wesley Longman. ISBN 978-0-201-02115-8.
- Fleisch, Daniel (2008). A Student’s Guide to Maxwell’s Equations. Cambridge, UK: Cambridge University Press. ISBN 978-0-521-70147-1.
- I.S. Grant; W.R. Phillips; Manchester Physics (2008). Electromagnetism (2nd ed.). John Wiley & Sons. ISBN 978-0-471-92712-9.
- Griffiths, David J. (1998). Introduction to Electrodynamics (3rd ed.). Prentice Hall. ISBN 978-0-13-805326-0.
- Jackson, John D. (1998). Classical Electrodynamics (3rd ed.). Wiley. ISBN 978-0-471-30932-1.
- Moliton, André (2007). Basic electromagnetism and materials. 430 pages. New York: Springer-Verlag New York. ISBN 978-0-387-30284-3.
- Purcell, Edward M. (1985). Electricity and Magnetism Berkeley, Physics Course Volume 2 (2nd ed.). McGraw-Hill. ISBN 978-0-07-004908-6.
- Purcell, Edward M and Morin, David. (2013). Electricity and Magnetism, 820p (3rd ed.). Cambridge University Press, New York. ISBN 978-1-107-01402-2.
{{cite book}}: CS1 maint: multiple names: authors list (link) - Rao, Nannapaneni N. (1994). Elements of engineering electromagnetics (4th ed.). Prentice Hall. ISBN 978-0-13-948746-0.
- Rothwell, Edward J.; Cloud, Michael J. (2001). Electromagnetics. CRC Press. ISBN 978-0-8493-1397-4.
- Tipler, Paul (1998). Physics for Scientists and Engineers: Vol. 2: Light, Electricity and Magnetism (4th ed.). W.H. Freeman. ISBN 978-1-57259-492-0.
- Wangsness, Roald K.; Cloud, Michael J. (1986). Electromagnetic Fields (2nd ed.). Wiley. ISBN 978-0-471-81186-2.
General coverage
- A. Beiser (1987). Concepts of Modern Physics (4th ed.). McGraw-Hill (International). ISBN 978-0-07-100144-1.
- L.H. Greenberg (1978). Physics with Modern Applications. Holt-Saunders International W.B. Saunders and Co. ISBN 978-0-7216-4247-5.
- R.G. Lerner; G.L. Trigg (2005). Encyclopaedia of Physics (2nd ed.). VHC Publishers, Hans Warlimont, Springer. pp. 12–13. ISBN 978-0-07-025734-4.
- J.B. Marion; W.F. Hornyak (1984). Principles of Physics. Holt-Saunders International Saunders College. ISBN 978-4-8337-0195-2.
- H.J. Pain (1983). The Physics of Vibrations and Waves (3rd ed.). John Wiley & Sons. ISBN 978-0-471-90182-2.
- C.B. Parker (1994). McGraw Hill Encyclopaedia of Physics (2nd ed.). McGraw Hill. ISBN 978-0-07-051400-3.
- R. Penrose (2007). The Road to Reality. Vintage books. ISBN 978-0-679-77631-4.
- P.A. Tipler; G. Mosca (2008). Physics for Scientists and Engineers: With Modern Physics (6th ed.). W.H. Freeman and Co. ISBN 978-1-4292-0265-7.
- P.M. Whelan; M.J. Hodgeson (1978). Essential Principles of Physics (2nd ed.). John Murray. ISBN 978-0-7195-3382-2.
External links
- Magnetic Field Strength Converter
- Electromagnetic Force – from Eric Weisstein’s World of Physics
From Wikipedia, the free encyclopedia
«Electromagnetic» redirects here. Electromagnetic may also refer to the use of an electromagnet.
«Electromagnetic force» redirects here. For the force exerted on particles by electromagnetic fields, see Lorentz force.
Electromagnetic interactions are responsible for the glowing filaments in this plasma globe
In physics, electromagnetism is an interaction that occurs between particles with electric charge via electromagnetic fields. The electromagnetic force is one of the four fundamental forces of nature. It is the dominant force in the interactions of atoms and molecules. Electromagnetism can be thought of as a combination of electrostatics and magnetism, two distinct but closely intertwined phenomena. Electromagnetic forces occur between any two charged particles, causing an attraction between particles with opposite charges and repulsion between particles with the same charge, while magnetism is an interaction that occurs exclusively between charged particles in relative motion. These two effects combine to create electromagnetic fields in the vicinity of charge particles, which can accelerate other charged particles via the Lorentz force. At high energy, the weak force and electromagnetic force are unified as a single electroweak force.
The electromagnetic force is responsible for many of the chemical and physical phenomena observed in daily life. The electrostatic attraction between atomic nuclei and their electrons holds atoms together. Electric forces also allow different atoms to combine into molecules, including the macromolecules such as proteins that form the basis of life. Meanwhile, magnetic interactions between the spin and angular momentum magnetic moments of electrons also play a role in chemical reactivity; such relationships are studied in spin chemistry. Electromagnetism also plays a crucial role in modern technology: electrical energy production, transformation and distribution, light, heat, and sound production and detection, fiber optic and wireless communication, sensors, computation, electrolysis, electroplating and mechanical motors and actuators.
Electromagnetism has been studied since ancient times. Many ancient civilizations, including the Greeks and the Mayans created wide-ranging theories to explain lightning, static electricity, and the attraction between magnetized pieces of iron ore. However, it wasn’t until the late 18th century that scientists began to develop a mathematical basis for understanding the nature of electromagnetic interactions. In the 18th and 19th centuries, prominent scientists and mathematicians such as Coulomb, Gauss and Faraday developed namesake laws which helped to explain the formation and interaction of electromagnetic fields. This process culminated in the 1860s with the discovery of Maxwell’s equations, a set of four partial differential equations which provide a complete description of classical electromagnetic fields. Besides providing a sound mathematical basis for the relationships between electricity and magnetism that scientists had been exploring for centuries, Maxwell’s equations also predicted the existence of self-sustaining electromagnetic waves. Maxwell postulated that such waves make up visible light, which was later shown to be true. Indeed, gamma-rays, x-rays, ultraviolet, visible, infrared radiation, microwaves and radio waves were all determined to be electromagnetic radiation differing only in their range of frequencies.
In the modern era, scientists have continued to refine the theorem of electromagnetism to take into account the effects of modern physics, including quantum mechanics and relativity. Indeed, the theoretical implications of electromagnetism, particularly the establishment of the speed of light based on properties of the «medium» of propagation (permeability and permittivity), helped inspire Einstein’s theory of special relativity in 1905. Meanwhile, the field of quantum electrodynamics (QED) has modified Maxwell’s equations to be consistent with the quantized nature of matter. In QED, the electromagnetic field is expressed in terms of discrete particles known as photons, which are also the physical quanta of light. Today, there exist many problems in electromagnetism that remain unsolved, such as the existence of magnetic monopoles and the mechanism by which some organisms can sense electric and magnetic fields.
History of the theory
Cover of A Treatise on Electricity and Magnetism
Originally, electricity and magnetism were considered to be two separate forces. This view changed with the publication of James Clerk Maxwell’s 1873 A Treatise on Electricity and Magnetism[1] in which the interactions of positive and negative charges were shown to be mediated by one force. There are four main effects resulting from these interactions, all of which have been clearly demonstrated by experiments:
- Electric charges attract or repel one another with a force inversely proportional to the square of the distance between them: unlike charges attract, like ones repel.[2]
- Magnetic poles (or states of polarization at individual points) attract or repel one another in a manner similar to positive and negative charges and always exist as pairs: every north pole is yoked to a south pole.[3]
- An electric current inside a wire creates a corresponding circumferential magnetic field outside the wire. Its direction (clockwise or counter-clockwise) depends on the direction of the current in the wire.[4]
- A current is induced in a loop of wire when it is moved toward or away from a magnetic field, or a magnet is moved towards or away from it; the direction of current depends on that of the movement.[4]
In April 1820, Hans Christian Ørsted observed that an electrical current in a wire caused a nearby compass needle to move. At the time of discovery, Ørsted did not suggest any satisfactory explanation of the phenomenon, nor did he try to represent the phenomenon in a mathematical framework. However, three months later he began more intensive investigations.[5][6] Soon thereafter he published his findings, proving that an electric current produces a magnetic field as it flows through a wire. The CGS unit of magnetic induction (oersted) is named in honor of his contributions to the field of electromagnetism.[7]
His findings resulted in intensive research throughout the scientific community in electrodynamics. They influenced French physicist André-Marie Ampère’s developments of a single mathematical form to represent the magnetic forces between current-carrying conductors. Ørsted’s discovery also represented a major step toward a unified concept of energy.
This unification, which was observed by Michael Faraday, extended by James Clerk Maxwell, and partially reformulated by Oliver Heaviside and Heinrich Hertz, is one of the key accomplishments of 19th-century mathematical physics.[8] It has had far-reaching consequences, one of which was the understanding of the nature of light. Unlike what was proposed by the electromagnetic theory of that time, light and other electromagnetic waves are at present seen as taking the form of quantized, self-propagating oscillatory electromagnetic field disturbances called photons. Different frequencies of oscillation give rise to the different forms of electromagnetic radiation, from radio waves at the lowest frequencies, to visible light at intermediate frequencies, to gamma rays at the highest frequencies.
Ørsted was not the only person to examine the relationship between electricity and magnetism. In 1802, Gian Domenico Romagnosi, an Italian legal scholar, deflected a magnetic needle using a Voltaic pile. The factual setup of the experiment is not completely clear, nor if current flowed across the needle or not. An account of the discovery was published in 1802 in an Italian newspaper, but it was largely overlooked by the contemporary scientific community, because Romagnosi seemingly did not belong to this community.[9]
An earlier (1735), and often neglected, connection between electricity and magnetism was reported by a Dr. Cookson.[10] The account stated:
A tradesman at Wakefield in Yorkshire, having put up a great number of knives and forks in a large box … and having placed the box in the corner of a large room, there happened a sudden storm of thunder, lightning, &c. … The owner emptying the box on a counter where some nails lay, the persons who took up the knives, that lay on the nails, observed that the knives took up the nails. On this the whole number was tried, and found to do the same, and that, to such a degree as to take up large nails, packing needles, and other iron things of considerable weight …
E. T. Whittaker suggested in 1910 that this particular event was responsible for lightning to be «credited with the power of magnetizing steel; and it was doubtless this which led Franklin in 1751 to attempt to magnetize a sewing-needle by means of the discharge of Leyden jars.»[11]
Fundamental forces
Representation of the electric field vector of a wave of circularly polarized electromagnetic radiation.
The electromagnetic force is one of the four known fundamental forces and the second strongest (after the strong nuclear force), operating with infinite range;[12] The other fundamental forces are:
- the strong nuclear force, which binds quarks to form nucleons, and binds nucleons to form nuclei; it is the strongest of the four known fundamental forces, but operates only at short range;[12]
- the weak nuclear force, which binds to all known particles in the Standard Model, and causes certain forms of radioactive decay; it is the second weakest of the four fundamental forces and, like the strong nuclear force, operates only at short range (note that in particle physics, the electroweak interaction is the unified description of two of the four known fundamental interactions of nature: electromagnetism and the weak interaction);[12]
- the gravitational force is the only one of the four fundamental forces that is not part of the Standard Model of particle physics; while by far the weakest of the four fundamental forces, the gravitational force, along with the electromagnetic force, operates at infinite range.[12]
All other forces (e.g., friction, contact forces) are derived from these four fundamental forces and they are known as non-fundamental forces.[13]
Roughly speaking, all the forces involved in interactions between atoms can be explained by the electromagnetic force acting between the electrically charged atomic nuclei and electrons of the atoms. Electromagnetic forces also explain how these particles carry momentum by their movement. This includes the forces we experience in «pushing» or «pulling» ordinary material objects, which result from the intermolecular forces that act between the individual molecules in our bodies and those in the objects. The electromagnetic force is also involved in all forms of chemical phenomena.
A necessary part of understanding the intra-atomic and intermolecular forces is the effective force generated by the momentum of the electrons’ movement, such that as electrons move between interacting atoms they carry momentum with them. As a collection of electrons becomes more confined, their minimum momentum necessarily increases due to the Pauli exclusion principle. The behaviour of matter at the molecular scale including its density is determined by the balance between the electromagnetic force and the force generated by the exchange of momentum carried by the electrons themselves.[14]
Classical electrodynamics
In 1600, William Gilbert proposed, in his De Magnete, that electricity and magnetism, while both capable of causing attraction and repulsion of objects, were distinct effects.[15] Mariners had noticed that lightning strikes had the ability to disturb a compass needle. The link between lightning and electricity was not confirmed until Benjamin Franklin’s proposed experiments in 1752 were conducted on 10 May 1752 by Thomas-François Dalibard of France using a 40-foot-tall (12 m) iron rod instead of a kite and he successfully extracted electrical sparks from a cloud.[16][17]
One of the first to discover and publish a link between man-made electric current and magnetism was Gian Romagnosi, who in 1802 noticed that connecting a wire across a voltaic pile deflected a nearby compass needle. However, the effect did not become widely known until 1820, when Ørsted performed a similar experiment.[18] Ørsted’s work influenced Ampère to produce a theory of electromagnetism that set the subject on a mathematical foundation.[19]
A theory of electromagnetism, known as classical electromagnetism, was developed by various physicists during the period between 1820 and 1873 when it culminated in the publication of a treatise by James Clerk Maxwell, which unified the preceding developments into a single theory and discovered the electromagnetic nature of light.[20] In classical electromagnetism, the behavior of the electromagnetic field is described by a set of equations known as Maxwell’s equations, and the electromagnetic force is given by the Lorentz force law.[21]
One of the peculiarities of classical electromagnetism is that it is difficult to reconcile with classical mechanics, but it is compatible with special relativity. According to Maxwell’s equations, the speed of light in vacuum is a universal constant that is dependent only on the electrical permittivity and magnetic permeability of free space. This violates Galilean invariance, a long-standing cornerstone of classical mechanics. One way to reconcile the two theories (electromagnetism and classical mechanics) is to assume the existence of a luminiferous aether through which the light propagates. However, subsequent experimental efforts failed to detect the presence of the aether. After important contributions of Hendrik Lorentz and Henri Poincaré, in 1905, Albert Einstein solved the problem with the introduction of special relativity, which replaced classical kinematics with a new theory of kinematics compatible with classical electromagnetism. (For more information, see History of special relativity.)
In addition, relativity theory implies that in moving frames of reference, a magnetic field transforms to a field with a nonzero electric component and conversely, a moving electric field transforms to a nonzero magnetic component, thus firmly showing that the phenomena are two sides of the same coin. Hence the term «electromagnetism». (For more information, see Classical electromagnetism and special relativity and Covariant formulation of classical electromagnetism.)
Extension to nonlinear phenomena
The Maxwell equations are linear, in that a change in the sources (the charges and currents) results in a proportional change of the fields. Nonlinear dynamics can occur when electromagnetic fields couple to matter that follows nonlinear dynamical laws.[22] This is studied, for example, in the subject of magnetohydrodynamics, which combines Maxwell theory with the Navier–Stokes equations.[23]
Quantities and units
Here is a list of common units related to electromagnetism:[24]
- ampere (electric current)
- coulomb (electric charge)
- farad (capacitance)
- henry (inductance)
- ohm (resistance)
- siemens (conductance)
- tesla (magnetic flux density)
- volt (electric potential)
- watt (power)
- weber (magnetic flux)
In the electromagnetic CGS system, electric current is a fundamental quantity defined via Ampère’s law and takes the permeability as a dimensionless quantity (relative permeability) whose value in vacuum is unity.[25] As a consequence, the square of the speed of light appears explicitly in some of the equations interrelating quantities in this system.
|
SI electromagnetism units
|
||||
|---|---|---|---|---|
| Symbol[26] | Name of quantity | Unit name | Symbol | Base units |
| E | energy | joule | J = C⋅V | kg⋅m2⋅s−2 |
| Q | electric charge | coulomb | C | A⋅s |
| I | electric current | ampere | A = C/s = W/V | A |
| J | electric current density | ampere per square metre | A/m2 | A⋅m−2 |
| ΔV; Δφ; ε | potential difference; voltage; electromotive force | volt | V = J/C | kg⋅m2⋅s−3⋅A−1 |
| R; Z; X | electric resistance; impedance; reactance | ohm | Ω = V/A | kg⋅m2⋅s−3⋅A−2 |
| ρ | resistivity | ohm metre | Ω⋅m | kg⋅m3⋅s−3⋅A−2 |
| P | electric power | watt | W = V⋅A | kg⋅m2⋅s−3 |
| C | capacitance | farad | F = C/V | kg−1⋅m−2⋅A2⋅s4 |
| ΦE | electric flux | volt metre | V⋅m | kg⋅m3⋅s−3⋅A−1 |
| E | electric field strength | volt per metre | V/m = N/C | kg⋅m⋅A−1⋅s−3 |
| D | electric displacement field | coulomb per square metre | C/m2 | A⋅s⋅m−2 |
| ε | permittivity | farad per metre | F/m | kg−1⋅m−3⋅A2⋅s4 |
| χe | electric susceptibility | (dimensionless) | 1 | 1 |
| G; Y; B | conductance; admittance; susceptance | siemens | S = Ω−1 | kg−1⋅m−2⋅s3⋅A2 |
| κ, γ, σ | conductivity | siemens per metre | S/m | kg−1⋅m−3⋅s3⋅A2 |
| B | magnetic flux density, magnetic induction | tesla | T = Wb/m2 = N⋅A−1⋅m−1 | kg⋅s−2⋅A−1 |
| Φ, ΦM, ΦB | magnetic flux | weber | Wb = V⋅s | kg⋅m2⋅s−2⋅A−1 |
| H | magnetic field strength | ampere per metre | A/m | A⋅m−1 |
| L, M | inductance | henry | H = Wb/A = V⋅s/A | kg⋅m2⋅s−2⋅A−2 |
| μ | permeability | henry per metre | H/m | kg⋅m⋅s−2⋅A−2 |
| χ | magnetic susceptibility | (dimensionless) | 1 | 1 |
| µ | magnetic dipole moment | ampere square meter | A⋅m2 = J⋅T−1 | A⋅m2 |
| σ | mass magnetization | ampere square meter per kilogram | A⋅m2/kg | A⋅m2⋅kg−1 |
Formulas for physical laws of electromagnetism (such as Maxwell’s equations) need to be adjusted depending on what system of units one uses. This is because there is no one-to-one correspondence between electromagnetic units in SI and those in CGS, as is the case for mechanical units. Furthermore, within CGS, there are several plausible choices of electromagnetic units, leading to different unit «sub-systems», including Gaussian, «ESU», «EMU», and Heaviside–Lorentz. Among these choices, Gaussian units are the most common today, and in fact the phrase «CGS units» is often used to refer specifically to CGS-Gaussian units.[27]
Applications
The study of electromagnetism informs electric circuits and semiconductor devices’ construction.
See also
- Abraham–Lorentz force
- Aeromagnetic surveys
- Computational electromagnetics
- Double-slit experiment
- Electromagnet
- Electromagnetic induction
- Electromagnetic wave equation
- Electromagnetic scattering
- Electromechanics
- Geophysics
- Introduction to electromagnetism
- Magnetostatics
- Magnetoquasistatic field
- Optics
- Relativistic electromagnetism
- Wheeler–Feynman absorber theory
References
- ^ «A Treatise on Electricity and Magnetism». Nature. 7 (182): 478–480. 24 April 1873. Bibcode:1873Natur…7..478.. doi:10.1038/007478a0. ISSN 0028-0836. S2CID 10178476.
- ^ «Why Do Like Charges Repel And Opposite Charges Attract?». Science ABC. 2019-02-06. Retrieved 2022-08-22.
- ^ «What Makes Magnets Repel?». Sciencing. Retrieved 2022-08-22.
- ^ a b Jim Lucas Contributions from Ashley Hamer (2022-02-18). «What Is Faraday’s Law of Induction?». livescience.com. Retrieved 2022-08-22.
- ^ «History of the Electric Telegraph». Scientific American. 17 (425supp): 6784–6786. 1884-02-23. doi:10.1038/scientificamerican02231884-6784supp. ISSN 0036-8733.
- ^ Volta and the history of electricity. Fabio Bevilacqua, Enrico A. Giannetto. Milano: U. Hoepli. 2003. ISBN 88-203-3284-1. OCLC 1261807533.
{{cite book}}: CS1 maint: others (link) - ^ Roche, John J. (1998). The mathematics of measurement : a critical history. London: Athlone Press. ISBN 0-485-11473-9. OCLC 40499222.
- ^ Darrigol, Olivier (2000). Electrodynamics from Ampère to Einstein. New York: Oxford University Press. ISBN 0198505949.
- ^ Martins, Roberto de Andrade. «Romagnosi and Volta’s Pile: Early Difficulties in the Interpretation of Voltaic Electricity» (PDF). In Fabio Bevilacqua; Lucio Fregonese (eds.). Nuova Voltiana: Studies on Volta and his Times. Vol. 3. Università degli Studi di Pavia. pp. 81–102. Archived from the original (PDF) on 2013-05-30. Retrieved 2010-12-02.
- ^ VIII. An account of an extraordinary effect of lightning in communicating magnetism. Communicated by Pierce Dod, M.D. F.R.S. from Dr. Cookson of Wakefield in Yorkshire.
Phil. Trans. 1735 39, 74-75, published 1 January 1735 - ^ Whittaker, E.T. (1910). A History of the Theories of Aether and Electricity from the Age of Descartes to the Close of the Nineteenth Century. Longmans, Green and Company.
- ^ a b c d Rehm, Jeremy; published, Ben Biggs (2021-12-23). «The four fundamental forces of nature». Space.com. Retrieved 2022-08-22.
- ^ Browne, «Physics for Engineering and Science,» p. 160: «Gravity is one of the fundamental forces of nature. The other forces such as friction, tension, and the normal force are derived from the electric force, another of the fundamental forces. Gravity is a rather weak force… The electric force between two protons is much stronger than the gravitational force between them.»
- ^ Purcell, «Electricity and Magnetism, 3rd Edition,» p. 546: Ch 11 Section 6, «Electron Spin and Magnetic Moment.»
- ^ Malin, Stuart; Barraclough, David (2000). «Gilbert’s De Magnete: An early study of magnetism and electricity». Eos, Transactions American Geophysical Union. 81 (21): 233. Bibcode:2000EOSTr..81..233M. doi:10.1029/00EO00163. ISSN 0096-3941.
- ^ «Lightning! | Museum of Science, Boston».
- ^ Tucker, Tom (2003). Bolt of fate : Benjamin Franklin and his electric kite hoax (1st ed.). New York: PublicAffairs. ISBN 1-891620-70-3. OCLC 51763922.
- ^ Stern, Dr. David P.; Peredo, Mauricio (2001-11-25). «Magnetic Fields – History». NASA Goddard Space Flight Center. Retrieved 2009-11-27.
- ^ «Andre-Marie Ampère». ETHW. 2016-01-13. Retrieved 2022-08-22.
- ^ Purcell, p. 436. Chapter 9.3, «Maxwell’s description of the electromagnetic field was essentially complete.»
- ^ Purcell: p. 278: Chapter 6.1, «Definition of the Magnetic Field.» Lorentz force and force equation.
- ^ Jufriansah, Adi; Hermanto, Arief; Toifur, Moh.; Prasetyo, Erwin (2020-05-18). «Theoretical study of Maxwell’s equations in nonlinear optics». AIP Conference Proceedings. 2234 (1): 040013. Bibcode:2020AIPC.2234d0013J. doi:10.1063/5.0008179. ISSN 0094-243X. S2CID 219451710.
- ^ Hunt, Julian C. R. (1967-07-27). Some aspects of magnetohydrodynamics (Thesis thesis). University of Cambridge. doi:10.17863/cam.14141.
- ^ «Essentials of the SI: Base & derived units». physics.nist.gov. Retrieved 2022-08-22.
- ^ «Tables of Physical and Chemical Constants, and some Mathematical Functions». Nature. 107 (2687): 264. April 1921. Bibcode:1921Natur.107R.264.. doi:10.1038/107264c0. ISSN 1476-4687.
- ^ International Union of Pure and Applied Chemistry (1993). Quantities, Units and Symbols in Physical Chemistry, 2nd edition, Oxford: Blackwell Science. ISBN 0-632-03583-8. pp. 14–15. Electronic version.
- ^ «Conversion of formulae and quantities between unit systems» (PDF). www.stanford.edu. Retrieved 29 January 2022.
Further reading
Web sources
- Nave, R. «Electricity and magnetism». HyperPhysics. Georgia State University. Retrieved 2013-11-12.
- Khutoryansky, E. «Electromagnetism – Maxwell’s Laws». YouTube. Retrieved 2014-12-28.
Textbooks
- G.A.G. Bennet (1974). Electricity and Modern Physics (2nd ed.). Edward Arnold (UK). ISBN 978-0-7131-2459-0.
- Browne, Michael (2008). Physics for Engineering and Science (2nd ed.). McGraw-Hill/Schaum. ISBN 978-0-07-161399-6.
- Dibner, Bern (2012). Oersted and the discovery of electromagnetism. Literary Licensing, LLC. ISBN 978-1-258-33555-7.
- Durney, Carl H.; Johnson, Curtis C. (1969). Introduction to modern electromagnetics. McGraw-Hill. ISBN 978-0-07-018388-9.
- Feynman, Richard P. (1970). The Feynman Lectures on Physics Vol II. Addison Wesley Longman. ISBN 978-0-201-02115-8.
- Fleisch, Daniel (2008). A Student’s Guide to Maxwell’s Equations. Cambridge, UK: Cambridge University Press. ISBN 978-0-521-70147-1.
- I.S. Grant; W.R. Phillips; Manchester Physics (2008). Electromagnetism (2nd ed.). John Wiley & Sons. ISBN 978-0-471-92712-9.
- Griffiths, David J. (1998). Introduction to Electrodynamics (3rd ed.). Prentice Hall. ISBN 978-0-13-805326-0.
- Jackson, John D. (1998). Classical Electrodynamics (3rd ed.). Wiley. ISBN 978-0-471-30932-1.
- Moliton, André (2007). Basic electromagnetism and materials. 430 pages. New York: Springer-Verlag New York. ISBN 978-0-387-30284-3.
- Purcell, Edward M. (1985). Electricity and Magnetism Berkeley, Physics Course Volume 2 (2nd ed.). McGraw-Hill. ISBN 978-0-07-004908-6.
- Purcell, Edward M and Morin, David. (2013). Electricity and Magnetism, 820p (3rd ed.). Cambridge University Press, New York. ISBN 978-1-107-01402-2.
{{cite book}}: CS1 maint: multiple names: authors list (link) - Rao, Nannapaneni N. (1994). Elements of engineering electromagnetics (4th ed.). Prentice Hall. ISBN 978-0-13-948746-0.
- Rothwell, Edward J.; Cloud, Michael J. (2001). Electromagnetics. CRC Press. ISBN 978-0-8493-1397-4.
- Tipler, Paul (1998). Physics for Scientists and Engineers: Vol. 2: Light, Electricity and Magnetism (4th ed.). W.H. Freeman. ISBN 978-1-57259-492-0.
- Wangsness, Roald K.; Cloud, Michael J. (1986). Electromagnetic Fields (2nd ed.). Wiley. ISBN 978-0-471-81186-2.
General coverage
- A. Beiser (1987). Concepts of Modern Physics (4th ed.). McGraw-Hill (International). ISBN 978-0-07-100144-1.
- L.H. Greenberg (1978). Physics with Modern Applications. Holt-Saunders International W.B. Saunders and Co. ISBN 978-0-7216-4247-5.
- R.G. Lerner; G.L. Trigg (2005). Encyclopaedia of Physics (2nd ed.). VHC Publishers, Hans Warlimont, Springer. pp. 12–13. ISBN 978-0-07-025734-4.
- J.B. Marion; W.F. Hornyak (1984). Principles of Physics. Holt-Saunders International Saunders College. ISBN 978-4-8337-0195-2.
- H.J. Pain (1983). The Physics of Vibrations and Waves (3rd ed.). John Wiley & Sons. ISBN 978-0-471-90182-2.
- C.B. Parker (1994). McGraw Hill Encyclopaedia of Physics (2nd ed.). McGraw Hill. ISBN 978-0-07-051400-3.
- R. Penrose (2007). The Road to Reality. Vintage books. ISBN 978-0-679-77631-4.
- P.A. Tipler; G. Mosca (2008). Physics for Scientists and Engineers: With Modern Physics (6th ed.). W.H. Freeman and Co. ISBN 978-1-4292-0265-7.
- P.M. Whelan; M.J. Hodgeson (1978). Essential Principles of Physics (2nd ed.). John Murray. ISBN 978-0-7195-3382-2.
External links
- Magnetic Field Strength Converter
- Electromagnetic Force – from Eric Weisstein’s World of Physics






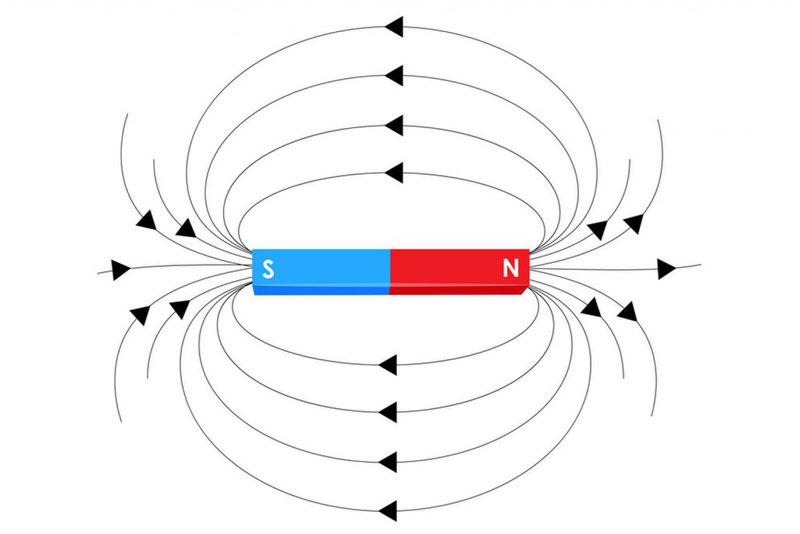
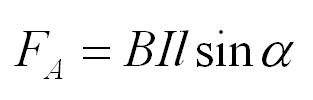
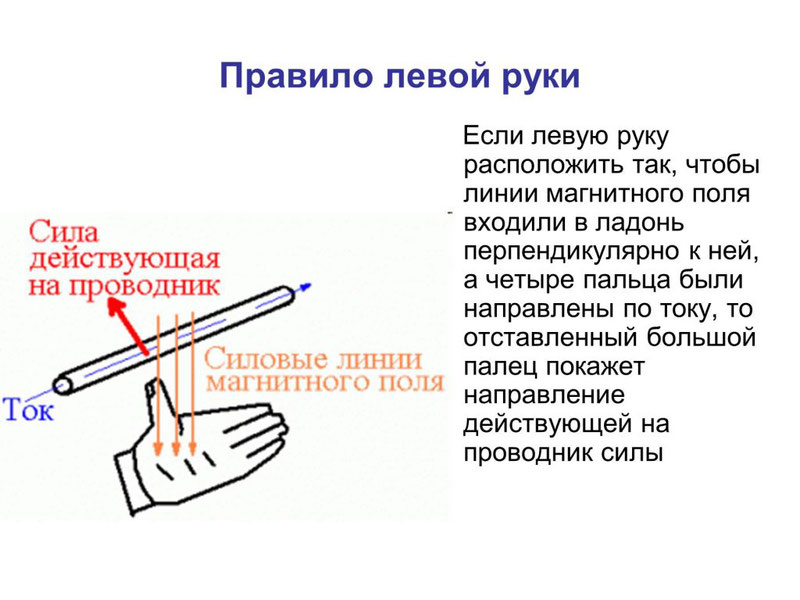
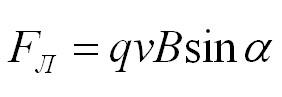

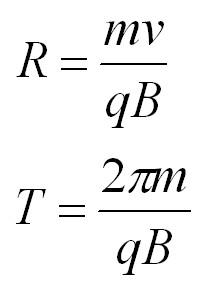
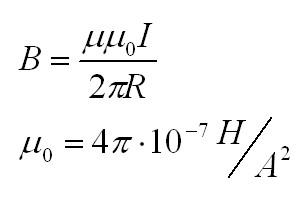
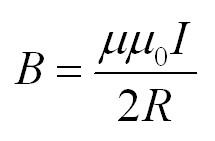
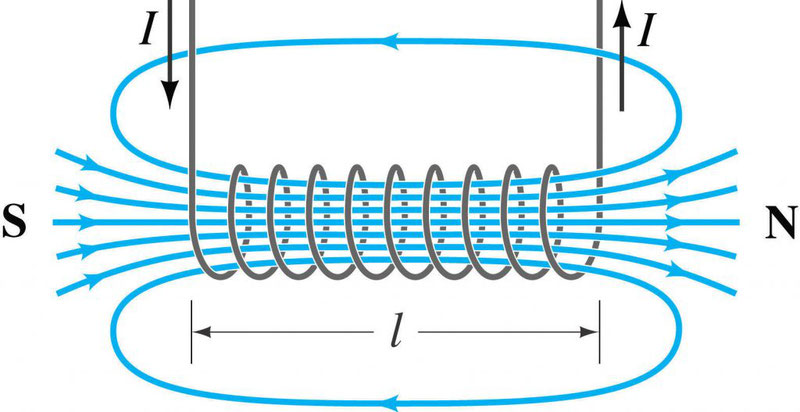
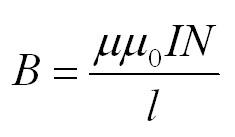
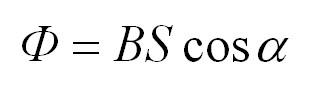
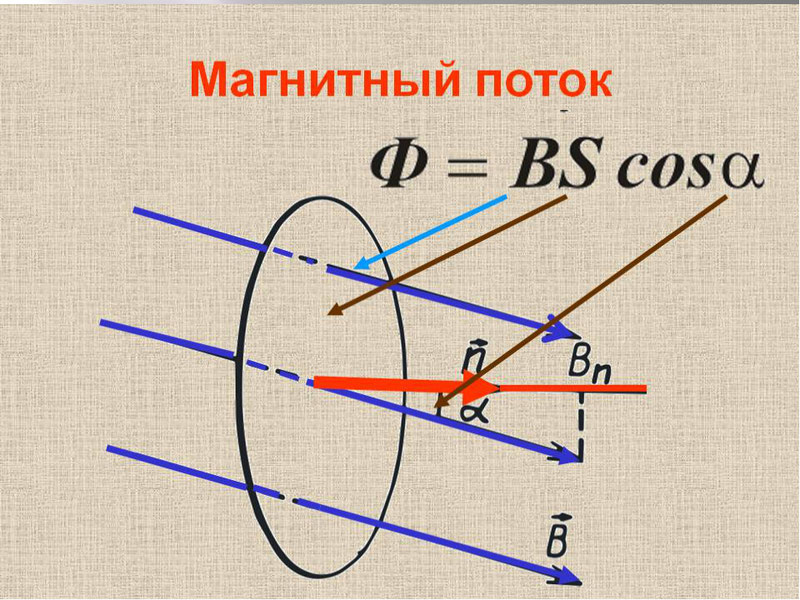
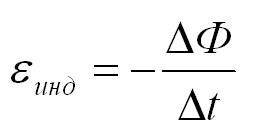
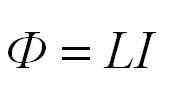
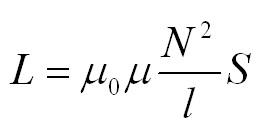
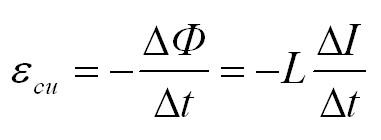
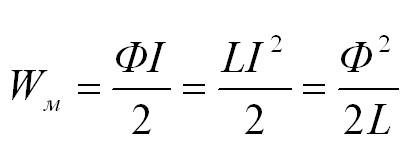
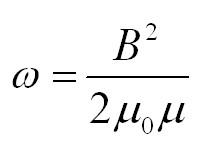




















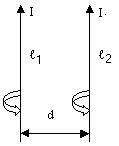
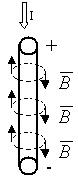
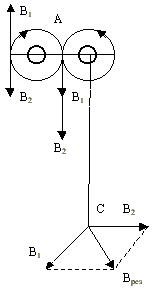
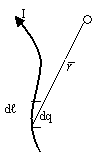
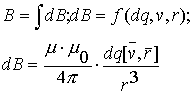
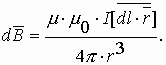
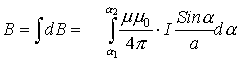
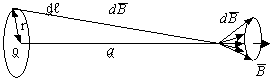
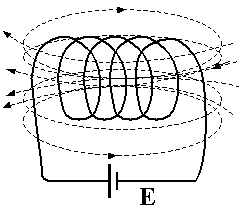
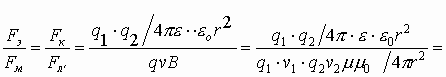
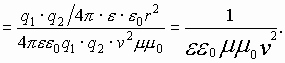
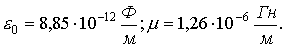
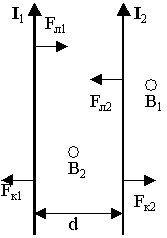
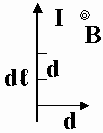
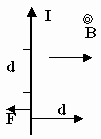
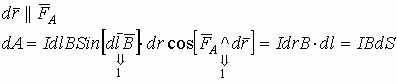
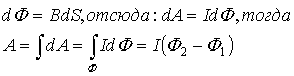
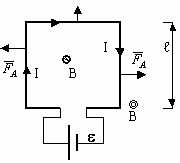
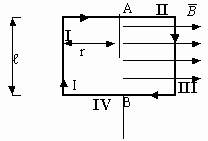
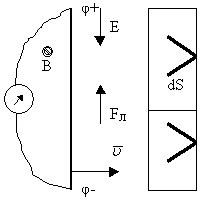
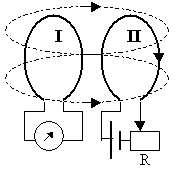
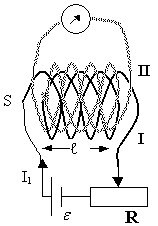
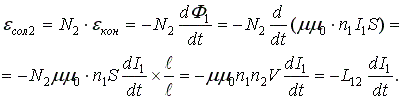
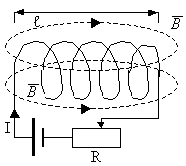
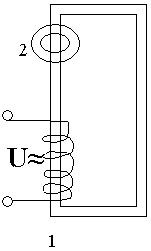
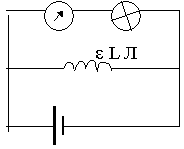
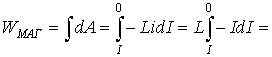
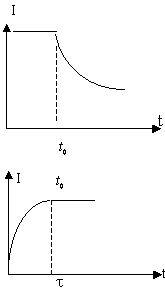
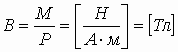 — тесла.
— тесла.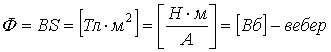 .
.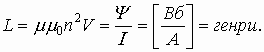
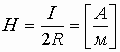 или для соленоида
или для соленоида 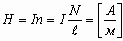 .
.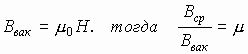 — безразмерная.
— безразмерная.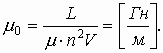
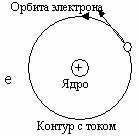
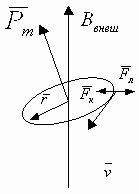
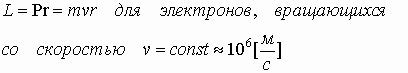
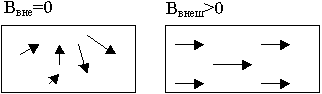
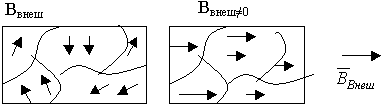
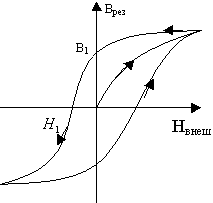
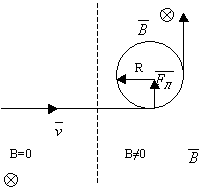
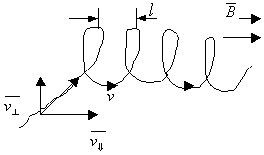
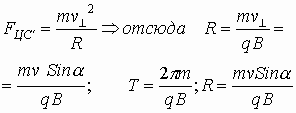
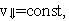
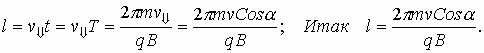
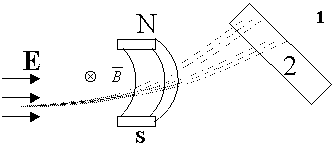
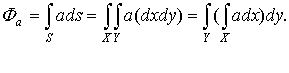
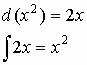
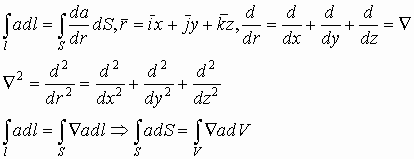
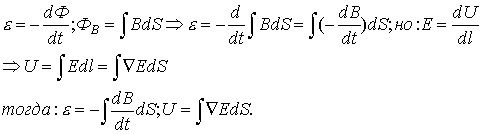
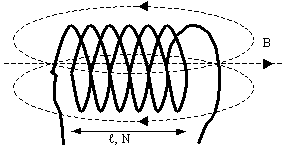
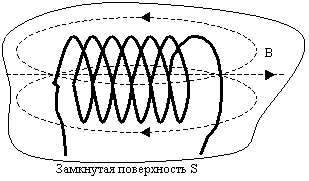
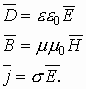

 , где
, где 

 , где
, где  — электрическая постоянная
— электрическая постоянная







 — модуль (нет знака)
— модуль (нет знака) — проекция (есть знак
— проекция (есть знак 




















 , затем вносим заряд под знак интеграла, делим силу на заряд и получаем напряженность:
, затем вносим заряд под знак интеграла, делим силу на заряд и получаем напряженность:






 — скорость изменения вдоль координаты
— скорость изменения вдоль координаты  — это взятое с обратным знаком производная от потенциала по этому направлению и по этой координате.
— это взятое с обратным знаком производная от потенциала по этому направлению и по этой координате. — скорость изменения вдоль координаты
— скорость изменения вдоль координаты  — для
— для 










 , где
, где 
 — поверхностная плотность
— поверхностная плотность , заряд/площадь поверхности, на которую он распределен.
, заряд/площадь поверхности, на которую он распределен.








