Элементы составных многогранников решу егэ

Каталог заданий.
Элементы составных многогранников


Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

1

Тип 2 № 245370

На рисунке изображён многогранник, все двугранные углы многогранника прямые. Найдите расстояние между вершинами A и C_2 .

Аналоги к заданию № 245370: 274953 275367 274955 274957 274959 274961 274963 274965 274967 274969 … Все

Кодификатор ФИПИ/Решу ЕГЭ: 5.5.3 Длина отрезка, ломаной, окружности, периметр многоугольника

Решение

·

·

Курс Д. Д. Гущина

·

Сообщить об ошибке · Помощь

2

Тип 2 № 245371

Найдите квадрат расстояния между вершинами D и C_2 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.

Аналоги к заданию № 245371: 275369 275859 275863 275867 275371 275373 275375 275377 275379 275381 … Все

Кодификатор ФИПИ/Решу ЕГЭ: 5.5.3 Длина отрезка, ломаной, окружности, периметр многоугольника

Решение

·

·

Курс Д. Д. Гущина

·

1 комментарий · Сообщить об ошибке · Помощь

3

Тип 2 № 245372

На рисунке изображён многогранник, все двугранные углы многогранника прямые. Найдите расстояние между вершинами B_1 и D_2 .

Аналоги к заданию № 245372: 275869 276367 275871 275875 275877 275879 275881 275883 275885 275887 … Все

Кодификатор ФИПИ/Решу ЕГЭ: 5.5.3 Длина отрезка, ломаной, окружности, периметр многоугольника

Решение

·

·

Курс Д. Д. Гущина

·

Сообщить об ошибке · Помощь

4

Тип 2 № 245373

Найдите угол CAD2 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах.

Аналоги к заданию № 245373: 276369 276867 276371 276373 276375 276377 276379 276381 276383 276385 … Все

Кодификатор ФИПИ/Решу ЕГЭ: 5.5.2 Угол между прямыми в пространстве; угол между прямой и плоскостью

Решение

·

·

Курс Д. Д. Гущина

·

Сообщить об ошибке · Помощь

5

Тип 2 № 245374

Найдите угол ABD многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах.

Аналоги к заданию № 245374: 276869 277367 276871 276873 276875 276877 276879 276881 276883 276885 … Все

Кодификатор ФИПИ/Решу ЕГЭ: 5.5.2 Угол между прямыми в пространстве; угол между прямой и плоскостью

Решение

·

·

Курс Д. Д. Гущина

·

Сообщить об ошибке · Помощь

Пройти тестирование по этим заданиям

Источник
Skip to content

ЕГЭ Профиль №8. Элементы составных многогранников

ЕГЭ Профиль №8. Элементы составных многогранниковadmin2018-08-14T13:31:55+03:00

Источник

Задание 1014

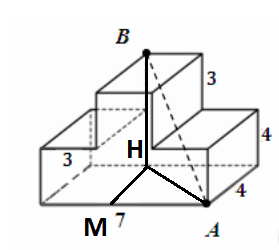
В многограннике, приведенном на рисунке, все двугранные углы прямые. Найдите расстояние между точками А и В.

Ответ: 9

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Скрыть

Для этого рассмотрим прямоугольный треугольник BHA: BH = 3 + 4 = 7. HA неизвестно, найдем ее из треугольника прямоугольного HMA: $$HA = sqrt{HM^2+MA^2}$$

$$HA = sqrt{HM^2+MA^2}=sqrt{4^2+(7-3)^2}=sqrt{32}$$

$$AB = sqrt{BH^2+AH^2}=sqrt{7^2+sqrt{32}^2}=sqrt{49+32}=sqrt{81}=9$$

Задание 2900

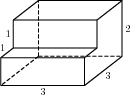
Найдите расстояние между вершинами B1 и D2 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.

Ответ: 3

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Скрыть

$$B_{1}D_{2}=sqrt{BD^{2}+D_{1}C_{2}^{2}}=$$ $$=sqrt{BC^{2}+CD^{2}+D_{1}C_{2}^{2}}=sqrt{2^{2}+2^{2}+1^{2}}=sqrt{9}=3$$

Задание 3695

На ри­сун­ке изоб­ражён мно­го­гран­ник, все дву­гран­ные углы мно­го­гран­ни­ка пря­мые. Най­ди­те рас­сто­я­ние между вер­ши­на­ми $$A$$ и $$C_{2}$$.

Ответ: 3

Задание 3696

Най­ди­те квад­рат рас­сто­я­ния между вер­ши­на­ми $$D$$ и $$C_{2}$$ мно­го­гран­ни­ка, изоб­ра­жен­но­го на ри­сун­ке. Все дву­гран­ные углы мно­го­гран­ни­ка пря­мые.

Ответ: 5

Задание 3697

На ри­сун­ке изоб­ражён мно­го­гран­ник, все дву­гран­ные углы мно­го­гран­ни­ка пря­мые. Най­ди­те рас­сто­я­ние между вер­ши­на­ми $$B_{1}$$ и $$D_{2}$$.

Ответ: 3

Задание 3698

Най­ди­те угол CAD2 мно­го­гран­ни­ка, изоб­ра­жен­но­го на ри­сун­ке. Все дву­гран­ные углы мно­го­гран­ни­ка пря­мые. Ответ дайте в гра­ду­сах.

Ответ: 60

Задание 3699

Най­ди­те угол ABD мно­го­гран­ни­ка, изоб­ра­жен­но­го на ри­сун­ке. Все дву­гран­ные углы мно­го­гран­ни­ка пря­мые. Ответ дайте в гра­ду­сах.

Ответ: 45

Задание 3700

На ри­сун­ке изоб­ражён мно­го­гран­ник, все дву­гран­ные углы мно­го­гран­ни­ка пря­мые. Най­ди­те тан­генс угла B2A2C2.

Ответ: 2

Задание 3701

На ри­сун­ке изоб­ражён мно­го­гран­ник, все дву­гран­ные углы мно­го­гран­ни­ка пря­мые. Най­ди­те квад­рат рас­сто­я­ния между вер­ши­на­ми $$B_{2}$$ и$$D_{3}$$.

Ответ: 11

Задание 3702

На ри­сун­ке изоб­ражён мно­го­гран­ник, все дву­гран­ные углы мно­го­гран­ни­ка пря­мые. Най­ди­те квад­рат рас­сто­я­ния между вер­ши­на­ми B и D2 

Ответ: 14

Задание 3703

На ри­сун­ке изоб­ражён мно­го­гран­ник, все дву­гран­ные углы мно­го­гран­ни­ка пря­мые. Най­ди­те квад­рат рас­сто­я­ния между вер­ши­на­ми $$A$$ и $$C_{3}$$.

Ответ: 17

Задание 3705

На ри­сун­ке изоб­ражён мно­го­гран­ник, все дву­гран­ные углы мно­го­гран­ни­ка пря­мые. Най­ди­те тан­генс угла ABB3.

Ответ: 2

Задание 3706

На ри­сун­ке изоб­ражён мно­го­гран­ник, все дву­гран­ные углы мно­го­гран­ни­ка пря­мые. Най­ди­те тан­генс угла C3D3B3.

Ответ: 3

Задание 3707

На ри­сун­ке изоб­ражён мно­го­гран­ник, все дву­гран­ные углы мно­го­гран­ни­ка пря­мые. Най­ди­те квад­рат рас­сто­я­ния между вер­ши­на­ми D и C2 

Ответ: 6

Задание 3708

Най­ди­те угол D2EF мно­го­гран­ни­ка, изоб­ра­жен­но­го на ри­сун­ке. Все дву­гран­ные углы мно­го­гран­ни­ка пря­мые. Ответ дайте в гра­ду­сах.

Ответ: 45

Источник

Многогранники

Многогранник – это поверхность, составленная из многоугольников, ограничивающая некоторое геометрическое тело.

В данной теме мы рассмотрим составные многогранники (многогранники, состоящие обычно из нескольких параллелепипедов).

Объемы различных многогранников:

  • Призма $V=S_{осн}·h$
  • Пирамида $V={1}/{3}S_{осн}·h$
  • Параллелепипед $V=a·b·c$, где $a, b$ и $c$ — длина, ширина и высота.
  • Куб $V=а^3$, где $а$ — сторона куба

Задачи на нахождение объема составного многогранника:

  • Первый способ.
  1. Составной многогранник надо достроить до полного параллелепипеда или куба.
  2. Найти объем параллелепипеда.
  3. Найти объем лишней части фигуры.
  4. Вычесть из объема параллелепипеда объем лишней части.

Пример:

Найдите объём многогранника, изображённого на рисунке (все двугранные углы прямые).

Решение:

1. Достроим составной многогранник до параллелепипеда.

Найдем его объем. Для этого перемножим все три измерения параллелепипеда:

$V=10·9·4=360$

2. Найдем объем лишнего маленького параллелепипеда:

Его длина равна $9-4=5$

Ширина равна $4$

Высота равна $7$

$V=7·4·5=140$

3. Вычтем из объема параллелепипеда объем лишней части и получим объем заданной фигуры:

$V=360-140=220$

Ответ: $220$

  • Второй способ
  1. Разделить составной многогранник на несколько параллелепипедов.
  2. Найти объем каждого параллелепипеда.
  3. Сложить объемы.

Задачи на нахождение площади поверхности составного многогранника.

— Если можно составной многогранник представить в виде прямой призмы, то находим площадь поверхности по формуле:

$S_{полн.пов.}=P_{осн}·h+2S_{осн}$

Чтобы найти площадь основания призмы, надо разделить его на прямоугольники и найти площадь каждого.

Пример:

Найдите площадь поверхности многогранника, изображённого на рисунке (все двугранные углы прямые).

Представим данный многогранник как прямую призму с высотой равной $12$.

$S_{полн.пов.}=P_{осн}·h+2S_{осн}$

$P_{осн}=8+6+6+2+2+4=28$

Чтобы найти площадь основания, разделим его на два прямоугольника и найдем площадь каждого:

$S_1=6·6=36$

$S_2=2·4=8$

$S_осн=36+8=44$

Далее подставим все данные в формулу и найдем площадь поверхности многогранника

$S_{полн.пов.}=28·12+2·44=336+88=424$

Ответ: $424$

— Если составной многогранник нельзя представить в виде призмы, то площадь полной поверхности можно найти как сумму площадей всех граней, ограничивающих поверхность.

Задачи на нахождение расстояния между точками составного многогранника.

В данных задачах приведены составные многогранники, у которых двугранные углы прямые. Надо соединить расстояние между заданными точками и достроить его до прямоугольного треугольника. Далее остается воспользоваться теоремой Пифагора для нахождения нужной стороны.

Теорема Пифагора

В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.

$АС^2+ВС^2=АВ^2$

Задачи на нахождение угла или значения одной из тригонометрических функций обозначенного в условии угла составного многогранника.

Так как в данных задачах приведены составные многогранники, у которых все двугранные углы прямые, то достроим угол до прямоугольного треугольника и найдем его значение по тригонометрическим значениям.

Соотношение между сторонами и углами в прямоугольном треугольнике:

В прямоугольном треугольнике $АВС$, с прямым углом $С$:

Для острого угла $В: АС$ — противолежащий катет; $ВС$ — прилежащий катет.

Для острого угла $А: ВС$ — противолежащий катет; $АС$ — прилежащий катет.

  1. Синусом ($sin$) острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
  2. Косинусом ($cos$) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
  3. Тангенсом ($tg$) острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету.

Значения тригонометрических функций некоторых углов:

$α$ $30$ $45$ $60$
$sinα$ ${1}/{2}$ ${√2}/{2}$ ${√3}/{2}$
$cosα$ ${√3}/{2}$ ${√2}/{2}$ ${1}/{2}$
$tgα$ ${√3}/{3}$ $1$ $√3$
$ctgα$ $√3$ $1$ ${√3}/{3}$

Задачи на рассмотрение подобия фигур.

При увеличении всех линейных размеров многогранника в $k$ раз, площадь его поверхности увеличится в $k^2$ раз.

При увеличении всех линейных размеров многогранника в $k$ раз, его объём увеличится в $k^3$ раз.

Источник

07
Сен 2013

Категория: 02 Стереометрия

02. Составные многогранники. Площадь поверхности. Объем

2013-09-07
2022-09-11

Задача 1. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

pic

Решение: + показать

Задача 2. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Решение: + показать

Задача 3. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Решение: + показать

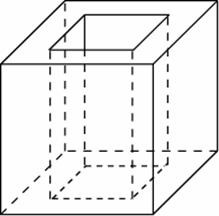
Задача 4.  Из единичного куба вырезана правильная четырехугольная призма со стороной основания 0,4 и боковым ребром 1. Найдите площадь поверхности оставшейся части куба.

311e2e2c481259de758d25b442f2ba60

Решение: + показать

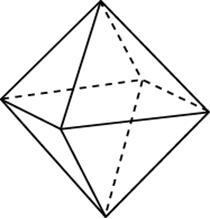
Задача 5. Во сколько раз увеличится площадь поверхности октаэдра, если все его ребра увеличить в 6 раз?

рп

Решение: + показать

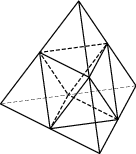
Задача 6. Площадь поверхности тетраэдра равна 1. Найдите площадь поверхности многогранника, вершинами которого являются середины сторон данного тетраэдра Видео*

pic-1

Решение: + показать

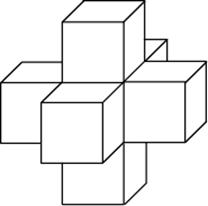
Задача 7.  Найдите объем пространственного креста, изображенного на рисунке и составленного из единичных кубов.

82173e2a373c19b17d150ef830c57ce7

Решение: + показать

Задача 8.  Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

pic-2

Решение: + показать

Задача 9.  Объем тетраэдра равен 1,5.  Найдите объем многогранника, вершинами которого являются середины сторон данного тетраэдра.

pic-1

Решение: + показать

Задача 10.  Найдите объем многогранника, вершинами которого являются точки A,;B,;C,;A_1,;C_1  правильной треугольной призмы ABCA_1B_1C_1, площадь основания которой равна 3, а боковое ребро равно 7.

xcvb

Решение: + показать

тестВы можете пройти тест “Cоставные многогранники”

Автор: egeMax |

комментариев 14

Источник

Канал видеоролика: Виктор Осипов

Элементы составных многогранников. Подготовка ЕГЭ. Задание 5.

Смотреть видео:

#математикаогэ #гвэ #егэответы #числа #математика #алгебра #егэпоматематике #ответы_егэ #ответы_огэ

Свежая информация для ЕГЭ и ОГЭ по Математике (листай):

С этим видео ученики смотрят следующие ролики:

Площадь поверхности составных многогранников. Подготовка ЕГЭ. Задание 5.

Площадь поверхности составных многогранников. Подготовка ЕГЭ. Задание 5.

Виктор Осипов

Объемы составных многогранников. Подготовка ЕГЭ. Задание 5.

Объемы составных многогранников. Подготовка ЕГЭ. Задание 5.

Виктор Осипов

Задание 13 урок 1 ЕГЭ 2019 математика профильный уровень подготовка

Задание 13 урок 1 ЕГЭ 2019 математика профильный уровень подготовка

Кирилл Макаров

задание 13 урок 2 ЕГЭ 2019 математика профильный уровень подготовка

задание 13 урок 2 ЕГЭ 2019 математика профильный уровень подготовка

Кирилл Макаров

Облегчи жизнь другим ученикам — поделись! (плюс тебе в карму):

10.11.2021

Источник

Слайды презентации

Слайд 1

Практикум Практикум
№3№3
по решению по решению
стереометрических задач

стереометрических задач
(базовый уровень)

(базовый уровень)

элементов на вычисление элементов
составных многогранниковсоставных многогранников

и

площади их поверхностии площади их поверхности

Слайд 3

Содержание
•
Задача №1
•
Задача №2
•
Задача №3
•
Задача №4
•
Задача №5
•
Задача №6
•
Задача №7 •
Задача

№8
•
Задача №9
•
Задача №10
•
Задача №11
•
Задача №12
•
Задача №13
•
Задача №14 •
Задача

№15
•
Задача №16
•
Задача №17
•
Задача №18
•
Задача №19
•
Задача

№20
•
Задача №21
•
Задача №22
•
Задача №23
•
Для сам. реш.

№20 • Задача №21 • Задача №22 • Задача №23 • Для сам. реш.

Слайд 4

Задача №1
Найдите расстояние между вершинами А и С2

многогранника,
изображенного на рисунке. Все двугранные углы многогранника

прямые.
Решение.Решение.
По теореме Пифагора имеем:По теореме Пифагора имеем:

Слайд 5

Задача №2
Найдите квадрат расстояния между вершинами D и

С2
многогранника, изображенного на рисунке. Все
двугранные углы

многогранника прямые.
Решение.Решение.
Рассмотрим прямоуголь ный
треугольник DD 2 C 2.

По теореме
Пифагора

По теореме Пифагора

Слайд 6

Задача №3
Найдите расстояние между вершинами В1 и D 2

многогранника, изображенного на рисунке. Все двугранные
углы многогранника

прямые.
Решение.Решение. Треугольник KD 2 B 1 = прямоуг.

По теореме
Пифагора :

По теореме Пифагора :

Слайд 7

Задача №4
Найдите угол CAD2 многогранника, изображенного на
рисунке.

Все двугранные углы многогранника прямые.
Ответ дайте в градусах.

Решение.Решение. Рассмотрим треугольник
CAD 2 где

AC=CD 2 =AD 2 т. к.
являются диагоналями равных
квадратов. Следовательно,
треугольник CAD 2 –
равносторонний, поэтому все его
углы равны 60 ° .

AC=CD 2 =AD 2 т. к. являются диагоналями равных квадратов. Следовательно, треугольник CAD 2 – равносторонний, поэтому все его углы равны 60 ° .

Слайд 8

Задача №5
Найдите угол АВ D многогранника, изображенного на

рисунке. Все двугранные углы многогранника прямые.
Ответ дайте в

градусах.
Решение.Решение.
ABCD квадрат со стороной 2, а BD —

его
диагональ. Значит, треугольник ABD —
прямоугольный и равнобедренный,
AB=AD . Угол ABD равен 45 °

его диагональ. Значит, треугольник ABD — прямоугольный и равнобедренный, AB=AD . Угол ABD равен 45 °

Слайд 9

Найдите угол D2EF многогранника, изображенного на
рисунке.

Все двугранные углы многогранника прямые.
Ответ дайте в градусах.

D 2 E — диагональ квадрата со
стороной 2, значит,

треугольник D 2 EF –
прямоугольный и
равнобедренный, угол D 2 EF
равен 45 ° .

треугольник D 2 EF – прямоугольный и равнобедренный, угол D 2 EF равен 45 ° .

Слайд 10

Найдите угол EAD 2 многогранника, изображенного на

рисунке. Все двугранные углы многогранника прямые.
Ответ дайте в

градусах.
Рассмотрим треугольник EAD 2 . В нем
AE=ED

2 =D 2 A , т.к. это диагонали
равных квадратов.
Таким образом, треугольник EAD 2 —
равносторонний, все его углы
равны 60° .

2 =D 2 A , т.к. это диагонали равных квадратов. Таким образом, треугольник EAD 2 — равносторонний, все его углы равны 60° .

Слайд 11

Задача № 8
Найдите тангенс угла

В 2 А 2 С 2 многогранника,
изображенного

на рисунке. Все двугранные углы
многогранника прямые.
Решение.Решение. Треугольник

В 2 А 2 С 2 прямоугольный.
Значит

В 2 А 2 С 2 прямоугольный. Значит

Слайд 12

Найдите тангенс угла С 2 С 3 В 2

многогранника,
изображенного на рисунке. Все двугранные углы
многогранника

прямые.

Слайд 13

Найдите тангенс угла АВВ 3 многогранника,
изображенного на

рисунке. Все двугранные углы
многогранника прямые.
к Опустим перпендикуляр

В 3 К из
точки В 3

на отрезок АВ . Угол
АВВ 3 равен углу КВВ 3 . В
прямоугольном треугольнике
В 3 КВ имеем:

на отрезок АВ . Угол АВВ 3 равен углу КВВ 3 . В прямоугольном треугольнике В 3 КВ имеем:

Слайд 14

Задача № 11
Найдите квадрат расстояния между вершинами В2 и

D3
многогранника, изображенного на рисунке. Все двугранные
углы

многогранника прямые.
Решение.Решение.
Ответ: 11

Слайд 15

Задача № 12
Найдите квадрат расстояния между вершинами В и

D 2
многогранника, изображенного на рисунке. Все
двугранные

углы многогранника прямые.
Решение.Решение.
Треугольник ВС1 D 2 прямоугольный =>

Слайд 16

Задача № 13
Найдите квадрат расстояния между вершинами А и

С 3
многогранника, изображенного на рисунке. Все
двугранные

углы многогранника прямые.
Решение.Решение.

Слайд 17

Задача №1 4
Найдите квадрат расстояния между вершинами D

и С 2
многогранника, изображенного на рисунке. Все

двугранные углы многогранника прямые.

Слайд 18

Задача №15
Найдите площадь поверхности многогранника,
изображенного на рисунке (все

двугранные углы
прямые).
Площадь поверхности заданного многогранника
равна разности

площади поверхности
прямоугольного параллелепипеда с ребрами
2, 3, 1 и

двух площадей прямоугольников со
сторонами 2, 1 :

двух площадей прямоугольников со сторонами 2, 1 :

Слайд 19

Задача №16
Найдите площадь поверхности многогранника,
изображенного на рисунке (все

двугранные углы
прямые).
Разность площадей параллелепипеда с ребрами 3,

3, 5 и двух площадей квадратов со стороной
1:

Слайд 20

Задача №17
Найдите площадь поверхности многогранника,
изображенного на рисунке (все

двугранные углы
прямые).
Площадь поверхности заданного
многогранника равна площади

поверхности прямоугольного
параллелепипеда с ребрами 3, 5, 5:

Слайд 21

Задача №18
Найдите площадь поверхности многогранника,
изображенного на рисунке (все

двугранные углы
прямые).
Площадь поверхности заданного
многогранника равна площади

поверхности прямоугольного
параллелепипеда с ребрами 3, 5, 4:

Слайд 22

Задача №19
Найдите площадь поверхности многогранника,
изображенного на рисунке (все

двугранные углы
прямые).
Площадь поверхности заданного
многогранника равна сумме

площадей
большого и маленького параллелепипедов с
ребрами 1, 5, 7

и 1, 1, 2, уменьшенной на 4
площади прямоугольника со сторонами 1,
2 — передней грани маленького
параллелепипеда, излишне учтенной при
расчете площадей поверхности
параллелепипедов :

и 1, 1, 2, уменьшенной на 4 площади прямоугольника со сторонами 1, 2 — передней грани маленького параллелепипеда, излишне учтенной при расчете площадей поверхности параллелепипедов :

Слайд 23

Задача №20
Найдите площадь поверхности многогранника, изображенного на
рисунке (все

двугранные углы прямые).
Площадь поверхности тела равна
сумме поверхностей

трех составляющих
ее параллелепипедов с ребрами 2,5,6 ;
2,5,3 и

2,2,3 , уменьшенная на
удвоенные площади прямоугольников со
сторонами 5 ,3 и 2, 3:

2,2,3 , уменьшенная на удвоенные площади прямоугольников со сторонами 5 ,3 и 2, 3:

Слайд 24

Задача №21
Найдите площадь поверхности многогранника, изображенного на
рисунке (все

двугранные углы прямые).
Площадь поверхности данной детали —
есть

сумма площади поверхности двух
многогранников: со сторонами 1,2,5 и

2,2,2 за вычетом 2 площадей
прямоугольников со сторонами 2,2 (т. к.
данная площадь учитывается два раза при
сложении площадей многогранников, а
как видно из рисунка, данных площадей в
итоговой детали нет). Значит:

2,2,2 за вычетом 2 площадей прямоугольников со сторонами 2,2 (т. к. данная площадь учитывается два раза при сложении площадей многогранников, а как видно из рисунка, данных площадей в итоговой детали нет). Значит:

Слайд 25

Задача №22
Найдите площадь поверхности многогранника, изображенного на
рисунке (все

двугранные углы прямые).
Площадь поверхности данной детали — есть

площадь поверхности многогранника со
сторонами 6,5,5 за вычетом площади

двух
«боковых прямоугольников» со сторонами
3,2 и прибавления 2 площадей «верхнего» и
«нижнего прямоугольников» со сторонами
2,5. Получаем:

двух "боковых прямоугольников" со сторонами 3,2 и прибавления 2 площадей "верхнего" и "нижнего прямоугольников" со сторонами 2,5. Получаем:

Слайд 26

Задача №23
Найдите площадь поверхности пространственного
креста, изображенного на рисунке

и составленного из
единичных кубов .
Поверхности креста составлена

из
шести поверхностей кубов , у
каждого из которых отсутствует

одна
грань . Тем самым, поверхность
креста состоит из 30 единичных
квадратов, поэтому ее площадь
равна 30.

одна грань . Тем самым, поверхность креста состоит из 30 единичных квадратов, поэтому ее площадь равна 30.

Слайд 27

Задачи Задачи
для самостоятельного для самостоятельного
решениярешения

Слайд 28

Задача №1 Решите самостоятельно
1) Найдите
расстояние

между
вершинами D и B 2
многогранника,

изображенного на
рисунке. Все
двугранные углы
многогранника
прямые.

Ответ: 33.

Ответ: 33.

Слайд 29

Задача №1 Решите самостоятельно
2) Найдите
расстояние

между
вершинами А и С2
многогранника,
изображенного на

рисунке. Все
двугранные углы
многогранника
прямые.

Слайд 30

Задача №1 Решите самостоятельно
3) Найдите
расстояние между

вершинами D и B 2
многогранника,
изображенного

на
рисунке. Все
двугранные углы
многогранника
прямые.

Слайд 31

Задача №2 Решите самостоятельно
Найдите квадрат расстояния между

вершинами А и В1 многогранника,
изображенного на рисунке.

Все двугранные углы многогранника прямые.
Ответ:37

Слайд 32

Задача №5 Решите самостоятельно
Найдите угол АВ D

многогранника, изображенного на
рисунке. Все двугранные углы многогранника

прямые.
Ответ дайте в градусах.
Ответ: 45

Слайд 33

Задача №8 Решите самостоятельно
Найдите тангенс угла

D 1 А 1 С 2 многогранника,
изображенного

на рисунке. Все двугранные углы
многогранника прямые.
Ответ: 1

Слайд 34

Задача № 15 Решите самостоятельно
Найдите площадь поверхности многогранника,

изображенного на рисунке (все двугранные углы
прямые).
Ответ:

Слайд 35

Задача № 20 Решите самостоятельно
Найдите площадь поверхности многогранника,

изображенного на рисунке (все двугранные углы
прямые).
Ответ:

Слайд 36

Найдите площадь поверхности многогранника, изображенного
на рисунке (все двугранные

углы прямые).
Ответ: 162

Слайд 37

Найдите площадь поверхности многогранника, изображенного
на рисунке (все двугранные

углы прямые).
Ответ:

Слайд 38

Найдите площадь поверхности многогранника, изображенного
на рисунке (все двугранные

углы прямые).
Ответ: 124

Слайд 39

Найдите площадь поверхности многогранника, изображенного
на рисунке (все двугранные

углы прямые).
Ответ: 84

Слайд 40

Найдите площадь поверхности многогранника, изображенного
на рисунке (все двугранные

углы прямые).
Ответ: 48

Слайд 41

Используемые ресурсы
•
Шаблон п одготовила учитель русского языка и литературы

Тихонова Надежда Андреевна
http://sch-53.ru/files/director/GIA/2016/%D0%95%D0%93%D0%AD%202016.jpg
«Решу ЕГЭ» Образовательный портал для подготовки к

ЕГЭ и ОГЭ. Режим
доступа: http://mathb.reshuege.ru
http://lib2.znate.ru/pars_docs/refs/324/323424/323424_html_m22f8f945.gif
Автор и источник заимствования неизвестен

Чтобы скачать презентацию — поделитесь ей с друзьями с помощью
социальных кнопок.

Источник

Понравилась статья? Поделить с друзьями:
  • Элементы системы права егэ обществознание
  • Элементы с проскоком электронов список егэ
  • Элементы религии обществознание егэ
  • Элементы прививки растений егэ
  • Элементы при сдаче экзамена в гаи