Элементы высшей математики
- Материалы к курсу
Векторы AC = a и BD = b служат диагоналями параллелограмма ABCD. Выразите вектор DA через векторы a и b
Тип ответа: Одиночный выбор
- 1) DA = (a − b) / 2
- 2) DA = (a + b) / 2
- 3) DA = −(a + b) / 2
Вертикальные асимптоты к графику функции y = (x + 2) / (x² — 4x)
Тип ответа: Одиночный выбор
- имеют вид …
- x= -2
- x = 0
- x = 4
- x = 4, x = 0
Вычислите (3 12/17 + 4 5/21) — 1 12/17
Тип ответа: Одиночный выбор
- 1) 6 1/3
- 2) 6 2/3
- 3) 6 12/17
- 4) 6 5/21
Вычислите выражение ((13 1/4 — 2 5/27 — 10 5/6) ⋅ 230,04 + 46,75) / 0,01
Тип ответа: Одиночный выбор
- 10000
- 100
- 10
- 1000
Вычислите интеграл J = ∫ cos(lnx)dx / x
Тип ответа: Одиночный выбор
- sin (lnx)+C
- ln sin x+C
- cos ln x+C
- -sin ln x+C
Вычислите определенный интеграл ∫ (eˣ — cosx)dx, x=0..π
Тип ответа: Одиночный выбор
- e^π-1
- e^π-2
- e^π
- e^π+ 1
Вычислите определенный интеграл ∫ √(1 — x)dx, x = 0..1
Тип ответа: Одиночный выбор
- 1) 2/3
- 2) 1,5
- 3) 2 2/3
- 4) 0
Вычислите определенный интеграл ∫ √(x)dx, x = 1..4
Тип ответа: Одиночный выбор
- 1) 4 2/3
- 2) 2 2/3
- 3) 4
- 4) 2
Вычислите определенный интеграл ∫ 2dt / cos²t, t = 0..π/4
Тип ответа: Одиночный выбор
- 1) 2 1/2
- 2) 2
- 3) 4
- 4) 1
Вычислите определенный интеграл ∫ dx / (1 — 2x)³, x = -2..0
Тип ответа: Одиночный выбор
- 0,24
- 0,3
- 0,4
- 0,008
Вычислите определенный интеграл ∫ eˣdx / (eˣ + 5), x = 0..1
Тип ответа: Одиночный выбор
- 1) ln((e + 5) / 6)
- 2) lne + 5
- 3) e^x + 5
- 4) 1 / (e + 5)
Вычислите определенный интеграл ∫ x²dx, x=0..3
Тип ответа: Одиночный выбор
- 9
- 7
- 6
- 3
Вычислите определитель │(1, 3, -2), (5, 1, 4), 3, 2, 1)│
Тип ответа: Одиночный выбор
- 56
- 1
- 0
- -42
Вычислите определитель │(5, −1), (2, 4)│
Тип ответа: Одиночный выбор
- 18
- 22
- 3
- 6
Вычислите определитель матрицы системы {2x — 4y = 1; 3x + 5y = -2
Тип ответа: Одиночный выбор
- -2
- -3
- 22
- -7
Вычислите определитель D =│(1, -2, 3), (3, 5, -1), (4, 1, 2)│
Тип ответа: Одиночный выбор
- -20
- 20
- 10
- -10
Вычислите площадь фигуры, ограниченной линиями 4y=x^2 и y^2=4x
Тип ответа: Одиночный выбор
- 16/3
- 3/16
- 16
- 3
Вычислите предел по правилу Лопиталя lim (√(5 — x) — 2) / (√(2 — x) — 1), x⟶1
Тип ответа: Одиночный выбор
- 1) -1/3
- 2) 1/3
- 3) -1/2
- 4) 1/2
Вычислите предел по правилу Лопиталя lim (3x² + 2x — 1) / (-x² + x + 2), x⟶-1
Тип ответа: Одиночный выбор
- 1) 4
- 2) 4/3
- 3) 1/3
- 4) -4/3
Вычислите предел по правилу Лопиталя lim lnx / ctgx, x⟶0
Тип ответа: Одиночный выбор
- 7
- 2
- 1
- 0
Вычислите предел по правилу Лопиталя lim x² / (1 — cos6x), x⟶0
Тип ответа: Одиночный выбор
- 11
- 1
- 2
- 1/18
Вычислите произведение матриц ((1, 2), (-2, -1)) ⋅ ((3, 0), (-2, 1))
Тип ответа: Одиночный выбор
- 1) ((3, 0), (4, −1))
- 2) ((−1, 2), (−4, −1))
- 3) ((3, 0), (−4, −1))
- 4) ((−1, 2), (4, 1))
Вычислите с точностью до десятых (3/5 + 0,425 — 0,005) : 0,1 / (30,5 + 1/3 + 3 1/3)
Тип ответа: Одиночный выбор
- 0,1
- 0,2
- 0,3
- 0,4
Дана функция f(x) = 4x + 8 / x. Решите уравнение f'(x) = 0
Тип ответа: Одиночный выбор
- 1) 0; 2
- 2) -2; 2
- 3) −√2; √2
- 4) √2
Дано: |a₁| = 3, |a₂| = 4, (a₁,᷍ a₂) = 2π/3. Вычислите (a₁ + a₂)²
Тип ответа: Одиночный выбор
- 144
- 12
- 11
- 13
Дано: a ⋅ b Найдите |a| = 8, |b| = 8, (a, ᷍ b) = π/3.
Тип ответа: Одиночный выбор
- -20
- 40
- 10
- 32
Даны вершины треугольника ABC: A(3; -1), B(4; 2) и C(-2; 0). Укажите уравнения его сторон
Тип ответа: Одиночный выбор
- 1) x − y + 10 = 0, 3x − 3y + 2 = 0, x + 5y + 2 = 0
- 2) 3x − y = 0, x + 3y − 6 = 0, x − 5y + 3 = 0
- 3) 3x − y − 10 = 0, x − 3y + 2 = 0, x + 5y + 2 = 0
Даны прямые (x + 2) / 2 = y / -3 = (z — 1) / 4 и (x — 3) / α = (y — 1) / 4 = (z — 7) / 2. При каком значении α они перпендикулярны?
Тип ответа: Одиночный выбор
- α = — 2
- α = 1
- α = 4
- α = 2
Даны точки M (-5; 7; -6), N (7; -9; 9). Вычислите проекцию вектора a = {1; -3; 1} на вектор MN
Тип ответа: Одиночный выбор
- 4
- 25
- 75
- 3
Для функции y = sinx / x
Тип ответа: Одиночный выбор
- точка x=0 является точкой …
- непрерывности
- разрыва 2-го рода
- устранимого разрыва
- экстремума
Каково необходимое условие возрастания функции?
Тип ответа: Одиночный выбор
- 1) если функция y=f(x) лифференцируема и возрастает на интервале (a;b), то f'(x)=0 для всех x их этого интервала
- 2) если функция y=f(x) лифференцируема и возрастает на интервале (a;b), то f'(x)≤0 для всех x их этого интервала
- 3) если функция y=f(x) лифференцируема и возрастает на интервале (a;b), то f'(x)≥0 для всех x их этого интервала
Какое из перечисленных чисел является иррациональным?
Тип ответа: Одиночный выбор
- 1) 1 1/2
- 2) 4,99
- 3) 5,4(15)
- 4) 3,141592…
Какой из перечисленных векторов коллинеарен вектору AB = (4; -8)?
Тип ответа: Одиночный выбор
- 1) MK = (2/3; −3/2)
- 2) LN = (3/2; −2/3)
- 3) EF = (3/2; −3/4)
- 4) CD = (2/3; −4/3)
Коллинеарными называются векторы, …
Тип ответа: Одиночный выбор
- лежащие на перпендикулярных прямых
- лежащие исключительно на одной прямой
- лежащие на одной прямой или на параллельных прямых
Матрица А^-1 является обратной матрицей к матрице А, если
Тип ответа: Одиночный выбор
- только А^-1⸱А=Е
- А^-1⸱А=А⸱А^-1=Е
- только А⸱А^-1=Е
- А^-1⸱А=А⸱А^-1=1
Матрица называется невырожденной, если ее определитель …
Тип ответа: Одиночный выбор
- равен нулю
- равен единице
- не равен нулю
- равен положительному числу
Матричное уравнение А⸱Х =В имеет решение …
Тип ответа: Одиночный выбор
- X=A^-1B
- X=BA^-1
- X=A-B
- X=B-A
Метод Гаусса решения системы линейных уравнений предполагает использование …
Тип ответа: Одиночный выбор
- алгебраического сложения
- определителей системы
- формул для вычисления неизвестных
- последовательного исключения неизвестных
Найдите ∛(-8)
Тип ответа: Одиночный выбор
- 2
- -24
- -2
Найдите ∫ (3 + 5x)⁴dx
Тип ответа: Одиночный выбор
- 1) 1/16 ⋅ (3 + 5x)³ + C
- 2) 1/15 ⋅ (3 + 5x)³ + C
- 3) 1/25 ⋅ (3 + 5x)⁵ + C
- 4) 1/25 ⋅ (3 + 5x)⁴ + C
Найдите ∫ (x — 3)dx, если при x= 2 первообразная функция равна
Тип ответа: Одиночный выбор
- 1) 2x² — 3x + 13
- 2) 2x² + 3x — 13
- 3) 1/2 ⋅ x² — 3x + 13
- 4) 1/2 ⋅ x + 3x + 13
Найдите ∫ √(x)dx / (1 + x)
Тип ответа: Одиночный выбор
- 1) 2 ⋅ (√x − arctg√x) + C
- 2) √x − arctg√x + C
- 3) 2 ⋅ (√x + arctg√x) + C
- 4) 1/2 ⋅ (√x − arctg√x) + C
Найдите ∫ √(x)dx
Тип ответа: Одиночный выбор
- 1) x√x + C
- 2) 2/3 ⋅ √x + C
- 3) 2/3 ⋅ x√x + C
- 4) 3/2 ⋅ x√x + C
Найдите ∫ 2xdx
Тип ответа: Одиночный выбор
- 4x^2 + С
- x + С
- x^2 + С
- 2x^2+C
Найдите ∫ 3dt / 2t
Тип ответа: Одиночный выбор
- 1) 3ln|t| + C
- 2) 2ln|t| + C
- 3) 3/2 ⋅ ln|t| + C
- 4) 2/3 ⋅ ln|t| + C
Найдите
Тип ответа: Одиночный выбор
- 1) tg(2x — 1) + C
- 2) 1/2 ⋅ ctg(2x — 1) + C
- 3) 1/2 ⋅ tg(2x — 1) + C
- 4) ctg(2x — 1) + C
Найдите ∫ lnxdx / x
Тип ответа: Одиночный выбор
- 1) 1/2 ⋅ lnx + C
- 2) -1/2 ⋅ lnx + C
- 3) 1/2 ⋅ ln²x + C
- 4) -1/2 ⋅ ln²x + C
Найдите ∫ sin³x cosx dx
Тип ответа: Одиночный выбор
- 1) x√x + C
- 2) 2/3 ⋅ √x + C
- 3) 2/3 ⋅ x√x + C
- 4) 3/2 ⋅ x√x + C
Найдите ∫ x²sin3x³dx
Тип ответа: Одиночный выбор
- 1) 1/6 ⋅ cos3x³ + C
- 2) -1/6 ⋅ cos3x² + C
- 3) 1/9 ⋅ cos3x³ + C
- 4) -1/9 ⋅ cos3x³ + C
Найдите ∫ xe^(x²)dx
Тип ответа: Одиночный выбор
- 1) 2xeˣ + C
- 2) 2xeˣ² + C
- 3) 1/2 ⋅ xeˣ² + C
- 4) 1/2 ⋅ eˣ² + C
Найдите ∫ xⁿ⁻¹dx
Тип ответа: Одиночный выбор
- 1) xⁿ + C
- 2) 1/n ⋅ x + C
- 3) 1/n ⋅ xⁿ + C
- 4) 1 / (n − 1) ⋅ xⁿ + C
Найдите А · В, где A = ((5, 0, 2, 3), (4, 1, 5, 3), (3, 1, -1, 2)); B = ((6), (-2), (7), (4))
Тип ответа: Одиночный выбор
- 1) ((5, 6), (6, 9), (2, 7))
- 2) ((5, 6), (6, 6), (1, 7))
- 3) ((5, 6), (4, 9), (1, 7))
- 4) ((5, 6), (6, 9), (1, 7))
Найдите АВ — АС, где A = ((2, -3), (0, 1)); B = ((1, 3), (0, 4))
Тип ответа: Одиночный выбор
- 1) ((4, −2), (−3, 1))
- 2) ((4, 2), (3, −1))
- 3) ((4, 2), (3, 1))
- 4) ((−2, 3), (0, −1))
Найдите значение выражения -3 ⋅ (2/3)² — 0,5²
Тип ответа: Одиночный выбор
- 1) 1 11/12
- 2) -1 2/9
- 3) -1 5/12
- 4) -1 7/12
Найдите значение выражения ((a + 1)² / (a² — 1) — 1) ⋅ (1 — a / (a + 1)) при a=2
Тип ответа: Одиночный выбор
- 1) 2
- 2) 1
- 3) 1/3
- 4) 2/3
Найдите координаты точки пересечения прямых 2x — y — 3 = 0 и 4x + 3y — 11 = 0
Тип ответа: Одиночный выбор
- (1; 3)
- (1; 2)
- (2; 2)
- (2; 1)
Найдите координаты точки K пересечения прямой (x — 1) / 2 = (y — 2) / 3 = (z — 3) / 4 с плоскостью 2x + 5y — 3z = 0
Тип ответа: Одиночный выбор
- 1) K(1/7; 5/7; 9/7)
- 2) K(2/7; 5/7; 9/7)
- 3) K(1/7; 5/7; 3/7)
- 4) K(1/7; 2/7; 9/7)
Найдите наибольшее и наименьшее значения функции Y=x^2 на промежутке [-1; 3]
Тип ответа: Одиночный выбор
- Yнаиб = 9,Yнаим = 1
- Yнаиб = 6,Yнаим = -2
- Yнаиб = 9, Yнаим = 0
Найдите обратную матрицу для матрицы A = ((2, 2, 3), (1, -1, 0), (-1, 2, 1))
Тип ответа: Одиночный выбор
- 1) A⁻¹ = ((1, −2, 7), (0, 1, −2), (0, 0, 1))
- 2) A⁻¹ = ((1, −4, −3), (1, −5, −3), (−1, 6, 4))
- 3) A⁻¹ = ((−3, 1, −4), (−3, 1, −5), (4, −1, 4))
- 4) A⁻¹ = ((1, 4, 3), (1, −5, 3), (1, 6, −4))
Найдите общее решение системы {9x₁ − 3x₂ + 5x₃ + 6x₄ = 4; 6x₁ − 2x₂ + 3x₃ + 4x₄ = 5; 3x₁ − x₂ + 3x₃ + 14x₄ = −8
Тип ответа: Одиночный выбор
- 1) {x₁ = c; x₂ = 11 + c; x₃ = −7; x₄ = 0
- 2) {x₁ = c; x₂ = 13 + c; x₃ = −7; x₄ = 1
- 3) {x₁ = 1 − c; x₂ = 13 + c; x₃ = −7; x₄ = 0
- 4) {x₁ = c; x₂ = 3c − 13; x₃ = −7; x₄ = 0
Найдите общее решение уравнения (x + y)dx + xdy = 0
Тип ответа: Одиночный выбор
- 1) y = (C − x²) / 2x
- 2) y = (x² − C) / 2x
- 3) y = (C − x²) / x
Найдите общее решение уравнения x² ⋅ d²y / dx² = 2
Тип ответа: Одиночный выбор
- 1) y = lnx + Cx + C₁
- 2) y = 2lnx + Cx + C₁
- 3) y = -lnx + Cx + C₁
Найдите общее решение уравнения xy^2dy = (x^3 + y^3)dx
Тип ответа: Одиночный выбор
- 1) y³ = 3x³ln|Cx|
- 2) y³ = 3xln|Cx|
- 3) y³ = 3x³lnCx
Найдите общее решение уравнения y’ — y / x = x
Тип ответа: Одиночный выбор
- 1) y = x² + Cx
- 2) y = x² − Cx
- 3) y = 2x² + Cx
Найдите общее решение уравнения y» — 4y’ + 3y = 0
Тип ответа: Одиночный выбор
- 1) y=C₁e³ˣ+C₂e⁻ˣ
- 2) y=C₁eˣ+C₂e⁻ˣ
- 3) y=C₁eˣ+C₂e³ˣ
Найдите общее решение уравнения y» — 9y = e²ˣ
Тип ответа: Одиночный выбор
- 1) y = C₁e³ˣ + C₂e⁻³ˣ — 1/5 ⋅ e²ˣ
- 2) y = C₁e³ˣ + C₂ — 1/2 ⋅ e²ˣ
- 3) y = e³ˣ(C₁ + C₂x) — 1/2 ⋅ e²ˣ
- 4) y = C₁e³ˣ + C₂e⁻³ˣ + e²ˣ
Найдите общее решение уравнения y» — y = 0
Тип ответа: Одиночный выбор
- 1) y = Ceˣ − C₁e⁻ˣ
- 2) y = C₁eˣ + C₂eˣ
- 3) y = C₁eˣ + C₂e⁻ˣ
Найдите острый угол между прямыми (x — 1) / 1 = (y + 2) / -1 = z / √2 и (x + 2) / 1 = (y — 3) / 1 = (z + 5) / √2
Тип ответа: Одиночный выбор
- 60°
- 30°
- 20°
- 45°
Найдите площадь фигуры, заключенной между прямыми y = 4x — 5, x = -3, x = -2 и осью Ox
Тип ответа: Одиночный выбор
- 15
- 12
- 10
- 7
Найдите площадь фигуры, ограниченной прямыми y = 5x, x = 2 и осью Ox
Тип ответа: Одиночный выбор
- 10
- 7
- 12
- 15
Найдите предел lim ((2 + x) / (3 + x))ˣ, x⟶∞
Тип ответа: Одиночный выбор
- 1) 0
- 2) −1
- 3) ∞
- 4) 1/e
Найдите предел lim (√(1 + 6x) — 5) / (√x — 2), x⟶∞
Тип ответа: Одиночный выбор
- 1) √6
- 2) 12/5
- 3) 2
- 4) 3/20
Найдите предел lim (√(1 + 6x) — 5) / (√x — 2), x⟶4
Тип ответа: Одиночный выбор
- 1) √6
- 2) 12/5
- 3) 2
- 4) 3/20
Найдите предел lim (√(x² + 4x + 2) — √(x² — 2x + 2)), x⟶∞
Тип ответа: Одиночный выбор
- 1) 1
- 2) -1
- 3) 3
- 4) ∞
Найдите предел lim (1 — 5 / x)ˣ, x⟶∞
Тип ответа: Одиночный выбор
- e^3
- e^2
- e^5
- e^-5
Найдите предел lim (2x + 1) / (x² — 3), x⟶∞
Тип ответа: Одиночный выбор
- 1) ∞
- 2) 1
- -3) -1/3
- 4) 0
Найдите предел lim (2x + 1) / (x² — 3), x⟶0
Тип ответа: Одиночный выбор
- 1) ∞
- 2) 2
- 3) -1/3
- 4) 0
Найдите предел lim (2x² + 1) / (x² — 3), x⟶∞
Тип ответа: Одиночный выбор
- 1) ∞
- 2) 1
- 3) -1/3
- 4) 2
Найдите предел lim (3n² + n — 1) / (2n² + 3), n⟶∞
Тип ответа: Одиночный выбор
- 3
- 0,5
- 0
- 1,5
Найдите предел lim (3n³ + n — 1) / (2n² — 3), n⟶∞
Тип ответа: Одиночный выбор
- 1) ∞
- 2) 0,5
- 3) 0
- 4) 1,5
Найдите предел lim (5n² + n + 1) / (3n² — n — 4), n⟶∞
Тип ответа: Одиночный выбор
- 1) 1
- 2) 5/3
- 3) -1
Найдите предел lim (5ˣ — cosx), x⟶0
Тип ответа: Одиночный выбор
- 0
- 1
- 4
- 5
- -1
Найдите предел lim (x² — 2) / (2x² + 5x — 7), x⟶1
Тип ответа: Одиночный выбор
- 1) 0,5
- 2) 1
- 3) 0
- 4) ∞
Найдите предел lim (x² — 4), x⟶3
Тип ответа: Одиночный выбор
- -5
- 1
- -1
- 5
Найдите предел lim (x² + x — 3) / (2x — 1), x⟶-1
Тип ответа: Одиночный выбор
- -1
- 0
- 1
Найдите предел lim 2 / (3x + 2), x⟶∞
Тип ответа: Одиночный выбор
- 1) ∞
- 2) 1
- 3) 0
Найдите предел lim 2x / (x — 1), x⟶0
Тип ответа: Одиночный выбор
- 1) 2
- 2) ∞
- 3) -2
- 4) 0
Найдите предел lim sin5x / x, x⟶0
Тип ответа: Одиночный выбор
- 5
- 1/5
- 1
- 0
Найдите предел lim tg3x / sin5x, x⟶0
Тип ответа: Одиночный выбор
- 1) −1/5
- 2) 1/5
- 3) −3/5
- 4) 3/5
Найдите предел lim tg5x / x, x⟶0
Тип ответа: Одиночный выбор
- 1) 1
- 2) −1
- 3) 5
- 4) ∞
Найдите предел lim x / 5, x⟶0
Тип ответа: Одиночный выбор
- 1) 1/5
- 2) 1
- 3) 0
Найдите производную функции f(x) = (1 + cosx)sinx
Тип ответа: Одиночный выбор
- 1+cos2x
- cosx+sin2x
- cosx+cos 2x
Найдите производную функции f(x) = ln(1 + a / x)
Тип ответа: Одиночный выбор
- 1) −1/x
- 2) a / (a + x)
- 3) −a / (x(a + x))
Найдите производную функции y = (3eˣ + x)cosx
Тип ответа: Одиночный выбор
- -(3e^x + 1) · sin x
- (3e^x-1+ 1) · cos x — (3e^x+x) · sin x
- (3e^x + 1) · cos x + (3e^x + x) · sin x
- (3e^x + 1) · cos x — (3e^x + x) · sin x
Найдите производную функции y = sin(2x² + 3)
Тип ответа: Одиночный выбор
- sin2x^2
- 4xcos4x
- cos(2x^2 + 3)
- 4xcos(2x^2 + 3)
Найдите производную функции y = xe^x — e^x
Тип ответа: Одиночный выбор
- xe
- e^x
- xe^x
Найдите производную функции y=2tgx
Тип ответа: Одиночный выбор
- 1) 2ᵗᶢˣ / (ln2 ⋅ cos²x)
- 2) 1 / (2^cos²x ⋅ ln2)
- 3) tgx2ᵗᶢˣ⁻¹ ⋅ 1 / cos²x
- 4) 2ᵗᶢˣln2 ⋅ 1 / cos²x
Найдите производную функции y=ln sin x
Тип ответа: Одиночный выбор
- ctg x
- tg x
- sin x
- cos x
Найдите промежутки возрастания или убывания функции y = — 2x^2 + 8x — 1
Тип ответа: Одиночный выбор
- убывает при x > -2, возрастает при x < -2
- убывает при x < 2, возрастает при x > 2
- убывает при x > 2, возрастает при x < 2
Найдите промежутки возрастания или убывания функции y = x^2 — 3x + 1
Тип ответа: Одиночный выбор
- 1) убывает при x>3/2, возрастает при x<3/2
- 2) убывает при x<2/3, возрастает при x>2/3
- 3) убывает при x<3/2, возрастает при x>3/2
Найдите скорость тела, движущегося по закону S = 3t — 5
Тип ответа: Одиночный выбор
- 1
- 5
- 3
Найдите точки максимума (минимума) функции y = x^2 — 2x
Тип ответа: Одиночный выбор
- (0; -1) – точка максимума
- (1; -1) – точка максимума
- (1; -1) – точка минимума
Найдите точки максимума (минимума) функции y= -5x^2- 2x + 2
Тип ответа: Одиночный выбор
- (-0,2; 0) – точка максимума
- (2,2; -0,2) – точка минимума
- (-0,2; 2,2) – точка максимума
Найдите точки перегиба кривой y = x^4 — 12x^3 + 48x^2 — 50
Тип ответа: Одиночный выбор
- (2; 4) и (4; 06)
- (2; 206) и (4; 2)
- (2; 2) и (4; 06)
Найдите точку перегиба кривой y = 1/3 ⋅ x³ — x
Тип ответа: Одиночный выбор
- (-1; 0)
- (0; 1)
- (1; 1)
- (0; 0)
Найдите угол между векторами α = 2m + 4n и b = m — n, где m и n – единичные векторы и угол между m и n равен 120
Тип ответа: Одиночный выбор
- 90
- 180
- 100
- 120
Найдите уравнение прямой, проходящей через точки M1(3; 2), M2(4; -1)
Тип ответа: Одиночный выбор
- x+y-12=0
- 3x+2y-11=0
- 3x+y-11=0
- 3x-y+11=0
Найдите уравнение прямой, проходящей через точку пересечения прямых 2x + 3y — 8 = 0 и x — 4y + 5 = 0 и через точку M1(-2; 3)
Тип ответа: Одиночный выбор
- 5x+13y-29=0
- 5x+3y-29=0
- 5x+13y-9=0
- 3x+8y-18=0
Найти решение системы {2x — 4y + 3z = 1; x — 2y + 4z = 3; 3x — y + 5z = 2
Тип ответа: Одиночный выбор
- {(-1; 0; -1)}
- {(1; 0; -1)}
- {(1; 0; 1)}
- {(-1; 0; 1)}
Напишите каноническое уравнение гиперболы, фокусы которой лежат на оси Ox, если даны a = 6 и b = 2
Тип ответа: Одиночный выбор
- 1) x² / 36 + y² / 4 = 1
- 2) x² / 6 − y² / 2 = 1
- 3) x² / 36 − y² / 4 = 1
Напишите каноническое уравнение эллипса, если даны его полуоси a = 5 и b = 4
Тип ответа: Одиночный выбор
- 1) x²/15 — y²/8 = 1
- 2) x²/5 + y²/2 = 1
- 3) x²/25 + y²/16 = 1
Неравенству — 8 < x < 4 удовлетворяют … целых чисел
Тип ответа: Одиночный выбор
- 12
- 10
- 11
- 9
Общий член последовательности 1 / (1 ⋅ 3), 2 / (3 ⋅ 5), 3 / (5 ⋅ 7), 4 / (7 ⋅ 9), … имеет вид …
Тип ответа: Одиночный выбор
- 1) aₙ = 3n / ((3n − 1)(2n + 1))
- 2) aₙ = n / (2n + 1)
- 3) aₙ = n / ((2n − 1)(2n + 1))
Определите полуоси гиперболы x² / 16 — y² = 1
Тип ответа: Одиночный выбор
- a = 4, b= 6
- a = 4, b = 1
- a = 3, b = 8
- a = 6, b = 1
Определите уравнение прямой, отсекающей на оси Oy отрезок b = 2 и составляющей с осью Ox угол = 45°
Тип ответа: Одиночный выбор
- y = 2x — 2
- y = 2x + 2
- y = x — 2
- y = x + 2
Определитель системы трех линейных неоднородных уравнений с тремя неизвестными равен 5. Это означает, что …
Тип ответа: Одиночный выбор
- система имеет нулевое решение
- система имеет множество решений
- система не имеет решения
- система имеет единственное решение
Первообразная для функции x² + x имеет вид …
Тип ответа: Одиночный выбор
- 1) 1/3 ⋅ x³ + 1/2 ⋅ x² + 1
- 2) 1/3 ⋅ x³ — 1/2 ⋅ x² + 1
- 3) -1/3 ⋅ x³ + 1/2 ⋅ x² + 1
- 4) 2x + 1
При каком значении l векторы MP и KD коллинеарны, если M(-3; 2), P(-1; -2), K(2; 1), D(5; l)?
Тип ответа: Одиночный выбор
- 1) -3 5/6
- 2) -4
- 3) -4,5
- 4) -5
При каком положительном значении параметра t прямые, заданные уравнениями 3tx — 8y +1 = 0 и (1 + t)x — 2ty = 0, параллельны?
Тип ответа: Одиночный выбор
- 2
- 3
- 2/3
- 3/2
производную (x − 5) / (2x − 5)
Тип ответа: Одиночный выбор
- 1) 2 / (2x − 5)
- 2) 1 / (2x − 5)
- 3) 5 / (2x − 5)²
- 4) 4x / (2x − 5)²
Разрыв функции в точке x0 называется разрывом первого рода, если …
Тип ответа: Одиночный выбор
- предел функции в точке x0 равен ∞
- левосторонний предел функции в точке x0 равен ∞, а правосторонний предел функции в точке x0 – конечный
- правосторонний предел функции в точке x0 равен ∞, а левосторонний предел функции в точке x0 – конечный
- левосторонний и правосторонний пределы функции в точке x0 – конечные
- функция не определена в точке x0
Раскройте определитель |(a, b), (b, a)|
Тип ответа: Одиночный выбор
- (a + b)^2
- (a — b^)2
- a^2 + b^2
- (a + b)(a — b)
Расширенная матрица системы {2x + 3y — 5 = 0; -x + 4y = z; x — y + 2z = 1 имеет вид …
Тип ответа: Одиночный выбор
- 1) ((2, 3, 0), (−1, 4, −1), (1, −1, 2))│((5), (0), (1))
- 2) ((2, 3, −5), (−1, 4, 0), (1, −1, 2))│((0), (1), (1))
- 3) ((2, 3, −5), (−1, 4, −1), (1, −1, 2))│((0), (0), (1))
- 4) ((2, 3, 0), (−1, 4, 0), (1, −1, −1))│((5), (1), (−2))
Решение, полученное из общего при конкретных значениях произвольных постоянных, называется …
Тип ответа: Одиночный выбор
- частным решением
- единичным решением
- множественным решением
- универсальным решением
Решите матричное уравнение AX + AXA = B, где A = ((1, 2), (0, 3)); B = ((4, 8), (6, 6))
Тип ответа: Одиночный выбор
- 1) ((0, 1), (1, 1))
- 2) ((0, −1), (1, 0))
- 3) ((0, 1), (−1, 0))
- 4) ((0, 1), (1, 0))
С помощью метода Крамера (определителей) можно найти решение …
Тип ответа: Одиночный выбор
- любой системы линейных алгебраических уравнений
- системы линейных алгебраических уравнений с невырожденной матрицей
- системы линейных алгебраических уравнений с вырожденной матрицей
- системы однородных уравнений
Система линейных уравнений называется определенной, если она …
Тип ответа: Одиночный выбор
- имеет хотя бы одно решение
- имеет ровно два решения
- имеет единственное решение
- имеет бесконечное множество решений
Система линейных уравнений называется совместной, если она …
Тип ответа: Одиночный выбор
- имеет только нулевое решение
- не имеет решений
- имеет только одно решение
- имеет хотя бы одно решение
Скалярным произведением двух векторов называется …
Тип ответа: Одиночный выбор
- 1) число, определяемое по формуле a ⋅ b = |a| ⋅ |b|
- 2) число, определяемое по формуле a ⋅ b = |a| ⋅ |b| ⋅ sinφ
- 3) число, определяемое по формуле a ⋅ b = |a| ⋅ |b| ⋅ cosφ
Смешанной периодической является дробь …
Тип ответа: Одиночный выбор
- 7,(3)
- 8,(11)
- 3,14
- 2,75(12)
Составьте уравнение плоскости, зная, что точка А(1, -1,3) служит основанием перпендикуляра, проведенного из начала координат к этой плоскости.
Тип ответа: Одиночный выбор
- x-y+3z-11=0
- -x+y+3z-11=0
- x-y-3z+11=0
- x-y+11z-3=0
Среди перечисленных дифференциальных уравнений укажите однородное уравнение
Тип ответа: Одиночный выбор
- 1) x²y’ = xy + y²
- 2) 2xy’ = y² — x
- 3) ax» = y’
- 4) y’ + y = e⁻ˣ / (1 — x)
Среди перечисленных дифференциальных уравнений укажите уравнение Бернулли
Тип ответа: Одиночный выбор
- 1) y’ + y / (x + 2) = 2
- 2) y’ + y / x = sinx / x
- 3) y’ + y² / x
- 4) y’ + y / x = e ⋅ y / x
Укажите канонические уравнения прямой {x + 3y — 5z — 7 = 0; 2x — 3y + 3z + 4 = 0
Тип ответа: Одиночный выбор
- 1) (x − 1) / −6 = (y − 2) / −13 = z / −9
- 2) (x − 1) / 24 = (y − 2) / 7 = z / 3
- 3) (x + 1) / −6 = (y + 2) / −13 = z / −9
- 4) (x − 1) / −6 = (y − 2) / 13 = z / −9
Укажите каноническое уравнение эллипса, расстояние между фокусами которого равно 8, а малая полуось b = 3
Тип ответа: Одиночный выбор
- 1) x² / 9 + y² / 25 = 1
- 2) x² / 5 + y² / 3 = 1
- 3) x² / 25 — y² / 9 = 1
- 4) x² / 25 + y² / 9 = 1
Укажите натуральный ряд чисел
Тип ответа: Одиночный выбор
- -1, -2, -3, -4, -5, -6, -7, -8, -9
- …, -9, -8, -7, -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, …
- 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, …
- 1, 2, 3, 4, 5, 6, 7, 8, 9, …
Укажите уравнение окружности радиуса R = 8 с центром в точке C(2; -5)
Тип ответа: Одиночный выбор
- (x — 2)^2 + (y + 5)^2 = 8^2
- (x + 2)^2 — (y + 5)^2 = 8^2
- (x + 2)^2 + (y — 5)^2 = 8^2
- (x — 2)^2 — (y + 5)^2 = 8^2
Укажите уравнение окружности, для которой точки А(3; 2) и В(-1; 6) являются концами одного из диаметров
Тип ответа: Одиночный выбор
- (x — 1)^2 — (y + 4)^2 = 8
- (x — 1)^2 + (y — 4)^2 = 8
- (x — 1)^2 — (y + 4)^2 = 64
- (x — 1)^2 + (y — 4)^2 = 16
Укажите уравнение окружности, которая проходит через точку А(2; 6) и центр которой совпадает с точкой C(-1; 2)
Тип ответа: Одиночный выбор
- (x+1)^2+(y-2)^2=25
- (x-1)^2-(y+2)^2=5
- (x-1)^2+(y+2)^2=25
- (x+1)^2+(y-2)^2=36
Укажите уравнение окружности, которая проходит через точку А(3;1), а ее центр лежит на прямой 3x — y — 2 = 0
Тип ответа: Одиночный выбор
- (x- 2)^2 + (y — 4)^2 = 16
- (x — 2)^2- (y+ 4)^2 = 5
- (x — 2)^2 — (y + 4)^2 = 10
- (x — 2)^2 + (y — 4)^2 = 10
Укажите уравнение окружности, проходящей через точку (4; 5), с центром в точке (1; -3)
Тип ответа: Одиночный выбор
- (x — 4)^2 + (y — 5)^2 =49
- (x — 1)^2 + (y+ 3)^2 = 7
- (x — 1)^2+ (y+ 3)^2 = 49
- (x — 1)^2 + (y + 3)^2 = 73
Укажите уравнение окружности, центр которой совпадает с началом координат, а прямая 3x — 4y + 20 = 0 является касательной к окружности
Тип ответа: Одиночный выбор
- x^2+y^2=16
- x^2+y^2=8
- x^2+y^2=9
- x^2-y^2=16
Укажите уравнение параболы с вершиной в точке O и фокусом F(4; 0)
Тип ответа: Одиночный выбор
- y^2=16x
- x^2=16y
- y^2=8x
- y^2=4x
Упростите выражение 5 / (1 + 4 / x) ⋅ ((x − 4) / (x² + 4x) − 16 / (16 − x²))
Тип ответа: Одиночный выбор
- 1) 5 / (x + 4)
- 2) 4x / (x + 4)
- 3) 4x / (x − 4)
- 4) 5 / (x − 4)
Упростите иррациональное выражение √((-22)²)
Тип ответа: Одиночный выбор
- 22
- -22
- √22
- -√22
Уравнение 3x — 4y + 12 = 0 преобразуйте к уравнению в отрезках
Тип ответа: Одиночный выбор
- 1) x / 4 − y / 3 = 1
- 2) x / −4 − y / 3 = 1
- 3) x / 4 + y / 3 = 1
- 4) x / −4 + y / 3 = 1
Уравнение вида P1(x)Q1(y)dx + P2(x)Q2(y)dy =0 является …
Тип ответа: Одиночный выбор
- дифференциальным уравнением с разделяющимися переменными
- дифференциальным уравнением в частных производных
- алгебраическим уравнением первого порядка
- дифференциальным уравнением второго порядка
Уравнение y + xy’ -2 = 0 является …
Тип ответа: Одиночный выбор
- дифференциальным уравнением Бернулли
- линейным неоднородным дифференциальным уравнением второго порядка с постоянными коэффициентами
- линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами
- дифференциальным уравнением с разделяющимися переменными
Уравнение y” — 4y = ex является …
Тип ответа: Одиночный выбор
- дифференциальным уравнением Бернулли
- линейным неоднородным дифференциальным уравнением второго порядка с постоянными коэффициентами
- линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами
- дифференциальным уравнением с разделяющимися переменными
Уравнение y” — y’ — 3y = 0 является …
Тип ответа: Одиночный выбор
- дифференциальным уравнением Бернулли
- линейным неоднородным дифференциальным уравнением второго порядка с постоянными коэффициентами
- линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами
- дифференциальным уравнением с разделяющимися переменными
Уравнение, связывающее независимую переменную x, искомую функцию y и ее первую производную y′, называется …
Тип ответа: Одиночный выбор
- дифференциальным уравнением второго порядка
- дифференциальным уравнением в частных производных
- дифференциальным уравнением первого порядка
- алгебраическим уравнением первого порядка
Установите взаимное расположение прямых (x — 2) / 4 = (y + 1) / -3 = (z — 1) / -2 и (x — 7) / 5 = (y — 1) / 6 = (z — 3) / 1
Тип ответа: Одиночный выбор
- прямые пересекаются, но не перпендикулярны
- прямые скрещиваются
- прямые параллельны
- прямые перпендикулярны
Функция y = (x — 2) / (x + 2) бесконечно малая в точке
Тип ответа: Одиночный выбор
- 1) x = 2
- 2) x = -2
- 3) x = 1
Целыми называются …
Тип ответа: Одиночный выбор
- только положительные числа
- только натуральные числа и числа, противоположные натуральным
- натуральные числа; числа, противоположные натуральным; число 0
- числа, оканчивающиеся на 0
Число f(x0) называется наибольшим значением функции на отрезке [a;b], если …
Тип ответа: Одиночный выбор
- 1) для всех x из этого отрезка выполняется неравенство f(x)=f(x₀)
- 2) для всех x из этого отрезка выполняется неравенство f(x)≥f(x₀)
- 3) для всех x из этого отрезка выполняется неравенство f(x)≤f(x₀)
Математика. Элементы высшей математики (ответы Синергия тест) 1 курс 30 вопросов оценка 90/100 баллов
СКАЧАТЬ ОТВЕТЫ ПО ССЫЛКЕ
1.Метод Гаусса решения системы линейных уравнений предполагает использование …
алгебраического сложения
определителей системы
Формул для вычисления неизвестных
последовательного исключения неизвестных
2.Найдите предел
1
2
3
3.Вычислите определенный интеграл
1
2
3
4
4.Найдите:
1
2
3
4
5.Найдите предел:
1
2
3
4
6.Найдите:
1
2
3
4
7.Среди перечисленных дифференциальных уравнений укажите однородное уравнение
1
2
3
4
8.Уравнение у” – 4у = ех является …
дифференциальным уравнением Бернулли
линейным неоднородным дифференциальным уравнением второго порядка с постоянными коэффициентами
линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами
дифференциальным уравнением с разделяющимися переменными
9.Напишите каноническое уравнение эллипса, если даны его полуоси : а = 5 и b = 4
1
2
3
10.Составьте уравнение плоскости, зная, что точка А(1, -1,3) служит основанием перпендикуляра, проведенного из начала координат к этой плоскости.
x-y+3z-11 =0
-x+y+3z-11=0
x-y-3z+11=0
x-y+11z-3=0
11.Даны вершины треугольника АВС: А(3; -1), В(4; 2) и С(-2; 0). Укажите уравнения его сторон
1) я – у + 10 = 0, Зх – Зу + 2 = 0, х + 5у + 2 = 0
2) Зя — у = 0, я + Зу — 6 = 0, х — 5у + 3 = 0
3) Зх-у- 10 = 0,я — Зу + 2 = 0,я + 5у + 2 = О
1
2
3
12.Найдите производную функции у = хелх – елх
хе
елх
хелх
13.Найти предел
1
2
3
4
14.Найти предел:
1
2
3
4
15.Найдите точки максимума (минимума) функции у = хл2 – 2х
0; -1) – точка максимума
1; -1) – точка максимума
1; -1) – точка минимума
16.Вычислите предел по правилу Лопиталя
1
2
3
4
17.Укажите натуральный ряд чисел
-1, -2, -3, -4, -5, -6, -7, -8. -9
-9, -8, -7, -6, -5, -4, -3, -2, -1, О, 1, 2, 3, 4, 5, б, 7, 8, 9,…
0, 1, 2, 3, 4, 5, б, 7, 8, 9,…
1, 2, 3, 4, 5, б, 7, 8, 9..
18.Найти предел:
1
2
3
4
19.Найти предел:
1
2
3
4
20.Найти предел:
5
1/5
1
0
21.Найдите площадь фигуры, заключенной между прямыми у = 4х – 5, х = -3, х = -2 и осью Ох
15
12
10
7
22.Найдите общее решение уравнения xyA2dy = (хA3 + yA3)dx
у3 = 3x3 ln | Сх |
у3= Зх3 ln | Cx
у3=Зх3 ln Cx
1
2
3
23.Вычислить определитель
-20
20
10
-10
24.Найдите производную функции у=2tgx
1
2
3
4
25.Укажите уравнение окружности, для которой точки А(3: 2) и В(-1; 6) являются концами одного из диаметров
(X- 1)л2 – (у + 4)л2 = 8
(X – 1)л2 + (у – 4)л2 = 8
(X- 1)л2-(у+ 4)л2 = 64
(X- 1)л2 + (у-4)л2 = 16
26.Найдите уравнение прямой, проходящей через точку пересечения прямых 2х + Зу-8 = 0их-4у + 5 = 0и через точку М1 (-2; 3)
5х+13у-29=0
5x+3y-29=0
5х+13у-9=0
Зх+8у-18=0
27.Вычислить определитель:
5 -1
2 4
18
22
3
6
28.Даны точки М (-5; 7; -6), N (7; -9; 9). Вычислите проекцию вектора а = {1; -3; 1} на вектор MN
4
25
75
3
29.Найдите предел lim (1-5/х)x
ел3
ел2
ел5
ел-5
30.Определитель системы трех линейных неоднородных уравнений с тремя неизвестными равен 5. Это означает, что …
система имеет нулевое решение
система имеет множество решений
система не имеет решения
система имеет единственное решение
Медицина
Финансы
Экономика
Биология
Ветеринария
Сельское хозяйство
Юриспруденция
Право
Языкознание
Языки
Логика
Философия
Религия
Этика
Политология
Социология
История
Информатика
Вычислительная техника
Физика
Математика
Промышленность
Энергетика
Искусство
Культура
Химия
Электротехника
Связь
Автоматика
Геология
Экология
Начальные классы
Строительство
образование
Механика
Воспитательная работа
Русский язык и литература
Дошкольное образование
Реферат
Урок
Программа
Отчет
Закон
Курсовая
Задача
Занятие
Лекция
Решение
Протокол
ОТВЕТЫ. ВЫСШАЯ МАТЕМАТИКА 97 БАЛЛОВ. тест синергия высшая математика 1 симестр 1 курс
|
Единственный в мире Музей Смайликов |
|
Предварительный просмотр недоступен. Но вы можете скачать оригинальный файл.
Подборка по базе: Бойко передел математика.docx, международная олимпиада по математика 1 класс.pdf, Специальная математика и основы статистики — демо.docx, промежуточный тест 1.docx, Итоговое тестирование по Модулю 5_ просмотр попытки.pdf, НГ. Тест 3. Часть 1. Тема «Пересечение поверхности с плоскостью», Контроллинг и управление затратами на предприятии Тестовые задан, Тема 4. Речь как высшая психическая функция.pdf, Тест Синергия. Физическая культура 2022.docx, Безопасность жизнедеятельности Синергия 1 курс 2023.rtf
Вступительное испытание по математике Вариант 1 Синергия
Бесплатные ответы на вступительный тест Синергии по математики. Верные ответы отмечены знаком «+»
При выполнении заданий в бланке ответов рядом с номером выполняемого вами задания (А1–А25) поставьте знак «х» в клеточку, номер которой соответствует номеру выбранного вами ответа.
А1. Футболка стоила 800 рублей. После снижения цены она стала стоить 680рублей. На сколько процентов была снижена цена на футболку?
- 1) 15 +
- 2) 17
- 3) 19
А2. На рисунке показано изменение температуры воздуха на протяжении трех суток. По горизонтали указывается дата и время суток, по вертикали —значение температуры в градусах Цельсия. Определите по рисунку наибольшую температуру воздуха 15 октября. Ответ дайте в градусах Цельсия.
- 1) 5
- 2) 9
- 3) 11+
А3. Найдите площадь параллелограмма, изображенного на рисунке.
- 1) 5
- 2) 10+
- 3) 20
А4. Строительной фирме нужно приобрести 40 кубометров строительного бруса у одного из трех поставщиков. Какова наименьшая стоимость такой покупки с доставкой (в рублях)? Цены и условия доставки приведены в таблице.
- 1) 150000
- 2) 152000 +
- 3) 200000
А5. Найдите корень уравнения:
- 1) 7 +
- 2) 17
- 3) -11
А6. В треугольнике ABC AC=BC, AB=15 , AH— высота, BH=3. Найдите cosBAC.
- 1) 0
- 2) 0,5+
- 3) 1
А7. Найдите значение выражения:
- 1) 1
- 2) 27 +
- 3) 147
А8. На рисунке изображен график y=f(x) — производной функции f(x),определенной на интервале (-2;10). Найдите количество точек, в которых касательная к графику функции f(x) параллельна прямой y=x-17 или совпадает с ней.
- 1) 1
- 2) 3 +
- 3) 4
А9. Найдите квадрат расстояния между вершинами и многогранника,изображенного на рисунке. Все двугранные углы многогранника прямые.
- 1) 2
- 2) 4
- 3) 5 +
А10. Найдите значение выражения
- 1) 1
- 2) 2+
- 3) 32
А11. Представьте в виде степени выражениеОтвет — 1
А12. Найдите значение выражения
- 1) 10
- 2) 5 +
- 3) log2* 10
А13. На одном из следующих рисунков изображен график нечетной функции.Укажите этот рисунок.
Ответ — 3
А14. Найдите область определения функции
- 1) (0; 2)+
- 2) (-∞; 0) U (2;+∞)
- 3) [0; 2]
А15. Укажите наибольшее значение функцииy=1-cos3x
- 1) 1
- 2) 2 +
- 3) 0
А16. На рисунке изображены графики функций y = f (x) и y = g (x), заданных на промежутке [-3; 6]. Найдите все значения х, для которых выполняется неравенство f (x) ≤ g (x).
- 1) [3; 1] U [1; 6]
- 2) [-1; 1] +
- 3) [-3; -2] U [2; 6]
А17. Укажите множество решений неравенства
- 1) (-∞;2] U [1,5; 6) +
- 2) (-∞; -1,5] U [2; 6)
- 3) (-∞; -2] U [3; 6)
А18. Вычислите значение производной функции у = sinx – 2х в точке х0 = 0.
- 1) 1
- 2) 0
- 3) –1 +
А19. Найдите область определения функции
- 1) [0,7; +∞) +
- 2) (0; 0,7]
- 3) (–∞; 0,7]
А20. Найдите множество значений функции у = 6х–12.
- 1) (0; +∞)
- 2) (–12; +∞) +
- 3) [–12; +∞)
А21. Фабрика выпускает сумки. В среднем на 150 качественных сумок приходится пятнадцать сумок со скрытыми дефектами. Найдите вероятность покупки качественной сумки. Результат округлите до сотых.
- 1) 0,91
- 2) 0,90 +
- 3) 0,1
А22. Правильная четырехугольная призма описана около цилиндра, радиус основания которого равен 3. Площадь боковой поверхности призмы равна 288. Найдите высоту цилиндра.
- 1) 48
- 2)24
- 3) 12+
А23. Сила тока в цепи I (в амперах) определяется напряжением в цепи исопротивлением электроприбора по закону Ома: , где U — напряжение ввольтах, R — сопротивление электроприбора в омах. В электросеть включенпредохранитель, который плавится, если сила тока превышает 25 А.Определите, какое минимальное сопротивление должно быть уэлектроприбора, подключаемого к розетке в 220 вольт, чтобы сеть продолжалаработать. Ответ выразите в омах.
- 1) 0,11
- 2) 8,8 +
- 3) 5500
А24. Из пункта А в пункт В, расстояние между которыми 60 км, одновременновыехали автомобилист и велосипедист. Известно, что в час автомобилистпроезжает на 35 км больше, чем велосипедист. Определите скоростьвелосипедиста, если известно, что он прибыл в пункт В на 2 часа 48 минутпозже автомобилиста. Ответ дайте в км/ч.
- 1) 20
- 2) 15 +
- 3) 10
А25. Найдите наименьшее значение функции на отрезке
- 1) -154 +
- 2) -14,5
- 3) 0
Другие тесты Синергии:
- Вступительное испытание по русскому языку Вариант 1
- Стратегический менеджмент – вступительный тест Синергии
- Тесты МОИ (МТИ) -вступительный тест по предмету “математика”
- Вступительное испытание по информатике Вариант 1- Синергия
Математика синергия
Тема 1. Функция. Способы задания.
Неявная функция. Обратная функция. Классификация функций
Тема 2. Теория пределов
Тема 3. Предел функции.
Непрерывность функции. Разрыв функции. Основные свойства непрерывных функций
Тема 4. Замечательные пределы.
Сравнение бесконечно малых величин. Эквивалентные бесконечно малые величины
Тема 5. Дифференцирование функций
Тема 6. Дифференцирование функций
Тема 7. Дифференциал функции.
Производные и дифференциалы высших порядков
Тема 8. Аналитические приложения
дифференцируемых функций
Тема 9. Экстремум функции
Тема 10. Неопределенный интеграл.
Основные свойства. Таблица неопределенных интегралов. Метод непосредственного
интегрирования
Тема 11. Неопределенный интеграл.
Основные методы интегрирования
Тема 12. Определенный интеграл.
Определенный интеграл. Задачи, приводящие к понятию определенного интеграла
Тема 13. Приложения определенного
интеграла
Тема 14. Основы линейной алгебры.
Матрицы. Виды матриц. Операции над матрицами
Тема 15. Теория определителей.
Основные свойства определителей. Вычисление определителей произвольного порядка
n. Формулы разложения
Тема 16. Обратная матрица. Ранг
матрицы. Понятие обратной матрицы
Тема 17. Системы линейных
алгебраических уравнений
Ссылка на Ответы по Математике Синергия СКАЧАТЬ
Обращайтесь к нам за помощью и консультацией. Мы обязательно поможем Вам!
Пишите: WhatsApp: +7 915 133-11-08 , Почта: studxelp@yandex.ru
ОТПРАВИТЬ ЗАЯВКУ
Mathematics Synergy 1 course (Elements of higher mathematics) score 90/100 points
The Gauss method for solving a system of linear equations involves the use of …
algebraic addition
system determinants
Formulas for calculating unknowns
successive elimination of unknowns
Find the limit
Calculate the definite integral
Among the listed differential equations, indicate the homogeneous equation
The equation y «- 4y = ex is …
differential Bernoulli equation
linear inhomogeneous differential equation of the second order with constant coefficients
linear homogeneous differential equation of the second order with constant coefficients
separable differential equation
Write the canonical equation of an ellipse if its semiaxes are given: a = 5 and b = 4
Equate the plane, knowing that point A (1, -1.3) is the base of the perpendicular drawn from the origin to this plane.
The vertices of the triangle ABC are given: A (3; -1), B (4; 2) and C (-2; 0). Indicate the equations of its sides
Find the derivative of the function
Find the maximum (minimum) points of the function
Calculate the limit by L´Hôpital´s rule
Specify a natural series of numbers
Find the area of the figure enclosed between the straight lines y = 4x — 5, x = -3, x = -2 and the Ox axis
Find the general solution to the equation xyA2dy = (хA3 yA3) dx
Calculate the determinant
Find the derivative of the function y = 2tgx
Specify the equation of a circle for which points A (3: 2) and B (-1; 6) are the ends of one of the diameters
Find the equation of the straight line passing through the point of intersection of the lines
The determinant of a system of three linear inhomogeneous equations with three unknowns is 5. This means that …
the system has a zero solution
the system has many solutions
the system has no solution
the system has only one solution
Тестовое задание по математике. На тему : «Элементы высшей математики». Тест вступительный. Набрано 52 балла из 100. Было выполнено на зачёт. После оплаты вы сможете скачать готовые ответы по тесту . Так же могу выполнять данную работу индивидуально. Делайте индивидуальный заказ
1.Смешанная производная (?^2 f)/?x?y для функции f=sinx-6x^2 y равна
0
-12х
cosx-12xy
cosx
2.Уравнение прямой, содержащей точку А(6;-1) и параллельной прямой х/(-5)=y/1
x+5y=2
x+5y=1
5x+y=0
x-5y=0
3.Определитель – это …
матрица
число
вектор
прямоугольная таблица чисел
4.Достаточным условием выпуклости функции y(x) на интервале (a;b) является
y//>0 на (a;b)
y/ <0 на (a;b)
y//<0 на (a;b)
y/ ?0 на (a;b)
5.Из векторов а(2;7;5), b=(7; -2,5) и c=(5;0; -7), ортогональными являются
b и c
a и b
a и c
a и b; b и c
6.Производная функции f(x)=(9x+5)/(x-10) равна
9/(x-10)^2
9ln(x-10)
-95/(x-10)^2
5x/(x-10)^2
7.Длина медианы АМ в треугольнике АВС с вершинами А(11;3), В(15;23), С(31;15) равна
8
20
10
9
8.Система линейных уравнений х_1+2х_2-2х_3=0 3х_1+7х_2-х_3=0 3х_1-2х_2-4х_3=0 имеет
одно нулевое решение
бесконечно много решений
одно ненулевое решение
нет решений
9.Общее решение неоднородного линейного дифференциального уравнения (ДУ) равно:
общему решению однородного линейного ДУ плюс произвольная функция;
частному решению линейного неоднородного ДУ плюс произвольная функция
частному решению линейного неоднородного ДУ
сумме частного решения линейного неоднородного ДУ и общего решения линейного однородного ДУ
10.Производная функции f(x)=x•cos(x+3)+7 равна
cos(x+3)-x•sin(x+3)
x•sin?(x+3)+7
sin(x+3)
sin(x+3)-x•cos(x+3)
11.Несобственный интеграл ?-?_0^2? 3dx/x равен
1
0
3
12.Предел limT???(x>?) ? ((x+9)/x)^x
1
0
9
13.Найдите корень уравнения 8(6+х)+2х=8
-6
4
-4
6
14.Какое понятие не связано с суммой ряда?
Частичная сумма
Приближенные суммы
Дискретная сумма
Сумма n первых членов
15.Частной производной ?f/?x для функции f=15ln(x+y^2) является
30x/(x+y^2)
15/(x+y^2)
30y/(x+y^2)
1/(x+y^2)
16.Дифференциальное уравнение y? + a(x)?y = b(x) – это:
уравнение с разделяющимися переменными
однородное уравнение
уравнение линейное, однородное
уравнение линейное, неоднородное
17.Заданы векторы p(5;3;1) и q(2;6;2). Выражение p•(q-p) равно
-5
31
32
8
18.Предел limT(x>?) 12x^6+7x^4-32x+36 / 7x^6-32x^4+12x+36 равен
12 / 7
1
-1/32
?
19.Модуль смешанного произведения трех векторов равен
площади треугольника, построенного на этих векторах
объему пирамиды, построенной на этих векторах
объему тетраэдра , построенного на этих векторах
объему параллелепипеда, построенного на этих векторах
20.Частным решением системы линейных уравнений x_1+x_2+2х_3=7 ?-х? _1-х_3=-3 х_1+2х_2-2х_3=6 является
(3;-7;1)
(2;3;1)
(0;0;0)
(-8;4;1)
21.Найдите значение выражения (7x^3)^2:7x^6
7
49
6
1
22.Уравнение прямой, содержащей точку А(6;-1) и параллельной прямой х/(-5)=у/1 является
x+5y=2
x+5y=1
5x+y=0
x-5y=0
23.Определитель матрицы равен ((7&9 5&10))
25
10
115
50
24.Произведение z1z2, если z1=5+2i,z2=1-2i, равно
10-8i
9-7i
9-8i
9-9i
25.Сумма 3z1-5z2 если z1=2+2i, z2=1+i, равна
1+i
2+i
1+2i
2+2i




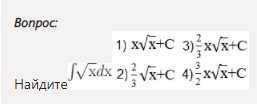

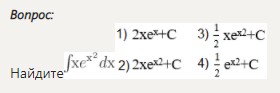
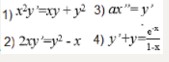
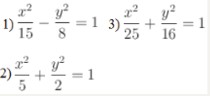
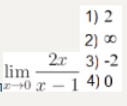

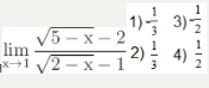
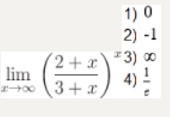
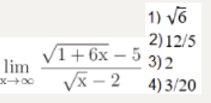
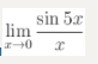

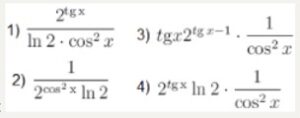

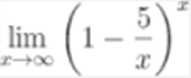

 Скачать 2.27 Mb.
Скачать 2.27 Mb.
















