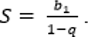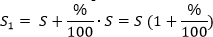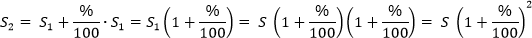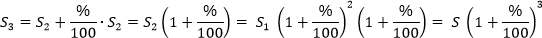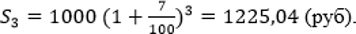Арифметическая прогрессия в задачах ЕГЭ по математике
Анна Малкова
Арифметическая прогрессия — это последовательность, каждый член которой, начиная со второго, равен сумме предыдущего члена и некоторого фиксированного числа d:
Фиксированное число называется разностью арифметической прогрессии.
Формула n-го члена арифметической прогрессии:
Сумма первых членов арифметической прогрессии
вычисляется по формуле:
Каждый член арифметической прогрессии, начиная со второго, есть среднее арифметическое соседних:
1. Максим решил накопить на айфон последней модели и 1 марта положил в копилку 10 рублей. С этого дня Максим ежедневно опускает в копилку на 10 рублей больше, чем в предыдущий день. Сколько рублей будет в копилке 31 мая, после того как Максим, как обычно, положит туда деньги?
По условию, 1 марта в копилке у Максима 10 рублей.
2 марта Максим опускает в копилку на 10 рублей больше, чем в предыдущий день, то есть 20 рублей.
3 марта он добавляет еще 30 рублей,
4 марта 40 рублей,
5 марта 50 рублей.
Мы имеем дело с арифметической прогрессией.
В нашей прогрессии В марте 31 день, в апреле 30, в мае 31 день. Значит,
31 мая Максим положит в копилку рублей.
Всего в копилке в этот день будет рублей.
Видите, как удобно пользоваться формулами для вычисления n-ного члена и суммы арифметической прогрессии. Намного проще, чем складывать 92 слагаемых.
2. (Задача ЕГЭ) Улитка ползет от одного дерева до другого. Каждый день она проползает на одно и то же расстояние больше, чем в предыдущий день. Известно, что за первый и последний дни улитка проползла в общей сложности 10 метров. Определите, сколько дней улитка потратила на весь путь, если расстояние между деревьями равно 150 метрам.
Пусть улитка проползла в первый день метров, в последний –
метров, причем
. Тогда за n дней она преодолела
метров. Отсюда
Ответ: 30
3. (Задача ЕГЭ) Васе надо решить 434 задачи. Ежедневно он решает на одно и то же количество задач больше по сравнению с предыдущим днем. Известно, что за первый день Вася решил 5 задач. Определите, сколько задач решил Вася в последний день, если со всеми задачами он справился за 14 дней
Это обычная задача на арифметическую прогрессию. В первый день Вася решил задач, в последний
задач. Запишем формулу для суммы арифметической прогрессии:
. Отсюда
4. (Задача ЕГЭ) Бригада маляров красит забор длиной 150 метров, ежедневно увеличивая норму покраски на одно и то же число метров. Известно, что за первый и последний день в сумме бригада покрасила 75 метров забора. Определите, сколько дней бригада маляров красила весь забор.
В первый день бригада покрасила метров забора, во второй
метров, в последний
метров.
По формуле суммы арифметической прогрессии: . По условию,
. Отсюда n = 4.
5. (Задача ОГЭ) Дана арифметическая прогрессия: -4; -2; 0… Найдите сумму первых десяти её членов.
Найдем d – разность арифметической прогрессии.
Найдем сумму первых 10 членов прогрессии по формуле:
У нас n = 10.
Задачи ЕГЭ для самостоятельного решения
- Турист идет из одного города в другой, каждый день проходя больше, чем в предыдущий день, на одно и то же расстояние. Известно, что за первый день турист прошел 10 километров. Определите, сколько километров прошел турист за третий день, если весь путь он прошел за 6 дней, а расстояние между городами составляет 120 километров.
- Рабочие прокладывают тоннель длиной 99 метров, ежедневно увеличивая норму прокладки на одно и то же число метров. Известно, что за первый день рабочие проложили 7 метров туннеля. Определите, сколько метров туннеля проложили рабочие в последний день, если вся работа была выполнена за 9 дней.
- Грузовик перевозит партию щебня массой 210 тонн, ежедневно увеличивая норму перевозки на одно и то же число тонн. Известно, что за первый день было перевезено 2 тонны щебня. Определите, сколько тонн щебня было перевезено за девятый день, если вся работа была выполнена за 14 дней.
- Вере надо подписать 640 открыток. Ежедневно она подписывает на одно и то же количество открыток больше по сравнению с предыдущим днем. Известно, что за первый день Вера подписала 10 открыток. Определите, сколько открыток было подписано за четвертый день, если вся работа была выполнена за 16 дней.
Ответы к задачам:
- Ответ: 18
- Ответ: 15
- Ответ: 18
- Ответ: 22.
Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Арифметическая прогрессия в задачах ЕГЭ по математике» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
08.03.2023
Прогрессии
Термин «прогрессия» имеет латинское происхождение («progression», что означает «движение вперед»), был введен римским математиком Боэцием в 6 веке.
Что такое прогрессия? Это тип последовательности. А что такое последовательность? Это бесконечный набор чисел, подчиняющийся определенному правилу. Например, последовательность составляют все числа, делящиеся на 2. Их бесконечно много, и они подчиняются определенному правилу. Последовательность можно задать формулой n-го члена, где n – номер члена последовательности.
Например,
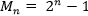
Последовательность также может задаваться правилом, по которому находят каждый ее член, если известны предыдущие. Например, первые два члена последовательности равны единице, а каждый следующий равен сумме двух непосредственно предшествующих ему. Тогда получаем последовательность чисел:
1, 1, 2, 3, 5, 8, 13, 21, … (называемых числами Фибоначчи)
Есть два вида последовательностей, которые изучаются в курсе математики– это арифметические и геометрические прогрессии.
Арифметическая прогрессия
Арифметической прогрессией называют такую числовую последовательность, каждый следующий член которой отличается от предшествующего члена на одно и то же число d.
Например, 1, 3, 5, 7…
Число d называют разностью арифметической прогрессии.
Отметим, что если d > 0, то арифметическая прогрессия является возрастающей последовательностью, если d < 0, то — убывающей последовательностью. А если d = 0 ? Это тоже прогрессия, называют ее в математике постоянной прогрессией.
Ряд натуральных чисел дает пример бесконечной арифметической прогрессии с разностью d = 1, а последовательность нечетных и четных чисел – примеры бесконечных арифметических прогрессий, у каждой из которых разность d = 2 (отличие только в первом члене прогрессии).
Если известен первый член арифметической прогрессии a1 и ее разность d, то можно найти любой член этой последовательности по формуле:
- an = a1 + d · (n−1) — формула n-го члена,
Пример: найдите члены а8, а1000 арифметической прогрессии, у которой а1 = -2, d = 5
Решение:
Найдем по записанной нами формуле:
а8 = a1 + d · (8 −1) = -2 + 7 · 5 = 33.
а1000 = a1 + d · (1000 −1) = -2 + 999 · 5 = 4993.
Запишем формулы суммы n первых членов прогрессии:
Пример: определить сумму k первых нечетных чисел, начиная с единицы.
Решение:
Последовательность нечетных чисел – арифметическая прогрессия с a1 = 1 и d = 2
Например, сумма первых пяти нечетных чисел:
Можно убедиться, что 1 + 3 + 5 + 7 + 9 = 25.
Каждый член арифметической прогрессии равен среднему арифметическому его соседних членов (исключение составляют первый и последний члены, т.к. у них только по одному соседнему члену)
— свойство n-го члена.
Геометрическая прогрессия
Геометрической прогрессией называют такую числовую последовательность, каждый член которой, начиная со второго, равен предшествующему члену, умноженному на одно и то же (определенное для данной последовательности) число q. Число q называют знаменателем геометрической прогрессии. Предполагается, что q ≠ 0.
Например, 1, 3, 9, 27…
Если q > 0, то прогрессия считается знакоположительной, при q < 0 – знакопеременной.
Если |q |>1, прогрессия возрастающая, если |q | <1 – убывающая. Заметим, что при q < 0 сами члены геометрической прогрессии попеременно меняют знак и убывающей последовательности не образуют, хотя такую прогрессию все равно называют убывающей.
Если b1 — первый член прогрессии (b1 ≠ 0), а q — знаменатель прогрессии (q ≠ 0), то справедливы следующие формулы:
- bn = b1 · q n -1 формула n-го члена
Пример: найдите b4, b11 геометрической прогрессии, если b1 = 3, q = 2
Решение:
По формуле найдем:
b4 = b1 · q 4 — 1= 3 · 2 3 = 24,
b11 = b1 · q 11 — 1= 3 · 2 10 = 3072.
— формула суммы n первых членов;
Пример: найдите сумму пяти членов геометрической прогрессии, у которой b1 = 2, q = 3
Решение:
Каждый член знакоположительной геометрической прогрессии представляет собой среднее геометрическое его соседних членов (исключение составляют первый и последний члены, т.к. у них только по одному соседнему члену):
— свойство n-го члена.
Если | q | < 1, то имеем бесконечную убывающую геометрическую прогрессию, сумму которой находят по формуле
Замечание:
Формула n-го члена прогрессии:
- арифметической:an = a1 + d · (n − 1)
- геометрической: bn = b1 · q n — 1
Зная одну формулу, легко можно получить другую – надо лишь сложение заменить умножением и умножение заменить возведением в степень, и из формулы для арифметической прогрессии получится формула для геометрической прогрессии.
Сложные проценты
Есть два вида процентов доходности – простые и сложные.
Чтобы с ними разобраться, представим двух братьев: Расчетливого Сашу и Простака Петю. Их отец дал каждому по 1000 рублей, и оба кладут их в банк. Расчетливый Саша всегда пользуется счетом со сложными процентами, а Простак Петя больше любит поступать по старинке и предпочитает счета с простыми процентами.
Сложный процент — это проценты с процентов.
У простого процента такой особенности нет, его рассчитывают от стартовой суммы, которую называют «основным капиталом». Пете легко в этом разобраться: основной капитал зарабатывает каждый год одну и ту же сумму.
Если вы откладываете деньги, занимаете их, пользуетесь кредитной картой, берёте в ипотеку или покупаете пожизненную ренту, формула сложного процента работает на (или против) вас.
Давайте выведем формулу сложных процентов. Допустим, у нас есть некоторая сумма S, в конце года мы ее увеличиваем на некоторый процент (%). Полученную сумму S1 после начисления процентов можно посчитать так:
В следующем году полученную сумму снова увеличим на тот же процент. Тогда можем записать верное равенство:
Аналогично мы можем посчитать полученную сумму еще через год:
Таким образом, если периодов n, то можем записать формулу вычисления сложных процентов:
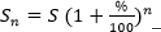
Тогда последовательность остатков долга будет следующей:
Видим, что это геометрическая прогрессия.
Итак, Саша размещает свои 1000 рублей на счете и получает ежегодно 7% дохода. Давайте посчитаем, сколько он получит за три года? В данном случае S = 1000, % = 7, n = 3, 
Счет Пети – тоже 7%-ный, но процент у него простой. Какие деньги заработает за три года Петя? В первый год он получит 70 рублей, столько же – во второй и в третий. Таким образом, проценты составят 3 · 70 = 210 рублей, итого общая сумма на счете — 1210 рублей. Инвестиционное решение Саши, очевидно, выгоднее.
Павел Бердов
уроки математики
5 июня 2016
Смотрите также:
- Задача 19: арифметическая прогрессия из пробного ЕГЭ
- Что такое функции с целыми значениями и как их применять для решения задач 19 из ЕГЭ по математике?
- Метод Гаусса
- Тест к уроку «Знаки тригонометрических функций» (1 вариант)
- Материалы для подготовки к ЕГЭ по математике
- Задача B2: Сложный процент и стандартная формула

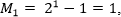
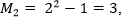
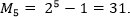
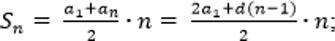
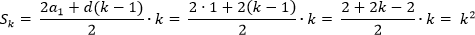
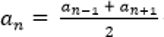 — свойство n-го члена.
— свойство n-го члена.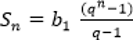 — формула суммы n первых членов;
— формула суммы n первых членов;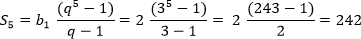
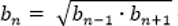 — свойство n-го члена.
— свойство n-го члена.