ЕГЭ по математике профильного уровня — один из самых сложных экзаменов. Планируете сдавать его, но не знаете, с чего начать? Этот экзамен не покажется вам таким трудным, если вы узнаете про него побольше и грамотно подготовитесь. В этой статье обсудим, что нужно знать про ЕГЭ по математике 2023, из каких разделов он состоит и как к нему подготовиться.
Какие темы важно знать для ЕГЭ по математике 2023?
В математике, как и в любом предмете, есть опорные темы. Если вы их выучите, будет легче справиться с экзаменом.
Формулы тригонометрии
Очень важно знать формулы тригонометрии и уметь применять их. Хорошая новость: в справочных материалах можно найти несколько тригонометрических формул.
Но формул гораздо больше. Я советую не зубрить их, а научиться выводить: приходить к формулам шаг за шагом, опираясь на тождества. Кстати, мы учим выводить формулы на курсах подготовки к ЕГЭ: это полезно, чтобы оказаться на экзамене во всеоружии и ничего не перепутать.
Квадратные уравнения
Эти уравнения мы учимся решать еще в 7 классе. Они встречаются в ЕГЭ по математике постоянно: и как самостоятельные задания, и внутри более сложных уравнений или неравенств. Квадратные уравнения могут встретиться в математических моделях № 9 и № 15, в задачах на геометрию и стереометрию, в задании № 17 с параметром.
Самое главное — хорошо знать универсальные методы решения. Первый — через формулу дискриминанта, второй — через теорему Виета, которая может сэкономить время на экзамене.
Треугольники
Эта замечательная тема, которую проходят в 7 классе — основа основ всей геометрии. Она нужна и для решения стереометрии, и для простейших планиметрических задач. Еще треугольники необходимы, чтобы освоить огромное количество теорем. Выучите все, что с ними связано! Особое внимание обратите на прямоугольные треугольники, которые встречаются чаще остальных — тогда геометрические задачи сразу станут проще.
Проценты
Самая нелюбимая тема моих учеников после тригонометрии, которую необходимо хорошо знать. Проценты нужны для реальной математики — это № 9 (с кратким ответом) и № 15 (с развернутым ответом). Понимание этой темы может принести вам 3 первичных балла.
План успешной подготовки к ЕГЭ по математике 2023
Если вы хотите получить больше 80 баллов на ЕГЭ, нужно идеально решать часть с кратким ответом, а также справляться с большинством заданий с развернутым ответом.
Чтобы постепенно прорабатывать материал, воспользуйтесь кодификатором. В нем обратите внимание на таблицу 2, а именно на блоки:
- Алгебра
- Уравнения и неравенства
- Элементы комбинаторики, статистики и теории вероятностей
- Функции
- Начала математического анализа
- Геометрия
Ориентируйтесь на указанную последовательность, но геометрию изучайте параллельно с остальными блоками — на нее нужно больше времени.
Самое главное — ни в коем случае не ограничивайтесь теорией. Ее у вас не спросят на экзамене, а вот задания решать придется. Поэтому тренируйте практические навыки: актуальные задания вы сможете найти в открытом банке заданий на сайте ФИПИ или в нашем тренажере «Решутест».
Как решать часть с кратким ответом
Ни в коем случае не пренебрегайте частью с кратким ответом! Иначе будет обидно: например, вы наберете за экономическую задачу № 15 полные 2 балла, но потеряете их в двух заданиях первой части. Это актуально для всех ЕГЭ: подробнее о том, как идеально справляться с первой частью экзамена, читайте здесь.
Еще одно заблуждение: «часть с кратким ответом простая, к ней можно не готовиться». Даже в первой части иногда встречаются такие задания, которые ученики даже не решают, потому что не готовились к ним.
Как я уже говорила, часть с кратким ответом содержит 11 заданий. Начинать подготовку необходимо именно с заданий базового уровня сложности, потому что это та основа, на которую потом накладывается более сложная теория.
Что касается задач повышенного уровня сложности, то среди каждого номера есть лайфхаки, например, в этой статье я уже рассказывала про № 11, в котором нужно работать с производной.
Задания с развернутым ответом: немного статистики
Многие думают, что эта часть ЕГЭ по математике очень сложная. Поэтому ребята, которые не рассчитывают на высокие баллы, даже не приступают к ней. И очень зря! С помощью этих заданий можно заработать дополнительные баллы и побороться за высокое место в рейтинге.
Сейчас будет немного статистики. В среднем около 35% учеников получают полные 2 балла за решение № 12, а вот неравенство № 14 дается хуже, только около 12% с ним справляются на полный балл. Геометрия даётся ещё хуже: стереометрию № 13 полностью решают 2% выпускников, планиметрию (№ 16) менее 5%. А вот с экономической задачей (№ 15) справляются около 20%, а это целых 2 балла! Что касается № 17 и 18, то они даются ещё хуже, но на то они и самые сложные, хотя 1 балл за № 18 по статистике получают около 25% сдающих — там нужно просто привести пример.
Особенности уровней ЕГЭ по математике
В 2015 году ЕГЭ по математике разделили на базовый и профильный уровни. Это упростило жизнь выпускникам, которые не планируют поступать на специальности, связанные с математикой. Если ЕГЭ по математике нужен только для получения аттестата, можно сдать его облегченную версию, оставив время и силы для профильных экзаменов.
Базовый уровень ЕГЭ по математике
Как устроен базовый ЕГЭ по математике? Экзамен идет 180 минут, он состоит из 21 задания, за каждое из которых можно получить 1 балл. Этот экзамен единственный, который переводится не в 100-бальную систему, а в оценки.
В ЕГЭ по математике базового уровня 6 тематических блоков:
Также обратите внимание, что базовый ЕГЭ по математике не поменялся с точки зрения наполнения, изменился лишь порядок заданий. Вот что пишут ФИПИ:
Подробнее про базовый ЕГЭ по математике, включая разбор всех заданий, читайте здесь, а мы перейдём к профильному.
Профильный уровень ЕГЭ по математике
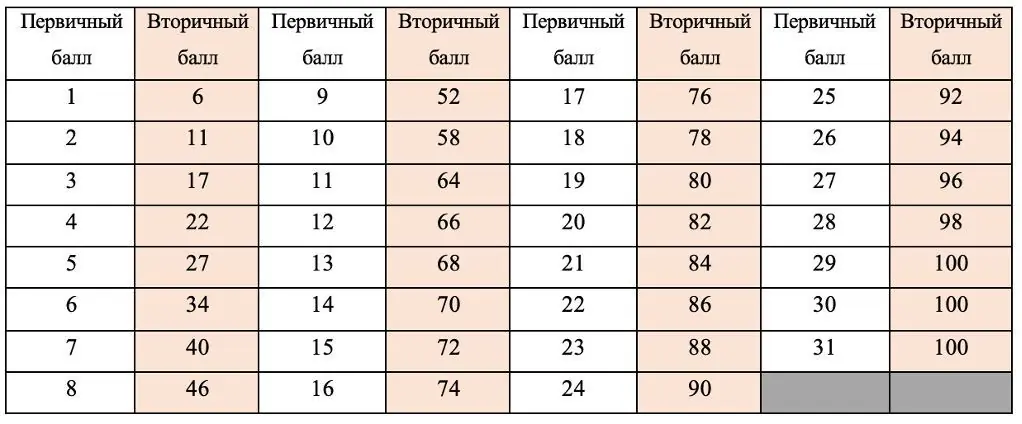
Данный экзамен, как и остальные ЕГЭ, переводится в 100-бальную систему:
Экзамен состоит из двух частей: Часть 1 с кратким ответом, а Часть 2 — с развернутым. Длится он 235 минут. Всего есть 18 заданий, которые разделены на 3 блока: алгебра, геометрия и реальная математика. Максимальное количество первичных баллов — 31.
База, профиль — неважно, к какому именно уровню вы готовитесь. В любом случае надо не только правильно решить каждое задание, но и оформить его так, чтобы проверяющие ни к чему не придрались. Нарисовать и описать график, расписать решение уравнения или задачи… И это не все: нужно еще и внести ответы в бланк без ошибок. И все это — за ограниченный период времени! Так можно перенервничать и запороть даже самую простую задачку. А на ЕГЭ — каждый балл на счету.
Поэтому на своих занятиях я сразу показываю своим ученикам, как правильно оформлять каждое задание в ЕГЭ по математике. Мы разбираем все критерии и учимся правильно отвечать на вопросы. А еще я всегда помогаю ученикам закрыть пробелы в знаниях и объясняю сложные темы столько раз, сколько нужно. И куда же без лайфхаков? Всегда рассказываю лучший способ решения типичных заданий. Так что мои ученики приходят на экзамены подготовленными и не нервничают, когда видят задачу. Хотите также? Приходите ко мне на курсы подготовки к ЕГЭ по математике — научу!
Структура ЕГЭ по математике 2023
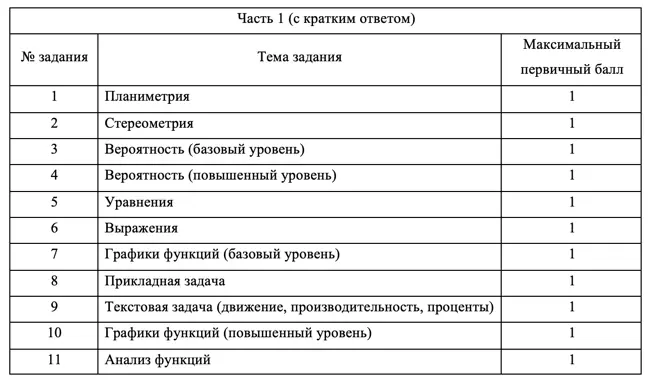
Часть 1:
- Приносит 11 баллов, то есть 35% всего экзамена
- 11 заданий с кратким ответом
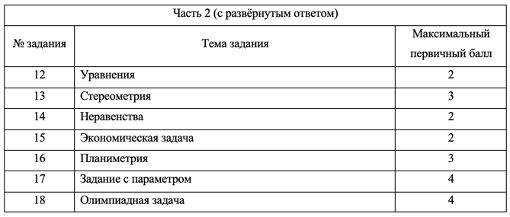
Часть 2:
- Приносит 20 баллов, то есть 65% всего экзамена
- 7 заданий с развернутым ответом
Внимание! Вся нумерация заданий в статье соответствует ЕГЭ 2023 года.
В заданиях с кратким ответом нужно лишь записать верное число в бланк. Заданий с развернутым ответом 7, в них нужно подробно расписать решение, которое должно соответствовать критериям оценивания.
ЕГЭ — стандартизированный экзамен, поэтому каждое задание всегда соответствует определенной теме.
Обратите внимание, что по сравнению с 2022 годом, в части 1 изменился только порядок заданий. Сами сотрудники ФИПИ говорят следующее:
Задания с кратким ответом принесут вам до 11 первичных баллов (64 вторичных). Если не понимаете, что это за баллы и откуда они берутся, почитайте эту статью. Самая популярная цель на ЕГЭ по математике — набрать 80 баллов, для этого раньше было необходимо 19 первичных баллов. Ранее многие ученики пользовались рабочей стратегией — решить всю часть с кратким ответом, а также № 12, 14 и 15. Если хорошо разбирались в геометрии, выбирали № 13 и 16 — или использовали их как запасные задания. Сейчас стратегия должна быть другая, так как № 13 (стереометрия) стал стоить дороже — 3 балла вместо 2, а № 15 (экономическая задача) — подешевел с 3 баллов до 2. Изменилась также шкала перевода баллов, поэтому подумайте, какими заданиями вы сможете набрать необходимое количество первичных баллов.
Разделы ЕГЭ по математике
- Алгебра и начала анализа — 8 заданий, 13 первичных баллов
- Геометрия — 4 задания, 8 первичных баллов
- Реальная математика — 6 заданий, 10 первичных баллов
Какие задания входят в ЕГЭ по математике?
Здесь вам на помощь приходят документы с официального сайта ФИПИ: кодификатор, демоверсия и спецификация.
- Кодификатор — это краткий перечень всех блоков и тем, которые включены в экзамен.
Сейчас кодификатор общий для обоих уровней экзамена, как базового, так и профильного. Он снова представляет собой единый документ, так что не запутаетесь.
- Демоверсия — типовой вариант ЕГЭ. Он показывает уровень экзамена и ориентировочную сложность заданий.
- Спецификация — это документ, описывающий структуру экзамена и разбалловку.
Что в итоге
Теперь вы знаете больше про ЕГЭ по математике 2023. Вы познакомились со структурой и поняли, на что стоит обращать внимание при подготовке. А еще узнали, что первую часть обязательно решать на максимум, а вторая не такая страшная, как кажется. Но наверняка у вас еще осталась куча вопросов: по оформлению и конкретному решению каких-то заданий точно.
Обо всем этом я подробно рассказываю своим ученикам во время подготовки к ЕГЭ по математике. Мы изучаем все непонятные темы, а потом прорешиваем много однотипных заданий — так легче запоминается формат. Еще мы всегда проводим пробные экзамены, чтобы выявить слабые места. Я анализирую ошибки каждого ученика и индивидуально разбираю их с ними. Благодаря этому мои выпускники гарантированно сдают ЕГЭ на 80+. Если вы хотите оказаться среди них — записывайтесь на курсы!
Привет! На связи методический отдел федеральной сети курсов ЕГЭ и ОГЭ Lancman School («Ланцман скул»). Сегодня мы расскажем о том, как готовиться к ЕГЭ по профильной математике 2022 года.
Все таблицы в сопроводительных к демоверсии документов указывают на то, что интегралы на ЕГЭ будут, и надо учить еще и эту тему.
Но на практике, правда, все не очень однозначно.
Проблема в том, что эти таблицы – как бы теоретические доводы. Или, вернее сказать, бюрократические: они есть на бумаге. Ещё в сборниках от ФИПИ.
Но за последние лет 5 (а то и больше) на ЕГЭ основной волны интегралы не встречались.
Как же справляться с такой противоречивой ситуацией?
Ведь не хочется тратить зря время на все-таки весьма обширные по меркам 1 части ЕГЭ темы. Но есть опасения: вдруг в этом году раз — и дадут-таки эти темы в №6.
Вот наши советы:
• Выделите время в конце подготовки: займитесь этой темой в мае.
Какой смысл разбирать редкую тему осенью-зимой, если весной на нее все равно придется тратить время, чтоб повторить? Раз уж она вряд ли встретится – экономьте на ней время, разберитесь с типовыми задачами один раз незадолго до экзамена, чтобы больше уже к этому не возвращаться.
• Задачи по этим темам не очень сложные, тут скорее вопрос во времязатратах. Поэтому перенесите их в онлайн.
Мы, например, весной так и делаем. Преподаватель записывает ролики с кратким объяснением теории и решением типовых задач. Обычно интегралы занимают ~30 мин.
Если вы преподаватель – запишите видео и отправьте своим ученикам.
Если сами готовитесь к экзамену – поищите в интернете, есть немало узконаправленных роликов, посвященным интегралам и условиям касания именно на ЕГЭ.
Надеемся, теперь вы уверенно чувствуете себя в этом вопросе и подберете подходящее для себя решение.
Хочешь БЕСПЛАТНО разобрать с опытным преподавателем все детали новых усложнённых вариантов ЕГЭ по профильной математике 2022 года — приходи на пробное занятие в Lancman School. Мы 13 лет готовим к ЕГЭ на высокие баллы и знаем об экзаменах и поступлении в хорошие вузы буквально всё. Решишь продолжить готовиться к ЕГЭ вместе с нами весь год — дадим скидку после бесплатного пробного занятия. Любой вопрос смело пиши сюда.
Если ты живешь не в Москве, но хочешь заниматься с лучшими столичными репетиторами и сдать ЕГЭ на 80+ баллов, то регистрируйся на наши онлайн-курсы. В этом году мы включили в договор пункт, гарантирующий поступление на бюджет в любой вуз страны. Если ученик будет соблюдать все обговоренные условия, он обязательно поступит. В противном случае мы вернём деньги. Первое пробное занятие БЕСПЛАТНО.
Рассылка «Lancman School»
Мы отправляем нашу интересную и очень полезную рассылку
два раза в неделю: во вторник и пятницу
Похожие статьи:
24 августа вышла демоверсия ЕГЭ 2023 по профильной математике. Для тех, кто пока не готов вникать в тему основательно, успокоительный спойлер: почти ничего не изменилось, принципиально новых заданий нет. Всё в порядке.
А для тех, кто давно был на низком старте и ждал разбор демо ЕГЭ, математик Эйджей провёл стрим с решением заданий из демоверсии ЕГЭ 2023 по профильной математике. В этой статье собраны резюме по заданиям экзамена, которые составители ЕГЭ представили в демоверсии.
https://youtu.be/RFQwP8DW8sA
Что изменилось в ЕГЭ 2023 по профильной математике
По сути, никаких критически важных изменений в демоверсии ЕГЭ 2023 нет, о чём составители написали прямо: «Изменения в содержании КИМ отсутствуют». Но есть момент: все задания из первой части, кроме 11, изменили свои номера.
Будем искать позитивные моменты: если в 2022 году вы не смогли запомнить номера заданий в тесте — ничего страшного, запомните новые в 2023 году.
Главное, что новых заданий не появилось.
Важный момент в самостоятельной подготовке к ЕГЭ по профильной математике — выбор качественных сборников задач. Делимся лучшими ресурсами для повторения теории и отработки практики.
1, 2 задания
В демоверсии ЕГЭ 2023 по профильной математике всё начинается с простой геометрии и стереометрии. Составители хотят, чтобы геометрические задачи научились решать как можно больше ребят, поэтому поместили эти задания вперёд как одни из самых простых, чтобы поднять решаемость.
3, 4 задания
Задания 3–4 посвящены теории вероятности.
Задание 3 — обычная задача наподобие задачи из ОГЭ, а задание 4 — задача про монеты и проценты из КИМа 2022 года.
5, 6 задания
После вероятностей составители ЕГЭ 2023 по профильной математике решили поставить уравнения и выражения. Уравнения ожидаются не супер лёгкие, но вполне решаемые: будут корни, логарифмы и степени. В выражениях в демоверсии ЕГЭ встретилась тригонометрия и степени.
7 задание
Ура, 7 задание осталось на своём месте: это задание с графиком и производными. Почему-то его не объединили в общий блок с 11 заданием, тоже посвящённым производным.
Далее в разборе демоверсии ЕГЭ 2023 по профильной математике выпускников ждут две задачи.
8 задание
8 задача на подстановку: нужно подставить в формулу известные числа и вычислить какую-либо величину. Ничего сложного, главное внимательность.
9 задание
Ещё одна текстовая задача. Здесь могут встретиться темы «Движение по прямой», «Движение по окружности», «Движение по реке» и «Сплавы, смеси, растворы». Такие задачи считаются не самыми простыми. Вместе с Эйджеем разберём этот номер в Телеграме.
10 задание
10 задание в демо ЕГЭ 2023 — «новое старое задание». Этот тип заданий с графиком впервые появился в 2022 году, и в КИМ 2023 попал без изменений. Возможно, стоит ждать усложнения этого задания.
11 задание
Традиционное задание с производными и точками минимума и максимума, которое почему-то не объединили в блок с другим заданием на производные.
Итак, обобщим всё, что мы узнали про первую часть демоверсии ЕГЭ по математике: в 2023 году в экзамене не появились ни вектора, ни комплексные числа. Можно немного расслабиться! Осталось выучить новую нумерацию, и всё будет хорошо.
Нумерация второй части в демоверсии ЕГЭ 2023 осталась без изменений, и это радует: не придётся переучивать номера и переживать. Посмотрим, что приготовили составители в этом году.
12 задание
Традиционно в разборе демоверсии ЕГЭ 2023 по профильной математике в 12 задании выпускников ждёт тригонометрическое уравнение.
13 задание
В 13 задании осталась стереометрия: в демоверсии представлена треугольная призма.
14 задание
В 14 задании всё по плану, там остались неравенства с логарифмами, ничего нового.
Это задание вместе с 12-ым составляет «джентльменский набор» из второй части — их под силу решить каждому, и этому нужно обязательно научиться, чтобы набрать 70+ баллов за ЕГЭ по профильной математике.
15 задание
15 задание также считается вполне решаемым. В демоверсии это экономическая задача про человека, который взял кредит в банке и рассчитывает выплаты и проценты.
16 задание
В задании 16 демоверсии ЕГЭ 2023 представлена планиметрическая задача про две окружности.
17 задание
Задача на параметр. Как показывает практика прошлых лет, параметр — самое решаемое задание из сложных заданий ЕГЭ.
18 задание
Задача на целые числа. Из трёх пунктов, А и Б решить может каждый, если хорошо подготовиться.
Чтобы получить 80+ баллов по профильной математике, нужно без ошибок решить первую часть и выполнить 12, 14, 15 и 18аб задания. А планиметрия, стереометрия, параметр и 18 задание полностью помогут получить заветную сотку. Как повысить свои шансы на успешную сдачу ЕГЭ по математике, рассказали в нашей статье.
Мы разобрали демоверсию ЕГЭ 2023 по математике, и теперь вы знаете, что приготовили для вас составители экзамена. Можно смело начинать подготовку! Эйджей уже составил план занятий и ждёт вас на курсе «Основа». Это возможность разобраться во всех темах и набить руку в решении заданий в компании единомышленников и с личным наставником.
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter. Мы обязательно поправим!
Образовательный портал для подготовки к экзаменам
Математика профильного уровня
Математика профильного уровня
Сайты, меню, вход, новости
Каталог заданий.
Первообразная
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
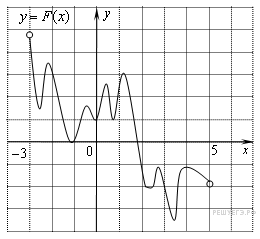
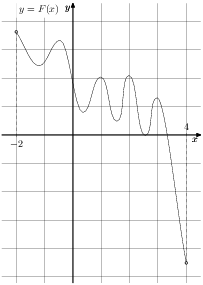
На рисунке изображён график функции y = F(x) — одной из первообразных функции f(x), определённой на интервале (−3; 5). Найдите количество решений уравнения f(x) = 0 на отрезке [−2; 4].
Источник: Пробный экзамен по математике. Санкт-Петербург 2013. Вариант 2.
2
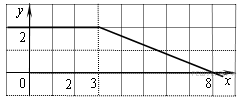
На рисунке изображён график некоторой функции 
(два луча с общей начальной точкой). Пользуясь рисунком, вычислите F(8) − F(2), где F(x) — одна из первообразных функции f(x).
Источник: Пробный экзамен по математике. Санкт-Петербург 2013. Вариант 1., Пробный экзамен по математике Санкт-Петербург 2014. Вариант 1.
3
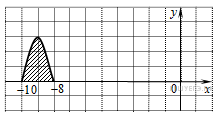
На рисунке изображён график функции y = f(x). Функция 
— одна из первообразных функции y = f(x). Найдите площадь закрашенной фигуры.
4
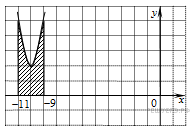
На рисунке изображён график некоторой функции y = f(x). Функция 
— одна из первообразных функции f(x). Найдите площадь закрашенной фигуры.
Пройти тестирование по этим заданиям
Первообразной для функции $f(x)$ называется такая функция $F(x)$, для которой выполняется равенство: $F'(x)=f(x)$
Таблица первообразных
Первообразная нуля равна $С$
| Функция | Первообразная |
| $f(x)=k$ | $F(x)=kx+C$ |
| $f(x)=x^m, m≠-1$ | $F(x)={x^{m+1}}/{m+1}+C$ |
| $f(x)={1}/{x}$ | $F(x)=ln|x|+C$ |
| $f(x)=e^x$ | $F(x)=e^x+C$ |
| $f(x)=a^x$ | $F(x)={a^x}/{lna}+C$ |
| $f(x)=sinx$ | $F(x)-cosx+C$ |
| $f(x)=cosx$ | $F(x)=sinx+C$ |
| $f(x)={1}/{sin^2x}$ | $F(x)=-ctgx+C$ |
| $f(x)={1}/{cos^2x}$ | $F(x)=tgx+C$ |
| $f(x)=√x$ | $F(x)={2x√x}/{3}+C$ |
| $f(x)={1}/{√x}$ | $F(x)=2√x+C$ |
Если $y=F(x)$ – это первообразная для функции $y=f(x)$ на промежутке $Х$, то $у$ $у=f(x)$ бесконечно много первообразных и все они имеют вид $y=F(x)+C$
Правила вычисления первообразных:
- Первообразная суммы равна сумме первообразных. Если $F(x)$ — первообразная для $f(x)$, а $G(x)$ – первообразная для $g(x)$, то $F(x)+G(x)$ — первообразная для $f(x)+g(x)$.
- Постоянный множитель выносится за знак первообразной. Если $F(x)$ — первообразная для $f(x)$, а $k$ – постоянная величина, то $k$ $F(x)$ — первообразная для $k$ $f(x)$.
- Если $F(x)$ — первообразная для $f(x)$, $а, k, b$ — постоянные величины, причем $k≠0$, то ${1}/{k}$ $F(kx+b)$ — это первообразная для $f(kx+b)$.
Пример:
Найти первообразную для функции $f(x)=2sinx+{4}/{x}-{cosx}/{3}$.
Решение:
Чтобы было проще найти первообразную от функции, выделим коэффициенты каждого слагаемого
$f(x)=2sinx+{4}/{x}-{cosx}/{3}=2∙sinx+4∙{1}/{x}-{1/3}∙cosx$
Далее, воспользовавшись таблицей первообразных, найдем первообразную для каждой функции, входящих в состав $f(x)$
$f_1=sinx$
$f_2={1}/{x}$
$f_3=cosx$
Для $f_1=sinx$ первообразная равна $F_1=-cosx$
Для $f_2={1}/{x}$ первообразная равна $F_2=ln|x|$
Для $f_2=cosx$ первообразная равна $F_3=sinx$
По первому правилу вычисления первообразных получаем:
$F(x)=2F_1+4F_2-{1}/{3}F_3=2∙(-cosx)+4∙ln|x|-{1}/{3}∙sinx$
Итак, общий вид первообразной для заданной функции
$F(x)=-2cosx+4ln|x|-{sin x}/{3}+C$
Связь между графиками функции и ее первообразной:
- Если график функции $f (x) > 0$ на промежутке, то график ее первообразной $F(x)$ возрастает на этом промежутке.
- Если график функции $f (x) < 0$ на промежутке, то график ее первообразной $F(x)$ убывает на этом промежутке.
- Если $f(x)=0$, то график ее первообразной $F(x)$ в этой точке меняется с возрастающего на убывающий (или наоборот).
Пример:
На рисунке изображен график функции $y=F(x)$ – одной из первообразных некоторой функции $f(x)$, определенной на интервале $(-3;5)$. Пользуясь рисунком, определите количество решений $f(x)=0$ на отрезке $(-2;2]$
Если $f(x)=0$, то график ее первообразной $F(x)$ в этой точке меняется с возрастающего на убывающий(или наоборот).
Выделим отрезок $(-2;2]$ и отметим на нем экстремумы.
У нас получилось $6$ таких точек.
Ответ: $6$
Неопределенный интеграл
Если функция $у=f(x)$ имеет на промежутке $Х$ первообразную $у=F(x)$, то множество всех первообразных $у=F(x)+С$, называют неопределенным интегралом функции $у=f(x)$ и записывают:
$∫f(x)dx$
Определенный интеграл – это интеграл с пределами интегрирования (на отрезке)
$∫_a^bf(x)dx$, где $a,b$ — пределы интегрирования
Площадь криволинейной трапеции или геометрический смысл первообразной
Площадь $S$ фигуры, ограниченной осью $Oх$, прямыми $х=а$ и $х=b$ и графиком неотрицательной функции $у=f(x)$ на отрезке $[a;b]$, находится по формуле
$S=∫_a^bf(x)dx$
Формула Ньютона — Лейбница
Если функция $у=f(x)$ непрерывна на отрезке $[a;b]$, то справедливо равенство
$∫_a^bf(x)dx=F(x)|_a^b=F(b)-F(a)$, где $F(x)$ — первообразная для $f(x)$
Пример:
На рисунке изображен график некоторой функции $у=f(x)$. Одна из первообразных этой функции равна $F(x)={2х^3}/{3}-2х^2-1$. Найдите площадь заштрихованной фигуры.
Решение:
Площадь выделенной фигуры равна разности значений первообразных, вычисленных в точках $1$ и $-2$
$S=F(1)-F(-2)$
Первообразная нам известна, следовательно, осталось только подставить в нее значения и вычислить
$F(1)={2∙1}/{3}-2∙1-1={2}/{3}-2-1={2}/{3}-3$
$F(-2)={2(-2)^3}/{3}-2(-2)^2-1={2∙(-8)}/{3}-8-1=-{16}/{3}-9$
$S={2}/{3}-3-(-{16}/{3}-9)={2}/{3}-3+{16}/{3}+9={18}/{3}+6=6+6=12$
Ответ: $12$
Изменения в ЕГЭ-2023 по русскому языку
Экзаменационных материалов по русскому языку коснулось больше всего обновлений. Вот что изменится в 2023 году:
-
Порядок первых трёх заданий. Теперь задание 1 проверяет понимание логико-смысловых отношений между фрагментами текста, задание 2 — лексическое значение слов, а задание 3 — умение верно определять стилистические характеристики текста. Кроме того, третье задание теперь имеет статус повышенной сложности.
-
21-е и 26-е задания первой части экзамена теперь тоже имеют повышенную сложность, так как расширился языковой материал, на основе которого их нужно выполнить. Максимальное число баллов за выполнение 26-го задания уменьшилось с 4 до 3.
-
Изменилась формулировка 4-го задания первой части (на знание орфоэпических норм) и система ответов на него: если раньше нужно было выбрать один вариант ответа, то теперь их может быть несколько. Также расширен языковой материал для 4-го и 5-го заданий.
-
За задание под номером 8 первой части экзаменуемые теперь могут получить максимум 3 балла (раньше — 5).
-
Изменилась формулировка в 9-м задании первой части (правописание гласных и согласных в корне), а также языковой материал задания.
-
Задание номер 27 из второй части экзамена теперь имеет другую формулировку. Изменились критерии оценки и максимальный балл по одному из них.
-
Изменились критерии оценки сочинения К1–К3 и К12. Изменения касаются фактических ошибок в тексте. Кроме того, сочинение больше не ограничено по объёму.
-
Максимально возможный первичный балл на ЕГЭ по этому предмету в 2023 году составит 54 (вместо 58).
Подготовка к ЕГЭ по русскому языку
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Демоурок по подготовке к экзаменам
Составим ваш личный путь к высоким баллам — учтем сроки, уровень знаний и цель.
Изменения в ЕГЭ-2023 по математике (база)
Сами задания по предмету не изменились, но теперь практические задания, которые проверяют знания из разных разделов математики, предшествуют блокам по геометрии и алгебре.
Как поясняется в материалах на сайте ФИПИ, это обновление поможет экзаменуемому эффективнее организовать работу над выполнением заданий.
Изменения в ЕГЭ-2023 по математике (профиль)
КИМ профильного экзамена по этому предмету также не изменились, но теперь задания в 1-й части сгруппированы иначе: сначала геометрия, потом элементы комбинаторики, статистика и теория вероятностей, в финале — алгебра, в том числе уравнения и неравенства, функции и начала анализа. Вторая часть экзамена осталась без изменений.
Подготовка к ЕГЭ по математике
Изменения в ЕГЭ-2023 по физике
-
Интегрированные задания из 1-й части экзамена, в которых проверяется знание не меньше чем из 3 разделов школьного курса по предмету, перенесены с 1-й и 2-й линий на 20-ю и 21-ю.
-
Вторая часть ЕГЭ тоже изменилась: раньше в 30-м задании могли встретиться только задачи по темам «Законы Ньютона» и «Законы сохранения в механике», а теперь в этот список добавили и задачи по теме «Статика».
Подготовка к ЕГЭ по физике
Изменения в ЕГЭ-2023 по химии
-
В 2023 году иначе будет выглядеть условие в 23-м задании, которое проверяет умение рассчитывать концентрации веществ в равновесной системе. Данные теперь записывают текстом, а не в формате таблицы, как было раньше.
-
Задания 33 и 34 в ЕГЭ по этому предмету поменялись местами. Теперь задание 33 проверяет умение определять молекулярную и структурную формулы вещества, а задание 34 содержит расчётную задачу.
-
Повысилась сложность заданий 9 (взаимосвязь неорганических веществ), 12, 16.
Подготовка к ЕГЭ по химии
Изменения в ЕГЭ-2023 по биологии
-
В 1-ю часть экзамена по этому предмету добавили еще одно задание на тему «Многообразие организмов», а задания 5–8, 9–12 и 13–16 были сгруппированы в тематические модули.
-
Из 2-й части ЕГЭ по биологии в 2023 году исключили одно задание — раньше оно было под номером 24. Задания 23 и 24 (по новой нумерации) сгруппированы в мини-модуль.
Изменения в ЕГЭ-2023 по истории
-
В экзамен по истории в 2023 году добавили два новых задания. Задание под номером 8 проверит знания экзаменуемого об истории ВОВ. В 20-м задании необходимо сравнить исторические события, явления или процессы. Помимо отдельных заданий о Великой Отечественной войне, знания об этом историческом периоде будут проверять в других заданиях. Факты о ВОВ встретятся не менее чем в 20% экзаменационных заданий.
-
Верхняя граница первичных баллов по этому предмету увеличилась с 38 до 42.
-
Скорректированы критерии оценки 18-го и 19-го заданий.
-
У экзаменуемых будет больше времени на сдачу ЕГЭ по истории — 210 минут вместо 180.
Изменения в ЕГЭ-2023 по географии
Изменения в заданиях в 2023 году коснутся всех предметов, кроме географии. Тут всё просто: по сравнению с 2022 годом в экзамене по географии ничего не поменяется.
Изменения в ЕГЭ-2023 по обществознанию
-
В 2023 году скорректирована формулировка 18-го задания экзамена по обществознанию.
-
Также изменилась формулировка последнего, 25-го задания — добавлены детали, а максимально возможный балл за это задание увеличен до 6 (в прошлом году — 4).
-
За 3-е задание экзаменуемые теперь могут получить максимум 1 балл (вместо 2).
-
Последнее изменение на ЕГЭ по обществу в 2023 году касается максимального первичного балла за работу — теперь это 58 баллов вместо 57.
Подготовка к ЕГЭ по обществознанию
Изменения в ЕГЭ-2023 по литературе
Изменения по этому предмету коснулись 9-го задания: если раньше нужно было выбрать три верных ответа из пяти, то теперь их число может быть от 2 до 4 — зависит от того, какое произведение попалось экзаменуемому.
Изменения в ЕГЭ-2023 по иностранным языкам (кроме китайского)
-
Раздел «Грамматика и лексика» в ЕГЭ по этим предметам уменьшился с 20 до 18 заданий.
-
За задания под номерами 1 и 11 экзаменуемые теперь могут получить максимум 3 балла, за задания 2 и 10 — 4 балла. Также изменилась верхняя граница первичных баллов — 86 вместо 100.
-
Изменения коснулись формулировок некоторых заданий, а именно — 38 (письменная часть) и 4 (устная часть).
-
Обновлены критерии оценки 37-го (письменная часть) и 3-го (устная часть) заданий.
Подготовка к ЕГЭ по английскому
Изменения в ЕГЭ-2023 по китайскому языку
-
Во 2-м задании раздела «Говорение» по этому предмету ответ теперь должен быть объёмнее: 10–12 фраз вместо 8–9.
-
Скорректирована формулировка 3-го задания из раздела «Говорение».
-
В 17-м задании письменной части вместо определения лишней лексической единицы нужно заполнить пропуск подходящей по смыслу лексической единицей.
-
В задании 23 письменной части нужно будет заполнить пропуск в приведённом фрагменте подходящей результативной морфемой (вместо дополнительного элемента, как в прошлом году).
-
В 26-м письменном задании ранее нужно было определить, какое из предложений построено грамматически верно. Теперь — выбрать корректную последовательность приведённых фрагментов одного предложения.
-
Сократилось количество вариантов ответов в заданиях 15–18, 22 и 23 письменной части — с пяти до четырёх.
Изменения в ЕГЭ-2023 по информатике
-
Изменилась тематика задания номер 6 по этому предмету: если раньше с его помощью проверяли знание основных конструкций ЯП, понятия переменной и оператора присваивания, то теперь оно касается работы с алгоритмами.
-
В задании 22 вместо анализа алгоритма, содержащего ветвление и цикл, теперь требуется построить математическую модель, чтобы решить практическую задачу, при этом нужно использовать приложенный файл.
Подготовка к ЕГЭ по информатике
Первообразные
| Первообразная: | `F'(x)=f(x)` | |||
| Неопределённый интеграл: | `intf(x)dx=F(x)+C` | |||
| Определённый интеграл (формула Ньютона-Лейбница): | `int_a^bf(x)dx=F(b)-F(a)` |  |
Таблица первообразных
| `f(x)` | `F(x)` | `f(x)` | `F(x)` | |
|---|---|---|---|---|
| `a` | `ax` | |||
| `x^n` | `x^(n+1)/(n+1)` | `1/x` | `lnx` | |
| `e^x` | `e^x` | `a^x` | `a^x/lna` | |
| `sinx` | `-cosx` | `cosx` | `sinx` | |
| `1/cos^2x` | `text(tg)x` | `1/sin^2x` | `-text(ctg)x` | |
| `1/(x^2+a^2)` | `1/atext(arctg)x/a` | `1/(x^2-a^2)` | `1/(2a)ln|(x-a)/(x+a)|` | |
| `1/sqrt(a^2-x^2)` | `text(arcsin)x/a` | `1/sqrt(x^2+a)` | `ln|x+sqrt(x^2+a)|` |
Все формулы для профильного ЕГЭ-2022 по математике
Все формулы для базового ЕГЭ-2022 по математике
В (12) задании ЕГЭ предлагается решить уравнение и выбрать корни, принадлежащие заданному промежутку. За это задание можно получить (2) балла.
Пример:
a) реши уравнение (x2+4x−2)(43x+1+82x−1−11)=0.
б) Найди все корни этого уравнения, принадлежащие отрезку [−0,5; 0,5].
Алгоритм выполнения задания
1. Определи вид уравнения, выбери метод решения.
2. Реши уравнение, используя соответствующие виду уравнения свойства и правила. Все найденные корни должны принадлежать области определения уравнения.
3. Выбери корни уравнения, принадлежащие указанному промежутку. Обоснуй выбор корней.
4. Запиши все шаги решения на чистовик разборчиво и кратко.
5. Запиши ответ по обоим пунктам.
Если ход решения верный и обоснованно получены верные ответы в обоих пунктах, то решение оценивается в (2) балла. Если верна последовательность всех шагов решения, но допущена описка или вычислительная ошибка, и в результате получены неверные ответы, можно получить (1) балл.
Как решить задание из примера
1. (x2+4x−2)(43x+1+82x−1−11)=0.
Уравнение является распадающимся, x∈ℝ. Произведение равно нулю, когда хотя бы один из множителей равен нулю:
x2+4x−2=0,(1)43x+1+82x−1−11=0.(2)
Нам нужны формулы степеней:
amn=amn;am+n=aman.
2. Решим каждое уравнение отдельно. Уравнение ((1)) является квадратным. Найдём его корни через дискриминант:
x1=−2−6;x2=−2+6.
Уравнение ((2)) является показательным. Приведём степени к одинаковому основанию:
22(3x+1)+23(2x−1)−11=0;
26x+2+26x−3−11=0.
Преобразуем степени, чтобы показатели тоже были равными:
26x−3+5+26x−3−11=0;
25⋅26x−3+26x−3−11=0;
33⋅26x−3=11;
26x−3=13;
6x−3=log213;
6x−3=log21−log23;
6x−3=−log23;
6x=3−log23;
x=12−log236.
Итак, уравнение имеет три корня −2−6, −2+6 и 12−log236.
3. Отберём корни уравнения, принадлежащие отрезку [−0,5; 0,5].
4<6<9;2<6<3;−5<−2−6<−4.
Корень −2−6 не принадлежит отрезку [−0,5; 0,5].
5,76<6<6,25;2,4<6<2,5;0,4<−2+6<0,5.
Корень −2+6 принадлежит отрезку [−0,5; 0,5].
log22<log23<log24;1<log23<2;−2<−log23<−1;−13<−log236<−16;−0,5<16<12−log236<13<0,5.
Корень 12−log236 принадлежит отрезку [−0,5; 0,5].
4. Перепишем шаги решения в чистовик.
5. Запишем ответ.
Ответ: а) −2−6; −2+6; 12−log236; б) −2+6; 12−log236.
Первообразная
1. На рисунке изображён график функции 
— одной из первообразных функции
, определённой на интервале 
. Найдите количество решений уравнения 
на отрезке 
.
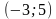
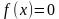
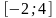
2. На рисунке изображён график некоторой функции 
. Пользуясь рисунком, вычислите 
, где 
— одна из первообразных функции .
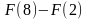
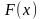
3. На рисунке изображён график функции . Функция 
— одна из первообразных функции . Найдите площадь закрашенной фигуры.
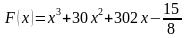
4. На рисунке изображён график некоторой функции . Функция 
— одна из первообразных функции . Найдите площадь закрашенной фигуры.
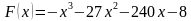
5. На рисунке изображён график функции , одной из первообразных некоторой функции , определённой на интервале 
Пользуясь рисунком, определите количество решений уравнения 
на отрезке 
6. На рисунке изображён график функции , одной из первообразных некоторой функции , определённой на интервале 
Пользуясь рисунком, определите количество решений уравнения на отрезке 
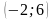
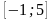
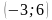
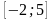
7. На рисунке изображён график функции , одной из первообразных некоторой функции , определённой на интервале 
Пользуясь рисунком, определите количество решений уравнения на отрезке 
8. На рисунке изображён график функции , одной из первообразных некоторой функции , определённой на интервале Пользуясь рисунком, определите количество решений уравнения на отрезке
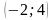
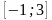
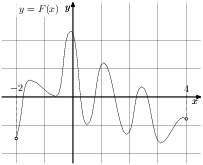
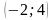
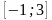
9. На рисунке изображён график функции , одной из первообразных некоторой функции , определённой на интервале Пользуясь рисунком, определите количество решений уравнения на отрезке
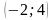
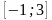
10. На рисунке изображён график функции , одной из первообразных некоторой функции , определённой на интервале 
Пользуясь рисунком, определите количество решений уравнения на отрезке 
11. На рисунке изображён график функции , одной из первообразных некоторой функции , определённой на интервале Пользуясь рисунком, определите количество решений уравнения на отрезке
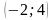
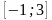
12. . На рисунке изображён график некоторой функции . Пользуясь рисунком, вычислите 
, где — одна из первообразных функции .
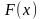
13. На рисунке изображён график некоторой функции . Пользуясь рисунком, вычислите 
, где — одна из первообразных функции .
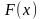
14. . На рисунке изображён график некоторой функции . Пользуясь рисунком, вычислите 
, где — одна из первообразных функции .
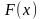
15. На рисунке изображён график функции . Функция — одна из первообразных функции . Найдите площадь закрашенной фигуры.
16. На рисунке изображён график функции .
Функция — одна из первообразных функции . Найдите площадь закрашенной фигуры.
17. На рисунке изображён график функции . Функция — одна из первообразных функции . Найдите площадь закрашенной фигуры.
18. На рисунке изображён график функции . Функция — одна из первообразных функции . Найдите площадь закрашенной фигуры.
19. На рисунке изображён график функции . Функция — одна из первообразных функции . Найдите площадь закрашенной фигуры.
20. На рисунке изображён график функции . Функция — одна из первообразных функции . Найдите площадь закрашенной фигуры.
21. На рисунке изображён график функции . Функция — одна из первообразных функции . Найдите площадь закрашенной фигуры.
22. На рисунке изображен график некоторой функции . Пользуясь рисунком, вычислите определенный интеграл 
23. На рисунке изображён график функции — одной из первообразных функции , определённой на интервале 
Найдите количество решений уравнения на отрезке 
.
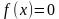
24. На рисунке изображён график функции — одной из первообразных функции , определённой на интервале 
. Найдите количество решений уравнения на отрезке 
.
Решу ЕГЭ 2022 математика, профильный уровень, задания, ответы
Ну что, давайте вместе решать ЕГЭ 2022 года по математике! А что бы выпускные экзамены удалось вам решить легко на 5 баллов, тогда нужно немного подготовиться к ним! Здесь можно бесплатно скачать демоверсии заданий и вопросов с ответами, которые будут на едином государственном экзамене в школе для учеников 11 класса. Все варианты для решения ЕГЭ были взяты с официального сайта ФИПИ. После домашнего изучения КИМ и тестовых вариантов, вы смело сможете сказать себе, что я РЕШУ ЕГЭ!
Официальный сайт. Единый Государственный Экзамен. Открытый банк заданий ЕГЭ-22. ФИПИ ШКОЛЕ. ФГОС. ОРКСЭ. МЦКО. Школа России. 21 век. ГДЗ. Решебник. Перспектива. Школа 2100. Планета знаний. Россия. Беларусь.
Скачать бесплатно новые задания, тесты, тренировочные варианты, ответы и решения Решу ЕГЭ-2022
Демонстрационный вариант реальных заданий контрольных измерительных материалов единого государственного экзамена 2022 года по Математике. Профильный уровень . Формат PDF
Скачать бесплатно
Кодификатор элементов содержания по Математике. База для составления контрольных измерительных материалов для проведения единого государственного экзамена
Скачать бесплатно
Кодификатор требований к уровню подготовки выпускников образовательных организаций для проведения единого государственного экзамена по математике
Скачать бесплатно
Спецификация контрольных измерительных материалов для проведения в 2022 году единого государственного экзамена по Математике Профиль.
Скачать бесплатно
Правильные ответы и решения заданий ЕГЭ-2022
Скачать бесплатно
С вопросами,мнением об экзаменах обращайтесь через форму для письма, рисунок конверта кликабелен.
И, пожалуйста, напишите об ошибке, если обнаружите таковую в моих решениях.
Узнайте, как можно поддержать сайт и помочь его развитию.
Внимание: в обсуждаемом варианте еще могут быть изменения.
Предлагаемый вариант профильного ЕГЭ по математике в следующем году заметно отличается от вариантов прошлых лет, как в части заданий с кратким ответом, так и в части заданий с развёрнутым ответом.
Основные отличия варианта 2022 от ЕГЭ 2021:
- Из варианта удалены первые три задания по темам: простейшие текстовые задачи, задания на анализ статистических графиков и диаграмм, задачи по геометрии на клетчатой бумаге.
- В первую часть добавлены задания на график функции, на решение обратных задач теории вероятностей, на комплексные числа. Последние два задания вызывают вопросы у педагогов и еще подлежат общественно-профессиональному обсуждению.
- Соответственно изменён порядок следования оставшихся заданий первой части. К некоторым заданиям добавлены иные образцы формулировок задачи, у некоторых число образцов уменьшено. При этом сохранилось правило – задания 1–7 имеют базовый уровень сложности.
- Задание на решение уравнений (13) представлено без второго пункта — выбор корней, принадлежащих заданному отрезку.
- Задание на решение неравенств (15) стало многоплановым. Оно состоит из трёх пунктов и включает независимое решение неравенства и уравнения, а затем решение системы, состоящей из тех же выражений.
- Прежние задания 16 (планиметрия) и 17 (экономическая задача) поменялись номерами, что больше соответствует структуре варианта
– задания 8–16 имеют повышенный уровень сложности; задания 17, 18 и 19 относятся к высокому уровню сложности.
Во второй части изменения менее явные.
На мой взгляд, экономическая задача, действительно, существенно проще, чем предлагаемые в этом разделе задачи по планиметрии.
Интерактивные страницы с Демо-версиями для экзамена 2022 будут обновляться осенью, когда окончательно утвердят контрольно-измерительные материалы ЕГЭ по математике. Здесь рассматриваются только предлагаемые новые задания и их решения.
Задания, которых не было в прошлом году
Задание 3.
Задача.
На рисунке изображён график функции вида (f(x)= ax^2 + bx + c,) где числа (a, b; и ;c) — целые. Найдите значение (f(-12)).
Решение.
Формула функции – квадратный трёхчлен, график функции – парабола. Требуется определить значение функции в точке, которая не видна на графике, поэтому нужно воспользоваться формулой. Для этого сначала нужно определить неизвестные коэффициенты квадратного трёхчлена.
Три неизвестных коэффициента можно найти путём решения системы трёх линейных уравнений. Чтобы составить такую систему уравнений, берём на графике три «удобные» точки и подставляем их координаты в формулу функции.
Точки «удобны», если их координаты хорошо считываются, например, находятся в узлах сетки, или мы о них что-то знаем из теории. Для параболы очень хорошими точками являются вершина и точка пересечения с осью ординат. К сожалению, последняя на заданном участке графика также не видна.
На рисунке показаны выбранные мною точки, которые задают следующие соотношения
[x_в=-4;Rightarrow;-frac{b}{2a} = -4; f(-3)=-2; Rightarrow;a(-3)^2 + b(-3) + c = -2; f(-2)=1;Rightarrow;a(-2)^2 + b(-2) + c = 1.]
Получили ситему уравнений [ begin{cases} -dfrac{b}{2a} = -4, 9a -3b + c = -2, 4a -2b + c = 1. end{cases}]
Решаем её [begin{cases} b = 8a,9a -24a + c = -2,4a -16a + c = 1; end{cases};
begin{cases} b = 8a,c = 15a-2,c = 12a+1; end{cases}; begin{cases} b = 8a, = 3a-3,c = 12a+1; end{cases};
begin{cases} b = 8,a = 1,c = 13. end{cases}]
Таким образом, уравнение функции имеет вид (f(x)= x^2 + 8x + 13), чтобы найти её значение в заданной точке, подставляем −12 в формулу [f(-12)= (-12)^2 + 8cdot(-12) +13 = 144-96+13 = 61.]
Замечание: Внимательные пользователи заметили, что полезность точки «Вершина параболы» в представленном решении использована не на все сто процентов. Постарайтесь вспомнить, что еще вы знаете о вершине параболы, и подумать о том, как сократить объём вычислений. Затем перейдите по ссылке, чтобы посмотреть второй вариант решения этой задачи.
Ответ:
Задание 7с.
Дополнительный образец формулировки задания на геометрический смысл производной.
Задача.
На рисунке изображён график (y = f'(x)) — производной функции (f(x)),
определённой на интервале (−9;12). В какой точке отрезка [−8;11] функция (f(x)) принимает наибольшее значение?
Решение.
Задачу лучше решать, делая отметки на чертеже.
Выделим на чертеже отрезок, на котором требуется найти искомое значение. Наибольшее значение непрерывной функции может быть достигнуто в одной из крайних точек отрезка, либо в одной из точек максимума функции внутри отрезка.
Крайние точки отрезка x = −8 и x = 11.
Внутренние точки отрезка, в которых функция имеет экстремальные значения, совпадают с точками, в которых её производная равна нулю. Эти точки также отмечаем на чертеже (здесь красными кружками).
Чтобы определиться, в каких точках экстремум является максимумом, нам нужно определить знак производной в окрестности каждой из этих точек. Знаки производной хорошо видны по её графику. Делаем соответствующие отметки на интервалах. Интервалу, где производная положительна соответствует интервал возрастания функции, интервалу, где производная отрицательна соответствует интервал убывания функции. Отмечаем свои наблюдения стрелочками. Обратите внимание, стрелочки относятся не к тому графику, который мы видим на чертеже, не к графику производной, а к графику исходной функции. Максимум функции может быть только в тех точках, левее которых функция возрастала, а правее стала убывать. Таким образом, кандидаты на ответ – точки максимума внутри отрезка: x = −7, x = 0, x = 7, x = 10.
Вернёмся к крайним точкам. Точка x = −8 находится на участке возрастания функции, поэтому во внутренних точках отрезка, расположенных правее её, значения функции будут больше. Точка x = 11 находится на участке убывания функции, и соответственно во внутренних точках отрезка, расположенных левее её, значения функции будут больше. Т.е. в крайних точках отрезка, наибольшего значения функция не достигает.
Итак, наибольшее значение функции может быть в одной из четырёх точек, но для однозначного ответа (ведь у нас I-я часть ЕГЭ) требуется выбрать одну из них. Для этого нужно вспомнить, что функция связана со своей производной через первообразную (неопределённый интеграл) (f(x) = int{f'(x)}dx + C), а она, в свою очередь, связана с площадью под кривой через определённый интеграл. Например, площадь под кривой на отрезке [2;7], отмеченную на рисунке светлозелёным цветом, можно вычислить по формуле (S = intlimits_2^7{f'(x)}dx = f(7) — f(2).)
Оценивая по клеточкам площади криволинейных трапеций между кривой и осью абсцисс на интервалах между точками экстремумов, мы можем прикинуть сколько единиц «теряет» функция на этом интервале, если участок отмечен знаком минус, и сколько «приобретает» там, где участок отмечен знаком «+».
Предположим, что наибольшее значение функции f(−7). Далее прибавляем и вычитаем примерные значения площадей, двигаясь к следующим точкам предполагаемого ответа слева направо. Как видно из рисунка, покрашенный участок имеет наибольшую площадь и соответственно добавит к значению функции больше, чем остальные, тем более, что часть из них с плюсом, другая с минусом, и они друг друга компенсируют. Таким образом, наибольшее значение функции будет достигнуто в точке x = 7.
Ответ:
Всё понятно? Остались ли у вас вопросы по этому заданию? А у меня остался вопрос к разработчикам из ФИПИ:
ПОЧЕМУ ЭТА ЗАДАЧА ОТНОСИТСЯ К БАЗОВОМУ УРОВНЮ СЛОЖНОСТИ?
Если я ошибаюсь, и есть решение проще представленного, напишите мне об этом на почту. (Жми конвертик!)
Задание 10.
Следующие задания, в которых требуется определить вероятность некого события при условии, что другое связанное с ним событие уже произошло, и мы об этом знаем, в теории вероятностей решаются с использованием теоремы Байеса (или формулы Байеса). Не уверена, что все школьники знают, а тем более понимают эту теорему, поэтому привожу альтернативные способы решения этих задач. Такие более «школьные» способы существуют для случаев, когда взаимосвязанных событий, упоминаемых в условии задачи немного.
Задача.
Симметричную игральную кость бросили три раза. Известно, что в сумме
выпало 6 очков. Какова вероятность события «хотя бы раз выпало три очка»?
Решение.
Постараемся решить, используя лишь классическое определение вероятности (P =dfrac{m}{n},) где (n -) общее число исходов, (m -) число исходов, благоприятствующих запрашиваемому событию.
Для этого рассмотрим, из каких трёх слагаемых может состоять число 6.
1) 6 = 1+2+3;
2) 6 = 2+2+2;
3) 6 = 4+1+1.
При трёхкратном бросании игральной кости вариант 1 может реализоваться 6-ю способами, т.к. очки могут выпадать в любом порядке: перестановки из 3-ёх элементов 3! = 6.
Вариант 2 может реализоваться только одним способом.
Вариант 3 реализуется 3-мя способами: 4 очка могут выпасть при первом, или при втором, или при третьем бросании.
Итого (n = 6+1+3 = 10.)
В первом варианте тройка присутствует по одному разу в каждом из 6-ти способов. Во втором и третьем вариантах тройки вообще нет.
Итого (m = 6.) [P =frac{m}{n} = frac{6}{10} = 0,6.]
Ответ: 0,6
Задача.
В городе 48% взрослого населения мужчины. Пенсионеры составляют 12,6% взрослого населения, причем доля пенсионеров среди женщин равна 15%. Для проведения исследования социологи случайным образом выбрали взрослого мужчину, проживающего в этом городе. Найдите вероятность события «выбранный мужчина является пенсионером».
Решение.
Эту задачу постараемся решить, используя лишь И/ИЛИ-правила (правила умножения/сложения вероятностей).
От долей населения в процентах перейдём к соответствующим вероятностям в десятичных дробях. (Это можно сделать, опираясь на такое доказа если в городе живёт N взрослых человек и 48% из них мужчины, то мужчин в городе живёт (dfrac{Ncdot48}{100},) тогда вероятность встретить взрослого мужчину составляет (dfrac{Ncdot48}{100cdot N} = dfrac{48}{100} = 0,48).)
Неизвестную вероятность события «выбранный мужчина является пенсионером» обозначим x. А находить будем вероятность другого, более общего события «выбранный взрослый житель города является пенсионером». Это событие можно записать так:
«Житель города является пенсионером, если он мужчина И при этом пенсионер ИЛИ она женщина И при этом пенсионер».
Учитывая независимость и несовместимость событий (один человек не может быть одновременно женщиной и мужчиной, быть и не быть персионером), к «И» применяем правило умножения вероятностей, к «ИЛИ» — правило сложения вероятностей. Получим формулу для вероятностей
P(П) = P(М)·P(МП) + P(Ж)·P(ЖП).
В этой формуле введены такие обозначения
- Событие П — «Житель города является пенсионером». Вероятность этого события P(П) = 0,126 находим в условии задачи (пенсионеры составляют 12,6% взрослого населения).
- Событие М — «Этот житель города является мужчиной». Вероятность этого события P(М) = 0,48 находим в условии задачи.
- Событие МП — «Выбранный мужчина является пенсионером». Вероятность этого события мы приняли за x
- Событие Ж — «Этот житель города является женщиной». Вероятность этого события P(Ж) = 1 − 0,48 = 0,52, так как оно противоположно событию «житель города мужчина».
- Событие ЖП — «Выбранная женщина является пенсионеркой». Вероятность этого события P(ЖП) = 0,15 находим в условии задачи (доля пенсионеров среди женщин равна 15%).
Получаем уравнение 0,126 = 0,48·x + 0,52·0,15,
из которого находим 0,48x = 0,126 − 0,52·0,15 = 0,048;
x = 0,048/0,48 = 0,1.
Ответ: 0,1.
Задание 11.
Задание по теме «Комплексные числа» вызывает больше всего вопросов у школьников и учителей, так как эта тема слабо представлена в действующих учебниках. Тем не менее, рассмотрим решение задачи из перспективного демонстрационного варианта.
Задача.
Про комплексное число (z) известно, что (|z — 4 — 7i| = | z + 4 — i|). Найдите наименьшее значение (|z|).
Решение.
Пусть (z = a+ib), тогда [|z| = sqrt{a^2+b^2}; z-4 — 7i = (a-4) +(b-7)i; ;; |z-4 — 7i| = sqrt{(a-4)^2 +(b-7)^2};
z+4 — i = (a+4) +(b-1)i; ;; |z+4 — i| = sqrt{(a+4)^2 +(b-1)^2};
|z — 4 — 7i| = | z + 4 — i| ;; Leftrightarrow ;; sqrt{(a-4)^2 +(b-7)^2} = sqrt{(a+4)^2 +(b-1)^2}.]
Из последнего равенства следует ((a-4)^2 +(b-7)^2 = (a+4)^2 +(b-1)^2.)
Преобразуем это уравнение, чтобы выразить одну из неизвестных переменных через другую
[(a-4)^2 — (a+4)^2 = (b-1)^2 — (b-7)^2 ; (a-4 -a-4)(a-4 +a+4) = (b-1-b+7)(b-1+b-7); -8cdot2a = 6cdot(2b-8);
a = -frac{3(b-4)}{4}.] Теперь можем записать (|z|) как функцию одной переменной [|z| = sqrt{a^2+b^2} = sqrt{left( -frac{3(b-4)}{4} right)^2+b^2} = sqrt{frac{9(b-4)^2 + 16b^2}{16}.} ]
Теперь видно, что наименьшее значение (|z|) будет достигнуто при таких значениях (b), при которых выражение (9(b-4)^2 + 16b^2) минимально. Ищем минимум этого выражения через производную.
[(9(b-4)^2 + 16b^2)’ = 9cdot2(b-4)+16cdot2b = 18b — 72 + 32b = 0; 50b = 72; ;; b = 1,44; |z| = sqrt{frac{9(b-4)^2 + 16b^2}{16} } = sqrt{frac{9(1,44-4)^2 + 16(1,44)^2}{16}} = 2,4.]
Ответ: 2,4
Моё мнение по этому заданию – требует существенных затрат времени на вычисление и проверку. Для I-ой части с учётом того, что нужно решить ещё 8 больших заданий, это может оказаться проблемой многих школьников. Если есть более простые подходы, напишите мне о них. (Жми на конвертик!)
Спасибо посетителям сайта, которые откликнулись и присылают мне свои варианты решения. Чтобы ознакомиться с вариантом геометрического решения этой задачи перейдите по ссылке.
Что касается первой части в целом, то, на мой взгляд, она стала сложнее, трудозатратнее, требует больше времени на выполнение. Действительно базовый уровень ушел.
Задание 15.
Примеры решения заданий второй части представлены непосредственно в демонстрационном варианте. Но для неравенств и их систем имеет большое значение прорисовка множеств на числовой оси, поэтому привожу здесь решение этого задания с рисунками. Другие типы неравенств можно найти здесь по ссылкам на этот номер.
Задача.
а) Решите неравенство [ log_{11}{(8x^2+7)} — log_{11}{(x^2+x+1)} ge log_{11}{left(frac{x}{x+5} + 7right)}.]
б) Решите уравнение [ sqrt{x^2+28x+196}+sqrt{x^2 +8x+16} =10.]
в) Решите систему [begin{cases} log_{11}{(8x^2+7)} — log_{11}{(x^2+x+1)} ge log_{11}{left(dfrac{x}{x+5} +7right)},sqrt{x^2+28x+196}+sqrt{x^2 +8x+16} =10.end{cases}]
Решение.
a) Решаем систему неравенств [begin{cases}8x^2+7>0; ;;(1)x^2+x+1>0; ;;(2)dfrac{x}{x+5}+7>0; ;;(3)
log_{11}{dfrac{8x^2+7}{x^2+x+1}} ge log_{11}{(dfrac{x}{x+5} +7)}, ;;(4)end{cases}]
где первые 3 неравенства следуют из ограниченности области определения логарифма, т.е. это ОДЗ выражения, а 4-е неравенство уже частично преобразованно с использованием свойства разности логарифмов с одинаковым основанием.
(1) (8x^2+7>0 ; Leftrightarrow ; x in (-infty;infty),) т.к. состоит из положительных слагаемых;
(2) (x^2+x+1>0; ; Leftrightarrow ; x in (-infty;infty),) т.к. дискриминант квадратного трёхчлена (D = 1^2-4cdot1cdot1 < 0) и ветви соответствующей параболы направлены вверх, т.е. у графика нет отрицательной части;
(3) Решаем методом интервалов [ frac{x}{x+5}+ ^{frac{x+5}}7>0; frac{8x+35}{x+5}>0;]
[ x in (-infty;-5)cup(-frac{35}{8};+infty).]
(4) Так как основание логарифма 11>1, то переходим от логарифмического наравенства к рациональному («отбраcываем логарифм») с сохранением знака неравенства [frac{8x^2+7}{x^2+x+1} ge frac{x}{x+5} +7].
Преобразуем и также решаем методом интервалов
[frac{8x^2+7}{x^2+x+1} — frac{x}{x+5}-7 ge 0; frac{(8x^2+7)(x+5) -x(x^2+x+1) -7(x^2+x+1)(x+5)}{(x^2+x+1)(x+5)} ge 0;
frac{-3x^2-36x}{(x^2+x+1)(x+5)} ge 0; frac{-3x(x+12)}{(x^2+x+1)(x+5)} ge 0;]
[ x in (-infty;-12]cup(-5;0].]
Чтобы завершить решение системы пересекаем все полученные множества. Фактически, это потребуется только для пунктов (3) и (4), потому что в (1) и (2) вся числовая ось.
Итак, ответ на задание пункта a) виден из рисунка
Ответ a) ( x in ( — infty ; — 12];left( — dfrac{35} {8};0 right]. ).
б) Квадратный корень имеет ограниченную область определения, поэтому иррациональное уравнение надо начинать решать с ОДЗ, т.е. с анализа подкоренных выражений. В данном случае замечаем, что оба квадратных трёхчлена образуют полные квадраты, поэтому область допустимых значений выражения (x in R).
Преобразуем уравнение [sqrt{x^2+28x+196}+sqrt{x^2 +8x+16} =10, sqrt{x^2+2cdot14cdot{x} + 14^2}+sqrt{x^2 +2cdot4cdot{x} + 4^2} =10, sqrt{(x+14)^2}+sqrt{(x+4)^2} =10, |x+14|+|x+4| =10.]
Уравнение свелось к сумме модулей по определению арифметического квадратного корня. Нужно определить знаки постоянства подмодульных выражений, чтобы упростить уравнение дальше.[|x+14|+|x+4| ; Leftrightarrow ;; left[ begin{array} {l}
-(x+14)-(x+4),text{ при } x le -14; (x+14)-(x+4),text{ при } -14 < x < -4; (x+14)+(x+4),text{ при } x ge -4. end{array} right.] Таким образом, наше уравнение будет равносильно совокупности
[ left[ begin{array} {l} -2x-18 = 10,text{ при } x le -14; 10 = 10,text{ при } -14 < x < -4; 2x+18 = 10,text{ при } x ge -4.end{array} right.] Корни первого и третьего уравнений (x= -14) и (x = -4) являются границами интервала, на котором уравнение выродилось в тождество. Таким образом, оно верно для всех точек отрезка [−14;−4].
Ответ б) ( x in [-14;-4]).
в) Чтобы решить систему, представленную в последнем пункте задания достаточно пересечь множества из предыдущих двух ответов.
Как видно из рисунка, решением этой системы будут промежутки [−14;−12] и (left( -dfrac{35}{8};-4 right].)
Ответ в) ( x in [-14;-12]cup left( — dfrac{35}{8};-4 right]).
Вывод по варианту в целом: изменения делают вариант более интересным и насыщенным, но распределение заданий не соответствует заявленному уровню сложности, а главное, все представленные новые задания времяёмкие.
Задание 1
Найдите корень уравнения $$9^{2x+5}=3,24cdot 5^{2x+5}$$
Ответ: -1,5
Задание 2
На экзамене по геометрии школьник отвечает на один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос по теме «Вписанная окружность», равна 0,25. Вероятность того, что это вопрос по теме «Площадь», равна 0,3. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
Ответ: 0,55
Задание 3
В тупоугольном треугольнике АВС известно, что АС=ВС, высота АН равна 3, $$CH=sqrt{7}$$. Найдите синус угла АСВ.
Ответ: 0,75
Задание 4
Найдите значение выражения $$frac{4cos 121^{circ}}{cos 59^{circ}}$$
Ответ: -4
Задание 5
Цилиндр вписан в правильную шестиугольную призму. Радиус основания цилиндра равен $$sqrt{3}$$, а высота равна 2. Найдите площадь боковой поверхности призмы.
Ответ: 24
Задание 6
На рисунке изображён график y=f(x). На оси абсцисс отмечены точки -2, -1, 1, 4. В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.
Ответ: 4
Задание 7
При температуре 0°C рельс имеет длину l=15 м. При возрастании температуры происходит тепловое расширение рельса, и его длина, выраженная в метрах, меняется по закону $$l(t_{0})=l_{0}(1+alphacdot t^{circ})$$, где $$alpha=1,2cdot 10^{-5}$$(оС)-1 — коэффициент теплового расширения, t° — температура (в градусах Цельсия). При какой температуре рельс удлинится на 7,2 мм? Ответ дайте в градусах Цельсия.
Ответ: 40
Задание 8
Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 135 км. На следующий день он отправился обратно со скоростью на 9 км/ч больше прежней. По дороге он сделал остановку на 4 часа. В результате он затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из А в В. Ответ дайте в км/ч.
Ответ: 13,5
Задание 9
На рисунке изображён график функции $$f(x)=ax^{2}+bx+c$$. Найдите $$f(-9)$$.
Ответ: -23
Задание 10
Две фабрики выпускают одинаковые стёкла для автомобильных фар. Первая фабрика выпускает 25% этих стёкол, вторая — 75%. Первая фабрика выпускает 5 % бракованных стёкол, а вторая — 1 %. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.
Ответ: 0,02
Задание 11
Найдите точку минимума функции $$y=frac{4}{3}xsqrt{x}-5x+4$$
Ответ: 6,25
Задание 12
а) Решите уравнение $$2cos^{3}(x-pi)=sin (frac{3pi}{2}+x)$$
б) Найдите все корни этого уравнения, принадлежащие отрезку $$[frac{9pi}{2};frac{11pi}{2}]$$
Ответ: а)$$frac{pi}{2}+pi k;frac{pi}{4}+frac{pi n}{2}$$ б)$$frac{9pi}{2};frac{19pi}{4};frac{21pi}{4};frac{11pi}{2}$$
Задание 13
В правильной четырёхугольной пирамиде SABCD сторона основания AD равна 10, высота SH равна 12. Точка К — середина бокового ребра SD. Плоскость АКB пересекает боковое ребро SC в точке Р.
а) Докажите, что площадь четырёхугольника CDKP составляет $$frac{3}{4}$$ треугольника SCD.
б) Найдите объём пирамиды ACDKP.
Ответ: 150
Задание 14
Решите неравенство $$(25^{x}-4cdot 5^{x})+8cdot 5^{x}<2cdot 25^{x}+15$$
Ответ: $$(-infty;0);(log_{5}3;1)$$
Задание 15
В июле 2023 года планируется взять кредит на 10 лет на некоторую сумму. Условия возврата таковы:
— каждый январь с 2024 по 2028 год долг возрастает на 18 % по сравнению с концом предыдущего года;
— каждый январь с 2029 по 2033 год долг возрастает на 16 % по сравнению с концом предыдущего года;
— с февраля по июнь необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года;
— к июлю 2033 года кредит должен быть полностью погашен.
Найдите сумму, которую планируется взять в кредит, если общая сумма выплат по кредиту должна составить 1470 тыс. рублей.
Ответ: 750 тыс. руб.
Задание 16
Точки А, В, С, D и Е лежат на окружности в указанном порядке, причём ВС=CD=DE, а AC $$perp$$ BE. Точка К — пересечение прямых BE и AD.
а) Докажите, что прямая СЕ делит отрезок KD пополам.
б) Найдите площадь треугольника АВК, если AD=4, $$DC=sqrt{3}$$ .
Ответ: $$frac{25sqrt{39}}{64}$$
Задание 17
Найдите все значения а, при каждом из которых уравнение $$|x^{2}-a^{2}|=|x+a|sqrt{x^{2}-5ax+4a}$$ имеет ровно два различных корня
Ответ: $$a<-2;-2<a<-frac{2}{3};a>0$$
Задание 18
На доске написаны три различных натуральных числа. Второе число равно сумме цифр первого, а третье равно сумме цифр второго.
а) Может ли сумма этих чисел быть равна 3456?
б) Может ли сумма этих чисел быть равна 2345?
в) В тройке чисел первое число трёхзначное, а третье равно 5. Сколько существует таких троек?
Ответ: а) да б) нет в) 85