Есть ли переменный ток в егэ по физике - Помощь в подготовке к экзаменам и поступлению

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Задания Д9 B15 № 1629

Если, при подключении неизвестного элемента электрической цепи к выходу генератора переменного тока с изменяемой частотой гармонических колебаний при неизменной амплитуде колебаний напряжения, обнаружена зависимость амплитуды колебаний силы тока от частоты, представленная на рисунке, то этот элемент электрической цепи является

1)  активным сопротивлением

2)  конденсатором

3)  катушкой

4)  последовательно соединенными конденсатором и катушкой

Задания Д9 B15 № 1630

обнаружена зависимость амплитуды колебаний силы тока от частоты, представленная на рисунке, то этот элемент электрической цепи является

1)  активным сопротивлением

2)  конденсатором

3)  катушкой

4)  последовательно соединенными конденсатором и катушкой

Задания Д9 B15 № 1631

1)  активным сопротивлением

2)  конденсатором

3)  катушкой

4)  последовательно соединенными конденсатором и катушкой

Задания Д9 B15 № 1632

1)  активным сопротивлением

2)  конденсатором

3)  катушкой

4)  последовательно соединенными конденсатором и катушкой

Задания Д9 B15 № 1633

Как изменится индуктивное сопротивление катушки при уменьшении частоты переменного тока в 4 раза?

1)  не изменится

2)  увеличится в 4 раза

3)  уменьшится в 2 раза

4)  уменьшится в 4 раза

Пройти тестирование по этим заданиям

Источник

15. Магнитное поле. Оптика

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Переменный ток

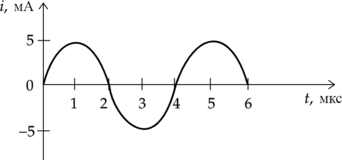
На рисунке приведён график зависимости силы тока от времени в колебательном контуре, состоящем из последовательно соединённых конденсатора и катушки, индуктивность которой равна 0,2 Гн. Каково максимальное значение энергии магнитного поля катушки? (Ответ дать в мкДж.)

Энергия магнитного поля: [W=frac{LI^2}{2},] где (L) – индуктивность катушки, (I) – сила тока на катушке.
Максимальная сила тока: [I_{max}=5 text{ мА}]
Подставим в формулу энергии магнитного поля: [W=frac{0,2text{ Гн}cdot5^2cdot10^{-6}text{ А$^2$}}{2}=2,5 text{ мкДж}]

Ответ: 2,5

К конденсатору, заряд которого 250 пКл, подключили катушку индуктивности. Определите максимальную силу тока (в мА), протекающего через катушку, если циклическая частота свободных колебаний в контуре (8cdot10^7) рад/с.

Период колебаний электромагнитного контура вычисляется по формуле Томсона: [T=2pisqrt{LC},] где (L) – индуктивность катушки, (C) – ёмкость конденсатора.
Циклическая частота: [omega=frac{1}{sqrt{LC}} Rightarrow LC=frac{1}{omega^2}]
Закон сохранения для колебательного контура [W_{L}=W_C] [frac{LI_{max}^2}{2}=frac{CU_{max}^2}{2}=frac{q_{max}^2}{2C},] где (L) – индуктивность катушки, (I-{max}) – максимальная сила тока на катушке, (C) – ёмкость конденсатора, (U_{max}) – максимальное напряжение, (q_{max}) – максимальный заряд на конденсаторе.
Тогда максимальная сила тока равна [I_{max}=sqrt{frac{q_{max}^2}{LC}}=q_{max}omega=250cdot10^{-12}text{ Кл}cdot8cdot10^7text{ рад/с}=20 text{ мА}]

Ответ: 20

Заряженный конденсатор емкостью 4 мкФ подключили к катушке с индуктивностью 90 мГн. Через какое минимальное время (в мкс) от момента подключения заряд конденсатора уменьшится в 2 раза?

Период колебаний электромагнитного контура вычисляется по формуле Томсона: [T=2pisqrt{LC},] где (L) – индуктивность катушки, (C) – ёмкость конденсатора. Циклическая частота: [omega=frac{1}{sqrt{LC}}] Так как конденсатор изначально заряжен, то колебания можно описывать законом: [q=q_{max}cos(omega t)] [q=0,5q_{max}] Заменим циклическую частоту на (frac{1}{sqrt{LC}}) и получим [0,5q_{max}=q_{max}cosleft(frac{1}{sqrt{LC}} tright) Rightarrow frac{1}{sqrt{LC}} t=frac{pi}{3}] [t=frac{pi sqrt{LC}}{3}=628 text{мкс}]

Ответ: 628

Напряжение на концах участка цепи, по которому течет переменный ток, изменяется со временем по закону: (displaystyle U = U_0sinleft(omega t + frac{2pi}{3}right)). В момент времени (t = T/12) мгновенное значение напряжения равно 9 В. Определите амплитуду напряжения.

Зависимость напряжения: [U = U_0sinleft(omega t + frac{2pi}{3}right),] (omega) – циклическая частота. [U=U_0sinleft(frac{2pi}{T}cdotfrac{T}{12}+frac{2pi}{3}right)] [U=frac{U_0}{2}] [U_0=2U=18 text{ В}]

Ответ: 18

Напряжение, при котором зажигается или гаснет неоновая лампа, включенная в сеть переменного тока, соответствует действующему значению напряжения этой сети. В течение каждого полупериода лампа горит 2/3 мс. Найдите частоту переменного тока.

Зависимость напряжения: [U = U_0sin(omega t),] (omega) – циклическая частота. Действующее напряжение: [U_{text{д}}=frac{U_0}{sqrt{2}}] [U_{text{д}} < U_0sin(omega t)] [frac{U_0}{sqrt{2}} < U_0sin(omega t )] [sin(omega t)>frac{sqrt{2}}{2}] [sin(frac{2pi}{T} t)>frac{sqrt{2}}{2}] Решая это тригонометрическое неравенство на одном периоде синусоиды получаем, что [frac{pi}{4}<frac{2pi}{T} t<frac{3pi}{4}] [frac{1}{8}<frac{1}{T} t<frac{3}{8}] [t=frac{T}{4}] [T=4t] [nu=frac{1}{4t}=frac{3}{2cdot4cdot10^{-3}}=375 text{ Гц}]

Ответ: 375 Гц

Сила тока в первичной обмотке трансформатора 2 А, напряжение на ее концах 220 В. Напряжение на концах вторичной обмотки 40 В. Определите силу тока во вторичной обмотке. Потерями в трансформаторе пренебречь.

Для идеального трансформатора можно записать ((P_1=P_2)): [I_1U_1=I_2U_2] где (I_1) и (I_2) – силы тока на первичной и вторичной обмотках, (U_1) и (U_2) – напряжения на первичной и вторичной обмотках, тогда сила тока на вторичной обмотке равна [I_2=frac{I_1U_1}{U_2}=frac{2text{ А}cdot220text{ В}}{40text{ В}}=11 text{ А}]

Ответ: 11

Под каким напряжением находится первичная обмотка трансформатора, имеющая 1000 витков, если во вторичной обмотке 3500 витков и напряжение на ней 105 В?

Для трансформатора справедливо: [frac{U_2}{U_1}=frac{N_2}{N_1},] где (U_2) и (U_1) – напряжения на вторичной и первичной обмотках, (N_2) и (N_1) – количество витков на вторичной и первичной обмотках, тогда напряжение на первичной обмотке [U_1=frac{U_2N_1}{N_2}=frac{105text{ В}cdot1000}{3500}=30 text{ В}]

Ответ: 30

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Источник

Темы кодификатора ЕГЭ: переменный ток, вынужденные электромагнитные колебания.
Условие квазистационарности
Резистор в цепи переменного тока
Конденсатор в цепи переменного тока
Катушка в цепи переменного тока

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: переменный ток, вынужденные электромагнитные колебания.

Переменный ток — это вынужденные электромагнитные колебания, вызываемые в электрической цепи источником переменного (чаще всего синусоидального) напряжения.

Переменный ток присутствует всюду. Он течёт по проводам наших квартир, в промышленных электросетях, в высоковольтных линиях электропередач. И если вам нужен постоянный ток, чтобы зарядить аккумулятор телефона или ноутбука, вы используете специальный адаптер, выпрямляющий переменный ток из розетки.

Почему переменный ток распространён так широко? Оказывается, он прост в получении и идеально приспособлен для передачи электроэнергии на большие расстояния. Подробнее об этом мы поговорим в листке, посвящённом производству, передаче и потреблению электрической энергии.

А сейчас мы рассмотрим простейшие цепи переменного тока. Будем подключать к источнику переменного напряжения поочерёдно: резистор сопротивлением , конденсатор ёмкости и катушку индуктивности . Изучив поведение этих элементов, мы в следующем листке «Переменный ток. 2» подключим их одновременно и исследуем прохождение переменного тока через колебательный контур, обладающий сопротивлением.

Напряжение на клеммах источника меняется по закону:

(1)

Как видим, напряжение может быть положительным и отрицательным. Каков смысл знака напряжения?

Всегда подразумевается, что выбрано положительное направление обхода контура. Напряжение считается положительным, если электрическое поле зарядов, образующих ток, имеет положительное направление. В противном случае напряжение считается отрицательным.

Начальная фаза напряжения не играет никакой роли, поскольку мы рассматриваем процессы, установившиеся во времени. При желании вместо синуса в выражении (1) можно было бы взять косинус — принципиально от этого ничего не изменится.

Текущее значение напряжения U(t) в момент времени называется мгновенным значением напряжения.

к оглавлению ▴

Условие квазистационарности

В случае переменного тока возникает один тонкий момент. Предположим, что цепь состоит из нескольких последовательно соединённых элементов.

Если напряжение источника меняется по синусоидальному закону, то сила тока не успевает мгновенно принимать одно и то же значение во всей цепи — на передачу взаимодействий между заряженными частицами вдоль цепи требуется некоторое время.

Между тем, как и в случае постоянного тока, нам хотелось бы считать силу тока одинаковой во всех элементах цепи. К счастью, во многих практически важных случаях мы действительно имеем на это право.

Возьмём, к примеру, переменное напряжение частоты nu = 50 Гц (это промышленный стандарт России и многих других стран). Период колебаний напряжения: с.

Взаимодействие между зарядами передаётся со скоростью света: м/с. За время, равное периоду колебаний, это взаимодействие распространится на расстояние:

м = 6000 км.

Поэтому в тех случаях, когда длина цепи на несколько порядков меньше данного расстояния, мы можем пренебречь временем распространения взаимодействия и считать, что сила тока мгновенно принимает одно и то же значение во всей цепи.

Теперь рассмотрим общий случай, когда напряжение колеблется с циклической частотой omega . Период колебаний равен , и за это время взаимодействие между зарядами передаётся на расстояние . Пусть — длина цепи. Мы можем пренебречь временем распространения взаимодействия, если много меньше :

(2)

Неравенство (2) называется условием квазистационарности. При выполнении этого условия можно считать, что сила тока в цепи мгновенно принимает одно и то же значение во всей цепи. Такой ток называется квазистационарным.

В дальнейшем мы подразумеваем, что переменный ток меняется достаточно медленно и его можно считать квазистационарным. Поэтому сила тока во всех последовательно включённых элементах цепи будет принимать одинаковое значение — своё в каждый момент времени. Оно называется мгновенным значением силы тока.

к оглавлению ▴

Резистор в цепи переменного тока

Простейшая цепь переменного тока получится, если к источнику переменного напряжения подключить обычный резистор (мы полагаем, разумеется, что индуктивность этого резистора пренебрежимо мала, так что эффект самоиндукции можно не принимать во внимание) , называемый также активным сопротивлением (рис. 1)

Рис. 1. Резистор в цепи переменного тока

Положительное направление обхода цепи выбираем против часовой стрелки, как показано на рисунке. Напомним, что сила тока считается положительной, если ток течёт в положительном направлении; в противном случае сила тока отрицательна.

Оказывается, мгновенные значения силы тока и напряжения связаны формулой, аналогичной закону Ома для постоянного тока:

$I = frac{displaystyle U}{displaystyle R vphantom{1^a}} = frac{displaystyle U_0}{displaystyle R vphantom{1^a}} sin omega t.$

Таким образом, сила тока в резисторе также меняется по закону синуса:

Амплитуда тока I_0 равна отношению амплитуды напряжения U_0 к сопротивлению :

$I_0 = frac{displaystyle U_0}{displaystyle R vphantom{1^a}}.$

Мы видим, что сила тока через резистор и напряжение на нём меняются «синхронно», точнее говоря — синфазно (рис. 2).

Рис. 2. Ток через резистор совпадает по фазе с напряжением

Фаза тока равна фазе напряжения, то есть сдвиг фаз между током и напряжением равен нулю.

к оглавлению ▴

Конденсатор в цепи переменного тока

Постоянный ток через конденсатор не течёт — для постоянного тока конденсатор является разрывом цепи. Однако переменному току конденсатор не помеха! Протекание переменного тока через конденсатор обеспечивается периодическим изменением заряда на его пластинах.

Рассмотрим конденсатор ёмкости , подключённый к источнику синусоидального напряжения (рис. 3). Активное сопротивление проводов, как всегда, считаем равным нулю. Положительное направление обхода цепи снова выбираем против часовой стрелки.

Рис. 3. Конденсатор в цепи переменного тока

Как и ранее, обозначим через заряд той пластины конденсатора, на которую течёт положительный ток — в данном случае это будет правая пластина. Тогда знак величины совпадает со знаком напряжения . Кроме того, как мы помним из предыдущего листка, при таком согласовании знака заряда и направления тока будет выполнено равенство .

Напряжение на конденсаторе равно напряжению источника:

$frac{displaystyle q}{displaystyle C vphantom{1^a}} = U = U_0 sin omega t.$

Отсюда

Дифференцируя это равенство по времени, находим силу тока через конденсатор:

$I = dot{q} = CU_0 omega cos omega t.$ (3)

Графики тока и напряжения представлены на рис. 4. Мы видим, что сила тока каждый раз достигает максимума на четверть периода раньше, чем напряжение. Это означает, что фаза силы тока на pi/2 больше фазы напряжения (ток опережает по фазе напряжение на pi/2 ).

Рис. 4. Ток через конденсатор опережает по фазе напряжение на pi/2

Найти сдвиг фаз между током и напряжением можно также с помощью формулы приведения:

$cos varphi = sin left ( varphi + frac{displaystyle pi}{displaystyle 2 vphantom{1^a}} right ).$

Используя её, получим из (3):

$I = CU_0 omegasin left ( omega t + frac{displaystyle pi}{displaystyle 2 vphantom{1^a}} right ).$

И теперь мы чётко видим, что фаза тока больше фазы напряжения на pi/2 .

Для амплитуды силы тока имеем:

$I_0 = CU_0 omega = frac{displaystyle U_0}{displaystyle 1/left ( omega C right ) vphantom{1^a}}.$

Таким образом, амплитуда силы тока связана с амплитудой напряжения соотношением, аналогичным закону Ома:

$I_0 = frac{displaystyle U_0}{displaystyle X_C vphantom{1^a}},$

где

$X_C = frac{displaystyle 1}{displaystyle omega C vphantom{1^a}}.$

Величина X_C называется ёмкостным сопротивлением конденсатора. Чем больше ёмкостное сопротивление конденсатора, тем меньше амплитуда тока, протекающего через него, и наоборот.

Ёмкостное сопротивление обратно пропорционально циклической частоте колебаний напряжения (тока) и ёмкости конденсатора. Попробуем понять физическую причину такой зависимости.

1. Чем больше частота колебаний (при фиксированной ёмкости ), тем за меньшее время по цепи проходит заряд CU_0 ; тем больше амплитуда силы тока и тем меньше ёмкостное сопротивление. При ёмкостное сопротивление стремится к нулю: . Это означает, что для тока высокой частоты конденсатор фактически является коротким замыканием цепи.

Наоборот, при уменьшении частоты ёмкостное сопротивление увеличивается, и при имеем . Это неудивительно: случай отвечает постоянному току, а конденсатор для постоянного тока представляет собой бесконечное сопротивление (разрыв цепи).

2. Чем больше ёмкость конденсатора (при фиксированной частоте), тем больший заряд CU_0 проходит по цепи за то же время (за ту же четверть периода); тем больше амплитуда силы тока и тем меньше ёмкостное сопротивление.

Подчеркнём, что, в отличие от ситуации с резистором, мгновенные значения тока и напряжения в одни и те же моменты времени уже не будут удовлетворять соотношению, аналогичному закону Ома. Причина заключается в сдвиге фаз: напряжение меняется по закону синуса, а сила тока — по закону косинуса; эти функции не пропорциональны друг другу. Законом Ома связаны лишь амплитудные значения тока и напряжения.

к оглавлению ▴

Катушка в цепи переменного тока

Теперь подключим к нашему источнику переменного напряжения катушку индуктивности (рис. 5). Активное сопротивление катушки считается равным нулю.

Рис. 5. Катушка в цепи переменного тока

Казалось бы, при нулевом активном (или, как ещё говорят, омическом) сопротивлении через катушку должен потечь бесконечный ток. Однако катушка оказывает переменному току сопротивление иного рода.
Магнитное поле тока, меняющееся во времени, порождает в катушке вихревое электрическое поле $vec{E_B}$ , которое, оказывается, в точности уравновешивает кулоновское поле vec{E} движущихся зарядов:

$vec{E} + vec{E_B} = vec{0}.$ (4)

Работа кулоновского поля vec{E} по перемещению единичного положительного заряда по внешней цепи в положительном направлении — это как раз напряжение . Аналогичная работа вихревого поля — это ЭДС индукции .

Поэтому из (4) получаем:

(5)

Равенство (5) можно объяснить и с энергетической точки зрения. Допустим, что оно не выполняется. Тогда при перемещении заряда по цепи совершается ненулевая работа, которая должна превращаться в тепло. Но тепловая мощность I^2R равна нулю при нулевом омическом сопротивлении цепи. Возникшее противоречие показывает, что равенство (5) обязано выполняться.

Вспоминая закон Фарадея $mathcal E_i = -L dot{I}$ , переписываем соотношение (5):

откуда

$dot{I} = frac{displaystyle U}{displaystyle L vphantom{1^a}} = frac{displaystyle U_0}{displaystyle L vphantom{1^a}} sin omega t.$ (6)

Остаётся выяснить, какую функцию, меняющуюся по гармоническому закону, надо продифференцировать, чтобы получить правую часть выражения (6). Сообразить это нетрудно (продифференцируйте и проверьте!):

$I = -frac{displaystyle U_0}{displaystyle omega L vphantom{1^a}} cos omega t.$ (7)

Мы получили выражение для силы тока через катушку. Графики тока и напряжения представлены на рис. 6.

Рис. 6. Ток через катушку отстаёт по фазе от напряжения на pi/2

Как видим, сила тока достигает каждого своего максимума на четверть периода позже, чем напряжение. Это означает, что сила тока отстаёт по фазе от напряжения на pi/2 .

Определить сдвиг фаз можно и с помощью формулы приведения:

$sin left ( varphi -frac{displaystyle pi}{displaystyle 2 vphantom{1^a}} right ) = -cos varphi.$

Получаем:

$I = frac{displaystyle U_0}{displaystyle omega L vphantom{1^a}} sin left ( omega t -frac{displaystyle pi}{displaystyle 2 vphantom{1^a}} right ).$

Непосредственно видим, что фаза силы тока меньше фазы напряжения на pi/2 .

Амплитуда силы тока через катушку равна:

$I_0 = frac{displaystyle U_0}{displaystyle omega L vphantom{1^a}}.$

Это можно записать в виде, аналогичном закону Ома:

$I_0 = frac{displaystyle U_0}{displaystyle X_L vphantom{1^a}},$

где

Величина X_L называется индуктивным сопротивлением катушки. Это и есть то самое сопротивление, которое наша катушка оказывает переменному току (при нулевом омическом сопротивлении).

Индуктивное сопротивление катушки пропорционально её индуктивности и частоте колебаний. Обсудим физический смысл этой зависимости.

1. Чем больше индуктивность катушки, тем большая в ней возникает ЭДС индукции, противодействующая нарастанию тока; тем меньшего амплитудного значения достигнет сила тока. Это и означает, что X_L будет больше.

2. Чем больше частота, тем быстрее меняется ток, тем больше скорость изменения магнитного поля в катушке, и тем большая возникает в ней ЭДС индукции, препятствующая возрастанию тока. При имеем , т. е. высокочастотный ток практически не проходит через катушку.

Наоборот, при имеем X_L = 0 . Для постоянного тока катушка является коротким замыканием цепи.

И снова мы видим, что закону Ома подчиняются лишь амплитудные, но не мгновенные значения тока и напряжения. Причина та же — наличие сдвига фаз.

Резистор, конденсатор и катушка, рассмотренные пока что по отдельности, теперь соберутся вместе в колебательный контур, подключённый к источнику переменного напряжения. Читайте следующий листок — «Переменный ток. 2».

Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Переменный ток. 1» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена:
09.03.2023

Источник

Тема 14.

Оптика. Электромагнитные колебания и волны

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.

Готовиться с нами — ЛЕГКО!

Подтемы раздела

оптика. электромагнитные колебания и волны

14.01Колебательный контур

14.02Переменный ток

14.03Геометрическая оптика (Законы отражения и преломления)

14.04Геометрическая оптика (Линзы)

14.05Волновая оптика

Решаем задачи

Первичная обмотка силового трансформатора для накала радиолампы имеет 2200 витков и включена в сеть с напряжением 220 В.
Какое количество витков должна иметь вторичная обмотка, если ее активное сопротивление 0,5 Ом, а напряжение накала лампы 3,5
В при силе тока накала 1 А?

Показать ответ и решение

Для трансформатора справедливо:

U2 N2
U1 = N1-

где и – напряжения на вторичной и первичной обмотках, и – количество витков на вторичной и первичной
обмотках Напряжение на вторичной обмотке:

где Uтр – напряжение на активном сопротивлении второго обмотка, – напряжение на лампе

Напряжение на второй обмотке

Количество витков на второй обмотке

U2N1 4 В ⋅2200
N2 = -U1--= -220-В--= 40

Сила тока в первичной обмотке трансформатора 0,5 А, напряжение на ее концах 220 В. Сила тока во вторичной обмотке 11 А,
напряжение на ее концах 9,5 В. Определите КПД (в процентах) трансформатора.

Показать ответ и решение

КПД трансформатора:

P2 U2I2
η = P1 = U1I1,

где и – напряжение на вторичной и первичных обмотках, и – силы тока на первичной и вторичной обмотках,
и – напряжения на первичной и вторичной обмотках, тогда КПД равно

η = 9,5 В-⋅11 А-=95%
220 В⋅0,5 А

Под каким напряжением находится первичная обмотка трансформатора, имеющая 1000 витков, если во вторичной обмотке 3500
витков и напряжение на ней 105 В?

Показать ответ и решение

Для трансформатора справедливо:

U2 N2
U1 = N1,

где и – напряжения на вторичной и первичной обмотках, и – количество витков на вторичной и первичной
обмотках, тогда напряжение на первичной обмотке

Сила тока в первичной обмотке трансформатора 2 А, напряжение на ее концах 220 В. Напряжение на концах вторичной обмотки 40
В. Определите силу тока во вторичной обмотке. Потерями в трансформаторе пренебречь.

Показать ответ и решение

Для идеального трансформатора можно записать ( P1 = P2 ):

где и – силы тока на первичной и вторичной обмотках, и – напряжения на первичной и вторичной обмотках,
тогда сила тока на вторичной обмотке равна

I1U1 2 А ⋅220 В
I2 =-U2- = --40-В---= 11 А

Напряжение, при котором зажигается или гаснет неоновая лампа, включенная в сеть переменного тока, соответствует действующему
значению напряжения этой сети. В течение каждого полупериода лампа горит 2/3 мс. Найдите частоту переменного
тока.

Показать ответ и решение

Зависимость напряжения:

– циклическая частота. Действующее напряжение:

U0
Uд = √2-

U√0-< U0sin(ωt)
2

√2
sin(ωt) > 2--

√ -
sin(2πt)> --2
T 2

Решая это тригонометрическое неравенство на одном периоде синусоиды получаем, что

π- 2π 3π-
4 < T t< 4

1 1 3
8 < Tt < 8

T
t= 4-

T = 4t

ν = 1-= ---3--−3 =375 Гц
4t 2⋅4⋅10

Показать ответ и решение

Зависимость напряжения:

( 2π)
U =U0sin ωt+ 3- ,

где – амплитуда колебаний, – циклическая частота.
Циклическая частота находится по формуле:

ω = 2π .
T

Подставим и :

(2π T 2π) (5π)
U = U0sin T- ⋅12 +-3 = U0sin -6

Тогда

U = U0
2

Источник

Трансформатор

В статье собраны задачи из задачника Никуловой и Москалева по теме «трансформатор». Теоретические сведения позволят ответить на все предлагаемые вопросы, ознакомьтесь со статьей внимательно.
Задача 1.
Почему сердечники в трансформаторе делают
А)из ферромагнитной стали;
Б) не сплошными, а из тонких изолированных пластин?
1) для усиления магнитного поля и…

Рамки в магнитном поле

В этой статье вы найдете и несложные, и среднего уровня задачи. В основном задачи связаны с рамками в поле, однако вторая — на тему «переменный ток» и связана с определением полного комплексного сопротивления цепи и его модуля. Для школьников она довольно сложна.
Задача 1.
Рамка…

28.11.2017 09:20:02 | Автор: Анна

Переменный ток

«Стартовые» задачи по теме «переменный ток». Познакомимся с понятиями индуктивного и емкостного сопротивлений, полного сопротивления, узнаем, что такое амплитудное и действующее значение тока и напряжения.
Задача 1.
В цепь переменного тока последовательно включены конденсатор, резистор и катушка индуктивности. Как соотносятся по фазе колебания напряжения на…

16.11.2017 19:26:45 | Автор: Анна

Колебания в резонансном контуре

Электромагнитные колебания в контуре — одна из сложных тем ЕГЭ. Энергия переходит из одной формы в другую и концентрируется то в конденсаторе, то в катушке. Период колебаний энергии — вдвое меньше, чем период колебаний в контуре (энергия колеблется с двойной частотой).
Задача 1.
Колебательный контур…

12.11.2017 12:46:53 | Автор: Анна

Источник

Инфоурок

›

Физика

›Презентации›Презентация к уроку по теме «Переменный ток. Подготовка к ЕГЭ»

Презентация к уроку по теме «Переменный ток. Подготовка к ЕГЭ»

Скачать материал

Сейчас обучается 34 человека из 20 регионов

Сейчас обучается 97 человек из 42 регионов

Описание презентации по отдельным слайдам:

1 слайд

Переменный ток
Обобщение по теме, варианты ЕГЭ
21 слайд

Успехов на экзамене!

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 153 771 материал в базе

Выберите категорию:
Выберите учебник и тему

Выберите класс:
Тип материала:
- Все материалы
- Статьи
- Научные работы
- Видеоуроки
- Презентации
- Конспекты
- Тесты
- Рабочие программы
- Другие методич. материалы

Найти материалы

Материал подходит для УМК

«Физика (базовый уровень)», Мякишев Г.Я., Буховцев Б.Б., Чаругин В.М. / Под ред. Парфентьевой Н.А.

Тема

§ 31. Переменный электрический ток

Больше материалов по этой теме

Другие материалы

Рейтинг:
5 из 5

17.08.2021
196
15

Рейтинг:
5 из 5

17.08.2021
2758
60

Вам будут интересны эти курсы:

Курс повышения квалификации «Информационные технологии в деятельности учителя физики»
Курс повышения квалификации «Разработка бизнес-плана и анализ инвестиционных проектов»
Курс повышения квалификации «Использование активных методов обучения в вузе в условиях реализации ФГОС»
Курс повышения квалификации «ЕГЭ по физике: методика решения задач»
Курс повышения квалификации «Методы и инструменты современного моделирования»
Курс профессиональной переподготовки «Организация деятельности помощника-референта руководителя со знанием иностранных языков»
Курс профессиональной переподготовки «Организация технической поддержки клиентов при установке и эксплуатации информационно-коммуникационных систем»
Курс повышения квалификации «Мировая экономика и международные экономические отношения»
Курс профессиональной переподготовки «Организация деятельности специалиста оценщика-эксперта по оценке имущества»
Курс повышения квалификации «Финансовые инструменты»
Курс профессиональной переподготовки «Организация процесса страхования (перестрахования)»
Курс профессиональной переподготовки «Организация и управление процессом по предоставлению услуг по кредитному брокериджу»

Настоящий материал опубликован пользователем Лиходеев Сергей Николаевич. Инфоурок является
информационным посредником и предоставляет пользователям возможность размещать на сайте
методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них
сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с
сайта, Вы можете оставить жалобу на материал.

Удалить материал
- На сайте: 4 года и 3 месяца
- Подписчики: 0
- Всего просмотров: 111152
- Всего материалов:
  
  291

Источник

Задачи на постоянный электрический ток у нас уже были. Пора заняться переменным! В сегодняшней статье рассмотрим несколько задач начального уровня на переменный ток.

Подпишитесь на наш телеграм, чтобы быть в курсе актуальных новостей и не упустить приятные скидки!

Задачи на переменный электрический ток

Прежде, чем мы перейдем непосредственно к примерам решения задач на переменный ток, скажем кое-что для тех, кто вообще не знает, с какой стороны подступиться к задачам по физике. У нас есть универсальный ответ – памятка по решению. А еще, вам могут пригодиться формулы.

Хотите разобраться в теории? Читайте в нашем блоге, что такое фаза и ноль в электричестве.

Задача№1. Переменный ток

Условие

Вольтметр, включённый в цепь переменного тока,показывает напряжение 220 В, а амперметр – ток 10 А.Чему равны амплитудные значения измеряемых величин?

Решение

Амперметр показывает мгновенные, действующие значения величин. Действующие значения силы тока и напряжения меньше амплитудных в 2 раз. Исходя из этого, рассчитаем:

IA=Iд·2=10·2=14,1 АUA=Uд·2=220·2=311 В

Ответ: 14,1 А; 311 В.

Задача№2. Переменный ток

Условие

Рамка вращается в однородном магнитном поле. ЭДС индукции, возникающая в рамке, изменяется по закону e=80sin25πt. Определите время одного оборота рамки.

Решение

Из условия можно найти угловую частоту вращения рамки:

e=εmsinωte=80sin25πtω=25π рад/с

Время одного оборота рамки – это период колебаний, связанный с угловой частотой:

T=2πω=2π25π=0,08 с

Ответ: 0,08 с.

Больше задач на тему ЭДС в нашем блоге.

Задача№3. Переменный ток

Условие

Сила тока в колебательном контуре изменяется по закону I =0,4sin(400πt) (А). Определите емкосьть конденсатора в контуре, если индуктивность катушки равна 125 мГн.

Решение

Запишем закон изменения силы тока в контуре:

I=IAsinωt

Учитывая исходное уравнение, можно найти угловую частоту и период колебаний:

ω=400π рад/с

T=2πω=2π400π=5·10-3c

Емкость конденсатора найдем из формулы Томпсона:

T=2πLCT2=4π2LCC=T24π2L=25·10-64·9,85·125·10-3=5·10-6 Ф

Ответ: 5 мкФ.

Задача№4. Переменный ток

Условие

Чему равна амплитуда силы тока в цепи переменного тока частотой 50 Гц, содержащей последовательно соединенные активное сопротивление 1 кОм и конденсатор емкости С = 1 мкФ, если действующее значение напряжения сети, к которой подключен участок цепи, равно 220 В?

Решение

Запишем закон Ома для цепи переменного тока:

I=UZ

Z – полное сопротивление цепи, которое складывается из активного и реактивного сопротивлений.

Z=R2+Xc2Xc=12πϑC

Найдем полное сопротивление, подставив в формулу данные из условия:

X=12·3.14·50·1·10-6=3,18 кОмZ=12·106+3,22·106=3,3 кОм

Далее по действующему значению напряжения найдем амплитудное:

UA=Uд·2=220·2=311 В

Теперь подставим апмлитудное значение напряжения в выражение для закона Ома и вычислим силу тока:

IA=UAZ=3113,3·103=0,09 А

Ответ: 0,09 А.

Задача№5. Переменный ток

Условие

Катушка с ничтожно малым активным сопротивлением включена в цепь переменного тока с частотой 50 Гц. При напряжении 125 В сила тока равна 3 А. Какова индуктивность катушки?

Решение

В данной задаче, исходя из условия, можно пренебречь активным сопротивлением катушки. Ее индуктивное сопротивоение равно:

xL=ωL

По закону Ома:

U=IxL=IωL

Отсюда находим индуктивность:

L=UIω=1253·314=0,13 Гн

Ответ: 0,13 Гн.

Все еще мало задач? Держите несколько примеров на мощность тока.

Вопросы на тему «Переменный ток»

Вопрос 1. Какой ток называют переменным?

Ответ.

Переменный ток – это электрический ток, изменяющийся с течением времени по гармоническому закону.

Вопрос 2. Какие преимущества переменный ток имеет перед постоянным?

Ответ. Переменный ток имеет ряд преимуществ по сравнению с постоянным:

генератор переменного тока значительно проще и дешевле;
переменный ток передается на большие расстояния с меньшими потерями.
переменный ток можно трансформировать;
переменный ток легко преобразуется в постоянный;
двигатели переменного тока значительно проще и дешевле, чем двигатели постоянного тока.

До конца XIX века повсеместо использовались только источники постоянного тока.

Вопрос 3. Кто стал популяризатором использования переменного тока?

Ответ. За активное использоваение переменного тока выступал Никола Тесла. Подробнее о войне токов между Теслой и Эдисоном вы можете почитать в нашей отдельной статье.

Вопрос 4. В обычной домашней розетке частота тока равна 50 Гц. Что это значит?

Ответ. Это значит, что за одну секунду ток меняет свое направление 50 раз.

Вопрос 5. Сформулируйте закон Ома для переменного тока.

Ответ. Закон Ома для цепи переменного тока гласит:

Значение тока в цепи переменного тока прямо пропорционально напряжению в цепи и обратно пропорционально полному сопротивлению цепи.

Полное сопротивоение цепи в общем случае состоит из активного, индуктивного и емкостного сопротивлений.

Проблемы с решением задач и выполнением других заданий по учебе? Добро пожаловать в профессиональный сервис для студентов за их решением!

Источник