Есть ли первообразная в егэ математика профиль 2023

ЕГЭ по математике профильного уровня — один из самых сложных экзаменов. Планируете сдавать его, но не знаете, с чего начать? Этот экзамен не покажется вам таким трудным, если вы узнаете про него побольше и грамотно подготовитесь. В этой статье обсудим, что нужно знать про ЕГЭ по математике 2023, из каких разделов он состоит и как к нему подготовиться.

Какие темы важно знать для ЕГЭ по математике 2023?

В математике, как и в любом предмете, есть опорные темы. Если вы их выучите, будет легче справиться с экзаменом.

Формулы тригонометрии

Очень важно знать формулы тригонометрии и уметь применять их. Хорошая новость: в справочных материалах можно найти несколько тригонометрических формул.

Но формул гораздо больше. Я советую не зубрить их, а научиться выводить: приходить к формулам шаг за шагом, опираясь на тождества. Кстати, мы учим выводить формулы на курсах подготовки к ЕГЭ: это полезно, чтобы оказаться на экзамене во всеоружии и ничего не перепутать.

Квадратные уравнения

Эти уравнения мы учимся решать еще в 7 классе. Они встречаются в ЕГЭ по математике постоянно: и как самостоятельные задания, и внутри более сложных уравнений или неравенств. Квадратные уравнения могут встретиться в математических моделях № 9 и № 15, в задачах на геометрию и стереометрию, в задании № 17 с параметром.

Самое главное — хорошо знать универсальные методы решения. Первый — через формулу дискриминанта, второй — через теорему Виета, которая может сэкономить время на экзамене.

Треугольники

Эта замечательная тема, которую проходят в 7 классе — основа основ всей геометрии. Она нужна и для решения стереометрии, и для простейших планиметрических задач. Еще треугольники необходимы, чтобы освоить огромное количество теорем. Выучите все, что с ними связано! Особое внимание обратите на прямоугольные треугольники, которые встречаются чаще остальных — тогда геометрические задачи сразу станут проще.

Проценты

Самая нелюбимая тема моих учеников после тригонометрии, которую необходимо хорошо знать. Проценты нужны для реальной математики — это № 9 (с кратким ответом) и № 15 (с развернутым ответом). Понимание этой темы может принести вам 3 первичных балла.

План успешной подготовки к ЕГЭ по математике 2023

Если вы хотите получить больше 80 баллов на ЕГЭ, нужно идеально решать часть с кратким ответом, а также справляться с большинством заданий с развернутым ответом.

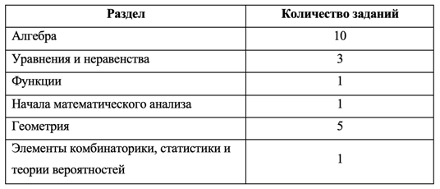
Чтобы постепенно прорабатывать материал, воспользуйтесь кодификатором. В нем обратите внимание на таблицу 2, а именно на блоки:

• Алгебра
• Уравнения и неравенства
• Элементы комбинаторики, статистики и теории вероятностей
• Функции
• Начала математического анализа
• Геометрия

Ориентируйтесь на указанную последовательность, но геометрию изучайте параллельно с остальными блоками — на нее нужно больше времени.

Самое главное — ни в коем случае не ограничивайтесь теорией. Ее у вас не спросят на экзамене, а вот задания решать придется. Поэтому тренируйте практические навыки: актуальные задания вы сможете найти в открытом банке заданий на сайте ФИПИ или в нашем тренажере «Решутест».

Как решать часть с кратким ответом

Ни в коем случае не пренебрегайте частью с кратким ответом! Иначе будет обидно: например, вы наберете за экономическую задачу № 15 полные 2 балла, но потеряете их в двух заданиях первой части. Это актуально для всех ЕГЭ: подробнее о том, как идеально справляться с первой частью экзамена, читайте здесь.

Еще одно заблуждение: «часть с кратким ответом простая, к ней можно не готовиться». Даже в первой части иногда встречаются такие задания, которые ученики даже не решают, потому что не готовились к ним.

Как я уже говорила, часть с кратким ответом содержит 11 заданий. Начинать подготовку необходимо именно с заданий базового уровня сложности, потому что это та основа, на которую потом накладывается более сложная теория.

Что касается задач повышенного уровня сложности, то среди каждого номера есть лайфхаки, например, в этой статье я уже рассказывала про № 11, в котором нужно работать с производной.

Задания с развернутым ответом: немного статистики

Многие думают, что эта часть ЕГЭ по математике очень сложная. Поэтому ребята, которые не рассчитывают на высокие баллы, даже не приступают к ней. И очень зря! С помощью этих заданий можно заработать дополнительные баллы и побороться за высокое место в рейтинге.

Сейчас будет немного статистики. В среднем около 35% учеников получают полные 2 балла за решение № 12, а вот неравенство № 14 дается хуже, только около 12% с ним справляются на полный балл. Геометрия даётся ещё хуже: стереометрию № 13 полностью решают 2% выпускников, планиметрию (№ 16) менее 5%. А вот с экономической задачей (№ 15) справляются около 20%, а это целых 2 балла! Что касается № 17 и 18, то они даются ещё хуже, но на то они и самые сложные, хотя 1 балл за № 18 по статистике получают около 25% сдающих — там нужно просто привести пример.

Особенности уровней ЕГЭ по математике

В 2015 году ЕГЭ по математике разделили на базовый и профильный уровни. Это упростило жизнь выпускникам, которые не планируют поступать на специальности, связанные с математикой. Если ЕГЭ по математике нужен только для получения аттестата, можно сдать его облегченную версию, оставив время и силы для профильных экзаменов.

Базовый уровень ЕГЭ по математике

Как устроен базовый ЕГЭ по математике? Экзамен идет 180 минут, он состоит из 21 задания, за каждое из которых можно получить 1 балл. Этот экзамен единственный, который переводится не в 100-бальную систему, а в оценки.

В ЕГЭ по математике базового уровня 6 тематических блоков:

Также обратите внимание, что базовый ЕГЭ по математике не поменялся с точки зрения наполнения, изменился лишь порядок заданий. Вот что пишут ФИПИ:

Подробнее про базовый ЕГЭ по математике, включая разбор всех заданий, читайте здесь, а мы перейдём к профильному.

Профильный уровень ЕГЭ по математике

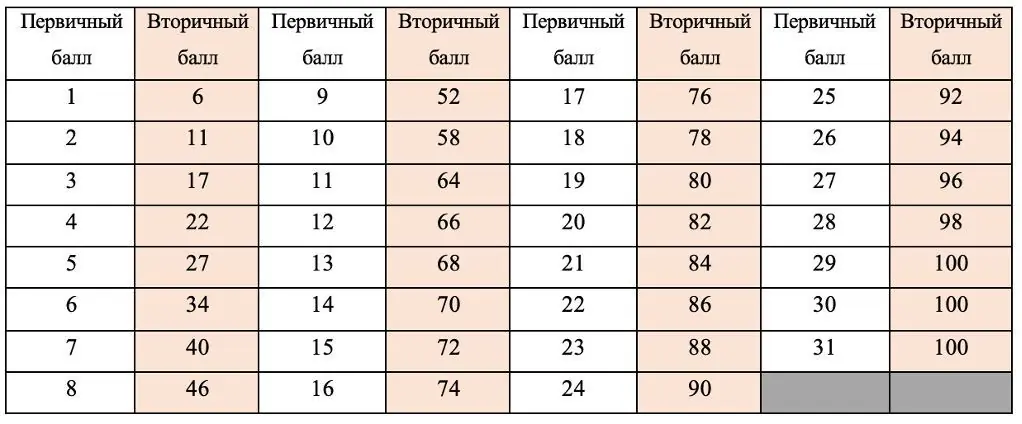
Данный экзамен, как и остальные ЕГЭ, переводится в 100-бальную систему:

Экзамен состоит из двух частей: Часть 1 с кратким ответом, а Часть 2 — с развернутым. Длится он 235 минут. Всего есть 18 заданий, которые разделены на 3 блока: алгебра, геометрия и реальная математика. Максимальное количество первичных баллов — 31.

Структура ЕГЭ по математике 2023

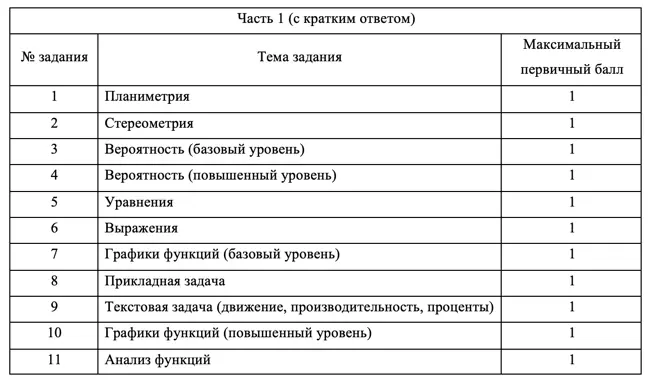
Часть 1:

• Приносит 11 баллов, то есть 35% всего экзамена
• 11 заданий с кратким ответом

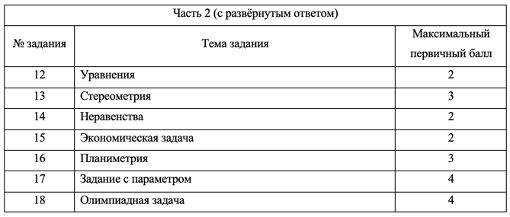
Часть 2:

• Приносит 20 баллов, то есть 65% всего экзамена
• 7 заданий с развернутым ответом

Внимание! Вся нумерация заданий в статье соответствует ЕГЭ 2023 года.

В заданиях с кратким ответом нужно лишь записать верное число в бланк. Заданий с развернутым ответом 7, в них нужно подробно расписать решение, которое должно соответствовать критериям оценивания.

ЕГЭ — стандартизированный экзамен, поэтому каждое задание всегда соответствует определенной теме.

Обратите внимание, что по сравнению с 2022 годом, в части 1 изменился только порядок заданий. Сами сотрудники ФИПИ говорят следующее:

Задания с кратким ответом принесут вам до 11 первичных баллов (64 вторичных). Если не понимаете, что это за баллы и откуда они берутся, почитайте эту статью. Самая популярная цель на ЕГЭ по математике — набрать 80 баллов, для этого раньше было необходимо 19 первичных баллов. Ранее многие ученики пользовались рабочей стратегией — решить всю часть с кратким ответом, а также № 12, 14 и 15. Если хорошо разбирались в геометрии, выбирали № 13 и 16 — или использовали их как запасные задания. Сейчас стратегия должна быть другая, так как № 13 (стереометрия) стал стоить дороже — 3 балла вместо 2, а № 15 (экономическая задача) — подешевел с 3 баллов до 2. Изменилась также шкала перевода баллов, поэтому подумайте, какими заданиями вы сможете набрать необходимое количество первичных баллов.

Разделы ЕГЭ по математике

• Алгебра и начала анализа — 8 заданий, 13 первичных баллов
• Геометрия — 4 задания, 8 первичных баллов
• Реальная математика — 6 заданий, 10 первичных баллов

Какие задания входят в ЕГЭ по математике?

Здесь вам на помощь приходят документы с официального сайта ФИПИ: кодификатор, демоверсия и спецификация.

• Кодификатор — это краткий перечень всех блоков и тем, которые включены в экзамен.

  Сейчас кодификатор общий для обоих уровней экзамена, как базового, так и профильного. Он снова представляет собой единый документ, так что не запутаетесь.

• Демоверсия — типовой вариант ЕГЭ. Он показывает уровень экзамена и ориентировочную сложность заданий.
• Спецификация — это документ, описывающий структуру экзамена и разбалловку.

Что в итоге

Необходимая теория:

Производная функции

Таблица производных

Первообразная функции

Задание 7 Профильного ЕГЭ по математике — это задачи на геометрический и физический смысл производной. Это задачи о том, как производная связана с поведением функции. И еще (правда, очень редко) в этих задачах встречаются вопросы о первообразной.

Геометрический смысл производной 

Вспомним, что производная — это скорость изменения функции.

Производная функции в точке равна угловому коэффициенту касательной, проведенной к графику функции в этой точке. Производная также равна тангенсу угла наклона касательной.

1. На рисунке изображён график функции и касательная к нему в точке с абсциссой Найдите значение производной функции в точке

Производная функции в точке равна тангенсу угла наклона касательной, проведенной в точке .

Достроив до прямоугольного треугольника АВС, получим:

Ответ: 0,25.

2. На рисунке изображён график функции и касательная к нему в точке с абсциссой
Найдите значение производной функции в точке

Начнём с определения знака производной. Мы видим, что в точке функция убывает, следовательно, её производная отрицательна. Касательная в точке образует тупой угол с положительным направлением оси . Поэтому из прямоугольного треугольника мы найдём тангенс угла , смежного с углом .

Мы помним, что тангенс угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему: Поскольку , имеем:

Ответ: −0, 25.

Касательная к графику функции

3. Прямая является касательной к графику функции

Найдите абсциссу точки касания.

Запишем условие касания функции и прямой в точке

При значения выражений и равны.

При этом производная функции равна угловому коэффициенту касательной, то есть .

Из второго уравнения находим или Первому уравнению удовлетворяет только .

Физический смысл производной

Мы помним, что производная — это скорость изменения функции.

Мгновенная скорость — это производная от координаты по времени. Но это не единственное применение производной в физике. Например, cила тока — это производная заряда по времени, то есть скорость изменения заряда. Угловая скорость — производная от угла поворота по времени.

Множество процессов в природе, экономике и технике описывается дифференциальными уравнениями — то есть уравнениями, содержащими не только сами функции, но и их производные.

4. Материальная точка движется прямолинейно по закону , где — расстояние от точки отсчета в метрах, — время в секундах, измеренное с начала движения. Найдите ее скорость (в м/с) в момент времени с.

Мгновенная скорость движущегося тела является производной от его координаты по времени. Это физический смысл производной. В условии дан закон изменения координаты материальной точки, то есть расстояния от точки отсчета:

Найдем скорость материальной точки как производную от координаты по времени:

В момент времени получим:

.

Ответ: 3.

Применение производной к исследованию функций

Каждый год в вариантах ЕГЭ встречаются задачи, в которых старшеклассники делают одни и те же ошибки.

Например, на рисунке изображен график функции — а спрашивают о производной. Кто их перепутал, тот задачу не решил.

Или наоборот. Нарисован график производной — а спрашивают о поведении функции.

И значит, надо просто внимательно читать условие. И знать, как же связана производная с поведением функции.

Если , то функция возрастает.

Если , то функция убывает.

В точке максимума производная равна нулю и меняет знак с «плюса» на «минус».

В точке минимума производная тоже равна нулю и меняет знак с «минуса» на «плюс».

	возрастает	точка максимума	убывает	точка минимума	возрастает
		0		0

5. На рисунке изображен график функции , определенной на интервале Найдите количество точек, в которых производная функции равна 0.

Производная функции в точках максимума и минимума функции Таких точек на графике 5.

Ответ: 5.

6. На рисунке изображён график — производной функции , определённой на интервале . В какой точке отрезка функция принимает наибольшее значение?

Не спешим. Зададим себе два вопроса: что изображено на рисунке и о чем спрашивается в этой задаче?

Изображен график производной, а спрашивают о поведении функции. График функции не нарисован. Но мы знаем, как производная связана с поведением функции.

На отрезке производная функции положительна.

Значит, функция возрастает на этом отрезке. Большим значениям х соответствует большее значение Наибольшее значение функции достигается в правом конце отрезка, то есть в точке 3.

Ответ: 3.

7. На рисунке изображён график функции , определённой на интервале . Найдите количество точек, в которых касательная к графику функции параллельна прямой

Прямая параллельна оси абсцисс. Найдем на графике функции точки, в которых касательная параллельна оси абсцисс, то есть горизонтальна. Таких точек на графике 7. Это точки максимума и минимума.

Ответ: 7.

8. На рисунке изображен график производной функции , определенной на интервале Найдите количество точек максимума функции на отрезке

Очень внимательно читаем условие задачи. Изображен график производной, а спрашивают о точках максимума функции. В точке максимума производная равна нулю и меняет знак с «плюса» на «минус». На отрезке такая точка всего одна! Это

Ответ: 1.

9. На рисунке изображен график производной функции , определенной на интервале Найдите точку экстремума функции на отрезке

Точками экстремума называют точки максимума и минимума функции. Если производная функции в некоторой точке равна нулю и при переходе через эту точку меняет знак, то это точка экстремума. На отрезке график производной (а именно он изображен на рисунке) пересекает ось абсцисс в точке В этой точке производная меняет знак с минуса на плюс.

Значит, является точкой экстремума.

Первообразная и формула Ньютона-Лейбница

Функция , для которой является производной, называется первообразной функции Функции вида образуют множество первообразных функции

10. На рисунке изображён график — одной из первообразных некоторой функции , определённой на интервале Пользуясь рисунком, определите количество решений уравнения на отрезке

Функция для которой является производной, называется первообразной функции

Это значит, что на графике нужно найти такие точки, принадлежащие отрезку , в которых производная функции равна нулю. Это точки максимума и минимума функции На отрезке таких точек 4.

Ответ: 4.

Больше задач на тему «Первообразная. Площадь под графиком функции» — в этой статье

Первообразная функции. Формула Ньютона-Лейбница.

А вы знаете, как безошибочно читать графики функций, искать производную и определять количество целых точек при ее положительном или отрицательном значении? В нашей серии обучающих видеороликов эксперт ЕГЭ по математике разберет задачи с производной и наглядно на графике покажет, что нужно делать, чтобы получить правильный ответ. Это поможет в поиске быстрого решения 7 задания ЕГЭ по математике.

7 задание ЕГЭ по математике профильный уровень 2023 года – задача №1

Перед вами график функции, на котором определен интервал значений. Преподаватель нашего учебного центра за несколько минут разбирает этот пример, отвечая на самые популярные вопросы по задачам с производной. Для того чтобы решить задачу №1, достаточно внимательно прочитать задание и правильно выделить положительную/отрицательную производную. В целом, ничего сложного, если посмотреть видео целиком и вникнуть в детали.

Разбор задания 7 по математике ЕГЭ профиль 2023 года – задача №2

Еще один пример, показывающий, как быстро находить точки производной функции. Зная теорию по графикам, можно без длительной подготовки решить задачу №2, опираясь на аналогичные примеры. Разбор задания 7 ЕГЭ по математике еще раз повторяет азы для закрепления результата.

Если вы хотите получить 80+ баллов по сложнейшему школьному предмету – математике, вам не обойтись без поддержки. Наш учебный центр Годограф поможет каждому ученику, независимо от уровня начальной подготовки, правильно найти решение 7 задания ЕГЭ по математике, а также другим задачам экзамена и получить высокий балл. Запишитесь на пробный урок уже сегодня!

Сайты, меню, вход, новости

Первообразной для функции $f(x)$ называется такая функция $F(x)$, для которой выполняется равенство: $F'(x)=f(x)$

Таблица первообразных

Первообразная нуля равна $С$

Функция	Первообразная
$f(x)=k$	$F(x)=kx+C$
$f(x)=x^m, m≠-1$	$F(x)={x^{m+1}}/{m+1}+C$
$f(x)={1}/{x}$	$F(x)=ln|x|+C$
$f(x)=e^x$	$F(x)=e^x+C$
$f(x)=a^x$	$F(x)={a^x}/{lna}+C$
$f(x)=sinx$	$F(x)-cosx+C$
$f(x)=cosx$	$F(x)=sinx+C$
$f(x)={1}/{sin^2x}$	$F(x)=-ctgx+C$
$f(x)={1}/{cos^2x}$	$F(x)=tgx+C$
$f(x)=√x$	$F(x)={2x√x}/{3}+C$
$f(x)={1}/{√x}$	$F(x)=2√x+C$

Если $y=F(x)$ – это первообразная для функции $y=f(x)$ на промежутке $Х$, то $у$ $у=f(x)$ бесконечно много первообразных и все они имеют вид $y=F(x)+C$

Правила вычисления первообразных:

1. Первообразная суммы равна сумме первообразных. Если $F(x)$ — первообразная для $f(x)$, а $G(x)$ – первообразная для $g(x)$, то $F(x)+G(x)$ — первообразная для $f(x)+g(x)$.
2. Постоянный множитель выносится за знак первообразной. Если $F(x)$ — первообразная для $f(x)$, а $k$ – постоянная величина, то $k$ $F(x)$ — первообразная для $k$ $f(x)$.
3. Если $F(x)$ — первообразная для $f(x)$, $а, k, b$ — постоянные величины, причем $k≠0$, то ${1}/{k}$ $F(kx+b)$ — это первообразная для $f(kx+b)$.

Связь между графиками функции и ее первообразной:

1. Если график функции $f (x) > 0$ на промежутке, то график ее первообразной $F(x)$ возрастает на этом промежутке.
2. Если график функции $f (x) < 0$ на промежутке, то график ее первообразной $F(x)$ убывает на этом промежутке.
3. Если $f(x)=0$, то график ее первообразной $F(x)$ в этой точке меняется с возрастающего на убывающий (или наоборот).

Неопределенный интеграл

Если функция $у=f(x)$ имеет на промежутке $Х$ первообразную $у=F(x)$, то множество всех первообразных $у=F(x)+С$, называют неопределенным интегралом функции $у=f(x)$ и записывают:

$∫f(x)dx$

Определенный интеграл – это интеграл с пределами интегрирования (на отрезке)

$∫_a^bf(x)dx$, где $a,b$ — пределы интегрирования

Площадь криволинейной трапеции или геометрический смысл первообразной

Площадь $S$ фигуры, ограниченной осью $Oх$, прямыми $х=а$ и $х=b$ и графиком неотрицательной функции $у=f(x)$ на отрезке $[a;b]$, находится по формуле

$S=∫_a^bf(x)dx$ 

Формула Ньютона — Лейбница

Если функция $у=f(x)$ непрерывна на отрезке $[a;b]$, то справедливо равенство

$∫_a^bf(x)dx=F(x)|_a^b=F(b)-F(a)$, где $F(x)$ — первообразная для $f(x)$

24 августа вышла демоверсия ЕГЭ 2023 по профильной математике. Для тех, кто пока не готов вникать в тему основательно, успокоительный спойлер: почти ничего не изменилось, принципиально новых заданий нет. Всё в порядке. 

А для тех, кто давно был на низком старте и ждал разбор демо ЕГЭ, математик Эйджей провёл стрим с решением заданий из демоверсии ЕГЭ 2023 по профильной математике. В этой статье собраны резюме по заданиям экзамена, которые составители ЕГЭ представили в демоверсии. 

https://youtu.be/RFQwP8DW8sA 

Что изменилось в ЕГЭ 2023 по профильной математике

По сути, никаких критически важных изменений в демоверсии ЕГЭ 2023 нет, о чём составители написали прямо: «Изменения в содержании КИМ отсутствуют». Но есть момент: все задания из первой части, кроме 11, изменили свои номера. 

Будем искать позитивные моменты: если в 2022 году вы не смогли запомнить номера заданий в тесте — ничего страшного, запомните новые в 2023 году. 

Главное, что новых заданий не появилось.

Важный момент в самостоятельной подготовке к ЕГЭ по профильной математике — выбор качественных сборников задач. Делимся лучшими ресурсами для повторения теории и отработки практики.

1, 2 задания

В демоверсии ЕГЭ 2023 по профильной математике всё начинается с простой геометрии и стереометрии. Составители хотят, чтобы геометрические задачи научились решать как можно больше ребят, поэтому поместили эти задания вперёд как одни из самых простых, чтобы поднять решаемость.

3, 4 задания

Задания 3–4 посвящены теории вероятности. 

Задание 3 — обычная задача наподобие задачи из ОГЭ, а задание 4 — задача про монеты и проценты из КИМа 2022 года. 

5, 6 задания

После вероятностей составители ЕГЭ 2023 по профильной математике решили поставить уравнения и выражения. Уравнения ожидаются не супер лёгкие, но вполне решаемые: будут корни, логарифмы и степени. В выражениях в демоверсии ЕГЭ встретилась тригонометрия и степени.

7 задание 

Ура, 7 задание осталось на своём месте: это задание с графиком и производными. Почему-то его не объединили в общий блок с 11 заданием, тоже посвящённым производным. 

Далее в разборе демоверсии ЕГЭ 2023 по профильной математике выпускников ждут две задачи. 

8 задание

8 задача на подстановку: нужно подставить в формулу известные числа и вычислить какую-либо величину. Ничего сложного, главное внимательность.

9 задание

Ещё одна текстовая задача. Здесь могут встретиться темы «Движение по прямой», «Движение по окружности», «Движение по реке» и «Сплавы, смеси, растворы». Такие задачи считаются не самыми простыми. Вместе с Эйджеем разберём этот номер в Телеграме.

10 задание

10 задание в демо ЕГЭ 2023 — «новое старое задание». Этот тип заданий с графиком впервые появился в 2022 году, и в КИМ 2023 попал без изменений. Возможно, стоит ждать усложнения этого задания. 

11 задание

Традиционное задание с производными и точками минимума и максимума, которое почему-то не объединили в блок с другим заданием на производные. 

Итак, обобщим всё, что мы узнали про первую часть демоверсии ЕГЭ по математике: в 2023 году в экзамене не появились ни вектора, ни комплексные числа. Можно немного расслабиться! Осталось выучить новую нумерацию, и всё будет хорошо.

Нумерация второй части в демоверсии ЕГЭ 2023 осталась без изменений, и это радует: не придётся переучивать номера и переживать. Посмотрим, что приготовили составители в этом году. 

12 задание

Традиционно в разборе демоверсии ЕГЭ 2023 по профильной математике в 12 задании выпускников ждёт тригонометрическое уравнение. 

13 задание

В 13 задании осталась стереометрия: в демоверсии представлена треугольная призма.

14 задание

В 14 задании всё по плану, там остались неравенства с логарифмами, ничего нового. 

Это задание вместе с 12-ым составляет «джентльменский набор» из второй части — их под силу решить каждому, и этому нужно обязательно научиться, чтобы набрать 70+ баллов за ЕГЭ по профильной математике. 

15 задание

15 задание также считается вполне решаемым. В демоверсии это экономическая задача про человека, который взял кредит в банке и рассчитывает выплаты и проценты.

16 задание

В задании 16 демоверсии ЕГЭ 2023 представлена планиметрическая задача про две окружности. 

17 задание

Задача на параметр. Как показывает практика прошлых лет, параметр — самое решаемое задание из сложных заданий ЕГЭ. 

18 задание

Задача на целые числа. Из трёх пунктов, А и Б решить может каждый, если хорошо подготовиться.

Чтобы получить 80+ баллов по профильной математике, нужно без ошибок решить первую часть и выполнить 12, 14, 15 и 18аб задания. А планиметрия, стереометрия, параметр и 18 задание полностью  помогут получить заветную сотку. Как повысить свои шансы на успешную сдачу ЕГЭ по математике, рассказали в нашей статье.

Мы разобрали демоверсию ЕГЭ 2023 по математике, и теперь вы знаете, что приготовили для вас составители экзамена. Можно смело начинать подготовку! Эйджей уже составил план занятий и ждёт вас на курсе «Основа». Это возможность разобраться во всех темах и набить руку в решении заданий в компании единомышленников и с личным наставником.