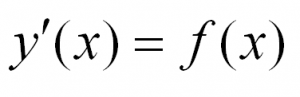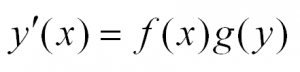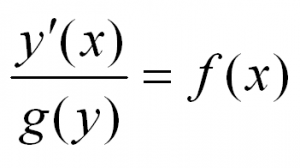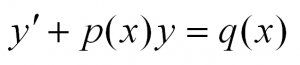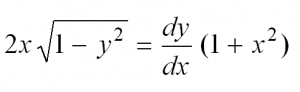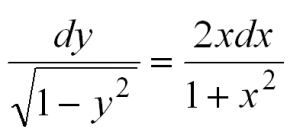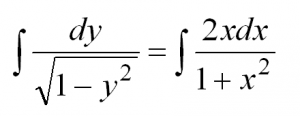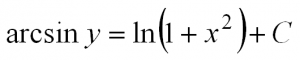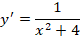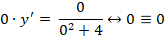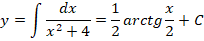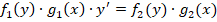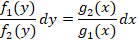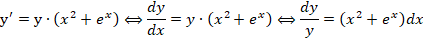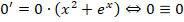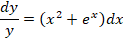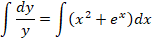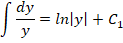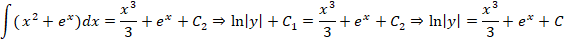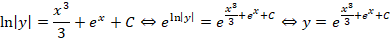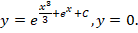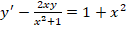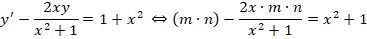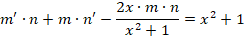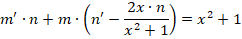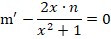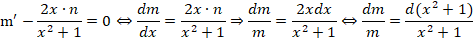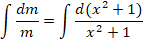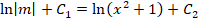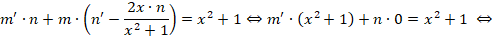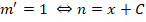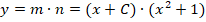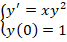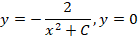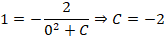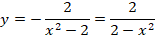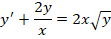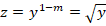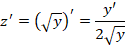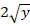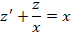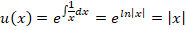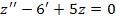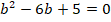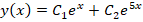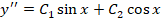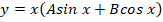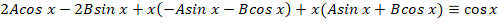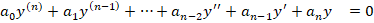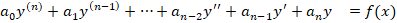Есть ли в егэ дифференциальные уравнения

Каталог заданий.
Линейные, квадратные, кубические уравнения

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Пройти тестирование по этим заданиям

Часто одно лишь упоминание дифференциальных уравнений вызывает у студентов неприятное чувство. Почему так происходит? Чаще всего потому, что при изучении основ материала возникает пробел в знаниях, из-за которого дальнейшее изучение диффуров становиться просто пыткой. Ничего не понятно, что делать, как решать, с чего начать?

Однако мы постараемся вам показать, что диффуры – это не так сложно, как кажется.

Основные понятия теории дифференциальных уравнений

Со школы нам известны простейшие уравнения, в которых нужно найти неизвестную x. По сути дифференциальные уравнения лишь чуточку отличаются от них – вместо переменной х в них нужно найти функцию y(х), которая обратит уравнение в тождество.

Дифференциальные уравнения имеют огромное прикладное значение. Это не абстрактная математика, которая не имеет отношения к окружающему нас миру. С помощью дифференциальных  уравнений описываются многие реальные природные процессы. Например, колебания струны, движение гармонического осциллятора, посредством дифференциальных уравнений в задачах механики находят скорость и ускорение тела. Также ДУ находят широкое применение в биологии, химии, экономике и многих других науках.

Дифференциальное уравнение (ДУ) – это уравнение, содержащее производные функции y(х), саму функцию, независимые переменные и иные параметры в различных комбинациях.

Существует множество видов дифференциальных уравнений: обыкновенные дифференциальные уравнения, линейные и нелинейные, однородные и неоднородные, дифференциальные уравнения первого и высших порядков, дифуры в частных производных и так далее.

Решением дифференциального уравнения является функция, которая обращает его в тождество. Существуют общие и частные решения ДУ.

Общим решением ДУ является общее множество решений, обращающих уравнение в тождество. Частным решением дифференциального уравнения называется решение, удовлетворяющее дополнительным условиям, заданным изначально.

Порядок дифференциального уравнения  определяется наивысшим порядком производных, входящих в него.

Обыкновенные дифференциальные уравнения

Обыкновенные дифференциальные уравнения – это уравнения, содержащие одну независимую переменную.

Рассмотрим простейшее обыкновенное дифференциальное уравнение первого порядка. Оно имеет вид:

Решить такое уравнение можно, просто проинтегрировав его правую часть.

Примеры таких уравнений:

Уравнения с разделяющимися переменными

В общем виде этот тип уравнений выглядит так:

Приведем пример:

Решая такое уравнение, нужно разделить переменные, приведя его к виду:

После этого останется проинтегрировать обе части и получить решение.

Линейные дифференциальные уравнения первого порядка

Такие уравнения имеют вид:

Здесь p(x) и q(x) – некоторые функции независимой переменной, а y=y(x) – искомая функция. Приведем пример такого уравнения:

Решая такое уравнение, чаще всего используют метод вариации произвольной постоянной либо представляют искомую функцию в виде произведения двух других функций y(x)=u(x)v(x).

Для решения таких уравнений необходима определенная подготовка и  взять их “с наскока” будет довольно сложно.

Пример решения ДУ с разделяющимися переменными

Вот мы и рассмотрели простейшие типы ДУ. Теперь разберем решение одного из них. Пусть это будет уравнение с разделяющимися переменными.

Сначала  перепишем производную в более привычном виде:

Затем разделим переменные, то есть в одной части уравнения соберем все «игреки», а в другой – «иксы»:

Теперь осталось проинтегрировать обе части:

Интегрируем и получаем общее решение данного уравнения:

Конечно, решение дифференциальных уравнений – своего рода искусство. Нужно уметь понимать, к какому типу относится уравнение, а также научиться видеть, какие преобразования нужно с ним совершить, чтобы привести к тому или иному виду, не говоря уже просто об умении дифференцировать и интегрировать. И чтобы преуспеть в решении ДУ, нужна практика (как и во всем). А если у Вас в данный момент нет времени разбираться с тем, как решаются дифференциальные уравнения или задача Коши встала как кость в горле или вы не знаете, как правильно оформить презентацию, обратитесь к нашим авторам. В сжатые сроки мы предоставим Вам готовое и подробное решение, разобраться в подробностях которого Вы сможете в любое удобное для Вас время. А пока предлагаем посмотреть видео на тему «Как решать дифференциальные уравнения»:

Необходимая теория:

Производная функции

Таблица производных

Первообразная функции

Задание 7 Профильного ЕГЭ по математике — это задачи на геометрический и физический смысл производной. Это задачи о том, как производная связана с поведением функции. И еще (правда, очень редко) в этих задачах встречаются вопросы о первообразной.

Геометрический смысл производной 

Вспомним, что производная — это скорость изменения функции.

Производная функции в точке равна угловому коэффициенту касательной, проведенной к графику функции в этой точке. Производная также равна тангенсу угла наклона касательной.

1. На рисунке изображён график функции и касательная к нему в точке с абсциссой Найдите значение производной функции в точке

Производная функции в точке равна тангенсу угла наклона касательной, проведенной в точке .

Достроив до прямоугольного треугольника АВС, получим:

Ответ: 0,25.

2. На рисунке изображён график функции и касательная к нему в точке с абсциссой
Найдите значение производной функции в точке

Начнём с определения знака производной. Мы видим, что в точке функция убывает, следовательно, её производная отрицательна. Касательная в точке образует тупой угол с положительным направлением оси . Поэтому из прямоугольного треугольника мы найдём тангенс угла , смежного с углом .

Мы помним, что тангенс угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему: Поскольку , имеем:

Ответ: −0, 25.

Касательная к графику функции

3. Прямая является касательной к графику функции

Найдите абсциссу точки касания.

Запишем условие касания функции и прямой в точке

При значения выражений и равны.

При этом производная функции равна угловому коэффициенту касательной, то есть .

Из второго уравнения находим или Первому уравнению удовлетворяет только .

Физический смысл производной

Мы помним, что производная — это скорость изменения функции.

Мгновенная скорость — это производная от координаты по времени. Но это не единственное применение производной в физике. Например, cила тока — это производная заряда по времени, то есть скорость изменения заряда. Угловая скорость — производная от угла поворота по времени.

Множество процессов в природе, экономике и технике описывается дифференциальными уравнениями — то есть уравнениями, содержащими не только сами функции, но и их производные.

4. Материальная точка движется прямолинейно по закону , где — расстояние от точки отсчета в метрах, — время в секундах, измеренное с начала движения. Найдите ее скорость (в м/с) в момент времени с.

Мгновенная скорость движущегося тела является производной от его координаты по времени. Это физический смысл производной. В условии дан закон изменения координаты материальной точки, то есть расстояния от точки отсчета:

Найдем скорость материальной точки как производную от координаты по времени:

В момент времени получим:

.

Ответ: 3.

Применение производной к исследованию функций

Каждый год в вариантах ЕГЭ встречаются задачи, в которых старшеклассники делают одни и те же ошибки.

Например, на рисунке изображен график функции — а спрашивают о производной. Кто их перепутал, тот задачу не решил.

Или наоборот. Нарисован график производной — а спрашивают о поведении функции.

И значит, надо просто внимательно читать условие. И знать, как же связана производная с поведением функции.

Если , то функция возрастает.

Если , то функция убывает.

В точке максимума производная равна нулю и меняет знак с «плюса» на «минус».

В точке минимума производная тоже равна нулю и меняет знак с «минуса» на «плюс».

	возрастает	точка максимума	убывает	точка минимума	возрастает
		0		0

5. На рисунке изображен график функции , определенной на интервале Найдите количество точек, в которых производная функции равна 0.

Производная функции в точках максимума и минимума функции Таких точек на графике 5.

Ответ: 5.

6. На рисунке изображён график — производной функции , определённой на интервале . В какой точке отрезка функция принимает наибольшее значение?

Не спешим. Зададим себе два вопроса: что изображено на рисунке и о чем спрашивается в этой задаче?

Изображен график производной, а спрашивают о поведении функции. График функции не нарисован. Но мы знаем, как производная связана с поведением функции.

На отрезке производная функции положительна.

Значит, функция возрастает на этом отрезке. Большим значениям х соответствует большее значение Наибольшее значение функции достигается в правом конце отрезка, то есть в точке 3.

Ответ: 3.

7. На рисунке изображён график функции , определённой на интервале . Найдите количество точек, в которых касательная к графику функции параллельна прямой

Прямая параллельна оси абсцисс. Найдем на графике функции точки, в которых касательная параллельна оси абсцисс, то есть горизонтальна. Таких точек на графике 7. Это точки максимума и минимума.

Ответ: 7.

8. На рисунке изображен график производной функции , определенной на интервале Найдите количество точек максимума функции на отрезке

Очень внимательно читаем условие задачи. Изображен график производной, а спрашивают о точках максимума функции. В точке максимума производная равна нулю и меняет знак с «плюса» на «минус». На отрезке такая точка всего одна! Это

Ответ: 1.

9. На рисунке изображен график производной функции , определенной на интервале Найдите точку экстремума функции на отрезке

Точками экстремума называют точки максимума и минимума функции. Если производная функции в некоторой точке равна нулю и при переходе через эту точку меняет знак, то это точка экстремума. На отрезке график производной (а именно он изображен на рисунке) пересекает ось абсцисс в точке В этой точке производная меняет знак с минуса на плюс.

Значит, является точкой экстремума.

Первообразная и формула Ньютона-Лейбница

Функция , для которой является производной, называется первообразной функции Функции вида образуют множество первообразных функции

10. На рисунке изображён график — одной из первообразных некоторой функции , определённой на интервале Пользуясь рисунком, определите количество решений уравнения на отрезке

Функция для которой является производной, называется первообразной функции

Это значит, что на графике нужно найти такие точки, принадлежащие отрезку , в которых производная функции равна нулю. Это точки максимума и минимума функции На отрезке таких точек 4.

Ответ: 4.

Больше задач на тему «Первообразная. Площадь под графиком функции» — в этой статье

Первообразная функции. Формула Ньютона-Лейбница.

Алгоритм решения дифференциальных уравнений

Дифференциальные уравнения не так сильно отличаются от привычных уравнений, где необходимо найти переменную x, как кажется на первый взгляд. Всё различие лишь в том, что в дифференциальных уравнениях мы ищем не переменную, а функцию у(х), с помощью которой можно обратить уравнение в равенство.

Дифференциальное уравнение – это уравнение, содержащее саму функцию (y=y(x)), производные функции или дифференциалы (y′, y″) и независимые переменные (наиболее распространённая – х). Обыкновенным дифференциальным уравнением называют уравнение, в котором содержится неизвестная функция под знаком производной или под знаком дифференциала.

Чтобы решить ДУ, необходимо найти множество всех функций, которые удовлетворяют данному уравнению. Это множество в большинстве случаев выглядит следующим образом:y=f(x; С), где С – произвольная постоянная.

Проверить решённое ДУ можно, подставив найденную функцию в изначальное уравнение и убедившись, что уравнение обращается в тождество (равенство).

Примеры решения дифференциальных уравнений

Задание

Решить дифференциальное уравнение xy’=y.

Решение

В первую очередь, необходимо переписать уравнение в другой вид. Пользуясь 

   

переписываем дифференциальное уравнение, получаем

   

Дальше смотрим, насколько реально разделить переменные, то есть путем обычных манипуляций (перенос слагаемых из части в часть, вынесение за скобки и пр.) получить выражение, где «иксы» с одной стороны, а «игреки» с другой. В данном уравнении разделить переменные вполне реально, и после переноса множителей  по правилу пропорции получаем

   

Далее интегрируем полученное уравнение:

   

В данном случае интегралы берём из таблицы:

   

После того, как взяты интегралы, дифференциальное уравнение считается решённым. Решение дифференциального уравнения в неявном виде называется общим интегралом дифференциального уравнения.

То есть,

   

– это общий интеграл. Также для удобства и красоты, его можно переписать в другом виде: y=Cx, где С=Const

Ответ

y=Cx, где С=Const.

Задание

Найти частное решение дифференциального уравнения

   

.

Решение

Действуем по тому же алгоритму, что и в предыдущем решении.

Переписываем производную в нужном виде, разделяем переменные и интегрируем полученное уравнение:

   

   

   

   

Получили общий интеграл.Далее, воспользуемся свойством степеней, выразим у в «общем» виде и перепишем функцию:

   

   

Если  – это константа, то

   

– тоже некоторая константа, заменим её буквой С:

   

– убираем модуль и теперь константа может принимать и положительные, и отрицательные значения.

Получаем общее решение:

   

где С=const.

Ответ

   

где С=const.

Задание

Решить дифференциальное уравнение

   

Решение

В первую очередь необходимо переписать производную в необходимом виде:

   

Второй шаг – разделение переменных и перенос со сменой знака второго слагаемого в правую часть:

   

   

После разделения переменных, интегрируем уравнение, как в примерах выше.

   

Чтобы решить интегралы из левой части, применим метод подведения функции под знак дифференциала:

   

   

   

В ответе мы получили одни логарифмы и константу, их тоже определяем под логарифм.

Далее упрощаем общий интеграл:

   

   

   

   

Приводим полученный общий интеграл к виду: F(x,y)=C:

   

Чтобы ответ смотрелся красивее, обе части необходимо возвести в квадрат.

Ответ

Общий интеграл:

   

где С=const.

Задание

Найти частное решение дифференциального уравнения

   

удовлетворяющее начальному условию y(0)=ln2.

Решение

Первый шаг – нахождение общего решения. То, что в исходном уравнении уже находятся готовые дифференциалы dy и dx значительно упрощает нам решение.

Начинаем разделять переменные и интегрировать уравнение:

   

   

   

   

   

   

   

Мы получили общий интеграл и следующий шаг – выразить общее решение. Для этого необходимо прологарифмировать обе части. Знак модуля не ставим, т.к. обе части уравнения положительные.

   

   

Получаем общее решение:

   

где С=const

Далее необходимо найти частное решение, которое соответствует заданному начальному условию y(0)=ln2.

В общее решение вместо «икса» подставляем ноль, а вместо «игрека» логарифм двух:

   

   

Подставляем найденное значение константы C=1 в общее решение.

Ответ

Частное решение:

   

.

Задание

Решить дифференциальное уравнение

   

.

Решение

При внимательном разборе данного уравнения видно, что можно разделить переменные, что и делаем, после интегрируем:

   

   

   

   

   

В данном случае константу C считается  не обязательным определять под логарифм.

Ответ

Общий интеграл:

   

Задание

Найти частное решение дифференциального уравнения

   

удовлетворяющее начальному условию y(1)=e. Выполнить проверку.

Решение

Как и в предыдущих примерах первым шагом будет нахождение общего решения. Для этого начинаем разделять переменные:

   

   

Интегрируем:

   

   

   

Общий интеграл получен, осталось упростить его. Упаковываем логарифмы и избавляемся от них:

   

Используя

   

можно выразить функцию в явном виде.

Общее решение:

   

где С=const.

Осталось найти частное решение, удовлетворяющее начальному условию y(1)=e.

   

Подставляем найденное значение константы C=1 в общее решение.

Ответ

Частное решение:

   

Проверка

Необходимо проверить, выполняется ли начальное условие:

   

Из равенства выше видно, что начальное условие y(1)=e выполнено.

Далее проводим следующую проверку: удовлетворяет ли вообще частное решение

   

дифференциальному уравнению. Для этого находим производную:

   

Подставим полученное частное решение

   

и найденную производную  в исходное уравнение

   

   

   

0=0

Получено верное равенство, значит, решение найдено правильно.

Задание

Найти общий интеграл уравнения

   

Решение

Данное уравнение допускает разделение переменных. Разделяем переменные и интегрируем:

   

   

   

   

Ответ

Общий интеграл:

   

Задание

Найти частное решение ДУ.

   

Решение

Данное ДУ допускает разделение переменных. Разделяем переменные:

   

   

   

Интегрируем:

   

   

Общий интеграл:

   

Найдем частное решение (частный интеграл), соответствующий заданному начальному условию

   

Подставляем в общее решение

   

   

   

   

Ответ

Частный интеграл:

   

Задание

Решить дифференциальное уравнение

   

Решение

Данное уравнение допускает разделение переменных. Разделяем переменные и интегрируем:

   

   

Левую часть интегрируем по частям:

   

   

   

В интеграле правой части проведем замену:

   

   

   

Таким образом:

   

   

(здесь дробь раскладывается методом неопределенных коэффициентов)

   

Обратная замена:

   

   

   

Ответ

Общий интеграл:

   

где С=const.

Задание

Решить дифференциальное уравнение

   

Решение

Данное уравнение допускает разделение переменных.

Разделяем переменные и интегрируем:

   

   

   

   

   

Методом неопределенных коэффициентов разложим подынтегральную функцию в сумму элементарных дробей:

   

   

   

   

   

   

   

   

   

   

   

Ответ

Общее решение:

   

где С=const.

Дифференциальные уравнения первого порядка

Обыкновенное диффуравнение (ДУ) 1-го порядка задается относительно некой функции, имеющей вид у(х):

F(x,y(x),y´(x)) = 0,

здесь, F(x,y,y^’) – это функция, задающаяся для трех аргументов (в этом примере для х, у и у^’).Таково строгое математическое определение ДУ.

Для примера можно привести следующее уравнение:

xy'(x) — y(x)² = 0

функция вида F(x,y,p) = xp — y²

Простейшие ДУ первого порядка

Общепринятый механизм нахождения решения таких выражений (чаще всего похожи на y’ = f(x)) – это интегрирование левой и правой части такого уравнения на заданном промежутке Х. 

После интегрирования получим такое выражение:

∫ y’dx = ∫ f(x)dx

Воспользовавшись свойствами, которые относятся к интегральным выражениям, упростим выражение до вида:

y = F(x) + N

здесь, F(x) – это первообразная от функции f(x) на заданном интервале Х, а N – случайным образом выбранная константа.

Задача №1

Необходимо определить все возможные варианты решения диффуравнения, имеющего вид 

Последовательно рассмотрим решение.

Представленное диффуравнение может иметь смысл только при действительных значениях параметра х. Примем условие, что x ≠ 0, тогда выражение легко преобразовывается в следующее:

Если же, напротив, принять, что х = 0, то выражение приобретет следующий вид, характерный для любых функций y’, удовлетворяющих данному условию:

Можно заключить, что решением при справедливости условия х = 0 будет любая функция у, найденная, когда аргумент равен нулю. Остается только проинтегрировать полученное диффуравнение:

Данное выражение – это решение для приведенного диффуравнения.

ДУ с разделяющимися переменными

Среди дифуров 1-го порядка можно выделить такие, где все переменные х и у можно преобразовать так, что они окажутся по разные стороны от знака равенства. 

Соответственно уравнения, где путем преобразований это возможно сделать, называются диффуравнениями с разделяющимися переменными. 

Их общий вид следующий:

После проведения нескольких преобразований, это выражение может быть сведено к следующему виду:

При составлении преобразований необходимо внимательно разделять переменные, не допуская, чтобы функции обращались в ноль, иначе возможна потеря некоторых значений.

Задача №2

Рассмотрим обыкновенный пример. Необходимо определить все возможные решения диффуравнения y’ = y(x² + e^x)

Как решать? В первую очередь проводим разделение переменных в разные части уравнения:

Данные преобразования справедливы, если у ≠ 0.

Если рассмотреть вариант решения при нулевом показателе функции, то можно заметить ,что

Это означает, что y = 0 – одно из возможных решений задачи.

Рассмотрим другие варианты решений, для чего произведем интегрирование диффуравнения:

Финальная часть преобразований будет вторым решением диффуравнения. Останется только потенциировать это выражение, чтобы привести его к более явному виду:

Правильными решениями, в результате преобразований, будут:

 

Кроме того, можно воспользоваться онлайн системой для нахождения ответа. Подробные объяснения даны в решебниках Филиппова и Понтрягина.

Линейные неоднородные ДУ первого порядка

Линейные неоднородные уравнения – это такие выражения, которые можно записать в формате y’ + b(x)y = f(x), при этом функции b(x) и f(x) – непрерывные.

Основной принцип при нахождении решения сводится к следующим шагам:

1. Первым делом для уравнения необходимо произвести поиск решения, которое бы соответствовало линейному однородному диффуравнению.

2. Затем необходимо варьировать произвольной постоянной, производя ее замену на функцию.

3. На финальном этапе функция подставляется в первоначальное уравнение, откуда, решая ДУ, получается ответ.

Задача №3

Рассмотрим применение методики решения на примере. 

Необходимо найти решение дифференциального уравнения вида 

Решение заключается в следующем. Первоначально примем, что y = m∗n, следовательно, получается:

На следующем этапе нужно определить, что такое m (оно обязательно не должно быть равным нулю), при котором все выражение внутри скобок будет равно нулю. 

Получаем дополнительное дифференциальное уравнение:

Теперь необходимо принять одно из частных решений n = x² + 1, которое соответствует равенству С₂ — С₁=0.

Выполняем оставшиеся преобразования:

Вполне очевидно, что ответом на условие задачи будет функция:

Задача Коши для ДУ

При рассмотрении решения практически любого диффуравнения, имеющего вид F(m,n,n’) = 0, становится очевидно, что это бесконечно большое количество решений (это следствие самого возникновения диффуравнения). 

На данном этапе математики сталкиваются с вопросом о выборе конкретного решения и способе его выделения из множества.Иными словами, если представить решения в виде бесконечного множества интегральных кривых, то необходимо найти среди них нужную. 

Чтобы это сделать, необходимо рассмотреть плоскость X_oy, где должна быть задана некая точка D₀, имеющая координаты (x₀, y₀) – именно через них и должна пройти интегральная кривая, чтобы стать искомым ответом.

Когда мы с самого начала задаем точку D₀(x₀, y₀) – это означает, задание начального условия y(x₀) = y₀. Диффуравнение, для которого определено начальное условие в представленном формате, называется уравнением с заданной задачей Коши.

Задача №4

Рассмотрим примеры с объяснениями. Необходимо определить решения задачи Коши вида:

Ход решения строится в три этапа. На первом этапе решаем диффуравнение y’ = xy² стандартным методом. Его решение приводить не будем, приведем только ответ:

Производим подстановку начального значения (х = 0, у = 1) в решение и находим значение С:

Производим подстановку полученного значения в ответ диффуравнения и получаем одно из частных решений:

Полученная функция – ответ на задачу Коши в этом примере.

Дифференциальные уравнения Бернулли

ДУ Бернулли обычно представлено в следующем виде:

y’ + b(x)y = c(x)yⁿ

Обязательное условие, что функции b(x) и c(x) – являются непрерывными.

Задача №5

Рассмотрим общее решение данного типа на примере. Необходимо выполнить поиск всех возможных решений уравнения:

Во время оценки уравнения в нем можно идентифицировать ДУ Бернулли с параметром ½. Оно легко сводится к линейному ДУ, для этого достаточно заменить выражения:

Находим производную:

Выполним деление по начальному уравнению Бернулли на 

и выполним необходимые преобразования:

Произведем замену параметра х на параметр у:

Теперь вычисляем интегрирующий модуль для данной функции, он будет равен:

Теперь производим ряд преобразований для вычисления решения диффуравнения:

Переписываем полученную функцию в неявном виде и получаем ответ:

Дифференциальные уравнения второго порядка

Отличить ДУ 2-го порядка от таковых 1-го порядка достаточно просто – в их составе присутствует вторая производная (y’’) и не содержится производных более высокого уровня. 

Общий вид таких уравнений таков:

F(m,n,n’,n») = 0  

Линейные однородные ДУ второго порядка с постоянными коэффициентами

Определение линейных дифференциальных однородных уравнений 2-го порядка крайне просто – они имеют вид:

y» + ry’ + k = 0

При это важным условием теории является причисление r и k к действительным числам.

Задача №6

Рассмотрим решение однородных диффуравнений 2-го порядка с постоянными коэффициентами на примере.

Найти решение диффуравнения 2-го порядка вида:

Во всех таких случаях начинаем с поиска характеристического уравнения:

Методы решения данного уравнения достаточно простые, можно воспользоваться калькулятором или быстро решить на листочке, поэтому их приводить не будем, запишем лишь корни – 1, 5. 

Поскольку это все действительные, неодинаковые числа, то можно записать функцию-решение в следующем виде:

 

Линейные неоднородные ДУ второго порядка с постоянными коэффициентами

Общий вид неоднородных диффуравнений второго порядка легко определить по представленному образцу:

y» + ry’ + ky = f(x)

Переменные r и k должны быть вещественными и постоянными числами.

Задача №7

Рассмотрим подробное решение. Необходимо определить все решения для уравнения y» + y = cos x.

На первом этапе находим в составе неоднородного уравнения его однородную часть – это будет y» — y = 0. 

Для него уже выполняем поиск характеристического уравнения – оно будет иметь вид k² + 1 = 0.

Корнями для данного характеристического уравнения являются k₁ = -i и k₂ = i. 

Исходя из этого записываем решение для однородного уравнения:

Из-за отсутствия параметра с производной первого порядка также будет справедливо записать:

Теперь остается только подставить найденные выражения:

Частное и общее решение для уравнения можно записать:

Дифференциальные уравнения высших порядков

Дифференциальные однородные уравнения высших порядков легко отличить, если они совпадают со следующим видом:

Для неоднородных справедлив другой формат:

Для выбора корректного пути решения ДУ, необходимо четко и правильно определить его тип. 

Для этого необходимо решить уравнение относительно его производной и проверить, возможно ли разложение функции на множители. После этого достаточно сравнить с одним из типов, приведенным в данной статье.

>

Примеры решения дифференциальных уравнений с ответами

Простое объяснение принципов решения дифференциальных уравнений и 10 наглядных примеров. В каждом примере поэтапный ход решения и ответ.

Алгоритм решения дифференциальных уравнений

Дифференциальные уравнения не так сильно отличаются от привычных уравнений, где необходимо найти переменную x , как кажется на первый взгляд. Всё различие лишь в том, что в дифференциальных уравнениях мы ищем не переменную, а функцию у(х) , с помощью которой можно обратить уравнение в равенство.

Дифференциальное уравнение – это уравнение, содержащее саму функцию (y=y(x)), производные функции или дифференциалы (y′, y″) и независимые переменные (наиболее распространённая – х). Обыкновенным дифференциальным уравнением называют уравнение, в котором содержится неизвестная функция под знаком производной или под знаком дифференциала.

Чтобы решить ДУ, необходимо найти множество всех функций, которые удовлетворяют данному уравнению. Это множество в большинстве случаев выглядит следующим образом:y=f(x; С), где С – произвольная постоянная.

Проверить решённое ДУ можно, подставив найденную функцию в изначальное уравнение и убедившись, что уравнение обращается в тождество (равенство).

Примеры решения дифференциальных уравнений

Задание

Решить дифференциальное уравнение xy’=y.

Решение

В первую очередь, необходимо переписать уравнение в другой вид. Пользуясь

переписываем дифференциальное уравнение, получаем

Дальше смотрим, насколько реально разделить переменные, то есть путем обычных манипуляций (перенос слагаемых из части в часть, вынесение за скобки и пр.) получить выражение, где «иксы» с одной стороны, а «игреки» с другой. В данном уравнении разделить переменные вполне реально, и после переноса множителей по правилу пропорции получаем

Далее интегрируем полученное уравнение:

В данном случае интегралы берём из таблицы:

После того, как взяты интегралы, дифференциальное уравнение считается решённым. Решение дифференциального уравнения в неявном виде называется общим интегралом дифференциального уравнения.

– это общий интеграл. Также для удобства и красоты, его можно переписать в другом виде: y=Cx, где С=Const

Ответ

Задание

Найти частное решение дифференциального уравнения

Решение

Действуем по тому же алгоритму, что и в предыдущем решении.

Переписываем производную в нужном виде, разделяем переменные и интегрируем полученное уравнение:

Получили общий интеграл.Далее, воспользуемся свойством степеней, выразим у в «общем» виде и перепишем функцию:

Если – это константа, то

0]» title=»Rendered by QuickLaTeX.com» />

– тоже некоторая константа, заменим её буквой С:

– убираем модуль и теперь константа может принимать и положительные, и отрицательные значения.

Получаем общее решение:

Ответ

Задание

Решить дифференциальное уравнение

Решение

В первую очередь необходимо переписать производную в необходимом виде:

Второй шаг – разделение переменных и перенос со сменой знака второго слагаемого в правую часть:

После разделения переменных, интегрируем уравнение, как в примерах выше.

Чтобы решить интегралы из левой части, применим метод подведения функции под знак дифференциала:

В ответе мы получили одни логарифмы и константу, их тоже определяем под логарифм.

Далее упрощаем общий интеграл:

Приводим полученный общий интеграл к виду: F(x,y)=C:

Чтобы ответ смотрелся красивее, обе части необходимо возвести в квадрат.

Ответ

Задание

Найти частное решение дифференциального уравнения

удовлетворяющее начальному условию y(0)=ln2.

Решение

Первый шаг – нахождение общего решения. То, что в исходном уравнении уже находятся готовые дифференциалы dy и dx значительно упрощает нам решение.

Начинаем разделять переменные и интегрировать уравнение:

Мы получили общий интеграл и следующий шаг – выразить общее решение. Для этого необходимо прологарифмировать обе части. Знак модуля не ставим, т.к. обе части уравнения положительные.

Получаем общее решение:

Далее необходимо найти частное решение, которое соответствует заданному начальному условию y(0)=ln2.

В общее решение вместо «икса» подставляем ноль, а вместо «игрека» логарифм двух:

Подставляем найденное значение константы C=1 в общее решение.

Ответ

Задание

Решить дифференциальное уравнение

Решение

При внимательном разборе данного уравнения видно, что можно разделить переменные, что и делаем, после интегрируем:

В данном случае константу C считается не обязательным определять под логарифм.

Ответ

Задание

Найти частное решение дифференциального уравнения

удовлетворяющее начальному условию y(1)=e. Выполнить проверку.

Решение

Как и в предыдущих примерах первым шагом будет нахождение общего решения. Для этого начинаем разделять переменные:

Общий интеграл получен, осталось упростить его. Упаковываем логарифмы и избавляемся от них:

можно выразить функцию в явном виде.

Осталось найти частное решение, удовлетворяющее начальному условию y(1)=e.

Подставляем найденное значение константы C=1 в общее решение.

Ответ

Проверка

Необходимо проверить, выполняется ли начальное условие:

Из равенства выше видно, что начальное условие y(1)=e выполнено.

Далее проводим следующую проверку: удовлетворяет ли вообще частное решение

дифференциальному уравнению. Для этого находим производную:

Подставим полученное частное решение

и найденную производную в исходное уравнение

Получено верное равенство, значит, решение найдено правильно.

Задание

Найти общий интеграл уравнения

Решение

Данное уравнение допускает разделение переменных. Разделяем переменные и интегрируем:

Ответ

Задание

Найти частное решение ДУ.

Решение

Данное ДУ допускает разделение переменных. Разделяем переменные:

Найдем частное решение (частный интеграл), соответствующий заданному начальному условию

Подставляем в общее решение

Ответ

Задание

Решить дифференциальное уравнение

Решение

Данное уравнение допускает разделение переменных. Разделяем переменные и интегрируем:

Левую часть интегрируем по частям:

В интеграле правой части проведем замену:

(здесь дробь раскладывается методом неопределенных коэффициентов)

Ответ

Задание

Решить дифференциальное уравнение

Решение

Данное уравнение допускает разделение переменных.

Разделяем переменные и интегрируем:

Методом неопределенных коэффициентов разложим подынтегральную функцию в сумму элементарных дробей:

Дифференциальные уравнения (ДУ) — методы и примеры решения уравнений разного порядка

Многих людей, хоть как-то изучавших курс высшей математики в учебном заведении, приводит в ужас словосочетание «дифференциальные уравнения». Согласно строгому научному определению в книгах – так именуются математические выражения, где в состав входят функция, ее производная или параметр. Имеется достаточно большое количество типов этих равенств, рассмотрим подходы к их решению так, чтобы они были понятны даже для «чайников».

Дифференциальные уравнения первого порядка

Обыкновенное диффуравнение (ДУ) 1-го порядка задается относительно некой функции, имеющей вид у(х):

здесь, F(x,y,y ’ ) – это функция, задающаяся для трех аргументов (в этом примере для х, у и у ’ ).Таково строгое математическое определение ДУ.

Для примера можно привести следующее уравнение:

функция вида F(x,y,p) = xp — y 2

Простейшие ДУ первого порядка

Общепринятый механизм нахождения решения таких выражений (чаще всего похожи на y’ = f(x)) – это интегрирование левой и правой части такого уравнения на заданном промежутке Х.

После интегрирования получим такое выражение:

Воспользовавшись свойствами, которые относятся к интегральным выражениям, упростим выражение до вида:

здесь, F(x) – это первообразная от функции f(x) на заданном интервале Х, а N – случайным образом выбранная константа.

Задача №1

Необходимо определить все возможные варианты решения диффуравнения, имеющего вид

Последовательно рассмотрим решение.

Представленное диффуравнение может иметь смысл только при действительных значениях параметра х. Примем условие, что x ≠ 0, тогда выражение легко преобразовывается в следующее:

Если же, напротив, принять, что х = 0, то выражение приобретет следующий вид, характерный для любых функций y’, удовлетворяющих данному условию:

Можно заключить, что решением при справедливости условия х = 0 будет любая функция у, найденная, когда аргумент равен нулю. Остается только проинтегрировать полученное диффуравнение:

Данное выражение – это решение для приведенного диффуравнения.

ДУ с разделяющимися переменными

Среди дифуров 1-го порядка можно выделить такие, где все переменные х и у можно преобразовать так, что они окажутся по разные стороны от знака равенства.

Соответственно уравнения, где путем преобразований это возможно сделать, называются диффуравнениями с разделяющимися переменными.

Их общий вид следующий:

После проведения нескольких преобразований, это выражение может быть сведено к следующему виду:

При составлении преобразований необходимо внимательно разделять переменные, не допуская, чтобы функции обращались в ноль, иначе возможна потеря некоторых значений.

Задача №2

Рассмотрим обыкновенный пример. Необходимо определить все возможные решения диффуравнения y’ = y(x 2 + e x )

Как решать? В первую очередь проводим разделение переменных в разные части уравнения:

Данные преобразования справедливы, если у ≠ 0.

Если рассмотреть вариант решения при нулевом показателе функции, то можно заметить ,что

Это означает, что y = 0 – одно из возможных решений задачи.

Рассмотрим другие варианты решений, для чего произведем интегрирование диффуравнения:

Финальная часть преобразований будет вторым решением диффуравнения. Останется только потенциировать это выражение, чтобы привести его к более явному виду:

Правильными решениями, в результате преобразований, будут:

Кроме того, можно воспользоваться онлайн системой для нахождения ответа. Подробные объяснения даны в решебниках Филиппова и Понтрягина.

Линейные неоднородные ДУ первого порядка

Линейные неоднородные уравнения – это такие выражения, которые можно записать в формате y’ + b(x)y = f(x), при этом функции b(x) и f(x) – непрерывные.

Основной принцип при нахождении решения сводится к следующим шагам:

Первым делом для уравнения необходимо произвести поиск решения, которое бы соответствовало линейному однородному диффуравнению.

Затем необходимо варьировать произвольной постоянной, производя ее замену на функцию.

На финальном этапе функция подставляется в первоначальное уравнение, откуда, решая ДУ, получается ответ.

Задача №3

Рассмотрим применение методики решения на примере.

Необходимо найти решение дифференциального уравнения вида

Решение заключается в следующем. Первоначально примем, что y = m∗n, следовательно, получается:

На следующем этапе нужно определить, что такое m (оно обязательно не должно быть равным нулю), при котором все выражение внутри скобок будет равно нулю.

Получаем дополнительное дифференциальное уравнение:

Теперь необходимо принять одно из частных решений n = x 2 + 1, которое соответствует равенству С₂ — С₁=0.

Выполняем оставшиеся преобразования:

Вполне очевидно, что ответом на условие задачи будет функция:

Задача Коши для ДУ

При рассмотрении решения практически любого диффуравнения, имеющего вид F(m,n,n’) = 0, становится очевидно, что это бесконечно большое количество решений (это следствие самого возникновения диффуравнения).

На данном этапе математики сталкиваются с вопросом о выборе конкретного решения и способе его выделения из множества.Иными словами, если представить решения в виде бесконечного множества интегральных кривых, то необходимо найти среди них нужную.

Чтобы это сделать, необходимо рассмотреть плоскость X_oy, где должна быть задана некая точка D₀, имеющая координаты (x₀, y₀) – именно через них и должна пройти интегральная кривая, чтобы стать искомым ответом.

Когда мы с самого начала задаем точку D₀(x₀, y₀) – это означает, задание начального условия y(x₀) = y₀. Диффуравнение, для которого определено начальное условие в представленном формате, называется уравнением с заданной задачей Коши.

Задача №4

Рассмотрим примеры с объяснениями. Необходимо определить решения задачи Коши вида:

Ход решения строится в три этапа. На первом этапе решаем диффуравнение y’ = xy 2 стандартным методом. Его решение приводить не будем, приведем только ответ:

Производим подстановку начального значения (х = 0, у = 1) в решение и находим значение С:

Производим подстановку полученного значения в ответ диффуравнения и получаем одно из частных решений:

Полученная функция – ответ на задачу Коши в этом примере.

Дифференциальные уравнения Бернулли

ДУ Бернулли обычно представлено в следующем виде:

Обязательное условие, что функции b(x) и c(x) – являются непрерывными.

Задача №5

Рассмотрим общее решение данного типа на примере. Необходимо выполнить поиск всех возможных решений уравнения:

Во время оценки уравнения в нем можно идентифицировать ДУ Бернулли с параметром ½. Оно легко сводится к линейному ДУ, для этого достаточно заменить выражения:

Выполним деление по начальному уравнению Бернулли на

и выполним необходимые преобразования:

Произведем замену параметра х на параметр у:

Теперь вычисляем интегрирующий модуль для данной функции, он будет равен:

Теперь производим ряд преобразований для вычисления решения диффуравнения:

Переписываем полученную функцию в неявном виде и получаем ответ:

Дифференциальные уравнения второго порядка

Отличить ДУ 2-го порядка от таковых 1-го порядка достаточно просто – в их составе присутствует вторая производная (y’’) и не содержится производных более высокого уровня.

Общий вид таких уравнений таков:

Линейные однородные ДУ второго порядка с постоянными коэффициентами

Определение линейных дифференциальных однородных уравнений 2-го порядка крайне просто – они имеют вид:

При это важным условием теории является причисление r и k к действительным числам.

Задача №6

Рассмотрим решение однородных диффуравнений 2-го порядка с постоянными коэффициентами на примере.

Найти решение диффуравнения 2-го порядка вида:

Во всех таких случаях начинаем с поиска характеристического уравнения:

Методы решения данного уравнения достаточно простые, можно воспользоваться калькулятором или быстро решить на листочке, поэтому их приводить не будем, запишем лишь корни – 1, 5.

Поскольку это все действительные, неодинаковые числа, то можно записать функцию-решение в следующем виде:

Линейные неоднородные ДУ второго порядка с постоянными коэффициентами

Общий вид неоднородных диффуравнений второго порядка легко определить по представленному образцу:

Переменные r и k должны быть вещественными и постоянными числами.

Задача №7

Рассмотрим подробное решение. Необходимо определить все решения для уравнения y» + y = cos x.

На первом этапе находим в составе неоднородного уравнения его однородную часть – это будет y» — y = 0.

Для него уже выполняем поиск характеристического уравнения – оно будет иметь вид k 2 + 1 = 0.

Корнями для данного характеристического уравнения являются k₁ = -i и k₂ = i.

Исходя из этого записываем решение для однородного уравнения:

Из-за отсутствия параметра с производной первого порядка также будет справедливо записать:

Теперь остается только подставить найденные выражения:

Частное и общее решение для уравнения можно записать:

Дифференциальные уравнения высших порядков

Дифференциальные однородные уравнения высших порядков легко отличить, если они совпадают со следующим видом:

Для неоднородных справедлив другой формат:

Для выбора корректного пути решения ДУ, необходимо четко и правильно определить его тип.

Для этого необходимо решить уравнение относительно его производной и проверить, возможно ли разложение функции на множители. После этого достаточно сравнить с одним из типов, приведенным в данной статье.

Что такое дифференциальное уравнение и зачем оно нужно?

На сегодняшний день одним из важнейших навыков для любого специалиста является умение решать дифференциальные уравнения. Решение дифференциальных уравнений – без этого не обходится ни одна прикладная задача, будь это расчет какого-либо физического параметра или моделирование изменений в результате принятой макроэкономической политики. Эти уравнения также важны для ряда других наук, таких как химия, биология, медицина и т.д. Ниже мы приведем пример использования дифференциальных уравнений в экономике, но перед этим кратко расскажем об основных типах уравнений.

Дифференциальные уравнения – простейшие виды

Мудрецы говорили, что законы нашей вселенной написаны на математическом языке. Конечно, в алгебре есть много примеров различных уравнений, но это, большей частью, учебные примеры, неприменимые на практике. По-настоящему интересная математика начинается, когда мы хотим описать процессы, протекающие в реальной жизни. Но как отразить фактор времени, которому подчиняются реальные процессы – инфляция, выработка продукции или демографические показатели?

Вспомним одно важное определение из курса математики, касающееся производной функции. Производная является скоростью изменения функции, следовательно, она может помочь нам отразить фактор времени в уравнении.

То есть, мы составляем уравнение с функцией, которая описывает интересующий нас показатель и добавляем в уравнение производную этой функции. Это и есть дифференциальное уравнение. А теперь перейдем к простейшим типам дифференциальных уравнений для чайников.

Простейшее дифференциальное уравнение имеет вид $y’(x)=f(x)$, где $f(x)$ – некоторая функция, а $y’(x)$ – производная или скорость изменения искомой функции. Оно решается обычным интегрированием: $$y(x)=int f(x)dx.$$

Второй простейший тип называется дифференциальным уравнением с разделяющимися переменными. Такое уравнение выглядит следующим образом $y’(x)=f(x)cdot g(y)$. Видно, что зависимая переменная $y$ также входит в состав конструируемой функции. Уравнение решается очень просто – нужно «разделить переменные», то есть привести его к виду $y’(x)/g(y)=f(x)$ или $dy/g(y)=f(x)dx$. Остается проинтегрировать обе части $$int frac=int f(x)dx$$ – это и есть решение дифференциального уравнения разделяющегося типа.

Последний простой тип – это линейное дифференциальное уравнение первого порядка. Оно имеет вид $y’+p(x)y=q(x)$. Здесь $p(x)$ и $q(x)$ – некоторые функции, а $y=y(x)$ – искомая функция. Для решения такого уравнения применяют уже специальные методы (метод Лагранжа вариации произвольной постоянной, метод подстановки Бернулли).

Есть более сложные виды уравнений – уравнения второго, третьего и вообще произвольного порядка, однородные и неоднородные уравнения, а также системы дифференциальных уравнений. Для их решения нужна предварительная подготовка и опыт решения более простых задач.

Большое значение для физики и, что неожиданно, финансов имеют так называемые дифференциальные уравнения в частных производных. Это значит, что искомая функция зависит от нескольких переменных одновременно. Например, уравнение Блека-Шоулса из области финансового инжиниринга описывает стоимость опциона (вид ценной бумаги) в зависимости от его доходности, размера выплат, а также сроков начала и конца выплат. Решение дифференциального уравнения в частных производных довольно сложное, обычно нужно использовать специальные программы, такие как Matlab или Maple.

Пример применения дифференциального уравнения в экономике

Приведем, как и было обещано, простой пример решения дифференциального уравнения. Вначале поставим задачу.

Для некоторой фирмы функция маржинальной выручки от продажи своей продукции имеет вид $MR=10-0,2q$. Здесь $MR$ – маржинальная выручка фирмы, а $q$ – объем продукции. Нужно найти общую выручку.

Как видно из задачи, это прикладной пример из микроэкономики. Множество фирм и предприятий постоянно сталкивается с подобными расчетами в ходе своей деятельности.

Приступаем к решению. Как известно из микроэкономики, маржинальная выручка представляет собой производную от общей выручки, причем выручка равна нулю при нулевом уровне продаж.

С математической точки задача свелась к решению дифференциального уравнения $R’=10-0,2q$ при условии $R(0)=0$.

Проинтегрируем уравнение, взяв первообразную функцию от обеих частей, получим общее решение: $$R(q) = int (10-0,2q)dq = 10 q-0,1q^2+C. $$

Чтобы найти константу $C$, вспомним условие $R(0)=0$. Подставим: $$R(0) =0-0+C = 0. $$ Значит C=0 и наша функция общей выручки принимает вид $R(q)=10q-0,1q^2$. Задача решена.

Другие примеры по разным типам ДУ собраны на странице: Дифференциальные уравнения с решениями онлайн.

Как решать дифференциальные уравнения

Дифференциальные уравнения бывают обыкновенными и в частных производных. В этой статье мы будем говорить об обыкновенных уравнениях и о том, как их решать.

Основные понятия и определения

Определения

Обыкновенные дифференциальные уравнения – это уравнения, содержащие функцию $y(x)$ только от одной неизвестной переменной (например, $x$).

Рассмотрим это на следующих практических примерах. $$ y’ = xy $$ $$ y» = 1 $$

Итак, в первом диффуре присутствует независимая переменная $x$, неизвестная функция $y(x)$ и производная этой функции $y'(x)$. А во втором случае нет $x, y(x),y'(x)$, а есть только вторая производная функции $y»(x)$. Значит, для того, чтобы уравнение называлось дифференциальным необязательно иметь $y(x)$ и $x$, а должно быть производная $y(x)$ любого порядка.

Порядок дифференциального уравнения – это порядок старшей производной неизвестной функции $y(x)$ в уравнении.

В первом случае максимальная производная первого порядка, значит, и само ДУ первого порядка. А во втором случае уравнение имеет вторую производную $y»(x)$, поэтому это ДУ второго порядка. 

Общее решение дифференциального уравнения – это семейство функций $y = f(x,C)$, при подстановке которых в заданное исходное уравнение мы получаем равенство левой и правой части. Здесь $C$ произвольная константа. Процесс нахождения таких решений называется интегрированием дифференциального уравнения.

Частное решение дифференциального уравнения – это решение, полученное из общего решения, путем нахождения константы $C$ из дополнительных условий в задаче.

Типы уравнений

1. ДУ первого порядка
   – с разделяющимися переменными
   – однородные
   – линейные неоднородные
   – уравнение Бернулли
2. ДУ второго порядка
   – уравнения допускающие понижение порядка
   – однородные с постоянными коэффициентами
   – неоднородные с постоянными коэффициентами 

Алгоритм решения

1. По старшей производной функции $y(x)$ определить порядок ДУ
2. Зная порядок, определить тип уравнения
3. Узнав тип, подобрать подходящий метод решения
4. Используя метод, найти общее решение
5. Получить частное решение из общего путем вычисления неизвестной $C$

В некоторых случаях для решения дифференциальных уравнений удобно переписать производные в таком виде (например, это нужно для ДУ с разделяющимися переменными). $$y’ = frac{dy}{dx}$$

ОБЯЗАТЕЛЬНО! Чтобы успешно решать дифференциальные уравнения необходимо уметь находить интегралы. Поэтому, если вы забыли данную тему, то её нужно вспомнить!

Пример 1

Дана функция $y = Ce^{frac{x^2}{2}} $. Проверить является ли функция решением дифференциального уравнения $y’ = xy$

Решение

Для того, чтобы проверить является ли функция решением нужно подставить её в исходное ДУ. Найдем производную функции. $$y’ = (Ce^{frac{x^2}{2}})’ = Ce^{frac{x^2}{2}} cdot (frac{x^2}{2})’ = Ce^{frac{x^2}{2}} cdot x = Cxe^{frac{x^2}{2}}$$ Теперь подставим $y’$ и $y$ в исходное уравнение. $$ Cxe^{frac{x^2}{2}} = x Ce^{frac{x^2}{2}} $$ Получили равенство левой и правой части, значит, функция $y = Ce^{frac{x^2}{2}} $ является общим решением ДУ.

Ответ

$$y = Ce^{frac{x^2}{2}} $$

Дифференциальные уравнения первого порядка

ДУ с разделяющимися переменными

Уравнения такого типа имеют следующий вид: $$ f_1(x)g_1(y)dy = f_2(x)g_2(y)dx$$ Общее решение такого ДУ нужно находить путем разделения переменных с иксами и с игреками: $$int frac{g_1(y)}{g_2(y)}dy = int frac{f_2(x)}{f_1(x)}dx$$

СОВЕТ: Если не удается определить тип диффура первого порядка, то рекомендуем мысленно попытаться разделить переменные иксы от игреков. Возможно перед вами хитрое дифференциальное уравнение с разделяющимися переменными.

Алгоритм нахождения общего решения:

1. Переписываем производные через $y’ = frac{dy}{dx}$
2. Разделяем все $y$ в левую часть уравнения, а все $x$ в правую
3. Интегрируем обе части уравнения

Пример 2

Найти общее решение дифференциального уравнения первого порядка с разделяющимися переменными $y’ = xy$

Решение

Видим, что в условии задачи присутствует производная от неизвестной функции $y(x)$ первого порядка. Значит, перед нами диффур 1-го порядка.  Забегая вперед скажем, что данный диффур из задачи является дифференциальным уравнением с разделяющимися переменными. Что это означает? Это означает, что можно в уравнении перенести всё что содержит $y$ в левую часть равенства, а то, что содержит $x$ перенести в правую часть. То есть разделить «игрики» от «иксов» по разные стороны. Но прежде, чем это делать стоит переписать производную таким образом: $$y’ = frac{dy}{dx}$$ После замены производной игрека исходное уравнение приобретает такой формат: $$frac{dy}{dx} = xy$$ Теперь, как сказали ранее, начинаем отделять игрики от иксов по разные стороны. Для этого обе части уравнения необходимо умножить на $dx$, а ещё разделить на $y$. $$ frac{dy}{y} = xdx $$ Теперь необходимо проинтегрировать обе части уравнения, чтобы получить функцию $y$. Для этого навешиваем значок интеграла на обе части уравнения. $$ int frac{dy}{y} = int xdx $$ Вспоминаем, что левый интеграл равен натуральному логарифму, а правый интеграл $frac{x^2}{2}$. А так как интеграл неопределенный, то необходимо прибавить константу $C$. $$ ln|y| = frac{x^2}{2} + C $$ Теперь необходимо вытащить $y$ для того, чтобы записать окончательный ответ в виде общего решения. Для этого вспоминаем, что игрик в $ln|y| = x$ равен $y = e^x$. Поэтому продолжая решать наше уравнение получаем. $$ y = e^{frac{x^2}{2} + C} $$ Далее вспоминаем свойство степеней $a^{x+y} = a^x cdot a^y$. Таким образом делаем преобразования нашего уравнения. $$ y = e^{frac{x^2}{2}} cdot e^C $$ Так как $e^C$ это константа, то её можно переписать следующим видом $e^C = C$. И после этого получаем окончательный ответ исходного уравнения, называемый общим решением. $$ y = Ce^{frac{x^2}{2}} $$

Ответ

$$ y = Ce^{frac{x^2}{2}} $$

Пример 3

Найти частное решение дифференциального уравнения первого порядка с разделяющимися переменными $y’ = frac{2x}{1+x^2}$, если $y(0) = 0$.

Решение

Начнем решать с того, что представим производную в исходном уравнении в виде $y’ = frac{dy}{dx}$: $$ frac{dy}{dx} = frac{2x}{1+x^2} $$ Теперь разделяем переменные иксы от игреков по разные стороны равенства путем умножения обеих частей уравнения на $dx$: $$ dy = frac{2x}{1+x^2} dx $$ Навешиваем знак интеграла на левую и правую часть, а затем решаем интегралы: $$ int dy = int frac{2x}{1+x^2} dx $$ $$ y =  int frac{2x}{1+x^2} dx $$ Замечаем, что $(1+x^2)’ = 2x$. Поэтому $2x$ можно занести под знак дифференциала, чтобы решить интеграл: $$ y = int frac{d(1+x^2)}{1+x^2} = ln (1+x^2) + C $$ Получили общее решение $y = ln (1+x^2) + C$. В условии задачи просят найти частное решение при условии $y(0) = 0$. Это означает, что нужно из последного условия найти константу $C$. Из $y(0) = 0$ видно, что $x = 0$, а $y = 0$. Подставляем их в общее решение дифференциального уравнения и вычисляем $C$: $$ln(1+0^2)+C = 0$$ $$ln 1+C = 0$$ $$0 + C = 0$$ $$C=0$$ Теперь заменив в общем решении $C$ на ноль, получаем частное решение: $$y = ln(1+x^2)$$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$y = ln(1+x^2)$$

Однородные ДУ

Чтобы проверить является ли предложенное уравнение однородным нужно заменить $x$ и $y$ на $lambda x$ и $lambda y$. Производную $y’$ заменять не нужно. Если все $lambda$ после элементарных преобразований удастся уничтожить, то перед вами однородное дифференциальное уравнение первого порядка.

Решается по следующему алгоритму:

1. Проверить уравнение на однородность с помощью $lambda$
2. Привести уравнение к виду $y’ = f(frac{y}{x})$
3. Выполнить замену $frac{y}{x} = t$ и $y’ = t’x+t$
4. Решить уравнение методом разделяющихся переменных

Пример 4

Найти общее решение дифференциального уравнения первого порядка $$y’ = frac{y}{x} — 1$$

Решение

Так как разделить переменные не получается, то проверим уравнение на однородность. Для этого вместо $x$ и $y$ выполним подстановку $lambda x$ и $lambda y$: $$y’ = frac{lambda y}{lambda x} — 1$$ Выполняем сокращение $lambda$ в числителе и знаменателе: $$y’ = frac{y}{x} — 1$$ После сокращения все $lambda$ уничтожились, значит перед нами однородное дифференциальное уравнение первого порядка. Решим его с помощью замены $frac{y}{x} = t$ и $y’ = t’x + t$: $$ t’x + t = t — 1$$ Переносим $t$ в одну сторону и тем самым уничтожаем его: $$ t’x = -1 $$ Теперь это ДУ с разделяющимися переменными. Запишем его в привычном для него виде: $$ frac{dt}{dx} x = -1 $$ Разделим переменные домножением на $dx$ и делением на $x$ обеих частей равенства: $$dt = -frac{dx}{x}$$ Интегрируем обе части: $$int dt = — int frac{dx}{x}$$ $$t = -ln|x|+C$$ Выполняем назад замену $t = frac{y}{x}$: $$frac{y}{x} = -ln|x|+C$$ Умножаем обе части на $x$, чтобы получить окончательный ответ общего решения: $$y = -xln|x| +Cx$$

Ответ

$$y = -xln|x| +Cx$$

Пример 5

Решить дифференциальное уравнение первого порядка $xy+y^2=(2x^2+xy)y’$

Решение

Сперва проверим уравнение на однородность. Подставляем $lambda$ вместо $x$ и $y$. $$lambda x cdot lambda y + (lambda y)^2 = (2 (lambda x)^2 + lambda xcdot lambda y)y’$$ После вынесения $lambda$ слева и справа за скобки получаем $$ lambda^2(xy+y^2) = lambda^2(2x^2+xy)y’,$$ где все $lambda$ сокращаются. А это подтвержает однородность уравнения. Перед тем, как выполнить замену $t = frac{y}{x}$ нужно привести исходное уравнение к виду $y = f(frac{y}{x})$. Для этого разделим левую и правую часть равенства на $x^2$: $$frac{y}{x}+frac{y^2}{x^2} = (2+frac{y}{x})y’.$$ Теперь производим замену $t = frac{y}{x}$ и $y’ = t’x+t$ в преобразованном уравнении: $$t+t^2=(2+t)(t’x+t).$$ Раскрываем скобки и сокращаем одинаковые слагаемые $$t+t^2 = 2t’x+2t+t’xt+t^2$$ $$2t’x+t’xt=-t.$$ Далее в полученном уравнении разделяем переменные $t$ и $x$ по разные стороны знака равенства. Для этого выносим за скобку $t’x$ $$t’x(2+t)=-t.$$ Делим на $t$ обе части уравнения $$t’xfrac{2+t}{t}=-1.$$ Представляем производную $t’ = frac{dt}{dx}$ и переносим $dx$ и $x$ в правую часть равенства $$frac{2+t}{t}dt = -frac{dx}{x}.$$ Интегрируем обе части уравнения $$int frac{2+t}{t}dt = — int frac{dx}{x}$$ $$int frac{2}{t}dt+int dt = -int frac{dx}{x}$$ $$2ln|t|+t = -ln|x|+C.$$ Выполняем обратную замену $t = frac{y}{x}$: $$2ln|frac{y}{x}|+frac{y}{x}=-ln|x|+C.$$ Упрощаем полученное равенство с помощью элементарных преобразований и свойств натурального логарифма $$2ln|y|-2ln|x|+frac{y}{x} = -ln|x|+C$$ $$2ln|y|+frac{y}{x}=ln|x|+C$$ $$2ln|y|+frac{y}{x}=ln|x|+ln|C|$$ $$2ln|y|+frac{y}{x}=ln|Cx|$$ $$ln y^2+frac{y}{x}=ln|Cx|$$ $$ln y^2 = ln|Cx|-frac{y}{x}$$ $$y^2 = Cxe^frac{-y}{x}.$$ Привели решение к такому виду через $y^2$. Это называется общим интегралом дифференциального уравнения. Ответ в таком виде остается в таком формате. Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$y^2 = Cxe^frac{-y}{x}$$

Линейные неоднородные ДУ

Линейное неоднородное дифференциальное уравнение 1-го порядка имеет следующий вид $$y’+p(x)y=q(x).$$

Для его решения существует два способа: метод Бернулли и вариация произвольной постоянной. В первом методе нужно сделать замену на произведение двух функций $y = uv$, а во втором способе необходимо найти неизвестную функцию $C(x)$. 

Алгоритм метода Бернулли:

1. Выполняем замену $y=uv$ и $y’ = u’v+uv’$
2. Находим функции $u(x)$ и $v(x)$ с помощью решения системы двух уравнений
3. Подставляем найденные $u(x)$ и $v(x)$ в уравнение $y=uv$, чтобы получить ответ

Алгоритм метода вариации произвольной постоянной:

1. Решаем исходное уравнение в качестве однородного методом разделяющихся переменных
2. В полученном общем решении заменяем константу $C$ на функцию $C(x)$
3. Подставляем общее решение и его производную в исходное уравнение, чтобы найти $C(x)$
4. Полученное $C(x)$ подставляем в общее решение однородного уравнения и записываем ответ

Пример 6

Найти частное решение дифференциального уравнения первого порядка методом Бернулли $xy’-2y=2x^4$, если $y(1)=0$.

Решение

Приводим уравнение к виду $y’+p(x)y=q(x)$ путем деления на $x$ обеих частей равенства $$y’-2frac{y}{x}=2x^3.$$ Делаем замену в полученном уравнении на $y=uv$ и $y’=u’v+uv’$ $$u’v+uv’-2frac{uv}{x}=2x^3.$$Выносим за скобку $u$, чтобы в дальнейшем составить систему уравнений: $$u’v+u(v’-2frac{v}{x})=2x^3.$$ Теперь приравниваем к нулю выражение в скобках и составляем систему уравнений $$begin{cases} v’ — 2frac{v}{x} = 0 \ u’v = 2x^3 end{cases},$$ в которой начнем сначала решать первое уравнение для нахождения функции $v(x)$. Разделяем в нём переменные $$begin{cases} frac{dv}{dx} = 2frac{v}{x} \ u’v = 2x^3 end{cases} Leftrightarrow begin{cases} frac{dv}{v} = 2frac{dx}{x} \ u’v = 2x^3 end{cases}.$$ Интегрируем первое уравнение в системе, чтобы получить функцию $v(x)$ $$begin{cases} ln|v| = 2ln|x| \ u’v = 2x^3 end{cases} Leftrightarrow begin{cases} v = x^2 \ u’v = 2x^3 end{cases}.$$ Теперь, зная, чему равно $v$ подставляем его во второе уравнение $$begin{cases} v=x^2 \ u’x^2 = 2x^3 end{cases} Leftrightarrow begin{cases} v=x^2 \ u = x^2+C end{cases}.$$ Записываем общее решение дифференциального уравнения $$y = uv Rightarrow y = x^4+Cx^2.$$ В условии задачи требуется найти частное решение из условия $y(1)=0$. Подставим в найденное общее решение $x=1$ и $y=0$, чтобы вычислить $C$ $$1^4+Ccdot 1^2 = 0 Rightarrow C = -1. $$ С учётом, что $C=-1$ записываем частное решение дифференциального уравнения $$y = x^4 — x^2.$$

Ответ

$$y = x^4 — x^2$$

Пример 7

Найти общее решение дифференциального уравнения первого порядка $y’sin x-ycos x = 1$ методом вариации произвольной постоянной $C$.

Решение

Перепишем уравнение в виде $$ y’ — y frac{cos x}{sin x} = frac{1}{sin x} .$$ Теперь записываем однородное дифференциальное уравнение $$y’ — y frac{cos x}{sin x} = 0,$$ решим его методом разделяющихся переменных: $$frac{dy}{dx} = y frac{cos x}{sin x}$$ $$int frac{dy}{y} = int frac{cos x}{sin x} dx.$$ Слева получается натуральный логарифм, а справа заносим косинус под знак дифференциала, чтобы получить логарифм синуса: $$ln|y| = ln|sin x| + C$$ $$y = Csin x.$$ Теперь заменяем константу $C$ на функцию $C(x)$ в полученном решении и находим производную $$y = C(x)sin x Rightarrow y’ = C'(x)sin x+ C(x)cos x.$$ Подставляем $y$ и $y’$ в неоднородное уравнение и решаем его относительно $C(x)$: $$C'(x)sin x+ C(x)cos x — C(x)sin x frac{cos x}{sin x} = frac{1}{sin x}$$ $$C'(x)sin x = frac{1}{sin x}$$ $$C'(x) = frac{1}{sin^2 x}.$$ В последнем уравнении можно разделить переменные, что и делаем, а затем интегрируем: $$ d(C(x)) = int frac{dx}{sin^2 x}$$ $$C(x) = -ctg x + C.$$ Берем решение $y = C(x)sin x$ и подставляем в него найденное $C(x) = -ctg x + C$ $$y = (-ctg x + C) sin x = Csin x — cos x.$$ Таким образом получили общее решение дифференциального уравнения $y = Csin x — cos x$. Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$y = Csin x — cos x$$

ДУ Бернулли

Дифференциальное уравнение Бернулли имеет следующий вид $$y’ + g(x)y = f(x)y^alpha qquad (alpha neq 0), (alpha neq 1).$$

Алгоритм решения: 

1. Выполняем подстановку $y = z^frac{1}{1-alpha}$
2. После подстановки получаем линейное уравнение $z’+p(x)z=q(x)$
3. Решив линейное уравнение делаем обратную замену $z = y^{1-alpha}$

Пример 8

Найти общее решение дифференциального уравнения первого порядка $y’+y=xy^2$.

Решение

Это уравнение Бернулли. Видим, что $alpha = 2$. Значит делаем замену на $y = z^frac{1}{1-alpha} = z^{-1}$. Отсюда $y’ = -frac{1}{z^2} cdot z’$. После подстановки в исходное уравнение имеем $$ -frac{z’}{z^2}+frac{1}{z}=frac{x}{z^2}.$$ Умножаем обе части равенства на $(-z^2)$, чтобы привести уравнение к линейному ДУ $$z’-z=-x, $$ которое можно решить методом Бернулли, либо вариацией произвольной постоянной. Выберем первый способ. Применяем подстановку $y=uv$ и $y’=u’v+uv’$ для последнего уравнения $$u’v+uv’-uv=-x.$$ Выносим за скобку $u$, чтобы затем построить систему уравнений для нахождения функций $u(x)$ и $v(x)$ $$u’v+u(v’-v) = -x.$$ Приравниваем к нулю скобку и получаем систему $$begin{cases} v’-v = 0 \ u’v = -x end{cases}.$$ Начинаем решать её с первого уравнения. Разделяем в нем переменные и затем интегрируем $$begin{cases} int frac{dv}{v} = int dx \ u’v = -x end{cases} Leftrightarrow begin{cases} ln|v| = x \ u’v = -x end{cases} Leftrightarrow begin{cases} v = e^x \ u’v = -x end{cases}. $$ Зная, что $v = e^x$ подставляем его во второе уравнение системы и решаем $$begin{cases} v = e^x \ u’ = -frac{x}{e^x} end{cases} Leftrightarrow begin{cases} v = e^x \ u = int (-x)e^{-x} dx end{cases}.$$ Для взятия интеграла воспользуемся методом интегрирования по частям $$u = int (-x)e^{-x} dx = begin{vmatrix} u = -x & du = -dx \ dv = e^{-x}dx & v = -e^{-x} end{vmatrix} = xe^{-x} — int e^{-x} dx = xe^{-x} +e^{-x} + C$$ Итак, получаем, что $$z = uv Rightarrow z = (xe^{-x} + e^{-x}+C) e^x = Ce^x +x + 1. $$ Вспоминаем, что была ещё одна замена в самом начале решения задачи $y = z^{-1}$, поэтому общее решение выглядит следующим образом $$y = frac{1}{Ce^x + x + 1}.$$

Ответ

$$y = frac{1}{Ce^x + x + 1}$$

ДУ в полных дифференциалах

Дифференциальные уравнения в полных дифференциалах имеют следующий вид $$P(x,y) dx + Q(x,y) dy = 0, $$ при выполнении условия $frac{partial P}{partial y} = frac{partial Q}{partial x} $.

Алгоритм решения заключается в том, чтобы найти функцию $U(x,y)=C$, полный дифференциал которой, есть исходное ДУ:

1. Проверяем условие, подтверждающее, что перед нами ДУ в полных дифференциалах
2. Получаем $U(x,y)$ интегрируя функцию $P(x,y)$ по переменной $x$. В результате этого появится неизвестная функция $varphi(y)$ 
3. Дифференцируем $U(x,y)$ по $y$ и приравниваем к $Q(x,y)$, чтобы найти $varphi(y)$

Пример 9

Найти общий интеграл $U(x,y)=C$ дифференциального уравнения $$(2x+5y)dx+(5x+3y^2)dy=0.$$

Решение

Убедимся, что данное уравнение в полных дифференциалах. Для этого проверим условие $frac{partial P}{partial y} = frac{partial Q}{partial x} $. Находим производные $$ P’_y = (2x+5y)’_y = 5, Q’_x = (5x+3y^2)’_x = 5, $$ и видим, что условие выполняется $P’_y=P’_x=5$. Находим функцию $U(x,y)$ беря интеграл по $x$ от функции $P(x,y)$ $$U(x,y) = int (2x+5y) dx = x^2 + 5yx + varphi(y).$$ Далее необходимо продифференцировать найденную $U(x,y)$ по $y$ $$U’_y = 5x + varphi'(y).$$  Осталось найти неизвестную функцию $varphi(y)$ приравняв $U’_y$ к $Q(x,y)$: $$5x + varphi'(y) = 5x+3y^2$$ $$varphi'(y) = 3y^2$$ $$varphi(y) = int 3y^2 dy = y^3 + C.$$ Теперь зная чему равна $varphi(y)$ подставляем её в $U(x,y)$ $$U(x,y)=x^2+5xy+y^3+C.$$ Записываем ответ в таком виде $$x^2+5xy+y^3 = C.$$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$x^2+5xy+y^3 = C.$$

Дифференциальные уравнения второго порядка

ДУ допускающие понижение порядка

Дифференциальные уравнения, допускающие понижение порядка бывают двух видов:

1. Без функции $y$: $F(x,y’,y»)=0$
2. Без переменной $x$: $F(y,y’,y»)=0$

Для решения таких диффуров в первом случае делаем замену $y’ = p(x)$, а во втором $y’ = p(y)$.

Пример 10

Найти частное решение дифференциального уравнения второго порядка $xy»+y’=0$ при условиях $y(1) = 0$ и $y'(1)=1$.

Решение

Видим, что данный дифур попадает под первый случай, когда отсутствует в уравнении $y$, а есть только его производные. Значит, делаем замену $y’ = p(x)$ $$xp’+p=0.$$ Данное уравнение имеет разделяющиеся переменные. Начнем с того, что перепишем уравнение через $p’ = frac{dp}{dx}$ $$xfrac{dp}{dx} = -p.$$ Разделяем переменные налево и направо от знака равенства и затем интегрируем: $$ frac{dp}{p} = -frac{dx}{x}$$ $$ int frac{dp}{p} = -int frac{dx}{x}$$ $$ln|p| = -ln|x|+C_1.$$ Теперь избавимся от логарифмов, чтобы получить $p$: $$p = e^{-ln|x| + C_1}$$ $$p = frac{C_1}{x}.$$ Вспоминаем про ранее выполненную замену $$y’ = p(x) = frac{C_1}{x}.$$ Интегрируем для того, чтобы найти $y$ $$y = int frac{C_1}{x} dx = C_1 ln|x| + C_2.$$ Таким образом, общее решение дифференциального уравнения $$y = C_1 ln|x| + C_2.$$ Займемся поиском частного решения. Для этого используем два дополнительных равенства из условия задачи: $$y(1) = 0 Rightarrow C_1 ln|1| + C_2 = 0 Rightarrow C_2 = 0$$ $$y'(1)=1 Rightarrow frac{C_1}{1} = 1 Rightarrow C_1 = 1.$$ Записываем частное решение дифференциального уравнения $$y = ln|x|.$$

Ответ

$$y = ln|x|$$

Пример 11

Найти частное решение дифференциального уравнения второго порядка $$yy»+y’^2 = 1, qquad y(0) = 1, y'(0) = 1.$$

Решение

Видим, что в диффуре отсутствует в явном виде переменная $x$, поэтому необходимо сделать замену $y’ = p(y)$ и отсюда $y» = p'(y)cdot y’ = p'(y)p$. Делаем замену и получаем уравнение $$yp'(y)p + p^2 = 1,$$ которое решим методом разделения переменных: $$ypfrac{dp}{dy} = 1-p^2$$ $$frac{p}{1-p^2}dp = frac{1}{y}dy.$$ Далее по плану необходимо проинтегрировать обе части уравнения, чтобы получить $p$ $$int frac{p}{1-p^2}dp = int frac{1}{y}dy.$$ В первом интеграле заносим под знак дифференциала $1-p^2$, чтобы получился натуральный логарифм, а во втором, используя таблицу интегрирования можно сразу записать ответ: $$-frac{1}{2} int frac{d(1-p^2)}{1-p^2} = ln|y| + C $$ $$-frac{1}{2} ln|1-p^2| = ln|y| + C.$$  Необходимо избавиться от логарифмов. Умножим обе части равенства на $(-2)$, а затем занесем эту двойку над икреком: $$ln|1-p^2| = -2ln|y|+C$$ $$ln|1-p^2| = ln frac{1}{y^2} + C.$$ Итак, теперь убирая логарифмы получаем: $$1-p^2 = C frac{1}{y^2}$$ $$p^2 = 1 — Cfrac{1}{y^2}$$ $$(y’)^2 = 1 — Cfrac{1}{y^2}.$$ Теперь найдем значение константы $C$ благодаря дополнительным условиям задачи $y = 1$ и $y’ = 1$. Подставляем их в последнее уравнение $$1^2 = 1 — Cfrac{1}{1^2} Rightarrow C = 0.$$ Зная теперь, что $C=0$ подставляем его в уравнение $(y’)^2 = 1 — Cfrac{1}{y^2}$: $$(y’)^2 = 1$$ $$y’ = pm 1.$$ Из условия помним, что $y’ = 1 > 0$, значит, берем только решение $y’ = 1$ и продолжаем его решать интегрированием $$y = int 1 dx = x + C.$$ Осталось найти снова постоянную $C$ теперь уже из условия $y(0) = 1$ $$y(0) = 0 + C = 1 Rightarrow C = 1.$$ Вот теперь можно записать ответ в виде частного решения, которое требовалось найти по условию данной задачи $$y = x + 1.$$

Ответ

$$y = x + 1$$

Линейные однородные ДУ с постоянными коэффицентами

Линейность дифференциального уравнения заключается в том, что в уравнение входит неизвестная функция $y(x)$ и её производные только в первой степени, между собой не перемножаясь. Однородность определяется тем, что уравнение не содержит свободного члена. То есть он равен нулю.

Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами выглядит следующим образом $$y»+py’+qy = 0.$$ Чтобы его решить необходимо составить характиристический многочлен и найти его корни. Для этого нужно заменить $y$ на $lambda$, степень которых будет соответствовать порядку производной $$y» Rightarrow lambda^2, qquad y’ Rightarrow lambda, qquad y Rightarrow 1.$$

В зависимости от получившихся корней имеем общее решение в различных видах:

1. Действительные корни $lambda_1 neq lambda_2$, тогда $y = C_1e^{lambda_1 x}+C_2e^{lambda_2 x}$
2. Действительные корни $lambda_1 = lambda_2$, тогда $y = C_1e^{lambda_1 x}+C_2xe^{lambda_1 x}$
3. Комплексные корни $lambda_{1,2} = alphapmbeta i$, тогда $y = C_1e^{alpha x}cos beta x + C_2e^{alpha x}sin beta x$.

Пример 12

Найти общее решение дифференциального уравнения второго порядка $y»+y’-2y = 0$.

Решение

Первым делом составляем характеристический многочлен. Заменяем $y$ на $lambda$ со степенями соответствующими порядку производной $y$ $$lambda^2 + lambda -2 = 0.$$ Обратите внимание, что $y$ имеет производную нулевого порядка, поэтому он заменяется на $lambda^0 = 1$. Итак, перед нами квадратное уравнение, начинаем решать: $$lambda_{1,2} = frac{-1pm sqrt{1^2-4cdot 1 cdot (-2)}}{2cdot 1} = frac{-1pm 3}{2}$$ $$lambda_1 = -2, qquad lambda_2 = 1.$$ Так как получили отличающиеся действительные корни, то общее решение записывается следующим образом $$y = C_1 e^{-2x} + C_2 e^{x}.$$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$y = C_1 e^{-2x} + C_2 e^{x}$$

Линейные неоднородные ДУ с постоянными коэффициентами

Линейное неоднородное ДУ с постоянными коэффициентами отличается от предыдущего типа уравнений наличием правой части от знака равенства $$y»+py’+q = f(x).$$

Общее решение такого диффура складывается из двух частей: общего решения однородного уравнения и частного решения неоднородного уравнения $$y_text{о.н.} = y_text{о.о.} + y_text{ч.н.}.$$

Частное решение неоднородного уравнения $y_text{ч.н.}$ подбирается исходя из вида правой части дифференциального уравнения. Затем в нём неизвестные постоянные находятся методом неопределенных коэффициентов.

№	Правая часть	Корни характеристического многочлена	Вид частного решения
1	$$P_n (x)$$	Число 0 не является корнем характеристического уравнения.	$$tilde{P_n}(x)$$
Число 0 – корень характеристического уравнения кратности $S$.	$$x^s tilde{P_n}(x)$$
2	$$P_n (x) e^{alpha x}$$	Число $alpha$ не является корнем характеристического уравнения.	$$tilde{P_n} (x) e^{alpha x}$$
Число $alpha$ является корнем характеристического уравнения кратности $S$.	$$x^s tilde{P_n} (x) e^{alpha x}$$
3	$$P_n (x) cos beta x + Q_m (x) sin beta x$$	Число $pm ibeta$ не является корнем характеристического уравнения.	$$tilde {P_n} cos beta x + tilde{Q_m} sin beta x$$
Число $pm ibeta$ является корнем характеристического уравнения кратности $S$.	$$x^s (tilde {P_n} cos beta x + tilde{Q_m} sin beta x)$$
4	$$e^{alpha x}[P_n (x) cos beta x + Q_m (x) sin beta x]$$	Число $alpha pm ibeta$ не является корнем характеристического уравнения.	$$e^{alpha x}[P_n (x) cos beta x + Q_m (x) sin beta x]$$
Число $alpha pm ibeta$ является корнем характеристического уравнения.	$$x^s e^{alpha x}[P_n (x) cos beta x + Q_m (x) sin beta x]$$

Пример 13

Найти общее решение дифференциального уравнения второго порядка $y»+y = 4xcos x$.

Решение

Сначала находим общее решение однородного уравнения $$y» + y = 0.$$ Строим характеристический многочлен $$lambda^2 + 1 = 0,$$ и находим его корни $$lambda_{1,2}=pm i.$$ Записываем получившееся общее решение однородного уравнения $$y_text{о.о.} = C_1 cos x + C_2 sin x.$$ Теперь необходимо подобрать частное решение неоднородного уравнения. Для этого смотрим на правую часть исходного уравнения и видим, что здесь многочлен первой степени умножается на косинус. Значит, необходимо выбрать из таблицы 3й случай. Причем корень характеристического уравнения совпадает с аргументом косинуса. Это значит, что требуется домножение на $x$ $$y_text{ч.н.} = x[(Ax+B)cos x + (Cx+D)sin x].$$Упростим последнее равенство и найдем от него вторую производную: $$y_text{ч.н.} = (Ax^2+Bx)cos x + (Cx^2 + Dx) sin x$$ $$y’_text{ч.н.} = (2Ax+B)cos x-(Ax^2+Bx)sin x + (2Cx+D)sin x + (Cx^2 + Dx) cos x.$$ Упростим $y’_text{ч.н}$ для удобства нахождения второй производной $$y’_text{ч.н.} = (2Ax+B+Cx^2+Dx)cos x + (2Cx+D-Ax^2-Bx)sin x.$$ Теперь можно найти вторую производную $$y»_text{ч.н.} = (2A+2Cx+D)cos x-(2Ax+B+Cx^2+Dx)sin x + (2C-2Ax-B)sin x + (2Cx+D-Ax^2-Bx)cos x.$$ Упрощаем последнее выражение $$y»_text{ч.н.} = (2A+4Cx+2D-Ax^2-Bx)cos x + (2C-4Ax-2B-Cx^2-Dx)sin x.$$ Подставляем найденные $y_text{ч.н.}$ и $y»_text{ч.н.}$ в исходный диффур из «дано» задачи $$(2A+4Cx+2D-Ax^2-Bx)cos x + (2C-4Ax-2B-Cx^2-Dx)sin x + (Ax^2+Bx)cos x + (Cx^2 + Dx) sin x = 4xcos x.$$ Упрощаем его $$(2A+4Cx+2D)cos x + (2C-4Ax-2B)sin x = 4xcos x.$$ Теперь подгоняем левую часть под правую, так чтобы можно было применить метод неопределенных коэффициентов и найти неизвестные $A,B,C,D$ $$(2A+2D)cos x+4Cxcos x + (2C-2B)sin x+(-4Ax)sin x = 4xcos x.$$ Смотрим на левую и правую часть и составляем систему $$begin{cases} 2A+2D = 0 \ 4C=4 \ 2C-2B=0 \ -4A = 0 end{cases} Leftrightarrow begin{cases} D=0 \ C= 1 \ B=1 \ A = 0end{cases}.$$ Подставляем полученные коэффициенты в частное решение неоднородного уравнения $$y_text{ч.н.} = xcos x + x^2sin x.$$ Теперь вспоминая, что $y_text{о.н.} = y_text{о.о.} + y_text{ч.н.}$ можем записать окончательный ответ $$y_text{о.н.} = C_1 cos x + C_2 sin x + xcos x + x^2sin x.$$

Ответ

$$y = C_1 cos x + C_2 sin x + xcos x + x^2sin x$$

Пример 14

Найти общее решение дифференциального уравнения второго порядка $y»+y’=5x+2e^x$.

Решение

Сначала найдем общее решение однородного дифференциального уравнения $$y»+y’=5x+2e^x.$$ Составляем характеристический многочлен однородного уравнения и находим его корни: $$lambda^2 + lambda = 0$$ $$lambda(lambda + 1) = 0$$ $$lambda_1 = 0, qquad lambda_2=-1.$$ Теперь можно записать общее решение $$y_text{о.о.} = C_1 + C_2e^{-x}.$$ Далее необходимо по правой части исходного неоднородного уравнения найти его частное решение путем подбора, используя данные таблицы. Первое слагаемое есть многочлен первой степени. И так как один из корней характеристического уравнения является нулем кратности 1, то решение ищем в виде $y = (Ax+B)x$. Второе слагаемое представляет собой произведение многочлена нулевой степени на экспоненту. Так как аргумент экспоненты не совпадает с одним из корней характеристического многочлена, то подбор будем делать в виде $y = Ce^x$. В итоге правую часть будем искать в виде суммы $$y_text{ч.н.} = (Ax+B)x+Ce^x.$$ Находим первую и вторую производную последней функции: $$y’ = 2Ax+B+Ce^x$$ $$y»=2A+Ce^x.$$ Подставляем полученные производные $y’$ и $y»$ в исходное дифференциальное уравнение: $$2A+Ce^x+2Ax+B+Ce^x = 5x+2e^x$$ $$2Ax+B+2A+2Ce^x=5x+2e^x.$$ Далее необходимо, используя метод неопределенных коэффициентов, найти значения $A,B,C$ составив систему уравнений $$begin{cases} 2A=5 \ 2C=2 \ B+2A = 0 end{cases} Leftrightarrow begin{cases} A=frac{5}{2} \ C=1 \ B=-5 end{cases}.$$ Подставляем найденные коэффициенты и получаем частное решение неоднородного уравнения $$y_text{ч.н.} = (frac{5}{2}x-5)x + e^x = frac{5}{2}x^2 — 5x + e^x.$$ Таким образом теперь можно записать общее решение неоднородного диффура $$y_text{о.н.} = y_text{о.о.} + y_text{ч.н.}=C_1 + C_2e^{-x} + frac{5}{2}x^2 — 5x + e^x.$$

Ответ

$$y = C_1 + C_2e^{-x} + frac{5}{2}x^2 — 5x + e^x$$

Метод Лагранжа

Данный метод позволяет решать линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами даже в тех, случаях, когда правая часть уравнения не подходит под табличный вид. В этом случае целесообразно применить данный метод решения.

1. Находим общее решение однородного уравнения $y = C_1 y_1(x) + C_2 y_2(x)$
2. Варьируем постоянные $C_1$ и $C_2$ на функции $C_1(x)$ и $C_2(x)$
3. Решаем систему методом Крамера $begin{cases} C_1 ‘(x) y_1 (x) + C_2 ‘(x) y_2 (x) = 0 \ C_1 ‘(x) y_1 ‘(x) + C_2 ‘(x) y_2 ‘(x) = f(x) end{cases} $
4. Получаем $C_1(x)$ и $C_2(x).$

Пример 15

Найти частное решение дифференциального уравнения $$y»-2y’+y=frac{e^x}{x}, text{ при } y(1)=e, y'(1)=3e.$$

Решение

Так как правая часть диффура не подходит под табличный формат, то не получится подбирать частное решение по правой части как делали это в предыдущем примере. Воспользуется методом Лагранжа или как его еще называют вариация произвольной постоянной. Для начала найдем общее решение однородного уравнения $$y»-2y’+y=0.$$ Составляем характеристический многочлен и находим его корни: $$lambda^2-2lambda+1=0$$ $$(lambda-1)^2 = 0 Rightarrow lambda = 1 text{ с кратностью 2}.$$ Так как корень кратный, то общее решение однородного уравнения записывается следующим образом $$y = C_1 e^x + C_2 xe^x.$$ Теперь необходимо варьировать постоянные $C_1$ и $C_2$ на соответствующие функции $C_1 (x)$ и $C_2 (x)$. Теперь получившееся решение следует записать в виде $y = C_1 (x) e^x + C_2 (x) xe^x$. Здесь заметим, что $y_1 = e^x$ и $y_2 = xe^x$. Это нужно для дальнейшего хода решения, а именно построения системы уравнений. Составляем систему уравнений и решаем её методом Крамера $$begin{cases} C_1 ‘(x) e^x+C_2 ‘(x) xe^x = 0 \C_1 ‘(x) e^x + C_2 ‘(x) (e^x+xe^x) = frac{e^x}{x} end{cases}.$$ Находим главный определитель системы $$Delta = begin{vmatrix} e^x & xe^x \ e^x & e^x+xe^x end{vmatrix} = e^x(e^x+xe^x)-xe^{2x} = e^{2x}.$$ Вычисляем дополнительные определители: $$Delta_1 = begin{vmatrix} 0 & xe^x \ frac{e^x}{x} & e^x + xe^x end{vmatrix} = -xe^x frac{e^x}{x} = e^{2x}$$ $$Delta_2 = begin{vmatrix} e^x & 0 \ e^x & frac{e^x}{x} end{vmatrix} = e^x frac{e^x}{x} = frac{e^{2x}}{x}.$$ Итак, получаем решение системы уравнений $$C_1 ‘(x) = frac{Delta_1}{Delta} = frac{e^{2x}}{e^{2x}} = 1, qquad C_2 ‘(x) = frac{Delta_2}{Delta} = frac{e^{2x}}{x} frac{1}{e^{2x}} = frac{1}{x}.$$ Далее интегрируем полученные решения, чтобы избавиться от производной: $$C_1(x) = int 1 dx = x+tilde{C_1}$$ $$C_2(x)=int frac{dx}{x}=ln|x|+tilde{C_2}.$$ Подставляем полученные $C_1(x)$ и $C_2(x)$ в общее решение однородного уравнения и записываем общее решение неоднородного дифференциального уравнения $$y = (x+tilde{C_1}) e^x + (ln|x|+tilde{C_2}) xe^x.$$ По условию нам требуется найти частное решение при условиях $y(1)=e$ и $y'(1)=3e$. Поэтому находим сначала производную $$y’=e^x+(x+tilde{C_1})e^x+e^x+(ln|x|+tilde{C_2})(e^x+xe^x), $$ раскрываем скобки $$y’ = 2e^x+xe^x+tilde{C_1}e^x+e^xln|x|+xe^xln|x|+tilde{C_2}e^x+tilde{C_2}xe^x,$$ а затем составляем систему уравнений $$begin{cases} y'(1)=3e+tilde{C_1}e+2tilde{C_2}e = 3e \ y(1) = e+tilde{C_1}e + tilde{C_2}e = e end{cases} Rightarrow begin{cases} tilde{C_1}+2tilde{C_2}=0 \ tilde{C_1}+tilde{C_2}=0 end{cases} Rightarrow begin{cases} tilde{C_2} = 0 \ tilde{C_1}=0 end{cases}.$$ Теперь можно записать частное решение к задаче $$y = xe^x + xln|x|e^x = xe^x(1+ln|x|).$$

Ответ

$$y = xe^x(1+ln|x|)$$