Есть ли вектора на егэ по математике

Векторы

Отрезок, для которого указано, какая из его граничных точек является началом, а какая — концом, называется вектором.

Вектор с началом в точке A и концом в точке B обозначают $<(АВ)>↖<→>$ или строчной (маленькой) буквой, например $<а>↖<→>$

Любая точка плоскости является вектором. В этом случае вектор называется нулевым.

Модуль (длину) вектора обозначают $|АВ|↖<→>$.

Ненулевые векторы называются коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых.

Два коллинеарных вектора называются сонаправленными, если они направлены в одну сторону.

Векторы называются равными , если они сонаправлены и их длины равны.

Сумма векторов — это вектор, который можно получить двумя способами.

1. Правило треугольника (А)
2. Правило параллелограмма (Б)

Для любых векторов $a↖<→>, b↖<→>, c↖<→>$ справедливы равенства:

Разность векторов тоже можно получить двумя способами:

Если надо найти разность двух векторов, их необходимо отложить из одной точки. Результирующий вектор направлен к уменьшаемому.

Для любых $a↖<→>$ и $b↖<→>$ справедливо равенство $a↖<→>-b↖<→>=a↖<→>+(<-b>↖<→>)$

Скалярное произведение векторов равно произведению длин векторов на косинус угла между ними.$a↖<→>⋅b↖<→>=|a↖<→>|·|b↖<→>|·cos⁡α$

Ненулевые векторы $a↖<→>$ и $b↖<→>$ перпендикулярны, если их произведение равно нулю.

Метод координат

Координаты вектора равны разностям соответствующих координат конца и начала данного вектора.

Для того чтобы векторы $a↖<→>$ и $b↖<→>$ были коллинеарными, необходимо и достаточно, чтобы выполнялось равенство $a↖<→>=k·b↖<→>$, где $k$ — это некоторое число.

Координаты середины вектора равны средним арифметическим координат его концов.

Каждая координата суммы двух или более векторов равна сумме соответствующих координат этих векторов.

Каждая координата разности двух векторов равна разности соответствующих координат этих векторов.

Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число.

Скалярное произведение векторов $a↖<→>$ и $b↖<→>$ в координатах находится по формуле $a↖<→>·b↖<→>= x1·x2+y1·y2$

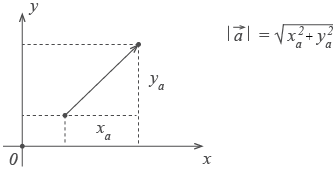
Длина вектора $a↖<→>$ вычисляется по формуле: $|a↖<→>|=√$

Расстояние между двумя точками $M1(x1;y1)$ и $M2(x2; y2)$ находится по формуле $|M1M2|=√<(x2-x1)^2+(y2-y1)^2>$

Найдите угол между векторами $a↖<→>$ и $b↖<→>$

1. Сначала нужно найти координаты векторов $a↖<→>$ <2-0;6-0>$b↖<→>$
2. Найдем скалярное произведение векторов $a↖<→>·b↖ <→>= 2·8+6·4=16+24=40$
3. Найдем длины каждого вектора $|a↖<→>|= √<4+36>=√<40>; |b↖<→>|=√<64+16>=√<80>$
4. Найдем косинус угла между векторами $cosα=<40>/<√<40>·√<80>>=<40>/<√<40·40·2>>=<1>/<√2>=<√2>/<2>$
5. Найдем угол $α=arccos<√2>/<2>=45$

Векторы на ЕГЭ по математике. Действия над векторами

Стандартное определение: «Вектор — это направленный отрезок». Обычно этим и ограничиваются знания выпускника о векторах. Кому нужны какие-то «направленные отрезки»?

А в самом деле, что такое векторы и зачем они?
Прогноз погоды. «Ветер северо-западный, скорость 18 метров в секунду». Согласитесь, имеет значение и направление ветра (откуда он дует), и модуль (то есть абсолютная величина) его скорости.

Величины, не имеющие направления, называются скалярными. Масса, работа, электрический заряд никуда не направлены. Они характеризуются лишь числовым значением — «сколько килограмм» или «сколько джоулей».

Физические величины, имеющие не только абсолютное значение, но и направление, называются векторными.

Скорость, сила, ускорение — векторы. Для них важно «сколько» и важно «куда». Например, ускорение свободного падения направлено к поверхности Земли, а величина его равна 9,8 м/с 2 . Импульс, напряженность электрического поля, индукция магнитного поля — тоже векторные величины.

Вы помните, что физические величины обозначают буквами, латинскими или греческими. Стрелочка над буквой показывает, что величина является векторной:

Вот другой пример.
Автомобиль движется из A в B . Конечный результат — его перемещение из точки A в точку B , то есть перемещение на вектор .

Теперь понятно, почему вектор — это направленный отрезок. Обратите внимание, конец вектора — там, где стрелочка. Длиной вектора называется длина этого отрезка. Обозначается: или

До сих пор мы работали со скалярными величинами, по правилам арифметики и элементарной алгебры. Векторы — новое понятие. Это другой класс математических объектов. Для них свои правила.

Когда-то мы и о числах ничего не знали. Знакомство с ними началось в младших классах. Оказалось, что числа можно сравнивать друг с другом, складывать, вычитать, умножать и делить. Мы узнали, что есть число единица и число ноль.
Теперь мы знакомимся с векторами.

Понятия «больше» и «меньше» для векторов не существует — ведь направления их могут быть разными. Сравнивать можно только длины векторов.

А вот понятие равенства для векторов есть.
Равными называются векторы, имеющие одинаковые длины и одинаковое направление. Это значит, что вектор можно перенести параллельно себе в любую точку плоскости.
Единичным называется вектор, длина которого равна 1 . Нулевым — вектор, длина которого равна нулю, то есть его начало совпадает с концом.

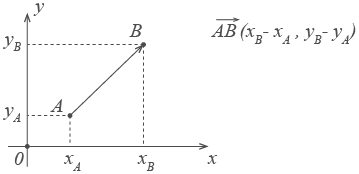
Удобнее всего работать с векторами в прямоугольной системе координат — той самой, в которой рисуем графики функций. Каждой точке в системе координат соответствуют два числа — ее координаты по x и y , абсцисса и ордината.
Вектор также задается двумя координатами:

Здесь в скобках записаны координаты вектора — по x и по y .
Находятся они просто: координата конца вектора минус координата его начала.

Если координаты вектора заданы, его длина находится по формуле

Сложение векторов

Для сложения векторов есть два способа.

1 . Правило параллелограмма. Чтобы сложить векторы и , помещаем начала обоих в одну точку. Достраиваем до параллелограмма и из той же точки проводим диагональ параллелограмма. Это и будет сумма векторов и .

Помните басню про лебедя, рака и щуку? Они очень старались, но так и не сдвинули воз с места. Ведь векторная сумма сил, приложенных ими к возу, была равна нулю.

2 . Второй способ сложения векторов — правило треугольника. Возьмем те же векторы и . К концу первого вектора пристроим начало второго. Теперь соединим начало первого и конец второго. Это и есть сумма векторов и .

По тому же правилу можно сложить и несколько векторов. Пристраиваем их один за другим, а затем соединяем начало первого с концом последнего.

Представьте, что вы идете из пункта А в пункт В , из В в С , из С в D , затем в Е и в F . Конечный результат этих действий — перемещение из А в F .

При сложении векторов и получаем:

Вычитание векторов

Вектор направлен противоположно вектору . Длины векторов и равны.

Теперь понятно, что такое вычитание векторов. Разность векторов и — это сумма вектора и вектора .

Умножение вектора на число

При умножении вектора на число k получается вектор, длина которого в k раз отличается от длины . Он сонаправлен с вектором , если k больше нуля, и направлен противоположно , если k меньше нуля.

Скалярное произведение векторов

Векторы можно умножать не только на числа, но и друг на друга.

Скалярным произведением векторов называется произведение длин векторов на косинус угла между ними.

Обратите внимание — перемножили два вектора, а получился скаляр, то есть число. Например, в физике механическая работа равна скалярному произведению двух векторов — силы и перемещения:

Если векторы перпендикулярны, их скалярное произведение равно нулю.
А вот так скалярное произведение выражается через координаты векторов и :

Из формулы для скалярного произведения можно найти угол между векторами:

Эта формула особенно удобна в стереометрии. Например, в задаче 14 Профильного ЕГЭ по математике нужно найти угол между скрещивающимися прямыми или между прямой и плоскостью. Часто векторным методом задача 14 решается в несколько раз быстрее, чем классическим.

В школьной программе по математике изучают только скалярное произведение векторов.
Оказывается, кроме скалярного, есть еще и векторное произведение, когда в результате умножения двух векторов получается вектор. Кто сдает ЕГЭ по физике, знает, что такое сила Лоренца и сила Ампера. В формулы для нахождения этих сил входят именно векторные произведения.

Векторы — полезнейший математический инструмент. В этом вы убедитесь на первом курсе.

Онлайн-курс «Математика 10+11 100 баллов»

— Теория: учебник Анны Малковой + 70 ч. видеоразборов.
— 144 ч. мастер-классов: 8 онлайн мастер-классов с Анной Малковой в месяц.
— Тренажер для отработки задач ЕГЭ (800+ задач): автоматическая + ручная проверки.
— Связь с Анной Малковой (чаты и почта).
— 9 репетиционных ЕГЭ: ежемесячно.
— Контроль: страница личных достижений учащегося, отчеты родителям.
— Личный кабинет.

Задачи по теме «Векторы»(для подготовки к ЕГЭ по математике профильный уровень)
консультация по математике (11 класс) на тему

Скачать:

Вложение	Размер
vektory.docx	479.51 КБ

Подготовка к ЕГЭ за 4 месяца

Репетиторы Учи.Дома помогут подготовиться к ЕГЭ. Приходите на бесплатный пробный урок, на котором репетиторы определят ваш уровень подготовки и составят индивидуальный план обучения.

попробовать бесплатно, онлайн, 40 минут

Предварительный просмотр:

1. Найдите квадрат длины вектора .

1. Стороны правильного треугольника ABC равны . Найдите длину вектора + .

1. Найдите сумму координат вектора .

Вектор с началом в точке A (2, 4) имеет координаты (6, 2). Найдите ординату точки B .

Вектор с концом в точке B (5, 3) имеет координаты (3, 1). Найдите абсциссу точки A .

Вектор с концом в точке B (5, 4) имеет координаты (3, 1). Найдите сумму координат точки A .

Найдите квадрат длины вектора + .

Найдите квадрат длины вектора .

Найдите длину вектора (6; 8).

Найдите квадрат длины вектора .

Стороны правильного треугольника равны . Найдите длину вектора .

Стороны правильного треугольника равны 3. Найдите длину вектора .

Стороны правильного треугольника равны 3. Найдите скалярное произведение векторов и .

. Найдите сумму координат вектора .

. Вектор с началом в точке (2; 4) имеет координаты (6; 2). Найдите абсциссу точки .

Вектор с началом в точке (2; 4) имеет координаты (6; 2). Найдите ординату точки .

Вектор с началом в точке (3; 6) имеет координаты (9; 3). Найдите сумму координат точки .

Вектор с концом в точке (5; 3) имеет координаты (3; 1). Найдите абсциссу точки .

Вектор с концом в точке (5; 3) имеет координаты (3; 1). Найдите ординату точки .

Вектор с концом в точке (5; 4) имеет координаты (3; 1). Найдите сумму координат точки .

Найдите сумму координат вектора + .

Найдите квадрат длины вектора + .

. Найдите сумму координат вектора .

Найдите квадрат длины вектора .

Найдите скалярное произведение векторов и .

Найдите угол между векторами и . Ответ дайте в градусах.

Найдите сумму координат вектора + .

Найдите квадрат длины вектора + .

Найдите сумму координат вектора .

Найдите квадрат длины вектора .

Найдите скалярное произведение векторов и .

Найдите угол между векторами и . Ответ дайте в градусах.

Векторы ЕГЭ по математике

08.11.2013

Материал для подготовки к ЕГЭ по математике на тему: «Векторы».

Содержание темы:

19.  ВЕКТОРЫ
19.1.  Основные понятия и определения
19.2.  Линейные действия над векторами
19.3.  Скалярное произведение векторов
Тест для проверки теоретических знаний
Примеры
Задачи для самостоятельного решения
Контрольный тест 

Рекомендуем использовать этот материал при тщательной подготовке к сдаче ЕГЭ на высокий балл.

В теме содержатся теория и практические задания различного уровня сложности.

Смотреть в PDF:

Или прямо сейчас: Скачайте в pdf файле.

Стандартное
определение: «Вектор — это направленный
отрезок». Обычно этим и ограничиваются
знания выпускника о векторах. Кому
нужны какие-то «направленные отрезки»?

А в самом
деле, что такое векторы и зачем
они?

Прогноз погоды. «Ветер
северо-западный, скорость 18 метров
в секунду». Согласитесь, имеет значение
и направление ветра (откуда он дует),
и модуль (то есть абсолютная
величина) его скорости.

Величины,
не имеющие направления, называются
скалярными. Масса, работа, электрический
заряд никуда не направлены. Они
характеризуются лишь числовым значением —
«сколько килограмм» или «сколько
джоулей».

Физические
величины, имеющие не только абсолютное
значение, но и направление,
называются векторными.

Скорость,
сила, ускорение — векторы. Для них
важно «сколько» и важно «куда».
Например, ускорение свободного падения

направлено
к поверхности Земли, а величина
его равна 9,8 м/с². Импульс,
напряженность электрического поля,
индукция магнитного поля — тоже
векторные величины.

Вы помните,
что физические величины обозначают
буквами, латинскими или греческими.
Стрелочка над буквой показывает, что
величина является векторной:

Вот
другой пример.

Автомобиль движется
из A в B. Конечный результат —
его перемещение из точки A в точку B,
то есть перемещение на вектор

.

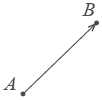
Теперь
понятно, почему вектор — это
направленный отрезок. Обратите внимание,
конец вектора — там, где стрелочка.
Длиной вектора называется длина
этого отрезка. Обозначается:

или

До сих
пор мы работали со скалярными
величинами, по правилам арифметики
и элементарной алгебры. Векторы —
новое понятие. Это другой класс
математических объектов. Для них свои
правила.

Когда-то
мы и о числах ничего не знали.
Знакомство с ними началось в младших
классах. Оказалось, что числа можно
сравнивать друг с другом, складывать,
вычитать, умножать и делить. Мы узнали,
что есть число единица и число
ноль.

Теперь мы знакомимся
с векторами.

Понятия
«больше» и «меньше» для векторов
не существует — ведь направления
их могут быть разными. Сравнивать
можно только длины векторов.

А вот
понятие равенства для векторов
есть.

Равными называются векторы,
имеющие одинаковые длины и одинаковое
направление. Это значит, что вектор
можно перенести параллельно себе в любую
точку плоскости.

Единичным
называется вектор, длина которого равна
1. Нулевым — вектор, длина которого
равна нулю, то есть его начало совпадает
с концом.

Удобнее
всего работать с векторами
в прямоугольной системе координат —
той самой, в которой рисуем графики
функций. Каждой точке в системе
координат соответствуют два числа —
ее координаты по x и y, абсцисса
и ордината.

Вектор также задается
двумя координатами:

Здесь
в скобках записаны координаты вектора

—
по x и по y.

Находятся они
просто: координата конца вектора минус
координата его начала.

Если
координаты вектора заданы, его длина
находится по формуле

Сложение векторов

Для
сложения векторов есть два способа.

1.
Правило параллелограмма. Чтобы сложить
векторы

и

,
помещаем начала обоих в одну точку.
Достраиваем до параллелограмма
и из той же точки проводим
диагональ параллелограмма. Это и будет
сумма векторов

и

.

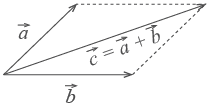
Помните
басню про лебедя, рака и щуку? Они
очень старались, но так и не сдвинули
воз с места. Ведь векторная сумма
сил, приложенных ими к возу, была
равна нулю.

2.
Второй способ сложения векторов —
правило треугольника. Возьмем те же
векторы

и

.
К концу первого вектора пристроим
начало второго. Теперь соединим начало
первого и конец второго. Это и есть
сумма векторов

и

.

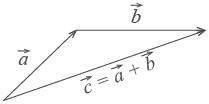
По тому же
правилу можно сложить и несколько
векторов. Пристраиваем их один
за другим, а затем соединяем начало
первого с концом последнего.

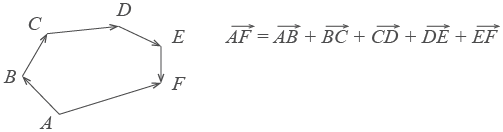
Представьте,
что вы идете из пункта А в пункт В,
из В в С, из С в D, затем в Е
и в F. Конечный результат этих
действий — перемещение из А в F.

При
сложении векторов

и

получаем:

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #