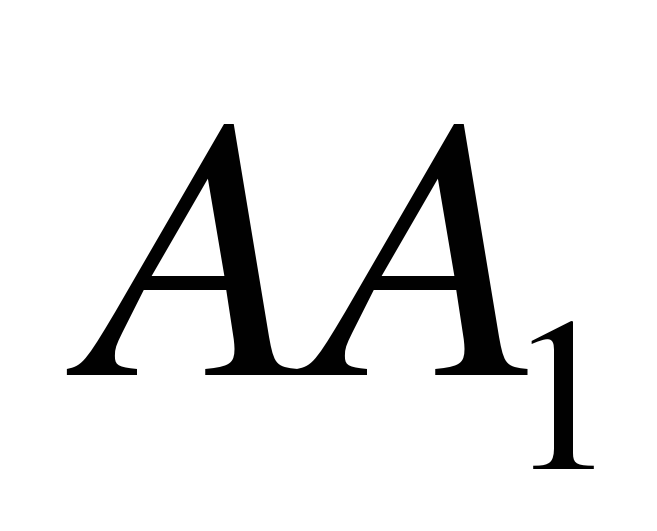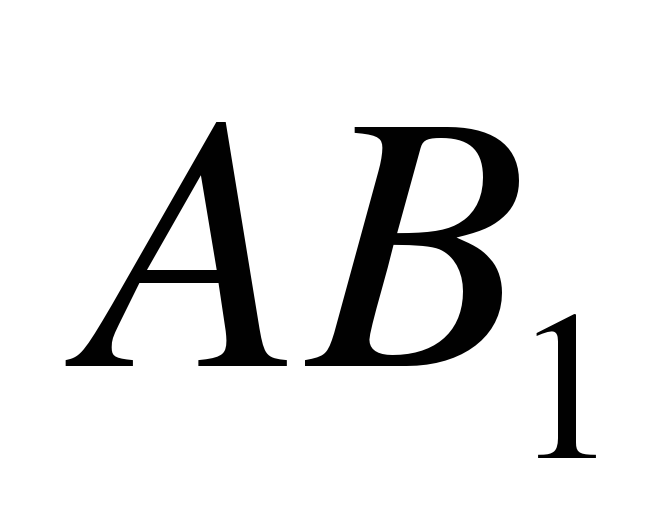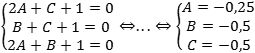Есть ли векторы в егэ профильная математика

Метод координат в егэ по математике профиль

Векторы

Отрезок, для которого указано, какая из его граничных точек является началом, а какая — концом, называется Вектором.

Вектор с началом в точке A и концом в точке B обозначают $↖$ или строчной (маленькой) буквой, например $↖$

Любая точка плоскости является вектором. В этом случае вектор называется Нулевым.

Модуль (длину) вектора обозначают $|АВ|↖$.

Ненулевые векторы называются Коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых.

Два коллинеарных вектора называются Сонаправленными, если они направлены в одну сторону.

Векторы называются Равными , если они сонаправлены и их длины равны.

Сумма векторов — это вектор, который можно получить двумя способами.

Правило треугольника (А) Правило параллелограмма (Б)

Для любых векторов $a↖, b↖, c↖$ справедливы равенства:

$a↖+b↖=b↖+a↖$(переместительный закон) $(a↖+b↖)+c↖=a↖+(b↖+c↖)$ (сочетательный закон)

Разность векторов тоже можно получить двумя способами:

Если надо найти разность двух векторов, их необходимо отложить из одной точки. Результирующий вектор направлен к уменьшаемому.

Для любых $a↖$ и $b↖$ справедливо равенство $a↖-b↖=a↖+(↖)$

Скалярное произведение векторов равно произведению длин векторов на косинус угла между ними.$a↖⋅b↖=|a↖|·|b↖|·cos⁡α$

Ненулевые векторы $a↖$ и $b↖$ перпендикулярны, если их произведение равно нулю.

Метод координат

Координаты вектора равны разностям соответствующих координат конца и начала данного вектора.

Для того чтобы векторы $a↖$ и $b↖$ были коллинеарными, необходимо и достаточно, чтобы выполнялось равенство $a↖=k·b↖$, где $k$ — это некоторое число.

Координаты середины вектора равны средним арифметическим координат его концов.

Каждая координата суммы двух или более векторов равна сумме соответствующих координат этих векторов.

Каждая координата разности двух векторов равна разности соответствующих координат этих векторов.

Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число.

Скалярное произведение векторов $a↖$ и $b↖$ в координатах находится по формуле $a↖·b↖= x1·x2+y1·y2$

Длина вектора $a↖$ вычисляется по формуле: $|a↖|=√$

Расстояние между двумя точками $M1(x1;y1)$ и $M2(x2; y2)$ находится по формуле $|M1M2|=√$

В правильной шестиугольной призме все ребра равны 1, найдите расстояние от точки А до плоскости.

3. В кубе ABCDA1B1C1D1 найдите угол между Плоскостями ABC и BDD1

Самое популярное. Тригонометрия и площади фигур

A b c a b c сочетательный закон.

Examer. ru

09.09.2017 3:20:00

2017-09-09 03:20:00

Лучшие шпаргалки по математике. Качественно. Ничего лишнего.

Просто кликните по картинке. Подробно — в разделе «Решение задач ЕГЭ по математике».

Самое популярное. Тригонометрия и площади фигур

Геометрия на ЕГЭ по математике. Треугольники, четырехугольники, окружности.

Стереометрия: формулы объема и площади поверхности.

Классическая стереометрия и метод координат

Алгебра

Внимание! Тотальная распродажа! Именно сейчас вы можете получить все 5 дисков видеокурса по минимальной цене 5000 2500 рублей. Количество комплектов ограничено. Не опоздайте! Заказать

Это полезно

Узнаете, чем отличаются официально-деловой, публицистический, научный, художественный и разговорный стили.

Узнаете, чем отличаются официально-деловой, публицистический, научный, художественный и разговорный стили.

Наш онлайн-курс по Физике

Все темы ЕГЭ с нуля

Можно не только читать, но и смотреть новые объяснения и разборы на нашем YouTube канале!

Пожалуйста, подпишитесь на канал и нажмите колокольчик, чтобы не пропустить новые видео

Задавайте свои вопросы в комментариях и оставляйте задачи, которые вы хотите, чтобы мы разобрали.

Мы обязательно ответим!

Мы заметили, что Вы регулярно пользуетесь нашими материалами для подготовки по физике.

В правильной шестиугольной призме все ребра равны 1, найдите расстояние между прямыми и.

Геометрия на ЕГЭ по математике. Треугольники, четырехугольники, окружности.

Внимание! Тотальная распродажа! Именно сейчас вы можете получить все 5 дисков видеокурса по минимальной цене 5000 2500 рублей. Количество комплектов ограничено. Не опоздайте! Заказать

Узнаете, чем отличаются официально-деловой, публицистический, научный, художественный и разговорный стили.

Узнаете, чем отличаются официально-деловой, публицистический, научный, художественный и разговорный стили.

Наш онлайн-курс по Физике

Все темы ЕГЭ с нуля

Можно не только читать, но и смотреть новые объяснения и разборы на нашем YouTube канале!

Пожалуйста, подпишитесь на канал и нажмите колокольчик, чтобы не пропустить новые видео

Задавайте свои вопросы в комментариях и оставляйте задачи, которые вы хотите, чтобы мы разобрали.

Мы обязательно ответим!

Мы заметили, что Вы регулярно пользуетесь нашими материалами для подготовки по физике.

В кубе найдите угол между плоскостями АВС и.

Метод координат

В правильной треугольной призме все ребра равны 1, найдите угол между прямой и плоскостью.

Ege-study. ru

08.02.2019 12:51:28

2019-02-08 12:51:28

Метод координат в пространстве (самостоятельная работа)

1. В кубе ABCDA1B1C1D1 найдите Угол между прямыми AA1 и BC1.

3. В кубе ABCDA1B1C1D1 найдите угол между Плоскостями ABC и BDD1

4. В кубе ABCDA1B1C1D1 найдите расстояние от точки А до плоскости BDA1

5. В правильной треугольной призме ABCA1B1C1 все ребра равны 1, найдите расстояние между прямыми AA1 и BC.

Весь материал — в документе.

Содержимое разработки

Самостоятельная работа по теме

«Метод координат в пространстве»

Вариант 1.

В кубе найдите угол между прямыми и.

В кубе найдите угол между прямой и плоскостью.

В кубе найдите угол между плоскостями АВС и.

В кубе найдите расстояние от точки А до плоскости.

В правильной треугольной призме все ребра равны 1, найдите расстояние между прямыми и.

Вариант 2.

В кубе найдите угол между прямыми и.

В кубе найдите угол между прямой и плоскостью.

В кубе найдите угол между плоскостями АВС и.

В кубе найдите расстояние от точки А до плоскости.

В правильной треугольной призме все ребра равны 1, найдите расстояние между прямыми и.

Вариант 3.

В правильной треугольной призме все ребра равны 1, найдите угол между прямыми и.

В правильной треугольной призме все ребра равны 1, найдите угол между прямой и плоскостью.

В кубе найдите угол между плоскостями АВС и.

В правильной шестиугольной призме все ребра равны 1, найдите расстояние от точки А до плоскости.

В правильной шестиугольной призме все ребра равны 1, найдите расстояние между прямыми и.

Вариант 4.

1. В правильной треугольной призме все ребра равны 1, найдите

Угол между прямыми и.

2. В правильной треугольной призме все ребра равны 1, найдите

Угол между прямой и плоскостью.

В кубе найдите угол между плоскостями и.

В правильной шестиугольной призме все ребра равны 1, найдите расстояние от точки А до плоскости.

В правильной шестиугольной призме все ребра равны 1, найдите расстояние между прямыми и.

-80%

Ненулевые векторы называются Коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых.

Отрезок, для которого указано, какая из его граничных точек является началом, а какая — концом, называется Вектором.

Два коллинеарных вектора называются сонаправленными, если они направлены в одну сторону.

Videouroki. net

06.05.2017 9:20:08

2017-05-06 09:20:08

Источники:

Https://examer. ru/ege_po_matematike/teoriya/vector

Https://ege-study. ru/ru/ege/materialy/matematika/shpargalki/

Https://videouroki. net/razrabotki/metod-koordinat-v-prostranstve-samostoyatelnaya-rabota. html

Презентация по математике Решение заданий 14 профиль ЕГЭ методом координат » /> » /> .keyword { color: red; } Метод координат в егэ по математике профиль

Презентация по математике Решение заданий 14 профиль ЕГЭ методом координат

Презентация по математике «Решение заданий 14 профиль ЕГЭ методом координат»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Международный конкурс по экологии «Экология России»

Доступно для всех учеников 1-11 классов и дошкольников

Описание презентации по отдельным слайдам:

Метод координат
В решении заданий 14 ЕГЭ (профильный уровень)

Повторение. Метод координат на плоскости.
Задача 1. Дана прямоугольная трапеция с основаниями a и b. Найдите расстояние между серединами ее диагоналей.
Решение. 1. Введем систему координат как указано на рисунке 3. Тогда вершины трапеции будут иметь координаты: A(0,0), B(0,y), C(b, y) и D(a,0). (y – высота трапеции, АВ).
2. Найдем координаты середин
Диагоналей. Для точки О, для точки О1:
.
По формуле найдем расстояние между точками О и О1:
Ковалева Ирина Константиновна
(0,0)
(0,y)
(b, y)
(a,0)

Ковалева Ирина Константиновна
Задача 2. Медиана, проведенная к основанию равнобедренного треугольника, равна 160 см, а основание треугольника равно 80 см.
Найдите две другие медианы этого треугольника.
Решение. 1. Введем прямоугольную систему координат так, как показано на рисунке 4. В этой системе вершины треугольника будут иметь координаты:
А(-40,0), В(0, 160), С(40,0), а точка М2(0,0).
.
Вычислим длины отрезков АМ1 и СМ3, используя формулу (6). Для АМ1 получим:
.
(-40,0)
(0, 160)
(40,0)
(0,0)

Ковалева Ирина Константиновна
Задача 3. В прямоугольном равнобедренном треугольнике проведены медианы острых углов. Вычислите косинус угла между ними.
Решение. 1. Введем систему координат так, как показано на рисунке. В этом случае вершины треугольника будут иметь координаты: С(0,0), А(а,0), В(0,а), а середины катетов (Здесь а – длина катета.):

2. По формуле (4) вычислим координаты векторов
(0,0)
(а,0)
0,а)

Метод координат
Приведём основные формулы.
1. Расстояние между точками
2. Координаты середины С отрезка АВ равны средним арифметическим соответствующих координат его концов:
Координаты точки пересечения медиан треугольника равны средним арифметическим соответствующих координат его вершин.
3. Скалярным произведением векторов называется число

4. Если — ненулевые векторы, а —угол между ними, то
Векторы перпендикулярны (ортогональны) тогда и только тогда, когда а • b = 0, или
5. Уравнение плоскости, проходящей через точку перпендикулярно ненулевому вектору ( вектору нормали плоскости), имеет вид
Любое линейное уравнение с тремя неизвестными Ax + By + Cz + D = 0,
Где числа А, В и С одновременно не равны нулю, есть уравнение некоторой плоскости, причём п (А; В; С) — вектор нормали этой плоскости.
6. (Уравнение плоскости в отрезках.) Если плоскость не проходит через начало координат, то её уравнение можно представить в виде
Где (р; 0; 0), (0; q; 0), (0; 0;r ) — точки пересечения плоскости с осями Ох, Оу и Oz соответственно.

7. Косинус угла между плоскостями равен модулю косинуса угла между векторами нормалей этих плоскостей, т. е. если — угол между плоскостями, заданными уравнениями
8. Параметрические уравнения прямой, проходящей через точку параллельно ненулевому вектору (направляющий вектор прямой), имеют вид
9. Расстояние d от точки до плоскости, заданной уравнением Ах + By + Cz + D = 0, находится по формуле

Если — угол между прямой с направляющим вектором и плоскостью Ах + Ву + Cz + D = 0 с вектором нормали
То равен модулю косинуса угла между этими векторами, т. е.

Для решения задачи по стереометрии координатным методом нужно выбрать декартову систему координат. Ее можно выбрать как угодно, главное, чтобы она была удобной. Приведем примеры выбора системы координат в кубе, пирамиде и конусе:
Примеры выбора системы координат

Далее необходимо найти координаты основных точек в выбранной системе координат. Это могут быть вершины объемной фигуры, середины ребер или любые другие точки, указанные в условии задачи. Найдем координаты куба и правильной пирамиды (предположим, что все ребра равны 4):
Очевидно, что координаты точки A (0;0;0) т. B — (4;0;0), т. G — (4;4;4) и т. д. (Рис. 1).

Рассмотрим правильную пирамиду ABCD с ребром 4: т. A (0;0;0),
Координату x точки С можно получить, опустив перпендикуляр из т. С на ось OX. (Рис. 2), искомая координата 2.
Координата y т. С равна длине отрезка AF=CE. Найдем его по теореме Пифагора из треугольника AFC:

Координата z точки C равна 0, потому что т. С лежит в плоскости XOY
C(2;√12;0).
E

Найдем координаты вершины D. Координаты X и Y т. D совпадают с координатами X и Y т. H. Высота правильной треугольной пирамиды падает в точку пересечения медиан, биссектрис и высот. Отрезок EH=1/3CE=1/3∗√12 (медианы точкой пересечения делятся в отношении как 1:3) и равен координате т. D поY. Отрезок IH=2 координата т. D по X. А координата по оси Z равна высоте пирамиды:

Угол между скрещивающимися прямыми
И так, мы научились находить координаты точек, и при помощи них определять координаты векторов.

Пример: Дан куб ABCDA1B1C1D1. Точка М — середина В1С1.
Найдите угол между прямыми АС1 и ВМ.
Пусть ребро куба равно 2. Найдём координаты точек: А(0; 0; 0),
С1(2; 2; 2),
В(0; 2; 0),
М(1; 2; 2),
Решение.
Найдём координаты векторов

Угол между плоскостями
Иногда в задачах по стереометрии просят найти угол между плоскостями. В этом случае вам нужно найти уравнения этих плоскостей и воспользоваться формулой.
Пусть даны два уравнения плоскостей:
Тогда угол между этими плоскостями можно найти по формуле:
Пример: Найдите угол между плоскостями, заданными уравнениями:
Решение: исходя из данных уравнений: А=3; В=2; С=3
А1=1; В1=-1; С1=2
Подставим в формулу для нахождения угла между плоскостями:

Уравнение плоскости
В задачах №14 (С2) ЕГЭ часто требуется найти угол между прямой и плоскостью и расстояние между скрещивающимися прямыми. Но для этого вы должны уметь выводить уравнение плоскости. В общем виде уравнение плоскости задается формулой: ,где A, B,C, D – какие-то числа. Если найти A, B,C, D, то мы найдем уравнений плоскости. Плоскость однозначно задается тремя точками в пространстве, значит нужно найти координаты трех точек, лежащий в данной плоскости, а потом подставить их в общее уравнение плоскости.
Например, пусть даны три точки:
Подставим координаты точек в общее уравнение плоскости:

Получилась система из трех уравнений, но неизвестных 4: A, B,C, D.
Если наша плоскость не проходит через начало координат, то мы можем D приравнять 1, если же проходит, то D=0. Объяснение этому простое: вы можете поделить каждое ваше уравнения на D, от этого уравнение не изменится, но вместо D будет стоять 1, а остальные коэффициенты будут в D раз меньше. Теперь у нас есть три уравнения и три неизвестные – можем решить систему:

Пример: Найти уравнение плоскости, проходящей через точки K(1;2;3); P(0;1;0); L(1;1;1).
Получаем искомое уравнение плоскости:
−0.5x−y+0.5z+1=0.

Решение: Подставим координаты точек в уравнение плоскости D=1:
K(1;2;3)
P(0;1;0)
L(1;1;1)

Для составления уравнения плоскости можно использовать определитель
Третьего порядка, который можно просчитать правилом Саррюса.
Пусть наша плоскость проходит через точки: М1(х1;у1;z1), М2(х2;у2;z2),
М3(х3;у3;z3). Уравнение этой плоскости в координатной форме будет иметь вид:
Теперь нам нужно найти многочлен от элементов квадратной матрицы
С помощью специальных правил. Рассмотрим лишь один из способов –
Правило Саррюса. Для этого дополним наш определитель матрицей:

Пример 2. Найти уравнение плоскости, проходящей через точки K(1;2;3); P(0;1;0); L(1;1;1).
Получаем искомое уравнение плоскости:

Решение: Подставим координаты точек в определитель:
K(1;2;3)
P(0;1;0)
L(1;1;1)
Х – 1 у – 2 z – 3
0 – 1 1 – 2 0 – 3 = 0
1 – 0 1 – 1 1 — 0
Дополним определитель матрицей:
Х – 1 у – 2 z – 3 х – 1 у – 2
0 – 1 1 – 2 0 – 3 0 – 1 1 – 2 =
1 – 0 1 – 1 1 – 0 1 – 0 1 – 1
4 5 6 + + +
1 2 3 — — —
=(х – 1)(1 -2)(1- 0)+(у – 2)(0 – 3)(1 – 0)+(z – 3)(0 – 1)(1 – 1) — (z – 3)(1 – 2)(1 – 0) –
(х – 1)(0 -3)(1- 1) — (у – 2)(0 – 1)(1 – 0) = — х + 1 — 3у + 6 + z – 3 + у – 2=
= — х – 2у + z + 2
Х – 2у + z + 2 = 0 / 2
— 0,5х – у + 0,5z + 1 = 0

Пример: Дан прямоугольный параллелепипед ABCDA1B1C1D1 с рёбрами АВ = 2, AD = 4, АА1 = 6. Найдите расстояние от середины ребра D1C1 до плоскости, проходящей через середины рёбер АВ, AD и ССг.
Решение. Пусть К, L, М и Р — середины рёбер АВ, AD, СС1 и C1D1 соответственно. Введём прямоугольную систему координат, взяв за её начало вершину А. Найдём координаты следующих точек: L(2; 0; 0), К(0; 1; 0), М(4; 2;3), Р(4; 1; 6).
Тогда уравнение плоскости KLM имеет вид
Расстояние от точки Р (4; 1; 6) до плоскости равно

Пример: В правильной четырехугольной пирамиде SАВСD сторона основания равна 2, а высота равна 1. Найдите угол между плоскостями SBС и MNP, где M — середина AB, N – середина ребра AD, P — середина SC.
Решение. Выберем систему координат (рис.). Определим координаты точек:
(-1;0;0)
(0;0;1)
(1;1;0)
(1;-1;0)
(0;-1;0)
Запишем уравнение плоскости SBC:
Запишем уравнение плоскости MNP:
Косинус угла между плоскостями равен модулю косинуса угла между векторами нормалей этих плоскостей
Cos (SBC;MNP)=ا-0,5ا = 0,5
Ответ: 60º

Пример: Дана правильная треугольная призма АВСА1В1С1 со стороной основания и боковым ребром. Точка М — середина ребра ВВ1. Найдите угол между плоскостями АМС и А1ВС1
Решение. Пусть К и N — середины рёбер АС и А1С1 соответственно. На прямой, проходящей через вершину В параллельно АС, отметим точку Т.
Введём прямоугольную систему координат, взяв за её начало вершину В, оси Вх, By и Bz по лучам ВК, ВТ и ВВ1 соответственно.
Найдём координаты точек: В(0; 0; 0), K(√21; 0; 0), N(√21; 0; 2√15), М(0; 0; √15).
Продолжить решение задачи самостоятельно

Расстояние от точки до плоскости
Зная координаты некоторой точки M(xM;yM;zM), легко найти расстояние до плоскости Ax+By+Cz+D=0:
Пример: Найдите расстояние от т. H(1;2;0) до плоскости, заданной уравнением: 2∗x+3∗y−√2∗z+4=0.
Решение: Из уравнения плоскости сразу находим коэффициенты:
A=2, B=3, C=−√2, D=4.
Подставим их в формулу для нахождения расстояния от точки до плоскости.

Расстояние между скрещивающимися прямыми

Расстояние между скрещивающимися прямыми – это расстояние от любой точки одной из прямых до параллельной ей плоскости, проходящей через вторую прямую.
Таким образом, если требуется найти расстояние между скрещивающимися прямыми, то нужно через одну из них провести плоскость параллельно второй прямой. Затем найти уравнение этой плоскости и по формуле расстояния от точки до плоскости найти расстояние между скрещивающимися прямыми. Точку на прямой можно выбрать произвольно (у которой легче всего найти координаты).

Решение:
Решим задачу полностью методом координат. Нарисуем рисунок и выберем декартову систему координат.

Пример: Дана правильная треугольная призма ABCFDE, ребра которой равны 2.
Точка G — середина ребра CE.
А)Докажите, что прямые AD и BG перпендикулярны.
Б)Найдите расстояние между прямыми AD и BG.
Определим координаты точек A, D, B и G. Координаты точки G по осям x и y совпадают с координатами точки C.
Мы нашли координаты векторов. Теперь воспользуемся формулой для нахождения косинуса угла между скрещивающимися прямыми. Если косинус получится равен 0, это будет значить, что прямые перпендикулярны.

Так как ADHE параллелограмм по построению, то DH=AB: H(4;0;2). Уравнение плоскости получим из системы уравнений, подставив в общее уравнение плоскости найденные координаты точек B, G и H.
Б)Для того, чтобы найти расстояние между скрещивающимися прямыми необходимо провести плоскость, проходящую через одну из прямых параллельно первой прямой.
Выполним параллельный перенос прямой DA в точку B. Получим прямую BН, где точка H лежит на продолжении ребра FD, потому что BH, очевидно, лежит в плоскости грани ABD, как прямая параллельная AD, и проходящая через точку B.
Искомая плоскость, проходящая через прямую BG, и параллельная прямой AD, будет проходить через три точки: B, G и H. Найдем координаты точки H.
, H(4;0;2)
Из системы уравнений находим:
Составляем уравнение плоскости:
Найдем расстояние от любой точки на прямой AD до найденной плоскости, это и будет искомым расстоянием между прямыми AD и BG. На прямой AD удобно выбрать т. A(0;0;0).

Ответ: Наибольшее давление будет в точке 1.

Ι A Ι ≥ 0

Ох, уж эти неравенства.

Где давление газа будет наибольшим.

Infourok. ru

27.09.2019 17:09:14

2019-09-27 17:09:14

Метод координат в стереометрических задачах профильного ЕГЭ по математике

Метод координат… Что же это такое и зачем он нужен? Можно ли без него обойтись при сдаче ЕГЭ? Можно, безусловно! Все стереометрические задачи второй части профильного ЕГЭ по математике решаются и без привязки фигур к системе координат. Но… координатный метод может значительно упростить решение самых сложных вопросов, таких, как определение расстояний и углов между прямыми и плоскостями в пространстве, так как там все эти расчеты сводятся, практически, к одной формуле.

Будем разбираться!

Вспомните, как вас знакомили с системой координат и объясняли, что положение каждой точки в системе координат можно определять координатами Х и у. Это точки M(xm; ym) и N(xn; Yn)

Как известно, прямую можно провести через две точки, и при том, только одну. Задача по определению уравнения прямой на плоскости, проходящей через две точки, координаты которых известны, решалась очень просто. В этом случае в уравнение прямой Y=Kx+B подставляли сначала координаты точки М, Затем – точки N.

Получали систему двух линейных уравнений относительно неизвестных коэффициентов K и B, которые находили при решении этой системы.

Но уравнение прямой на плоскости можно задать и по-другому:

Ax + By + C = 0, (A² + B² ≠ 0)

И суть от этого не изменится, изменятся только коэффициенты. Условие в скобках означает, что А и В не могут быть равны нулю одновременно.

Стереометрия рассматривает фигуры в пространстве, где каждая точка описывается уже тремя координатами – (X, Y, Z).

Привязка фигур к системе координат позволяет не только определять координаты точек, но и записать Уравнение плоскости. Как известно, на трех точках можно построить плоскость, притом, только одну. Соответственно, можно и записать плоскость уравнением. Выглядит это уравнение следующим образом:

Ax + By + Cz + D = 0

Очень похоже на вторую запись уравнения прямой на плоскости. Значит, и коэффициенты А, В, С И D мы будем находить также, как и коэффициенты для прямой на плоскости, По точкам.

Это действие сродни тому, что вы производили, определяя уравнение прямой, проходящей через две точки, заданные координатами.

Прямую можно провести через Две точки, и мы составляли два уравнения для двух точек.

Плоскость можно провести через Три Точки, значит, и уравнений будет три!

Но уравнений три, а неизвестных – четыре! Ну, и что! Мы же можем разделить все уравнения на D, при этом они не изменятся, будут равнозначны первоначальным! Так и будем поступать! Тогда вместо D будет единица, а все остальные коэффициенты будут делиться на D, назовем их также, А, В, С. И это уже вполне решаемая система!

Здесь значения всех X, Y и Z известны, это координаты точек, принадлежащих данной плоскости.

Итак, точку описать можем, прямую описать можем, плоскость – можем. Осталось вспомнить сами векторы и их координаты, они нам тоже пригодятся при решении задач.

Векторы и их координаты

Вектор – это математический объект, характеризующийся величиной и направлением. Например, в геометрии и в естественных науках вектор есть направленный отрезок прямой.

Мы можем «привязать» вектор к системе координат, т. е. мы можем его определять в пространстве координатами его проекций на координатные плоскости.

Если даны две точки в пространстве А(xa; ya; za) и B(xb; yb; zb), то дан и вектор

, где АХ, аУ и АZ – координаты вектора. Осталось определить значения аХ, АУ и аZ. Определяем:

АХ = XB – XA

АУ = YB – YA

АZ = ZB – ZА

Теперь, зная длины проекций вектора, мы можем легко найти длину вектора, которая, как видно из чертежа, есть не что иное, как диагональ параллелепипеда, сторонами которого являются координаты этого вектора. Его длина, модуль вектора, будет равна:

А что есть длина вектора, как не расстояние между двумя точками: началом и концом вектора? То есть выведенная формула определяет Расстояние между двумя точками в декартовой системе координат.

По морю параллельными курсами в одном направлении следуют два сухогруза: первый длиной 110 метров, второй – длиной 90 метров. Сначала второй сухогруз отстает от первого, и в некоторый момент времени расстояние от кормы первого сухогруза до носа второго составляет 1000 метров. Через 16 минут после этого уже первый сухогруз отстает от второго так, что расстояние от кормы второго сухогруза до носа первого равно 400 метрам. На сколько километров в час скорость первого сухогруза меньше скорости второго?

Давление насыщенного пара величина постоянная для заданной температуры. Она меняется только с изменением температуры: увеличивается с увеличением температуры и уменьшается с уменьшением температуры.

ЕГЭ физика. Решаем задачи с изопроцессами в графиках

Значит, и коэффициенты А, В, С и D мы будем находить также, как и коэффициенты для прямой на плоскости, по точкам.

Zagalina. ru

01.05.2017 15:03:39

2017-05-01 15:03:39

Метод координат в егэ по математике профиль

Сегодня будем решать текстовые задачи из профильного ЕГЭ по математике. А именно — задачи на движение. Убиваем сразу двух зайцев: решаем текстовые задачи и вспоминаем кинематику, а именно относительную систему координат.

Задача 1:

По морю параллельными курсами в одном направлении следуют два сухогруза: первый длиной 110 метров, второй – длиной 90 метров. Сначала второй сухогруз отстает от первого, и в некоторый момент времени расстояние от кормы первого сухогруза до носа второго составляет 1000 метров. Через 16 минут после этого уже первый сухогруз отстает от второго так, что расстояние от кормы второго сухогруза до носа первого равно 400 метрам. На сколько километров в час скорость первого сухогруза меньше скорости второго?

Решение:

Итак, мы имеем два движущихся с разной скоростью теплохода, и нам эту разницу скоростей нужно определить. Она и будет нашей неизвестной

На картинке оба теплохода движутся по неподвижной воде. Системой отсчета, она же — система координат, является море. Читать далее →

Задача с параметром и производная

Задача:

Найдите все значения а, при которых уравнение

Имеет два различных корня. укажите эти корни.

Для начала мы должны посмотреть на это уравнение. Для этого чертим графики левой части уравнения У = и правой части уравнения У = а(х — 1). Именно точки пересечения этих графиков и определят корни уравнения.

График правой части — линейная функция, проходящая через точку 1 на оси 0х, угловой коэффициент которой K = a, которую мы и ищем. Получается, что эта прямая как бы вращается вокруг точки А(1: 0), меняя угол наклона к оси 0х при изменении А. На графике представлены четыре из всего множества прямых: фиолетовая, красная, синяя и бирюзовая, а также пунктирная..

Второй график, График с модулем, преобразуем, сначала без модуля.

У = х 2 — 4х + 3 = ( х 2 — 2·2·х + 2 2 ) — 2 2 +3 = (х — 2) 2 — 1.

Отсюда получается, что это — парабола У = х 2 , вершина которой смещена в точку (2: -1). Модуль «переворачивает» отрицательную часть графика в положительную половину. График, который получился, начерчен зеленым цветом. Читать далее →

Производная. Что нужно о ней понимать?

Производная есть предел отношения приращения функции при бесконечно малом приращении аргумента.

А теперь посмотрим на линейную функцию Y = kx + b. Напоминаю, линейная функция на графике X 0 y — это прямая, а K — угловой коэффициент, определяемый тангенсом угла наклона графика к оси 0х. В нашем случае прямые — это три секущие и касательная. А для них отношение = k.

Получается, что при уменьшении Δх→ 0 секущая становится касательной. Следовательно

Производная функции в точке — это угловой коэффициент касательной к данной точке функции.

Решаем задачи ЕГЭ по МКТ и термодинамике

Задача 1:

На высоте 200км давление воздуха составляет примерно 10 -9 от нормального давления, а температура воздуха примерно 1200К. Оцените плотность воздуха на этой высоте. Ответ дайте 10 -10 , Округлите до десятых

Начнем! Сначала преобразуем уравнение Менделеева-Клайперона для данного конкретного случая:

PV = νRT

Заменим M = ρV, получим

Очевидно, что можно разделить все уравнение на V, получим

Выделяем из этого уравнения плотность, получим

= 291· 10 -12 ≈ 2,9· 10 -10

Ответ: 2,9

Задача 2:

Абсолютная температура воздуха в сосуде под поршнем повысилась в 2 раза, и воздух перешел из состояния 1 в состояние 2. Сквозь зазор между поршнем и сосудом мог просачиваться воздух. Рассчитайте отношение N2 / N1 числа молекул газа в конце и в начале опыта.

Посмотрим, что мы имеем в относительных величинах, используем приложенный график: Читать далее →

ЕГЭ физика. Решаем задачи с изопроцессами в графиках

Изопроцессы в МКТ — это процессы, протекающие в газах с каким-нибудь неизменным параметром. Рассмотрим, как решаются некоторые задачи, представленные в графиках, при наличии неизменных параметров.

Задача 1 : Постоянная масса идеального газа участвует в процессе, указанном на рисунке. Где давление газа будет наибольшим?

Приступаем. Фраза «постоянная масса газа» означает, что мы имеем задачу с изопроцессом. Смотрим.

1-2: Температура не меняется (изотерма), но при этом увеличивается объем. В изотермическом процессе увеличение объема ведет к уменьшению давления и наоборот. Давление обратно пропорционально объему. Следовательно, в точке 2 давление ниже, чем в точке.

2-3: Не меняется объем (изохора), но при этом температура уменьшается. А в изохорном процессе давление прямо пропорционально температуре. То есть, в нашем случае — уменьшается. Давление в точке 3 будет меньше, чем в точке 2.

Ответ: Наибольшее давление будет в точке 1.

Задача 2 : Зависимость объема идеального газа от температуры показана на V-P диаграмме. Масса газа постоянна. Выберите два верных утверждения о процессе, происходящем с газом: Читать далее →

Изопроцессы и их графики

Изопроцессы в МКТ — это процессы, протекающие в газах с каким-нибудь неизменным параметром. Для начала мы рассмотрим газ, у которого постоянная масса и химический состав. То есть в газе не меняется количество вещества Ν . В этом случае мы можем упростить уравнение Менделеева-Клайперона.

Я не буду углубляться в названия газовых законов, вы это прочтете в учебниках. Займемся чистой математикой

Итак, у нас есть некий газ постоянной массы. Основные характеристики его состояния определяются. То есть, если мы будем на этот газ как-то воздействовать, меняя его характеристики, то

Получается, что все три его характеристики связаны. Но можно рассмотреть случаи, когда один из этих компонентов не меняется. это и будут изопроцессы. Посмотрим, как будут выглядеть графики изопроцессов в осях p(V), p(T), V(T).

Определяем угол между скрещивающимися прямыми

Задача из варианта №304 Ларина:

В правильном тетраэдре ABCD с ребром, равным 6, точки M и N – середины
Ребер АВ и CD.

А) Докажите, что угол между прямыми MN и BC равен 45°

Решать будем при помощи координат. Для этого присоединим к пирамиде систему координат, произвольно. Я выбрала вариант, показанный на рисунке: Нулевая точка декартовой системы находится в точке М.

Определяем координаты всех точек пирамиды. Воспользуемся чертежом проекции пирамиды на плоскость ХОу (вид сверху). В этом случае вершина пирамиды D совпадает на чертеже с точкой Н основания пирамиды. Точки основания пирамиды отмечены не чертеже в скобках.

Проекция пирамиды — это равносторонний треугольник со стороной, равной 6, а точка Н здесь — центр вписанной и описанной окружностей.. Определяем координаты точек относительно точки М. Углы треугольника по 60º.

Н — точка пересечения медиан, делит медиану на отрезки, которые относятся 2:1. Точка N делит сторону DC пополам, следовательно, проекция СН тоже делится пополам. Следовательно,

Координаты точек основания будут:

Определяем расстояние от точки до плоскости

Основанием призмы АВСА1В1С1 является правильный треугольник АВС со стороной 6. Боковое ребро АА1 Призмы равно 6 и образует со сторонами АВ и АС углы По 60 0 .
Определите расстояние от точки B1 до плоскости А1СВ;

Будем решать, применяя координатный метод. Присоединим к нашей призме систему координат, определим координаты узловых точек и найдем, все что нужно по координатам прямых и плоскостей.

Чтобы сделать рисунок более понятным, я закрасила грани и основания разным цветом. Предлагаю посмотреть на призму в проекциях на координатные плоскости, как бы со всех сторон. Соответственно на рисунке 1 смотрим на плоскость Х0у, на рисунке 2 — Z0y, а на рисунках 3 и 4 — плоскость Z0x слева и справа от призмы.

Переходим к расчету координат узловых точек. Вспомним, что наша призма состоит их двух треугольников (основания призмы), двух ромбов (боковые грани) и квадрата (третья боковая грань). Чтобы определиться, насколько отстоит верхнее основание от нижнего, нам необходимо выяснить положение точки А1. Читать далее →

Решаем тригонометрическое уравнение с помощью вспомогательного угла

Для начала найдем сумму квадратов коэффициентов при синусе и косинусе и разделим все уравнение на корень квадратный из этой суммы:

⇒

А теперь заменяем φ, a φ. Или φ, a φ. Я возьму первый вариант, но вы выбираете, какой хотите.

Определяем значения с помощью тригонометрического круга

Следует напомнить, что тригонометрический круг позволяет определиться с любыми значениями синусов, косинусов, тангенсов (подробнее здесь). Котангенсы тоже можно определять, только зачем нам загружать еще одну ось на нашу шпаргалку, когда любое уравнение с котангенсом можно превратить в уравнение с тангенсом, поскольку

На приведенном справа рисунке тригонометрического круга прорисованы все углы, значения которых мы знаем еще из геометрии, а именно: Π/6, Π/4 и Π/3, и те, которые можно определить через эти углы. Как определяются эти углы, можно увидеть ниже: Читать далее →

ЕГЭ физика. Решаем задачи на влажность

Среди задач ЕГЭ по физике некоторую трудность при всей своей простоте представляют задачи на влажность. По всей видимости существует некоторое недопонимание сути проблемы. Попробуем разобраться.

В воздухе всегда находится некоторое количество воды в газообразном виде, в виде пара. Это происходит потому, что над поверхностью любой жидкости происходит испарение и конденсация жидкости. В открытом сосуде процесс испарения может преобладать над процессом конденсации. Испаряться вода может до тех пор, пока не наступит динамическое равновесие между испарением и конденсацией молекул воды.

Относительная влажность — это отношение плотности пара в воздухе к плотности насыщенного пара.

Но если вспомнить, что плотность газа пропорциональна давлению газа, то получим формулу определения влажности:

Где Р — парциальное давление, Р0 — давление насыщенного пара.

Давление насыщенного пара величина постоянная для заданной температуры. Она меняется только с изменением температуры: увеличивается с увеличением температуры и уменьшается с уменьшением температуры.

Задача 1: Относительная влажность воздуха в закрытом сосуде 30 %. Какой станет относительная влажность, если объём сосуда при неизменной температуре уменьшить в 2 раза? (Ответ дать в процентах.)

Решение : Относительная влажность определяется отношением парциального давления пара к давлению насыщенного пара

Когда вы начинаете изучать газовые законы, тепло и т. д., первое, с чем вы сталкиваетесь, это понятие МОЛЕКУЛЯРНО-КИНЕТИЧЕСКАЯ ТЕОРИЯ. Так вот, ее название и есть отражение сути этого раздела физики. Нас интересуют молекулы газов и их движение в разных обстоятельствах. Появляется понятие идеального газа, газа, столкновения молекул у которого абсолютно упругие, и силой взаимодействия молекул в котором можно пренебречь.

Уравнение состояния идеального газа — уравнение Менделеева-Клайперона:

PV = νRT

Где P — давление (Па); V — объем газа (м 3 ); Ν — количество вещества (моли); R — газовая постоянная; T — температура (абсолютная).

Разберемся сначала с понятием количества вещества. Количество вещества измеряется молями. Что же такое моль? В общем-то 1 моль — это 6,1 • 10 23 штук молекул какого-то вещества. Грубо говоря, если нам сказано, что добавили один моль газа к смеси, то это значит, что туда запустили 6,1 • 10 23 штук молекул этого газа. Конечно же эти 6,1 • 10 23 молекул у разных газов имеют разную массу, но в данном случае масса обезличена, интересуют только количество молекул.
Читать далее →

Ох, уж эти неравенства.

Какое-то наваждение! Оказалось, проблемы у будущих выпускников школы появляются там, где не ждали! В решении неравенств! А ведь это одно из самых предсказуемых заданий сложной части профильного ЕГЭ. Что ж, разберемся.

С простыми неравенствами проблем, как правило, не бывает: решаем уравнение относительно нуля, расставляем точки, соответствующие корням, рисуем интервалы, определяем знаки… Все правильно, вопросов вроде, как нет.

Но вот, например, такое неравенство

Почему-то здесь вдруг эти вопросы появляются. Читать далее →

Абсолютная величина или модуль числа

Начну с известной всем формулировки:

Модуль числа A равен числу A, если A ≥ 0, и равен –A, если A < 0.

Про это помнят все, а вот что за минус, почему он появился, толком не понимают многие.

Сразу же главное: выражения с модулем не решаются как-нибудь отдельным способом, его раскрывают, но раскрывают в зависимости от того, какое выражение записано под модулем: положительное или отрицательное.

Модуль или абсолютная величина числа это его численное значение без учета каких-либо знаков. Просто число. У векторов, кстати, модуль вектора тоже просто число, которое определяет длину вектора независимо от его положения в пространстве. Отсюда Модуль числа — это всегда неотрицательное число. То есть

Ι A Ι ≥ 0

Так откуда минус? Читать далее →

Метод координат в стереометрических задачах профильного ЕГЭ по математике

Метод координат… Что же это такое и зачем он нужен? Можно ли без него обойтись при сдаче ЕГЭ? Можно, безусловно! Все стереометрические задачи второй части профильного ЕГЭ по математике решаются и без привязки фигур к системе координат. Но… координатный метод может значительно упростить решение самых сложных вопросов, таких, как определение расстояний и углов между прямыми и плоскостями в пространстве, так как там все эти расчеты сводятся, практически, к одной формуле.

Будем разбираться!

Вспомните, как вас знакомили с системой координат и объясняли, что положение каждой точки в системе координат можно определять координатами Х и у. Это точки M(xm; ym) и N(xn; Yn)

Как известно, прямую можно провести через две точки, и при том, только одну. Задача по определению уравнения прямой на плоскости, проходящей через две точки, координаты которых известны, решалась очень просто. В этом случае в уравнение прямой Y=Kx+B подставляли сначала координаты точки М, Затем – точки N.

Получали систему двух линейных уравнений относительно неизвестных коэффициентов K и B, которые находили при решении этой системы.

Но уравнение прямой на плоскости можно задать и по-другому:

Ax + By + C = 0, (A² + B² ≠ 0)

И суть от этого не изменится, изменятся только коэффициенты. Условие в скобках означает, что А и В не могут быть равны нулю одновременно. Читать далее →

Решение: Подставим координаты точек в определитель:
K(1;2;3)
P(0;1;0)
L(1;1;1)
Х – 1 у – 2 z – 3
0 – 1 1 – 2 0 – 3 = 0
1 – 0 1 – 1 1 — 0
Дополним определитель матрицей:
Х – 1 у – 2 z – 3 х – 1 у – 2
0 – 1 1 – 2 0 – 3 0 – 1 1 – 2 =
1 – 0 1 – 1 1 – 0 1 – 0 1 – 1
4 5 6 + + +
1 2 3 — — —
=(х – 1)(1 -2)(1- 0)+(у – 2)(0 – 3)(1 – 0)+(z – 3)(0 – 1)(1 – 1) — (z – 3)(1 – 2)(1 – 0) –
(х – 1)(0 -3)(1- 1) — (у – 2)(0 – 1)(1 – 0) = — х + 1 — 3у + 6 + z – 3 + у – 2=
= — х – 2у + z + 2
Х – 2у + z + 2 = 0 / 2
— 0,5х – у + 0,5z + 1 = 0

Координата z точки C равна 0, потому что т. С лежит в плоскости XOY
C(2;√12;0).
E

Векторы и их координаты

В этом случае вершина пирамиды D совпадает на чертеже с точкой Н основания пирамиды.

Zagalina. ru

12.07.2018 18:58:12

2018-07-12 18:58:12

Источники:

Https://infourok. ru/prezentaciya-po-matematike-reshenie-zadanij-14-profil-ege-metodom-koordinat-5255198.html

Https://zagalina. ru/2019/04/06/metod-koordinat-v-zadachakh-n14-profiln/

Https://zagalina. ru/ege/

Метод координат в пространстве » /> » /> .keyword { color: red; } Метод координат в егэ по математике профиль

Метод координат в пространстве

Метод координат в пространстве

Для того, чтобы использовать метод координат, надо хорошо знать формулы. Их три:

Главная формула — косинус угла φ между векторами a = (x1; y1; z1) и b = (x2; y2; z2):

На первый взгляд, выглядит угрожающе, но достаточно немного практики — и все будет работать великолепно.

Задача. Найти косинус угла между векторами a = (4; 3; 0) и b = (0; 12; 5).

Решение. Поскольку координаты векторов нам даны, подставляем их в первую формулу:

Задача. Составить уравнение плоскости, проходящей через точки M = (2; 0; 1), N = (0; 1; 1) и K = (2; 1; 0), если известно, что она не проходит через начало координат.

Решение. Общее уравнение плоскости: Ax + By + Cz + D = 0, но, поскольку искомая плоскость не проходит через начало координат — точку (0; 0; 0) — то положим D = 1. Поскольку эта плоскость проходит через точки M, N и K, то координаты этих точек должны обращать уравнение в верное числовое равенство.

Подставим вместо x, y и z координаты точки M = (2; 0; 1). Имеем:
A · 2 + B · 0 + C · 1 + 1 = 0 ⇒ 2A + C + 1 = 0;

Аналогично, для точек N = (0; 1; 1) и K = (2; 1; 0) получим уравнения:
A · 0 + B · 1 + C · 1 + 1 = 0 ⇒ B + C + 1 = 0;
A · 2 + B · 1 + C · 0 + 1 = 0 ⇒ 2A + B + 1 = 0;

Итак, у нас есть три уравнения и три неизвестных. Составим и решим систему уравнений:

Получили, что уравнение плоскости имеет вид: − 0,25x − 0,5y − 0,5z + 1 = 0.

Задача. Плоскость задана уравнением 7x − 2y + 4z + 1 = 0. Найти координаты вектора, перпендикулярного данной плоскости.

Решение. Используя третью формулу, получаем n = (7; − 2; 4) — вот и все!

Вычисление координат векторов

А что, если в задаче нет векторов — есть только точки, лежащие на прямых, и требуется вычислить угол между этими прямыми? Все просто: зная координаты точек — начала и конца вектора — можно вычислить координаты самого вектора.

Чтобы найти координаты вектора, надо из координат его конца вычесть координаты начала.

Эта теорема одинаково работает и на плоскости, и в пространстве. Выражение «вычесть координаты» означает, что из координаты x одной точки вычитается координата x другой, затем то же самое надо сделать с координатами y и z. Вот несколько примеров:

Задача. В пространстве расположены три точки, заданные своими координатами: A = (1; 6; 3), B = (3; − 1; 7) и C = (− 4; 3; − 2). Найти координаты векторов AB, AC и BC.

Рассмотрим вектор AB: его начало находится в точке A, а конец — в точке B. Следовательно, чтобы найти его координаты, надо из координат точки B вычесть координаты точки A:
AB = (3 − 1; − 1 − 6; 7 − 3) = (2; − 7; 4).

Аналогично, начало вектора AC — все та же точка A, зато конец — точка C. Поэтому имеем:
AC = (− 4 − 1; 3 − 6; − 2 − 3) = (− 5; − 3; − 5).

Наконец, чтобы найти координаты вектора BC, надо из координат точки C вычесть координаты точки B:
BC = (− 4 − 3; 3 − (− 1); − 2 − 7) = (− 7; 4; − 9).

Ответ: AB = (2; − 7; 4); AC = (− 5; − 3; − 5); BC = (− 7; 4; − 9)

Обратите внимание на вычисление координат последнего вектора BC: очень многие ошибаются, когда работают с отрицательными числами. Это касается переменной y: у точки B координата y = − 1, а у точки C y = 3. Получаем именно 3 − (− 1) = 4, а не 3 − 1, как многие считают. Не допускайте таких глупых ошибок!

Вычисление направляющих векторов для прямых

Если вы внимательно прочитаете задачу C2, то с удивлением обнаружите, что никаких векторов там нет. Там только прямые да плоскости.

Для начала разберемся с прямыми. Здесь все просто: на любой прямой найдутся хотя бы две различные точки и, наоборот, любые две различные точки задают единственную прямую.

Кто-нибудь понял, что написано в предыдущем абзаце? Я и сам не понял, поэтому объясню проще: в задаче C2 прямые всегда задаются парой точек. Если ввести систему координат и рассмотреть вектор с началом и концом в этих точках, получим так называемый для прямой:

Зачем нужен этот вектор? Дело в том, что — это угол между их направляющими векторами. Таким образом, мы переходим от непонятных прямых к конкретным векторам, координаты которых легко считаются. Насколько легко? Взгляните на примеры:

Задача. В кубе ABCDA1B1C1D1 проведены прямые AC и BD1. Найдите координаты направляющих векторов этих прямых.

Поскольку длина ребер куба в условии не указана, положим AB = 1. Введем систему координат с началом в точке A и осями x, y, z, направленными вдоль прямых AB, AD и AA1 соответственно. Единичный отрезок равен AB = 1.

Теперь найдем координаты направляющего вектора для прямой AC. Нам потребуются две точки: A = (0; 0; 0) и C = (1; 1; 0). Отсюда получаем координаты вектора AC = (1 − 0; 1 − 0; 0 − 0) = (1; 1; 0) — это и есть направляющий вектор.

Теперь разберемся с прямой BD1. На ней также есть две точки: B = (1; 0; 0) и D1 = (0; 1; 1). Получаем направляющий вектор BD1 = (0 − 1; 1 − 0; 1 − 0) = (− 1; 1; 1).

Ответ: AC = (1; 1; 0); BD1 = (− 1; 1; 1)

Задача. В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, проведены прямые AB1 и AC1. Найдите координаты направляющих векторов этих прямых.

Введем систему координат: начало в точке A, ось x совпадает с AB, ось z совпадает с AA1, ось y образует с осью x плоскость OXY, которая совпадает с плоскостью ABC.

Для начала разберемся с прямой AB1. Тут все просто: у нас есть точки A = (0; 0; 0) и B1 = (1; 0; 1). Получаем направляющий вектор AB1 = (1 − 0; 0 − 0; 1 − 0) = (1; 0; 1).

Теперь найдем направляющий вектор для AC1. Все то же самое — единственное отличие в том, что у точки C1 иррациональные координаты. Итак, A = (0; 0; 0), поэтому имеем:

Небольшое, но очень важное замечание насчет последнего примера. Если начало вектора совпадает с началом координат, вычисления резко упрощаются: координаты вектора просто равны координатам конца. К сожалению, это верно лишь для векторов. Например, при работе с плоскостями присутствие на них начала координат только усложняет выкладки.

Вычисление нормальных векторов для плоскостей

Нормальные векторы — это не те векторы, у которых все в порядке, или которые чувствуют себя хорошо. По определению, нормальный вектор (нормаль) к плоскости — это вектор, перпендикулярный данной плоскости.

Другими словами, — это вектор, перпендикулярный любому вектору в данной плоскости. Наверняка вы встречали такое определение — правда, вместо векторов речь шла о прямых. Однако чуть выше было показано, что в задаче C2 можно оперировать любым удобным объектом — хоть прямой, хоть вектором.

Еще раз напомню, что всякая плоскость задается в пространстве уравнением Ax + By + Cz + D = 0, где A, B, C и D — некоторые коэффициенты. Не умаляя общности решения, можно полагать D = 1, если плоскость не проходит через начало координат, или D = 0, если все-таки проходит. В любом случае, координаты нормального вектора к этой плоскости равны n = (A; B; C).

Итак, плоскость тоже можно успешно заменить вектором — той самой нормалью. Всякая плоскость задается в пространстве тремя точками. Как найти уравнение плоскости (а следовательно — и нормали), мы уже обсуждали в самом начале статьи. Однако этот процесс у многих вызывает проблемы, поэтому приведу еще парочку примеров:

Задача. В кубе ABCDA1B1C1D1 проведено сечение A1BC1. Найти нормальный вектор для плоскости этого сечения, если начало координат находится в точке A, а оси x, y и z совпадают с ребрами AB, AD и AA1 соответственно.

Поскольку плоскость не проходит через начало координат, ее уравнение выглядит так: Ax + By + Cz + 1 = 0, т. е. коэффициент D = 1. Поскольку эта плоскость проходит через точки A1, B и C1, то координаты этих точек обращают уравнение плоскости в верное числовое равенство.

Подставим вместо x, y и z координаты точки A1 = (0; 0; 1). Имеем:
A · 0 + B · 0 + C · 1 + 1 = 0 ⇒ C + 1 = 0 ⇒ C = − 1;

Аналогично, для точек B = (1; 0; 0) и C1 = (1; 1; 1) получим уравнения:
A · 1 + B · 0 + C · 0 + 1 = 0 ⇒ A + 1 = 0 ⇒ A = − 1;
A · 1 + B · 1 + C · 1 + 1 = 0 ⇒ A + B + C + 1 = 0;

Но коэффициенты A = − 1 и C = − 1 нам уже известны, поэтому остается найти коэффициент B:
B = − 1 − A − C = − 1 + 1 + 1 = 1.

Получаем уравнение плоскости: − A + B − C + 1 = 0, Следовательно, координаты нормального вектора равны n = (− 1; 1; − 1).

Задача. В кубе ABCDA1B1C1D1 проведено сечение AA1C1C. Найти нормальный вектор для плоскости этого сечения, если начало координат находится в точке A, а оси x, y и z совпадают с ребрами AB, AD и AA1 соответственно.

В данном случае плоскость проходит через начало координат, поэтому коэффициент D = 0, а уравнение плоскости выглядит так: Ax + By + Cz = 0. Поскольку плоскость проходит через точки A1 и C, координаты этих точек обращают уравнение плоскости в верное числовое равенство.

Подставим вместо x, y и z координаты точки A1 = (0; 0; 1). Имеем:
A · 0 + B · 0 + C · 1 = 0 ⇒ C = 0;

Аналогично, для точки C = (1; 1; 0) получим уравнение:
A · 1 + B · 1 + C · 0 = 0 ⇒ A + B = 0 ⇒ A = − B;

Положим B = 1. Тогда A = − B = − 1, и уравнение всей плоскости имеет вид: − A + B = 0, Следовательно, координаты нормального вектора равны n = (− 1; 1; 0).

Вообще говоря, в приведенных задачах надо составлять систему уравнений и решать ее. Получится три уравнения и три переменных, но во втором случае одна из них будет свободной, т. е. принимать произвольные значения. Именно поэтому мы вправе положить B = 1 — без ущерба для общности решения и правильности ответа.

Координаты середины отрезка

Очень часто в задаче C2 требуется работать с точками, которые делят отрезок пополам. Координаты таких точек легко считаются, если известны координаты концов отрезка.

Итак, пусть отрезок задан своими концами — точками A = (xa; ya; za) и B = (xb; yb; zb). Тогда координаты середины отрезка — обозначим ее точкой H — можно найти по формуле:

Другими словами, координаты середины отрезка — это среднее арифметическое координат его концов.

Задача. Единичный куб ABCDA1B1C1D1 помещен в систему координат так, что оси x, y и z направлены вдоль ребер AB, AD и AA1 соответственно, а начало координат совпадает с точкой A. Точка K — середина ребра A1B1. Найдите координаты этой точки.

Поскольку точка K — середина отрезка A1B1, ее координаты равных среднему арифметическому координат концов. Запишем координаты концов: A1 = (0; 0; 1) и B1 = (1; 0; 1). Теперь найдем координаты точки K:

Задача. Единичный куб ABCDA1B1C1D1 помещен в систему координат так, что оси x, y и z направлены вдоль ребер AB, AD и AA1 соответственно, а начало координат совпадает с точкой A. Найдите координаты точки L, в которой пересекаются диагонали квадрата A1B1C1D1.

Из курса планиметрии известно, что точка пересечения диагоналей квадрата равноудалена от всех его вершин. В частности, A1L = C1L, т. е. точка L — это середина отрезка A1C1. Но A1 = (0; 0; 1), C1 = (1; 1; 1), поэтому имеем:

Обозначим центры треугольников ACD1 и BC1A1 через точки О и О1 соответственно. Точка D равноудалена от вершин треугольника ACD1, поэтому проекция точки D на плоскость ACD1 совпадает с О. Аналогично проекция точки D на плоскость BC1A1 совпадает с О1, а проекции точки В1 на плоскости ACD1 и BC1A1 также совпадают с точками О и О1 соответственно. Значит, прямая DB1 перпендикулярна плоскостям ACD1 и BC1A1 и содержит точки О и О1.

Задача. Составить уравнение плоскости, проходящей через точки M = (2; 0; 1), N = (0; 1; 1) и K = (2; 1; 0), если известно, что она не проходит через начало координат.

Демонстрационные варианты ЕГЭ и ОГЭ

Наконец, чтобы найти координаты вектора BC, надо из координат точки C вычесть координаты точки B BC 4 3; 3 1 ; 2 7 7; 4; 9.

Www. berdov. com

21.08.2017 10:21:44

2017-08-21 10:21:44

Метод координат на плоскости

С понятием Декартовых координат точек плоскости и Уравнением окружности можно ознакомиться в разделе «Декартовы координаты точек плоскости. Уравнение окружности» нашего справочника.

Графики прямых на координатной плоскости представлены в разделе «Прямые на координатной плоскости» нашего справочника.

Графики парабол представлены в разделе «Парабола на координатной плоскости. Решение квадратных неравенств» нашего справочника.

Графики гипербол представлены в разделе «Гипербола на координатной плоскости. График дробно-линейной функции» нашего справочника.

Способы получения графиков функций из «базовых» графиков приведены в разделе «Элементарные преобразования графиков функций» нашего справочника.

Демонстрационные варианты ЕГЭ и ОГЭ

С демонстрационными вариантами ЕГЭ и ОГЭ по всем предметам, опубликованными на официальном информационном портале Единого Государственного Экзамена, можно ознакомиться на специальной страничке нашего сайта.

Электронный справочник по математике для школьников

При подготовке к ЕГЭ и ОГЭ по математике большую помощь может оказать наш Электронный справочник по математике для школьников.

В справочник включены Все разделы школьной программы, а также множество сведений для углубленного изучения курса математики.

Каждый раздел нашего справочника содержит не только теоретические сведения, но и Решения типовых примеров и задач.

Теперь найдем направляющий вектор для AC1. Все то же самое — единственное отличие в том, что у точки C1 иррациональные координаты. Итак, A = (0; 0; 0), поэтому имеем:

Демонстрационные варианты ЕГЭ и ОГЭ

С демонстрационными вариантами ЕГЭ и ОГЭ по всем предметам, опубликованными на официальном информационном портале Единого Государственного Экзамена, можно ознакомиться на специальной страничке нашего сайта.

При подготовке к ЕГЭ и ОГЭ по математике большую помощь может оказать наш Электронный справочник по математике для школьников.

В справочник включены Все разделы школьной программы, а также множество сведений для углубленного изучения курса математики.

Каждый раздел нашего справочника содержит не только теоретические сведения, но и Решения типовых примеров и задач.

Обратите внимание на вычисление координат последнего вектора BC: очень многие ошибаются, когда работают с отрицательными числами. Это касается переменной y: у точки B координата y = − 1, а у точки C y = 3. Получаем именно 3 − (− 1) = 4, а не 3 − 1, как многие считают. Не допускайте таких глупых ошибок!

Вычисление нормальных векторов для плоскостей

Если начало вектора совпадает с началом координат, вычисления резко упрощаются координаты вектора просто равны координатам конца.

Www. resolventa. ru

29.05.2018 21:18:57

2018-05-29 21:18:57

Метод координат в егэ по математике профиль

Уско­рен­ная под­го­тов­ка к ЕГЭ с ре­пе­ти­то­ра­ми Учи. До­ма. За­пи­сы­вай­тесь на бес­плат­ное за­ня­тие!

—>

Задание 13 № 514520

В правильной четырёхугольной пирамиде SABCD сторона AB основания равна а высота SH пирамиды равна 3. Точки M и N — середины рёбер CD и AB, соответственно, а NT — высота пирамиды NSCD с вершиной N и основанием SCD.

А) Докажите, что точка T является серединой SM.

Б) Найдите расстояние между NT и SC.

А) Точка H лежит на отрезке MN. Так как NC = ND, то TC = TD. Это означает, что точка T лежит на SM. Таким образом, точки T и H лежат в плоскости SNM, перпендикулярной плоскости ABC.

Значит, треугольник SNM равносторонний, а NT — его высота и, следовательно, медиана, T — середина SM.

Б) Пусть E — основание перпендикуляра, опущенного из точки T на прямую SC. Прямые NT и TE перпендикулярны, так как NT — высота пирамиды NSCD. Поскольку отрезок TE перпендикулярен как прямой SC, так и прямой NT, его длина и есть искомое расстояние.

Прямоугольные треугольники SET и SMC подобны, следовательно, откуда

Источник: Задания 14 (С2) ЕГЭ 2016, ЕГЭ по математике 06.06.2016. Основная волна. Вариант 512 (C часть).

Задание 13 № 517563

Основанием прямой треугольной призмы ABCA1B1C1 является прямоугольный треугольник ABC с прямым углом C. Грань ACC1A1 является квадратом.

А) Докажите, что прямые CA1 и AB1 перпендикулярны.

Б) Найдите расстояние между прямыми CA1 и AB1, если AC = 4, BC = 7.

А) Заметим, что B1 C1 ⊥ C1 A1 как катеты прямоугольного треугольника, и B1 C1 ⊥ C1 C, поскольку призма прямая. Тогда по признаку перпендикулярности прямой и плоскости Кроме того, как диагонали квадрата. AB1 − наклонная, AC1 − ее проекция на плоскость ACA1, − прямая в плоскости перпендикулярная проекции. Тогда по теореме о трёх перпендикулярах что и требовалось доказать.

Б) Пусть M − середина AC1. Тогда искомое расстояние равно расстоянию от точки M до прямой AB1, поскольку прямая A1C перпендикулярна плоскости AB1C1. Это расстояние равно половине высоты прямоугольного треугольника AB1C1, проведённой к гипотенузе, то есть

Здравствуйте. В решении нельзя применить теорему о трех перпендикулярах, так как прямая А1С не проходит через основание наклонной АВ1 точку А.

Разные формулировки есть.

Задание 13 № 519515

В правильной четырёхугольной пирамиде PABCD сторона основания ABCD равна 12, боковое ребро PA ― Через вершину A проведена плоскость α, перпендикулярная прямой PC и пересекающая ребро PC в точке K.

А) Докажите, что плоскость α делит высоту PH пирамиды PABCD в отношении 2 : 1, считая от вершины P.

Б) Найдите расстояние между прямыми PH и BK.

А) Пусть прямая AK пересекает прямую PH в точке M. Так как и то Поскольку то AK ― высота и медиана правильного треугольника PAC. Следовательно, M ― точка пересечения медиан этого треугольника, откуда и получаем PM : MH = 2 : 1.

Б) Пусть точка L ― проекция точки K на плоскость ABC. Так как KL || PH и PK = KC, то и L ― середина CH. Отрезок BL ― проекция отрезка BK на плоскость ABC. Поскольку точка H ― проекция прямой PH на плоскость ABC. Значит, расстояние между прямыми PH и BK равно расстоянию от точки H до прямой BL, то есть высоте H треугольника BHL проведенной из вершины H.

Задание 13 № 520822

В кубе ABCDA1B1C1D1 все ребра равны 6.

А) Докажите, что угол между прямыми AC и BC1 равен 60°.

Б) Найдите расстояние между прямыми AC и BC1.

А) Прямые ВС1 и AD1 параллельны, поэтому угол между прямыми АС и ВС1 равен углу CAD1. Треугольник CAD1 равносторонний, поэтому все его углы равны 60°.

Б) Заметим, что прямые АС и ВС1 содержатся в параллельных плоскостях ACD1 и BC1A1. Значит, искомое расстояние равно расстоянию между этими плоскостями.

Обозначим центры треугольников ACD1 и BC1A1 через точки О и О1 соответственно. Точка D равноудалена от вершин треугольника ACD1, поэтому проекция точки D на плоскость ACD1 совпадает с О. Аналогично проекция точки D на плоскость BC1A1 совпадает с О1, а проекции точки В1 на плоскости ACD1 и BC1A1 также совпадают с точками О и О1 соответственно. Значит, прямая DB1 перпендикулярна плоскостям ACD1 и BC1A1 и содержит точки О и О1.

Объем тетраэдра DACD1 равен 36, а площадь его основания Значит, высота Аналогично Кроме того, Значит,

Источник: ЕГЭ — 2018. Основная волна 01.06.2018. Вариант 991 (C часть). Он же: вариант 751 (резервный день 25.06.2018), Задания 14 (С2) ЕГЭ 2018

Задача. В кубе ABCDA1B1C1D1 проведены прямые AC и BD1. Найдите координаты направляющих векторов этих прямых.

Задание 13 № 519515

Вычисление координат векторов

Единичный отрезок равен AB 1.

Ege. sdamgia. ru

05.08.2020 17:47:37

2020-08-05 17:47:37

Источники:

Https://www. berdov. com/ege/solid_geometry/method/

Https://www. resolventa. ru/index. php/metod-koordinat

Https://ege. sdamgia. ru/test? theme=280