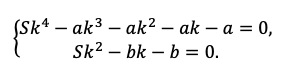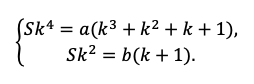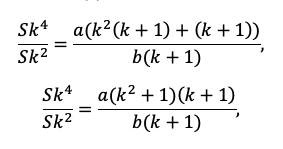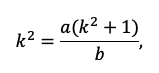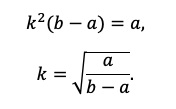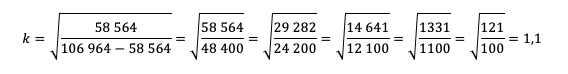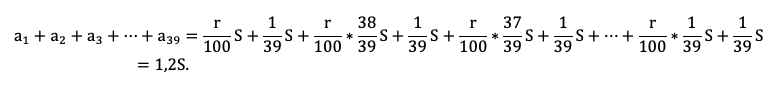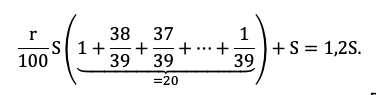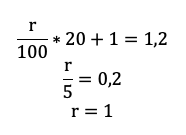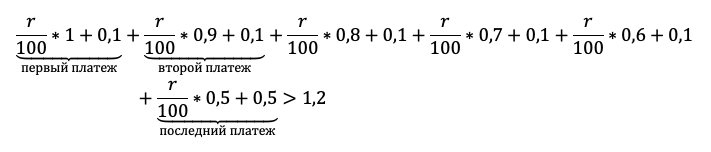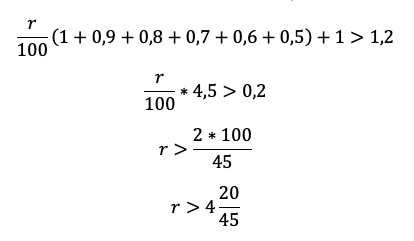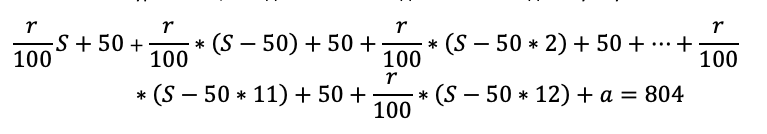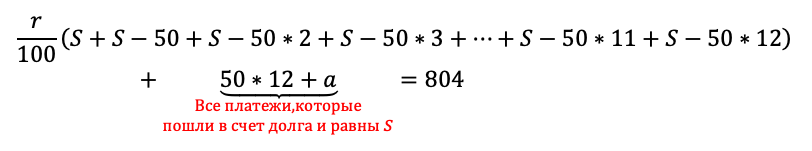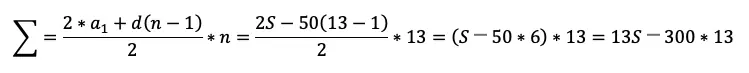Муниципальное казенное общеобразовательное учреждение гимназия
г. Вятские Поляны Кировской области, ул. Гагарина, д.17, факс/телефон
(83334) 6-29-29 e-mail: vpschool3@mail.ru, сайт: гимназия-вп.рф
Решение экономических задач с помощью таблицы в ЕГЭ
Составила: Гатауллина Гульфия Анасовна
учитель математики
МКОУ гимназии г. Вятские Поляны
Кировской области
2019
Оглавление
Введение 3
Примеры решения задач 4
Задачи для самостоятельного решения 11
Заключение 12
Список литературы 13
Введение
В условиях современных требований к выпускникам средней школы при поступлении в ВУЗы, профилирующие предметы которых связаны с математической наукой, ЕГЭ по математике профильного уровня расширен.
С 2015 года в него добавлено экономическая (банковская) задача. Эта задача ориентирована на реальную жизнь. В этих заданиях рассматриваются идеализированные жизненные ситуации, которые являются некоторыми текстовыми упрощениями, моделями, реально возникающих, например, при обращении в банк, покупке или продаже ценных бумаг, выпуск производственной продукции и получение прибыли.
За правильное решение задания № 17 на ЕГЭ можно получить три балла.
В своей работе я решила обратиться к рассмотрению решения таких задач, потому, что с одной стороны по ним представлено не много материала в открытых источниках, а с другой – было большое желание разобраться в их решении на собственном опыте.
Рассмотрим один из подходов к решению задач с «экономическим содержанием» с помощью таблицы на примере следующих задач.
Примеры решения задач
1) В июле планируется взять кредит в банке на сумму 28 млн рублей на некоторый срок (целое число лет). Условия его возврата таковы:
-каждый январь долг возрастает на 25% по сравнению с концом предыдущего года;
- с февраля по июнь каждого года необходимо выплатить часть долга;
- в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
Чему будет равна общая сумма выплат после полного погашения кредита, если наибольший годовой платёж составит 9 млн рублей?
Решение:
Пусть 𝑛− срок кредита
Составим таблицу:
|
Год |
Долг на начало года |
Основной платёж |
Дополнительный платёж |
|
1 |
28 |
|
|
|
… |
|||
|
𝑛 |
|
|
|
Очевидно, что наибольший годовой платёж будет в первом году (потому что платежи равномерно уменьшаются в течение 𝑛 лет)
Наибольший годовой платёж = 9 млн
𝑛 = 14
В таблице все значения становятся известными:
|
Год |
Долг на начало года |
Основной платёж |
Дополнительный платёж |
|
1 |
28 |
|
7 |
|
… |
|||
|
14 |
2 |
2 |
|
Общая сумма выплат (ОСВ) – это все основные платежи и все дополнительные платежи (сумму всех дополнительных платежей найдём с помощью формулы суммы первых 𝑛 членов арифметической прогрессии)
Сумма первых n членов арифметической прогрессии
80,5
Ответ: 80,5 млн
2) В июле планируется взять кредит в банке на сумму 9 млн рублей на некоторый срок (целое число лет). Условия его возврата таковы:
– каждый январь долг возрастает на 25% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить часть долга;
– в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
Чему будет равна общая сумма выплат после полного погашения кредита, если наименьший годовой платёж составит 1,25 млн рублей?
Решение:
Пусть 𝑛− срок кредита
Составим таблицу:
|
Год |
Долг на начало года |
Основной платёж |
Дополнительный платёж |
|
1 |
9 |
|
|
|
… |
|||
|
𝑛 |
|
|
|
Очевидно, что наименьший годовой платёж будет в последнем году (потому что платежи равномерно уменьшаются в течение 𝑛 лет)
Наибольший годовой платёж = 1.25 млн
𝑛 = 9
В таблице все значения становятся известными:
|
Год |
Долг на начало года |
Основной платёж |
Дополнительный платёж |
|
1 |
9 |
|
2.25 |
|
… |
|||
|
9 |
1 |
1 |
|
Общая сумма выплат (ОСВ) – это все основные платежи и все дополнительные платежи (сумму всех дополнительных платежей найдём с помощью формулы суммы первых 𝑛 членов арифметической прогрессии)
Сумма первых n членов арифметической прогрессии
20.25
Ответ: 20.25 млн
3) В июле планируется взять кредит в банке на сумму 16 млн рублей на некоторый срок (целое число лет). Условия его возврата таковы:
– каждый январь долг возрастает на 25% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить часть долга;
– в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
На сколько лет планируется взять кредит, если известно, что общая сумма выплат после его полного погашения составит 38 млн рублей?
Решение:
Пусть 𝑛− срок кредита
Составим таблицу:
|
Год |
Долг на начало года |
Основной платёж |
Дополнительный платёж |
|
1 |
16 |
|
|
|
… |
|||
|
𝑛 |
|
|
|
Общая сумма выплат (ОСВ) – это все основные платежи и все дополнительные платежи (сумму всех дополнительных платежей найдём с помощью формулы суммы первых 𝑛 членов арифметической прогрессии)
Сумма первых n членов арифметической прогрессии
Ответ: 10
4) 15-го января планируется взять кредит в банке на 19 месяцев. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на 𝑟% по сравнению с концом предыдущего месяца;
– со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.
Известно, что общая сумма выплат после полного погашения кредита на
30% больше суммы, взятой в кредит. Найдите 𝑟.
Решение:
Пусть 𝑥 − сумма кредита
Тогда 1,3𝑥 − общая сумма выплат, превышающая сумму кредита на 30%
Составим таблицу:
|
Месяц |
Долг на начало месяца |
Основной платёж |
Дополнительный платёж |
|
1 |
𝑥 |
|
|
|
2 |
|
|
|
|
… |
|||
|
19 |
|
|
|
Общая сумма выплат (ОСВ) – это все основные платежи и все дополнительные платежи (сумму всех дополнительных платежей найдём с помощью формулы суммы первых 𝑛 членов арифметической прогрессии)
Сумма первых n членов арифметической прогрессии
Ответ: 3
5) К 15 декабря планируется взять кредит в банке на 21 месяц. Условия возврата таковы:
— 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца с 1-го по 20-й долг должен быть на 30 тыс. рублей меньше долга на 15-ечисло предыдущего месяца;
— к 15 –му числу 21 месяца кредит должен быть полностью погашен.
Какую сумму планируется взять в кредит, если общая сумма выплат после полного погашения составит 1604 тыс. рублей.
S тыс.руб – сумма, которую планируют взять в кредит.
3%=0,03
|
№ |
Долг по кредиту на начало месяца |
Сумма, на которую возрастает долг на 1-е число каждого месяца |
Выплата |
|
1. |
s |
s∙0,03=0,03 s |
30+0,03 s |
|
2. |
s-30 |
0,03 (s-30) |
30+0,03 (s-30) |
|
3. |
s-2∙30 |
0,03(s-2∙30) |
30+0,03(s-2∙30) |
|
4. |
s-3∙30 |
0,03(s-3∙30) |
30+0,03(s-3∙30) |
|
5. |
s-4∙30 |
0,03(s-4∙30) |
30+0,03(s-4∙30) |
|
… |
…. |
…. |
… |
|
20 |
s-19∙30 |
0,03(s-19∙30) |
30+0,03(s-19∙30) |
|
21 |
s-20∙30 |
0,03(s-20∙30) |
s-20∙30+0,03(s-20∙30) |
|
Итого: |
1604 тыс. рублей |
Составим и решим уравнение:
Общая сумма выплат представляет собой сумму суммы, которую планируют взять в кредит, и сумму сумм, на которые возрастает долг на 1-е число каждого месяца.
s +0,03 s +0,03 (s-30)+ 0,03(s-2∙30)+….+ 0,03(s-20∙30)=1604
s +0,03∙(s+( s-30)+(s-2∙30)+… (s-20∙30))=1604
s+0,03∙( 21s- (30+2∙30+…20∙30)+=1604
30;2∙30;…;20∙30-арифметическая прогрессия, а1 =30, а21 =20∙30
S=*20=6300
s+0,03∙( 21s-6300)=1604
1,63 s-189=1604
1,63s=1793
s=1793:1,63
s=1100
Ответ: 1100 тыс. Рублей
Задачи для самостоятельного решения
- Жанна взяла в банке в кредит 1,2 млн рублей на срок 24 месяца. По договору Жанна должна возвращать банку часть денег в конце каждого месяца. Каждый месяц общая сумма долга возрастает на 2 %, а затем уменьшается на сумму, уплаченную Жанной банку в конце месяца. Суммы, выплачиваемые Жанной, подбираются так, чтобы сумма долга уменьшалась равномерно, то есть на одну и ту же величину каждый месяц. Какую сумму Жанна вернёт банку в течение первого года кредитования?
- Александр взял кредит в банке на срок 9 месяцев. В конце каждого месяца общая сумма оставшегося долга увеличивается на 12%, а затем уменьшается на сумму, уплаченную Александром. Суммы, выплачиваемые в конце каждого месяца, подбираются так, чтобы в результате сумма долга каждый месяц уменьшалась равномерно, то есть на одну и ту же величину.
Сколько процентов от суммы кредита составила общая сумма, уплаченная Александром банку (сверх кредита)?
3) 15-го января планируется взять кредит в банке на некоторый срок (целое число месяцев). Условие его выплаты таковы:
— 1-го числа каждого месяца долго возрастёт на 3% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.
На сколько месяцев планируется взять кредит, если известно, что общая сумма выплат после полного погашения кредита на 30% больше суммы, взятой в кредит?
Заключение
Я считаю введение таких задач чрезвычайно полезным так как, работая над моделями, сформулированными в условиях, они заставляют задумываться о реальной жизни. О том, что кредиты, отношения с банками, игра на бирже, колебания курсов ценных бумаг, начисление процентов дело сложное и требует больших знаний. К этому нельзя относиться легкомысленно. С чего начинать решать экономические задачи – очень внимательно читать условия задачи и по шагам распределить действия, затем постараться математически выразить их и постараться прийти к ответу.
Список литературы
1. Ященко И. В. и др. Подготовка к ЕГЭ по математике в 2018 году. Базовый и профильный уровни. Методические указания / И. В. Ященко, С. А. Шестаков, А. С. Трепалин. – М.: МЦНМО, 2015. – 288 с.
2. Демонстрационный вариант контрольно-измерительных материалов единого государственного экзамена 2018 года по математике. Профильный уровень. Сайт http://www.ege.edu.ru/
3. Спецификация контрольно-измерительных материалов для проведения в 2018 году единого государственного экзамена по математике. Профильный уровень. Сайт http://www.ege.edu.ru/
В части с развернутым ответом в ЕГЭ по профильной математике есть уникальный номер, к которому школьник почти готов сразу после освоения материала для первых 12-ти заданий. Речь об экономической задаче под номером 17 в ЕГЭ по математике. Конечно, поготовиться придется, но, если повезет с прототипом, баллы можно урвать почти даром!
Прототипы для 17-го номера делятся на три большие группы:
- банковские задачи,
- на ценные бумаги,
- задачи на оптимальный выбор.
В этой статье мы расскажем, как научить ученика структурировать условие любой банковской задачи, как составить по этим данным математическую модель и найти решение. Расскажем, на что обратить внимание ученика, чтобы школьник не потерял баллы из-за неверного оформления.
Главная трудность — школьник плохо понимает условие, ведь с кредитами и вкладами он пока не сталкивался.
- Как работает процент по кредиту?
- На какую сумму начисляется?
- Из каких частей состоит платеж?
- Как уменьшается долг?
На все эти вопросы вам придется ответить. Это отличная возможность показать пользу уроков математики, ведь 17-ый номер — едва ли не самая прикладная задача за весь школьный курс!
Например, можно рассказать о том, какие бывают образовательные кредиты. Вы в курсе, что их дают с 14 лет, а платеж первые годы может быть ничтожным? Школьник об этом точно не знает.
С чего начать разбор экономической (банковской) задачи в ЕГЭ по математике
Экзамен немного утрирует реальную ситуацию, в жизни кредит работает сложнее. Однако грустно упускать возможность рассказать школьнику что-то из реальности! Если у вас есть опыт с кредитованием, самое время им поделиться. Если нет, то воспользуйтесь нашим:
- Например, расскажите, что клиенту придется сверх купить страховку на случай потери работоспособности, ведь банк не хочет терять прибыль даже если на заемщика кирпич упадет. Ваши ученики знают, как работает страховка?
- Расскажите о механизме аннуитетного платежа: как часть денег банк забирает себе в качестве дохода, то есть на погашение процентов за пользование кредитом; а на вторую часть уменьшает ваш долг. В реальности это разделение считается по специальной формуле, и совсем не в пользу заемщика.
- Например, по нашему опыту, в ипотеке на 10 лет из 20 тысяч ежемесячного платежа на первых порах всего 5 000 рублей идет в счет уменьшения долга, а 15 000 — забирает себе банк! Но каждый раз платеж чуть ребалансируется, и в счет долга идет чуть больше. Так в последних платежах через 10 лет в счет процентов идет буквально пара сотен, а все остальное гасит долг.
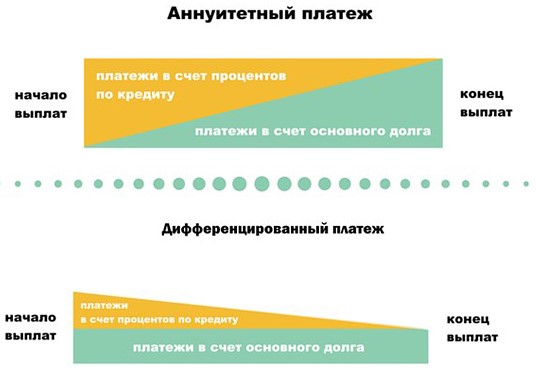
Хорошая новость в том, что в экзаменационных задачах подобной вакханалии не бывает. Долг и проценты или гасятся равномерно, или по заранее известному алгоритму, достаточно просто внимательно прочитать условие.
Еще одно частое упрощение в ЕГЭ — процент там обычно не годовой, а ежемесячный! То есть своим платежом заемщик гасит набежавший за этот месяц процент и уменьшает долг на заданную величину. Удобно.
Мы предлагаем научить школьника упорядочивать данные банковской задачи в ЕГЭ по математике с помощью таблицы. Табличка — не единственный способ решить 17-ый номер, кто-то использует последовательности, кто-то — считает прикладным методом как заправский бухгалтер. Однако наш метод универсален, а значит вы дадите школьнику один алгоритм на все типы банковских задач. Согласитесь, работать с одним алгоритмом проще, чем подбирать разные по ситуации.
Тип 1. Равные платежи
Особенность этого типа заданий в том, что заемщик всегда вносит одинаковые суммы.
В июле 2020 года планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:
— каждый январь долг увеличивается на r % по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга.
Если ежегодно выплачивать по 58 564 рубля, то кредит будет полностью погашен за 4 года, а если ежегодно выплачивать по 106 964 рубля, то кредит будет полностью погашен за 2 года. Найдите r.
Очевидно, что эта схема должна оказаться у школьника в тетради. Ведь вы же знаете: того, чего нет в тетради, и на уроке-то не было!
Заполняем всю табличку. Учитываем обе ситуации из условия. Для наглядности каждую выделим жирной рамкой.
Теперь остался еще один непростой шаг — перейти от структурированных данных к математической модели. Дайте ученику возможность увидеть, что уже почти составил ее.
Мы получили два уравнения, которые подсветили в табличке оранжевым. Объединим их в систему и решим!
Напомните выпускнику о культуре вычислений! Порой эти задачи составлены так, что неудачная последовательность действий сделает их нерешаемыми без калькулятора. Потому не надо спешить делать первое попавшееся действие, пусть школьник тренируется думать на пару ходов вперед.
Например, разделим одно уравнение на другое, ведь так мы избавимся от одной неизвестной S:
Наше решение не зависит от суммы кредита, S сокращается.
По сути, мы получили уравнение с одной неизвестной, ведь платежи a и b знаем из условия. Выразим k:
Пожалуй, все, проще уже некуда. Подставляем значения!
Тут можно обратить внимание ученика на то, как составители экзамена на самом деле заботятся о нем! Ведь будь задачка хоть чуть-чуть другой, посчитать без калькулятора было бы невозможно.
Вспоминаем, что k=1+r/100, а найти нам надо r.
Ответ: 10%.
Не забудьте после решения расставить акценты в задаче:
Чтобы решить задачу и получить 3 балла, мы:
— Воспользовались простым алгоритмом упорядочивания данных,
— Составили математическую модель,
— Нашли удобный способ решить ее, ВСЕ!
Это и есть алгоритм решения банковской задачи.
Тип 2. Равномерно убывающий долг
В прошлой задаче заемщик платил одинаковую сумму каждый месяц. Тут ему нужно уменьшать долг на одну и ту же величину. То есть за месяц пользования деньгами банк начислил на них процент, клиент теперь должен чуть больше. Своим платежом он оплатит банку проценты, чтобы заем стал таким, как ДО их начисления. А сверху внесет сумму, которая как раз и пойдет на то самое РАВНОМЕРНОЕ уменьшение долга.
15-го января планируется взять кредит в банке на 39 месяцев. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на r % по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.
Известно, что общая сумма выплат после полного погашения кредита на 20% больше суммы, взятой в кредит. Найдите r.
(Считайте, что округления при вычислении платежей не производятся.)
Тут главный элемент в задаче — равномерно убывающий долг. Если мы взяли сумму S на 39 месяцев, и каждый месяц долг должен быть меньше на одинаковую величину, то что это за величина? Пусть правильный ответ 1/39 S даст ученик.
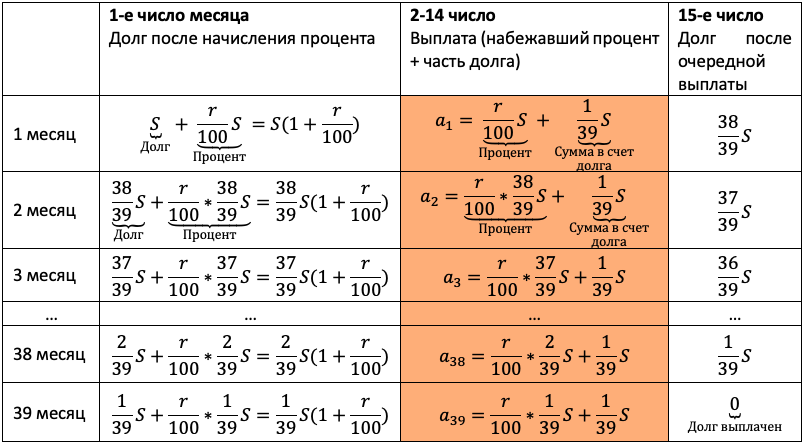
Проиллюстрируйте школьнику, как здорово работает наш алгоритм. Пусть выпускник проговаривает пункты вслух, а вы их выполняйте. Следите, чтобы каждый шаг подопечный фиксировал в тетради:
Продолжаем заполнять табличку. Пусть дальше пробует выпускник, ведь пока сам не попробуешь, не научишься:
Осталось увязать добытую информацию в уравнение или неравенство. Обратите внимание подопечного на то, что ненужных подробностей в задачах ЕГЭ не бывает! Единственная информация в задаче, которую мы до сих пор не использовали — общая сумма выплат. По условию она на 20% больше суммы кредита, то есть равна 1,2S:
Приведем подобные, вынесем общий множитель за скобку:
Решение в итоге снова не зависит от того, какую сумму взяли в долг. Разделим обе части на S и упростим выражение:
Ответ: 1%.
И снова все по нашему алгоритму, ничего нового, кроме него, мы не используем! Не забудьте излучать восторг, иначе школьник не проникнется мощью вашего метода решения.
Тип 3. Долг, убывающий согласно табличке
Задача похожа на прошлую. Разница лишь в том, что кроме процентов нам каждый месяц придется гасить не равную долю долга, а долю согласно таблице.
15-го января планируется взять кредит в банке на шесть месяцев в размере 1 млн рублей. Условия его возврата таковы:
— 1-го числа каждого месяца долг увеличивается на r процентов по сравнению с концом предыдущего месяца, где r — целое число;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей.
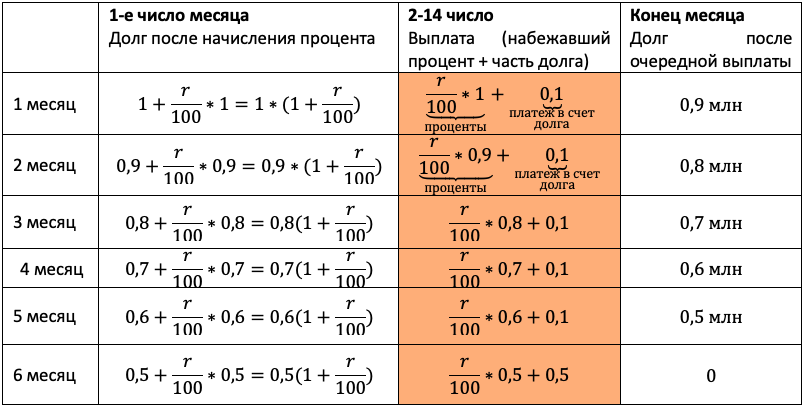
| Дата | 15.01 | 15.02 | 15.03 | 15.04 | 15.05 | 15.06 | 15.07 |
| Долг(в млн рублей) | 1 | 0,9 | 0,8 | 0,7 | 0,6 | 0,5 | 0 |
Найдите наименьшее значение r, при котором общая сумма выплат будет больше 1,2 млн рублей.
Протестируем нашу универсальную табличку в третий раз, доверьте это непростое занятие школьнику. Пусть процессом командует он! По ответам будет ясно, ловит ли он суть.
Отличие от прошлого типа будет лишь в том, что в третий столбец мы будем записывать не равномерно убывающий долг, а перенесем остаток долга из таблицы условия. Чтобы не таскать по решению нули, считать будем в миллионах:
Чтобы долг убывал согласно табличке, нам снова каждый раз придется гасить набежавшие проценты и первые 5 месяцев добавлять сверху 0,1 млн. После останется погасить весь остаток.
Акцентируйте внимание на механизме погашения, для школьника он не всегда очевиден.
«По условию нам снова дана общая сумма выплат, значит достаточно просуммировать оранжевый столбец, и уравнение готово», — вероятно, подумает школьник. Подловите его! Уравнение в этой задаче — прямой путь потерять балл! Сумма выплат должна быть БОЛЬШЕ 1,2 млн. Отразим это в модели с помощью неравенства:
Подопечный должен быть уверен в каждом символе в бланке ответа. Даже не пригодившиеся промежуточные вычисления с ошибкой приведут к катастрофе.
Приведем подобные и вынесем общие множители за скобку:
Последний шаг – не забыть, что по условию процент должен быть целым и округлить в верную сторону.
Ответ: 5%.
Правильная математическая модель — это суперважно! К ней проверяющие обязательно придерутся.
Тип 4. Погашение кредита в два этапа.
По сути, это та же прошлая задача, но месяцев больше
В 2017-2018 учебном году составителей экзамена посетило вдохновение, на свет родился вот этот тип банковских задач. Школьники были в шоке, и от страха завалили 17-ый номер. Хотя всего-то нужно было догадаться воспользоваться знаниями об арифметической прогрессии и достать из условия одно немного неочевидное дано!
15-го декабря планируется взять кредит в банке на 13 месяцев. Условия возврата таковы:
— 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца с 1-го по 12-й долг должен быть на 50 тысяч рублей меньше долга на 15-е число предыдущего месяца;
— к 15-му числу 13-го месяца кредит должен быть полностью погашен.
Какую сумму планируется взять в кредит, если общая сумма выплат после полного его погашения составит 804 тысячи рублей?
И снова пусть по возможности командует школьник. По крайней мере он уже точно в курсе, что происходит первые 13 месяцев.
Последовательно начисляем процент на остаток долга – считаем выплату – фиксируем остаток долга после выплаты. Сумму кредита возьмем за S.
Научите школьника не спешить с вычислениями. Например, вместо того чтобы написать S-600, мы пишем S-50*12, потому что так удобнее: нам сразу ясно, что речь идет о двенадцатом месяце. Да и потом вычисления будут проще, если мы оставим маленькие числа.
Осталось составить уравнение, и модель готова. В задаче нам снова дали сумму всех выплат:
Как обычно, сгруппируем отдельно слагаемые с r/100, отдельно слагаемые без них:
Вот именно последняя группировка всех платежей в счет долга и оказалась неочевидной. Без нее в задаче остается одна лишняя неизвестная величина, которая рушит все решение.
Осталось привести уравнение к решаемому виду. Для этого надо просуммировать то, что получилось в скобках. Если внимательно приглядеться, то видно, что это сумма арифметической прогрессии:
Посчитаем эту сумму:
Подставляем выражение для суммы в уравнение, заметим, что по условию r=2:

Мы сокращали дробь, пока это было возможно, и в итоге довольно просто получили ответ даже без калькулятора. Ваш подопечный должен научиться также!
Ответ: 700 тысяч.
Зачем использовать формулу суммы прогрессии, если можно посчитать вручную? Все верно, можно. Но это только в данном случае кредит взяли всего на 13 месяцев. А бывают прототипы, когда срок – 21 и больше месяцев. В какой-то момент считать вручную станет совсем долго и неудобно, потому воспользоваться формулой суммы – более универсальный метод.
Чем закончить разбор экономической (банковской) задачи № 17 в ЕГЭ по математике
Чтобы у ученика окончательно сложилась картинка занятия, пробегитесь еще раз по основным выводам:
- Повторите алгоритм заполнения таблицы и решения задачи (да, пятый раз);
- Повторите типы задач и механизм распределения платежа на проценты и долг;
- Напомните, как важно считать культурно и быть уверенным в каждой циферке в бланке;
- Проговорите, что математическая модель должна точно отражать условие задачи.
Как показывает практика, чем больше повторяешь, тем больше шансов, что в голове выпускника останется хоть что-то.
За что дают баллы?
Знание критериев оценивания экономической (банковской) задачи № 17 в ЕГЭ по математике поможетученику чувствовать себя увереннее, ведь выставление баллов — это не какая-то магия и не вредность экспертов. Все правила игры прописаны в нормативных документах.
17-ый номер стоит 3 балла. Чтобы узнать, как их присуждают, мы залезли в методические рекомендации для членов предметных комиссий.
Согласно пояснениям из документа, для получения одного балла мало просто обоснованно составить математическую модель по задаче, надо предложить правильный метод ее анализа.
Два балла получит школьник, который ошибся в вычислениях или не обосновал появление математической модели в решении. Например, согласно методическим рекомендациям, решение на 2 балла выглядит так:
А вот отсутствие промежуточных вычислений хоть и усложняет проверку, но баллы не снимает.
Идеально выполненная первая часть ЕГЭ по профильной математике принесет школьнику всего 62 тестовых балла. Добавим сюда пару ошибок по невнимательности, и останутся совсем крохи — баллов 50, не больше. Для поступления на бюджет мало, а значит необходимо планировать делать вторую часть! Чем раньше школьник это осознает, тем проще будет с ним работать. А банковская задача поможет получить дополнительные баллы с минимальными усилиями.
Однако кредиты – не единственный прототип 17-го номера, и в следующий раз мы расскажем, как научить школьника решать задачи на оптимальный выбор и ценные бумаги.
Всего: 71 1–20 | 21–40 | 41–60 | 61–71
Добавить в вариант
15-го января планируется взять кредит в банке на некоторый срок (целое число месяцев). Условие его выплаты таковы:
− 1-го числа k-ого месяца долг возрастёт на 1% по сравнению с концом предыдущего месяца;
− со 2-го по 14-е число k-того месяца необходимо выплатить часть долга;
− 15-го числа k-того месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.
На сколько месяцев планируется взять кредит, если известно, что общая сумма выплат после полного погашения кредита на 20% больше суммы, взятой в кредит?
Источник: Задания 17 (С5) ЕГЭ 2017, ЕГЭ — 2017. Основная волна 02.06.2017. Вариант 402 (C часть).
В июле планируется взять кредит в банке на сумму 20 млн рублей на некоторый срок (целое число лет). Условия его возврата таковы:
— каждый январь долг возрастает на 30% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года.
На сколько лет был взят кредит, если известно, что общая сумма выплат после его погашения равнялась 47 млн рублей?
Источник: А. Ларин: Тренировочный вариант № 238.
Банк планирует вложить на 1 год 40% имеющихся у него средств клиентов в проект Х, а остальные 60% в проект Y. Проект Х может принести прибыль в размере от 19% до 24% годовых, а проект Y — от 29% до 34% годовых. В конце года банк обязан вернуть деньги клиентам и выплатить им проценты по заранее установленной ставке. Определить наименьший и наибольший возможные уровни процентной ставки, при которых чистая прибыль банка составит не менее 10% и не более 15% годовых от суммарных вложений в проекты Х и Y.
Источник: А. Ларин. Тренировочный вариант № 366.
15‐го января планируется взять кредит в банке на 14 месяцев. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на r% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15 число предыдущего месяца. Известно, что общая сумма выплат после полного погашения кредита на 15% больше суммы, взятой в кредит. Найдите r.
Источник: ЕГЭ — 2015. Основная волна по математике 04.06.2015. Вариант Ларина.
Семья Ивановых ежемесячно вносит плату за коммунальные услуги, телефон и электричество. Если бы коммунальные услуги подорожали на 50%, то общая сумма платежа увеличилась бы на 35%. Если бы электричество подорожало на 50%, то общая сумма платежа увеличилась бы на 10%. Какой процент от общей суммы платежа приходится на телефон?
Источник: А. Ларин: Тренировочный вариант № 106.
В июле планируется взять кредит в банке на сумму 28 млн рублей на некоторый срок (целое число лет). Условия его возврата таковы:
— каждый январь долг возрастает на 25% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
Чему будет равна общая сумма выплат после полного погашения кредита, если наибольший годовой платёж составит 9 млн рублей?
Источник: Материалы для экспертов ЕГЭ 2016
В июле планируется взять кредит в банке на сумму 9 млн рублей на некоторый срок (целое число лет). Условия его возврата таковы:
— каждый январь долг возрастает на 10% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
Чему будет равна общая сумма выплат после полного погашения кредита, если наибольший годовой платёж составит 1,5 млн рублей?
Источник: Материалы для экспертов ЕГЭ 2016
В июле планируется взять кредит в банке на сумму 17 млн рублей на некоторый срок (целое число лет). Условия его возврата таковы:
— каждый январь долг возрастает на 10% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
Чему будет равна общая сумма выплат после полного погашения кредита, если наибольший годовой платёж составит 3,4 млн рублей?
Источник: Материалы для экспертов ЕГЭ 2016
Планируется выдать льготный кредит на целое число миллионов рублей на пять лет. В середине каждого года действия кредита долг заёмщика возрастает на 10% по сравнению с началом года. В конце 1-го, 2-го и 3-го годов заёмщик выплачивает только проценты по кредиту, оставляя долг неизменно равным первоначальному. В конце 4-го и 5-го годов заёмщик выплачивает одинаковые суммы, погашая весь долг полностью. Найдите наибольший размер кредита, при котором общая сумма выплат заёмщика будет меньше 8 млн.
В июле 2016 года планируется взять кредит в банке на пять лет в размере S тыс рублей. Условия его возврата таковы:
− каждый январь долг возрастает на 25% по сравнению с концом предыдущего года;
− с февраля по июнь каждого года необходимо выплатить часть долга;
− в июле 2017,2018 и 2019 долг остаётся равным S тыс. рублей;
− выплаты в 2020 и 2021 годах равны по 625 тыс. рублей;
− к июлю 2021 долг будет выплачен полностью.
Найдите общую сумму выплат за пять лет.
Источник: ЕГЭ по математике 06.06.2016. Основная волна. Вариант 509 (C часть).
Алексей взял кредит в банке на срок 17 месяцев. По договору Алексей должен вернуть кредит ежемесячными платежами. В конце каждого месяца к оставшейся сумме долга добавляется r % этой суммы и своим ежемесячным платежом Алексей погашает эти добавленные проценты и уменьшает сумму долга. Ежемесячные платежи подбираются так, чтобы долг уменьшался на одну и ту же величину каждый месяц (на практике такая схема называется «схемой с дифференцированными платежами»). Известно, что общая сумма, выплаченная Алексеем банку за весь срок кредитования, оказалась на 27% больше, чем сумма, взятая им в кредит. Найдите r.
15-го января планируется взять кредит в банке на 39 месяцев. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастёт на r% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца. Известно, что общая сумма выплат после полного погашения кредита на 20% больше суммы, взятой в кредит. Найдите r.
Источник: ЕГЭ — 2015. Основная волна по математике 04.06.2015. Вариант 2 (Часть С).
15-го января планируется взять кредит в банке на 39 месяцев. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастёт на r% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца. Известно, что общая сумма выплат после полного погашения кредита на 20% больше суммы, взятой в кредит. Найдите r.
Источник: ЕГЭ — 2015. Основная волна по математике 04.06.2015. Вариант 2 (Часть С)., Задания 17 (С4) ЕГЭ 2015
15 января планируется взять кредит в банке на 6 месяцев в размере 1 млн руб. Условия его возврата таковы:
− Первого числа месяца долг увеличивается на r% по сравнению с концом предыдущего месяца, где r целое число.
− Со 2 по 14 число необходимо выплатить часть долга.
− 15 числа каждого месяца долг должен составлять некоторую сумму в соответствии с таблицей
| Месяц | Январь | Февраль | Март | Апрель | Май | Июнь | Июль |
| Долг | 1 | 0,6 | 0,4 | 0,3 | 0,2 | 0,1 | 0 |
Найдите наибольшее r, при котором сумма выплат будет меньше 1,25 млн руб.
Источник: ЕГЭ по математике 06.06.2016. Основная волна. Вариант 412. Запад (C часть).
В июле 2016 года планируется взять кредит в банке на пять лет в размере S тыс. рублей. Условия его возврата таковы:
− каждый январь долг возрастает на 20%;
− с февраля по июнь каждого года необходимо выплатить часть долга;
− в июле 2017-2019 долг остаётся S
− в 2020, 2021 выплаты по 360 тыс. руб.
− к июлю 2021 долг будет выплачен полностью
Найдите общую сумму выплат за 5 лет.
Источник: ЕГЭ по математике 06.06.2016. Основная волна.
В июле планируется взять кредит в банке на сумму 5 млн рублей на некоторый срок (целое число лет). Условия его возврата таковы:
— каждый январь долг возрастает на 20% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
На сколько лет планируется взять кредит, если известно, что общая сумма выплат после его полного погашения составит 7,5 млн рублей?
Источник: Задания 17 (С5) ЕГЭ 2017, ЕГЭ — 2017. Основная волна 02.06.2017. Вариант 419 (C часть)., Задания 17 ЕГЭ–2020
В июле 2018 года планируется взять кредит в банке на шесть лет в размере S тыс. рублей. Условия его возврата таковы:
— каждый январь долг увеличивается на 2% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;
— в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей.
Найдите S, если общая сумма выплат после полного погашения кредита составила 327 тысяч рублей.
В июле 2018 года планируется взять кредит в банке на шесть лет в размере S тыс. рублей. Условия его возврата таковы:
— каждый январь долг увеличивается на 1% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;
— в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей.
Найдите S, если общая сумма выплат после полного погашения кредита составила 836 тысяч рублей.
В июле 2016 года планируется взять кредит в банке в размере S тыс. рублей, где S — натуральное число, на 3 года. Условия его возврата таковы
− каждый январь долг увеличивается на 17,5% по сравнению с концом предыдущего года;
− с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;
− в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей.
| Месяц и год | Июль 2016 | Июль 2017 | Июль 2018 | Июль 2019 |
| Долг (в тыс. рублей) |
S | 0,9S | 0,4S | 0 |
Найдите наименьшее значение S, при котором каждая из выплат будет составлять целое число тысяч рублей.
Источник: ЕГЭ по математике 06.06.2016. Основная волна. Вариант 703 (C часть).
По бизнес-плану предполагается вложить в четырёхлетний проект целое число миллионов рублей. По итогам каждого года планируется прирост средств вкладчика на 20% по сравнению с началом года. Начисленные проценты остаются вложенными в проект. Кроме этого, сразу после начислений процентов нужны дополнительные вложения: по 20 миллионов рублей в первый и второй годы, а также по 10 миллионов в третий и четвёртый годы. Найдите наименьший размер первоначальных вложений, при котором общая сумма средств вкладчика за два года станет больше 100 миллионов, а за четыре года станет больше 170 миллионов рублей.
Всего: 71 1–20 | 21–40 | 41–60 | 61–71
Задание 15 Профильного ЕГЭ по математике — «экономическая» задача. Как вы уже поняли, речь пойдет о деньгах. О кредитах и вкладах. О ситуациях, где нужно узнать, при каких значениях переменной будет максимальна прибыль или минимальны издержки. С 2022 года задание 15 оценивается на ЕГЭ в 2 первичных балла.
В этой статье:
Как научиться решать «экономические» задачи. С чего начать.
Две схемы решения задач на кредиты и как их распознать.
Комбинированные задачи.
В чем основная сложность «экономической» задачи.
Задания на оптимальный выбор. В том числе — с применением производной.
Если материал покажется вам сложным — вернитесь к теме «Задачи на проценты» из первой части ЕГЭ по математике.
Надеемся, что вы уже сейчас сможете ответить на такие вопросы:
- Что принимается за 100%?
- Величина х увеличилась на p%. Как это записать?
- Величина y дважды уменьшилась на р%. Как это записать?
Ответы на вопросы, а также подготовительные задачи — в статье «Задача 17 Профильного ЕГЭ по математике. Кредиты и вклады. Начисление процентов». Повторите эту тему.
Запомним, что есть всего две схемы решения задач на кредиты
Первая схема: кредит погашается равными платежами. Или известна информация о платежах. Подробно здесь.
Вторая схема: равномерно уменьшается сумма долга. Или дана информация об изменении суммы долга. Подробно здесь.
В задачах первого типа обычно применяется формула для суммы геометрической прогрессии. В задачах второго типа — формула суммы арифметической прогрессии.
Посмотрите, чем эти схемы отличаются друг от друга. На какие ключевые слова в условии надо обратить внимание.
Потому что первое, что надо сделать, когда решаете «экономическую» задачу на кредиты или вклады, — определить, к какому типу она относится.
Давайте потренируемся.
1. 31 декабря 2014 года Аристарх взял в банке 6 902 000 рублей в кредит под 12,5% годовых. Схема выплаты кредита следующая — 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 12,5%), затем Аристарх переводит в банк X рублей. Какой должна быть сумма X, чтобы Аристарх выплатил долг четырьмя равными платежами (то есть за четыре года)?
Конечно, это задача первого типа. Есть информация о платежах. В условии сказано, что Аристарх выплатит долг четырьмя равными платежами.
Введем обозначения:
тыс. рублей — сумма долга. Расчеты будем вести в тысячах рублей.
— процент банка,
— коэффициент, показывающий, во сколько раз увеличилась сумма долга после начисления процентов,
— сумма ежегодного платежа.
Составим схему погашения кредита. Заметим, что здесь 4 раза (то есть в течение 4 лет) повторяются одни и те же действия:
— сумма долга увеличивается в раз;
— Аристарх вносит на счет сумму в счет погашения кредита, и сумма долга уменьшается на
.
Вот что получается:
Раскроем скобки:
Что у нас в скобках? Да, это геометрическая прогрессия, и ее проще записать как
. В этой прогрессии первый член равен 1, а каждый следующий в k раз больше предыдущего, то есть знаменатель прогрессии равен k.
Применим формулу суммы геометрической прогрессии:
И выразим из этой формулы
.
Что же, можно подставить численные данные. Стараемся, чтобы наши вычисления были максимально простыми. Поменьше столбиков! Например, коэффициент k лучше записать не в виде десятичной дроби 1,125 — а в виде обыкновенной дроби
, Иначе у вас будет 12 знаков после запятой!
И конечно, не спешить возводить эту дробь в четвертую степень или умножать на S = 6902000 рублей.
тыс.руб.
Ответ: 2296350 рублей.
Вот следующая задача.
2. Жанна взяла в банке в кредит 1,8 млн рублей на срок 24 месяца. По договору Жанна должна возвращать банку часть денег в конце каждого месяца. Каждый месяц общая сумма долга возрастает на 1 %, а затем уменьшается на сумму, уплаченную Жанной банку в конце месяца. Суммы, выплачиваемые Жанной, подбираются так, чтобы сумма долга уменьшалась равномерно, то есть на одну и ту же величину каждый месяц. Какую сумму Жанна вернёт банку в течение первого года кредитования?
В этой задаче сумма долга уменьшается равномерно — задача второго типа.
Пусть S — первоначальная сумма долга, S = 1800 тысяч рублей.
Нарисуем схему начисления процентов и выплат. И заметим некоторые закономерности.
Как обычно,
Сумма долга уменьшается равномерно. Можно сказать — равными ступеньками. И каждая ступенька равна После первой выплаты сумма долга равна
после второй
Тогда первая выплата вторая выплата
,
Последняя в году выплата
Сумма всех выплат в течение первого года:
В первой «скобке» — сумма 12 членов арифметической прогрессии, в которой Обозначим эту сумму
Во второй скобке — также сумма 12 членов арифметической прогрессии, в которой Эту сумму обозначим
Общая сумма выплат за год:
тыс. рублей.
Ответ: 1066500 рублей.
Еще одна задача — комбинированная. Здесь мы рисуем такую же схему выплаты кредита, как в задачах второго типа.
3. В июле 2016 года планируется взять кредит в банке на пять лет в размере S тыс. рублей. Условия его возврата таковы:
− каждый январь долг возрастает на 25% по сравнению с концом предыдущего года;
− с февраля по июнь каждого года необходимо выплатить часть долга;
− в июле 2017, 2018 и 2019 долг остаётся равным S тыс. рублей;
− выплаты в 2020 и 2021 годах равны по 625 тыс. рублей;
− к июлю 2021 долг будет выплачен полностью.
Найдите общую сумму выплат за пять лет.
Введем переменные: тысяч рублей. Рисуем схему погашения кредита:
Общая сумма выплат: Кроме того, долг был полностью погашен последней выплатой
.
Это значит, что и тогда
тысяч рублей.
Ответ: 1925 тыс. рублей.
Но не только задачи на кредиты и вклады могут встретиться в задании 15 Профильного ЕГЭ по математике. Есть еще задачи на оптимальный выбор. Например, нужно найти максимальную прибыль (при соблюдении каких-либо дополнительных условий), или минимальные затраты. Сначала в такой задаче нужно понять, как одна из величин зависит от другой (или других). Другими словами, нужна та функция, наибольшее или наименьшее значение которой мы ищем. А затем — найти это наибольшее или наименьшее значение. Иногда — с помощью производной. А если повезет и функция получится линейная или квадратичная — можно просто воспользоваться свойствами этих функций.
4. Консервный завод выпускает фруктовые компоты в двух видах тары—стеклянной и жестяной. Производственные мощности завода позволяют выпускать в день 90 центнеров компотов в стеклянной таре или 80 центнеров в жестяной таре. Для выполнения условий ассортиментности, которые предъявляются торговыми сетями, продукции в каждом из видов тары должно быть выпущено не менее 20 центнеров. В таблице приведены себестоимость и отпускная цена завода за 1 центнер продукции для обоих видов тары.
| Вид тары | Себестоимость, 1 центнера |
Отпускная цена, 1 центнера |
| стеклянная | 1500 руб | 2100 руб |
| жестяная | 1100 руб | 1750 руб |
Предполагая, что вся продукция завода находит спрос (реализуется без остатка), найдите максимально возможную прибыль завода за один день (прибылью называется разница между отпускной стоимостью всей продукции и её себестоимостью).
По условию, завод не может выпускать компот только в стеклянных банках или только в жестяных — должны быть и те, и другие.
Пусть x — доля мощностей завода, занятых под поизводство компотов в стеклянных банках, а y — доля мощностей, занятых под производство компотов в жестяных банках, Тогда x+y=1. (Например, х=0,3 и у = 0,7 — то есть 30% производства — это компот в стеклянных банках, а 70% — компот в жестяных банках).
Если бы завод выпускал только компот в стеклянных банках, их бы получилось 90 центнеров в сутки. Однако выпускаются и те, и другие, и компотов в стеклянных банках производится 90x центнеров, а в жестяных банках — 80y центнеров в сутки.
Составим таблицу.
| Вид тары | Доля в общем количестве | Производится в сутки | Прибыль за 1 центнер |
| стеклянная | 2100 — 1500 = 600 руб | ||
| жестяная | 1750 — 1100 = 650 руб |
Общая прибыль завода за сутки равна
По условию, и
, то есть
и
Нужно найти наибольшее значение выражения при выполнении следующих условий:
Подставим в выражение для прибыли завода за сутки. Получим, что она равна
Это линейная функция от x. Она монотонно возрастает и свое наибольшее значение принимает при
Тогда
и максимально возможная прибыль завода за день равна
руб.
Ответ: 53500 руб.
Больше задач по финансовой математике на нахождение наибольших и наименьших значений функций и применение производной — здесь:
Задача 15 Профильного ЕГЭ по математике. Исследование функций и производная
Вот такая она, задача с экономическим содержанием. Мы рассказали о ней самое главное. Если готов осваивать ее самостоятельно — желаем удачи. А если не все будет сразу получаться — приходи к нам в ЕГЭ-Студию на интенсивы, курсы или Онлайн-курс.
Если вам понравился наш материал — записывайтесь на курсы подготовки к ЕГЭ по математике онлайн
Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Задание 15. Финансовая математика u0026#8212; профильный ЕГЭ по математике» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
09.03.2023
Муниципальное
бюджетное общеобразовательное учреждение
«Средняя общеобразовательная школа № 34»
поселка
Краснобродского
Экономические
задачи ЕГЭ
Методические
рекомендации
Руководитель: Агеева Светлана Никитична,
учитель математики
2022
год
Оглавление
Введение……………………………………………………………………………………………. 3
1. Теория……………………………………………………………………………………………. 5
1.2 Проценты.………………………………………………………………………………… 6
1.3 Платежи.…………………………………………………………………………………….. 7
1.4 Таблицы.…………………………………………………………………………………….. 7
1.5 Арифметическая и геометрическая
прогрессии.…………………….. 10
1.6 Производная…………………………………………………………………………… 11
2. Практическое решение экономических задач…………………………………….. 13
2.1 Кредиты.…………………………………………………………………………………… 13
1 тип:
Нахождение количества лет (месяцев) выплаты кредита.…………. 13
2.тип:
Вычисление процентной ставки по кредиту.…………………………… 14
3.тип.
Нахождение суммы кредита………………………………………………….. 15
4 тип:
Нахождение ежегодного ( ежемесячного) транша.…………………… 16
5 тип:
Нахождение разницы. (Аннуитетные платежи)……………………….. 17
6 тип:
Задачи с таблицей в условии…………………………………………………. 19
7 тип:
Задачи, связанные с дифференцированными платежами.…………. 20
2.2 Вклады.…………………………………………………………………………………….. 25
2.3 Задачи на оптимизацию.……………………………………………………………… 29
Заключение………………………………………………………………………………………. 31
Список использованной литературы…………………………………………………….. 32
“Чтобы научиться решать задачи,
надо их решать” Д.Пойа
Введение
Современная экономическая обстановка
актуализирует проблему экономического воспитания подрастающего поколения.
Экономические знания современной молодежи носят сугубо теоретический характер,
оторванный от реальной действительности. Причем все больше осознается
необходимость в формировании экономической грамотности у старшеклассников, тех,
кто стоит на пороге самостоятельной жизни и которым в ближайшем будущем
предстоит занять активную позицию в обществе. От экономической грамотности
выпускников школы во многом будет зависеть их успешная адаптация к социально –
экономическим условиям общества. Проблема обучения старшеклассников решению
задач с экономическим содержанием складывается из нескольких составляющих:
наличие в таких задачах большого количества терминов, неизвестных учащимся;
старшеклассники плохо ориентируются в материале, изученном в 5-9 классах и
необходимом для решения задач с экономическим содержанием: темы процентов,
арифметической, геометрической прогрессий вызывают затруднения.
Актуальность исследовательской работы определяется
необходимостью уметь решать экономические задачи при сдаче ЕГЭ. Решение экономических
задач очень полезно, так как жизнь современного человека тесно связана с
финансовыми операциями.
Проблема заключается
в отсутствии навыков применения математических и экономических знаний на
практике в расчетах платежей банковских кредитов и прочих операций, а также
неумение и боязнь решать экономические задачи на ЕГЭ.
Предмет исследования:
различные подходы к решению задач о кредитах, в зависимости от условия
задачи.
Цель исследования –
исследование методов решения задач с экономическим содержанием.
Задачи:
1. Изучить
теоретический материал по выбранной теме;
2. Научиться
решать задачи с процентами разных видов сложности;
3. Разобрать
основные типы задач с примерами решений;
4. Создать
таблицы для различных видов платежей;
5. Показать
на примерах поиск решения реальной практической задачи (кредит с разными видами
платежей – аннуитетные, фиксированные и дифференцированные);
Методы исследования – теоретический
анализ и синтез научной и учебной литературы по теме исследования, сравнение,
систематизация информации, обобщение, вывод, подбор и решение задач.
1.Теория
Решение финансовых задач основывается
на использовании различных математических моделей: уравнений, неравенств, их
систем с привлечением процентов, арифметической и геометрической прогрессий и
производной.
Основными ошибками, которыми
допускали учащиеся при решении задач финансовой математики, являются:
·
неверное составление модели;
·
вычислительные, или
арифметические (самая распространённая ошибка);
·
прекращение решения на промежуточном шаге,
то есть без доведения ответа до числового значения;
·
решение методом перебора без обоснования
единственности;
·
решение без вывода формул. В ряде случаев
трактуется как неумение строить математическую модель.
С целью подготовки учащихся к
успешной ЕГЭ имеет смысл подробно рассмотреть типы экономических задач и методы
их решения.
Конечно, на различных сайтах и в
математической литературе можно найти решения таких задач, но зачастую либо они
содержат много лишней информации, либо они решены непонятным для меня способом.
Я же использовала табличный метод, так как считаю его самым наглядным и
простым.
Из необходимых знаний и умений мне
понадобились:
1)
Понятие «Процент»;
2)
Определение понятий «Фиксированные
платежи», «Аннуитетные платежи» и «Дифференцируемые платежи»;
3)
Виды таблиц для решения задач
4)
Определение, формулы n-ого члена и суммы n
первых членов арифметической и геометрической прогрессий
5)
Знание алгоритмов нахождения
промежутков возрастания (убывания) функций и точек экстремума.
Всего
я решила примерно 50 задач, выбрала из них 14 задач, разделив их условно на
типы:
Кредиты.
1
тип: Нахождение количества лет (месяцев)
выплаты кредита(Аннуитетные платежи) — 1 задача.
2
тип: Вычисление процентной ставки по кредиту.
(Фиксированные платежи) – 1 задачи.
3
тип: Нахождение суммы кредита. (Аннуитетные
платежи) — 1 задачи.
4
тип: Нахождение ежегодного (ежемесячного)
транша. (Аннуитетные платежи) — 1 задача.
5
тип: Нахождение разницы. (Аннуитетные
платежи) – 1 задача.
6
тип: Задачи, связанные с известным
остатком. (Фиксированные платежи) — 1 задача.
7
тип: Задачи, связанные с
дифференцированными платежами. — 3 задачи.
Вклады.
– 3 задачи.
Задачи на оптимизацию.
— 2 задачи.
1.2 Проценты.
Определение: один процент – это одна
сотая доля. Чтобы найти данное число процентов от числа, нужно проценты
записать десятичной дробью, а затем число умножить на эту десятичную дробь.
Пример: 5% от 80 это будет 0,05× 80 = 4, r%
от 14 это будет 0,01r× 14 = 0,14𝑟
При решении задач необходимо понимать
механизм начисления процентов по вкладам или кредитам. Например, если банк
выдаѐт кредит (S) клиенту, то через год клиент должен банку не только сумму
кредита, но и некий процент (r). Возникает необходимость введения нового
коэффициента b, b=1+0,01r. С учётом этого, долг клиента банку через год можно
записать следующим образом:
S + r% от
S = S + 0,01r× 𝑆
= S (1 + 0,01r) = bS
1.3 Платежи.
В задачах по теме «Кредит» используют
о три основных вида платежа:
1.
Фиксированные платежи —
платежи, которые чѐтко оговариваются в условии задачи.
2.
Аннуитетные платежи— это такая система выплат, при которой
кредит выплачивается раз в год равными платежами (иногда в условии задачи год
заменяется на месяц). При этом каждый год до внесения платежа банк начисляет на
оставшуюся часть долга некоторый процент, то есть оставшаяся сумма долга
увеличивается на это количество процентов.
3.
Дифференцируемые платежи–
это такая система выплат, при которой ежемесячные или ежегодные платежи,
уменьшающиеся к концу срока кредитования и обеспечивающие уменьшение суммы
долга на одну и ту же величину.
1.4 Таблицы
1) Аннуитетные платежи подразумевают
наличие выплат равными частями на протяжении всего срока
кредитования. Решать задачи,
связанные с аннуитетными платежами удобно с помощью таблицы
платежей. Приложение 1.
В таблице используются
обозначения: S – сумма; r% — годовые (ежемесячные); b=1+0,01r — коэффициент;
х- ежегодная (ежемесячная) выплата.
2) При решении задач,
связанных с дифференцированными платежами используется таблица r-процент кредита.
Приложение 2.
3)Таблица для начисления
процентов по вкладам. Приложение 3.
4) Таблица для решении задач, в которых осуществлялись
какие-либо действия (пополнение или снятие денег с вклада). Приложение 4.
х –
действие
1.5 Арифметическая
и геометрическая прогрессии.
Арифметическая прогрессия
Определение. Последовательность
чисел, в которой каждое следующее отличается от предыдущего ровно на одну и ту
же величину, называется арифметической прогрессией.
Любой член арифметической прогрессии
вычисляется по формуле:
𝑎𝑛
= 𝑎1
+ (n-1)d
Формула суммы n-первых членов
арифметической прогрессии
Sn
С
учётом этой формулы: (n-1) + (n-2) +…+3+2+1 =
Геометрическая прогрессия
Определение. Геометрической прогрессией называется
последовательность отличных от нуля чисел, каждый член которой, начиная со
второго, равен предыдущему члену, умноженному на одно и то же число.
Любой член геометрической
прогрессии вычисляется по формуле: bn
=b1· qn-1
Формула суммы n-первых членов
геометрической прогрессии
Sn
Из этой формулы следует: bn-
1.6 Производная
Достаточные признаки возрастания и
убывания функции:
Если производная данной функции
положительна для всех значений х в интервале (а;
в), т.е. f'(x) > 0, то функция в этом
интервале возрастает.
Если производная данной функции
отрицательна для всех значений х в интервале (а; в), т.е. f'(x) < 0, то
функция в этом интервале убывает.
Алгоритм нахождения промежутков
монотонности:
1.Найти область
определения функции.
2.Найти производную
функции.
3. Найти критические
точки (точки, в которых производная не существует) и стационарные (точки, в
которых производная равна нулю).
4. Исследовать знак
производной в промежутках, на которые найденные точки делят область определения
функции.
Достаточное условие существования
максимума состоит в смене знака производной при переходе через критическую
точку с «+» на «-«, а для минимума с «-» на
«+». Если при переходе через критическую точку смены знака
производной не происходит, то в данной точке экстремума нет
Пример:
Найдём производную.
Критические точки = 1,
= -1
Стационарные точки
Ответ: возрастает
на промежутках , убывает
; xmin
= xmax
=
2.Практическое решение
экономических задач.
2.1 Кредиты.
1 тип: Нахождение количества лет (месяцев)
выплаты кредита.
Задача
№1. 1 января 2015 года Павел
Витальевич взял в банке 1 млн рублей в кредит. Схема выплаты кредита следующая:
1 числа каждого следующего месяца банк начисляет 1 процент на оставшуюся сумму
долга (то есть увеличивает долг на 1%), затем Павел Витальевич переводит в банк
платёж. На какое минимальное количество месяцев Павел Витальевич может взять
кредит, чтобы ежемесячные выплаты были не более 125 тыс. рублей?
Решение.
Кредит: 1000000 руб.
Ставка (r) 3% годовых.
Введём коэффициент b=1+0,01r
Ежемесячная выплата (х)
≤125000 руб.
Сколько месяцев (n)-?
Ясно, что чем больше
годовые выплаты, тем быстрее будет выплачен долг. Значит, срок кредита будет
минимален в том случае, когда выплаты составляют 330 тыс. рублей.
|
Месяц |
Долг до % |
Долг с % |
Платёж |
Долг после выплаты |
|
1 |
1000000 |
1000000*1,01=1010000 |
125000 |
885000 |
|
2 |
885000 |
885000 *1,01=893850 |
125000 |
768850 |
|
3 |
768850 |
768850*1,01=776538,5 |
125000 |
651538,5 |
|
4 |
651538,5 |
651538,5*1,01=589515,79 |
125000 |
526538,5 |
|
5 |
526538,5 |
526538,5*1,01=531803,885 |
125000 |
406803,885 |
|
6 |
406803,885 |
406803,885 *1,01=410871,924 |
125000 |
285871,924 |
|
7 |
285871,924 |
285871,924*1,01=288730,643 |
125000 |
163730,643 |
|
8 |
163730,643 |
163730,643*1,01=165367,96 |
125000 |
40367,9495 |
|
9 |
40367,9495 |
40367,9495*1,01=40771,629 |
40771,629 |
0 |
Из таблицы видно, что
минимальный срок кредита в условиях задачи составляет 9 месяцев.
Ответ: 9 месяцев.
2.тип: Вычисление процентной ставки по кредиту.
r-? (Фиксированные
платежи)
Задача №1.
(ЕГЭ основная волна 2020) В июле
2026 года планируется взять кредит на пять лет в размере 630 тыс. рублей.
Условия его возврата таковы:
-каждый январь долг возрастает на r% по сравнению с концом
предыдущего года;
-с февраля по июнь каждого года необходимо выплатить одним платежом
часть долга;
— в июле 2027,2028 и 2029 годов долг остаётся равным 630 тыс.
рублей;
-выплаты в 2030 и 2031 годах равны;
-к июлю 2031 года долг будет выплачен полностью.
Найдите r, если известно, что долг будет выплачен полностью и общий
размер выплат составит 915 тыс. рублей.
Решение:
Кредит (S) 630 тыс. руб. Введём коэффициент b=1+0,01r
В 2030 и в 2031 выплаты равны = x
|
Год |
Долг до % |
Долг с % |
Платёж |
Долг после выплаты |
|
2027 |
S |
S+S*0,01r |
S*0,01r |
Sb-x1 |
|
2028 |
S |
S+S*0,01r |
S*0,01r |
S |
|
2029 |
S |
S+S*0,01r |
S*0,01r |
S |
|
2030 |
S |
Sb |
x |
Sb-x |
|
2031 |
Sb-x |
S |
x |
S |
1) Общий размер выплат: 3*S*0,01r+2x=915
2) S-xb-x=0
3* S*0,01r+2x=915
b=1+0,01r, отсюда 0,01r=b-1
3*S*(b-1)+2x=915
3*630b-630*3+2x=915
1890b-1890+2x=915
x==1402,5-945b
2)S-xb-x=0
630*-(1402,5-945b)b-1402,5-945b=0
210-61b-187=0
D=+840*187=160801=
=
…- не подходит
по условию
b=1+0,01r=1,1;0,01r=1,1-1=0,1; r=10%
Ответ: r =10
3.тип. Нахождение суммы кредита
Задача №1. В июле 2020 года планируется взять кредит в
банке на некоторую сумму. Условия его возврата таковы:
-каждый январь долг возрастает на 30% по сравнению с концом
предыдущего года;
-с февраля по июнь каждого года необходимо выплатить часть
долга;
Определите сумму кредита, если известно, что кредит будет
выплачен тремя равными платежами (за 3 года) и общая сумма выплат на 78030
рублей больше суммы, взятой в кредит.
Решение:
Ставка
(r) — 30% , b=1,3. Ежегодная выплата х
Количество лет (n) 3 года. Сумма кредита (S) -?
|
Год |
Долг до % |
Долг с % |
Выплата |
Долг после выплаты |
|
1 год |
S |
Sb |
х |
Sb-x |
|
2 год |
Sb-x |
b(Sb-x)= Sb2-xb |
х |
Sb2-xb-x |
|
3 год |
Sb2-xb-x |
b(Sb2-xb-x |
х |
Sb3_ хb2—xb-x=0 |
По условию дано, что сумма выплат больше взятого кредита на
78030, отсюда следует, что 3x=S+78030; x= =
+26010
Sb3-хb2-xb-x=0
S*1,33—x-1,3x-x =0
S*2,197-1,69x-1,3x-x=0
S*2,197-3,99(+26010)=0
S*2,197-1,33S-3,33*26010=0
S==119700рублей
Ответ: 119700рублей.
4 тип: Нахождение ежегодного ( ежемесячного) транша.
х-? (Аннуитетные
платежи)
Задача
№1. Для покупки квартиры
Алексею не хватало 1209600 рублей, поэтому в январе 2015 года он решил взять в
банке кредит под 10% годовых на 2 года. Условия пользования кредитом таковы: –
раз в год 15 декабря банк начисляет на оставшуюся сумму долга проценты (т.е.
долг увеличивается на 10%); – в период с 16 по 31 декабря Алексей обязан
перевести в банк некоторую сумму x рублей (сделать платеж). Какова должна быть
сумма x, чтобы Алексей выплатил долг равными платежами?
Сумма кредита (S)- 1209600рубля . Ставка (а)=10%, b=1,1.
Количество лет (n) 2 года . Ежегодная выплата ( транш) Х
-?
|
Год |
Долг |
Долг с % |
Выплата |
Долг |
|
1 год |
S |
Sb |
x |
Sb-x |
|
2 год |
Sb-x |
(Sb-x)b=Sb2-xb |
x |
Sb2-xb-x=0 |
1209600*1,12-1,1x-x=0
2,1x=1209600*1,21
x==696960рублей
Ответ:696960рублей
5 тип: Нахождение разницы. (Аннуитетные платежи)
Задача
№1. 31 декабря 2014 года Федор взял в банке 6 951 000 рублей в кредит под 10%
годовых. Схема выплаты кредита следующая:31 декабря каждого следующего года
банк начисляет проценты на оставшуюся сумму долга(то есть увеличивает долг на
10%)затем Федор переводит в банк платеж. Весь долг Федор выплатил за 3 равных
платежа. На сколько рублей меньше он бы отдал банку, если бы мог выплатить долг
за 2 равных платежа?
Решение:
Сумма
кредита (S) – 6951000 рублей. Ставка (r) -10%, b=1,1.
3
равных платежа
|
Год |
Долг до % |
Долг с % |
Платёж |
Долг |
|
1 год |
S |
Sb |
х |
Sb-x |
|
2 год |
Sb-x |
b(Sb-x)= |
х |
Sb2-xb-x |
|
3 год |
Sb2-xb-x |
b(Sb2-xb-x )=Sb3_ хb2xb |
х |
Sb3-хb2-xb-x=0 |
Sb3-
хb2-xb-x=0
Sb3-x(b2+b+1)=0
S*1,13-x(1,12+1,1+1)=0
x==2100000*1,331=2795100
2
равных платежа
|
Год |
Долг до % |
Долг |
Платёж |
Долг после выплаты |
|
1 |
S |
Sb |
х |
Sb-x |
|
2 |
Sb-x |
b(Sb-x)= Sb2-xb |
х |
Sb2-xb-x=0 |
Sb2-xb-x=0
Sb2-x(b+1)=0
S*1,12-x(1,1+1)=0
x==4005100
За
три года: 2795100*3=8385300 За два года:4005100*2=8010200 Разница:
8385300-8010200=375100
Ответ: на 375100 рублей.
6 тип:
Задачи с таблицей в условии
Задача №1. В июле 2026
года планируется взять кредит в банке на три года в размере S млн
рублей, где S — целое число. Условия его возврата таковы:
—
каждый январь долг увеличивается на 20% по сравнению с концом предыдущего года;
—
с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;
—
в июле каждого года долг должен составлять часть кредита в соответствии со
следующей таблицей.
|
Месяц и год |
Июль 2026 |
Июль 2027 |
Июль 2028 |
Июль 2029 |
|
Долг (в млн рублей) |
S |
0,8S |
0,4S |
0 |
Найдите
наибольшее S, при котором каждая из выплат будет меньше 5 млн руб.
Решение:
S – сумма кредита
1,2-множитель
увеличения на 20%
|
Месяц |
Долг до % |
Долг с % |
Выплата |
Долг после выплаты |
|
2026 |
S |
1,2S |
0,4S |
0,8S |
|
2027 |
0,8S |
0,96S |
0,56S |
0,4S |
|
2028 |
0,4S |
0,48S |
0,48S |
0 |
Каждая
из выплат меньше 5 млн руб., следовательно

0,4>0,48>0,56 => S<; S<8
=> S=8млн
Ответ:8млн. рублей.
7 тип: Задачи,
связанные с дифференцированными платежами.
Задача №1. (Аналог ЕГЭ
2018 основная волна) 15 января планируется взять кредит в банке
на 9 месяцев. Условия его возврата таковы:
—
1-го числа каждого месяца долг возрастает на т% по сравнению с концом
предыдущего
месяца;
—
с 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
—
15-го числа каждого месяца долг должен быть на одну и ту же сумму
меньше
долга на 15-е число предыдущего месяца (на практике такая схема называется
«схемой с дифференцированными платежами);
Найдите
т, если известно, что общая сумма выплат после погашения долга
на
25% больше суммы кредита.
Сумма
кредита (S), ставка (r) -?
|
№ |
Долг |
Долг |
Основная |
Процентная |
Долг |
|
1 |
S |
|
|
|
|
|
2 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
… |
… |
… |
… |
… |
… |
|
8 |
|
|
|
|
|
|
9 |
|
|
|
|
0 |
(1+0,25)S=1,25S-
увеличение S на 25 %
Составим
равнение, зная, что сумма вышла больше взятого кредита на 25%:
9+S*
(9+8+7+…+2+1)=1,25S
В
скобках мы наблюдаем арифметическую прогрессию, следуя формуле Sn получаем:
S+S*(
*9)=1,25S
S+=1,25S
r=5
Ответ:5%.
Задача
№2.
15-го
декабря планируется взят кредит в банке на 1500000 на (n + 1) месяц. Условия
его возврата таковы:
—
1-го числа каждого месяца долг возрастает на 3% по сравнению с концом
предыдущего месяца;
—
cо 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
—
15-го числа каждого месяца с 1-го по n-й долг должен быть на x тысяч рублей
меньше долга на 15-е число предыдущего месяца;
—
15-го числа n-го месяца долг составит 300 тысяч рублей;
—
к 15-му числу (n + 1)-го месяца кредит должен быть полностью погашен.
Найдите
x, если известно, что общая сумма выплат после полного погашения кредита
составит 2067 тысяч рублей.
Решение:
Сумма
кредита S=1500000
Ставка (r) -3 %, b=1,03x— основная выплата=Сумма одной
выплаты (x) =?
|
№ |
Долг до % |
Долг с % |
Основная часть В |
Процентная часть В |
Долг после выплаты |
|
1 |
S |
|
|
|
S-x |
|
2 |
S-x |
(S-x) |
|
|
|
|
… |
… |
… |
… |
… |
… |
|
n |
(S-(n-1)x) |
(S-(n-1)x)+(S-(n-1)x)*0,03 |
|
(S-(n-1)x)*0,03 |
|
|
n+1 |
S-nx |
S-(nx)+S-nx*0,03 |
S-(nx) |
S-nx*0,03 |
0 |
2)
15-числа т-го месяца долг составит 300тысяй, следовательно
S—nx=300
1500-nx=300
nx=1200
3)
Общая сумма выплат после полного погашения кредита составит 2067 тысяч рублей,
составим уравнение
xn+S-nx+0,03(S+(S-x)+(S-2x)+…+S-(n-2)x+S-(n-1)x+S+nx)=2067
В
скобках видим арифметическую прогрессию, равномерное уменьшение на x
S+0,03()=2067
1500+0,03()=2067
1500+0,03*900(n+1)=2067
27(n+1)=567
n+1=
n+1=21
=>n=20
4)
nx=1200
20x=1200
x=60
тысяч
Ответ:60тысяч.
Задача
№ 3.
В
феврале планируется взять кредит в банке в размере 2,4 млн рублей сроком на 12
месяцев. Условия его возврата таковы:
—
1-го числа каждого месяца долг возрастает на r% по сравнению с концом
предыдущего месяца;
—
со 2-го по 14 число каждого месяца необходимо выплатить часть долга;
—
15-го числа каждый месяц долг должен уменьшиться на одну и ту же величину.
Известно, что с 3 по 7 месяц включительно, нужно выплатить банку 1,096 млн
рублей. Найдите процент банка r. Сколько будет выплачено банку за первые 9
месяцев?
1.Так как долг уменьшался равномерно на
протяжении 12 месяцев, значит каждый долг уменьшался на
|
№ |
Долг |
Долг |
Основная |
Процентная |
Долг |
|
1 |
2,4 |
|
|
|
|
|
2 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
… |
… |
… |
… |
… |
… |
|
7 |
|
|
|
|
|
|
… |
… |
… |
… |
… |
… |
|
9 |
|
|
|
|
|
|
… |
… |
… |
… |
… |
… |
|
12 |
|
|
|
|
0 |
2) С 3 по 7 месяц
нужно выплатить 1,096 млн.р
*2,4*5+2,4*
(
1+(
=0,096
=1,2%
Сумма
выплат за 9 месяцев:
=
=
Ответ:
1,9728 млн.рулей
2.2 Вклады.
Задача
№1. В банк помещена сумма 3900 тысяч рублей под 50% годовых. В конце каждого из
первых четырех лет хранения после начисления процентов вкладчик дополнительно
вносил на счет одну и ту же фиксированную сумму. К концу пятого года после
начисления процентов оказалось, что размер вклада увеличился по сравнению с
первоначальным на 725%. Какую сумму вкладчик ежегодно добавлял к вкладу?
Решение:
S=3900
тысяч – сумма вклада
r% — годовые (ежемесячные) проценты, r=10%
b=1+0,5r – коэффициент, b=1,5 n=5 лет, х =? – действие
|
Год |
Вклад с % |
Действие |
Вклад |
|
1 год |
Sb |
+х |
Sb+x |
|
2 год |
b(Sb+x)= Sb2+xb |
+х |
Sb2+xb+x |
|
3 год |
b(Sb2+xb+x)=Sb3+хb2+xb |
+х |
Sb3+хb2+xb+x |
|
4 год |
b(Sb3+xb2+xb+x)=Sb4+хb3+xb2+xb |
+х |
Sb4+хb3+xb2+xb+x |
|
5 год |
b(Sb4+хb3+xb2+xb)= |
Снял вклад |
Известно,
что размер вклада увеличился по сравнению с первоначальным на 725%.Это
значит, что он стал составлять 825% от начального, т.е. увеличился
в 8,25 раз
Sb5+хb4+xb3+xb2+xb=8,25S
3900*1,55+x*1,54+x*1,53+x*1,52+x*1,5=8,25*3900
3900*1,55+x(1,54+1,53+1,52+1,5)=
8,25*3900
3900*1,55+12,1875x=8,25*3900
12,1875x=2559,375
x=210
Ответ:
210 тысяч рублей.
Задача
№2.
В банк был положен вклад под 10%
годовых. Через год, после начисления процентов, вкладчик снял со счета 2000
рублей, а еще через год (опять после начисления процентов) снова внес 2000
рублей. Вследствие этих действий через три года со времени открытия вклада
вкладчик получил сумму меньше запланированной (если бы не было промежуточных
операций со вкладом). На сколько рублей меньше запланированной суммы он
получил?
В данной задаче мы заполним две
таблицы, где будут учитываться все действия вкладчика и где не будут
учитываться действия вкладчика.
Решение:
S– сумма вклада. r% —
годовые (ежемесячные) проценты, r=10% ; 1+0,1=1,1 – коэффициент n=3 года.
|
Год |
Вклад с % |
Действие |
Вклад после действия. |
|
1 год |
S*1,1 |
-2000 |
S*1,1-2000 |
|
2 год |
1,1(S*1,1-2000)= S*1,12-2000*1,1 |
+2000 |
S1,12-2000*1,1+2000 |
|
3 год |
1,1(S1,12-2000*1,1+2000)=S*1,13-2000*1,12+2000*1,1 |
— |
S*1,13-2000*1,12+2000*1,1 |
S*1,13-2000*1,12+2000*1,1=S*1,331-1,21*2000+1,1*2000=S*1,331
-220
Теперь
составим вторую таблицу:
|
Год |
Вклад с % |
Действие |
Вклад после действия. |
|
1 год |
S*1,1 |
— |
S*1,1 |
|
2 год |
S*1,1 |
— |
S1,12 |
|
3 год |
S1,12 |
— |
S*1,13 |
Чтобы узнать на сколько вклад без
действий вкладчика оказался бы прибыльнее, нужно из него вычесть вклад с
действиями
1,331S-(1,331S-220)=1,331S=1,331S+220=220
Ответ: на 220 рублей.
Задача
№3. Близнецы Саша и Паша
положили в банк по 50 000 рублей на три года под 10% годовых. Однако через год
и Саша, и Паша сняли со своих счетов соответственно 10% и 20% имеющихся денег.
Еще через год каждый из них снял со своего счета соответственно 20 000 рублей и
15 000 рублей. У кого из братьев к концу третьего года на счету окажется
большая сумма денег? На сколько рублей?
Решение:
S=50000 – сумма вклада . r% — годовые (ежемесячные) проценты, r=10%
b=1+0,01r – коэффициент, b=1,1 n=3 года, х – действие
Саша
|
Год |
Вклад с % |
Действие |
Вклад после действия. |
|
1 |
Sb |
— 0,1Sb |
0,9Sb |
|
2 |
0,9Sb*b=0,9Sb2 |
-20000 |
0,9Sb2— 20000 |
|
3 |
(0,9Sb2— |
Снял вклад |
0,9Sb3_
20000b = 0,9*50000*1,331–20000*1,1 = 59895–22000 = 37895рублей
Паша
|
Год |
Вклад с % |
Действие |
Вклад после действия. |
|
1 |
Sb |
— 0,2Sb |
0,8Sb |
|
2 |
0,8Sb*b=0,9Sb2 |
-15000 |
0,8Sb2- 15000 |
|
3 |
(0,8Sb2- 15000)*b = |
Снял вклад |
0,8Sb3_
15000b = 0,8*50000*1,331–15000*1,1 = 53240–16500 = 36740рублей
37895 – 36740 = 1155
рублей
Ответ: у Саши на 1155 рублей.
2.3 Задачи на оптимизацию.
Задача №1. На заводе по
изготовлению автозапчастей затраты на производство Q единиц товара составляют
300Q + 100000 рублей. При этом, зависимость количества Q (шт. 0 <= Q <=
1500), купленного у завода товара, можно выразить формулой Q = 1500 — P. Помимо
затрат на производство завод обязан выплатить налог t рублей (0 <t<1000)
с каждой произведенной автозапчасти. Отсюда прибыль фирмы составляет PQ — 300Q
— 100000 — tQ рублей, а общая сумма налогов, уплаченных в казну государства,
равна tQ рублей. Известно, что завод изготавливает такое количество
автозапчастей, чтобы прибыль была максимальной. При каком значении t общая
сумма налогов будет максимальной? P — цена товара (в руб. за штуку).
Решение:
По условию P = 1500 — Q, значит,
прибыль компании составит: (1500 — Q) • Q — 300Q — 100000 — tQ = -Q2 + (1200 —
t)Q — 100000.
Функция f(Q) = -Q2 + (1200 — t)Q —
100000 является параболой с ветвями вниз. Максимальное значение эта функция
достигает в точке вершины параболы. Тогда Qмакс = (-1200 + t) /(-2) = 600 —
t/2.
Сумма налогов: tQ = t • (600 — t/2) =
600t — t2/2 Функция f(t) является параболой с ветвями вниз. Тогда максимальное
значение достигается в точке вершины параболы: tmax = -600/(-1) = 600.Значит,
общая сумма налогов будет максимальной при t = 600.
Ответ: 600.
Задача №2. Андрей владеет предприятием по производству
настольных игр. Он заключил договор с компанией «ФЛЕШ» на доставку 50 коробок с
настольными играми на сумму 1000 тыс. рублей. Чтобы мотивировать грузчиков
работать быстрее, в условиях договора Андрей указал, что за каждый час погрузки
из этой суммы вычитается 40 тыс. рублей. Компания «ФЛЕШ» также мотивирует своих
сотрудников: по результатам погрузки она выделяет премию в размере 20v тыс.
рублей, где v – скорость погрузки (коробок в час). Найдите наибольшее значение
прибыли (в рублях), которую может получить компания «ФЛЕШ».
S – Прибыль компании
|
Количество товаров |
Скорость погрузки |
Время погрузки |
Штраф |
Премия |
|
50 |
x |
|
40* |
20*x |
Составим
уравнение прибыль компании, учитывая все затраты и премию
S=1000-40* -20x
Для
того чтобы найти наибольшее значение прибыли, найдём производную S
S’=-40*( )’-20(x)’+1000’=-40*
)-20=
-20
Найдём
экстремумы. Для этого приравняем производную к нулю:
-20=0
2000-20x2=0
x2=100
x=±10
 |
x=10
S принимает
наибольшее значение при x = 10
S=1000-40* -20*10=600тысяч рублей.
Ответ: 600 тысяч рублей.
Задача
№3. Пенсионный фонд владеет
ценными бумагами, которые стоят t2 тыс. рублей в конце года t
(t = 1; 2; …). В конце любого года пенсионный фонд может продать ценные
бумаги и положить деньги на счёт в банке, при этом в конце каждого следующего
года сумма на счёте будет увеличиваться в 1 + r раз. Пенсионный фонд хочет
продать ценные бумаги в конце такого года, чтобы в конце двадцать пятого года
сумма на его счёте была наибольшей. Расчеты показали, что для этого ценные
бумаги нужно продавать строго в конце двадцать первого года. При каких положительных
значениях r это возможно?
За год ценные бумаги увеличиваются в цене в=(
)2раз
Видно, что
относительное увеличение стоимости замедляется с каждым годом. Продавать бумаги
и класть деньги в банк имеет смысл в том случае, когда в банке прирост за год
(а, значит, и за все последующие годы) станет больше. По условию, продавать
бумаги нужно в конце 21-го года, значит, за 21-ый год прирост стоимости ценных
бумаг еще больше банковского процента, а в 22-м году – уже нет. Записываем:
|
21-ый год |
22-й год |
|
|
|
> 1+r<
> 1+r<
Ответ:
> 1+r<
Заключение
В ходе выполнения данного
исследования, я считаю, что поставлення цель мною достигнута. Исследовала,
какие виды экономических задач предлагаются на ЕГЭ, какие математические
понятия потребуются для решения таких задач. Рассмотрела основные методы
решения задач на кредит, вклады и оптимизацию. Научилась решать задачи разных
видов, выбрав оптимальный для меня способ (с помощью составления таблиц).
Умение решать такие задачи позволяет,
учащимся рассчитать платежи по кредитам и прибыль по вкладам, применять эти
знания в повседневной жизни. И конечно получить более высокий бал на ЕГЭ.
Также я улучшила свои навыки работы с офисными приложениями Microsoft Word, Microsoft PowerPoint.
Тема
работы очень актуальна, так как все рассматриваемые задачи взяты из материалов
по подготовке к ЕГЭ по математике «Профиль». Надеюсь, что данная работа будет
полезна учащимся 10-11 класса, а также преподавателям математики.
Список литературы
1.
Балабанов, И. Т. Основы финансового
менеджмента, математика: Финансы и статистика. [Текст]/ И. Т. Балабанов — М. :«Дрофа»,2001
г.-420с.
2.
Гусев, В.А. Математика. Справочные
материалы/ В.А. Гусев, А.Г. Мордкович — М.: Просвещение, 1988, 372с.
3.
Семенов, А.Л. Математика ЕГЭ. Профильный
уровень [Текст]/
А. Л. Семенов, И.В. Ященко-М.: Издательство «Национальное наследие», 2022-
192с.
4.
Чертышкин, Е. М., Васильева, Н. Е.
Финансовые – экономические расчеты. Справочное пособие. [Текст]/ Е. М. Чертышкин,
Н. Е. Васильева, М.:Финансы и статистика, 1990 г.- 300с.
5.
В.Е. Черкасов «Практическое руководство по
финансово – экономическим расчетам». Москва: Метаинформ, 1995 г.
6.
Открытый банк задач по
математике. ЕГЭ –
Режим доступа:.https://fipi.ru/ (ресурсы
удаленного доступа (Internet))
7.
Математика профильного уровня –
Режим доступа:. https://math-ege.sdamgia.ru/problem
. (ресурсы удаленного доступа (Internet))
8.
Тренировочные варианты ЕГЭ –
Режим доступа:.. https://alexlarin.net/
(ресурсы удаленного доступа (Internet))
Приложение 1.
Таблица для решения задач, связанных с а аннуитетными платежами
|
Год |
Долг до % |
Долг |
Выплата |
Долг после выплаты |
|
1 год |
S |
Sb |
x |
Sb-x |
|
2 год |
Sb-x |
(Sb-x)b=Sb2-xb |
x |
Sb2-xb-x |
|
3 год |
Sb2-xb-x |
(Sb2-xb-x)b=Sb3-x |
x |
Sb3-x b2-xb-x |
|
4 год |
Sb3-x b2-xb-x |
(Sb3-x b2-xb-x)b= |
x |
Sb4-xb3-xb2-xb-x |
|
5 год |
Sb4-xb3-xb2-xb-x |
(Sb4-xb3-xb2-xb-x)b=Sb5xb4-xb3-xb2-xb |
x |
Sb5-xb4-xb3-xb2-xb-x |
|
6 год |
Sb5-xb4-xb3-xb2-xb-x |
(Sb5-xb4-xb3-xb2-xb-x)b=Sb6-xb5-xb4-xb-3xb2-xb |
x |
Sb6-xb5-xb4-xb-3xb2— xb-x |
|
n год |
Sb6-xb5-xb4-xb-3xb2-xb-x |
Sbn-xbn-1-xbn-2-…-xb2-xb |
x |
Полная выплата, долг равен 0 |
Приложение 2.
Таблица
|
Год |
Долг |
Долг |
Основная |
Процентная |
Долг после выплаты |
|
1 |
S |
|
|
|
|
|
2 |
|
|
|
|
|
|
33 |
|
|
|
|
|
|
… |
… |
… |
… |
… |
|
|
Nn |
|
|
|
|
0 |
Приложение 3
Таблица для начисления процентов по
вкладам
|
Год |
Вклад |
Действия |
Вклад с % и после действий |
|
1 |
S |
— |
Sb |
|
2 |
Sb |
— |
Sb2 |
|
n |
|
— |
Sbn |
Приложение 4
Таблица для решении
задач, в которых осуществлялись какие-либо действия (пополнение или снятие
денег с вклада)
|
Год |
Вклад |
Вклад с % |
Действие |
Вклад после действия. |
|
1 |
S |
Sb |
+х |
Sb+x |
|
2 |
Sb+x |
b(Sb+x)= |
+х |
Sb2+xb+x |
|
3 |
Sb2+xb+x |
b(Sb2+xb+x)=Sb3_+хb2+xb |
Снял вклад |
Методичка по решению экономических задач
(задание 17 ЕГЭ)
Составитель: Мокина В.С.,
учитель математики
МАОУ гимназия №83
Тюмень 2021 год
Содержание
l. Задачи на оптимальный выбор.
2. Задачи на кредит с аннуитетным платежом
3. Задачи на дифференцированный платеж
4. Задачи на нахождение суммы кредита
5. Задачи на нахождение суммы вклада
Все представленные в банке ЕГЭ задачи (задание 17), можно условно разделить на группы и подгруппы:
Задачи, не связанные с банковскими операциями (задачи на оптимизацию)
Банковские задачи на вклады
1) нахождение срока вклада;
2) вычисление процентной ставки по вкладу;
3) нахождение суммы вклада;
4) нахождение ежегодной суммы пополнения вклада
Банковские задачи на кредиты:
1) нахождение количества лет выплаты кредита;
2) вычисление процентной ставки по кредиту;
3) нахождение суммы кредита;
4) нахождение ежегодного транша.
В методичке показаны методы решения задач экономического содержания, связанные с банковскими кредитами, оптимизацией производства товаров и услуг.
Рассмотрим решение задач (задание 17), в которых требуется оптимальным образом распределить производство продукции для получения максимальной прибыли.
Задачи на оптимальный выбор. Например, нужно найти максимальную прибыль (при соблюдении каких-либо дополнительных условий), или минимальные затраты. Сначала в такой задаче нужно понять, как одна из величин зависит от другой (или других). Другими словами, нужна та функция, наибольшее или наименьшее значение которой мы ищем. А затем — найти это наибольшее или наименьшее значение. Иногда — с помощью производной. А если функция получится линейная или квадратичная — можно просто воспользоваться свойствами этих функций.
У фермера есть два поля, каждое площадью 10 гектаров. На каждом поле можно выращивать картофель и свёклу, поля можно делить между этими культурами в любой пропорции. Урожайность картофеля на первом поле составляет 500 ц/га, а на втором – 300 ц/га. Урожайность свёклы на первом поле составляет 300 ц/га, а на втором – 500 ц/га. Фермер может продать картофель по цене 5000 руб. за центнер, а свёклу – по цене 8000 руб. за центнер. Какой наибольший доход может получить фермер?
Решение:
Величина дохода фермера будет зависеть от того как будет распределена площадь поля между картофелем и свёклой. Пусть х га, засажено картофелем на первом поле, тогда (10 – х) га, засаженных свеклой на первом поле. Полученная прибыль с первого поля, равна:
S(х) = х·500·5000 + (10 – х)·300·8000 = 24000000 + 100000х (руб.)
Функция возрастающая, т.к. к>0, значит, наибольшая доходность будет достигнута при наибольшем значении х = 10 га и прибыль с первого поля составит: S(10) = 24000000 + 100000·10 = 25000000 рублей.
Обозначим через у — количество гектар, засаженных картофелем на втором поле, а (10- у) — количество гектар, засаженных свеклой на втором поле. Прибыль со второго поля составит:
S(у) = 300·5000·у + (10 – у)·500·8000 = 40000000 – 2500000у ( руб.)
Функция убывающая, т.к. к<0, значит, наибольшая доходность будет достигнута при наименьшем значении х = 0 га и прибыль с первого поля составит: S(10) = 40000000 рублей.
Таким образом, максимальная прибыль с обоих полей, равна: S = 25000000 + 40000 = 65000000 рублей, что составляет 65 млн. рублей.
Ответ: 65млн. рублей.
Реши самостоятельно:
У фермера есть два поля, каждое площадью 10 гектаров. На каждом поле можно выращивать картофель и свёклу, поля можно делить между этими культурами в любой пропорции. Урожайность картофеля на первом поле составляет 400 ц/га, а на втором — 300 ц/га. Урожайность свёклы на первом поле составляет 300 ц/га, а на втором — 400 ц/га.
Фермер может продавать картофель по цене 10 000 руб. за центнер, а свёклу — по цене 11 000 руб. за центнер. Какой наибольший доход может получить фермер?
У фермера есть два поля, каждое площадью 10 гектаров. На каждом поле можно выращивать картофель и свёклу, поля можно делить между этими культурами в любой пропорции. Урожайность картофеля на первом поле составляет 300 ц/га, а на втором — 200 ц/га. Урожайность свёклы на первом поле составляет 200 ц/га, а на втором — 300 ц/га.
Фермер может продавать картофель по цене 10 000 руб. за центнер, а свёклу — по цене 13 000 руб. за центнер. Какой наибольший доход может получить фермер?
У фермера есть два поля, каждое площадью 10 гектаров. На каждом поле можно выращивать картофель и свёклу, поля можно делить между этими культурами в любой пропорции. Урожайность картофеля на первом поле составляет 200 ц/га, а на втором — 300 ц/га. Урожайность свёклы на первом поле составляет 250 ц/га, а на втором — 200 ц/га.
Фермер может продавать картофель по цене 15 000 руб. за центнер, а свёклу — по цене 18 000 руб. за центнер. Какой наибольший доход может получить фермер?
Консервный завод выпускает фруктовые компоты в двух видах тары — стеклянной и жестяной. Производственные мощности завода позволяют выпускать в день 90 центнеров компотов в стеклянной таре или 80 центнеров в жестяной таре. Для выполнения условий ассортиментности, которые предъявляются торговыми сетями, продукции в каждом из видов тары должно быть выпущено не менее 20 центнеров. В таблице приведены себестоимость и отпускная цена завода за 1 центнер продукции для обоих видов тары.
|
Вид тары |
Себестоимость за 1 ц |
Отпускная цена за 1 ц |
|
стекло |
1500 рублей |
2100 рублей |
|
жесть |
1100 рублей |
1750 рублей |
Предполагая, что вся продукция завода находит спрос (реализуется без остатка), найдите максимально возможную прибыль завода за один день (прибылью называется разница между отпускной стоимостью всей продукции и её себестоимостью).
5) Фабрика, производящая пищевые полуфабрикаты, выпускает блинчики со следующими видами начинки: ягодная и творожная. В данной ниже таблице приведены себестоимость и отпускная цена, а также производственные возможности фабрики по каждому виду продукта при полной загрузке всех мощностей только данным видом продукта.
|
Вид начинки |
Себестоимость за 1 тонну |
Отпускная цена за 1тонну |
Производственные возможности |
|
ягоды |
70000 рублей |
100000 рублей |
90т/месс. |
|
творог |
100000 рублей |
135000 рублей |
75 т/месс. |
Для выполнения условий ассортиментности, которые предъявляются торговыми сетями, продукции каждого вида должно быть выпущено не менее 15 тонн. Предполагая, что вся продукция фабрики находит спрос (реализуется без остатка), найдите максимально возможную прибыль, которую может получить фабрика от производства блинчиков за 1 месяц.
Предприниматель купил здание и собирается открыть в нём отель. В отеле могут быть стандартные номера площадью 27 квадратных метров и номера «люкс» площадью 45 квадратных метров. Общая площадь, которую можно отвести под номера, составляет 981 квадратный метр. Предприниматель может поделить эту площадь между номерами различных типов, как хочет. Обычный номер будет приносить отелю 2000 рублей в сутки, а номер «люкс» — 4000 рублей в сутки. Какую наибольшую сумму денег сможет заработать в сутки на своём отеле предприниматель?
Решение:
Пусть у — число номеров «люкс», а х — число стандартных номеров и S = 981м2. Тогда должно соблюдаться неравенство: 27х + 45у = 981
Выразим число обычных номеров т.е.
х = 981 – 45у, х = 

Найдем решение этого уравнения подбором, где х, у 
Если у = 2, то х = 33 у = 14, то х = 15
у = 5, то х = 28 у = 17, то х = 8
у = 11, то х =18 у = 20, то х = 3
f(х,у) = 2000х + 4000у.
Очевидно, что максимальная прибыль будет при максимальном числе номеров «люкс», поэтому выбираем у = 20, х = 3.
Тогда в сутки предприниматель получит:
4000·20 + 2000·3 = 80000 + 6000 = 86000 рублей.
Проверим оставшиеся варианты
2·4000 + 33·2000 = 74000 рублей
5·4000 + 28·2000 = 76000 рублей
11·4000 + 18·2000 = 74000 рублей
2·4000 + 33·2000 = 80000 рублей
14·4000 + 15·2000 = 86000 рублей
17·4000 + 8·2000 = 84000 рублей
Ответ: 86000 рублей
Реши самостоятельно:
Предприниматель купил здание и собирается открыть в нем отель. В отеле могут быть стандартные номера площадью 30 квадратных метров и номера «люкс» площадью 40 квадратных метров. Общая площадь, которую можно отвести под номера, составляет 940 квадратных метров. Предприниматель может определить эту площадь между номерами различных типов, как хочет. Обычный номер будет приносить отелю 4000 рублей в сутки, а номер «люкс» — 5000 рублей в сутки. Какую наибольшую сумму денег сможет заработать в сутки на своем отеле предприниматель?
Предприниматель купил здание и собирается открыть в нем отель. В отеле могут быть стандартные номера площадью 21 квадратный метр и номера «люкс» площадью 49 м2. Общая площадь, которую можно отвести под номера, составляет 1099 м2. Предприниматель может поделить эту площадь между номерами различных типов, как хочет. Обычный номер будет приносить отелю 2000 рублей в сутки, а номер «люкс» — 4500 рублей в сутки. Какую наибольшую сумму денег сможет заработать в сутки на своем отеле предприниматель?
Предприниматель купил здание и собирается открыть в нём отель. В отеле могут быть стандартные номера площадью 27 квадратных метров и номера «люкс» площадью 45 квадратных метров. Общая площадь, которую можно отвести под номера, составляет 981 квадратный метр. Предприниматель может поделить эту площадь между номерами различных типов, как хочет. Обычный номер будет приносить отелю 2200 рублей в сутки, а номер «люкс» — 4000 рублей в сутки. Какую наибольшую сумму денег сможет заработать в сутки на своём отеле предприниматель?
Производство некоторого товара облагалось налогом в размере t0 руб. за ед. товара. Государство увеличило налог в 2.5 раза (t1= 2.5t0), но сумма налоговых поступлений не изменилась. На сколько процентов государству следует изменить налог, чтобы добиться максимальных налоговых сборов. если известно, что при налоге равном t руб. за ед. товара, объем производства товара составляет 9000 – 2t ед., если это число положительно, и 0 единиц?
Решение:
Обозначим Q(t) = 9000- 2t единиц товара, Q(t)- объем производства. Тогда налоговые сборы составляют S(t) = Q ·t, S(t) = (9000 — 2t)·t = 9000t – 2t2 руб. Рассмотрим функцию S(t) = 9000t – 2t2. Это квадратичная функция, графиком является парабола, ветви которой направлены вниз. Максимального значения эта функция достигает в вершине параболы. t = 





Значит государству необходимо на 30% уменьшить налог, чтобы добиться максимальных налоговых сборов.
Ответ: уменьшить на 30%
Решить самостоятельно
Производство некоторого товара облагалось налогом в размере t0 руб. за ед. товара. Государство увеличило налог в 2.5 раза (t1= 2.5t0),но сумма налоговых поступлений не изменилась. На сколько процентов государству следует изменить налог, чтобы добиться максимальных налоговых сборов. если известно, что при налоге равном t руб. за ед. товара, объем производства товара составляет 7000–2t ед., если это число положительно, и 0 единиц?
Производство некоторого товара облагалось налогом в размере t0 рублей за единицу товара. После того как государство, стремясь нарастить сумму налоговых поступлений, увеличило налог вдвое (до 2t0 рублей за единицу товара), сумма налоговых поступлений не изменилась. На сколько процентов государству следует изменить налог после такого увеличения, чтобы добиться максимальных налоговых поступлений, если известно, что при налоге, равном t рублей за единицу товара, объём производства составляет 10 000 – 2t единиц и это число положительно?
lll. 1. В начале 2001 года Алексей приобрел ценную бумагу за 11 000 рублей. В конце каждого года цена бумаги возрастает на 4 000 рублей. В начале любого года Алексей может продать бумагу и положить вырученные деньги на банковский счет. Каждый год сумма на счете будет увеличиваться на 10%. В начале каждого года Алексей должен продать ценную бумагу, чтобы через 15 лет после покупки этой бумаги сумма на счете была наибольшей?
Решение:
Используем арифметическую прогрессию, в которой а1=11000 — цена за бумагу в первый год покупки году, d=4000 — увеличение стоимости бумаги, аn — пока еще неизвестный нам год продажи бумаги (по счету от года покупки), n — номер года.
Формула n-ого члена арифметической прогрессии: an=a1+d(n-1).
Используя ее находим числа, отвечающие за стоимость бумаги на начало n-го года (по счету от года покупки).
Каждый год сумма на счете будет увеличиваться на 10% = 0,1 от данной суммы, и эти 10% должны быть больше или равны 4000.
Составим неравенство: 0,1·(a1+d(n-1)) ≥ 4000.
Подставим а1=11000, d=4000 и решим неравенство:
0,1·(11000+4000(n-1)) ≥ 4000 обе части неравенства умножим на 10, чтобы избавится от десятичной дроби, получим
11000+4000(n — 1) ≥ 40000;
11000+4000n — 4000 ≥ 40000;
4000n ≥ 33000;
n ≥ 8,25, n ∈Ν ⇒ n=8
через 8 лет надо продать бумагу, т.е. в 2001+8=2009 году
Или рассуждаем так: на восьмом году (т.е. в 2008) 10% от стоимости будет больше 4000, значит бумагу надо продать в следующем (т.е. 2009)).
Ответ: 2009 год.
Другое решение этой задачи.
Чтобы извлечь наибольшую прибыль, Алексей должен воспользоваться банковским депозитом, когда 10% от суммы, вырученной за ценную бумагу, превысит 4000 руб. Найдем значение суммы, от которой 10% будут равны 4000, получим: х·0,1 = 4000
х = 4000: 0,1 = 40000
То есть ценную бумагу в 11000 рублей нужно довести до суммы большей или равной 40000 рублей и полученную сумму положить в банк. Ценная бумага дойдет до этого уровня через 40000 – 11000 = 4000·n
n = 29000: 4000 = 7,25 n ∈Ν ⇒ n=8
то есть через 8 лет, и в начале 2009-го года полученную сумму нужно положить на банковский депозит.
Ответ: 2009.
Реши самостоятельно:
В начале 2001 года Алексей приобрел ценную бумагу за 7000 рублей. В конце каждого года цена бумаги возрастает на 2000 рублей. В начале любого года Алексей может продать бумагу и положить вырученные деньги на банковский счет. Каждый год сумма на счет будет увеличиваться на 10%. В начале какого года Алексей должен продать ценную бумагу, чтобы через пятнадцать лет после покупки этой бумаги сумма на банковском счете была наибольшей?
В начале 2001 года Алексей приобрел ценную бумагу за 19000руб. В конце каждого года цена бумаги возрастает на 3000 руб. В начале любого года Алексей может продать бумагу и положить вырученные деньги на банковский счет. Каждый год сумма на счете будет увеличиваться на 10%. В начале какого года Алексей должен продать ценную бумагу, чтобы через пятнадцать лет после покупки этой бумаги сумма на банковском счете была наибольшей?
Решение экономических задач: банки, проценты, кредиты.
1. Аннуитетный платеж – представляет собой равные ежемесячные платежи, растянутые на весь срок кредитования. В сумму платежа включены: часть ссудной задолженности и начисленный процент. При этом, в первые месяцы (или годы) кредита большую часть транша составляют проценты, а меньшую – погашаемая часть основного долга. Ближе к концу кредитования пропорция меняется: большая часть транша идет на погашение «тела» кредита, меньшая – на проценты. При этом общий размер платежа всегда остается одинаковым.
Задачи на кредит с аннуитетным платежом
1 января 2015 года Александр Сергеевич взял в банке 1,1 млн. рублей в кредит. Схема выплаты кредита следующая – 1-го числа каждого следующего месяца банк начисляет 1% на оставшуюся сумму долга (то есть увеличивает долг на 1%), затем Александр Сергеевич переводит в банк платёж. На какое минимальное количество месяцев Александр Сергеевич может взять кредит, чтобы ежемесячные выплаты были не более 275 тыс. рублей?
Решение:
|
№ месяца |
Остаток после начисления процентов и платежа |
|
0 |
1100000руб. |
|
1 |
1100000 ·1,02 – 275000 = 836000 руб. |
|
2 |
836000 ·1,02 – 275000 = 569360 руб. |
|
3 |
569360 ·1,02 – 275000 = 300053,6 руб. |
|
4 |
300053,6·1,02 – 275000 = 28054,13 руб. |
|
5 |
28054,13 ·1,02 = 28334,67 — 28334,67 = 0 |
Ответ: 5 месяцев
Реши самостоятельно:
1 января 2015 года Иван Сергеевич взял в банке 1 млн. рублей в кредит. Схема выплаты кредита следующая: 1-го числа каждого следующего месяца банк начисляет 2% на оставшуюся сумму долга (то есть увеличивает долг на 2%), затем Иван Сергеевич переводит в банк платёж. На какое минимальное количество месяцев Иван Сергеевич может взять кредит, чтобы ежемесячные выплаты были не более 200 тыс. рублей.
1 января 2015 года Андрей Владимирович взял в банке 1,1 млн. рублей в кредит. Схема выплаты кредита следующая: 1 числа каждого следующего месяца банк начисляет 3 процента на оставшуюся сумму долга (то есть увеличивает долг на 3%), затем Андрей Владимирович переводит в банк платёж. На какое минимальное количество месяцев Андрей Владимирович может взять кредит, чтобы ежемесячные выплаты были не более 220 тыс. рублей?
1 января 2019 года Павел Васильевич взял в банке 1 млн. рублей в кредит. Схема выплаты кредита следующая: 1 числа каждого следующего месяца банк начисляет 1 процент на оставшуюся сумму долга (то есть увеличивает долг на 1%), затем Павел Васильевич переводит в банк платёж. На какое минимальное количество месяцев Павел Васильевич может взять кредит, чтобы ежемесячные выплаты были не более 125 тыс. рублей?
1 января 2018 года Тимофей Ильич взял в банке 1,1 млн. рублей в кредит. Схема выплаты кредита следующая — 1 числа каждого следующего месяца банк начисляет 2 процента на оставшуюся сумму долга (то есть увеличивает долг на 2%), затем Тимофей Ильич переводит в банк платёж. На какое минимальное количество месяцев Тимофей Ильич может взять кредит, чтобы ежемесячные выплаты были не более 220 тыс. рублей?
IV.1. 31 декабря 2014 года Алексей взял в банке 9282000 рублей в кредит под 10% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 10%) затем Алексей переводит в банк X рублей. Какой должна быть сумма X, чтобы Алексей выплатил долг четырьмя равными платежами (то есть за 4 года)?
Решение:
Пусть S = 9282000 рублей размер взятого в банке кредита. 31 декабря каждого года размер кредита увеличился на 10%, а затем, Алексей переводит в банк X рублей, т.е. остаток через четыре года будет равен нулю.
|
год |
дата |
долг |
|
0 |
31 декабря 2014 |
S = 9282000 рублей |
|
31 декабря 2015 |
1,1S |
|
|
1 |
1 января 2016 |
1,1S — х |
|
31 декабря 2016 |
(1,1S – х)1,1 |
|
|
2 |
1 января 2017 |
1,12 S – 1,1х -х |
|
31 декабря 2017 |
(1,12 S – 1,1х –х)1,1 |
|
|
3 |
1 января 2018 |
(1,12 S – 1,1х –х)1,1 — х |
|
31 декабря 2018 |
((1,12 S – 1,1х –х)1,1 – х)1,1 |
|
|
4 |
1 января 2019 |
((1,12 S – 1,1х –х)1,1 – х)1,1 — х |
Решим уравнение: ((1,12 S – 1,1х –х)1,1 – х)1,1 – х = 0
1,14 S – 1,13 х — 1,12 х — 1,1х –х = 0
Х =
Х =
Х = 2928200
Ответ: 2928200.
31 декабря 2018 года Роман взял в банке 8599000 рублей в кредит под 14% годовых. Схема выплаты кредита следующая – 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга(то есть увеличивает долг на 14%), затем Роман переводит в банк Х рублей. Какой должна быть сумма Х, чтобы Роман выплатил долг тремя равными платежами (то есть за 3 года)?
31 декабря 2019 года Виктор взял в банке 3276000 рублей в кредит под 20 % годовых. Схема выплаты кредита следующая – 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 20 %), затем Виктор переводит в банк Х рублей. Какой должна быть сумма Х, чтобы Виктор выплатил долг тремя равными платежами (то есть за 3 года)?
31 декабря 2020 года Георгий взял в банке 2648000 рублей в кредит под 10 % годовых. Схема выплаты кредита следующая – 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 10 %), затем Георгий переводит в банк Х рублей. Какой должна быть сумма Х, чтобы Георгий выплатил долг тремя равными платежами (то есть за 3 года)?
IV.2. В августе 2020 года взяли кредит. Условия возврата таковы:
— каждый январь долг увеличивается на r %;
— с февраля по июль необходимо выплатить часть долга. Кредит можно выплатить за три года равными платежами по 56 595 рублей, или за два года равными платежами по 81 095 рублей. Найдите r.
Решение:
Пусть S рублей сумма кредита, ежегодные выплаты x руб., r % годовых,
к = 1 + r/100. Выплаты: b = 81095 руб., х = 56595 руб. По условию долг на июль меняется так:
|
год |
Долг (руб.) |
|
1 |
кS — b |
|
2 |
(кS – b)к — b |
Если долг выплачен двумя равными платежами b руб., то (кS – b)к – b = 0
к2 S – кb — b = 0; к2 S = (к + 1)b; S = ((к+1) b)/к2
Если долг выплачен тремя равными платежами х руб., то
|
год |
Долг (руб.) |
|
1 |
кS — х |
|
2 |
(кS – х)к — х |
|
3 |
((кS – х)к – х)к — х |
((кS – х)к – х)к – х = 0
к3 S – к2 х – кх — х = 0
S = ((к2 + к+1) х)/к3
Решим систему уравнений


(к+1)к b = х(к2 + к+1)
(к2 + к) b = х(к2 + к) + х
(к2 + к) b — х(к2 + к) – х = 0
(к2 + к)( b – х) –х = 0
(81095 – 56595) (к2 + к) – 56595 = 0
24500к2 + 24500к — 56595 = 0
100к2 + 100к – 231 = 0
D = 102400, к = 1,1 к = -21 не удовлетворяет условию
к = 1 + r/100, r = 10%
Ответ: 10
Реши самостоятельно:
31 декабря 2017 года Пётр взял в банке некоторую сумму в кредит под некоторый процент годовых. Схема выплаты кредита следующая — 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на а %), затем Пётр переводит очередной транш. Если он будет платить каждый год по 2 592 000 рублей, то выплатит долг за 4 года. Если по 4 392 000 рублей, то за 2 года. Под какой процент Пётр взял деньги в банке?
В августе 2017 года взяли кредит. Условия возврата таковы:
— каждый январь долг увеличивается на r %;
— с февраля по июль необходимо выплатить часть долга.
Кредит можно выплатить за три года равными платежами по 38 016 рублей, или за два года равными платежами по 52 416 рублей.
Найдите r.
В августе 2020 года взяли кредит. Условия возврата таковы: — каждый год долг увеличивается на r — процентов с февраля по июнь необходимо выплатить часть долга Кредит можно выплатить за 4 года равными платежами по 777600 руб. или за 2 года равными платежами по 1317600 руб. Найдите r.
В июле 2020 года планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:
— каждый январь долг увеличивается на r % по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга.
Если ежегодно выплачивать по 58 564 рубля, то кредит будет полностью погашен за 4 года, а если ежегодно выплачивать по 106 964 рубля, то кредит будет полностью погашен за 2 года. Найдите r.
2. Дифференцированный платеж – представляет собой неравные ежемесячные транши, пропорционально уменьшающиеся в течение срока кредитования. Наибольшие платежи – в первой четверти срока, наименьшие – в четвертой четверти. «Срединные» платежи обычно сравнимы с аннуитетом. Ежемесячно тело кредита уменьшается на равную долю, процент же насчитывается на остаток задолженности. Поэтому сумма транша меняется от выплаты к выплате. Если в задаче присутствуют слова «равными платежами» или «долг уменьшается на одну и ту же величину», то речь идет о дифференцированном платеже.
V. Планируется выдать льготный кредит на целое число миллионов рублей на четыре года. В середине каждого года действия кредита долг заёмщика возрастает на 25 % по сравнению с началом года. В конце 1-го и 2-го годов заёмщик выплачивает только проценты по кредиту, оставляя долг неизменно равным первоначальному. В конце 3-го и 4-го годов заёмщик выплачивает одинаковые суммы, погашая весь долг полностью. Найдите наименьший размер кредита, при котором общая сумма выплат заёмщика превысит 9 млн. рублей.
Решение:
Пусть S млн. рублей сумма первоначального кредита. В середине каждого года действия кредита долг возрастает на 25 %, x млн.рублей заёмщик выплачивает в конце 3-го и 4-го годов. В конце 1-го и 2-го годов заёмщик выплачивает только проценты по кредиту, оставляя долг неизменно равным первоначальному.
|
1 год |
начало |
S млн. рублей |
2 год |
начало |
S млн. рублей |
|
середина |
S + 0,25 S = 1,25 S |
середина |
S + 0,25 S = 1,25 S |
||
|
конец |
1,25 S — 0,25 S = S |
конец |
1,25 S — 0,25 S = S |
В сумме за 2 года он погашает сумму 0,25S + 0,25S = 0,5S.
В последние два года (3-й и 4-й) сумма долга сначала возрастает в 1,25 раза, а затем, погашается равными долями в x млн.рублей.
|
3 год |
начало |
S млн. рублей |
4 год |
начало |
(1,25 S – х) млн. руб. |
|
середина |
S + 0,25 S = 1,25 S |
середина |
(1,25 S – х)1,25 |
||
|
конец |
1,25 S — х |
конец |
1,252 S — 1,25 х -х |
На конец 4-го года, сумма долга составляет 0 рублей. Отсюда получаем
1,252 S — 1,25 х –х = 0,
1,252 S — 2,25 х = 0, х = 
За 4 года сумма выплат составила 0,5S + 2х. По условию общая сумма выплат превышает 9 млн. рублей, то есть, 0,5S + 2
17S > 81, S > 4
Ответ: 5 000 000
Реши самостоятельно:
Планируется выдать льготный кредит на целое число миллионов рублей на четыре года. В середине каждого года действия кредита долг заемщика возрастает на 20% по сравнению с началом года. В конце 1-го и 2-го годов заемщик выплачивает только проценты по кредиту, оставляя долг неизменно равным первоначальному. В конце 3-го и 4-го годов заемщик выплачивает одинаковые суммы, погашая весь долг полностью. Найдите наименьший размер кредита, при котором общая сумма выплат заемщика превысит 10 млн. рублей.
Планируется выдать льготный кредит на целое число миллионов рублей на четыре года. В середине каждого года действия кредита долг заемщика возрастает на 25% по сравнению с началом года. В конце 1-го и 2-го годов заемщик выплачивает только проценты по кредиту, оставляя долг неизменно равным первоначальному. В конце 3-го и 4-го годов заемщик выплачивает одинаковые суммы, погашая весь долг полностью. Найдите наименьший размер кредита, при котором общая сумма выплат заемщика превысит 5 млн. рублей.
Планируется выдать льготный кредит на целое число миллионов рублей на четыре года. В середине каждого года действия кредита долг заемщика возрастает на 15% по сравнению с началом года. В конце 1-го и 2-го годов заемщик выплачивает только проценты по кредиту, оставляя долг неизменно равным первоначальному. В конце 3-го и 4-го годов заемщик выплачивает одинаковые суммы, погашая весь долг полностью. Найдите наименьший размер кредита, при котором общая сумма выплат заемщика превысит 7 млн. рублей.
Планируется выдать льготный кредит на целое число миллионов рублей на четыре года. В середине каждого года действия кредита долг заёмщика возрастает на 10 % по сравнению с началом года. По договоренности с банком в конце 1-го и 3 – го года заемщик выплачивает только проценты по кредиту, начисленные за соответствующий текущий год. В конце 2‐го и 4‐го годов заёмщик выплачивает одинаковые суммы, погашая к концу 4‐го года весь долг полностью. Найдите наименьший размер кредита, при котором общая сумма выплат заёмщика превысит 100 млн. рублей.
Планируется выдать льготный кредит на целое число миллионов рублей на пять лет. В середине каждого года действия кредита долг заемщика возрастает на 10% по сравнению с началом года. В конце 1-го и 2-го и 3-го годов заемщик выплачивает только проценты по кредиту, оставляя долг неизменно равным первоначальному. В конце 4-го и 5-го годов заемщик выплачивает одинаковые суммы, погашая весь долг полностью. Найдите наибольший размер кредита, при котором общая сумма выплат будет меньше 8 млн. рублей.
Решение банковских задач на нахождение суммы кредита
VI. В июле 2026 года планируется взять кредит в банке на три года в размере S млн. руб., где S — целое число. Условия его возврата таковы:
— каждый январь долг увеличивается на 25% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;
-в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей.
|
Месяц, год |
Июль 2026 |
Июль 2027 |
Июль 2028 |
Июль 2029 |
|
Долг (в млн. руб.) |
S |
0,8S |
0,5S |
0 |
Найдите наибольшее значение S, при котором каждая из выплат будет меньше 4 млн. рублей.
Решение:
Долг перед банком (в млн. рублей) на июль каждого года должен уменьшаться до нуля следующим образом: S; 0,8S; 0,5S; 0
По условию, в январе каждого года долг увеличивается на 25%, значит, долг в январе каждого года равен: 1,25S; 1,25∙0,8S; 1,25∙0,5S
Следовательно, выплаты с февраля по июнь каждого года составляют:
1,25S — 0,8S = 0,45S 1,25∙0,8S — 0,5S = 0,5S 1,25∙0,5S – 0 = 0,725S
По условию, каждая из выплат должна быть меньше 4 млн. рублей. Это будет верно, если максимальная из выплат меньше 4 млн.рублей, т. е.
0,725S< 4; S< 6,4 S = 6
Наибольшее целое решение этого неравенства – число 6. Значит, искомый размер кредита 6 млн. рублей.
Ответ: 6 млн. рублей.
Реши самостоятельно:
В июле 2026 года планируется взять кредит в банке на три года в размере S млн. руб., где S — целое число. Условия его возврата таковы:
— каждый январь долг увеличивается на 25% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;
-в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей.
|
Месяц, год |
Июль 2026 |
Июль 2027 |
Июль 2028 |
Июль 2029 |
|
Долг (в млн. руб.) |
S |
0,7S |
0,4S |
0 |
Найдите наименьшее значение S, при котором каждая из выплат будет больше 5 млн. рублей.
В июле 2020 года планируется взять кредит в банке на три года в размере S млн. руб., где S — целое число. Условия его возврата таковы:
— каждый январь долг увеличивается на 15% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;
-в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей.
|
Месяц, год |
Июль 2020 |
Июль 2021 |
Июль 2022 |
Июль 2023 |
|
Долг (в тыс. руб.) |
S |
0,7S |
0,4S |
0 |
Найдите наименьшее значение S, при котором каждая из выплат будет составлять целое число тысяч рублей.
В июле планируется взять кредит в банке в размере S тыс. рублей (S – натуральное число) сроком на 3 года. Условия возврата кредита таковы: ‐ каждый январь долг увеличивается на 22,5% по сравнению с концом предыдущего года; ‐ в июне каждого года необходимо выплатить одним платежом часть долга; ‐ в июле каждого года величина долга задается таблицей
|
Месяц, год |
2018 |
2019 |
2020 |
2021 |
|
Долг (в тыс. руб.) |
S |
0,7S |
0,4S |
0 |
Найдите наименьшее значение S, при котором каждая из выплат будет составлять целое число тысяч рублей.
В июле 2016 года планируется взять кредит в банке на четыре года в размере S млн. рублей, где S — целое число. Условия его возврата таковы:
— каждый январь долг увеличивается на 15% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей.
|
Месяц, год |
Июль 2016 |
Июль 2017 |
Июль 2018 |
Июль 2019 |
Июль 2020 |
|
Долг (в млн. руб.) |
S |
0,8S |
0,5S |
0,1 S |
0 |
Найдите наибольшее значение S, при котором общая сумма выплат будет меньше 50 млн. рублей.
В июле 2016 года планируется взять кредит в банке на четыре года в размере S млн. рублей, где S — натуральное число. Условия его возврата таковы:
— каждый январь долг увеличивается на 25% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей.
|
Месяц, год |
Июль 2016 |
Июль 2017 |
Июль 2018 |
Июль 2019 |
Июль 2020 |
|
Долг (в млн. руб.) |
S |
0,7S |
0,5S |
0,3 S |
0 |
Найдите наименьшее значение S, при котором общая сумма выплат будет составлять целое число миллионов рублей.
Решение банковских задач на нахождение суммы вклада
VII. 15-го января планируется взять кредит в банке на 24 месяца. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.
Известно, что в течении первого года кредитования нужно вернуть банку 466,5 тыс. руб. Какую сумму планируется взять в кредит?
Решение:
Обозначим через Х размер кредита, взятого в банке. Во втором месяце долг увеличивается на 3% и, затем, осуществляется выплата так, чтобы долг уменьшался на одну и ту же величину, т.е. в первый раз выплата будет составлять 
1,03х – (



1,03·




Вторая выплата будет равна:
Аналогично третья выплата:
Аналогично четвертая выплата: 
………………………………………………………..
12- тая выплата:
Сумма выплат за первые 12 месяцев составит:

В скобках получилась арифметическая прогрессия сумму, которой находим по формуле 

=



По условию в течении первого года нужно выплатить 466,5 тыс. руб.


Ответ: 600000 руб.
Реши самостоятельно:
15-го января планируется взять кредит в банке на 20 месяца. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.
Известно, что за первые 10 месяцев нужно вернуть банку 1179 тыс. руб. Какую сумму планируется взять в кредит?
15-го января планируется взять кредит в банке на 24 месяца. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на 1% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.
Известно, что за последние 12 месяцев нужно вернуть банку 1597,5 тыс. руб. Какую сумму планируется взять в кредит?
15-го января планируется взять кредит в банке на 16 месяца. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на 4% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.
Известно, что за первые 8 месяцев нужно вернуть банку 900 тыс. руб. Какую сумму планируется взять в кредит?
5-го января планируется взять кредит в банке на 24 месяца. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.
Какую сумму следует взять в кредит, чтобы общая сумма выплат после полного его погашения равнялась 1 млн рублей?
5)15 января планируется взять кредит в банке на 24 месяца. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.
Известно, что в течение второго года кредитования нужно вернуть банку 339 тыс. рублей. Какую сумму нужно вернуть банку в течение первого года кредитования?
VIII. 15-го января планируется взять кредит в банке на 26 месяцев. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца с 1- го по 25 – й месяц долг должен быть на 40 тыс. руб. меньше долга на 15-е число предыдущего месяца.
— к 15 – му числу 26 – го месяца кредит должен быть полностью погашен.
Какую сумму планируется взять в кредит, если общая сумма выплат после полного его погашения составит 1924 тыс. руб.
Решение:
Обозначим через S исходную сумму кредита. В течение первого месяца эта сумма возрастает на 3%, становится равной S+0,03S = 1,03 S. Выплату нужно сделать так, чтобы исходная сумма S уменьшилась на 40 тыс. рублей, то есть, нужно выплатить
0,03S+40 тыс. рублей.
Оставшаяся сумма S-40 в следующем месяце снова увеличивается на 3%, становится равной 1,03(S-40), и следует выплатить0,03(S-40) + 40 тыс. руб., Таким образом, в течении 25-ти месяцев, сумма выплат составит:
0,03S+40 + (0,03(S-40) + 40) + (0,03(S-2·40) + 40) + (0,03(S-2·40) + 40) +… + (0,03(S-24·40) + 40) = 0,03S·25 + 40·25 – 0,03·40·( 1 + 2 + 3 +… + 24) =
S24 = 1 + 2 + 3 +… + 24 = 
= 0,75 S + 1000 – 360 =0,75 S + 640
В последний 26-й месяц выплачивается остаток 1,03(S -25·40) = 1,03(S – 1000)
В сумме за 26 месяцев имеем: 0,75 S + 640 +1,03(S – 1000). По условию общая сумма выплат после полного его погашения составит 1924 тыс. руб. Составим и решим уравнение: 0,75 S + 640 +1,03(S – 1000) = 1924
1,78 S = 1924 + 390
S = 2314/ 1,78
S = 1300 тыс.руб.
Ответ: 1300000 руб.
Реши самостоятельно:
15-го декабря планируется взять кредит в банке на 11 месяцев. Условия возврата таковы:
— 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца с 1-го по 10-й долг должен быть на 80 тысяч рублей меньше долга на 15-е число предыдущего месяца;
— к 15-му числу 11-го месяца кредит должен быть полностью погашен.
Какой долг будет 15-го числа 10-го месяца, если общая сумма выплат после полного погашения кредита составит 1198 тысяч рублей?
15-го декабря планируется взять кредит в банке на сумму 300 тысяч рублей на 21 месяц. Условия возврата таковы:
— 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца с 1-го по 20-й долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца;
— 15-го числа 20-го месяца долг составит 100 тысяч рублей;
— к 15-му числу 21-го месяца кредит должен быть полностью погашен.
Найдите общую сумму выплат после полного погашения кредита.
15-го декабря планируется взять кредит в банке на 21 месяц. Условия возврата таковы:
— 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца с 1-го по 20-й долг должен быть на 30 тысяч рублей меньше долга на 15-е число предыдущего месяца;
— к 15-му числу 21-го месяца кредит должен быть полностью погашен.
Какую сумму планируется взять в кредит, если общая сумма выплат после полного его погашения составит 1604 тысяч рублей?
Ответы:
1) 84 млн. руб., 2) 69 млн. руб., 3) 90 млн. руб., 4)53500 руб., 5) 2685000 руб.
1) 125000 руб., 2)104500 руб. 3)86600 рублей.
1) 2 2) 25
III. l. 1) 2008 2) 2005
1) 6 месяцев 2) 6 месяцев 3) 9 месяцев 4) 6 месяцев
IV.1. 1) 3703860 рублей 2) 155520 рублей 3) 1064800 рублей
IV.2. 1) 20% 2) 20% 3) 20% 4) 10%
1) 6 млн. руб., 2) 3 млн. руб., 3) 5 млн. руб., 4) 77 млн. руб.,
5 млн. руб.
VI. 1) 11млн.руб. 2) 200 тыс. руб. 3) 400 тыс. руб. 4) 36 млн.руб.
5) 8 млн.руб.
VII. 1) 1200000руб. 2) 3000000 руб. 3) 1200000руб. 4) 0,8 млн. руб.
5) 411000 руб.
VIII. 1) 200000 руб. 2) 384000 руб. 3) 1100000 руб.
Используемая литература:
Шестаков С.А. ЕГЭ 2017. Математика. Задачи с экономическим содержанием. Задачи 17(профильный уровень)/Под ред.И.В.Ященко.-М.:МЦНМЩ, 2017
30 тренировочных вариантов ЕГЭ под редакцией И. В. Ященко» – 2021.
Основные формулы в задачах на вклады и кредиты
12 марта 2015
Сегодня мы немного отвлечемся от стандартных логарифмов, интегралов, тригонометрии и т.д., а вместе этого рассмотрим более жизненную задачу из ЕГЭ по математике, которая имеет прямое отношение к нашей отсталой российской сырьевой экономике. А если быть точным, мы рассмотрим задачу про вклады, проценты и кредиты. Потому что именно задачи с процентами с недавних пор добавлены во вторую часть единого государственного экзамена по математике. Сразу оговорюсь, что за решение этой задачи согласно спецификациям ЕГЭ предлагается сразу три первичных балла, т. е. экзаменаторы считают эту задачу одной из самых сложных.
Вместе с тем, для решения любой из указанных задач из ЕГЭ по математике необходимо знать всего лишь две формулы, каждая из которых вполне доступна любому школьному выпускнику, однако по непонятным мне причинам эти формулы начисто игнорируются как школьными учителями, так и составителями всевозможных задач для подготовки к ЕГЭ. Поэтому сегодня я не просто расскажу вам, что это за формулы и как их применять, а выведу каждую из этих формул буквально у вас на глазах, взяв за основу задачи из открытого банка ЕГЭ по математике.
Поэтому урок получился довольно объемный, довольно содержательный, поэтому устраивайтесь поудобнее, и мы начинаем.
Вкладываем деньги в банк
Прежде всего, хотелось бы сделать небольшое лирическое отступление, связанное с финансами, банками, кредитами и вкладами, на основании которых мы и получим те формулы, которые будем использовать для решения данной задачи. Итак, давайте немного отвлечемся от экзаменов, от предстоящих школьных проблем, и посмотрим в будущее.
Допустим, вы выросли и собираетесь покупать квартиру. Допустим, вы собираетесь покупать не какую-то плохую квартиру на окраине, а хорошую качественную квартиру за 20 миллионов рублей. При этом также предположим, что вы устроились на более-менее нормальную работу и зарабатываете по 300 тысяч рублей в месяц. В этом случае за год вы сможете отложить примерно три миллиона рублей. Разумеется, зарабатывая по 300 тысяч рублей в месяц, за год у вас получится чуть большая сумма — 3600000 — но эти 600000 пусть будут потрачены на еду, на одежду и на прочие ежедневные бытовые радости. Итого вводные данные таковы: необходимо заработать двадцать миллионов рублей, у нас же в распоряжении имеется лишь три миллиона рублей в год. Возникает естественный вопрос: сколько лет нам необходимо откладывать по три миллиона, чтобы получить эти самые двадцать миллионов. Считается это элементарно:
[frac{20}{3}=6,….to 7]
Однако как мы уже с вами отмечали, вы зарабатываете 300 тысяч рублей в месяц, это значит, что вы умные люди и не будете откладывать деньги «под подушку», а отнесете их в банк. И, следовательно, ежегодно на те вклады, которые вы принесете в банк, будут начисляться проценты. Допустим, вы выберете надежный, но при этом более-менее прибыльный банк, и поэтому ваши вклады ежегодно будут расти на 15% годовых. Другими словами можно сказать, что сумма на ваших счетах ежегодно будет увеличиваться в 1,15 раза. Напомню формулу:
[Ktext{%} to 1+frac{K}{100}]
Давайте посчитаем, сколько денег будет на ваших счетах после каждого года:
В первый год, когда вы только начнете откладывать деньги, никакие проценты не накопятся, т. е. в конце года вы отложите три миллиона рублей:
[3m]
В конце второго года на те три миллиона рублей, которые остались с первого года, уже будут начислены проценты, т.е. нам нужно умножить на 1,15. Однако в течение второго года вы также доложили еще три миллиона рублей. Разумеется, на эти три миллиона еще не были начислены проценты, потому что к концу второго года эти три миллиона только появились на счету:
[3mcdot 1,15+3m]
Итак, третий год. В конце третьего года на эту сумму будут начислены проценты, т. е. необходимо всю эту сумму умножить на 1,15. И опять же, в течение всего года вы усердно работали и еще отложили три миллиона рублей:
[left( 3mcdot 1,15+3m right)cdot 1,15+3m]
Давайте рассчитаем еще четвертый год. Опять же, вся сумма, которая оказалась у нас к концу третьего года, умножается на 1,15, т.е. на всю сумму будут начислены проценты. В том числе, будут начислены проценты на проценты. И к этой сумме добавляется еще три миллиона, потому что в течение четвертого года вы также работали и также откладывали деньги:
[left( left( 3mcdot 1,15+3m right)cdot 1,15+3m right)cdot 1,15+3m]
А теперь давайте раскроем скобки и посмотрим, какая у нас будет сумма к концу четвертого года откладывания денег:
[begin{align}& left( left( 3mcdot 1,15+3m right)cdot 1,15+3m right)cdot 1,15+3m= \& =left( 3mcdot {{1,15}^{2}}+3mcdot 1,15+3m right)cdot 1,15+3m= \& =3mcdot {{1,15}^{3}}+3mcdot {{1,15}^{2}}+3mcdot 1,15+3m= \& =3mleft( {{1,15}^{3}}+{{1,15}^{2}}+1,15+1 right)= \& =3mleft( 1+1,15+{{1,15}^{2}}+{{1,15}^{3}} right) \end{align}]
Как видим, в скобках у нас стоят элементы геометрической прогрессии, т. е. у нас стоит сумма элементов геометрической прогрессии.
Напомню, что если геометрическая прогрессия задана элементом ${{b}_{1}}$, а также знаменателем $q$, то сумма элементов будет считаться по следующей формуле:
[{{S}_{n}}={{b}_{1}}cdot frac{{{q}^{n}}-1}{q-1}]
Эту формулу обязательно нужно знать и четко применять.
Обратите внимание: формула n-го элемента звучит следующим образом:
[{{b}_{n}}={{b}_{1}}cdot {{q}^{n-1}}]
Из-за этой степени многие ученики путаются. В сумме у нас стоит просто nдля суммы n-элементов, а сам n-й элемент имеет степень $n-1$. Другими словами, если мы сейчас попытаемся посчитать сумму геометрической прогрессии, то нужно учитывать следующее:
[begin{align}& {{b}_{1}}=1 \& q=1,15 \end{align}]
Теперь мы можем посчитать сумму:
[{{S}_{4}}=1cdot frac{{{1,15}^{4}}-1}{1,15-1}]
Посчитаем числитель отдельно:
[{{1,15}^{4}}={{left( {{1,15}^{2}} right)}^{2}}={{left( 1,3225 right)}^{2}}=1,74900625approx 1,75]
Итого, возвращаясь к сумме геометрической прогрессии, мы получим:
[{{S}_{4}}=1cdot frac{1,75-1}{0,15}=frac{0,75}{0,15}=frac{75}{15}=5]
В итоге мы получаем, что за четыре года накоплений наша исходная сумма увеличится не в четыре раза, как если бы мы не клали деньги в банк, а в пять раз, т. е. пятнадцать миллионов. Давайте запишем это отдельно:
4 года → 5 раз
Забегая вперед, скажу, что если бы мы копили не четыре года, а пять лет, то в итоге наша сумма накоплений увеличилась бы в 6,7 раза:
5 лет → 6,7 раз
Другими словами, к концу пятого года мы бы получили на счету следующую сумму:
[6,7cdot 3=20,1]
Т. е. к концу пятого года накоплений с учетом процентов по вкладу мы бы уже получили свыше двадцати миллионов рублей. Таким образом, общий счет накоплений за счет банковских процентов снизился бы с почти семи лет до пяти лет, т. е. почти на два года.
Таким образом, даже, несмотря на то, что банк начисляет достаточно низкий процент на наши вклады (15%), уже через пять лет эти самые 15% дают прибавку, существенно превышающую наш ежегодный заработок. При этом основной мультипликационный эффект приходится на последние годы и даже, скорее, на последний год накоплений.
К чему я это все писал? Разумеется, не к тому, чтобы агитировать вас нести деньги в банк. Потому что если вы действительно хотите приумножить свои сбережения, то вкладывать их нужно не в банк, а в реально действующий бизнес, где эти самые проценты, т. е. рентабельность в условиях российской экономики редко опускается ниже 30%, т. е. вдвое больше банковских вкладов.
А вот что действительно полезно во всех этих рассуждениях, так это формула, которая позволяет нам найти итоговую сумму вклада через размер ежегодных платежей, а также через проценты, которые начисляет банк. Так и запишем:
[text{Vklad}=text{platezh}frac{{{text{%}}^{n}}-1}{text{%}-1}]
Сам по себе % считается по следующей формуле:
[Ktext{%}to 1+frac{K}{100}]
Эту формулу также необходимо знать, как и основную формулу суммы вклада. А, в свою очередь, основная формула способна значительно сократить вычисления в тех задачах с процентами, где требуется посчитать именно вклад.
Почему стоит пользоваться формулами, а не таблицами?
У многих наверняка возникнет вопрос, а к чему вообще все эти сложности, нельзя ли просто расписать каждый год в табличке, как это делают во многих учебниках, посчитать отдельно каждый год, а затем посчитать общую сумму вклада? Конечно, можно вообще забыть про сумму геометрической прогрессии и все считать с помощью классических табличек — так сделано в большинстве сборников для подготовки к ЕГЭ. Однако, во-первых, резко увеличивается объем вычислений, а во-вторых, как следствие, увеличивается вероятность допустить ошибку.
Да и вообще, использовать таблицы вместо этой замечательной формулы — это то же самое, что на стройке копать траншеи руками вместо того, чтобы использовать стоящий рядом и полностью работающий экскаватор.
Ну, или то же самое, что умножить пятерку на десятку не с помощью таблицы умножения, а складывать пятерку с самой собой десять раз подряд. Впрочем, это я уже отвлекся, поэтому еще раз повторю самую главную мысль: если есть какой-то способ упростить и сократить вычисления, то именно этим способом и надо воспользоваться.
Проценты по кредитам
С вкладами мы разобрались, поэтому переходим к следующей теме, а именно — к процентам по кредитам.
Итак, пока вы копите деньги, скрупулезно планируете свой бюджет, думаете о своей будущей квартире, ваш одноклассник, а нынче простой безработный, решил жить сегодняшним днем и просто взял кредит. При этом он еще будет подкалывать и смеяться над вами, мол, у него кредитный телефон и подержанный автомобиль, взятый в кредит, а вы до сих пор ездите на метро и пользуетесь старым кнопочным телефоном. Разумеется, за все эти дешевые «понты» вашему бывшему однокласснику придется дорого расплатится. Насколько дорого — вот это именно сейчас мы и посчитаем.
Для начала краткая вводная информация. Допустим, ваш бывший одноклассник взял два миллиона рублей в кредит. При этом согласно договору он должен платить xрублей в месяц. Допустим, что кредит он взял по ставке 20% годовых, что в нынешних условиях выглядит вполне прилично. Кроме того, предположим, что срок кредита составляет всего три месяца. Давайте попробуем связать все эти величины в одну формулу.
Итак, в самом начале, как только ваш бывший одноклассник вышел из банка у него в кармане два миллиона, и это и есть его долг. При этом не год прошел, и не месяц, а это только самое начало:
[2m]
Затем спустя один месяц на сумму задолженности будут начислены проценты. Как мы уже знаем для вычисления процентов достаточно умножить исходную задолженность на коэффициент, который считается по следующей формуле:
[Ktext{%}to 1+frac{K}{100}]
В нашем случае речь идет о ставке 20% годовых, т. е. мы можем записать:
[1+frac{20}{100}=1,2]
Это коэффициент суммы, которая будет начисляться в год. Однако наш одноклассник не очень умный и он не читал договор, и на деле кредит ему выдали не под 20% в год, а под 20% в месяц. И уже к концу первого месяца на эту сумму будут начислены проценты, и она увеличится в 1,2 раза. Сразу после этого человеку будет необходимо оплатить оговоренную сумму, т. е. xрублей в месяц:
[2mcdot 1,2- x]
Далее к концу второго месяца уже на эту сумму будут вновь начислены проценты:
[left( 2mcdot 1,2- xright)cdot 1,2-x]
И вновь наш паренек вносит платеж в размере $x$ рублей.
Затем к концу третьего месяца сумма его задолженности еще раз увеличивается на 20%:
[left( left( 2mcdot 1,2- xright)cdot 1,2- xright)1,2- x]
И по условию за три месяца он должен полностью расплатиться, т. е. после внесения последнего третьего платежа его объем задолженности должен быть равен нулю. Мы можем записать такое уравнение:
[left( left( 2mcdot 1,2- xright)cdot 1,2- xright)1,2 — x=0]
Давайте решать:
[begin{align}& left( 2mcdot {{1,2}^{2}}- xcdot 1,2- xright)cdot 1,2- x=0 \& 2mcdot {{1,2}^{3}}- xcdot {{1,2}^{2}}- xcdot 1,2- x=0 \& 2mcdot {{1,2}^{3}}=cdot {{1,2}^{2}}+cdot 1,2+ \& 2mcdot {{1,2}^{3}}=left( {{1,2}^{2}}+1,2+1 right) \end{align}]
Перед нами вновь геометрическая прогрессия, а точнее, сумма трех элементов геометрической прогрессии. Давайте перепишем ее в порядке возрастания элементов:
[2mcdot {{1,2}^{3}}=left( 1+1,2+{{1,2}^{2}} right)]
Теперь нам нужно найти сумму трех элементов геометрической прогрессии. Давайте запишем:
[begin{align}& {{b}_{1}}=1; \& q=1,2 \end{align}]
Теперь найдем сумму геометрической прогрессии:
[{{S}_{3}}=1cdot frac{{{1,2}^{3}}-1}{1,2-1}]
Следует напомнить, что сумма геометрической прогрессии с такими параметрами $left( {{b}_{1}};q right)$ считается по формуле:
[{{S}_{n}}={{b}_{1}}cdot frac{{{q}^{n}}-1}{q-1}]
Вот этой формулой мы только что и воспользовались. Подставляем эту формулу в наше выражение:
[2mcdot {{1,2}^{3}}=cdot frac{{{1,2}^{3}}-1}{1,2-1}]
Для дальнейших вычислений нам следует узнать, чему равна ${{1,2}^{3}}$. К сожалению, в этом случае мы уже не можем расписать как в прошлый раз в виде двойного квадрата, но зато можем посчитать так:
[begin{align}& {{1,2}^{3}}={{1,2}^{2}}cdot 1,2 \& {{1,2}^{3}}=1,44cdot 1,2 \& {{1,2}^{3}}=1,728 \end{align}]
Переписываем наше выражение:
[2mcdot 1,728=cdot frac{0,728}{0,2}]
Это классическое линейное выражение. Давайте вернемся к следующей формуле:
[2cdot {{1,2}^{3}}=cdot frac{{{1,2}^{3}}-1}{1,2-1}]
По сути, если обобщить ее, то мы получим формулу, связывающую проценты, кредиты, платежи и сроки. Формула звучит следующим образом:
[kreditcdot {{%}^{n}}=platezhcdot frac{{{%}^{n}}-1}{%-1}]
Вот она, самая главная формула сегодняшнего видеоурока, с помощью которой считается не менее 80% всех экономических задач из ЕГЭ по математике во второй части.
Чаще всего в реальных задачах у вас будет спрашиваться платеж, либо чуть реже кредит, т. е. общая сумма задолженности, которая была у нашего одноклассника в самом начале платежей. В более сложных задачах вас попросят найти процент, ну а совсем сложных, которые мы разберем в отдельном видеоуроке от вас попросят найти сроки, в течение которых при данных параметрах кредита и платежа наш безработный одноклассник сможет полностью расплатится с банком.
Возможно, кто-то сейчас подумает, что я являюсь яростным противником кредитов, финансов и вообще банковской системы. Так вот, ничего подобного! Напротив, я считаю, что кредитные инструменты очень полезны и крайне необходимы нашей экономике, но только при условии, что кредит берется на развитие бизнеса. В крайнем случае, можно взять кредит на покупку жилья, т. е. ипотеку либо на неотложное медицинское лечение — все, других причин взять кредит просто не существует. А всевозможные безработные, которые берут кредиты на покупку «понтов» и при этом совершенно не задумываются о последствиях в итоге и становятся причиной кризисов и проблем в нашей экономике.
Возвращаясь к теме сегодняшнего урока, хотел бы отметить, что знать эту формулу, связывающую кредиты платежи и проценты, также необходимо как и сумму геометрической прогрессии. Именно с помощью этих формул решаются реальные экономические задачи из ЕГЭ по математике. Ну, а теперь, когда вы все это прекрасно знаете, когда понимаете, что такое кредит и почему его не стоит брать, переходим к решению реальных экономических задач из ЕГЭ по математике.
Решаем реальные задачи из ЕГЭ по математике
Пример № 1
Итак, первая задача:
31 декабря 2014 года Алексей взял в банке 9282000 рублей в кредит под 10% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (т .е. увеличивает долг на 10%), затем Алексей переводит в банк Х рублей. Какой должна быть сумма Х, чтобы Алексей выплатил долг четырьмя равными платежами (т .е. за четыре года)?
Итак, это задача про кредит, поэтому сразу записываем нашу формулу:
[kreditcdot {{%}^{n}}=platezhcdot frac{{{%}^{n}}-1}{%-1}]
Кредит нам известен — 9282000 рублей.
С процентами мы сейчас разберемся. У нас речь идет о 10% в задаче. Следовательно, мы можем их перевести:
[10text{%}to 1+frac{10}{100}=1,1]
Мы можем составить уравнение:
[9289000cdot {{1,1}^{4}}=xcdot frac{{{1,1}^{4}}-1}{1,1-1}]
У нас получилось обычное линейное уравнение относительно $x$, хотя с достаточно грозными коэффициентами. Давайте попробуем его решить. Для начала найдем выражение ${{1,1}^{4}}$:
$begin{align}& {{1,1}^{4}}={{left( {{1,1}^{2}} right)}^{2}} \& 1,1cdot 1,1=1,21 \& {{1,1}^{4}}=1,4641 \end{align}$
Теперь перепишем уравнение:
[begin{align}& 9289000cdot 1,4641=xcdot frac{1,4641-1}{0,1} \& 9282000cdot 1,4641=xcdot frac{0,4641}{0,1}|:10000 \& 9282000cdot frac{14641}{10000}=xcdot frac{4641}{1000} \& frac{9282cdot 14641}{10}=xcdot frac{4641}{1000}|:frac{4641}{1000} \& x=frac{9282cdot 14641}{10}cdot frac{1000}{4641} \& x=frac{2cdot 14641cdot 1000}{10} \& x=200cdot 14641 \& x=2928200 \end{align}][]
Все, наша задача с процентами решена.
Разумеется, что это была лишь самая простая задача с процентами из ЕГЭ по математике. В настоящем экзамене такой задачи, скорее всего, не будет. А если и будет, то считайте, что вам очень повезло. Ну, а для тех, кто любит считать и не любит рисковать, переходим к следующим более сложным задачам.
Пример № 2
31 декабря 2014 года Степан взял в банке 4004000 рублей в кредит под 20% годовых. Схема выплаты кредиты следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (т. е.) увеличивает долг на 20%), затем Степан производит в банк платеж. Весь долг Степан выплатил за 3 равных платежа. На сколько рублей меньше он бы отдал банку, если бы смог выплатить долг за 2 равных платежа.
Перед нами задача про кредиты, поэтому записываем нашу формулу:
[][kreditcdot {{%}^{n}}=platezhcdot frac{{{%}^{n}}-1}{%-1}]
Что нам известно? Во-первых, нам известен общий кредит. Также нам известны проценты. Давайте найдем коэффициент:
[20%to 1+frac{20}{100}=1,2]
Что касается $n$, то нужно внимательно прочитать условие задачи. Т. е. сначала нам необходимо посчитать, сколько он заплатил за три года, т. е. $n=3$, а затем выполнить еще раз те же самые действия но рассчитать платежи за два года. Давайте запишем уравнение для того случай, когда платеж выплачивается за три года:
[4004000cdot {{1,2}^{3}}=xcdot frac{{{1,2}^{3}}-1}{1,2-1}]
Давайте решать это уравнение. Но для начала найдем выражение ${{1,2}^{3}}$:
[begin{align}& {{1,2}^{3}}=1,2cdot {{1,2}^{2}} \& {{1,2}^{3}}=1,44cdot 1,2 \& {{1,2}^{3}}=1,728 \end{align}]
Переписываем наше выражение:
[begin{align}& 4004000cdot 1,728=xcdot frac{1,728-1}{0,2} \& 4004000cdot frac{1728}{1000}=xcdot frac{728}{200}|:frac{728}{200} \& x=frac{4004cdot 1728cdot 200}{728} \& x=frac{4004cdot 216cdot 200}{91} \& x=44cdot 216cdot 200 \& x=8800cdot 216 \& x=1900800 \end{align}]
Итого, наш платеж составит 1900800 рублей. Однако обратите внимании: в задаче от нас требовалось найти не ежемесячный платеж, а сколько всего Степан заплатит за три равных платежа, т. е. за все время пользования кредитом. Поэтому полученную величину необходимо еще раз умножить на три. Давайте посчитаем:
[3x=5702400]
Итого за три равных платежа Степан заплатит 5702400 рублей. Вот во сколько ему обойдется пользование кредитом в течение трех лет.
Теперь рассмотрим вторую ситуацию, когда Степан поднапрягся, собрался и выплатил весь кредит не за три, а за два равных платежа. Записываем все ту же нашу формулу:
[begin{align}& 4004000cdot {{1,2}^{2}}=xcdot frac{{{1,2}^{2}}-1}{1,2-1} \& 4004000cdot frac{144}{100}=xcdot frac{11}{5}|cdot frac{5}{11} \& x=frac{40040cdot 144cdot 5}{11} \& x=3640cdot 144cdot 5=3640cdot 720 \& x=2620800 \end{align}]
Но это еще не все, потому что сейчас мы посчитали лишь один из двух платежей, поэтому всего Степан заплатит ровно в два раза больше:
[2x=5241600]
Прекрасно, вот теперь мы и приблизились к окончательному ответу. Но обратите внимание: ни в коем случае мы еще не получили окончательный ответ, потому что за три года платежей Степан заплатит 5702400 рублей, а за два года платежей он заплатит 5241600 рублей, т. е. чуть-чуть поменьше. Насколько меньше? Чтобы это узнать, нужно из первого размера платежей вычесть второй размер платежей:
[5702400-5241600=460800]
Итого окончательный ответ — 460800 рублей. Именно сколько сэкономит Степан, если будет платить не три года, а два.
Как видите, формула, связывающая проценты, сроки и платежи, существенно упрощает вычисления по сравнению с классическими таблицами и, к сожалению, по непонятным причинам в большинстве сборников задач, тем не менее, до сих пор используются именно таблицы.
Отдельно хотел бы обратить ваше внимание на срок, на который взят кредит, и размером ежемесячных платежей. Дело в том, что эта связь напрямую не просматривается из тех формул, которые мы записали, однако ее понимание необходимо для быстрого и эффективного решения настоящих задач на экзамене. На самом деле эта связь очень проста: чем на больший срок берется кредит, тем меньшая сумма будет в ежемесячных платежах, но тем большая сумма накопится за все время пользования кредитом. И наоборот: чем меньше срок, тем больше ежемесячный платеж, однако при этом меньше итоговая переплата и меньше общая стоимость кредита.
Разумеется, все эти утверждения будут равны лишь при условии, что сумма кредита и процентная ставка в обоих случаях одна и та же. В общем, пока просто запомните этот факт — он будет использоваться для решения самых сложных задач на эту тему, а пока мы разберем более простую задачу, где как раз и требуется найти общую сумму исходного кредита.
Пример № 3
Итак, еще одна задача на кредит и по совместительству последняя задача в сегодняшнем видеоуроке.
31 декабря 2014 года Василий взял в банке некоторую сумму в кредит под 13% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (т.е. увеличивает долг на 13%), затем Василий переводит в банк 5 107 600 рублей. Какую сумму взял Василий в банке, если он выплатил долг двумя равными платежами (за два года)?
Итак, в первую очередь, эта задача вновь про кредиты, поэтому записываем нашу замечательную формулу:
[kreditcdot {{%}^{n}}=platezhcdot frac{{{%}^{n}}-1}{%-1}]
Посмотрим, что нам известно из условия задачи. Во-первых, платеж — он равен 5107600 рублей в год. Во вторых проценты, поэтому мы можем найти коэффициент:
[13%to 1+frac{13}{100}=1,13]
Кроме того, согласно условию задачи Василий взял в банке кредит на два года, т.е. выплатил двумя равными платежами, следовательно, $n=2$. Давайте все подставим и также заметим, что кредит нам неизвестен, т.е. та сумма, которую он взял, и обозначим ее за $x$. Получим:
[xcdot {{1,13}^{2}}=5107600cdot frac{{{1,13}^{2}}-1}{1,13-1}]
Знаменатель мы можем тут же посчитать — это будет 1,13, а вот в числителе, а также слева перед переменной $x$ у нас стоит коэффициент ${{1,13}^{2}}$. Предлагаю посчитать данное выражение отдельно:
[{{1,13}^{2}}=1,2769]
Перепишем наше уравнение с учетом этого факта:
[begin{align}& xcdot frac{12769}{10000}=5107600cdot frac{1,2769-1}{0,13} \& xcdot frac{12769}{10000}=frac{5107600cdot 2769}{1300}|:frac{12769}{10000} \& x=frac{51076cdot 2769}{13}cdot frac{10000}{12769} \& x=4cdot 213cdot 10000 \& x=8520000 \end{align}]
Все, это и есть окончательный ответ. Именно такую сумму Василий взял в кредит в самом начале.
Теперь понятно, почему в этой задаче нам предлагается взять кредит лишь на два года, потому что здесь фигурируют двузначные проценты, а именно 13%, которые в квадрате дают уже довольно «зверское» число. Но и это еще не предел — в следующем отдельном уроке мы рассмотрим более сложные задачи, где будет требоваться найти срок кредита, а ставка будет составлять один, два или три процента.
В общем, учитесь решать задачи на вклады и кредиты, готовьтесь к экзаменам и сдавайте их «отлично». А если что-то непонятно в материалах сегодняшнего видеоурока, то не стесняйтесь — пишите, звоните, и я постараюсь вам помочь.
Смотрите также:
- Задача на производительность труда
- ЕГЭ по математике 2016: задача про кредиты с фиксированным платежом
- Тест к уроку «Что такое логарифм» (тяжелый)
- Комбинированные задачи B12
- Как решать задачи про летающие камни?
- Задача C1: тригонометрия и показательная функция — 1 вариант