|
VI районная научно-исследовательская конференция обучающихся обучающихся общеобразовательных организаций Октябрьского муниципального района |
|
Финансовая математика в задачах ЕГЭ. Решение задач на кредиты |
|
Исследовательская работа по математике |
Автор работы: Кутепова Анна, ученица 10 класса
Руководитель: Моторина Ольга Робертовна, преподаватель математики «МОУ ОСОШ №1»
с. Октябрьское, 2022 г.
СОДЕРЖАНИЕ
Введение 2
Банковские кредиты и математика 4
Схемы решения экономических задач на кредиты 8
- Задача на определение величины выплаты/дифференцированные платежи 8
- Задача на определение ежегодной (ежемесячной) выплаты /аннуитетные платежи 10
- Определение величины процента ставки кредита /долг, убывающий согласно таблице в условие задачи 12
- Задача на определение суммы кредита/аннуитетные платежи 14
- Нахождение количества лет (месяцев) выплаты кредита /дифференцированные платежи 16
Заключение 20
Список информационных источников 22
Введение
В современном, информационно-развитом мире, встречаются люди, которые не умеют правильно распоряжаться своими финансами и контролировать свои доходы и расходы. В этих случаях необходима финансовая грамотность, ведь благодаря данным знаниям мы сможем не только управлять деньгами, правильно инвестировать свои средства, но также будем в безопасности во время сложных жизненных обстоятельств и не потеряем свои доходы. Наша жизнь сегодня настоятельно требует, чтобы каждый человек имел развитое экономическое мышление и был готов к жизни в условиях рыночных отношений. Финансовая грамотность необходима при решении экономических задач в ЕГЭ профильного уровня по математике. Данные задания проверяют практические навыки применения математики в повседневной жизни, навыки построения и исследования математических моделей.
Учащиеся при подходе к итоговой аттестации в 9-х и 11-х классах сталкиваются с проблемой решения задач на проценты, а они есть и в ОГЭ и в ЕГЭ. На данный момент я являюсь ученицей 10 класса. В следующем году мне предстоит сдать ЕГЭ. Я уже ознакомлена с заданиями данного экзамена и знаю, что среди них есть задачи экономической направленности повышенного уровня сложности, которые в курсе старшей общеобразовательной школы не рассматриваются. Для меня стал актуален вопрос о том, каким образом подойти к решению таких задач. Кроме того я выбрала эту тему еще и потому, что в 7 классе мной был выполнен проект «Сам себе финансист: проценты и скидки».В этой исследовательской работе я хочу углубить и расширить свои знания в области финансовой математики. На выбор темы повлияло и то, что в будущем я планирую поступить на экономический факультет ВУЗа.
Тема моей работы: Финансовая математика в экономических задачах ЕГЭ. Решение задач на кредиты.
Гипотеза: Не смотря многообразие типов экономических задач профильного экзамена по математике, их можно классифицировать и вывести единую схему решения.
Цель работы: Изучить основные типы экономических задач на кредиты ЕГЭ по профильной математике и научиться их решать.
Задачи:
- Изучить теоретические аспекты решения экономических задач;
- Познакомиться с прототипами экономических задач, представленных в открытом банке заданий ЕГЭ;
- Создать обучающую презентацию по различным типам задач на кредиты.
Объект исследования: Экономические задачи на кредиты №15 в ЕГЭ.
Предмет исследования: Схемы и алгоритмы решения задач на кредиты.
Методы исследования:
- Изучение и анализ литературы и интернет-источников по данной теме.
- Математическое моделирование
- Классификация
- Анализ
Банковские кредиты и математика
Финансовая математика – раздел прикладной математики, имеющий дело с математическими задачами, связанными с экономическими расчётами.
В единый государственный экзамен по математике (ЕГЭ) профильного уровня экономические задачи были включены в 2015 г. Это задания высокого уровня сложности с практическим содержанием, проверяющее навыки применения математики в повседневной жизни, навыки построения и исследования математических моделей.
Экономические задачи предполагают:
- Умение работать с процентами, частями и долями.
- Владение понятием «Математическая модель».
- Умение строить математическую модель задачи.
- Владение вычислительными навыками.
- Умение применять математические методы для решения содержательных задач из различных областей науки и практики.
- Умение интерпретировать полученный результат, учитывать реальные ограничения.
Экономические задачи под номером 15 в ЕГЭ по профильной математике делятся на три основные группы:
- Задачи на кредиты.
- Задачи на вклады и ценные бумаги.
- Задачи на оптимальный выбор.
Данную работу я посвятила разбору примеров задач первого типа.
Банковский кредит – денежная сумма, предоставляемая банком на определённый срок и на определённых условиях; определённая технология удовлетворения заявленной заёмщикомфинансовой потребности.
Потребность в кредите возникает при оплате значительныхпо стоимости объектов потребления без предварительного накопления достаточных ресурсов, необходимости обеспечения своевременных платежей по товарам, приобретенным в рассрочку, оплате эксклюзивных покупок случайного характера, кассовых разрывах при замене старых объектов потребления на новые, покрытии потерь при наступлении рисков, оплате значительных расходов и т. д.
Понимание и структурирование данных условия задачи – важный шаг на пути правильного ее решения. Для упорядочивания данных условия задачи я использовала таблицы, хотя это и не единственный способ решения 15-го задания, можно использовать и другие методы: последовательности, прикладные методы. Метод решения текстовых задач с помощью таблиц универсальный, знаком каждому школьнику. С помощью таблицможно выработать единый алгоритм решения большинства банковских задач.
В решениях, представленных в работе задач,мною будут использоваться следующие обозначения:
выплатить кредит
Кредитные операции играют основную роль в деятельности банков. Экономические задачи, конечно, несколько упрощают реальную ситуацию, в жизни банковские операции по кредитам значительно сложнее, тем не менее, именно они дают начальные представления о действиях в мире финансов. При решении экономических задач не обойтись без вычисления процентов, при этом используются «простые» и «сложные проценты». Задачи простые проценты изучаются в школьном курсе математике и включены в тестовую часть заданий профильного экзамена. Вычислять же «сложные проценты» приходится в тех случаях, когда в задаче идет речь о величине, подверженной поэтапному изменению. При этом каждый раз ее изменениесоставляет определенное число процентов от значения, которое эта величина имела на предыдущем этапе.Существуют разные формулы, по которым происходит вычисление сложных процентов. При выдаче кредитов на срок n проценты могут, например, начисляться по формуле:

Проанализировав условия задач на кредиты профильного ЕГЭ, я обнаружила, что классифицировать задачи можно разными способами:
- По типу ежемесячных (ежегодных) платежей.
- Разделить на простые (используется одна формула) или сложные (применяются несколько формул, используются системы, неравенства).
- По неизвестной величине, которую требуется найти в условии (процентной ставке, величине выплаты, суммы кредита и др.)
По типу платежей задачи ЕГЭ задачами самыми распространенными являются задачи на фиксированный, аннуитетный и дифференцированный платежи.
Фиксированный платеж – это платеж, величина которого четко определена в задаче.
Аннуитетный платеж– это платеж, которыйустанавливается в равной сумме через равные промежутки времени, то есть остаётся постоянным на всём периоде кредитования. Ежемесячный платёж, при аннуитетной схеме погашения кредита состоит из двух частей. Первая часть платежа идёт на погашение процентов за пользование кредитом, авторая часть идёт на погашение суммы долга. Главная особенность таких платежей в том, что вначале ежемесячный платеж практически полностью состоит из суммы процентов, тогда как основной долг заемщика не уменьшается. Постепенно это соотношение выравнивается: если первое времязаемщик гасит в основном проценты, то потом основные средства идут в счет погашения задолженности.
Дифференцированный платеж – это способ ежемесячного платежа по кредиту, при котором размер ежемесячной выплаты по погашению кредита постепенно уменьшается к концу периода кредитования. Ежемесячный платёж, как и при аннуитетной схеме погашения кредита, складывается тоже из двух составляющих. Но в дифференцированной схеме первая часть называется основным платежом, размер которого не изменяется на всём сроке кредитования. Этот платёж идет на погашение основного долга по кредиту. Вторая часть платежа непостоянная, она уменьшается к концу срока кредитования. Данная часть платежа при дифференцированной схеме идет на погашение процентов по кредиту. При дифференцированной схеме погашения кредита, ежемесячный платеж рассчитывается как сумма основного платежа и проценты, начисляемые на оставшийся размер долга. Естественно, что оставшийся размер долга уменьшается к концу срока кредитования, отсюда и получается уменьшение размера ежемесячной выплаты.
Схемы решения экономических задач на кредиты
В практической части своей работы я представляюпримеры решений нескольких задач на кредиты. Это задачи на нахождение: процентной ставки, суммы долга, суммы переплаты, ежегодных (ежемесячных, еженедельных т.д.) выплат, определения срока кредитования.
-
Задача на определение величины выплаты
/дифференцированные платежи
15-го января планируется взять кредит в банке на сумму 2,4 млн. рублей на 24 месяца. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;
– со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.
Какую сумму нужно выплатить банку в первые 12 месяцев?
Решение:
Фраза «15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца» — это означает, что каждый месяц мы должны выплачивать часть начального долга 

|
№ мес. |
Начальная сумма, млн. руб. |
Сумма начисленных процентов, млн. руб. |
Выплата, млн. руб. |
Конечная сумма, млн. руб. |
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
24 |
… |
… |
… |
0 |
Первая сумма 



Ответ: 1 866 000 рублей
Примеры задач банка ЕГЭ на определение величины выплаты:
1. В июле планируется взять кредит в банке на сумму 28 млн. рублей на некоторыйсрок (целое число лет). Условия его возврата таковы:
– каждый январь долг возрастает на 25% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить часть долга;
– в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июльпредыдущего года.
Чему будет равна общая сумма выплат после полного погашения кредита, если наибольший годовой платёж составит 9 млн. рублей?
2. В июле планируется взять кредит в банке на сумму 9 млн. рублей на некоторый срок(целое число лет). Условия его возврата таковы:
– каждый январь долг возрастает на 25% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить часть долга;
– в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июльпредыдущего года.
Чему будет равна общая сумма выплат после полного погашения кредита, если наименьший годовой платёж составит 1,25 млн. рублей?
-
Задача на определение ежегодной (ежемесячной) выплаты/аннуитетные платежи
В июле планируется взять кредит на сумму 6409000 рублей. Условия его возврата таковы:
— Каждый январь долг возрастает на 12,5% по сравнению с концом предыдущего года.
— С февраля по июнь каждого года необходимо выплатить некоторую часть долга.
Сколько рублей нужно платить ежегодно, чтобы кредит был полностью погашен двумя равными платежами.
Решение:
|
№ года |
Начальная сумма, руб. |
Сумма долга после начисления процентов, руб. |
Выплата, руб. |
Конечная сумма, руб. |
|
1 год |
|
|
x |
|
|
2 год |
|
|
x |
|
Ответ: 3817125 руб.
Примеры задач банка ЕГЭна определение ежегодной (ежемесячной) выплаты:
- В июле планируется взять кредит на сумму 8052000 рублей. Условия его возврата таковы:
– каждый январь долг возрастает на 20% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить некоторую часть долга.
Сколько рублей нужно платить ежегодно, чтобы кредит был полностью погашен четырьмя равными платежами (то есть за 4 года)?
-
Определение величины процента ставки кредита /долг, убывающий согласно таблице в условие задачи
15-го января планируется взять кредит в банке на шесть месяцев в размере 
– 1-го числа каждого месяца долг увеличивается на

– со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей:
|
Дата |
|
|
|
|
|
|
|
|
Долг (млн. руб.) |
|
|
|
|
|
|
|
Найдите наибольшее значение
Решение:
|
|
Начальная сумма, млн. руб. |
Сумма долга после начисления процентов,млн. руб. |
Выплата, млн. руб. |
Конечная сумма,млн. руб. |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Учитывая, что общая сумма выплат меньше 1,2 млн. руб., составим и решим неравенство:
Ответ: 7%
Примеры задач банка ЕГЭна определение величины процента ставки кредита:
- 15-го января планируется взять кредит в банке на шесть месяцев в размере 1 млн. рублей. Условия его возврата таковы:
– 1-го числа каждого месяца долг увеличивается на r процентов по сравнению с концом предыдущего месяца, где r – целое число;
– со 2-го по 14-е число каждого месяца необходимо выплатить часть долга; – 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей.
|
Дата |
15.01 |
15.02 |
15.03 |
15.04 |
15.05 |
15.06 |
15.07 |
|
Долг (в млн. руб.) |
1 |
0,9 |
0,8 |
0,7 |
0,6 |
0,5 |
0 |
Найдите наименьшее значение r, при котором общая сумма выплат будет больше 1,2 млн. рублей.
- В июле планируется взять кредит в банке на сумму 4,5 млн. рублей на срок 9 лет. Условия его возврата таковы:
– каждый январь долг возрастает на r % по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить часть долга;
– в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
Найдите r, если известно, что наибольший годовой платёж по кредиту составит не более 1,4 млн. рублей, а наименьший – не менее 0,6 млн рублей.
-
Задача на определение суммы кредита
/аннуитетные платежи
В июле 2020 года планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:
– каждый январь долг увеличивается на 30% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить одним платежом часть долга.
Сколько рублей планируется взять в банке, если известно, что кредит будет полностью погашен тремя равными платежами (то есть за три года) и общая сумма выплат после полного погашения кредита на 156 060 рублей больше суммы, взятой в кредит?
Решение:
|
№ года |
Начальная сумма, руб. |
Сумма долга после начисления процентов, руб. |
Выплата, руб. |
Конечная сумма, руб. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Определим величину ежегодной выплаты, решив уравнение относительно x:
Известно, что сумма трех выплат на 156060 руб. больше суммы кредита:
Ответ: 239 400руб.
Примеры задач банка ЕГЭна определение суммы кредита:
- В июле 2020 года планируется взять кредит в банке на сумму 419 375 рублей. Условия его возврата таковы:
– каждый январь долг увеличивается на 20% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить одним платежом часть долга.
Сколько рублей будет выплачено банку, если известно, что кредит будет полностью погашен четырьмя равными платежами (то есть за четыре года)?
- В июле 2020 года планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:
– каждый январь долг увеличивается на 10% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить одним платежом часть долга.
Сколько рублей планируется взять в банке, если известно, что кредит будет полностью погашен тремя равными платежами (то есть за три года) и общая сумма выплат после полного погашения кредита на 40 980 рублей больше суммы, взятой в кредит?
-
Нахождение количества лет (месяцев) выплаты кредита/дифференцированные платежи
В июле планируется взять кредит в банке на сумму 5 млн. рублей на некоторый срок (целое число лет). Условия его возврата таковы:
– каждый январь долг возрастает на 20% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить часть долга;
– в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
На сколько лет планируется взять кредит, если известно, что общая сумма выплат после его полного погашения составит 7,5 млн. рублей?
Решение:
«В июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года» — это означает, что каждый год мы должны выплачивать часть начального долга 

|
№ года |
Начальная сумма, руб. |
Сумма долга после начисления процентов, руб. |
Выплата, руб. |
Конечная сумма, руб. |
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
Сложим все платежи, чтобы определить общую сумму выплат по кредиту:
Сложив все слагаемые 


Выражение в скобках – арифметическая прогрессия.Найдём её сумму по формуле:
Подставим полученную сумму в выражение для нахождения общей выплаты:
Вместо буквенных символов подставим известные нам значения величин и найдем n:
Ответ: 4 года
Примеры задач банка ЕГЭна нахождение срокавыплаты кредита:
- В июле планируется взять кредит в банке на сумму 14 млн. рублей на некоторый срок (целое число лет). Условия его возврата таковы:
– каждый январь долг возрастает на 25% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить часть долга; – в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
На сколько лет планируется взять кредит, если известно, что общая сумма выплат после его полного погашения составит 24,5 млн. рублей?
- В июле планируется взять кредит в банке на сумму 16 млн. рублей на некоторый срок (целое число лет). Условия его возврата таковы:
– каждый январь долг возрастает на 25% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить часть долга; – в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
На сколько лет планируется взять кредит, если известно, что общая сумма выплат после его полного погашения составит 38 млн. рублей?
Заключение
Подводя итоги своей работы, целью которой было познакомиться с типами задач с экономическим содержанием и научиться решать задачи на кредиты, я считаю, что мне удалось достичь этой цели, хотя есть еще к чему стремиться, так как предстоит изучить и задачи других видов.
Проанализировав условия и решения банковских задач, я пришла к заключению, что в большинстве случаев схему решения можно использовать таблицу такого вида:
В ходе своего исследования, разбирая примеры задач и решая задачи самостоятельно, я заметила, что:
- Практически все экономические задачи из банка ЕГЭ можно разделить на несколько основных видов
- Решение экономических задач можно выполнять по одному алгоритму, а именно:
- Занести данные условия задачи в таблицу.
- Составить уравнение или неравенство (систему уравнений/неравенств).
- В ходе решения появится формула, с помощью которой будет найден ответ на вопрос задачи.
Моя гипотеза о том, что, несмотря на сложность и многообразие типов экономических задач их можно классифицировать и вывести единую схему решения, подтвердилась. Я убедилась в ее истинности на примере изучения задач на кредиты.Работу по изучению экономических задач буду продолжать и дальше, так как впереди экзамен по профильной математике и, кроме того, считаю, что решение таких задач позволило мне лучше разобраться в базовых понятиях банковских процессов, что будет полезно мне в моей будущей профессии.
Думаю, что эта работа будет полезна ученикам 10 и 11 класса, учителям для подготовки к ЕГЭ профильного уровня по математике. В ходе работы мною была создана презентация с примерами задач на кредиты и их подробными решениями. Эту презентацию можно предложить ребятам для самостоятельной подготовки, кроме решенных примеров она содержит задачи из банка ЕГЭ по математике.
Список информационных источников
- Лукашин Ю.П. Финансовая математика / Московский международный институт эконометрики, информатики, финансов и права. — М., 2003. https://kpsu.ru/upload/medialibrary/606/606fd86fd3cd2272b6f1f3f1b0e4f96c.pdf
- https://ru.wikipedia.org
- https://ege.sdamgia.ru/
- http://fipi.ru/
- Курс лекций по финансовой математике https://lfirmal.com/predmet-finansovaya-matematika/
- Материалы для подготовки к ЕГЭ по математике https://www.time4math.ru/ege
Финансовая математика (задачи ЕГЭ)
- Авторы
- Руководители
- Файлы работы
- Наградные документы
Зырянов Д.А. 1
1Забайкальский краевой лицей-интернат
Ульзутуева С.А. 1
1Забайкальский краевой лицей-интернат
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
Введение
В нашем современном обществе огромную роль играет экономика. Она требует от человека глубоких знаний и умений при работе с массивными числовыми потоками информации. Проценты, вклады, кредиты стали неотъемлемой частью нашей жизни. Подтверждением этому служит то, к примеру, что понятие «процент» широко используется как в реальной жизни, так и в различных областях науки. Без процентов невозможно обойтись ни в финансовом анализе, ни в жизни. Чтобы начислить зарплату работнику необходимо знать процент налоговых отчислений; мы интересуемся размером процентных начислений на сумму вклада, чтобы открыть депозитный счет в банке; чтобы знать приблизительный рост цен в будущем году, мы интересуемся процентом инфляции.
Для того, чтобы развить навыки экономической грамотности, её основы закладываются в школе. Но, особое внимание экономическим задачам уделяется на Едином Государственном Экзамене, где данные задачи представлены в задании №17. Одними из особенностей данных задач является их нестандартность и повышенная сложность решения. Умение эффективно решать задачи на сложные и простые проценты, понимание различия дифференцированных и аннуитетных платежей, а также владение основными теоретическими знаниями в экономике, способствуют правильному решению задач в области экономики на ЕГЭ. Решение многих задач школьного курса, нестандартных задач, практических задач помогает разобраться в новых экономических веяниях жизни.
Исследование данной темы очень важно по нескольким причинам.
Во-первых, я, являюсь учеником старшей школы на физико-математическом профиле, и успешная сдача ЕГЭ для меня приоритетна, что подразумевает под собой умение эффективно решать все типы заданий, в том числе и те, которые связаны с экономикой.
Во-вторых, решение финансовых задач очень полезно, так как вся жизнь современного человека тесно связана с экономическими операциями. Большинство людей в мире совершают банковские операции, вклады, берут кредиты, поэтому рассмотрение данного вопроса поможет не допустить финансовых ошибок в жизни с моей стороны.
Цель проекта: Изучить способы решения экономических задач. Сформировать схемы задач на кредиты и вклады по финансовой математике, показать приемы быстрого счета.
Достижение поставленной цели будет реализовано с помощью решения таких задач как:
Проанализировать научную литературу по данной теме.
Систематизировать все задачи по способам решений.
Разработать наглядные схемы по решению данного вида задач.
Подобрать несколько задач по данным схемам
На основе рассмотренных задач подготовить и создать памятку для учеников по решению данных задач.
Предмет исследования: Способы решения экономических задач ЕГЭ на проценты и вклады.
Объект исследования: Экономические задачи на ЕГЭ.
Целевая аудитория: Ученики 10-11 классов.
Методы:
Теоретический: изучение литературных и Интернет источников, анализ данных, систематизация материала,
Практическая значимость: с помощью составленных схем для учеников старшей школы можно повысить их уровень знания в области задач, связанных с расчётами кредитов, вкладов, подготовку к решению задания № 17, а также увеличить шансы выпускников на хорошую сдачу Единого Государственного Экзамена.
Основная часть
Теоретическая часть
Арифметическая и геометрическая прогрессии
Для того, чтобы начинать разбираться в задании № 17, нужно повторить как арифметическую, так и геометрическую прогрессии, так как они напрямую используются при финансовых расчетах в экономике и применяются в данном задании.
Арифметическая прогрессия
Арифметической называется последовательность, каждый член которой, начиная со второго, равен сумме предыдущего члена и некоторого фиксированного числа d: , где n принадлежит множеству натуральных чисел;
Фиксированным числом d называется разность арифметическом прогрессии;
Формула n-ого члена арифметической прогрессии: ;
Сумма первых n членов в арифметической прогрессии вычисляется по формуле: ;
В арифметической прогрессии каждый ее член, начиная со второго, является средним арифметическим соседних ему членов: .
Геометрическая прогрессия
Геометрической называется последовательность, каждый член которой, начиная со второго, равен произведению предыдущего члена и некоторого фиксированного числа q:, где n принадлежит множеству натуральных чисел;
Фиксированным числом q называется знаменатель геометрической прогрессии;
Формула n-ого члена геометрической прогрессии: ;
Квадрат каждого члена геометрической прогрессии, начиная со второго, равен произведению соседних: ;
Формула суммы первых n членов геометрической прогрессии можно вычислить по формуле: .
Проценты
В математике, в том числе экономических задачах, мы часто сталкиваемся с понятием «процент». Под этим термином подразумевается сотая часть числа. 1%=0,01 А, где А- некоторое число. В данном задании ученикам встречаются несколько видов задач на проценты. Итак, разберемся с методом решения некоторых из них.
I тип задач — нахождение q% от некоторого числа А.
— Число А умножаем на 0,01*q, и получаем искомое число;
II тип задач — нахождение некоторого числа А по его q%, где q%=B.
— Число B делим на 0,01*q, и получаем искомое число;
III тип задач — сколько процентов составляет число А от числа В.
— Делим число А на число В и умножаем на 100%;
IV тип задач — Вычислить число B, если число A меньше него на q%.
— B = A(1+q/100)
V тип задач — Вычислить число B, если число A больше него на q%.
— B = A(1-q/100)
Разберем несколько типовых задач на проценты.
Найти 15% от 80: 80*0,15=12;
Найти A, если 47%равны 94: 94/0,47=200;
Сколько % составляет 78 от 300:78/300*100%=0,26%
Для того, чтобы рационализировать расчеты, важно помнить, что проценты имеют свойство обратимости. То есть q% от числа А равны p% от числа A. К примеру, 10% от 50 равны 50% от 10 (10% от 50 = 5, 50% от 10 = 5).
Вклады: Простые и сложные проценты
Современная экономическая система определяет два способа начисления доходов на вклады: простые и сложные проценты.
Для начала работы с вкладами и процентами, нужно дать определение вкладам, а также процентам: сложным и простым.
Банковский вкладом (или банковским депозитом) называется сумма денег, переданная лицом кредитному учреждению (банку) с целью получения дохода в виде процентов, образующихся в ходе финансовых операций с вкладом.
Простые проценты — метод начисления доходов на вклад, при котором размер вклада увеличивается на одну и ту же сумму, равную определенному количеству процентов от исходного. За один расчетный период, как правило, принимается один год. Если A — исходное количество денег, q процентов годовых – процентная ставка, то по истечении k лет клиент получит сумму .
Формула для нахождения же простого процента напоминает формулу k-того члена арифметической прогрессии c разностью Разность умножается на k, а не на k-1 по той же причине, что будет показана и для сложных процентов.
Теперь следует обратиться к вкладам и второму методу начисления доходов: сложным процентам.
Сложные проценты — это способ начисления процентов, при котором происходит начисление как на исходную сумму, так и на уже начисленные проценты, то есть на прирост. Более полно понять это определение поможет следующий пример.
Пусть клиент положил на счет сумму A0на n периодов, ив конце каждого периода на имеющуюся на счете сумму начисляется q%.Тогда через 1 период на счете окажется сумма
В конце второго периода имеющаяся сумма снова увеличится на q%, то есть
Аналогично в конце третьего периода на счете окажется сумма
Несложно заметить, что появляется определённая закономерность. Выведем общую формулу количества денег на счете клиента по истечении nпрошедших периодов:
Формула, которую мы получили, напоминает формулу нахождения n-ного члена геометрической прогрессии, с той лишь разницей, что знаменатель прогрессии в нашем случае в степени n, а не n-1. Это можно объяснить тем, что сумму, лежащую в самом начале, мы обозначили за , а не за .
Обобщая выше сказанное, необходимо отметить тот неоспоримый факт о том, что начисление сложных процентов на сумму вклада более выгодно клиенту, так как в этом случае сумма вклада будет расти в геометрической прогрессии. Банку же, в свою очередь, более выгодно начисление простых процентов на сумму счёта клиента, так как она будет увеличиваться только лишь в арифметической прогрессии. Все это можно проследить на нижеуказанном рисунке (см. приложение 1).
Кредиты: Аннуитетные и дифференцированные платежи
В современном мире в экономике немаловажную роль играют кредиты. Под определением «кредит» подразумевают заем в банке определенной суммы денег с возвращением долга, а также начисленных на него процентов. В зависимости от способа начисления процентов, выплаты по кредитам осуществляются дифференцированными, либо аннуитетными платежами. В каждом из этих случаев начисление процентов всегда происходит на остаток от долга, то есть методом сложных процентов.
Аннуитетный платеж — способ выплаты по кредиту, при котором сумма выплат делится на равные части (столько, сколько планируется платежей), а сумма одной выплаты состоит из остатка по кредиту и процентов, начисленных на остаток долга. При таком способе погашения основной долг, являющийся телом кредита, при первых платежах практически не погашается, а выплачиваются только проценты.
Дифференцированный платеж — способ выплаты по кредиту, при котором сумма долга клиента делится на равные части (столько, сколько планируется платежей для его выплаты), к каждой из которых прибавляются проценты, начисленные на оставшуюся сумму долга. При этом с каждым разом сумма выплаты уменьшается, а в последний раз клиент платит наименьшую сумму.
Более понятно разъяснить суть разницы двух видов платежей поможет следующий рисунок (см. приложение 2).
Дифференцированные платежи более выгодны клиенту, так как переплата в этом случае для намного меньше, чем в случае выбора клиентом аннуитетной схемы. Но при этом стоит учитывать то, что первые платежи могут оказаться слишком большими для клиента. Кроме того, сумму каждого следующего дифференцированного платежа необходимо отслеживать. Все это делает аннуитетную схему выплат более удобной как для клиента, так и более выгодной для банков, а потому и наиболее популярной.
После того, как мы познакомились с определениями кредита, а также двух типов платежей, разберем схемы решения задач на кредиты:
Пусть A — сумма кредита, x — очередная выплата n — количество платёжных периодов, q — процент по кредиту, начисляемый банком. В нашем случае коэффициент показывает то, во сколько раз увеличивается сумма долга после начисления по нему процентов.
Выплата кредита равными платежами (аннуитетные платежи)
Схема погашения кредита:
Преобразуем выражение:
Применим формулу суммы геометрической прогрессии и получим:
=0.
Схема с дифференцированными платежами (равномерное уменьшение суммы долга по кредиту)
Схема погашения для n платёжных периодов:
1-я выплата:
2-я выплата:
…
n-я выплата:
Посчитаем сумму всех выплат:
Теперь применяем формулу суммы для арифметической прогрессии. Тогда общая сумма выплат равна:
В данном случае Z— величина переплаты,
Практическая часть
Примеры решения задач на аннуитетный платёж
Вклад планируется открыть на четыре года. Первоначальный вклад составляет целое число миллионов рублей. В конце каждого года вклад увеличивается на 10% по сравнению с его размером в начале года, а, кроме этого, в начале третьего и четвёртого годов вклад ежегодно пополняется на 2 млн рублей. Найдите наибольший размер первоначального вклада, при котором через четыре года вклад будет меньше 15 млн рублей.
Решение
Пусть S— первоначальная сумма вклада, а по условию q=10%, k=1,1.
Расчёты, для удобства следует проводить в миллионах рублей: по ранее представленной формуле для аннуитетных платежей получаем:
;
;
;
, следовательно, S=7 миллионов рублей.
Ответ:7 миллионов рублей.
31 декабря 2020 года Максим взял в банке 6 902 000 рублей в кредит под 12,5% годовых. Схема выплат кредита следующая — 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга, то есть увеличивает долг на 12,5%, затем Максим переводит в банк X рублей. Какой должна быть сумма x, чтобы Максим выплатил долг четырьмя равными платежами, то есть за четыре года?
Решение
Данная задача также решается с помощью формулы аннуитетных платежей, так как по условию сказано, что долг выплачивается равными платежами.
Пусть S=6902 тыс. рублей;
Применим формулу геометрической прогрессии:
следовательно,
.
Ответ: 2296350 рублей.
Ольга хочет взять в кредит 100 000 рублей под 10% годовых. Погашение кредита происходит раз в год равными суммами, кроме, может быть, последней, после начисления процентов. На какое минимальное количество лет Ольга может взять кредит, чтобы ежегодные выплаты были не более 24 000 рублей?
Решение
Пусть Оля берет кредит на n лет. Если же последняя выплата по кредиту будет меньше предыдущих, то погасится все тело кредита. Но возьмём, к примеру, что последняя выплата будет всё же равна предыдущим, тогда долг клиента не только погасится полностью, но и станет отрицательным
(на карте останутся некоторые средства). Для удобства будем вести расчёты в тысячах рублей.
.
Тогда следует для такого случая записать неравенство по формуле для расчетов аннуитетного платежа:
Так как в скобках- сумма n членов геометрической прогрессии, то тогда данная сумма равна ;
Тогда: ;
Домножим обе части неравенства на (k-1) и подставим числовые значения:
получаем .
Переведем, округляя до сотых, данную дробь в десятичную и получаем, что ,71.
Теперь, для того, чтобы вычислить значение n, нам необходимо воспользоваться биномом Ньютона, следовательно, и треугольником Паскаля (см. приложение 3).
Выражение есть бином Ньютона и расписывается следующим образом: .
Нам необходимо найти минимальное значение n. Распишем же 1,1 так, чтобы воспользоваться треугольником Паскаля:
Возьмём n=5, тогда ;
Возьмём n=6,тогда .
Следовательно, .
Ответ:6 лет.
Примеры решения задач на дифференцированный платёж
Жанна взяла в банке в кредит 1,8 млн рублей на срок 24 месяца. По договору Жанна должна возвращать банку часть денег в конце каждого месяца. Каждый месяц общая сумма долга возрастает на 1 %, а затем уменьшается на сумму, уплаченную Жанной банку в конце месяца. Суммы, выплачиваемые Жанной, подбираются так, чтобы сумма долга уменьшалась равномерно, то есть на одну и ту же величину каждый месяц. Какую сумму Жанна вернёт банку в течение первого года кредитования?
Решение
Пусть S— первоначальная сумма долга, при этом, .
Для начала нарисуем схему начисления процентов и выплат. Заметим некоторые закономерности:
S … 0
Начисление 1-ая 2-ая посл.
процентов выплата выплата выплата
Sk …
Как обычно, коэффициент показывает то, во сколько раз увеличивается сумма долга после начисления по нему процентов.
Сумма долга уменьшается равными долями, равномерно. Каждая доля равна
.
Тогда первая выплата *S;
Вторая выплата ;
…
Последняя выплата в году равна .
Посчитаем общую сумму всех выплат в течение первого года:
.
Видим, что в первой скобке находится сумма 12 членов арифметической прогрессии, в которой , . Пусть эта сумма равна .
Видим, что во второй скобке аналогично находится сумма 12 членов арифметической прогрессии, в которой , . Пусть эта сумма равна .
Тогда общая сумма выплат за 1 год:
Ответ:1066500 рублей.
Алексей взял кредит в банке на срок 17 месяцев. По договору Алексей должен вернуть кредит ежемесячными платежами. В конце каждого месяца к оставшейся сумме долга добавляется q % этой суммы и своим ежемесячным платежом Алексей погашает эти добавленные проценты и уменьшает сумму долга. Ежемесячные платежи подбираются так, чтобы долг уменьшался на одну и ту же величину каждый месяц (на практике такая схема называется «схемой с дифференцированными платежами»). Известно, что общая сумма, выплаченная Алексеем банку за весь срок кредитования, оказалась на 27 % больше, чем сумма, взятая им в кредит. Найдите q.
Решение
Применим формулу для задач с дифференцированными процентами, выведенной в теоретической части.
Пусть на n платежных периодов в кредит взята сумма S, но при этом имеем то, что платежи подобраны таким образом, что сумма долга уменьшается равномерно. Тогда величина переплаты F и полная сумма выплат G за все время выплаты кредита представлены формулами:
; .
Применяя формулу к данной задаче, получаем (величина переплаты)
.
Ответ: q=3.
В июле 2016 года планируется взять кредит в банке на четыре года в размере S млн рублей, где S — целое число. Условия его возврата таковы:
— каждый январь долг увеличивается на 15% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей.
|
Месяц и год |
Июль 2016 |
Июль 2017 |
Июль 2018 |
Июль 2019 |
Июль 2020 |
|
Долг (в млн рублей) |
S |
0,8S |
0,5S |
0,1S |
0 |
Решение
В данной задаче .
Составим схему выплат для дифференцированных платежей:
Год 2016 2017 2018 2019 2020
Июль S 0
1-ая 2-ая 3-я 4-ая
процентов выплата Х1 выплата Х2 выплата Х3 выплата Х4
ЯнварьkS …
Общая сумма X выплат:
.
По условию S— целое число, а . Для удобства произведем расчеты в миллионах рублей.
, значит
Ответ: 29 млн. рублей
Заключение
Цели исследования достигнуты. В данной работе были показаны основные методы решения задач на кредиты, вклады. Тема исследования остается актуальной по причине того, что все рассматриваемые задачи взяты из материалов по подготовке к ЕГЭ по математике «Профиль».
Исследование и рассмотрение задания №17 ЕГЭ показало, что отличное знание теоретического аспекта темы, умение оперировать этими знаниями, позволяют решать задачи повышенной сложности из Единого Государственного Экзамена по теме «Экономические задачи» ученикам старшей школы.
Также, для успешного решения таких задач, необходимо отработать аппарат стандартных вычислений, так как все экономические задачи направлены на серьёзные вычисления. Экономические задачи – это не просто задачи из математики, это часть нашей жизни в современном мире. Умение их решать будет полезно в будущем, как для проверки банковских операций при оформлении кредитов или вкладов, так и в простых жизненных ситуациях, что поможет не совершать мелких и фатальных ошибок.
Составленные схемы по решению задач (см. приложение 4) помогут разобраться и справиться с заданием, посвященным экономике в ЕГЭ, как старшеклассникам, сдающим экзамен в этом году, так и ученикам девятых и десятых классов.
Библиографический список
https://ru.wikipedia.org/wiki/Аннуитет;
https://ru.wikipedia.org/wiki/Дифференцированный_платёж;
https://math-ege.sdamgia.ru/test?theme=293;
https://math-ege.sdamgia.ru/test?theme=292.
Математика: задания высокой и повышенной сложности/ A. Г. Малкова — Изд. 2-е — Ростов н/Д: Феникс, 2019. — 221, с.: ил. — (ЕГЭ. Высший балл).
Приложения
Приложение 1
Приложение 2
Приложение 3
Треугольник Паскаля
Приложение 4
Общие схемы решения задач ЕГЭ задания №17
(аннуитетные и дифференцированные платежи)
A — сумма кредита;
x — очередная выплата;
n — количество платёжных периодов;
q — процент по кредиту, начисляемый банком;
коэффициент показывает то, во сколько раз увеличивается сумма долга после начисления по нему процентов.
Схема выплат кредита равными платежами (аннуитетные платежи)
=0.
Схема с дифференцированными платежами (равномерное уменьшение суммы долга по кредиту)
V— величина переплаты,
Просмотров работы: 1061
4 декабря 2020
В закладки
Обсудить
Жалоба
Финансовая математика в задачах ЕГЭ
В данном проекте «Финансовая математика в задачах ЕГЭ» разработаны алгоритмы решения задач №17 ЕГЭ на банковские вклады, кредиты и проценты. Задачи выбраны из Открытого банка заданий.
Подбор задач:
а) на банковские вклады;
б) выплата банковских кредитов по различным схемам;
в) выбор более выгодных условий кредитования.
fin-m.docx
fin-m.pdf
ПРОЕКТ ПО МАТЕМАТИКЕ
«50 ЭКОНОМИЧЕСКИХ ЗАДАЧ»
Выполнила: Позднякова Полина,
ученица 11 «А» класса
МБОУ Щёлковский лицей №7.
Руководитель: Позднякова Ольга Вячеславовна.
2018 год
2
Оглавление
1. Введение ……………………………………………………………………………………….. 3
2. Теория
2.1 Проценты ………………………………………………………………………………… 5
2.2 Платежи ………………………………………………………………………………….. 5
2.3 Таблицы …………………………………………………………………………………. 5
2.4 Арифметическая и геометрическая прогрессии ………………………… 7
2.5 Производная ……………………………………………………………………………. 8
3. Практическое решение экономических задач
3.1 Кредиты
1 тип: Нахождение количества лет (месяцев) выплаты кредита.
(Аннуитетные платежи) ………………………………………………………………. 10
2 тип: Вычисление процентной ставки по кредиту. (Фиксированные
платежи) ……………………………………………………………………………………… 13
3 тип: Нахождение суммы кредита. (Аннуитетные платежи) ………… 16
4 тип: Нахождение ежегодного ( ежемесячного)
транша.(Аннуитетные платежи) …………………………………………………… 19
5 тип: Нахождение разницы. (Аннуитетные платежи) ………………….. 22
6 тип: Задачи, связанные с известным остатком. (Фиксированные
платежи) ……………………………………………………………………………………… 25
7 тип: Задачи, связанные с дифференцированными платежами …….. 28
8 тип: Нестандартные задачи, связанные с кредитом ……………………. 32
3.2 Вклады …………………………..………………………………………………………. 36
3.3 Задачи на оптимизацию ………………………………………………………….. 44
3.4 Нестандартные задачи ……………………………………………………………. 56
4.Заключение ……………………………………………………….…………………………. 61
5.Список литературы ……………………………………………………………………….. 61
3
1. Введение
Экономическую задачу ввели в экзамен ЕГЭ «Профиль по математике» только
с 2015 года. Она стала называться заданием номер 17 и по своей сложности
находится на одном уровне с заданиями на параметры и теорию чисел.
Приведу примеры статистики сдачи ЕГЭ по математике (профильный
уровень) за 2016 и 2017 годы (использовала данные с сайта ФИПИ)
Набрали
ненулевой
балл (от
сдавших
экзамен
учащихся)
Набрали
ненулевой
балл (от
всех
учащихся)
Набрали
максимальный
балл (от
сдавших
экзамен
учащихся)
Набрали
максимальный
балл (от всех
учащихся)
Такая статистика решения экономической задачи объясняется и сложностью
задания и просто тем, что такой темы просто нет в наших учебниках по алгебре.
Поэтому у меня и появилась идея написать методичку «50 экономических задач для
подготовки к сдаче ЕГЭ «Профиль по математике»», целью которой является
подготовка учащихся к ЕГЭ.
Конечно, на различных сайтах и в математической литературе можно найти
решения таких задач, но зачастую либо они содержат много лишней информации,
либо они решены непонятным для меня способом. Я же использовала табличный
метод, так как считаю его самым наглядным и простым.
4
Из необходимых знаний и умений мне понадобились:
1) Определение понятия «Процент»
2) Определение понятий «Фиксированные платежи», «Аннуитетные платежи» и
«Дифференцируемые платежи».
3) Виды мною созданных таблиц
4) Определение, формулы n-ого члена и суммы n первых членов арифметической
и геометрической прогрессий
5) Знание алгоритмов нахождения промежутков возрастания (убывания)
функций и точек экстремума.
Каждую неделю, начиная с сентября 2016 года, я решала по две
экономических задачи. Условия таких задач я брала:
1. ЕГЭ 2018 под редакцией А. Л. Семенова, И.В. Ященко
2. Открытый банк заданий ЕГЭ fipi.ru
3. Сайт «Решу ЕГЭ»
4. И мой любимый сайт «Алекс Ларин»
Всего я решила примерно 152 задачи, выбрала из них 50 задач, разделив их
условно на типы:
Кредиты.
1 тип: Нахождение количества лет (месяцев) выплаты кредита.
(Аннуитетные платежи) — 3 задачи
2 тип: Вычисление процентной ставки по кредиту. (Фиксированные платежи)
– 3 задачи
3 тип: Нахождение суммы кредита. (Аннуитетные платежи)— 3 задачи
4 тип: Нахождение ежегодного (ежемесячного) транша. (Аннуитетные
платежи)— 3 задачи
5 тип: Нахождение разницы. (Аннуитетные платежи) – 3 задачи
6 тип: Задачи, связанные с известным остатком. (Фиксированные платежи)— 3
задачи
7 тип: Задачи, связанные с дифференцированными платежами.— 3 задачи
8 тип: Нестандартные задачи, связанные с кредитом.— 4 задачи
Вклады. – 8 задач
Задачи на оптимизацию. —12 задач
Нестандартные задачи.-5 задач
Конечно, наиболее трудными среди экономических задач считаются задачи на тему
«Оптимизация» и нестандартные задачи с сайта «Алекс Ларин».
5
2.Теория.
Решение финансовых задач основывается на использовании различных
математических моделей: уравнений, неравенств, их систем с привлечением
процентов, арифметической и геометрической прогрессий и производной.
Приведу основные определения, понятия, таблицы и формулы.
2.1 Проценты.
Определение: один процент – это одна сотая доля. Чтобы найти данное число
процентов от числа, нужно проценты записать десятичной дробью, а затем число
умножить на эту десятичную дробь.
Пример: 5% от 80 это будет 0,05
r% от 14 это будет 0,01r
При решении задач необходимо понимать механизм начисления процентов по
вкладам или кредитам. Например, если банк выдаёт кредит (S) клиенту, то через год
клиент должен банку не только сумму кредита, но и некий процент (r). Возникает
необходимость введения нового коэффициента b, b=1+0,01r. С учётом этого , долг
клиента банку через год можно записать следующим образом:
S + r% от S = S + 0,01r = S (1 + 0,01r) = bS
2.2 Платежи.
В задачах по теме «Кредит» используют о три основных вида платежа:
1. Фиксированные платежи (платежи, которые чётко оговариваются в
условии задачи)
2. Аннуитетные платежи (постоянные ежемесячные или ежегодные
платежи, которые не меняются на протяжении всего периода кредитования)
3. Дифференцируемые платежи (ежемесячные или ежегодные платежи,
уменьшающиеся к концу срока кредитования и обеспечивающие
уменьшение суммы долга на одну и ту же величину)
2.3 Таблицы.
При решении задач, связанных с аннуитетными платежами мне было очень
удобно заполнять следующую таблицу:
S – сумма кредита
r% — годовые (ежемесячные) проценты
6
b=1+0,01r – коэффициент
х – ежегодная (ежемесячная) выплата
(Sb
3
-x b
2
-xb-x)b= Sb
4
-xb
3
—
xb
2
-xb
(Sb
4
-xb
3
-xb
2
-xb-x)b= Sb
5
—
xb
4-
xb
3
-xb
2
-xb
(Sb
5
-xb
4-
xb
3
-xb
2
-xb-x)b=
Sb
6
-xb
5
-xb
4-
xb-
3
xb
2
-xb
Полная выплата, долг
равен 0
При решении задач, связанных с дифференцированными платежами я
использовала следующую таблицу:
7
При решении задач по теме «Вклады»:
При решении задач, в которых осуществлялись какие—либо действия
(пополнение или снятие денег с вклада):
х – действие
2.4 Арифметическая и геометрическая прогрессии.
Арифметическая прогрессия
Определение. Последовательность чисел, в которой каждое следующее отличается
от предыдущего ровно на одну и ту же величину, называется арифметической
прогрессией.
Любой член арифметической прогрессии вычисляется по формуле:
=
+ (n-1)d
Формула суммы n—первых членов арифметической прогрессии
S
n
=
С учётом этой формулы : (n-1) + (n-2) +…+3+2+1 =
=
=
=
=
=
8
Геометрическая прогрессия
Определение. Геометрической прогрессией называется последовательность
отличных от нуля чисел, каждый член которой, начиная со второго, равен
предыдущему члену, умноженному на одно и то же число.
Любой член геометрической прогрессии вычисляется по формуле:
b
n
=b
1
· q
n-1
Формула суммы n—первых членов геометрической прогрессии
S
n
=
Из этой формулы следует: b
n-1
+b
n-2
+…+b
2
+b+1=
2.5 Производная.
Достаточные признаки возрастания и убывания функции:
Если производная данной функции положительна для всех значений х в интервале
(а; в), т.е. f'(x) > 0, то функция в этом интервале возрастает.
Если производная данной функции отрицательна для всех значений х в интервале (а;
в), т.е. f'(x) < 0, то функция в этом интервале убывает
Порядок нахождения промежутков монотонности:
Найти область определения функции.
1. Найти производную функции.
2. Найти критические точки (точки, в которых производная не существует) и
стационарные (точки, в которых производная равна нулю). Исследовать знак
производной в промежутках, на которые найденные точки делят область
определения функции.
Достаточное условие существования максимума состоит в смене знака производной
при переходе через критическую точку с «+» на «—«, а для минимума с «—» на «+».
Если при переходе через критическую точку смены знака производной не
происходит, то в данной точке экстремума нет
Пример:
f(x) =
Найдём производную.
9
=(
)
,
=
=
=
=
Критические точки
= 1,
= -1
Стационарные точки
=
= —
,
= 0
Ответ: возрастает (—
;+
убывает
; —
=
;
=
.
10
3.Практическое решение экономических задач.
3.1 Кредиты.
1 тип: Нахождение количества лет ( месяцев) выплаты кредита.
n-? (Аннуитетные платежи)
Задача №1
Максим хочет взять кредит 1,5 млн рублей. Погашение кредита происходит раз
в год равными суммами ( кроме, может быть, последней) после начисления
процентов. Ставка процента 10% годовых. На какое минимальное количество
лет может Максим взять кредит, чтобы ежегодные выплаты были не более
350 тысяч рублей?
Решение:
Кредит (S) 1500000 руб.
Ставка (r) 10% годовых. Введём коэффициент b=1+0,01r
Ежегодная выплата (х) ≤350000 руб.
Сколько лет (n)-?
11
Задача №2
1 января 2015 года Андрей Владимирович взял в банке 1,1 млн. рублей в кредит.
Схема выплаты кредита следующая: 1 числа каждого следующего месяца банк
начисляет 3% на оставшуюся сумму долга (то есть увеличивает долг на 3%),
затем Андрей Владимирович переводит в банк платеж. На какое минимальное
количество месяцев Андрей Владимирович может взять кредит, чтобы
ежемесячные выплаты были не более 220 тыс. рублей?
Решение.
Кредит (S) 1100000 руб.
Ставка (r) 3% годовых. Введём коэффициент b=1+0,01r
Ежемесячная выплата (х) ≤220000 руб.
Сколько месяцев (n)-?
12
Задача №3.
1 января 2015 года Павел Витальевич взял в банке 1 млн. рублей в кредит. Схема
выплаты кредита следующая: 1 числа каждого следующего месяца банк начисляет
1% на оставшуюся сумму долга (то есть увеличивает долг на 1%), затем Павел
Витальевич переводит в банк платеж. На какое минимальное количество месяцев
Павел Витальевич может взять кредит, чтобы ежемесячные выплаты были не
более 125 тыс. рублей?
Решение.
Кредит (S) 1000000 руб.
Ставка (r) 1% годовых. Введём коэффициент b=1+0,01r
Ежемесячная выплата (х) ≤125000 руб.
Сколько лет –(n)-?
13
2 тип: Вычисление процентной ставки по кредиту.
r-? (Фиксированные платежи)
Задача №1
31 декабря 2014 года Борис взял в банке 1 млн. рублей в кредит. Схема выплаты
кредита следующая: 31 декабря каждого следующего года банк начисляет
проценты на оставшуюся сумму долга ( то есть увеличивает долг на
определенное количество процентов), затем Борис переводит очередной транш.
Борис выплатил кредит за два транша, переводя в первый раз 560 тыс. рублей,
во второй – 661,1 тыс. рублей. Под какой процент банк выдал кредит Борису?
Решение Кредит (S) 1000000 руб.
Введём коэффициент b=1+0,01r
1 год выплата – x
1
=560000руб.
2 год выплата – x
2=
644100 руб.
r-?
Sb
2
-x
1
b=x
2
1000000b
2
-560000b-644100=0
10000b
2
-5600b-6441=0
D=5600
2
+4•10000•6441=31360000+257640000=289000000
b
1
= =1,13
b
2
= =-0,57 не подходит по условию задачи.
b=1+0,01r
r=13
Ответ: 13
14
Задача №2.
31 декабря 2014 года Антон взял в банке 1 млн. рублей в кредит. Схема выплаты
кредита следующая: 31 декабря каждого следующего года банк начисляет
проценты на оставшуюся сумму долга ( то есть увеличивает долг на определенное
количество процентов), затем Антон переводит очередной транш. Антон
выплатил кредит за два транша, переводя в первый раз 510 тыс. рублей, во второй
– 649 тыс. рублей. Под какой процент банк выдал кредит Антону?
Решение:
Кредит (S) 1000000 руб.
Введём коэффициент b=1+0,01r
1 год выплата – x
1
=510000руб.
2 год выплата – x
2=
649000 руб.
r-?
Sb
2
-x
1
b=x
2
1000000b
2
—510000b-649000=0
10000b
2
—5100b-649=0
D=5100
2
+4•10000•649=260100+2596000=2856100
b
1
= =1,1
b
2
= =-0,59 не подходит по условию задачи.
Ответ: r =10
15
Задача№3.
31 декабря 2014 года Арсений взял в банке 1 млн. рублей в кредит. Схема выплаты
кредита следующая: 31 декабря каждого следующего года банк начисляет
проценты на оставшуюся сумму долга ( то есть увеличивает долг на определённое
количество процентов), затем Арсений переводит очередной транш. Арсентий
выплатил кредит за два транша, переводя в первый раз 550 тыс. рублей, во второй
– 638,4 тыс. рублей. Под какой процент банк выдал кредит Арсению?
Решение:
Кредит (S) 1000000 руб.
Введём коэффициент b=1+0,01r
1 год выплата – x
1
=550000руб.
2 год выплата – x
2=
638400 руб.
r-?
Sb
2
-x
1
b=x
2
1000000b
2
-550000b-638400=0
10000b
2
-5500b-6384=0
D=5500
2
+4•10000•6384=30250000+255360000=285610000
b
1
= =1,12
b
2
= =-0,57 не подходит по условию задачи.
Ответ: r=12.
16
3 тип: Нахождение суммы кредита.
S-? (Аннуитетные платежи)
Задача №1.
31 декабря 2014 года Сергей взял в банке некоторую сумму в кредит под 12%
годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего
года банк начисляет проценты на оставшуюся сумму долга ( то есть
увеличивает долг на 12%), затем Сергей переводит в банк 3512320 рублей. Какую
сумму взял Сергей в банке, если он выплатил долг тремя равными платежами (
то есть за три года)?
Решение:
Ставка (r) — 12% , b=1,12
Ежегодная выплата (х) — 3512320 рублей
Количество лет (n) 3 года
Сумма кредита (S) —?
Sb
3_
хb
2
—xb =x
Sb
3
-(1+b+b
2
)x=0
S=
Ответ: 8436000рублей.
рублей
b
xbb
8436000
404928,1
3744,33512320
404928,1
)2544,112,11(3512320)1(
3
2
=
•
=
++•
=
++
17
Задача №2.
31 декабря 2014 года Игорь взял в банке некоторую сумму в кредит под 13%
годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года
банк начисляет проценты на оставшуюся сумму долга ( то есть увеличивает долг
на 13%), затем Игорь переводит в банк 5107600 рублей. Какую сумму взял Игорь в
банке, если он выплатил долг двумя равными платежами ( то есть за два года)?
Решение:
Ставка (r) — 13%, b=1,13
Ежегодная выплата (х) — 5107600 рублей
Количество лет (n) 2 года
Сумма кредита (S) —?
Sb
2
-xb=x
Sb
2
-(1+b)x=0
S=
Ответ: 8520000 рублей.
рублей
b
bx
8520000
2769,1
13,25107600
13,1
)13,11(5107600)1(
22
=
•
=
+•
=
+
18
Задача№3.
31 декабря 2014 года Михаил взял в банке некоторую сумму в кредит под 10%
годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего
года банк начисляет проценты на оставшуюся сумму долга ( то есть
увеличивает долг на 10%), затем Михаил переводит в банк 2928200 рублей.
Какую сумму взял Михаил в банке, если он выплатил долг четырьмя равными
платежами ( то есть за четыре года)?
Решение:
Ставка (r) — 10%
b=1,1
Ежегодная выплата (х) — 2928200 рублей
Количество лет (n) 4 года
Сумма кредита (S) -?
(Sb
3
-x b
2
-xb-x)b= Sb
4
-xb
3
—
xb
2
-xb
Полная выплата —
остаток 0
Sb
4
-xb
3
-xb
2
-xb =x
Sb
4
-(1+b+b
2+
b
3
)x=0
S=
Ответ: 9282000 рублей.
9282000
1,1
)1,11,11,11(*2928200)1(
4
32
4
32
=
+++
=
+++
b
bbbx
19
4 тип: Нахождение ежегодного ( ежемесячного) транша.
х-? (Аннуитетные платежи)
Задача №1.
31 декабря 2014 года Алексей взял в банке 9282000рублей в кредит по 10% годовых.
Схема выплат кредита следующая: 31 декабря каждого следующего года банк
начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на
10%), затем Алексей переводит в банк Х рублей. Какой должна быть сумма Х,
чтобы Алексей выплатил долг четырьмя равными платежами ( то есть за четыре
года)?
Решение:
Сумма кредита (S)- 9282000рубля
Ставка (а)=10%, b=1,1
Количество лет (n) 4 года
Ежегодная выплата ( транш) Х -?
(Sb
3
-x b
2
—xb-x)b= Sb
4
—xb
3
—
xb
2
—xb
Полная выплата —
остаток 0
Sb
4
—xb
3
—xb
2
-xb =x
Sb
4
-(b+b
2
+b
3
)x=x
Sb
4
-(1+b+b
2
+b
3
)x=0
X=
X=
Ответ: 2928200 рублей.
рублей2928200
641,4
4641,19282000
331,121,11,11
4641,19282000
1,11,11,11
1,19282000
32
4
=
•
=
+++
•
=
+++
•
20
Задача №2.
31 декабря 2014 года Иван взял в банке 4230000 рублей в кредит по 11,5% годовых.
Схема выплат кредита следующая: 31 декабря каждого следующего года банк
начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на
11,5%), затем Иван переводит в банк Х рублей. Какой должна быть сумма Х,
чтобы Иван выплатил долг двумя равными платежами ( то есть за два года)?
Сумма кредита (S)- 4230000рубля
Ставка (а)=11,5%, b=1,115
Количество лет (n) 2 года
Ежегодная выплата ( транш) Х -?
Sb
2
-xb=x
Sb
2
-(1+b)x=0
X=
X=
Ответ: 2486450рублей.
рублей2486450
115,2
243225,14230000
115,11
115,14230000
2
=
•
=
+
•
21
Задача №3.
31 декабря 2014 года Павел взял в банке 6327000 рублей в кредит по 12%
годовых. Схема выплат кредита следующая: 31 декабря каждого следующего
года банк начисляет проценты на оставшуюся сумму долга (то есть
увеличивает долг на 12%), затем Павел переводит в банк Х рублей. Какой
должна быть сумма Х, чтобы Павел выплатил долг тремя равными платежами
( то есть за три года)?
Решение:
Сумма кредита (S)- 6327000 рубля
Ставка (а)=12%,b=1,12
Количество лет (n) 3 года
Ежегодная выплата ( транш) Х -?
Sb
3_
хb
2
—xb =x
Sb
3
—(b
2
-b)x=x
Sb
3
-(1+b+b
2
)x=0
X= =
Ответ: 2634240 рублей.
2634240
112,112,1
12,1*632700
2
3
=
++
22
5 тип: Нахождение разницы. (Аннуитетные платежи)
Задача №1.
31 декабря 2014 года Федор взял в банке 6951000рублей в кредит под 10% годовых.
Схема выплат кредита следующая: 31 декабря каждого следующего года банк
начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на
10%), затем Федор переводит в банк платеж. Весь долг Федор выплатил за 3
равных платежа. На сколько рублей меньше он бы отдал банку, если бы смог
выплатить долг за 2 равных платежа?
Решение: Сумма кредита (S) – 6951000 рублей
Ставка (r) —10%, b=1,1
3 равных платежа
Sb
3
— хb
2
—xb=x
Sb
3
-(b
2
+b+1)x=0
X=
2 равных платежа
Sb
2
-xb=x
Sb
2
-(1+b)x=0
X=
За три года: 2795100 3=8385300
За два года:4005100 2=8010200
Разница: 8385300-8010200=375100
Ответ: на 375100 рублей.
2795100
31,3
331,16951000
11,11,1
331,16951000
1
22
3
=
•
=
++
•
=
++ bb
Sb
4005100
1,2
21,16951000
1,11
1,16951000
1
22
=
•
=
+
•
=
+ b
Sb
23
Задача №2.
31 декабря 2014 года Степан взял в банке 4004000 рублей в кредит под 20%
годовых. Схема выплат кредита следующая: 31 декабря каждого следующего года
банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг
на 20%), затем Степан переводит в банк платеж. Весь долг Степан выплатил за 3
равных платежа. На сколько рублей меньше он бы отдал банку, если бы смог
выплатить долг за 2 равных платежа?
Решение: Сумма кредита (S) – 4004000 рублей
Ставка (r) —20%, b=1,2
3 равных платежа
Sb
3
—хb
2
—xb=x
Sb
3
-(b
2
+b+1)x=0
X=
2 равных платежа
Sb
2
-xb=x
Sb
2
-(1+b)x=0
X=
За 3 года выплатил: 3*1900800=5702400
За два года: 2*2620800=5241600
Разница: 5702400-5241600=460800
Ответ: 460800 рублей.
1900800
12,144,1
728,1*4004000
12,12,1
2,1*4004000
1
2
3
2
3
=
++
=
++
=
++ bb
Sb
2620800
12,1
2,1*4004000
1
22
=
+
=
+b
Sb
24
Задача №3.
31 декабря 2014 года Алексей взял в банке 3689000 рублей в кредит под 12,5%
годовых. Схема выплат кредита следующая: 31 декабря каждого следующего года
банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг
на 12,5%), затем Алексей переводит в банк платеж. Весь долг Алексей выплатил за
3 равных платежа. На сколько рублей меньше он бы отдал банку, если бы смог
выплатить долг за 2 равных платежа?
Решение: Сумма кредита (S) – 3689000 рублей
Ставка (r) -12,5%, b=1,125
3 равных платежа
Sb
3
—хb
2
—xb=x
Sb
3
-(b
2
+b+1)x=0
X=
2 равных платежа
Sb
2
-xb=x
Sb
2
-(1+b)x=0
X=
За три года: 1549125 3=4647375
За два года:2197125 2=4394250
Разница: 4647375-4394250=253125
Ответ: 253125 рублей.
1549125
1125,1125,1
125,1*3689000
2
3
=
++
2197125
1
8
1
1
)
8
1
1(*3689000
1
2
2
=
+
=
+b
Sb
25
6 тип: Задачи, связанные с известным остатком. (Фиксированные платежи)
Задача №1.
15—го января был выдан полугодовой кредит на развитие бизнеса. В таблице
представлен график его погашения.
Долг (в процентах от кредита)
В конце каждого месяца, начиная с января, текущий долг увеличивался на 5%, а
выплаты по погашению кредита происходили в первой половине каждого месяца,
начиная с февраля. На сколько процентов общая сумма выплат при таких условиях
больше суммы самого кредита?
Решение: S – сумма кредита
r% — годовые (ежемесячные) проценты (5%)
b=1+0,01r – коэффициент (1,05)
Полная выплата —
остаток 0
Общая сумма выплат:
(Sb+0,9Sb+0,8Sb+0,7Sb+0,6Sb+0,5Sb)-(0,9S+0,8S+0,7S+0,6S+0,5S)=
4,5Sb-3,5S=S(4,5b-3,5)=S(4,5*1,05-3,5)=1,225S
Ответ: 22,5 процента.
26
Задача №2.
15—го января планируется взять кредит в банке на 1 млн рублей на 6 месяцев.
Условия его возврата таковы:
− 1-го числа каждого месяца долг возрастает на целое число r процентов по
сравнению с концом предыдущего месяца;
− со 2—го по 14—е число каждого месяца необходимо выплатить часть долга;
− 15—го числа каждого месяца долг должен составлять некоторую сумму в
соответствии со следующей таблицей
Найдите наибольшее значение r, при котором общая сумма выплат будет
составлять менее 1,2 млн рублей.
Решение: S – сумма кредита (1000000рублей)
Найти : r% — годовые (ежемесячные) проценты
b=1+0,01r – коэффициент
Полная выплата —
остаток 0
Общая сумма выплат:
(Sb+0,6Sb+0,4Sb+0,3Sb+0,2Sb+0,1Sb)-(0,6S+0,4S+0,3S+0,2S+0,1S)=
2,6Sb-1,6S=S(2,6b-1,6)=1*(2,6b-1,6)=2,6b-1,6
2,6b-1,6<1,2 ; 2,6b<2,8 ; b<1,076 ; b=1,07 ; r=7
Ответ: 7 процентов.
27
Задача №3.
В июле 2016 года планируется взять кредит в банке в размере S тыс. рублей,
где S — натуральное число, на 3 года. Условия его возврата таковы
− каждый январь долг увеличивается на 15% по сравнению с концом предыдущего
года;
− с февраля по июнь каждого года необходимо выплатить одним платежом часть
долга;
− в июле каждого года долг должен составлять часть кредита в соответствии со
следующей таблицей.
Найдите наименьшее значение S, при котором каждая из выплат будет
составлять целое число тысяч рублей.
Решение: S – сумма кредита
r% — годовые (ежемесячные) проценты (15%)
b=1+0,01r – коэффициент (1,15)
Полная выплата —
остаток 0
1 выплата 1,15S-0,7S= 0,45S=
2 выплата 0,7*1,15S-0,4S= 0,405S=
3 выплата 0,4*1,15S= 0,46S=
По условию, все выплаты должны быть целыми. Значит, число S должно делиться
на 20, 200 и 50. Наименьшее общее кратное этих чисел равно 200.
Ответ: 200 тысяч.
28
7 тип: Задачи, связанные с дифференцированными платежами.
Задача №1.
Алексей взял кредит в банке на срок 12 месяцев. По договору Алексей должен
вернуть кредит ежемесячными платежами. В конце каждого месяца к оставшейся
сумме долга добавляется r % этой суммы и своим ежемесячным платежом
Алексей погашает эти добавленные проценты и уменьшает сумму долга.
Ежемесячные платежи подбираются так, чтобы долг уменьшался на одну и ту же
величину каждый месяц (на практике такая схема называется «схемой с
дифференцированными платежами»). Известно, что общая сумма, выплаченная
Алексеем банку за весь срок кредитования, оказалась на 13 % больше, чем сумма,
взятая им в кредит. Найдите r.
Решение: Сумма кредита (S), ставка (r) —? %, b=1+0,01r
29
Sb(1+
)-S
)=1,13S
—
=1,13S /S
—
=1,13
78b=1,13*12+66
b=1,02
r=2%
Ответ:2%.
Задача 2.
15 января планируется взять кредит в банке на 9 месяцев. Условия его возврата
таковы:
— 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом
предыдущего месяца;
— со 2—го по 14—е число каждого месяца необходимо выплатить часть долга;
— 15—го числа каждого месяца долг должен быть на одну и ту же величину меньше
долга на 15—е число предыдущего месяца.
Известно, что на пятый месяц кредитования нужно выплатить 57,5 тыс. рублей.
Какую сумму нужно вернуть банку в течение всего срока кредитования?
Решение: Сумма кредита (S)
Ставка (r) -3 %, b=1,03 n=9 Сумма всех выплат =?
=57,5
5Sb-4S=517,5
S(5b-4)=517,5
S(5*1,03-4)=517,5
S=450
Sb(1+
)-S
)=5Sb-4S=
450*(5*1,03-4)=450*1,15=517,5
Ответ:517,5 тысяч.
Задача 3.
15—го января планируется взять кредит в банке на несколько месяцев. Условия его
возврата таковы:
— 1-го числа каждого месяца долг возврастает на 5% по сравнению с концом
предыдущего месяца;
— со 2—го по 14—е число месяца необходимо выплатить часть долга;
— 15—го числа каждого месяца долг должен быть на одну и ту же сумму меньше
долга на 15—е число предыдущего месяца.
На сколько месяцев можно взять кредит, если известно, что общая сумма выплат
после полного погашения кредита на 25% больше суммы, взятой в кредит. (решение
с помощью формулы суммы арифметической прогрессии)
Решение: Сумма кредита (S) , ставка (r) -5 %, b=1,05 n=?
Sb(
)-S
)=1,25S
По формуле суммы арифметической прогрессии получаем
Sb*
— S*
=1,25S /S
b*
—
=1,25
1,05*(n+1)-(n-1)=2,5
1,05n+1,05-n+1=2,5
0,05n=0,45
n=9
Ответ: 9 месяцев.
32
8 тип: Нестандартные задачи, связанные с кредитом.
Задача 1.
В июле 2016 года планируется взять кредит в размере 6,6 млн. руб. Условия
возврата таковы:
— каждый январь долг возрастает на r% по сравнению с концом предыдущего года.
— с февраля по июнь необходимо выплатить часть долга.
— в июле 2017, 2018 и 2019 годов долг остается равным 6,6 млн. руб.
— суммы выплат 2020 и 2021 годов равны.
Найдите r, если в 2021 году долг будет выплачен полностью и общие выплаты
составят 12,6 млн. рублей.
Решение: S=6,6
r% =? b=1+0,01r
1)Sb
2
—xb=x
2)3Sb-3S+2x=12,6
19,8b-19,8+2x=12,6
x=16,2-9.9b
1)6,6 b
2
–(16,2-9,9b)b=16,2-9,9b
6,6 b
2
-16,2b+9,9 b
2
=16,2-9,9b
16,5 b
2
-6,3b-16,2=0
165 b
2
—63b-162=0
D=63
2
+4•162•165=110889
b
1
=1,2
b
2
= —0,81не подходит по условию задачи.
Ответ: r=20.
33
Задача №2.
1 марта 2010 года Аркадий взял в банке кредит под 10% годовых. Схема выплаты
кредита следующая: 1 марта каждого следующего года банк начисляет проценты
на оставшуюся сумму долга (то есть увеличивает долг на 10%), затем Аркадий
переводит в банк платеж. Весь долг Аркадий выплатил за 3 платежа, причем
второй платеж оказался в два раза больше первого, а третий – в три раза больше
первого. Сколько рублей взял в кредит Аркадий, если за три года он выплатил банку
2 395 800 рублей?
Решение:
Сумма кредита (S)-?
Ставка (а)=10%, b=1,1
Количество лет (n) 3 года
Полная выплата —
остаток 0
x+2x+3x=2395800
6x=2395800
x=399300
Sb
3_
хb
2
-2xb =3x
Sb
3
-(3+2b+b
2
)x=0
S=
Ответ: 1923000рублей.
Задача №3.
Анатолий решил взять кредит в банке 331000 рублей на 3 месяца под 10% в месяц.
Существуют две схемы выплаты кредита.
По первой схеме банк в конце каждого месяца начисляет проценты на оставшуюся
сумму долга (то есть увеличивает долг на 10%), затем Анатолий переводит в банк
фиксированную сумму и в результате выплачивает весь долг тремя равными
платежами (аннуитетные платежи).
рублей
b
xbb
1923000
331,1
41,6399300
331,1
)21,12,23(399300)23(
3
2
=
•
=
++•
=
++
34
По второй схеме тоже сумма долга в конце каждого месяца увеличивается на 10%,
а затем уменьшается на сумму, уплаченную Анатолием. Суммы, выплачиваемые в
конце каждого месяца, подбираются так, чтобы в результате сумма долга
каждый месяц уменьшалась равномерно, то есть на одну и ту же величину
(дифференцированные платежи). Какую схему выгоднее выбрать Анатолию?
Сколько рублей будет составлять эта выгода?
Решение: Сумма кредита (S) – 331000 рублей
Ставка (r) —10%, b=1,1
Аннуитетные платежи.
Sb
3_
хb
2
—xb=x
Sb
3
-(b
2
+b+1)x=0
3х=399300
Дифференцированные платежи.
Sb(1+
)-S
)=2Sb-S
2*331000*1,1- 331000=331000*1,2=397200
399300 – 397200= 2100
Ответ: дифференцированные платежи, выгода 2100 рублей.
133100
11,11,1
1,1*331000
2
3
=
++
=x
35
Задача №4.
Петр Иванович взял кредит на несколько лет и выплатил его равными ежегодными
платежами по 200000 руб. При этом в начале каждого
года сумма текущего долга увеличивалась на 10 %, а в конце года производился пла
тёж. Если бы Петр Иванович не делал платежей, то за это время вследствие начи
сления процентов сумма кредита составила бы 928200 руб. На сколько лет был взя
т кредит?
Решение:
Кредит (S)
Введём коэффициент b=1+0,01r
Sb
n
=928200,
ставка (r) —10%, b=1,1
х= 200000рублей, аннуитетные платежи.
Полная выплата,
долг равен 0
Sb
n
—xb
n-1
—xb
n-2-
…—xb
2
—xb-x=0
Sb
n
-x(b
n-1
+b
n-2
+…+b
2
+b+1)=0
По формуле суммы геометрической прогрессии
b
n-1
+b
n-2
+…+b
2
+b+1=
Sb
n
— x
=0
928200- 200000
=0
2000000
-1)=928200
=1+0,4641,
=1,4641
n=4
Ответ:4 года.
36
3.2 Вклады.
Задача №1.
Владимир поместил в банк 3600 тысяч рублей под 10% годовых. В конце каждого из
первых двух лет хранения после начисления процентов он дополнительно вносил на
счет одну и ту же фиксированную сумму. К концу третьего года после начисления
процентов оказалось, что размер вклада увеличился по сравнению с первоначальным
на 48,5%. Какую сумму Владимир ежегодно добавлял к вкладу?
Решение:
S=3600 тысяч – сумма вклада
r% — годовые (ежемесячные) проценты, r=10%
b=1+0,01r – коэффициент, b=1,1
n=3 года, х =? – действие
Sb
3
+хb
2
+xb = 1,485S
х(b
2
+b) = 1,485S — Sb
3
х(1,21+1,1) = 1,485S – 1,331S
2,31х = 0,154*3600
2,31х = 554,4
х = 240
Ответ: 240000.
37
Задача №2.
Василий кладет в банк 1 000 000 рублей под 10% годовых на 4 года (проценты
начисляются один раз после истечения года) с правом докладывать три раза (в
конце каждого года) на счет фиксированную сумму 133 000 рублей. Какая сумма
будет на счете у Василия через 4 года? (Решение с помощью формулы суммы
геометрической прогрессии)
Решение:
S=1000000 – сумма вклада
r% — годовые (ежемесячные) проценты, r=10%
b=1+0,01r – коэффициент, b=1,1
n=4 года, х =133000 – действие
b(Sb
3_
+хb
2
+xb+х)=
Sb
4_
+хb
3
+xb
2
+хb
Sb
4_
+хb
3
+xb
2
+хb=Sb
4_
+хb(b
2
+b+1)=
Ответ: 1948353 рублей.
рублей
b
b
xbSb 1948353
11,1
)1331,1(1,1133000
10000004641,1
1
)1(
3
4
=
−
−••
+•=
−
−
+=
38
Задача №3.
Близнецы Саша и Паша положили в банк по 50 000 рублей на три года под 10%
годовых Однако через год и Саша, и Паша сняли со своих счетов соответственно
10% и 20% имеющихся денег. Еще через год каждый из них снял со своего счета
соответственно 20 000 рублей и 15 000 рублей. У кого из братьев к концу третьего
года на счету окажется большая сумма денег? На сколько рублей?
Решение:
S=50000 – сумма вклада
r% — годовые (ежемесячные) проценты, r=10%
b=1+0,01r – коэффициент, b=1,1
n=3 года, х – действие
Саша
(0,9Sb
2
— 20000)*b =
0,9Sb
3_
20000b
0,9Sb
3_
20000b = 0,9*50000*1,331–20000*1,1 = 59895–22000 = 37895рублей
Паша
(0,8Sb2— 15000)*b =
0,8Sb3_ 15000b
0,8Sb
3_
15000b = 0,8*50000*1,331–15000*1,1 = 53240–16500 = 36740рублей
37895 – 36740 = 1155 рублей
Ответ: у Саши на 1155 рублей.
39
Задача №4.
Миша и Маша положили в один и тот же банк одинаковые суммы под 10%
годовых. Через год сразу после начисления процентов Миша снял со своего счета
5000 рублей, а еще через год снова внес 5000 рублей. Маша, наоборот, через год
доложила на свой счет 5000 рублей, а еще через год сразу после начисления
процентов сняла со счета 5000 рублей. Кто через три года со времени
первоначального вложения получит большую сумму и на сколько рублей?
Решение:
S – сумма вклада
r% — годовые (ежемесячные) проценты, r=10%
b=1+0,01r – коэффициент, b=1,1
n=3 года, х – действие
Миша
(Sb2-5000b+5000)*b =
Sb3-5000b2+5000b
Sb
3
-5000b
2
+5000b = 1,331S-5000*1,21+5000*1,1=1,331S-6050+5500=1,331S-550
Маша
(Sb2+5000b-5000)*b =
Sb3+5000b2-5000b
Sb
3
+5000b
2
-5000b = 1,331S+5000*1,21-5000*1,1=1,331S+6050-5500=1,331S+550
Ответ: у Маши на 1100 рублей.
40
Задача №5.
Гражданка Васильева вложила 44 млрд. рублей в два оффшорных банка на 3 года:
часть денег в банк А, остальное в банк Б. Известно, что банк А ежегодно
начисляет 10% годовых; банк Б в первый год начисляет 5% годовых, во второй –
10%, а в третий – 15%. Сколько рублей было вложено в каждый из банков, если
через три года доход гражданки Васильевой от вложения денег составил 14 520
млн. рублей.
Решение:
S=44000млн – сумма вклада
r% — годовые (ежемесячные) проценты,
b=1+0,01r – коэффициент,
n=3 года
1 банк
1,05*1,1*1,15S=1,32825(44000-S)
1,331S+1,32825(44000-S)-44000=14520
1,331S-1,32825S=14520-58443+44000
0,00275S=77
S=28000 млн=28 млрд положила в 1 банк
44—28=16 положила во 2 банк
Ответ: 28 млрд и 16 млрд рублей.
41
Задача №6.
1 ноября 2017 года Николай открыл в банке счёт «Управляй», вложив S тысяч
рублей (S – целое число) сроком на 4 года под 10% годовых. По договору с банком
проценты по вкладу должны начисляться 31 октября каждого последующего года.
1 ноября 2019 года и 1 ноября 2020 года Николай планирует снять со счёта 100
тысяч и 50 тысяч рублей соответственно. 1 ноября 2021 года Николай собирается
закрыть счёт в банке и забрать все причитающиеся ему деньги.
Найдите наименьшее значение S, при котором доход Николая от вложений в банк з
а эти 4 года окажется более 70 тысяч рублей.
Решение:
S – сумма вклада
r% — годовые (ежемесячные) проценты, r=10%
b=1+0,01r – коэффициент, b=1,1
n=4 года, х – действие
b(Sb3_100b-50)=
Sb4_100b2-50b
Sb
4_
100b
2
-50b –S+150
70
S(b
4_
1)-100b
2
-50b +150
70
S(1,1
4_
1)
70-150+55+121
0,4641S
96
S
206,9
S=207
Ответ: 207тысяч рублей.
42
Задача №7.
За время хранения вклада в банке проценты по нему начислялись ежемесячно
сначала в размере 5%, затем 12%, потом 11
и, наконец, 12,5% в месяц. Известно,
что под действием каждой новой процентной ставки вклад находился целое число
месяцев, а по истечении срока хранения первоначальная сумма увеличилась на
104
%. Определите срок хранения вклада.
Решение:
S – сумма вклада
1,125p×
k 1,12m 1,05nS
Пусть n месяцев лежал вклад под 5%, m месяцев – под 12%, k месяцев – под 11
,
p месяцев – под 12,5 %.
1,125
p
k
1,12
m
1,05
n
S =
S
1,125
p
=
p
=
p
=
=
k
=
=
1,12
m
=
m
=
m
=
=
1,05
n
=
n
=
n
=
=
=
=
=
—2n+2m+k-3p=-3 n=1
=
n-2k+2p = -1 m=1
=
-n+k-2m = 0 k=3
=
m+ n = 2 p=2
1+1+3+2 = 7
Ответ: 7 месяцев.
43
Задача №8
Алексей приобрёл ценную бумагу за 7 тыс. рублей. Цена бумаги каждый год
возрастает на 2 тыс. рублей. В любой момент Алексей может продать бумагу и
положить вырученные деньги на банковский счёт. Каждый год сумма на счёте
будет увеличиваться на 10 %. В течение какого года после покупки Алексей должен
продать ценную бумагу, чтобы через тридцать лет после покупки этой бумаги
сумма на банковском счёте была наибольшей?
Решение:
Чтобы сумма на банковском счёте была наибольшей необходимо, чтобы процент (r)
от стоимости ценной бумаги в n-ом году был больше, чем 2000 рублей
r(7000+(n-1)2000)2000
0,1(7000+2000n-2000)2000
500+200n2000
200n
n
n=8
Ответ: 8 года.
44
3.3 Задачи на оптимизацию.
Задача №1.
У фермера есть два поля, каждое площадью 100 гектаров. На каждом поле можно
выращивать картофель и свёклу, поля можно делить между этими культурами в
любой пропорции. Урожайность картофеля на первом поле составляет 400 ц/га, а
на втором — 300 ц/га. Урожайность свёклы на первом поле составляет 300 ц/га, а
на втором — 400 ц/га. Фермер может продавать картофель по цене 10 000 руб. за
центнер, а свёклу — по цене 11 000 руб. за центнер. Какой наибольший доход
может получить фермер?
Решение:
Вся площадь: 100 га
Составим функцию полного дохода:
∑(x,k) = 4000000x+3300000kx→наиб
Заметим, что x+kx=100, т.е. x=
где k
∑(k) =
+
→наиб
∑(k) =
→наиб
Возьмём производную этой функции
=
=
Значит функция убывает во всей области определения, т.е. принимает своё
наибольшее значение при k=0. Это означает, что всё первое поле нужно засадить
картофелем, при этом доход будет 4000000 рублей
Из второй таблицы видно, что свекла имеет, как большую урожайность, так и
большую цену за центнер, следовательно, второе поле нужно засадить свеклой. При
этом доход будет 40011000 рублей
Полный доход составляет 400 млн + 440 млн = 840 млн рублей.
Ответ: 840 млн рублей.
45
Задача №2.
У фермера есть два поля, каждое площадью 10 гектаров. На каждом поле можно
выращивать картофель и свёклу, поля можно делить между этими культурами в
любой пропорции. Урожайность картофеля на первом поле составляет 500 ц/га, а
на втором — 300 ц/га. Урожайность свёклы на первом поле составляет 300 ц/га, а
на втором – 500 ц/га. Фермер может продать картофель по цене 5000 руб. за
центнер, а свёклу — по цене 8000 руб. за центнер. Какой наибольший доход может
получить фермер?
Вся площадь: 10 га
Составим функцию полного дохода:
∑(x,k) = 2500000x+2400000kx→наиб
Заметим, что x+kx=10, т.е. x=
где k
∑(k) =
+
→наиб
∑(k) =
→наиб
Возьмём производную этой функции
=
=
Значит функция убывает во всей области определения, т.е. принимает своё
наибольшее значение при k=0. Это означает, что всё первое поле нужно засадить
картофелем, при этом доход будет 2500000 рублей
Из второй таблицы видно, что свекла имеет, как большую урожайность, так и
большую цену за центнер, следовательно, второе поле нужно засадить свеклой. При
этом доход будет 5008000 рублей
Полный доход составляет 25 млн + 40 млн = 65 млн рублей.
Ответ: 65 млн рублей.
46
Задача №3.
Предприниматель купил здание и собирается открыть в нём отель. В отеле могут
быть стандартные номера площадью 27 квадратных метров и номера «люкс»
площадью 45 квадратных метров. Общая площадь, которую можно отвести под
номера, составляет 981 квадратный метр. Предприниматель может поделить
эту площадь между номерами различных типов, как хочет. Обычный номер будет
приносить отелю 2000 рублей в сутки, а номер «люкс» — 4000 рублей в сутки.
Какую наибольшую сумму денег сможет заработать в сутки на своём отеле
предприниматель?
Решение:
Общая площадь: 981
Составим функцию полного дохода:
∑(x,y) = 2000x+4000y→наиб
Заметим, что 27x+45y981, т.е. x
где y
, т.е. y
∑(y) =
+4000y→наиб
∑(y) =
→наиб
Возьмём производную этой функции
=
Значит функция возрастает во всей области определения, т.е. принимает своё
наибольшее значение при y=21. Это означает, что номеров люкс будет 21. Проверим
общую площадь: 45
ер. При этом полный доход
будет рублей.
Ответ: 86000 рублей.
47
Задача №4.
Предприниматель купил здание и собирается открыть в нем отель. В отеле могут
быть стандартные номера площадью 30 квадратных метров и номера «люкс»
площадью 40 квадратных метров. Общая площадь, которую можно отвести под
номера, составляет 940 квадратных метров. Предприниматель может
определить эту площадь между номерами различных типов, как хочет. Обычный
номер будет приносить отелю 4000 рублей в стуки, а номер «люкс» — 5000 рублей
в сутки. Какую наибольшую сумму денег сможет заработать в сутки на своем
отеле предприниматель?
Решение: Общая площадь : 940
Составим функцию полного дохода:
∑(x,y) = 4000x+5000y→наиб
Заметим, что 30x+40y940, т.е. x
где y
, т.е. y
∑(y) =
+5000y→наиб
∑(y) =
→наиб
Возьмём производную этой функции
=
Значит функция убывает во всей области определения, т.е. принимает своё
наибольшее значение при y=0. Это означает, что стандартных номеров будет 940
. Проверим общую площадь: 30
ер на номер люкс.
При этом полный доход будет рублей.
Ответ: 125000 рублей.
48
Задача №5.
Антон является владельцем двух заводов в разных городах. На заводах
производится абсолютно одинаковые товары при использовании одинаковых
технологий. Если рабочие на одном из заводов трудятся суммарно t
2
часов в
неделю, то за эту неделю они производят t единиц товара. За каждый час работы
на заводе, расположенном в первом городе, Антон платит рабочему 250 рублей, а
на заводе, расположенном во втором городе, — 200 рублей. Антон готов выделять
900 000 рублей в неделю на оплату труда рабочих. Какое наибольшее количество
единиц товара можно произвести за неделю на этих двух заводах?
Решение: Оплата труда в неделю : 900000рублей
Составим функцию количества единиц товара:
∑(x,y) = x+y→наиб
Заметим, что 250
+200
900000, т.е. x
где y
∑(y) =
+y→наиб
Возьмём производную этой функции
=
+1 =
Найдём нули производной:
=0
=0
0,64
=(3600—
)
1,44
=3600
y=50
Функция принимает своё наибольшее значение при y=50 (точка максимума).
x
=
=40
Найдём количество единиц товара : +50 = 90
Ответ: 90 единиц товара.
49
Задача №6.
Григорий является владельцем двух заводов в разных городах. На заводах
производятся абсолютно одинаковые товары, но на заводе, расположенном во
втором городе, используется более совершенное оборудование. В результате, если
рабочие на заводе, расположенном в первом городе, трудятся суммарно t
2
часов в
неделю, то за эту неделю они производят 3t единиц товара; если рабочие на заводе,
расположенном во втором городе, трудятся суммарно t
2
часов в неделю, то за эту
неделю они производят 4t единиц товара. За каждый час работы (на каждом из
заводов) Григорий платит рабочему 500 рублей. Готов выделять 5 000 000 рублей в
неделю на оплату труда рабочих. Какое наибольшее количество единиц товара
можно произвести за неделю на этих двух заводах?
Решение: Оплата труда в неделю: 5000000рублей
Составим функцию количества единиц товара:
∑(x,y) = 3x+4y→наиб
Заметим, что 500
+500
5000000, т.е. x
где y
∑(y) =3
+4y→наиб
Возьмём производную этой функции
= 3
+4 =
Найдём нули производной:
=0
=0
9
=16(10000-
)
25
=1600000
y=80
Функция принимает своё наибольшее значение при y=80 (точка максимума).
x
=
=60
Найдём количество единиц товара: 3 +480 = 180+320 = 500
Ответ: 500 единиц товара.
50
Задача №7.
Борис является владельцем двух заводов в разных городах. На заводах производятся
абсолютно одинаковые товары при использовании одинаковых технологий. Если
рабочие на одном из заводов трудятся суммарно t
2
часов в неделю, то за эту
неделю они производят t единиц товара. За каждый час работы на заводе,
расположенном в первом городе, Борис платит рабочему 500 рублей, а на заводе,
расположенном во втором городе, — 200 рублей. Борису нужно каждую неделю
производить 70 единиц товара. Какую наименьшую сумму придётся тратить
еженедельно на оплату труда рабочих?
Решение: 70 единиц товара
Составим функцию еженедельной оплаты труда:
∑(x,y) = 500
→наим
Заметим, что x+y70, т.е. x где y
∑(y) =500
→ наим
∑(y) =500
=700
-70000y+2450000
Возьмём производную этой функции
= 1400y-70000
Найдём нули производной: 1400y-70000=0
y=50
Функция принимает своё наименьшее значение при y=50 (точка минимума).
x
Найдём еженедельную оплату труда:
+200
= 500 +200
500000=700000
Ответ: 700 тысяч рублей .
51
Задача №8.
Фёдор является владельцем двух заводов в разных городах. На заводах
производятся абсолютно одинаковые приборы, но на заводе,
расположенном в первом городе, используется более совершенное оборудование. В р
езультате, если рабочие на заводе, расположенном в первом городе, трудятся
суммарно 3t
2
часов в неделю, то за эту неделю они производят t приборов; если
рабочие на заводе, расположенном во втором городе, трудятся суммарно 4t
2
часов в неделю, они производят t приборов.
За каждый час работы (на каждом из заводов) Фёдор платит рабочему 1 тысячу
руб. Необходимо, чтобы за неделю суммарно производилось 30 приборов. Какую
наименьшую сумму придется тратить владельцу
заводов еженедельно на оплату труда рабочих?
Решение: 30 единиц товара
Составим функцию еженедельной оплаты труда:
∑(x,y) = 3000
→наим
Заметим, что x+y30, т.е. x где y
∑(y) =3000
→наим
∑(y) =3000
=7000
—180000y+2700000
Возьмём производную этой функции
= 14000y—180000
Найдём нули производной: 14000y-180000=0
y =
=12
Функция принимает своё наименьшее значение при y=12
(точка минимума).
Пусть y=12, тогда x=18
Найдём еженедельную оплату труда:
+400
= 3000 +4000
000=1548000
Пусть y=13, тогда x=17
Найдём еженедельную оплату труда:
+400
= 3000 4000
000=1543000
Ответ: 1543000 рублей .
52
Задача №9.
В двух областях есть по 160 рабочих, каждый из которых готов трудиться по 5
часов в сутки на добыче алюминия или никеля. В первой области один рабочий за
час добывает 0,1 кг алюминия или 0,1 кг никеля. Во второй области для добычи x кг
алюминия в день требуется x
2
человеко—часов труда, а для добычи у кг никеля в день
требуется у
2
человеко—часов труда.
Для нужд промышленности можно использовать или алюминий, или никель, причём
1 кг алюминия можно заменить 1 кг никеля. Какую наибольшую массу металлов
можно за сутки суммарно добыть в двух областях?
Решение:
Из таблицы видно, что в первой области совершенно одинаковые условия
добывания алюминия и никеля. Это означает, что в первой области алюминия и
никеля будут добывать поровну по
= 40 кг. Всего 80 кг.
Во второй области: x
2
+y
2
=160
x
2
+y
2
=800
x=20, y=20. Всего 40 кг.
Ответ: 120кг.
Задача №10.
В двух шахтах добывают алюминий и никель. В первой шахте имеется 60 рабочих,
каждый из которых готов трудиться 5 часов в день. При этом один рабочий за час
добывает 2 кг алюминия или 3 кг никеля. Во второй шахте имеется 260 рабочих,
каждый из которых готов трудиться 5 часов в день. При этом один рабочий за час
добывает 3 кг алюминия или 2 кг никеля.
Обе шахты поставляют добытый металл на завод, где для нужд промышленности
производится сплав алюминия и никеля, в котором на 2 кг алюминия приходится 1
кг никеля. При этом шахты договариваются между собой вести добычу металлов
так, чтобы завод мог произвести наибольшее количество сплава. Сколько
килограммов сплава при таких условиях ежедневно сможет произвести завод?
Решение: 60 человек по 5 часов в день
260 человек по 5 часов в день
Получаем, что всего алюминия производят 10x+15y
никеля: 15(60-x)+ 10(260-y)=3500-15x-10y
Так как для сплава необходимо , чтобы на2 кг алюминия приходился 1 кг никеля,
то: 10x+15y=2(3500-15x-10y)
10x+15y=7000-30x-20y
40x=7000-35y
x =
=
Составим функцию массы сплава:
∑(x,y) = 10x+15y +3500-15x-10y →наиб
∑(x,y) = 3500-5x+5y →наиб
∑(y) = 3500-5
+5y →наиб
∑(y) = 3500-5
+5y →наиб
∑(y) =
→наиб
Возьмём производную этой функции
=
Значит функция возрастает во всей области определения, т.е. принимает своё
наибольшее значение при наибольшем значении y.
Так как x =
то 1400-7y0 , y.
Проверим значение у=200, тогда x=0.
Масса сплава: 3500-5 +5 =4500
Ответ: 4500 кг.
54
Задача №11.
Фабрика, производящая пищевые полуфабрикаты, выпускает блинчики со
следующими видами начинки: ягодная и творожная. В данной ниже таблице
приведены себестоимость и отпускная цена, а также производственные
возможности фабрики по каждому виду продукта при полной загрузке всех
мощностей только данным видом продукта.
Себестоимость
(за 1 тонну)
Отпускная цена
(за 1 тонну)
Производственные
возможности
Для выполнения условий ассортиментности, которые предъявляются торговыми
сетями, продукции каждого вида должно быть выпущено не менее 15 тонн.
Предполагая, что вся продукция фабрики находит спрос (реализуется без
остатка), найдите максимально возможную прибыль, которую может получить
фабрика от производства блинчиков за 1 месяц
Решение
Пусть x тонн выпускает фабрика блинчиков с ягодами, а y тонн – с творогом. Тогда
по условию имеем : x
Составим функцию прибыли:
∑(x,y) = 30x+35y→наиб
Пусть производственная возможность равна 1, тогда
+
= 1
75x + 90y = 6750
x = 90 – 1,2y
∑(y) = 30(90 – 1,2y)+35y→наиб
∑(y) = 2700 — y→наиб
Возьмём производную этой функции
=
Значит функция убывает во всей области определения, т.е. принимает своё
наибольшее значение при y=15. Тогда x = 90-1,2
При этом максимальная прибыль будет рублей.
Ответ: 2685000 рублей.
55
Задача №12.
Консервный завод выпускает фруктовые компоты в двух видах тары — стеклянной
и жестяной. Производственные мощности завода позволяют выпускать в день 90
центнеров компотов в стеклянной таре или 80 центнеров в жестяной таре. Для
выполнения условий ассортиментности, которые предъявляются торговыми
сетями, продукции в каждом из видов тары должно быть выпущено не менее 20
центнеров. В таблице приведены себестоимость и отпускная цена завода за 1
центнер продукции для обоих видов тары.
Предполагая, что вся продукция завода находит спрос (реализуется без остатка),
найдите максимально возможную прибыль завода за один день (прибылью
называется разница между отпускной стоимостью всей продукции и её
себестоимостью).
Решение
Пусть x центнеров выпускает фабрика в стеклянной таре, а y центнеров – в
жестяной. Тогда по условию имеем : x
Составим функцию прибыли:
∑(x,y) = 600x+650y→наиб
Пусть производственная возможность равна 1, тогда
+
= 1
80x + 90y = 7200
x = 90 – 1,125y
∑(y) = 600(90 – 1,125y)+650y→наиб
∑(y) = 54000 — 25y→наиб
Возьмём производную этой функции
=
Значит функция убывает во всей области определения, т.е. принимает своё
наибольшее значение при y=20. Тогда x = 90-1,12
При этом максимальная прибыль будет рублей.
Ответ: 53500 рублей.
56
3.4 Нестандартные задачи
Задача №1.
Два велосипедиста равномерно движутся по взаимно перпендикулярным дорогам по
направлению к перекрестку этих дорог. Один из них движется со скоростью 40
км/ч и находится на расстоянии 5 км от перекрестка, второй движется со
скоростью 30 км/ч и находится на расстоянии 3 км от перекрестка. Через сколько
минут расстояние между велосипедистами станет наименьшим? Каково будет
это наименьшее расстояние?
Решение:
Составим функцию квадрата расстояния между велосипедистами:
∑(t) =
→наим, где t
∑(t) = 25-400t+1600
→наим
∑(t) = 2500
→наим
Возьмём производную этой функции
= 5000t-580
Найдём нули производной: 5000t-580=0
t =
=
=
Функция принимает своё наименьшее значение при t=
ч = 60
(точка минимума).
Найдём расстояние между велосипедистами:
=
=
=
=
= 0,6
Ответ: 0,6км, 6,96 минут .
57
Задача №2 .
Бриллиант массой 20 карат был разбит на две части после чего его стоимость
уменьшилась на 25,5%.а) Найдите массы частей на которые был разбит
бриллиант если известно, что цена бриллианта пропорциональна квадрату его
массы.б) На какое максимальное число процентов может уменьшиться цена
бриллианта разбитого на две части.
Решение:
M=20 карат, S- стоимость бриллианта
S=km ,S
1
=km
1
,S
2
=km
2
Пусть m =x, тогда m =20-x
1) S1+S2=0,745S
kx
2
+k(20-x)
2
=0,745k20
2
x
2
+(20-x)
2
=298
x
2
+400-40x+102=0
x
2
-20x+51=0
x
1
=17, x
2
=3
Ответ: массы частей 17 и 3 карат.
2) Цена бриллианта максимально снизится, если обе части будут по 10 карат
S
1
+S
2
=aS
k10
2
+k10
2
=a20
2
k
100+100=a400
a=200/400=0,5
Ответ: на 50%
58
Задача №3
В одной стране в обращении находились 1000000 долларов, 20% из которых были
фальшивыми. Некая нехорошая структура стала ввозить в страну по 100000
долларов в месяц, 10% из которых были фальшивыми. В это время другая
структура стала вывозить из страны 50000 долларов ежемесячно, из которых
30% оказались фальшивыми. Через сколько месяцев содержания фальшивых
долларов в стране составит 5%?
Решение:
n — количество месяцев
200000-5000n =0,05(1000000+50000n )
200000-5000n =50000+2500n
-7500n = -150000
n=20
Ответ: 20 месяцев
59
Задача №4
Два брокера купили акции одного достоинства на сумму 3640 рублей. Когда цена
на эти акции возросла, они продали часть акций на сумму 3927 рублей. Первый
брокер продал 75% своих акций, а второй – 80%. При этом сумма от продажи
акций, полученная вторым брокером, на 140% больше суммы первого. На сколько
процентов возросла цена одной акции?
Решение:
k- первоначальная цена 1 акции
x – штук купил первый брокер
y – штук купил второй
z – конечная цена 1 акции
Составим систему уравнений:
3)
y =
= 2,25x
1) k(x+y)=3640
k(x+2.25x)=3640
k =
=
=
2) z(0,75x+0,8y)=3927
z(0,75х+1,8x)=3927
z2,55x=3927
z=
=
=
4) Найдём, на сколько процентов возросла цена одной акции
k =
— 100%
z =
— a%
a=
137,5%
Ответ: на 37,5%
60
Задача №5.
Строительство нового завода стоит 115 млн рублей. Затраты на
производство x тыс. единиц продукции на таком заводе равны 0,5 x
2
+x+9 млн
рублей в год. Если продукцию завода продать по цене p тыс. рублей за единицу, то
прибыль фирмы (в млн рублей) за один год составит
px-(0,5 x
2
+x+9). Когда завод будет построен, фирма будет выпускать продукцию
в таком количестве, чтобы прибыль была наибольшей. При каком наименьшем
значении p строительство завода окупится не более чем за 5 лет?
Решение
Составим функцию прибыли:
∑(x,p) = px-(0,5 x
2
+x+9)→наиб
∑(x,p) = px-0,5 x
2
-x-9
Возьмём производную этой функции
= p-x-1
Найдём нули производной: p-x-1=0
x = p-1
Функция принимает своё наибольшее значение при x = p-1
(точка минимума).
Найдём прибыль:
∑(p) = p(p-1)-0,5 (p-1)
2
-(p-1)—9 = 0,5p
2
-p-8,5
По условию строительство завода должно окупиться не более, чем за 5 лет. То есть
за 5 лет прибыль должна быть не меньше 115 млн рублей.
5(0,5p
2
-p-8,5115
0,5p
2
-p-8,5-23=0
p
2
-2p-63=0
p
1
=9, p
2
=-7
Ответ: 9 тысяч рублей.
61
4.Заключение
В данной работе рассмотрены основные методы решения задач на кредит, вклады и
оптимизацию. Тема работы очень актуальна, так как все рассматриваемые задачи взяты
из материалов по подготовке к ЕГЭ по математике «Профиль». Надеюсь, что данная
работа будет полезна учащимся 10—11 класса, а также преподавателям математики.
5.Список использованной литературы:
1. ЕГЭ 2018 под редакцией А. Л. Семенова, И.В. Ященко
2. Открытый банк заданий ЕГЭ fipi.ru
3. Сайт «Решу ЕГЭ»
4. Сайт «Алекс Ларин»
Департамент образования мэрии города Новосибирска
Дворец творчества детей и учащейся молодежи «Юниор»
XXXVIII городская открытая научно-практическая
конференция НОУ «Сибирь»
Секция: математика
Тема: Экономические задачи на ЕГЭ
Авторы:
Галахова Анастасия Александровна,
Прокопенко Анна Павловна
10 класс МБОУ СОШ № 141 с углублённым изучением математики
Первомайского района
города Новосибирска
Научные руководители:
Туленкова Елена Сергеевна,
учитель математики в.к.к.
МБОУ СОШ № 141 с углублённым изучением математики
конт. тел. 8-913-749-25-03,
Петрунина Вера Андреевна,
учитель математики в.к.к.
МБОУ СОШ № 141 с углублённым изучением математики
конт. тел. 8-913-482-02-86
Новосибирск 2018
Содержание
-
Введение…………………………………………………………………….3
-
Об экономических задачах…………………………………………………4
-
Решение экономических задач……………………………………………11
-
Заключение………………………………………………………………..18
-
Список литературы……………………………………………………….19
-
Приложение……………………………………………………………….20
Введение
В экзаменационных заданиях по математике (профильный уровень) во II части содержится задание № 17 – задача с экономическим содержанием. Она относится к повышенному уровню сложности и оценивается максимально в 3 балла.
По статистике это задание на 3 балла выполняют только 7,8% учащихся, на 2 балла – 2,4%, на 1 балл – 2,7%.
В следующем году и нам предстоит сдавать экзамен по математике. Чтобы попасть в эти 7,8 %, мы решили уже в 10 классе разобраться, что необходимо знать и уметь для решения экономических задач.
Более того, мы уверены, что умение решать такие задачи поможет нам и в повседневной жизни, например, в управлении личными финансами. Любому человеку необходимо повышать свою финансовую грамотность и разбираться в таких вопросах, как начисление заработной платы, налоговые отчисления, инфляция, потребительские и ипотечные кредиты, кредиты на образование и др. Часто финансово грамотное решение в реальной жизни вырабатывается не методом проб и ошибок, а путём аккуратных расчётов.
Цель нашей работы: выяснить, какие задачи называют экономическими, выявить основные типы задач на ЕГЭ и научиться их решать.
Задачи:
-
Изучить теоретический материал;
-
Проанализировать виды экономических задач;
-
Научиться применять полученные знания на практике.
Объект исследования:
Экономические задачи повышенного уровня сложности.
Методы:
-
поисковый метод с использованием научной и учебной литературы, интернета;
-
исследовательский метод при определении видов задач;
-
практический метод решения задач;
-
анализ полученных в ходе исследования данных.
План работы:
-
Работа с литературой
-
Анкетирование учащихся
-
Изучение видов задач на проценты
-
Изучение способов решения задач
-
Выводы
Об экономических задачах
Начиная с 2015 года, в заданиях ЕГЭ по математике профильного уровня появилась новая экономическая задача №17.
Экономические задачи — задачи, решаемые в процессе экономического анализа, планирования, проектирования, связанные с определением искомых неизвестных величин на основе исходных данных. Их решение сопровождается поиском недостающих данных, экспертными оценками, обсуждением, принятием решений.
Мы изучили теоретический материал и выяснили, что эти задачи условно разделяют на два типа: непрерывные модели (производство товаров, протяжённое во времени, оптимизация производства, и т.п.) и дискретные модели (налоги, банковские проценты, вклады, погашение кредитов, и т.п.).
Непрерывные модели
-
Использование свойств функции
Решение различных экономических задач в формате ЕГЭ часто сводится к отысканию экстремальных (минимальных или максимальных) значений некоторой функции на заданном или получаемом из условия промежутке.
Нередко такими функциями являются линейная функция y=px+q(p ≠ 0) или квадратичная функция y= ax2+bx+c (a≠0). Линейная функция принимает экстремальное значение на одном из концов промежутка, которому принадлежат значения х.
Если линейная функция рассматривается только на множестве целых чисел, то число из этого промежутка, при котором функция принимает наибольшее или наименьшее значение, будет ближайшим целым числом к тому концу промежутка, на котором она принимает соответствующее экстремальное значение. Это следует из того, что линейная функция при ненулевом значении углового коэффициента является монотонно возрастающей или убывающей.
Пример. Подрядчику выделили 30000 рублей на уборку микрорайона к приезду губернатора. Из этих денег нужно выдать 2000 рублей бригадиру и по 450 рублей зарплаты каждому рабочему. Какую наибольшую сумму может потратить подрядчик на зарплату?
Решение. Пусть всего х рабочих. Зарплата рабочих и бригадира равна 2000+450х, по условию она не должна превышать 30000, т.е. 2000+450х≤30000
x ≤ 62 
Линейная функция y = 2000+450х возрастающая, поэтому наибольшее значение она примет на правом конце промежутка. По условию х – число натуральное, значит, наибольшее значение будет достигаться при х = 62, тогда наибольшее значение равно 2000+450×62 = 29900 рублей.
Ответ: 29900 рублей.
Квадратичная функция y=ax2+bx+c принимает экстремальное значение при х0= —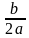
Пример. Производительность отдела в зависимости от количества сотрудников х, находящихся в офисе, описывается формулой y = -2х2+25х-8. Найдите, при каком числе сотрудников, находящихся в офисе, производительность отдела наибольшая.
Решение. Графиком функции y = -2х2+25х-8 является парабола, ветви которой направлены вниз. Значит, наибольшее значение она принимает в вершине параболы. Найдём абсциссу вершины
х0 =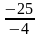
Количество сотрудников – число натуральное, значит наибольшее значение функция будет принимать при натуральном значении х, ближайшем к вершине, в данном случае х = 6.
Ответ:6
-
Применение производной
Для исследования свойств функции используют производную.
Дискретные модели
Некоторые задачи удобно решать с помощью дискретных математических моделей, то есть моделей, переменные в которых могут принимать некоторое, практически всегда конечное число наперед известных значений.
-
Простые экономические задачи. Проценты, доли и соотношения.
Часто такие задачи требуют умения обращаться с процентами — находить процент от числа, число по его процентам, а также величину и изменение величины в процентах. Это объясняется тем, что проценты широко распространены в реальной жизни при проведении различных операций, где возникают банковские проценты, проценты от зарплаты в качестве налога и т.д.
При решении задач на анализ динамики экономических показателей всегда устанавливается взаимно однозначное соответствие между процентами и коэффициентами. Выражение «величина увеличилась (уменьшилась) на x процентов» нужно воспринимать в виде «величина умножилась на коэффициент k» и наоборот. В общем виде это можно представить так:
-
увеличился на х% — умножился на коэффициент k =
;
-
уменьшился на х% — умножился на коэффициент k =
.
Пример. Налог на доходы составляет 13% от заработной платы. Заработная плата Николая Ивановича равна 22 500 рублей. Какую сумму он получит после вычета налога на доходы?
Решение. После вычета налога на доходы Николай получит 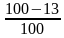
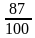
22 500×0,87 = 19 575 рублей.
Ответ: 19 575 рублей.
Но следует помнить, что если происходит последовательное изменение какой-либо величины, то каждый раз проценты берутся от ее последнего (перед очередным изменением) значения, и на соответствующий коэффициент каждый раз умножается последнее (перед очередным изменением) значение величины.
-
Вклады
Вкладом является денежная сумма или другие ценности, которые человек отдает в банк на определенных условиях, подразумевающих начисление процентов за определенный период на вложенную сумму.
Например, если в банк вложена сумма А под p% на некоторый период времени t, то по истечении этого времени вложенная сумма увеличится на р% от числа А, значит, станет равной:
А + А × 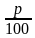
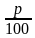
Другими словами, вклад увеличится в 1 + 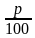
Ставка по вкладу с учетом капитализации.
Часто банк применяет ставку по вкладу с учетом капитализации, то есть если в банк была вложена сумма А под р% годовых, то каждый месяц банк увеличивает сумму, находящуюся к этому моменту на счете клиента на 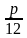
Формула расчета суммы вклада, размещенного с учетом ежемесячной капитализации под р% годовых: 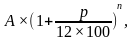
Пример. Ольга Викторовна поместила 250 000 рублей в банк на 3 месяца под 24% годовых с учетом капитализации процентов, то есть по истечении каждого месяца к ее вкладу были добавлены деньги, начисленные в качестве процентов. Какая сумма будет на счете Ольги Викторовны через 3 месяца? На сколько рублей увеличился ее первоначальный вклад?
Решение. На счете Ольги через 3 месяца будет
250000 × (1 + 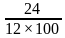
Её первоначальный вклад увеличился на 265302 – 250000 = 15302 рубля.
Ответ: 265302 рубля, на 15302 рубля.
-
Кредиты
Кредит – это финансовая сделка, в результате которой кредитор (банк или другое финансовое учреждение) предоставляет на определенный срок деньги заемщику. За пользование деньгами заемщик, кроме погашения основного долга (называемого в финансовой литературе телом кредита), выплачивает также кредитору проценты. Разделение погашающих платежей на две части, отвечающие за погашение долга (тела кредита) и погашение процентных денег, принципиально важно, поскольку от этого зависят уплачиваемые налоги.
Пример. Клиент взял в банке 135000 рублей на год под 12%. Он должен погашать кредит, внося в банк ежемесячно одинаковую сумму денег, с тем, чтобы через год выплатить всю сумму, взятую в кредит, вместе с процентами. Сколько рублей он должен вносить в банк ежемесячно?
Решение. Через год долг увеличится в 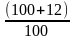
Клиент будет должен банку 135000×1,12 = 151200 рублей.
Ежемесячно он будет вносить 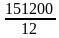
Ответ: 12600 рублей.
Дифференцированная схема
При дифференцированной (или регрессивной) схеме процент и периодичность обязательных платежей фиксируются (например, ежегодные, ежеквартальные или ежемесячные платежи), а фиксированный процент начисляется на ещё не выплаченную к моменту очередного обязательного платежа часть кредита (долг). В этом случае каждый платёжный период сумма выплат уменьшается, поскольку она состоит из фиксированной части и процентов, начисляемых на остаток долга по кредиту, величина которого каждый платёжный период уменьшается. Таким образом, при схеме с дифференцированными платежами клиент возвращает банку до истечения каждого платёжного периода 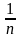
Пусть S0 – сумма кредита, который был взят на n лет под k% годовых.
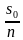
(фиксированная часть)
Процент на остаток долга
(изменяющаяся часть)
Платеж = +
|
Года |
1 |
2 |
3 |
4 |
… |
n |
|
Фиксированная часть (выплаты) |
|
|
|
|
… |
|
|
Сумма на которую начисляется процент |
|
|
|
|
… |
|
|
Начисленные проценты |
|
|
|
|
… |
|
Общая сумма начисленных процентов:
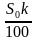
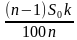
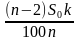
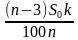
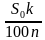
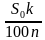
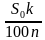
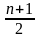
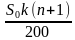
Общая сумма S всех выплат по кредиту: S = S0 + 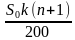
Пример. Величина предоставленного потребительского кредита – 12000руб. Процентная ставка – 12% годовых, срок погашения – 6 месяцев, схема погашения – рецессивная (т.е. в конце каждого месяца заемщик выплачивает процент на оставшуюся часть долга и одну шестую часть основного долга). Какую сумму выплатит заемщик в итоге банку?
Решение. Воспользуемся формулой, где К=12000, р=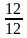
Х=12000 + 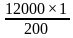
Ответ: 12420 рублей.
Но следует заметить, что чтобы использовать данную формулу на экзамене, ее нужно будет вывести самостоятельно, используя приведенные в условии данные. Но вывод формулы довольно сложный и не каждый ученик сможет его воспроизвести, поэтому существует ещё один способ решения таких задач – таблица
|
Месяц |
Долг |
Процентный платеж |
Выплата долга |
Месячный взнос |
|
Д |
П=0,01Д |
В |
П+В |
|
|
1 |
12000 |
120 |
2000 |
2120 |
|
2 |
10000 |
100 |
2000 |
2100 |
|
3 |
8000 |
80 |
2000 |
2080 |
|
4 |
6000 |
60 |
2000 |
2060 |
|
5 |
4000 |
40 |
2000 |
2040 |
|
6 |
2000 |
20 |
2000 |
2020 |
|
Всего |
420 |
12000 |
12420 |
Ответ:12420 рублей.
Аннуитетная схема
На сегодняшний день большим спросом среди заёмщиков пользуется аннуитетная схема: заёмщику удобно, когда сумма ежемесячного (ежеквартального, ежегодного) платежа фиксируется на весь срок кредитования.
Пусть кредит в размере S0 рублей выдан на n лет под k% годовых и пусть х рублей – ежегодный платеж. Тогда полная выплата по кредиту составит Х = nx рублей. Ежегодное начисление р% на остаток долга соответствует умножению этого остатка на коэффициент m=1+0,01k. Тогда
S1 = S0m – x;
S2 = mS1 – x = m2S0 – mx – x;
S3 = mS2 – x = m3S0 – m2x – mx – x;
Sn = mSn — 1 – x = mnS0 – mn — 1x – mx – x.
Поскольку по истечении платёжного периода долг равен 0, то Sn = 0, т.е.
mnS0 – mn — 1x – …–mx – x = 0.
Отсюда mn — 1x + …+ mx + x = mnS0, а после вынесения общего множителя
x(mn — 1 + …+ m + 1) = mnS0. Сумма mn — 1 + …+ m + 1 вычисляется формуле суммы s первых n членов геометрической прогрессии {bn}: S = b1×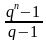
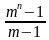
= mnS0, откуда х =
S0. (1)
m=1+0,01k, 0,01k часто обозначают буквой p. Тогда m = 1+p, формула (1) примет вид х = S0.
Пример. Клиент взял 15960000рублей в кредит под 30% годовых. По истечению каждого следующего года банк начисляет проценты на оставшуюся сумму долга (т.е. увеличивает долг на 30%), затем клиент переводит в банк определенную сумму ежегодного платежа. Какой должна быть сумма ежегодного платежа, чтобы клиент выплатил долг тремя равными ежегодными платежами?
Решение. Используем формулу
S=15960000, n=3, q=1+ =
x= = 8788000
Ответ: 8788000 рублей.
2-й способ. Эту задачу также можно решить без использования формулы.
Пусть ежегодный платеж составляет х рублей. Тогда
1-й год: 1,3×15960000-х=20748000-х
2-й год: 1,3(20748000-х)-х=26972400-2,3х
3-й год: 1,3(26972400-2,3х) –х= 35064120-3,99х.
По условию клиент должен выплатить кредит тремя равными платежами, т.е. в конце третьего года его долг составит 0 рублей. Тогда 35064120-3,99х=0. Решим уравнение и получим х=8788000.
Ответ: 8788000 рублей.
Решение экономических задач
Дискретные модели
Задача №1. Взяли кредит в банке на сумму 250000 рублей под р% годовых и выплатили за 2 года платежами 150000 рублей в первый год и 180000 рублей- во второй. Найдите р.
Решение. 1-й год: 250000 + 250000×0,01р – 150000 =100000+2500р.
2-й год: 100000+2500р + (100000+2500р)0,01р – 180000 = 25р2+3500р-80000.
Решим уравнение 25р2 + 3500р – 80000 = 0 и получим р1=20%
р2= -160% — п.к., т.к. р≥0.
Ответ: 20
Задача №2. 31 декабря 2014 года Евгений взял в банке 1 млн. рублей в кредит. Схема выплаты кредита следующая – 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (т.е. увеличивает долг на а%), затем Евгений переводит очередной транш. Евгений выплатил кредит за два транша, переведя в первый раз 540 тыс. рублей, во второй 649,6 тыс. рублей. Найдите а.
Решение. Евгений выплатил кредит за два транша, т.е. за два года. Тогда
31.12.15. 1000000 + 1000000×0,01а – 540000 = 460000+10000а
31.12.16. 460000+1000а+(460000+1000а)0,01а– 649600 = 100а2+14600а -18900.
Решим уравнение 100а2+14600а-18900=0 и получим а1=12%
а2= -158%, п.к., т.к. а≥0.
Ответ: 12
Задача №3. Банк выдал заемщику кредит в размере 30000 рублей, ежегодная выплата по кредиту составляет 10000 рублей (последний платеж может отличаться от стальных в меньшую сторону), процентная ставка – 20% годовых. Через сколько лет кредит будет погашен? Сколько составит переплата?
Решение. Решим с помощь таблицы
|
Сумма по кредиту А |
Процент по кредиту 0,2А |
Ежегодная выплата |
Погашение тела кредита В=1000-0,2А |
Тело кредита на начало след.года А-В |
|
30000 |
6000 |
10000 |
4000 |
26000 |
|
26000 |
5200 |
10000 |
4800 |
21200 |
|
21200 |
4240 |
10000 |
5760 |
15440 |
|
15440 |
3088 |
10000 |
6912 |
8528 |
|
8528 |
1705,6 |
10000 |
8294,4 |
233,6 |
|
233,6 |
46,72 |
280, 32 |
233,6 |
0 |
|
Итого |
50280,32 |
30000 |
Кредит будет погашен через 6 лет. Переплата составит 50280,32-30000=20280,32 рублей.
Ответ: 6 лет; 20280,32 рублей.
Задача №4. 31 декабря 2014 года Дмитрий взял в банке 4290000 рублей в кредит по 14,5% годовых. Схема выплаты кредита следующая – 31 декабря каждого следующего года в банк начисляется проценты на оставшуюся сумму долга, затем Дмитрий переводит в банк х рублей. Какой должна быть сумма х, чтобы Дмитрий выплатил долг двумя равными платежами (т.е. за два года)?
Решение. 31.12.15 — 4290000×1,145 – х=4912050 – х.
31.12.16 – (4912050 – х)1,145 – х= 5624297,25 – 2,145х.
Т.к. долг погашен за два года то 5624297,25 – 2,145х=0
х=2622050 рублей.
Ответ: 2622050 рублей.
Задача №5. 15-го января планируется взять кредит в банке на 15 месяцев. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на 1% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.
Известно, что восьмая выплата составила 108 тыс. рублей. Какую сумму нужно вернуть банку в течение всего срока кредитования?
Решение. Пусть S0 – сумма кредита. Составим схему выплат:
1-й месяц: + 0,01S0
2-й месяц: + 0,01(S0 —
) =
+ 0,01
S0
3-й месяц: + 0,01
S0
…
8-й месяц: + 0,01
S0
Известно, что восьмая выплата составила 108 тыс. рублей, значит
+ 0,01
S0 = 108
(1 + 0,08) = 108
1,08 = 108
S0 = = 1500 тыс. рублей – сумма кредита. По выведенной нами формуле:
S = S0 + 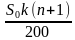
S = 1500 + = 1500 + = 1500 + 120 = 1620 тыс. рублей = 1620000рублей.
Ответ: 1620000 рублей.
Задача №6. 15-го декабря планируется взять кредит в банке на 21 месяц. Условия возврата таковы:
— 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца с 1-го по 20-й долг должен быть на 30 тысяч рублей меньше долга на 15-е число предыдущего месяца;
— к 15-му числу 21-го месяца кредит должен быть полностью погашен. Какую сумму планируется взять в кредит, если общая сумма выплат после полного его погашения составит 1604 тысяч рублей?
Решение. Пусть S – сумма, которую планируется взять в кредит, Х — сумма на которую уменьшается основной долг, Х = 30 (тысяч рублей). После каждого начисления процентов сумма долга увеличивается в 1,03 раза, т.е. k = 1,03.
Рассмотрим схему
После первого начисления процентов сумма долга равна kS. Затем, после первой выплаты, сумма долга равна S – X, где Х = 30 (тысяч рублей).
Значит, первая выплата равна kS – (S – X)
Вторая выплата: k (S – X ) – ( S – 2X).
…
Последняя выплата: k ( S – 20 X).
Найдём общую сумму выплат: kS – (S – X) + k (S – X ) – ( S – 2X) + … + k ( S – 20X) =
= k ( S + S – X + S – 2X + … + S – 20 X) – ( S – X + S – 2X + … + S – 20X).
Упростим выражения в скобках:
k (21S – X (1 + 2 + 3+ … + 20)) – (20S – X (1 + 2 + 3+ … + 20))
Используя сумму арифметической прогрессии найдём ;
Получим:
k (21 S – 210X ) – 20 S + 210 Х = 1604
Осталось подставить числовые значения.
1,03(21S – 210×30) – 20S + 210×30 = 1604
1,63S = 1793
S = 1100 тысяч рублей = 1 100 000 рублей.
Ответ: 1100000 рублей.
Непрерывные модели
Задача №7. По бизнес-плану предполагается вложить в четырехлетний проект 20 млн рублей. По итогам каждого года планируется прирост вложенных средств на 13% по сравнению с началом года. Начисленные проценты остаются вложенными в проект. Кроме этого, сразу после начислений процентов нужны дополнительные вложения: целое число n млн рублей в первый и второй годы, а также целое число m млн рублей в третий и четвертый годы. Найдите наименьшие значения n и m, при которых первоначальные вложения за два года как минимум удвоятся, а за четыре года как минимум утроятся.
Решение. 1-й год: 20×1,13 + n = 22,6 + n.
2-й год: (22,6+n)1,13+n = 25,538+2,13n.
По условию 25,538+2,13n ≥ 2×20
25,538+2,13n ≥ 40
n 6,78…
Наименьшее целое решение n=7.
3-й год (25,538+2,13n)1,13 + m=(25,538+2,13×7)1,13 + m=45,70624 + m
4-й год (конец проекта): (45,70624 + m)1,13 + m=51,6480512 + 2,13m
По условию 51,6480512 + 2,13m≥3×20
51,6480512 + 2,13m≥60
m≥3,92…
Наименьшее целое решение m=4.
Ответ: 7 млн рублей; 4 млн рублей.
Задача №8. По бизнес-плану предполагается вложить в четырехлетний проект целое число миллионов рублей. По итогам каждого года планируется прирост средств вкладчика на 20% по сравнению с началом года. Начисленные проценты остаются вложенными в проект. Кроме этого, сразу после начисления процентов нужна дополнительные вложения: по 20 миллионов рублей в первый и второй годы, а также по 10 миллионов в третий и четвертый годы. Найдите наименьший размер первоначальных вложений, при котором они за два года станут больше 125 миллионов, а за четыре года станут больше 200 миллионов рублей.
Решение. Пусть х млн рублей – первоначальные вложения. Тогда
1-й год: 1,2х + 20.
2-й год: (1,2х + 20)1,2 + 20=1,44х + 44.
По условию 1,44х + 44˃125
х˃56,25
Наименьшее целое решение х=57.
3-й год: (1,44х + 44)1,2+10=1,728х+62,8
4-й год (конец проекта): (1,728х+62,8)1,2+10=2,0736х+85,36
По условию 2,0736х+85,36˃200
х˃55,28…
Наименьшее целое число (также удовлетворяющее условию на два года) х=57.
Ответ: 57 млн рублей.
Задача №9. Зависимость объема спроса q (единиц в месяц) на продукцию предприятия-монополиста от цены p (тыс. руб.) задается формулой q=280-2p. Выручка предприятия за меся r ( в тыс. руб.) вычисляется по формуле r(p)=qp. Определите цену, при которой месячная выручка r(p) будет наибольшей. Найдите наибольшую возможную выручку.
Решение. r = qp = (280-2p)p = 280p — p2. Графиком полученной функции является парабола, ветви которой направлены вниз. Значит, наибольшее значение она принимает при p0 = = 70.
При цене 70 тыс. рублей выручка будет наибольшей и будет равна
(280-2×70)70=140×70=9800 тыс. рублей.
Ответ: 70тыс. рублей; 9800 тыс. рублей.
Задача №10. Вклад в размере 6 млн рублей планируется открыть на четыре года. В конце каждого года вклад увеличивается на 10% по сравнению с его размером в начале года, а, кроме этого, в начале третьего и четвертого годов вклад ежегодно пополняется на одну и ту же фиксированную сумму, равную целому числу миллионов рублей. Найдите наименьший возможный размер такой суммы, при котором через четыре года вклад станет не меньше 15 млн рублей.
Решение. Пусть искомая сумма равна х рублей.
1-й год: 1,1×6=6,6 млн рублей.
2-й год: 1,1×6,6=7,26млн рублей.
3-й год: 1,1×7,26+х=7,986+х
4-й год: 1,1(7,986+х)+х=8,7846+2,1х.
По условию 8,7846+2,1х≥15
х≥2,95…
Наименьшее целое число х=3.
Ответ: 3 млн рублей.
Задача №11. В распоряжении начальника имеется бригада рабочих в составе 24 человек. Их нужно распределить на день на два объекта. Если на первом объекте работает t человек, то их суточная зарплата составляет 4t2 у. е. Если на втором объекте работает t человек, то их суточная зарплата составляет t2 у. е. Как нужно распределить на эти объекты бригаду рабочих, чтобы выплаты на их суточную зарплату оказались наименьшими? Сколько у. е. в этом случае придется заплатить рабочим?
Решение: Пусть I объект — х рабочих, суточная зарплата: f1(x) = 4x2.
Тогда II объект 24 – x рабочих — суточная заработная плата: f2(24 – x)2 = 576 – 48x + x2.
В день начальник будет должен платить рабочим
f(x) = f1(x) + f2(x) = 4x2 + 576 – 48x + x2 = 5x2— 48x + 576, 0 є N.
Квадратичная функция f(x) принимает наименьшее значение при
х0 = =
= 4,8. Число х является натуральным числом, поэтому функция достигает наименьшего значения в точках 4 или 5. Найдем и сравним эти значения:
f(4) = 5×16 – 48×4 +576 = 80 – 192 + 576 = 464
f(5) = 5×25 – 48×5 + 576 = 125 – 240 + 576 = 461
Наименьшее значение функции достигается в точке 5. Поэтому необходимо направить 5 рабочих на первый объект, 24 – 5 = 19 рабочих — на второй объект. Зарплата рабочих составит 461 у. е.
Ответ: I объект – 5 рабочих, II объект – 19 рабочих, 461 у.е.
Задача №12. У фермера есть два поля, каждое площадью 10 гектаров. На каждом поле можно выращивать картофель и свёклу, поля можно делить между этими культурами в любой пропорции. Урожайность картофеля на первом поле составляет 500 ц/га, а на втором — 300 ц/га. Урожайность свёклы на первом поле составляет 300 ц/га, а на втором — 500 ц/га.
Фермер может продать картофель по цене 5000 руб. за центнер, а свёклу — по цене 8000 руб. за центнер. Какой наибольший доход может получить фермер?
Решение. Продавать свеклу более выгодно, поэтому второе поле, где ее урожайность выше, следует засадить только свеклой. Она принесет доход 10 га · 500 ц/га · 8000 руб/ц = 40 млн руб.
Пусть на первом поле – х га свеклы, тогда картофеля 10 – х га, составим функцию: f(x) = x×300×8000 + (10 – x)500×5000 = 2400000x + 25000000 – 2500000x = -100000x + 25000000 = -x + 250, х є [0; 10].
Линейная функция убывающая, значит, наибольшее значение она будет принимать на левом конце промежутка, т.е. при х = 0, значит, первое поле нужно засадить только картофелем.
Тогда доход составит: 10×500×500 = 25 млн руб.
Общий доход: 40 + 25 = 65 млн. рублей.
Ответ: 65 млн руб.
Задача №13. Подрядчику выделили 30000 рублей на уборку микрорайона к приезду губернатора. Из этих денег нужно выдать 2000 рублей бригадиру и по 450 рублей зарплаты каждому рабочему. Какую наибольшую сумму может потратить подрядчик на зарплату?
Решение. Пусть всего х рабочих. Зарплата рабочих и бригадира равна 2000+450х, по условию она не должна превышать 30000, т.е. 2000+450х≤30000
x ≤ 62 
Линейная функция y = 2000+450х возрастающая, поэтому наибольшее значение она примет на правом конце промежутка. По условию х – число натуральное, значит, наибольшее значение будет достигаться при х = 62, тогда наибольшее значение равно 2000+450×62 = 29900 рублей.
Ответ: 29900 рублей.
Задача №14. Производительность отдела в зависимости от количества сотрудников х, находящихся в офисе, описывается формулой y = -2х2+25х-8. Найдите, при каком числе сотрудников, находящихся в офисе, производительность отдела наибольшая.
Решение. Графиком функции y = -2х2+25х-8 является парабола, ветви которой направлены вниз. Значит, наибольшее значение она принимает в вершине параболы. Найдём абсциссу вершины
х0 =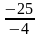
Количество сотрудников – число натуральное, значит наибольшее значение функция будет принимать при натуральном значении х, ближайшем к вершине, в данном случае х = 6.
Ответ:6
Заключение
В процессе нашей работы мы узнали, какие задачи относятся к экономическим, каких типов они бывают. В результате решения таких задач, мы поняли, что главное — это ориентироваться в базовых экономических понятиях и уметь составить математическую модель задачи. Таким образом своей цели мы достигли.
Результатами нашей работы мы планируем поделиться с учащимися 10 классов. Надеемся, что наш опыт поможет им в освоении экономических задач.
Список литературы
-
ЕГЭ. Математика. Профильный уровень : типовые экзаменационные варианты : 36 вариантов / под ред. И.В.Ященко. – М. : Издательство «Национальное образование», 2019.
-
ЕГЭ 2017. Математика. Профильный уровень. 50 вариантов типовых тестовых заданий/ И. В. Ященко, М. А. Волчкевич, И. Р. Высоцкий, Р. К. Гордин, П. В. Семёнов, О. Н. Косухин, Д. А. Фёдоровых, А. И. Суздальцев, А. Р. Рязановский, И. Н. Сергеев, В. А. Смирнов, А. В. Хачатурян, С. А. Шестаков, Д. Э. Шноль; под ред. И. В. Ященко. – М. : издательство «Экзамен», 2017.
-
Математика. ЕГЭ. Алгебра; задания с развернутым ответом: учебно – методическое пособие/ Под ред. Ф.Ф.Лысенко, С.Ю.Кулабухова. – Ростов-на-Дону: Легион, 2016.
-
Математика. ЕГЭ. Задача с экономическим содержанием: учебно – методическое пособие/ Под. ред. Ф. Ф. Лысенко и С. Ю. Кулабухова. – Изд. 2 – е., перераб. и доп. – Ростов н/Д: Легион, 2016.
-
Ященко И. В. Я сдам ЕГЭ! Математика. Курс самоподготовки. Технология решения заданий. Учеб. пособие для общеобразоват. организаций. Проф. Уровень. В 3 ч. Ч. 2. Алгебра и начала математического анализа/ И. В. Ященко, С. А. Шестаков. – М. : Просвещение, 2018.
-
http://www.fipi.ru
-
https://ege.sdamgia.ru
-
https://dic.academic.ru/dic.nsf/dic_economic_law/
22












































































































































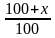 ;
;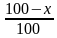 .
.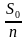
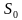
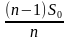
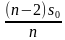
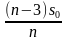
 =
=