Тренировочные варианты профильного ЕГЭ 2023 по математике с ответами.
Пробные и тренировочные варианты по математике профильного уровня в формате ЕГЭ 2023 из различных источников.
Варианты составлены в соответствии с демоверсией 2023 года
Тренировочные варианты ЕГЭ 2023 по математике (профиль)
| vk.com/pezhirovschool | |
| Вариант 1 | решения |
| Вариант 2 | решения |
| Вариант 3 | решения |
| Вариант 4 | решения |
| Вариант 5 (с ответами) | |
| Вариант 6 (с ответами) | |
| Вариант 7 (с ответами) | |
| Вариант 8 (с ответами) | |
| egemath.ru | |
| вариант 1 | скачать |
| вариант 2 | скачать |
| вариант 3 | скачать |
| вариант 4 | скачать |
| вариант 5 | скачать |
| вариант 6 | скачать |
| вариант 7 | скачать |
| вариант 8 | скачать |
| вариант 9 | скачать |
| вариант 10 | скачать |
| вариант 11 | скачать |
| вариант 12 | скачать |
| вариант 13 | скачать |
| вариант 14 | скачать |
| вариант 15 | скачать |
| вариант 16 | скачать |
| вариант 17 | скачать |
| вариант 18 | скачать |
| вариант 19 | скачать |
| вариант 20 | скачать |
| time4math.ru | |
| вариант 1-2 | ответы |
| вариант 3-4 | ответы |
| вариант 5-6 | ответы |
| вариант 7-8 | |
| yagubov.ru | |
| вариант 33 (сентябрь) | ege2023-yagubov-prof-var33 |
| вариант 34 (октябрь) | ege2023-yagubov-prof-var34 |
| вариант 35 (ноябрь) | ege2023-yagubov-prof-var35 |
| вариант 36 (декабрь) | ege2023-yagubov-prof-var36 |
| вариант 37 (январь) | ege2023-yagubov-prof-var37 |
| вариант 38 (февраль) | ege2023-yagubov-prof-var38 |
| math100.ru (с ответами) | |
| variant 179 | скачать |
| variant 180 | скачать |
| variant 181 | скачать |
| variant 182 | скачать |
| variant 183 | скачать |
| variant 184 | скачать |
| variant 185 | скачать |
| variant 186 | скачать |
| variant 187 | скачать |
| variant 188 | скачать |
| variant 189 | скачать |
| variant 190 | скачать |
| variant 191 | скачать |
| variant 192 | скачать |
| variant 193 | скачать |
| variant 194 | скачать |
| variant 195 | скачать |
| variant 196 | скачать |
| variant 197 | скачать |
| variant 198 | скачать |
| variant 199 | скачать |
| variant 200 | скачать |
| variant 201 | скачать |
| variant 202 | скачать |
| variant 203 | скачать |
| variant 204 | скачать |
| variant 205 | скачать |
| alexlarin.net | |
| Вариант 397 | проверить ответы |
| Вариант 398 | проверить ответы |
| Вариант 399 | проверить ответы |
| Вариант 400 | проверить ответы |
| Вариант 401 | проверить ответы |
| Вариант 402 | проверить ответы |
| Вариант 403 | проверить ответы |
| Вариант 404 | проверить ответы |
| Вариант 405 | проверить ответы |
| Вариант 406 | проверить ответы |
| Вариант 407 | проверить ответы |
| Вариант 408 | проверить ответы |
| Вариант 409 | проверить ответы |
| Вариант 410 | проверить ответы |
| Вариант 411 | проверить ответы |
| Вариант 412 | проверить ответы |
| Вариант 413 | проверить ответы |
| vk.com/ege100ballov | |
| вариант 1 | скачать |
| вариант 2 | скачать |
| вариант 3 | скачать |
| вариант 4 | скачать |
| вариант 5 | скачать |
| вариант 6 | скачать |
| вариант 7 | скачать |
| вариант 8 | скачать |
| вариант 9 | скачать |
| вариант 10 | скачать |
| вариант 11 | скачать |
| vk.com/math.studying | |
| Вариант 1 | ответы |
| vk.com/marsel_tutor | |
| Вариант 1 | разбор |
| Вариант 2 | конспект / разбор |
| Вариант 3 | конспект / разбор |
| Вариант 4 | конспект / разбор |
| Вариант 5 | конспект / разбор |
| Вариант 6 | разбор |
| vk.com/shkolkovo_easy_math | |
| Вариант 1 | решение |
| Вариант 2 | решение |
| Вариант 3 | решение |
| Вариант 5 | решение |
| Вариант 6 | решение |
| vk.com/mathlearn_ru | |
| вариант 1 | разбор |
| vk.com/ekaterina_chekmareva | |
| Вариант 1 | ответы |
| Вариант 2 | ответы |
| Вариант 3 | ответы |
| Вариант 4 | ответы |
| Вариант 5 | ответы |
| Вариант 6 | ответы |
| Вариант 7 | ответы |
| Вариант 8 | ответы |
Структура варианта КИМ ЕГЭ 2023 по математике профильного уровня
Экзаменационная работа состоит из двух частей и включает в себя 18 заданий, которые различаются по содержанию, сложности и количеству заданий:
– часть 1 содержит 11 заданий (задания 1–11) с кратким ответом в виде целого числа или конечной десятичной дроби;
– часть 2 содержит 7 заданий (задания 12–18) с развёрнутым ответом (полная запись решения с обоснованием выполненных действий).
Задания части 1 направлены на проверку освоения базовых умений и практических навыков применения математических знаний в повседневных ситуациях. Посредством заданий части 2 осуществляется проверка освоения математики на профильном уровне, необходимом для применения математики в профессиональной деятельности и на творческом уровне.
Задания части 1 предназначены для определения математических компетентностей выпускников образовательных организаций, реализующих программы среднего (полного) общего образования на базовом уровне. Задание с кратким ответом (1–11) считается выполненным, если в бланке ответов № 1 зафиксирован верный ответ в виде целого числа или конечной десятичной дроби.
Задания 12–18 с развёрнутым ответом, в числе которых 5 заданий повышенного уровня и 2 задания высокого уровня сложности, предназначены для более точной дифференциации абитуриентов вузов.
Примеры заданий:
1. Перед началом первого тура чемпионата по бадминтону участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 76 бадминтонистов, среди которых 22 спортсмена из России, в том числе Игорь Чаев. Найдите вероятность того, что в первом туре Игорь Чаев будет играть с каким-либо бадминтонистом из России.
2. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орёл не выпадет ни разу
3. На доске написали несколько не обязательно различных двузначных натуральных чисел без нулей в десятичной записи. Сумма этих чисел оказалась равной 363. Затем в каждом числе поменяли местами первую и вторую цифры (например, число 17 заменили на число 71).
а) Приведите пример исходных чисел, для которых сумма получившихся чисел ровно в 4 раза больше, чем сумма исходных чисел.
б) Могла ли сумма получившихся чисел быть ровно в 2 раза больше, чем сумма исходных чисел?
в) Найдите наибольшее возможное значение суммы получившихся чисел.
Смотрите также:
Критерии
Оценивание
| № задания | 1-11 | 12, 14, 15 | 13, 16 | 17, 18 | Всего |
|---|---|---|---|---|---|
| Баллы | 1 | 2 | 3 | 4 | 31 |
Экзаменационная работа состоит из двух частей, включающих в себя 18 заданий. Часть 1 содержит 11 заданий базового уровня сложности с кратким ответом. Часть 2 содержит 7 заданий с развёрнутым ответом повышенного и высокого уровней сложности.
На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).
Ответы к заданиям 1–11 записываются в виде целого числа или конечной десятичной дроби. Числа запишите в поля ответов в тексте работы, а затем перенесите в бланк ответов № 1, выданный на экзамене!
При выполнении работы Вы можете воспользоваться справочными материалами, выдаваемыми вместе с работой.
Разрешается использовать только линейку, но можно сделать циркуль своими руками. Запрещается использовать инструменты с нанесёнными на них справочными материалами. Калькуляторы на экзамене не используются.
На экзамене при себе надо иметь документ удостоверяющий личность (паспорт), пропуск и капиллярную или гелевую ручку с черными чернилами! Разрешают брать с собой воду (в прозрачной бутылке) и еду (фрукты, шоколадку, булочки, бутерброды), но могут попросить оставить в коридоре.
| № задания | 1-11 | 12, 14, 15 | 13, 16 | 17, 18 | Всего |
|---|---|---|---|---|---|
| Баллы | 1 | 2 | 3 | 4 | 31 |
Экзаменационная работа состоит из двух частей, включающих в себя 18 заданий. Часть 1 содержит 11 заданий базового уровня сложности с кратким ответом. Часть 2 содержит 7 заданий с развёрнутым ответом повышенного и высокого уровней сложности.
На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).
Ответы к заданиям 1–11 записываются в виде целого числа или конечной десятичной дроби. Числа запишите в поля ответов в тексте работы, а затем перенесите в бланк ответов № 1, выданный на экзамене!
При выполнении работы Вы можете воспользоваться справочными материалами, выдаваемыми вместе с работой.
Разрешается использовать только линейку, но можно сделать циркуль своими руками. Запрещается использовать инструменты с нанесёнными на них справочными материалами. Калькуляторы на экзамене не используются.
На экзамене при себе надо иметь документ удостоверяющий личность (паспорт), пропуск и капиллярную или гелевую ручку с черными чернилами! Разрешают брать с собой воду (в прозрачной бутылке) и еду (фрукты, шоколадку, булочки, бутерброды), но могут попросить оставить в коридоре.
Шкалирование
| Первичный | Тестовый | Оценка |
|---|---|---|
| 5-6 | 27-34 | 3 |
| 7-8 | 40-46 | 4 |
| 9-10 | 52-58 | |
| 11-12-13 | 64-66-68 | 5 |
| 14-15-16 | 70-72-74 | |
| 17-18-19 | 76-78-80 | |
| 20-21-22 | 82-84-86 | |
| 23-24-25 | 88-90-92 | |
| 26-27-28 | 94-96-98 | |
| 29-30-31 | 100 |
| Первичный балл / Тестовый балл |
5/27 | 6/34 | 7/40 | 8/46 | 9/52 | 10/58 | 11/64 | 12/66 | 13/68 | 14/70 |
|---|---|---|---|---|---|---|---|---|---|---|
| 15/72 | 16/74 | 17/76 | 18/78 | 19/80 | 20/82 | X / 2X+42 | 29+ / 100 |
Математика Профильный уровень
Об экзамене
Профильная математика – довольно коварная, обманчивая вещь. Вроде бы смотришь на задания первой части, думаешь, лол, что это за детский сад? А потом открываешь вторую часть, и в голове начинают крутиться совершенно другие мысли… И ведь подсознательно понимаешь, что это далеко не самые сложные вещи, но сколько всевозможных тонких моментов, о которые начинаешь сходу спотыкаться. Так что не впадайте в крайности, готовьтесь планомерно, по чуть-чуть повышайте сложность заданий и стремитесь к большему! Ведь профильная математика – это круто!
Структура
Часть 1 содержит 8 заданий (задания 1–8) с кратким ответом; часть 2 содержит 4 задания (задания 9–12) с кратким ответом заданий (задания 13–19) с развернутым ответом. По уровню сложности задания распределяются следующим образом: задания 1–8 имеют базовый уровень; задания 9–17 – повышенный уровень; задания 18 и 19 относятся к высокому уровню сложности.
На выполнение экзаменационной работы отводится 3 часа 55 минут (235 минут).
Пояснения к оцениванию заданий
Правильное решение каждого из заданий 1–12 оценивается 1 баллом. Задание считается выполненным верно, если экзаменуемый дал правильный ответ в виде целого числа или конечной десятичной дроби. Решения заданий с развернутым ответом оцениваются от 0 до 4 баллов. Полное правильное решение каждого из заданий 13–15 оценивается 2 баллами; каждого из заданий 16 и 17 – 3 баллами; каждого из заданий 18 и 19 – 4 баллами. Проверка выполнения заданий 13–19 проводится разработанной системы критериев оценивания.
| Тема | Результат | Задания | |||
|---|---|---|---|---|---|
| 1. | Простейшие текстовые задачи
Вычисления Округление с недостатком Округление с избытком Проценты Проценты и округление |
Не изучена | Отработать | ||
| 2. | Чтение графиков и диаграмм
Определение величины по графику Определение величины по диаграмме Вычисление величин по графику или диаграмме |
Не изучена | Отработать | ||
| 3. | Планиметрия: вычисление длин и площадей
Многоугольники: вычисление длин и углов Многоугольники: вычисление площадей Круг и его элементы Координатная плоскость |
Не изучена | Отработать | ||
| 4. | Начала теории вероятностей
Классическое определение вероятности Теоремы о вероятностях событий |
Не изучена | Отработать | ||
| 5. | Простейшие уравнения
Линейные, квадратные, кубические уравнения Рациональные уравнения Иррациональные уравнения Показательные уравнения Логарифмические уравнения Тригонометрические уравнения |
Не изучена | Отработать | ||
| 6. | Планиметрия
Прямоугольные треугольники Равнобедренные треугольники Треугольники общего вида Параллелограмм Трапеция Центральные и вписанные углы Касательная, хорда, секущая Вписанные окружности Описанные окружности |
Не изучена | Отработать | ||
| 7. | Производная и первообразная
Физический смысл производной Производная и касательная Применение производной к исследованию функций Определение свойств производной по заданной функции Определение свойств функции по заданной производной Первообразная |
Не изучена | Отработать | ||
| 8. | Стереометрия
Куб Прямоугольный параллелепипед Элементы составных многогранников Площадь поверхности составного многогранника Объем составного многогранника Призма Пирамида Комбинации тел Цилиндр Конус Сфера, шар |
Не изучена | Отработать | ||
| 9. | Вычисления и преобразования
Алгебраические выражения Рациональные выражения Иррациональные выражения Степенные выражения Логарифмические выражения Тригонометрические выражения |
Не изучена | Отработать | ||
| 10. | Задачи с прикладным содержанием
Разные задачи Линейные уравнения и неравенства Квадратные и степенные уравнения и неравенства Иррациональные уравнения и неравенства Рациональные уравнения и неравенства Логарифмические уравнения и неравенства Тригонометрические уравнения и неравенства Показательные уравнения и неравенства |
Не изучена | Отработать | ||
| 11. | Текстовые задачи
Задачи на сплавы и смеси Задачи на движение по прямой Задачи на движение по окружности Задачи на движение по воде Задачи на производительность Задачи на прогрессии Задачи на проценты |
Не изучена | Отработать | ||
| 12. | Наибольшее и наименьшее значение функций
Исследование степенных и иррациональных функций Исследование частных Исследование произведений Исследование показательных и логарифмических функций Исследование тригонометрических функций Исследование функций без помощи производной |
Не изучена | Отработать | ||
| Часть 2 | |||||
| 13. | Уравнения
Рациональные и иррациональные уравнения Логарифмические и показательные уравнения Тригонометрические уравнения Тригонометрические уравнения, исследование ОДЗ Уравнения смешанного типа |
Отработать | |||
| 14. | Углы и расстояния в пространстве
Задача на доказательство и вычисление Угол между скрещивающимися прямыми Угол между прямой и плоскостью Угол между плоскостями Расстояние от точки до прямой и до плоскости Расстояние между прямыми и плоскостями Сечения многогранников Объёмы многогранников Тела вращения: цилиндр, конус, шар |
Отработать | |||
| 15. | Неравенства
Рациональные неравенства Иррациональные неравенства Показательные неравенства Логарифмические неравенства Неравенства с логарифмами по переменному основанию Неравенства с модулем Смешанные неравенства |
Отработать | |||
| 16. | Планиметрическая задача
Многоугольники и их свойства Окружности и треугольники Окружности и четырёхугольники Окружности и системы окружностей Задача на доказательство и вычисление |
Отработать | |||
| 17. | Практические задачи
Банки, вклады, акции Кредиты (с установленными размерами платежей) Кредиты (с установленной схемой уменьшения долга) Задачи на оптимальный выбор Разные задачи |
Отработать | |||
| 18. | Уравнения, неравенства, системы с параметром
Комбинация «кривых» Кусочное построение графика функции Комбинация прямых Координаты (x, a) Левая и правая части в качестве отдельных графиков Перебор случаев Подвижная галочка Расстояние между точками Симметрия в решениях Уравнение окружности Функции, зависящие от параметра Уравнения с параметром Расположение корней квадратного трехчлена Использование симметрий, оценок, монотонности |
Отработать | |||
| 19. | Числа и их свойства
Числа и их свойства Числовые наборы на карточках и досках Последовательности и прогрессии Сюжетные задачи |
Отработать |
Любой учитель или репетитор может отслеживать результаты своих учеников по всей группе или классу.
Для этого нажмите ниже на кнопку «Создать класс», а затем отправьте приглашение всем заинтересованным.
Ознакомьтесь с подробной видеоинструкцией по использованию модуля.
Решение и ответы заданий демонстрационного варианта Проекта ЕГЭ 2023 по математике (профильный уровень). Полное решение. Демоверсия от ФИПИ для 11 класса профиль. Демовариант.
Задание 1.
Треугольник ABC вписан в окружность с центром О. Угол ВАС равен 32°. Найдите угол ВОС. Ответ дайте в градусах.
ИЛИ
Площадь треугольника ABC равна 24, DE – средняя линия, параллельная стороне АВ. Найдите площадь треугольника CDE.
ИЛИ
В ромбе ABCD угол DBA равен 13°. Найдите угол BCD. Ответ дайте в градусах.
ИЛИ
Стороны параллелограмма равны 24 и 27. Высота, опущенная на меньшую из этих сторон, равна 18. Найдите высоту, опущенную на большую сторону параллелограмма.
Задание 2.
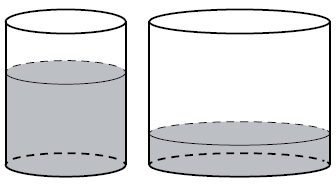
В первом цилиндрическом сосуде уровень жидкости достигает 16 см. Эту жидкость перелили во второй цилиндрический сосуд, диаметр основания которого в 2 раза больше диаметра основания первого. На какой высоте будет находиться уровень жидкости во втором сосуде? Ответ дайте в сантиметрах.
ИЛИ
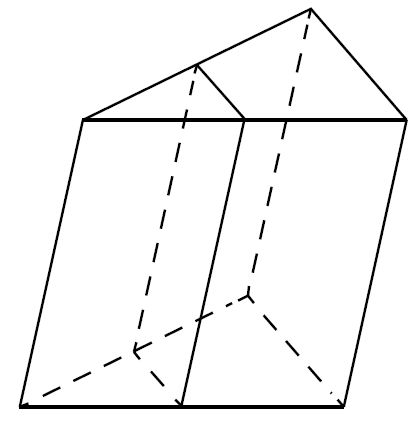
Площадь боковой поверхности треугольной призмы равна 24. Через среднюю линию основания призмы проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсечённой треугольной призмы.
ИЛИ
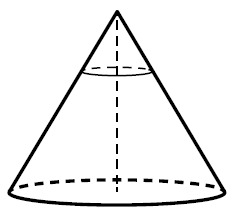
Через точку, лежащую на высоте прямого кругового конуса и делящую её в отношении 1:2, считая от вершины конуса, проведена плоскость, параллельная его основанию и делящая конус на две части. Каков объём той части конуса, которая примыкает к его основанию, если объём всего конуса равен 54?
Задание 3.
В сборнике билетов по биологии всего 25 билетов. Только в двух билетах встречается вопрос о грибах. На экзамене школьнику достаётся один случайно выбранный билет из этого сборника. Найдите вероятность того, что в этом билете будет вопрос о грибах.
ИЛИ
Вероятность того, что мотор холодильника прослужит более 1 года, равна 0,8, а вероятность того, что он прослужит более 2 лет, равна 0,6. Какова вероятность того, что мотор прослужит более 1 года, но не более 2 лет?
Задание 4.
Симметричную игральную кость бросили три раза. Известно, что в сумме выпало 6 очков. Какова вероятность события «хотя бы раз выпало три очка»?
ИЛИ
В городе 48% взрослого населения мужчины. Пенсионеры составляют 12,6% взрослого населения, причем доля пенсионеров среди женщин равна 15%. Для проведения исследования социологи случайным образом выбрали взрослого мужчину, проживающего в этом городе. Найдите вероятность события «выбранный мужчина является пенсионером».
Задание 5.
Найдите корень уравнения 3x–5 = 81
ИЛИ
Найдите корень уравнения sqrt{3x+49}=10.
ИЛИ
Найдите корень уравнения log8 (5x + 47) = 3
ИЛИ
Решите уравнение sqrt{2x+3}=x. Если корней окажется несколько, то в ответ запишите наименьший из них.
Задание 6.
Найдите sin2α, ecли cosα = 0,6 и π < α < 2π.
ИЛИ
Найдите значение выражения 16cdot log_{7}sqrt[4]{7}.
ИЛИ
Найдите значение выражения 4^{frac{1}{5}}cdot 16^{frac{9}{10}}.
Задание 7.
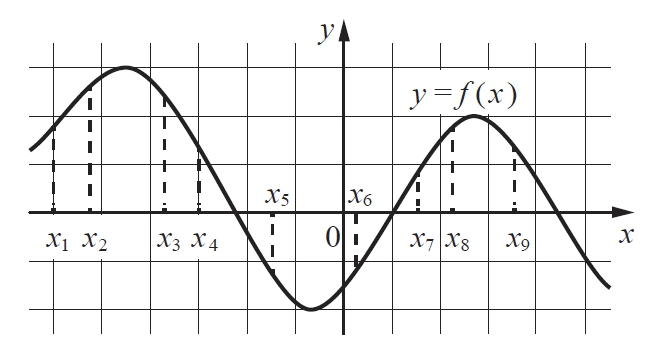
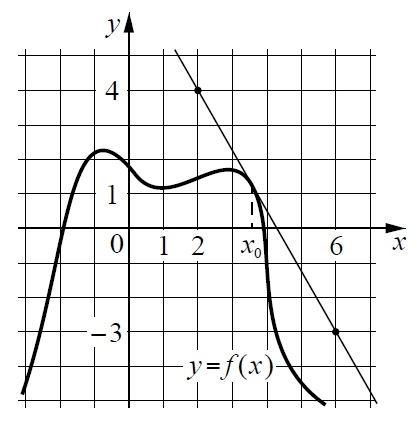
На рисунке изображён график дифференцируемой функции у = f(x). На оси абсцисс отмечены девять точек: x1, x2, … x9. 
Найдите все отмеченные точки, в которых производная функции f(x) отрицательна. В ответе укажите количество этих точек.
ИЛИ
На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой х0. Найдите значение производной функции f(x) в точке х0.
Задание 8.
Локатор батискафа, равномерно погружающегося вертикально вниз, испускает ультразвуковой сигнал частотой 749 МГц. Приёмник регистрирует частоту сигнала, отражённого от дна океана. Скорость погружения батискафа (в м/с) и частоты связаны соотношением
v=ccdot frac{f–f_{0}}{f+f_{0}},
где с = 1500 м/с – скорость звука в воде, f0 – частота испускаемого сигнала (в МГц), f – частота отражённого сигнала (в МГц). Найдите частоту отражённого сигнала (в МГц), если батискаф погружается со скоростью 2 м/с.
Задание 9.
Весной катер идёт против течения реки в 1frac{2}{3} раза медленнее, чем по течению. Летом течение становится на 1 км/ч медленнее. Поэтому летом катер идёт против течения в 1frac{1}{2} раза медленнее, чем по течению. Найдите скорость течения весной (в км/ч).
ИЛИ
Смешав 45-процентный и 97-процентный растворы кислоты и добавив 10 кг чистой воды, получили 62-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 72-процентный раствор кислоты. Сколько килограммов 45-процентного раствора использовали для получения смеси?
ИЛИ
Автомобиль, движущийся с постоянной скоростью 70 км/ч по прямому шоссе, обгоняет другой автомобиль, движущийся в ту же сторону с постоянной скоростью 40 км/ч. Каким будет расстояние (в километрах) между этими автомобилями через 15 минут после обгона?
Задание 10.
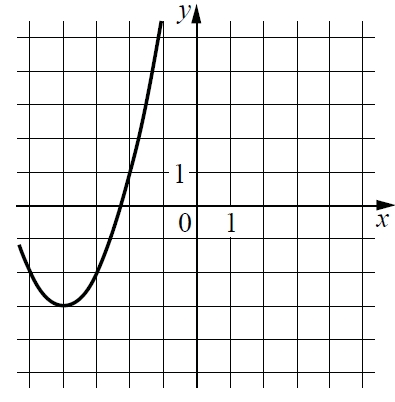
На рисунке изображён график функции вида f(x) = ax2 + bx + c, где числа a, b и c – целые. Найдите значение f(−12).
Задание 11.
Найдите наименьшее значение функции
y = 9x – 9ln(x + 11) + 7
на отрезке [–10,5 ; 0].
ИЛИ
Найдите точку максимума функции y = (x + 
2 ∙ e3–x
ИЛИ
Найдите точку минимума функции y=–frac{x}{x^{2}+256}.
Задание 12.
а) Решите уравнение 2sin(x+frac{pi}{2})+cos2x=sqrt{3}cosx+1.
б) Укажите корни этого уравнения, принадлежащие отрезку [-3pi;-frac{3pi}{2}].
Задание 13.
Все рёбра правильной треугольной призмы ABCA1B1C1 имеют длину 6. Точки M и N – середины рёбер AA1 и A1C1 соответственно.
а) Докажите, что прямые BM и MN перпендикулярны.
б) Найдите угол между плоскостями BMN и ABB1.
Задание 14.
Решите неравенство log_{11}(8x^{2}+7)-log_{11}(x^{2}+x+1)ge log_{11}(frac{x}{x+5}+7).
Задание 15.
15 января планируется взять кредит в банке на шесть месяцев в размере 1 млн рублей. Условия его возврата таковы:
– 1-го числа каждого месяца долг увеличивается на r процентов по сравнению с концом предыдущего месяца, где r – целое число;
– со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей.
Найдите наибольшее значение r, при котором общая сумма выплат будет меньше 1,2 млн рублей.
Задание 16.
Две окружности касаются внешним образом в точке K. Прямая AB касается первой окружности в точке A, а второй – в точке B. Прямая BK пересекает первую окружность в точке D, прямая AK пересекает вторую окружность в точке C.
а) Докажите, что прямые AD и BC параллельны.
б) Найдите площадь треугольника AKB, если известно, что радиусы окружностей равны 4 и 1.
Задание 17.
Найдите все положительные значения a, при каждом из которых система
begin{cases} (|x|-5)^{2}+(y-4)^{2}=9, \ (x+2)^{2}+y^{2}=a^{2} end{cases}
имеет единственное решение.
Задание 18.
В школах № 1 и № 2 учащиеся писали тест. В каждой школе тест писали по крайней мере 2 учащихся, а суммарно тест писали 9 учащихся. Каждый учащийся, писавший тест, набрал натуральное количество баллов. Оказалось, что в каждой школе средний балл за тест был целым числом. После этого один из учащихся, писавших тест, перешёл из школы № 1 в школу № 2, а средние баллы за тест были пересчитаны в обеих школах.
а) Мог ли средний балл в школе № 1 уменьшиться в 10 раз?
б) Средний балл в школе № 1 уменьшился на 10%, средний балл в школе № 2 также уменьшился на 10%. Мог ли первоначальный средний балл в школе № 2 равняться 7?
в) Средний балл в школе № 1 уменьшился на 10%, средний балл в школе № 2 также уменьшился на 10%. Найдите наименьшее значение первоначального среднего балла в школе № 2.
Источник варианта: fipi.ru
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 5 / 5. Количество оценок: 1
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
Математика 36 вариантов ЕГЭ 2023 ФИПИ школе Ященко профильный уровень 🔥
Таблица соответствия заданий ЕГЭ 2023 по математике профильного уровня по сравнению с ЕГЭ 2022
Федеральный институт ПИ в очередной раз славно потрудился и порадовал изменениями номеров заданий первой части в ЕГЭ по профильной математике.
Цитата от ФИПИ:
«В структуру части 1 КИМ внесены изменения, позволяющие участнику экзамена более эффективно организовать работу над заданиями за счет перегруппировки заданий по тематическим блокам…».
Итак, «новое» от перегруппировщиков:
| 2023 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 2022 | 3 | 5 | 2 | 10 | 1 | 4 | 6 | 7 | 8 | 9 | 11 |
| Планиметрия | Стереометрия | Вероятность | Вероятность | Уравнения | Выражения | Смысл производной | Прикладная физическая | Текстовая | График функции | Исследование функции |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| Уравнения | Стереометря | Неравенства | Экономическая | Планиметрия | Параметры | Числа и их свойства |
Планируемые изменения в КИМ ЕГЭ 2023 года
Планируемые изменения в КИМ ЕГЭ 2023 года
Демонстрационный вариант контрольных измерительных материалов единого государственного экзамена 2023 года по МАТЕМАТИКЕ Профильный уровень
ФИПИ Демовариант по математике профиль ЕГЭ 2023 года
Демонстрационный вариант контрольных измерительных материалов единого государственного экзамена 2023 года по Русскому языку
ФИПИ Демовариант по Русскому языку ЕГЭ 2023 года Проект
Критерии оценивания ЕГЭ для апелляции
Критерии оценивания 2 части ЕГЭ по математике профильного уровня ФИПИ
Скачать в PDF
ЕГЭ по математике 2022 основная волна 02.06.2022
Решение заданий вариантов ЕГЭ по математике профильного уровня основной волны 2 июня 2022 года
ОГЭ по математике 2022
Решение заданий вариантов ОГЭ по математике основной волны 23 мая 2022 года
Досрочный ЕГЭ по математике 2022
Решение заданий вариантов досрочного ЕГЭ по математике основной волны профильного уровня 18 марта 2022 года
Математика 36 вариантов ЕГЭ 2022 ФИПИ школе Ященко профильный уровень
Математика 50 вариантов заданий ЕГЭ 2022 Ященко
Таблица соответствия заданий ЕГЭ 2022 профильного уровня по сравнению с ЕГЭ 2021
| Стало | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| Было | 5 | 4 | 6 | 9 | 8 | 7 | 10 | 11 | — | 4 | 12 | 13 | 14 | 15 | 17 | 16 | 18 | 19 |
| Баллы | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 2 | 3 | 2 | 2 | 3 | 4 | 4 |
Демонстрационный вариант ЕГЭ 2022 года ФИПИ КИМ по математике профильного уровня (Проект). Критерии, ответы
Решение заданий демонстрационного варианта ЕГЭ 2022 года ФИПИ по математике профильного уровня
Скачать в PDF Демонстрационный вариант ЕГЭ 2022 года ФИПИ по математике профильного уровня (Проект)
Демонстрационный вариант ЕГЭ 2022 года ФИПИ КИМ по математике базового уровня (Проект). Ответы
Скачать в PDF Демонстрационный вариант ЕГЭ 2022 года ФИПИ по математике базового уровня (Проект)
ЕГЭ по математике профильного уровня 07.06.2021 основная волна
Решение заданий вариантов ЕГЭ по математике 2021 года основной волны профильного уровня 7 июня
ЕГЭ по математике 2021 профильного уровня резервный день
Решение заданий вариантов ЕГЭ по математике 2021 года резервного дня
Открытые варианты КИМ ЕГЭ 2021
Открытый вариант КИМ ЕГЭ по математике 2021 (профильная)
Скачать в PDF Открытый вариант КИМ ЕГЭ 2021 по математике (профильная)
Решение открытого варианта КИМ ЕГЭ по математике 2021 (профильного уровня) ФИПИ
Открытый вариант КИМ ЕГЭ по русскому языку 2021
Скачать в PDF Открытый вариант КИМ ЕГЭ 2021 по русскому языку
Открытый вариант КИМ ЕГЭ по физике 2021
Скачать в PDF Открытый вариант КИМ ЕГЭ 2021 по физике
Открытый вариант КИМ ЕГЭ по информатике 2021
Скачать в PDF Открытый вариант КИМ ЕГЭ 2021 по информатике
Открытый вариант КИМ ЕГЭ по обществознанию 2021
Скачать в PDF Открытый вариант КИМ ЕГЭ 2021 по обществознанию
Математика 50 вариантов заданий ЕГЭ 2021 Ященко
Математика 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко профильный уровень
Демонстрационный вариант ЕГЭ 2021 года ФИПИ КИМ по математике профильного уровня (Проект). Критерии, ответы
Скачать в PDF Демонстрационный вариант ЕГЭ 2021 года ФИПИ по математике профильного уровня
Решение заданий демонстрационного варианта ЕГЭ 2021 года ФИПИ по математике профильного уровня
Демонстрационный вариант ЕГЭ 2021 года ФИПИ КИМ по математике базового уровня (Проект). Ответы
Скачать в PDF Демонстрационный вариант ЕГЭ 2021 года ФИПИ по математике базового уровня
Демонстрационный вариант ОГЭ 2021 года ФИПИ КИМ по математике (Проект). Критерии, ответы
Скачать в PDF Демонстрационный вариант ОГЭ 2021 года ФИПИ по математике
Открытые варианты досрочного (отменённого) ЕГЭ 2020
Открытые варианты досрочного (отменённого) ЕГЭ 2020 по математике профильного уровня
Открытые варианты досрочного (отменённого) ЕГЭ 2020 по информатике
Открытые варианты досрочного (отменённого) ЕГЭ 2020 по физике
Открытые варианты досрочного (отменённого) ЕГЭ 2020 по обществознанию