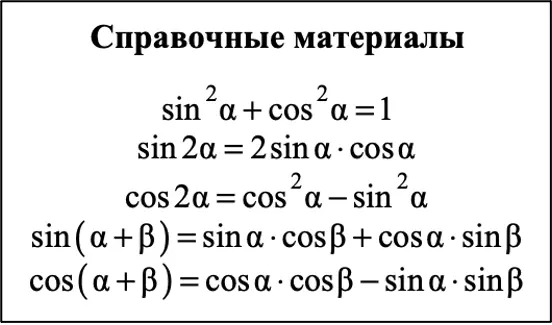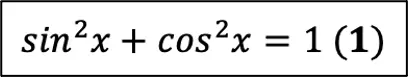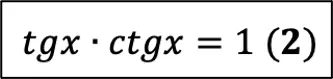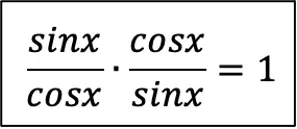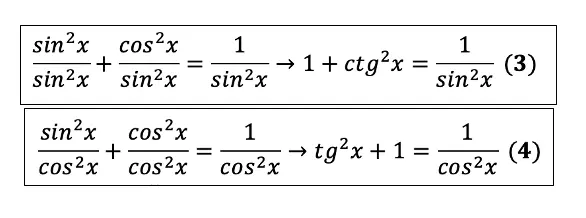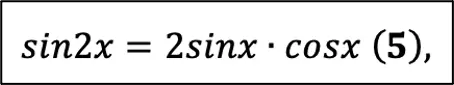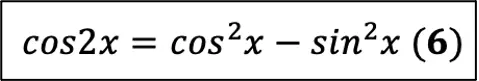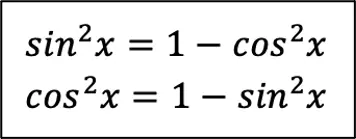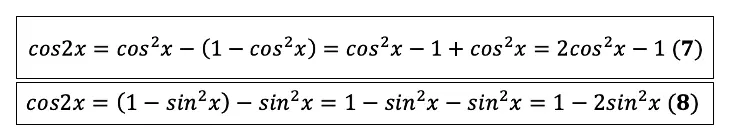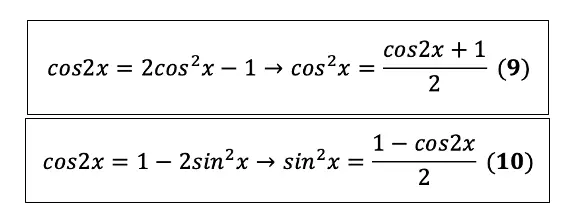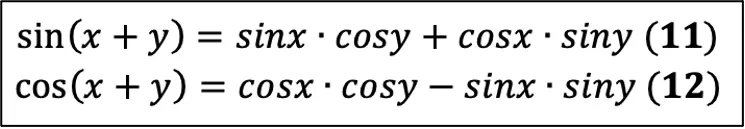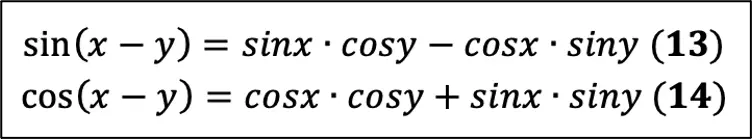Фипи егэ тригонометрия

Сайты, меню, вход, новости

23 марта 2022

В закладки

Обсудить

Жалоба

Задачи ЕГЭ с тригонометрией

Подборка заданий для тренировки профильного уровня.

Без ответов.

Задание 1. Простейшие уравнения
Задание 4. Вычисления и преобразования
Задание 7. Задачи с прикладным содержанием
Задание 11. Наибольшее и наименьшее значение функций
Задание 12

s-tr.pdf

Источник: vk.com/trigonometrics2122

Чуть больше 30% выпускников справляется с тригонометрией на ЕГЭ по математике. И неудивительно: для решения заданий из базы и профиля надо знать очень много формул, которые сложно освоить за 1-2 года. На самом деле, это миф! Чтобы решить задания по тригонометрии, нужно знать всего 5 формул — и просто уметь ими пользоваться.

Тригонометрия на ЕГЭ: основные проблемы темы

Чаще всего тригонометрию начинают изучать в 10 классе — но в некоторых школах оставляют до 11. В первом случае у учеников есть 2 года, чтобы освоить новую тему. А во втором, к сожалению, всего год. И это проблема. Дело в том, что в тригонометрии очень много формул, которые нужно знать, чтобы успешно решать задания. Если за 2 года их можно успеть выучить, то за год это будет сделать проблематично.

Ситуация осложняется ещё двумя факторами. Во-первых, в самой математике много формул, признаков, теорем и т.д. Во-вторых, кроме математики есть и другие экзамены, для которых нужно выучить большой объём информации.

Именно поэтому я всегда советую своим ученикам не учить формулы для тригонометрии на ЕГЭ, а выводить! Но об этом мы поговорим чуть позже, а сейчас давайте обсудим, почему тригонометрия так важна и где в ЕГЭ ее можно встретить.

Задания по тригонометрии в базе и профиле на ЕГЭ

Так как ЕГЭ по математике делится на базовый и профильный, а тригонометрия встречается в обоих, то давайте рассмотрим оба уровня экзамена.

Тригонометрия в базе

Что касается Базового уровня, то в нём всего 3 задания, в которых можно столкнуться с тригонометрией:

В № 7 в виде простейшего выражения

Как правило, для успешного решения таких заданий достаточно воспользоваться формулами из справочного материала.

В № 8 в виде формулы прикладной задачи

Стоит отметить, что в базовом ЕГЭ в прикладных задачах тригонометрия попадается редко, но нужно быть готовыми.

В № 15 как тригонометрия в геометрии

В справочном материале есть вся необходимая информация для успешного решения данного задания, а именно определение всех тригофункций в прямоугольном треугольнике.

Тригонометрия в профиле

Базовый уровень мы рассмотрели, теперь перейдём к профильному. Здесь уже больше вариантов, в которых можно встретиться с тригонометрией. Давайте посмотрим на Части 1 и 2.

В № 3 как тригонометрия в геометрии (Часть 1)

То же самое задание, как в базовом ЕГЭ, вот только в справочном материале уже нет необходимой информации.

В № 4 в виде выражения (Часть 1)

То же самое задание, как в базовом ЕГЭ.

В № 7 в виде формулы прикладной задачи (Часть 1)

То же самое задание, как в базовом ЕГЭ. Для успешного решения подойдут базовые навыки работы с тригонометрией.

В № 11 как часть функции (Часть 1)

Функцию нужно проанализировать для поиска наибольшего/наименьшего значения или точек максимума/минимума.

Если с Частью 1 профиля всё более-менее очевидно, то во второй части бывают сюрпризы, о которых ученики даже не подозревают. Да-да, тригонометрия на ЕГЭ умеет прятаться и в Части 2. Давайте посмотрим на эти задания.

В № 12 (Часть 2)

Тут сюрпризов нет. Это уравнение второй части, в котором ученики как раз ожидают увидеть тригонометрию, хотя она там бывает не всегда!

В № 13 — стереометрия (Часть 2)

Да, тригонометрия может встретиться здесь в виде теоремы синусов или теоремы косинусов, а ещё в виде формул в методе координат (для любителей решать этим методом).

В № 16 — планиметрия (Часть 2)

Здесь всё аналогично стереометрии: есть геометрические формулы, в которых прячется тригонометрия. Ведь, как я и сказала выше, в геометрии она тоже бывает!

5 формул тригонометрии: теория для ЕГЭ

А теперь предлагаю перейти к самому интересному — а именно к формулам. К сожалению, их действительно много. А ещё они похожи, и если их просто учить (или бездумно зубрить), то велик риск перепутать «+» с «–» или забыть какую-нибудь единичку.

Именно поэтому я рекомендую не учить формулы, а выводить. Это очень удобно тем более, что в профильном ЕГЭ по математике весь справочный материал состоит из 5-ти формул тригонометрии, из которых очень легко выводятся все остальные.

Но прежде чем я расскажу вам, как выводятся тригонометрические формулы, пообещайте, что обязательно отработаете все правила выведения! Для этого нужно будет регулярно выводить формулы по указанным ниже схемам.

Вот формулы, которые будут у вас в справочном материале:

Формула № 1 и как она пригодится в поиске котангенса и тангенса

Первая формула — основное тригонометрическое тождество (ОТТ):

Обычно ученики знают ее очень хорошо. Она связывает синус и косинус и помогает найти одну функцию через другую.

С этой формулой косвенно связана другая (ее нет в справочном материале), которая тоже легко дается школьникам:

Эту формулу очень легко запомнить, если знать, как можно расписать тангенс и котангенс через синус и косинус:

Эти 2 формулы связывают по отдельности синус с косинусом и тангенс с котангенсом. Но иногда требуется, чтобы были связаны все 4 функции, и здесь на помощь приходят следствия из ОТТ (как раз та самая формула № 1).

Чтобы вывести следствия нужно всего лишь разделить ОТТ на sin² и cos²:

Теперь можно легко найти:

• котангенс, зная синус,
• или тангенс, зная косинус.

Формула № 2 и что из нее можно вывести

С тождествами разобрались, давайте перейдём к формулам двойного угла. Что касается синуса двойного угла (вторая формула в справочном материале):

Здесь всё просто, берёте и применяете формулу, если видите, что она нужна для задания.

Формула № 3 и что из нее можно вывести

А вот с косинусом двойного угла (третья формула в справочном материале) всё интереснее. Безусловно, косинус двойного угла:

в чистом виде встречается, и тогда вы делаете всё тоже самое, что с синусом. Но на самом деле есть ещё 2 формулы, которые очень просто вывести, используя ОТТ (формулу № 1). Для начала нужно выразить квадрат синуса и квадрат косинуса из ОТТ (Шаг 1):

А потом нужно подставить эти значения в формулу (6, или третья формула справочного материала) (Шаг 2):

Вот мы вывели ещё 2 формулы! А сейчас я покажу вам как практически ничего не делая получить ещё 2. Мы будем выводить формулы понижения степени из формул двойного угла. Смотрите, нужно всего лишь выразить одно из другого:

Формулы № 4 и 5 и что из них можно вывести

Давайте посмотрим на справочный материал, у нас там ещё целых 2 формулы, из которых мы получим конечно же ещё 2! Сейчас вообще ничего удивительного не будет. Вот формулы, которые уже даны:

Как вы заметили, они для суммы углов, а чтобы получить формулы для разности углов, нам нужно всего лишь поменять знаки в формуле на противоположные (разумеется, я говорю про «+» и «–»):

Вот так при помощи нехитрых преобразований из 5-ти формул справочного материала мы получили целых 14!

Все скриншоты взяты из открытого банка заданий ФИПИ или из демоверсий ЕГЭ по математике 2022.

Что еще пригодится вам для тригонометрии на ЕГЭ

Скажу по секрету, что это далеко не все формулы тригонометрии, которые существуют. Есть и другие:

• некоторые можно вывести из вышеуказанных,
• некоторые можно обобщить и вместо огромного количества формул использовать короткое правило.

Но мне кажется, что пока этого и так много!

А чтобы отрабатывать выведение было не так скучно, держите моего котика, который любезно согласился позировать в позе котангенса:

1. Найдите значение выражения .

2. Найдите значение выражения .

3. Найдите , если  и .

4. Найдите значение выражения .

5. Найдите значение выражения .

6. Найдите значение выражения .

7. Найдите , если  и .

8. Найдите значение выражения .

9. Найдите значение выражения .

10. Найдите , если .

11. Найдите , если  и .

12. Найдите значение выражения .

13. Найдите значение выражения 

14. Найдите значение выражения .

15. Найдите значение выражения .

16. Найдите , если .

17. Найдите , если  и .

18. Найдите значение выражения .

19. Найдите значение выражения .

20. Найдите значение выражения , если .

21. Найдите , если  и .

22. Найдите , если  и .

23. Найдите , если  и .

24. Найдите значение выражения .

25. Найдите значение выражения .

26. Найдите значение выражения .

27. Найдите , если .

28. Найдите значение выражения .

29. Найдите , если 

30. Найдите значение выражения .

31. Найдите значение выражения .

32. Найдите значение выражения .

33. Найдите значение выражения .

34. Найдите значение выражения .

35. Найдите , если .

36. Найдите , если  и .

37. Найдите , если  и .

38. Найдите значение выражения .

39. Найдите значение выражения .

40. Найдите значение выражения .

41. Найдите значение выражения .

42. Найдите значение выражения 

43. Найдите значение выражения .

44. Найдите , если .

45. Найдите значение выражения .

46. Найдите значение выражения .

47. Найдите значение выражения .

48. Найдите значение выражения 

49. Найдите , если .

50 Найдите значение выражения .

51. Найдите значение выражения .

52. Найдите значение выражения .

53. Найдите значение выражения 

54. Найдите значение выражения 

55. Найдите , если .

56. Найдите , если .

57. Найдите , если 

58. Найдите , если .

59. Найдите , если  и 

60. Найдите значение выражения 

61. Найдите значение выражения .

62. Найдите значение выражения .

63. Найдите , если  и .

64. Найдите , если 

65. Найдите , если .

66. Найдите , если  и .

67. Найдите значение выражения .

68. Найдите значение выражения .

69. Найдите , если .

70. Найдите значение выражения .

71. Найдите значение выражения .

72. Найдите значение выражения .

73. Найдите значение выражения , если .

74. Найдите значение выражения .

75. Найдите , если  и .

76. Найдите , если  и .

77. Найдите значение выражения .

78. Найдите значение выражения .

79. Найдите значение выражения .

80. Найдите значение выражения .

81. Найдите значение выражения .

82. Найдите значение выражения , если .

83. Найдите значение выражения .

84. Найдите значение выражения .

85 Найдите значение выражения .

86. Найдите значение выражения .

87. Найдите , если .

88. Найдите значение выражения .

89. Найдите значение выражения .

90. Найдите значение выражения .

91. Найдите значение выражения: 

92. Найдите , если .

93. Найдите , если  и .

94. Найдите значение выражения .

95. Найдите значение выражения .

96. Найдите значение выражения .

97. Найдите значение выражения .

98. Найдите значение выражения .

99. Найдите значение выражения .

100. Найдите значение выражения .

101. Найдите значение выражения .

102. Найдите значение выражения .

103. Найдите значение выражения: .

104. Найдите значение выражения: .

105. Найдите значение выражения .

106. Найдите значение выражения .

107. Найдите значение выражения .

109. Найдите корень уравнения . В ответе напишите наименьший положительный корень.

• Задание №77413

Найдите значение
выражения 5sin74∘cos37∘⋅cos53∘.

• Задание №26784

Найдите sin(7π/2−α), если sinα=0,8 и α∈(π/2;π).

• Задание №26773

Найдите значение
выражения 6cos²23∘+cos²113∘.

• Задание №26780

Найдите 10sin6α3cos3α, если sin3α=0,6.

• Задание №26763

Найдите значение
выражения −182√sin(−135∘).

• Задание №26762

Найдите значение
выражения 23√tg(−300∘).

• Задание №26755

Найдите значение
выражения 12sin11∘⋅cos11∘sin22∘.

• Задание №139A29

Найдите значение
выражения 30tg3°⋅tg87°−43 .

• Задание №26766

Найдите значение
выражения 4cos146∘cos34∘.

• Задание №26759

Найдите значение
выражения 42√cosπ4cos7π3.

• Задание №26791

Найдите tgα, если 3sinα−5cosα+2sinα+3cosα+6=13.

• Задание №26760

Найдите значение
выражения 8sin(−27π4)cos(31π4).

• Задание №26785

Найдите 26cos(3π2+α), если cosα=1213 и α∈(3π2;2π).

• Задание №26774

Найдите значение
выражения 12sin227∘+cos2207∘.

• Задание №26776

Найдите tgα, если sinα=−526√ и α∈(π;3π2).

• Задание №77412

Найдите значение
выражения 5sin98∘sin49∘⋅sin41∘.

• Задание №26770

Найдите значение
выражения 5tg17∘⋅tg107∘.

• Задание №26787

Найдите tg2α, если 5sin2α+13cos2α=6.

• Задание №26781

Найдите значение
выражения 3cos(π−β)+sin(π2+β)cos(β+3π).

• Задание №26769

Найдите значение
выражения 14sin409∘sin49∘.

• Задание №26758

Найдите значение
выражения 366√tgπ6sinπ4.

• Задание №26786

Найдите tg(α+5π2), если tgα=0,4.

• Задание №26792

Найдите значение
выражения 7cos(π+β)−2sin(π2+β), если cosβ=−13.

• Задание №0220E4

Найдите tgα, если cosα=529√29 и α∈(3π2; 2π).

• Задание №26765

Найдите значение
выражения 14sin19∘sin341∘.

• Задание №26761

Найдите значение
выражения −43√cos(−750∘).

• Задание №26771

Найдите значение
выражения 7tg13∘⋅tg77∘.

• Задание №26793

Найдите значение
выражения 5sin(α−7π)−11cos(3π2+α), если sinα=−0,25.

• Задание №26782

Найдите значение
выражения 2sin(α−7π)+cos(3π2+α)sin(α+π).

• Задание №26775

Найдите tgα, если cosα=10√10 и α∈(3π2;2π).

• Задание №26757

Найдите значение
выражения 5cos29∘sin61∘.

• Задание №26779

Найдите 24cos2α, если sinα=−0,2.

• Задание №26789

Найдите 10cosα+4sinα+152sinα+5cosα+3, если tgα=−2,5.

• Задание №26764

Найдите значение
выражения 242√cos(−π3)sin(−π4).

• Задание №26778

Найдите 5sinα, если cosα=26√5 и α∈(3π2;2π).

• Задание №26772

Найдите значение
выражения 12sin237∘+sin2127∘.

• Задание №26783

Найдите значение
выражения 5tg(5π−γ)−tg(−γ), если tgγ=7.

• Задание №26794

Найдите 9cos2α, если cosα=13.

• Задание №77414

Найдите значение
выражения: 12sin150∘⋅cos120∘.

• Задание №26756

Найдите значение
выражения 24(sin217∘−cos217∘)cos34∘.

• Задание №26790

Найдите tgα, если 7sinα+13cosα5sinα−17cosα=3.

• Задание №26767

Найдите значение
выражения 5tg163∘tg17∘.

• Задание №26777

Найдите 3cosα, если sinα=−22√3 и α∈(3π2;2π).

• Задание №26788

Найдите 3cosα−4sinα2sinα−5cosα, если tgα=3.

• Задание №4C550F

Найдите cosα, если sinα=− 51√10 и α∈(π; 3π2).