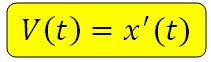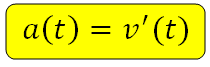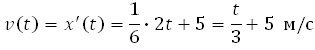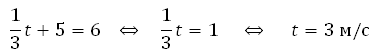Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Материальная точка движется прямолинейно по закону (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). Найдите ее скорость (в м/с) в момент времени t = 9 с.
2
Материальная точка движется прямолинейно по закону (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). Найдите ее скорость в (м/с) в момент времени t = 6 с.
3
Материальная точка движется прямолинейно по закону (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). Найдите ее скорость в (м/с) в момент времени
с.
4
Материальная точка движется прямолинейно по закону (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). В какой момент времени (в секундах) ее скорость была равна 3 м/с?
5
Материальная точка движется прямолинейно по закону (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). В какой момент времени (в секундах) ее скорость была равна 2 м/с?
Пройти тестирование по этим заданиям
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Материальная точка движется прямолинейно по закону (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). Найдите ее скорость (в м/с) в момент времени t = 9 с.
2
Материальная точка движется прямолинейно по закону (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). Найдите ее скорость в (м/с) в момент времени t = 6 с.
3
Материальная точка движется прямолинейно по закону (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). Найдите ее скорость в (м/с) в момент времени
с.
4
Материальная точка движется прямолинейно по закону (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). В какой момент времени (в секундах) ее скорость была равна 3 м/с?
5
Материальная точка движется прямолинейно по закону (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). В какой момент времени (в секундах) ее скорость была равна 2 м/с?
Пройти тестирование по этим заданиям
Лучшие репетиторы для сдачи ЕГЭ
Задания по теме «Физический смысл производной»
Открытый банк заданий по теме физический смысл производной. Задания B7 из ЕГЭ по математике (профильный уровень)
Геометрические фигуры на плоскости: вычисление величин с использованием углов
Геометрические фигуры в пространстве: нахождение длины, площади, объема
Задание №1148
Тип задания: 7
Тема:
Физический смысл производной
Условие
Материальная точка движется прямолинейно по закону x(t)=frac14t^3-4t^2+t, где x —расстояние от точки отсчёта в метрах, t — время в секундах, измеренное с начала движения. В какой момент времени (в секундах) её скорость была 13 м/с?
Показать решение
Решение
Согласно физическому смыслу производной необходимо решить уравнение x'(t)=13.
x'(t)=frac34t^2-8t+1. Решаем уравнение:
frac34t^2-8t+1=13,
frac34t^2-8t-12=0,
3t^2-32t-48=0,
t_{1,2}= frac{16pmsqrt{256+3cdot48}}{3}= frac{16pmsqrt{400}}{3}= frac{16pm20}{3}.
t_1=-frac43, t_2=12.
Так как tgeqslant0, то t=12.
Ответ
12
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1138
Тип задания: 7
Тема:
Физический смысл производной
Условие
Материальная точка движется прямолинейно по закону x(t)=-t^4+7t^3+6t+16, где x — расстояние от точки отсчёта в метрах, t — время в секундах, измеренное с начала движения. Найдите её скорость (в метрах в секунду) в момент времени t=5 с.
Показать решение
Решение
Согласно физическому смыслу производной необходимо найти x'(5).
x'(t)=-4t^3+21t^2+6.
x'(5)= -4cdot 5^3+21cdot 5^2+6= -500+525+6= 31.
Ответ
31
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №899
Тип задания: 7
Тема:
Физический смысл производной
Условие
Материальная точка движется прямолинейно по закону x(t)=frac14t^3-4t^2+t, где
х — расстояние от точки отсчёта в метрах,
t — время в секундах, измеренное с начала движения.
Найдите её скорость (в метрах в секунду) в момент времени t = 12 с.
Показать решение
Решение
Согласно физическому смыслу производной необходимо найти x'(12).
x'(t) = frac34t^2-8t+1,
x'(12) = frac34cdot12^2-8cdot12+1= 108-96+1=13.
Ответ
13
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №304
Тип задания: 7
Тема:
Физический смысл производной
Условие
Материальная точка движется прямолинейно по закону x(t)=frac13 t^3-t^2-5t+18, где
x — расстояние от точки отсчета в метрах,
t — время в секундах, измеряемое с начала движения.
В какой момент времени (в секундах) ее скорость была равна 10 м/с?
Показать решение
Решение
Найдем скорость движения точки: v(t)=x'(t)=t^2-2t-5.
По условию v(t)=10 м/с, значит, t^2-2t-5=10,
t^2-2t-15=0,
t_1=5,;t_2=-3.
По смыслу задачи tgeq 0, следовательно, t=5 с.
Ответ
5
Источник: «Математика. Подготовка к ЕГЭ-2016. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №89
Тип задания: 7
Тема:
Физический смысл производной
Условие
Закон прямолинейного движения материальной точки равен x(t)=-frac13t^4+4t^3-7t^2-5t-5, где
x – расстояние от точки отсчета (м);
t – время с начала движения (с).
Найдите скорость точки в момент времени t = 6 с. Ответ выразите в метрах в секунду
Показать решение
Решение
Скорость точки в определенный момент времени определяется как производная ее координаты в этот момент времени:
V(t)=frac{dx(t)}{dt}=-frac43t^3+12t^2-14t-5.
Найдем скорость в момент времени t = 6:
V(6)=-frac43cdot 216+12cdot 36-14cdot 6-5=-377+432=55 м/с
Ответ
55
Задание №88
Тип задания: 7
Тема:
Физический смысл производной
Условие
Закон прямолинейного движения материальной точки равен x(t)=frac12t^2+2t-15, где
x – расстояние от точки отсчета (м);
t – время с начала движения (с).
Найдите скорость точки в момент времени t = 7 с. Ответ выразите в метрах в секунду
Показать решение
Решение
Скорость точки в определенный момент времени определяется как производная ее координаты в этот момент времени:
V(t)=frac{dx(t)}{dt}=t+2.
Найдем скорость в момент времени t = 7:
V (7) = 7 + 2 = 9 м/с
Ответ
9
Лучшие репетиторы для сдачи ЕГЭ
Сложно со сдачей ЕГЭ?
Звоните, и подберем для вас репетитора: 78007750928
15 мая 2014
Иногда в задаче 6 из ЕГЭ по математике вместо всеми любимых графиков функции или производной дается просто уравнение расстояния от точки до начала координат. Что делать в этом случае? Как по расстоянию найти скорость или ускорение.
На самом деле все просто. Скорость — это производная от расстояния, а ускорение — это производная скорости (или, что то же самое, вторая производная от расстояния). В этом коротком видео вы убедитесь, что такие задачи решаются ничуть не сложнее «классических» заданий 6.
Сегодня мы разберем две задачи на физический смысл производных из ЕГЭ по математике. Эти задания встречаются в части Bи существенно отличаются от тех, что большинство учеников привыкло видеть на пробниках и экзаменах. Все дело в том, что они требуют понимать физический смысл производной функции. В данных задачах речь пойдет о функциях, выражающих расстояния.
Если $S=xleft( t right)$, то $v$ мы можем посчитать следующим образом:
[v={S}’={x}’left( t right)]
Точно так же мы можем посчитать и ускорение:
[a={v}’={{S}’}’={{x}’}’left( t right)]
Эти три формулы – все, что вам потребуется для решения таких примеров на физический смысл производной. Просто запомните, что $v$ — это производная от расстояния, а ускорение — это производная от скорости.
Давайте посмотрим, как это работает при решении реальных задач.
Пример № 1
Материальная точка движется по закону:
[xleft( t right)=-frac{1}{5}{{t}^{5}}+{{t}^{4}}-{{t}^{3}}+5t]
где $x$ — расстояние от точки отсчета в метрах, $t$ — время в секундах, прошедшее с начала движения. Найдите скорость точки (в м/с) в момент времени $t=2c$.
Это означает, что у нас есть функция, задающая расстояние, а нужно посчитать скорость в момент времени $t=2c$. Другими словами, нам нужно найти $v$, т.е.
[v={S}’={x}’left( 2 right)]
Вот и все, что нам нужно было выяснить из условия: во-первых, как выглядит функция, а во-вторых, что от нас требуется найти.
Давайте решать. В первую очередь, посчитаем производную:
[{x}’left( t right)=-frac{1}{5}cdot 5{{t}^{4}}+4{{t}^{3}}-3{{t}^{2}}+5]
[{x}’left( t right)=-{{t}^{4}}+4{{t}^{3}}-3{{t}^{2}}+5]
Нам требуется найти производную в точке 2. Давайте подставим:
[{x}’left( 2 right)=-{{2}^{4}}+4cdot {{2}^{3}}-3cdot {{2}^{2}}+5=]
[=-16+32-12+5=9]
Вот и все, мы нашли окончательный ответ. Итого, скорость нашей материальной точки в момент времени $t=2c$ составит 9 м/с.
Пример № 2
Материальная точка движется по закону:
[xleft( t right)=frac{1}{3}{{t}^{3}}-4{{t}^{2}}+19t-11]
где $x$ — расстояние от точки отсчета в метрах, $t$ — время в секундах, измеренное с начала движения. В какой момент времени ее скорость была равна 3 м/с?
Взгляните, в прошлый раз от нас требовалось найти $v$ в момент времени 2 с, а в этот раз от нас требуется найти тот самый момент, когда эта скорость будет равна 3 м/с. Можно сказать, что нам известно конечное значение, а по этому конечному значению нам требуется найти исходное.
В первую очередь, вновь ищем производную:
[{x}’left( t right)=frac{1}{3}cdot 3{{t}^{2}}-4cdot 2t+19]
[{x}’left( t right)={{t}^{2}}-8t+19]
От нас просят найти, в какой момент времени скорость будет равна 3 м/с. Составляем и решаем уравнение, чтобы найти физический смысл производной:
[{{t}^{2}}-8t+19=3]
[{{t}^{2}}-8t+16=0]
[{{left( t-4 right)}^{2}}=0]
[t-4=0]
[t=4]
Полученное число означает, что в момент времени 4 с $v$ материальной точки, движущейся по выше описанному закону, как раз и будет равна 3 м/с.
Ключевые моменты
В заключении давайте еще раз пробежимся по самому главному моменту сегодняшней задачи, а именно, по правилу преобразования расстояние в скорость и ускорение. Итак, если нам в задаче прямо описан закон, прямо указывающий расстояние от материальной точки до точки отсчета, то через эту формулу мы можем найти любую мгновенную скорость (это просто производная). И более того, мы можем найти еще и ускорение. Ускорение, в свою очередь, равно производной от скорости, т.е. второй производной от расстояния. Такие задачи встречаются довольно редко, поэтому сегодня мы их не разбирали. Но если вы увидите в условии слово «ускорение», пусть оно вас не пугает, достаточно просто найти еще одну производную.
Надеюсь, этот урок поможет вам подготовиться к ЕГЭ по математике.
Смотрите также:
- Не допускайте таких ошибок, когда видите график производной в задаче 6 из ЕГЭ по математике!
- ЕГЭ 2022, задание 6. Касательная и квадратичная функция с параметром
- Схема Бернулли. Примеры решения задач
- Комбинаторика в задаче B6: средний тест
- Как решать задачи про летающие камни?
- B4: счетчики на электричество
Производной функции $y = f(x)$ в данной точке $х_0$ называют предел отношения приращения функции к соответствующему приращению его аргумента при условии, что последнее стремится к нулю:
$f'(x_0)={lim}↙{△x→0}{△f(x_0)}/{△x}$
Дифференцированием называют операцию нахождения производной.
Таблица производных некоторых элементарных функций
| Функция | Производная |
| $c$ | $0$ |
| $x$ | $1$ |
| $x^n$ | $nx^{n-1}$ |
| ${1}/{x}$ | $-{1}/{x^2}$ |
| $√x$ | ${1}/{2√x}$ |
| $e^x$ | $e^x$ |
| $lnx$ | ${1}/{x}$ |
| $sinx$ | $cosx$ |
| $cosx$ | $-sinx$ |
| $tgx$ | ${1}/{cos^2x}$ |
| $ctgx$ | $-{1}/{sin^2x}$ |
Основные правила дифференцирования
1. Производная суммы (разности) равна сумме (разности) производных
$(f(x) ± g(x))’= f'(x)±g'(x)$
Найти производную функции $f(x)=3x^5-cosx+{1}/{x}$
Производная суммы (разности) равна сумме (разности) производных.
$f'(x) = (3x^5 )’-(cos x)’ + ({1}/{x})’ = 15x^4 + sinx — {1}/{x^2}$
2. Производная произведения
$(f(x) · g(x))’= f'(x) · g(x)+ f(x) · g(x)’$
Найти производную $f(x)=4x·cosx$
$f'(x)=(4x)’·cosx+4x·(cosx)’=4·cosx-4x·sinx$
3. Производная частного
$({f(x)}/{g(x)})’={f'(x)·g(x)-f(x)·g(x)’}/{g^2(x)}$
Найти производную $f(x)={5x^5}/{e^x}$
$f'(x)={(5x^5)’·e^x-5x^5·(e^x)’}/{(e^x)^2}={25x^4·e^x-5x^5·e^x}/{(e^x)^2}$
4. Производная сложной функции равна произведению производной внешней функции на производную внутренней функции
$f(g(x))’=f'(g(x))·g'(x)$
$f(x)= cos(5x)$
$f'(x)=cos'(5x)·(5x)’=-sin(5x)·5= -5sin(5x)$
Физический смысл производной
Если материальная точка движется прямолинейно и ее координата изменяется в зависимости от времени по закону $x(t)$, то мгновенная скорость данной точки равна производной функции.
$v(t) = x'(t)$
Точка движется по координатной прямой согласно закону $x(t)= 1,5t^2-3t + 7$, где $x(t)$ — координата в момент времени $t$. В какой момент времени скорость точки будет равна $12$?
Решение:
1. Скорость – это производная от $x(t)$, поэтому найдем производную заданной функции
$v(t) = x'(t) = 1,5·2t -3 = 3t -3$
2. Чтобы найти, в какой момент времени $t$ скорость была равна $12$, составим и решим уравнение:
$3t-3 = 12$
$3t = 15$
$t = 5$
Ответ: $5$
Геометрический смысл производной
Напомним, что уравнение прямой, не параллельной осям координат, можно записать в виде $y = kx + b$, где $k$ – угловой коэффициент прямой. Коэффициент $k$ равен тангенсу угла наклона между прямой и положительным направлением оси $Ох$.
$k = tgα$
Производная функции $f(x)$ в точке $х_0$ равна угловому коэффициенту $k$ касательной к графику в данной точке:
$f'(x_0) = k$
Следовательно, можем составить общее равенство:
$f'(x_0) = k = tgα$
На рисунке касательная к функции $f(x)$ возрастает, следовательно, коэффициент $k > 0$. Так как $k > 0$, то $f'(x_0) = tgα > 0$. Угол $α$ между касательной и положительным направлением $Ох$ острый.
На рисунке касательная к функции $f(x)$ убывает, следовательно, коэффициент $k < 0$, следовательно, $f'(x_0) = tgα < 0$. Угол $α$ между касательной и положительным направлением оси $Ох$ тупой.
На рисунке касательная к функции $f(x)$ параллельна оси $Ох$, следовательно, коэффициент $k = 0$, следовательно, $f'(x_0) = tg α = 0$. Точка $x_0$, в которой $f ‘(x_0) = 0$, называется экстремумом.
На рисунке изображён график функции $y=f(x)$ и касательная к этому графику, проведённая в точке с абсциссой $x_0$. Найдите значение производной функции $f(x)$ в точке $x_0$.
Решение:
Касательная к графику возрастает, следовательно, $f'(x_0) = tg α > 0$
Для того, чтобы найти $f'(x_0)$, найдем тангенс угла наклона между касательной и положительным направлением оси $Ох$. Для этого достроим касательную до треугольника $АВС$.
Найдем тангенс угла $ВАС$. (Тангенсом острого угла в прямоугольном треугольнике называется отношение противолежащего катета к прилежащему катету.)
$tg BAC = {BC}/{AC} = {3}/{12}= {1}/{4}=0,25$
$f'(x_0) = tg ВАС = 0,25$
Ответ: $0,25$
Производная так же применяется для нахождения промежутков возрастания и убывания функции:
Если $f'(x) > 0$ на промежутке, то функция $f(x)$ возрастает на этом промежутке.
Если $f'(x) < 0$ на промежутке, то функция $f(x)$ убывает на этом промежутке.
На рисунке изображен график функции $y = f(x)$. Найдите среди точек $х_1,х_2,х_3…х_7$ те точки, в которых производная функции отрицательна.
В ответ запишите количество данных точек.
Решение:
Отрицательным значениям производной соответствуют интервалы, на которых функция $f (x)$ убывает. Поэтому, выделим на рисунке интервалы, на которых функция убывает.
В выделенных интервалах находятся точки $х_2, х_4$. В ответ напишем их количество $2$.
Ответ: $2$
ЕГЭ Профиль №6. Физический смысл производной
Скачать файл в формате pdf.
ЕГЭ Профиль №6. Физический смысл производной
| Задача 1. Материальная точка движется прямолинейно по закону (xleft( t right) = — frac{1}{3}{t^2} + 4t + 15), где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени (t = 3;{text{c}}).
Ответ
ОТВЕТ: 2. |
|
| Задача 2. Материальная точка движется прямолинейно по закону (xleft( t right) = frac{1}{3}{t^3} + 2{t^2} — 15), где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени (t = 2;{text{c}}).
Ответ
ОТВЕТ: 12. |
|
| Задача 3. Материальная точка движется прямолинейно по закону (xleft( t right) = {t^4} + 9{t^2} — 3t + 23), где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени (t = 1;{text{c}}{text{.}})
Ответ
ОТВЕТ: 19. |
|
| Задача 4. Материальная точка движется прямолинейно по закону (xleft( t right) = — frac{1}{6}{t^2} + 5t — 19), где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 4 м/с?
Ответ
ОТВЕТ: 3. |
|
| Задача 5. Материальная точка движется прямолинейно по закону (xleft( t right) = frac{1}{3}{t^3} + {t^2} — 9t + 12), где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 15 м/с?
Ответ
ОТВЕТ: 4. |
|
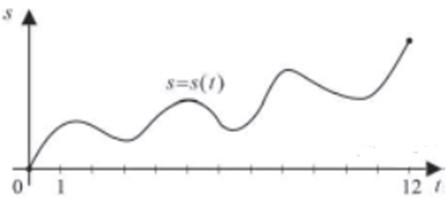
| Задача 6. Материальная точка M начинает движение из точки A и движется по прямой на протяжении 12 секунд. График показывает, как менялось расстояние от точки A до точки M со временем. На оси абсцисс откладывается время t в секундах, на оси ординат — расстояние S. Определите, сколько раз за время движения скорость точки M обращалась в ноль (начало и конец движения не учитывайте). Ответ
ОТВЕТ: 6. |
 |
Физический смысл производной. В состав ЕГЭ по математике входит группа задач для решения которых необходимо знание и понимание физического смысла производной. В частности, есть задачи, где дан закон движения определённой точки (объекта), выраженный уравнением и требуется найти его скорость в определённый момент времени движения, либо время, через которое объект приобретёт определённую заданную скорость. Задачи очень простые, решаются они в одно действие. Итак:
Пусть задан закон движения материальной точки x (t) вдоль координатной оси, где x координата движущейся точки, t – время.
Скорость в определённый момент времени – это производная координаты по времени. В этом и состоит механический смысл производной.
Аналогично, ускорение – это производная скорости по времени:
Таким образом, физический смысл производной это скорость. Это может быть скорость движения, скорость изменения какого-либо процесса (например роста бактерий), скорость совершения работы (и так далее, прикладных задач множество).
Кроме того, необходимо знать таблицу производных (знать её нужно также, как таблицу умножения) и правила дифференцирования. Если конкретно, то для решения оговоренных задач необходимо знание первых шести производных (см. таблицу):
Рассмотрим задачи:
Материальная точка движется прямолинейно по закону
x (t) = t2 – 7t – 20
где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t = 5 c.
Физический смысл производной это скорость (скорость движения, скорость изменения процесса, скорость работы и т.д.)
Найдем закон изменения скорости: v (t) = x′(t) = 2t – 7 м/с.
При t = 5 имеем:
Ответ: 3
Решить самостоятельно:
Материальная точка движется прямолинейно по закону x (t) = 6t2 – 48t + 17, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t = 9 c.
Посмотреть решение
Материальная точка движется прямолинейно по закону x (t) = 0,5t3 – 3t2 + 2t, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t = 6 с.
Посмотреть решение
Материальная точка движется прямолинейно по закону
x (t) = –t4 + 6t3 + 5t + 23
где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t = 3 с.
Посмотреть решение
Материальная точка движется прямолинейно по закону
x (t) = (1/6) t2 + 5t + 28
где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 6 м/с?
Найдем закон изменения скорости:
Для того, чтобы найти, в какой момент времени t скорость была равна 3 м/с, необходимо решить уравнение:
Ответ: 3
Решите самостоятельно:
Материальная точка движется прямолинейно по закону x (t) = t2 – 13t + 23, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 3 м/с?
Посмотреть решение
Материальная точка движется прямолинейно по закону
x (t) = (1/3) t3 – 3t2 – 5t + 3
где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 2 м/с?
Посмотреть решение
Отмечу, что ориентироваться только на такой тип задач на ЕГЭ не стоит. Могут совершенно неожиданно ввести задачи обратные представленным. Когда дан закон изменения скорости и будет стоять вопрос о нахождении закона движения.
Подсказка: в этом случае необходимо найти интеграл от функции скорости (это так же задачи в одно действие). Если потребуется найти пройденное расстояние за определённый момент времени, то необходимо подставить время в полученное уравнение и вычислить расстояние. Впрочем, мы такие задачи тоже будем разбирать, не пропустите! Успехов вам!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.