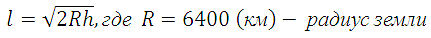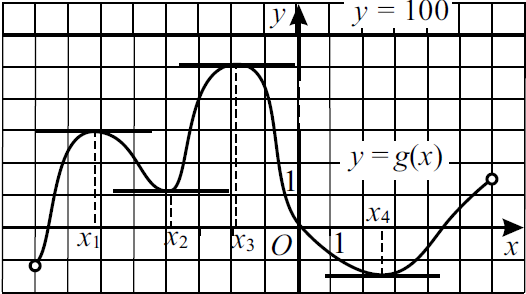Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Материальная точка движется прямолинейно по закону (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). Найдите ее скорость (в м/с) в момент времени t = 9 с.
2
Материальная точка движется прямолинейно по закону (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). Найдите ее скорость в (м/с) в момент времени t = 6 с.
3
Материальная точка движется прямолинейно по закону (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). Найдите ее скорость в (м/с) в момент времени
с.
4
Материальная точка движется прямолинейно по закону (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). В какой момент времени (в секундах) ее скорость была равна 3 м/с?
5
Материальная точка движется прямолинейно по закону (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). В какой момент времени (в секундах) ее скорость была равна 2 м/с?
Пройти тестирование по этим заданиям
Категория: Физические задачи
Расстояние от наблюдателя, находящегося
263802. Расстояние от наблюдателя, находящегося на небольшой высоте h километров над землей до наблюдаемой им линии горизонта вычисляется по формуле: С какой высоты горизонт виден на расстоянии 4 километра? Ответ выразите в километрах.
Дата: 2015-02-02
3536
Категория: Физические задачи
Метка: ЕГЭ-№8
Далее
263802. Расстояние от наблюдателя, находящегося на небольшой…
Скорость колеблющегося на пружине
28014. Скорость колеблющегося на пружине груза меняется по закону: t — время в секундах. Какую долю времени из первой секунды скорость движения превышала 2,5 см/с? Ответ выразите десятичной дробью, если нужно, округлите до сотых.
Дата: 2015-02-02
12068
Категория: Физические задачи
Метка: ЕГЭ-№8
Далее
28014. Скорость колеблющегося на пружине груза меняется по з…
Груз массой 0,08 кг колеблется
28013. Груз массой 0,08 кг колеблется на пружине со скоростью, меняющейся по закону Кинетическая энергия груза вычисляется по формуле: Определите, какую долю времени из первой секунды после начала движения кинетическая энергия груза будет не менее 5∙10–3Дж….
Дата: 2015-02-02
8000
Категория: Физические задачи
Метка: ЕГЭ-№8
Далее
28013. Груз массой 0,08 кг колеблется на пружине со скорост…
Скейтбордист прыгает на стоящую
28011. Скейтбордист прыгает на стоящую на рельсах платформу, со скоростью v=3м/с под острым углом α к рельсам. От толчка платформа начинает ехать со скоростью m=80 кг — масса скейтбордиста со скейтом, а М = 400…
Дата: 2015-02-02
10660
Категория: Физические задачи
Метка: ЕГЭ-№8
Далее
28011. Скейтбордист прыгает на стоящую на рельсах платформу,…
Катер должен пересечь реку шириной
28010. Катер должен пересечь реку шириной L =100 м и со скоростью течения u = 0,5 м/с так, чтобы причалить точно напротив места отправления. Он может двигаться с разными скоростями, при этом время в пути,…
Дата: 2015-02-01
6803
Категория: Физические задачи
Метка: ЕГЭ-№8
Далее
28010. Катер должен пересечь реку шириной L =100 м и со скор…
Два тела массой m = 2 кг каждое
28009. Два тела массой m = 2 каждое, движутся с одинаковой скоростью v=10 м/с под углом 2α друг к другу. Энергия (в джоулях), выделяющаяся при их абсолютно неупругом соударении определяется выражением: Под каким наименьшим углом 2α…
Дата: 2015-02-01
15121
Категория: Физические задачи
Метка: ЕГЭ-№8
Далее
28009. Два тела массой m = 2 каждое, движутся с одинаковой …
При нормальном падении света
28008. При нормальном падении света с длиной волны λ = 400 нм на дифракционную решётку с периодом d нм наблюдают серию дифракционных максимумов. При этом угол φ (отсчитываемый от перпендикуляра к решётке), под которым наблюдается…
Дата: 2015-02-01
13423
Категория: Физические задачи
Метка: ЕГЭ-№8
Далее
28008. При нормальном падении света с длиной волны λ = 400 н…
Трактор тащит сани с силой
28007. Трактор тащит сани с силой F=50 кН, направленной под острым углом a к горизонту. Мощность (в киловаттах) трактора при скорости v = 3 м/с равна: При каком максимальном угле α (в градусах) эта мощность будет не менее 75 кВт.
Дата: 2015-02-01
7704
Категория: Физические задачи
Метка: ЕГЭ-№8
Далее
28007. Трактор тащит сани с силой F=50 кН, направленной под …
Плоский замкнутый контур площадью
28005. Плоский замкнутый контур площадью S = 0,5м2 находится в магнитном поле, индукция которого равномерно возрастает. При этом согласно закону электромагнитной индукции Фарадея в контуре появляется ЭДС индукции, значение которой, выраженное в вольтах, определяется формулой:…
Дата: 2015-02-01
7715
Категория: Физические задачи
Метка: ЕГЭ-№8
Далее
28005. Плоский замкнутый контур площадью S = 0,5м2 находится…
Небольшой мячик бросают
28004. Небольшой мячик бросают под острым углом α к плоской горизонтальной поверхности земли. Расстояние, которое пролетает мячик, вычисляется по формуле V0=20 м/с — начальная скорость мячика, а g — ускорение свободного падения (считайте g =10 м/с2). При каком…
Дата: 2015-02-01
13042
Категория: Физические задачи
Метка: ЕГЭ-№8
Далее
28004. Небольшой мячик бросают под острым углом α к плоской …
Используя этот сайт, Вы соглашаетесь с тем, что мы сохраняем и используем файлы cookies, а также используем похожие технологии для улучшения работы сайта.
Ok
Скачать материал

Скачать материал


- Сейчас обучается 166 человек из 48 регионов


- Сейчас обучается 342 человека из 70 регионов


- Сейчас обучается 139 человек из 41 региона


Описание презентации по отдельным слайдам:
-
1 слайд
Решение физических задач ЕГЭ по математике.
МОУ «СОШ № 34 с углубленным изучением
художественно-эстетических предметов»
Н.И. Хренникова,
учитель математики
Саратов
2014 -
2 слайд
Задания с наибольшим количеством аналогов
-
3 слайд
Задание B12 (№ 28643)
Два тела массой кг каждое движутся с одинаковой скоростью м/с под углом друг к другу. Энергия (в джоулях), выделяющаяся при их абсолютно неупругом соударении определяется выражением . Под каким наименьшим углом (в градусах) должны двигаться тела, чтобы в результате соударения выделилось не менее 108 джоулей?
Задание B12 (№ 28613)
Трактор тащит сани с силой кН, направленной под острым углом к горизонту. Работа трактора (в килоджоулях) на участке длиной м вычисляется по формуле . При каком максимальном угле (в градусах) совершeнная работа будет не менее 2800 кДж?
Задание B12 (№ 28053)
Зависимость объeма спроса q (единиц в месяц) на продукцию предприятия-монополиста от цены p (тыс. руб.) задаeтся формулой . Выручка предприятия за месяц r (в тыс. руб.) вычисляется по формуле . Определите наибольшую цену p, при которой месячная выручка составит не менее 360 тыс. руб. Ответ приведите в тыс. руб. -
4 слайд
Задания с наименьшим количеством аналогов
-
5 слайд
Задание B12 (№ 41991)
Сила тока в цепи I (в амперах) определяется напряжением в цепи и сопротивлением электроприбора по закону Ома: , где U — напряжение в вольтах, R — сопротивление электроприбора в омах. В электросеть включeн предохранитель, который плавится, если сила тока превышает 1 А. Определите, какое минимальное сопротивление должно быть у электроприбора, подключаемого к розетке в 220 вольт, чтобы сеть продолжала работать. Ответ выразите в омах.
Задание B12 (№ 28083)
В боковой стенке высокого цилиндрического бака у самого дна закреплeн кран. После его открытия вода начинает вытекать из бака, при этом высота столба воды в нeм, выраженная в метрах, меняется по закону , гдеt — время в секундах, прошедшее с момента открытия крана, м — начальная высота столба воды, — отношение площадей поперечных сечений крана и бака, а g — ускорение свободного падения (считайте м/с ). Через сколько секунд после открытия крана в баке останется четверть первоначального объeма воды?
Задание B12 (№ 28393)
Скорость автомобиля, разгоняющегося с места старта по прямолинейному отрезку пути длиной l км с постоянным ускорением a км/ч , вычисляется по формуле . Определите, с какой наименьшей скоростью будет двигаться автомобиль на расстоянии 0,4 километра от старта, если по конструктивным особенностям автомобиля приобретаемое им ускорение не меньше 12500 км/ч . Ответ выразите в км/ч. -
6 слайд
Шаги решения В12
Решение задач В12 условно можно разделить на несколько шагов:а) анализ условия и вычленение формулы, описывающей заданную ситуацию, а также значений параметров, констант или начальных условий, которые необходимо подставить в эту формулу;
б) математическая интерпретация задачи — сведение её к уравнению или неравенству и его решение;
в) анализ полученного решения.
Задания В12 отличаются от других тем, что очень высок процент тех, кто даже не приступал к решению.
Основные проблемы — трудности с арифметикой, логические ошибки, невнимательное чтение условия. -
7 слайд
линейному уравнению или неравенству
степенному уравнению или неравенству
показательному уравнению или неравенству
логарифмическому уравнению и неравенству
тригонометрическому уравнению или неравенству
Задачи, решение которых сводятся к стандартным уравнениям и неравенствам
-
8 слайд
При температуре 0oС рельс имеет длину lo= 20 м. При возрастании температуры происходит тепловое расширение рельса, и его длина, выраженная в метрах, меняется по закону l(to) = l0 ( 1+α·to), где α = 1,2·10-5(oC)-1 – коэффициент теплового расширения, to — температура (в градусах Цельсия). При какой температуре рельс удлинится на 9 мм? Ответ выразите в градусах Цельсия.
Задание B12 (№ 28017) -
9 слайд
Функция:
Данные:
Получаем уравнение:
Найти:
Ответ: 37,5. -
10 слайд
Задание B12 (№ 28027)
Некоторая компания продает свою продукцию по цене p = 600 руб. за единицу, переменные затраты на производство одной единицы продукции составляют ν = 400 руб., постоянные расходы предприятия f = 600000 руб. в месяц. Месячная операционная прибыль (в рублях) вычисляется по формуле π(q) = q( p — ν)- f . Определите наименьший месячный объём производства q (единиц продукции), при котором месячная операционная прибыль предприятия будет не меньше 500000 руб.
-
11 слайд
Данные:
Функция:
Найти:
Решаем неравенство:
Ответ:
5500. -
12 слайд
Для обогрева помещения, температура в котором Тп = 20°С, через радиатор пропускают горячую воду температурой Т= 60°С. Через радиатор проходит m= 0,3 кг/с воды. Проходя по радиатору расстояние х = 84 м, вода охлаждается до температуры T(°С), причём
где с = 4200 — теплоёмкость воды, γ= 21 — коэффициент теплообмена,
а α = 0,7 — постоянная. До какой температуры (в градусах Цельсия) охладится вода?
Задание B12 (№ 28027) -
13 слайд
Данные:
Функция:
Найти:
Получаем уравнение:
Тп = 20°С
Т-?°С
х = 84 м
m= 0,3 кг/с
с = 4200
α = 0,7
Ответ: 30 -
14 слайд
Находящийся в воде водолазный колокол, содержащий ν= 4 моля воздуха при давлении р1 = 1,2 атмосферы, медленно опускают на дно водоёма. При этом происходит изотермическое сжатие воздуха. Работа (в джоулях), совершаемая водой при сжатии воздуха, определяется выражением
где α = 5,75 — постоянная, Т = 300 К—температура воздуха, P1 (атм) — начальное давление, а р2 (атм) — конечное давление воздуха в колоколе. До какого наибольшего давления р2 (в атм) можно сжать воздух в колоколе, если при сжатии воздуха совершается работа не более чем
20 700 Дж?
Задание B12 (№ 28027) -
15 слайд
Функция:
Данные:
Получаем неравенство:
Найти:
Ответ: 9,6
ν= 4
р1 = 1,2
α = 5,75
Т = 300
, при -
16 слайд
Трактор тащит сани с силой F = 80 кН, направленной под острым углом а к горизонту. Работа трактора, выраженная в килоджоулях, на участке длиной S = 50 м равна
А = FS cos α.
При каком максимальном угле а (в градусах) совершённая работа будет
не менее 2000 кДж?
,
Задание B12 (№ 28006) -
17 слайд
Данные:
Функция:
Найти:
Получаем неравенство:
Ответ: 60
А ≥ 2000
F =80
80•50• cos α ≥ 2000
cos α ≥
0°< α≤ 60
°
А = FS cos α.
S = 50
а (в градусах), при -
18 слайд
В ходе распада радиоактивного изотопа его масса уменьшается по закону
m(t) = m0.2-t/T,
где m0 — начальная масса изотопа, t — время, прошедшее от начала распада,
Т — период полураспада в минутах. В лаборатории получили вещество, содержащее m0 = 40 мг изотопа азота-13, период полураспада которого
Т = 10 мин. В течение скольких минут масса изотопа азота-13 будет
не меньше 10 мг?
Задание B12 (№ 27991) -
19 слайд
Данные:
Функция:
Найти:
Получаем неравенство:
Ответ: 20
m(t) ≥ 10
m0 = 40 мг
Т = 10 мин
40 *2 -t/10 ≥ 10 ,
2 -t/10 ≥ 2-2 ,
t ≤ 20
m(t) = m0.2-t/T,
t , если -
20 слайд
Задачи, решения которых сводятся к квадратным уравнениям и неравенствам.
-
21 слайд
Мотоциклист, движущийся по городу со скоростью v0 = 57 км/ч, выезжает из него и сразу после выезда начинает разгоняться с постоянным ускорением a = 12 км/ч2. Расстояние от мотоциклиста до города, измеряемое в километрах, определяется выражением
Определите наибольшее время, в течение которого мотоциклист будет находиться в зоне функционирования сотовой связи, если оператор гарантирует покрытие на расстоянии не далее чем в 30 км от города. Ответ выразите в минутах.
Задание B12 (№ 28135)
at2
2
v0t
S
+
=
30 км -
22 слайд
Решаем неравенство:
Функция:
Данные:
Найти:
Ответ:
30. -
23 слайд
Задание B12 (№ 28125)
Лебёдка — механизм, тяговое усилие которого передается посредством каната, цепи, троса
или иного гибкого элемента от приводного барабана.
βt2
2
ωt
φ
+
=
Для сматывания кабеля на заводе используют лебёдку, которая равноускоренно наматывает кабель на катушку. Угол, на который поворачивается катушка, изменяется со
временем по закону , где t — время в
минутах, ω = 750/мин — начальная угловая скорость вращения катушки, а β = 100/мин2 — угловое ускорение, с которым наматывается кабель. Рабочий должен
проверить ход его намотки не позже того момента,
когда угол намотки φ достигнет 22500. Определите время после начала
работы лебёдки, не позже которого
рабочий должен проверить её работу.
Ответ выразите в минутах. -
24 слайд
Функция:
Данные:
Найти:
Ответ:
15.
Решаем неравенство: -
25 слайд
(m+2M)R2
2
+ M(2Rh + h2).
I
=
Деталью некоторого прибора является вращающаяся катушка. Она состоит из трёх однородных соосных цилиндров: центрального массой m = 8 кг и радиуса R = 5 см, и двух боковых с массами M = 2 кг и с радиусами R + h. При этом момент инерции катушки относительно оси вращения, выражаемый в кг· см2 , даётся формулой
.
При каком максимальном значении h момент инерции катушки не превышает предельного значения 1900 кг· см2 ? Ответ выразите в сантиметрах.
Задание B12 (№ 28165) -
26 слайд
Данные:
Функция:
Найти:
Решаем неравенство:
Ответ:
25. -
27 слайд
Зависимость объёма спроса q (тыс. руб.) на продукцию предприятия-монополиста от цены p (тыс. руб.) задаётся формулой q = 130 — 10p . Выручка предприятия за месяц r (в тыс. руб.) вычисляется по формуле r(p) = q · p. Определите наибольшую цену p, при которой месячная выручка составит не менее 360 тыс. руб. Ответ приведите в тыс. руб.
Задание B12 (№ 28053) -
28 слайд
Данные:
Функция:
Найти:
Получаем неравенство:
Ответ:
9. -
29 слайд
60
-1
a
=
6
7
b
=
Камнеметательная машина выстреливает камни под некоторым острым углом к горизонту. Траектория полёта камня описывается формулой y = ax2 + bx ,
где м-1, — постоянные параметры,
x (м) — смещение камня по горизонтали, y (м) — высота камня над землёй. На каком наибольшем расстоянии (в метрах) от крепостной стены высотой 9 м нужно расположить машину, чтобы камни пролетали над стеной на высоте не менее 1 метра?
Задание B12 (№ 28105) -
30 слайд
y = 10
Функция:
Данные:
Найти:Ответ:
60.
Решаем неравенство: -
31 слайд
Задание B12 (№ 28091)
H0
В боковой стенке высокого цилиндрического бака у самого дна закреплён кран. После его открытия вода начинает вытекать из бака, при этом высота столба воды в нём, выраженная в метрах, меняется по закону H(t) = H0 + bt + at2 , где Н0 = 2 м — начальный уровень воды,
м/мин2, м/мин, t — время в минутах,
прошедшее с момента открытия крана. В течение какого времени вода будет вытекать из бака? Ответ приведите в минутах.
50
1
a
=
5
-2
b
= -
32 слайд
Функция:
Данные:
Решаем уравнение:
Найти:
Ответ:
10. -
33 слайд
В боковой стенке высокого цилиндрического бака у самого дна закреплён кран. После его открытия вода начинает вытекать из бака, при этом высота столба воды в нём, выраженная в метрах, меняется по закону
, где t — время в секундах,
прошедшее с момента открытия крана, —
отношение площадей поперечных сечений крана и бака, Н0 = 5 м — начальная высота столба воды, а g — ускорение свободного падения (считайте g = 10 м/с2). Через сколько секунд после открытия крана в баке останется четверть первоначального объёма воды?
Задание B12 (№ 28081)
2
gH
2
2
0
0
2
)
(
t
k
g
kt
H
t
H
+
—
=
k
200
1
= -
34 слайд
Найти:
H0
4
1
H0
Данные:
Функция:
Решаем уравнение:
Ответ:
100. -
35 слайд
Задание B12 (№ 28115)
Зависимость температуры (в градусах Кельвина) от времени для нагревательного элемента некоторого прибора была получена экспериментально и на исследуемом интервале температур определяется выражением T(t) = T0 + bt + at2 , где t — время в минутах, T0 = 1450 К, a = — 12,5 К/мин2 , b = 175 К/мин. Известно, что при температуре нагревателя свыше 1750 К прибор может испортиться, поэтому его нужно отключать. Определите, через какое наибольшее время после начала работы нужно отключать прибор. Ответ выразите в минутах.
Пирометр — прибор для беcконтактного измерения температуры тел. -
36 слайд
Данные:
y = T(t)
y
t
0
1450
Функция:
Найти:
Схематичный график:
1750
tнаиб.
Необходимоотключить
Ответ:
2. -
37 слайд
Задачи, в которых необходимо найти длину промежутка.
-
38 слайд
1,1 с
1,2 с
Задание B12 (№ 28039)
После дождя уровень воды в колодце может повыситься. Мальчик измеряет время t падения небольших камешков в колодец и рассчитывает расстояние до воды по формуле h = 5t2, где h — расстояние в метрах, t — время падения в секундах. До дождя время падения камешков составляло 1,2 с. На сколько должен подняться уровень воды после дождя, чтобы измеряемое время изменилось на 0,1 с? -
39 слайд
Найти:
Ответ:
Данные:
Функция:
1,15.
Решение: -
40 слайд
Высота над землёй подброшенного вверх мяча меняется по закону h(t) = 1,4 + 9t — 5t2 , где h — высота в метрах, t — время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее 3 метров?
Задание B12 (№ 28059) -
41 слайд
Данные:
Функция:
Найти:
Получаем неравенство:
Ответ: 1,4 -
42 слайд
Задачи, в которых присутствуют несколько переменных
-
43 слайд
g
L
v
m
P
—
=
2
(
)
Задание B12 (№ 28071)
Если достаточно быстро вращать ведёрко с водой на верёвке в вертикальной плоскости, то вода не будет выливаться. При вращении ведёрка сила давления воды на дно не остаётся постоянной: она максимальна в нижней точке и минимальна в верхней. Вода не будет выливаться, если сила её давления на дно будет положительной во всех точках траектории кроме верхней, где она может быть равной нулю. В верхней точке сила давления, выраженная
в ньютонах, равна , где m — масса воды в
килограммах, v — скорость движения ведёрка в м/с, L — длина верёвки в метрах, g — ускорение свободного падения (считайте, g = 10 м/с2 ). С какой наименьшей скоростью надо вращать ведёрко, чтобы вода не выливалась, если длина верёвки равна 62,5 cм? Ответ выразите в м/с. -
44 слайд
Функция:
Данные:
Решаем неравенство:
Ответ:
2,5
Найти: -
45 слайд
В презентации использованы задачи из открытого банка заданий ЕГЭ по математике.
Краткое описание документа:
Презентация «Решение физических задач ЕГЭ по математике « может быть полезна в использована при подготовке учащихся к итоговой аттестации в 10 — 11 классах . Задачи физического содержания всегда вызывают затруднения у выпускников. Работа поможет классифицировать задачи по способам решения задачи, тем самым преодолеть страх перед решением таких задач. Наличие анимации в презентации будет помогать запоминанию разновидностей прототипов задач, подходу к решению различных прототипов задач. Желаю удачи!
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 156 989 материалов в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Другие материалы
- 26.03.2014
- 942
- 0
Рейтинг:
5 из 5
- 26.03.2014
- 3051
- 1
- 26.03.2014
- 1557
- 3
- 26.03.2014
- 1827
- 8
- 26.03.2014
- 1260
- 0
- 26.03.2014
- 2649
- 20
- 26.03.2014
- 2621
- 4
Вам будут интересны эти курсы:
-
Курс повышения квалификации «Внедрение системы компьютерной математики в процесс обучения математике в старших классах в рамках реализации ФГОС»
-
Курс повышения квалификации «Педагогическое проектирование как средство оптимизации труда учителя математики в условиях ФГОС второго поколения»
-
Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
-
Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Специфика преподавания основ финансовой грамотности в общеобразовательной школе»
-
Курс повышения квалификации «Специфика преподавания информатики в начальных классах с учетом ФГОС НОО»
-
Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
-
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
-
Курс профессиональной переподготовки «Инженерная графика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Развитие элементарных математических представлений у детей дошкольного возраста»
-
Курс повышения квалификации «Методика преподавания курса «Шахматы» в общеобразовательных организациях в рамках ФГОС НОО»
-
Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
-
Курс профессиональной переподготовки «Черчение: теория и методика преподавания в образовательной организации»
Лучшие репетиторы для сдачи ЕГЭ
Задания по теме «Физический смысл производной»
Открытый банк заданий по теме физический смысл производной. Задания B7 из ЕГЭ по математике (профильный уровень)
Геометрические фигуры на плоскости: вычисление величин с использованием углов
Геометрические фигуры в пространстве: нахождение длины, площади, объема
Задание №1148
Тип задания: 7
Тема:
Физический смысл производной
Условие
Материальная точка движется прямолинейно по закону x(t)=frac14t^3-4t^2+t, где x —расстояние от точки отсчёта в метрах, t — время в секундах, измеренное с начала движения. В какой момент времени (в секундах) её скорость была 13 м/с?
Показать решение
Решение
Согласно физическому смыслу производной необходимо решить уравнение x'(t)=13.
x'(t)=frac34t^2-8t+1. Решаем уравнение:
frac34t^2-8t+1=13,
frac34t^2-8t-12=0,
3t^2-32t-48=0,
t_{1,2}= frac{16pmsqrt{256+3cdot48}}{3}= frac{16pmsqrt{400}}{3}= frac{16pm20}{3}.
t_1=-frac43, t_2=12.
Так как tgeqslant0, то t=12.
Ответ
12
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1138
Тип задания: 7
Тема:
Физический смысл производной
Условие
Материальная точка движется прямолинейно по закону x(t)=-t^4+7t^3+6t+16, где x — расстояние от точки отсчёта в метрах, t — время в секундах, измеренное с начала движения. Найдите её скорость (в метрах в секунду) в момент времени t=5 с.
Показать решение
Решение
Согласно физическому смыслу производной необходимо найти x'(5).
x'(t)=-4t^3+21t^2+6.
x'(5)= -4cdot 5^3+21cdot 5^2+6= -500+525+6= 31.
Ответ
31
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №899
Тип задания: 7
Тема:
Физический смысл производной
Условие
Материальная точка движется прямолинейно по закону x(t)=frac14t^3-4t^2+t, где
х — расстояние от точки отсчёта в метрах,
t — время в секундах, измеренное с начала движения.
Найдите её скорость (в метрах в секунду) в момент времени t = 12 с.
Показать решение
Решение
Согласно физическому смыслу производной необходимо найти x'(12).
x'(t) = frac34t^2-8t+1,
x'(12) = frac34cdot12^2-8cdot12+1= 108-96+1=13.
Ответ
13
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №304
Тип задания: 7
Тема:
Физический смысл производной
Условие
Материальная точка движется прямолинейно по закону x(t)=frac13 t^3-t^2-5t+18, где
x — расстояние от точки отсчета в метрах,
t — время в секундах, измеряемое с начала движения.
В какой момент времени (в секундах) ее скорость была равна 10 м/с?
Показать решение
Решение
Найдем скорость движения точки: v(t)=x'(t)=t^2-2t-5.
По условию v(t)=10 м/с, значит, t^2-2t-5=10,
t^2-2t-15=0,
t_1=5,;t_2=-3.
По смыслу задачи tgeq 0, следовательно, t=5 с.
Ответ
5
Источник: «Математика. Подготовка к ЕГЭ-2016. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №89
Тип задания: 7
Тема:
Физический смысл производной
Условие
Закон прямолинейного движения материальной точки равен x(t)=-frac13t^4+4t^3-7t^2-5t-5, где
x – расстояние от точки отсчета (м);
t – время с начала движения (с).
Найдите скорость точки в момент времени t = 6 с. Ответ выразите в метрах в секунду
Показать решение
Решение
Скорость точки в определенный момент времени определяется как производная ее координаты в этот момент времени:
V(t)=frac{dx(t)}{dt}=-frac43t^3+12t^2-14t-5.
Найдем скорость в момент времени t = 6:
V(6)=-frac43cdot 216+12cdot 36-14cdot 6-5=-377+432=55 м/с
Ответ
55
Задание №88
Тип задания: 7
Тема:
Физический смысл производной
Условие
Закон прямолинейного движения материальной точки равен x(t)=frac12t^2+2t-15, где
x – расстояние от точки отсчета (м);
t – время с начала движения (с).
Найдите скорость точки в момент времени t = 7 с. Ответ выразите в метрах в секунду
Показать решение
Решение
Скорость точки в определенный момент времени определяется как производная ее координаты в этот момент времени:
V(t)=frac{dx(t)}{dt}=t+2.
Найдем скорость в момент времени t = 7:
V (7) = 7 + 2 = 9 м/с
Ответ
9
Лучшие репетиторы для сдачи ЕГЭ
Сложно со сдачей ЕГЭ?
Звоните, и подберем для вас репетитора: 78007750928
За это задание ты можешь получить 1 балл. На решение дается около 5 минут. Уровень сложности: базовый.
Средний процент выполнения: 61.5%
Ответом к заданию 7 по математике (профильной) может быть целое число или конечная десятичная дробь.
Разбор сложных заданий в тг-канале
Задачи для практики
Задача 1
На рисунке изображён график функции $y=f'(x)$ производной функции $f(x)$, определённой на интервале $(-7;4)$. В какой точке отрезка $[-3;2]$ функция $f(x)$ принимает наибольшее значение?
Решение
На отрезке $[-3; 2]$ производная $y = f′(x)$ равна нулю в точке $x = -2$ и при переходе через неё меняет свой знак с «+» на «-», поэтому точка $x = -2$ — точка максимума функции на отрезке $[−3; 2]$. Так как она, кроме того, единственная точка экстремума на отрезке $[−3; 2]$, то в ней функция принимает наибольшее значение на данном отрезке.
Ответ: -2
Задача 2
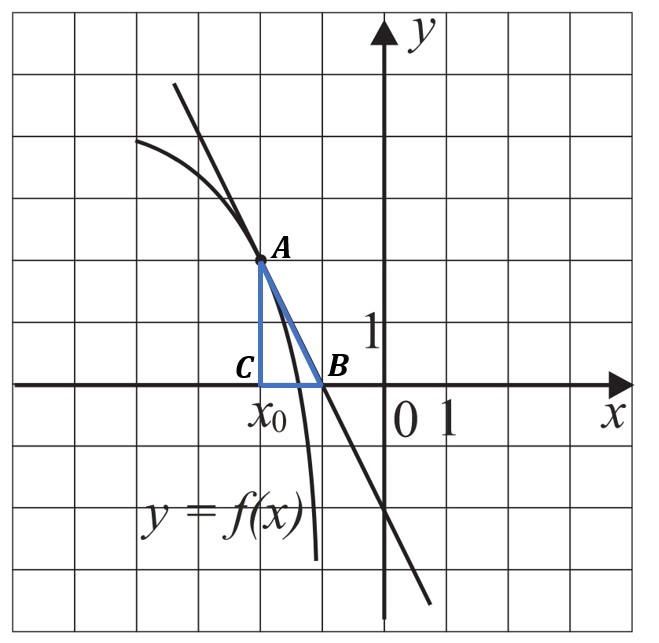
На рисунке изображён график функции $y=f(x)$ и касательная к нему в точке с абсциссой $x_0$. Найдите значение производной функции $f(x)$ в точке $x_0$.
Решение
По рисунку определяем, что касательная проходит через точки $A(-2; 2)$ и $B(-1; 0)$. Построим прямоугольный треугольник $ABC$ , где $C$ имеет координаты (-2; 0). Заметим, что прямая AB образует с положительным направлением оси Ox тупой уголα. Учитывая, что $f′(x_0) = tgα$, имеем $tgα = tg(180° — ∠ABC ) = — tg ∠ABC = -{AC}/{BC} = -{2}/{1} = -2$.
Ответ: -2
Задача 3
На рисунке изображён график функции $y=f(x)$ и отмечены точки $-7$; $-5$; $-1$;$1$. В какой из этих точек значение производной наибольшее?
Решение
Проводим касательные к графику в точках с указанными абсциссами (см. рис.).
Определяем, под каким углом $α$ они наклонены к положительному направлению оси $Ox$.
Согласно геометрическому смыслу производной $f'(x_0)=tg α$, то есть значения тангенсов построенных углов — это и есть значения производной в указанных точках
Замечаем, в точках $-7$ и $1$ касательные наклонены под острым углом, поэтому в этих точках значение производной положительно.
Учитывая, что касательная, проведённая к графику функции в точке с абсциссой $1$, образует больший угол с положительным направлении оси $Ox$, значит, значение производной в этой точке наибольшее.
Ответ: 1
Задача 4
На рисунке изображён график $y=f'(x)$ — производной функции $f(x)$, определённой на интервале $(-6;9)$. Найдите промежутки возрастания функции $f(x)$. В ответе укажите длину наибольшего из них.
Решение
Так как производная функции $y = f′(x)$ положительна на промежутках $(-6; -3)$ и $(8,5; 9)$, то функция $y = f(x$) возрастает на этих промежутках. Длина наибольшего из них $(-6; -3)$ равна $-3 — (-6) = 3$
Ответ: 3
Задача 5
На рисунке изображён график $y=f'(x)$ — производной функции $f(x)$, определённой на интервале $(-6;9)$. Найдите промежутки убывания функции $f(x)$. В ответе укажите длину наибольшего из них.
Решение
Так как на промежутке $(-3;8)$ производная функции $y=f'(x)$ отрицательна, то на этом промежутке функция $y=f(x)$ убывает. Длина этого промежутка равна $8-(-3)=11$.
Ответ: 11
Задача 6
На рисунке изображён график $y=f'(x)$ — производной функции $f(x)$, определённой на интервале $(-8;5)$. Найдите промежутки убывания функции $f(x)$. В ответе укажите сумму целых точек, входящих в эти промежутки.
Решение
Так как на промежутке (-6.5; -3.5) производная функции y = f′(x) отрицательна, то на этом промежутке функция y = f (x) убывает. В этот промежуток входят целые точки: -6; -5; -4. Их сумма равна -15.
Ответ: -15
Задача 7
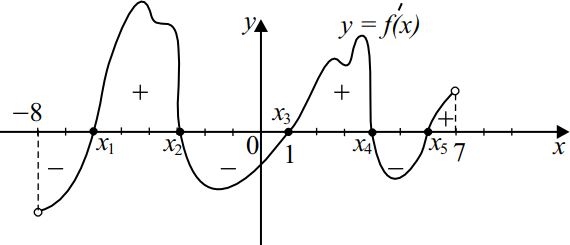
На рисунке изображён график $y=f'(x)$ — производной функции $f(x)$, определённой на интервале $(-8;7)$. Найдите количество точек экстремума функции $f(x)$ на заданном интервале.
Решение
Из графика видно, что производная $f′(x)$ функции $f(x)$ равна нулю в пяти точках причём при переходе через эти точки она меняет знак. То есть на заданном промежутке таких точек $5: x_1 , x_2 , x_3 , x_4 , x_5$. Таким образом, функция $f (x)$ имеет $5$ точек экстремума на заданном промежутке.
Ответ: 5
Задача 8
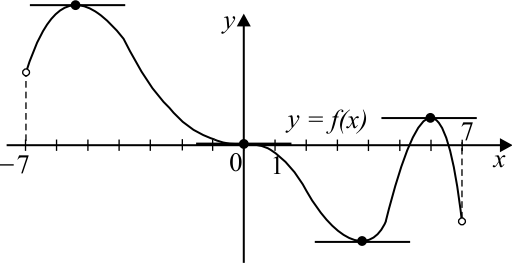
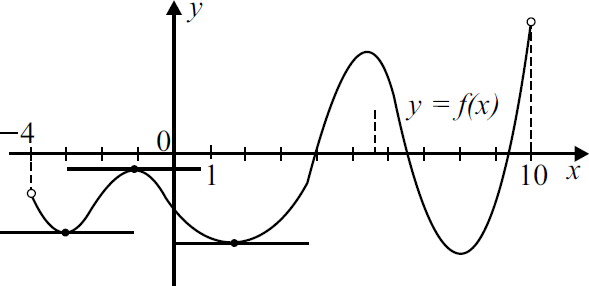
На рисунке изображён график функции $y=f(x)$, определённой на интервале $(-7;7)$. Найдите количество решений уравнения $f'(x)=0$.
Решение
Производная функции y = f′(x) на интервале (-7; 7) равна нулю в 4-х точках, в которых касательная к графику функции y = f(x) параллельна оси абсцисс.
Ответ: 4
Задача 9
На рисунке изображён график функции $y=f(x)$, определённой на интервале $(-4;10)$. Найдите количество решений уравнения $f'(x)=0$ на интервале $(-4;3)$.
Решение
Так как угловой коэффициент касательной $k = tg α = f′(x_0) = 0$, то это означает, что касательная к графику данной функции параллельна оси абсцисс.
На интервале $(-4; 3)$ построены три касательные, параллельные оси абсцисс.
Ответ: 3
Задача 10
Прямая $y=38x-28$ параллельна касательной к графику функции $y=3x^2+8x-2$. Найдите абсциссу точки касания.
Решение
Угловой коэффициент касательной к графику функции $y = 3x^2+8x-2$ в некоторой точке $x_0$ равен $y′(x_0). y′ = (3x^2 + 8x — 2)′ = 6x + 8$, значит, $y′(x_0) = 6x_0+8$. Угловой коэффициент прямой $y = 38x-28$ равен $38$. По условию, эта прямая параллельна касательной, значит, их угловые коэффициенты равны. Найдём значение $x_0$ из условия $6x_0 + 8 = 38, x_0 = 5$.
Ответ: 5
Задача 11
На рисунке изображён график $y=f'(x)$ — производной функции $f(x)$. На оси абсцисс отмечено десять точек: $x_1$, $x_2$, $x_3$, … , $x_8$, $x_9$, $x_{10}$. Сколько из этих точек лежит на промежутках убывания функции $f(x)$?
Решение
Так как производная функции $y = f′(x)$ отрицательна в точках $x_1, x_2, x_3$ и $x_8, x_9, x_{10}$, то на промежутках убывания лежат $6$ точек.
Ответ: 6
Задача 12
На рисунке изображён график $y=f'(x)$ — производной функции $f(x)$. На оси абсцисс отмечено десять точек: $x_1$, $x_2$, $x_3$, … , $x_8$, $x_9$, $x_{10}$. Сколько из этих точек лежит на промежутках возрастания функции $f(x)$?
Решение
Так как производная $y=f'(x)$ положительна в точках $x_4$, $x_5$, $x_6$, $x_7$, а в остальных точках — отрицательна, то на промежутке возрастания лежат $4$ точки.
Ответ: 4
Задача 13
На рисунке изображён график функции $y=f(x)$ и восемь точек на оси абсцисс: $x_1$, $x_2$, $x_3$, … ,$x_8$. В скольких из этих точек производная функции $f(x)$ отрицательна?
Решение
Производная отрицательна только в тех точках, которые принадлежат промежуткам убывания функции, если касательные в них не горизонтальны. Таких точек $3: x_3, x_5, x_8$.
Ответ: 3
Задача 14
Материальная точка движется прямолинейно по закону
$x(t)={1} / {3}t^3-{7} / {2}t^2-3t+5$, где $x$ — расстояние от точки отсчёта в метрах, $t$ — время в секундах, измеренное с начала движения. В какой момент времени (в секундах) её скорость была равна $5$ м/с?
Решение
Найдём скорость движения материальной точки $v(t) = x′(t) = t^2-7t-3$.
Найдём в какой момент времени (в секундах) её скорость была равна $5$ м/с, решив уравнение $t^2-7t-3 = 5$.
$t^2 — 7t — 8 = 0$;
$t_1 + t_2 = 7$,
$t_1·t_2 = -8$.
$t_1 = 8, t_2 = -1$ не удовлетворяет условию задачи.
Скорость материальной точки была равна $5$ м/с в момент времени $8$ секунд.
Ответ: 8
Задача 15
Материальная точка движется прямолинейно по закону
$x(t)=t^2-t-12$, где $x$ — расстояние от точки отсчёта в метрах, $t$ — время в секундах, измеренное с начала движения. Найдите её скорость (в метрах в секунду) в момент времени $t=7$ с.
Решение
Согласно физическому смыслу производной, мгновенная скорость равна $v(t) = x′(t).
v(t) = (t^2-t-12)′ = 2t-1. v(7) = 2·7-1 = 13$. Скорость материальной точки была $13$ м/с в момент времени $7$ секунд.
Ответ: 13
Задача 16
На рисунке изображён график функции $y=g(x)$, определённой и дифференцируемой на интервале $(-8; 6)$. Найдите количество точек, в которых касательная к графику этой функции параллельна прямой $y=100$.
Решение
Построим прямую y = 100. По графику определяем, что касательная к графику функции y = g(x) параллельна прямой y = 100 в четырёх точках.
Ответ: 4
Задача 17
На рисунке изображён график функции $y=f(x)$, определённой и дифференцируемой на интервале $(-6;7)$. Найдите количество точек, в которых касательная к графику функции $f(x)$ параллельна прямой $y=4$.
Решение
Построим прямую $y=4$. По графику находим, что касательная к графику функции $y=f(x)$ параллельна прямой $y=4$ в $6$ точках (см. рис.).
Ответ: 6
Рекомендуемые курсы подготовки
ЕГЭ Профиль №6. Физический смысл производной
Скачать файл в формате pdf.
ЕГЭ Профиль №6. Физический смысл производной
| Задача 1. Материальная точка движется прямолинейно по закону (xleft( t right) = — frac{1}{3}{t^2} + 4t + 15), где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени (t = 3;{text{c}}).
Ответ
ОТВЕТ: 2. |
|
| Задача 2. Материальная точка движется прямолинейно по закону (xleft( t right) = frac{1}{3}{t^3} + 2{t^2} — 15), где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени (t = 2;{text{c}}).
Ответ
ОТВЕТ: 12. |
|
| Задача 3. Материальная точка движется прямолинейно по закону (xleft( t right) = {t^4} + 9{t^2} — 3t + 23), где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени (t = 1;{text{c}}{text{.}})
Ответ
ОТВЕТ: 19. |
|
| Задача 4. Материальная точка движется прямолинейно по закону (xleft( t right) = — frac{1}{6}{t^2} + 5t — 19), где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 4 м/с?
Ответ
ОТВЕТ: 3. |
|
| Задача 5. Материальная точка движется прямолинейно по закону (xleft( t right) = frac{1}{3}{t^3} + {t^2} — 9t + 12), где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 15 м/с?
Ответ
ОТВЕТ: 4. |
|
| Задача 6. Материальная точка M начинает движение из точки A и движется по прямой на протяжении 12 секунд. График показывает, как менялось расстояние от точки A до точки M со временем. На оси абсцисс откладывается время t в секундах, на оси ординат — расстояние S. Определите, сколько раз за время движения скорость точки M обращалась в ноль (начало и конец движения не учитывайте). Ответ
ОТВЕТ: 6. |
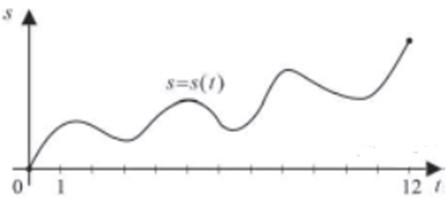 |
Задача 3. Начала теории вероятностей
Задача 3. Начала теории вероятностей
Задача 4. Вероятности сложных событий
Задача 4. Вероятности сложных событий
Задача 5. Простейшие уравнения
Задача 5. Простейшие уравнения
Задача 6. Вычисления и преобразования
Задача 6. Вычисления и преобразования
Задача 7. Производная и первообразная
Задача 7. Производная и первообразная
Задача 8. Задачи с прикладным содержанием
Задача 8. Задачи с прикладным содержанием
Задача 9. Текстовые задачи
Задача 9. Текстовые задачи
Задача 10. Графики функций
Задача 10. Графики функций
Задача 11. Наибольшее и наименьшее значение функций
Задача 11. Наибольшее и наименьшее значение функций