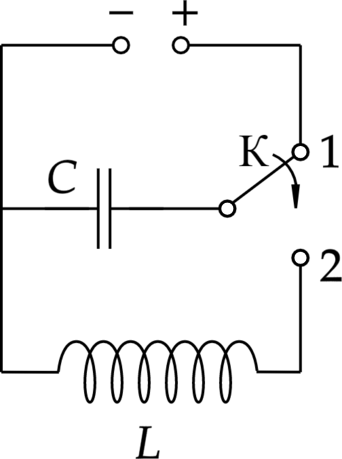
В колебательном контуре (см. рис.) индуктивность катушки L = 12 мГн. Какой должна быть индуктивность Lx второй катушки, чтобы при переводе ключа К из положения 1 в положение 2 период собственных электромагнитных колебаний в контуре уменьшился в
раза? Ответ приведите в миллигенри.
Спрятать решение
Решение.
Период собственных колебаний колебательного контура равен следовательно, для уменьшения периода колебаний в
раз необходимо уменьшить индуктивность в 3 раза, то есть индуктивность Lx должна быть равна 12 мГн/3 = 4 мГн.
Ответ: 4.
Источник: ЕГЭ по физике 2020. Досрочная волна. Вариант 1
Канал видеоролика: Математик МГУ
Смотреть видео:
#математикаогэ #гвэ #егэответы #репетиторпоматематике #репетитор_по_математике #огэматематика #огэответы #подготовкакогэ #подготовкакегэ
Свежая информация для ЕГЭ и ОГЭ по Математике (листай):
С этим видео ученики смотрят следующие ролики:

Магнетизм. Расчётная задача С5 | Физика ЕГЭ | Pi-Fi
Математика ОГЭ и ЕГЭ с Пифагором

ЕГЭ 2023. Физика. Структура экзамена и метод размерностей
Математик МГУ

ЕГЭ 2023 Физика. Игра в карты с механикой
Математик МГУ

ЕГЭ 2023 Физика. Электричество и электрические схемы
Математик МГУ
Облегчи жизнь другим ученикам — поделись! (плюс тебе в карму):
22.08.2022
- Комментарии
RSS
Написать комментарий
Нет комментариев. Ваш будет первым!
Ваше имя:
Загрузка…
Задание 18045
Внимательно прочитайте текст задания и выберите верный ответ из списка
Решение
→
Задание 18103
Внимательно прочитайте текст задания и выберите верный ответ из списка
Решение
→
Задание 18111
Внимательно прочитайте текст задания и выберите верный ответ из списка
Решение
→
Задание 18142
Внимательно прочитайте текст задания и выберите верный ответ из списка
Решение
→
Задание 18243
Внимательно прочитайте текст задания и выберите верный ответ из списка
Решение
→
Задание 18615
Установление соответствия
Решение
→
Задание 18684
Установление соответствия
Решение
→
Задание 18789
Установление соответствия
Решение
→
Задание 18478
Внимательно прочитайте текст задания и выберите верный ответ из списка
Решение
→
Задание 18533
Введите ответ в поле ввода
Решение
→
Задание 18190
Установление соответствия
Решение
→
Задание 18785
Установление соответствия
Решение
→
Задание 17495
Внимательно прочитайте текст задания и выберите верный ответ из списка
Решение
→
Задание 18143
Внимательно прочитайте текст задания и выберите верный ответ из списка
Решение
→
Задание 18207
Внимательно прочитайте текст задания и выберите верный ответ из списка
Решение
→
Задание 18176
Внимательно прочитайте текст задания и выберите верный ответ из списка
Решение
→
Задание 18473
Внимательно прочитайте текст задания и выберите верный ответ из списка
Решение
→
Из двух городов навстречу друг…
К системе из кубика массой М…
Шарик массой 400 г падает…
Колеблющаяся струна издаёт звук с…
Автомобиль массой 3 т проезжает…
На поверхности пресной воды плотностью…
Груз, привязанный к нити, отклонили…
При уменьшении абсолютной температуры на…
У идеального теплового двигателя Карно…
В воздухе комнаты парциальное давление…
На рисунке приведены графики двух…
Одноатомный идеальный газ в количестве…
На рисунке показаны два параллельных…
По проводнику течёт постоянный электрический…
На рисунке приведена зависимость силы…
Две параллельные металлические пластины больших…
Протон движется по окружности в…
Два резистора с сопротивлениями R1…
На рисунке представлен фрагмент Периодической…
Период полураспада одного из изотопов…
Для некоторых атомов характерной особенностью…
Определите показания вольтметра (см. рисунок),…
Необходимо сделать нитяной маятник и…
Рассмотрите таблицу, содержащую характеристики планет…
В начале процесса температура куска…
Сколько фотонов падает на сетчатку…
Две порции одного и того…
Нить, удерживающая вертикально расположенную лёгкую…
Два тела подвешены за нерастяжимую…
Одноатомный идеальный газ совершает циклический…
В электрической цепи, показанной на…
Квадратная проволочная рамка со стороной I…
ЕГЭ профильный уровень. №5 Логарифмические уравнения. Задача 10
Задача 10. Решите уравнение ({log _{x + 6}}32 = 5.) Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
({log _{x + 6}}32 = 5,,,,,, Leftrightarrow ,,,,,,left{ {begin{array}{*{20}{c}}{{{left( {x + 6} right)}^5} = 32}\{x + 6 > 0,,,,,,,,,,}\{x + 6 ne 1,,,,,,,,,,,}end{array}} right.,,,,,,, Leftrightarrow ,,,,,,left{ {begin{array}{*{20}{c}}{{{left( {x + 6} right)}^5} = {2^5}}\{x + 6 > 0,,,,,,,,}\{x + 6 ne 1,,,,,,,,}end{array}} right.,,,,,, Leftrightarrow )
( Leftrightarrow ,,,,,,,left{ {begin{array}{*{20}{c}}{x + 6 = 2}\{x + 6 > 0}\{x + 6 ne 1}end{array},,,,,, Leftrightarrow } right.,,,,,,,,x + 6 = 2,,,,,,, Leftrightarrow ,,,,,,,x = — 4.)
Ответ: – 4.
18. Электродинамика и СТО (установление соответствия)
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Колебательный контур
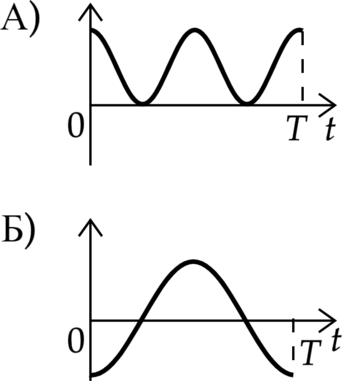
Конденсатор идеального колебательного контура длительное время подключён к источнику постоянного напряжения (см. рисунок). В момент (t=0) переключатель К переводят из положения 1 в положение 2. Графики А и Б отображают изменения физических величин, характеризующих возникшие после этого электромагнитные колебания в контуре (T – период колебаний). 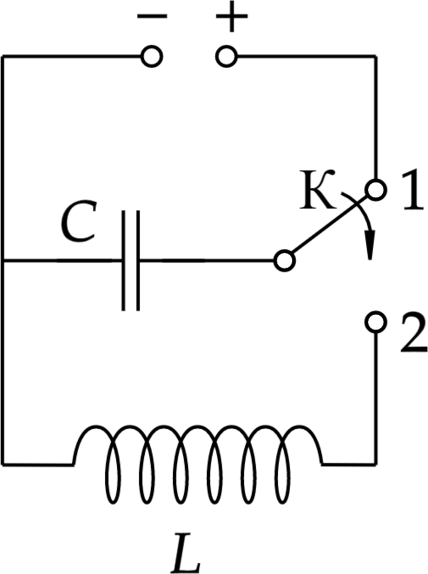
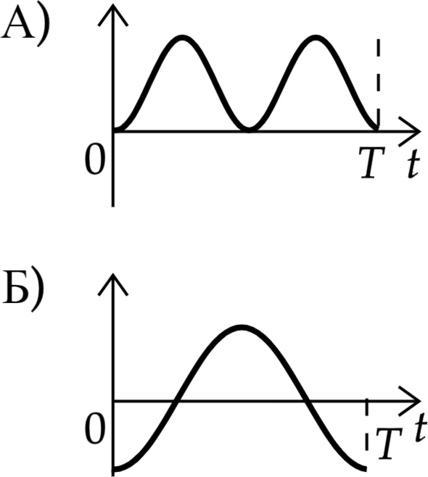
1) энергия магнитного поля катушки
2) сила тока в катушке
3) заряд правой обкладки конденсатора
4) энергия электрического поля конденсатора
“Демоверсия 2021”
А) Энергия магнитного поля катушки в начальный момент равна 0, при этом она не может быть отрицательна Б) Сила тока должна выходить из 0, а энергия эектрического поля конденсатора не может быть равна 0, остается вариант 3
Ответ: 13
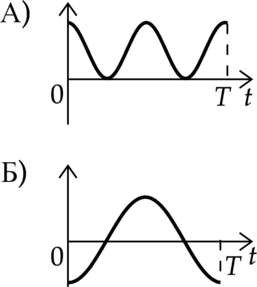
Конденсатор колебательного контура длительное время подключён к источнику постоянного напряжения (см. рисунок). В момент t = 0 переключатель К переводят из положения 1 в положение 2. Графики А и Б представляют изменения физических величин, характеризующих электромагнитные колебания в контуре после этого (Т — период колебаний).
Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
1) сила тока в контуре
2) энергия магнитного поля катушки
3) энергия электрического поля конденсатора
4) заряд левой обкладки конденсатора
[begin{array}{|c|c|}
hline
text{А}&text{Б}\
hline
& \
hline
end{array}]
“Досрочная волна 2019 вариант 1”
А) Во-первых, это энергия, так как заряд могжет быть отрицательным, а сила тока изменяется с меньшим периодом. При этом это зард конденсатора, так как он первоначально заряжен.
Б) Единственное, что из списка может быть отрицательным – заряд.
Ответ: 34
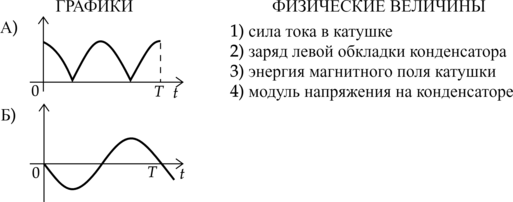
Перекидной ключ находится в положении 1 в течение долгого времени. Далее ключ переключают в положение 2 и начинают наблюдение за возникшими колебаниями. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут отражать.
К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами. 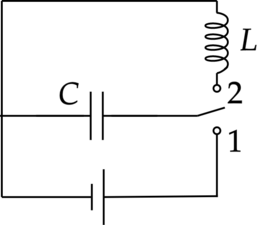
Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
1) Энергия конденсатора
2) Модуль напряжения на конденсаторе
3) Ток через катушку
4) Заряд левой обкладки конденсатора
[begin{array}{|c|c|}
hline
text{А}&text{Б}\
hline
& \
hline
end{array}]
“Досрочная волна 2019 вариант 2”
Гррафик Б – ни одна из данных величин не может быть отрицательным, кроме заряда.
Заметим, что период колебаний заряда в 2 раза больше, чем период колебаний величины графика А, следовательно, это энергия конденсатора: [W=dfrac{q^2}{2C}]
Ответ: 14
Конденсатор колебательного контура длительное время подключён к источнику постоянного напряжения (см. рисунок). В момент t = 0 переключатель К переводят из положения 1 в положение 2. На графиках А и Б представлены изменения физических величин, характеризующих колебания в контуре после этого. (T) – период электромагнитных колебаний.
Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять.
К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
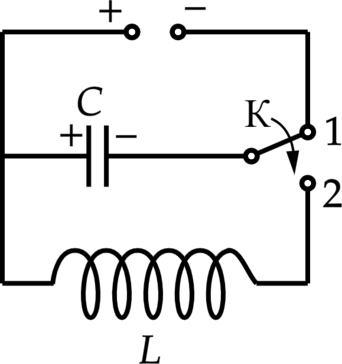
В начальный момент времени весь заряд сосредоточен на обкладках конденсатора. Значит график А, соответствует либо заряду на левой обкладке конденсаторе, либо модулю напряжения на нем, но так как заряд на обкладках при колебаниях будет отрицательный, а модуль напряжения будет вычислять по формуле: [|U|=|U_{max}cos (dfrac{t}{sqrt{LC}})|]. А – 4.
Сила тока на катушке будет вычисляться по формуле: [I(t)=I_m sin(dfrac{t}{sqrt{LC}})] Энергия на катушке [W=dfrac{LI^2}{2}=dfrac{LI^2_msin^2(dfrac{t}{sqrt{LC}})}{2}] Энергия не может быть отрицательно, а сила тока может быть, значит Б – 1
Ответ: 41
Катушка идеального колебательного контура длительное время подключена к источнику постоянного напряжения, поэтому конденсатор не заряжен (см. рисунок). В момент t=0 ключ К размыкают. Графики А и Б отображают изменения физических величин, характеризующих возникшие после этого электромагнитные колебания в контуре (Т — период колебаний).
Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут отображать.

Первоначально ток на катушке максимален, а заряд на конденсаторе равен 0, кроме того, энергия конденсатора и катушки не может быть отрицательной, значит графики соответствуют А –4, Б –1
Ответ: 41
В идеальном колебательном контуре, состоящем из катушки индуктивности и конденсатора, происходят свободные незатухающие электромагнитные колебания.
Из приведённого ниже списка выберите две величины, которые остаются постоянными при этих колебаниях.
1) период колебаний силы тока в контуре
2) заряд конденсатора
3) фаза колебаний напряжения на конденсаторе
4) амплитуда колебаний силы тока в катушке энергия магнитного поля катушки
5) энергия магнитного поля катушки
1) Да, период колебаний T в идеальном колебательном контуре является постоянной величиной.
2) Заряд конденсатора постоянно меняется: сначала уменьшается, затем, снова увеличивается.
3) Фаза колебаний (не путать с начальной фазой колебаний) меняется со временем по закону .
4) Да, амплитуда колебаний заряда остается прежней, так как в идеальном колебательном контуре заряд никуда не исчезает.
5) Энергия магнитного поля катушки периодически то уменьшается, то увеличивается.
Ответ: 14
Катушка идеального колебательного контура длительное время подключена к источнику постоянного напряжения, поэтому конденсатор не заряжен (см. рисунок). В момент t=0 ключ К размыкают. Графики А и Б отображают изменения физических величин, характеризующих возникшие после этого электромагнитные колебания в контуре (Т — период колебаний).
Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут отображать.

Первоначально ток на катушке максимален, а заряд на конденсаторе равен 0. Значит, первоначально энергия катушки максимальна, а энергия конденсатора минимальна.
А) График всюду положителен (значит, это или энергия конденсатора или катушки) и имеет ненулевое начальное значение, значит, этот график может отражать только энергию магнитного поля катушки.
Б) График также всюду положителен и имеет нулевое начальное значение. Подходит только энергия электрического поля конденсатора.
Ответ: 23

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
К однородному медному цилиндрическому проводнику длиной 40 м приложили разность потенциалов 10 В. Каким будет изменение температуры проводника DT через 15 с? Изменением сопротивления проводника и рассеянием тепла при его нагревании пренебречь. (Удельное сопротивление меди 1,7´10–8 Ом´м.)
На рисунке показана схема устройства для предварительного отбора заряженных частиц для последующего детального исследования. Устройство представляет собой конденсатор, пластины которого изогнуты дугой радиусом см. Предположим, что в промежуток между обкладками конденсатора из источника заряженных частиц (и. ч.) влетают ионы, как показано на рисунке. Напряжённость электрического поля в конденсаторе по модулю равна 5 кВ/м. Скорость ионов равна 105 м/с. При каком значении отношения заряда к массе ионы пролетят сквозь конденсатор, не коснувшись его пластин? Считать, что расстояние между обкладками конденсатора мало, напряжённость электрического поля в конденсаторе всюду одинакова по модулю, а вне конденсатора электрическое поле отсутствует. Влиянием силы тяжести пренебречь.
По прямому горизонтальному проводнику длиной 1 м с площадью поперечного сечения подвешенному с помощью двух одинаковых невесомых пружинок жёсткостью 100 Н/м, течёт ток
(см. рисунок).
Какой угол составляют оси пружинок с вертикалью после включения вертикального магнитного поля с индукцией
если абсолютное удлинение каждой из пружинок при этом составляет
? (Плотность материала проводника
)
В электрической цепи, показанной на рисунке, ЭДС источника тока равна 12 В, емкость конденсатора 2 мФ, индуктивность катушки 5 мГн, сопротивление лампы 5 Ом и сопротивление резистора 3 Ом.
В начальный момент времени ключ К замкнут. Какая энергия выделится в лампе после размыкания ключа? Внутренним сопротивлением источника тока, и проводов пренебречь.
Пылинка, имеющая массу и заряд
влетает в электрическое поле вертикального высокого конденсатора в точке, находящейся посередине между его пластинами (см. рисунок, вид сверху).
Чему должна быть равна минимальная скорость, с которой пылинка влетает в конденсатор, чтобы она смогла пролететь его насквозь? Длина пластин конденсатора 10 см, расстояние между пластинами 1 см, напряжение на пластинах конденсатора 5 000 В. Система находится в вакууме.
Плоская горизонтальная фигура площадью 0,1 м2, ограниченная проводящим контуром, имеющим сопротивление 5 Ом, находится в однородном магнитном поле. Проекция вектора магнитной индукции на вертикальную ось Оz медленно и равномерно возрастает от некоторого начального значения B1z до конечного значения B2z = 4,7 Тл. За это время по контуру протекает заряд Δq= 0,08 Кл. Найдите B1z.
В электрической схеме, показанной на рисунке, ключ К замкнут.
Заряд конденсатора ЭДС батарейки
её внутреннее сопротивление
сопротивление резистора
Найдите количество теплоты, которое выделяется на резисторе после размыкания ключа К в результате разряда конденсатора. Потерями на излучение пренебречь.
Тонкий алюминиевый брусок прямоугольного сечения, имеющий длину L = 0,5 м, соскальзывает из состояния покоя по гладкой наклонной плоскости из диэлектрика в вертикальном магнитном поле индукцией В = 0,1 Тл (см. рисунок). Плоскость наклонена к горизонту под углом a = 30°. Продольная ось бруска при движении сохраняет горизонтальное направление. Найдите величину ЭДС индукции на концах бруска в момент, когда брусок пройдёт по наклонной плоскости расстояние l = 1,6 м.
Проводящий стержень длиной l = 20 см движется поступательно в однородном магнитном поле со скоростью v = 1 м/с так, что угол между стержнем и вектором скорости = 30° (см. рисунок). ЭДС индукции в стержне равна 0,05 В. Какова индукция магнитного поля?
Как и во сколько раз изменится мощность, выделяющаяся на резисторе в цепи, схема которой изображена на рисунке, если перевести ключ К из положения 1 в положение 2? Параметры цепи:
На уроке физики школьник собрал схему, изображенную на рисунке. Ему было известно, что сопротивления резисторов равны и
Токи, измеренные школьником при помощи идеального амперметра А при последовательном подключении ключа К к контактам 1, 2 и 3, оказались равными, соответственно,
Чему было равно сопротивление резистора
?
В цепи, схема которой изображена на рисунке, вначале замыкают ключ а затем, спустя длительное время, ключ
Известно, что после этого через ключ
протек заряд, равный по модулю
Чему равна ЭДС
источника тока, если
? Источник считайте идеальным.
В цепи, изображённой на рисунке, сопротивление диода в прямом направлении пренебрежимо мало, а в обратном многократно превышает сопротивление резисторов. При подключении к точке А положительного полюса, а к точке В отрицательного полюса батареи с ЭДС 12 В и пренебрежимо малым внутренним сопротивлением потребляемая мощность равна 14,4 Вт. При изменении полярности подключения батареи потребляемая мощность оказалась равной 21,6 Вт. Укажите, как течёт ток через диод и резисторы в обоих случаях, и определите сопротивления резисторов в этой цепи.
В цепи, изображённой на рисунке, сопротивления резисторов равны между собой: R1= R2 = R3 = R. При разомкнутом ключе К через резистор R3 течёт ток I0 =1,4 А. Загорится ли лампа после замыкания ключа, если она загорается при силе тока I = 0,5 А? Сопротивление лампы в этом режиме Rл = 3R. Внутренним сопротивлением источника пренебречь, диод считать идеальным.
Решение
1. Из рисунка видно, что диод включен противоположно направлению тока. Так как диод идеальный, то ток через него и резистор не потечёт.
2. При разомкнутом ключе резисторы и
подключены последовательно, а значит, сила тока в этом случае по закону Ома равна
3. Когда ключ замыкают, лампа включается параллельно резистору а значит, сопротивление участка с параллельным соединением проводов будет:
Ток в цепи в этом случае:
Напряжение на параллельных участках одинаково и равно
Тогда через лампу будет проходить ток:
что меньше величины необходимого тока, а значит, лампа не загорится.
Задача 16
Одни и те же элементы соединены в электрическую цепь сначала по схеме 1, а затем по схеме 2 (см. рисунок). Сопротивление резистора равно R, сопротивление амперметра сопротивление вольтметра
Найдите отношение мощностей
выделяемых на резисторах в этих схемах. Внутренним сопротивлением источника и сопротивлением проводов пренебречь.
Решение
Пусть — сопротивление амперметра,
— сопротивление вольтметра,
— ЭДС источника. В схеме 1 напряжение на резисторе определяется с помощью закона Ома для замкнутой цепи:
где
— сопротивление участка цепи, содержащего резистор и вольтметр. Отсюда:
В схеме 2 с помощью закона Ома найдём силу тока через резистор:
Отношение мощностей
Задача 17
Маленький шарик с зарядом и массой 3 г, подвешенный на невесомой нити с коэффициентом упругости 100 Н/м, находится между вертикальными пластинами плоского воздушного конденсатора. Расстояние между обкладками конденсатора 5 см. Какова разность потенциалов между обкладками конденсатора, если удлинение нити 0,5 мм?
Решение
Условия равновесия:
Возведем оба равенства в квадрат и сложим их:
откуда
Напряженность электрического поля в конденсаторе:
Таким образом,
Задача 18
По П-образному проводнику постоянного сечения скользит со скоростью
медная перемычка
длиной
из того же материала и такого же сечения.
Проводники, образующие контур, помещены в постоянное однородное магнитное поле, вектор индукции которого направлен перпендикулярно плоскости проводников (см. рисунок). Какова индукция магнитного поля если в тот момент, когда
разность потенциалов между точками
и
равна
? Сопротивление между проводниками в точках контакта пренебрежимо мало, а сопротивление проводов велико.
Решение
При движении перемычки в ней возникает ЭДС
Закон Ома для замкнутой цепи :
где — сопротивление перемычки
Следовательно,
Задача 19
Два плоских конденсатора ёмкостью С и 2С соединили параллельно и зарядили до напряжения U. Затем ключ К разомкнули, отключив конденсаторы от источника (см. рисунок). Пространство между их обкладками заполнено жидким диэлектриком с диэлектрической проницаемостью ε. Какой будет разность потенциалов между обкладками, если из правого конденсатора диэлектрик вытечет?
Решение
В соответствии с определением понятия «ёмкость» для суммарного заряда конденсаторов имеем:
где 3С — суммарная ёмкость конденсаторов, когда оба они заполнены жидким диэлектриком. После вытекания диэлектрика из правого конденсатора суммарный заряд останется прежним. Так как для плоского конденсатора C~ε, то суммарная ёмкость станет равной (С + 2С/ε), а напряжение будет равно U1, так что
Решая систему уравнений (1) и (2), получим ответ:
Задача 20
Катод фотоэлемента с работой выхода освещается светом частотой
Вылетевшие из катода электроны попадают в однородное магнитное поле с индукцией
перпендикулярно линиям индукции этого поля. Чему равен максимальный радиус окружности R, по которой движутся электроны?
Решение
| № этапа | Содержание этапа решения | Чертёж, график, формула | Оценка этапа в баллах |
| 1 | Записано уравнение Эйнштейна для фотоэффекта: | 1 | |
| 2 | Записано уравнение, связывающее силу Лоренца, действующую на электрон, с величиной центростремительного ускорения:
Уравнение преобразовано к виду, устанавливающему связь между кинетической энергией электрона и радиусом орбиты: |
1 | |
| 3 | Решена система уравнений и получен ответ в алгебраической форме:
Подставлены значения констант и параметров и получен ответ в числовой форме: |
1 | |
| Максимальный балл | 3 |
Задача 21
В однородном магнитном поле, индукция которого протон движется перпендикулярно вектору магнитной индукции В по окружности радиусом 5 м. Определите скорость протона.
Решение
Из уравнения, связывающего на основе второго закона Ньютона силу Лоренца, действующую на протон, с модулем центростремительного ускорения: . Откуда выражаем искомую скорость.
Задача 22
К одному концу лёгкой пружины жёсткостью k = 100 Н/м прикреплён массивный груз, лежащий на горизонтальной плоскости, другой конец пружины закреплён неподвижно (см. рисунок). Коэффициент трения груза по плоскости Груз смещают по горизонтали, растягивая пружину, затем отпускают с начальной скоростью, равной нулю. Груз движется в одном направлении и затем останавливается в положении, в котором пружина уже сжата. Максимальное растяжение пружины, при котором груз движется таким образом, равно d = 15 см. Найдите массу m груза.
Решение
1. Начальная энергия системы равна потенциальной энергии растянутой пружины: После того, как пружину отпустили, она остановится в положении, при котором она сжата на величину
Тогда конечная энергия системы равна потенциальной энергии сжатой пружины:
Приращение полной энергии системы равно работе силы трения
где — модуль силы реакции опоры.
2. В момент, когда груз остановился, по второму закону Ньютона равнодействующая всех сил стала равна нулю. Пружина сжата, поэтому сила упругости пружины направлена вправо. Её уравновешивает сила трения покоя, которая направлена против возможного движения, причём эта сила максимальна, т. к. по условию начальное положение пружины соответствует максимальному растяжению пружины, при котором груз движется таким образом.
Запишем закон Ньютона для вертикальной и горизонтальной оси:
3. Подставим полученное выражение для в равенство из пункта 1:
После подстановки получим
Задача 23
Хорошо проводящая рамка площадью вращается в однородном магнитном поле с индукцией
перпендикулярной оси вращения рамки, с частотой
Скользящие контакты от рамки присоединены к цепи, состоящей из резистора сопротивлением
к которому последовательно присоединены два параллельно соединенных резистора сопротивлениями
и
(см. рис.). Найти максимальную силу тока, текущего через резистор
в процессе вращения рамки. Индуктивностью цепи можно пренебречь.
Решение
При вращении рамки в магнитном поле в ней возникает ЭДС индукции, равная, по закону электромагнитной индукции Фарадея,
(здесь — угловая частота вращения рамки).
В цепи из резисторов, присоединенной к рамке, под действием этой ЭДС возникает ток, равный, согласно закону Ома для полной цепи, где согласно формулам для сопротивления цепи, состоящей из последовательно и, параллельно соединенных резисторов,
Поскольку падение напряжения на параллельно соединенных резисторах и
одинаково, по закону Ома для участка цепи
причем в точке разветвления тока
Из всех записанных уравнений следует, что
откуда искомая максимальная сила тока равна, очевидно,
Подставляя числовые данные и проверяя размерность, получаем:
Задача 24
На двух вертикальных лёгких проводах длиной l каждый подвешен в горизонтальном положении массивный проводящий стержень длиной L. Верхние концы проводов присоединены к обкладкам конденсатора ёмкостью С. Система находится в вертикальном однородном магнитном поле с индукцией В (см. рисунок). Стержень отклоняют от положения равновесия параллельно самому себе на небольшое расстояние и отпускают с нулевой начальной скоростью. Найдите зависимость от времени t заряда q конденсатора, считая, что в начальный момент, при
конденсатор был не заряжен. Трением, сопротивлением всех проводников и контактов между ними, а также силами взаимодействия токов в проводниках с магнитным полем пренебречь.
Решение
Согласно условию задачи, взаимодействие токов в проводниках с магнитным полем пренебрежимо мало. Поэтому после отпускания стержень будет совершать свободные колебания, как математический маятник, с круговой частотой по закону
где x — текущее отклонение стержня от положения равновесия.
Поток вектора магнитной индукции через замкнутый контур, содержащий все проводники и конденсатор, равен
По закону электромагнитной индукции Фарадея при колебаниях стержня в данном контуре будет возникать ЭДС индукции, равная
Поскольку сопротивлением проводников мы также пренебрегаем, то по закону Ома для полной цепи эта ЭДС равняется напряжению между обкладками конденсатора: откуда
Задача 25
В однородном магнитном поле с индукцией протон движется перпендикулярно вектору
индукции со скоростью
Определите радиус траектории протона.
Задача 26
Ядро изотопа водорода — дейтерия — движется в однородном магнитном поле индукцией
перпендикулярно вектору В индукции по окружности радиусом 10 м. Определите скорость ядра.
Задача 27
В однородном магнитном поле с индукцией B, направленной вертикально вниз, равномерно вращается в горизонтальной плоскости против часовой стрелки положительно заряженный шарик массой m, подвешенный на нити длиной l (конический маятник). Угол отклонения нити от вертикали равен скорость движения шарика равна v. Найдите заряд шарика q.
Решение
Задача 28
На непроводящей горизонтальной поверхности стола проводящая жёсткая рамка массой m из однородной тонкой проволоки, согнутая в виде квадрата ACDE со стороной (см. рисунок). Рамка находится в однородном горизонтальном магнитном поле, вектор индукции
которого перпендикулярен сторонам АЕ и CD и равен по модулю В. По рамке течёт ток в направлении, указанном стрелками (см. рисунок). При какой минимальной силе тока рамка начнет поворачиваться вокруг стороны CD?
Решение
Для того, чтобы рамка начала поворачиваться вокруг оси CD, вращательный момент сил, действующих на рамку и направленных вверх, должен быть не меньше суммарного момента сил, направленных вниз.
На проводник с током в магнитном поле действует сила Ампера Если направление тока и магнитного поля параллельны, то сила Ампера не действует. В данном случае на сторону АЕ действует сила Ампера
которая по правилу буравчика направлена вверх (на рисунке — на нас). На каждую из сторон действует сила тяжести
т. к. масса всего квадрата равна
Запишем условие моментов: где
и
— плечи сил относительно оси CD.
Отсюда находим минимальную силу тока
Задача 29
Ион ускоряется в электрическом поле с разностью потенциалов кВ и попадает в однородное магнитное поле перпендикулярно к вектору его индукции
(см. рисунок). Радиус траектории движения иона в магнитном поле
м, модуль индукции магнитного поля равен 0,5 Тл. Определите отношение массы иона к его электрическому заряду
Кинетической энергией иона при его вылете из источника пренебрегите.
Решение
Разность потенциалов сообщает иону кинетическую энергию
В магнитном поле, на движущийся ион действует сила Лоренца, которая сообщает ему центростремительное ускорение:
Приравнивая правые части полученных равенств, имеем
Задача 30
Горизонтальный проводящий стержень прямоугольного сечения поступательно движется с ускорением вверх по гладкой наклонной плоскости в вертикальном однородном магнитном поле (см. рисунок).
По стержню протекает ток I. Угол наклона плоскости Отношение массы стержня к его длине
Модуль индукции магнитного поля
Ускорение стержня
Чему равна сила тока в стержне?
Решение
1) На рисунке показаны силы, действующие на стержень с током:
— сила тяжести направленная вертикально вниз;
— сила реакции опоры направленная перпендикулярно к наклонной плоскости;
— сила Ампера направленная горизонтально вправо, что вытекает из условия задачи.
2) Модуль силы Ампера
3) Систему отсчёта, связанную с наклонной плоскостью, считаем инерциальной. Для решения задачи достаточно записать второй закон Ньютона в проекциях на ось х (см. рисунок):
Отсюда находим
Задача 31
В зазоре между полюсами электромагнита вращается с угловой скоростью ω = 100 с–1проволочная рамка в форме полуокружности радиусом r = 5 см, содержащая N = 20 витков провода. Ось вращения рамки проходит вдоль оси О рамки и находится вблизи края области с постоянным однородным магнитным полем с индукцией В = 1 Тл (см. рисунок), линии которого перпендикулярны плоскости рамки. Концы обмотки рамки замкнуты через скользящие контакты на резистор с сопротивлением R = 25 Ом. Пренебрегая сопротивлением рамки, найдите тепловую мощность, выделяющуюся в резисторе.
Решение
При вращении рамки в магнитном поле в ней возникает ЭДС индукции, равная по модулю
За малое время рамка поворачивается на угол
и её площадь, находящаяся в магнитном, поле увеличивается на
так что
Так происходит до тех пор, пока площадь рамки в поле увеличивается. После того как вся рамка окажется в поле, эта площадь начнёт уменьшаться с такой же скоростью, так что ЭДС поменяет знак, но сохранит своё значение.
Таким образом, согласно закону Ома для замкнутой цепи, в рамке всё время будет течь ток с одинаковым значением периодически изменяя своё направление на противоположное.
По закону Джоуля — Ленца тепловая мощность, выделяющаяся при этом процессе в резисторе, не зависит от направления тока и равняется
Задача 32
На шероховатой плоскости, наклонённой под углом к горизонту, находится однородный цилиндрический проводник массой от
г и длиной
см (см. рисунок). По проводнику пропускают ток в направлении «от нас», за плоскость рисунка, и вся система находится в однородном магнитном поле с индукцией
направленной вертикально вниз. При какой силе тока
цилиндр будет оставаться на месте, не скатываясь с плоскости и не накатываясь на неё?
РешениеНарисуем силы, действующие на проводник с током: силу тяжести
направленную вертикально вниз, силу нормального давления
перпендикулярную плоскости, и силу Ампера
равную по модулю
и направленную в данном случае, согласно правилу левой руки, горизонтально влево (см. рисунок). Заметим, что все эти три силы приложены таким образом, что они не создают моментов сил относительно оси цилиндра. Поэтому в равновесии сила сухого трения цилиндра о шероховатую наклонную плоскость децствительно должна равняться нулю — иначе он бы покатился.
Спроецируем эти силы на направление вдоль плоскости и на перпендикуляр к ней. Условия равновесия имеют вид
Из первого уравнения находим искомую величину силы тока при равновесии цилиндра: Подставляя это значение
во второе уравнение, находим
(хотя эту величину находить по условию не требовалось).
Задача 33
Проводник движется равноускоренно в однородном вертикальном магнитном поле. Направление скорости перпендикулярно проводнику. Длина проводника — 2 м. Индукция перпендикулярна проводнику и скорости его движения. Проводник перемещается на 3 м за некоторое время. При этом начальная скорость проводника равна нулю, а ускорение 5 м/с2. Найдите индукцию магнитного поля, зная, что ЭДС индукции на концах проводника в конце движения равна 2 В.
Решение
При движении проводника в магнитном поле на электроны в проводнике действует сила Лоренца. Сила Лоренца равна Напряжённость поля внутри проводника можно рассчитать по формуле
Напряжение на концах проводника равно
Движение равноускоренное, поэтому путь, пройденный проводником рассчитывается по формуле
откуда
Следовательно,
откуда
Задача 34
Плоская горизонтальная фигура площадью 0,1 м2, ограниченная проводящим контуром, имеющим сопротивление 5 Ом, находится в однородном магнитном поле. Проекция вектора магнитной индукции на вертикальную ось Оz медленно и равномерно возрастает от некоторого начального значения B1z до конечного значения B2z = 4,7 Тл. За это время по контуру протекает заряд Δq= 0,08 Кл. Найдите B1z.
Решение
Выражение для модуля ЭДС индукции в случае однородного поля: где S — площадь фигуры;
Закон Ома: E = IR, где R — сопротивление контура; — ток в контуре за время Δt изменения магнитного поля.
Выражение для заряда, протекающего по цепи:
Задача 35
К конденсатору С1 через диод и катушку индуктивности L подключён конденсатор ёмкостью С2 = 2 мкФ. До замыкания ключа К конденсатор С1 был заряжен до напряжения U = 50 В, а конденсатор С2 не заряжен. После замыкания ключа система перешла в новое состояние равновесия, в котором напряжение на конденсаторе С2 оказалось равным U2 = 20 В. Какова ёмкость конденсатора С1? (Активное сопротивление цепи пренебрежимо мало.)
Решение
Энергия заряженного конденсатора С1 до замыкания ключа К:
q = C1U.
Суммарная энергия заряженных конденсаторов после замыкания ключа К:
Так как процесс зарядки конденсатора С2 происходит медленно, нет потерь энергии на излучение, а следовательно, после замыкания ключа К первоначальная энергия заряженного конденсатора С1 в новом состоянии равновесия распределяется между конденсаторами:
Wэ = Wэ1 + Wэ2.
Кроме того, выполняется закон сохранения заряда: q = q1 + q2 = C1U1 + C2U2. Объединяя соотношения, получаем систему уравнений
Решая эту систему, получаем
Задача 36
Математический маятник, грузик которого имеет массу m = 8 г, совершает малые колебания в поле силы тяжести с периодом T1 = 0,7 с. Грузик зарядили и включили направленное вниз однородное вертикальное электрическое поле, модуль напряжённости которого равен E = 3 кВ/м. В результате этого период колебаний маятника стал равным T2 = 0,5 с. Найдите заряд q грузика.
Решение
1. В первом случае период колебаний математического маятника равен где l — длина нити подвеса маятника.
2. Во втором случае период колебаний шарика в электрическом поле, направленном вниз, уменьшился, значит, сила натяжения нити подвеса увеличилась и заряд шарика — положительный.
3. При малых колебаниях математического маятника с грузиком массой m и с зарядом q в поле тяготения модуль F силы натяжения нити близок к mg + qE. Уравнение движения грузика в проекции на горизонтальную ось Х имеет вид: где
— угол отклонения нити от вертикали, x — смещение грузика. Отсюда получаем уравнение гармонических колебаний:
или
где
Период этих колебаний равен
4. Из последнего уравнения находим заряд шарика маятника:
мкКл.
Задача 37
По горизонтально расположенным шероховатым рельсам с пренебрежимо малым сопротивлением могут скользить два одинаковых стержня массой и сопротивлением
каждый. Расстояние между рельсами
а коэффициент трения между стержнями и рельсами
Рельсы со стержнями находятся в однородном вертикальном магнитном поле с индукцией
(см. рисунок). Под действием горизонтальной силы, действующей на первый стержень вдоль рельс, оба стержня движутся поступательно равномерно с разными скоростями. Какова скорость движения первого стержня относительно второго? Самоиндукцией контура пренебречь.
Решение
Задача 38
Два параллельных друг другу рельса, лежащих в горизонтальной плоскости, находятся в однородном магнитном поле, индукция B которого направлена вертикально вниз (см. рисунок, вид сверху). На рельсах находятся два одинаковых проводника. Левый проводник движется вправо со скоростью V, а правый — покоится. С какой скоростью v надо перемещать правый проводник направо, чтобы в три раза уменьшить силу Ампера, действующую на левый проводник? (Сопротивлением рельсов пренебречь.)
Решение