Задания
Версия для печати и копирования в MS Word
Тип 18 № 2109
Какая доля радиоактивных ядер распадается через интервал времени, равный половине периода полураспада? Ответ приведите в процентах и округлите до целых.
Спрятать решение
Решение.
Согласно закону радиоактивного распада, по истечении времени от первоначального количества радиоактивных атомов
останется примерно
Тем самым доля ядер, не претерпевших радиоактивного распада, составит Доля же распавшихся ядер, очевидно, окажется равной
Ответ: 29.
Раздел кодификатора ФИПИ/Решу ЕГЭ: 5.3.5 Закон радиоактивного распада
Спрятать решение
·
·
Сообщить об ошибке · Помощь
Тренировочный вариант №2 КИМ №210927 ЕГЭ 2022 по физике 11 класс для подготовки на 100 баллов от 27 сентября 2021 года.
Вариант с ответами: скачать
Данный вариант составлен по новой демоверсии ФИПИ экзамена ЕГЭ 2022 года, к тренировочным заданиям прилагаются решения и правильные ответы.
Для выполнения экзаменационной работы по физике отводится 3 часа 55 минут (235 минут). Работа состоит из двух частей, включающих в себя 30 заданий.
Решу ЕГЭ 2022 по физике 11 класс вариант 100 баллов №210927:
Сложные задания и ответы с варианта
1)Выберите все верные утверждения о физических явлениях, величинах и закономерностях. Запишите цифры, под которыми они указаны.
- 1) При неупругом столкновении двух тел механическая энергия не сохраняется.
- 2) Равномерное движение – это такое движение, при котором тело за равные промежутки времени проходит равные расстояния.
- 3) Электрический ток – направленное движение электронов.
- 4) При преломлении электромагнитных волн на границе воздух-вода скорость волны уменьшается.
- 5) Удельная теплота плавления показывает какое количество теплоты надо подвести к телу массой 1 кг, чтобы расплавить его.
Ответ: 14
2)Даны следующие зависимости величин: А) зависимость температуры идеального газа от объема при изотермическом процессе; Б) зависимость количества нераспавшихся частиц при радиоактивном распаде; В) зависимость координаты х при движении тела, брошенного под углом к горизонту. Установите соответствие между этими зависимостями и видами графиков, обозначенных цифрами 1–5. Для каждой зависимости А–В подберите соответствующий вид графика и запишите в таблицу выбранные цифры под соответствующими буквами.
Ответ: 345
3)На рисунке приведены графики зависимости проекции скорости от времени для легкового автомобиля (I) и микроавтобуса (II), движущихся по прямой дороге, вдоль которой и направлена ось Ох. Определите отношение модулей.
Ответ: 2
4)Пластилиновый шар массой 0,1 кг имеет скорость 1 м/с. Он налетает на неподвижную тележку массой 0,1 кг, прикрепленную к пружине, и прилипает к тележке (см. рисунок). Чему равна полная механическая энергия системы при ее дальнейших колебаниях? Трением пренебречь.
Ответ: 0,025
5)Два груза массами 2m и m закреплены на невесомом стержне длиной 60 см. Чтобы стержень оставался в равновесии, его следует подвесить в точке О, находящейся на расстоянии Х от левого груза. Определите, чему равно Х.
Ответ: 20
6)При подвешивании груза массой m к стальному тросу длина троса возрастает на ∆L. Из приведенного ниже списка выберите все верные утверждения, соответствующих данным графикам. 1) Величина ∆L не изменится, если L будет вдвое больше, а m – вдвое меньше. 2) Величина ∆L не изменится, если L и m будут вдвое меньше. 3) Величина ∆L увеличится в четыре раза, если L и m будут вдвое больше. 4) Величина ∆L уменьшится в четыре раза, если L и m – вдвое больше. 5) Величина ∆L уменьшится в два раза, если L будет вчетверо меньше, а m – вдвое меньше.
Ответ: 13
7)На поверхности воды плавает сплошной деревянный брусок. Как изменятся глубина погружения бруска и сила Архимеда, действующая на брусок, если его заменить сплошным бруском той же плотности и высоты, но большей массы? Для каждой величины определите соответствующий характер изменения: 1) увеличивается 2) уменьшается 3) не изменится
Ответ: 31
8)Тело массой 100 г движется вдоль оси Ох, при этом его координата изменяется во времени в соответствии с формулой х(t) = 10 + 5t – 3t2 (все величины выражены в СИ). Установите соответствие между физическими величинами и формулами, выражающими их зависимости от времени в условиях данной задачи. К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
Ответ: 12
9)В одном из опытов стали закачивать воздух в стеклянный сосуд, одновременно охлаждая его. При этом температура воздуха в сосуде понизилась в 2 раза, а его давление возросло в 3 раза. Во сколько раз увеличилась масса воздуха в сосуде?
Ответ: 6
10)В кубическом метре воздуха в помещении при температуре 20 °С находится 1,1245⋅10-2 г водяных паров. Пользуясь таблицей плотности насыщенных паров воды, определите относительную влажность воздуха.
Ответ: 65
11)На графике показана зависимость давления одноатомного идеального газа от объема. Газ совершает работу, равную 3 кДж. Определите количество теплоты, полученное газом при переходе из состояния 1 в состояние 2.
Ответ: 3000
12)При переводе идеального газа из состояния 1 в состояние 2 концентрация молекул n пропорциональна давлению р (см. рисунок). Масса газа в процессе остаётся постоянной. Выберите из предложенного перечня все верные утверждения, которые сделать анализируя данный график:
- 1) Плотность газа возрастает.
- 2) Происходит изотермическое расширение газа.
- 3) Газ совершает работу без изменения внутренней энергии.
- 4) Плотность газа уменьшается.
- 5) Внутренняя энергия газа уменьшается.
Ответ: 234
13)В ходе адиабатного процесса внутренняя энергия одного моля разреженного гелия увеличивается. Как изменяются при этом температура гелия и его объём? Для каждой величины определите соответствующий характер изменения: 1) увеличивается 2) уменьшается 3) не изменится
Ответ: 12
14)По участку цепи, состоящему из резистора R = 4 кОм, течёт постоянный ток I = 100мА. За какое время на этом участке выделится количество теплоты Q = 2,4 кДж?
Ответ: 60
16)Если ключ находится в положении 1, то период собственных электромагнитных колебаний в контуре (см. рисунок) равен 6 мс. Насколько увеличится период собственных электромагнитных колебаний в контуре, если ключ перевести из положения 1 в положение 2?
Ответ: 6
17)Ученик, изучая законы геометрической оптики, провел опыт по преломлению света (см. рисунок). Для этого он направил узкий пучок света на стеклянную пластину. Пользуясь приведенной таблицей, выберите из приведенного ниже списка два правильных утверждения, описывающих наблюдаемое явление.
Ответ: 14
18)Электрический колебательный контур радиоприемника настроен на длину волны λ. Как изменятся частота колебаний в контуре и соответствующая им длина волны, если площадь пластин конденсатора уменьшить? Для каждой величины определите соответствующий характер изменения: 1) увеличится 2) уменьшится 3) не изменится
Ответ: 12
19)Конденсатор колебательного контура длительное время подключён к источнику постоянного напряжения (см. рисунок). В момент времени t = 0 переключатель К переводят из положения 1 в положение 2. Графики А и Б представляют изменения физических величин, характеризующих колебания в контуре после этого. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять. К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
Ответ: 21
20)Какая доля радиоактивных атомов распадется через интервал времени, равный двум периодам полураспада? Ответ выразите в процентах.
Ответ: 75
21)В опытах по фотоэффекту взяли пластину из металла с работой выхода 3,5 эВ и стали освещать ее светом частоты 3⋅1015Гц. Затем частоту падающей на пластину световой волны уменьшили в 4 раза, увеличив в 2 раза интенсивность светового пучка. Как изменится в результате этого число фотоэлектронов, покидающих пластину за 1 с и их скорость. Для каждой величины определите соответствующий характер изменения: 1) увеличивается 2) уменьшается 3) не изменится
Ответ: 33
22)С помощью линейки с миллиметровыми делениями измерили толщину стопки из 25 шайб. Толщина стопки оказалась равной примерно 45 мм. Определите толщину одной шайбы, если погрешность измерений равна половине цены деления линейки. Запишите ответ с учетом погрешности.
Ответ: 1,800,04
23)Пучок белого света, пройдя через призму, разлагается в спектр. Была выдвинута гипотеза, что ширина спектра, получаемого на стоящем за призмой экране, зависит от угла при вершине призмы. Необходимо экспериментально проверить эту гипотезу. Какие два опыта нужно провести для такого исследования?
Ответ: 13
24)Намагниченный стальной стержень начинает свободное падение с нулевой начальной скоростью из положения, изображённого на рис. 1. Пролетая сквозь закреплённое проволочное кольцо, стержень создаёт в нём электрический ток, сила которого изменяется со временем так, как показано на рис. 2. Почему в моменты времени t1 и t2 ток в кольце имеет различные направления? Ответ поясните, указав, какие физические явления и закономерности Вы использовали для объяснения. Влиянием тока в кольце на движение магнита пренебречь.
25)Небольшой камень, брошенный с ровной горизонтальной поверхности земли под углом к горизонту, упал обратно на землю в 20 метрах от места броска. Сколько времени прошло от броска до того момента, когда его скорость была направлена горизонтально и равна 10 м/с?
26)Напряжение на концах первичной обмотки трансформатора 220 В, сила тока в ней 1 А. Напряжение на концах вторичной обмотки 22 В. Какой была бы сила тока во вторичной обмотке при коэффициенте полезного действия трансформатора 95 %?
27)В водонепроницаемый мешок, лежащий на дне моря на глубине 73,1 м закачивается сверху воздух. Вода вытесняется из мешка через нижнее отверстие, и когда объём воздуха в мешке достигает 28,0 м3 , мешок всплывает вместе с прикреплённым к нему грузом. Масса оболочки 2710 кг. Опреде-лите массу груза. Температура воды равна 7°С. Атмосферное давление на уровне моря равно 105 Па. Объёмом груза и стенок мешка пренебречь.
28)К конденсатору С1 через диод и катушку индуктивности L подключён конденсатор ёмкостью С2 = 2 мкФ. До замыкания ключа К конденсатор С1 был заряжен до напряжения U = 50 В, а конденсатор С2 не заряжен. После замыкания ключа система перешла в новое состояние равновесия, в котором напряжение на конденсаторе С2 оказалось равным U2 = 20 В. Какова ёмкость конденсатора С1? (Активное сопротивление цепи пренебрежимо мало.)
29)На поверхности воды плавает надувной плот шириной 4 м и длиной б м. Небо затянуто сплошным облачным покровом, полностью рассеивающим солнечный свет. На какой максимальной глубине под плотом должна находиться маленькая рыбка, чтобы ее не увидели плавающие вокруг плота хищники? Глубиной погружения плота, рассеиванием света водой и его отражением от дна водоема пренебречь. Показатель преломления воды относительно воздуха принять равным 4/3.
30)В изображенной на рисунке системе нижний брусок может двигаться по наклонной плоскости, составляющей с горизонтом угол α = 30°, а верхний брусок — вдоль наклонной плоскости, составляющей с горизонтом некоторый угол β. Коэффициент трения между нижним бруском и плоскостью равен μ = 0,2, трение между верхним бруском и наклонной плоскостью отсутствует. Считая соединяющую бруски нить очень легкой и нерастяжимой, и пренебрегая массой блока и трением в его оси найдите, при каких значениях угла β нить будет натянута.
Другие тренировочные варианты ЕГЭ 2022 по физике:
Физика 11 класс итоговая контрольная работа 2 варианта с ответами
12.07.2021 Тест по физике для 11 класса повторение 1 четверть 4 варианта с ответами
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
На рисунке показан график зависимости…
По горизонтальному полу по прямой…
Под действием постоянной силы, равной…
У входа в вертикальную шахту…
Два одинаковых бруска толщиной 5…
Высота полёта искусственного спутника над…
Тело движется вдоль оси Ох,…
При повышении абсолютной температуры средняя…
Тепловая машина за цикл получает…
На рисунке показан график изменения…
На рV-диаграмме показаны два процесса,…
Один моль одноатомного идеального газа…
Квадратная проволочная рамка расположена в…
Одинаковые положительные точечные заряды, величина…
Энергия магнитного поля катушки с…
Алюминиевый проводник АБ подвешен на…
При настройке колебательного контура генератора,…
Установите соответствие между физическими величинами…
Ядро бериллия может захватить альфа-частицу,…
На рисунке изображена упрощённая диаграмма…
Необходимо экспериментально изучить зависимость силы…
Рассмотрите таблицу, содержащую характеристики планет…
В стакан калориметра, содержащий воду…
Лазер излучает в импульсе 1019…
Прямолинейный проводник с током и…
Два груза, связанные нерастяжимой и…
В установке, изображённой на рисунке,…
Идеальный одноатомный газ в количестве…
Батарея из четырёх конденсаторов электроёмкостью…
В дно водоёма глубиной 3…
За это задание ты можешь получить 1 балл. Уровень сложности: базовый.
Средний процент выполнения: 69.1%
Ответом к заданию 1 по физике может быть целое число или конечная десятичная дробь.
Алгоритм решения задания 1:
- Первым делом определите, на какой вид движения задача (равномерное, равноускоренное и т.д).
- Далее посмотрите, что вам необходимо найти. Обратите внимания на ключевые слова: МОДУЛЬ, ПРОЕКЦИЯ, ПУТЬ, ПЕРЕМЩЕНИЕ. Так как именно на этих словах вас хотят подловить.
- Выбирайте наиболее подходящую для решения формулу.
Разбор сложных заданий в тг-канале
Задачи для практики
Задача 1
Уравнение движения тела имеет вид x = 2t + 0,5t2. Найдите, с каким ускорением двигалось тело. Ответ выразите в (м/с2).
Решение
Дано:
$x=2t+0.5t^2$
$a-?$
Решение:
Запишем уравнение движения в общем виде и сравнив с имеющимся: $x=2t+0.5t^2; x=υ_0t+{at^2}/{2}$, тогда ${at^2}/{2}=0.5t^2; a=0.5·2$ или $a=1м/с^2$.
Ответ: 1
Задача 2
Первую четверть пути поезд прошёл со скоростью 60 км/ч. Средняя скорость на всём пути оказалась равной 40 км/ч. С какой скоростью поезд двигался на оставшейся части пути? Ответ выразите в (км/ч).
Решение
Дано:
$υ_1=60$км/ч
$S_1={1}/{4}S$
$S_2={3S}/{4}$
$υ_{ср}=40$км/ч
$υ_2-?$
Решение:
Средняя скорость определяется выражением: $υ_{ср}={S_{общ}}/{t_{общ}}$(1), где $S_{общ}=S_1+S_2={S}/{4}+{3S}/{4}={4S}/{4}=S$(2), $t_{общ}=t_1+t_2={S_1}/{υ_1}+{S_2}/{υ_2}={S}/{4υ_1}+{3S}/{4υ_2}={Sυ_2+3Sυ_1}/{4υ_1υ_2}$(3).
Подставим выражения (2) и (3) в (1), получим: $υ_{ср}={S}/{1}:{S(3υ_1+υ_2)}/{4υ_1υ_2}={S}/{1}·{4υ_1υ_2}/{S(3υ_1+υ_2)}={4υ_1υ_2}/{(3υ_1+υ_2)}$(4). Из (4) выразим скорость $υ_2$: $υ_{ср}(3υ_1+υ_2)=4υ_1υ_2⇒3υ_1υ_{ср}+υ_{ср}υ_2=4υ_1υ_2⇒4υ_1υ_2-υ_{ср}υ_2=3υ_1υ_{ср}⇒υ_2(4υ_1-υ_{ср})=3υ_1υ_{ср}⇒υ_2={3υ_1υ_{ср}}/{(4υ_1-υ_{ср})}$(5). Подставим числовые значения в (5): $υ_2={3·60·40}/{4·60-40}={7200}/{200}=36км/ч$.
Ответ: 36
Задача 3
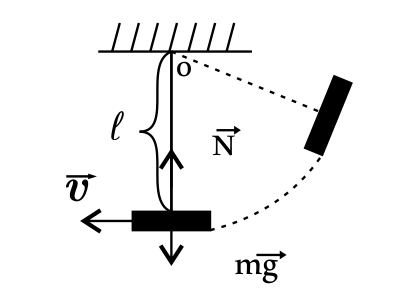
Цирковая гимнастка массой 50 кг качается на качелях с длиной верёвок 5 м. С какой силой она давит на сиденье при прохождении положения равновесия со скоростью 6 м/с? Ответ выразите в (Н). Ускорение свободного падения считать равным 10 м/с^2
Решение
Дано:
$m=50$кг
$g=10м/с^2$
$l=5$м
$υ=6$м/c
$N-?$
Решение:
При прохождении качелями среднего положения второй закон Ньютона в проекции на вертикальное направление иммет вид: $ma=N-mg$(1), здесь $a$ — ускорение гимнастики, совпадающее с центростремительным, $m$ — масса гимнастики, $N$ — сила реакции опоры (сиденья), равная по модулю, согласно третьему закону Ньютона, силе, с которой мальчик давит на сиденье. Так как центростремительное ускорение равно $a_{ц.с.}={υ^2}/{l}$(2), то сила, действующая на сиденье, равна: $N=ma+mg=m(a+g)=m({υ^2}/{l}+g)$(3). Подставим числовые значения в (3): $N=50·({36}/{5}+10)=50·17=860H$.
Ответ: 860
Задача 4
Из начала координат одновременно начинают движение две точки. Первая движется вдоль оси Ox со скоростью 3 м/с, а вторая — вдоль оси Oy со скоростью 4 м/с. (Оси перпендикулярны). С какой скоростью они будут удаляться друг от друга? Ответ выразите в (м/с).
Решение
Дано:
$υ_1=3$м/с
$υ_2=4$м/с
$υ_{отн}-?$
Решение:
Вектор относительной скорости $υ_{отн}$ есть разность векторов скоростей двух точек. По правилу вычитания векторов, вектор относительной скорости будет ижти от конца вектора скорости одной точки к концу векторая скорости другой точки. Так как скорости точек направлены перпендикулярно, длина вектора относительной скорости является гипотенузой прямоугольного треугольника и находится по теореме Пифагора: $υ_{отн}=√{υ_1^2+υ_2^2}=√{(3)^2+(4)^2}=√{9+16}=√{25}=5$м/с.
Ответ: 5
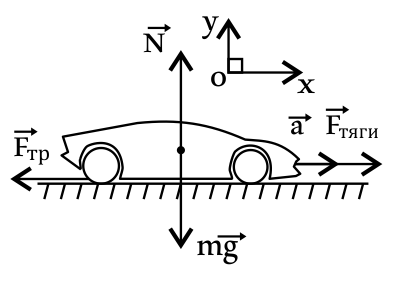
Задача 5
Автобус, масса которого 15 т, движется с ускорением 0,7 м/с2. Чему равна сила тяги двигателя, если коэффициент сопротивления движению равен 0,03? Ответ выразите в (кН).
Решение
Дано:
$m=15·10^3$кг
$a=0.7м/с^2$
$μ=0.03$
$F_{тяги}-?$
Решение:
На автомобиль действуют силы: тяги, трения, тяжести и силы реакции опоры. Запишем второй закон Ньютона: $ma↖{→}={F_{тяги}}↖{→}+{F_{тр}}↖{→}+mg↖{→}+N↖{→}$(1).
В проекциях на оси координат имеем: $Ox:ma=F_{тяги}-F_{тр}$(2), откуда $F_{тяги}=ma+F_{тр}$(3). $Oy:O=N-mg$(4), откуда $N=mg$(5). Учитывая, что сила трения $F_{тр}=μN$, то с учетом (5) получим: $F_{тр}=μmg$(6). Подставим (6) в (3) и найдем $F_{тяги}:F_{тяги}=ma+μmg=m(a+μg)$(7), где $g≈10м/с^2$ — ускорение свободного падения.
Подставим числовые значения в (7), получим: $F_{тяги}=15·10^3·(0.7+0.03·10)=15·10^3·(0.7+0.3)=15·10^3·1=15·10^3=15$кН.
Ответ: 15
Задача 6
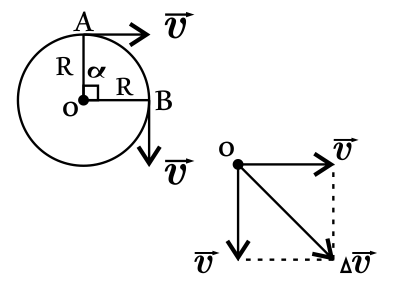
Тело движется по окружности равномерно. Радиус окружности 1 м. Найдите изменение вектора скорости при перемещении тела на угол 90◦. Период обращения 3,14 с. Ответ округлите до десятых. Ответ выразите в (м/с). Число ${π}$ принять равным 3,14
Решение
Дано:
$R=1$м
$α=90°$
$T=3.14$c
$∆υ-?$
Решение:
Изменение вектора скорости при перемещении тела на угол $90°$ равно по теореме Пифагора: $∆υ=√{υ^2+υ^2}=√{2υ^2}=√{2}υ$(1).
Найдем величину скорости $υ$: $υ={S}/{t}={2πR}/{T}={3.14·2·1}/{3.14}=2$м/с(2).
Подставим числовые значения в (1), получим: $∆υ=√2·υ=1.41·2=2.82=2.8$м/с.
Ответ: 2.8
Задача 7
Тело движется вдоль оси Ox. Чему равна проекция скорости тела vx, координата x которого меняется с течением времени по закону x = 3 − 2t, где все величины выражены в системе СИ? Ответ выразите в (м/c).
Решение
Дано:
$x=3-2t$
$υ_х-?$
Решение:
Известно, что $υ_x=x'(t)$, тогда $x'(t)=-2·1=-2$.
Ответ: -2
Задача 8
Подъёмный кран поднимает груз вверх со скоростью 3 м/с. В некоторый момент времени трос обрывается и груз начинает падать вниз. Определите скорость груза в момент падения на землю, если время падения составляет 4 с. Ответ выразить в (м/с). Ускорение свободного падения принять равным $10м/с^2$
Решение
Дано:
$υ=3$м/с
$t=4$c
$υ_к-?$
Решение:
На тело действует сила тяжести и ускорение свободного падения $g=const=10м/с^2$
$g={υ_к-(-υ_0)}/{t}$, т.к. ускорение $g$ и $υ_0$ разнонаправлены. $υ_к=gt-υ_0=10·4-3=37$м/с.
Ответ: 37
Задача 9
Тело движется вдоль оси Ox. Чему равно перемещение тела за 10 с, координата x которого меняется с течением времени по закону x = 3 − 2t + t2, где все величины выражены в системе СИ? Ответ выразить в (м).
Решение
Дано:
$t=10$c
$x=3-2t+t^2$
$x_0=3$
$r-?$
Решение:
$x=-20+100=80+3=83$
$r=x-x_0=83-3=80$м, т.к. изначально тело уже прошло 3м.
Ответ: 80
Задача 10
Планета имеет радиус в 2 раза меньший радиуса Земли. Найдите массу этой планеты, если известно, что ускорение свободного падения на поверхности этой планеты такое же, как и на Земле. Масса Земли 6 · 1024 кг. Ответ выразить в (·1024 кг).
Решение
Дано:
$R_n={R_3}/{2}$
$M_n-?$
$g_n=g_3$
$M_3=6·10^{24}$м
Решение:
${tableg_n=G{M_n}/{R_r^2}; g_3=G{M_3}/{R_3^2};$ ${M_n}/{R_n^2}={M_3}/{R_3^2}; M_n=M_3·{R_n^2}/{R_3^2}=6·10^{24}·{1}/{4}=1.5·10^{24}$кг
Ответ: 1.5
Задача 11
Материальная точка движется по окружности радиусом ${1.5}/{π}$ м. Найдите перемещение точки за 2 полных оборота. Ответ выразить в (м).
Решение
Дано:
$R={1.5}{π}$
Решение:
Точка делает 2 полных оборота и возвращается в начальную точку, ее перемещение равно 0.
Ответ: 0
Задача 12
Планета имеет массу в 4 раза меньшую массы Земли. Найдите радиус этой планеты, если известно, что ускорение свободного падения на поверхности этой планеты такое же, как на Земле, радиус Земли 6,4 · 106 м. Ответ выразите в (км).
Решение
Дано:
$M_n={M_3}/{4}$
$R_n-?$
$g_n=g_3$
$R_3=6.4·10^6$м
Решение:
${tableg_n=G{M_n}/{R_n^2}; g_3=G{M_3}/{R_3^2};$ ${M_n}/{M_3}={R_n^2}/{R_3^2}; {1}/{2}={R_n}/{R_3}$
$R_n=3200$км
Ответ: 3200
Задача 13
Найдите, чему равно ускорение свободного падения на некоторой планете, если период колебаний секундного земного математического маятника на ней оказался равным 1,41 с. Ответ выразите в (м/с2).
Решение
Дано:
$g_n-?$
$T_n=1.41$с
$T_3=1c$
Решение:
${tableT_n=2π√{{l}/{g_n}}; T_3=2π√{{l}/{g_3}};$ ${T_n}/{T_3}=√{{g_3}/{g_n}}; {1.41^2}/{1}={10}/{g_n}$
$g_n=5м/с^2$
Ответ: 5
Задача 14
Мяч массой 800 г брошен под углом 90◦ к горизонту с начальной скоростью 5 м/с. Найдите модуль силы тяжести, действующей на мяч сразу после броска. Ответ выразите в (Н).
Решение
Дано:
$m=0.8$кг
$υ=5$м/с
$F_{тяж}-?$
Решение:
Модуль силы тяжести, равна: $m·g=0.8·10=8H$
Ответ: 8
Задача 15
Найдите значение ускорения свободного падения на некоторой планете, плотность которой в два раза меньше плотности Земли, если радиусы планет одинаковы. Ответ выразите в (м/с2). Ускорение свободного падения на Земле принять равным 10 м/с^2
Решение
Дано:
$R_n=R_3$
${ρ_3}/{2}=ρ_n$
$ρ_n-?$
Решение:
${tableg^3=G{M_3}/{r^2}; g_n=G{M_n}/{r_n^2};$
а $V={4}/{3}π·R^3$, то и $V_n=V_3$.
${g_3}/{g_n}={ρ_3·V_3·r_n^2}/{ρ_n·V_n·r_3^2}⇒g_3=2·g_n; g_n=5м/с^2$.
Ответ: 5
Задача 16
Висящий на пружинке груз массой 400 г растягивает её на 10 см. На сколько сантиметров растянется пружина, если груз заменить на другой, массой 300 г? Ускорение свободного падения принять равным $10 м/{с^2}$. Ответ выразите в (см).
Решение
Дано:
$m_1=0.4$кг
$m_2=0.3$кг
$x_1=10^{-1}$ м=10 см
$x_2-?$
Решение:
${tablem_1g=kx_1; m_2g=kx_2;$ $⇒x_2={m_2g}/{m_1g}·x_1={0.3}/{0.4}·10см=7.5$
Ответ: 7.5
Задача 17
Велосипедист за 30 мин проехал 4 км, затем полчаса отдыхал, а затем проехал ещё 4 км за 15 мин. Какой была его средняя скорость на всём пути? Ответ выразите в (км/ч).
Решение
Известно, $υ_{ср}={∆S}/{∆t}={4+0+4}/{30+30+15}={8}/{1.25}=6.4{км}/ч$.
Ответ: 6.4
Задача 18
Найдите жёсткость пружины, если под действием силы 2 Н она растянулась на 4 см. Ответ выразите в (Н/м).
Решение
Дано:
$А=2·H$
$∆x=4·10^{-2}$
$K-?$
Решение:
По закону Гука $K={F}/{∆x}={2}/{4·10^{-2}}=50Н/м$.
Ответ: 50
Задача 19
Материальная точка равномерно движется по окружности. Найдите отношение пути к модулю перемещения за половину периода. Ответ округлить до сотых.
Решение
Дано:
${L}/{|S↖{→}|}-?$
$t={T}/{2}$
Решение:
1) За полпериода тело проходит половину окружности, поэтому пройденный путь равен половине дуги окружности: $L=π·R$
2) Модуль перемещения равен длине прямой, соединяющей начальную и конечную точки: $|S↖{→}|=2·R$
3) ${L}/{|S↖{→}|}={π·R}/{2·R}=1.57$
Ответ: 1.57
Задача 20
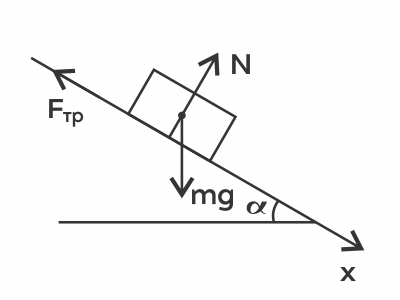
Брусок массой 2 кг покоится на наклонной плоскости с углом наклона 30◦ к горизонту. Определите силу трения, действующую на брусок, если коэффициент трения равен 0,7. Ответ выразите в (H). Ускорение свободного падения считать равным 10 $м/с^2$.
Решение
Дано:
$m=2$кг
$α=30°$
$μ=0.7$
Найти:$F_{тр}-?$
Решение:
Запишем 2-й закон Ньютона для тела: $ma↖{→}=mg↖{→}+N↖{→}+F_{тр}↖{→}=0$ (т.к. брусок покоится)
Направим ось х параллельно плоскости. 2-й закон Ньютона в проекции на ось х: $mg·sinα-F_{тр}=0⇒$
$F_{тр}=mgsinα=2·10·{1}/{2}=10Н$
Внимание! Многие при решении этой задачи используют неверную формулу $F_{тр}=μmgcosα$ — эта формула не может быть использована в этой задаче, потому что она описывает максимальную(!) силу трения покоя или силу трения скольжения. А в данной задаче тело покоится под действием силы трения, поэтому применять нужно формулы, указанные выше в решении.
Ответ: 10
Рекомендуемые курсы подготовки
Варианты ЕГЭ по физике
Об экзамене
С физикой дела обстоят по-особенному. С одной стороны, если сдал данный предмет, то открывается колоссальный выбор всевозможных специальностей и направлений, и даже таких, где особенно она и не нужна, с другой стороны, если сдаешь слабо, набирая в районе 50 баллов или даже меньше, то высока вероятность дальнейшего отчисления после первой же сессии. Поэтому выбор должен быть по-настоящему осознанный. Не сказать, что в школьном курсе физики очень много теории, как например, по биологии или истории. В ЕГЭ по истории логика особенно-то и не нужна, просто учи себе, зубри, а вот физику надо понимать, уметь оперировать базовыми формулами, по которым затем выстраивается работа над задачами. Если раньше все сводилось к заучиванию формул и штудированию учебников, то сейчас есть огромное количество цифрового контента (в первую очередь видео). Полюбить физику стало проще!
Да и сложность заданий из года в год остается примерно на одном уровне, поэтому не ленитесь, готовьтесь и получайте от всего этого процесса удовольствие!
Структура
Часть 1 содержит 23 задания с кратким ответом. Из них 13 заданий с записью ответа в виде числа, слова или двух чисел, 10 заданий на установление соответствия и множественный выбор, в которых ответы необходимо записать в виде последовательности цифр.
Часть 2 содержит 8 заданий, объединенных общим видом деятельности – решение задач. Из них 3 задания с кратким ответом (24–26) и 5 заданий (27–31), для которых необходимо привести развернутый ответ.
На выполнение всей экзаменационной работы отводится 3 часа 55 минут (235 минут).
Пояснения к оцениванию заданий
Задания 1–4, 8–10, 13–15, 19, 20, 22 и 23 части 1 и задания 24–26 части 2 оцениваются 1 баллом.
Задания 5–7, 11, 12, 16–18 и 21 части 1 оцениваются 2 баллами, если верно указаны оба элемента ответа; 1 баллом, если допущена ошибка в указании одного из элементов ответа, и 0 баллов, если допущено две ошибки.
Любой учитель или репетитор может отслеживать результаты своих учеников по всей группе или классу.
Для этого нажмите ниже на кнопку «Создать класс», а затем отправьте приглашение всем заинтересованным.
Ознакомьтесь с подробной видеоинструкцией по использованию модуля.
Закон радиоактивного распада
Какая доля радиоактивных ядер распадается через интервал времени, равный половине периода полураспада? Ответ приведите в процентах и округлите до целых.
Закон радиоактивного распада: [N=N_0cdot2^{ -(t/T)}=N_0cdot2^{-(1/2)}=0,71N_0] Следовательно, (0,29N_0) распадается.
Ответ: 29
В образце, содержащем большое количество атомов углерода (_6^{14}C), через 5 700 лет останется половина начального количества атомов. Каков период полураспада ядер атомов углерода? (Ответ дать в годах.)
Период полураспада (T=5700) лет.
Ответ: 5700
Период полураспада изотопа ртути ( _{80}^{190}Hg) равен 20 минутам. Если изначально было 40 мг этого изотопа, то сколько примерно его будет через 1 час? Ответ приведите в миллиграммах.
Закон радиоактивного распада: [N=N_0cdot2^{ -(t/T)}=40text{ мг}cdot2^{-60text{ мин}/20text{ мин}}=5text{ мг}]
Ответ: 5
Определите отношение числа распавшихся ядер некоторого радиоактивного изотопа к числу нераспавшихся ядер через время, равное пяти периодам полураспада этого изотопа.
Закон радиоактивного распада: [N=N_0cdot2^{ -(t/T)}]
Тогда отношение нераспавшихся ядер к числу распавшихся : [frac{N_0-N}{N}=dfrac{N_0}{N}-1=2^{t/T}-1=2^5-1=31]
Ответ: 31
Образец радиоактивного радия (_{88}^{224}Ra) находится в закрытом сосуде, из которого откачан воздух. Ядра радия испытывают (alpha)–распад с периодом полураспада 2,5 суток. Определите число моль радия-224 в сосуде через 5 суток, если образец в момент его помещения в сосуд имел в своём составе (1,6cdot 10^{23}) атомов. Ответ округлите до сотых.
Закон радиоактивного распада: [N=N_0cdot2^{ -(t/T)}=1,6cdot 10^{23}cdot 2^{-dfrac{5}{2,5}}=0,4cdot 10^{23}]
–количество распавшегося радия.
Тогда число моль оставшегося газа: [dfrac{N}{N_A}=dfrac{0,4cdot 10^{23}}{6cdot 10^{23}}approx 0,07]
Ответ: 0,07
Период полураспада (Т) изотопа европия (_{63}^{156}Eu) равен 10 дням. Какая масса этого изотопа распалась за 30 дней в образце, содержавшем первоначально 100 мг (_{63}^{156}Eu)?
[N=N_0cdot2^{ -(t/T)}=100cdot 2^{-dfrac{30}{10}}=0,4cdot 10^{23}=12,5text{ мг}]
Тогда за 30 дней в образце распалась масса, равная: [100-12,5=87,5text{ мг}]
Ответ: 87,5
Период полураспада ядер радиоактивного изотопа висмута 19 мин. Через какое время распадется 75% ядер висмута в исследуемом образце? (Ответ дать в минутах.)
75% ядер висмута распадутся за два периода полураспада. Значит, (t=38) мин.
Ответ: 38