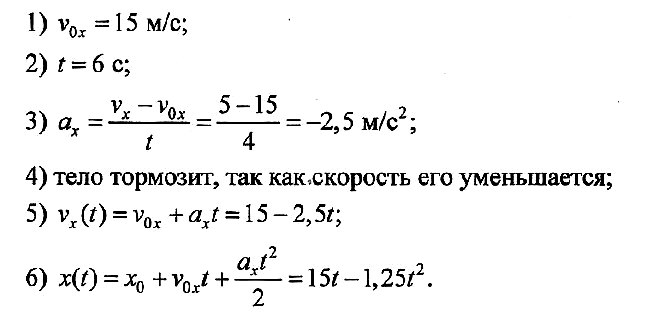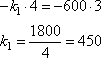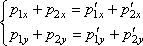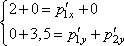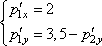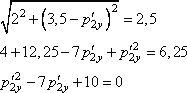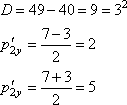Физика егэ 3600

Задания

Версия для печати и копирования в MS Word

В таблице представлены данные о положении шарика, прикреплённого к пружине и колеблющегося вдоль горизонтальной оси Ох, в различные моменты времени.Из приведённого ниже списка выберите два правильных утверждения относительно этих колебаний.

1) Потенциальная энергия пружины в момент времени 2,0 с максимальна.
2) Частота колебаний шарика равна 0,25 Гц.
3) Потенциальная энергия шарика в момент времени 3,0 с минимальна.
4) Амплитуда колебаний шарика равна 30 мм.
5) Полная механическая энергия маятника, состоящего из шарика и пружины, в момент времени 3,0 с минимальна.

Видео (Разбор решения 5 задания)

Решание

Хозяин договорился с рабочими, что они выкопают ему колодец на следующих условиях: за первый метр он заплатит им (3600) рублей, а за каждый следующий метр будет платить на (1400) рублей больше, чем за предыдущий. Сколько рублей хозяин должен будет заплатить рабочим, если они выкопают колодец глубиной (8) метров?

---

Решение

Первый вариант решения:

За первый метр оплата (3600) рублей;

Второй метр – (3600+1400=5000) рублей;

Третий метр – (5000+1400=6400) рублей;

Четвертый метр – (6400+1400=7800) рублей;

Пятый метр – (7800+1400=9200) рублей;

Шестой метр – (9200+1400=10600) рублей;

Седьмой метр – (10600+1400=12000) рублей;

Восьмой метр – (12000+1400=13400) рублей.

Значит, за выкопанный колодец глубиной (8) метров хозяин должен заплатить рабочим сумму в размере (3600+5000+6400+7800) (+9200+10600+12000+13400=68000) рублей.

Второй вариант решения:

Если бы пришлось выкапывать колодец очень длинный, то задачу бы пришлось решать очень долго, поэтому есть другой способ решения данной задачи.

Т.к. оплата каждого следующего метра отличается от оплаты предыдущего на одно и то же число, то перед нами представлена арифметическая прогрессия, сумма nn-первых членов которой находится по формуле:

(S_n=frac{2a_1+d(n-1)}{2}⋅n), где (n) – число суммируемых членов, (a_1) – первый член прогрессии, (d) – разность прогрессии.

В нашем случае (n=8) – глубина колодца, (a_1=3600) – оплата за первый метр, (d=1400) – разница в оплате за каждый последующий метр. Подставим известные данные в формулу и найдем сумму, которую должен заплатить хозяин рабочим:

(S_8=frac{2⋅3600+1400⋅(8-1)}{2}⋅8=68000) рублей.

Ответ: (68000).

---

Источник: ЕГЭ-2017. Математика. Базовый уровень. 30 вариантов. Типовые экзаменационные варианты. (вариант №8) (Купить книгу)

ЗАДАЧИ на Прямолинейное равноускоренное
движение с решениями

Формулы, используемые в 9-11 классах по теме
«ЗАДАЧИ на Прямолинейное равноускоренное движение».

Название величины	Обозначение	Единица измерения	Формула
Время	t	с
Проекция начальной скорости	v0x	м/с
Проекция мгновенной скорости	vx	м/с
Проекция ускорения	ax	м/с2
Проекция перемещения	Sx	м
Координата	x	м

1 мин = 60 с;   1 ч = 3600 с;   1 км = 1000 м;   1 м/с = 3,6 км/ч.

---

---

ПРИМЕРЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ

---

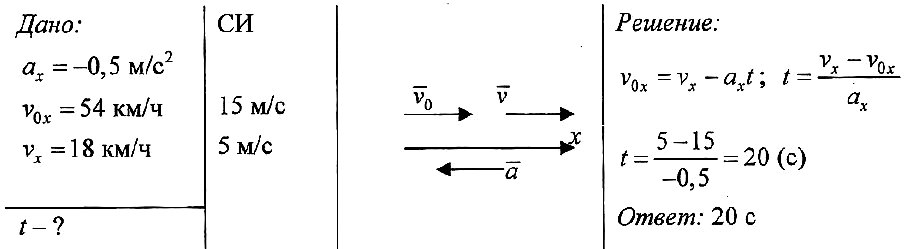
Задача № 1.
 Автомобиль, двигаясь с ускорением –0,5 м/с², уменьшил свою скорость от 54 до 18 км/ч. Сколько времени ему для этого понадобилось?

---

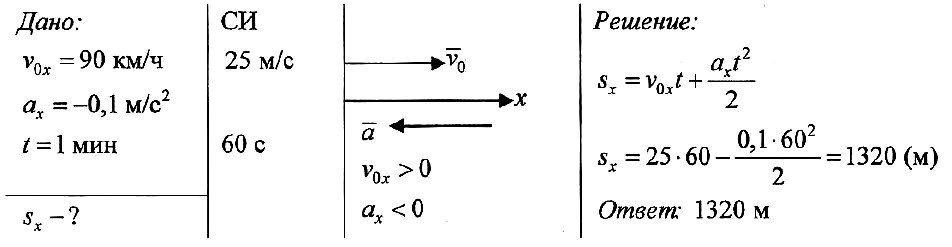
Задача № 2.
 При подходе к станции поезд начал торможение с ускорением 0,1 м/с², имея начальную скорость 90 км/ч. Определите тормозной путь поезда, если торможение длилось 1 мин.

---

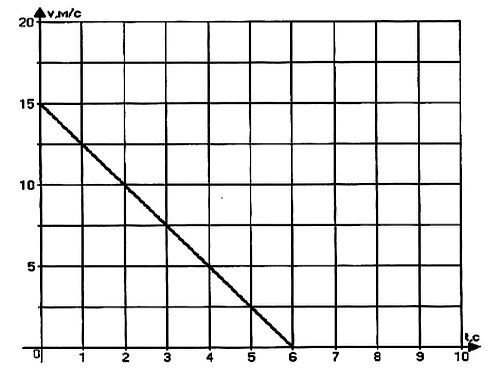
Задача № 3.
 По графику проекции скорости определите: 1) начальную скорость тела; 2) время движения тела до остановки; 3) ускорение тела; 4) вид движения (разгоняется тело или тормозит);  5) запишите уравнение проекции скорости; 6) запишите уравнение координаты (начальную координату считайте равной нулю).

Решение:

---

Задача № 4.
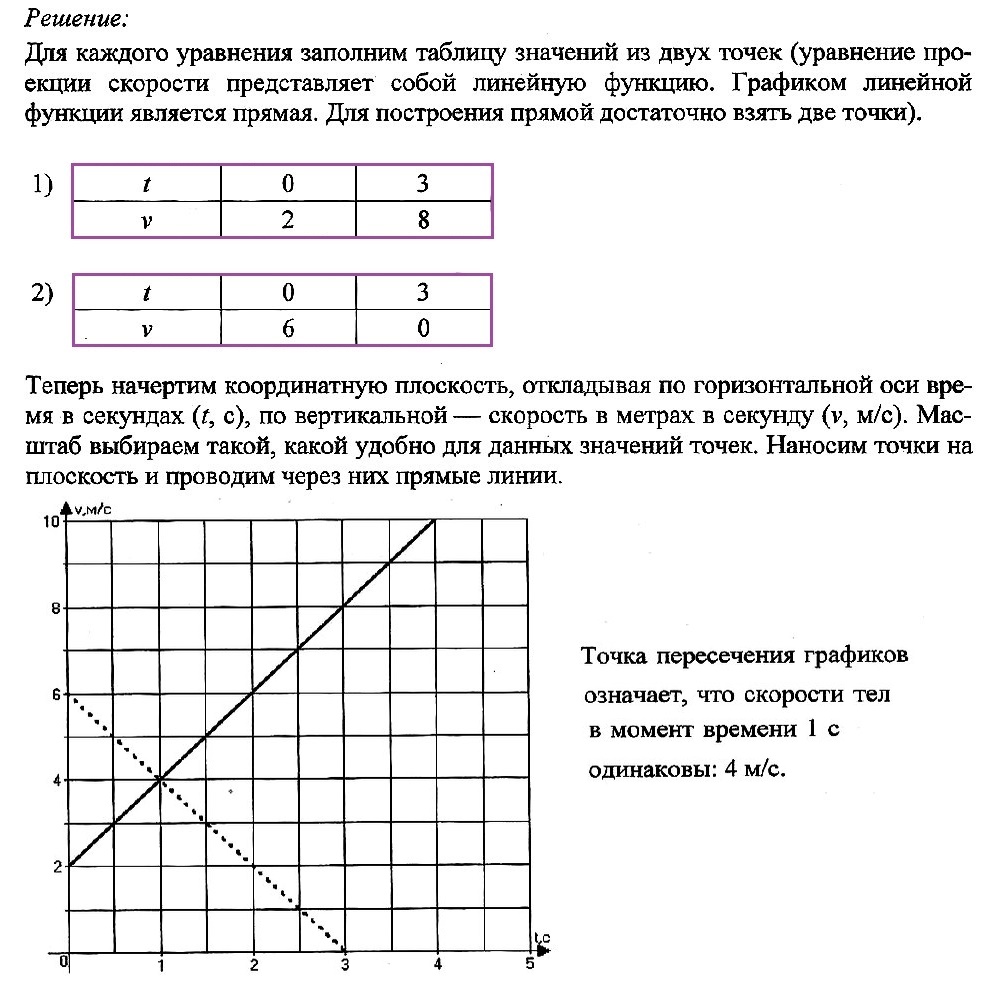
 Движение двух тел задано уравнениями проекции скорости:
v_1x(t) = 2 + 2t
v_2x(t) = 6 – 2t
В одной координатной плоскости постройте график проекции скорости каждого тела. Что означает точка пересечения графиков?

---

Задача № 5.
 Движение тела задано уравнением x(t) = 5 + 10t — 0,5t².  Определите:  1) начальную координату тела;  2) проекцию скорости тела;  3) проекцию ускорения;  4) вид движения (разгоняется тело или тормозит);  5) запишите уравнение проекции скорости;  6) определите значение координаты и скорости в момент времени t = 4 с.  Сравним уравнение координаты в общем виде с данным уравнением и найдем искомые величины.

Решение:

---

---

---

Задача № 6.
 Вагон движется равноускоренно с ускорением -0,5 м/с². Начальная скорость вагона равна 54 км/ч. Через сколько времени вагон остановится? Постройте график зависимости скорости от времени.

---

Задача № 7.
 Самолет, летевший прямолинейно с постоянной скоростью 360 км/ч, стал двигаться с постоянным ускорением 9 м/с² в течение 10 с в том же направлении. Какой скорости достиг самолет и какое расстояние он пролетел за это время? Чему равна средняя скорость за время 10 с при ускоренном движении?

---

Задача № 8.
 Трамвай двигался равномерно прямолинейно со скоростью 6 м/с, а в процессе торможения — равноускоренно с ускорением 0,6 м/с². Определите время торможения и тормозной путь трамвая. Постройте графики скорости v(t) и ускорения a(t).

---

Задача № 9.
 Тело, имея некоторую начальную скорость, движется равноускоренно. За время t = 2 с тело прошло путь S = 18 м, причём его скорость увеличилась в 5 раз. Найти ускорение и начальную скорость тела.

---

Задача № 10. (повышенной сложности)
 Прямолинейное движение описывается формулой х = –4 + 2t – t². Опишите движение, постройте для него графики v_x(t), s_x(t), l(t).

---

Задача № 11.
  ОГЭ
 Поезд, идущий со скоростью v₀ = 36 км/ч, начинает двигаться равноускоренно и проходит путь S = 600 м, имея в конце этого участка скорость v = 45 км/ч. Определить ускорение поезда а и время t его ускоренного движения.

---

Краткое пояснение для решения
ЗАДАЧИ на Прямолинейное равноускоренное движение.

Равноускоренным движением называется такое движение, при котором тело за равные промежутки времени изменяет свою скорость на одну и ту же величину. Движение, при котором скорость равномерно уменьшается, тоже считают равноускоренным (иногда его называют равнозамедленным).

Величины, участвующие в описании равноускоренного движения, почти все векторные. При решении задач формулы записывают обычно через проекции векторов на координатные оси. Если тело движется по горизонтали, ось обозначают буквой х, если по вертикали — буквой у.

Если векторы скорости и ускорения сонаправлены (их проекции имеют одинаковые знаки), тело разгоняется, т. е. его скорость увеличивается. Если же векторы скорости и ускорения противоположно направлены, тело тормозит.

---

Это конспект по теме «ЗАДАЧИ на Прямолинейное равноускоренное движение с решениями». Выберите дальнейшие действия:

• Перейти к теме: ЗАДАЧИ на Свободное падение тел с решениями
• Посмотреть конспект по теме КИНЕМАТИКА: вся теория для ОГЭ (шпаргалка)
• Вернуться к списку конспектов по Физике.
• Проверить свои знания по Физике (онлайн-тесты).

Разбор 5 задания ЕГЭ 2020 по физике из демонстрационного варианта. Проверяемые элементы содержания: механика (объяснение явлений; интерпретация результатов опытов, представленных в виде таблицы или графиков).

В таблице представлены данные о положении шарика, прикрепленного к пружине и колеблющегося вдоль горизонтальной оси Ох, в различные моменты времени.

Из приведенного ниже списка выберите два правильных утверждения относительно этих колебаний.

1) Потенциальная энергия пружины в момент времени 2,0 с максимальна.
2) Период колебаний шарика равен 4,0 с.
3) Кинетическая энергия шарика в момент времени 1,0 с минимальна.
4) Амплитуда колебаний шарика равна 30 мм.
5) Полная механическая энергия маятника, состоящего из шарика и пружины, в момент времени 2,0 с минимальна.

Проверим правильность всех утверждений.

1. Потенциальная энергия пружины в момент времени 2,0 с максимальна.

В момент времени 2,0 с деформация пружины равна 0, и, значит, ее потенциальная энергия не может быть максимальной. Это утверждение неверно.

2. Период колебаний шарика равен 4,0 с.

Из таблицы видно, что за время от 0,0 до 2,0 с совершилась половина колебания, значит, период равен 4 с. Это утверждение верно.

3. Кинетическая энергия шарика в момент времени 1,0 с минимальна.

Кинетическая энергия шарика минимальна в точках наибольшего отклонения шарика (где его скорость равна 0). В момент времени 1,0 с x = 15 мм, то есть шарик находится в точке наибольшего отклонения. В этой точке его скорость равна 0, следовательно, его кинетическая энергия минимальна. Это утверждение верно.

4. Амплитуда колебаний шарика равна 30 мм.

Из таблицы видно, что максимальное отклонение от равновесия составляет 15 мм. Это утверждение неверно.

5. Полная механическая энергия маятника, состоящего из шарика и пружины, в момент времени 2,0 с минимальна.

Полная механическая энергия маятника постоянна. Это утверждение неверно.

Ответ:
23

Опубликовано: 25.11.2019
Обновлено: 25.11.2019

ЕГЭ 2017. Физика. Демидова М. Ю. 30 вариантов. Вариант 1. Решение

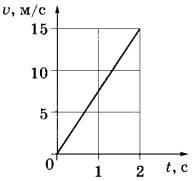
Задание 1. Используя график зависимости модуля скорости тела от времени (см. рисунок), определите ускорение прямолинейно движущегося тела в момент времени t = 1 с.

Решение.

Из графика видно, что скорость линейно возрастает со временем. Это означает, что тело движется с постоянным ускорением, равным . Из графика видно, что за время  секунды тело приобрело скорость  м/с, следовательно, ускорение равно

 м/с2.

Ответ: 7,5.

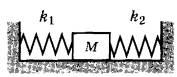
Задание 2. Кубик массой 1 кг покоится на гладком горизонтальном столе, сжатый с боков пружинами (см. рисунок). Первая пружина сжата на 4 см, а вторая сжата на 3 см. Жёсткость второй пружины k2 = 600 Н/м. Чему равна жёсткость первой пружины k1?

Решение.

Так как тело находится в состоянии покоя, то равнодействующая сила равна 0. На тело с одной стороны действует сила от первой пружины, равная (согласно закону Гука) , а с другой,  и . В задаче сказано, что , тогда из равенства сил имеем следующее уравнение:

Ответ: 450.

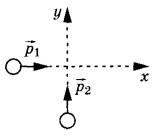
Задание 3. По гладкой горизонтальной плоскости движутся вдоль осей х и у две шайбы с импульсами, равными по модулю p1 =2 кг*м/с и p2 = 3,5 кг*м/с (см. рисунок). После их соударения вторая шайба продолжает двигаться по оси у в прежнем направлении. Модуль импульса первой шайбы после удара равен р’1 = 2,5 кг*м/с. Найдите модуль импульса второй шайбы после удара.

Решение.

Согласно закону сохранения импульса, суммарный импульс шайб до удара и после удара равны по каждой координате x и y, то есть будет справедливо равенство:

где  — импульсы шайб до удара по координатам x и y;  — импульсы шайб после удара. В задаче сказано, что изначально первая шайба двигалась по оси Ox, то есть ее импульс , а второй вдоль оси Oy с импульсом . После удара импульс первой шайбы стал равен , а вторая шайба продолжила движение по оси Oy, то есть . Подставим эти величины в систему, получим:

откуда имеем:

Учитывая, что , получаем уравнение:

Решаем квадратное уравнение, получаем:

Предполагая, что первая шайба продолжила свое движение в прежнем направлении, ее импульс , следовательно, .

Ответ: 2.

Задание 4. Частота свободных вертикальных гармонических колебаний пружинного маятника равна 4 Гц. Какой будет частота таких колебаний маятника, если увеличить жёсткость его пружины в 4 раза?

Решение.

Период колебания пружинного маятника определяется выражением

где m – масса маятника; k – жесткость пружины. Так как частота связана с периодом колебания выражением , то для частоты имеем выражение:

.

Из последней формулы видно, что если жесткость пружины увеличить в 4 раза, то есть взять 4k, то частота станет равной

,

то есть увеличится в 2 раза. Так как изначально частота колебаний была равна 4 Гц, то после увеличения жесткости пружины в 4 раза, она станет равной

 Гц.

Ответ: 8.

Задание 5. В инерциальной системе отсчёта вдоль оси Ох движется тело массой 20 кг. На рисунке приведён график зависимости проекции скорости Vx этого тела от времени t. Из приведённого ниже списка выберите два правильных утверждения и укажите их номера.

1) Модуль ускорения тела в промежутке времени от 0 до 20 с в два раза больше модуля ускорения тела в промежутке времени от 60 до 80 с.

2) В промежутке времени от 0 до 10 с тело переместилось на 20 м.

3) В момент времени 40 с равнодействующая сил, действующих на тело, равна 0.

4) В промежутке времени от 80 до 100 с импульс тела уменьшился на 60 кг • м/с.

5) Кинетическая энергия тела в промежутке времени от 10 до 20 с увеличилась в 2 раза.

Решение.

1) На участке от 0 до 20 с тело достигло скорости 4 м/с, а на участке от 60 до 80 с, скорость тела изменилась на 4-3=1 м/с. Следовательно, ускорения были разными.

2) Тело переместилось бы за 10 с на 20 метров, если бы оно постоянно двигалось со скоростью 2 м/с, здесь же тело набирало скорость до 2 м/с, то есть оно прошло меньше 20 м.

3) Да, верно, так как скорость тела остается постоянной, следовательно, и равнодействующая всех сил должна быть равна 0 согласно второму закону Ньютона.

4) Импульс тела на 80-й секунде был равен , а на 100-й секунде , следовательно, изменение импульса составило 60.

5) Кинетическая энергия тела определяется выражением  и так как скорость с 10-й по 20-ю секунду изменилась в 2 раза, то кинетическая энергия изменилась в 4 раза.

Ответ: 34.

Задание 6. В результате перехода искусственного спутника Земли с одной круговой орбиты на другую его центростремительное ускорение уменьшается. Как изменяются в результате этого перехода радиус орбиты спутника и его скорость движения по орбите вокруг Земли?

Для каждой величины определите соответствующий характер изменения:

1) увеличивается

2) уменьшается

3) не изменяется

Решение.

На спутник действует только сила притяжения земли

,

где M — масса земли; m — масса спутника; R — радиус орбиты. В соответствии со вторым законом Ньютона, можем записать:

,

где a – играет роль центростремительного ускорения. Отсюда видно, что при уменьшении ускорения, радиус орбиты должен увеличиваться.

Теперь рассмотрим как изменится скорость движения спутника в зависимости от радиуса орбиты. Подставим вместо ускорения , получим:

.

То есть, при увеличении R, скорость спутника уменьшается.

Ответ: 12.

Задание 7. Верхний конец пружины идеального пружинного маятника неподвижно закреплён, как показано на рисунке. Масса груза маятника равна m, жёсткость пружины равна k. Груз оттянули вниз на расстояние x от положения равновесия и отпустили с начальной скоростью, равной нулю. Формулы А и Б позволяют рассчитать значения физических величин, характеризующих колебания маятника.

Установите соответствие между формулами и физическими величинами, значение которых можно рассчитать по этим формулам.

К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.

ФОРМУЛЫ

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ 1) амплитуда колебаний скорости 2) циклическая частота колебаний 3) максимальная кинетическая энергия груза 4) период колебаний

Решение.

А) Имеем пружинный маятник массой m и жесткостью пружины k, тогда период свободных колебаний этого маятника определяется по формуле , а частота как . Циклическая частота , следовательно, для буквы А имеем ответ под номером 2.

Б) Для пружинного маятника известны формулы кинетической энергии  и потенциальной энергии . Ответ под номером 3 (в таблице ошиблись, написали кинетическую энергию).

Ответ: 23.

Задание 8. В сосуде содержится гелий под давлением 100 кПа. Концентрацию гелия увеличили в 2 раза, а среднюю кинетическую энергию его молекул уменьшили в 4 раза. Определите установившееся давление газа.

Решение.

Основное уравнение молекулярно-кинетической теории дает связь между кинетической энергией молекул газа и его давлением:

,

где n – концентрация газа; p – давление; E – кинетическая энергия. Эта формула показывает, что если концентрация молекул увеличивается в 2 раза, то есть равна 2n, а кинетическая энергия уменьшается в 4 раза, то есть E/4, то давление становится равным

,

то есть уменьшается в 2 раза по сравнению с начальным и равна

 кПа.

Ответ: 50.

Задание 9. Кусок металла удельной теплоёмкостью 500 Дж / (кг • К) нагрели от 20 °С до 80 °С, затратив количество теплоты, равное 75 кДж. Чему равна масса этого куска металла?

Решение.

Найдем массу металла из формулы зависимости количества переданной теплоты для нагревания материала от 20 °С до 80 °С, получим:

,

откуда

.

Подставляя числовые значения, получаем:

 кг.

Ответ: 2,5.

Задание 10. Идеальный одноатомный газ участвует в процессе 1-2-3, график которого приведен на рисунке (V — объём газа, Т — абсолютная температура газа). Масса газа в ходе процесса не меняется. В процессе 1-2 газу сообщают количество теплоты, равное 8 кДж. Определите изменение внутренней энергии в процессе 1-2.

Решение.

Из первого закона термодинамики известно, что изменение внутренней энергии одноатомного газа связано количеством переданной ему теплоты и совершенной им работой, определяется формулой

.

Так как в данном опыте газ не совершает никакую работу, то  и получаем, что

 кДж.

Ответ: 8.

Задание 11. На рисунке показан график циклического процесса, проведённого с одноатомным идеальным газом, в координатах р-Т, где p — давление газа, Т — абсолютная температура газа. Количество вещества газа постоянно.

Из приведённого ниже списка выберите два правильных утверждения, характеризующие процессы на графике, и укажите их номера.

1) Газ за цикл совершает положительную работу.

2) В процессе АВ газ получает некоторое количество теплоты.

3) В процессе ВС внутренняя энергия газа уменьшается.

4) В процессе CD над газом совершают работу внешние силы.

5) В процессе DA газ изотермически расширяется.

Решение.

Любой процесс изменения состояния идеального газа протекает в соответствии с уравнением Менделеева-Клайперона:

.           (1)

На отрезке AB имеем линейную зависимость давления газа от его температуры, причем прямая условно начинается в начале координат в точке (0,0). Тогда будет справедлива запись , где  — некоторый коэффициенты. Выразим теперь из формулы (1) объем газа и посмотрим как он меняется на участке AB, получим:

,

то есть объем остается неизменным и имеем изохорный процесс. По аналогии на прямой DC происходит также изохорный процесс, но в обратном направлении.

На участках AD и BC температура газа не меняется, но происходит изменение давления, следовательно, из формулы  имеем  и изменение давления ведет к обратно пропорциональному изменению объема.

1) Таким образом, получаем, на участке AB газ увеличивает давление и температуру при сохранении объема, следовательно, ему сообщают энергию. Затем на BC давление газа падает при постоянной температуре, то есть происходит увеличение объема – газ совершает работу. После этого на DC внутренняя энергия газа уменьшается и на AD давление газа увеличивается при неизменной температуре, то есть объем уменьшается – над газом совершают работу. Из рисунка видно, что совершенная газом работа больше работы, совершенной над газом, следовательно, газ совершил положительную работу.

2) Как уже сказано в п. 1 газу на участке AB передают некоторое количество теплоты.

3) На участке BC температура газа остается неизменной, а уменьшение давления связано с увеличением объема, следовательно, внутренняя энергия газа постоянна.

4) На участке CD происходит остывание газа, работа не совершается.

5) На участке DA происходит увеличение давление и уменьшение объема, изотермическое сжатие.

Ответ: 12.

Задание 12. В сосуде неизменного объёма находилась при комнатной температуре смесь двух идеальных газов, по 1 моль каждого. Половину содержимого сосуда выпустили, а затем добавили в сосуд 3 моль первого газа. Как изменились в результате парциальное давление первого газа и суммарное давление газов, если температура в сосуде поддерживалась неизменной?

Для каждой величины определите соответствующий характер изменения:

1) увеличилась

2) уменьшилась

3) не изменилась

Решение.

Парциальное давление – это давление отдельно взятого газа. Пусть изначально, парциальное давление первого газа было равно p. После того как половину газа выпустили, осталось 0,5 моль первого газа, следовательно, его давление упало вдвое и стало равно p:2. Затем, в сосуд добавили 3 моль первого газа (p – это начальное давление 1-го моля), тогда давление первого газа стало равно

,

то есть оно увеличилось в 3,5 раз.

Суммарное давление стало равно , а изначально было , то есть суммарное давление в итоге выросло.

Ответ: 11.

Задание 13. Заряд +q 0 находится на равном расстоянии от неподвижных точечных зарядов +Q 0 и -Q, расположенных на концах тонкой стеклянной палочки (см. рисунок). Куда направлено (вверх, вниз, влево, вправо, от наблюдателя, к наблюдателю) ускорение заряда +q в этот момент времени, если на него действуют только заряды +Q и -Q? Ответ запишите словом (словами).

Решение.

Известно, что разноименные заряды притягиваются, а одноименные – отталкиваются. Кроме того, согласно закону Кулона сила, действующая на точечный заряд +q со стороны другого точечного заряда +Q, равна

,

где k – коэффициент пропорциональности; r – расстояние между зарядами.

Аналогично для силы, действующей со стороны заряда –Q:

.

Так как расстояния до зарядов равны r, то и силы  и  равны, но направлены под углом в разные стороны (см. рисунок ниже).

И результирующая сила направлена вправо (синяя линия).

Ответ: вправо.

Задание 14. Пять одинаковых резисторов с сопротивлением 1 Ом соединены в электрическую цепь, через которую течёт ток I = 2 А (см. рисунок). Какое напряжение показывает идеальный вольтметр?

Решение.

Из рисунка видно, что вольтметр будет показывать падение напряжения на первом сопротивлении плюс падение напряжение на втором сопротивлении. Через первое сопротивление в 1 Ом проходит ток 2 А, тогда по закону Ома падение напряжения составит

 В.

Затем, ток разделяется пополам, так как суммарное сопротивление каждой из ветвей цепи одинаково, и на следующее сопротивление попадает ток в 1 А, а падение напряжения на нем будет равно

 В.

Таким образом, вольтметр покажет напряжение

 В.

Ответ: 3.

Задание 15. В опыте по наблюдению электромагнитной индукции квадратная рамка из одного витка тонкого провода находится в однородном магнитном поле, перпендикулярном плоскости рамки. Индукция магнитного поля равномерно возрастает от 0 до максимального значения Bмакс за время T. При этом в рамке возбуждается ЭДС индукции, равная 8 мВ. Определите ЭДС индукции, возникающую в рамке, если Т увеличить в 2 раза, а Bмакс в 2 раза уменьшить.

Решение.

Для провода из одного витка, ЭДС индукции, создаваемое потоком , проходящим перпендикулярно рамки, равна

.

Если значение  уменьшить в 2 раза, а время  увеличить в 2 раза, то ЭДС будет равен

то есть 2 мВ.

Ответ: 2.

Задание 16. На рисунке изображены графики зависимости мощности лампы накаливания Р = Р(Т) и сопротивления её спирали R = R(T) от температуры. Выберите два верных утверждения, которые можно сделать, анализируя эти графики.

1) Напряжение на спирали лампы при подводимой мощности Р = 200 Вт меньше 150 В.

2) Сопротивление спирали лампы при подводимой мощности Р = 100 Вт равно 80 Ом.

3) С уменьшением мощности, подводимой к лампе, напряжение на ней падает.

4) Напряжение на лампе возрастает прямо пропорционально подводимой к ней мощности.

5) Напряжение на спирали лампы при подводимой мощности Р = 100 Вт равно 100 В.

Решение.

Электрическая мощность определяется выражением

,

где U – напряжение; R – сопротивление; I – сила тока.

1) Из графика видно, что при P=200 имеем температуру T=3600 К. Найдем сопротивление спирали лампы при этой же температуре на правом графике. Наклонная линия имеет коэффициент наклона  (это видно из графика), а одно деление по вертикали равно 20, следовательно, при температуре T=3600 К имеем сопротивление, равное  Ом. И напряжение на спирали лампы равно

2) При P=100 сопротивление равно R=80 Ом и напряжение

3) Из формулы  видно, что при уменьшении мощности, напряжение также уменьшается.

4) Напряжение лампы не имеет линейную зависимость от мощности, что следует из формулы .

5) При P=100 сопротивление равно R=100 Ом и напряжение

Ответ: 35.

Задание 17. По проволочному резистору течёт ток. Резистор заменили на другой, с проволокой из того же металла и той же длины, но имеющей вдвое меньшую площадь поперечного сечения, и пропустили через него вдвое меньший ток. Как изменятся при этом напряжение на резисторе и его сопротивление? Для каждой величины определите соответствующий характер изменения:

1) увеличится

2) уменьшится

3) не изменится

Решение.

Сопротивление провода длины  с поперечным сечением S определяется выражением

,

где  — удельное сопротивление материала провода. Если площадь поперечного сечения уменьшить вдвое, то сопротивление резистора станет

,

то есть увеличится вдвое.

Найдем изменение напряжения из закона Ома . В задаче сказано, что ток уменьшили в 2 раза, следовательно, напряжение станет равным

,

то есть оно не изменится.

Ответ: 31.

Задание 18. По участку цепи постоянного тока с сопротивлением R течёт ток I. Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать.

К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ А) мощность тока, выделяющаяся на резисторе Б) напряжение на резисторе

ФОРМУЛЫ

Решение.

А) Мощность тока, выделяемая на сопротивлении определяется формулой , что соответствует формуле 2.

Б) Напряжение на резисторе определяется по закону Ома и равно  — формула под номером 1.

Ответ: 21.

Задание 19. Укажите число протонов и число нейтронов в ядре изотопа аргона .

Решение.

Для изотопа аргона  имеем массовое число, равное 39 и порядковый номер, равный 18. Известно, что массовое число – это число протонов и нейтронов в атоме изотопа. Порядковый номер – это число протонов в атоме. Таким образом, имеем 18 протонов и 39-18=21 нейтронов.

Ответ: 1821.

Задание 20. Период полураспада изотопа кислорода  составляет 71с. Какая доля от исходного большого количества этих ядер остаётся нераспавшейся через интервал времени, равный 142 с?

Решение.

Формула радиоактивного распада имеет вид:

,

где  — период полураспада;  — время распада;  — начальная концентрация изотопа (масса изотопа). Чтобы найти долю нераспавшихся ядер, нужно найти отношение , получим:

 %.

Ответ: 25.

Задание 21. При исследовании зависимости кинетической энергии фотоэлектронов от длины волны падающего света фотоэлемент освещался через различные светофильтры. В первой серии опытов использовался светофильтр, пропускающий только зелёный свет, а во второй — пропускающий только фиолетовый свет. В каждом опыте наблюдали явление фотоэффекта и измеряли запирающее напряжение.

Как изменяются длина световой волны и запирающее напряжение при переходе от первой серии опытов ко второй? Для каждой величины определите соответствующий характер изменения:

1) увеличивается

2) уменьшается

3) не изменяется

Решение.

Согласно формуле Эйнштейна по фотоэффекту работа выхода и кинетическая энергия частиц (фотоэлектронов) связана с частотой падающего света соотношением:

,

а запирающее напряжение равно

,

где e – элементарный заряд; U – запирающее напряжение.

Кинетическая энергия связана с частотой падающего света: чем выше частота, тем больше кинетическая энергия. Так, зеленый свет имеет меньшую частоту (большую длину волны), чем фиолетовый, соответственно, кинетическая энергия при фиолетовом свете будет выше и соответственно увеличивается запирающее напряжение U.

Ответ: 21.

Задание 22. Ученик измерял температуру воздуха в классе. Показания термометра приведены на фотографии. Погрешность измерения температуры равна цене деления термометра. Чему равна температура воздуха в классе по результатам этих измерений?

Запишите в ответ показания термометра с учётом погрешности измерений.

Решение.

Из рисунка видно, что одна шкала деления равна одному градусу. Термометр показывает 23 градуса, а цена деления – это 1 градуса, следовательно, погрешность измерения термометром температуры равна  градус.

Ответ: .

Задание 23. Ученик изучает силу Архимеда, действующую на тела, полностью погружённые в жидкость. В его распоряжении имеются пять установок, состоящие из ёмкостей с различными жидкостями и сплошных шариков разного объёма, сделанных из разных материалов (см. таблицу). Какие две установки необходимо использовать ученику для того, чтобы на опыте обнаружить зависимость силы Архимеда от объёма тела?

№ установки	Жидкость, налитая в ёмкость	Объём шарика	Материал, из которого сделан шарик
1	керосин	30 см3	сталь
2	вода	20 см3	алюминий
3	керосин	20 см3	алюминий
4	подсолнечное масло	30 см3	сталь
5	вода	30 см3	алюминий

В ответ запишите номера выбранных установок.

Решение.

Сила Архимеда определяется выражением:

,

где  — плотность жидкости; V – объем погруженного в жидкость тела; g – ускорение свободного падения. Для исследования силы Архимеда от объема V нужно взять одинаковые жидкости, одинаковые материалы, но разные объемы тел. Этому условию соответствуют установки под номером 2 и 5.

Ответ: 25.

Задание 24. Груз массой 1 кг, лежащий на столе, связан лёгкой нерастяжимой нитью, переброшенной через идеальный блок, с грузом массой 0,25 кг. На первый груз действует горизонтальная постоянная сила F, равная по модулю 1 Н (см. рисунок). При этом второй груз движется с ускорением 0,8 м/с2, направленным вниз. Каков коэффициент трения скольжения первого груза по поверхности стола?

Решение.

Два груза связаны между собой нерастяжимой нитью через блок. На первый груз действует сила  Н и сила трения , направленная в противоположную сторону движения груза. На второй груз действует только сила тяжести, равная  Н. Равнодействующая этих тел равна силе , которая вызывает движение системы из двух грузов с ускорением . Тогда, согласно второму закону Ньютона можно записать:

,

где  — массы первого и второго грузов соответственно. Отсюда находим силу трения:

и коэффициент трения равен

.

Ответ: 0,05.

Задание 26. В однородном магнитном поле по вертикальным направляющим без трения скользит прямой горизонтальный проводник массой 0,2 кг, по которому течёт ток 2 А. Вектор магнитной индукции направлен горизонтально перпендикулярно проводнику (см. рисунок), В = 2 Тл. Чему равна длина проводника, если известно, что ускорение проводника направлено вниз и равно 2 м/с2?

Решение.

На проводник с током, помещенный в магнитное поле, действует сила Ампера, направление которой можно определить по правилу «левой руки» (см. рисунок).

Величина силы Ампера определяется выражением

,

где  — индукция магнитного поля;  — сила  тока в проводнике;  — длина проводника  — угол между вектором магнитной индукции и проводником. По условию задачи угол  и , поэтому в данном случае

.

В соответствии с правилом «левой руки», сила Ампера будет направлена вверх, то есть в противоположную сторону силе тяжести, равной , где  м/с2 – ускорение свободного падения. Таким образом, перемещение проводника вертикально вниз будет описываться вторым законом Ньютона

,

где в качестве силы  будет выступать сумма силы Ампера и силы тяжести, т.е.

и получаем выражение

,

откуда

Подставляем числовые значения, получаем длину проводника

 метра.

Ответ: 0,4.

Задание 26. Предмет расположен перпендикулярно главной оптической оси тонкой собирающей линзы с оптической силой 10 дптр. Расстояние от предмета до линзы равно 30 см. Определите расстояние от линзы до изображения предмета.

Решение.

Оптическая сила линзы в d=10 диоптрий означает, что ее фокусное расстояние F равно

 метр

что составляет 10 см. Найдем расстояние от линзы до изображения предмета, используя соотношение для тонкой линзы:

,

где  — расстояние от предмета до линзы;  — расстояние от линзы до изображения предмета. Из последней формулы имеем:

 см.

Ответ: 15.

Задание 27. Стеклянный сосуд, содержащий воздух с относительной влажностью 50 % при t1 = 30 °С, плотно закрыли крышкой и нагрели до t2 = 50 °С. Опираясь на законы молекулярной физики, объясните, как изменятся при этом парциальное давление водяного пара и относительная влажность воздуха в сосуде.

Решение.

Учитывая, что сосуд с паром жесткий, получаем изохорный процесс, при котором объем остается неизменным. Тогда из уравнения Менделеева-Клайперона следует отношение

,

где  — парциальные давления паров при температурах  соответственно. При увеличении температуры получаем, что  и из соотношения следует, что и , то есть давление увеличивается.

При увеличении температуры плотность насыщенного пара  будет увеличиваться, а плотность пара в сосуде  не изменяется (так как сосуд герметичный, масса газов не меняется). Так как относительная влажность воздуха определяется выражением

,

то относительная влажность воздуха уменьшится.

Ответ: парциальное давление увеличится, относительная влажность уменьшится.

Задание 28. Небольшой брусок массой m = 1 кг начинает соскальзывать с высоты Н = 3 м по гладкой горке, переходящей в мёртвую петлю (см. рисунок). Определите радиус петли R, если на высоте h = 2,5 м от нижней точки петли брусок давит на её стенку с силой F = 4 Н. Сделайте рисунок с указанием сил, поясняющий решение.

Решение.

Пусть скорость бруска на высоте h равна v, а в нижней точке петли потенциальная энергия равна нулю. Тогда по закону сохранения механической энергии, получаем:

,

откуда

.      (1)

Когда брусок находится на высоте h, на него действую две силы: сила тяжести  и сила реакции опоры N. Запишем второй закон Ньютона в проекциях на радиальное направление (Ox на рисунке):

,                   (2)

где  — центростремительное ускорение. По третьему закону Ньютона . Из рисунка видно, что , тогда из выражения (2) получаем:

.

Подставив полученное значение  из (1), найдем:

и после подстановки числовых значений, имеем:

 м.

Ответ: 2,5.

Задание 29. Сосуд объёмом 10 л содержит смесь водорода и гелия общей массой 2 г при температуре 27 °С и давлении 200 кПа. Каково отношение массы водорода к массе гелия в смеси?

Решение.

Запишем уравнение Менделеева-Клайперона для водорода и гелия в смеси:

Согласно закону Дальтона давление смеси равно

,

а масса смеси равна

.

Объединяя полученные выражения, имеем:

,

подставляя числовые значения, получаем:

.

Ответ: 1,5.

Задание 30. На рис. 1 изображена зависимость силы тока через светодиод D от приложенного к нему напряжения, а на рис. 2 — схема его включения. Напряжение на светодиоде практически не зависит от силы тока через него в интервале значений 0,05 А

Решение.

Как следует из рисунка 1, при силе тока  А напряжение на светодиоде  В. По закону Ома для участка цепи напряжение на резисторе, будет равно . По закону Ома для полной (замкнутой) цепи, имеем:

.

Таким образом, получаем:

,

и сопротивление резистора равно

 Ом.

Напряжение на светодиоде не зависит от силы тока, проходящего через него в интервале значений  (это следует из графика рис. 1), поэтому  для любой силы тока из этого интервала значений, следовательно, сила тока в цепи при изменении ЭДС источника

Ответ: 0,05.

Задание 31. Металлическую пластину освещают монохроматическим светом с длиной волны λ = 531 нм. Каков максимальный импульс фотоэлектронов, если работа выхода электронов из данного металла Авых = 1,73 • 10^-19 Дж?

Решение.

Согласно уравнению Эйнштейна для фотоэффекта

,

где h – постоянная Планка; c – скорость света в вакууме;  — кинетическая энергия фотоэлектронов. Кинетическая энергия определяется также выражением

,

где  — масса электрона;  — максимальная скорость фотоэлектронов. Объединяя данные формулы, имеем:

Ответ: .