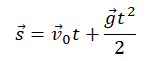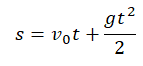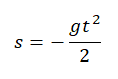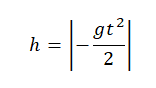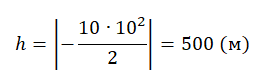Архитектор, инженер, программист, технолог — это далеко не полный список специальностей, для которых нужно сдавать экзамен по физике. Задание 1 из ЕГЭ по этому предмету кажется школьникам простым, однако для его решения нужно выучить большой блок теории. Все задачи из первого номера относятся к теме «Движение». Выпускник должен разбираться в видах движения, уметь анализировать графики и знать принцип относительности. Если вы понимаете эту тему и хотите освежить знания перед ЕГЭ, наша статья напомнит вам основные формулы и правила. Также стоит обратить внимание на курсы подготовки к ЕГЭ: там преподаватель объяснит все подробно, с нуля. А чтобы быть уверенным в высоких баллах, можно выбрать комплексную программу, включающую также занятия по русскому языку и профильной математике.
Кинематика

Если материальная точка перемещается в пространстве, у нее есть траектория — это условная линия, описывающая движение. Форма траектории зависит от выбранной системы отсчета, в задачах ЕГЭ траектории обычно рассматривают относительно Земли. Если мы свяжем траекторию с часами, то получим путь — то, что прошло тело за определенный временной промежуток. Путь, как и траектория, может иметь любую форму, но у него есть начальная и конечная точка. Соединив их прямой линией, мы нарисуем вектор перемещения. Он не может быть больше пути, а иногда вовсе равняется нулю (в том случае, когда тело двигалось по замкнутой линии). Теория к заданию 1 из ЕГЭ по физике не будет полной без описания принципа относительности движения. Для этого представим, что мы сидим в поезде и видим еще один на соседнем пути. Сначала наш поезд стоит неподвижно, а потом трогается. Если посмотреть на ситуацию относительно Земли, мы двигаемся: были на станции, а теперь отъехали от нее. Относительно самого поезда мы стоим на месте — как сидели у окна, так и сидим. А если взглянуть на соседний состав? Он постепенно удаляется от нас. Несмотря на то, что он по-прежнему стоит на станции, нам кажется, что он перемещается. Вывод: движение зависит от того, в какой системе координат его изучают.
Виды движения
От теории мы переходим к решению задач. Чаще всего в них фигурируют два понятия: скорость и ускорение. Скорость — это быстрота и направление перемещения. Средняя скорость перемещения находится по формуле u = s / t, средняя путевая — u = l / t. Здесь u — скорость, l — путь, s — перемещение. Первая величина будет векторной, вторая — скалярной. Существует также мгновенная скорость, то есть скорость в определенной точке. Ее можно найти по графику или из уравнения u = u0 + at. a — ускорение, то есть изменение скорости за единицу времени. Это векторная величина, она рассчитывается следующим образом: a = u / t. При ускоренном движении она направлена так же, как и скорость, при замедленном — противоположно ей. В случае с движением по окружности эти величины перпендикулярны. Перечислим несколько формул для задания 1 ЕГЭ по физике, связанных с видами движения:
равномерное прямолинейное:
- x = x0 + ut (x — координата точки в данный момент времени).
- s = ut.
- u = const.
- a = 0.
- прямолинейное равноускоренное:
- x = x0 + u0t + аt2 / 2.
- s = u0t + аt2 / 2.
- u= uox+ at.
- a = const.
движение по окружности (u = const):
- T = t / N = 1 / v — период.
- v = N / t = 1 / T — частота.
- u = l / t = 2πR / T = 2πRv — линейная скорость.
- ω = ϕ / t = 2π / T = 2πv — угловая скорость.
- a = u2 / R = ω2R = ωu — ускорение.
- движение по параболе с ускорением свободного падения:
- x = xo + uoxt + gt2 / 2.
- y = yo + uoyt +gt2 / 2.
- ux= uox+ gt.
- uy= uoy+ gt.
- uоx = u0 cosα.
- uоy = u0 sinα.
Частные случаи равноускоренного движения под действием силы тяжести
В рамках теории к заданию 1 ЕГЭ по физике нужно знать два частных случая:
движение по вертикали:
- при u0 = 0 высота h = gt2 / 2 и u = gt.
- при u0↑ и движении вверх h = u0t — gt2 / 2 и u = u0 – gt.
- при u0↑ и движении вниз h = -u0t + gt2 / 2 и u = -u0 + gt.
- при υ0↓ h = u0t + gt2 / 2 и υ = υ0 + gt.
- движение тела, брошенного горизонтально:
- h = gt2 / 2 — высота полета.
- s = uоt — дальность полета.
- υy= gt — скорость относительно оси OY.
Дополнительная информация для частных случаев решения задач
Еще несколько формул для задания 1 ЕГЭ по физике:
- модуль вектора: S=sx2+sy2.
- средняя скорость: uср = (s1 + s2 + … + sn ) / (t1 + t2 + … + tn) = 2u1u2 / (u1 + u2).
- площадь фигуры равна пройденному пути: S = S1 — S2.
- физический смысл производной: ux = x΄ и uy = y΄, ах = u΄x = x΄΄ и аy = u΄y = y΄΄.
- движение колеса без проскальзывания: uпост = uвращ и u = uпост + uвращ.
Пример решения задач

Решение: В момент встречи велосипедистов их координаты совпадут: x1 = x2, следовательно, 3t = 12 — t. Решив уравнение, найдем, что t = 3 с. Чтобы найти координату, подставим значение в любое из уравнений (для самопроверки лучше подставить в оба): x1 = 3 • 3 = 9.
Ответ: 9.
Задача 2: Первую половину пути супермен пролетел со скоростью 30 км/ч, вторую — со скоростью 50 км/ч. Найти среднюю скорость супермена.
Решение: Нам известны две скорости: u1 и u2, поэтому мы можем воспользоваться формулой uср = 2u1u2 / u1 + u2 = 2 • 30 • 50 / (30 + 50) = 37,5 км/ч.
Ответ: 37,5.
Теперь вы знаете больше теории для ЕГЭ по физике в 2020 году. Задание 1 только кажется очень простым, в нем бывают нетипичные задачи, поэтому стоит уделить внимание его разбору. Грамотно подготовиться к ЕГЭ вам помогут курсы ЦМДО «Уникум» . На них вы разберете каждую тему из экзамена, переходя от простого к сложному. Много времени преподаватели уделяют решению задач, объяснению сложных моментов. Но независимо от того, какой способ подготовки вы выберете, мы желаем вам удачи, высоких баллов и поступления в вуз мечты.
Механическое движение. Относительность механического движения. Система отсчета
Под механическим движением понимают изменение с течением времени взаимного расположения тел или их частей в пространстве: например, движение небесных тел, колебания земной коры, воздушные и морские течения, движение летательных аппаратов и транспортных средств, машин и механизмов, деформации элементов конструкций и сооружений, движение жидкостей и газов и др.
Относительность механического движения
С относительностью механического движения мы знакомы с детства. Так, сидя в поезде и наблюдая за трогающимся с места поездом, стоявшим до этого на параллельном пути, мы часто не можем определить, какой из поездов на самом деле начал двигаться. И здесь сразу следует уточнить: двигаться относительно чего? Относительно Земли, конечно. Потому что относительно соседнего поезда мы начали двигаться независимо от того, какой из поездов начал свое движение относительно Земли.
Относительность механического движения заключается в относительности скоростей перемещения тел: скорости тел относительно разных систем отсчета будут различны (скорость человека, перемещающегося в поезде, пароходе, самолете, будет отличаться как по величине, так и по направлению, в зависимости от того, в какой системе отсчета эти скорости определяются: в системе отсчета, связанной с движущимся транспортным средством, или с неподвижной Землей).
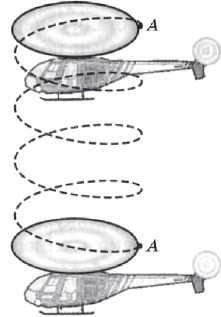
Различными будут и траектории движения тела в разных системах отсчета. Так, например, вертикально падающие на землю капли дождя оставят след в виде косых струй на окне вагона мчащегося поезда. Точно также любая точка на вращающемся пропеллере летящего самолета или спускающегося на землю вертолета описывает окружность относительно самолета и гораздо более сложную кривую — винтовую линию относительно Земли. Таким образом, при механическом движении относительной является также и траектория движения.
Путь, пройденный телом, также зависит от системы отсчета. Возвращаясь все к тому же пассажиру, сидящему в поезде, мы понимаем, что путь, проделанный им относительно поезда за время поездки, равен нулю (если он не передвигался по вагону) или, во всяком случае, намного меньше того пути, который он преодолел вместе с поездом относительно Земли. Таким образом, при механическом движении относительным является также и путь.
Осознание относительности механического движения (т. е. того, что движение тела можно рассматривать в разных системах отсчета) привело к переходу от геоцентрической системы мира Птолемея к гелиоцентрической системе Коперника. Птолемей, следуя наблюдаемому издревле движению Солнца и звезд на небосклоне, в центре Вселенной расположил неподвижную Землю с вращающимися вокруг нее остальными небесными телами. Коперник же считал, что Земля и другие планеты вращаются вокруг Солнца и одновременно вокруг своих осей.
Таким образом, изменение системы отсчета (Земля — в геоцентрической системе мира и Солнце — в гелиоцентрической) привело к гораздо более прогрессивной гелиоцентрической системе, позволяющей решить многие научные и прикладные задачи астрономии и изменить взгляды человечества на Вселенную.
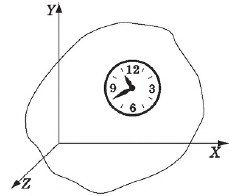
Система координат $X, У, Z$, тело отсчета, с которым она связана, и прибор для измерения времени (часы) образуют систему отсчета, относительно которой рассматривается движение тела.
Телом отсчета называется тело, относительно которого рассматривается изменение положения других тел в пространстве.
Систему отсчета можно выбрать произвольно. При кинематических исследованиях все системы отсчета равноправны. В задачах динамики также можно использовать любые произвольно движущиеся системы отсчета, но удобнее всего инерциальные системы отсчета, так как в них характеристики движения имеют более простой вид.
Материальная точка
Материальная точка — объект пренебрежимо малых размеров, имеющий массу.
Понятие «материальная точка» вводится для описания (с помощью математических формул) механического движения тел. Делается это потому, что описывать движение точки проще, чем реального тела, частицы которого к тому же могут двигаться с разными скоростями (например, при вращении тела или деформациях).
Если реальное тело заменяют материальной точкой, то этой точке приписывают массу этого тела, но пренебрегают его размерами, а заодно пренебрегают различием характеристик движения его точек (скоростей, ускорений и т. д.), если таковое имеется. В каких случаях это можно делать?
Практически любое тело можно рассматривать как материальную точку, если расстояния, проходимые точками тела, очень велики по сравнению с его размерами.
Например, материальными точками считают Землю и другие планеты при изучении их движения вокруг Солнца. В данном случае различия в движении различных точек любой планеты, вызванные ее суточным вращением, не влияют на величины, описывающие годовое движение.
Следовательно, если в изучаемом движении тела можно пренебречь его вращением вокруг оси, такое тело можно представить как материальную точку.
Однако при решении задач, связанных с суточным вращением планет (например, при определении восхода Солнца в разных местах поверхности земного шара), считать планету материальной точкой бессмысленно, так как результат задачи зависит от размеров этой планеты и скорости движения точек ее поверхности.
Материальной точкой правомерно считать самолет, если требуется, например, определить среднюю скорость его движения на пути из Москвы в Новосибирск. Но при вычислении силы сопротивления воздуха, действующей на летящий самолет, считать его материальной точкой нельзя, поскольку сила сопротивления зависит от размеров и формы самолета.
Если тело движется поступательно, даже если его размеры сопоставимы с расстояниями, которые оно проходит, это тело можно рассматривать как материальную точку (поскольку все точки тела движутся одинаково).
В заключение можно сказать: тело, размерами которого в условиях рассматриваемой задачи можно пренебречь, можно считать материальной точкой.
Траектория
Траектория — это линия (или, как принято говорить, кривая), которую описывает тело при движении относительно выбранного тела отсчета.
Говорить о траектории имеет смысл лишь в том случае, когда тело можно представить в виде материальной точки.
Траектории могут иметь разную форму. О форме траектории иногда удается судить по-видимому следу, который оставляет движущееся тело, например, летящий самолет или проносящийся в ночном небе метеор.
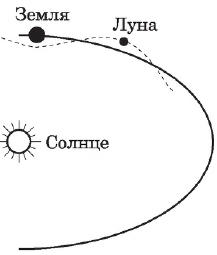
Форма траектории зависит от выбора тела отсчета. Например, относительно Земли траектория движения Луны представляет собой окружность, относительно Солнца — линию более сложной формы.
При изучении механического движения в качестве тела отсчета, как правило, рассматривается Земля.
Способы задания положения точки и описание ее движения
Положение точки в пространстве задается двумя способами: 1) с помощью координат; 2) с помощью радиус-вектора.
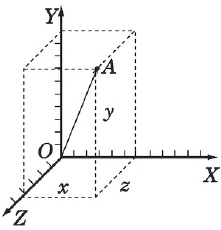
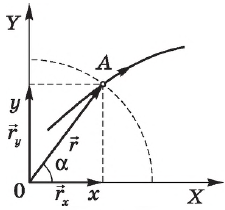
Положение точки с помощью координат задается тремя проекциями точки $х, у, z$ на оси декартовой системы координат $ОХ, ОУ, OZ$, связанные с телом отсчета. Для этого из точки А необходимо опустить перпендикуляры на плоскости $YZ$ (координата $х$), $ХZ$ (координата $у$), $ХУ$ (координата $z$) соответственно. Записывается это так: $А(х, у, z)$. Для конкретного случая, $(х=6, у=10.2, z= 4.5$), точка $А$ обозначается $А(6; 10; 4.5)$.
Наоборот, если заданы конкретные значения координат точки в данной системе координат, то для изображения самой точки необходимо отложить значения координат на соответствующие оси ($х$ на ось $ОХ$ и т. д.) и на этих трех взаимно перпендикулярных отрезках построить параллелепипед. Вершина его, противоположная началу координат $О$ и лежащая на диагонали параллелепипеда, и будет искомой точкой $А$.
Если точка движется в пределах некоторой плоскости, то через выбранные на теле отсчета точки достаточно провести две координатные оси: $ОХ$ и $ОУ$. Тогда положение точки на плоскости определяют двумя координатами $х$ и $у$.
Если точка движется вдоль прямой, достаточно задать одну координатную ось ОХ и направить ее вдоль линии движения.
Задание положения точки $А$ с помощью радиус-вектора осуществляется соединением точки $А$ с началом координат $О$. Направленный отрезок $ОА = r↖{→}$ называется радиус-вектором.
Радиус-вектор — это вектор, соединяющий начало отсчета с положением точки в произвольный момент времени.
Точка задана радиус-вектором, если известны его длина (модуль) и направление в пространстве, т. е. значения его проекций $r_x, r_у, r_z$ на оси координат $ОХ, ОY, OZ$, либо углы между радиус-вектором и осями координат. Для случая движения на плоскости имеем:
$x=r_x=rcosα,$
$y=r_y=rsinα.$
Здесь $r=|r↖{→}|$ — модуль радиус-вектора $r↖{→}, r_x$ и $r_y$ — его проекции на оси координат, все три величины — скаляры; хжу — координаты точки А.
Последние уравнения демонстрируют связь между координатным и векторным способами задания положения точки.
Вектор $r↖{→}$ можно также разложить на составляющие по осям $Х$ и $Y$, т. е. представить в виде суммы двух векторов:
$r↖{→}=r↖{→}_x+r↖{→}_y$
Таким образом, положение точки в пространстве задается либо ее координатами, либо радиус-вектором.
Способы описания движения точки
В соответствии со способами задания координат движение точки можно описать: 1) координатным способом; 2) векторным способом.
При координатном способе описания (или задания) движения изменение координат точки со временем записывается в виде функций всех трех ее координат от времени:
$x = x(t),$
$y = y(t),$
$z = z(t).$
Уравнения называют кинематическими уравнениями движения точки, записанными в координатной форме. Зная кинематические уравнения движения и начальные условия (т. е. положение точки в начальный момент времени), можно определить положение точки в любой момент времени.
При векторном способе описания движения точки изменение ее положения со временем задается зависимостью радиус-вектора от времени:
$r↖{→}=r↖{→}(t)$
Уравнение представляет собой уравнение движения точки, записанное в векторной форме. Если оно известно, то для любого момента времени можно рассчитать радиус-вектор точки, т. е. определить ее положение (как и в случае координатного способа). Таким образом, задание трех скалярных уравнений равносильно заданию одного векторного уравнения.
Для каждого случая движения вид уравнений будет вполне определенным. Если траекторией движения точки является прямая линия, движение называется прямолинейным, а если кривая — криволинейным.
Перемещение и путь
Перемещение в механике — это вектор, соединяющий положения движущейся точки в начале и в конце некоторого промежутка времени.
Понятие вектора перемещения вводится для решения задачи кинематики — определить положение тела (точки) в пространстве в данный момент времени, если известно его начальное положение.
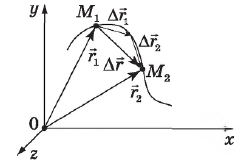
На рис. вектор ${М_1М_2}↖{-}$ соединяет два положения движущейся точки — $М_1$ и $М_2$ в моменты времени $t_1$ и $t_2$ соответственно и, согласно определению, является вектором перемещения. Если точка $М_1$ задана радиус-вектором $r↖{→}_1$, а точка $М_2$ — радиус-вектором $r↖{→}_2$, то, как видно из рисунка, вектор перемещения равен разности этих двух векторов, т. е. изменению радиус-вектора за время $∆t=t_2-t_1$:
$∆r↖{→}=r↖{→}_2-r↖{→}_1$.
Сложение перемещений (например, на двух соседних участках траектории) $∆r↖{→}_1$ и $∆r↖{→}_2$ осуществляется по правилу сложения векторов:
$∆r=∆r↖{→}_2+∆r↖{→}_1$
Путь — это длина участка траектории, пройденного материальной точкой за данный промежуток времени. Модуль вектора перемещения в общем случае не равен длине пути, пройденного точкой за время $∆t$ (траектория может быть криволинейной, и, кроме того, точка может менять направление движения).
Модуль вектора перемещения равен пути только при прямолинейном движении в одном направлении. Если направление прямолинейного движения меняется, модуль вектора перемещения меньше пути.
При криволинейном движении модуль вектора перемещения также меньше пути, т. к. хорда всегда меньше длины дуги, которую она стягивает.
Скорость материальной точки
Скорость характеризует быстроту, с которой происходят любые изменения в окружающем нас мире (движение материи в пространстве и времени). Движение пешехода по тротуару, полет птицы, распространение звука, радиоволн или света в воздухе, вытекание воды из трубы, движение облаков, испарение воды, нагрев утюга — все эти явления характеризуются определенной скоростью.
При механическом движении тел скорость характеризует не только быстроту, но и направление движения, т. е. является векторной величиной.
Скоростью $υ↖{→}$ точки называется предел отношения перемещения $∆r↖{→}$ к промежутку времени $∆t$, в течение которого это перемещение произошло, при стремлении $∆t$ к нулю (т. е. производной $∆r↖{→}$ по $t$):
$υ↖{→}={lim}↙{∆t→0}{∆r↖{→}}/{∆t}=r↖{→}_1’$
Составляющие вектора скорости по осям $X, Y, Z$ определяются аналогично:
$υ↖{→}_x={lim}↙{∆t→0}{∆x}/{∆t}=x’; υ_y=y’; υ_z=z’$
Определенное таким образом понятие скорости называют также мгновенной скоростью. Это определение скорости справедливо для любых видов движения — от криволинейного неравномерного до прямолинейного равномерного. Когда говорят о скорости при неравномерном движении, под ней понимают именно мгновенную скорость. Из этого определения непосредственно вытекает векторный характер скорости, поскольку перемещение — векторная величина. Вектор мгновенной скорости $υ↖{→}$ всегда направлен по касательной к траектории движения. Он указывает направление, по которому происходило бы движение тела, если бы с момента времени $t$ на него прекратилось действие любых других тел.
Средняя скорость
Средняя скорость точки вводится для характеристики неравномерного движения (т.е. движения с переменной скоростью) и определяется двояко.
1. Средняя скорость точки $υ_{ср}$ равна отношению всего пройденного телом пути $∆s$ ко всему времени движения $∆t$:
$υ↖{→}_{ср}={∆s}/{∆t}$
При таком определении средняя скорость — скаляр, т. к. пройденный путь (расстояние) и время — величины скалярные.
Такой способ определения дает представление о средней скорости движения на участке траектории (средней путевой скорости).
2. Средняя скорость точки равна отношению перемещения точки к промежутку времени, в течение которого это перемещение произошло:
$υ↖{→}_{ср}={∆r↖{→}}/{∆t}$
Средняя скорость перемещения — величина векторная.
Для неравномерного криволинейного движения такое определение средней скорости не всегда позволяет определить даже приблизительно реальные скорости на пути движения точки. Например, если точка двигалась по замкнутой траектории в течение некоторого времени, то перемещение ее равно нулю (но скорость явно отличалась от нуля). В этом случае лучше пользоваться первым определением средней скорости.
В любом случае следует различать эти два определения средней скорости и знать, о какой из них идет речь.
Закон сложения скоростей
Закон сложения скоростей устанавливает связь между значениями скорости материальной точки относительно различных систем отсчета, движущихся друг относительно друга. В нерелятивистской (классической) физике, когда рассматриваемые скорости малы по сравнению со скоростью света, справедлив закон сложения скоростей Галилея, который выражается формулой:
$υ↖{→}_2=υ↖{→}_1+υ↖{→}$
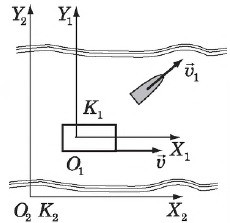
где $υ↖{→}_2$ и $υ↖{→}_1$ — скорости тела (точки) относительно двух инерциальных систем отсчета — неподвижной системы отсчета $K_2$ и системы отсчета $K_1$ движущейся со скоростью $υ↖{→}$ относительно $K_2$.
Формула может быть получена путем сложения векторов перемещений.
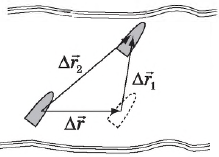
Для наглядности рассмотрим движение лодки со скоростью $υ↖{→}_1$ относительно реки (система отсчета $K_1$), воды которой движутся со скоростью $υ↖{→}$ относительно берега (система отсчета $K_2$).
Векторы перемещений лодки относительно воды $∆r↖{→}_1$, реки относительно берега $∆r↖{→}$ и суммарный вектор перемещения лодки относительно берега $∆r↖{→}_2$ изображены на рис..
Математически:
$∆r↖{→}_2=∆r↖{→}_1+∆r↖{→}$
Поделив обе части уравнения на интервал времени $∆t$, получим:
${∆r↖{→}_2}/{∆t}={∆r↖{→}_1}/{∆t}+{∆r↖{→}}/{∆t}$
В проекциях вектора скорости на оси координат уравнение имеет вид:
$υ_{2x}=υ_{1x}+υ_x,$
$υ_{2y}=υ_{1y}+υ_y.$
Проекции скоростей складываются алгебраически.
Относительная скорость
Из закона сложения скоростей следует, что если два тела движутся в одной и той же системе отсчета со скоростями $υ↖{→}_1$ и $υ↖{→}_2$, то скорость первого тела относительно второго $υ↖{→}_{12}$ равна разности скоростей этих тел:
$υ↖{→}_{12}=υ↖{→}_1-υ↖{→}_2$
Так, при движении тел в одном направлении (обгон) модуль относительной скорости равен разности скоростей, а при встречном движении — сумме скоростей.
Ускорение материальной точки
Ускорение — величина, характеризующая быстроту изменения скорости. Как правило, движение является неравномерным, т. е. происходит с переменной скоростью. На одних участках траектории тела могут иметь большую скорость, на других — меньшую. Например, поезд, отходящий от станции, со временем двигается все быстрее и быстрее. Подъезжая к станции, он, наоборот, замедляет свое движение.
Ускорение (или мгновенное ускорение) — векторная физическая величина, равная пределу отношения изменения скорости к промежутку времени, за который это изменение произошло, при стремлении $∆t$ к нулю, (т. е. производной $υ↖{→}$ по $t$):
$a↖{→}=lim↙{∆t→0}{∆υ↖{→}}/{∆t}=υ↖{→}_t’$
Составляющие $a↖{→} (а_х, а_у, а_z)$ равны соответственно:
$a_x=υ_x’;a_y=υ_y’;a_z=υ_z’$
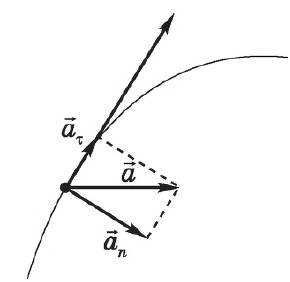
Ускорение, как и изменение скорости, направлено в сторону вогнутости траектории и может быть разложено на две составляющие — тангенциальную — по касательной к траектории движения — и нормальную — перпендикулярно к траектории.
В соответствии с этим проекцию ускорения $а_х$ на касательную к траектории называют касательным, или тангенциальным ускорением, проекцию $a_n$ на нормаль — нормальным, или центростремительным ускорением.
Касательное ускорение определяет величину изменения численного значения скорости:
$a_t=lim↙{∆t→0}{∆υ}/{∆t}$
Нормальное, или центростремительное ускорение характеризует изменение направления скорости и определяется по формуле:
$a_n={v^2}/{R}$
где R — радиус кривизны траектории в соответствующей ее точке.
Модуль ускорения определяется по формуле:
$a=√{a_t^2+a_n^2}$
При прямолинейном движении полное ускорение $а$ равно тангенциальному $a=a_t$, т. к. центростремительное $a_n=0$.
Единицей ускорения в СИ является такое ускорение, при котором за каждую секунду скорость тела изменяется на 1 м/с. Эту единицу обозначают 1 м/с2 и называют «метр на секунду в квадрате».
Равномерное прямолинейное движение
Движение точки называется равномерным, если за любые равные промежутки времени она проходит равные пути.
Например, если автомобиль за каждую четверть часа (15 мин) проходит 20 км, за каждые полчаса (30 мин) — 40 км, за каждый час (60 мин) — 80 км и т. д., то такое движение считается равномерным. При равномерном движении численная величина (модуль) скорости точки $υ$ — величина постоянная:
$υ=|υ↖{→}|=const$
Равномерное движение может происходить как по криволинейной, так и по прямолинейной траектории.
Закон равномерного движения точки описывается уравнением:
$s=s_0+υt$
где $s$ — расстояние, измеренное вдоль дуги траектории, от некоторой точки на траектории, принятой за начало отсчета; $t$ — время точки в пути; $s_0$ — значение $s$ в начальный момент времени $t=0$.
Путь, пройденный точкой за время $t$, определяется слагаемым $υt$.
Равномерное прямолинейное движение — это движение, при котором тело перемещается с постоянной по модулю и направлению скоростью:
$υ↖{→}=const$
Скорость равномерного прямолинейного движения — величина постоянная и может быть определена как отношение перемещения точки к промежутку времени, в течение которого это перемещение произошло:
$υ↖{→}={∆r↖{→}}/{∆t}$
Модуль этой скорости
$υ={|∆r↖{→}|}/{∆t}$
по смыслу есть расстояние $s=|∆r↖{→}|$, пройденное точкой за время $∆t$.
Скорость тела при равномерном прямолинейном движении — это величина, равная отношению пути $s$ ко времени, за которое этот путь пройден:
$υ={s}/{t}$
Перемещение при прямолинейном равномерном движении (по оси X) можно рассчитать по формуле:
$∆x=υ_xt$
где $υ_x$ — проекция скорости на ось X. Отсюда закон прямолинейного равномерного движения имеет вид:
$x=x_0+υ_xt$
Если в начальный момент времени $x_0=0$, то
$x=υ_xt$
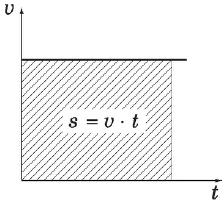
График зависимости скорости от времени — прямая, параллельная оси абсцисс, а пройденный путь — это площадь под этой прямой.
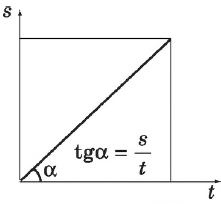
График зависимости пути от времени — прямая линия, угол наклона которой к оси времени $Ot$ тем больше, чем больше скорость равномерного движения. Тангенс этого угла равен скорости.
22 марта 2021
В закладки
Обсудить
Жалоба
Задание 1 — расчётная задача базового уровня сложности.
Проверяемые темы
→ Равномерное прямолинейное движение
→ Равноускоренное прямолинейное движение
→ Движение по окружности
Правильный ответ оценивается в 1 балл.
Примеры заданий
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания,
берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта
готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием
сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом
администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта
и представлены на сайте исключительно для ознакомления. Авторские права на материалы
принадлежат их законным авторам. Частичное или полное копирование материалов сайта без
письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой
зрения авторов.
За это задание ты можешь получить 1 балл. Уровень сложности: базовый.
Средний процент выполнения: 69.1%
Ответом к заданию 1 по физике может быть целое число или конечная десятичная дробь.
Алгоритм решения задания 1:
- Первым делом определите, на какой вид движения задача (равномерное, равноускоренное и т.д).
- Далее посмотрите, что вам необходимо найти. Обратите внимания на ключевые слова: МОДУЛЬ, ПРОЕКЦИЯ, ПУТЬ, ПЕРЕМЩЕНИЕ. Так как именно на этих словах вас хотят подловить.
- Выбирайте наиболее подходящую для решения формулу.
Разбор сложных заданий в тг-канале
Задачи для практики
Задача 1
Уравнение движения тела имеет вид x = 2t + 0,5t2. Найдите, с каким ускорением двигалось тело. Ответ выразите в (м/с2).
Решение
Дано:
$x=2t+0.5t^2$
$a-?$
Решение:
Запишем уравнение движения в общем виде и сравнив с имеющимся: $x=2t+0.5t^2; x=υ_0t+{at^2}/{2}$, тогда ${at^2}/{2}=0.5t^2; a=0.5·2$ или $a=1м/с^2$.
Ответ: 1
Задача 2
Первую четверть пути поезд прошёл со скоростью 60 км/ч. Средняя скорость на всём пути оказалась равной 40 км/ч. С какой скоростью поезд двигался на оставшейся части пути? Ответ выразите в (км/ч).
Решение
Дано:
$υ_1=60$км/ч
$S_1={1}/{4}S$
$S_2={3S}/{4}$
$υ_{ср}=40$км/ч
$υ_2-?$
Решение:
Средняя скорость определяется выражением: $υ_{ср}={S_{общ}}/{t_{общ}}$(1), где $S_{общ}=S_1+S_2={S}/{4}+{3S}/{4}={4S}/{4}=S$(2), $t_{общ}=t_1+t_2={S_1}/{υ_1}+{S_2}/{υ_2}={S}/{4υ_1}+{3S}/{4υ_2}={Sυ_2+3Sυ_1}/{4υ_1υ_2}$(3).
Подставим выражения (2) и (3) в (1), получим: $υ_{ср}={S}/{1}:{S(3υ_1+υ_2)}/{4υ_1υ_2}={S}/{1}·{4υ_1υ_2}/{S(3υ_1+υ_2)}={4υ_1υ_2}/{(3υ_1+υ_2)}$(4). Из (4) выразим скорость $υ_2$: $υ_{ср}(3υ_1+υ_2)=4υ_1υ_2⇒3υ_1υ_{ср}+υ_{ср}υ_2=4υ_1υ_2⇒4υ_1υ_2-υ_{ср}υ_2=3υ_1υ_{ср}⇒υ_2(4υ_1-υ_{ср})=3υ_1υ_{ср}⇒υ_2={3υ_1υ_{ср}}/{(4υ_1-υ_{ср})}$(5). Подставим числовые значения в (5): $υ_2={3·60·40}/{4·60-40}={7200}/{200}=36км/ч$.
Ответ: 36
Задача 3
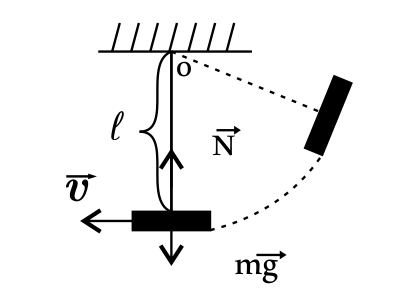
Цирковая гимнастка массой 50 кг качается на качелях с длиной верёвок 5 м. С какой силой она давит на сиденье при прохождении положения равновесия со скоростью 6 м/с? Ответ выразите в (Н). Ускорение свободного падения считать равным 10 м/с^2
Решение
Дано:
$m=50$кг
$g=10м/с^2$
$l=5$м
$υ=6$м/c
$N-?$
Решение:
При прохождении качелями среднего положения второй закон Ньютона в проекции на вертикальное направление иммет вид: $ma=N-mg$(1), здесь $a$ — ускорение гимнастики, совпадающее с центростремительным, $m$ — масса гимнастики, $N$ — сила реакции опоры (сиденья), равная по модулю, согласно третьему закону Ньютона, силе, с которой мальчик давит на сиденье. Так как центростремительное ускорение равно $a_{ц.с.}={υ^2}/{l}$(2), то сила, действующая на сиденье, равна: $N=ma+mg=m(a+g)=m({υ^2}/{l}+g)$(3). Подставим числовые значения в (3): $N=50·({36}/{5}+10)=50·17=860H$.
Ответ: 860
Задача 4
Из начала координат одновременно начинают движение две точки. Первая движется вдоль оси Ox со скоростью 3 м/с, а вторая — вдоль оси Oy со скоростью 4 м/с. (Оси перпендикулярны). С какой скоростью они будут удаляться друг от друга? Ответ выразите в (м/с).
Решение
Дано:
$υ_1=3$м/с
$υ_2=4$м/с
$υ_{отн}-?$
Решение:
Вектор относительной скорости $υ_{отн}$ есть разность векторов скоростей двух точек. По правилу вычитания векторов, вектор относительной скорости будет ижти от конца вектора скорости одной точки к концу векторая скорости другой точки. Так как скорости точек направлены перпендикулярно, длина вектора относительной скорости является гипотенузой прямоугольного треугольника и находится по теореме Пифагора: $υ_{отн}=√{υ_1^2+υ_2^2}=√{(3)^2+(4)^2}=√{9+16}=√{25}=5$м/с.
Ответ: 5
Задача 5
Автобус, масса которого 15 т, движется с ускорением 0,7 м/с2. Чему равна сила тяги двигателя, если коэффициент сопротивления движению равен 0,03? Ответ выразите в (кН).
Решение
Дано:
$m=15·10^3$кг
$a=0.7м/с^2$
$μ=0.03$
$F_{тяги}-?$
Решение:
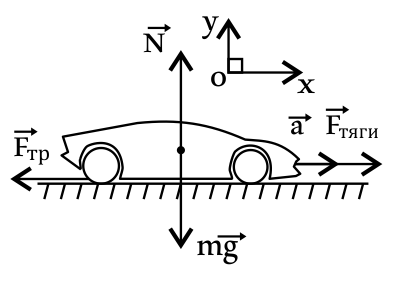
На автомобиль действуют силы: тяги, трения, тяжести и силы реакции опоры. Запишем второй закон Ньютона: $ma↖{→}={F_{тяги}}↖{→}+{F_{тр}}↖{→}+mg↖{→}+N↖{→}$(1).
В проекциях на оси координат имеем: $Ox:ma=F_{тяги}-F_{тр}$(2), откуда $F_{тяги}=ma+F_{тр}$(3). $Oy:O=N-mg$(4), откуда $N=mg$(5). Учитывая, что сила трения $F_{тр}=μN$, то с учетом (5) получим: $F_{тр}=μmg$(6). Подставим (6) в (3) и найдем $F_{тяги}:F_{тяги}=ma+μmg=m(a+μg)$(7), где $g≈10м/с^2$ — ускорение свободного падения.
Подставим числовые значения в (7), получим: $F_{тяги}=15·10^3·(0.7+0.03·10)=15·10^3·(0.7+0.3)=15·10^3·1=15·10^3=15$кН.
Ответ: 15
Задача 6
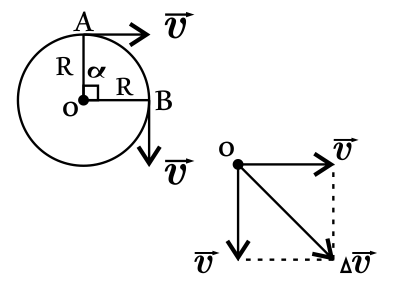
Тело движется по окружности равномерно. Радиус окружности 1 м. Найдите изменение вектора скорости при перемещении тела на угол 90◦. Период обращения 3,14 с. Ответ округлите до десятых. Ответ выразите в (м/с). Число ${π}$ принять равным 3,14
Решение
Дано:
$R=1$м
$α=90°$
$T=3.14$c
$∆υ-?$
Решение:
Изменение вектора скорости при перемещении тела на угол $90°$ равно по теореме Пифагора: $∆υ=√{υ^2+υ^2}=√{2υ^2}=√{2}υ$(1).
Найдем величину скорости $υ$: $υ={S}/{t}={2πR}/{T}={3.14·2·1}/{3.14}=2$м/с(2).
Подставим числовые значения в (1), получим: $∆υ=√2·υ=1.41·2=2.82=2.8$м/с.
Ответ: 2.8
Задача 7
Тело движется вдоль оси Ox. Чему равна проекция скорости тела vx, координата x которого меняется с течением времени по закону x = 3 − 2t, где все величины выражены в системе СИ? Ответ выразите в (м/c).
Решение
Дано:
$x=3-2t$
$υ_х-?$
Решение:
Известно, что $υ_x=x'(t)$, тогда $x'(t)=-2·1=-2$.
Ответ: -2
Задача 8
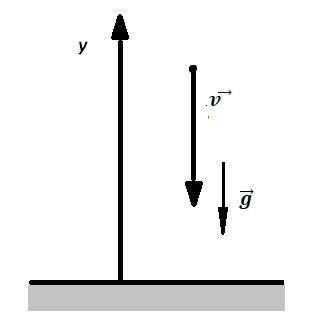
Подъёмный кран поднимает груз вверх со скоростью 3 м/с. В некоторый момент времени трос обрывается и груз начинает падать вниз. Определите скорость груза в момент падения на землю, если время падения составляет 4 с. Ответ выразить в (м/с). Ускорение свободного падения принять равным $10м/с^2$
Решение
Дано:
$υ=3$м/с
$t=4$c
$υ_к-?$
Решение:
На тело действует сила тяжести и ускорение свободного падения $g=const=10м/с^2$
$g={υ_к-(-υ_0)}/{t}$, т.к. ускорение $g$ и $υ_0$ разнонаправлены. $υ_к=gt-υ_0=10·4-3=37$м/с.
Ответ: 37
Задача 9
Тело движется вдоль оси Ox. Чему равно перемещение тела за 10 с, координата x которого меняется с течением времени по закону x = 3 − 2t + t2, где все величины выражены в системе СИ? Ответ выразить в (м).
Решение
Дано:
$t=10$c
$x=3-2t+t^2$
$x_0=3$
$r-?$
Решение:
$x=-20+100=80+3=83$
$r=x-x_0=83-3=80$м, т.к. изначально тело уже прошло 3м.
Ответ: 80
Задача 10
Планета имеет радиус в 2 раза меньший радиуса Земли. Найдите массу этой планеты, если известно, что ускорение свободного падения на поверхности этой планеты такое же, как и на Земле. Масса Земли 6 · 1024 кг. Ответ выразить в (·1024 кг).
Решение
Дано:
$R_n={R_3}/{2}$
$M_n-?$
$g_n=g_3$
$M_3=6·10^{24}$м
Решение:
${tableg_n=G{M_n}/{R_r^2}; g_3=G{M_3}/{R_3^2};$ ${M_n}/{R_n^2}={M_3}/{R_3^2}; M_n=M_3·{R_n^2}/{R_3^2}=6·10^{24}·{1}/{4}=1.5·10^{24}$кг
Ответ: 1.5
Задача 11
Материальная точка движется по окружности радиусом ${1.5}/{π}$ м. Найдите перемещение точки за 2 полных оборота. Ответ выразить в (м).
Решение
Дано:
$R={1.5}{π}$
Решение:
Точка делает 2 полных оборота и возвращается в начальную точку, ее перемещение равно 0.
Ответ: 0
Задача 12
Планета имеет массу в 4 раза меньшую массы Земли. Найдите радиус этой планеты, если известно, что ускорение свободного падения на поверхности этой планеты такое же, как на Земле, радиус Земли 6,4 · 106 м. Ответ выразите в (км).
Решение
Дано:
$M_n={M_3}/{4}$
$R_n-?$
$g_n=g_3$
$R_3=6.4·10^6$м
Решение:
${tableg_n=G{M_n}/{R_n^2}; g_3=G{M_3}/{R_3^2};$ ${M_n}/{M_3}={R_n^2}/{R_3^2}; {1}/{2}={R_n}/{R_3}$
$R_n=3200$км
Ответ: 3200
Задача 13
Найдите, чему равно ускорение свободного падения на некоторой планете, если период колебаний секундного земного математического маятника на ней оказался равным 1,41 с. Ответ выразите в (м/с2).
Решение
Дано:
$g_n-?$
$T_n=1.41$с
$T_3=1c$
Решение:
${tableT_n=2π√{{l}/{g_n}}; T_3=2π√{{l}/{g_3}};$ ${T_n}/{T_3}=√{{g_3}/{g_n}}; {1.41^2}/{1}={10}/{g_n}$
$g_n=5м/с^2$
Ответ: 5
Задача 14
Мяч массой 800 г брошен под углом 90◦ к горизонту с начальной скоростью 5 м/с. Найдите модуль силы тяжести, действующей на мяч сразу после броска. Ответ выразите в (Н).
Решение
Дано:
$m=0.8$кг
$υ=5$м/с
$F_{тяж}-?$
Решение:
Модуль силы тяжести, равна: $m·g=0.8·10=8H$
Ответ: 8
Задача 15
Найдите значение ускорения свободного падения на некоторой планете, плотность которой в два раза меньше плотности Земли, если радиусы планет одинаковы. Ответ выразите в (м/с2). Ускорение свободного падения на Земле принять равным 10 м/с^2
Решение
Дано:
$R_n=R_3$
${ρ_3}/{2}=ρ_n$
$ρ_n-?$
Решение:
${tableg^3=G{M_3}/{r^2}; g_n=G{M_n}/{r_n^2};$
а $V={4}/{3}π·R^3$, то и $V_n=V_3$.
${g_3}/{g_n}={ρ_3·V_3·r_n^2}/{ρ_n·V_n·r_3^2}⇒g_3=2·g_n; g_n=5м/с^2$.
Ответ: 5
Задача 16
Висящий на пружинке груз массой 400 г растягивает её на 10 см. На сколько сантиметров растянется пружина, если груз заменить на другой, массой 300 г? Ускорение свободного падения принять равным $10 м/{с^2}$. Ответ выразите в (см).
Решение
Дано:
$m_1=0.4$кг
$m_2=0.3$кг
$x_1=10^{-1}$ м=10 см
$x_2-?$
Решение:
${tablem_1g=kx_1; m_2g=kx_2;$ $⇒x_2={m_2g}/{m_1g}·x_1={0.3}/{0.4}·10см=7.5$
Ответ: 7.5
Задача 17
Велосипедист за 30 мин проехал 4 км, затем полчаса отдыхал, а затем проехал ещё 4 км за 15 мин. Какой была его средняя скорость на всём пути? Ответ выразите в (км/ч).
Решение
Известно, $υ_{ср}={∆S}/{∆t}={4+0+4}/{30+30+15}={8}/{1.25}=6.4{км}/ч$.
Ответ: 6.4
Задача 18
Найдите жёсткость пружины, если под действием силы 2 Н она растянулась на 4 см. Ответ выразите в (Н/м).
Решение
Дано:
$А=2·H$
$∆x=4·10^{-2}$
$K-?$
Решение:
По закону Гука $K={F}/{∆x}={2}/{4·10^{-2}}=50Н/м$.
Ответ: 50
Задача 19
Материальная точка равномерно движется по окружности. Найдите отношение пути к модулю перемещения за половину периода. Ответ округлить до сотых.
Решение
Дано:
${L}/{|S↖{→}|}-?$
$t={T}/{2}$
Решение:
1) За полпериода тело проходит половину окружности, поэтому пройденный путь равен половине дуги окружности: $L=π·R$
2) Модуль перемещения равен длине прямой, соединяющей начальную и конечную точки: $|S↖{→}|=2·R$
3) ${L}/{|S↖{→}|}={π·R}/{2·R}=1.57$
Ответ: 1.57
Задача 20
Брусок массой 2 кг покоится на наклонной плоскости с углом наклона 30◦ к горизонту. Определите силу трения, действующую на брусок, если коэффициент трения равен 0,7. Ответ выразите в (H). Ускорение свободного падения считать равным 10 $м/с^2$.
Решение
Дано:
$m=2$кг
$α=30°$
$μ=0.7$
Найти:$F_{тр}-?$
Решение:
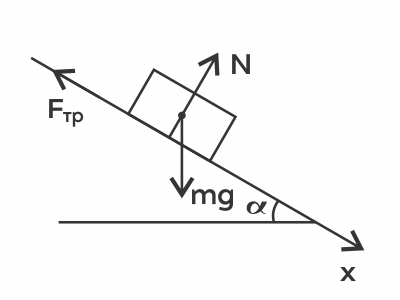
Запишем 2-й закон Ньютона для тела: $ma↖{→}=mg↖{→}+N↖{→}+F_{тр}↖{→}=0$ (т.к. брусок покоится)
Направим ось х параллельно плоскости. 2-й закон Ньютона в проекции на ось х: $mg·sinα-F_{тр}=0⇒$
$F_{тр}=mgsinα=2·10·{1}/{2}=10Н$
Внимание! Многие при решении этой задачи используют неверную формулу $F_{тр}=μmgcosα$ — эта формула не может быть использована в этой задаче, потому что она описывает максимальную(!) силу трения покоя или силу трения скольжения. А в данной задаче тело покоится под действием силы трения, поэтому применять нужно формулы, указанные выше в решении.
Ответ: 10
Рекомендуемые курсы подготовки
Статьи
Среднее общее образование
Линия УМК Г. Я. Мякишева, М.А. Петровой. Физика (10-11) (Б)
Физика
Представляем вашему вниманию разбор 1 задания ЕГЭ-2019 по физике
09 октября 2018
Задание 1
Это задание проверяет знания учащихся в области кинематики, к основным понятиям которой относятся понятия ускорение, скорости и перемещения. Так как это векторные величины, то в подавляющем большинстве учебников приведены формулы в векторном виде и подавляющее большинство моих коллег, с которыми мне доводилось общаться, также заставляют своих учеников учить формулы в векторном виде, что совершенно избыточно, на мой взгляд, и чаще мешает решать задания ЕГЭ, чем помогает. Конечно, важно знать, что скорость, ускорение и перемещение — это векторные величины, как и импульс, и сила. Но гораздо важнее, чтобы они понимали, что вычисляем мы, в конечном итоге, не вектора, а их проекции и модули. И вот с этим-то учащиеся часто путаются. К примеру, необходимо по графику скорости определить модуль или проекцию ускорения. Сколько формул для этого нужно учить — три, две или одну? Конечно же одну, для проекции ускорения. А модуль ускорения а = |ах|.
С перемещением ситуация ещё интереснее. Часто мне приходится сталкиваться с ситуацией, когда ученики из других школ, с которыми я занимаюсь подготовкой к экзамену по физике в центре подготовки к ЕГЭ в городе Ногинске, не понимают почему проекцию перемещения нужно находить по той или иной формуле. Они просто не могут понять откуда взялись те или иные формулы перемещения. Но зато они легко могут написать эти формулы в векторном виде, от которого, как правило, мало толку. Да, есть проблема — когда изучается кинематика, в 10 классе, дети ещё не знакомы с элементами математического анализа и не знают ни понятия производной, ни понятия интеграла. Но это и не обязательно. Достаточно показать на простом примере равномерного движения, что проекция перемещения может быть определена как площадь фигуры под графиком скорости и затем применить эту идею к равноускоренному движению. Это, в принципе, показано и в учебнике Пёрышкина для 9 класс, в разделе Кинематика, и в учебнике для 10 класса углублённого уровня Мякишева. Но тем не менее, почему-то многие ученики затрудняются с вычислением пройденного пути по графику скорости, который есть ни что иное как модуль перемещения при прямолинейном движении. Особенно, если график представляет собой ломаную линию.
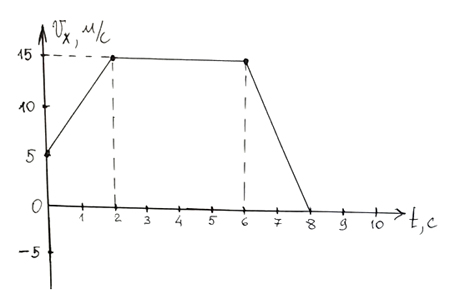
- Найти ax в промежутке времени от 0 до 2 с.
- Найти модуль ускорения в промежутке от 6 до 7 с.
- Найти пройденный путь за первые 5 с движения
Вот несколько примеров.
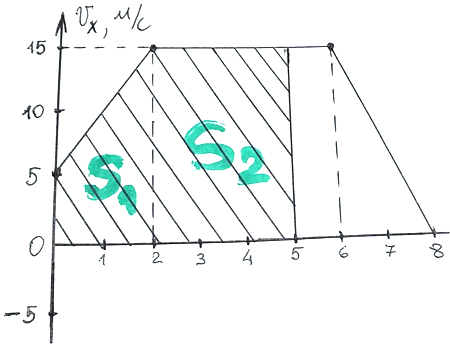
1) 
2) На промежутке от 6 до 7 с ускорение такое же как и на промежутке от 6 до 8 с, а он удобнее, поэтому

a = │ax│ = 7,5 м/с2
3) На графике площадь заштрихованной области и есть Sx, то есть:

ЕГЭ-2020. Физика. Решение задач
В книге содержатся материалы для успешной сдачи ЕГЭ: краткие теоретические сведения по всем темам, задания разных типов и уровней сложности, решение задач повышенного уровня сложности, ответы и критерии оценивания. Учащимся не придется искать дополнительную информацию в интернете и покупать другие пособия. В данной книге они найдут все необходимое для самостоятельной и эффективной подготовки к экзамену.
Купить
В задании №1 ЕГЭ по физике необходимо решить простую задачу по кинематике. Это может быть нахождение пути, скорости, ускорения тела или объекта по графику из условия.
Задание EF18273
Верхнюю точку моста радиусом 100 м автомобиль проходит со скоростью 20 м/с. Центростремительное ускорение автомобиля равно…
Алгоритм решения
- Записать исходные данные.
- Записать формулу для определения искомой величины.
- Подставить известные данные в формулу и произвести вычисления.
Решение
Записываем исходные данные:
- Радиус окружности, по которой движется автомобиль: R = 100 м.
- Скорость автомобиля во время движения по окружности: v = 20 м/с.
Формула, определяющая зависимость центростремительного ускорения от скорости движения тела:
Подставляем известные данные в формулу и вычисляем:
Ответ: 4
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF18741
Мальчик бросил стальной шарик вверх под углом к горизонту. Пренебрегая сопротивлением воздуха, определите, как меняются по мере приближения к Земле модуль ускорения шарика и горизонтальная составляющая его скорости?
Для каждой величины определите соответствующий характер изменения:
- увеличивается
- уменьшается
- не изменяется
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Алгоритм решения
- Сделать чертеж, иллюстрирующий ситуацию.
- Записать формулы, определяющие указанные в условии задачи величины.
- Определить характер изменения физических величин, опираясь на сделанный чертеж и формулы.
Решение
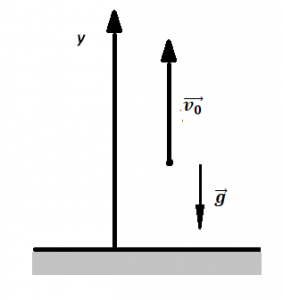
Выполняем чертеж:
Модуль ускорения шарика |g| — величина постоянная, так как ускорение свободного падения не меняет ни направления, ни модуля. Поэтому модуль ускорения не меняется (выбор «3»).
Горизонтальная составляющая скорости шарика определяется формулой:
vx = v0 cosα
Угол, под которым было брошено тело, поменяться не может. Начальная скорость броска тоже. Больше ни от каких величин горизонтальная составляющая скорости не зависит. Поэтому проекция скорости на ось ОХ тоже не меняется (выбор «3»).
Ответом будет следующая последовательность цифр — 33.
Ответ: 33
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF17519
С аэростата, зависшего над Землёй, упал груз. Через 10 с он достиг поверхности Земли. На какой высоте находился аэростат? Сопротивление воздуха пренебрежимо мало.
Алгоритм решения
- Записать исходные данные.
- Сделать чертеж, иллюстрирующий ситуацию.
- Записать формулу для определения искомой величины в векторном виде.
- Записать формулу для определения искомой величины в векторном виде.
- Подставить известные данные и вычислить скорость.
Решение
Записываем исходные данные:
- Начальная скорость v0 = 0 м/с.
- Время падения t = 10 c.
Делаем чертеж:
Перемещение (высота) свободно падающего тела, определяется по формуле:
В скалярном виде эта формула примет вид:
Учтем, что начальная скорость равна нулю, а ускорение свободного падения противоположно направлено оси ОУ:
Относительно оси ОУ груз совершил отрицательное перемещение. Но высота — величина положительная. Поэтому она будет равна модулю перемещения:
Вычисляем высоту, подставив известные данные:
Ответ: 500
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF17483
Тело брошено вертикально вверх с начальной скоростью 10 м/с. Если сопротивление воздуха пренебрежимо мало, то через одну секунду после броска скорость тела будет равна…
Алгоритм решения
- Записать исходные данные.
- Сделать чертеж, иллюстрирующий ситуацию.
- Записать формулу для определения скорости тела в векторном виде.
- Записать формулу для определения скорости тела в скалярном виде.
- Подставить известные данные и вычислить скорость.
Решение
Записываем исходные данные:
- Начальная скорость v0 = 10 м/с.
- Время движения t = 1 c.
Делаем чертеж:
Записываем формулу для определения скорости тела в векторном виде:
v = v0 + gt
Теперь запишем эту формулу в скалярном виде. Учтем, что согласно чертежу, вектор скорости сонаправлен с осью ОУ, а вектор ускорения свободного падения направлен в противоположную сторону:
v = v0 – gt
Подставим известные данные и вычислим скорость:
v = 10 –10∙1 = 0 (м/с)
Ответ: 0
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF17992
Начальная скорость автомобиля, движущегося прямолинейно и равноускоренно, равна 5 м/с. После прохождения расстояния 40 м его скорость оказалась равной 15 м/c. Чему равно ускорение автомобиля?
Алгоритм решения
- Записать исходные данные.
- Записать формулу, связывающую известные из условия задачи величины.
- Выразить из формулы искомую величину.
- Вычислить искомую величину, подставив в формулу исходные данные.
Решение
Запишем исходные данные:
- Начальная скорость v0 = 5 м/с.
- Конечная скорость v = 15 м/с.
- Пройденный путь s = 40 м.
Формула, которая связывает ускорение тела с пройденным путем:
Так как скорость растет, ускорение положительное, поэтому перед ним в формуле поставим знак «+».
Выразим из формулы ускорение:
Подставим известные данные и вычислим ускорение автомобиля:
Ответ: 2,5
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF17553
На рисунке представлены графики зависимости пройденного пути от времени для двух тел. Скорость второго тела v2 больше скорости первого тела v1 в n раз, где n равно…
Алгоритм решения
- Выбрать любой временной интервал.
- Выбрать для временного интервала начальные и конечные пути для каждого из графиков.
- Записать формулу скорости и вычислить ее для 1 и 2 тела.
- Найти n — отношение скорости второго тела к скорости первого тела
Решение
Рассмотрим графики во временном интервале от 0 до 4 с. Ему соответствуют следующие данные:
- Для графика 1: начальный путь s10 = 0 м. Конечный путь равен s1 = 80 м.
- Для графика 2: начальный путь s20 = 0 м. Конечный путь равен s2 = 120 м.
Скорость определяется формулой:
Так как начальный момент времени и скорость для обоих тел нулевые, формула примет вид:
Скорость первого тела:
Скорость второго тела:
Отношение скорости второго тела к скорости первого тела:
Ответ: 1,5
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF18831
На рисунке представлен график зависимости модуля скорости υ автомобиля от времени t. Определите по графику путь, пройденный автомобилем в интервале времени от t1=20 с до t2=50 с.
Алгоритм решения
- Охарактеризовать движение тела на различных участках графика.
- Выделить участки движения, над которыми нужно работать по условию задачи.
- Записать исходные данные.
- Записать формулу определения искомой величины.
- Произвести вычисления.
Решение
Весь график можно поделить на 3 участка:
- От t1 = 0 c до t2 = 10 с. В это время тело двигалось равноускоренно (с положительным ускорением).
- От t1 = 10 c до t2 = 30 с. В это время тело двигалось равномерно (с нулевым ускорением).
- От t1 = 30 c до t2 = 50 с. В это время тело двигалось равнозамедленно (с отрицательным ускорением).
По условию задачи нужно найти путь, пройденный автомобилем в интервале времени от t1 = 20 c до t2 = 50 с. Этому времени соответствуют два участка:
- От t1 = 20 c до t2 = 30 с — с равномерным движением.
- От t1 = 30 c до t2 = 50 с — с равнозамедленным движением.
Исходные данные:
- Для первого участка. Начальный момент времени t1 = 20 c. Конечный момент времени t2 = 30 с. Скорость (определяем по графику) — 10 м/с.
- Для второго участка. Начальный момент времени t1 = 30 c. Конечный момент времени t2 = 50 с. Скорость определяем по графику. Начальная скорость — 10 м/с, конечная — 0 м/с.
Записываем формулу искомой величины:
s = s1 + s2
s1 — путь тела, пройденный на первом участке, s2 — путь тела, пройденный на втором участке.
s1 и s2 можно выразить через формулы пути для равномерного и равноускоренного движения соответственно:
Теперь рассчитаем пути s1 и s2, а затем сложим их:
s1 + s2 = 100 + 100 = 200 (м)
Ответ: 200
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF17612
Тело начинает двигаться из состояния покоя с ускорением 4 м/с2. Через 2 с его скорость будет равна…
Алгоритм решения
- Записать исходные данные в определенной системе отсчета.
- Записать формулу ускорения.
- Выразить из формулы ускорения скорость.
- Найти искомую величину.
Решение
Записываем исходные данные:
- Тело начинает двигаться из состояния покоя. Поэтому его начальная скорость v0 = 0 м/с.
- Ускорение, с которым тело начинает движение, равно: a = 4 м/с2.
- Время движения согласно условию задачи равно: t = 2 c.
Записываем формулу ускорения:
Так как начальная скорость равна 0, эта формула принимает вид:
Отсюда скорость равна:
v = at
Подставляем имеющиеся данные и вычисляем:
v = 4∙2 = 8 (м/с)
Ответ: 8
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF17727
Два автомобиля движутся по прямому шоссе, первый — со скоростью v, второй — со скоростью –4v. Найти скорость второго автомобиля относительно первого.
Алгоритм решения
- Записать данные в определенной системе отсчета.
- Изобразить графическую модель ситуации задачи.
- Записать классический закон сложения скоростей в векторном виде.
- Записать классический закон сложения скоростей в векторном виде применительно к условиям задачи.
- Найти искомую величину.
Решение
Записываем данные относительно Земли:
- Скорость первого автомобиля относительно оси ОХ: v1 = v.
- Скорость второго автомобиля относительно оси ОХ: v2 = –4v.
Изображаем графическую модель ситуации. Так как у второго автомобиля перед вектором скорости стоит знак «–», первый и второй автомобили движутся во взаимно противоположных направлениях.
Записываем закон сложения скоростей в векторном виде:
v′ = v + u
v′ — скорость второго автомобиля относительно оси ОХ (v2), v — скорость второго автомобиля относительно системы отсчета, связанной с первым автомобилем, u — скорость движения первого автомобиля относительно оси ОХ (v1).
Закон сложения скоростей в векторном виде применительно к условиям задачи будет выглядеть так:
v2 = v + v1
Отсюда:
v = v2 — v1 = –4v – v = –5v
Ответ: -5v
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF17518
Два автомобиля движутся в одном направлении. Относительно Земли скорость первого автомобиля 110 км/ч, второго 60 км/ч. Чему равен модуль скорости первого автомобиля в системе отсчёта, связанной со вторым автомобилем?
Алгоритм решения
- Записать данные в определенной системе отсчета.
- Изобразить графическую модель ситуации задачи.
- Записать классический закон сложения скоростей в векторном виде.
- Выбрать систему отсчета.
- Записать классический закон сложения скоростей в скалярном виде.
- Найти искомую величину.
Решение
Записываем данные относительно Земли:
- Скорость первого автомобиля относительно неподвижной системы отсчета: v1 = 110 км/ч;
- Скорость второго автомобиля относительно Земли: v2 = 60 км/ч.
Изображаем графическую модель ситуации:
Записываем закон сложения скоростей в векторном виде:
v′ = v + u
v′ — скорость автомобиля относительно земли (v1), v — скорость второго автомобиля относительно системы отсчета, связанной со вторым автомобилем, u — скорость движения второго автомобиля относительно земли (v2).
По условию задачи в качестве системы отсчета нужно выбрать второй автомобиль. Так как система отсчета, связанная со вторым автомобилем, и первый автомобиль движутся в одном направлении, классический закон сложения скоростей в скалярном виде будет выглядеть так:
v’ = v + u
Отсюда скорость первого автомобиля в системе отсчёта, связанной со вторым автомобилем:
v = v’ – u = v1 – v2 = 110 – 60 = 50 (км/ч).
По условию задачи ответом должен быть модуль этой скорости. Модуль числа 50 есть 50.Ответ: 50
pазбирался: Алиса Никитина | обсудить разбор | оценить

 равномерное прямолинейное:
равномерное прямолинейное:  движение по окружности (u = const):
движение по окружности (u = const): движение по вертикали:
движение по вертикали: