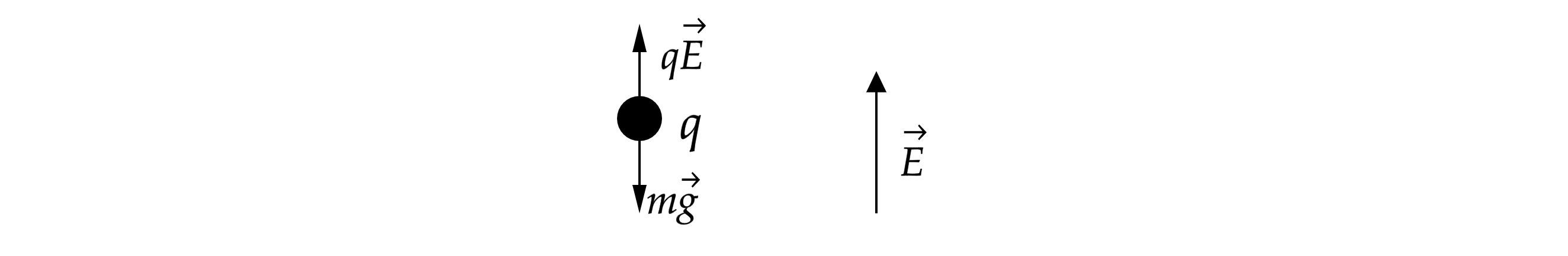Физика егэ потенциалы - Помощь в подготовке к экзаменам и поступлению

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Какова разность потенциалов между точками поля, если при перемещении заряда 12 мкКл из одной точки в другую электростатическое поле совершает работу 0,36 мДж? (Ответ дать в вольтах.)

Модуль напряженности однородного электрического поля равен 100 В/м. Каков модуль разности потенциалов между двумя точками, расположенными на одной силовой линии поля на расстоянии 5 см? (Ответ дать в вольтах.)

В электрическую цепь включена медная проволока длиной При напряженности электрического поля 50В/м сила тока в проводнике равна 2 А. Какое приложено напряжение к концам проволоки? (Ответ дать в вольтах.)

Шар радиусом 10 см равномерно заряжен электрическим зарядом. В таблице представлены результаты измерений модуля напряжённости E электрического поля от расстояния r до поверхности этого шара. Чему равен модуль заряда шара? (Ответ дать в нКл.) Коэффициент k принять равным 9·10⁹ Н·м²/Кл².

r, см	10	20	30	40	50
E, В/м	900	400	225	144	100

Шар радиусом 20 см равномерно заряжен электрическим зарядом. В таблице представлены результаты измерений модуля напряжённости E электрического поля от расстояния r до поверхности этого шара. Чему равен модуль заряда шара? (Ответ дать в нКл.) Коэффициент k принять равным 9·10⁹ Н·м²/Кл².

r, см	20	40	60	80	100
E, В/м	225	100	56,25	36	25

Пройти тестирование по этим заданиям

Источник

Предлагаю вашему вниманию сложные задачи ЕГЭ, которые могут встретиться под номерами 30 и 31. Надеюсь, подробный разбор укрепит вашу уверенность в том, что и с этими задачами вы справитесь.

Задача 1.

Расстояние между точечными зарядами нКл и нКл равно м. Найдите напряженность поля в точке на прямой, проходящей через заряды, в которой потенциал равен нулю.

Так как заряды разных знаков, то искомая точка располагается, вероятно, между ними. Обозначим за расстояние от второго заряда до этой искомой точки, тогда от первого заряда до нее расстояние будет . Так как потенциал в этой точке равен нулю, запишем:

Откуда

Отрицательный знак второго заряда уже учтен в уравнении, поэтому подставляем его модуль:

Таким образом, искомая точка – в метре от первого и в 10 см от второго заряда. Найдем напряженность поля в ней.

Ответ: 990 В/м.

Задача 2.

В вершинах равностороннего треугольника со стороной см расположены точечные заряды мкКл. Какую работу нужно совершить, чтобы переместить точечный заряд нКл из середины одной из сторон треугольника в его центр?

Узнаем потенциалы точек: первой – на середине стороны, и второй – в центре. В первой точке () сложатся три потенциала: два из трех зарядов располагаются на расстоянии , а третий – на расстоянии :

Точка располагается от зарядов на равных расстояниях, равных — так как медианы треугольника делятся точкой пересечения в отношении 2:1, считая от вершины. Тогда:

Высота правильного треугольника (она же и медиана) вычисляется по формуле:

Тогда:

Работа по перемещению заряда тогда будет такой:

Ответ: .

Задача 3.

Металлический шар радиусом см, заряженный до потенциала В, соединили проволокой с шаром емкостью пФ, на котором находится заряд Кл. Каков будет заряд на первом шаре после перераспределения зарядов?

На шарах после соединения их проводником заряды будут разными, но потенциалы – одинаковые. Вычислим потенциал второго шара:

Таким образом, потенциал второго шара – (-20 000) В.

Вычислим радиус этого шара:

Вычислим заряд первого шара:

При соединении проводников заряды сложатся и оставшийся нескомпенсированным заряд разделится пропорционально радиусам шаров:

Поэтому

Ответ: Кл.

Задача 4.

Протон, обладающий импульсом кгм/с, влетает в плоский конденсатор длиной 1 см под углом к пластинам. Расстояние между пластинами равно см. Определите величину напряжения на пластинах конденсатора, если при выходе из конденсатора протон будет двигаться параллельно пластинам.

Протон теряет вертикальную составляющую скорости – она становится равной нулю. То есть его импульс изменяется на величину . Чтобы изменить импульс, нужно воздействовать на протон с некоторой силой в течение некоторого времени. Поле конденсатора будет действовать на протон с силой , а время пролета через конденсатор будет равно

Тогда

Откуда

Ответ: 50 В.

Задача 5.

Электрон со скоростью см/с влетает в пространство между пластинами плоского конденсатора через маленькое отверстие в нижней пластине под углом к ней. Напряжение между пластинами В, расстояние между ними см. На какое максимальное расстояние электрон может удалиться от нижней пластины? Отношение заряда электрона к его массе равно Кл/кг.

На электрон будет воздействовать поле конденсатора, которое будет его тормозить. В итоге вертикальная составляющая скорости электрона должна стать равной 0. Сила, с которой поле воздействует на электрон, равна . Определим, с каким ускорением тормозит электрон.

Изменение скорости электрона — , время, за которое электрон снизил свою вертикальную составляющую скорости до нуля, равно . Здесь — горизонтальная составляющая скорости, а — расстояние, пройденное электроном по горизонтали. Тогда

Определим длину пройденного по горизонтали электроном расстояния из формулы:

Подставим в уравнение для ускорения:

Тогда

Ответ: 0,5 см

Задача решается проще, если приравнять работу поля и убыль кинетической энергии электрона:

Задача 6.

Между горизонтально расположенными пластинами плоского конденсатора с высоты см свободно падает незаряженный металлический шарик массой г. На какую высоту после абсолютно упругого удара о нижнюю пластину поднимется шарик, если в момент удара на него переходит заряд мк Кл? Разность потенциалов между пластинами конденсатора равна В, расстояние между ними см.

У шарика изначально есть запас потенциальной энергии . После отскока у него будет запас потенциальной энергии гравитационной, и запас потенциальной энергии взаимодействия с полем:

Откуда

Ответ: 1 см.

Задача 7.

Две частицы с массами и , имеющие одноименные заряды и соответственно, удерживают на расстоянии друг от друга. Какую максимальную скорость может приобрести частица , если обе отпустить одновременно без начальной скорости?

Частицы приобретут скорости, а следовательно, кинетические энергии. Эти энергии будут равны:

Приобретут они эти энергии за счет потенциальной энергии взаимодействия:

По закону сохранения импульса можно записать:

Или

Подставим это выражение в (1):

Ответ:

Задача 8.

В однородном электрическом поле, силовые линии которого направлены вертикально вверх, вращается в вертикальной плоскости на нити шарик массой и отрицательным зарядом , подвешенный на нити длиной . Заряд шарика не влияет на напряженность поля. Во сколько раз кинетическая энергия шарика в нижней точке траектории больше, чем в верхней?

В верхней точке траектории скорость такова, что сила натяжения нити минимальна. То есть скорость должна быть такой, чтобы нормальное ускорение могло противостоять и скомпенсировать силу тяжести и силу Кулона:

Откуда

Или, если мы хотим узнать кинетическую энергию в верхней точке, то

Теперь рассмотрим нижнюю точку. В этой точке скорость шарика другая, обозначим ее . В этой точке у шарика больше гравитационная потенциальная энергия (на ), и больше потенциальная энергия взаимодействия с полем (на ), поэтому закон сохранения энергии запишется так:

Так как из (2)

То

Тогда отношение энергий равно 5.

Ответ: 5.

Источник

Потенциал. Разность потенциалов. ЗАДАЧИ с решениями

Формулы, используемые на уроках «Решение задач на тему: Работа перемещения заряда в электрическом поле. Потенциал. Разность потенциалов» для подготовки к ЕГЭ.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача № 1.
Металлический шар диаметром d заряжен с поверхностной плотностью зарядов σ. Найти потенциал φ этого шара, если он окружен заземленной проводящей сферой, имеющей общий с шаром центр. Диаметр сферы D. Среда — воздух.

Задача № 2.
Потенциал заряженного шара φ₁ = 300 В. Чему равен потенциал φ₂ электрического поля этого шара в точке, отстоящей на расстоянии l = 50 см от его поверхности, если радиус шара R = 25 см?

Смотреть решение и ответ

Задача № 3.
Определить потенциал φ точки поля, находящейся на расстоянии а = 9 см от поверхности заряженного шара радиусом R = 1 см, если поверхностная плотность зарядов на шаре σ = 1 • 10^–11 Кл/см². Среда — воздух.

Задача № 4.
В точке 1 поля точечного заряда-источника потенциал φ₁ = 40 В, а в точке 2 φ₂ = 10 В. Найти потенциал φ в точке М, лежащей посередине между точками 1 и 2 (рис. 3-6).

Задача № 5.
В трех вершинах квадрата со стороной а = 20 см находятся заряды q₁ = 1 • 10^–8 Кл, q₂ = 2 • 10^–8 Кл и q₃ = 2 • 10^–8 Кл (рис. 3-7). Определить потенциал φ электрического поля, созданного этими зарядами в четвертой вершине.

Задача № 6.
Четыре одинаковых точечных заряда q расположены на одной прямой на расстоянии r друг от друга. Какую работу А надо совершить, чтобы переместить эти заряды в вершины тетраэдра со стороной r? Среда — вакуум.

Задача № 7.
Два одинаково заряженных шарика диаметрами d = 0,5 см каждый расположены на расстоянии l = 2 см между их поверхностями (рис. 3-14). До какого потенциала φ они заряжены, если сила их отталкивания друг от друга F = 2 мкН? Среда — воздух.

Задача № 8.
В однородном электрическом поле напряженностью Е = 2 кВ/см переместили заряд q = –20 нКл в направлении силовой линии поля на расстояние d = 10 см. Найти работу поля А, изменение потенциальной энергии поля ΔW_п и напряжение (разность потенциалов) U между начальной и конечной точками перемещения.

Смотреть решение и ответ

Задача № 9.
Между двумя горизонтальными плоскостями, заряженными разноименно и расположенными на расстоянии d = 5 мм друг от друга, находится в равновесии капелька масла массой 20 нг (нанограмм) (рис. 3-10). Найти число избыточных электронов N на этой капельке. Среда — воздух. Разность потенциалов между плоскостями U = 2 кВ.

Задача № 10.
На пластине М поддерживается потенциал φ₁ = +80 В, а на пластине N – φ₂ = –80 В (рис. 3-11, а). Расстояние между пластинами d = 10 см. На расстоянии d₁ = 4 см от пластины М помещают заземленную пластину Р (рис. 3-11, б). Найти изменение напряженности ΔЕ₁ поля на участке МР и изменение напряженности поля ΔЕ₂ на участке PN при этом. Построить графики зависимостей напряженностей Е = Е(х) и потенциала φ = φ(х) от расстояния между точками поля и пластинами.

Это конспект по теме «Потенциал. Разность потенциалов. ЗАДАЧИ с решениями». Выберите дальнейшие действия:

Вернуться к списку конспектов по Физике.
Проверить свои знания по Физике.

Источник

Работа сил электростатического поля. Потенциал и разность потенциалов. Связь разности потенциалов с напряженностью электростатического поля. Потенциал поля точечного заряда. Эквипотенциальные поверхности.

Работа сил электростатического поля

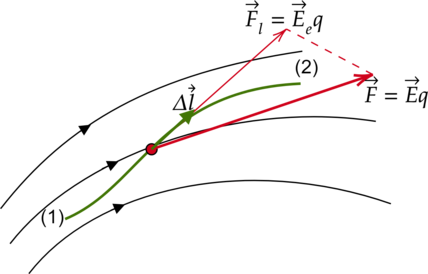
При перемещении пробного заряда (q) в электрическом поле электрические силы совершают работу. Эта работа при малом перемещении (Delta vec{l}) равна:

[Delta A=FDelta lcosalpha=EqDelta lcosalpha=E_1 qDelta l]

Рассмотрим работу сил в электрическом поле, создаваемом неизменным во времени распределенным зарядом, т.е. электростатическом поле.

Электростатическое поле обладает важным свойством:

Работа сил электростатического поля при перемещении заряда из одной точки поля в другую не зависит от формы траектории, а определяется только положением начальной и конечной точек и величиной заряда.

Следствием независимости работы от формы траектории является следующее утверждение:

Работа сил электростатического поля при перемещении заряда по любой замкнутой траектории равна нулю.

Силовые поля, обладающие этим свойством, называют или консервативными.

На замкнутой траектории работа кулоновских сил равна нулю.

Потенциальная энергия заряда (q), помещенного в любую точку (1) пространства, относительно фиксированной точки (0) равна работе (A_{10}), которую совершит электростатическое поле при перемещении заряда (q) из точки (1) в точку (0):

[W_{p1} = A_{10}]

Так же, как и в механике, потенциальная энергия определена с точностью до постоянной величины, зависящей от выбора опорной точки (0). Такая неоднозначность в определении потенциальной энергии не приводит к каким-либо недоразумениям, так как физический смысл имеет не сама потенциальная энергия, а разность ее значений в двух точках пространства.

Работа, совершаемая электростатическое полем при перемещении точечного заряда (q) из точки (1) в точку (2), равна разности значений потенциальной энергии в этих точках и не зависит от пути перемещения заряда и от выбора точки (0).

[A_{12} = A_{10} + A_{02} = A_{10} — A_{20} = W_{p_1} — W_{p_2}]

Физическую величину, равную отношению потенциальной энергии электрического заряда в электростатическом поле к величине этого заряда, называют (varphi) электрического поля:

[varphi=dfrac{W_p}{q}]

Потенциал (varphi) является энергетической характеристикой электростатического поля.

Работа (A_{12}) по перемещению электрического заряда (q) из начальной точки (1) в конечную точку (2) равна произведению заряда на разность потенциалов ((varphi_1-varphi_2)) начальной и конечной точек:

(A_{12} = W_{p1} — W_{p2} = qvarphi_1 — qvarphi_2 = q(varphi_1-varphi_2))

Единицы измерения: (displaystyle [text{В}]) (Вольт).

Во многих задачах электростатики при вычислении потенциалов за опорную точку (0) удобно принять бесконечно удаленную точку. В этом случае понятие потенциала может быть определено следующим образом:

Потенциал поля в данной точке пространства равен работе, которую совершают электрические силы при удалении единичного положительного заряда из данной точки в бесконечность.

[varphi_{infty}=dfrac{A_{infty}}{q}]

Поверхность, во всех точках которой потенциал электрического поля имеет одинаковые значения, называется или поверхностью равного потенциала.

Из принципа суперпозиции напряженностей полей, создаваемых электрическими зарядами, следует принцип суперпозиции для потенциалов:

[varphi =varphi_1 + varphi_2+ varphi_3 + …+varphi_n]

Источник

Энергия.

Работа.
Мощность.
Механическая энергия.
Кинетическая энергия.
Потенциальная энергия тела вблизи поверхности Земли.
Потенциальна яэнергия деформированной пружины.
Закон сохранения механической энергии.
Закон изменения механической энергии.

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: работа силы, мощность, кинетическая энергия, потенциальная энергия, закон сохранения механической энергии.

Мы приступаем к изучению энергии — фундаментального физического понятия. Но предварительно нужно разобраться с другой физической величиной — работой силы.

к оглавлению ▴

Работа.

Пусть на тело действует постоянная сила vec F и тело, двигаясь прямолинейно по горизонтальной поерхности, совершило перемещение vec s . Сила vec F не обязательно является непосредственной причиной перемещения (так, сила тяжести не является непосредственной причиной перемещения шкафа, который передвигают по комнате).

Предположим сначала, что векторы силы и перемещения сонаправлены (рис. 1; остальные силы, действующие на тело, не указаны)

Рис. 1.A=Fs

В этом простейшем случае работа определяется как произведение модуля силы на модуль перемещения:

A=Fs . (1)

Единицей измерения работы служит джоуль (Дж): Дж=Н cdot м. Таким образом, если под действием силы 1 Н тело перемещается на 1 м, то сила совершает работу 1 Дж.

Работа силы, перпендикулярной перемещению, по определению считается равной нулю. Так, в данном случае сила тяжести и сила реакции опоры не совершают работы.

Пусть теперь вектор силы образует с вектором перемещения острый угол alpha (рис. 2).

Разложим силу vec F на две составляющие: $vec F _{parallel }$ (параллельную перемещению) и $vec F _{perp }$ (перпендикулярную перемещению). Работу совершает только $vec F _{parallel }$ . Поэтому для работы силы vec F получаем:

$A=vec F _{parallel }s=Fcosalpha cdot s$ . Итак,

. (2)

Если вектор силы образует с вектором перемещения тупой угол alpha , то работа по-прежнему определяется формулой (2). В этом случае работа оказывается отрицательной.

Например, работа силы трения скольжения, действующей на тело в рассмотренных ситуациях, будет отрицательной, так как сила трения направлена противоположно перемещению. В этом случае имеем:

$alpha=180^{circ}, cos alpha=-1$ , и для работы силы трения получаем:

$A_{TP}=-F_{TP}s=-mu mgs$ ,

где — масса тела, — коэффициент трения между телом и опорой.

Соотношение (2) означает, что работа является скалярным произведением векторов силы и перемещения:

Это позволяет вычислять работу через координаты данных векторов:

$A=F_{displaystyle x}s_{displaystyle x}+F_{displaystyle y}s_{displaystyle y}+F_{displaystyle z}s_{displaystyle z}$ .

Пусть на тело действуют несколько сил $vec F_{1},vec F_{2},..,vec F_{n}$ и vec F — равнодействующая этих сил. Для работы силы vec F имеем:

$A=vec F vec s=(vec F_{1}+vec F_{2}+...+vec F_{n})vec s=vec F_{1}vec s+vec F_{2}vec s+...+vec F_{n}vec s$ ,

или

$A=A_{1}+A_{2}+...+A_{n}$ ,

где $A_{1}, A_{2},...,A_{n}$ — работы сил $F_{1}, F_{2},...,F_{n}$ . Итак, работа равнодействующей приложенных к телу сил равна сумме работ каждой силы в отдельности.

к оглавлению ▴

Мощность.

Часто имеет значение быстрота, с которой совершается работа. Скажем, на практике важно знать, какую работу сможет выполнить данное устройство за фиксированное время.

Мощность — это величина, характеризующая скорость совершения работы. Мощность есть отношение работы ко времени , за которое эта работа совершена:

$N=frac{displaystyle A}{displaystyle t}$ .

Мощность измеряется в ваттах (Вт). 1 Вт = 1 Дж/с, то есть 1 Вт — это такая мощность, при которой работа в 1 Дж совершается за 1 с.

Предположим, что силы, действующие на тело, уравновешены, и тело движется равномерно и прямолинейно со скоростью vec v . В этом случае существует полезная формула для мощности, развиваемой одной из действующих сил vec F .

За время тело совершит перемещение . Работа силы vec F будет равна:

Отсюда получаем мощность:

или

где alpha -угол между векторами силы и скорости.

Наиболее часто эта формула используется в ситуации, когда vec F — сила «тяги» двигателя автомобиля (которая на самом деле есть сила трения ведущих колёс о дорогу). В этом случае , и мы получаем просто:

N=Fv .

к оглавлению ▴

Механическая энергия.

Энергия является мерой движения и взаимодействия любых объектов в природе. Имеются различные формы энергии: механическая, тепловая, электромагнитная, ядерная. . .

Опыт показывает, что энергия не появляется ниоткуда и не исчезает бесследно, она лишь переходит из одной формы в другую. Это самая общая формулировка закона сохранения энергии.

Каждый вид энергии представляет собой некоторое математическое выражение. Закон сохранения энергии означает, что в каждом явлении природы определённая сумма таких выражений остаётся постоянной с течением времени.

Измеряется энергия в джоулях, как и работа.

Механическая энергия является мерой движения и взаимодействия механических объектов (материальных точек, твёрдых тел).

Мерой движения тела является кинетическая энергия. Она зависит от скорости тела. Мерой взаимодействия тел является потенциальная энергия. Она зависит от взаимного расположения тел.

Механическая энергия системы тел равна сумме кинетической энергии тел и потенциальной энергии их взаимодействия друг с другом.

к оглавлению ▴

Кинетическая энергия.

Кинетической энергией тела (принимаемого за материальную точку) называется величина

$K=frac{displaystyle mv^{displaystyle 2}}{displaystyle 2}$ ,

где — масса тела, — его скорость.

Кинетической энергией системы из тел называется сумма кинетических энергий каждого тела:

$K=frac{displaystyle m_{displaystyle 1}v_{displaystyle 1}^{displaystyle 2}}{displaystyle 2}+frac{displaystyle m_{displaystyle 2}v_{displaystyle 2}^{displaystyle 2}}{displaystyle 2}+...+frac{displaystyle m_{displaystyle N}v_{displaystyle N}^{displaystyle 2}}{displaystyle 2}$ .

Если тело движется под действием силы vec F , то кинетическая энергия тела, вообще говоря, меняется со временем. Оказывается, именение кинетической энергии тела за некоторый промежуток времени равно работе силы vec F . Покажем это для случая прямолинейного равноускоренного движения.

Пусть $vec{v_{1}}$ — начальная скорость, $vec{v_{2}}$ — конечная скорость тела. Выберем ось вдоль траектории тела (и, соответственно, вдоль вектора силы vec F ). Для работы силы vec F получаем:

$A=vec{F}vec{s}=F_{x}s_{displaystyle s}=ma_{displaystyle x}s_{displaystyle x}= ma_{displaystyle x}frac{{v_{displaystyle 2x}}^{displaystyle 2}-{v_{displaystyle 1x}}^{displaystyle 2}}{displaystyle 2a_{displaystyle x}}=frac{{displaystyle mv_{displaystyle 2x}}^{displaystyle 2}-{displaystyle mv_{displaystyle 1x}}^{displaystyle 2}}{displaystyle 2}$ .

(мы воспользовались формулой для $s_{x}$ , выведенной в статье «Равноускоренное движение»). Заметим теперь, что в данном случае проекция скорости отличается от модуля скорости разве что знаком; поэтому ${v_{displaystyle 1x}}^{displaystyle 2}={v_{displaystyle 1}}^{displaystyle 2}$ и ${v_{displaystyle 2x}}^{displaystyle 2}={v_{displaystyle 2}}^{displaystyle 2}$ . В результате имеем:

$A=frac{displaystyle mv_{displaystyle 2}^{displaystyle 2}}{displaystyle 2}-frac{displaystyle mv_{displaystyle 1}^{displaystyle 2}}{displaystyle 2}=K_{displaystyle 2}-K_{displaystyle 1}=Delta K$ ,

что и требовалось.

На самом деле соотношение справедливо и в самом общем случае криволинейного движения под действием переменной силы.

Теорема о кинетической энергии. Изменение кинетической энергии тела равно работе, совершённой приложенными к телу внешними силами за рассматриваемый промежуток времени.

Если работа внешних сил положительна, то кинетическая энергия увеличивается (, тело разгоняется).

Если работа внешних сил отрицательна, то кинетическая энергия уменьшается (, тело замедляет движение). Пример — торможение под действием силы трения, работа которой отрицательна.

Если же работа внешних сил равна нулю, то кинетическая энергия тела за это время не меняется. Нетривиальный пример — равномерное движение по окружности, совершаемое грузом на нити в горизонтальной плоскости. Сила тяжести, сила реакции опоры и сила натяжения нити всегда перпендикулярны скорости, и работа каждой из этих сил равна нулю в течение любого промежутка времени. Соответственно, кинетическая энергия груза (а значит, и его скорость) остаётся постоянной в процессе движения.

Задача. Автомобиль едет по горизонтальной дороге со скоростью и начинает резко тормозить. Найти путь , пройденный автомобилем до полной остановки, если коэффициент трения шин о дорогу равен .

Решение. Начальная кинетическая энергия автомобиля $K_{displaystyle 1}=frac{displaystyle mv^{displaystyle 2}}{displaystyle 2}$ , конечная кинетическая энергия $K_{displaystyle 2}=0$ . Изменение кинетической энергии $Delta K=K_{displaystyle 2}-K_{displaystyle 1}=-frac{displaystyle mv^{displaystyle 2}}{displaystyle 2}$ .

На автомобиль действуют сила тяжести m vec g , реакция опоры vec N и сила трения vec f . Сила тяжести и реакция опоры, будучи перпендикулярны перемещению автомобиля, работы не совершают. Работа силы трения:

Из теоремы о кинетической энергии теперь получаем:

$Delta K=A Rightarrow - frac{displaystyle mv^{displaystyle 2}}{displaystyle 2}=- mu mgs Rightarrow s=frac{displaystyle v^{displaystyle 2}}{displaystyle 2 mu g}$ .

к оглавлению ▴

Потенциальная энергия тела вблизи поверхности Земли.

Рассмотрим тело массы , находящееся на некоторой высоте над поверхностью Земли. Высоту считаем много меньше земного радиуса. Изменением силы тяжести в процессе перемещения тела пренебрегаем.

Если тело находится на высоте , то потенциальная энергия тела по определению равна:

W=mgh

где — ускорение свободного падения вблизи поверхности Земли.

Высоту не обязательно отсчитывать от поверхности Земли. Как мы увидим ниже (формулы (3), (4)), физическим смыслом обладает не сама по себе потенциальная энергия, но её изменение. А изменение потенциальной энергии не зависит от уровня отсчёта. Выбор нулевого уровня потенциальной энергии в конкретной задаче диктуется исключительно соображениями удобства.

Найдём работу, совершаемую силой тяжести при перемещении тела. Предположим, что тело перемещается по прямой из точки , находящейся на высоте $h_{1}$ , в точку , находящуюся на высоте $h_{2}$ (рис. 3).

Рис. 3.A=mg(h1-h2)[/math]

Угол между силой тяжести m vec g и перемещением тела vec s обозначим alpha . Для работы силы тяжести получим:

Но, как видно из рис. 3, $s cos alpha=h_{1}-h_{2}$ . Поэтому

$A=mg(h_{1}-h_{2})=mgh_{1}-mgh_{2}$ ,

или

$A=W_{1}-W_{2}$ . (3)

Учитывая, что $W_{1}-W_{2}=-(W_{2}-W_{1})=- Delta W$ , имеем также:

. (4)

Можно доказать, что формулы (3) и (4) справедливы для любой траектории, по которой тело перемещается из точки в точку , а не только для прямолинейного отрезка.

Работа силы тяжести не зависит от формы траектории, по которой перемещается тело, и равна разности значений потенциальной энергии в начальной и конечной точках траектории. Иными словами, работа силы тяжести всегда равна изменению потенциальной энергии с противоположным знаком. В частности, работа силы тяжести по любому замкнутому пути равна нулю.

Сила называется консервативной, если при перемещении тела работа этой силы не зависит от формы траектории, а определяется только начальным и конечным положением тела. Сила тяжести, таким образом, является консервативной. Работа консервативной силы по любому замкнутому пути равна нулю. Только в случае консервативной силы возможно ввести такую величину, как потенциальная энергия.

к оглавлению ▴

Потенциальна яэнергия деформированной пружины.

Рассмотрим пружину жёсткости . Начальная деформация пружины равна $x_{1}$ . Предположим,
что пружина деформируется до некоторой конечной величины деформации $x_{2}$ . Чему равна при этом работа силы упругости пружины?

В данном случае силу на перемещение не умножишь, так как сила упругости меняется в процессе деформации пружины. Для нахождения работы переменной силы требуется интегрирование. Мы не будем приводить здесь вывод, а сразу выпишем конечный результат.

Оказывается, сила упругости пружины также является консервативной. Её работа зависит лишь от величин $x_{1}$ и $x_{2}$ и определяется формулой:

$A=frac{kx_{displaystyle 1}^{displaystyle 2}}{displaystyle 2}-frac{displaystyle kx_{displaystyle 2}^{displaystyle 2}}{displaystyle 2}$ .

Величина

$W=frac{displaystyle kx^{displaystyle 2}}{displaystyle 2}$

называется потенциальной энергией деформированной пружины (x — величина деформации).

Следовательно,

$A=W_{1}-W_{2}=- Delta W$ ,

что полностью аналогично формулам (3) и (4).

к оглавлению ▴

Закон сохранения механической энергии.

Консервативные силы называются так потому, что сохраняют механическую энергию замкнутой системы тел.

Механическая энергия тела равна сумме его кинетической и потенциальной энергий:

E=K+W .

Механическая энергия системы тел равна сумме их кинетических энергий и потенциальной энергии их взаимодействия друг с другом.

Предположим, что тело совершает движение под действием силы тяжести и/или силы упругости пружины. Будем считать, что трения нет. Пусть в начальном положении кинетическая и потенциальная энергии тела равны $K_{1}$ и $W_{1}$ , в конечном положении — $K_{2}$ и $W_{2}$ . Работу внешних сил при перемещении тела из начального положения в конечное обозначим .

По теореме о кинетической энергии

$K_{2}-K_{1}=A$ .

Но работа консервативных сил равна разности потенциальных энергий:

$A=W_{1}-W_{2}$ .

Отсюда получаем:

$K_{2}-K_{1}=W_{1}-W_{2}$ ,

или

$K_{1}+W_{1}=K_{2}+W_{2}$ .

Левая и правая части данного равенства представляют собой механическую энергию тела в начальном и конечном положении:

$E_{1}=E_{2}$ .

Следовательно, при движении тела в поле силы тяжести и/или на пружине механическая энергия тела остаётся неизменной при отсутствии трения. Справедливо и более общее утверждение.

Закон сохранения механической энергии. Если в замкнутой системе действуют только консервативные силы, то механическая энергия системы сохраняется.

При этих условиях могут происходить лишь превращения энергии: из кинетической в потенциальную и наоборот. Общий запас механической энергии системы остаётся постоянным.

к оглавлению ▴

Закон изменения механической энергии.

Если между телами замкнутой системы имеются силы сопротивления (сухое или вязкое трение), то механическая энергия системы будет уменьшаться. Так, автомобиль останавливается в результате торможения, колебания маятника постепенно затухают и т. д. Силы трения неконсервативны: работа силы трения очевидным образом зависит от пути, по которому перемещается тело между данными точками. В частности, работа силы трения по замкнутому пути не равна нулю.

Снова рассмотрим движение тела в поле силы тяжести и/или на пружине. Вдобавок на тело действует сила трения, которая за рассматриваемый промежуток времени совершает отрицательную работу $A_{TP}$ . Работу консервативных сил (тяжести и упругости) по-прежнему обозначаем .

Изменение кинетической энергии тела равно работе всех внешних сил:

$K_{2}-K_{1}=A+A_{TP}$ .

Но $A=W_{1}-W_{2}$ , следовательно

$K_{2}-K_{1}=W_{1}-W_{2}+A_{TP}$ .

Отсюда

$K_{2}+W_{2}-(K_{1}+W_{1})=A_{TP}$ ,

или

$E_{2}-E_{1}=A_{TP}$ .

В левой части стоит величина $Delta E=E_{2}-E_{1}$ — изменение механической энергии тела:

$Delta E=A_{TP}$ .

Итак,при движении тела в поле силы тяжести и/или на пружине изменение механической энергии тела равно работе силы трения. Так как работа силы трения отрицательна,изменение механической энергии также отрицательно: механическая энергия убывает.
Справедливо и более общее утверждение.

Закон изменения механической энергии. Изменение механической энергии замкнутой системы равно работе сил трения, действующих внутри системы.

Ясно, что закон сохранения механической энергии является частным случаем данного утверждения.

Конечно, убыль механической энергии не противоречит общефизическому закону сохранения энергии. В данном случае механическая энергия превращается в энергию теплового движения частиц вещества и их потенциальную энергию взаимодействия друг с другом, т. е. переходит во внутреннюю энергию тел системы.

Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Энергия.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена:
09.03.2023

Источник

Тема 12.

Электрическое поле. Законы постоянного тока

Электростатика. Напряженность и потенциал электрического поля

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.

Готовиться с нами — ЛЕГКО!

Подтемы раздела

электрическое поле. законы постоянного тока

12.01Электростатика. Закон Кулона

12.02Электростатика. Напряженность и потенциал электрического поля

12.03Конденсаторы

12.04Электрический ток. Закон Ома

12.05Работа тока. Закон Джоуля – Ленца

Решаем задачи

Во сколько раз увеличится ускорение заряженной пылинки, движущейся в электрическом поле, если её заряд увеличить в 6 раз, а
напряжённость поля уменьшить в 2 раза? Силу тяжести и сопротивление воздуха не учитывать.

Показать ответ и решение

Электрическая сила, действующая на пылинку равна:

F =qE,

где – заряд, – напряженность.
Ускорение можно выразить из второго закона Ньютона:

F
a= m-,

где – масса пылинки.
Тогда

a= qE-,
m

при увеличении заряда 6 раз и уменьшении напряженности в 2, ускорение увеличится в 3 раза.

Точечный положительный заряд величиной = 2 мкКл помещён между двумя протяжёнными пластинами, равномерно
заряженными разноимёнными зарядами. Модуль напряжённости электрического поля, создаваемого положительно
заряженной пластиной, равен 103 кВ/м, а поля, создаваемого отрицательно заряженной пластиной, в 2 раза больше.
Определите модуль электрической силы, которая будет действовать на указанный точечный заряд. (Ответ дайте в
ньютонах.)

Показать ответ и решение

Согласно принципу суперпозиции:

По условию, напряженность поля, создаваемого отрицательно заряженной пластиной, в 2 раза больше, чем модуль
напряжённости электрического поля, создаваемого положительно заряженной пластиной:

Тогда напряженность поля системы равна:

Электрическая сила равна:

Какая работа совершается при переносе заряда 8 мкКл из точки поля с потенциалом 28 В в другую точку с потенциалом 12 В?
(Ответ дайте в мкДж)

Показать ответ и решение

Разность потенциалов есть напряжение. Напряжение — это работа по перемещению заряда:

A
U = -q ⇒ A= qU

где — заряд, — разность потенциалов или напряжение.

Какую работу совершает электростатическое поле при перемещении заряда 2 нКл из одной
точки поля в другую, если разность потенциалов между ними равна 1000 В? (Ответ дайте в
мкДж)

Показать ответ и решение

Разность потенциалов есть напряжение. Напряжение — это работа по перемещению заряда:

A
U = -q ⇒ A= qU

где — заряд, — разность потенциалов или напряжение.

Модуль напряженности однородного электрического поля равен 200 В/м. Каков модуль разности
потенциалов между двумя точками, расположенными на одной силовой линии поля на расстоянии 10
см? (Ответ дайте в вольтах.)

Показать ответ и решение

Модуль разности потенциалов это напряжение, оно находится по формуле:

U = Ed

где — напряженность, — расстояние между точками. Найдем напряжение:

Показать ответ и решение

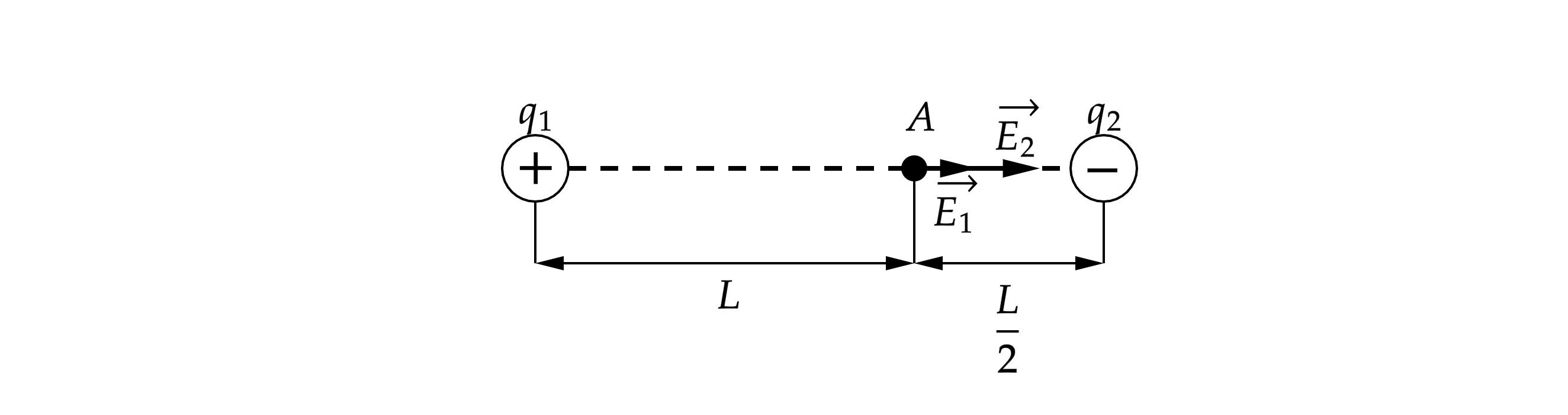
По принципу суперпозиции напряженность в точке будет равна сумме напряженностей, создаваемых точечными зарядами. Так
как q1 > 0 , то вектор напряженности направлен от заряда, а q2 < 0 – к заряду. (см. рис.)

Напряженность определяется по формуле:

kq
E = r2,

где – постоянная Кулона, – заряд, – расстояние от заряда до точки измерения напряженности.
Тогда по принципу суперпозиции:

Подставим числа из условия:

Показать ответ и решение

Работа по перемещению заряда может быть найдена по формуле:

где – заряд, – потенциал в точке , – потенциал в точке .
Подставляя числа из условия:

Разность потенциалов между точками, находящимися на расстоянии 10 см друг от друга на одной линии
напряженности однородного электростатического поля, равна 10 В. Чему равна напряженность (в В/м)
этого поля?

Показать ответ и решение

Напряженность можно найти по формуле:

U
E = d.

Здесь – разность потенциалов, – расстояние между точками.
Подставляя числа из условия

E = -10-В-= 100 В/м
0,1 м

При лечении электростатическим душем к электродам электрической машины прикладывается
разность потенциалов 10 кВ. Какой заряд (в Кл) проходит между электродами во время
процедуры, если известно, что электрическое поле совершает при этом работу, равную 3,6
кДж?

Показать ответ и решение

Работа по перемещению заряда равна:

A =qU,

где – заряд, который проходит между электродами, – разность потенциалов.
Тогда

A 3600 Дж
q = U-= 10000 В-= 0,36 К л

В вертикальном однородном электрическом поле с напряженностью 100 В/м, неподвижно висит
пылинка, заряд которой 10 нКл. Чему равна масса (в мг) пылинки?

Показать ответ и решение

Запишем второй закон Ньютона

где –вектор напряженности, – ускорение частицы, – масса частицы, – её заряд.
Так как скорость частицы равна нулю, то ее ускорение равно нулю, значит, второй закон Ньютона в проекции на вертикальную ось
запишется в виде:

−9
qE − mg = 0 ⇒ m = qE-= 100 В/м-⋅10⋅10-К-л= 0,1 мг.
g 10 м/c2

Напряженность в точке на поверхности сферы равна 200 В/м . Найдите напряженность в точке , если она расположена
диаметрально противоположно точке . Ответ дайте в В/м

Показать ответ и решение

Напряженность на поверхности проводника во всех местах одинаковая, следовательно, напряженность в точке равна 200
В/м.

Проводящий шар радиусом r =6 см имеет заряд равный 10 нКл. Найдите напряженность в точке

Показать ответ и решение

Напряженность внутри проводника равна 0.

Потенциал точки, находящейся на поверхности заряженной проводящего шара радиуса 5 см,
равен 24 В. Найдите потенциал внутри шара на расстоянии 2,5 см от центра. Ответ дайте в
В.

Показать ответ и решение

Потенциал внутри проводника равен потенциалу на поверхности проводника, следовательно, потенциал
в данном случае равен 24 В.

Потенциал точки, находящейся на поверхности заряженной проводящего шара радиуса 12 см, равен 12
В. Найдите потенциал в центре шара. Ответ дайте в В

Показать ответ и решение

Потенциал внутри проводника равен потенциалу на поверхности проводника, следовательно, потенциал
в центре шара равен 12 В.

Источник

Видеоурок: Работа электрического поля. Потенциал. Электрическое напряжение

Лекция: Потенциальность электростатического поля

Потенциальная энергия поля

Некоторую силу можно назвать консервативной только в том случае, когда она не зависит от траектории, по которой двигается тело. Работа всех консервативных сил равна разности потенциальных энергий рассматриваемого тела A = W1 — W2

Сила взаимодействия между зарядами также является консервативной, а так как это сила приводит к тому, что заряды начинают двигаться, то она так же выполняет работу. При этом существует важный факт — работа в данном случае абсолютно не зависит от траектории, по которой двигается данной тело, а определяется она только начальным и конечным положением тела. При этом, как и любая работа консервативных сил, если траектория перемещения — замкнутая линия, то работа равна нулю.

Потенциальная энергия поля равна:

Можно заметить, что практически вся теория электродинамики достаточно сильно напоминает механику. Постарайтесь вспомнить потенциальную энергию тела. Она зависела от массы, высоты и ускорения свободного падения. Можно провести аналогию. Более того, напряженность электрического поля из закона Кулона выводится точно так же, как и ускорение свободного падения из закона гравитационного взаимодействия.

Основным и главным отличием потенциальной энергии материальных точек от энергии зарядов являются граничные значения. Потенциальная энергия заряженных тел увеличивается с уменьшением расстояния между зарядами и стремится к нулю, когда заряды удаляют на бесконечность.

Потенциал

Исходя из формулы, можно сделать вывод, что потенциальная энергия поля пропорциональна величине рассматриваемого заряда. Величина, являющая коэффициентом пропорциональности, называется потенциалом поля. Как видно из формулы, он также зависит от величины заряда.

Потенциал обозначается буквой «фи» и измеряется в Вольтах (В).

Если напряженность — это силовая характеристика имеющегося поля, то потенциал является его энергетической характеристикой.

Разность потенциалов

Из полученной формулы можно вывести значение энергии через потенциал. И если учесть, что разность потенциальных энергий — это работа, получим:

Полученная величина называется

разностью потенциалов

. Если некоторый пробный заряд отдалять на какое-то расстояние от заряженного тела, то будет совершаться работа, позволяющая изменить энергетическую характеристику поля.

Разность потенциалов еще называют напряжением. Если некоторый заряд удаляют на бесконечное расстояние, то напряжение такого поля равно начальному потенциалу.

Для того, чтобы изменить потенциал поля необходимо совершить работу по перемещению заряда.

Эквипотенциальная поверхность

Для наглядного понимания того, что такое потенциалы и их изменения, используют эквипотенциальные поверхности. Это поверхности, которые расположены перпендикулярно к силовым линиям. На всей такой поверхности значение потенциала одинаково. Чем дальше эквипотенциальная поверхность находится от заряда, тем меньше там потенциал.

На рисунке мы можем наблюдать поперечное сечение поверхности. Они располагаются перпендикулярно к экрану, на который вы смотрите. Направление перемещения заряда всегда находится под углом 90 градусов к поверхностям.

Источник