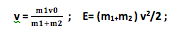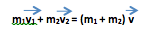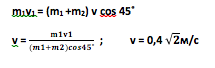Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
2
Система состоит из двух тел a и b. На рисунке стрелками в заданном масштабе указаны импульсы этих тел. Чему по модулю равен импульс всей системы? Ответ выразите в килограммах на метр в секунду и округлите до десятых.
3
Система состоит из двух тел a и b. На рисунке стрелками в заданном масштабе указаны импульсы этих тел. Чему по модулю равен импульс всей системы? (Ответ дайте в килограммах на метр в секунду.)
4
Система состоит из двух тел 1 и 2, массы которых равны 0,5 кг и 2 кг. На рисунке стрелками в заданном масштабе указаны скорости этих тел. Чему равен импульс всей системы по модулю? (Ответ дайте в килограммах на метр в секунду.)
5
Охотник массой 60 кг, стоящий на гладком льду, стреляет из ружья в горизонтальном направлении. Масса заряда 0,03 кг. Скорость дробинок при выстреле Какова скорость охотника после выстрела? (Ответ дайте в метрах в секунду.)
Пройти тестирование по этим заданиям
Закон сохранения импульса.
Задачи ЕГЭ с решениями
Формулы для решения задач по теме «Закон сохранения импульса. Задачи ЕГЭ».
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача 1.
Тело массой 2 кг свободно падает без начальной скорости с высоты 5 м на горизонтальную поверхность и отскакивает от нее со скоростью 5 м/с. Найдите абсолютную величину изменения импульса тела при ударе, g = 10 м/с2.
Задача 2.
Мячик массой 200 г летел со скоростью 20 м/с. После удара о стенку он отскочил под прямым углом к прежнему направлению со скоростью 15 м/с. Найдите модуль изменения импульса мячика при ударе.
Посмотреть РЕШЕНИЕ и ответ
Задача 3.
Стальной шарик массой 0,1 кг падает на горизонтальную плоскость с высоты 0,2 м и отскакивает после удара снова до высоты 0,2 м. Найдите среднюю силу давления шарика на плоскость при ударе, если его длительность 0,04 с. g = 10 м/с2.
Посмотреть РЕШЕНИЕ и ответ
Задача 4.
Стальной шарик массой 40 г, летящий горизонтально со скоростью 20 м/с, ударяется о наклонную плоскость, составляющую угол 30° с горизонтом. Считая удар абсолютно упругим, найдите среднюю силу взаимодействия шарика с наклонной плоскостью. Продолжительность удара 0,01 с. Действием силы тяжести за время удара пренебречь.
Посмотреть РЕШЕНИЕ и ответ
Задача 5.
Какова средняя сила давления на плечо при стрельбе из автомата, если масса пули 10 г, а скорость пули при вылете 300 м/с? Автомат делает 300 выстрелов в минуту.
Посмотреть РЕШЕНИЕ и ответ
Задача 6.
Ракета массой 2 т неподвижно висит над землей, выбрасывая вниз реактивную струю со скоростью 1250 м/с. Какая масса газов выбрасывается в струе за 1 с? g = 10 м/с2.
Посмотреть РЕШЕНИЕ и ответ
Замечание. Если ракета движется с ускорением, формула для реактивной силы имеет такой же вид. Проще всего убедиться в этом, перейдя в систему отсчета, в которой ракета в данный момент покоится.
Задача 7.
Тонкую мягкую цепочку массой 200 г удерживают за один конец так, что другой ее конец касается стола. Цепочку отпускают, и она падает на стол. Считая, что все элементы цепочки, находящиеся в воздухе, падают свободно, найдите силу давления на стол в тот момент, когда в воздухе находится половина цепочки, g = 10 м/с2.
Посмотреть РЕШЕНИЕ и ответ
Задача 8.
Конькобежец катил груженные сани по льду со скоростью 5 м/с, а затем толкнул их вперед и отпустил. С какой скоростью (в см/с) покатится конькобежец непосредственно после толчка, если скорость саней возросла до 8 м/с? Масса саней 90 кг, масса человека 60 кг. В ответе укажите модуль скорости.
Посмотреть РЕШЕНИЕ и ответ
Задача 9.
Три лодки массами 100 кг каждая идут одна за другой с одинаковыми скоростями. Из средней лодки одновременно в переднюю и заднюю бросают горизонтально со скоростью 2,2 м/с относительно лодки грузы массой 10 кг каждый. Найдите величину относительной скорости (в см/с) передней и задней лодок после попадания в них грузов.
Посмотреть РЕШЕНИЕ и ответ
Задача 10.
От поезда, идущего с постоянной скоростью 64 км/ч, отделяется пятая часть состава. Через некоторое время скорость отделившихся вагонов уменьшилась в 2 раза. Считая, что сила тяги при разрыве не изменилась, найдите скорость (км/ч) головной части поезда в этот момент. Сила трения пропорциональна весу.
Посмотреть РЕШЕНИЕ и ответ
Задача 11.
Снаряд, летящий с некоторой скоростью, распадается на два осколка. Скорость большего осколка по величине равна начальной скорости снаряда и направлена перпендикулярно к ней. Скорость другого осколка по величине в 5 раз больше первоначальной. Найдите отношение масс осколков.
Посмотреть РЕШЕНИЕ и ответ
Задача 12.
Снаряд массой 50 кг, летящий под углам 30° к вертикали со скоростью 600 м/с, попадает в платформу с пескам и застревает в ней. Найдите скорость платформы после попадания снаряда. Масса платформы 950 кг. Трением между платформой и рельсами пренебречь.
Посмотреть РЕШЕНИЕ и ответ
Задача 13.
В ящик с песком массой 9 кг, соскальзывающий с гладкой наклонной плоскости, попадает горизонтально летящее ядро массой 3 кг и застревает в нем. Найдите скорость ящика сразу же после попадания ядра, если непосредственно перед попаданием скорость ящика равнялась 6 м/с, а скорость ядра 12 м/с. Угол наклона плоскости к горизонту 60°.
Посмотреть РЕШЕНИЕ и ответ
Задача 14.
Тележка стоит на гладких рельсах. Человек переходит с одного ее конца на другой параллельно рельсам. На какое расстояние относительно земли переместится при этом тележка? Масса человека 60 кг, масса тележки 120 кг, ее длина 6 м.
Посмотреть РЕШЕНИЕ и ответ
Задача 15.
На стол поставили в вертикальном положении тонкую палочку длиной 80 см и отпустили. На сколько сантиметров сместится нижний конец палочки к тому моменту, когда она будет составлять с поверхностью стола угол 60°? Трением пренебречь.
Посмотреть РЕШЕНИЕ и ответ
Задача 16.
Веревку длиной 80 см и массой 200 г положили на гладкую горизонтальную поверхность и раскрутили вокруг одного из концов с угловой скоростью 10 рад/с. Чему равна сила натяжения веревки в середине ее длины?
Посмотреть РЕШЕНИЕ и ответ
Задача 17.
Два шарика массой 250г каждый, соединенные нитью длиной 1 м, движутся по гладкой горизонтальной поверхности. В некоторый момент один из шариков неподвижен, а скорость другого равна 4 м/с и направлена перпендикулярно нити. Чему равна сила натяжения нити?
Посмотреть РЕШЕНИЕ и ответ
Вы смотрели конспект по теме «Закон сохранения импульса. Задачи ЕГЭ». Ключевые слова конспекта: Определение импульса. Изменение импульса и средняя сила. Закон сохранения импульса. Сохранение проекции импульса. Комплексные задачи. Центр масс.
Автор задач и решений: Алексей Игоревич Черноуцан. Выберите дальнейшие действия:
- Перейти к теме:
- Вернуться к списку конспектов по Физике.
- Проверить свои знания по Физике.
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Закон сохранения импульса
Закон сохранения импульса
Импульс замкнутой системы, состоящей из (n), тел остается постоянным с течением времени при любых взаимодействиях тел внутри данной системы
[displaystylesum_{i=1}^{n}vec{p}_i=displaystylesum_{i=1}^{n}m_ivec{v}_i=const]
Охотник, стоящий на гладком льду, стреляет из ружья. Масса заряда (0,05 text{кг} ). Скорость снаряда (200 text{м/c}). Какова масса охотника, если его скорость после выстрела равна (0,1 text{м/c})
Так как до выстрела общий импульс системы равен нулю. По Закону Сохранения импульса: [m_1cdot upsilon_1 — m_2cdot upsilon_2 = 0] Где (m_2) – масса охотника, (m_1) – масса снаряда (v_1), (upsilon_2) – скорости снаряда и охотника соответственно [m_2 = frac {m_1 cdot upsilon_1} {upsilon_2}] [m_2= frac {0,05 text {кг} cdot 200 text{ м/с}}{0,1 text{м/c} } =100text{ кг}]
Ответ: 100
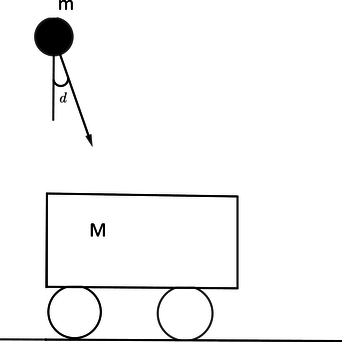
Камень массой (m =4 text { кг} ) падает под углом (alpha=30^circ) к вертикали со скоростью (10 text { м/с}) в тележку с песком общей массой ( M= 16 text { кг}), покоящуюся на горизонтальных рельсах. Определите скорость тележки с камнем после падения в неё камня.
В начале импульс тележки равен нулю. по Закону Сохранения Импульса(на горизонтальную ось): [m_1cdot upsilon_1sinalpha=(m+M)cdotupsilon’] [upsilon’=frac{m_1cdot upsilon_1sinalpha}{m+M}] [upsilon’=frac{4text{ кг}cdot 10text{ м/с} cdotdfrac 1 2 }{4text{ кг}+16text{ кг}}=1text{ м/c}]
Ответ: 1
С неподвижной лодки массой (M=50text{ кг } ) на берег прыгнул мальчик массой (m=40text{ кг } ) со скоростью (upsilon_1 = 1 text{ м/c } ) относительно берега, направленной горизонтально. Какую скорость (upsilon_2) относительно берега приобрела лодка?
Начальный импульс системы равен нулю. По закону Сохранения Импульса: [Mcdotupsilon_2-mcdotupsilon_1 = 0] [upsilon_2=frac{mcdotupsilon_1}{M}] [upsilon_2=frac{40 text{ кг }cdot 1 text{ м/с } } {50 text{ кг}} =0,8 text{ м/c }]
Ответ: 0, 8
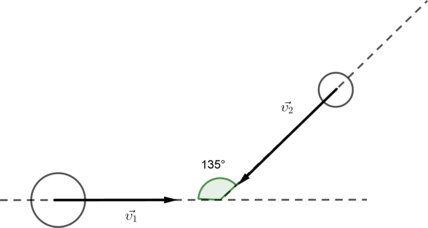
Одинаковые шары массой (m = 1 text{ кг } ) каждый движутся со скоростями, направления которых указаны на рисунке, и сталкиваются. Чему будет равен суммарный импульс шаров после столкновения, если (upsilon_1=16 text{ м/c }), а (upsilon_2=upsilon_1 cdot sqrt{2})?
Из рисунка видно, что углы между осями и вторым шаром равны (45^circ). По закону сохранения импульса суммапрный импульс системы до удара и после удара будет одинаковый. Найдем проекции суммарного импульса на каждую ось: (p_x’) – Суммарный импульс на ось Ox (p_y’) – суммарный импульс на ось Oy [p_{2x}-p_{1x}=p_x’] [p_{2y}-p_{1y} =p_y’] По рисунку (p_{1y}=0) По теореме Пифагора: [P_{text{итог}}’=sqrt{p_y’^2+p_x’^2}] Заменим (upsilon_2) на (upsilon_1 cdot sqrt{2} ). [p_y’=mcdotupsilon_1sqrt{2}cos{45^circ}] [p_x’=mcdot upsilon_1cdot (cos{45^circ} cdot sqrt{2}-1)] [p_y’= 1 text{кг} cdot 16 text{ м/c } cdot frac{sqrt2} 2cdot sqrt 2 = 16 frac{text{ кг }cdot text{ м }} {text{ c }}] [p_x’= 1 кг cdot 16 text{м/c} left(frac{sqrt2} {2} cdot sqrt2 — 1right)=0frac{text{ кг }cdot text{ м }} {text{ c }}] [P_{ итог } = sqrt{left(16frac{text{кг}cdot text{м}} { c}right)^2}=16frac{text{ кг }cdot text{ м }} { text{ c } }]
Ответ: 16
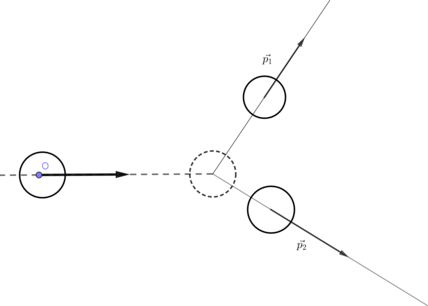
На неподвижный бильярдный шар налетел другой такой же. После удара шары разлетелись под углом (90^circ) так, что импульс одного равен (p_1=5dfrac {text{ кг }cdot text{ м }} {text{ c }} ), а другого (p_2 = 12dfrac{text{ кг }cdot text{ м }}{text{ c }}) (см.рисунок). Чему был равен импульс налетающего шара?
По закону сохранения импульса: [vec{p’}=vec{p_1}+vec{p_2}] Так как шары разлетелись под углом (90^{circ}), применим теорему Пифагора: [p’=sqrt{p_1^2 + p_2^2}] [p’=sqrt{left(5 frac {text{ кг }cdot text{ м }} {text{ c }} right)^2 + left(12frac {text{ кг }cdot text{ м }} {text{ c }} right)^2}=13frac {text{ кг }cdot text{ м }} {text{ c }}]
Ответ: 13
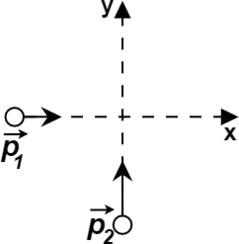
По гладкой горизонтальной плоскости по осям Оx и Оy движутся две шайбы с импульсами равными по модулю (p_1 =3 ) кг(cdot)м/с и (p_2 =6 ) кг(cdot)м/с (см.рисунок). После их соударения вторая шайба продолжает двигаться по оси y в прежнем направлении. Модуль импульса первой шайбы после удара равен (p_1’= 5 ) кг(cdot)м/с. Найдите модуль импульса второй шайбы после удара.
Запишем ЗСИ (закон сохранения импульса): [vec{p_1}+vec{p_2}=vec{p_1}’+vec{p_2}’ quad(1)] Спроецируем данное уравнение на ось Оx: [p_1=p_{1x}’ quad(2)] Спроецируем на ось Оy: [p_2=p_{1y}’+p_2′ quad(3)] После удара импульс первой шайбы стал равен [p_1’=sqrt{p_{1x}^{prime 2}+p_{1y}^{prime 2}} quad(4)] Из (2) следует, что (p_{1x}’ =3 ) кг(cdot)м/с. Из (4) следует, что [p_{1y}=sqrt{p_1^{prime 2}- p_{1x} ^{prime 2}}=sqrt{25-9} = 4 text{ кг$cdot$м/c}]
Найдем (p_2′) из (3): [p_2’=p_2-p_{1y}’= 6 — 4 = 2text{ кг·м/c}]
Ответ: 2
Снаряд, выпущенный вертикально вверх, мгновенно разрывается в высшей точке траектории на два осколка, массы которых (m) и (4m). Скорость лѐгкого осколка сразу после взрыва (upsilon_1=500) м/с. Найдите скорость (upsilon_2) второго осколка сразу после взрыва.
Суммарный импульс снаряда до взрыва равен 0 (так как взрыв происходит в наивысшей точки траектории), следовательно сразу после взрыва суммарный импульс тоже равен 0: [0=vec{p_1}+vec{p_2}] где (p_1) и (p_2) – это импульс первого и второго осколка. Найдем скорость второго осколка: [mupsilon_1=4mupsilon_2] [upsilon_2=frac{upsilon_1}{4}=frac{500}{4}=125 text{ м/с}]
Ответ: 125

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
|
Под действием постоянной силы, равной по модулю 6 Н, импульс тела изменился на 30 кг·м/с. Сколько времени потребовалось для этого? |
||
|
1) |
0,5 с |
|
|
2) |
5 с |
|
|
3) |
36 с |
|
|
4) |
180 с |
Навстречу друг другу летят шарики из пластилина. Модули их импульсов равны соответственно 510–2 кгм/с и 310–2 кгм/с. Столкнувшись, шарики слипаются. Импульс слипшихся шариков равен
1)
810–2 кгм/с
2)
410–2 кгм/с
3)
210–2 кгм/с
4)
10–2 кгм/с
Санки после толчка движутся по горизонтальной дорожке. Как изменится модуль импульса санок, если на них в течение 5 с действует сила трения о снег, равная 20 Н?
1)
ответить невозможно, так как неизвестна масса санок
2)
увеличится на 4 Н/с
3)
увеличится на 100 кгм/с
4)
уменьшится на 100 кгм/с
Шары одинаковой массы движутся так, как показано на рисунке, и абсолютно неупруго соударяются. Как будет направлен импульс шаров после соударения?
1)
2)
3)
4)
На неподвижный бильярдный шар налетел другой – такой же. После удара шары разлетелись под углом 90 так, что импульс одного Р1 = 0,3 кгм/с, а другого Р2 = 0,4 кгм/с (см. рисунок). Налетевший шар имел до удара импульс, равный
1)
0,1 кгм/с
2)
0,5 кгм/с
3)
0,7 кгм/с
4)
0,25 кгм/с
Ракета, состоящая из двух ступеней, двигалась со скоростью 0 = 6 км/с (рис. А). Первая ступень после отделения движется со скоростью 1 = 2 км/с (рис. Б). Масса первой ступени m1 = 1103 кг, масса второй m2 = 2103 кг. Вторая ступень после отделения первой имеет скорость
1)
2 км/с
2)
4 км/с
3)
6 км/с
4)
8 км/с
Если на вагонетку массой m, движущуюся по горизонтальным рельсам со скоростью v, сверху вертикально опустить груз, масса которого равна половине массы вагонетки, то скорость вагонетки с грузом станет равной
1)
2/3v
2)
3/2v
3)
1/2v
4)
1/4v
С балкона высотой 20 м упал на землю мяч массой 0,2 кг. Из-за сопротивления воздуха скорость мяча у земли оказалась на 20% меньше скорости тела, свободно падающего с высоты 20 м. Импульс мяча в момент падения равен
1)
4,0 кгм/с
2)
4,2 кгм/с
3)
3,2 кгм/с
4)
6,4 кгм/с
Шар массой 200 г падает с начальной скоростью 10 м/с на неподвижную, горизонтально расположенную платформу, под углом 45 к ней. Модуль изменения импульса шара в результате абсолютно упругого удара шара о платформу равен
1)
0 кгм/с
2)
2 кгм/с
3)
4 кгм/с
4)
2√2 кгм/с
На экране монитора в Центре управления полетов отображены графики скоростей двух космических аппаратов после их расстыковки (см. рис.). Масса первого из них равна 10 т, масса второго равна 15 т. С какой скоростью двигались аппараты перед их расстыковкой?

1)
2103 м/с
2)
7,4103 м/с
3)
1103 м/с
4)
7,6103 м/с
Две тележки движутся вдоль одной прямой в одном направлении. Массы тележек m и 2m, скорости – соответственно 2v и v. Какой будет их скорость после абсолютно неупругого столкновения?
1)
3/4v
2)
2/3v
3)
3v
4)
1/3v
После пережигания нити первая тележка, масса которой равна 0,6 кг, стала двигаться со скоростью 0,4 м/с (см. рисунок). С какой по модулю скоростью начала двигаться вторая тележка, масса которой равна 0,8 кг?
1)
0,2 м/с
2)
0,3 м/с
3)
0,4 м/с
4)
0,6 м/с
Тело массой 2 кг движется вдоль оси ОХ. Его координата меняется в соответствии с уравнением х = А +Bt + Ct2, где А = 2 м, В = 3 м/с, С = 5 м/с2. Чему равен импульс тела в момент времени t = 2 c?
1)
86 кгм/с
2)
48 кгм/с
3)
46 кгм/с
4)
26 кгм/с
Шар массой 200 г падает с начальной скоростью 10 м/с на неподвижную платформу под углом 45 к ней. Какой импульс будут иметь шар и платформа в результате абсолютно неупругого удара шара о платформу, если платформа может скользить по горизонтальной поверхности без трения?
1)
0 кгм/с
2)
2 кгм/с
3)
√2 кгм/с
4)
2√2 кгм/с
Два автомобиля одинаковой массы m движутся со скоростями v и 2v относительно Земли в противоположных направлениях. Чему равен модуль импульса второго автомобиля в системе отсчета, связанной с первым автомобилем?
1)
3mv
2)
2mv
3)
mv
4)
0
На сани, стоящие на гладком льду, с некоторой высоты прыгает человек массой 50 кг. Проекция скорости человека на горизонтальное направление в момент соприкосновения с санями 4 м/с. Скорость саней с человеком после прыжка составила 0,8 м/с. Какова масса саней?
1)
150 кг
2)
200 кг
3)
250 кг
4)
400 кг
На стоящие на горизонтальном льду сани массой 200 кг с разбега запрыгивает человек массой 50 кг. Скорость саней после прыжка составила 0,8 м/с. Какова проекция скорости человека на горизонтальное направление в момент касания саней?
1)
1 м/с
2)
8 м/с
3)
6 м/с
4)
4 м/с
Тело движется по прямой. Под действием постоянной силы величиной 4 Н за 2 с импульс тела увеличился и стал равен 20 кгм/с. Первоначальный импульс тела равен
1)
4 кгм/с
2)
8 кгм/с
3)
12 кгм/с
4)
28 кгм/с
На рисунке изображены графики изменения скорости двух взаимодействующих тележек разной массы (одна тележка догоняет и толкает другую). Какую информацию о тележках содержат эти графики?
1)
тележка 1 едет сзади и имеет бóльшую массу
2)
тележка 1 едет сзади и имеет меньшую массу
3)
тележка 2 едет сзади и имеет бóльшую массу
4)
тележка 2 едет впереди и имеет меньшую массу
Когда твои ученики учатся в ЗФТШ — считай, ты тоже там учишься. Что, кстати, очень полезно, ибо задачи олимпиадные, сложненькие.
Задача 1.
Материальная точка массой кг движется в однородном силовом поле. В некоторый момент времени ее скорость
м/с. В результате действия неизменной по величине и направлению силы
вектор импульса материальной точки за время
с повернулся на угол
и стал равен по величине начальному. Найдите величину
силы, действующей в однородном поле на материальную точку.
Решение. Так как вектор импульса повернулся на , то изменение импульса — вектор, равный разности конечного и начального – равен
Так как импульс силы
То
Ответ: Н.
Задача 2.
Снаряд массой кг, выпущенный со скоростью
м/с под углом
к горизонту, через
c разрывается на осколки. Через какое время
после разрыва снаряда суммарный импульс
осколков будет направлен горизонтально, если известно, что все осколки еще находятся в полете? Найдите модуль
импульса в этот момент времени. Силы сопротивления воздуха, действующие на снаряд и осколки, не учитывайте.
Решение. Выясним, в какой точке траектории находился снаряд через 10 с. Его вертикальная составляющая скорости равна
Она станет равной нулю в наивысшей точке подьема:
Итак, снаряд к наивысшей точке должен был лететь 20 с. И там, в этой точке, вектор его импульса стал бы горизонтальным – потому что у снаряда осталась бы только горизонтальная составляющая скорости. Таким образом, даже несмотря на то, что снаряд разорвался, суммарный импульс его осколков станет горизонтальным через 20 с после выстрела, или через 10 с после разрыва. В этот момент времени скорость снаряда была бы равна . А импульс был бы равен
— таким и будет суммарный импульс всех его осколков.
Ответ: 10 с, кг
м/с.
Задача 3.
Два свинцовых шарика одинаковой массы, летящие со скоростями м/с и
м/с, слипаются в результате абсолютно неупругого удара. Скорости шариков перед слипанием взаимно перпендикулярны.
Решение. Суммарный импульс шариков равен
Так как шарики слиплись, их общая масса , а значит, скорость равна 50 м/c.
Теперь выясним вопрос с температурой. Запишем закон сохранения энергии
С другой стороны,
Здесь 130 Дж/кг град – теплоемкость свинца.
Ответ: м/с,
.
Задача 4.
Движущаяся по гладкой горизонтальной поверхности шайба налетает на покоящуюся шайбу. После абсолютно упругого центрального удара шайбы движутся со скоростями, отличающимися по абсолютной величине в раза. Найдите отношение
масс покоившейся и налетевшей шайб.
Решение. Записываем закон сохранения импульса:
И закон сохранения энергии (удар – упругий):
Из закона сохранения импульса имеем:
А из ЗСЭ получаем
Разделим теперь второе на первое:
Откуда
Ответ: .
Задача 5.
Шайба, скользящая по гладкой горизонтальной поверхности, сталкивается с такой же по массе покоящейся шайбой. В результате абсолютно упругого соударения вектор скорости налетающей шайбы повернулся на угол . Под каким углом
к направлению движения налетающей шайбы будет двигаться вторая шайба?
Решение. Так как в сумме два вектора обеих шайб после удара должны давать первоначальный импульс налетающей шайбы, то можно сделать вывод, что импульс второй шайбы будет направлен под углом к направлению движения налетающей шайбы – так, чтобы три вектора образовали прямоугольный треугольник.
К задаче 5
Ответ: .
Закон сохранения импульса.
Алгоритм решения задач на закон сохранения импульса:
- Записать краткое условие задачи.
- Перевести единицы измерения в систему СИ.
- Выбрать систему отсчёта.
- Считать систему тел замкнутой.
- Нарисовать тела до взаимодействия и после, учитывая упругий удар или неупругий, указывая направления их скоростей.
- Выбрать оси координат.
- Записать Закон сохранения импульса в векторной форме.
- Спроецировать Закон сохранения импульса на оси координат.
- Решить систему уравнений.
- Оценить полученный результат.
Проверьте свои знания, пройдя Тренировочный тест по Законам Сохранения
Примеры решения задач
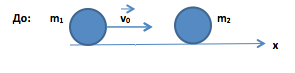
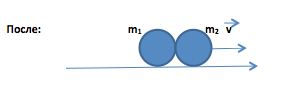
С2. Свинцовый шар массой 500 г, движущийся со скоростью 0, 6 м/с, сталкивается с неподвижным шаром из воска массой 100 г, после чего оба шара движутся вместе. Определите кинетическую энергию шаров после удара.
Решение: В инерциальной системе отсчёта, связанной с Землёй, считая систему тел замкнутой.
Закон сохранения импульса:
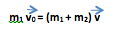
Проекция на ось Х:
m1v0 = (m1 + m2) v ;
Ответ: Е= 0,075 Дж
Закон сохранения энергии.
Алгоритм решения задач на закон сохранения энергии:
- Записать краткое условие задачи.
- Перевести единицы измерения в систему СИ.
- Выбрать систему отсчёта.
- Определить начальное и конечное положения тел, а так же, если необходимо, то промежуточные положения, о которых идёт речь в задаче.
- Выбрать нулевой уровень потенциальной энергии.
- Если на тела действуют только потенциальные силы, записать закон сохранения механической энергии: Е1= Е2. Если в системе тел действуют также и непотенциальные силы, то закон сохранения энергии записать в следующем виде: ΔЕ = Е2 — Е1 = А , где А А — работа непотенциальных сил.
- Выразить неизвестное.
- Произвести расчёт численного значения и единиц измерения.
- Оценить полученный результат.
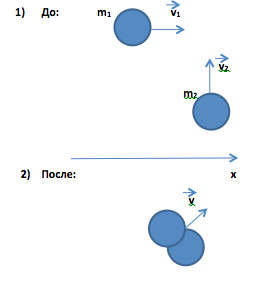
С2. Два пластилиновых шарика массами по 50 г движутся с одинаковыми по модулю скоростями 0,8 м/с, направленными под углом 90˚ друг к другу. Какая часть энергии перейдёт в тепло при абсолютно неупругом ударе?
Решение:
В инерциальной системе отсчёта, считая систему
замкнутой. Закон сохранения импульса:
Энергия системы до удара: Е1 = m1v12/2 + m2v22/2 ; E1 = 0,032 Дж
Энергия системы после удара: Е2 = (m1+m2) v2/2 ; E2 = 0,016 Дж
Количество теплоты, выделенное при ударе:
Q = E1— E2 ; Q = 0,016 Дж
Часть энергии, перешедшая в тепло после удара: Q/E1= 0,5
Ответ: 50%
Типичные ошибки в задачах на применение законов сохранения энергии, а также энергии и импульса:
- Неверное представление об импульсе и его изменении, носящих векторный характер.
- При неупругом столкновения не выполняется закон сохранения механической энергии. В этом случае следует применять закон сохранения импульса.
- Работа равнодействующей всех сил равна изменению кинетической энергии, произошедшему под действием этой силы.
- При выборе ответа полагаться только на физические законы, а не на интуицию.
- Применение закона сохранения энергии в совокупности с анализом графиков.