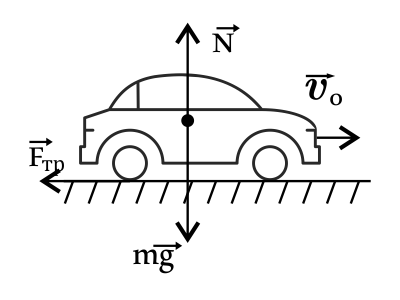
Силы в природе, законы Ньютона. Закон всемирного тяготения, закон Гука, сила трения
В. З. Шапиро
Второе задание ЕГЭ по физике проверяет знания по разделу «Динамика». Это задание базового уровня сложности, без возможности выбора ответа. Для его решения необходимо знать законы Ньютона, формулы, которые выражают силу тяжести, силу всемирного тяготения, силу упругости, вес тела, силу трения, силу реакции опоры на горизонтальной поверхности и на наклонной плоскости. Во многих задачах применяется одна и та же формула, но в различных ситуациях. Как правило, необходимо составить и решить систему из двух уравнений.
Применение закона всемирного тяготения
Необходимая теория: Сила тяготения
1. Две звезды одинаковой массы m притягиваются друг к другу с силами, равными по модулю F. Во сколько раз больше будет модуль сил притяжения между другими двумя звёздами, если расстояние между их центрами в два раза больше, а массы звёзд равны 2m и 3m?
Ответ: в _________________________ раз(а).
В этой задаче необходимо записать формулу закона всемирного тяготения для двух случаев:
(1).
(2).
Разделив (2) на (1), получим:
Ответ: в 1,5 раза.
Подобные задачи проверяют знания основных физических формул. Их необходимо записать в общем виде и в случае, когда происходит изменение какой-либо физической величины. Полученную систему уравнений решаем любым удобным способом. Задания такого типа часто встречаются в различных разделах курса физики.
Применение II закона Ньютона
Необходимая теория: Второй и третий законы Ньютона
2. На рисунке показаны силы (в заданном масштабе), действующие на материальную точку. Сторона клетки соответствует 1 Н. Определите модуль равнодействующей сил, приложенных к телу.
Равнодействующая сила равна геометрической сумме сил, приложенных к телу.
Следующий шаг – найти сумму проекций сил на оси OX и OY.
Сумма проекций сил на ось OX равна:
Сумма проекций сил на вертикальную ось равна:
По теореме Пифагора, модуль равнодействующей силы определяется:
Ответ: 2 Н.
Секрет решения: Многие задачи по динамике требует прочных знаний по геометрии. Теорема Пифагора, а также соотношения в прямоугольном треугольнике являются обязательными инструментами для тех, кто собирается сдавать экзамен по физике.
Применение формулы силы упругости (закон Гука)
Необходимая теория: Сила упругости
3. Подвешенная к потолку пружина под действием силы 5 Н удлинилась на 10 см. Чему равно удлинение этой пружины под действием силы 8 Н?
Ответ: ___________________________ см.
Запишем формулу закона Гука для двух случаев:
(1)
(2)
Разделим (2) на (1).
(м).
Ответ: 16 см.
Задача решается стандартным применением физической формулы для двух случаев. Обратите внимание на единицы измерения, которые требуются в ответе.
Применение формул для силы реакции опоры и силы трения
Необходимая теория: Сила трения
4. Тело движется по горизонтальной плоскости. Нормальная составляющая силы воздействия тела на плоскость равна 40 Н, сила трения равна 10 Н. Определите коэффициент трения скольжения.
Ответ: ___________________________.
Общая формула для силы трения имеет вид:
где N — сила реакции опоры.
Отсюда коэффициент трения можно выразить
Проведем расчет:
Ответ: 0,25.
Секрет решения: Помним, что коэффициент трения находится в интервале от 0 до 1. Это поможет вам более уверенно решать задачи на расчет коэффициента трения.
Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Задание 2 ЕГЭ по физике» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
09.03.2023
В результате выполнения задания 2 ЕГЭ по физике проверяются следующие требования/умения:
Коды проверяемых требований к уровню подготовки (по кодификатору):
Читать подробнее…
Коды проверяемых элементов содержания (по кодификатору):
Уровень сложности задания:
Максимальный балл за выполнение задания:
Примерное время выполнения задания выпускником, изучавшим предмет:
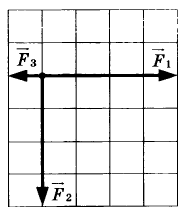
На рисунке представлены три вектора сил, приложенных к одной точке и лежащих в одной плоскости. Модуль вектора силы F1 равен 4 Н. Чему равен модуль равнодействующей векторов F1, F2, F3?
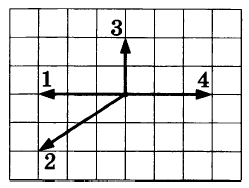
На рисунке представлены четыре вектора сил, действующих на тело. С исключением какой из четырёх сил ускорение тела будет равно нулю? В ответе укажите номер вектора этой силы.
Пружина жесткости k = 104 Н/м одним концом прикреплена к неподвижной опоре, а к другому ее концу приложили силу F = 1000 Н. Определите растяжение пружины.
Лифт движется вверх с ускорением 2 м/с2, в нем находится пассажир массой 50 кг. Чему равен модуль силы тяжести, действующей на пассажира?
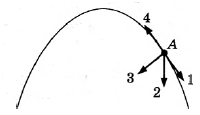
На рисунке показана траектория движения тела, брошенного под некоторым углом к горизонтальной поверхности Земли. В точке А этой траектории направление вектора скорости обозначено стрелкой 1; траектория движения тела и все векторы лежат в плоскости, перпендикулярной поверхности Земли. Сопротивление воздуха пренебрежимо мало. Какое направление имеет вектор ускорения
тела в системе отсчёта Земля? В ответе укажите номер соответствующей стрелки.
В инерциальной системе отсчета сила $$oversetrightharpoonup F$$ сообщает телу массой m ускорение, равное по модулю 8 м/с2. Чему равен модуль ускорения тела массой 2m под действием силы $$frac{oversetrightharpoonup F}2$$ в этой системе отсчета?
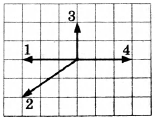
На рисунке представлены четыре вектора сил, действующих на тело. С исключением какой из четырёх сил ускорение тела будет равно нулю? В ответе укажите номер вектора этой силы.
Под действием одной силы $$vec{F_1}$$ тело движется с ускорением 4 м/с2. Под действием другой силы $$vec{F_2}$$, направленной противоположно силе $$vec{F_1}$$, ускорение тела равно 3 м/с2. С каким ускорением будет двигаться тело при одновременном действии сил $$vec{F_1}$$ и $$vec{F_2}$$ ?
В инерциальной системе отсчета сила $$oversetrightharpoonup F$$ сообщает телу массой m ускорение, равное по модулю 2 м/с2. Чему равен модуль ускорения тела массой $$frac m2$$ под действием силы 2$$oversetrightharpoonup F$$ в этой системе отсчета?
Среднее расстояние между центрами Луны и Земли примерно 60 земных радиусов. Во сколько раз уменьшится сила гравитационного взаимодействия предмета массой 1 кг и Земли, если сначала предмет находится на поверхности Земли, а затем на лунной орбите?
Ответ: в____________раз
За это задание ты можешь получить 1 балл. Уровень сложности: базовый.
Средний процент выполнения: 76.3%
Ответом к заданию 2 по физике может быть целое число или конечная десятичная дробь.
Разбор сложных заданий в тг-канале
Задачи для практики
Задача 1
Автомобиль массой 4 т движется со скоростью 36 км/ч. Какой путь прошёл автомобиль до полной остановки, если коэффициент трения колёс о дорогу равен 0,3? Движение считать равнозамедленным. Ответ выразите в (м). Ответ округлите до десятых
Решение
Дано:
$m=4000$кг
$μ=0.03$
$g=10м/с^2$
$υ_0=36=10$м/с
$υ_к=0$
$А-?$
Решение:
Работа силы трения равна: $A_{F_{тр}}=∆E_к$(1), где $A_{F_{тр}}=F_{тр}·S=μNS=μmgS$(2), где $S$ — путь автомобиля до полной остановки. $∆E_к={mυ_к^2}/{2}-{mυ_0^2}/{2}=-{mυ_0^2}/{2}$(3). Знак «минус» опустим так как он говорит, что сила трения направлена в сторону, противоположную движению, тогда имеем: $μmgS={mυ_0^2}/{2}⇒S={υ_0^2}/{2μg}={100}/{6}=16.66=16.7$м.
Ответ: 16.7
Задача 2
Пружину, жёсткость которой равна 1 · 104 Н/м, сжали с силой 400 Н. Вычислите потенциальную энергию, запасённую пружиной. Ответ выразите в (Дж).
Решение
Дано:
$k=10^4$Н/м
$F=400$Н
$E_{п}-?$
Решение:
Запишем закон Гука: $F=kx$(1), где $x$ — удлинение (в нашем случае, сжатие) пружины, $k$ — жесткость пружины. Откуда: $x={F}/{k}={400}/{10^4}=0.04$м(2).
Потенциальная энергия сжатой пружины определяется выражением: $E_{п}={kx^2}/{2}={10^4·16·10^{-4}}/{2}=8$Дж.
Ответ: 8
Задача 3
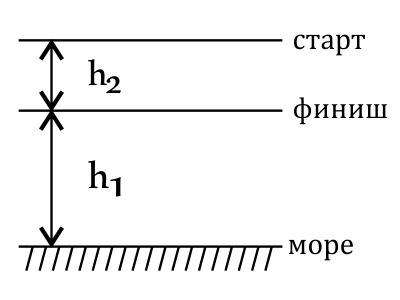
Точка финиша трассы горнолыжных соревнований находится на высоте 2 км над уровнем моря, а точка старта — на высоте 400 м над точкой финиша. Чему равна потенциальная энергия лыжника на старте относительно уровня моря? Масса лыжника 70 кг. Ответ выразите в (МДж).
Решение
Дано:
$m=70$кг
$g=10м/с^2$
$h_1=2000$м
$h_2=400$м
$E_{п}-?$
Решение:
Потенциальная энергия лыжника на старте относительно уровня моря по определению равна: $E_{п}=mg(h_1+h_2)=70·10·(2000+400)=700·2400=1680000=1.68$МДж.
Ответ: 1.68
Задача 4
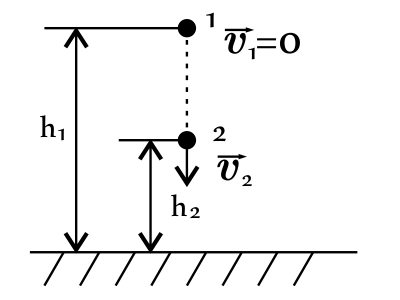
Тело массой 2 кг начинает свободно падать с высоты 5 м. Чему равна кинетическая энергия тела на высоте 2 м от земли? Ответ выразите в (Дж).
Решение
Дано:
$m=2$кг
$g=10м/с^2$
$h_1=5$м
$h_2=2$м
$E_{к_2}-?$
Решение:
Полная механическая энергия тела в точке 1 равна полной механической энергии тела в точке 2: $E_1=E_2$(1), где $E_1=E_{п_1}+E_{к_1}=mgh_1+{mυ_1^2}/{2}=mgh_1$(2), $E_2=E_{п_2}+E_{к_2}=mgh_2+E_{к_2}$(3).
Подставим (2) и (3) в (1) и найдем $E_{к_2}:mgh_1=mgh_2+E_{к_2}$, откуда $E_{к_2}=mg(h_1-h_2)$(4).
Подставим числовые значения в (4), получим: $E_{к_2}=2·10·(5-2)=60$Дж.
Ответ: 60
Задача 5
Материальная точка массой 4,6 кг равномерно движется по окружности. Чему равна её скорость, если изменение её импульса за два с половиной периода составило 18,4 кг·м/с? Ответ выразить в (м/с).
Решение
Дано:
$m=4.6$кг
$t=2.5T$
$Δp↖{→}=18.4кгм/с$
$υ-?$
Решение:
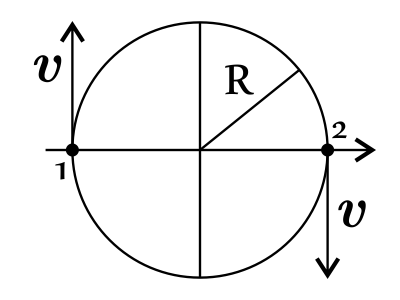
Исходя из рисунка $p_1$ и $p_2$ противонаправлены, тогда: $υ={Δp↖{→}}/{2·m}={18.4}/{2·4.6}=2м/с$
Ответ: 2
Задача 6
Падение тела массой 2 кг с некоторой высоты занимает 10 с. Найдите кинетическую энергию, которой будет обладать тело при падении на землю. Ответ выразите в (кДж).
Решение
Дано:
$m=2$кг
$t=10$с
$E_к-?$
Решение:
1) $E_к=E_n=mgh$ по закону сохранения
2) $S=H={gt^2}/{2}={10·100}/{2}=500$м
$E_n=mgh=2·10·500=10$кДж
Ответ: 10
Задача 7
Тело подбросили вертикально вверх с начальной скоростью 6 м/с. На какой высоте кинетическая энергия тела будет в два раза больше его потенциальной энергии? Ответ выразите в (м).
Решение
Дано:
$υ_0=6$м/с
$E_к=2·E_n$
$h-?$
Решение:
${table.{mυ_0^2}/{2}=E’_к+E’_n; .{E_к}/{2}=E_n;$
$⇒{mυ_0^2}/{2}=3E_n⇒{υ_0^2}/{2}=3gh$.
$h={υ_0^2}/{2g·3}={36}/{60}=0.6$м
Ответ: 0.6
Задача 8
На покоящуюся тележку массой 0,2 т налетает тележка массой 0,3 т со скоростью 8 км/ч . Найдите скорость, с которой эти тележки начали двигаться совместно после удара. Ответ выразите в (км/ч).
Решение
Дано:
$m_1=200$кг
$m_2=300$кг
$υ_1=8{км}/ч$
$υ_2-?$
Решение:
По закону сохранения энергии $m_1·0+m_2·υ_1=(m_1+m_2)υ_2$ выразим: $υ_2={m_2·υ_1}/{m_1+m_2}={300·8}/{200+300}=4.8{км}/ч$
Ответ: 4.8
Задача 9
Найдите, чему равно отношение масс большего тела к меньшему, если до абсолютного неупругого столкновения они двигались навстречу друг другу со скоростями 10 м/с каждое, а после — со скоростью 5 м/с.
Решение
Дано:
$υ_1=10м/с$
$υ_2=5м/с$
${M}/{m}-?$
Решение:
Запишем закон сохранения импульсов: $M·υ_1-m·υ_1=(M+m)υ_2$.
$10·M-10·m=5M+5m$
$5M=15m; {M}/{m}={15}/{5}=3$
Ответ: 3
Задача 10
Санки массой 50 кг из состояния покоя съезжают с гладкой наклонной плоскости высотой 5 м. После этого они продолжают двигаться по горизонтальной поверхности и спустя некоторое время останавливаются. Как при этом изменилась их механическая энергия? В ответе запишите: уменьшилась на _ (кДж).
Решение
Дано:
$m=50$кг
$h=5$м
$∆E_m-?$
$m_0=1·10^{-6}$кг
Решение:
По закону сохранения $∆E_m=∆E_h+∆E_к; ∆E_к=0$
$∆E_r=mgh=50·5·10=2.5$кДж. Тогда $∆E_{мех}=∆E_n=2.5$кДж.
Ответ: 2.5
Задача 11
Тела 1 и 2 взаимодействуют только друг с другом. Изменение кинетической энергии тела 1 за некоторый промежуток времени равно 15 Дж. Работа, которую совершили за этот же промежуток времени силы взаимодействия тел 1 и 2, равна 45 Дж. Чему равно изменение кинетической энергии тела 2 за это время? Ответ выразить в (Дж).
Решение
Дано:
$∆E_1=15$Дж
$∆E_в=45$Дж
$∆E_2-?$
Решение:
По закону сохранения энергии запишем уравнение взаимодействия: $∆E_1+∆E_2=∆E_в⇒∆E_2=∆E_в-∆E_1$
$∆E_2=45-15=30$Дж
Ответ: 30
Задача 12
Мальчик столкнул санки массой 2 кг с вершины горки. Сразу после толчка санки имели скорость 4 м/с, а у подножия горки она равнялась 8 м/с. Трение санок о снег пренебрежимо мало. Какова высота горки? Ответ выразите в (м).
Решение
Дано:
$υ_0=4$м/с
$υ_к=8$м/с
$F_{тр}=0$
$H-?$
Решение:
Запишем закон сохранения энергии для данного случая $E_{к_0}+E_п=E_к^к$. $E_{к_0}$ — кинетическая энергия в начальный момент; $E_п$ — потенциальная энергия в начальный момент; $E_к^к$ — кинетическая энергия в конце пути.
$E_п=E_к^к-E_{к_0}$
$mgH={m·υ_к^2}/{2}-{m·υ_0^2}/{2}$
$2·10·H=64-16⇒H=2.4$м
Ответ: 2.4
Задача 13
Легковой автомобиль и грузовик движутся со скоростями 108 км/ч и 72 км/ч соответственно. Масса грузовика 4500 кг. Какова масса легкового автомобиля, если импульс грузовика больше импульса легкового автомобиля в 2 раза? Ответ выразите в (кг).
Решение
Дано:
$υ_л=108$км/ч$=30м/с$
$υ_г=72$км/ч$=20м/с$
$m_г=4500кг$
$p_г=2p_л$
$m_л-?$
Решение:
По определению импульс тела равен: $p=mυ$(1), тогда $p_г=m_г·υ_г$(2) — импульс грузового автомобиля; $p_л=m_л·υ_л$(2) — импульс легкового автомобиля. По условию задачи: $p_г=2p_л$(4). Подставим (2) и (3) в (4): $m_г·υ_г=2m_лυ_л⇒m_л={m_г·υ_г}/{2υ_л}$(5). Подставим числовые значения в (5): $m_л={4500·20}/{30·2}=1500кг$.
Ответ: 1500
Задача 14
Автомобиль массой 1 т двигался со скоростью 72 км/ч. Максимальное значение коэффициента трения шин о дорожное покрытие равно 0,7. Каков минимальный тормозной путь автомобиля? Ответ округлите до целых. Ответ выразите в (м).
Решение
Дано:
$m=1000$кг
$υ=72км/ч=20м/с$
$g≈10м/c^2$
$μ_{max}=0.7$
$S_{min}-?$
Решение:
Работа силы трения равна изменению кинетической энергии автомобиля: $A_{F_{тр}}=∆E_к$(1), где $A_{F_{тр}}=F_{тр}·S_{min}·cos180°$(2). $∆E_к=0-{mυ^2}/{2}=-{mυ^2}/{2}$(3), т.к. автомобиль останавливается; $cos180°=-1$
$F_{тр}=μ_{max}·N=μ_{max}·mg$(4).
Подствим (2), (3), (4) в выражение (1): $-μ_{max}·mg·S_{min}=-{mυ^2}/{2}⇒S_{min}={υ^2}/{2μ_{max}·g}$(5)
$S_{min}={400}/{2·0.7·10}=28.57м=29м$
Ответ: 29
Задача 15
Ученик исследовал зависимость силы упругости F пружины от её растяжения x и получил следующие результаты:
| F, H | 0 | 0,5 | 1 | 1,5 | 2 | 2,5 |
| x, см | 0 | 2 | 4 | 6 | 8 | 10 |
По данным опыта определите, какую работу нужно совершить, чтобы растянуть пружину от 4 см до 8 см. Ответ выразите в (Дж).
Решение
Дано:
$x_1=4см=4·10^{-2}м$
$x_2=8см=8·10^{-2}м$
$A-?$
Решение:
Работа силы упругости пружины равна убыли ее потенциальной энергии: $A={kx_1^2}/{2}-{kx_2^2}/{2}$(1), где $k$ — жесткость пружины.
Найдем жесткость пружины $k$. Для этого возьмем любые значения силы упругости пружины и растяжения, отличные от нуля, например, $F_{тр}=1H, x=0.04м$. Тогда, по закону Гука имеем: $F_{упр}=kx⇒k={F_{упр}}/{х}$(2). $k={1}/{0.04}=25Н/м$
Подставим числовые значения в (1) и найдем работу $A$: $A={25}/{2}((4·10^{-2})^2-(8·10^{-2})^2)=12.5·(16·10^{-4}-64·10^{-4})=-600·10^{-4}=-0.06$Дж.
Зная, что «минус» говорит о том, что при растяжении сила упругости направлена противоположно растяжению пружины.
Ответ: 0.06
Задача 16
Шарик массой 100 г налетает со скоростью 2 м/с на покоящийся шар такой же массы. Каков импульс системы шаров после абсолютно неупругого удара? Ответ выразите в (кг·м/с).
Решение
Дано:
$m_1=m_2=m=0.1кг$
$υ_1=2{м}/{с}; υ_2=0{м}/{с}$
$p-?$
Решение:
По закону сохранения импульса: импульс системы до взаимодействия равен импульсу системы после взаимодействия: $p=p_1+p_2=m_1·υ_1+m_2·υ_2=m_1υ_1=0.1·2=0.2{кг·м}/{с}$
Ответ: 0.2
Задача 17
Кинетическая энергия равномерно движущегося тела массой 200 г равна 10 Дж. С какой скоростью движется тело? Ответ выразите в (м/с).
Решение
Дано:
$m=200г=0.2кг$
$Е_к=10Дж$
$υ-?$
Решение:
Кинетическая энергия определяется выражением:$Е_к={mυ^2}/{2}$(1), откуда выразим скорость $υ: $.
Учитывая, что $mυ^2=2Е_к$, $υ^2={2E_к}/{m}$, $υ=√{{2E_к}/{m}}$(2).
Подставим числовые значения в (2): $υ^2=√{{2·10}/{0.2}}=√{100}=10{м}/{с}$
Ответ: 10
Задача 18
Тело массой 200 г, двигаясь равномерно, обладает импульсом 4 кг·м/с. Какова его кинетическая энергия? Ответ выразите в (Дж).
Решение
Дано:
$m=200г=0.2кг$
$p=4{кг·м}/{с}$
$Е_к-?$
Решение:
Импульс по определению равен: $p=mυ$(1), а кинетическая энергия определяется выражением:$Е_к={mυ^2}/{2}$(2).
Учитывая, что $mυ^2={m^2υ^2}/{m}={(mυ)^2}/{m}={p^2}/{m}$(3), подставим (3) в (2): $Е_к={p^2}/{2m}$(4).
Подставим числовые значения в (4): $Е_к={4^2}/{2·0.2}={16}/{0.4}=40$Дж
Ответ: 40
Рекомендуемые курсы подготовки
Задача 1
В цистерне поливочной автомашины массой 4 т находится 5 м3 воды. Чему равен импульс машины, когда она движется со скоростью 18 км/ч? Ответ выразите в (кг·м/с).
Задача 2
Материальная точка равномерно движется по окружности со скоростью 2 м/с. Чему равна её масса, если изменение её импульса при повороте на 45◦ составило 9,2 · √2 кг·м/с? Ответ вырази…
Задача 3
Два шарика движутся по гладкой горизонтальной плоскости вдоль осей Ox и Oy. Найдите модуль импульса второго шарика, если модуль импульса первого p1 = 1, 6 кг·м/с, а импульс системы…
Задача 4
Два шарика движутся по гладкой горизонтальной плоскости вдоль осей Ox и Oy с импульсами, равными по модулю p1 = 0,8 кг·м/с и p2 = 0,6 кг·м/с. Найдите модуль импульса системы этих ш…
Задача 5
На экране монитора в Центре управления полётом отображены графики скоростей многоступенчатой ракеты массой 50 т и одной из ступеней массой 10 т. Чему равна скорость отделившейся вт…
Задача 6
Зависимость скорости от времени для материальной точки массой 200 г задана на рисунке. Какова её кинетическая энергия в момент времени 2,5 с? Ответ выразите в (Дж).
Задача 7
Зависимость скорости от времени для материальной точки массой 200 г задана на рисунке. Каков её импульс в момент времени 2,5 с? Ответ выразите в (кг·м/с).
Задача 8
Небольшое тело массой 200 г движется равноускоренно, при этом его скорость меняется по закону v = 6−4t. Какова кинетическая энергия тела в момент времени 1 с? Ответ в Дж.
Задача 9
Небольшое тело массой 200 г движется равноускоренно, при этом его скорость меняется по закону v = 6+4t. Каков импульс силы, действующей на это тело, за первые 3 с? Ответ в H$·$с.
Задача 10
Мяч массой 200 г налетает на вертикальную стенку со скоростью 1 м/с под углом 30$°$ по отношению к стенке и упруго с ней соударяется. Какой импульс при этом приобретает стенка? Ответ…
Задача 11
Груз массой 300 г свободно падает с высоты 12 м с нулевой начальной скоростью. Какова кинетическая энергия груза на высоте 8 м относительно земли? Сопротивлением воздуха пренебречь…
Задача 12
Лебёдка равномерно поднимает груз массой 50 кг на высоту 4 м за 10 с. Какова мощность двигателя лебёдки? Ответ в Вт.
Задача 13
Какую среднюю мощность развивает сила, если тело массой 200 г под действием данной силы приобретает скорость 5 м/с за 10 с? Ответ в Вт.
Задача 14
Камень массой 100 г бросают с высоты 5м над землёй со скоростью 10 м/с, направленной вертикально вверх. Какое максимальное значение принимает потенциальная энергия камня относитель…
Задача 15
Камень массой 100 г бросают с высоты 5 м со скоростью 10 м/с, направленной вертикально вверх. Какова кинетическая энергия камня в наивысшей точке? Ответ в Дж.
Задача 16
Кинетическая энергия груза массой 500 г равна 100 Дж. С какой скоростью движется груз? Ответ в м/с.
Задача 17
Домохозяйка развешивала бельё на балконе 8 этажа и уронила прищепку. Определите скорость прищепки, когда она пролетала 5 этаж дома. Считать высоту этажа равной 2,5 м. Ответ укажите…
Задача 18
Пуля массой 20 г, летящая под углом 30$°$ к горизонту, попадает в брусок массой 4 кг, лежащей на гладком горизонтальном столе, и застревает в нём. Чему равна скорость бруска после по…
Задача 19
Чему равно изменение импульса материальной точки массой 2 кг, движущейся по окружности со скоростью 2 м/с за шестую часть периода? Ответ в кг$·$м/с.
Задача 20
Рельс длиной 25 м лежит на земле. Какую работу нужно совершить, чтобы приподнять рельс краном за один из его концов на высоту 1 м? Прогибом рельса пренебречь, каждый метр рельса им…
Задание 2 ЕГЭ по физике посвящено силам, действующим в природе на предметы, а также законам Ньютона. При этом вопросы задания в разных билетах отличаются своей разнообразностью.
Так, если учащемуся попадется тема «Второй закон Ньютона», ему придется вычислять вес предмета, силу натяжения нитей, а также импульс материальной точки, а если темой вопроса будет «Равнодействующая», то и вопрос будет посвящен всему, что связано с уравновешиванием действующих на тело сил. В этом случае учащийся будет вычислять модуль равнодействующей сил или значение одной из сил, действующих на тело.
Если темой задание 2 ЕГЭ по физике будет «Сила трения», то основными вопросами задачи будут «Чему равна сила трения?» или «Какую направленную силу нужно приложить, чтобы сдвинуть тело с места?». Тема «Сила тяжести» содержит в себе задачи, связанные преимущественно с падениями предметов, а тема «Сила упругости» — с поведением пружин в различных условиях. Еще один вариант задания № 2 ЕГЭ по физике – «Закон всемирного тяготения», и его задачи подразумевают, в основном, задачи на силу притяжения.
Второй вопрос экзаменационного билета требует краткого ответа, выраженного точным числом.
К однородному медному цилиндрическому проводнику длиной 40 м приложили разность потенциалов 10 В. Каким будет изменение температуры проводника DT через 15 с? Изменением сопротивления проводника и рассеянием тепла при его нагревании пренебречь. (Удельное сопротивление меди 1,7´10–8 Ом´м.)
На рисунке показана схема устройства для предварительного отбора заряженных частиц для последующего детального исследования. Устройство представляет собой конденсатор, пластины которого изогнуты дугой радиусом см. Предположим, что в промежуток между обкладками конденсатора из источника заряженных частиц (и. ч.) влетают ионы, как показано на рисунке. Напряжённость электрического поля в конденсаторе по модулю равна 5 кВ/м. Скорость ионов равна 105 м/с. При каком значении отношения заряда к массе ионы пролетят сквозь конденсатор, не коснувшись его пластин? Считать, что расстояние между обкладками конденсатора мало, напряжённость электрического поля в конденсаторе всюду одинакова по модулю, а вне конденсатора электрическое поле отсутствует. Влиянием силы тяжести пренебречь.
По прямому горизонтальному проводнику длиной 1 м с площадью поперечного сечения подвешенному с помощью двух одинаковых невесомых пружинок жёсткостью 100 Н/м, течёт ток
(см. рисунок).
Какой угол составляют оси пружинок с вертикалью после включения вертикального магнитного поля с индукцией
если абсолютное удлинение каждой из пружинок при этом составляет
? (Плотность материала проводника
)
В электрической цепи, показанной на рисунке, ЭДС источника тока равна 12 В, емкость конденсатора 2 мФ, индуктивность катушки 5 мГн, сопротивление лампы 5 Ом и сопротивление резистора 3 Ом.
В начальный момент времени ключ К замкнут. Какая энергия выделится в лампе после размыкания ключа? Внутренним сопротивлением источника тока, и проводов пренебречь.
Пылинка, имеющая массу и заряд
влетает в электрическое поле вертикального высокого конденсатора в точке, находящейся посередине между его пластинами (см. рисунок, вид сверху).
Чему должна быть равна минимальная скорость, с которой пылинка влетает в конденсатор, чтобы она смогла пролететь его насквозь? Длина пластин конденсатора 10 см, расстояние между пластинами 1 см, напряжение на пластинах конденсатора 5 000 В. Система находится в вакууме.
Плоская горизонтальная фигура площадью 0,1 м2, ограниченная проводящим контуром, имеющим сопротивление 5 Ом, находится в однородном магнитном поле. Проекция вектора магнитной индукции на вертикальную ось Оz медленно и равномерно возрастает от некоторого начального значения B1z до конечного значения B2z = 4,7 Тл. За это время по контуру протекает заряд Δq= 0,08 Кл. Найдите B1z.
В электрической схеме, показанной на рисунке, ключ К замкнут.
Заряд конденсатора ЭДС батарейки
её внутреннее сопротивление
сопротивление резистора
Найдите количество теплоты, которое выделяется на резисторе после размыкания ключа К в результате разряда конденсатора. Потерями на излучение пренебречь.
Тонкий алюминиевый брусок прямоугольного сечения, имеющий длину L = 0,5 м, соскальзывает из состояния покоя по гладкой наклонной плоскости из диэлектрика в вертикальном магнитном поле индукцией В = 0,1 Тл (см. рисунок). Плоскость наклонена к горизонту под углом a = 30°. Продольная ось бруска при движении сохраняет горизонтальное направление. Найдите величину ЭДС индукции на концах бруска в момент, когда брусок пройдёт по наклонной плоскости расстояние l = 1,6 м.
Проводящий стержень длиной l = 20 см движется поступательно в однородном магнитном поле со скоростью v = 1 м/с так, что угол между стержнем и вектором скорости = 30° (см. рисунок). ЭДС индукции в стержне равна 0,05 В. Какова индукция магнитного поля?
Как и во сколько раз изменится мощность, выделяющаяся на резисторе в цепи, схема которой изображена на рисунке, если перевести ключ К из положения 1 в положение 2? Параметры цепи:
На уроке физики школьник собрал схему, изображенную на рисунке. Ему было известно, что сопротивления резисторов равны и
Токи, измеренные школьником при помощи идеального амперметра А при последовательном подключении ключа К к контактам 1, 2 и 3, оказались равными, соответственно,
Чему было равно сопротивление резистора
?
В цепи, схема которой изображена на рисунке, вначале замыкают ключ а затем, спустя длительное время, ключ
Известно, что после этого через ключ
протек заряд, равный по модулю
Чему равна ЭДС
источника тока, если
? Источник считайте идеальным.
В цепи, изображённой на рисунке, сопротивление диода в прямом направлении пренебрежимо мало, а в обратном многократно превышает сопротивление резисторов. При подключении к точке А положительного полюса, а к точке В отрицательного полюса батареи с ЭДС 12 В и пренебрежимо малым внутренним сопротивлением потребляемая мощность равна 14,4 Вт. При изменении полярности подключения батареи потребляемая мощность оказалась равной 21,6 Вт. Укажите, как течёт ток через диод и резисторы в обоих случаях, и определите сопротивления резисторов в этой цепи.
В цепи, изображённой на рисунке, сопротивления резисторов равны между собой: R1= R2 = R3 = R. При разомкнутом ключе К через резистор R3 течёт ток I0 =1,4 А. Загорится ли лампа после замыкания ключа, если она загорается при силе тока I = 0,5 А? Сопротивление лампы в этом режиме Rл = 3R. Внутренним сопротивлением источника пренебречь, диод считать идеальным.
Решение
1. Из рисунка видно, что диод включен противоположно направлению тока. Так как диод идеальный, то ток через него и резистор не потечёт.
2. При разомкнутом ключе резисторы и
подключены последовательно, а значит, сила тока в этом случае по закону Ома равна
3. Когда ключ замыкают, лампа включается параллельно резистору а значит, сопротивление участка с параллельным соединением проводов будет:
Ток в цепи в этом случае:
Напряжение на параллельных участках одинаково и равно
Тогда через лампу будет проходить ток:
что меньше величины необходимого тока, а значит, лампа не загорится.
Задача 16
Одни и те же элементы соединены в электрическую цепь сначала по схеме 1, а затем по схеме 2 (см. рисунок). Сопротивление резистора равно R, сопротивление амперметра сопротивление вольтметра
Найдите отношение мощностей
выделяемых на резисторах в этих схемах. Внутренним сопротивлением источника и сопротивлением проводов пренебречь.
Решение
Пусть — сопротивление амперметра,
— сопротивление вольтметра,
— ЭДС источника. В схеме 1 напряжение на резисторе определяется с помощью закона Ома для замкнутой цепи:
где
— сопротивление участка цепи, содержащего резистор и вольтметр. Отсюда:
В схеме 2 с помощью закона Ома найдём силу тока через резистор:
Отношение мощностей
Задача 17
Маленький шарик с зарядом и массой 3 г, подвешенный на невесомой нити с коэффициентом упругости 100 Н/м, находится между вертикальными пластинами плоского воздушного конденсатора. Расстояние между обкладками конденсатора 5 см. Какова разность потенциалов между обкладками конденсатора, если удлинение нити 0,5 мм?
Решение
Условия равновесия:
Возведем оба равенства в квадрат и сложим их:
откуда
Напряженность электрического поля в конденсаторе:
Таким образом,
Задача 18
По П-образному проводнику постоянного сечения скользит со скоростью
медная перемычка
длиной
из того же материала и такого же сечения.
Проводники, образующие контур, помещены в постоянное однородное магнитное поле, вектор индукции которого направлен перпендикулярно плоскости проводников (см. рисунок). Какова индукция магнитного поля если в тот момент, когда
разность потенциалов между точками
и
равна
? Сопротивление между проводниками в точках контакта пренебрежимо мало, а сопротивление проводов велико.
Решение
При движении перемычки в ней возникает ЭДС
Закон Ома для замкнутой цепи :
где — сопротивление перемычки
Следовательно,
Задача 19
Два плоских конденсатора ёмкостью С и 2С соединили параллельно и зарядили до напряжения U. Затем ключ К разомкнули, отключив конденсаторы от источника (см. рисунок). Пространство между их обкладками заполнено жидким диэлектриком с диэлектрической проницаемостью ε. Какой будет разность потенциалов между обкладками, если из правого конденсатора диэлектрик вытечет?
Решение
В соответствии с определением понятия «ёмкость» для суммарного заряда конденсаторов имеем:
где 3С — суммарная ёмкость конденсаторов, когда оба они заполнены жидким диэлектриком. После вытекания диэлектрика из правого конденсатора суммарный заряд останется прежним. Так как для плоского конденсатора C~ε, то суммарная ёмкость станет равной (С + 2С/ε), а напряжение будет равно U1, так что
Решая систему уравнений (1) и (2), получим ответ:
Задача 20
Катод фотоэлемента с работой выхода освещается светом частотой
Вылетевшие из катода электроны попадают в однородное магнитное поле с индукцией
перпендикулярно линиям индукции этого поля. Чему равен максимальный радиус окружности R, по которой движутся электроны?
Решение
| № этапа | Содержание этапа решения | Чертёж, график, формула | Оценка этапа в баллах |
| 1 | Записано уравнение Эйнштейна для фотоэффекта: | 1 | |
| 2 | Записано уравнение, связывающее силу Лоренца, действующую на электрон, с величиной центростремительного ускорения:
Уравнение преобразовано к виду, устанавливающему связь между кинетической энергией электрона и радиусом орбиты: |
1 | |
| 3 | Решена система уравнений и получен ответ в алгебраической форме:
Подставлены значения констант и параметров и получен ответ в числовой форме: |
1 | |
| Максимальный балл | 3 |
Задача 21
В однородном магнитном поле, индукция которого протон движется перпендикулярно вектору магнитной индукции В по окружности радиусом 5 м. Определите скорость протона.
Решение
Из уравнения, связывающего на основе второго закона Ньютона силу Лоренца, действующую на протон, с модулем центростремительного ускорения: . Откуда выражаем искомую скорость.
Задача 22
К одному концу лёгкой пружины жёсткостью k = 100 Н/м прикреплён массивный груз, лежащий на горизонтальной плоскости, другой конец пружины закреплён неподвижно (см. рисунок). Коэффициент трения груза по плоскости Груз смещают по горизонтали, растягивая пружину, затем отпускают с начальной скоростью, равной нулю. Груз движется в одном направлении и затем останавливается в положении, в котором пружина уже сжата. Максимальное растяжение пружины, при котором груз движется таким образом, равно d = 15 см. Найдите массу m груза.
Решение
1. Начальная энергия системы равна потенциальной энергии растянутой пружины: После того, как пружину отпустили, она остановится в положении, при котором она сжата на величину
Тогда конечная энергия системы равна потенциальной энергии сжатой пружины:
Приращение полной энергии системы равно работе силы трения
где — модуль силы реакции опоры.
2. В момент, когда груз остановился, по второму закону Ньютона равнодействующая всех сил стала равна нулю. Пружина сжата, поэтому сила упругости пружины направлена вправо. Её уравновешивает сила трения покоя, которая направлена против возможного движения, причём эта сила максимальна, т. к. по условию начальное положение пружины соответствует максимальному растяжению пружины, при котором груз движется таким образом.
Запишем закон Ньютона для вертикальной и горизонтальной оси:
3. Подставим полученное выражение для в равенство из пункта 1:
После подстановки получим
Задача 23
Хорошо проводящая рамка площадью вращается в однородном магнитном поле с индукцией
перпендикулярной оси вращения рамки, с частотой
Скользящие контакты от рамки присоединены к цепи, состоящей из резистора сопротивлением
к которому последовательно присоединены два параллельно соединенных резистора сопротивлениями
и
(см. рис.). Найти максимальную силу тока, текущего через резистор
в процессе вращения рамки. Индуктивностью цепи можно пренебречь.
Решение
При вращении рамки в магнитном поле в ней возникает ЭДС индукции, равная, по закону электромагнитной индукции Фарадея,
(здесь — угловая частота вращения рамки).
В цепи из резисторов, присоединенной к рамке, под действием этой ЭДС возникает ток, равный, согласно закону Ома для полной цепи, где согласно формулам для сопротивления цепи, состоящей из последовательно и, параллельно соединенных резисторов,
Поскольку падение напряжения на параллельно соединенных резисторах и
одинаково, по закону Ома для участка цепи
причем в точке разветвления тока
Из всех записанных уравнений следует, что
откуда искомая максимальная сила тока равна, очевидно,
Подставляя числовые данные и проверяя размерность, получаем:
Задача 24
На двух вертикальных лёгких проводах длиной l каждый подвешен в горизонтальном положении массивный проводящий стержень длиной L. Верхние концы проводов присоединены к обкладкам конденсатора ёмкостью С. Система находится в вертикальном однородном магнитном поле с индукцией В (см. рисунок). Стержень отклоняют от положения равновесия параллельно самому себе на небольшое расстояние и отпускают с нулевой начальной скоростью. Найдите зависимость от времени t заряда q конденсатора, считая, что в начальный момент, при
конденсатор был не заряжен. Трением, сопротивлением всех проводников и контактов между ними, а также силами взаимодействия токов в проводниках с магнитным полем пренебречь.
Решение
Согласно условию задачи, взаимодействие токов в проводниках с магнитным полем пренебрежимо мало. Поэтому после отпускания стержень будет совершать свободные колебания, как математический маятник, с круговой частотой по закону
где x — текущее отклонение стержня от положения равновесия.
Поток вектора магнитной индукции через замкнутый контур, содержащий все проводники и конденсатор, равен
По закону электромагнитной индукции Фарадея при колебаниях стержня в данном контуре будет возникать ЭДС индукции, равная
Поскольку сопротивлением проводников мы также пренебрегаем, то по закону Ома для полной цепи эта ЭДС равняется напряжению между обкладками конденсатора: откуда
Задача 25
В однородном магнитном поле с индукцией протон движется перпендикулярно вектору
индукции со скоростью
Определите радиус траектории протона.
Задача 26
Ядро изотопа водорода — дейтерия — движется в однородном магнитном поле индукцией
перпендикулярно вектору В индукции по окружности радиусом 10 м. Определите скорость ядра.
Задача 27
В однородном магнитном поле с индукцией B, направленной вертикально вниз, равномерно вращается в горизонтальной плоскости против часовой стрелки положительно заряженный шарик массой m, подвешенный на нити длиной l (конический маятник). Угол отклонения нити от вертикали равен скорость движения шарика равна v. Найдите заряд шарика q.
Решение
Задача 28
На непроводящей горизонтальной поверхности стола проводящая жёсткая рамка массой m из однородной тонкой проволоки, согнутая в виде квадрата ACDE со стороной (см. рисунок). Рамка находится в однородном горизонтальном магнитном поле, вектор индукции
которого перпендикулярен сторонам АЕ и CD и равен по модулю В. По рамке течёт ток в направлении, указанном стрелками (см. рисунок). При какой минимальной силе тока рамка начнет поворачиваться вокруг стороны CD?
Решение
Для того, чтобы рамка начала поворачиваться вокруг оси CD, вращательный момент сил, действующих на рамку и направленных вверх, должен быть не меньше суммарного момента сил, направленных вниз.
На проводник с током в магнитном поле действует сила Ампера Если направление тока и магнитного поля параллельны, то сила Ампера не действует. В данном случае на сторону АЕ действует сила Ампера
которая по правилу буравчика направлена вверх (на рисунке — на нас). На каждую из сторон действует сила тяжести
т. к. масса всего квадрата равна
Запишем условие моментов: где
и
— плечи сил относительно оси CD.
Отсюда находим минимальную силу тока
Задача 29
Ион ускоряется в электрическом поле с разностью потенциалов кВ и попадает в однородное магнитное поле перпендикулярно к вектору его индукции
(см. рисунок). Радиус траектории движения иона в магнитном поле
м, модуль индукции магнитного поля равен 0,5 Тл. Определите отношение массы иона к его электрическому заряду
Кинетической энергией иона при его вылете из источника пренебрегите.
Решение
Разность потенциалов сообщает иону кинетическую энергию
В магнитном поле, на движущийся ион действует сила Лоренца, которая сообщает ему центростремительное ускорение:
Приравнивая правые части полученных равенств, имеем
Задача 30
Горизонтальный проводящий стержень прямоугольного сечения поступательно движется с ускорением вверх по гладкой наклонной плоскости в вертикальном однородном магнитном поле (см. рисунок).
По стержню протекает ток I. Угол наклона плоскости Отношение массы стержня к его длине
Модуль индукции магнитного поля
Ускорение стержня
Чему равна сила тока в стержне?
Решение
1) На рисунке показаны силы, действующие на стержень с током:
— сила тяжести направленная вертикально вниз;
— сила реакции опоры направленная перпендикулярно к наклонной плоскости;
— сила Ампера направленная горизонтально вправо, что вытекает из условия задачи.
2) Модуль силы Ампера
3) Систему отсчёта, связанную с наклонной плоскостью, считаем инерциальной. Для решения задачи достаточно записать второй закон Ньютона в проекциях на ось х (см. рисунок):
Отсюда находим
Задача 31
В зазоре между полюсами электромагнита вращается с угловой скоростью ω = 100 с–1проволочная рамка в форме полуокружности радиусом r = 5 см, содержащая N = 20 витков провода. Ось вращения рамки проходит вдоль оси О рамки и находится вблизи края области с постоянным однородным магнитным полем с индукцией В = 1 Тл (см. рисунок), линии которого перпендикулярны плоскости рамки. Концы обмотки рамки замкнуты через скользящие контакты на резистор с сопротивлением R = 25 Ом. Пренебрегая сопротивлением рамки, найдите тепловую мощность, выделяющуюся в резисторе.
Решение
При вращении рамки в магнитном поле в ней возникает ЭДС индукции, равная по модулю
За малое время рамка поворачивается на угол
и её площадь, находящаяся в магнитном, поле увеличивается на
так что
Так происходит до тех пор, пока площадь рамки в поле увеличивается. После того как вся рамка окажется в поле, эта площадь начнёт уменьшаться с такой же скоростью, так что ЭДС поменяет знак, но сохранит своё значение.
Таким образом, согласно закону Ома для замкнутой цепи, в рамке всё время будет течь ток с одинаковым значением периодически изменяя своё направление на противоположное.
По закону Джоуля — Ленца тепловая мощность, выделяющаяся при этом процессе в резисторе, не зависит от направления тока и равняется
Задача 32
На шероховатой плоскости, наклонённой под углом к горизонту, находится однородный цилиндрический проводник массой от
г и длиной
см (см. рисунок). По проводнику пропускают ток в направлении «от нас», за плоскость рисунка, и вся система находится в однородном магнитном поле с индукцией
направленной вертикально вниз. При какой силе тока
цилиндр будет оставаться на месте, не скатываясь с плоскости и не накатываясь на неё?
РешениеНарисуем силы, действующие на проводник с током: силу тяжести
направленную вертикально вниз, силу нормального давления
перпендикулярную плоскости, и силу Ампера
равную по модулю
и направленную в данном случае, согласно правилу левой руки, горизонтально влево (см. рисунок). Заметим, что все эти три силы приложены таким образом, что они не создают моментов сил относительно оси цилиндра. Поэтому в равновесии сила сухого трения цилиндра о шероховатую наклонную плоскость децствительно должна равняться нулю — иначе он бы покатился.
Спроецируем эти силы на направление вдоль плоскости и на перпендикуляр к ней. Условия равновесия имеют вид
Из первого уравнения находим искомую величину силы тока при равновесии цилиндра: Подставляя это значение
во второе уравнение, находим
(хотя эту величину находить по условию не требовалось).
Задача 33
Проводник движется равноускоренно в однородном вертикальном магнитном поле. Направление скорости перпендикулярно проводнику. Длина проводника — 2 м. Индукция перпендикулярна проводнику и скорости его движения. Проводник перемещается на 3 м за некоторое время. При этом начальная скорость проводника равна нулю, а ускорение 5 м/с2. Найдите индукцию магнитного поля, зная, что ЭДС индукции на концах проводника в конце движения равна 2 В.
Решение
При движении проводника в магнитном поле на электроны в проводнике действует сила Лоренца. Сила Лоренца равна Напряжённость поля внутри проводника можно рассчитать по формуле
Напряжение на концах проводника равно
Движение равноускоренное, поэтому путь, пройденный проводником рассчитывается по формуле
откуда
Следовательно,
откуда
Задача 34
Плоская горизонтальная фигура площадью 0,1 м2, ограниченная проводящим контуром, имеющим сопротивление 5 Ом, находится в однородном магнитном поле. Проекция вектора магнитной индукции на вертикальную ось Оz медленно и равномерно возрастает от некоторого начального значения B1z до конечного значения B2z = 4,7 Тл. За это время по контуру протекает заряд Δq= 0,08 Кл. Найдите B1z.
Решение
Выражение для модуля ЭДС индукции в случае однородного поля: где S — площадь фигуры;
Закон Ома: E = IR, где R — сопротивление контура; — ток в контуре за время Δt изменения магнитного поля.
Выражение для заряда, протекающего по цепи:
Задача 35
К конденсатору С1 через диод и катушку индуктивности L подключён конденсатор ёмкостью С2 = 2 мкФ. До замыкания ключа К конденсатор С1 был заряжен до напряжения U = 50 В, а конденсатор С2 не заряжен. После замыкания ключа система перешла в новое состояние равновесия, в котором напряжение на конденсаторе С2 оказалось равным U2 = 20 В. Какова ёмкость конденсатора С1? (Активное сопротивление цепи пренебрежимо мало.)
Решение
Энергия заряженного конденсатора С1 до замыкания ключа К:
q = C1U.
Суммарная энергия заряженных конденсаторов после замыкания ключа К:
Так как процесс зарядки конденсатора С2 происходит медленно, нет потерь энергии на излучение, а следовательно, после замыкания ключа К первоначальная энергия заряженного конденсатора С1 в новом состоянии равновесия распределяется между конденсаторами:
Wэ = Wэ1 + Wэ2.
Кроме того, выполняется закон сохранения заряда: q = q1 + q2 = C1U1 + C2U2. Объединяя соотношения, получаем систему уравнений
Решая эту систему, получаем
Задача 36
Математический маятник, грузик которого имеет массу m = 8 г, совершает малые колебания в поле силы тяжести с периодом T1 = 0,7 с. Грузик зарядили и включили направленное вниз однородное вертикальное электрическое поле, модуль напряжённости которого равен E = 3 кВ/м. В результате этого период колебаний маятника стал равным T2 = 0,5 с. Найдите заряд q грузика.
Решение
1. В первом случае период колебаний математического маятника равен где l — длина нити подвеса маятника.
2. Во втором случае период колебаний шарика в электрическом поле, направленном вниз, уменьшился, значит, сила натяжения нити подвеса увеличилась и заряд шарика — положительный.
3. При малых колебаниях математического маятника с грузиком массой m и с зарядом q в поле тяготения модуль F силы натяжения нити близок к mg + qE. Уравнение движения грузика в проекции на горизонтальную ось Х имеет вид: где
— угол отклонения нити от вертикали, x — смещение грузика. Отсюда получаем уравнение гармонических колебаний:
или
где
Период этих колебаний равен
4. Из последнего уравнения находим заряд шарика маятника:
мкКл.
Задача 37
По горизонтально расположенным шероховатым рельсам с пренебрежимо малым сопротивлением могут скользить два одинаковых стержня массой и сопротивлением
каждый. Расстояние между рельсами
а коэффициент трения между стержнями и рельсами
Рельсы со стержнями находятся в однородном вертикальном магнитном поле с индукцией
(см. рисунок). Под действием горизонтальной силы, действующей на первый стержень вдоль рельс, оба стержня движутся поступательно равномерно с разными скоростями. Какова скорость движения первого стержня относительно второго? Самоиндукцией контура пренебречь.
Решение
Задача 38
Два параллельных друг другу рельса, лежащих в горизонтальной плоскости, находятся в однородном магнитном поле, индукция B которого направлена вертикально вниз (см. рисунок, вид сверху). На рельсах находятся два одинаковых проводника. Левый проводник движется вправо со скоростью V, а правый — покоится. С какой скоростью v надо перемещать правый проводник направо, чтобы в три раза уменьшить силу Ампера, действующую на левый проводник? (Сопротивлением рельсов пренебречь.)
Решение