Физика электростатика экзамен - Помощь в подготовке к экзаменам и поступлению

Основные теоретические сведения
- Электрический заряд и его свойства
- Закон Кулона
- Электрическое поле и его напряженность
- Принцип суперпозиции
- Потенциальная энергия взаимодействия зарядов
- Потенциал. Разность потенциалов. Напряжение
- Электрическая емкость. Плоский конденсатор
- Соединения конденсаторов
- Проводящая сфера
- Свойства проводника в электрическом поле
- Замечания к решению сложных задач

Основные теоретические сведения

Электрический заряд и его свойства

К оглавлению…

Электрический заряд – это физическая величина, характеризующая способность частиц или тел вступать в электромагнитные взаимодействия. Электрический заряд обычно обозначается буквами q или Q. В системе СИ электрический заряд измеряется в Кулонах (Кл). Свободный заряд в 1 Кл – это гигантская величина заряда, практически не встречающаяся в природе. Как правило, Вам придется иметь дело с микрокулонами (1 мкКл = 10^–6 Кл), нанокулонами (1 нКл = 10^–9 Кл) и пикокулонами (1 пКл = 10^–12 Кл). Электрический заряд обладает следующими свойствами:

1. Электрический заряд является видом материи.

2. Электрический заряд не зависит от движения частицы и от ее скорости.

3. Заряды могут передаваться (например, при непосредственном контакте) от одного тела к другому. В отличие от массы тела электрический заряд не является неотъемлемой характеристикой данного тела. Одно и то же тело в разных условиях может иметь разный заряд.

4. Существует два рода электрических зарядов, условно названных положительными и отрицательными.

5. Все заряды взаимодействуют друг с другом. При этом одноименные заряды отталкиваются, разноименные – притягиваются. Силы взаимодействия зарядов являются центральными, то есть лежат на прямой, соединяющей центры зарядов.

6. Существует минимально возможный (по модулю) электрический заряд, называемый элементарным зарядом. Его значение:

e = 1,602177·10^–19 Кл ≈ 1,6·10^–19 Кл.

Электрический заряд любого тела всегда кратен элементарному заряду:

где: N – целое число. Обратите внимание, невозможно существование заряда, равного 0,5е; 1,7е; 22,7е и так далее. Физические величины, которые могут принимать только дискретный (не непрерывный) ряд значений, называются квантованными. Элементарный заряд e является квантом (наименьшей порцией) электрического заряда.

7. Закон сохранения электрического заряда. В изолированной системе алгебраическая сумма зарядов всех тел остается постоянной:

Закон сохранения электрического заряда утверждает, что в замкнутой системе тел не могут наблюдаться процессы рождения или исчезновения зарядов только одного знака. Из закона сохранения заряда так же следует, если два тела одного размера и формы, обладающие зарядами q₁ и q₂ (совершенно не важно какого знака заряды), привести в соприкосновение, а затем обратно развести, то заряд каждого из тел станет равным:

С современной точки зрения, носителями зарядов являются элементарные частицы. Все обычные тела состоят из атомов, в состав которых входят положительно заряженные протоны, отрицательно заряженные электроны и нейтральные частицы – нейтроны. Протоны и нейтроны входят в состав атомных ядер, электроны образуют электронную оболочку атомов. Электрические заряды протона и электрона по модулю в точности одинаковы и равны элементарному (то есть минимально возможному) заряду e.

В нейтральном атоме число протонов в ядре равно числу электронов в оболочке. Это число называется атомным номером. Атом данного вещества может потерять один или несколько электронов, или приобрести лишний электрон. В этих случаях нейтральный атом превращается в положительно или отрицательно заряженный ион. Обратите внимание, что положительные протоны входят в состав ядра атома, поэтому их число может изменяться только при ядерных реакциях. Очевидно, что при электризации тел ядерных реакций не происходит. Поэтому в любых электрических явлениях число протонов не меняется, изменяется только число электронов. Так, сообщение телу отрицательного заряда означает передачу ему лишних электронов. А сообщение положительного заряда, вопреки частой ошибке, означает не добавление протонов, а отнимание электронов. Заряд может передаваться от одного тела к другому только порциями, содержащими целое число электронов.

Иногда в задачах электрический заряд распределен по некоторому телу. Для описания этого распределения вводятся следующие величины:

1. Линейная плотность заряда. Используется для описания распределения заряда по нити:

где: L – длина нити. Измеряется в Кл/м.

2. Поверхностная плотность заряда. Используется для описания распределения заряда по поверхности тела:

где: S – площадь поверхности тела. Измеряется в Кл/м².

3. Объемная плотность заряда. Используется для описания распределения заряда по объему тела:

где: V – объем тела. Измеряется в Кл/м³.

Обратите внимание на то, что масса электрона равна:

m_e = 9,11∙10^–31 кг.

Закон Кулона

К оглавлению…

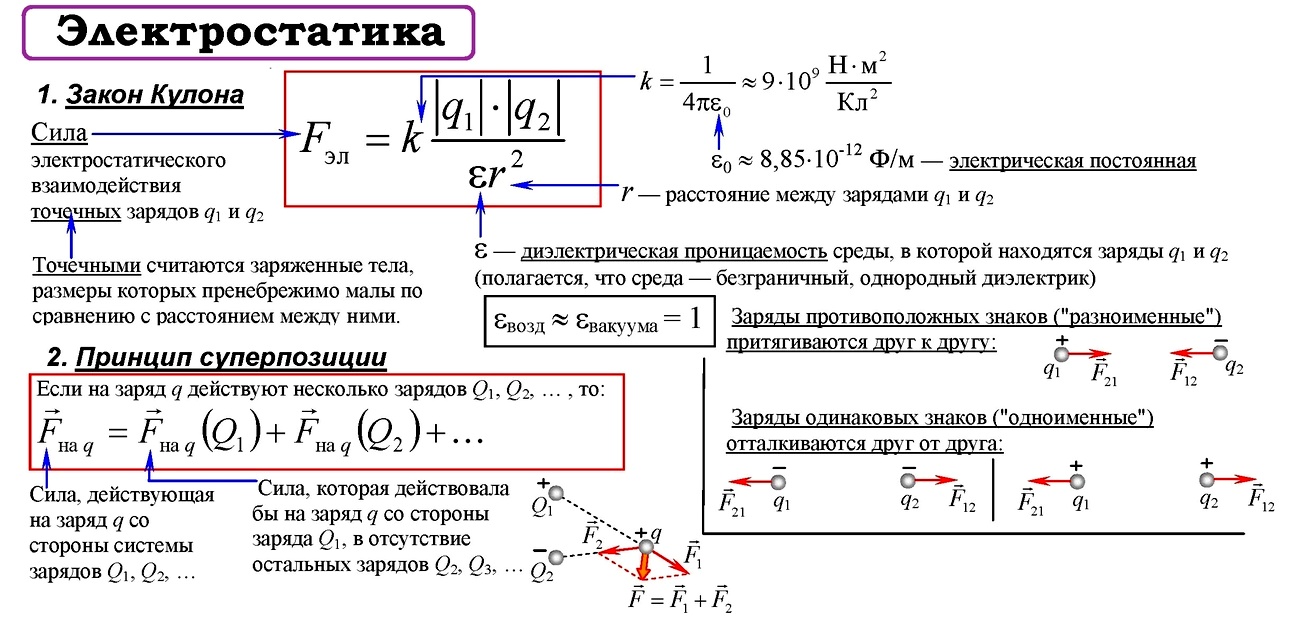
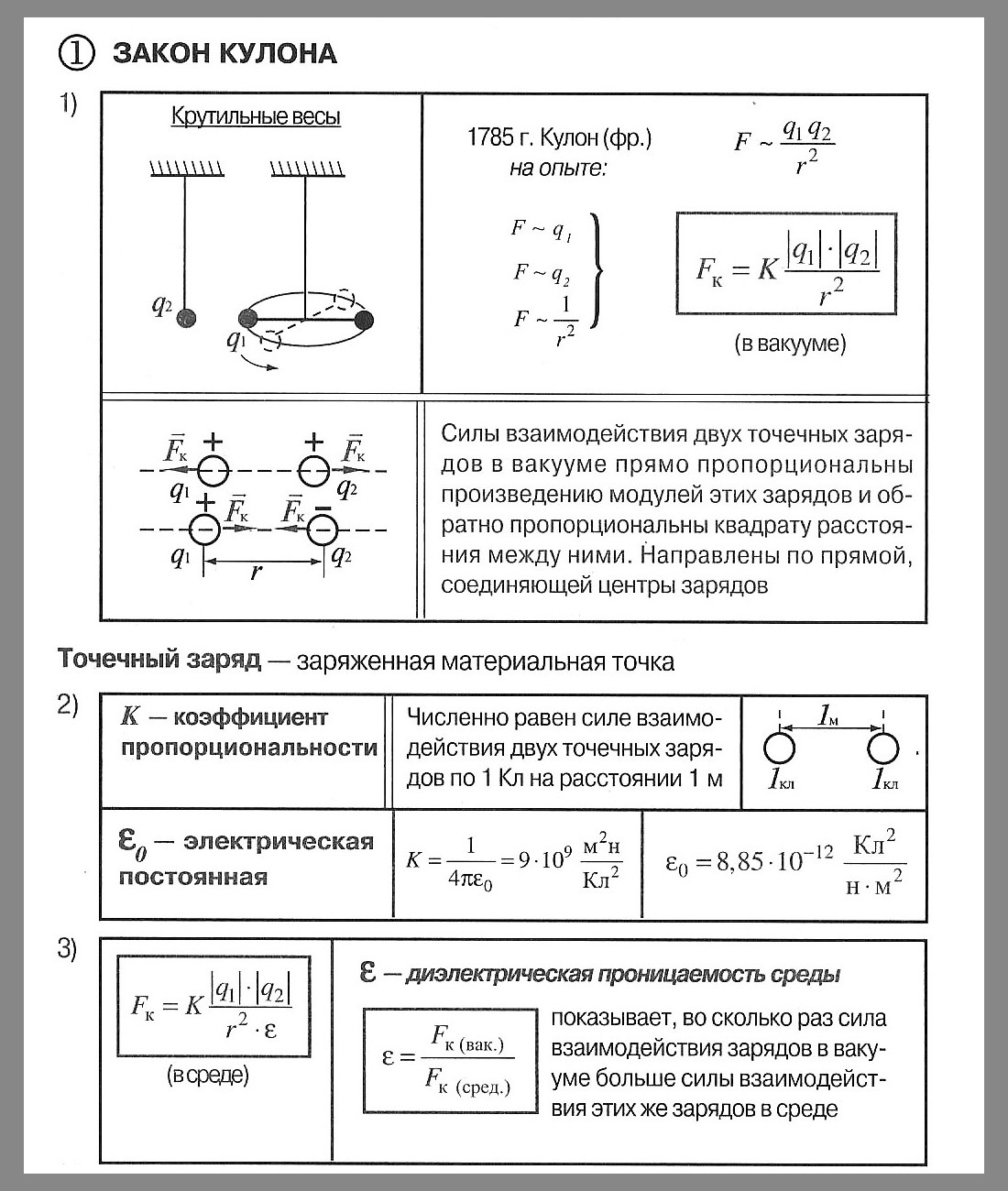
Точечным зарядом называют заряженное тело, размерами которого в условиях данной задачи можно пренебречь. На основании многочисленных опытов Кулон установил следующий закон:

Силы взаимодействия неподвижных точечных зарядов прямо пропорциональны произведению модулей зарядов и обратно пропорциональны квадрату расстояния между ними:

где: ε – диэлектрическая проницаемость среды – безразмерная физическая величина, показывающая, во сколько раз сила электростатического взаимодействия в данной среде будет меньше, чем в вакууме (то есть во сколько раз среда ослабляет взаимодействие). Здесь k – коэффициент в законе Кулона, величина, определяющая численное значение силы взаимодействия зарядов. В системе СИ его значение принимается равным:

k = 9∙10⁹ м/Ф.

Силы взаимодействия точечных неподвижных зарядов подчиняются третьему закону Ньютона, и являются силами отталкивания друг от друга при одинаковых знаках зарядов и силами притяжения друг к другу при разных знаках. Взаимодействие неподвижных электрических зарядов называют электростатическим или кулоновским взаимодействием. Раздел электродинамики, изучающий кулоновское взаимодействие, называют электростатикой.

Закон Кулона справедлив для точечных заряженных тел, равномерно заряженных сфер и шаров. В этом случае за расстояния r берут расстояние между центрами сфер или шаров. На практике закон Кулона хорошо выполняется, если размеры заряженных тел много меньше расстояния между ними. Коэффициент k в системе СИ иногда записывают в виде:

где: ε₀ = 8,85∙10^–12 Ф/м – электрическая постоянная.

Опыт показывает, что силы кулоновского взаимодействия подчиняются принципу суперпозиции: если заряженное тело взаимодействует одновременно с несколькими заряженными телами, то результирующая сила, действующая на данное тело, равна векторной сумме сил, действующих на это тело со стороны всех других заряженных тел.

Запомните также два важных определения:

Проводники – вещества, содержащие свободные носители электрического заряда. Внутри проводника возможно свободное движение электронов – носителей заряда (по проводникам может протекать электрический ток). К проводникам относятся металлы, растворы и расплавы электролитов, ионизированные газы, плазма.

Диэлектрики (изоляторы) – вещества, в которых нет свободных носителей заряда. Свободное движение электронов внутри диэлектриков невозможно (по ним не может протекать электрический ток). Именно диэлектрики обладают некоторой не равной единице диэлектрической проницаемостью ε.

Для диэлектрической проницаемости вещества верно следующее (о том, что такое электрическое поле чуть ниже):

Электрическое поле и его напряженность

К оглавлению…

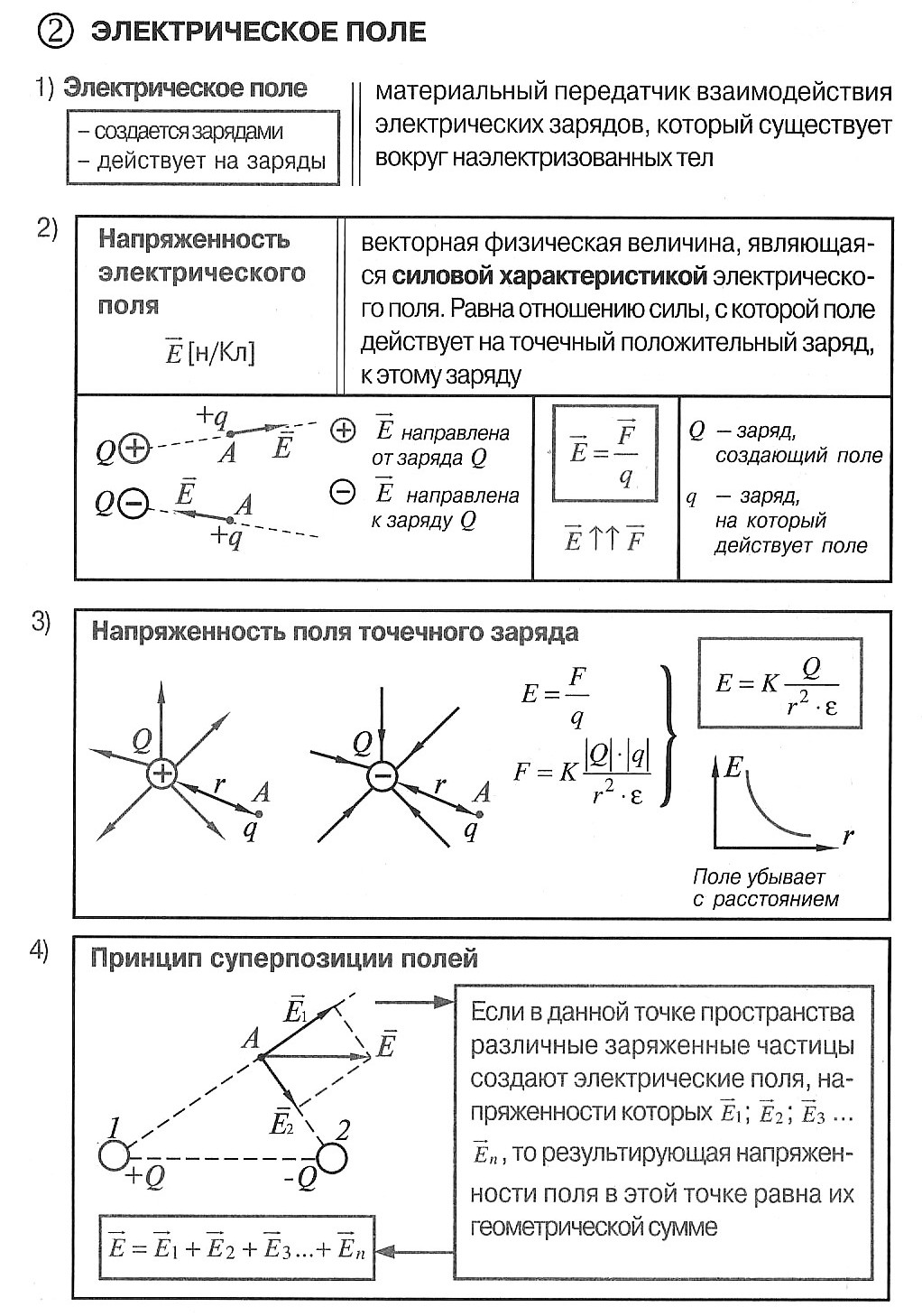
По современным представлениям, электрические заряды не действуют друг на друга непосредственно. Каждое заряженное тело создает в окружающем пространстве электрическое поле. Это поле оказывает силовое действие на другие заряженные тела. Главное свойство электрического поля – действие на электрические заряды с некоторой силой. Таким образом, взаимодействие заряженных тел осуществляется не непосредственным их воздействием друг на друга, а через электрические поля, окружающие заряженные тела.

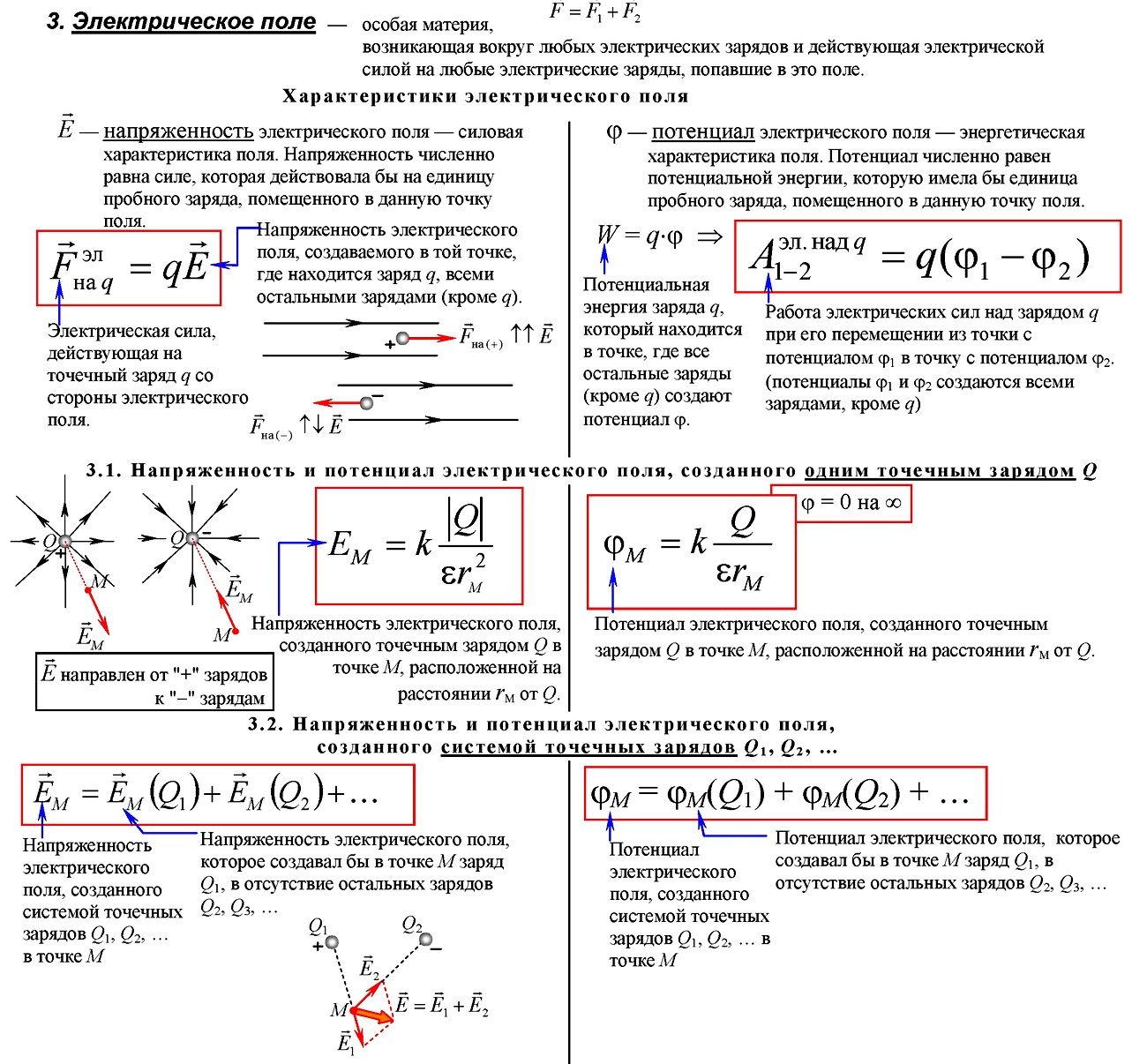
Электрическое поле, окружающее заряженное тело, можно исследовать с помощью так называемого пробного заряда – небольшого по величине точечного заряда, который не вносит заметного перераспределения исследуемых зарядов. Для количественного определения электрического поля вводится силовая характеристика — напряженность электрического поля E.

Напряженностью электрического поля называют физическую величину, равную отношению силы, с которой поле действует на пробный заряд, помещенный в данную точку поля, к величине этого заряда:

Напряженность электрического поля – векторная физическая величина. Направление вектора напряженности совпадает в каждой точке пространства с направлением силы, действующей на положительный пробный заряд. Электрическое поле неподвижных и не меняющихся со временем зарядов называется электростатическим.

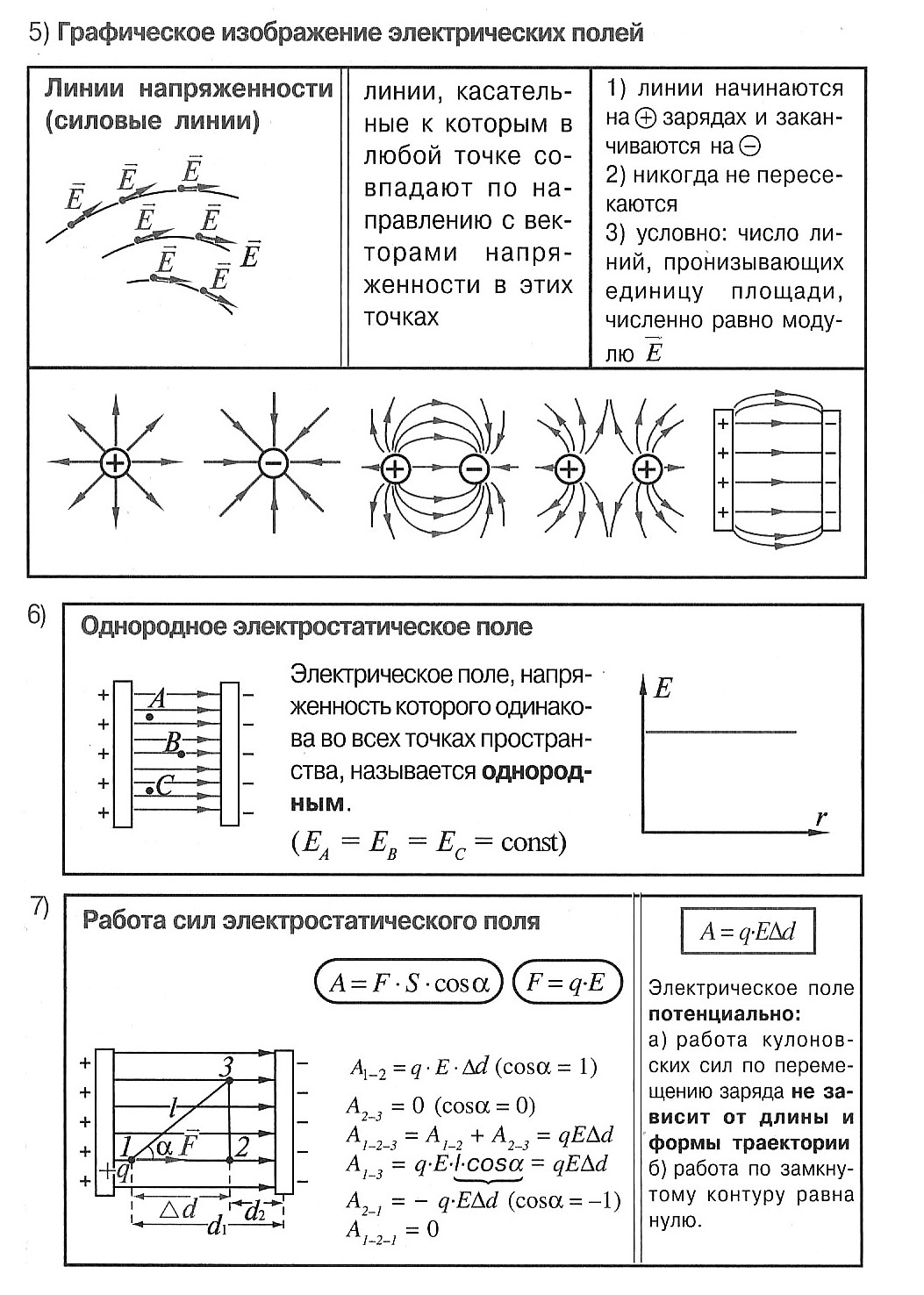
Для наглядного представления электрического поля используют силовые линии. Эти линии проводятся так, чтобы направление вектора напряженности в каждой точке совпадало с направлением касательной к силовой линии. Силовые линии обладают следующими свойствами.

Силовые линии электростатического поля никогда не пересекаются.
Силовые линии электростатического поля всегда направлены от положительных зарядов к отрицательным.
При изображении электрического поля с помощью силовых линий их густота должна быть пропорциональна модулю вектора напряженности поля.
Силовые линии начинаются на положительном заряде или бесконечности, а заканчиваются на отрицательном или бесконечности. Густота линий тем больше, чем больше напряжённость.
В данной точке пространства может проходить только одна силовая линия, т.к. напряжённость электрического поля в данной точке пространства задаётся однозначно.

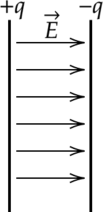
Электрическое поле называют однородным, если вектор напряжённости одинаков во всех точках поля. Например, однородное поле создаёт плоский конденсатор – две пластины, заряженные равным по величине и противоположным по знаку зарядом, разделённые слоем диэлектрика, причём расстояние между пластинами много меньше размеров пластин.

Во всех точках однородного поля на заряд q, внесённый в однородное поле с напряжённостью E, действует одинаковая по величине и направлению сила, равная F = Eq. Причём, если заряд q положительный, то направление силы совпадает с направлением вектора напряжённости, а если заряд отрицательный, то вектора силы и напряжённости противоположно направлены.

Силовые линии кулоновских полей положительных и отрицательных точечных зарядов изображены на рисунке:

Принцип суперпозиции

К оглавлению…

Если с помощью пробного заряда исследуется электрическое поле, создаваемое несколькими заряженными телами, то результирующая сила оказывается равной геометрической сумме сил, действующих на пробный заряд со стороны каждого заряженного тела в отдельности. Следовательно, напряженность электрического поля, создаваемого системой зарядов в данной точке пространства, равна векторной сумме напряжённостей электрических полей, создаваемых в той же точке зарядами в отдельности:

Это свойство электрического поля означает, что поле подчиняется принципу суперпозиции. В соответствии с законом Кулона, напряженность электростатического поля, создаваемого точечным зарядом Q на расстоянии r от него, равна по модулю:

Это поле называется кулоновским. В кулоновском поле направление вектора напряженности зависит от знака заряда Q: если Q > 0, то вектор напряженности направлен от заряда, если Q < 0, то вектор напряженности направлен к заряду. Величина напряжённости зависит от величины заряда, среды, в которой находится заряд, и уменьшается с увеличением расстояния.

Напряженность электрического поля, которую создает заряженная плоскость вблизи своей поверхности:

Итак, если в задаче требуется определить напряженность поля системы зарядов, то надо действовать по следующему алгоритму:

Нарисовать рисунок.
Изобразить напряженность поля каждого заряда по отдельности в нужной точке. Помните, что напряженность направлена к отрицательному заряду и от положительного заряда.
Вычислить каждую из напряжённостей по соответствующей формуле.
Сложить вектора напряжённостей геометрически (т.е. векторно).

Потенциальная энергия взаимодействия зарядов

К оглавлению…

Электрические заряды взаимодействуют друг с другом и с электрическим полем. Любое взаимодействие описывается потенциальной энергией. Потенциальная энергия взаимодействия двух точечных электрических зарядов рассчитывается по формуле:

Обратите внимание на отсутствие модулей у зарядов. Для разноименных зарядов энергия взаимодействия имеет отрицательное значение. Такая же формула справедлива и для энергии взаимодействия равномерно заряженных сфер и шаров. Как обычно, в этом случае расстояние r измеряется между центрами шаров или сфер. Если же зарядов не два, а больше, то энергию их взаимодействия следует считать так: разбить систему зарядов на все возможные пары, рассчитать энергию взаимодействия каждой пары и просуммировать все энергии для всех пар.

Задачи по данной теме решаются, как и задачи на закон сохранения механической энергии: сначала находится начальная энергия взаимодействия, потом конечная. Если в задаче просят найти работу по перемещению зарядов, то она будет равна разнице между начальной и конечной суммарной энергией взаимодействия зарядов. Энергия взаимодействия так же может переходить в кинетическую энергию или в другие виды энергии. Если тела находятся на очень большом расстоянии, то энергия их взаимодействия полагается равной 0.

Обратите внимание: если в задаче требуется найти минимальное или максимальное расстояние между телами (частицами) при движении, то это условие выполнится в тот момент времени, когда частицы движутся в одну сторону с одинаковой скоростью. Поэтому решение надо начинать с записи закона сохранения импульса, из которого и находится эта одинаковая скорость. А далее следует писать закон сохранения энергии с учетом кинетической энергии частиц во втором случае.

Потенциал. Разность потенциалов. Напряжение

К оглавлению…

Электростатическое поле обладает важным свойством: работа сил электростатического поля при перемещении заряда из одной точки поля в другую не зависит от формы траектории, а определяется только положением начальной и конечной точек и величиной заряда.

Следствием независимости работы от формы траектории является следующее утверждение: работа сил электростатического поля при перемещении заряда по любой замкнутой траектории равна нулю.

Свойство потенциальности (независимости работы от формы траектории) электростатического поля позволяет ввести понятие потенциальной энергии заряда в электрическом поле. А физическую величину, равную отношению потенциальной энергии электрического заряда в электростатическом поле к величине этого заряда, называют потенциалом φ электрического поля:

Потенциал φ является энергетической характеристикой электростатического поля. В Международной системе единиц (СИ) единицей потенциала (а значит и разности потенциалов, т.е. напряжения) является вольт [В]. Потенциал — скалярная величина.

Во многих задачах электростатики при вычислении потенциалов за опорную точку, где значения потенциальной энергии и потенциала обращаются в ноль, удобно принять бесконечно удаленную точку. В этом случае понятие потенциала может быть определено следующим образом: потенциал поля в данной точке пространства равен работе, которую совершают электрические силы при удалении единичного положительного заряда из данной точки в бесконечность.

Вспомнив формулу для потенциальной энергии взаимодействия двух точечных зарядов и разделив ее на величину одного из зарядов в соответствии с определением потенциала получим, что потенциал φ поля точечного заряда Q на расстоянии r от него относительно бесконечно удаленной точки вычисляется следующим образом:

Потенциал рассчитанный по этой формуле может быть положительным и отрицательным в зависимости от знака заряда создавшего его. Эта же формула выражает потенциал поля однородно заряженного шара (или сферы) при r ≥ R (снаружи от шара или сферы), где R – радиус шара, а расстояние r отсчитывается от центра шара.

Для наглядного представления электрического поля наряду с силовыми линиями используют эквипотенциальные поверхности. Поверхность, во всех точках которой потенциал электрического поля имеет одинаковые значения, называется эквипотенциальной поверхностью или поверхностью равного потенциала. Силовые линии электрического поля всегда перпендикулярны эквипотенциальным поверхностям. Эквипотенциальные поверхности кулоновского поля точечного заряда – концентрические сферы.

Электрическое напряжение это просто разность потенциалов, т.е. определение электрического напряжения может быть задано формулой:

В однородном электрическом поле существует связь между напряженностью поля и напряжением:

Работа электрического поля может быть вычислена как разность начальной и конечной потенциальной энергии системы зарядов:

Работа электрического поля в общем случае может быть вычислена также и по одной из формул:

В однородном поле при перемещении заряда вдоль его силовых линий работа поля может быть также рассчитана по следующей формуле:

В этих формулах:

φ – потенциал электрического поля.
∆φ – разность потенциалов.
W – потенциальная энергия заряда во внешнем электрическом поле.
A – работа электрического поля по перемещению заряда (зарядов).
q – заряд, который перемещают во внешнем электрическом поле.
U – напряжение.
E – напряженность электрического поля.
d или ∆l – расстояние на которое перемещают заряд вдоль силовых линий.

Во всех предыдущих формулах речь шла именно о работе электростатического поля, но если в задаче говорится, что «работу надо совершить», или идет речь о «работе внешних сил», то эту работу следует считать так же, как и работу поля, но с противоположным знаком.

Принцип суперпозиции потенциала

Из принципа суперпозиции напряженностей полей, создаваемых электрическими зарядами, следует принцип суперпозиции для потенциалов (при этом знак потенциала поля зависит от знака заряда, создавшего поле):

Обратите внимание, насколько легче применять принцип суперпозиции потенциала, чем напряженности. Потенциал – скалярная величина, не имеющая направления. Складывать потенциалы – это просто суммировать численные значения.

Электрическая емкость. Плоский конденсатор

К оглавлению…

При сообщении проводнику заряда всегда существует некоторый предел, более которого зарядить тело не удастся. Для характеристики способности тела накапливать электрический заряд вводят понятие электрической емкости. Емкостью уединенного проводника называют отношение его заряда к потенциалу:

В системе СИ емкость измеряется в Фарадах [Ф]. 1 Фарад – чрезвычайно большая емкость. Для сравнения, емкость всего земного шара значительно меньше одного фарада. Емкость проводника не зависит ни от его заряда, ни от потенциала тела. Аналогично, плотность не зависит ни от массы, ни от объема тела. Емкость зависит лишь от формы тела, его размеров и свойств окружающей его среды.

Электроемкостью системы из двух проводников называется физическая величина, определяемая как отношение заряда q одного из проводников к разности потенциалов Δφ между ними:

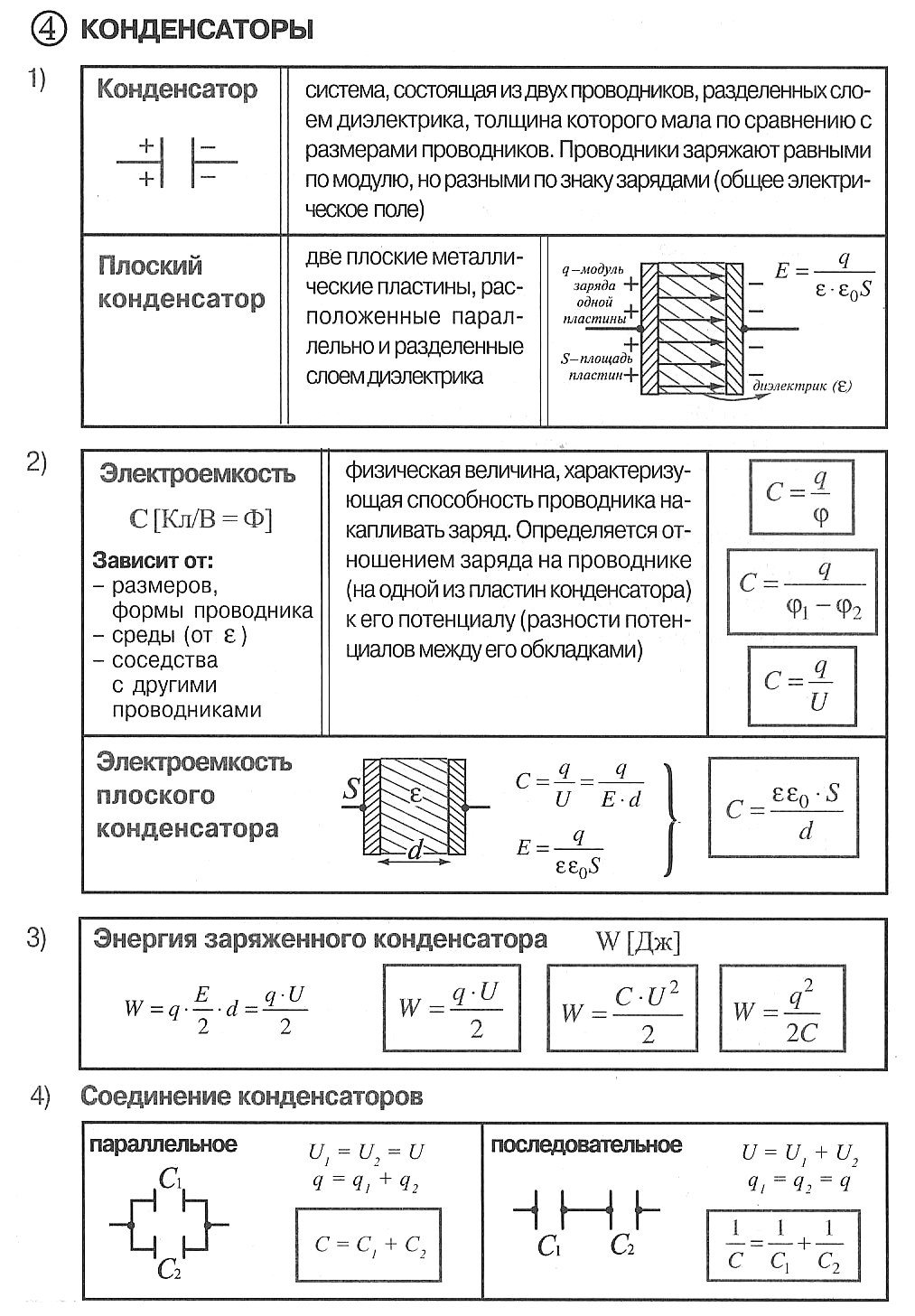
Величина электроемкости проводников зависит от формы и размеров проводников и от свойств диэлектрика, разделяющего проводники. Существуют такие конфигурации проводников, при которых электрическое поле оказывается сосредоточенным (локализованным) лишь в некоторой области пространства. Такие системы называются конденсаторами, а проводники, составляющие конденсатор, называются обкладками.

Простейший конденсатор – система из двух плоских проводящих пластин, расположенных параллельно друг другу на малом по сравнению с размерами пластин расстоянии и разделенных слоем диэлектрика. Такой конденсатор называется плоским. Электрическое поле плоского конденсатора в основном локализовано между пластинами.

Каждая из заряженных пластин плоского конденсатора создает вблизи своей поверхности электрическое поле, модуль напряженности которого выражается соотношением уже приводившимся выше. Тогда модуль напряженности итогового поля внутри конденсатора, создаваемого двумя пластинами, равен:

За пределами конденсатора, электрические поля двух пластин направлены в разные стороны, и поэтому результирующее электростатическое поле E = 0. Электроёмкость плоского конденсатора может быть рассчитана по формуле:

Таким образом, электроемкость плоского конденсатора прямо пропорциональна площади пластин (обкладок) и обратно пропорциональна расстоянию между ними. Если пространство между обкладками заполнено диэлектриком, электроемкость конденсатора увеличивается в ε раз. Обратите внимание, что S в этой формуле есть площадь только одной обкладки конденсатора. Когда в задаче говорят о «площади обкладок», то имеют в виду именно эту величину. На 2 умножать или делить её не надо никогда.

Еще раз приведем формулу для заряда конденсатора. Под зарядом конденсатора понимают только заряд его положительной обкладки:

Сила притяжения пластин конденсатора. Сила, действующая на каждую обкладку, определяется не полным полем конденсатора, а полем, созданным противоположной обкладкой (сама на себя обкладка не действует). Напряженность этого поля равна половине напряженности полного поля, и сила взаимодействия пластин:

Энергия конденсатора. Ее же называют энергией электрического поля внутри конденсатора. Опыт показывает, что заряженный конденсатор содержит запас энергии. Энергия заряженного конденсатора равна работе внешних сил, которую необходимо затратить, чтобы зарядить конденсатор. Существует три эквивалентные формы записи формулы для энергии конденсатора (они следуют одна из другой если воспользоваться соотношением q = CU):

Особое внимание обращайте на фразу: «Конденсатор подключён к источнику». Это означает, что напряжение на конденсаторе не изменяется. А фраза «Конденсатор зарядили и отключили от источника» означает, что заряд конденсатора не изменится.

Энергия электрического поля

Электрическую энергию следует рассматривать как потенциальную энергию, запасенную в заряженном конденсаторе. По современным представлениям, электрическая энергия конденсатора локализована в пространстве между обкладками конденсатора, то есть в электрическом поле. Поэтому ее называют энергией электрического поля. Энергия заряженных тел сосредоточена в пространстве, в котором есть электрическое поле, т.е. можно говорить об энергии электрического поля. Например, у конденсатора энергия сосредоточена в пространстве между его обкладками. Таким образом, имеет смысл ввести новую физическую характеристику – объёмную плотность энергии электрического поля. На примере плоского конденсатора, можно получить такую формулу для объёмной плотности энергии (или энергии единицы объёма электрического поля):

Соединения конденсаторов

К оглавлению…

Параллельное соединение конденсаторов – для увеличения ёмкости. Конденсаторы соединены одноименно заряженными обкладками, как бы увеличивая площадь одинаково заряженных пластин. Напряжение на всех конденсаторах одинаковое, общий заряд равен сумме зарядов каждого из конденсаторов, и общая ёмкость также равна сумме емкостей всех конденсаторов соединенных параллельно. Выпишем формулы для параллельного соединения конденсаторов:

При последовательном соединении конденсаторов общая ёмкость батареи конденсаторов всегда меньше, чем ёмкость наименьшего конденсатора, входящего в батарею. Применяется последовательное соединение для увеличения напряжения пробоя конденсаторов. Выпишем формулы для последовательного соединения конденсаторов. Общая емкость последовательно соединенных конденсаторов находится из соотношения:

Из закона сохранения заряда следует, что заряды на соседних обкладках равны:

Напряжение равно сумме напряжений на отдельных конденсаторах.

Для двух последовательно соединённых конденсаторов формула выше даст нам следующее выражение для общей емкости:

Для N одинаковых последовательно соединённых конденсаторов:

Проводящая сфера

К оглавлению…

Напряженность поля внутри заряженного проводника равна нулю. В противном случае на свободные заряды внутри проводника действовала бы электрическая сила, которая вынуждала бы эти заряды двигаться внутри проводника. Это движение, в свою очередь, приводило бы к разогреванию заряженного проводника, чего на самом деле не происходит.

Факт того, что внутри проводника нет электрического поля можно понять и по-другому: если бы оно было то заряженные частицы опять таки двигались бы, причем они бы двигались именно так, чтобы свести это поле к нолю своим собственным полем, т.к. вообще-то двигаться им не хотелось бы, ведь всякая система стремится к равновесию. Рано или поздно все двигавшиеся заряды остановились бы именно в том месте, чтобы поле внутри проводника стало равно нолю.

На поверхности проводника напряжённость электрического поля максимальна. Величина напряжённости электрического поля заряженного шара за его пределами убывает по мере удаления от проводника и рассчитывается по формуле, аналогичной формулам для напряженности поля точечного заряда, в которой расстояния отсчитываются от центра шара.

Так как напряженность поля внутри заряженного проводника равна нулю, то потенциал во всех точках внутри и на поверхности проводника одинаков (только в этом случае разность потенциалов, а значит и напряжённость равна нулю). Потенциал внутри заряженного шара равен потенциалу на поверхности. Потенциал за пределами шара вычисляется по формуле, аналогичной формулам для потенциала точечного заряда, в которой расстояния отсчитываются от центра шара.

Электрическая емкость шара радиуса R:

Если шар окружен диэлектриком, то:

Свойства проводника в электрическом поле

К оглавлению…

Внутри проводника напряженность поля всегда равна нулю.
Потенциал внутри проводника во всех точках одинаков и равен потенциалу поверхности проводника. Когда в задаче говорят, что «проводник заряжен до потенциала … В», то имеют в виду именно потенциал поверхности.
Снаружи от проводника вблизи от его поверхности напряженность поля всегда перпендикулярна поверхности.
Если проводнику сообщить заряд, то он весь распределится по очень тонкому слою вблизи поверхности проводника (обычно говорят, что весь заряд проводника распределяется на его поверхности). Это легко объясняется: дело в том, что сообщая заряд телу, мы передаем ему носители заряда одного знака, т.е. одноименные заряды, которые отталкиваются. А значит они будут стремиться разбежаться друг от друга на максимальное расстояние из всех возможных, т.е. скопятся у самых краев проводника. Как следствие, если из проводника удалить сердцевину, то его электростатические свойства никак не изменятся.
Снаружи проводника напряженность поля тем больше, чем кривее поверхность проводника. Максимальное значение напряженности достигается вблизи остриев и резких изломов поверхности проводника.

Замечания к решению сложных задач

К оглавлению…

1. Заземление чего-либо означает соединение проводником данного объекта с Землей. При этом потенциалы Земли и имеющегося объекта выравниваются, а необходимые для этого заряды перебегают по проводнику с Земли на объект либо наоборот. При этом нужно учитывать несколько факторов, которые следуют из того, что Земля несоизмеримо больше любого объекта находящегося не ней:

Общий заряд Земли условно равен нолю, поэтому ее потенциал также равен нолю, и он останется равным нолю после соединения объекта с Землей. Одним словом, заземлить – означает обнулить потенциал объекта.
Для обнуления потенциала (а значит и собственного заряда объекта, который мог быть до этого как положительным так и отрицательным), объекту придется либо принять либо отдать Земле некоторый (возможно даже очень большой) заряд, и Земля всегда сможет обеспечить такую возможность.

2. Еще раз повторимся: расстояние между отталкивающимися телами минимально в тот момент, когда их скорости становятся равны по величине и направлены в одну сторону (относительная скорость зарядов равна нулю). В этот момент потенциальная энергия взаимодействия зарядов максимальна. Расстояние между притягивающимися телами максимально, также в момент равенства скоростей, направленных в одну сторону.

3. Если в задаче имеется система, состоящая из большого количества зарядов, то необходимо рассматривать и расписывать силы, действующие на заряд, который не находится в центре симметрии.

Источник

ЭЛЕКТРОСТАТИКА
Теория и формулы (кратко и сжато)

Электростатика – раздел электродинамики, изучающий покоящиеся электрически заряженные тела. Существует два вида электрических зарядов: положительные (стекло о шелк) и отрицательные (эбонит о шерсть).

Элементарный заряд – минимальный заряд (е = 1,6∙10^-19Кл)

Заряд любого тела кратен целому числу элементарных зарядов: q = N∙е

Электризация тел – перераспределение заряда между телами. Способы электризации: трение, касание, влияние.

Закон сохранения электрического заряда – в замкнутой системе алгебраическая сумма зарядов всех частиц остается неизменной. q_{1 +} q ₂+ q ₃+ …..+ q_n = const

Пробный заряд – точечный положительный заряд.

Закон Кулона

Закон Кулона (установлен опытным путем в 1785 году) Сила взаимодействия двух неподвижных точечных зарядов в вакууме прямо пропорциональна произведению модулей зарядов и обратно пропорционально квадрату расстояния между ними.

Электрическое поле

Электрическое поле – вид материи, осуществляющий взаимодействие между электрическими зарядами, возникает вокруг зарядов, действует только на заряды

Силовые линии напряженности электрического поля – непрерывные линии, касательные к которым в каждой точке, через которые они проходят, совпадают с вектором напряженности.

Свойства силовых линий:

не замкнуты;
не пересекаются;
непрерывны;
направление совпадает с направлением вектора напряжённости;
начало на + q или в бесконечности, конец на – q или в бесконечности;
гуще вблизи зарядов (где больше напряжённость).
перпендикулярны поверхности проводника

Разность потенциалов или напряжение (Δφ или U) — это разность потенциалов в начальной и конечной точках траектории заряда Δφ = φ₁ – φ₂

Чем меньше меняется потенциал на отрезке пути, тем меньше напряженность поля.
Напряженность электрического поля направлена в сторону уменьшения потенциала.

Электроемкость

Электроемкость С — характеризует способность проводника накапливать электрический заряд на своей поверхности.

— не зависит от электрического заряда и напряжения.
— зависит от геометрических размеров проводников, их формы, взаимного расположения, электрических свойств среды между проводниками.

Проводники и диэлектрики

Конденсаторы

Конденсатор — электротехническое устройство, служащее для быстрого накопления электрического заряда и быстрой отдачи его в цепь (два проводника, разделенных слоем диэлектрика ).

Скачать таблицы по теме «Электростатика»

Конспект уроков по теме «Электростатика. Теория и формулы» + шпаргалка.

Еще конспекты для 10-11 классов:

Источник

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Какова разность потенциалов между точками поля, если при перемещении заряда 12 мкКл из одной точки в другую электростатическое поле совершает работу 0,36 мДж? (Ответ дать в вольтах.)

Модуль напряженности однородного электрического поля равен 100 В/м. Каков модуль разности потенциалов между двумя точками, расположенными на одной силовой линии поля на расстоянии 5 см? (Ответ дать в вольтах.)

В электрическую цепь включена медная проволока длиной При напряженности электрического поля 50В/м сила тока в проводнике равна 2 А. Какое приложено напряжение к концам проволоки? (Ответ дать в вольтах.)

Шар радиусом 10 см равномерно заряжен электрическим зарядом. В таблице представлены результаты измерений модуля напряжённости E электрического поля от расстояния r до поверхности этого шара. Чему равен модуль заряда шара? (Ответ дать в нКл.) Коэффициент k принять равным 9·10⁹ Н·м²/Кл².

r, см	10	20	30	40	50
E, В/м	900	400	225	144	100

Шар радиусом 20 см равномерно заряжен электрическим зарядом. В таблице представлены результаты измерений модуля напряжённости E электрического поля от расстояния r до поверхности этого шара. Чему равен модуль заряда шара? (Ответ дать в нКл.) Коэффициент k принять равным 9·10⁹ Н·м²/Кл².

r, см	20	40	60	80	100
E, В/м	225	100	56,25	36	25

Пройти тестирование по этим заданиям

Источник

Закон сохранения электрического заряда

В замкнутой системе тел алгебраическая сумма зарядов остается неизменной при любых процессах, происходящих с этими телами:

[q_1+q_2+…+q_n=const]

Закон Кулона в вакууме

Сила взаимодействия двух неподвижных точечный зарядов в вакууме прямо пропорциональна произведению абсолютных величин зарядов (q_1) и (q_2) и обратно пропорциональна квадрату расстояния (r) между ними.

[F=kdfrac{q_1q_2}{r^2}]

Где (k=9cdot 10^9) — коэффициент пропорциональности в законе Кулона.

[k=dfrac{1}{4pivarepsilon_0}]

(varepsilon_0=8,85cdot10^{-12} dfrac{text{Ф}}{text{м}}) — электрическая постоянная.

Закон Кулона в диэлектрике

[F=kdfrac{q_1q_2}{varepsilon r^2}]

Напряженность электрического поля — это отношение вектора силы (vec{F}), с которой поле действует на пробный заряд (q), к самому пробному заряду с учетом его знака.

[vec{E}=dfrac{vec{F}}{q}]

Единицы измерения: (displaystyle Big[dfrac{text{В}}{text{м}}Big]) (вольт на метр).

Линии напряженности всегда начинаются на положительных зарядах и заканчиваются на отрицательных.

Напряженность электростатического поля точечного заряда Q в точке A, удаленной на расстояние (r) от заряда (Q), определяется формулой:

[E=dfrac{kcdot |Q|}{r^2}]

Напряженность заряженной бесконечной пластины где (sigma):

[E=frac{sigma}{2varepsilon_0}]

Принцип суперпозиции полей

Пусть заряды (displaystyle q_1, q_2, q_3,… , q_n) по отдельности создают в данной точке поля (vec{E}_1), (vec{E}_2),…,(vec{E}_n). Тогда система этих зарядов создает в данной точке поле (vec{E}), равное векторной сумме напряженностей полей отдельных зарядов.

[vec{E}=vec{E}_1+vec{E}_2+…+vec{E}_n]

Физическую величину, равную отношению потенциальной энергии электрического заряда в электростатическом поле к величине этого заряда, называют (varphi) электрического поля:

[varphi=dfrac{W_p}{q}]

Единицы измерения: (displaystyle [text{В}]) (Вольт).

Работа сил электростатического поля при перемещении заряда по любой замкнутой траектории равна нулю.

Работа поля по перемещению заряда:

[A_{text{эл}}=q(varphi_1-varphi_2)=qU]

Поверхность, во всех точках которой потенциал электрического поля имеет одинаковые значения, называется .

Электроемкостью системы из двух проводников называется физическая величина, определяемая как отношение заряда (q) одного из проводников к разности потенциалов (Delta varphi) между ними:

[C=dfrac{q}{Delta varphi}]

Единицы измерения: (displaystyle [text{Ф}]) (фарад).

Плоский конденсатор — система из двух плоских проводящих пластин, расположенных параллельно друг другу на малом по сравнению с размерами пластин расстоянии и разделенных слоем диэлектрика.

Электроемкость плоского конденсатора

[C=dfrac{varepsilon_0S}{d}]

[C=dfrac{varepsilon_0varepsilon S}{d}]

Последовательное соединение конденсаторов

[U=U_1+U_2]

[q=q_1=q_2]

[dfrac{1}{C}=dfrac{1}{C_1}+dfrac{1}{C_2}]

Параллельное соединение конденсаторов

[U=U_1=U_2]

[q=q_1+q_2]

[C=C_1+C_2]

Энергия заряженного конденсатора

[W=dfrac{q^2}{2C}=dfrac{qU}{2}=dfrac{CU^2}{2}]

Источник

Вопросы
к экзамену по физике (АВТИ, весенний
семестр)

Электрический
заряд. Закон сохранения заряда.
Закон Кулона.
Напряженность
электростатического поля. Силовые
линии. Принцип суперпозиции. Пример
расчета (поле на оси кольца).
Потенциал
электростатического поля. Связь
напряженности
и потенциала. Поверхности равного
потенциала.
Теорема
Остроградского-Гаусса для Е
(для вакуума)
в интегральной форме.
Теорема
Остроградского-Гаусса для Е
(для вакуума)
в дифференциальной форме.
Диполь.
Дипольный момент. Диполь в однородном
и неоднородном электростатическом
поле.
Классификация
диэлектриков. Поляризованность
(вектор поляризации).

Диэлектрическая
восприимчивость. Расчет Р
для
однородного диэлектрика в однородном
электростатическом
поле.

Теорема Гаусса
для поляризованности (в интегральной
и дифференциальной форме).
Теорема
Остроградского-Гаусса для диэлектрика.
Вектор электрического смещения.
Относительная диэлектрическая
проницаемость
вещества.

Граничные условия
для векторов Е
и И
. Преломление
силовых линий на границе диэлектриков.
Проводники
в электростатическом поле (распределение
заряда, эффект стекания заряда).
Электроемкость
уединенного проводника и конденсатора.
Плоский, цилиндрический и сферический
конденсаторы.
Энергия
заряженного проводника и конденсатора.
Энергия взаимодействия системы
точечных зарядов.
Энергия
электростатического поля. Объемная
плотность энергии.
Электрический
ток (сила тока, плотность тока).
Уравнение непрерывности в интегральной
и дифференциальной форме.
Закон Ома для
однородного и неоднородного
участка цепи. Закон Джоуля-Ленца.
Классическая
теория электропроводности.
Магнитное
поле. Индукция магнитного поля
(вектор магнитной индукции).
Закон
Био-Савара-Лапласа. Поле отрезка прямого
тока.

Закон
Био-Савара-Лапласа. Поле на оси кругового
тока. Магнитный момент контура с током.
Закон
полного тока (в интегральной форме).
Поле
бесконечного соленоида. Поле тороида.

Теорема о циркуляции
вектора В в
дифференциальной форме.
Сила
Ампера. Контур с током в однородном
и неоднородном магнитном поле.
Работа
по перемещению проводника и контура
с током в магнитном поле.
Сила
Лоренца. Движение заряженной частицы
в однородном магнитном поле. Эффект
Холла.

20. Ускорители
частиц.

Явление
электромагнитной индукции. Закон
электромагнитной индукции. Правило
Ленца.
Явление самоиндукции.
Индуктивность.
Расчет индуктивности прямого
длинного соленоида. Взаимная индуктивность.
Магнитная
энергия тока. Магнитная энергия
двух контуров с током при наличии
магнитной
связи. Энергия магнитного поля.
Магнитный
момент атома. Атом в магнитном
поле. Классификация магнетиков.
Намагниченность.
Теорема о циркуляции

вектора 3.

32. Напряженность
магнитного поля. Теорема

о циркуляции Н.
Связь между
В,
3 и
Н.

Граничные условия
для В и
Н. Преломление
линий.
Ферромагнетики.
Кривая намагничивания. Гистерезис.
Температура Кюри. Природа ферромагнетизма.
Ток
смещения. Полный ток. Уравнения Максвелла
(в интегральной и дифференциальной
форме).
Относительность
электрического и магнитного
полей. Преобразование полей. Инварианты.
Свободные
гармонические колебания. Уравнение
гармонических колебаний.
Сложение
гармонических колебаний.
Затухающие
колебания: уравнение, декремент
затухания, логарифмический декремент
затухания, добротность системы.
Вынужденные
колебания. Резонанс.
Электромагнитные
волны. Волновое уравнение.
Вывод
волнового уравнения из уравнений
Максвелла.
Энергия
электромагнитной волны.

Источник

26.12.2008 02:58

Электростатика бгту военмех ответы:
Вопросы и ответы к экзамену
1. ЭЛЕКТРОСТАТИКА И ПОСТОЯННЫЙ ТОК
2. МАГНЕТИЗМ
3. КОЛЕБАНИЯ
+ фотки первой контрольной ( не проверенные), я ранее выкладывал те, что мне передавал Дима Танков…

Электростатика бгту военмех ответы:
Вопросы и ответы к экзамену

1. ЭЛЕКТРОСТАТИКА И ПОСТОЯННЫЙ ТОК
2. МАГНЕТИЗМ
3. КОЛЕБАНИЯ

+ фотки первой контрольной ( не проверенные), я ранее выкладывал те, что мне передавал Дима Танков…

Cкачать

< Предыдущая		Следующая >

Магнитное поле и его основные свойства

Итак, что нужно знать о магнитном поле. В первую очередь то, что источниками магнитного поля являются электрические движущиеся заряды. В отличие от электрического магнитное не воздействует на сам заряд, сила возникает только при движении.

Основные свойства магнитного поля, о которых стоит помнить для решения задач на ЕГЭ:

магнитное поле материально;
магнитное поле порождается только движущимся электрическим зарядом;
там, где двигается электрический заряд с определенной силой, всегда есть магнитное поле;
скорость магнитного поля конечна и равна скорости света в вакууме.

Электричество

Как проще освоить тему? Конечно, разбить ее на подтемы. Именно это и делает преподаватель учебного центра Годограф, чтобы облегчить понимание для каждого ученика.

Итак, электричество делим на 2 подтемы:

Электростатика. В этом случае заряды никуда не двигаются.
Электродинамика. Здесь заряды уже можно двигать, появляются различные схемы и т.д.

Электродинамика и электростатика в ЕГЭ – важный раздел, на который отводится немало задач. Внимательно изучив теорию по электростатике для ЕГЭ, вы сможете легче справиться с практическими заданиями и испытывать меньшую нагрузку на экзамене.

Электростатика на ЕГЭ: способы упрощение подготовки

Если вы только начинаете готовиться к экзамену, вооружите себя всеми доступными методическими материалами. Учебники, специальная литература, старые тесты, методички – все это станет вашим путеводителем в мир знаний. Кроме того, задачи на электростатику ЕГЭ прошлых годов помогут оценить сложность заданий.

Однако чтобы освоить нелегкую тему электромагнетизма самому, бывает недостаточно усидчивости и самоконтроля. В этом случае обратите внимание на курсы, которые предлагают учебные центры. С опытными педагогами, имеющими под рукой готовую программу и многолетний опыт, значительно проще получить желаемый результат на экзамене по физике.

О том, как выбрать репетитора для подготовки к ЕГЭ, вы можете почитать в нашей статье.

Опытные преподаватели физики учебного центра Годограф помогут восстановить пробелы в знаниях и подготовиться к ЕГЭ на 80+ баллов. Наш рейтинг на Яндекс.Картах – 5.0! Записывайтесь на пробный урок и продолжайте знакомиться с нашими видеообзорами по физике.