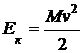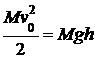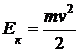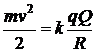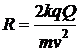в условии
в решении
в тексте к заданию
в атрибутах
Категория:
Атрибут:
Всего: 36 1–20 | 21–36
Добавить в вариант
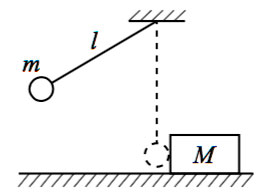
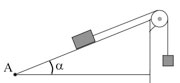
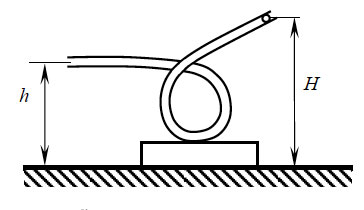
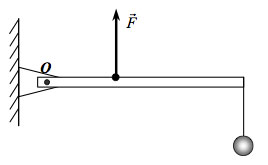
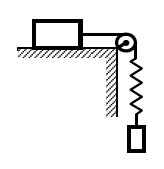
На гладком горизонтальном столе покоится брусок с прикреплённой к нему гладкой изогнутой в вертикальной плоскости тонкой жёсткой трубкой (см. рис.). Общая масса бруска с трубкой равна M = 0,8 кг. В верхний конец вертикальной части трубки, находящийся на высоте H = 70 см над бруском, опускают без начальной скорости маленький шарик массой m = 50 г. Другой конец трубки наклонён к горизонту под углом α = 30° и находится на высоте h = 20 см над бруском. Найдите модуль скорости, с которой будет двигаться брусок после того, как шарик вылетит из трубки.
Какие законы Вы используете для описания движения и взаимодействия трубки и шарика? Обоснуйте их применение к данному случаю.
Источник: Тренировочная работа по физике 28.04.2017, вариант ФИ10503
Задания Д1 B1 № 131
Лодка должна попасть на противоположный берег реки по кратчайшему пути в системе отсчета, связанной с берегом. Скорость течения реки u, а скорость лодки относительно воды Чему должен быть равен модуль скорости лодки относительно берега?
1)
2)
3)
4)
Автобус везёт пассажиров по прямой дороге со скоростью 10 м/с. Пассажир равномерно идёт по салону автобуса со скоростью 1 м/с относительно автобуса, двигаясь от задней двери к кабине водителя. Чему равен модуль скорости пассажира относительно дороги? (Ответ дайте в метрах в секунду.)
Задания Д29 C2 № 9072
На гладком горизонтальном столе покоится брусок с прикреплённой к нему гладкой изогнутой в вертикальной плоскости тонкой жёсткой трубкой (см. рис.). Общая масса бруска с трубкой равна M = 0,8 кг. В верхний конец вертикальной части трубки, находящийся на высоте H = 70 см над бруском, опускают без начальной скорости маленький шарик массой m = 50 г. Другой конец трубки наклонён к горизонту под углом α = 30° и находится на высоте h = 20 см над бруском. Найдите модуль скорости, с которой будет двигаться брусок после того, как шарик вылетит из трубки.
Задания Д1 B1 № 5952
Два камня одновременно бросили из одной точки: первый — вертикально вверх, второй — под углом 45° к горизонту. Сопротивление воздуха пренебрежимо мало. Как движется первый камень в системе отсчёта, связанной со вторым камнем?
1) покоится
2) движется по параболе
3) движется равномерно и прямолинейно
4) движется по дуге окружности
Задания Д1 B1 № 5987
Два камня одновременно бросили из одной точки: первый — вертикально вверх, второй — под углом 30° к горизонту. Сопротивление воздуха пренебрежимо мало. Как движется второй камень в системе отсчёта, связанной с первым камнем?
1) покоится
2) движется по параболе
3) движется равномерно и прямолинейно
4) движется по дуге окружности
Мотоцикл едет по прямой дороге с постоянной скоростью 50 км/ч. По той же дороге навстречу ему едет автомобиль с постоянной скоростью 70 км/ч. Чему равен модуль скорости движения мотоцикла относительно автомобиля? (Ответ дайте в километрах в час.)
Мотоцикл едет по прямой дороге с постоянной скоростью 50 км/ч. По той же дороге в том же направлении едет автомобиль с постоянной скоростью 70 км/ч. Чему равен модуль скорости движения мотоцикла относительно автомобиля? (Ответ дайте в километрах в час.)
Задания Д2 B2 № 6637
Маша взяла в руку монету и, стоя в комнате своей квартиры, выпустила её из пальцев без начальной скорости. Монета полетела вдоль вертикали и упала на пол комнаты. Затем Маша вышла из дома, села в подъехавший автобус и, дождавшись, пока он начнёт двигаться равномерно и прямолинейно по горизонтальной дороге, повторила опыт с бросанием монеты. Оказалось, что монета в равномерно движущемся автобусе падает точно так же, как и в квартире. Иллюстрацией какого закона или принципа может служить этот опыт?
1) первого закона Ньютона
2) второго закона Ньютона
3) третьего закона Ньютона
4) принципа относительности Галилея
Задания Д2 B2 № 6676
Саша взял в руку монету и, стоя в равномерно движущемся вниз лифте, выпустил её из пальцев без начальной скорости. Монета полетела вдоль вертикали и упала на пол лифта. Затем Саша вышел из дома, сел в подъехавший автобус и, дождавшись, пока он начнёт двигаться равномерно и прямолинейно по горизонтальной дороге, повторил опыт с бросанием монеты. Оказалось, что монета в равномерно движущемся автобусе падает точно так же, как и в равномерно опускающемся лифте. Иллюстрацией какого закона или принципа может служить этот опыт?
1) Первого закона Ньютона
2) Второго закона Ньютона
3) Третьего закона Ньютона
4) принципа относительности Галилея
Задания Д1 B1 № 125
Вертолет поднимается вертикально вверх. Какова траектория движения точки на конце лопасти винта вертолета в системе отсчета, связанной с винтом?
1) точка
2) прямая
3) окружность
4) винтовая линия
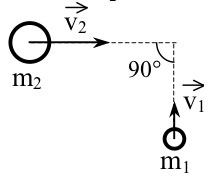
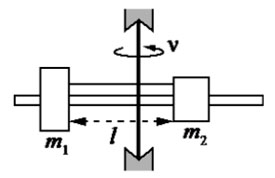
Задания Д3 B3 № 4412
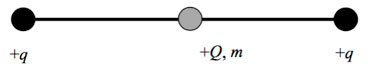
Два бруска массой m и
равномерно движутся вдоль прямой OX (см. рис.). В системе отсчёта, связанной с бруском
модуль импульса второго бруска равен
1)
2)
3)
4)
Задания Д3 B3 № 4447
Два бруска массой m и
равномерно движутся вдоль прямой OX (см. рис.). В системе отсчёта, связанной с бруском
модуль импульса первого бруска равен
1) mV
2)
3)
4)
Из двух городов навстречу друг другу с постоянной скоростью движутся два автомобиля. На графике показано изменение расстояния между автомобилями с течением времени. Каков модуль скорости первого автомобиля в системе отсчёта, связанной со вторым автомобилем? Ответ приведите в метрах в секунду.
Источник: Демонстрационная версия ЕГЭ—2020 по физике.
Задания Д1 B1 № 3357
Вертолет равномерно поднимается вертикально вверх. Какова траектория крайней точки лопасти вертолета в системе отсчета, связанной с корпусом вертолета?
1) прямая линия
2) винтовая линия
3) окружность
4) эллипс
Пловец плывет по течению реки. Определите скорость пловца относительно берега, если скорость пловца относительно воды 0,4 м/с, а скорость течения реки 0,3 м/с. (Ответ дайте в метрах в секунду.)
Из незакреплённой пушки стреляют снарядом массой 20 кг, который вылетает из ствола в горизонтальном направлении со скоростью 102 м/с относительно пушки. Пушка при этом откатывается, приобретая относительно земли скорость 2 м/с. Чему равна масса пушки, если массой сгоревшего порохового заряда можно пренебречь? Ответ дайте в килограммах.
Из незакреплённой пушки массой 800 кг стреляют снарядом, который вылетает из ствола в горизонтальном направлении со скоростью 102 м/с относительно пушки. Пушка при этом откатывается, приобретая относительно земли скорость 2 м/с. Чему равна масса снаряда, если массой сгоревшего порохового заряда можно пренебречь? Ответ дайте в килограммах.
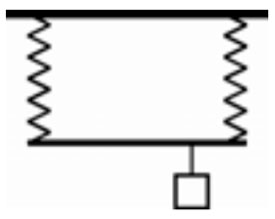
Пароход движется по реке против течения со скоростью 5 м/с относительно берега. Определите скорость течения реки, если скорость парохода относительно берега при движении в обратном направлении равна 8 м/с. (Ответ дайте в метрах в секунду.)
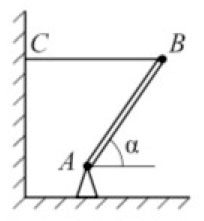
Всего: 36 1–20 | 21–36
Задача 1
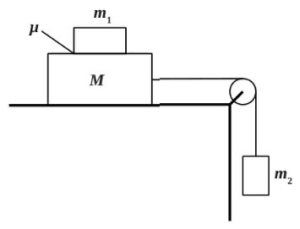
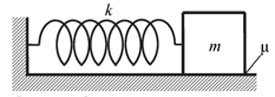
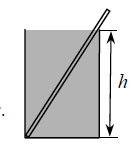
К одному концу лёгкой пружины жёсткостью k = 100 Н/м прикреплён массивный груз, лежащий на горизонтальной плоскости, другой конец пружины закреплён неподвижно (см. рисунок). Коэффициент трения груза по плоскости Груз смещают по горизонтали, растягивая пружину, затем отпускают с начальной скоростью, равной нулю. Груз движется в одном направлении и затем останавливается в положении, в котором пружина уже сжата. Максимальное растяжение пружины, при котором груз движется таким образом, равно d = 15 см. Найдите массу m груза.
Решение
1. Начальная энергия системы равна потенциальной энергии растянутой пружины: После того, как пружину отпустили, она остановится в положении, при котором она сжата на величину
Тогда конечная энергия системы равна потенциальной энергии сжатой пружины:
Изменение полной энергии системы равно работе силы трения
где — модуль силы реакции опоры.
2. В момент, когда груз остановился, по второму закону Ньютона равнодействующая всех сил стала равна нулю. Пружина сжата, поэтому сила упругости пружины направлена вправо. Её уравновешивает сила трения покоя, которая направлена против возможного движения, причём эта сила максимальна, т. к. по условию начальное положение пружины соответствует максимальному растяжению пружины, при котором груз движется таким образом.
Запишем закон Ньютона для горизонтальной и вертикальной осей:
3. Подставим полученное выражение для в равенство из пункта 1:
После подстановки получим
Ответ:
Задача 2
Из пружинного пистолета выстрелили вертикально вниз в мишень, находящуюся на расстоянии 2 м от него. Совершив работу 0,12 Дж, пуля застряла в мишени. Какова масса пули, если пружина была сжата перед выстрелом на 2 см, а ее жесткость 100 Н/м?
Решение
Согласно закону сохранения механической энергии, имеем два равенства:
где и
— скорости летящей пули соответственно на высоте и непосредственно перед мишенью. Вся энергия подлетевшей к мишени пули потрачена на механическую работу, так что
Решая полученную систему уравнений, находим массу пули:
Задача 3
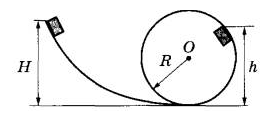
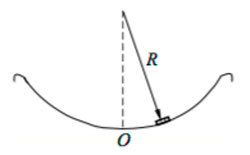
Небольшая шайба после толчка приобретает скорость v = 2 м/с и скользит по внутренней поверхности гладкого закрепленного кольца радиусом R = 0,14 м. На какой высоте h шайба отрывается от кольца и начинает свободно падать?
Решение
Согласно закону сохранения энергии:
, (1)
где — скорость шайбы в момент отрыва от кольца на высоте
.
В точке отрыва сила нормальной реакции опоры равна 0; . Центростремительное ускорение шайбы
найдём из второго закона Ньютона (см. рис.):
. (2)
. (3)
Объединяя (1), (2) и (3), получим:
м.
Ответ: 0,18.
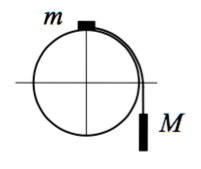
Задача 4
Грузы массами M = 1 кг и m связаны легкой нерастяжимой нитью, переброшенной через блок, по которому нить может скользить без трения (см. рис.). Груз массой М находится на шероховатой наклонной плоскости (угол наклона плоскости к горизонту а = 30°, коэффициент трения = 0,3). Чему равно минимальное значение массы m, при котором система грузов еще не выходит из первоначального состояния покоя?
Решение
Если масса m достаточно мала, но грузы ещё покоятся, то сила трения покоя, действующая на груз массой М, направлена вверх вдоль наклонной плоскости. Запишем второй закон Ньютона для каждого из покоящихся тел в проекциях на оси введенной системы координат. На первое тело действуют сила тяжести, сила нормальной реакции опоры, сила натяжения нити и сила трения:
(ось направлена вниз вдоль наклонной плоскости);
(ось направлена вверх перпендикулярно наклонной плоскости).
На второе тело действуют сила тяжести и сила натяжения нити:
(ось направлена вертикально вниз).
Учитывая, что (нить легкая, между блоком и нитью трения нет), то
(сила трения покоя). Получим:
кг.
Ответ: 0,24.
Задача 5
Тело, брошено с поверхности земли со скоростью v под углом a к горизонту. Сопротивление воздуха пренебрежимо мало.
Установите соответствие между физическими величинами, характеризующими движение тела, и формулами, по которым их можно определить.
К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры.

Решение
Рассмотрим динамику движения тела, брошенного под углом к горизонту с начальной скоростью
. В задаче нас интересует вертикальное движение тела.
Из рисунка видно, что проекция начальной скорости на ось Oy равна
.
Проекция ускорения равна
,
где м/с2 – ускорение свободного падения. Таким образом, скорость тела вдоль оси Oy будет меняться по закону
.
Можно заметить, что в точке максимального подъема скорость , получаем уравнение
То есть для буквы «А» соответствует формула под номером 4.
Для определения максимальной высоты , запишем формулу движения тела, подброшенного вертикально вверх:
и, учитывая, что ,
, а время для достижения максимальной высоты составляет
, получаем выражение:
.
То есть для буквы «Б» соответствует формула под номером 1.
Ответ: А4, Б1.
Задача 6
Воздушный шар объемом V = 2500 м3 с массой оболочки = 400 кг имеет внизу отверстие, через которое воздух в шаре нагревается горелкой. До какой минимальной температуры t1 нужно нагреть воздух в шаре, чтобы шар взлетел вместе с грузом (корзиной и воздухоплавателем) массой
= 200 кг? Температура окружающего воздуха t = 7 °С, его плотность
= 1,2 кг/м3. Оболочку шара считать нерастяжимой.
Решение
Шар взлетает, когда сила тяжести, действующая на него, равна силе Архимеда
, (1)
где m — масса воздуха в шаре. Из уравнения Менделеева-Клапейрона
,
, (2)
где ,
,
— молярная масса воздуха. Объединяя (1) и (2), получим:
К
соответственно °С.
Ответ: 350.
Задача 7
Брусок массой m1 = 500 г соскальзывает по наклонной плоскости с некоторой высоты h и, двигаясь по горизонтальной поверхности, сталкивается с неподвижным бруском массой m2 = 300 г. Считая столкновение абсолютно неупругим, определите высоту h, если общая кинетическая энергия брусков после столкновения равна 2,5 Дж. Трением при движении пренебречь. Считать, что наклонная плоскость плавно переходит в горизонтальную.
Решение
Кинетическая энергия брусков после столкновения где v — скорость системы после удара, определяемая из закона сохранения импульса на горизонтальном участке: m1v1 = (m1 + m2)v.
Исключая из системы уравнений скорость v, получим:
Кинетическая энергия первого бруска перед столкновением определяется из закона сохранения механической энергии при скольжении по наклонной плоскости: что даёт выражение
Подставляя значения масс и энергии из условия, получим численное значение h = 0,8 м
Ответ: h = 0,8 м.
Задача 8
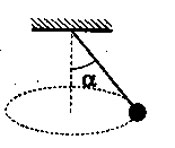
Небольшой груз, прикрепленный к нити длиной l = 15 см, вращается вокруг вертикальной оси так, что нить отклоняется от вертикали на угол a = 60°. С какой скоростью движется груз?
Решение
На груз действуют сила натяжения нити и сила тяжести
, как указано на рисунке.
В инерциальной системе отсчёта, связанной с Землёй, ускорение тела определяется вторым законом Ньютона:
Здесь — центростремительное ускорение. Решая полученную систему, получим:
м/с.
Ответ: 1,5.
Задача 9
Камень массой m = 4 кг падает под углом a = 30° к вертикали со скоростью 10 м/с в тележку с песком общей массой M = 16 кг, покоящуюся на горизонтальных рельсах. Определите скорость тележки с камнем после падения в нее камня.
Решение
Общая инерция камня, падающего в тележку, равна . Величина инерции, в горизонтальном направлении от падения камня составит
. Тогда из закона сохранения инерции, учитывая, что тележка вначале была неподвижной, а после падения в нее камня увеличила свою массу на массу камня, получаем
,
откуда
и

Ответ: 1.
Задача 10
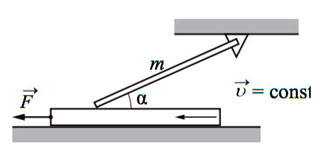
Два груза одинаковой массы М, связанные нерастяжимой и невесомой нитью, движутся прямолинейно по гладкой горизонтальной поверхности под действием горизонтальной силы F, приложенной к одному из грузов (см. рис.). Минимальная сила F, при которой нить обрывается, равна 12 Н. При какой силе натяжения обрывается нить?
Решение
Сила, под действием которой движутся грузы массой M – это равнодействующая, то есть учитывающая силу трения. Следовательно, из второго закона Ньютона можно записать , где
— ускорение, с которым движутся грузы. Сила натяжения нити T создается последним грузом, который перемещается с тем же ускорением
, но имеет массу M, т.е.
. Выражая ускорение как
, получаем силу натяжения, равную
Н.
Ответ: 6.
Задача 11
Груз, лежащий на столе, связан легкой нерастяжимой нитью, переброшенной через идеальный блок, с грузом массой 0,25 кг. На первый груз действует горизонтальная постоянная сила F, равная 9 Н (см. рис.). Второй груз движется с ускорением 2 м/с2, направленным вверх. Трением между грузом и поверхностью стола пренебречь. Какова масса первого груза?
Решение
На второй груз действует сила тяжести и противоположная сила тяги первого груза
Н (трение здесь не учитывается). Таким образом, для системы из двух грузов массами
и
можем записать
,
где — масса первого груза. Отсюда получаем:
Подставляем числовые значения, находим
кг.
Ответ: 3.
Задача 12
Маленький шарик падает сверху на наклонную плоскость и упруго отражается от неё. Угол наклона плоскости к горизонту равен На какое расстояние по горизонтали перемещается шарик между первым и вторым ударами о плоскость? Скорость шарика непосредственно перед первым ударом направлена вертикально вниз и равна 1 м/с.
Решение
Выберем следующую систему координат: ось направим вдоль плоскости, а ось
— перпендикулярно ей. Тогда кинематические уравнения движения шарика имеют вид:
В момент второго соударения шарика с плоскостью
Решая систему уравнений, получаем:
и
Из рисунка видно, что
Ответ:
Задача 13
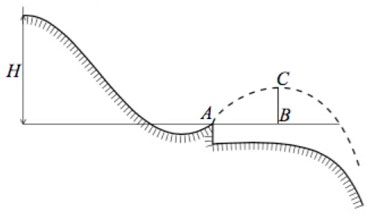
На гладкой горизонтальной поверхности стола покоится горка с двумя вершинами, высоты которых h и 5/2*h (см. рисунок). На правой вершине горки находится шайба. От незначительного толчка шайба и горка приходят в движение, причём шайба движется влево, не отрываясь от гладкой поверхности горки, а поступательно движущаяся горка не отрывается от стола. Скорость шайбы на левой вершине горки оказалась равной v. Найдите отношение масс шайбы и горки.
Решение
На систему тел «шайба + горка» действуют внешние силы (тяжести и реакции стола), направленные по вертикали, поэтому проекция импульса системы на горизонтальную ось Ох системы отсчёта, связанной со столом, сохраняется.
В начальный момент , а в момент
. Из закона сохранения импульса
получим:
, где m — масса шайбы, М — масса горки.
Работа сил тяжести определяется изменением потенциальной энергии, а суммарная работа сил реакции равна нулю, так как поверхности гладкие. Следовательно, полная механическая энергия системы тел, равная сумме кинетической и потенциальной, сохраняется. Так как потенциальная энергия горки не изменилась, получаем уравнение
.
Решение системы дает отношение масс
.
Ответ: .
Задача 14
Снаряд, движущийся со скоростью v0 разрывается на две равные части, одна из которых продолжает движение по направлению движения снаряда, а другая движется в противоположную сторону. В момент разрыва суммарная кинетическая энергия осколков увеличивается за счёт энергии взрыва на величину ∆E. Скорость осколка, движущегося вперёд по направлению движения снаряда, равна v1. Найдите массу m осколка.
Решение
Введём обозначение: v2 — модуль скорости летящего назад осколка снаряда. Система уравнений для решения задачи:
Выразим v2 из первого уравнения: — и подставим во второе уравнение. Получим:
. Отсюда следует:

Ответ: 
Задача 15
Снаряд массой 2m разрывается в полёте на две равные части, одна из которых продолжает движение по направлению движения снаряда, а другая — в противоположную сторону. В момент разрыва суммарная кинетическая энергия осколков увеличивается за счёт энергии взрыва на величину ∆Е. Модуль скорости осколка, движущегося по направлению движения снаряда, равен v1, а модуль скорости второго осколка равен v2. Найдите ∆Е.
Решение
Введём обозначение: v0 — модуль скорости снаряда до разрыва. Система уравнений для решения задачи:
Выразим v0 из первого уравнения: и подставим во второе уравнение. Получим:
.
Отсюда следует:
.
Ответ: .
Задача 16
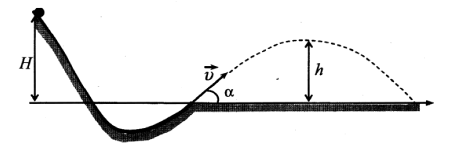
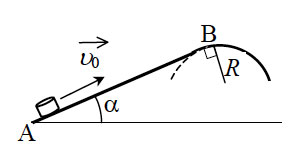
При выполнении трюка «Летающий велосипедист» гонщик движется по гладкому трамплину под действием силы тяжести, начиная движение из состояния покоя с некоторой высоты (см. рисунок). На краю трамплина скорость гонщика направлена под углом α = 60° к горизонту. Пролетев по воздуху, он приземляется на горизонтальный стол, поднявшись в полёте на высоту h над краем трамплина. С какой высоты H начинал движение гонщик?
Решение
Применим закон сохранения энергии и найдём скорость велосипедиста при отрыве от трамплина.
Рассмотрим проекции скорости на горизонтальную и вертикальную оси:
В тот момент, когда велосипедист достигнет наивысшей точки полёта вертикальная проекция его скорости станет равной нулю, при этом в горизонтальном направлении он пролетит половину пути. Найдём время, за которое велосипедист достигнет наивысшей точки.
Координата зависит от времени по закону
Значит, максимальная высота полёта велоспедиста
Откуда
Ответ:
Задача 17
После толчка льдинка закатилась в яму с гладкими стенками, в которой она может двигаться практически без трения. На рисунке приведен график зависимости энергии взаимодействия льдинки с Землей от её координаты в яме.
В некоторый момент времени льдинка находилась в точке А с координатой и двигалась влево, имея кинетическую энергию, равную 2 Дж. Сможет ли льдинка выскользнуть из ямы? Ответ поясните, указав, какие физические закономерности вы использовали для объяснения.
Решение
1) Льдинка сможет выскользнуть из ямы через ее правый край.
2) Трения при движении льдинки нет, поэтому ее механическая энергия сохраняется. Запас кинетической энергии льдинки в точке A позволяет ей подняться до уровня, где ее потенциальная энергия составит 4 Дж.
3) Левый край ямы поднят до большей высоты. Следовательно, этого края льдинка не достигнет и заскользит вправо. Правый же край ямы ниже: на верху этого края потенциальная энергия льдинки меньше 4 Дж. Поэтому льдинка выскользнет из ямы через правый край.
Задача 18
Гладкий клин массой M с углом при основании стоит на горизонтальной плоскости, часть которой под ним и левее — гладкая, а часть — справа от него — шероховатая (см. рис.). На вершине клина, на высоте H над плоскостью находится маленький брусок массой m, коэффициент трения которого о шероховатую часть плоскости равен
Брусок отпускают без начальной скорости, он скатывается по клину и далее скользит по шероховатой плоскости и останавливается на некотором расстоянии L по горизонтали от своего начального положения. Найдите это расстояние L, если в точке перехода с клина на плоскость есть гладкое закругление, так что скорость бруска при переходе с клина на плоскость не уменьшается.
Решение
При соскальзывании бруска с клина выполняются законы сохранения горизонтальной проекции импульса и механической энергии данной системы тел:
где v и V — скорости бруска и клина, соответственно, после соскальзывания бруска с клина. Из этих уравнений следует, что скорость бруска перед его попаданием на шероховатый участок плоскости равна:
До попадания на этот участок брусок сдвинется из начального положения по горизонтали без трения на расстояние равное, очевидно, длине основания клина, а затем пройдёт по шероховатой плоскости расстояние
на котором его кинетическая энергия будет израсходована на работу против силы сухого трения скольжения. По закону Амонтона — Кулона эта сила равна
так как сила N давления бруска на неподвижную горизонтальную плоскость равна mg. Таким образом,
и
Искомое расстояние L в результате равно сумме l1 и l2:
Ответ:
Задача 19
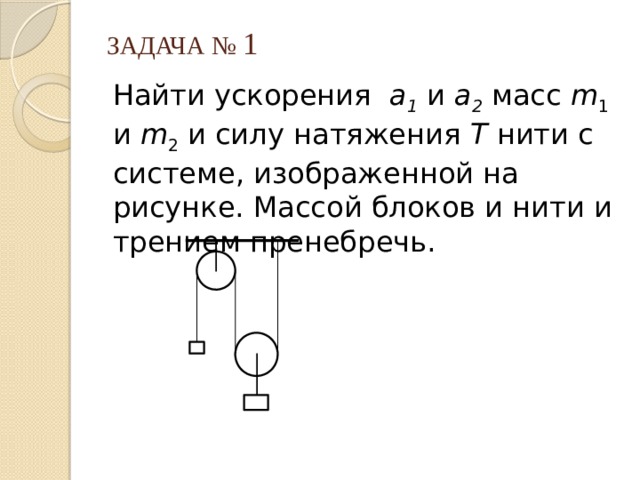
В системе, изображённой на рисунке, трения нет, блоки невесомы, нить невесома и нерастяжима, m1 = 2 кг, m2 = 4 кг, m3 = 1 кг. Найдите модуль и направление ускорения груза массой m3.
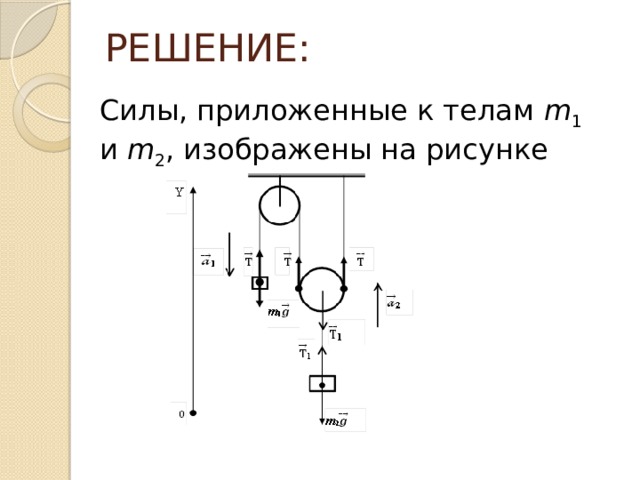
Решение
1. Введём на рисунке неподвижную систему координат, у которой ось x горизонтальна и направлена вправо, а ось y направлена вертикально вниз. Обозначим также силы, определяющие ускорения тел вдоль направлений их движения: силу T натяжения нити, которая, как следует из условия задачи, постоянна по модулю вдоль всей нити, и силу тяжести
2. Записывая второй закон Ньютона в проекциях на оси x и y для трёх грузов, имеем:
3. Поскольку нить нерастяжима, из постоянства её длины получаем следующее соотношение для координат грузов:
Отсюда следует связь между ускорениями грузов:
4. Решая полученную систему уравнений, находим модуль искомого ускорения:
вектор направлен вниз.
Ответ: вектор
направлен вниз.
Задача 20
К двум вертикально расположенным пружинам одинаковой длины подвесили однородный стержень длиной L = 30 см. Если к этому стержню подвесить груз массой m = 3 кг на расстоянии d = 5 см от правой пружины, то стержень будет расположен горизонтально, и растяжения обеих пружин будут одинаковы (см. рисунок). Жёсткость левой пружины в 2 раза меньше, чем правой. Чему равна масса стержня М? Сделайте рисунок с указанием используемых в решении сил.
Решение
1. Укажем на рисунке силы действующие на стержень. Приравняем моменты сил, действующих на стержень, относительно центра стержня, т.е. точки А:
Учтем, что стержень расположен горизонтально, т.е. удлинения пружин равны, а также, что жесткость правой пружины в два раза больше левой:
2. Приравняем моменты сил, действующих на стержень, относительно точки Б, которая находится в месте крепления правой пружины:
3. Найдем массу стержня:
Ответ:
Задача 21
Найдите модуль ускорения a груза массой m в системе, изображённой на рисунке. Трения нет, блоки невесомы, нити лёгкие и нерастяжимые, их участки, не лежащие на блоках, вертикальны, масса второго груза M, ускорение свободного падения равно g.
Решение
Введём координатную ось Х, направленную вниз, и отметим на ней координаты грузов М и m: xM и xm (см. рис.). Пронумеруем блоки цифрами 1, 2, 3 и укажем на рисунке силы натяжения нитей и силы тяжести, действующие на грузы. Согласно условию, в силу невесомости нитей и блоков, а также отсутствия сил трения, первая нить, охватывающая блоки 1 и 2, натянута с силой T, а вторая — с силой 2T, так что на груз m действует направленная вверх сила 4T. Если сместить груз М вдоль оси Х вниз на расстояние ΔxM, то в силу нерастяжимости нитей блок 2 сместится, как следует из рисунка, на −ΔxM/2, а блок 3 и груз m — на Δxm = −ΔxM/4. Таким образом, ΔxM + 4Δxm = 0.
Отсюда получаем уравнение кинематической связи: A + 4a = 0, где A и a — проекции ускорений грузов М и m на ось Х. Уравнения движения грузов (второй закон Ньютона) в проекциях на ось Х имеют вид: МA = Мg – T, ma = mg – 4T. Решая полученную систему из трех уравнений, находим, что модуль ускорения груза М равен:
Ответ:
Задача 22
Тонкий однородный стержень АВ шарнирно закреплён в точке А и удерживается горизонтальной нитью ВС (см. рисунок). Трение в шарнире пренебрежимо мало. Масса стержня m = 1 кг, угол его наклона к горизонту α = 45°. Найдите модуль силы действующей на стержень со стороны шарнира. Сделайте рисунок, на котором укажите все силы, действующие на стержень.
Решение
1. Изобразим на рисунке силы, действующие на стержень, и систему координат Оху.
Здесь — сила натяжения нити,
— сила тяжести,
и
— вертикальная и горизонтальная составляющие силы, действующей на стержень со стороны шарнира.
2. В положении равновесия равны нулю сумма моментов сил, действующих на стержень, относительно оси, проходящей через точку А перпендикулярно плоскости рисунка, сумма горизонтальных и сумма вертикальных составляющих сил, действующих на стержень:
где
— длина стержня; (1)
(2)
(3)
3. Модуль силы реакции шарнира
Из (1) получим Окончательно
Ответ:
Задача 23
Из двух ровных досок сделан желоб, представляющий собой двугранный угол с раствором Желоб закреплен так, что его ребро горизонтально, а доски симметричны относительно вертикали. В желобе на боковой поверхности лежит цилиндр массой
Коэффициент трения между досками и цилиндром равен
К торцу цилиндра приложена горизонтально направленная сила
Найдите модуль ускорения цилиндра.
Решение
Изобразим вид на желоб со стороны торца цилиндра. На цилиндр в плоскости чертежа действуют направленная вниз сила тяжести
и две равные по модулю силы реакции
досок, направленные перпендикулярно стенкам желоба. Так как цилиндр не движется в вертикальном направлении, то, в соответствии со вторым законом Ньютона, сумма проекций этих трех сил на вертикаль равна нулю:
где
Отсюда В горизонтальном направлении (вдоль желоба) на цилиндр действуют сила
а также, в противоположном направлении, две силы сухого трения
Предположим, что цилиндр будет двигаться по желобу. Тогда по закону Амонтона — Кулона для силы сухого трения скольжения можно записать:
Записывая второй закон Ньютона в проекции на горизонтальную ось, направленную вдоль ребра желоба, получим:
где — модуль искомого ускорения цилиндра. Заметим, что
Это означает, что приложенная к торцу цилиндра сила превышает силу трения покоя, то есть цилиндр и в самом деле будет скользить вдоль желоба.
Следовательно, Подставляя числовые данные и проверяя размерность, окончательно получим:
Ответ:
Задача 24
Равносторонний треугольник, состоящий из трёх жёстких лёгких стержней, может вращаться без трения вокруг горизонтальной оси, совпадающей с одной из его сторон. В точке пересечения двух других его сторон к треугольнику прикреплён массивный грузик (см. рисунок). Как и во сколько раз изменится период малых колебаний грузика около его положения равновесия, если ось вращения наклонить под углом к горизонту?
Решение
Обозначим расстояние от оси вращения треугольника до грузика через Тогда период колебаний при горизонтальном положении оси равен, очевидно,
После наклона оси на угол возвращающая сила при отклонении треугольника от положения равновесия уменьшится: составляющая силы тяжести вдоль оси, равная
(здесь
— масса грузика), будет компенсироваться силами реакции со стороны подшипников, в которых закреплена эта ось, а в направлении, перпендикулярном оси, будет действовать эффективная «сила тяжести», равна
Поэтому период малых колебаний грузика при наклоненной оси будет равен
Таким образом, период колебаний увеличится в раз.
Ответ: период колебаний увеличится в раз.
Задача 25
На гладкой горизонтальной плоскости лежат два груза массами и
соединённые невесомой нерастяжимой нитью, перекинутой через два неподвижных (А и В) и один подвижный (О) невесомые блоки, как показано на рисунке. Оси блоков горизонтальны, трения в осях блоков нет. К оси О подвижного блока приложена направленная вертикально вниз сила F = 4 Н. Найдите ускорение этой оси. Сделайте схематический рисунок с указанием сил, действующих на грузы и блок.
Решение
Нарисуем силы Т натяжения нити, одинаковые, в силу условия задачи, вдоль всей нити и действующие на грузы и блок О (см. рисунок). Введём систему координат XY, как показано на рисунке, и запишем уравнения движения грузов в проекции на ось X:
В силу невесомости блока О имеем или
В силу нерастяжимости нити (длиной L) и неподвижности блоков А и В (их координаты и
постоянны) имеется следующая кинематическая связь между координатами
и
грузов и координатой
блока О (здесь
— радиус блоков А и В, R — радиус блока О):
или
и значит
Решаем записанную систему уравнений и получаем ответ:
Ответ:
Задача 26
Два вращающихся вала соединены замкнутым ремнём, который не проскальзывает относительно валов. Радиус первого вала равен R, радиус второго вала равен 2R. Чему равно отношение угловой скорости точки A к угловой скорости вращения первого вала
Решение
Скорость движения точек первого вала, находящихся на расстоянии от его центра, даётся формулой
Угловая скорость вращения точки А равна угловой скорости вращения второго вала. Валы связаны ремнём, поэтому скорости ободов
у валов одинаковы, а их угловые скорости
В итоге получаем
Ответ: 0,5.
Задача 28
Два велосипедиста совершают кольцевую гонку с одинаковой угловой скоростью. Положения и траектории движения велосипедистов показаны на рисунке. Чему равно отношение центростремительных ускорений велосипедистов ?
Решение
При движении по окружности угловая и линейная
скорости тела связаны с радиусом окружности
соотношением:
Центростремительное ускорение равно
Поскольку велосипедисты едут с одинаковым угловыми скоростями, для отношения центростремительных ускорения велосипедистов имеем:
Ответ: 2.
Задача 29
Прибор наблюдения обнаружил летящий снаряд и зафиксировал его горизонтальную координату и высоту
м над Землёй (см. рисунок). Через 3 с снаряд упал на Землю и взорвался на расстоянии
м от места его обнаружения. Известно, что снаряды данного типа вылетают из ствола пушки со скоростью 800 м/с. Какова была максимальная высота Н траектории снаряда, если считать, что сопротивление воздуха пренебрежимо мало? Пушка и место взрыва находятся на одной горизонтали.
Первое решение
Найдём горизонтальную скорость снаряда:
Найдём вертикальную проекцию скорости снаряда в момент обнаружения:
Определим, за какое время снаряд долетел из верхней точки траектории в точку, в которой был зафиксирован:
Таким образом, время опускания снаряда составляет
Таким образом, максимальная высота снаряда:
Второе решение
Найдём горизонтальную скорость снаряда: эта скорость остается постоянной на протяжении всего полета. Определим величину вертикальной проекции скорости в начальный момент:
Используя формулу для максимальной высоты брошенного под углом к горизонту тела, получаем:
Ответ: около 16 км.
Задача 30
К концу вертикального стержня привязана лёгкая нерастяжимая нить с маленьким грузиком на конце. Грузик раскрутили на нити так, что она отклонилась от вертикали на угол α = 30º (см. рисунок). Как и во сколько раз надо изменить угловую скорость ω вращения грузика вокруг стержня для того, чтобы этот угол стал равным β = 60º?
Решение
1. Обозначим силу натяжения нити T, массу грузика m, длину нити l, радиус окружности, по которой вращается грузик, R, и изобразим систему на рисунке (см. рисунок).
2. Запишем уравнение движения грузика по окружности вокруг стержня в проекциях на вертикальную ось и на радиус окружности с учётом выражения для центростремительного ускорения грузика:
,
.
3. Из написанных соотношений следует, что , а
.
4. Для того, чтобы угол отклонения нити стал равным β, угловая скорость вращения грузика должна увеличиться в
раза.
Ответ: 1,3 раза.
Задача 31
В аттракционе человек массой 80 кг движется на тележке по рельсам и совершает «мертвую петлю» в вертикальной плоскости. Каков радиус круговой траектории, если при скорости 10 м/с, направленной вертикально вверх, сила нормального давления человека на сидение тележки равна 1 600 Н? Ускорение свободного падения равно
Задача 32
На рисунке приведен график зависимости проекции скорости тела от времени. Чему равна проекция ускорения тела в момент времени 45 с? Ответ выразите в м/с2.
Решение
Из графика видно, что скорость в интервале времени от 40 с до 50 с меняется линейно, значит, ускорение постоянно. На всём этом интервале времени ускорение такое же, как и в момент времени 45 с. Найдём это ускорение:
Ответ: 2.
Задача 32
Два небольших тела с массами 2 кг и 3 кг висят на разных концах невесомой нерастяжимой нити, перекинутой через гладкий неподвижный блок. Первое тело находится на высоте 40 см ниже второго. Тела пришли в движение без начальной скорости. Через какое время они окажутся на одной высоте? Сделайте схематический рисунок с указанием сил, действующих на тела. Обоснуйте применимость используемых законов к решению задачи.
Решение
Задача 33
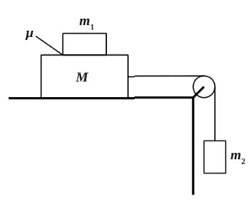
Система грузов M, m1 и m2, показанная на рисунке, движется из состояния покоя. Поверхность стола — горизонтальная гладкая. Коэффициент трения между грузами M и m1 равен μ = 0,3. Грузы M и m2 связаны легкой нерастяжимой нитью, которая скользит по блоку без трения. Пусть M = 2,4 кг, m1 = m2 = m. При каких значениях m грузы M и m1 движутся как одно целое? Сделайте рисунок с указанием сил, действующих на грузы.
Решение
Задача 34
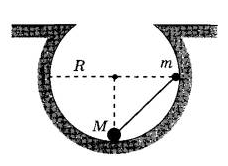
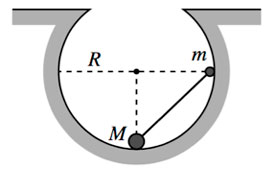
Небольшие шарики, массы которых m и M, соединены лёгким стержнем и помещены в гладкую сферическую выемку радиусом R = 20 см. В начальный момент шарики удерживаются в положении, изображённом на рисунке. Когда их отпустили без толчка, шарики стали скользить по поверхности выемки. Минимальная высота, на которой оказался шарик m в процессе движения, равна 4 см от нижней точки выемки. Определите отношение масс M и m.
Решение
Задача 35
Небольшой брусок массой m начинает соскальзывать с высоты H по гладкой горке, переходящей в мёртвую петлю (см. рисунок). Определите высоту отрыва бруска, если высота горки H. Радиус окружности R. Сделайте рисунок с указанием сил, поясняющий решение.
Решение
Направим ось Ох вдоль ускорения и пусть сила тяжести образует с этой осью угол α Запишем второй закон Ньютона для бруска на высоте h:
Выразим отсюда скорость бруска, учитывая, что и по третьему закону Ньютона
:
На высоте h брусок обладает как кинетической, так и потенциальной энергией. Из закона сохранения энергии найдём искомую высоту H:
откуда
Задача 36
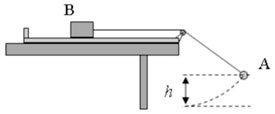
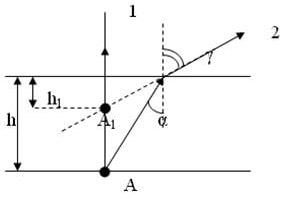
В маленький шар массой M=100г, висящий на нити длиной l=50 см, попадает и застревает в нем пулька массой m=20г, летящая под углом 30 град к горизонту (см рисунок). Какую скорость v имела пуля перед попаданием в шар, если после соударения шар с застрявшей в нем пулей отклонился по вертикали на угол 60 град? Сопротивлением воздуха пренебречь. Какие законы вы использовали для описания взаимодействия пульки с шаром и подьема тел? Обоснуйте их применимость к данному случаю.
Решение
Задача 37
При выполнение трюка летающий велосипедист гонщик движется по трамплину под действием силы тяжести, начиная движение из состояния покоя с высоты H. На краю трамплина скорость гонщика направлена под таим углом к горизонту, что дальность его полета максимальна. Пролетев по воздуху, гонщик приземляется на горизонтальный стол, находящейся на той же высоте, что и край трамплина. Какова высота полета h на этом трамплине? Сопротивлением воздуха и трением пренебречь.
Решение
Слайд 1
Механика
Слайд 2
Перед ребенком, решившим выбрать в своей жизни дорогу научно-технического направления, встают две задачи: ЭКЗАМЕНЫ (ГИА и ЕГЭ) . И для сдачи экзаменов в новых форматах успешной учебы в течение всех прошедших лет оказывается недостаточно. Проблема в том, что сдача экзаменов требует от ребенка особого алгоритма работы, повышенной интенсивности мыслительной деятельности, работы в измененном психофизическом стрессовом состоянии и работы с большим объемом информации. Можно уверенно сказать, что школьная программа на это не рассчитана.
Слайд 3
1. Поэтапно, в соответствии с последовательностью изучения 6 разделов школьного курса физики освоить все содержание основной триады (понятия-законы-границы применимости). Более того, в задачи школьной программы вовсе, не входит подготовка к ГИА и ЕГЭ. По действующему законодательству в задачи школы входит освоение учениками федеральных государственных образовательных стандартов (ФГОС) и не более. А экзамены ГИА и ЕГЭ – это уже проверка государством уровня подготовленности учеников по своим стандартам, которые попросту не связаны с ФГОС.
Слайд 4
2. После изучения триады соответствующего раздела физики освоить методы решения физических задач из этого раздела. 3. Проконтролировать освоение изученного раздела. «Подводные камни» Методика работает только при полной мотивации ребенка на обучение. Уговоры и принуждения при таком подходе попросту «не сработают». Школьнику необходимо выделить время на заучивание триады (понятия-законы-границы применимости), этого за него никто сделать не сможет. В случае же, если необходимые составляющие заучены не будут, все остальные учебные действия потеряют свою базовую опору и в сознании школьника не сохранятся.
Слайд 5
Существенные затруднения у учащихся ежегодно возникают при решении качественных задач. Порядка 70-75% экзаменуемых получали за ее решение ноль баллов. Дело в том, что примеры качественных заданий в пособиях для подготовки к экзамену и в опубликованном открытом сегменте КИМ присутствуют в минимальном количестве. Таким образом, возможности абитуриентов по целенаправленной подготовке к выполнению этой части экзаменационной работы были ограничены.. Результаты экзамены показали, что обучающиеся не умеют корректно использовать физические термины, ссылаясь при необходимости на физические законы.
Слайд 6
В качестве примера приведем подробное решение следующей задачи. Задача С1. Доказать, что крупные капли дождя падают быстрее, чем мелкие. Капли имеют форму шара, силу сопротивления воздуха считать пропорциональной площади поперечного сечения капли. Решение: Прежде всего, следует понять модель процесса. Совершенно ясно, что в данной задаче нельзя пренебречь силой сопротивления воздуха. Именно она и оказывает решающее влияние на скорость капли, и дело здесь не только в разной массе капель воды. Рассмотри силы, действующие на каплю при ее падении в воздухе
Слайд 7
На каплю вверх действует сила сопротивлении воздуха. пропорциональная квадрату радиуса (площади поперечного сечения), а вниз действует сила тяжести , пропорциональная массе тела, а следовательно объему тела, т.е. кубу радиуса капли. Таким образом, с ростом размера капли сила тяжести растет быстрее силы сопротивления воздуха., равнодействующая этих сил (направленная вниз) растет и растет ускорение капли. F т F сопр
Слайд 8
Основное затруднение при решении задач это создание алгоритма. К сожалению создать такой алгоритма невозможно. В некоторых разделах физики например в динамике некоторые элементы таких алгоритмов можно придумать. В динамике очень важно находить все силы. Действующие на тело и ускорение. Что является первичным в механике? Первичным является взаимодействие: гравитационное, электромагнитное, сильное и слабое. Результатом взаимодействия является сила. Определение сил и является построением модели задачи.
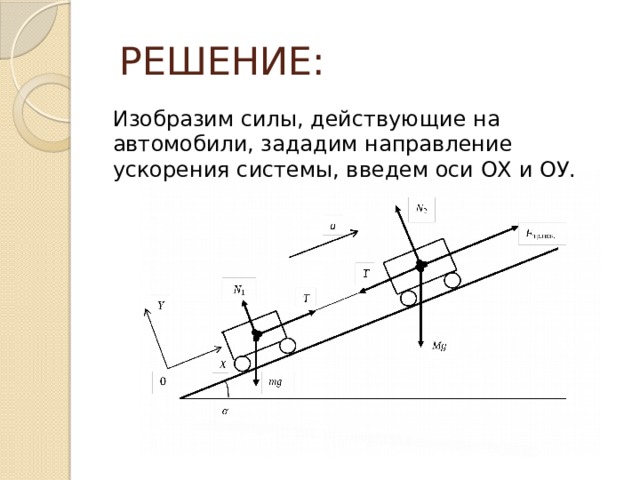
Слайд 9
Задача С2. Груз массой m располагается на поверхности клина с углом при основании α. К грузу прикреплена нить, другой конец которой привязан к гвоздю. Вбитому в вершину клина. Клин перемещается в горизонтальном направлении с ускорением а .Найти силу натяжения нити T силу давления груза на поверхность клина F д. Решение. На клин действует сила, вынуждающая его двигаться с ускорением а в горизонтальном направлении. Эта сила приложена именно к клину, но не к грузу на нем. Груз хоть и движется вместе с клином с таким же ускорением а , но под действием иных сил, приложенных к нему. Этими силами являются сила тяжести mg , сила натяжения нити Т и сила реакции опоры N . Совместное действие этих трех сил и сообщает грузу ускорение а .
Слайд 10
Y X N mg T cos α N sin α T N cos α T sin α α α α α α a
Слайд 11
Согласно второму закону Ньютона, применительно к грузу: ma = mg + T + N Запишем закон в скалярном виде. Спроецируем эти силы на оси координат ОХ и OY , сонаправив ось ОХ с ускорением груза и клин а . Тогда второй закон Ньютона в проекциях применительно к движению груза на клине имеет вид: ma = 0 + T cos α – N sin α ( 1 ) В этом уравнение есть две искомые величины N и T . Для их определения составим еще одно уравнение, спроецировав силы, приложенные к грузу , на ось OY : mg =T sin α +N cos α ( 2 ) Из уравнения ( 2 ) выразим силу N : N = (mg -T sin α ) / cos α ( 3 )
Слайд 12
и подставим в уравнение ( 1 ): ma = T cos α – (mg -T sin α ) sin α cos α преобразуем : ma cos α = T cos 2 α — mg sin α +T sin 2 α m (a cos α + g sin α ) = T ( sin 2 α + cos 2 α ) sin 2 α + cos 2 α = 1 отсюда: T = m (a cos α + g sin α ) – первая величина найдена. По третьему закону Ньютона сила давления груза F давл равна силе давления клина на груз, т.е. силе реакции опоры N , которая равна ( 3 ): N = (mg -T sin α ) / cos α – вторая величина найдена, Задача решена.
Слайд 13
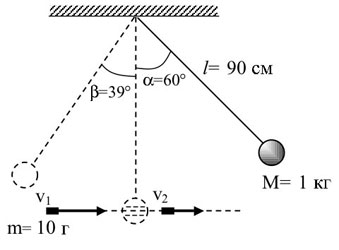
Задача С3 . Шар массой 1 кг, подвешенный на нити длиной 90 см, отводят от положения равновесия на угол 60° и отпускают. В момент прохождения шаром положения равновесия в него попадает пуля, летящая навстречу шару. Она пробивает его и продолжает двигаться горизонтально. После попадания пули в шар он продолжает движение в прежнем направлении, пока нить не составит с вертикалью угол 39°. Определите массу пули, если в результате попадания в шар скорость пули уменьшилась на 100 м/с. (Массу шара считать неизменной, диаметр шара – пренебрежимо малым по сравнению с длиной нити, с os 39 ° = 0,778.
Слайд 14
1. По закону сохранения импульса Mu 1 — m υ 1 = Mu 2 — m υ 2 , где m – масса пули, u 1 , u 2 – скорости шара до и после взаимодействия с пулей соответственно. Отсюда ∆ υ = υ 2 — υ 1 = ( u 2 — u 1 ) ( 1 ) 2. По закону сохранения энергии скорость шара в нижней точке траектории до попадания в него пули равна: u 1 = √ 2gl(1- cosa ) . 3. По закону сохранения энергии скорость шара в нижней точке траектории после вылета из него пули равна: u 2 = √ 2gl(1- cos β ) . m M
Слайд 15
4. Подставляя в формулу ( 1 ) изменение скорости шара, получим: ∆ υ = υ 2 — υ 1 = M √ 2gl(1- cos β ) — √ 2gl(1- cosa ) , откуда: m = M √ 2gl(1- cos β ) — √ 2gl(1- cosa ) 5. Проводя вычисления, получим: m = 1 √ 2 . 10 . 0,9 (1 – 0,778) — √ 2 . 10 . 0,9 ( 1 – 0,5) = 0,01 кг Ответ: 0,01 кг υ 2 — υ 1 m — 100
Слайд 16
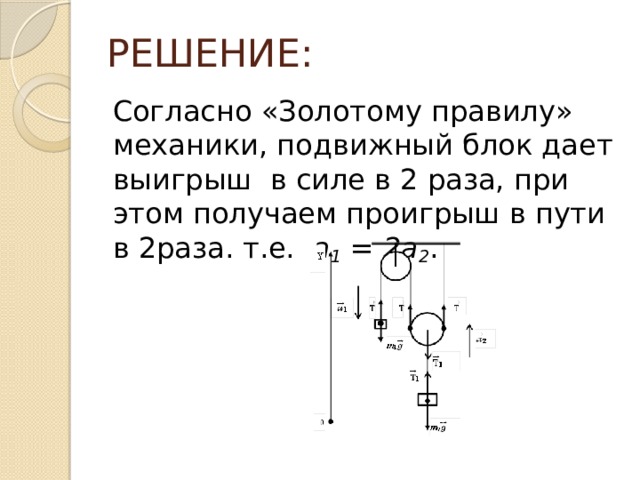
ЕЕЕЕЕЕ Е k Задача 4. Е k Е k Е P Задача решена.
Слайд 17
Задача 5. Тело массой m связано двумя пружинами одинаковой жесткости k , которые один раз соединяются параллельно, а второй- последовательно. В обеих случаях телу сообщается скорость υ . В каком отношении будут находится амплитуды колебаний грузов без учета трения и сопротивления ?
Слайд 18
Решение: 1. В первом случае пружины соединены параллельно, поэтому общая их жесткость равна k 1 = k + k = 2k . Закон сохранения энергии представится следующим образом: 2. При последовательном соединении пружин: 3.Отношение амплитуд собственных колебаний: Задача решена.
Слайд 19
Задача С6. Небольшой шар, надет на гладкую горизонтальную спицу, прикреплен к двум невесомым пружинам, вторые концы которых заделаны в неподвижную стену так, что в положении равновесия пружины не деформированы. Найти период колебаний тела, если при ее поочередном подвешивании к пружинам их удлинение составило ∆ x 1 и ∆ x 2 .
Слайд 20
Решение. 1. Жесткости пружин: 2. Пружины соединены параллельно. Поэтому их общая жесткость равна сумме жесткостей:
Слайд 21
3. Период колебания тела: Задача решена.
Слайд 22
Задача 6. Поднимая при помощи подвижного блока ведро с песком весом 200 Н на высоту 5 м, производят работу 1020 Дж. Какой процент составляет энергия, которая была затрачена непроизводительно? Решение: Полезная работа, которую нужно совершить, чтобы поднять груз весом Р на высоту h равна: А= Р . h = 200 . 5 = 1000 Дж . Общая совершенная работа составила А общ =1020 Дж. Таким образом, непроизводительно была затрачена энергия: ∆ А =А общ – А = 1020 — 1000 = 20 Дж. Эта величина составляет в процентном отношении: (∆ А /А общ ) . 100%= (20/100) . 100% = 2% То есть непроизводительно было затрачено 2% от общей энергии Задача решена.
Задачи из ДЕМОВАРИАНТОВ (с решениями)
1. Тело, свободно падающее с некоторой высоты
без начальной скорости, за время τ = 1 с после начала
движения проходит путь в n = 5 раз меньший, чем за
такой же промежуток времени в конце движения. Найдите полное
время движения.
Образец возможного решения
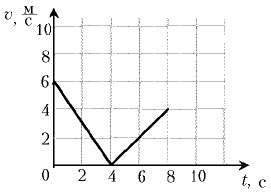
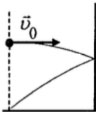
2. Шайба, брошенная вдоль наклонной плоскости,
скользит по ней, двигаясь вверх, а затем движется вниз. График
зависимости модуля скорости шайбы от времени дан на рисунке.
Найти угол наклона плоскости к горизонту.
Образец возможного решения
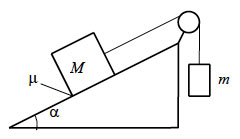
3. Грузы массами M
= 1 кг и m связаны лёгкой нерастяжимой нитью, переброшенной
через блок, по которому нить может скользить без трения (см.
рисунок). Груз массой M находится на шероховатой наклонной
плоскости (угол наклона плоскости к горизонту α = 30°,
коэффициент трения μ = 0,3). Чему равно максимальное значение
массы m, при котором система грузов ещё не выходит
из первоначального состояния покоя? Решение поясните схематичным
рисунком с указанием используемых сил.
Образец возможного решения
массы Земли, диаметр Марса вдвое меньше, чем диаметр Земли. Каково
отношение периодов обращения искусственных спутников Марса и Земли
ТM/ТЗ, движущихся по круговым
орбитам на небольшой высоте?
Образец
возможного решения
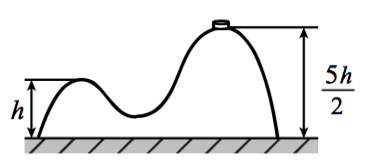
5. На гладкой горизонтальной поверхности стола покоится горка с двумя вершинами, высоты которых h и 5h/2 (см. рисунок). На правой вершине горки находится шайба. От незначительного толчка шайба и горка приходят в движение, причём шайба движется влево, не отрываясь от гладкой поверхности горки, а поступательно движущаяся горка не отрывается от стола. Скорость шайбы на левой вершине горки оказалась равной u. Найдите отношение масс шайбы и горки.
Образец возможного решения
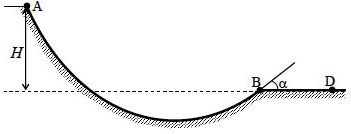
6. Шайба массой m
начинает движение по желобу AB из точки А из состояния покоя.
Точка А расположена выше точки В на высоте H = 6 м.
В процессе движения по желобу механическая энергия шайбы из-за
трения уменьшается на ΔE = 2 Дж. В точке В шайба
вылетает из желоба под углом α = 15° к горизонту и падает
на землю в точке D, находящейся на одной горизонтали с точкой
В (см. рисунок). BD = 4 м. Найдите массу шайбы m. Сопротивлением
воздуха пренебречь.
Образец возможного решения
7. Шарик скользит без трения по наклонному
желобу, а затем движется по «мертвой петле» радиуса R.
С какой силой шарик давит на желоб в нижней точке петли, если
масса шарика равна 100 г, а высота, с которой его отпускают,
равна 4R?
Образец возможного решения
8. Небольшая шайба после
удара скользит вверх по наклонной плоскости из точки А (см.
рисунок). В точке В наклонная плоскость без излома переходит
в наружную поверхность горизонтальной трубы радиусом R.
Если в точке А скорость шайбы превосходит υ0
= 4 м/с, то в точке В шайба отрывается от опоры. Длина наклонной
плоскости АВ = L = 1 м, угол α = 30°. Коэффициент
трения между наклонной плоскостью и шайбой μ = 0,2. Найдите
внешний радиус трубы R.
Образец возможного решения
9. Кусок пластилина
сталкивается со скользящим навстречу по горизонтальной поверхности
стола бруском и прилипает к нему. Скорости пластилина и бруска
перед ударом направлены противоположно и равны vпл
= 15 м/с и vбр = 5 м/с. Масса бруска в 4 раза больше
массы пластилина. Коэффициент трения скольжения между бруском
и столом μ = 0,17. На какое расстояние переместятся слипшиеся
брусок с пластилином к моменту, когда их скорость уменьшится
на 30%?
Образец возможного решения
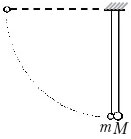
10. Система из грузов m и M и связывающей их лёгкой нерастяжимой нити в начальный момент покоится в вертикальной плоскости, проходящей через центр закреплённой сферы. Груз m находится в точке А на вершине сферы (см. рисунок). В ходе возникшего движения груз m отрывается от поверхности сферы, пройдя по ней дугу 30°. Найдите массу m, если М = 100 г. Размеры груза m ничтожно малы по сравнению с радиусом сферы. Трением пренебречь. Сделайте схематический рисунок с указанием сил, действующих на грузы.
Образец возможного решения
11. Шар массой 1 кг, подвешенный на нити
длиной 90 см, отводят от положения равновесия на угол 60o
и отпускают. В момент прохождения шаром положения равновесия
в него попадает пуля массой 10 г, летящая навстречу шару.
Она пробивает его и продолжает двигаться горизонтально. Определите
изменение скорости пули в результате попадания в шар, если
он, продолжая движение в прежнем направлении, отклоняется
на угол 39o. (Массу шара считать неизменной, диаметр
шара – пренебрежимо малым по сравнению с длиной нити, cos
39° = 7/9.)
Образец возможного решения
12. Два тела, массы которых соответственно
m1 = 1 кг и m2 = 2кг, скользят по гладкому
горизонтальному столу (см. рисунок). Скорость первого тела
v1 = 3 м/с, скорость второго тела v2
= 6 м/с. Какое количество теплоты выделится, когда они столкнутся
и будут двигаться дальше, сцепившись вместе? Вращения в системе
не возникает. Действием внешних сил пренебречь.
Образец возможного решения
13. Маленький шарик массой m = 0,3 кг подвешен на лёгкой нерастяжимой нити длиной l = 0,9 м, которая разрывается при силе натяжения T0 = 6 Н. Шарик отведён от положения равновесия (оно показано на рисунке пунктиром) и отпущен. Когда шарик проходит положение равновесия, нить обрывается, и шарик тут же абсолютно неупруго сталкивается с бруском массой M = 1,5 кг, лежащим неподвижно на гладкой горизонтальной поверхности стола. Какова скорость u бруска после удара? Считать, что брусок после удара движется поступательно.
Образец возможного решения

14. На рисунке представлена
фотография установки по исследованию скольжения каретки (1)
массой 40 г по наклонной плоскости под углом 30°. В момент начала
движения верхний датчик (2) включает секундомер (3). При прохождения
кареткой нижнего датчика (4) секундомер выключается. Оцените
количество теплоты, которое выделилось при скольжении каретки
по наклонной плоскости между датчиками.
Образец возможного решения
15. Однородный тонкий стержень массой m = 1 кг одним концом шарнирно прикреплён к потолку, а другим концом опирается на массивную горизонтальную доску, образуя с ней угол α = 30°. Под действием горизонтальной силы F доска движется поступательно влево с постоянной скоростью (см. рисунок). Стержень при этом неподвижен. Найдите F, если коэффициент трения стержня по доске μ = 0,2. Трением доски по опоре и трением в шарнире пренебречь.
Образец возможного решения
16. Деревянный шар привязан нитью ко дну цилиндрического сосуда с площадью дна S =100 см2. В сосуд наливают воду так, что шар полностью погружается в жидкость, при этом нить натягивается и действует на шар с силой T. Если нить перерезать, то шар всплывёт, а уровень воды изменится на h = 5 см. Найдите силу натяжения нити T.
Образец возможного решения
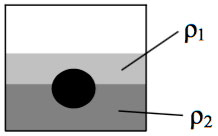
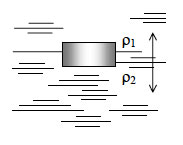
17. На границе раздела двух несмешивающихся жидкостей, имеющих плотности ρ1 = 900 кг/м3 и ρ2 = 3ρ1, плавает шарик (см. рисунок). Какой должна быть плотность шарика ρ, чтобы выше границы раздела жидкостей была одна треть его объёма?
Образец возможного решения
Избранные задачи прошлых лет
(с ответами)
18. В безветренную погоду самолёт затрачивает на перелёт между городами 6 часов. Если во время полёта дует боковой ветер перпендикулярно линии полёта, то самолёт затрачивает на перелёт на 9 минут больше. Найдите скорость ветра, если скорость самолёта относительно воздуха постоянная и равна 328 км/ч.
19. В последнюю секунду свободного падения тело прошло путь, в n = 2 раза больший, чем в предыдущую. Найдите полное время падения t, если начальная скорость равна нулю.
20. Под каким углом к горизонту надо бросить мяч, чтобы он перелетел через забор высотой h = 4 м, коснувшись его в верхней точке своей траектории, если мяч бросают с уровня h0 = 0,8 м над землей с расстояния S = 6,4 м от забора? Сопротивлением воздуха пренебречь.
21. Мяч бросают горизонтально с высоты 1,25 м по направлению к вертикальной стене, находящейся на расстоянии 2,5 м от точки бросания. Какова должна быть начальная скорость мяча, чтобы после упругого удара о стену он приземлился под точкой бросания (см. рисунок)?
22. С высоты
H = 30 м свободно падает стальной шарик. Через t
= 2 с после начала падения он сталкивается с неподвижной плитой,
плоскость которой наклонена под углом α = 30° к горизонту.
На какую высоту h от поверхности земли поднимется шарик
после удара? Удар шарика о плиту считать абсолютно упругим.
23. С края каменистого обрыва, расположенного на высоте h = 20 м над уровнем Земли, падает камень. Через 1 с падения камень упруго ударяется о плоский участок выступающей гранитной плиты, расположенной к горизонту под углом 30°, и далее летит в свободном полете. На каком расстоянии от вертикали, вдоль которой начинал падать камень, он упадет на Землю? Сопротивлением воздуха можно пренебречь.
24. Прибор наблюдения обнаружил летящий снаряд и зафиксировал его горизонтальную координату х1 и высоту h1 = 1655 м над Землёй (см. рисунок). Через 3 с снаряд упал на Землю и взорвался на расстоянии l = 1700 м от места его обнаружения. Известно, что снаряды данного типа вылетают из ствола пушки со скоростью 800 м/с. На каком расстоянии от точки взрыва снаряда находилась пушка, если считать, что сопротивление воздуха пренебрежимо мало? Пушка и место взрыва находятся на одной горизонтали.
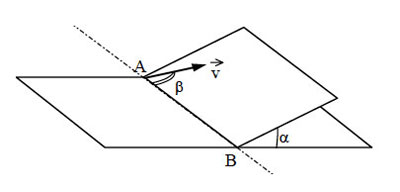
25. Наклонная плоскость
пересекается с горизонтальной плоскостью по прямой AB.
Угол между плоскостями α = 30°. Маленькая шайба начинает
движение вверх по наклонной плоскости из точки A с
начальной скоростью υ0 = 2 м/с под углом β
= 60° к прямой AB. В ходе движения шайба съезжает на
прямую AB в точке B. Пренебрегая трением между
шайбой и наклонной плоскостью, найдите расстояние AB.
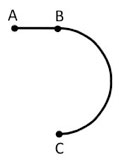
26. Стартуя из точки А (см. рисунок), спортсмен движется равноускоренно до точки В, после которой модуль скорости спортсмена остаётся постоянным вплоть до точки С. Во сколько раз время, затраченное спортсменом на участок ВС, больше, чем на участок АВ, если модуль ускорения на обоих участках одинаков? Траектория ВС – полуокружность.
27. Грузовой
автомобиль массой М = 4 т тянет за нерастяжимый трос
вверх по уклону легковой автомобиль, масса которого m
= 1 т. Двигатель легкового автомобиля выключен. С каким максимальным
ускорением могут двигаться автомобили, если угол уклона составляет
α = arcsin 0,1, а коэффициент трения между шинами грузового
автомобиля и дорогой μ = 0,2? Силой трения качения, действующей
на легковой автомобиль пренебречь.
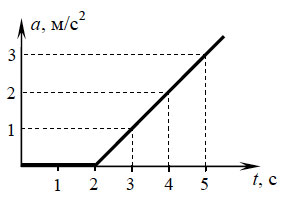
28. К покоящемуся на шероховатой
горизонтальной поверхности телу приложена нарастающая с течением
времени горизонтальная сила тяги F = bt, где
b – постоянная величина. На рисунке представлен график
зависимости ускорения тела от времени действия силы. Определите
коэффициент трения скольжения.
29. На горизонтальном столе лежит деревянный брусок. Коэффициент трения между поверхностью стола и бруском µ = 0,1. Если приложить к бруску силу, направленную вверх под углом α = 45° к горизонту, то брусок будет двигаться по столу равномерно. С каким ускорением будет двигаться этот брусок по столу, если приложить к нему такую же по модулю силу, направленную под углом β = 30° к горизонту?
30. После того, как брусок толкнули, он движется вверх по наклонной плоскости, а затем начинает соскальзывать вниз. При каких значениях коэффициента трения между бруском и наклонной плоскостью это возможно, если угол наклона плоскости к горизонту α = 30°?
31. Ученик исследовал движение бруска по наклонной плоскости. При помощи электронного секундомера он провёл пять опытов, измеряя время движения бруска из состояния покоя на одном и том же участке наклонной плоскости. Результаты опытов приведены в таблице.
| Опыт |
1 |
2 |
3 |
4 |
5 |
| t, c |
0,470 |
0,468 |
0,483 |
0,481 |
0,475 |
Угол между наклонной плоскостью и лабораторным столом составлял 30°. Расстояние, которое проходил брусок в каждом опыте, равно 400 мм. Определите примерное значение коэффициента трения между бруском и наклонной плоскостью. Сделайте рисунок с указанием сил, действующих на брусок.
32. Брусок массой m1 = 1 кг лежит на наклонной плоскости с углом при основании, равным α = 53°. Коэффициент трения бруска с плоскостью равен μ = 0,5. К бруску привязана невесомая нить, другой конец которой перекинут через неподвижный идеальный блок. К этому концу нити подвешивается груз массой m2 = 1 кг. Определите, придёт ли в движение брусок при подвешивании груза. Если придёт в движение, то в каком направлении? (sin53° = 0,8; cos53° = 0,6)
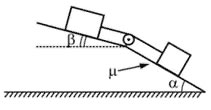
33. В изображенной на рисунке системе нижний брусок может двигаться по наклонной плоскости, составляющей с горизонтом угол α = 30°, а верхний брусок – вдоль наклонной плоскости, составляющей с горизонтом некоторый угол β. Коэффициент трения между нижним бруском и плоскостью равен μ = 0,2, трение между верхним бруском и наклонной плоскостью отсутствует. Считая соединяющую бруски нить очень легкой и нерастяжимой, и пренебрегая массой блока и трением в его оси найдите, при каких значениях угла β нить будет натянута.
34. На наклонной плоскости находится брусок, связанный с грузом перекинутой через блок невесомой нерастяжимой нитью (см. рисунок). Угол наклона α плоскости равен 30°; масса бруска 2 кг, коэффициент трения бруска о плоскость равна 0,23, масса груза 0,2 кг. В начальный момент времени брусок покоился на расстоянии 5 м от точки А у основания плоскости. Определите расстояние от бруска до точки А через 2 с.
35. Система грузов М, m1 и m2, показанная на рисунке, движется из состояния покоя. Поверхность стола – горизонтальная гладкая. Коэффициент трения между грузами М и m1 равен μ = 0,2. Грузы М и m2 связаны лёгкой нерастяжимой нитью, которая скользит по блоку без трения. Пусть М = 1,2 кг, m1 = m2 = m. При каких значениях m грузы М и m1 движутся как одно целое?
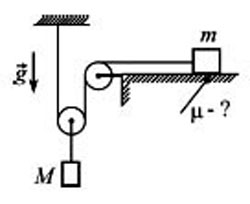
36. В системе, изображённой на рисунке, масса груза, лежащего на шероховатой горизонтальной плоскости, равна m = 3 кг. При подвешивании к оси подвижного блока груза массой M = 2 кг он движется вниз с ускорением a = 1 м/с2. Чему равен коэффициент трения μ между грузом массой m и плоскостью? Нити невесомы и нерастяжимы, блоки невесомы, трение в осях блоков и о воздух отсутствует.
37. К нижнему концу легкой
пружины подвешены связанные невесомой нитью грузы: верхний массой
m1 = 0,2 кг и нижний массой m2
= 0,1 кг. Нить, соединяющую грузы, пережигают. С каким ускорением
и в каком направлении начнет двигаться верхний груз?
38. На шероховатом горизонтальном диске, вращающемся вокруг вертикальной оси, покоится небольшое тело. Расстояние от оси вращения до тела r = 25 см. Угловую скорость вращения начали медленно увеличивать. Каков коэффициент трения μ между телом и диском, если тело начало скользить по диску при угловой скорости ω = 4,5 рад/с?
39. Грузики с точечными
массами m1 = 0,25 кг и m2=
0,5 кг прикреплены к невесомому стержню длиной l =
1 м (см. рисунок). Стержень может вращаться вокруг горизонтальной
оси, проходящей через точку О. В нижней точке траектории
грузик массой m2 имеет скорость υ =
2 м/с. Определите силу, с которой стержень действует на грузик
m1 в этот момент.
40. На вертикальной оси укреплена гладкая горизонтальная штанга, по которой могут перемещаться два груза массами m1 = 200 г и m2 = 300 г, связанные нерастяжимой невесомой нитью длиной l = 20 см. Нить закрепили на оси так, что грузы располагаются по разные стороны от оси и натяжение нити с обеих сторон от оси при вращении штанги одинаково (см. рисунок). Определите модуль силы натяжения Т нити, соединяющей грузы, при вращении штанги с частотой 600 об/мин.
41. Шарик массой m = 200 г подвешен к потолку на лёгкой нерастяжимой нити длиной L = 1,5 м. Шарик привели в движение так, что он движется по окружности в горизонтальной плоскости, образуя конический маятник (см. рисунок). Модуль силы натяжения нити Т = 2,7 Н. Чему равен период τ, за который шарик делает один оборот по окружности?
42. Полый конус с углом при вершине 2α вращается с угловой скоростью ω вокруг вертикальной оси, совпадающей с его осью симметрии. Вершина конуса обращена вверх. На внешней поверхности конуса находится небольшая шайба, коэффициент трения которой о поверхность конуса равен μ. При каком максимальном расстоянии L от вершины шайба будет неподвижна относительно конуса? Сделайте схематический рисунок с указанием сил, действующих на шайбу.
43. Определите
отношение веса тела на экваторе планеты к весу этого тела на
ее полюсе, если плотность вещества планеты ρ = 5200 кг/м3,
а период ее вращения вокруг собственной оси равен T
= 3•104 с. Планету считать однородным шаром.
44. Звезда
и массивная планета обращаются вокруг общего неподвижного центра
масс по круговым орбитам. Найдите радиус орбиты планеты r,
если известно, что масса планеты равна m, а скорость
движения звезды и радиус ее орбиты равны υ и R
соответственно.
45. Радиус планеты Плюк в 2 раза больше радиуса Земли, а средние плотности Плюка и Земли равны. Найдите отношение периода обращения спутника, движущегося вокруг Плюка по низкой орбите, к периоду обращения аналогичного спутника для Земли. Объем шара пропорционален кубу радиуса этого шара (V ~ R3).
46. Тело массой 100 г, свободно падающее на землю с некоторой высоты без начальной скорости, за первую секунду падения проходит путь, в 4 раза меньший, чем за последнюю секунду падения. Каков импульс тела в конце падения? Силой сопротивления движению пренебречь.
47. На космическом
аппарате, находящемся вдали от Земли, начал работать реактивный
двигатель. Из сопла ракеты ежесекундно выбрасывается 2 кг газа
(Δm/Δt = 2 кг/с) со скоростью υ
= 500 м/с. Исходная масса аппарата М = 500 кг. Какой
будет скорость аппарата через t = 6 c после старта?
Начальную скорость аппарата принять равной нулю. Изменением
массы аппарата за время движения пренебречь.
48. На озере два рыбака сидят в покоящейся лодке, масса которой М = 100 кг и длина L = 6 м: один — на носу, а второй — на корме. Их массы равны соответственно m1 = 60 кг и m2 = 80 кг. Насколько сместится лодка относительно берега озера, если второй рыбак перейдёт к первому? (Трением пренебречь.)
49. Начальная
скорость снаряда, выпущенного из пушки вертикально вверх, равна
υ0 = 10 м/с. В точке максимального подъема снаряд
разорвался на два осколка, массы которых относятся как 2 : 1.
Осколок большей массы упал на землю первым со скоростью υ1
= 2υ0. До какой максимальной высоты поднялся
осколок меньшей массы?
50. Начальная скорость снаряда, выпущенного из пушки вертикально вверх, равна 500 м/с. В точке максимального подъема снаряд разорвался на два осколка. Первый упал на землю вблизи точки выстрела, имея скорость в 2 раза больше начальной скорости снаряда, а второй в этом же месте – через 100 с после разрыва. Чему равно отношение массы первого осколка к массе второго осколка? Сопротивлением воздуха пренебречь.
51. Снаряд
массой 4 кг разорвался в полете на две равные части, одна из
которых продолжила движение по направлению движения снаряда,
а другая — в противоположную сторону. В момент разрыва суммарная
кинетическая энергия осколков увеличивается за счет энергии
взрыва на величину 0,5 МДж. Модуль скорости осколка, движущегося
по направлению движения снаряда, равен 900 м/с. Найдите скорость
снаряда перед разрывом.
52. На гладкой горизонтальной плоскости находится длинная доска массой М = 2 кг. По доске скользит шайба массой m = 0,5 кг. Коэффициент трения между шайбой и доской μ = 0,2. В начальный момент времени скорость шайбы υ0 = 2 м/с, а доска покоится. Сколько времени потребуется для того, чтобы шайба перестала скользить по доске?
53. Два шарика,
массы которых m1 = 200 г и m2
= 600 г, висят, соприкасаясь, на одинаковых нитях длиной l
= 80 см. Первый шар отклонили на угол 90° и отпустили. На какую
высоту поднимутся шарики после удара, если этот удар абсолютно
неупругий?
54. Брусок
массой m1 = 500 г соскальзывает по наклонной
поверхности с высоты h = 0,8 м и, двигаясь по горизонтальной
поверхности, сталкивается с неподвижным бруском массой m2
= 300 г. Считая столкновение абсолютно неупругим, определите
изменение кинетической энергии первого бруска в результате столкновения.
Трением при движении пренебречь. Считать, что наклонная плоскость
плавно переходит в горизонтальную.
55. Брусок
массой m1 = 600 г, движущийся со скоростью
υ = 2 м/с, сталкивается с неподвижным бруском массой m2
= 200 г. Какова скорость первого бруска после столкновения?
Удар считать центральным и абсолютно упругим.
56. Два шарика, массы которых отличаются в 3 раза, висят, соприкасаясь, на вертикальных нитях (см. рисунок). Лёгкий шарик отклоняют на угол 90° и отпускают без начальной скорости. Каким будет отношение кинетических энергий тяжёлого и лёгкого шариков тотчас после их абсолютно упругого центрального удара?
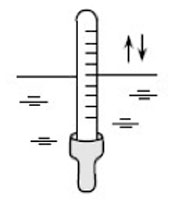
57. Пробирка массой 40 г, содержащая пары
эфира, закрыта пробкой и подвешена в горизонтальном положении
к штанге на нерастяжимых нитях. Расстояние от центра масс
пробирки до штанги L = 20 см. При нагревании пробирки
пробка вылетает из нее со скоростью 4 м/с. Какова масса пробки,
если нити отклонились от вертикали на максимальный угол 60°?
58. Пробирка массой 40 г, содержащая пары
эфира, закрыта пробкой массой 10 г и подвешена в горизонтальном
положении к штанге на нерастяжимых нитях. При нагревании пробирки
пробка вылетает из нее со скоростью 4 м/с, а нить обрывается.
Найдите максимально возможное в этих условиях расстояние L
от центра масс пробирки до штанги, если нити выдерживают суммарную
нагрузку не более 0,6 Н.
59. В установке, изображённой на рисунке, грузик А соединён перекинутой через блок нитью с бруском В, лежащим на горизонтальной поверхности трибометра, закреплённого на столе. Грузик отводят в сторону, приподнимая его на высоту h, и отпускают. Длина свисающей части нити равна L. Какую величину должна превзойти масса грузика, чтобы брусок сдвинулся с места в момент прохождения грузиком нижней точки траектории? Масса бруска M, коэффициент трения между бруском и поверхностью μ. Трением в блоке, а также размерами блока пренебречь.
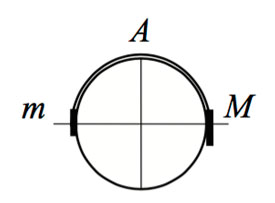
60. Система из грузов m и M и связывающей их лёгкой нерастяжимой нити в начальный момент покоится в вертикальной плоскости, проходящей перпендикулярно оси закреплённой цилиндрической трубы. Грузы находятся на горизонтальной прямой, пересекающей ось трубы (см. рисунок). В ходе возникшего движения груз m отрывается от поверхности трубы в её верхней точке А. Найдите массу М, если m = 100 г. Размеры грузов ничтожно малы по сравнению с радиусом трубы. Трением пренебречь. Сделайте схематический рисунок с указанием сил, действующих на грузы.
61. Небольшие шарики, массы которых m и M, соединены лёгким стержнем и помещены в гладкую сферическую выемку радиусом R = 20 см. В начальный момент шарики удерживаются в положении, изображённом на рисунке. Когда их отпустили без толчка, шарики стали скользить по поверхности выемки. Минимальная высота, на которой оказался шарик m в процессе движения, равна 4 см от нижней точки выемки. Определите отношение масс M и m.
62. Шарик скользит без трения по наклонному желобу, а затем движется по «мертвой петле» радиуса R. С какой силой шарик давит на желоб в нижней точке петли, если масса шарика равна 100 г, а высота, с которой его отпускают, равна 4R?
63. Небольшая шайба после
толчка приобретает скорость υ = 2 м/с и скользит по внутренней
поверхности гладкого закрепленного кольца радиусом R
= 0,14 м. На какой высоте h шайба отрывается от кольца
и начинает свободно падать?
64. Небольшой кубик массой m = 1 кг начинает скользить с нулевой начальной скоростью по гладкой горке, переходящей в «мёртвую петлю» радиусом R = 2 м (см. рисунок). С какой высоты Н был отпущен кубик, если на высоте h = 2,5 м от нижней точки петли сила давления кубика на стенку петли F = 5 Н? Сделайте рисунок с указанием сил, поясняющий решение.
65. Пуля летит
горизонтально со скоростью υ0 = 400 м/с , попадает
в лежащий на горизонтальной поверхности льда брусок и отскакивает
в обратном направлении со скоростью υ0/8. Масса
бруска в 90 раз больше массы пули. Коэффициент трения скольжения
между бруском и льдом μ = 0,1. На какое расстояние s
переместится брусок к моменту, когда его скорость уменьшится
на 20%?
66. В тело массой 4,8 кг, лежащее на гладком участке горизонтальной поверхности, попадает снаряд массой 0,2 кг, летящий под углом 60° к горизонту со скоростью 40 м/с, и застревает в нем. Попав на шероховатую часть поверхности, тело проходит до остановки путь, равный 12 см. Определите коэффициент трения скольжения между телом и поверхностью.
67. На краю стола высотой h = 1 м лежит пластилиновый шарик массой m = 50 г. На него со стороны стола налетает по горизонтали другой пластилиновый шарик, имеющий массу M = 100 г. Какой должна быть скорость второго шарика, чтобы точка приземления шариков на пол была дальше от стола, чем заданное расстояние L = 0,3 м? (Удар считать центральным.)
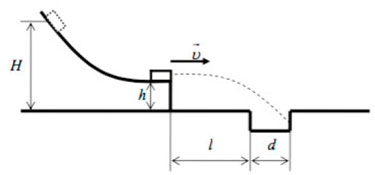
68. Маленькая шайба движется по гладкому трамплину из состояния покоя с высоты H над поверхностью земли. На высоте h = 1 м шайба отрывается от трамплина, причём в этот момент скорость шайбы направлена горизонтально (см. рисунок). При каких значениях H шайба упадёт в канаву, вырытую перед трамплином, если ширина канавы d = 1 м, а ближний край канавы находится на расстоянии l = 3 м от стенки трамплина? Сопротивлением воздуха пренебречь. Считать, что шайба не может закатиться в канаву, если не упала в нее сразу.
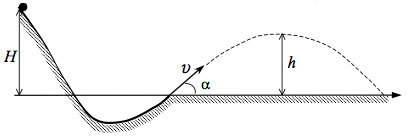
69. При выполнении трюка «Летающий велосипедист» гонщик движется по трамплину под действием силы тяжести, начиная движение из состояния покоя с высоты Н (см. рис.). На краю трамплина скорость гонщика направлена под таким углом к горизонту, что дальность его полета максимальна. Пролетев по воздуху, гонщик приземляется на горизонтальный стол, находящийся на той же высоте, что и край трамплина. Какова высота полета h на этом трамплине? Сопротивлением воздуха и трением пренебречь.
70. Лыжник массой 60 кг прыгает с трамплина высотой Н. На рисунке показана траектория полёта лыжника; параметры этой траектории: АВ = 10 м, ВС = 5 м. Модуль работы силы трения лыжника о снег при спуске равен 1,2 кДж. Определите высоту Н трамплина.
71. Пушка,
закрепленная на высоте 5 м, стреляет в горизонтальном направлении
снарядами массы 10 кг. Вследствие отдачи ее ствол, имеющий массу
1000 кг, сжимает на 1 м пружину жесткости 6000 Н/м, производящую
перезарядку пушки. Считая, что относительная доля η = 1/6
энергии отдачи идет на сжатие этой пружины, найдите дальность
полета снаряда.
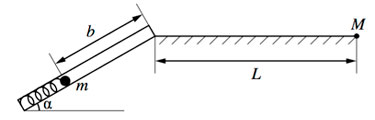
72. Пружинное ружьё наклонено под углом α = 30° к горизонту. Энергия сжатой пружины равна 0,41 Дж. При выстреле шарик массой m = 50 г проходит по стволу ружья расстояние b, вылетает и падает на расстоянии L = 1 м от дула ружья в точку М, находящуюся с ним на одной высоте (см. рис.). Найдите расстояние b. Трением в стволе и сопротивлением воздуха пренебречь.
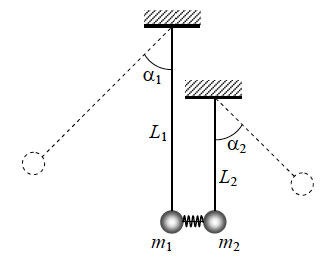
73. Два шарика подвешены
на вертикальных тонких нитях так, что они находятся на одной
высоте. Между ними находится сжатая и связанная нитью пружина.
При пережигании связывающей нити пружина распрямляется, отклоняя
шарики в разные стороны на одинаковые углы. Во сколько раз одна
нить длиннее другой, если отношение масс m2/m1
= 1,5? Считать величину сжатия пружины во много раз меньше длин
нитей.
74. От груза, неподвижно висящего на невесомой пружине жёсткостью k = 400 Н/м, отделился с начальной скоростью, равной нулю, его фрагмент, после чего оставшаяся часть груза поднялась на максимальную высоту h = 3 см относительно первоначального положения. Какова масса отделившегося от груза фрагмента?
75. К одному концу лёгкой пружины жёсткостью k = 100 Н/м прикреплён массивный груз, лежащий на горизонтальной плоскости, другой конец пружины закреплён неподвижно (см. рисунок). Коэффициент трения груза по плоскости μ = 0,2. Груз смещают по горизонтали, растягивая пружину, затем отпускают с начальной скоростью, равной нулю. Груз движется в одном направлении и затем останавливается в положении, в котором пружина уже сжата. Максимальное растяжение пружины, при котором груз движется таким образом, равно d = 15 см. Найдите массу m груза.
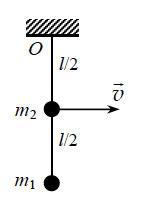
76. Изогнутая жесткая
трубка укреплена на платформе, находящейся на гладкой горизонтальной
поверхности стола (см. рисунок). В трубке на расстоянии H
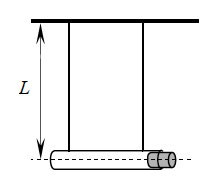
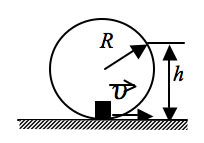
от стола удерживают шарик, который может скользить по трубке
без трения. Все тела покоятся. Шарик отпускают. В результате
платформа движется поступательно, не отрываясь от стола, и после
вылета шарика из трубки со скоростью υ приобретает
скорость υ/5. На каком расстоянии h от стола находится
левый горизонтальный конец трубки?
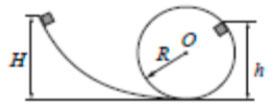
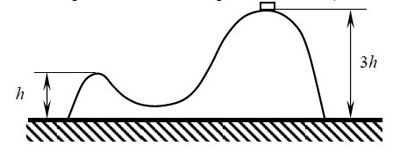
77. Горка с двумя вершинами,
высоты которых h и 3h, покоится на гладкой
горизонтальной поверхности стола (см. рисунок). На правой вершине
горки находится монета, масса которой в 12 раз меньше массы
горки. От незначительного толчка монета и горка приходят в движение,
причем монета движется влево, не отрываясь от гладкой поверхности
горки, а поступательно движущаяся горка не отрывается от стола.
Найдите скорость горки в тот момент, когда монета окажется на
левой вершине горки.
78. Пластилиновый шарик в момент t = 0 бросают с горизонтальной поверхности Земли с начальной скоростью u0 под углом α к горизонту. Одновременно с некоторой высоты над поверхностью Земли начинает падать из состояния покоя другой такой же шарик. Шарики абсолютно неупруго сталкиваются в воздухе. Сразу после столкновения скорость шариков направлена горизонтально. В какой момент времени τ шарики упадут на Землю? Сопротивлением воздуха пренебречь.
79. К двум вертикально расположенным пружинам одинаковой длины подвесили однородный стержень длиной L = 30 см. Если к этому стержню подвесить груз массой m = 3 кг на расстоянии d = 5 см от правой пружины, то стержень будет расположен горизонтально, и растяжения обеих пружин будут одинаковы (см. рисунок). Жёсткость левой пружины в 2 раза меньше, чем правой. Чему равна масса стержня М? Сделайте рисунок с указанием используемых в решении сил.
80. Тонкий однородный стержень АВ шарнирно закреплён в точке А и удерживается горизонтальной нитью ВС (см. рисунок). Трение в шарнире пренебрежимо мало́. Масса стержня m = 1 кг, угол его наклона к горизонту α = 45°. Найдите модуль силы F, действующей на стержень со стороны шарнира. Сделайте рисунок, на котором укажите все силы, действующие на стержень.
81. Стальной шарик массой m = 780 г удерживается силой F = 28 Н с помощью стержня, один конец которого на шарнире прикреплен к стене (см. рисунок). Длина стержня L = 80 см, масса M = 400 г. Затем шарик опускают в сосуд с водой. Как следует изменить точку приложения силы F, чтобы стержень при этом остался в горизонтальном положении?
82. В гладкий стакан высотой
h = 8 см и радиусом 3 см поставили однородную палочку
длиной 12 см. Стакан доверху наполнили жидкостью, плотность
которой в 5 раз меньше плотности материала палочки. Чему равна
масса палочки, если она давит на край стакана с силой 465 мН
?
83. Шарик массой m = 0,1 кг на нити длиной L = 0,4 м раскачивают так, что каждый раз, когда шарик проходит положение равновесия, на него в течение короткого промежутка времени t = 0,01 с действует сила F = 0,1 Н, направленная по скорости. Через сколько полных колебаний шарик на нити отклонится на 60°?
84. На планете Плюк местный школьник решил определить ускорение свободного падения g. Он взял чашу с очень скользким сферическим дном радиусом R = 0,5 м и положил неподалеку от нижней точки О дна маленькую монету (см. рисунок). Монета стала совершать колебания около точки О с частотой 0,5 Гц. Какое значение g школьник должен получить, если правильно провёл измерения?
85. Ареометр, погруженный в жидкость, совершает малые вертикальные гармонические колебания с частотой ν = 0,2 Гц (см. рисунок). Площадь сечения трубки ареометра S = 10 мм2, его масса m = 50 г. Пренебрегая сопротивлением жидкости, найдите плотность жидкости.
86. Однородный цилиндр
с площадью поперечного сечения 10-2 м2 плавает
на границе несмешивающихся жидкостей с плотностью 800 кг/м3
и 1000 кг/м3 (см. рисунок). Пренебрегая сопротивлением
жидкостей, определите массу цилиндра, если период его малых
вертикальных колебаний π /5 c.
87. Брусок, покоящийся на горизонтальном
столе, и пружинный маятник, состоящий из грузика и легкой
пружины, связаны легкой нерастяжимой нитью через идеальный
блок (см. рисунок). Коэффициент трения между основанием бруска
и поверхностью стола равен 0,25. Груз маятника совершает колебания
с периодом 0,5 с вдоль вертикали, совпадающей с вертикальным
отрезком нити. Максимально возможная амплитуда этих колебаний,
при которой они остаются гармоническими, равна 4 см. Чему
равно отношение массы бруска к массе грузика?
88. Брусок, покоящийся на горизонтальном
столе, и пружинный маятник, состоящий из грузика и легкой
пружины, связаны легкой нерастяжимой нитью через идеальный
блок (см. рисунок). Коэффициент трения между основанием бруска
и поверхностью стола равен 0,25. Груз маятника совершает колебания
с частотой 2,5 Гц вдоль вертикали, совпадающей с вертикальным
отрезком нити. Максимально возможная амплитуда этих колебаний,
при которой они остаются гармоническими, равна 4 см. Чему
равно минимальное значение отношения массы бруска к массе
грузика?
89. Шарик массой m = 20 г подвешен на шелковой нити и помещен над положительно заряженной плоскостью, создающей однородное вертикальное электрическое поле напряженностью Е = 104 В/м. Шарик имеет положительный заряд q = 10-5 Кл. Период малых колебаний шарика Т = 1 с. Какова длина нити?
90. По гладкой горизонтальной направляющей длины 2l скользит бусинка с положительным зарядом Q > 0 и массой m. На концах направляющей находятся положительные заряды q > 0 (см. рисунок). Бусинка совершает малые колебания относительно положения равновесия, период которых равен Т. Чему будет равен период колебаний бусинки, если ее заряд увеличить в 2 раза?
91. По гладкой горизонтальной направляющей скользит бусинка с отрицательным зарядом – q и массой m. На расстоянии l от направляющей находится шарик с положительным зарядом + Q (см. рисунок). Бусинка совершает малые гармонические колебания относительно положения равновесия, период которых равен Т. Заряды бусинки и шарика увеличили в 2 раза. Какой должна быть масса бусинки, чтобы период ее колебаний при этом остался прежним?
прошлых лет
| » Меню сайта |
|
| » Категории раздела | ||||
|
| » Подготовка к ЕГЭ |
 |
| » Кнопка сайта |
 |
| » Код кнопки сайта |
| Решение задач ЕГЭ части С | ||
 |
| » Вход на сайт |
 |
| » Статистика сайта |
|
|
| » Поиск | ||
|
|
| » Погода |
|
Новосибирск — погода |
| » Календарь | |||||||||||||||||||||||||||||||||||||||||
|
Примеры решений заданий части C ЕГЭ по физике.
ЕГЭ по физике с решениями, часть А
С1. Дно водоёма всегда кажется расположенным ближе к поверхностиводы для наблюдателя, находящегося в лодке. Объяснить это явление.
Ответ:
|
Образец возможного решения |
|
Рассмотрим ход лучей 1 и 2, отражённых от некоторой точки А, лежащей на дне водоёма. Луч 1 (взятый для удобства построения) падает перпендикулярно на границу раздела сред (вода-воздух) и не преломляется. Произвольный луч 2 падает на границу раздела под некоторым углом α и преломляется под углом γ (α<γ, т.к. луч переходит из оптически более плотной среды в оптически менее плотную среду). Находим пересечение луча 1 и продолжения луча 2 – точку А1. Из построения следует, что кажущаяся глубина h1 меньше глубины водоёма h. |
С2. Шар массой 1 кг свободно, без начальной скорости, падает с высоты 13,2 м. На высоте 10 м он насквозь простреливается горизонтально летящей пулей массой 10 г. Скорость пули за время движения в шаре изменяется от V1=700 м/с до V2=100 м/с. Найдите кинетическуюэнергию шара в момент удара о горизонтальную поверхность земли.
Ответ:
|
Образец возможного решения |
|
Кинетическая энергия шара в момент его падения на землю определяется следующим образом:
Вертикальную составляющую скорости определяем из закона сохранения полной механической энергии:
Горизонтальную составляющую скорости шара определяем из закона сохранения импульса:
Ек=150 Дж |
С3. Как изменится температура идеального газа, если увеличить его объем в 2 разапри осуществлении процесса, описываемого формулой pV4=const?
Ответ:
|
Образец возможного решения |
|
|
Выразим из уравнения Менделеева-Клапейрона давление p: Подставим (1) в формулу, описывающую данный процесс: https://5-ege.ru/reshenie-zadach-po-fizike-ege-chast-c/ |
С4. Электрическое поле образовано двумя неподвижными, вертикальнорасположенными, параллельными, разноименно заряженными непроводящимипластинами. Пластины распложены на расстоянии d = 5см друг от друга. Напряженность поля между пластинами Е =104В/м. Между пластинами, на равном расстоянии от них, помещен шарикс зарядом q = 10-5 Кл и массой m = 20г. После того как шарикотпустили, он начинает падать и ударяется об одну из пластин. На какоерасстояние Δh по вертикалисместится шарик к моменту его удара об одну из пластин?
Ответ:
|
Образец возможного решения |
|
Движение шарика можно «разложить» на равноускоренное движение по вертикали под действием силы тяжести и на равноускоренное движение по горизонтали под действием силы Кулона. За одно и то же время t шарик проходит путь Таким образом, |
С5. Маленький шарик массой 1 г, несущий заряд 0,15 мкКл, брошен издалека соскоростью 1 м/с в сферу, имеющую заряд 0,3 мкКл. При каком минимальном значениирадиуса сферы шарик достигнет ее поверхности?
Ответ:
|
Образец возможного решения |
|
В момент бросания шарик обладает кинетической энергией В тот момент, когда шарик достигнет поверхности сферы, его потенциальная энергия равна
Применяя закон сохранения энергии, получаем
|
С6. В вакууме находятся два покрытых кальцием электрода, к которым подключенконденсатор ёмкостью С. При длительном освещении катода светом с длиной волны λ=100нм фототок, возникший вначале, прекращается, а на конденсаторе появляется зарядq=9,6∙10-10 Кл.Работа выхода электрона из кальция А=4,42∙10-19 Дж. Определитеёмкость конденсатора С.
Ответ:
|
Образец возможного решения |
|
Напряжение на конденсаторе U будет равно задерживающей разности потенциалов Uз, которое можно найти из уравнения Эйнштейна для фотоэффекта: Отсюда: Находим емкость конденсатора: |
Рекомендуем:
Решение задач из ЕГЭ часть С «Механика»
Никифорова Наталья Владиленовна,
учитель физики МБУ «Лицей №51» г.о. Тольятти
ЗАДАЧА № 1
Найти ускорения a 1 и a 2 масс m 1 и m 2 и силу натяжения Т нити с системе, изображенной на рисунке. Массой блоков и нити и трением пренебречь.
РЕШЕНИЕ:
Силы, приложенные к телам m 1 и m 2 , изображены на рисунке
РЕШЕНИЕ:
Предполагая, что ускорения тел a 1 и a 2 направлены, как показано на рисунке, введем ось координат 0Y и запишем второй закон Ньютона.
Т – m 1 g = – m 1 a 1 , (1)
T 1 – m 2 g = m 2 a 2 . (2)
Запишем второй закон Ньютона для подвижного блока (массой блока можно пренебречь):
T 1 – 2Т = 0 , следовательно:
T 1 = 2Т.
РЕШЕНИЕ:
Согласно «Золотому правилу» механики, подвижный блок дает выигрыш в силе в 2 раза, при этом получаем проигрыш в пути в 2раза. т.е. a 1 = 2a 2 .
РЕШЕНИЕ:
Из уравнения (1) выразим Т
Т= m 1 g – m 1 a 1 . (4)
Из уравнения (2) выразим T 1
T 1 = m 2 g + m 2 a 2 , с учетом T 1 = 2Т получим
2T = m 2 g + m 2 a 2 . (5) Подставим формулу (3) a 1 = 2a 2 в (4):
Т= m 1 g – 2m 1 a 2 . (6)
Подставим формулу (6) в (5) и выразим a 2 :
2 ( m 1 g – 2m 1 a 2 ) = m 2 g + m 2 a 2 ,
a 2 = g ( 2m 1 – m 2 ) / (4 m 1 + m 2 ).
РЕШЕНИЕ:
Найдем a 1 = 2a 2 ,
a 1 = 2g ( 2m 1 – m 2 ) / (4 m 1 + m 2 ). (7)
Подставим формулу (7) в (4) и выразим Т :
Т = 3g m 1 m 2 / (4 m 1 + m 2 ).
Ответ: a 1 = 2g ( 2m 1 – m 2 ) / (4 m 1 + m 2 ),
a 2 = g ( 2m 1 – m 2 ) / (4 m 1 + m 2 ),
Т = 3g m 1 m 2 / (4 m 1 + m 2 ).
ЗАДАЧА № 2
Маленькое тело соскальзывает с нулевой начальной скоростью по внутренней поверхности полусферы с высоты, равной ее радиусу. Одна половина полусферы абсолютно гладкая, а другая — шероховатая, причем на этой половине коэффициент трения между телом и поверхностью μ = 0,15. Определить величину ускорения а тела в тот момент, когда оно перейдет на шероховатую поверхность. Ускорение свободного падения принять равным g = 10 м/с 2 .
РЕШЕНИЕ:
Изобразим силы, действующие на тело в момент, когда оно оказывается на шероховатой поверхности.
Ускорение тела а в рассматриваемый момент времени равно: =+.
а τ — касательное ускорение, направлено по касательной к траектории движения тела, а n — нормальное ускорение тела, направлено по радиусу к центру окружности.
РЕШЕНИЕ:
Введем систему координат, запишем второй закон Ньютона m + + m ,
и спроецируем его на оси 0Y и 0Х :
ma n = N – mg, (1)
ma τ = F тp . (2)
Поскольку a n =υ 2 /R, где υ — скорость тела, из уравнения (1) следует, что
N = ( mυ 2 /R ) + mg .
Сила трения равна
F тp = μN, F тp = μm(g + υ 2 /R) . (3)
РЕШЕНИЕ:
Подставляем (3) в (2), получаем
a τ = μ (g + υ 2 /R) (4)
При движении тела по гладкой поверхности справедлив закон сохранения энергии :
mυ 2 /2 = mgR,
Из него υ 2 = 2gR.
Из (4) получаем a τ =3μg; для a n =υ 2 /R, a n =2g.
Находим ускорение тела по формуле
a=(a τ 2 + а n 2 ) 1/2
Ответ: a= g (9 μ 2 + 4) ½ = 20,5 м/с 2
ЗАДАЧА № 3
К одному концу лёгкой пружины жёсткостью к = 100 Н/м прикреплён груз массой m = 1 кг, лежащий на горизонтальной плоскости, другой конец пружины закреплён неподвижно. Коэффициент трения груза по плоскости μ = 0,2. Груз смещают по горизонтали, растягивая пружину на величину d , затем отпускают с начальной скоростью, равной нулю. Найдите максимальное значение d , при котором груз движется в одном направлении и затем останавливается в положении, в котором пружина уже сжата.
РЕШЕНИЕ:
Начальная энергия системы равна потенциальной энергии растянутой пружины: W 1 = k d 2 /2. После того, как пружину отпустили, она остановится в положении, при котором она сжата на величину x . Тогда конечная энергия системы равна потенциальной энергии сжатой пружины: W 2 = k x 2 /2.
Изменение полной энергии системы равно работе силы трения:
W 2 — W 1 = А тр ,
А тр = F тр ( d + x ) cos 180° = – F тр ( d + x ), F тр = μN,
k /2 ( x 2 – d 2 ) = – μN ( d + x ), k /2 ( d 2 – x 2 ) = μN ( d + x ),
k /2 ( d – x ) = μN . (1)
РЕШЕНИЕ:
Для момента, когда груз остановился, запишем второй закон Ньютона для оси OY и OX:
N — mg = 0 , N= mg (2)
F у – F тр = 0, k x = μN (3)
Подставим (2) в (3) и выразим x :
x = μmg/ k. (4)
Подставим формулы (2) и (4) в k /2 ( d – x ) = μN :
k /2 ( d – μmg/ k ) = μmg , kd /2 = μmg + μmg/ 2,
kd = 3 μmg , d = 3 μmg/ k.
Ответ: d = 6 см .
ЗАДАЧА № 4
Грузовой автомобиль массой М = 4 т с двумя ведущими осями тянет за нерастяжимый трос вверх по склону легковой автомобиль массой m = 1 т, у которого выключен двигатель. С каким максимальным ускорением могут двигаться автомобили, если угол наклона составляет α = arcsin 0,1, а коэффициент трения между шинами грузового автомобиля и дорогой μ = 0,2? Силой трения качения, действующей на легковой автомобиль, пренебречь. Массой колес пренебречь.
РЕШЕНИЕ:
Изобразим силы, действующие на автомобили, зададим направление ускорения системы, введем оси ОХ и ОУ.
РЕШЕНИЕ:
Запишем уравнение второго закона Ньютона для грузового автомобиля в проекции на ось ОХ:
F тр.пок – Мg sinα – T = Ma , (1)
в проекции на ось ОУ:
N 2 – Мg cosα = 0 , отсюда N 2 = Мg cosα .
Максимальная сила трения покоя, действующая на грузовой автомобиль (сила сцепления колес с дорогой) равна:
( F тр.пок ) мах = μ N 2 = μМg cosα . (2)
РЕШЕНИЕ:
Запишем второй закон Ньютона для легкового автомобиля в проекции на ось ОХ:
Т – mg sinα = ma , отсюда
Т = m ( g sinα + a ). (3)
Подставим формулы (2) и (3) в (1):
μМg cosα – Мg sinα – m ( g sinα + a ) = Ma ,
и выразим ускорение автомобилей
a = ( Мg ( μ cosα – sinα ) – mg sinα ) / ( M + m ).
Получим численное значение ускорения
a = 0,6 м/с 2 .
Ответ: a = 0,6 м/с 2 .
Список литературы
- ЕГЭ 2010. Физика: сборник экзаменационных заданий/ Авт.-сост. М.Ю.Демидова, И.И. Нурминский. – М.: Эксмо, 2010.
- Отличник ЕГЭ. Физика. Решение сложных задач. под ред. В.А. Макарова, М.В. Семенова, А.А. Якуты; ФИПИ. – М.: Интеллект-Центр, 2010.
- Савченко Н.Е. Задачи по физике с анализом их решения. – М.: Просвещение: Учеб. лит., 1996.
Благодарю за внимание!