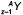Задания
Версия для печати и копирования в MS Word
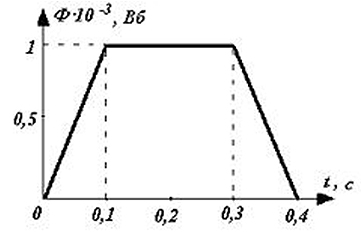
Система состоит из двух тел 1 и 2, массы которых равны 0,5 кг и 2 кг. На рисунке стрелками в заданном масштабе указаны скорости этих тел. Чему равен импульс всей системы по модулю? (Ответ дайте в килограммах на метр в секунду.)
Спрятать решение
Решение.
Используя масштаб рисунка, определим величины скоростей тел: и
Вычислим модули импульсов тел:
и
Импульс всей системы равен Так как вектора
и
перпендикулярны, то модуль импульса всей системы равен
Ответ: 10.
Подборка тренировочных вариантов ЕГЭ 2023 по физике для 11 класса с ответами из различных источников.
Соответствуют демоверсии ЕГЭ 2023 по физике
→ варианты прошлого года
Тренировочные варианты ЕГЭ 2023 по физике
| ЕГЭ 100 баллов (с ответами) | ||
| Вариант 1 | скачать | |
| Вариант 2 | скачать | |
| Вариант 3 | скачать | |
| Вариант 4 | скачать | |
| Вариант 5 | скачать | |
| Вариант 6 | скачать | |
| vk.com/shkolkovo_fiz | ||
| Вариант 1 | ответы | |
| Вариант 2 | разбор | |
| Вариант 3 | ответы | |
| easy-physic.ru | ||
| Вариант 110 | ответы | разбор |
| Вариант 111 | ответы | разбор |
| Вариант 112 | ответы | разбор |
| Вариант 113 | ответы | разбор |
| Вариант 114 | ответы | разбор |
| Вариант 115 | ответы | разбор |
| Вариант 116 | ответы | разбор |
Примеры заданий:
1. Цилиндрический сосуд разделён лёгким подвижным теплоизолирующим поршнем на две части. В одной части сосуда находится аргон, в другой – неон. Концентрация молекул газов одинакова. Определите отношение средней кинетической энергии теплового движения молекул аргона к средней кинетической энергии теплового движения молекул неона, когда поршень находится в равновесии.
2. Газ получил количество теплоты, равное 300 Дж, при этом внутренняя энергия газа уменьшилась на 100 Дж. Масса газа не менялась. Какую работу совершил газ в этом процессе?
3. Выберите все верные утверждения о физических явлениях, величинах и закономерностях. Запишите цифры, под которыми они указаны.
1) При увеличении длины нити математического маятника период его колебаний уменьшается.
2) Явление диффузии протекает в твёрдых телах значительно медленнее, чем в жидкостях.
3) Сила Лоренца отклоняет положительно и отрицательно заряженные частицы, влетающие под углом к линиям индукции однородного магнитного поля, в противоположные стороны.
4) Дифракция рентгеновских лучей невозможна.
5) В процессе фотоэффекта с поверхности вещества под действием падающего света вылетают электроны.
4. В запаянной с одного конца трубке находится влажный воздух, отделённый от атмосферы столбиком ртути длиной l = 76 мм. Когда трубка лежит горизонтально, относительная влажность воздуха ϕ1 в ней равна 80%. Какой станет относительная влажность этого воздуха ϕ2 , если трубку поставить вертикально, открытым концом вниз? Атмосферное давление равно 760 мм рт. ст. Температуру считать постоянно
5. Предмет расположен на главной оптической оси тонкой собирающей линзы. Оптическая сила линзы D = 5 дптр. Изображение предмета действительное, увеличение (отношение высоты изображения предмета к высоте самого предмета) k = 2. Найдите расстояние между предметом и его изображением.
Связанные страницы:
На чтение 1 мин Просмотров 3 Опубликовано 5 марта, 2023
Вариант 220404 пробный ЕГЭ 2022 по физике 11 класс 100 баллов с ответами Решение и ответы на задачи на официальном сайте источника онлайн.
Решу ЕГЭ 2022 физика 11 класс пробный тренировочный вариант 100 баллов №14 КИМ №220404 в форме типового экзамена ЕГЭ 2022
Варианты ответов и решение задачи ТУТ: https://100ballnik.com/%d0%b2%d0%b0%d1%80%d0%b8%d0%b0%d0%bd%d1%82-220404-%d0%bf%d1%80%d0%be%d0%b1%d0%bd%d1%8b%d0%b9-%d0%b5%d0%b3%d1%8d-2022-%d0%bf%d0%be-%d1%84%d0%b8%d0%b7%d0%b8%d0%ba%d0%b5-11-%d0%ba%d0%bb%d0%b0%d1%81%d1%81/
Ответы и решение задачи онлайн
Оставляйте комментарии на сайте, обсуждайте их решения и ответы, предлагайте альтернативные варианты ответов.
Тренировочная работа №4 пробный ЕГЭ 2022 статград по физике 11 класс составлена по образцу экзамена ЕГЭ 2022 года , тренировочные варианты ФИ2110401, ФИ2110402, ФИ2110403, ФИ2110404 с ответами и решением на все задания, официальная дата проведения работы 28 марта 2022 года.
Скачать варианты (задания)
Скачать ответы и решения на все задания
Для выполнения работы статград по физике отводится 3 часа 55 минут (235 минут). Работа состоит из двух частей, включающих в себя 30 заданий.
Тренировочная работа №4 статград по физике 11 класс ЕГЭ 2022:
Сложные задания с 1 варианта:
1)Выберите все верные утверждения о физических явлениях, величинах и закономерностях. Запишите цифры, под которыми они указаны.
- 1) При колебаниях пружинного маятника ускорение груза максимально по модулю в момент прохождения грузом положения равновесия.
- 2) При постоянной температуре давление насыщенных паров вещества возрастает при уменьшении объёма пара.
- 3) Если диэлектрик помещён во внешнее электростатическое поле, то напряжённость поля внутри диэлектрика больше, чем снаружи.
- 4) Собирающая линза может формировать как действительное, так и мнимое изображение.
- 5) При увеличении скорости частицы её длина волны де Бройля уменьшается.
Правильный ответ: 45
2)На рисунке изображены три графика: установите соответствие между этими графиками А), Б) и В) и зависимостями физических величин, обозначенных цифрами 1–5. Для каждого графика А–В подберите соответствующую зависимость и запишите в таблицу выбранные цифры под соответствующими буквами.
- 1) зависимость потенциальной энергии материальной точки от высоты её поднятия над уровнем земли (который принят за начало отсчёта потенциальной энергии)
- 2) зависимость кинетической энергии материальной точки массой m от её импульса
- 3) зависимость модуля силы гравитационного взаимодействия двух материальных точек от расстояния между ними
- 4) зависимость энергии фотона от длины его волны
- 5) зависимость модуля скорости камня, брошенного вертикально вверх, от времени (при движении от момента броска до момента подъёма на максимальную высоту)
Правильный ответ: 245
3)Тело состоит из двух частей, масса которых одинакова. Плотность первой части 3 г/см3 , плотность второй части 6 г/см3 . Чему равна средняя плотность этого тела?
Правильный ответ: 4
4)На горизонтальной гладкой поверхности покоится маленький брусок массой m = 1 кг, прикрепленный к стене при помощи нерастянутой пружины жёсткостью 100 Н/м. К бруску прикладывают постоянную силу F = 15 Н, направленную от стены вдоль оси пружины (см. рис.). На какую максимальную величину растянется пружина?
Правильный ответ: 30
5)На дне аквариума с гладким горизонтальным плоским дном лежит тонкий стеклянный диск, масса которого пренебрежимо мала. Высота уровня воды в аквариуме 40 см, площадь верхней поверхности диска 25 см2 . Диск хорошо отшлифован и плотно прижат к дну аквариума, и поэтому вода под диск не подтекает. Давление воздуха над поверхностью воды 105 Па. Какую минимальную направленную вверх силу нужно приложить к центру диска для того, чтобы оторвать его от дна аквариума?
Правильный ответ: 260
6)Небольшое тело массой 200 г, закреплённое на лёгкой пружине, совершает гармонические колебания вдоль оси OX. На рисунке показан график зависимости проекции скорости Vx этого тела на указанную ось от времени t. Из приведённого ниже списка выберите все верные утверждения, описывающие данное движение тела. Запишите цифры, под которыми они указаны.
- 1) Период колебаний тела равен 2 с.
- 2) Частота ν колебаний тела равна 0,25 Гц.
- 3) Жёсткость пружины примерно равна 0,5 Н/м.
- 4) Амплитуда колебаний тела примерно равна 13 мм.
- 5) Максимальная кинетическая энергия тела равна 20 мкДж.
Правильный ответ: 234
7)По гладкой горизонтальной поверхности движутся поступательно навстречу друг другу два одинаковых шара. Модули скоростей шаров одинаковые, сопротивление воздуха пренебрежимо мало. Между шарами происходит абсолютно неупругое лобовое соударение. Этот опыт повторяют с теми же шарами, увеличив модуль скорости каждого из них в два раза. Как для второго опыта по сравнению с первым изменились модуль суммарного импульса шаров и количество выделившейся при соударении теплоты? Для каждой величины определите соответствующий характер изменения:
- 1) увеличится
- 2) уменьшится
- 3) не изменится
Правильный ответ: 31
8)Небольшой камень бросили под углом α к горизонту с высоты h от поверхности земли с начальной скоростью υ0. Сопротивление воздуха пренебрежимо мало. Через время t после броска камень ещё не упал на землю. Установите соответствие между физическими величинами, характеризующими движение камня, и формулами, выражающими их в рассматриваемой задаче. К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры.
Правильный ответ: 42
9)В сосуде находится некоторое постоянное количество идеального газа. В некотором процессе объём сосуда уменьшился в 2 раза, а средняя кинетическая энергия теплового движения молекул газа увеличилась в 2 раза. Каким стало давление газа в сосуде, если начальное давление было равно 40 кПа?
Правильный ответ: 160
10)В цилиндре находится воздух с относительной влажностью 40 %. Во сколько раз концентрация насыщенного водяного пара при той же температуре превышает концентрацию водяных паров в цилиндре?
Правильный ответ: 2,5
11)Идеальный тепловой двигатель, работающий по циклу Карно, имеет КПД 60 %. Каким станет КПД этого теплового двигателя, если температуру его холодильника увеличить в 1,5 раза, а температуру нагревателя оставить прежней?
Правильный ответ: 40
12)С одним молем гелия проводят процесс 1-2-3, который изображён на pTдиаграмме (Т – абсолютная температура гелия, р – его давление). Выберите все верные утверждения о происходивших в системе процессах и о состояниях гелия.
- 1) В процессе 1-2 гелий совершил положительную работу.
- 2) В процессе 1-2 внутренняя энергия гелия увеличилась в 2 раза.
- 3) В процессе 2-3 гелий получил количество теплоты.
- 4) В процессе 2-3 концентрация гелия увеличивалась.
- 5) В состояниях 1 и 3 плотность гелия разная.
Правильный ответ: 235
13)В ходе адиабатного процесса внутренняя энергия идеального газа уменьшается. Как изменяются в этом процессе объём газа и его температура? Для каждой величины определите соответствующий характер изменения:
- 1) увеличивается
- 2) уменьшается
- 3) не изменяется
Правильный ответ: 12
14)Участок цепи состоит из трёх последовательно соединённых резисторов с сопротивлениями 2 Ом, 3 Ом и 5 Ом. Каким должно быть сопротивление четвёртого резистора, который включают в этот участок последовательно к первым трём, чтобы общее сопротивление участка увеличилось в 2,5 раза?
15)Индуктивность витка тонкой проволоки равна 4 мГн. При какой силе тока в этом витке магнитный поток через поверхность, ограниченную витком, равен 24 мВб?
16)Непрозрачный круг освещается точечным источником света, находящимся на расстоянии 1 м от центра круга. На экране, параллельном плоскости круга, образуется круглая тень, радиус которой в 2 раза больше радиуса круга. Определите расстояние от круга до экрана.
17)На рисунке изображён график зависимости напряжения U между обкладками конденсатора в колебательном контуре от времени t. Ёмкость конденсатора равна 10 мкФ. Выберите все верные утверждения об этом колебательном контуре.
- 1) Сила тока в колебательном контуре изменяется с частотой 250 Гц.
- 2) Период изменения энергии электрического поля конденсатора равен 4 мс.
- 3) Максимальный заряд конденсатора равен 20 мкКл.
- 4) Индуктивность катушки колебательного контура примерно равна 0,16 Гн.
- 5) В момент времени 4 мс сила тока в контуре равна нулю.
18)Дифракционная решётка освещается красным светом. На экране, установленном за решёткой параллельно ей, возникает дифракционная картина, состоящая из тёмных и светлых вертикальных полос. Как изменятся расстояние между соседними светлыми полосами и число наблюдаемых тёмных полос, если освещать эту же решётку зелёным светом? Для каждой величины определите соответствующий характер изменения:
- 1) увеличивается
- 2) уменьшается
- 3) не изменяется
19)Резистор и конденсатор соединены параллельно и подключены к аккумулятору с ЭДС, равной E, и внутренним сопротивлением r (см. рисунок). Электроёмкость конденсатора равна С, сопротивление резистора равно R. Установите соответствие между физическими величинами и формулами, выражающими их в рассматриваемой задаче. К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры.
20)Энергия первого фотона равна 10–20 Дж, а длина волны второго фотона λ = 0,5 мкм. Во сколько раз энергия второго фотона превышает энергию первого фотона? Ответ округлите до десятых долей.
21)Для некоторых атомов характерной особенностью является возможность захвата атомным ядром одного из ближайших к нему электронов из электронной оболочки атома. Как изменятся заряд ядра и число нуклонов в ядре при захвате электрона ядром? Для каждой величины определите соответствующий характер изменения: 1) увеличится 2) уменьшится 3) не изменится
22)На рисунке изображён термометр, показывающий температуру в комнате в градусах Цельсия. Чему равна абсолютная температура воздуха в комнате, если погрешность измерения температуры равна цене деления термометра?
23)Ученику необходимо провести лабораторную работу с целью исследования зависимости модуля силы Архимеда от объёма груза, полностью погружённого в жидкость. В распоряжении ученика имеется ряд установок, в которых используются сосуды с различными жидкостями и различные грузы. Какие две установки из перечисленных в таблице необходимо выбрать, чтобы провести такое исследование?
24)Обкладки плоского воздушного конденсатора изготовлены из двух тонких квадратных металлических пластин со стороной a (на рисунке показан вид сбоку). Расстояние между обкладками d << a. Этот конденсатор подключён к источнику постоянного напряжения U с пренебрежимо малым внутренним сопротивлением. Через пространство между обкладками начинают медленно протаскивать с постоянной скоростью V квадратную пластину со стороной a и толщиной d, сделанную из однородного непроводящего материала с диэлектрической проницаемостью ε. В некоторый момент всё пространство между обкладками конденсатора оказывается заполненным диэлектриком. Затем пластину продолжают двигать в том же направлении с той же скоростью до тех пор, пока она не покинет пространство между обкладками.
Опираясь на законы физики, изобразите график зависимости силы электрического тока I, протекающего через источник напряжения, от времени t. Искажениями электрического поля вблизи краёв обкладок и пластины можно пренебречь. Отсчёт времени начинается в момент, когда правый край пластины находится на уровне левых краёв обкладок конденсатора, а заканчивается, когда пластина оказывается полностью вынутой из конденсатора с противоположной стороны. Объясните построение графика, указав явления и закономерности, которые Вы при этом использовали. На осях координат обозначьте физические величины в «особых» точках графика (максимумы, минимумы, разрывы, точки излома графика), если они есть.
25)В велотренажерах для регулировки физической нагрузки тренирующихся на них спортсменов в настоящее время часто используются электродинамические тормозящие устройства, позволяющие плавно регулировать усилия, необходимые для вращения педалей с определённой скоростью. Вращение от педалей передаётся на массивный токопроводящий диск, находящийся между двумя сильными неподвижными магнитами, расстояние от которых до диска можно регулировать. Взаимодействие возникающих в диске индукционных токов с магнитами тормозит вращение диска, а, следовательно, и педалей, заставляя прикладывать к ним регулируемые по величине силы. Пусть спортсмен крутит педали, находящиеся на расстоянии R = 20 см от их оси вращения, с частотой ν = 15 оборотов в минуту, прикладывая к каждой из педалей в направлении её движения постоянную по модулю вращающую силу F = 50 Н. На сколько градусов нагреется алюминиевый диск массой m = 5 кг за время t = 30 минут работы в таком режиме? Считайте, что вся работа спортсмена расходуется только на равномерный разогрев диска.
26)На рисунке показана схема электрической цепи, состоящей из нескольких резисторов с одинаковыми сопротивлениями R, идеального диода Д, источника питания с постоянной ЭДС ε и малым внутренним сопротивлением, идеального амперметра А и переключателя П полярности источника питания. Во сколько раз изменится сила тока I через амперметр после перевода переключателя в другое положение?
27)На p–V диаграмме изображён процесс 1-2-3-1, проводимый с одним молем идеального одноатомного газа. Значения p и V на ней приведены в относительных единицах y = p/p0 и x = V/V0, где p0 и V0 – некоторые постоянные величины давления и объёма. Какую работу А1234 совершил газ в этом процессе при переходе из состояния 1 в состояние 4, в котором температура газа приняла максимальное значение? Известно, что температура газа в состоянии 2 была равна T2 = 150 К.
28)Квадратная проводящая рамка с длинами сторон 2a = 20 см закреплена на горизонтальной оси О, установленной в неподвижных подшипниках и проходящей через середины двух противоположных сторон рамки. К центру этой оси жёстко приделана лёгкая штанга длиной l = 10 см с маленьким грузиком массой m = 100 г на конце, перпендикулярная плоскости рамки. Вся эта конструкция может свободно вращаться на оси и находится в однородном горизонтальном магнитном поле с индукцией B = 1 Тл, направленной перпендикулярно оси рамки (см. рисунок, вид сбоку вдоль оси). По рамке с помощью гибких проводов начали пропускать постоянный ток, в результате чего в новом положении равновесия рамка со штангой повернулась вокруг оси на угол α = 45°. Чему равна сила тока I в рамке?
29)На стеклянную призму с преломляющим углом α = 30° нормально к её передней грани падает параллельный пучок монохроматического зелёного света, для которого показатель преломления n = 1,65 (стекло – тяжёлый флинт). После преломления в призме пучок идёт вдоль главной оптической оси тонкой линзы с фокусным расстоянием F = 30 см и после неё собирается в точку на экране, параллельном плоскости линзы. Затем при том же расположении элементов оптической системы по тому же направлению на призму пускают параллельный пучок монохроматического голубого света, для которого показатель преломления стекла из-за явления дисперсии света больше на Δn = 0,01. На какое расстояние Δl при этом сдвинется точка, в которой собираются лучи на экране?
30)На горизонтальном биллиардном столе маленький шарик 1 находится вблизи лузы на расстояниях Δx = 32 см от одного борта и Δy = 24 см от другого борта стола (см. рисунок). Немного дальше от бортов стоит такой же шарик 2, которому игрок сообщает ударом кия скорость V2 = 1,25 м/с в направлении к первому шарику, прицелившись так, чтобы после нелобового абсолютно упругого столкновения шарик 1 попал в лузу, находящуюся в точке x = y = 0. Первый шарик действительно попадает в лузу спустя время t1 = 0,4 с после столкновения. Спустя какое время t2 после столкновения шариков второй шарик ударится о борт стола? Какие законы Вы использовали для описания движения шариков? Обоснуйте их применимость к данному случаю.
Сложные задания с 2 варианта:
1)Выберите все верные утверждения о физических явлениях, величинах и закономерностях. Запишите цифры, под которыми они указаны.
- 1) При колебаниях пружинного маятника ускорение груза максимально по модулю в момент наибольшего удаления груза от положения равновесия.
- 2) При постоянной температуре давление насыщенных паров вещества уменьшается при увеличении объёма пара.
- 3) Если диэлектрик помещён во внешнее электростатическое поле, то напряжённость поля внутри диэлектрика такая же, как и снаружи.
- 4) Собирающая линза может формировать только действительное изображение.
- 5) При увеличении массы частицы её длина волны де Бройля уменьшается.
Правильный ответ: 15
2)На рисунке изображены три графика. Установите соответствие между этими графиками А), Б) и В) и зависимостями физических величин, обозначенных цифрами 1–5. Для каждого графика А–В подберите соответствующую зависимость и запишите в таблицу выбранные цифры под соответствующими буквами.
- 1) зависимость потенциальной энергии растянутой пружины от величины растягивающей силы
- 2) зависимость модуля импульса тела от модуля его скорости
- 3) зависимость электрической ёмкости плоского конденсатора от расстояния между его пластинами
- 4) зависимость давления столба однородной жидкости, находящейся в сосуде, от расстояния до дна сосуда
- 5) зависимость давления идеального газа от его температуры при постоянном объёме
Правильный ответ: 134
3)Тело состоит из двух частей, масса которых одинакова. Плотность первой части 1,5 г/см3 , плотность второй части 3,5 г/см3 . Чему равна средняя плотность этого тела?
Правильный ответ: 2,1
4)На горизонтальной гладкой поверхности покоится маленький брусок массой m = 0,5 кг, прикрепленный к стене при помощи нерастянутой пружины жёсткостью 200 Н/м. К бруску прикладывают постоянную силу F = 20 Н, направленную к стене вдоль оси пружины (так, как показано стрелкой на рисунке). На какую максимальную величину сожмётся пружина?
Правильный ответ: 20
5)На дне аквариума с гладким горизонтальным плоским дном лежит тонкий стеклянный диск, масса которого пренебрежимо мала. Высота уровня воды в аквариуме 50 см. Диск хорошо отшлифован и плотно прижат к дну аквариума, и поэтому вода под диск не подтекает. Давление воздуха над поверхностью воды 105 Па. Для того чтобы оторвать диск от дна аквариума, нужно приложить к центру диска минимальную направленную вверх силу, равную 630 Н. Чему равна площадь верхней поверхности диска?
Правильный ответ: 60
6)Небольшое тело, закреплённое на лёгкой пружине жёсткостью 1 Н/м, совершает гармонические колебания вдоль горизонтальной оси OX. На рисунке показан график зависимости проекции ускорения ax этого тела на указанную ось от времени t. Из приведённого ниже списка выберите все верные утверждения, описывающие данное движение тела. Запишите цифры, под которыми они указаны.
- 1) Период колебаний тела равен 4 с.
- 2) Амплитуда колебаний тела примерно равна 8 мм.
- 3) Максимальная потенциальная энергия пружины равна 16 мкДж.
- 4) Частота ν колебаний тела равна 2 Гц.
- 5) Масса тела примерно равна 400 г.
Правильный ответ: 125
7)По гладкой горизонтальной поверхности движутся поступательно навстречу друг другу два одинаковых шара. Модули скоростей шаров одинаковые, сопротивление воздуха пренебрежимо мало. Между шарами происходит абсолютно неупругое лобовое соударение. Этот опыт повторяют с теми же шарами, уменьшив модуль скорости каждого из них в три раза. Как для второго опыта по сравнению с первым изменились модуль суммарного импульса шаров и количество выделившейся при соударении теплоты? Для каждой величины определите соответствующий характер изменения:
- 1) увеличится
- 2) уменьшится
- 3) не изменится
Правильный ответ: 32
8)Небольшой камень бросили под углом α к горизонту с высоты h от поверхности земли с начальной скоростью υ0. Сопротивление воздуха пренебрежимо мало. Через время t после броска камень ещё не упал на землю. Установите соответствие между физическими величинами, характеризующими движение камня, и формулами, выражающими их в рассматриваемой задаче. К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры.
Правильный ответ: 23
9)В сосуде находится некоторое постоянное количество идеального газа. В некотором процессе объём сосуда увеличился в 2 раза, а средняя кинетическая энергия теплового движения молекул газа увеличилась в 4 раза. Каким стало давление газа в сосуде, если начальное давление было равно 60 кПа?
Правильный ответ: 120
10)В цилиндре находится воздух с относительной влажностью 20 %. Во сколько раз плотность насыщенного водяного пара при той же температуре превышает плотность водяных паров в цилиндре?
Правильный ответ: 5
11)Идеальный тепловой двигатель, работающий по циклу Карно, имеет КПД 60%. Каким станет КПД этого теплового двигателя, если температуру его нагревателя увеличить в 2 раза, а температуру холодильника оставить прежней?
Правильный ответ: 80
12)С одним молем гелия проводят процесс 1-2-3, который изображён на VTдиаграмме (Т – абсолютная температура гелия, V – его объём). Выберите все верные утверждения о происходивших в системе процессах и о состояниях гелия.
Правильный ответ: 124
13)В ходе адиабатного процесса внутренняя энергия идеального газа увеличивается. Как изменяются в этом процессе давление газа и его температура? Для каждой величины определите соответствующий характер изменения: 1) увеличивается 2) уменьшается 3) не изменяется
Правильный ответ: 11
14)Участок цепи состоит из трёх последовательно соединённых резисторов с сопротивлениями 2 Ом, 8 Ом и 10 Ом. Каким должно быть сопротивление четвёртого резистора, который включают в этот участок последовательно к первым трём, чтобы общее сопротивление участка увеличилось в 1,5 раза?
15)Индуктивность витка тонкой проволоки равна 4 мГн. Чему равен магнитный поток через поверхность, ограниченную этим витком, если сила тока в витке равна 2 А?
16)Непрозрачный круг освещается точечным источником света. На экране, параллельном плоскости круга, образуется круглая тень, радиус которой в 2 раза больше радиуса круга. Определите расстояние от центра круга до источника света, если расстояние от круга до экрана равно 80 см.
17)На рисунке изображён график зависимости напряжения U между обкладками конденсатора в колебательном контуре от времени t. Ёмкость конденсатора равна 15 мкФ. Выберите все верные утверждения об этом колебательном контуре.
- 1) Сила тока в колебательном контуре изменяется с частотой 250 Гц.
- 2) Период изменения энергии электрического поля конденсатора равен 4 мс.
- 3) Максимальный заряд конденсатора равен 15 мкКл.
- 4) Максимальная энергия магнитного поля катушки равна 30 мкДж.
- 5) В момент времени 4 мс сила тока в контуре равна нулю.
18)Дифракционная решётка с расстоянием между штрихами d освещается красным светом. На экране, установленном за решёткой параллельно ей, возникает дифракционная картина, состоящая из тёмных и светлых вертикальных полос. Как изменятся расстояние между соседними светлыми полосами и число наблюдаемых тёмных полос при освещении тем же светом другой решётки с расстоянием между штрихами 2d? Для каждой величины определите соответствующий характер изменения: 1) увеличивается 2) уменьшается 3) не изменяется
20)Модуль импульса первого фотона равен 10–28 кг⋅м/с, а длина волны второго фотона λ = 0,6 мкм. Во сколько раз модуль импульса второго фотона превышает модуль импульса первого фотона? Ответ округлите до целого числа.
21)В результате ядерной реакции ядро некоторого атома захватило быстрый нейтрон. Как изменятся заряд ядра и его массовое число при захвате нейтрона ядром? Для каждой величины определите соответствующий характер изменения: 1) увеличится 2) уменьшится 3) не изменится
22)На рисунке изображён термометр, показывающий уличную температуру в градусах Цельсия. Чему равна абсолютная температура воздуха на улице, если погрешность измерения температуры равна цене деления термометра?
23)Ученику необходимо провести лабораторную работу с целью исследования зависимости модуля силы Архимеда, действующей на полностью погруженный в жидкость груз, от плотности жидкости. В его распоряжении имеется ряд установок, в которых используются сосуды с различными жидкостями и различные грузы. Какие две установки из перечисленных в таблице необходимо выбрать, чтобы провести такое исследование?
24)Обкладки плоского воздушного конденсатора изготовлены из двух тонких квадратных металлических пластин со стороной a (на рисунке показан вид сбоку). Расстояние между обкладками d << a. Этот конденсатор подключён к источнику постоянного напряжения U с пренебрежимо малым внутренним сопротивлением. Через пространство между обкладками начинают медленно протаскивать с постоянной скоростью V квадратную пластину со стороной a и толщиной d, сделанную из однородного непроводящего материала с диэлектрической проницаемостью ε. В момент, когда всё пространство между обкладками конденсатора оказывается заполненным диэлектриком, пластину останавливают. Затем её начинают двигать в противоположном направлении с той же по модулю скоростью до тех пор, пока она не покинет пространство между обкладками.
Опираясь на законы физики, изобразите график зависимости силы электрического тока I, протекающего через источник напряжения, от времени t. Искажениями электрического поля вблизи краёв обкладок и пластины можно пренебречь. Отсчёт времени начинается в момент, когда правый край пластины находится на уровне левых краёв обкладок конденсатора, а заканчивается, когда пластина оказывается полностью вынутой из конденсатора с той же стороны, откуда начиналось движение пластины. Объясните построение графика, указав явления и закономерности, которые Вы при этом использовали. На осях координат обозначьте физические величины в «особых» точках графика (максимумы, минимумы, разрывы, точки излома графика), если они есть.
25)В велотренажерах для регулировки физической нагрузки тренирующихся на них спортсменов в настоящее время часто используются электродинамические тормозящие устройства, позволяющие плавно регулировать усилия, необходимые для вращения педалей с определённой скоростью. Вращение от педалей передаётся на массивный токопроводящий диск, находящийся между двумя сильными неподвижными магнитами, расстояние от которых до диска можно регулировать. Взаимодействие возникающих в диске индукционных токов с магнитами тормозит вращение диска, а, следовательно, и педалей, заставляя прикладывать к ним регулируемые по величине силы. Пусть спортсмен крутит педали, находящиеся на расстоянии R = 25 см от их оси вращения, с частотой ν = 12 оборотов в минуту, прикладывая к каждой из педалей в направлении её движения постоянную по модулю вращающую силу F = 40 Н. На сколько градусов нагреется железный диск массой m = 6 кг за время t = 20 минут работы в таком режиме? Считайте, что вся работа спортсмена расходуется только на равномерный разогрев диска.
26)На рисунке показана схема электрической цепи, состоящей из нескольких резисторов с одинаковыми сопротивлениями R, идеального диода Д, источника питания с постоянной ЭДС ε и малым внутренним сопротивлением, идеального амперметра А и переключателя П полярности источника питания. Во сколько раз изменится сила тока I через амперметр после перевода переключателя в другое положение?
27)На p–V диаграмме изображён процесс 1-2-3-1, проводимый с одним молем идеального одноатомного газа. Значения p и V на ней приведены в относительных единицах y = p/p0 и x = V/V0, где p0 и V0 – некоторые постоянные величины давления и объёма. Какую работу А1234 совершил газ в этом процессе при переходе из состояния 1 в состояние 4, в котором температура газа приняла максимальное значение? Известно, что температура газа в состоянии 2 была равна T2 = 200 К.
28)Квадратная проводящая рамка с длинами сторон 2a = 24 см закреплена на горизонтальной оси О, установленной в неподвижных подшипниках и проходящей через середины двух противоположных сторон рамки. К центру этой оси жёстко приделана лёгкая штанга длиной l = 12 см с маленьким грузиком массой m = 150 г на конце, перпендикулярная плоскости рамки. Вся эта конструкция может свободно вращаться на оси и находится в однородном горизонтальном магнитном поле с индукцией B = 0,8 Тл, направленной перпендикулярно оси рамки (см. рисунок, вид сбоку вдоль оси). По рамке с помощью гибких проводов начали пропускать постоянный ток, в результате чего в новом положении равновесия рамка со штангой повернулась вокруг оси на угол α = 40°. Чему равна сила тока I в рамке?
29)На стеклянную призму с преломляющим углом α = 35° нормально к её передней грани падает параллельный пучок монохроматического красного света, для которого показатель преломления n = 1,51 (стекло – лёгкий крон). После преломления в призме пучок идёт вдоль главной оптической оси тонкой линзы с фокусным расстоянием F = 40 см и после неё собирается в точку на экране, параллельном плоскости линзы. Затем при том же расположении элементов оптической системы по тому же направлению на призму пускают параллельный пучок монохроматического синего света, для которого показатель преломления стекла из-за явления дисперсии света больше на Δn = 0,015. На какое расстояние Δl при этом сдвинется точка, в которой собираются лучи на экране?
30)На горизонтальном биллиардном столе маленький шарик 1 находится вблизи лузы на расстояниях Δx = 24 см от одного борта и Δy = 18 см от другого борта стола (см. рисунок). Немного дальше от бортов стоит такой же шарик 2, которому игрок сообщает ударом кия скорость V2 = 1 м/с в направлении к первому шарику, прицелившись так, чтобы после нелобового абсолютно упругого столкновения шарик 1 попал в лузу, находящуюся в точке x = y = 0. Первый шарик действительно попадает в лузу спустя время t1 = 0,4 с после столкновения. Спустя какое время t2 после столкновения шариков второй шарик ударится о борт стола? Какие законы Вы использовали для описания движения шариков? Обоснуйте их применимость к данному случаю.
Другие тренировочные варианты ЕГЭ 2022 по физике 11 класс:
Статград варианты ФИ2110301-ФИ2110304 физика 11 класс ЕГЭ 2022 с ответами
Физика 11 класс пробный ЕГЭ 2022 статград 4 варианта ФИ2110201-ФИ2110204 с ответами
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
ЕГЭ профильный уровень. №5 Логарифмические уравнения. Задача 10
Задача 10. Решите уравнение ({log _{x + 6}}32 = 5.) Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
({log _{x + 6}}32 = 5,,,,,, Leftrightarrow ,,,,,,left{ {begin{array}{*{20}{c}}{{{left( {x + 6} right)}^5} = 32}\{x + 6 > 0,,,,,,,,,,}\{x + 6 ne 1,,,,,,,,,,,}end{array}} right.,,,,,,, Leftrightarrow ,,,,,,left{ {begin{array}{*{20}{c}}{{{left( {x + 6} right)}^5} = {2^5}}\{x + 6 > 0,,,,,,,,}\{x + 6 ne 1,,,,,,,,}end{array}} right.,,,,,, Leftrightarrow )
( Leftrightarrow ,,,,,,,left{ {begin{array}{*{20}{c}}{x + 6 = 2}\{x + 6 > 0}\{x + 6 ne 1}end{array},,,,,, Leftrightarrow } right.,,,,,,,,x + 6 = 2,,,,,,, Leftrightarrow ,,,,,,,x = — 4.)
Ответ: – 4.
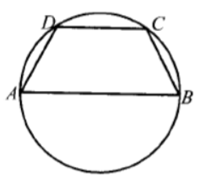
Задание 1
Боковая сторона равнобедренной трапеции равна её меньшему основанию, угол при основании трапеции равен 60°, большее основание равно 18. Найдите радиус описанной окружности этой трапеции
Ответ: 9
Скрыть
Рассмотрим треугольник ADC, в котором AD=DC по условию задания, а угол D равен:
$$angle D=frac{360^{circ}-angle A-angle B}{2}=frac{360^{circ}-60^{circ}-60^{circ}}{2}=120^{circ}.$$
Найдем сторону AD=DC из треугольника ADH:
$$AD=frac{AH}{cos60^{circ}}=frac{(AB-DC):2}{0,5}=AB-DC$$
$$2AD=AB=18$$
$$AD=frac{18}{2}=9$$
Радиус описанной окружности можно найти по теореме синусов для треугольника ADC, имеем:
$$R=frac{AD}{2sinangle DCA}=frac{9}{2cdotsin30^{circ}}=9.$$
Задание 2
Цилиндр вписан в правильную шестиугольную призму. Радиус основания цилиндра равен $$sqrt{3},$$ а высота равна 2. Найдите площадь боковой поверхности призмы.
Ответ: 24
Скрыть
В основании правильной четырёхугольной призмы лежит правильный шестиугольник:
Найдем сторону этого шестиугольника из треугольника, у которого известен угол 120 градусов между сторонами и противолежащая сторона $$D = 2sqrt{3}.$$ По теореме косинусов можно записать:
$$D^2=a^2+a^2-2cdot acdot acdotcos120$$
$$(2sqrt{3})^2=2a^2-2a^2cdot(-frac{1}{2})$$
$$12=3a^2$$
$$a=2$$
Площадь боковой поверхности правильной шестиугольной призмы со стороной a = 2 и высотой h = 3, равна:
Площадь боковой поверхности правильной призмы со стороной a = 6 и высотой h = 2, равна:
$$S=6cdot acdot h=6cdot2cdot2=24$$
Задание 3
Какова вероятность того, что последние три цифры номера случайно выбранного паспорта одинаковы?
Ответ: 0,01
Скрыть
Цифры меняются от 0 до 9, значит, совпадение трех последних цифр – это одно из $$m = 10$$ событий:
$$000, 111, 222, …, 999.$$
Всего возможных комбинаций из трех цифр $$n=10^3=1000.$$ Получаем значение искомой вероятности:
$$P=frac{m}{n}=frac{10}{1000}=0,01$$
Задание 4
Игральную кость бросали до тех пор, пока сумма всех выпавших очков не превысила число 9. Какова вероятность того, что для этого потребовалось три броска? Ответ округлите до сотых.
Ответ: 0,46
Скрыть
Пусть первое число — результат первого броска, второе — второго, третье — третьего. Тогда возможные варианты превысить число 9 в сумме за три броска:
1 3…6 6 — четыре исхода: $$frac{1}{6}cdotfrac{1}{6}cdotfrac{1}{6}cdot4=frac{4}{216}$$
1 4…6 5 — три исхода: $$frac{1}{6}cdotfrac{1}{6}cdotfrac{1}{6}cdot3=frac{3}{216}$$
1 5…6 4 — два исхода: $$frac{1}{6}cdotfrac{1}{6}cdotfrac{1}{6}cdot2=frac{2}{216}$$
1 6 3 — один исход: $$frac{1}{6}cdotfrac{1}{6}cdotfrac{1}{6}=frac{1}{216}$$
Аналогично рассматривается с первой двойкой (15 исходов всего $$frac{15}{216}$$), тройкой — 21 исход $$frac{21}{216}$$
4 1…5 6 — 5 исходов: $$frac{5}{216}$$
4 1…5 5 — 5 исходов: $$frac{5}{216}$$
4 2…5 4 — 4 исхода: $$frac{4}{216}$$
4 3…5 3 — 3 исхода: $$frac{3}{216}$$
4 4…5 2 — 2 исхода: $$frac{2}{216}$$
4 5 1 — 1 исход: $$frac{1}{216}$$
Заметьте, что 4 6 не рассматриваем уже, т.к. тогда на втором броске уже будет больше 9.
Аналогично с пятеркой: 18 исходов: $$frac{18}{216}$$ и шестеркой: 15 исходов: $$frac{15}{216}$$
В итоге получили: $$10+15+21+20+18+15=99$$ исходов с вероятность $$frac{1}{216}$$
$$P(A)=frac{99}{216}=0,458(3)approx0,46$$
Задание 5
Решите уравнение $$sqrt{2log_8(-x)}-log_8sqrt{x^2}=0.$$ Если уравнение имеет несколько корней, в ответе укажите их сумму.
Ответ: -65
Скрыть
Учтём, что $$log_8sqrt{x^2}=log_8|x|.$$ Так как есть $$log_8(-x),$$ то $$-x>0Rightarrow x<0.$$ Тогда $$log_8|x|=log_8(-x)$$
Пусть $$log_8(-x)=y.$$ Получим: $$sqrt{2y}=yRightarrowleft{begin{matrix} 2y=y^2\ ygeq0 end{matrix}right.Leftrightarrowleft[begin{matrix} y=0\ y=2 end{matrix}right.$$
Обратная замена:
$$left[begin{matrix} log_8(-x)=0\ log_8(-x)=2 end{matrix}right.Leftrightarrowleft[begin{matrix} -x=1\ -x=64 end{matrix}right.Leftrightarrowleft[begin{matrix} x=-1\ x=-64 end{matrix}right.$$
Сумма корней $$(-1)+(-64)=-65.$$
Задание 6
Найдите значение выражения $$frac{p(b)}{p(frac{1}{b})},$$ если $$p(b)=(b+frac{3}{b})(3b+frac{1}{b})$$ при $$bneq0$$
Ответ: 1
Скрыть
$$frac{p(b)}{p(frac{1}{b})}=frac{(b+frac{3}{b})(3b+frac{1}{b})}{(frac{1}{b}+3b)(frac{3}{b}+b)}=1$$
Задание 7
Прямая $$y=x+7$$ является касательной к графику функции $$y=ax^2-15x+15.$$ Найдите $$a.$$
Ответ: 8
Скрыть
Приравниваем производные и функции:
$$left{begin{matrix} (x+7)’=(ax^2-15x+15)’\ x+7=ax^2-15x+15 end{matrix}right.Leftrightarrowleft{begin{matrix} 1=2ax-15\ ax^2-16x+8 end{matrix}right.Leftrightarrowleft{begin{matrix} x=frac{8}{a}\ acdotfrac{64}{a^2}-frac{16cdot8}{a}+8=0 end{matrix}right.$$
$$frac{64}{a}-frac{128}{a}=-8Rightarrow -frac{64}{a}=-8Rightarrow a=8$$
Задание 8
Если достаточно быстро вращать ведёрко с водой на верёвке в вертикальной плоскости, то вода не будет выливаться. При вращении ведёрка сила давления воды на дно не остаётся постоянной: она максимальна в нижней точке и минимальна в верхней. Вода не будет выливаться, если сила её давления на дно будет положительной во всех точках траектории, кроме верхней, где она может быть равной нулю. В верхней точке сила давления, выраженная в ньютонах, равна $$P=m(frac{v^2}{L}-g),$$ где $$m$$ — масса воды в килограммах, $$v$$ — скорость движения ведёрка в м/с, $$L$$ — длина верёвки в метрах, $$g$$ — ускорение свободного падения (считайте, что $$g = 10$$ м/с2). С какой минимальной скоростью надо вращать ведёрко, чтобы вода не выливалась, если длина верёвки равна 0,625 м? Ответ выразите в м/с.
Ответ: 2,5
Скрыть
Чем выше скорость вращения, тем больше давление воды ⇒ нужно найти минимальную скорость, давление должно быть равно 0.
$$m(frac{v_2}{0,625}-10)=0$$
Произведение равно 0, когда один из множителей равен 0. m ≠ 0
$$frac{v_2}{0,625}-10=0$$
$$frac{v_2}{0,625}=10$$
$$v_2 = 10cdot0,625$$
$$v_2 = 6,25$$
$$v = 2,5$$
Задание 9
Трем рабочим поручили изготовить одинаковые партии деталей. Производительность первого рабочего была на 10% меньше, чем у второго, и на 20% больше, чем у третьего. Первым приступил к работе третий рабочий, спустя 6 минут начал свою работу первый рабочий и они закончили свои задания одновременно. На сколько минут позже третьего рабочего начал работать второй, если он свое задание выполнил на 2 минуты раньше, чем первый и третий рабочий?
Ответ: 7
Скрыть
Пусть производительность третьего рабочего $$x$$ раб/мин, тогда производительность первого рабочего — $$(x+0,2x)=1,2x$$ раб/мин, а производительность третьего считаем по пропорции
1,2x — 90%
пр.тр. — 100%
пр.тр. $$=frac{1,2xcdot100}{90}=frac{4x}{3}$$ — производительность третьего рабочего.
Всю работу примем за 1. Тогда время на выполнение работы первым рабочим $$frac{1}{1,2x}$$ минут, третьим — $$frac{1}{x}$$ минут. Первый рабочий выполнил работу на 6 минут быстрее третьего. Составим и решим уравнение:
$$frac{1}{x}-frac{1}{1,2x}=6$$
$$frac{6-5}{6x}=6$$
$$frac{1}{6x}=6$$
$$36x=1$$
$$x=frac{1}{36}$$ раб/мин — производительность третьего рабочего, значит, всю работу он выполнит за 36 минут.
$$frac{4}{3}cdotfrac{1}{36}=frac{1}{27}$$ раб/мин — производительность второго рабочего, значит, всю работу он выполнит за 27 минут.
$$36-27=9$$ минут — на столько дольше работу выполняет третий рабочий, чем второй.
Если второй выполнил работу на 2 минуты раньше третьего, то
$$9-2=7$$ минут — на столько позже третьего второй начал работу.
Задание 10
На рисунке изображен график функции $$f(x)=b+log_a(-frac{1}{x}),$$ где $$a, b$$ — целые числа. Найдите значение $$x,$$ при котором $$f(x)=5.$$
Ответ: -0,25
Скрыть
График проходит через (-4;1) и (-1;3). Получим:
$$left{begin{matrix} 1=b+log_afrac{1}{4}\ 3=b+log_a 1 end{matrix}right.Leftrightarrowleft{begin{matrix} log_afrac{1}{4}=-2\ b=3 end{matrix}right.Leftrightarrowleft{begin{matrix} a=2\ b=3 end{matrix}right.$$
Получили $$f(x)=3+log_2(-frac{1}{x})=5Rightarrow log_2(-frac{1}{x})=2Rightarrow -frac{1}{x}=4Rightarrow x=-0,25$$
Задание 11
Найдите наименьшее значение функции $$f(x)=3x^4+4x^3-12x^2-12$$ на отрезке $$[-0,5;2].$$
Ответ: -17
Скрыть
Найдем производную и приравняем ее к нулю
$$12x^3+12x^2−24x=0$$
$$x(12x^2+12x−24)=0$$
$$x=0$$
$$x=1$$
$$x=−2$$ – не попадет в промежуток
Проверяем методом интервалов точка 1 – точка минимума
$$f(1)=−17$$
Задание 12
А) Решите уравнение $$(-2cos^2x+sin x+1)cdotlog_{0,5}(-0,8cos x)=0$$
Б) Найдите все корни уравнения, принадлежащие отрезку $$[-6pi;-4pi]$$
Ответ: А)$$frac{5pi}{6}+2pi n,nin Z$$ Б)$$-frac{31pi}{6}$$
Задание 13
Конус и полусфера имеют общее основание, радиус которого относится к высоте конуса как 1:3.
А) Докажите, что поверхность полусферы делит образующую конуса в отношении 4:1, считая от вершины конуса.
Б) Найдите площадь поверхности полусферы, находящейся внутри конуса, если радиус их общего основания равен 5.
Ответ: $$20pi$$
Задание 14
Решите неравенство: $$sqrt{2-log_{frac{1}{2}}x}cdotfrac{(x-1)(x+7)}{x+2}geq0$$
Ответ: $$left{frac{1}{4}right},[1;infty)$$
Задание 15
Строительство нового цеха по производству роботов-пылесосов стоит 300 млн рублей. Затраты на производство $$x$$ тыс. единиц продукции на такой линии равны $$0,1x^2+3x+100$$ млн рублей в год. Если продукцию продавать по цене $$р$$ тыс. рублей за единицу, то прибыль фирмы (в млн рублей) за один год составит $$px-(0,1x^2+3x+100).$$ Когда цех будет построен, каждый год фирма будет выпускать продукцию в таком количестве, чтобы прибыль была наибольшей. В первый год после постройки цеха цена продукции $$p = 12$$ тыс. руб. за единицу, каждый следующий год цена продукции увеличивается на 1 тыс. руб. за единицу. За сколько лет окупится строительство цеха?
Ответ: 3
Задание 16
Дана равнобедренная трапеция ABCD. На боковой стороне АВ и большем основании AD взяты соответственно точки К и L так, что KL||CD и CK=DL.
А) Докажите, что $$angle BCK = angle AKL$$
Б) Найдите площадь трапеции ABCD, если $$KL = 12,DL = 2,5BK, S_{CDLK} = 26sqrt{6}$$
Ответ: $$frac{196sqrt{6}}{5}$$
Задание 17
Найдите все положительные значения параметра $$a,$$ при каждом из которых любое значение $$x$$ из отрезка $$[-1;1]$$ будет являться решением неравенства
$$3a^{2x}-16^x+2cdot(4a)^xgeq0$$
Ответ: $$[frac{4}{3};12]$$
Задание 18
В натуральном числе $$n$$ между всеми парами соседних цифр вставили одну и ту же цифру $$c.$$ Получилось число $$m,$$ которое делится на $$n.$$ Их частное равно $$k.$$
А) Может ли быть $$k = 10$$?
Б) Может ли быть $$k = 2$$?
В) Чему может быть равно наименьшее значение числа $$k$$?
Ответ: А) да, Б) нет, В) 6

В работе представлены задания разных уровней сложности: базового, повышенного и высокого. Задания базового уровня, это простые задания, проверяющие усвоение наиболее важных физических понятий, моделей, явлений и законов. Задания повышенного уровня направлены на проверку умения использовать понятия и законы физики для анализа различных процессов и явлений, а также умения решать задачи на применение одного-двух законов (формул) по какой-либо из тем школьного курса физики. В работе 4 задания части 2 являются заданиями высокого уровня сложности и проверяют умение использовать законы и теории физики в измененной или новой ситуации. Выполнение таких заданий требует применения знаний сразу из двух трех разделов физики, т.е. высокого уровня подготовки. Данный вариант полностью соответствует демонстрационному варианту ЕГЭ 2017 года, задания взяты из открытого банка заданий ЕГЭ.
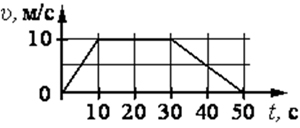
Задание 1. На рисунке представлен график зависимости модуля скорости от времени t. Определите по графику путь, пройденный автомобилем в интервале времени от 0 до 30 с.
Решение. Путь, пройденный автомобилем в интервале времени от 0 до 30 с проще всего определить как площадь трапеции, основаниями которой являются интервалы времени (30 – 0) = 30 c и (30 – 10) = 20 с, а высотой является скорость v = 10 м/с, т.е.
| S = | (30 + 20) с | 10 м/с = 250 м. |
| 2 |
Ответ. 250 м.
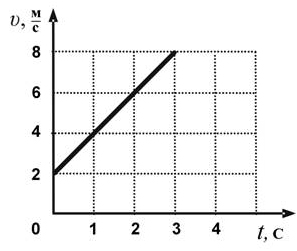
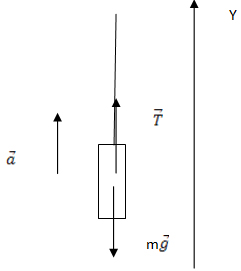
Задание 2. Груз массой 100 кг поднимают вертикально вверх с помощью троса. На рисунке приведена зависимость проекции скорости V груза на ось, направленную вверх, от времени t. Определите модуль силы натяжения троса в течение подъема.
Рис. 1
Рис. 2
Решение. По графику зависимости проекции скорости v груза на ось, направленную вертикально вверх, от времени t, можно определить проекцию ускорения груза
| a = | ∆v | = | (8 – 2) м/с | = 2 м/с2. |
| ∆t | 3 с |
На груз действуют: сила тяжести 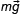
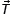
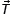
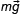
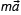
Запишем уравнение для проекции векторов в системе отсчета, связанной с землей, ось OY направим вверх. Проекция силы натяжения положительная, так как направление силы совпадает с направлением оси OY, проекция силы тяжести отрицательная, так как вектор силы противоположно направлен оси OY, проекция вектора ускорения тоже положительная, так тело движется с ускорением вверх. Имеем
T – mg = ma (2);
из формулы (2) модуль силы натяжения
Т = m(g + a) = 100 кг (10 + 2) м/с2 = 1200 Н.
Ответ. 1200 Н.
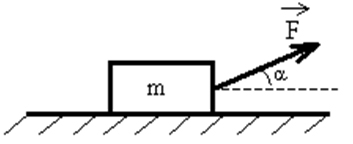
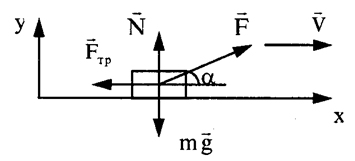
Задание 3. Тело тащат по шероховатой горизонтальной поверхности с постоянной скоростью 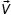
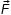
Рис. 1
Рис. 2
Решение. Представим себе физический процесс, заданный в условии задачи и сделаем схематический чертеж с указанием всех сил, действующих на тело (рис.2). Запишем основное уравнение динамики.
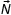
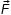
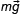
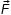
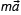
Выбрав систему отсчета, связанную с неподвижной поверхностью, запишем уравнения для проекции векторов на выбранные координатные оси. По условию задачи тело движется равномерно, так как его скорость постоянна и равна 1,5 м/с. Это значит, ускорение тела равно нулю. По горизонтали на тело действуют две силы: сила трения скольжения 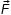
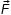
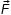
N = 16 Н · 1,5 м/с = 24 Вт.
Ответ. 24 Вт.
Задание 4. Груз, закрепленный на легкой пружине жесткостью 200 Н/м, совершает вертикальные колебания. На рисунке представлен график зависимости смещения x груза от времени t. Определите, чему равна масса груза. Ответ округлите до целого числа.
Решение. Груз на пружине совершает вертикальные колебания. По графику зависимости смещения груза х от времени t, определим период колебаний груза. Период колебаний равен Т = 4 с; из формулы Т = 2π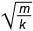
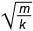 = = |
T | ; | m | = | T2 | ; m = k | T2 | ; m = 200 H/м | (4 с)2 | = 81,14 кг ≈ 81 кг. |
| 2π | k | 4π2 | 4π2 | 39,438 |
Ответ: 81 кг.
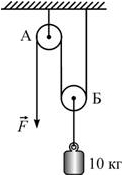
Задание 5. На рисунке показана система из двух легких блоков и невесомого троса, с помощью которого можно удерживать в равновесии или поднимать груз массой 10 кг. Трение пренебрежимо мало. На основании анализа приведенного рисунка выберите два верных утверждения и укажите в ответе их номера.
- Для того чтобы удерживать груз в равновесии, нужно действовать на конец веревки с силой 100 Н.
- Изображенная на рисунке система блоков не дает выигрыша в силе.
- Для того чтобы медленно поднять груз на высоту h, нужно вытянуть участок веревки длиной 3h.
- Для того чтобы медленно поднять груз на высоту h, нужно вытянуть участок веревки длиной 2h.
- Для того чтобы удерживать груз в равновесии, нужно действовать на конец веревки с силой 50 Н.
Решение. В данной задаче необходимо вспомнить простые механизмы, а именно блоки: подвижный и неподвижный блок. Подвижный блок дает выигрыш в силе в два раза, при этом участок веревки нужно вытянуть в два раза длиннее, а неподвижный блок используют для перенаправления силы. В работе простые механизмы выигрыша не дают. После анализа задачи сразу выбираем нужные утверждения:
- Для того чтобы медленно поднять груз на высоту h, нужно вытянуть участок веревки длиной 2h.
- Для того чтобы удерживать груз в равновесии, нужно действовать на конец веревки с силой 50 Н.
Ответ. 45.
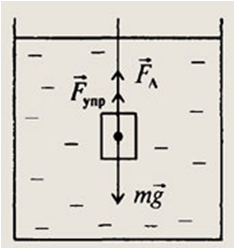
Задание 6. В сосуд с водой полностью погружен алюминиевый груз, закрепленный на невесомой и нерастяжимой нити. Груз не касается стенок и дна сосуда. Затем в такой же сосуд с водой погружают железный груз, масса которого равна массе алюминиевого груза. Как в результате этого изменятся модуль силы натяжения нити и модуль действующей на груз силы тяжести?
Для каждой величины определите соответствующий характер изменения:
- Увеличивается;
- Уменьшается;
- Не изменяется.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
|
Модуль силы натяжения нити |
Модуль действующей на груз силы тяжести |
Рис. 1
Решение. Анализируем условие задачи и выделяем те параметры, которые не меняются в ходе исследования: это масса тела и жидкость, в которую погружают тело на нити. После этого лучше выполнить схематический рисунок и указать действующие на груз силы: сила натяжения нити Fупр, направленная вдоль нити вверх; сила тяжести 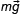
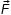
Плотность железа 7800 кг/м3, а алюминиевого груза 2700 кг/м3. Следовательно, Vж < Va. Тело в равновесии, равнодействующая всех сил, действующих на тело равна нулю. Направим координатную ось OY вверх. Основное уравнение динамики с учетом проекции сил запишем в виде Fупр + Fa – mg = 0; (1) Выразим силу натяжения Fупр = mg – Fa (2); архимедова сила зависит от плотности жидкости и объема погруженной части тела Fa = ρgV п.ч.т. (3); Плотность жидкости не меняется, а объем тела из железа меньше Vж < Va, поэтому архимедова сила, действующая на железный груз будет меньше. Делаем вывод о модуле силы натяжения нити, работая с уравнение (2), он возрастет.
Ответ. 13.
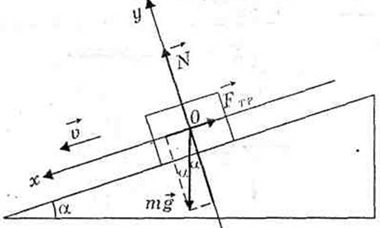
Задание 7. Брусок массой m соскальзывает с закрепленной шероховатой наклонной плоскости с углом α при основании. Модуль ускорения бруска равен a, модуль скорости бруска возрастает. Сопротивлением воздуха можно пренебречь.
Установите соответствие между физическими величинами и формулами, при помощи которых их можно вычислить. К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
|
ФИЗИЧЕСКАЯ ВЕЛИЧИНА |
ФОРМУЛА |
|
А) Модуль силы реакции, действующей на брусок со стороны наклонной плоскости |
1) mg |
|
Б) Коэффициент трения бруска о наклонную плоскость |
3) mg cosα |
Решение. Данная задача требует применение законов Ньютона. Рекомендуем сделать схематический чертеж; указать все кинематические характеристики движения. Если возможно, изобразить вектор ускорения и векторы всех сил, приложенных к движущемуся телу; помнить, что силы, действующие на тело, – результат взаимодействия с другими телами. Затем записать основное уравнение динамики. Выбрать систему отсчета и записать полученное уравнение для проекции векторов сил и ускорений;
Следуя предложенному алгоритму, сделаем схематический чертеж (рис. 1). На рисунке изображены силы, приложенные к центру тяжести бруска, и координатные оси системы отсчета, связанной с поверхностью наклонной плоскости. Так как все силы постоянны, то движение бруска будет равнопеременным с увеличивающейся скоростью, т.е. вектор ускорения направлен в сторону движения. Выберем направление осей как указано на рисунке. Запишем проекции сил, на выбранные оси.
Рис. 1
Запишем основное уравнение динамики:
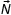
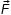
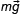
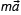
Запишем данное уравнение (1) для проекции сил и ускорения.
На ось OY: проекция силы реакции опоры положительная, так как вектор совпадает с направлением оси OY Ny = N; проекция силы трения равна нулю так как вектор перпендикулярен оси; проекция силы тяжести будет отрицательная и равная mgy = –mgcosα; проекция вектора ускорения ay = 0, так как вектор ускорения перпендикулярен оси. Имеем N – mgcosα = 0 (2) из уравнения выразим силу реакции действующей на брусок, со стороны наклонной плоскости. N = mgcosα (3). Запишем проекции на ось OX.
На ось OX: проекция силы N равна нулю, так как вектор перпендикулярен оси ОХ; Проекция силы трения отрицательная (вектор направлен в противоположную сторону относительно выбранной оси); проекция силы тяжести положительная и равна mgx = mgsinα (4) из прямоугольного треугольника. Проекция ускорения положительная ax = a; Тогда уравнение (1) запишем с учетом проекции mgsinα – Fтр = ma (5); Fтр = m(gsinα – a) (6); Помним, что сила трения пропорциональна силе нормального давления N.
По определению Fтр = μN (7), выразим коэффициент трения бруска о наклонную плоскость.
| μ = | Fтр | = | m(gsinα – a) | = tgα – | a | (8). |
| N | mgcosα | gcosα |
Выбираем соответствующие позиции для каждой буквы.
Ответ. A – 3; Б – 2.
Задание 8. Газообразный кислород находится в сосуде объемом 33,2 литра. Давление газа 150 кПа, его температура 127° С. Определите массу газа в этом сосуде. Ответ выразите в граммах и округлите до целого числа.
Решение. Важно обратить внимание на перевод единиц в систему СИ. Температуру переводим в Кельвины T = t°С + 273, объем V = 33,2 л = 33,2 · 10–3 м3; Давление переводим P = 150 кПа = 150 000 Па. Используя уравнение состояния идеального газа
| PV = | m | RT, (уравнение Менделеева –Клапейрона) |
| μ |
выразим массу газа.
и подставим числовые значения в полученное уравнение.
| m = | 1,5 · 105 ·33,2 · 10–3 · 32 · 10–3 | = 0,0479 кг = 47,9 г ≈ 48 г |
| 8,31 · 400 |
Обязательно обращаем внимание, в каких единица просят записать ответ. Это очень важно.
Ответ. 48 г.
Задание 9. Идеальный одноатомный газ в количестве 0,025 моль адиабатически расширился. При этом его температура понизилась с +103°С до +23°С. Какую работу совершил газ? Ответ выразите в Джоулях и округлите до целого числа.
Решение. Во-первых, газ одноатомный число степеней свободы i = 3, во-вторых, газ расширяется адиабатически – это значит без теплообмена Q = 0. Газ совершает работу за счет уменьшения внутренней энергии. С учетом этого, первый закон термодинамики запишем в виде 0 = ∆U + Aг; (1) выразим работу газа Aг = –∆U (2); Изменение внутренней энергии для одноатомного газа запишем как
Проведем вычисления подставив (3) в (2). Не забываем перевести температуру из градусов Цельсия в Кельвины.
| Aг = – | 3 | 0,025 · 8,31 · (–80) = 24,93 (Дж) ≈ 25Дж |
| 2 |
Ответ. 25 Дж.
Задание 10. Относительная влажность порции воздуха при некоторой температуре равна 10 %. Во сколько раз следует изменить давление этой порции воздуха для того, чтобы при неизменной температуре его относительная влажность увеличилась на 25 %?
Решение. Вопросы, связанные с насыщенным паром и влажностью воздуха, чаще всего вызывают затруднения у школьников. Воспользуемся формулой для расчета относительной влажности воздуха
| φ = | Pв.п. | · 100 % (1); |
| Pн.п. |
По условию задачи температура не изменяется, значит, давление насыщенного пара остается тем же. Запишем формулу (1) для двух состояний воздуха.
| φ1 = | P1в.п. | · 100 % (2); |
| Pн.п. |
и
| φ2 = | P2в.п. | · 100 % (3); |
| Pн.п. |
φ1 = 10 % ; φ2 = 35 %
Выразим давления воздуха из формул (2), (3) и найдем отношение давлений.
| P2 | = | φ2 | = | 35 | = 3,5 |
| P1 | φ1 | 10 |
Ответ. Давление следует увеличить в 3,5 раза.
Задание 11. Горячее вещество в жидком состоянии медленно охлаждалось в плавильной печи с постоянной мощностью. В таблице приведены результаты измерений температуры вещества с течением времени.
|
Время, мин |
0 |
5 |
10 |
15 |
20 |
25 |
30 |
35 |
|
Температура, °С |
250 |
242 |
234 |
232 |
232 |
232 |
230 |
216 |
Выберите из предложенного перечня два утверждения, которые соответствуют результатам проведенных измерений и укажите их номера.
- Температура плавления вещества в данных условиях равна 232°С.
- Через 20 мин. после начала измерений вещество находилось только в твердом состоянии.
- Теплоемкость вещества в жидком и твердом состоянии одинакова.
- Через 30 мин. после начала измерений вещество находилось только в твердом состоянии.
- Процесс кристаллизации вещества занял более 25 минут.
Решение. Так как вещество охлаждалось, то его внутренняя энергия уменьшалась. Результаты измерения температуры, позволяют определить температуру, при которой вещество начинает кристаллизоваться. Пока вещество переходит из жидкого состояния в твердое, температура не меняется. Зная, что температура плавления и температура кристаллизации одинаковы, выбираем утверждение:
1. Tемпература плавления вещества в данных условиях равна 232°С.
Второе верное утверждение это:
4. Через 30 мин. после начала измерений вещество находилось только в твердом состоянии. Так как температура в этот момент времени, уже ниже температуры кристаллизации.
Ответ. 14.
Задание 12. В изолированной системе тело А имеет температуру +40°С, а тело Б температуру +65°С. Эти тела привели в тепловой контакт друг с другом. Через некоторое время наступило тепловое равновесие. Как в результате изменилась температура тела Б и суммарная внутренняя энергия тела А и Б?
Для каждой величины определите соответствующий характер изменения:
- Увеличилась;
- Уменьшилась;
- Не изменилась.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
|
Температура тела Б |
Суммарная внутренняя энергия тел А и Б |
Решение. Если в изолированной системе тел не происходит никаких превращений энергии кроме теплообмена, то количество теплоты, отданное телами, внутренняя энергия которых уменьшается, равно количеству теплоты, полученному телами, внутренняя энергия которых увеличивается. (По закону сохранения энергии.) При этом суммарная внутренняя энергия системы не меняется. Задачи такого типа решаются на основании уравнения теплового баланса.
| ∆U = ∑ | n | ∆Ui = 0 (1); |
i = 1 |
где ∆U – изменение внутренней энергии.
В нашем случае в результате теплообмена внутренняя энергия тела Б уменьшается, а значит уменьшается температура этого тела. Внутренняя энергия тела А увеличивается, так как тело получило количество теплоты от тела Б, то температура его увеличится. Суммарная внутренняя энергия тел А и Б не изменяется.
Ответ. 23.
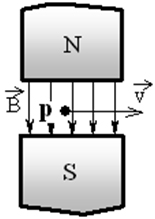
Задание 13. Протон p, влетевший в зазор между полюсами электромагнита, имеет скорость 
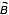
Решение. На заряженную частицу магнитное поле действует с силой Лоренца. Для того чтобы определить направление этой силы, важно помнить мнемоническое правило левой руки, не забывать учитывать заряд частицы. Четыре пальца левой руки направляем по вектору скорости, для положительно заряженной частицы, вектор 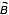
Ответ. от наблюдателя.
Задание 14. Модуль напряженности электрического поля в плоском воздушном конденсаторе емкостью 50 мкФ равен 200 В/м. Расстояние между пластинами конденсатора 2 мм. Чему равен заряд конденсатора? Ответ запишите в мкКл.
Решение. Переведем все единицы измерения в систему СИ. Емкость С = 50 мкФ = 50 · 10–6 Ф, расстояние между пластинами d = 2 · 10–3 м. В задаче говорится о плоском воздушном конденсаторе – устройстве для накопления электрического заряда и энергии электрического поля. Из формулы электрической емкости
выразим электрический заряд q = C · U (2). Используя связь напряженности электрического поля E и напряжения U, запишем формулу
где d – расстояние между пластинами.
Выразим напряжение U = E · d (4); Подставим (4) в (2) и рассчитаем заряд конденсатора.
q = C · Ed = 50 · 10–6 · 200 · 0,002 = 20 мкКл
Обращаем внимание, в каких единицах нужно записать ответ. Получили в кулонах, а представляем в мкКл.
Ответ. 20 мкКл.
Задание 15.
Рис. 1
Ученик провел опыт по преломлению света, представленный на фотографии. Как изменяется при увеличении угла падения угол преломления света, распространяющегося в стекле, и показатель преломления стекла?
- Увеличивается
- Уменьшается
- Не изменяется
- Запишите в таблицу выбранные цифры для каждого ответа. Цифры в ответе могут повторяться.
|
Угол преломления |
Показатель преломления стекла |
Решение. В задачах такого плана вспоминаем, что такое преломление. Это изменение направления распространения волны при прохождении из одной среды в другую. Вызвано оно тем, что скорости распространения волн в этих средах различны. Разобравшись из какой среды в какую свет распространяется, запишем закона преломления в виде
где n2 – абсолютный показатель преломления стекла, среда куда идет свет; n1 – абсолютный показатель преломления первой среды, откуда свет идет. Для воздуха n1 = 1. α – угол падения луча на поверхность стеклянного полуцилиндра, β – угол преломления луча в стекле. Причем, угол преломления будет меньше угла падения, так как стекло оптически более плотная среда – среда с большим показателем преломления. Скорость распространения света в стекле меньше. Обращаем внимание, что углы измеряем от перпендикуляра, восстановленного в точке падения луча. Если увеличивать угол падения, то и угол преломления будет расти. Показатель преломления стекла от этого меняться не будет.
Ответ.
Задание 16. Медная перемычка в момент времени t0 = 0 начинает двигаться со скоростью 2 м/с по параллельным горизонтальным проводящим рельсам, к концам которых подсоединен резистор сопротивлением 10 Ом. Вся система находится в вертикальном однородном магнитном поле. Сопротивление перемычки и рельсов пренебрежимо мало, перемычка все время расположена перпендикулярно рельсам. Поток Ф вектора магнитной индукции через контур, образованный перемычкой, рельсами и резистором, изменяется с течением времени t так, как показано на графике.
Используя график, выберите два верных утверждения и укажите в ответе их номера.
- К моменту времени t = 0,1 с изменение магнитного потока через контур равно 1 мВб.
- Индукционный ток в перемычке в интервале от t = 0,1 с t = 0,3 с максимален.
- Модуль ЭДС индукции, возникающей в контуре, равен 10 мВ.
- Сила индукционного тока, текущего в перемычке, равна 64 мА.
- Для поддержания движения перемычки к ней прикладывают силу, проекция которой на направление рельсов равна 0,2 Н.
Решение. По графику зависимости потока вектора магнитной индукции через контур от времени определим участки, где поток Ф меняется, и где изменение потока равно нулю. Это позволит нам определить интервалы времени, в которые в контуре будет возникать индукционный ток. Верное утверждение:
1) К моменту времени t = 0,1 с изменение магнитного потока через контур равно 1 мВб ∆Ф = (1 – 0) · 10–3 Вб; Модуль ЭДС индукции, возникающей в контуре определим используя закон ЭМИ
| Ɛ = | – | ∆Ф | = | – | 1 ·10–3 | = 0,01 В = 10 мВ |
| ∆t | 0,1 |
Ответ. 13.
Задание 17.
По графику зависимости силы тока от времени в электрической цепи, индуктивность которой равна 1 мГн, определите модуль ЭДС самоиндукции в интервале времени от 5 до 10 с. Ответ запишите в мкВ.
Решение. Переведем все величины в систему СИ, т.е. индуктивность 1 мГн переведем в Гн, получим 10–3 Гн. Силу тока, показанной на рисунке в мА также будем переводить в А путем умножения на величину 10–3.
Формула ЭДС самоиндукции имеет вид
где L – индуктивность цепи; ∆I – изменение тока; ∆t – интервал времени (при котором происходит изменение тока).
Модуль ЭДС самоиндукции будет иметь вид
при этом интервал времени дан по условию задачи
∆t = 10 c – 5 c = 5 c
секунд и по графику определяем интервал изменения тока за это время:
∆I = 30 · 10–3 – 20 · 10–3 = 10 · 10–3 = 10–2 A.
Подставляем числовые значения в формулу (2), получаем
|Ɛ| = 2 ·10–6 В, или 2 мкВ.
Ответ. 2.
Задание 18. Две прозрачные плоскопараллельные пластинки плотно прижаты друг к другу. Из воздуха на поверхность первой пластинки падает луч света (см. рисунок). Известно, что показатель преломления верхней пластинки равен n2 = 1,77. Установите соответствие между физическими величинами и их значениями. К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
|
ФИЗИЧЕСКАЯ ВЕЛИЧИНА |
ЕЕ ЗНАЧЕНИЕ |
|
А) Синус угла падения луча на границу 2-3 между пластинами |
1) ≈ 0,698 |
|
2) ≈ 0,433 |
|
|
Б) Угол преломления луча при переходе границы 3-1 ( в радианах) |
3) ≈ 0,363 |
|
4) ≈ 0,873 |
Решение. Для решения задач о преломлении света на границе раздела двух сред, в частности задач на прохождение света через плоскопараллельные пластинки можно рекомендовать следующий порядок решения: сделать чертеж с указанием хода лучей, идущих из одной среды в другую; в точке падения луча на границе раздела двух сред провести нормаль к поверхности, отметить углы падения и преломления. Особо обратить внимание на оптическую плотность рассматриваемых сред и помнить, что при переходе луча света из оптически менее плотной среды в оптически более плотную среду угол преломления будет меньше угла падения. На рисунке дан угол между падающим лучом и поверхностью, а нам нужен угол падения. Помним, что углы определяются от перпендикуляра, восстановленного в точке падения. Определяем, что угол падения луча на поверхность 90° – 40° = 50°, показатель преломления n2 = 1,77; n1 = 1 (воздух).
Запишем закон преломления
для границы 1-2:
| sinβ = | sin50 | = 0,4327 ≈ 0,433 |
| 1,77 |
Построим примерный ход луча через пластинки. Используем формулу (1) для границы 2–3 и 3–1. В ответе получаем
А) Синус угла падения луча на границу 2–3 между пластинками – это 2) ≈ 0,433;
Б) Угол преломления луча при переходе границы 3–1 (в радианах) – это 4) ≈ 0,873.
Ответ. 24.
Задание 19. Определите, сколько α – частиц и сколько протонов получается в результате реакции термоядерного синтеза



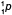
|
Количество α-частиц |
Количество протонов |
Решение. При всех ядерных реакциях соблюдаются законы сохранения электрического заряда и числа нуклонов. Обозначим через x – количество альфа частиц, y– количество протонов. Составим уравнения



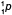
решая систему имеем, что x = 1; y = 2
Ответ. 1 – α-частица; 2 – протона.
Задание 20. Модуль импульса первого фотона равен 1,32 · 10–28 кг·м/с, что на 9,48 · 10–28 кг·м/с меньше, чем модуль импульса второго фотона. Найдите отношение энергии E2/E1 второго и первого фотонов. Ответ округлите до десятых долей.
Решение. Импульс второго фотона больше импульса первого фотона по условию значит можно представить p2 = p1 + Δp (1). Энергию фотона можно выразить через импульс фотона, используя следующие уравнения. Это E = mc2 (1) и p = mc (2), тогда
E = pc (3),
где E – энергия фотона, p – импульс фотона, m – масса фотона, c = 3 · 108 м/с – скорость света. С учетом формулы (3) имеем:
Ответ округляем до десятых и получаем 8,2.
Ответ. 8,2.
Задание 21. Ядро атома претерпело радиоактивный позитронный β – распад. Как в результате этого изменялись электрический заряд ядра и количество нейтронов в нем?
Для каждой величины определите соответствующий характер изменения:
- Увеличилась;
- Уменьшилась;
- Не изменилась.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
|
Электрический заряд ядра |
Количество нейтронов в ядре |
Решение. Позитронный β – распад в атомном ядре происходит при превращений протона в нейтрон с испусканием позитрона. В результате этого число нейтронов в ядре увеличивается на единицу, электрический заряд уменьшается на единицу, а массовое число ядра остается неизменным. Таким образом, реакция превращения элемента следующая:
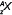
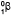
Ответ. 21.
Задание 22. В лаборатории было проведено пять экспериментов по наблюдению дифракции с помощью различных дифракционных решеток. Каждая из решеток освещалась параллельными пучками монохроматического света с определенной длиной волны. Свет во всех случаях падал перпендикулярно решетке. В двух из этих экспериментов наблюдалось одинаковое количество главных дифракционных максимумов. Укажите сначала номер эксперимента, в котором использовалась дифракционная решетка с меньшим периодом, а затем – номер эксперимента, в котором использовалась дифракционная решетка с большим периодом.
|
Номер эксперимента |
Период дифракционной решетки |
Длина волны падающего света |
|
1 |
2d |
λ/2 |
|
2 |
d |
λ |
|
3 |
2d |
λ |
|
4 |
d/2 |
λ/2 |
|
5 |
d/2 |
2λ |
Решение. Дифракцией света называется явление светового пучка в область геометрической тени. Дифракцию можно наблюдать в том случае, когда на пути световой волны встречаются непрозрачные участки или отверстия в больших по размерам и непрозрачных для света преградах, причем размеры этих участков или отверстий соизмеримы с длиной волны. Одним из важнейших дифракционных устройств является дифракционная решетка. Угловые направления на максимумы дифракционной картины определяются уравнением
dsinφ = k λ (1),
где d – период дифракционной решетки, φ – угол между нормалью к решетке и направлением на один из максимумов дифракционной картины, λ – длина световой волны, k – целое число, называемое порядком дифракционного максимума. Выразим из уравнения (1)
Подбирая пары согласно условию эксперимента, выбираем сначала 4 где использовалась дифракционная решетка с меньшим периодом, а затем – номер эксперимента, в котором использовалась дифракционная решетка с большим периодом – это 2.
Ответ. 42.
Задание 23. По проволочному резистору течет ток. Резистор заменили на другой, с проволокой из того же металла и той же длины, но имеющей вдвое меньшую площадь поперечного сечения, и пропустили через него вдвое меньший ток. Как изменятся при этом напряжение на резисторе и его сопротивление?
Для каждой величины определите соответствующий характер изменения:
- Увеличится;
- Уменьшится;
- Не изменится.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
|
Напряжение на резисторе |
Сопротивление резистора |
Решение. Важно помнить от каких величин зависит сопротивление проводника. Формула для расчета сопротивления имеет вид
где ρ – удельное сопротивление проводника; l – длина проводника; S – площадь поперечного сечения. Для полного ответа на вопрос задачи необходимо записан формулу
закона Ома для участка цепи, из формулы (2), выразим напряжение
U = IR (3).
По условию задачи второй резистор изготовлен из проволоки того же материала, той же длины, но разной площади поперечного сечения. Площадь в два раза меньшая. Подставляя в (1) получим, что сопротивление увеличивается в 2 раза, а сила тока уменьшается в 2 раза, следовательно, напряжение не изменяется.
Ответ. 13.
Задание 24. Период колебаний математического маятника на поверхности Земли в 1, 2 раза больше периода его колебаний на некоторой планете. Чему равен модуль ускорения свободного падения на этой планете? Влияние атмосферы в обоих случаях пренебрежимо мало.
Решение. Математический маятник – это система, состоящая из нити, размеры которой много больше размеров шарика и самого шарика. Трудность может возникнуть если забыта формула Томсона для периода колебаний математического маятника.
T = 2π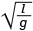
l – длина математического маятника; g – ускорение свободного падения.
По условию
Используя формулу Томсона для периода колебаний математического маятника T = 2π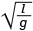
| Tз | =  (4). (4). |
| Tп |
Выразим из (3) gп = 14,4 м/с2. Надо отметить, что ускорение свободного падения зависит от массы планеты и радиуса
Ответ. 14,4 м/с2.
Задание 25. Прямолинейный проводник длиной 1 м, по которому течет ток 3 А, расположен в однородном магнитном поле с индукцией В = 0,4 Тл под углом 30° к вектору 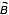
Решение. Если в магнитное поле, поместить проводник с током, то поле на проводник с током будет действовать с силой Ампера. Запишем формулу модуля силы Ампера
FА = ILBsinα;
FА = 0,6 Н
Ответ. FА = 0,6 Н.
Задание 26. Энергия магнитного поля, запасенная в катушке при пропускании через нее постоянного тока, равна 120 Дж. Во сколько раз нужно увеличить силу тока, протекающего через обмотку катушки, для того, чтобы запасенная в ней энергия магнитного поля увеличилась на 5760 Дж.
Решение. Энергия магнитного поля катушки рассчитывается по формуле
По условию W1 = 120 Дж, тогда W2 = 120 + 5760 = 5880 Дж.
| I12 = | 2W1 | ; I22 = | 2W2 | ; |
| L | L |
Тогда отношение токов
Ответ. Силу тока нужно увеличить в 7 раз. В бланк ответов Вы вносите только цифру 7.
Задание 27. Электрическая цепь состоит из двух лампочек, двух диодов и витка провода, соединенных, как показано на рисунке. (Диод пропускает ток только в одном направлении, как показано на верхней части рисунка). Какая из лампочек загорится, если к витку приближать северный полюс магнита? Ответ объясните, указав, какие явления и закономерности вы использовали при объяснении.
Решение. Линии магнитной индукции выходят из северного полюса магнита и расходятся. При приближении магнита магнитный поток через виток провода увеличивается. В соответствии с правило Ленца магнитное поле, создаваемое индукционным током витка, должно быть направлено вправо. По правилу буравчика ток должен идти по часовой стрелке (если смотреть слева). В этом направлении пропускает диод, стоящий в цепи второй лампы. Значит, загорится вторая лампа.
Ответ. Загорится вторая лампа.
Задание 28. Алюминиевая спица длиной L = 25 см и площадью поперечного сечения S = 0,1 см2 подвешена на нити за верхний конец. Нижний конец опирается на горизонтальное дно сосуда, в который налита вода. Длина погруженной в воду части спицы l = 10 см. Найти силу F, с которой спица давит на дно сосуда, если известно, что нить расположена вертикально. Плотность алюминия ρа = 2,7 г/см3, плотность воды ρв = 1,0 г/см3. Ускорение свободного падения g = 10 м/с2
Решение. Выполним поясняющий рисунок.
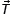
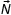
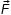
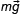
По определению масса спицы m и модуль архимедовой силы выражаются следующим образом : m = SLρa (1);
Fa = Slρвg (2)
Рассмотрим моменты сил относительно точки подвеса спицы.
М(Т) = 0 – момент силы натяжения; (3)
М(N) = NLcosα – момент силы реакции опоры; (4)
| М(Fa) = Slρв g (L – | 1 | ) cosα – момент архимедовой силы ; (5) |
| 2 |
| М(mg) = SLρa g | L | cosα – момент силы тяжести; (6) |
| 2 |
С учетом знаков моментов запишем уравнение
| NLcosα + Slρв g (L – | l | ) cosα = SLρa g | L | cosα (7) |
| 2 | 2 |
учитывая, что по третьему закону Ньютона сила реакции дна сосуда равна силе Fд с которой спица давит на дно сосуда запишем N = Fд и из уравнения (7) выразим эту силу:
| Fд = [ | 1 | Lρa – (1 – | l | )lρв]Sg (8). |
| 2 | 2L |
Подставим числовые данные и получим, что
Fд = 0,025 Н.
Ответ. Fд = 0,025 Н.
Задание 29. Баллон, содержащий m1 = 1 кг азота, при испытании на прочность взорвался при температуре t1 = 327°С. Какую массу водорода m2 можно было бы хранить в таком баллоне при температуре t2 = 27°С, имея пятикратный запас прочности? Молярная масса азота M1 = 28 г/моль, водорода M2 = 2 г/моль.
Решение. Запишем уравнение состояния идеального газа Менделеева – Клапейрона для азота
Из уравнения состояния азота следует, что давление, при котором взорвался баллон,
| p1 = | m1 | · | RT1 | , (2) |
| M1 | V |
где V – объем баллона, T1 = t1 + 273°C. По условию водород можно хранить при давлении p2 = p1/5; (3) Учитывая, что
| p2 = | m2 | · | RT2 | (4) |
| M2 | V |
можем выразить массу водорода работая сразу с уравнениями (2), (3), (4). Конечная формула имеет вид:
| m2 = | m1 | M2 | T1 | (5). | ||
| 5 | M1 | T2 |
После подстановки числовых данных m2 = 28 г.
Ответ. m2 = 28 г.
Задание 30. В идеальном колебательном контуре амплитуда колебаний силы тока в катушке индуктивности Im = 5 мА, а амплитуда напряжения на конденсаторе Um = 2,0 В. В момент времени t напряжение на конденсаторе равно 1,2 В. Найдите силу тока в катушке в этот момент.
Решение. В идеальном колебательном контуре сохраняется энергия колебаний. Для момента времени t закон сохранения энергий имеет вид
| C | U2 | + L | I2 | = L | Im2 | (1) |
| 2 | 2 | 2 |
Для амплитудных (максимальных) значений запишем
| C | Um2 | = L | Im2 | (2) |
| 2 | 2 |
Из равенства (1) следует :
а из уравнения (2) выразим
Подставим (4) в (3). В результате получим:
I = Im 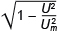
Таким образом, сила тока в катушке в момент времени t равна
I = 4,0 мА.
Ответ. I = 4,0 мА.
Задание 31. На дне водоема глубиной 2 м лежит зеркало. Луч света, пройдя через воду, отражается от зеркала и выходит из воды. Показатель преломления воды равен 1,33. Найдите расстояние между точкой входа луча в воду и точкой выхода луча из воды, если угол падения луча равен 30°
Решение. Сделаем поясняющий рисунок
α – угол падения луча;
β – угол преломления луча в воде;
АС – расстояние между точкой входа луча в воду и точкой выхода луча из воды.
По закону преломления света
где n2 – показатель преломления воды; n1 – показатель преломления воздуха. n1 = 1. Тогда формулу (1) можно записать
Выразим
Рассмотрим прямоугольный ΔАDВ. В нем АD = h, тогда DВ = АD
| tgβ = htgβ = h | sinα | = h | sinβ | = h | sinα | (4) |
| cosβ |  |
 |
Получаем следующее выражение:
| АС = 2 DВ = 2h | sinα | (5) |
 |
Подставим числовые значения в полученную формулу (5)
АС = 1,63 м
Ответ. 1,63 м.