На рисунке приведён график зависимости модуля индукции B магнитного поля от времени t. В это поле перпендикулярно линиям магнитной индукции помещён проводящий прямоугольный контур сопротивлением R = 0,2 Ом. Длина прямоугольника равна 4 см, а ширина — 2,5 см. Найдите величину индукционного тока, протекающего по этому контуру в интервале времени от 1 с до 2 с. Ответ выразите в миллиамперах.
Спрятать решение
Решение.
Согласно закону электромагнитной индукции, ЭДС индукции, возникающая в контуре, пропорциональна скорости изменения магнитного потока через контур:
Используя закон Ома, найдем индукционный ток:
Ответ: 1.
Прочитайте текст и вставьте на место пропусков слова (словосочетания) из приведённого списка.
Для изучения электрических свойств стержня проведём следующий опыт. Возьмём два электрометра. Один из них зарядим, а другой, наоборот, разрядим (см. рис.).
Теперь возьмём стержень с помощью пластмассовой ручки и соединим стержнем шары электрометров. Пластмасса является _________(А) и выполняет роль _________(Б) между стержнем и кожей человека. Если материал стрежня относится к _________(В), то листочки незаряженного электрометра практически моментально отклонятся от вертикального положения. Это объясняется _________(Г) между двумя электрометрами.
Список слов и словосочетаний:
1) вещество
2) проводник
3) материал
4) электризация металлического стержня через влияние
5) диэлектрик
6) протекание свободного электрического заряда
7) изолятор
Запишите в таблицу выбранные цифры под соответствующими буквами.
Варианты, ответы и решения ФИ2210401, ФИ2210402, ФИ2210403, ФИ2210404 тренировочная работа №4 статград пробник ЕГЭ 2023 по физике 11 класс в формате реального экзамена ЕГЭ 2023 года, которая прошла 7 марта 2023 года.
Скачать тренировочные варианты
Скачать ответы для вариантов
ФИ2210401_ФИ2210402_ФИ2210403_ФИ2210404
Вариант ФИ2210401 с ответами
1. Два маленьких тела, находившиеся в состоянии покоя, одновременно начинают двигаться из одной точки по плоскости YOX с разными по модулю постоянными ускорениями. На рисунке изображены векторы 1 a и 2 a ускорений этих тел (масштабы координатной сетки вдоль горизонтальной и вертикальной осей одинаковы). Чему равно отношение путей S1/S2, пройденных этими телами за первые 2 секунды их движения?
2. Ускорение свободного падения на поверхности Юпитера в 2,6 раза больше, чем на поверхности Земли. Первая космическая скорость для Юпитера в 5,4 раза больше, чем для Земли. Во сколько раз радиус Юпитера больше радиуса Земли? Ответ округлите до целого числа.
3. На горизонтальном столе лежит лист бумаги, на котором нарисован равнобедренный треугольник с длиной боковой стороны 12 см и углом 30° при основании. В его вершинах расположены одинаковые маленькие тяжёлые бусинки. На каком расстоянии от основания данного треугольника расположен центр тяжести системы, состоящей из этих трёх бусинок?
4. Небольшая шайба массой 50 г соскальзывает с наклонной плоскости с углом при основании 30°. Сопротивление воздуха пренебрежимо мало. В таблице приведены значения модуля скорости V шайбы в различные моменты времени t. Выберите все верные утверждения о результатах этого опыта на основании данных, содержащихся в таблице.
1) Сухое трение между шайбой и плоскостью отсутствует.
2) Модуль ускорения шайбы приблизительно равен 3 м/с2 .
3) За первую секунду движения шайба прошла путь менее 1 м.
4) В момент времени t = 0,4 с модуль импульса шайбы примерно равен 0,06 кг⋅м/с.
5) Если в момент времени t = 1,4 с шайба столкнётся с абсолютно неупругим препятствием, то выделится количество теплоты ≈ 0,44 Дж.
5. На двух узких опорах покоится тяжёлая горизонтальная однородная доска. На доске посередине между опорами лежит гиря. Гирю перекладывают так, что она оказывается лежащей на доске ближе к правой опоре. Как после перекладывания гири изменяются модуль силы реакции правой опоры и момент силы тяжести гири относительно левой опоры? Для каждой величины определите соответствующий характер изменения:
1) увеличивается
2) уменьшается
3) не изменяется
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
6. На горизонтальном столе установлена в вертикальном положении лёгкая пружина жёсткостью k. Её нижний конец прикреплён к столу, а к верхнему концу прикреплена горизонтальная платформа массой M. На высоте H над платформой удерживают маленький пластилиновый шарик массой m. Шарик отпускают без начальной скорости, после чего он свободно падает и прилипает к покоившейся платформе. В результате этого платформа с шариком начинают совершать колебания, в ходе которых ось пружины остаётся вертикальной, а платформа не касается стола. Установите соответствие между физическими величинами и формулами, выражающими их в рассматриваемой задаче (g – ускорение свободного падения). К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
7. В сосуде объёмом 8,31 л находится 0,35 моль идеального газа при давлении 100 кПа. Газ сначала изотермически расширяют в 2 раза, а затем изохорически нагревают на 120 К. Чему равно давление газа в конечном состоянии? Ответ выразите в кПа и округлите до целого числа.
8. На рисунке приведена зависимость температуры T однородного твёрдого тела массой 2 кг от времени t в процессе нагревания. Чему равна удельная теплоёмкость вещества этого тела? Подводимую к телу тепловую мощность можно считать постоянной и равной 450 Вт.
9. На Т–р-диаграмме показан процесс изменения состояния идеального одноатомного газа. Газ отдал в этом процессе количество теплоты 80 кДж. Масса газа не менялась. Определите работу, совершённую внешними силами над газом в этом процессе, если р1 = 80 кПа, р2 = 200 кПа, Т0 =300 К.
10. С постоянной массой идеального одноатомного газа происходит циклический процесс 1−2−3−4−1, p–V-диаграмма которого представлена на рисунке. Максимальная температура газа в этом процессе составляет 400 К. На основании анализа этого циклического процесса выберите все верные утверждения.
1) Работа, совершённая газом при его изобарическом расширении, равна 200 Дж.
2) Количество вещества газа, участвующего в циклическом процессе, больше 0,45 моль.
3) Работа, совершённая над газом при его изобарическом сжатии, равна 200 Дж.
4) Изменение внутренней энергии газа в процессе 1–2–3–4–1 равно нулю.
5) Количество теплоты, переданное газу при изохорическом нагревании, равно 400 Дж.
11. В закрытом сосуде под подвижным поршнем находятся влажный воздух и немного воды. Перемещая поршень, объём сосуда медленно увеличивают при постоянной температуре. Как изменяются в этом процессе относительная влажность воздуха и концентрация пара? Известно, что в конечном состоянии в сосуде остаётся вода. Для каждой величины определите соответствующий характер изменения:
1) увеличивается
2) уменьшается
3) не изменяется
12. Участок электрической цепи состоит из трёх резисторов, соединённых так, как показано на рисунке. Сила тока I = 3 А. Сопротивления резисторов равны R1 = 20 Ом и R2 = 30 Ом. Каким должно быть сопротивление резистора R, чтобы сила текущего через него тока была равна 2 А?
13. На рисунке показан график зависимости магнитного потока Φ, пронизывающего проводящий контур, от времени t. Сопротивление контура равно 5 Ом. Чему равна сила тока, текущего в контуре, в промежутке времени от 0 до 10 с?
15. Две маленькие закреплённые бусинки, расположенные в точках А и В, несут на себе заряды +q > 0 и +4q соответственно (см. рисунок). Расстояние от точки С до точки А в два раза меньше, чем расстояние от точки С до точки В: СВ = 2 АС . Выберите все верные утверждения, соответствующие приведённым данным.
1) Модуль силы Кулона, действующей на бусинку в точке А, в 4 раза больше, чем модуль силы Кулона, действующей на бусинку в точке В.
2) Если бусинки соединить тонким проводником, то они будут притягиваться друг к другу.
3) Напряжённость результирующего электростатического поля в точке С равна нулю.
4) Если бусинки соединить стеклянной палочкой, то их заряды не изменятся.
5) Если бусинку с зарядом +4q заменить на бусинку с зарядом –4q, то напряжённость результирующего электростатического поля в точке С будет направлена вправо.
16. В первом опыте лазерный луч красного цвета падает перпендикулярно на дифракционную решётку, содержащую 50 штрихов на 1 мм. При этом на удалённом экране наблюдают дифракционную картину. Во втором опыте проводят эксперимент с тем же лазером, заменив решётку на другую, содержащую 100 штрихов на 1 мм, и оставив угол падения лазерного луча на решётку тем же. Как изменяются во втором опыте по сравнению с первым расстояние между дифракционными максимумами первого порядка на экране и количество наблюдаемых дифракционных максимумов? Для каждой величины определите соответствующий характер изменения:
- 1) увеличивается
- 2) уменьшается
- 3) не изменяется
17. В однородном вертикальном магнитном поле находится наклонная плоскость с углом α при основании. На этой плоскости закреплён П-образный проводник, по которому скользит вниз с постоянной скоростью V проводящая перемычка длиной L. Взаимное расположение наклонной плоскости, проводника и перемычки показано на рисунке. Сопротивление перемычки равно R, сопротивление П-образного проводника мало. Модуль индукции магнитного поля равен В. Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать.
К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
18. Какая доля радиоактивных ядер (в процентах от первоначального числа ядер) остаётся нераспавшейся через интервал времени, равный двум периодам полураспада?
19. В опыте по изучению фотоэффекта металлическая пластина облучалась светом с частотой ν. Работа выхода электронов из металла равна Авых. Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать (h – постоянная Планка, с – скорость света в вакууме, me – масса электрона). К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
20. Выберите все верные утверждения о физических явлениях, величинах и закономерностях. Запишите цифры, под которыми они указаны.
- 1) При равномерном прямолинейном движении за любые равные промежутки времени тело совершает одинаковые перемещения.
- 2) Средняя кинетическая энергия теплового движения молекул гелия уменьшается при увеличении абсолютной температуры газа.
- 3) В однородном электростатическом поле работа по перемещению электрического заряда между двумя положениями в пространстве не зависит от траектории.
- 4) При переходе электромагнитной волны из воды в воздух период колебаний вектора напряжённости электрического поля в волне уменьшается.
- 5) При испускании протона электрический заряд ядра уменьшается.
21. Даны следующие зависимости величин:
- А) зависимость модуля импульса материальной точки от её кинетической энергии при неизменной массе;
- Б) зависимость количества теплоты, выделяющегося при конденсации пара, от его массы;
- В) зависимость периода колебаний силы тока в идеальном колебательном контуре от индуктивности катушки.
Установите соответствие между этими зависимостями и графиками, обозначенными цифрами 1–5. Для каждой зависимости А–В подберите соответствующий вид графика и запишите в таблицу выбранные цифры под соответствующими буквами. Цифры в ответе могут повторяться.
22. Для определения массы порции подсолнечного масла ученик измерил её объём с использованием мерного цилиндра и получил результат: V = (12 ±1) см3 . Чему равна масса данной порции масла с учётом погрешности измерений?
23. Ученик изучает свойства силы трения скольжения. В его распоряжении имеются установки, состоящие из горизонтальной опоры и сплошного бруска. Площадь соприкосновения бруска с опорой при проведении всех опытов одинакова. Параметры установок приведены в таблице. Какие из этих установок нужно использовать для того, чтобы на опыте обнаружить зависимость коэффициента трения от модуля силы нормального давления тела на опору?
24. В боковой стенке покоящейся на столе бутылки проделано маленькое отверстие, в которое вставлена затычка. В бутылку налита вода, а горлышко бутылки закрыто резиновой пробкой, через которую пропущена вертикальная тонкая трубка. Нижний конец трубки находится выше отверстия в стенке бутылки, но ниже поверхности воды, а верхний конец сообщается с атмосферой (см. рис.). Затычку из отверстия в боковой стенке вынимают, и вода вытекает из бутылки через отверстие. При этом через трубку в бутылку входят пузырьки воздуха. Затем трубку начинают медленно опускать вниз и делают это до тех пор, пока нижний конец трубки не окажется на одном уровне с отверстием. Опишите, как будет изменяться скорость вытекания воды из отверстия по мере опускания трубки. Считайте, что уровень воды всегда находится выше нижнего конца трубки и выше отверстия в стенке. Ответ обоснуйте, указав, какие физические закономерности Вы использовали для объяснения.
25. В механической системе, изображённой на рисунке, все блоки, пружины и нити невесомые, нити нерастяжимые, трения в осях блоков нет, все участки нитей, не лежащие на блоках, вертикальны. Известно, что после подвешивания груза массой M = 40 кг к оси самого правого блока левая пружина в состоянии равновесия растянулась на величину Δx1 = 10 см. Найдите коэффициент жёсткости k1 левой пружины.
26. В центре металлической сферической оболочки толщиной 0,5 см поместили точечный заряд q = 2 мкКл, а на её внешнюю поверхность радиусом R = 10 см – заряд Q = – 1 мкКл. Найдите для равновесного состояния модуль напряжённости E электрического поля на расстоянии r = 1 м от центра оболочки и укажите, куда направлен вектор E – к центру оболочки или от неё.
27. В большом помещении с размерами 6 × 10 × 3 м3 в зимние холода при температуре Т1 парциальное давление водяного пара в воздухе составляло pп1 = 700 Па, а относительная влажность воздуха равнялась при этом φ1 = 50 %. После обогрева помещения температура в нём поднялась до значения T2 = 25 °С, а относительная влажность снизилась до φ2 = 25 %. Используя приведённый на рисунке график, найдите, как и на сколько в результате обогрева изменилась масса m паров воды в данном помещении.
28. Иногда для измерения индукции магнитного поля используют следующий способ: маленькую плоскую круглую катушку с большим числом витков быстро вводят в область измеряемого поля так, что её плоскость перпендикулярна линиям индукции. Катушка присоединена к входным клеммам баллистического гальванометра, который может измерять электрический заряд Δq, протекший по образовавшейся замкнутой цепи за время ввода измерительной катушки в исследуемое магнитное поле. Этот заряд связан с изменением магнитного потока Ф через катушку, поэтому данный гальванометр часто используют в качестве «флюксметра». Зная поток магнитной индукции и параметры катушки, можно найти величину В проекции индукции на ось катушки. Пусть измеренное таким способом значение В = 0,5 Тл, входное сопротивление гальванометра rф = 0,1 кОм, сопротивление измерительной катушки rк = 900 Ом, диаметр её витков d = 1 см. Определите число N витков в катушке, если протекший через цепь суммарный заряд qΣ = 15 мкКл.
29. Вдоль оптической оси тонкой выпуклой собирающей линзы распространяется в воздухе параллельный приосевой пучок света, собирающийся в точку справа от неё на расстоянии F1. Линза изготовлена из стекла с показателем преломления n1 = 1,4 и ограничена справа и слева сферическими поверхностями радиусами R1 = 15 см. На какое расстояние и в какую сторону сместится точка схождения лучей этого пучка, если заменить линзу на другую, с показателем преломления стекла n2 = 1,6 и радиусами поверхностей R2 = 24 см? Положения обеих линз относительно пучка света одинаковые. Все углы падения и преломления можно считать малыми и использовать для них приближённую формулу sin α ≈ α.
30. На даче у школьника на горизонтальном полу террасы стояла пластмассовая кубическая ёмкость для воды, иногда протекающей с крыши. Когда ёмкость заполнилась наполовину, дедушка попросил внука вылить воду из неё, наклонив вокруг одного из нижних рёбер куба, чтобы вода переливалась через соседнее верхнее ребро. Какую работу А совершил внук к моменту начала вытекания воды из ёмкости, если процесс подъёма был очень медленным, так что поверхность воды всё время оставалась горизонтальной? Объём воды вначале был равен V = 108 л, квадратные стенки ёмкости и её днище тонкие, однородные, массой m = 4 кг каждая (сверху ёмкость открыта). Сделайте рисунки с указанием положения центров масс воды, днища и стенок ёмкости до начала наклона ёмкости и в момент, когда вода начинает выливаться. Обоснуйте применимость используемых законов к решению задачи.
Вариант ФИ2210402 с ответами
1. Два маленьких тела, находившиеся в состоянии покоя, одновременно начинают двигаться из одной точки по плоскости YOX с разными по модулю постоянными ускорениями. На рисунке изображены векторы 1 a и 2 a ускорений этих тел (масштабы координатной сетки вдоль горизонтальной и вертикальной осей одинаковы). Чему равно отношение путей S1/S2, пройденных этими телами за первые 3 секунды их движения?
2. Ускорение свободного падения на поверхности Земли в 2,65 раза больше, чем на поверхности Марса. Вторая космическая скорость для Земли в 2,24 раза больше, чем для Марса. Во сколько раз радиус Земли больше радиуса Марса? Ответ округлите до целого числа.
3. На горизонтальном столе лежит лист бумаги, на котором нарисован равнобедренный треугольник ABC с основанием BC. Длина боковой стороны этого треугольника 18 см, угол при основании 30°. В его вершинах расположены одинаковые маленькие тяжёлые бусинки. На каком расстоянии от вершины A расположен центр тяжести системы, состоящей из этих трёх бусинок?
4. Небольшая шайба массой 100 г соскальзывает с наклонной плоскости с углом при основании 45°. Сопротивление воздуха пренебрежимо мало. В таблице приведены значения модуля скорости V шайбы в различные моменты времени t. Выберите все верные утверждения о результатах этого опыта на основании данных, содержащихся в таблице.
- 1) Между шайбой и плоскостью есть сухое трение.
- 2) Модуль ускорения шайбы приблизительно равен 7 м/с2 .
- 3) За первую секунду движения шайба прошла путь менее 2 м.
- 4) В момент времени t = 0,6 с модуль импульса шайбы примерно равен 0,36 кг⋅м/с.
- 5) Если в момент времени t = 1,2 с шайба столкнётся с абсолютно неупругим препятствием, то выделится количество теплоты ≈ 2,6 Дж.
5. На двух узких опорах покоится тяжёлая горизонтальная однородная доска. На доске посередине между опорами лежит гиря. Гирю перекладывают так, что она оказывается лежащей на доске ближе к правой опоре. Как после перекладывания гири изменяются модуль силы реакции левой опоры и момент силы тяжести гири относительно правой опоры? Для каждой величины определите соответствующий характер изменения:
- 1) увеличивается
- 2) уменьшается
- 3) не изменяется
6. На горизонтальном столе установлена в вертикальном положении лёгкая пружина жёсткостью k. Её нижний конец прикреплён к столу, а к верхнему концу прикреплена горизонтальная платформа массой M. На высоте H над платформой удерживают маленький пластилиновый шарик массой m. Шарик отпускают без начальной скорости, после чего он свободно падает и прилипает к покоившейся платформе. В результате этого платформа с шариком начинают совершать колебания, в ходе которых ось пружины остаётся вертикальной, а платформа не касается стола. Установите соответствие между физическими величинами и формулами, выражающими их в рассматриваемой задаче (g – ускорение свободного падения). К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
7. В сосуде объёмом 8,31 л находится 0,35 моля идеального газа при давлении 100 кПа. Газ сначала изотермически расширяют в 2 раза, а затем изобарически нагревают на 24 К. Чему равен объём газа в конечном состоянии?
8. На рисунке приведена зависимость температуры t однородного твёрдого тела массой 5 кг от времени τ в процессе нагревания. Чему равна удельная теплоёмкость вещества этого тела? Подводимую к телу тепловую мощность можно считать постоянной и равной 520 Вт.
9. На Т–V-диаграмме показан процесс изменения состояния идеального одноатомного газа. Газ получил в этом процессе количество теплоты 120 кДж. Масса газа не менялась. Определите работу, совершённую газом в этом процессе, если V1 = 8 л, V2 = 20 л, Т0 = 300 К.
10. С постоянной массой идеального одноатомного газа происходит циклический процесс 1−2−3−4−1, p–V-диаграмма которого представлена на рисунке. Максимальная температура газа в этом процессе составляет 600 К. На основании анализа этого циклического процесса выберите все верные утверждения.
- 1) Работа, совершённая газом при его изобарическом расширении, равна 400 Дж.
- 2) Количество вещества газа, участвующего в циклическом процессе, больше 0,45 моля.
- 3) Суммарное количество теплоты, которым газ обменялся с окружающими телами в процессе 1–2–3–4–1, равно 200 Дж.
- 4) Изменение внутренней энергии газа в процессе 4–1 равно 600 Дж.
- 5) Температура газа в состоянии 4 равна 225 К.
11. В закрытом сосуде под подвижным поршнем находятся влажный воздух и немного воды. Перемещая поршень, объём сосуда медленно уменьшают при постоянной температуре. Как изменяются в этом процессе относительная влажность воздуха и плотность пара? Для каждой величины определите соответствующий характер изменения:
- 1) увеличивается
- 2) уменьшается
- 3) не изменяется
12. Участок электрической цепи состоит из трёх резисторов, соединённых так, как показано на рисунке. Сила тока I = 6 А. Сопротивления резисторов равны R1 = 10 Ом и R2 = 30 Ом. Каким должно быть сопротивление резистора R, чтобы сила тока, текущего через него, была равна 2 А?
13. На рисунке показан график зависимости магнитного потока Φ, пронизывающего проводящий контур, от времени t. Сопротивление контура равно 3 Ом. Чему равна сила тока, текущего в контуре в промежутке времени от 10 до 20 с?
14. Сила тока i в идеальном колебательном контуре меняется со временем t по закону 0,02cos(5 10 ) 6 i = ⋅ t , где все величины выражены в единицах СИ. Чему равен максимальный заряд одной из пластин конденсатора, включённого в этот колебательный контур?
15. Две маленькие закреплённые бусинки, расположенные в точках А и В, несут на себе заряды +q > 0 и –4q соответственно (см. рисунок). Точка С расположена посередине отрезка АВ. Выберите все верные утверждения, соответствующие приведённым данным.
- 1) Сила Кулона, действующая на бусинку в точке А равна по модулю силе Кулона, действующей на бусинку в точке В.
- 2) Если бусинки соединить проводником, то они станут отталкиваться друг от друга.
- 3) Напряжённость результирующего электростатического поля в точке С направлена влево.
- 4) Если бусинки соединить стеклянной палочкой, то их заряды станут одинаковыми.
- 5) Если бусинку с зарядом –4q заменить на бусинку с зарядом +3q, то модуль напряжённости результирующего электростатического поля в точке С уменьшится в 2,5 раза.
16. В первом опыте лазерный луч красного цвета падает перпендикулярно на дифракционную решётку, содержащую 100 штрихов на 1 мм. При этом на удалённом экране наблюдают дифракционную картину. Во втором опыте проводят эксперимент с тем же лазером, заменив решётку на другую, содержащую 50 штрихов на 1 мм, и оставив угол падения лазерного луча на решётку тем же. Как изменяются во втором опыте по сравнению с первым расстояние между дифракционными максимумами второго порядка на экране и угол, под которым наблюдается первый дифракционный максимум? Для каждой величины определите соответствующий характер изменения:
- 1) увеличивается
- 2) уменьшается
- 3) не изменяется
17. В однородном вертикальном магнитном поле находится наклонная плоскость с углом α при основании. На этой плоскости закреплён П-образный проводник, по которому скользит вниз с постоянной скоростью V проводящая перемычка длиной L. Взаимное расположение наклонной плоскости, проводника и перемычки показано на рисунке. Сопротивление перемычки равно R, сопротивление П-образного проводника мало. Модуль индукции магнитного поля равен В. Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать.
18. Какая доля радиоактивных ядер (в процентах от первоначального числа ядер) остаётся нераспавшейся через интервал времени, равный трём периодам полураспада?
19. В опыте по изучению фотоэффекта металлическая пластина облучалась светом с частотой ν. Работа выхода электронов из металла равна Авых. Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать (h – постоянная Планка, с – скорость света в вакууме, me – масса электрона). К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
20. Выберите все верные утверждения о физических явлениях, величинах и закономерностях. Запишите цифры, под которыми они указаны.
- 1) При равномерном движении по окружности перемещение тела за один период обращения равно нулю.
- 2) При увеличении средней кинетической энергии теплового движения молекул гелия его давление в закрытом сосуде неизменного объёма уменьшается.
- 3) При движении заряда по окружности в однородном магнитном поле сила Лоренца, действующая на этот заряд, не совершает работу.
- 4) При переходе электромагнитной волны из воздуха в воду период колебаний вектора индукции магнитного поля в волне не изменяется.
- 5) При испускании нейтрона электрический заряд ядра увеличивается.
21. Даны следующие зависимости величин:
- А) зависимость кинетической энергии материальной точки от модуля её импульса при неизменной массе;
- Б) зависимость количества теплоты, выделяющегося при кристаллизации воды, от её массы;
- В) зависимость энергии конденсатора постоянной ёмкости от его заряда.
Установите соответствие между этими зависимостями и графиками, обозначенными цифрами 1–5. Для каждой зависимости А–В подберите соответствующий вид графика и запишите в таблицу выбранные цифры под соответствующими буквами. Цифры в ответе могут повторяться.
22. Для определения массы порции керосина ученик измерил её объём с использованием мерного цилиндра и получил результат: V = (30,0 ± 0,5) см3 . Чему равна масса данной порции керосина с учётом погрешности измерений?
23. Ученик изучает свойства силы трения скольжения. В его распоряжении имеются установки, состоящие из горизонтальной опоры и сплошного бруска. Площадь соприкосновения бруска с опорой при проведении всех опытов одинакова. Параметры установок приведены в таблице. Какие из установок нужно использовать для того, чтобы на опыте обнаружить зависимость коэффициента трения от материала опоры?
24. В боковой стенке покоящейся на столе бутылки проделано маленькое отверстие, в которое вставлена затычка. В бутылку налита вода, а горлышко бутылки закрыто резиновой пробкой, через которую пропущена вертикальная тонкая трубка. Нижний конец трубки находится ниже поверхности воды на уровне отверстия в стенке бутылки, а верхний конец сообщается с атмосферой (см. рис.). Затычку из отверстия в боковой стенке вынимают и начинают медленно поднимать трубку вверх. При этом вода вытекает из бутылки через отверстие, а через трубку в бутылку входят пузырьки воздуха. Опишите, как будет изменяться скорость вытекания воды из отверстия по мере поднимания трубки. Считайте, что уровень воды всегда находится выше нижнего конца трубки и выше отверстия в стенке. Ответ обоснуйте, указав, какие физические закономерности Вы использовали для объяснения.
25. В механической системе, изображённой на рисунке, все блоки, пружины и нити невесомые, нити нерастяжимые, трения в осях блоков нет, все участки нитей, не лежащие на блоках, вертикальны. Известно, что после подвешивания груза M к оси самого правого блока левая пружина, имеющая коэффициент жёсткости k1 = 500 Н/м, в состоянии равновесия растянулась на величину Δx1 = 10 см. На какую величину Δx2 удлинилась при этом правая пружина, если её коэффициент жёсткости равен k2 = 1000 Н/м?
26. В центре металлической сферической оболочки толщиной 0,2 см поместили точечный заряд q = 1 мкКл, а на её внешнюю поверхность радиусом R = 10 см – заряд Q = – 3 мкКл. Найдите для равновесного состояния модуль E напряжённости электрического поля на расстоянии r = 2 м от центра оболочки и укажите, куда направлен вектор E – к центру оболочки или от неё.
27. В большом помещении с размерами 5 × 10 м2 (пол) и 3,5 м (высота потолка) температура T1 во время зимних холодов понизилась, парциальное давление водяного пара в воздухе опустилось до значения pп1 = 600 Па, а относительная влажность воздуха равнялась при этом φ1 = 50 %. После обогрева помещения температура в нём поднялась до значения T2 = 24 °С, а относительная влажность снизилась до φ2 = 30 %. Используя приведённый на рисунке график, найдите, как и во сколько раз в результате обогрева изменилась масса m паров воды в данном помещении.
28. Иногда для измерения индукции магнитного поля используют следующий способ: маленькую плоскую круглую катушку с большим числом витков быстро вводят в область измеряемого поля так, что её плоскость перпендикулярна линиям индукции. Катушка присоединена к входным клеммам баллистического гальванометра, который может измерять электрический заряд Δq, протекший по образовавшейся замкнутой цепи за время ввода измерительной катушки в исследуемое магнитное поле. Этот заряд связан с изменением магнитного потока Ф через катушку, поэтому данный гальванометр часто используют в качестве «флюксметра». Зная поток магнитной индукции и параметры катушки, можно найти величину В проекции индукции на ось катушки. Пусть входное сопротивление гальванометра rф = 0,2 кОм, сопротивление измерительной катушки rк = 600 Ом, диаметр её витков d = 0,95 см, число витков в ней N = 300. Чему равен измеренный модуль индукции магнитного поля, если протекший через цепь суммарный заряд qΣ = 12 мкКл.
29. Вдоль оптической оси тонкой выпуклой собирающей линзы распространяется в воздухе параллельный приосевой пучок света, собирающийся в точку справа от неё на расстоянии F1. Линза изготовлена из стекла с показателем преломления n1 = 1,5 и ограничена справа и слева сферическими поверхностями радиусами R1 = 20 см. На какое расстояние сместится точка схождения лучей этого пучка, если заменить линзу на другую, с показателем преломления стекла n2 = 1,7 и радиусами поверхностей R2 = 16 см? Положения обеих линз относительно пучка света одинаковые. Все углы падения и преломления можно считать малыми и использовать для них приближённую формулу sinα ≈ α.
30. На даче у школьника на горизонтальном полу террасы стояла пластмассовая кубическая ёмкость для воды, иногда протекающей с крыши. Когда ёмкость заполнилась наполовину, дедушка попросил своего сильного внука вылить воду из неё, наклонив вокруг одного из нижних рёбер куба, чтобы вода переливалась через соседнее верхнее ребро. Оцените, на какую величину ∆E внук увеличит механическую энергию ёмкости с водой к моменту начала вытекания воды из ёмкости, если процесс подъёма был очень медленным, так что поверхность воды всё время оставалась горизонтальной? Объём воды вначале был равен V = 63 л, квадратные стенки ёмкости и её днище тонкие, однородные, массой m = 3 кг каждая (сверху ёмкость открыта). Сделайте рисунки с указанием положения центров масс воды, днища и стенок ёмкости до начала наклона ёмкости и в момент, когда вода начинает выливаться. Обоснуйте применимость используемых законов к решению задачи.
Попробуйте решить другие варианты
Статград ФИ2210301-ФИ2210304 физика 11 класс ЕГЭ 2023 варианты и ответы
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
ЕГЭ профильный уровень. №5 Логарифмические уравнения. Задача 10
Задача 10. Решите уравнение ({log _{x + 6}}32 = 5.) Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
({log _{x + 6}}32 = 5,,,,,, Leftrightarrow ,,,,,,left{ {begin{array}{*{20}{c}}{{{left( {x + 6} right)}^5} = 32}\{x + 6 > 0,,,,,,,,,,}\{x + 6 ne 1,,,,,,,,,,,}end{array}} right.,,,,,,, Leftrightarrow ,,,,,,left{ {begin{array}{*{20}{c}}{{{left( {x + 6} right)}^5} = {2^5}}\{x + 6 > 0,,,,,,,,}\{x + 6 ne 1,,,,,,,,}end{array}} right.,,,,,, Leftrightarrow )
( Leftrightarrow ,,,,,,,left{ {begin{array}{*{20}{c}}{x + 6 = 2}\{x + 6 > 0}\{x + 6 ne 1}end{array},,,,,, Leftrightarrow } right.,,,,,,,,x + 6 = 2,,,,,,, Leftrightarrow ,,,,,,,x = — 4.)
Ответ: – 4.
- 10.03.2023
Четвертая тренировочная работа от Статграда по физике в формате ЕГЭ 2023 года. Работа проводилась 7 марта 2023 года. Разбираем все задания из варианта в формате видеоурока.
Ответы на каждое задание будут по ходу видео, вместе с разбором.
- Другие варианты ЕГЭ по физике
Есть вопросы? Задавайте в комментариях ниже.
Вариант с видеоразбором
Сохранить ссылку:
Комментарии (0)
Добавить комментарий
Добавить комментарий
Комментарии без регистрации. Несодержательные сообщения удаляются.
Имя (обязательное)
E-Mail
Подписаться на уведомления о новых комментариях
Отправить
За это задание ты можешь получить 1 балл. Уровень сложности: базовый.
Средний процент выполнения: 69.1%
Ответом к заданию 1 по физике может быть целое число или конечная десятичная дробь.
Алгоритм решения задания 1:
- Первым делом определите, на какой вид движения задача (равномерное, равноускоренное и т.д).
- Далее посмотрите, что вам необходимо найти. Обратите внимания на ключевые слова: МОДУЛЬ, ПРОЕКЦИЯ, ПУТЬ, ПЕРЕМЩЕНИЕ. Так как именно на этих словах вас хотят подловить.
- Выбирайте наиболее подходящую для решения формулу.
Разбор сложных заданий в тг-канале
Задачи для практики
Задача 1
Уравнение движения тела имеет вид x = 2t + 0,5t2. Найдите, с каким ускорением двигалось тело. Ответ выразите в (м/с2).
Решение
Дано:
$x=2t+0.5t^2$
$a-?$
Решение:
Запишем уравнение движения в общем виде и сравнив с имеющимся: $x=2t+0.5t^2; x=υ_0t+{at^2}/{2}$, тогда ${at^2}/{2}=0.5t^2; a=0.5·2$ или $a=1м/с^2$.
Ответ: 1
Задача 2
Первую четверть пути поезд прошёл со скоростью 60 км/ч. Средняя скорость на всём пути оказалась равной 40 км/ч. С какой скоростью поезд двигался на оставшейся части пути? Ответ выразите в (км/ч).
Решение
Дано:
$υ_1=60$км/ч
$S_1={1}/{4}S$
$S_2={3S}/{4}$
$υ_{ср}=40$км/ч
$υ_2-?$
Решение:
Средняя скорость определяется выражением: $υ_{ср}={S_{общ}}/{t_{общ}}$(1), где $S_{общ}=S_1+S_2={S}/{4}+{3S}/{4}={4S}/{4}=S$(2), $t_{общ}=t_1+t_2={S_1}/{υ_1}+{S_2}/{υ_2}={S}/{4υ_1}+{3S}/{4υ_2}={Sυ_2+3Sυ_1}/{4υ_1υ_2}$(3).
Подставим выражения (2) и (3) в (1), получим: $υ_{ср}={S}/{1}:{S(3υ_1+υ_2)}/{4υ_1υ_2}={S}/{1}·{4υ_1υ_2}/{S(3υ_1+υ_2)}={4υ_1υ_2}/{(3υ_1+υ_2)}$(4). Из (4) выразим скорость $υ_2$: $υ_{ср}(3υ_1+υ_2)=4υ_1υ_2⇒3υ_1υ_{ср}+υ_{ср}υ_2=4υ_1υ_2⇒4υ_1υ_2-υ_{ср}υ_2=3υ_1υ_{ср}⇒υ_2(4υ_1-υ_{ср})=3υ_1υ_{ср}⇒υ_2={3υ_1υ_{ср}}/{(4υ_1-υ_{ср})}$(5). Подставим числовые значения в (5): $υ_2={3·60·40}/{4·60-40}={7200}/{200}=36км/ч$.
Ответ: 36
Задача 3
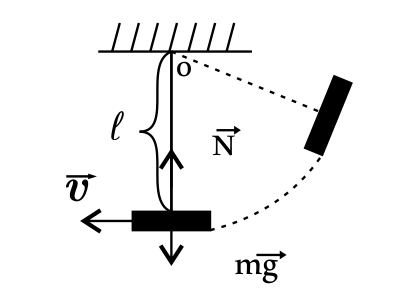
Цирковая гимнастка массой 50 кг качается на качелях с длиной верёвок 5 м. С какой силой она давит на сиденье при прохождении положения равновесия со скоростью 6 м/с? Ответ выразите в (Н). Ускорение свободного падения считать равным 10 м/с^2
Решение
Дано:
$m=50$кг
$g=10м/с^2$
$l=5$м
$υ=6$м/c
$N-?$
Решение:
При прохождении качелями среднего положения второй закон Ньютона в проекции на вертикальное направление иммет вид: $ma=N-mg$(1), здесь $a$ — ускорение гимнастики, совпадающее с центростремительным, $m$ — масса гимнастики, $N$ — сила реакции опоры (сиденья), равная по модулю, согласно третьему закону Ньютона, силе, с которой мальчик давит на сиденье. Так как центростремительное ускорение равно $a_{ц.с.}={υ^2}/{l}$(2), то сила, действующая на сиденье, равна: $N=ma+mg=m(a+g)=m({υ^2}/{l}+g)$(3). Подставим числовые значения в (3): $N=50·({36}/{5}+10)=50·17=860H$.
Ответ: 860
Задача 4
Из начала координат одновременно начинают движение две точки. Первая движется вдоль оси Ox со скоростью 3 м/с, а вторая — вдоль оси Oy со скоростью 4 м/с. (Оси перпендикулярны). С какой скоростью они будут удаляться друг от друга? Ответ выразите в (м/с).
Решение
Дано:
$υ_1=3$м/с
$υ_2=4$м/с
$υ_{отн}-?$
Решение:
Вектор относительной скорости $υ_{отн}$ есть разность векторов скоростей двух точек. По правилу вычитания векторов, вектор относительной скорости будет ижти от конца вектора скорости одной точки к концу векторая скорости другой точки. Так как скорости точек направлены перпендикулярно, длина вектора относительной скорости является гипотенузой прямоугольного треугольника и находится по теореме Пифагора: $υ_{отн}=√{υ_1^2+υ_2^2}=√{(3)^2+(4)^2}=√{9+16}=√{25}=5$м/с.
Ответ: 5
Задача 5
Автобус, масса которого 15 т, движется с ускорением 0,7 м/с2. Чему равна сила тяги двигателя, если коэффициент сопротивления движению равен 0,03? Ответ выразите в (кН).
Решение
Дано:
$m=15·10^3$кг
$a=0.7м/с^2$
$μ=0.03$
$F_{тяги}-?$
Решение:
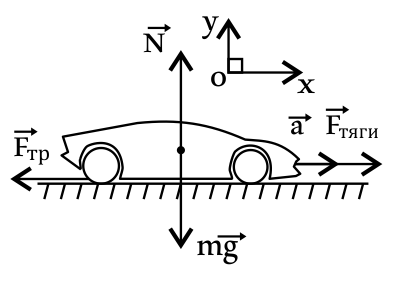
На автомобиль действуют силы: тяги, трения, тяжести и силы реакции опоры. Запишем второй закон Ньютона: $ma↖{→}={F_{тяги}}↖{→}+{F_{тр}}↖{→}+mg↖{→}+N↖{→}$(1).
В проекциях на оси координат имеем: $Ox:ma=F_{тяги}-F_{тр}$(2), откуда $F_{тяги}=ma+F_{тр}$(3). $Oy:O=N-mg$(4), откуда $N=mg$(5). Учитывая, что сила трения $F_{тр}=μN$, то с учетом (5) получим: $F_{тр}=μmg$(6). Подставим (6) в (3) и найдем $F_{тяги}:F_{тяги}=ma+μmg=m(a+μg)$(7), где $g≈10м/с^2$ — ускорение свободного падения.
Подставим числовые значения в (7), получим: $F_{тяги}=15·10^3·(0.7+0.03·10)=15·10^3·(0.7+0.3)=15·10^3·1=15·10^3=15$кН.
Ответ: 15
Задача 6
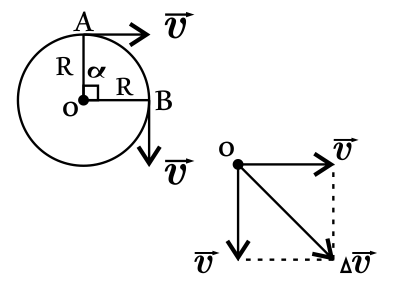
Тело движется по окружности равномерно. Радиус окружности 1 м. Найдите изменение вектора скорости при перемещении тела на угол 90◦. Период обращения 3,14 с. Ответ округлите до десятых. Ответ выразите в (м/с). Число ${π}$ принять равным 3,14
Решение
Дано:
$R=1$м
$α=90°$
$T=3.14$c
$∆υ-?$
Решение:
Изменение вектора скорости при перемещении тела на угол $90°$ равно по теореме Пифагора: $∆υ=√{υ^2+υ^2}=√{2υ^2}=√{2}υ$(1).
Найдем величину скорости $υ$: $υ={S}/{t}={2πR}/{T}={3.14·2·1}/{3.14}=2$м/с(2).
Подставим числовые значения в (1), получим: $∆υ=√2·υ=1.41·2=2.82=2.8$м/с.
Ответ: 2.8
Задача 7
Тело движется вдоль оси Ox. Чему равна проекция скорости тела vx, координата x которого меняется с течением времени по закону x = 3 − 2t, где все величины выражены в системе СИ? Ответ выразите в (м/c).
Решение
Дано:
$x=3-2t$
$υ_х-?$
Решение:
Известно, что $υ_x=x'(t)$, тогда $x'(t)=-2·1=-2$.
Ответ: -2
Задача 8
Подъёмный кран поднимает груз вверх со скоростью 3 м/с. В некоторый момент времени трос обрывается и груз начинает падать вниз. Определите скорость груза в момент падения на землю, если время падения составляет 4 с. Ответ выразить в (м/с). Ускорение свободного падения принять равным $10м/с^2$
Решение
Дано:
$υ=3$м/с
$t=4$c
$υ_к-?$
Решение:
На тело действует сила тяжести и ускорение свободного падения $g=const=10м/с^2$
$g={υ_к-(-υ_0)}/{t}$, т.к. ускорение $g$ и $υ_0$ разнонаправлены. $υ_к=gt-υ_0=10·4-3=37$м/с.
Ответ: 37
Задача 9
Тело движется вдоль оси Ox. Чему равно перемещение тела за 10 с, координата x которого меняется с течением времени по закону x = 3 − 2t + t2, где все величины выражены в системе СИ? Ответ выразить в (м).
Решение
Дано:
$t=10$c
$x=3-2t+t^2$
$x_0=3$
$r-?$
Решение:
$x=-20+100=80+3=83$
$r=x-x_0=83-3=80$м, т.к. изначально тело уже прошло 3м.
Ответ: 80
Задача 10
Планета имеет радиус в 2 раза меньший радиуса Земли. Найдите массу этой планеты, если известно, что ускорение свободного падения на поверхности этой планеты такое же, как и на Земле. Масса Земли 6 · 1024 кг. Ответ выразить в (·1024 кг).
Решение
Дано:
$R_n={R_3}/{2}$
$M_n-?$
$g_n=g_3$
$M_3=6·10^{24}$м
Решение:
${tableg_n=G{M_n}/{R_r^2}; g_3=G{M_3}/{R_3^2};$ ${M_n}/{R_n^2}={M_3}/{R_3^2}; M_n=M_3·{R_n^2}/{R_3^2}=6·10^{24}·{1}/{4}=1.5·10^{24}$кг
Ответ: 1.5
Задача 11
Материальная точка движется по окружности радиусом ${1.5}/{π}$ м. Найдите перемещение точки за 2 полных оборота. Ответ выразить в (м).
Решение
Дано:
$R={1.5}{π}$
Решение:
Точка делает 2 полных оборота и возвращается в начальную точку, ее перемещение равно 0.
Ответ: 0
Задача 12
Планета имеет массу в 4 раза меньшую массы Земли. Найдите радиус этой планеты, если известно, что ускорение свободного падения на поверхности этой планеты такое же, как на Земле, радиус Земли 6,4 · 106 м. Ответ выразите в (км).
Решение
Дано:
$M_n={M_3}/{4}$
$R_n-?$
$g_n=g_3$
$R_3=6.4·10^6$м
Решение:
${tableg_n=G{M_n}/{R_n^2}; g_3=G{M_3}/{R_3^2};$ ${M_n}/{M_3}={R_n^2}/{R_3^2}; {1}/{2}={R_n}/{R_3}$
$R_n=3200$км
Ответ: 3200
Задача 13
Найдите, чему равно ускорение свободного падения на некоторой планете, если период колебаний секундного земного математического маятника на ней оказался равным 1,41 с. Ответ выразите в (м/с2).
Решение
Дано:
$g_n-?$
$T_n=1.41$с
$T_3=1c$
Решение:
${tableT_n=2π√{{l}/{g_n}}; T_3=2π√{{l}/{g_3}};$ ${T_n}/{T_3}=√{{g_3}/{g_n}}; {1.41^2}/{1}={10}/{g_n}$
$g_n=5м/с^2$
Ответ: 5
Задача 14
Мяч массой 800 г брошен под углом 90◦ к горизонту с начальной скоростью 5 м/с. Найдите модуль силы тяжести, действующей на мяч сразу после броска. Ответ выразите в (Н).
Решение
Дано:
$m=0.8$кг
$υ=5$м/с
$F_{тяж}-?$
Решение:
Модуль силы тяжести, равна: $m·g=0.8·10=8H$
Ответ: 8
Задача 15
Найдите значение ускорения свободного падения на некоторой планете, плотность которой в два раза меньше плотности Земли, если радиусы планет одинаковы. Ответ выразите в (м/с2). Ускорение свободного падения на Земле принять равным 10 м/с^2
Решение
Дано:
$R_n=R_3$
${ρ_3}/{2}=ρ_n$
$ρ_n-?$
Решение:
${tableg^3=G{M_3}/{r^2}; g_n=G{M_n}/{r_n^2};$
а $V={4}/{3}π·R^3$, то и $V_n=V_3$.
${g_3}/{g_n}={ρ_3·V_3·r_n^2}/{ρ_n·V_n·r_3^2}⇒g_3=2·g_n; g_n=5м/с^2$.
Ответ: 5
Задача 16
Висящий на пружинке груз массой 400 г растягивает её на 10 см. На сколько сантиметров растянется пружина, если груз заменить на другой, массой 300 г? Ускорение свободного падения принять равным $10 м/{с^2}$. Ответ выразите в (см).
Решение
Дано:
$m_1=0.4$кг
$m_2=0.3$кг
$x_1=10^{-1}$ м=10 см
$x_2-?$
Решение:
${tablem_1g=kx_1; m_2g=kx_2;$ $⇒x_2={m_2g}/{m_1g}·x_1={0.3}/{0.4}·10см=7.5$
Ответ: 7.5
Задача 17
Велосипедист за 30 мин проехал 4 км, затем полчаса отдыхал, а затем проехал ещё 4 км за 15 мин. Какой была его средняя скорость на всём пути? Ответ выразите в (км/ч).
Решение
Известно, $υ_{ср}={∆S}/{∆t}={4+0+4}/{30+30+15}={8}/{1.25}=6.4{км}/ч$.
Ответ: 6.4
Задача 18
Найдите жёсткость пружины, если под действием силы 2 Н она растянулась на 4 см. Ответ выразите в (Н/м).
Решение
Дано:
$А=2·H$
$∆x=4·10^{-2}$
$K-?$
Решение:
По закону Гука $K={F}/{∆x}={2}/{4·10^{-2}}=50Н/м$.
Ответ: 50
Задача 19
Материальная точка равномерно движется по окружности. Найдите отношение пути к модулю перемещения за половину периода. Ответ округлить до сотых.
Решение
Дано:
${L}/{|S↖{→}|}-?$
$t={T}/{2}$
Решение:
1) За полпериода тело проходит половину окружности, поэтому пройденный путь равен половине дуги окружности: $L=π·R$
2) Модуль перемещения равен длине прямой, соединяющей начальную и конечную точки: $|S↖{→}|=2·R$
3) ${L}/{|S↖{→}|}={π·R}/{2·R}=1.57$
Ответ: 1.57
Задача 20
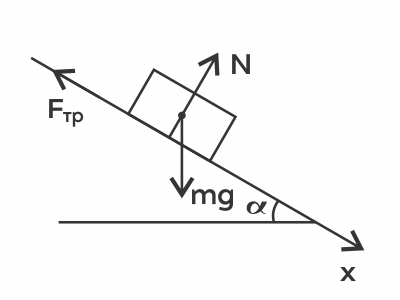
Брусок массой 2 кг покоится на наклонной плоскости с углом наклона 30◦ к горизонту. Определите силу трения, действующую на брусок, если коэффициент трения равен 0,7. Ответ выразите в (H). Ускорение свободного падения считать равным 10 $м/с^2$.
Решение
Дано:
$m=2$кг
$α=30°$
$μ=0.7$
Найти:$F_{тр}-?$
Решение:
Запишем 2-й закон Ньютона для тела: $ma↖{→}=mg↖{→}+N↖{→}+F_{тр}↖{→}=0$ (т.к. брусок покоится)
Направим ось х параллельно плоскости. 2-й закон Ньютона в проекции на ось х: $mg·sinα-F_{тр}=0⇒$
$F_{тр}=mgsinα=2·10·{1}/{2}=10Н$
Внимание! Многие при решении этой задачи используют неверную формулу $F_{тр}=μmgcosα$ — эта формула не может быть использована в этой задаче, потому что она описывает максимальную(!) силу трения покоя или силу трения скольжения. А в данной задаче тело покоится под действием силы трения, поэтому применять нужно формулы, указанные выше в решении.
Ответ: 10