КИНЕМАТИКА.
Теория и формулы (кратко и сжато)
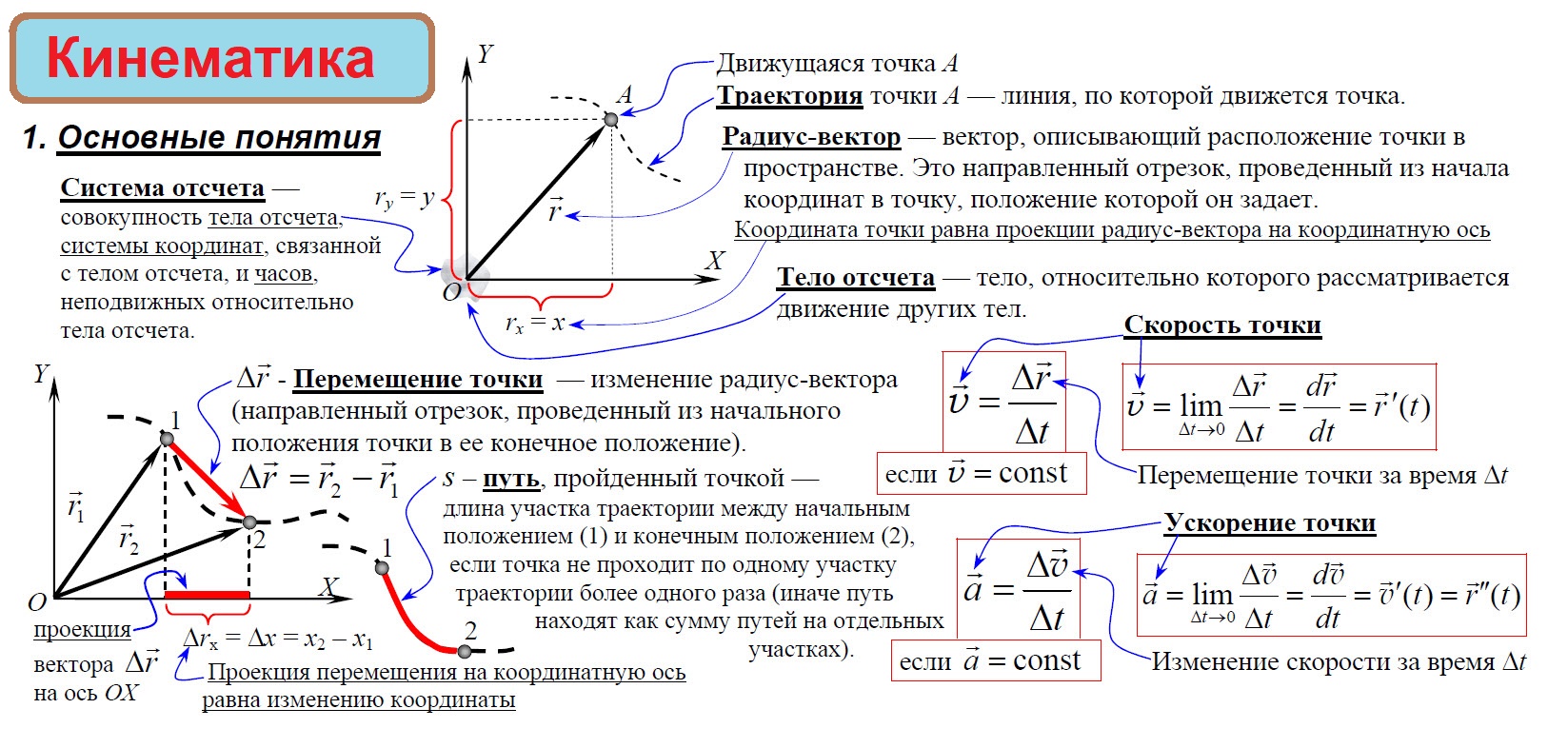
Кинематика – раздел физики, изучающий способы математического описания движения без выяснения его причин.
Механическое движение – изменение положения тела относительно других тел с течением времени. Способы описания: словесный, табличный, графический, формулами.
Материальная точка – тело, собственными размерами которого в данных условиях можно пренебречь.
Траектория – линия, которую описывает материальная точка при своём движении в пространстве. По виду траектории все движения делятся на прямолинейные и криволинейные.
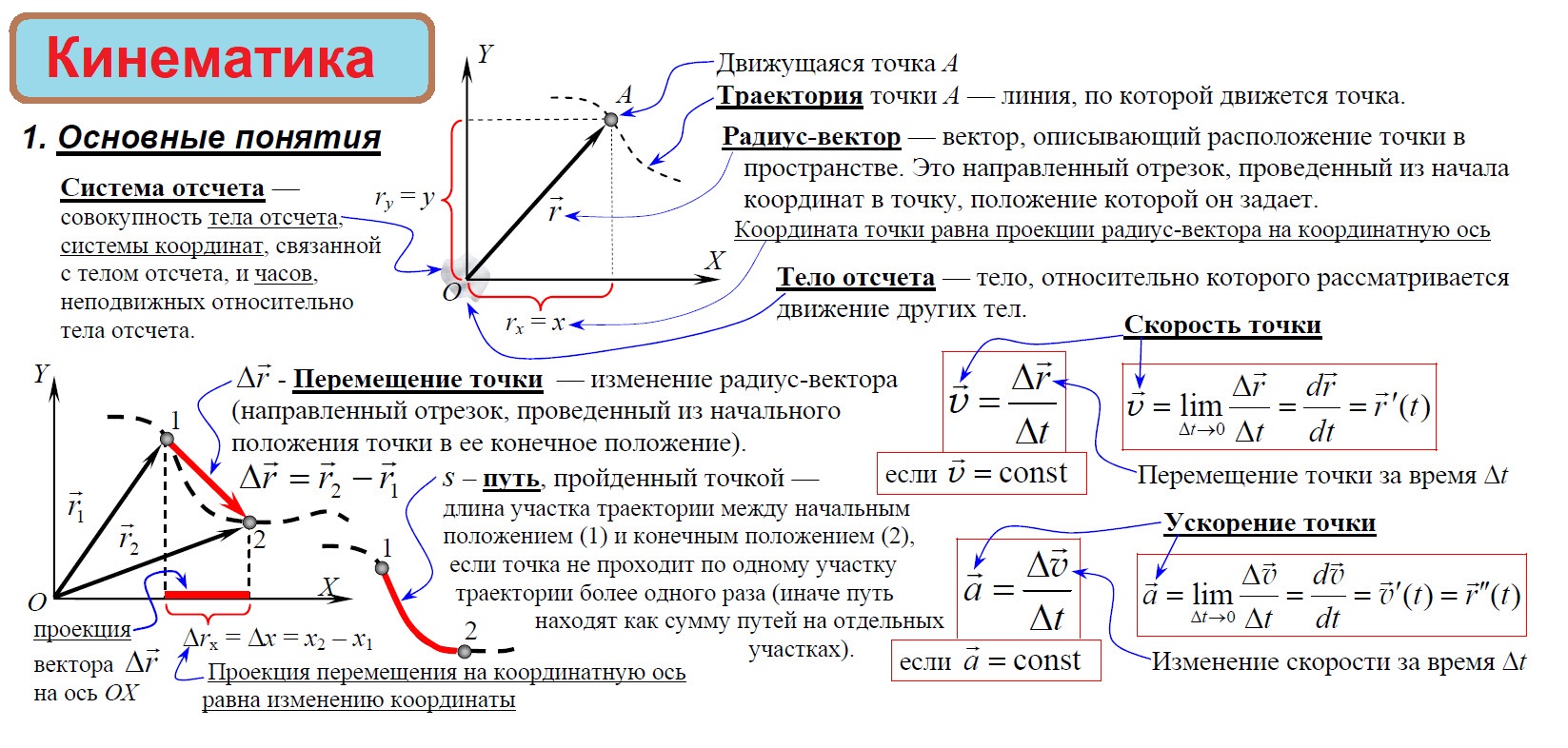
Система отсчёта – часы и система координат, связанные с условно выбираемым телом отсчёта (наблюдателем).
Относительность движения – различие скорости, направления и траектории движения в различных системах отсчёта.
Перемещение – вектор, проведённый из начального положения материальной точки в её конечное положение.
Типы движений
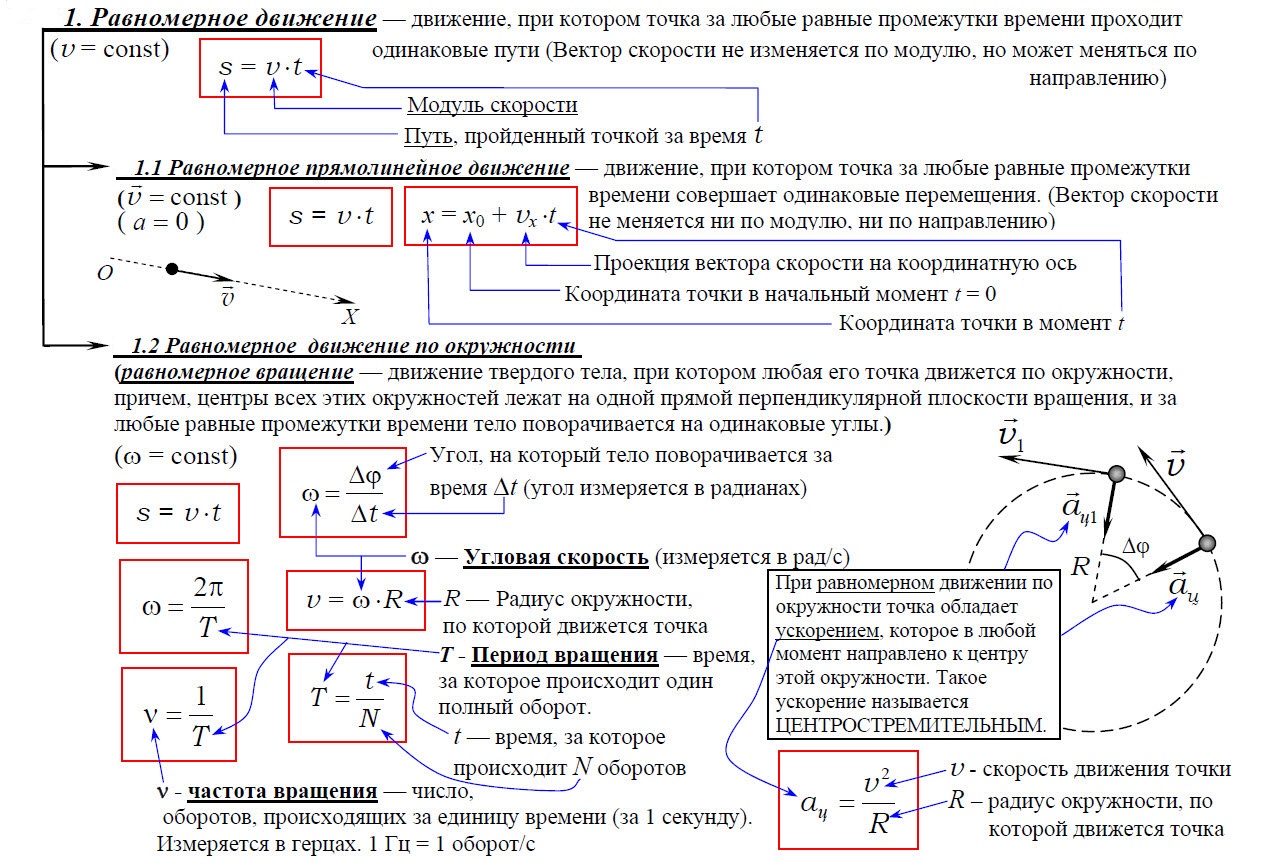
1. Равномерное движение
1.1. Равномерное прямолинейное движение
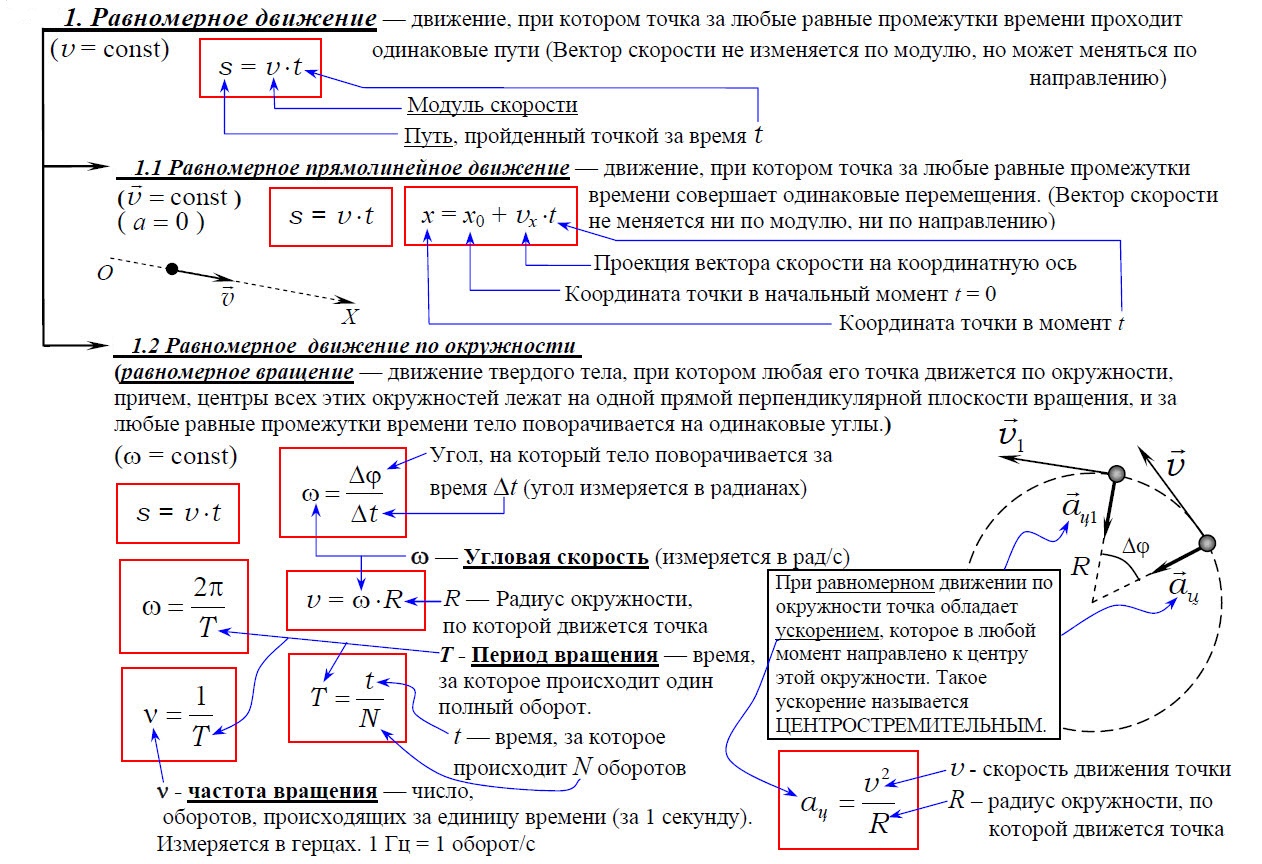
Равномерное движение – движение тела, при котором за равные интервалы времени оно преодолевает равные части пути.
Скорость равномерного движения равна отношению пройденного пути к интервалу времени, за который этот путь пройден.
Скорость равномерного прямолинейного движения равна отношению перемещения к интервалу времени его совершения.
Уравнение равно-прямолинейного движения x = xo + υoxt показывает, что координата линейно зависит от времени.
Мгновенная скорость равна отношению перемещения к бесконечно малому интервалу времени, за который оно произошло.
1.2 Равномерное движение по окружности (равномерное вращение)
Равномерное движение по окружности — это движение, при котором материальная точка за равные промежутки времени проходит равные по длине дуги окружности.
Равномерное движение тела по окружности — это частный и наиболее простой случай криволинейного движения. Хотя при таком движении модуль скорости остается постоянным, это движение с ускорением, которое является следствием изменения направления вектора скорости.
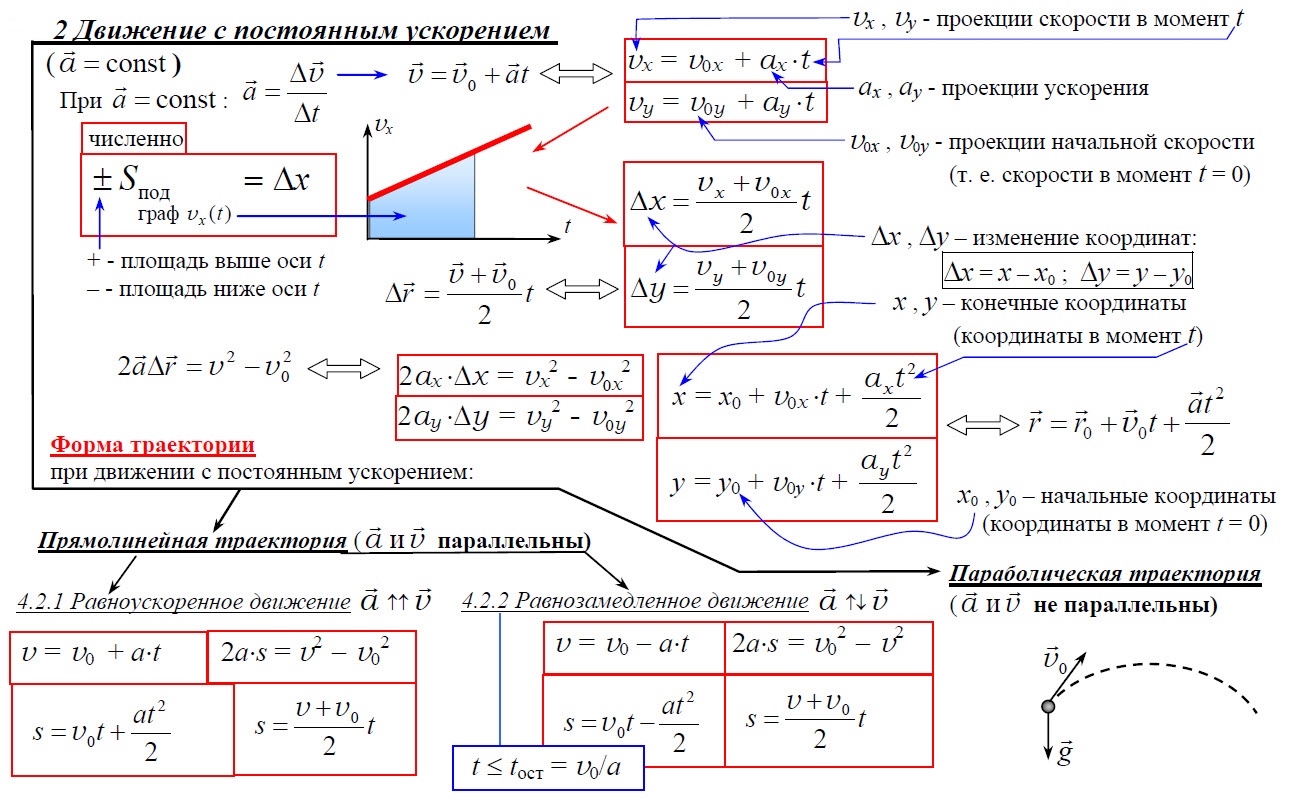
2. Движение с постоянным ускорением
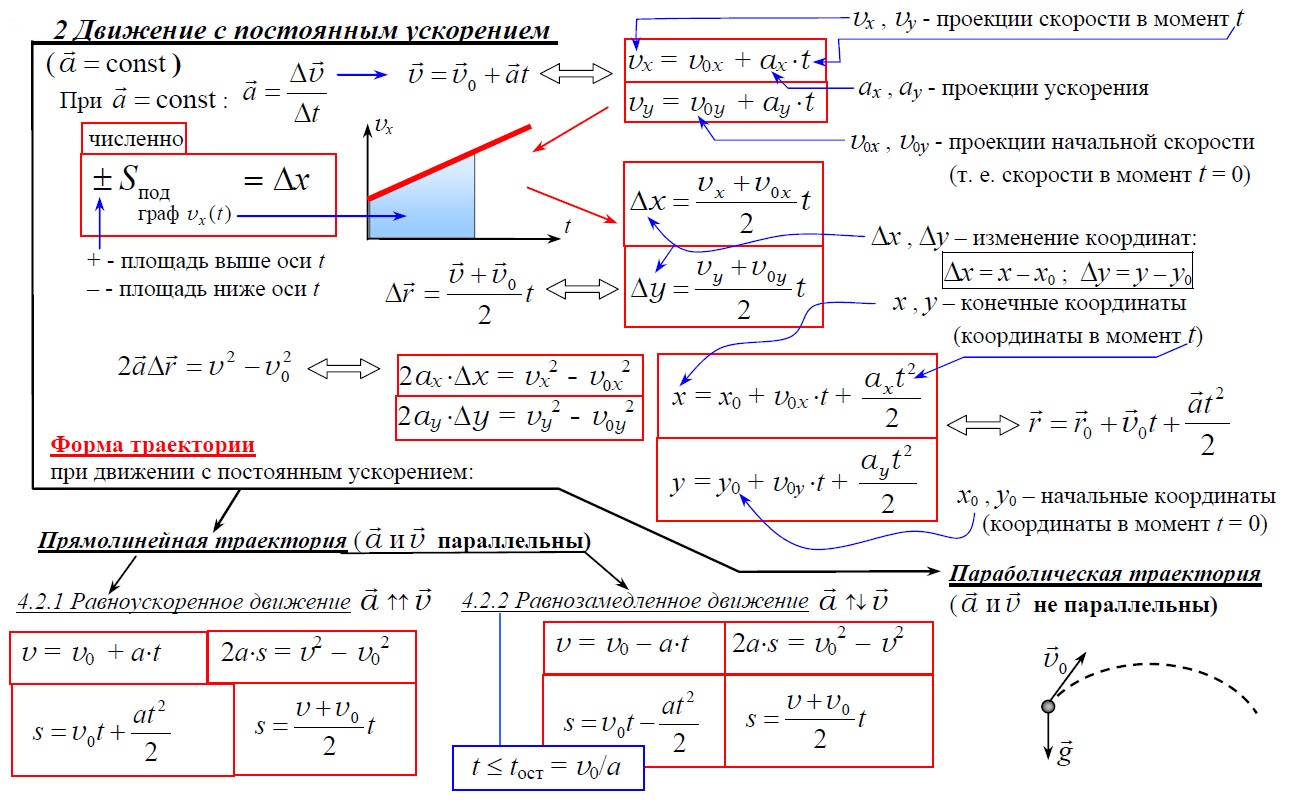
Равноускоренное движение – движение, при котором мгновенная скорость за любые равные интервалы времени меняется одинаково.
Мгновенное ускорение равно отношению изменения мгновенной скорости тела к бесконечно малому интервалу времени, за который это изменение произошло.
Ускорение равноускоренного движения равно отношению изменения мгновенной скорости тела к интервалу времени, за который это изменение произошло.
Уравнение равноускоренного движения y = yo + υoyt + ½ayt² показывает, что координата квадратично зависит от времени. Уравнение υy = υoy + ayt показывает, что скорость линейно зависит от времени.
Центростремительное ускорение – ускорение, всегда направленное к центру окружности при равномерном движении по ней материальной точки. Модуль центростремительного ускорения равен отношению квадрата модуля скорости равномерного движения по окружности к её радиусу.
3. Гармоническое движение
Виды движений
Прямолинейное движение
Криволинейное движение
Частные случаи равноускоренного движения под действием силы тяжести
Частные случаи решения задач
Дополнительные материалы по кинематике
Кинематика. Таблица кратко.
Это конспект по физике «Кинематика. Теория и формулы для ЕГЭ» + шпаргалка.
Еще конспекты для 10-11 классов:
Оглавление:
- Основные теоретические сведения
- Система СИ
- Путь и перемещение
- Средняя скорость
- Равноускоренное прямолинейное движение
- Свободное падение по вертикали
- Горизонтальный бросок
- Бросок под углом к горизонту (с земли на землю)
- Сложение скоростей
- Равномерное движение по окружности
Основные теоретические сведения
Система СИ
К оглавлению…
Основные единицы измерения величин в системе СИ таковы:
- единица измерения длины — метр (1 м),
- времени — секунда (1 с),
- массы — килограмм (1 кг),
- количества вещества — моль (1 моль),
- температуры — кельвин (1 К),
- силы электрического тока — ампер (1 А),
- Справочно: силы света — кандела (1 кд, фактически не используется при решении школьных задач).
При выполнении расчетов в системе СИ углы измеряются в радианах.
Если в задаче по физике не указано, в каких единицах нужно дать ответ, его нужно дать в единицах системы СИ или в производных от них величинах, соответствующих той физической величине, о которой спрашивается в задаче. Например, если в задаче требуется найти скорость, и не сказано в чем ее нужно выразить, то ответ нужно дать в м/с.
Для удобства в задачах по физике часто приходится использовать дольные (уменьшающие) и кратные (увеличивающие) приставки. их можно применять к любой физической величине. Например, мм – миллиметр, кт – килотонна, нс – наносекунда, Мг – мегаграмм, ммоль – миллимоль, мкА – микроампер. Запомните, что в физике не существует двойных приставок. Например, мкг – это микрограмм, а не милликилограмм. Учтите, что при сложении и вычитании величин Вы можете оперировать только величинами одинаковой размерности. Например, килограммы можно складывать только с килограммами, из миллиметров можно вычитать только миллиметры, и так далее. При переводе величин пользуйтесь следующей таблицей.
Таблица дольных и кратных приставок в физике:
Путь и перемещение
К оглавлению…
Кинематикой называют раздел механики, в котором движение тел рассматривается без выяснения причин этого движения.
Механическим движением тела называют изменение его положения в пространстве относительно других тел с течением времени.
Всякое тело имеет определенные размеры. Однако, во многих задачах механики нет необходимости указывать положения отдельных частей тела. Если размеры тела малы по сравнению с расстояниями до других тел, то данное тело можно считать материальной точкой. Так при движении автомобиля на большие расстояния можно пренебречь его длиной, так как длина автомобиля мала по сравнению с расстояниями, которое он проходит.
Интуитивно понятно, что характеристики движения (скорость, траектория и т.д.) зависят от того, откуда мы на него смотрим. Поэтому для описания движения вводится понятие системы отсчета. Система отсчета (СО) – совокупность тела отсчета (оно считается абсолютно твердым), привязанной к нему системой координат, линейки (прибора, измеряющего расстояния), часов и синхронизатора времени.
Перемещаясь с течением времени из одной точки в другую, тело (материальная точка) описывает в данной СО некоторую линию, которую называют траекторией движения тела.
Перемещением тела называют направленный отрезок прямой, соединяющий начальное положение тела с его конечным положением. Перемещение есть векторная величина. Перемещение может в процессе движения увеличиваться, уменьшаться и становиться равным нулю.
Пройденный путь равен длине траектории, пройденной телом за некоторое время. Путь – скалярная величина. Путь не может уменьшаться. Путь только возрастает либо остается постоянным (если тело не движется). При движении тела по криволинейной траектории модуль (длина) вектора перемещения всегда меньше пройденного пути.
При равномерном (с постоянной скоростью) движении путь L может быть найден по формуле:
где: v – скорость тела, t – время в течении которого оно двигалось. При решении задач по кинематике перемещение обычно находится из геометрических соображений. Часто геометрические соображения для нахождения перемещения требуют знания теоремы Пифагора.
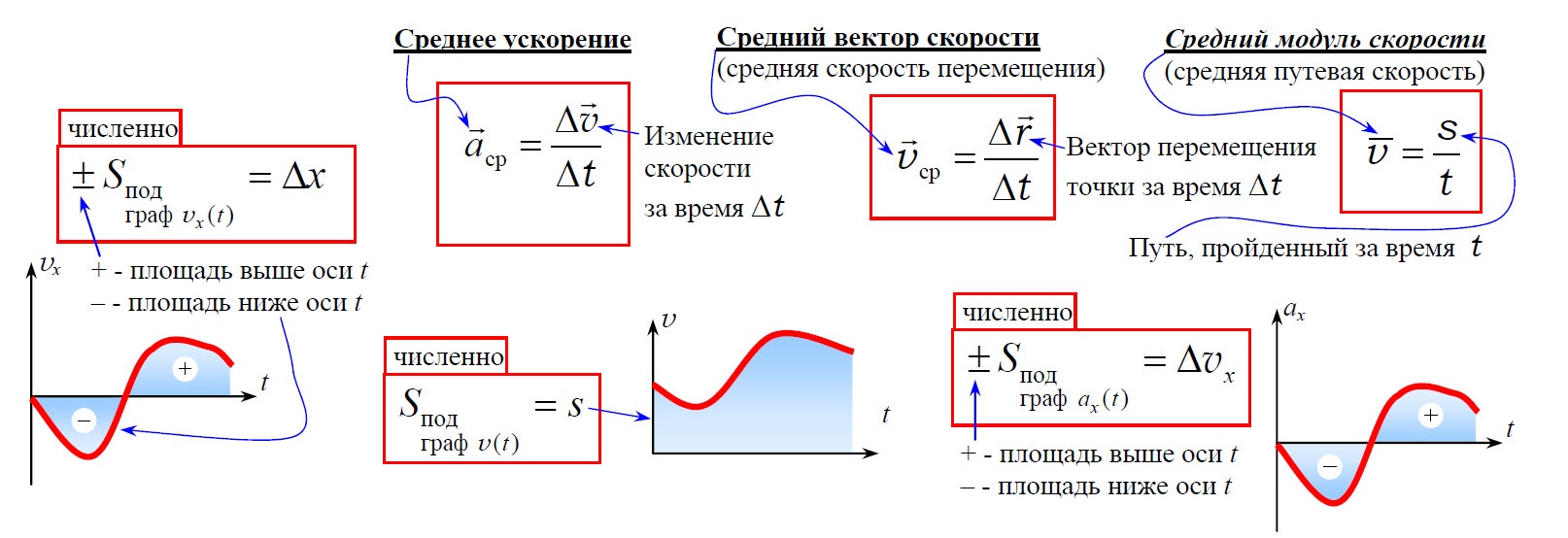
Средняя скорость
К оглавлению…
Скорость – векторная величина, характеризующая быстроту перемещения тела в пространстве. Скорость бывает средней и мгновенной. Мгновенная скорость описывает движение в данный конкретный момент времени в данной конкретной точке пространства, а средняя скорость характеризует все движение в целом, в общем, не описывая подробности движения на каждом конкретном участке.
Средняя скорость пути – это отношение всего пути ко всему времени движения:
где: Lполн – весь путь, который прошло тело, tполн – все время движения.
Средняя скорость перемещения – это отношение всего перемещения ко всему времени движения:
Эта величина направлена так же, как и полное перемещение тела (то есть из начальной точки движения в конечную точку). При этом не забывайте, что полное перемещение не всегда равно алгебраической сумме перемещений на определённых этапах движения. Вектор полного перемещения равен векторной сумме перемещений на отдельных этапах движения.
- При решении задач по кинематике не совершайте очень распространенную ошибку. Средняя скорость, как правило, не равна среднему арифметическому скоростей тела на каждом этапе движения. Среднее арифметическое получается только в некоторых частных случаях.
- И уж тем более средняя скорость не равна одной из скоростей, с которыми двигалось тело в процессе движения, даже если эта скорость имела примерно промежуточное значение относительно других скоростей, с которыми двигалось тело.
Равноускоренное прямолинейное движение
К оглавлению…
Ускорение – векторная физическая величина, определяющая быстроту изменения скорости тела. Ускорением тела называют отношение изменения скорости к промежутку времени, в течение которого происходило изменение скорости:
где: v0 – начальная скорость тела, v – конечная скорость тела (то есть спустя промежуток времени t).
Далее, если иное не указано в условии задачи, мы считаем, что если тело движется с ускорением, то это ускорение остается постоянным. Такое движение тела называется равноускоренным (или равнопеременным). При равноускоренном движении скорость тела изменяется на одинаковую величину за любые равные промежутки времени.
Равноускоренное движение бывает собственно ускоренным, когда тело увеличивает скорость движения, и замедленным, когда скорость уменьшается. Для простоты решения задач удобно для замедленного движения брать ускорение со знаком «–».
Из предыдущей формулы, следует другая более распространённая формула, описывающая изменение скорости со временем при равноускоренном движении:
Перемещение (но не путь) при равноускоренном движении рассчитывается по формулам:
В последней формуле использована одна особенность равноускоренного движения. При равноускоренном движении среднюю скорость можно рассчитывать, как среднее арифметическое начальной и конечной скоростей (этим свойством очень удобно пользоваться при решении некоторых задач):
С расчетом пути все сложнее. Если тело не меняло направления движения, то при равноускоренном прямолинейном движении путь численно равен перемещению. А если меняло – надо отдельно считать путь до остановки (момента разворота) и путь после остановки (момента разворота). А просто подстановка времени в формулы для перемещения в этом случае приведет к типичной ошибке.
Координата при равноускоренном движении изменяется по закону:
Проекция скорости при равноускоренном движении изменяется по такому закону:
Аналогичные формулы получаются для остальных координатных осей. Формула для тормозного пути тела:
Свободное падение по вертикали
К оглавлению…
На все тела, находящиеся в поле тяготения Земли, действует сила тяжести. В отсутствие опоры или подвеса эта сила заставляет тела падать к поверхности Земли. Если пренебречь сопротивлением воздуха, то движение тел только под действием силы тяжести называется свободным падением. Сила тяжести сообщает любым телам, независимо от их формы, массы и размеров, одинаковое ускорение, называемое ускорением свободного падения. Вблизи поверхности Земли ускорение свободного падения составляет:
Это значит, что свободное падение всех тел вблизи поверхности Земли является равноускоренным (но не обязательно прямолинейным) движением. Вначале рассмотрим простейший случай свободного падения, когда тело движется строго по вертикали. Такое движение является равноускоренным прямолинейным движением, поэтому все изученные ранее закономерности и фокусы такого движения подходят и для свободного падения. Только ускорение всегда равно ускорению свободного падения.
Традиционно при свободном падении используют направленную вертикально ось OY. Ничего страшного здесь нет. Просто надо во всех формулах вместо индекса «х» писать «у». Смысл этого индекса и правило определения знаков сохраняется. Куда направлять ось OY – Ваш выбор, зависящий от удобства решения задачи. Вариантов 2: вверх или вниз.
Приведем несколько формул, которые являются решением некоторых конкретных задач по кинематике на свободное падение по вертикали. Например, скорость, с которой упадет тело падающее с высоты h без начальной скорости:
Время падения тела с высоты h без начальной скорости:
Максимальная высота на которую поднимется тело, брошенное вертикально вверх с начальной скоростью v0, время подъема этого тела на максимальную высоту, и полное время полета (до возвращения в исходную точку):
Горизонтальный бросок
К оглавлению…
При горизонтальном броске с начальной скоростью v0 движение тела удобно рассматривать как два движения: равномерное вдоль оси ОХ (вдоль оси ОХ нет никаких сил препятствующих или помогающих движению) и равноускоренного движения вдоль оси OY.
Скорость в любой момент времени направлена по касательной к траектории. Ее можно разложить на две составляющие: горизонтальную и вертикальную. Горизонтальная составляющая всегда остается неизменной и равна vx = v0. А вертикальная возрастает по законам ускоренного движения vy = gt. При этом полная скорость тела может быть найдена по формулам:
При этом важно понять, что время падения тела на землю никоим образом не зависит от того, с какой горизонтальной скоростью его бросили, а определяется только высотой, с которой было брошено тело. Время падения тела на землю находится по формуле:
Пока тело падает, оно одновременно движется вдоль горизонтальной оси. Следовательно, дальность полета тела или расстояние, которое тело сможет пролететь вдоль оси ОХ, будет равно:
Угол между горизонтом и скоростью тела легко найти из соотношения:
Также иногда в задачах могут спросить о моменте времени, при котором полная скорость тела будет наклонена под определенным углом к вертикали. Тогда этот угол будет находиться из соотношения:
Важно понять, какой именно угол фигурирует в задаче (с вертикалью или с горизонталью). Это и поможет вам выбрать правильную формулу. Если же решать эту задачу координатным методом, то общая формула для закона изменения координаты при равноускоренном движении:
Преобразуется в следующий закон движения по оси OY для тела брошенного горизонтально:
При ее помощи мы можем найти высоту на которой будет находится тело в любой момент времени. При этом в момент падения тела на землю координата тела по оси OY будет равна нулю. Очевидно, что вдоль оси OХ тело движется равномерно, поэтому в рамках координатного метода горизонтальная координата изменятся по закону:
Бросок под углом к горизонту (с земли на землю)
К оглавлению…
Максимальная высота подъема при броске под углом к горизонту (относительно начального уровня):
Время подъема до максимальной высоты при броске под углом к горизонту:
Дальность полета и полное время полета тела брошенного под углом к горизонту (при условии, что полет заканчивается на той же высоте с которой начался, т.е. тело бросали, например, с земли на землю):
Минимальная скорость тела брошенного под углом к горизонту – в наивысшей точке подъёма, и равна:
Максимальная скорость тела брошенного под углом к горизонту – в моменты броска и падения на землю, и равна начальной. Это утверждение верно только для броска с земли на землю. Если тело продолжает лететь ниже того уровня, с которого его бросали, то оно будет там приобретать все большую и большую скорость.
Сложение скоростей
К оглавлению…
Движение тел можно описывать в различных системах отсчета. С точки зрения кинематики все системы отсчета равноправны. Однако кинематические характеристики движения, такие как траектория, перемещение, скорость, в разных системах оказываются различными. Величины, зависящие от выбора системы отсчета, в которой производится их измерение, называют относительными. Таким образом, покой и движение тела относительны. Классический закон сложения скоростей:
Таким образом, абсолютная скорость тела равна векторной сумме его скорости относительно подвижной системы координат и скорости самой подвижной системы отсчета. Или, другими словами, скорость тела в неподвижной системе отсчета равна векторной сумме скорости тела в подвижной системе отсчета и скорости подвижной системы отсчета относительно неподвижной.
Равномерное движение по окружности
К оглавлению…
Движение тела по окружности является частным случаем криволинейного движения. Такой вид движения также рассматривается в кинематике. При криволинейном движении вектор скорости тела всегда направлен по касательной к траектории. То же самое происходит и при движении по окружности (см. рисунок). Равномерное движение тела по окружности характеризуется рядом величин.
Период – время, за которое тело, двигаясь по окружности, совершает один полный оборот. Единица измерения – 1 с. Период рассчитывается по формуле:
Частота – количество оборотов, которое совершило тело, двигаясь по окружности, в единицу времени. Единица измерения – 1 об/с или 1 Гц. Частота рассчитывается по формуле:
В обеих формулах: N – количество оборотов за время t. Как видно из вышеприведенных формул, период и частота величины взаимообратные:
При равномерном вращении скорость тела будет определяется следующим образом:
где: l – длина окружности или путь, пройденный телом за время равное периоду T. При движении тела по окружности удобно рассматривать угловое перемещение φ (или угол поворота), измеряемое в радианах. Угловой скоростью ω тела в данной точке называют отношение малого углового перемещения Δφ к малому промежутку времени Δt. Очевидно, что за время равное периоду T тело пройдет угол равный 2π, следовательно при равномерном движении по окружности выполняются формулы:
Угловая скорость измеряется в рад/с. Не забывайте переводить углы из градусов в радианы. Длина дуги l связана с углом поворота соотношением:
Связь между модулем линейной скорости v и угловой скоростью ω:
При движении тела по окружности с постоянной по модулю скоростью изменяется только направление вектора скорости, поэтому движение тела по окружности с постоянной по модулю скоростью является движением с ускорением (но не равноускоренным), так как меняется направление скорости. В этом случае ускорение направлено по радиусу к центру окружности. Его называют нормальным, или центростремительным ускорением, так как вектор ускорения в любой точке окружности направлен к ее центру (см. рисунок).
Модуль центростремительного ускорения связан с линейной v и угловой ω скоростями соотношениями:
Обратите внимание, что если тела (точки) находятся на вращающемся диске, шаре, стержне и так далее, одним словом на одном и том же вращающемся объекте, то у всех тел одинаковые период вращения, угловая скорость и частота.
Полная теория по Кинематике, теория и практика ЕГЭ по физике
- 30.09.2013
Полный материал по физике на тему: Кинематика.
Материал содержит в себе необходимую теорию по теме, а также множество различных практических заданий и тестов, ориентированных на ЕГЭ.
Вместе с этим материалом вы сможете максимально качественно изучить раздел физики «Кинематика» для ЕГЭ.
Смотреть в PDF:
Или прямо сейчас: Скачайте в pdf файле.
Добавить комментарий
Комментарии без регистрации. Несодержательные сообщения удаляются.
Кинематика
Механика — это раздел физики, изучающий механическое движение тел.
Кинематика — это раздел механики, в котором изучается механическое движение тел без учета причин, вызывающих это движение.
Материальная точка — тело, обладающее массой, размерами которого в данной задаче можно пренебречь, если
- расстояние, которое проходит тело, много больше его размера;
- расстояние от данного тела до другого тела много больше его размера;
- тело движется поступательно.
Система отсчета — это тело отсчета, связанная с ним система координат и прибор для измерения времени.
Траектория — это линия, которую описывает тело при своем движении.
Путь — это скалярная величина, равная длине траектории.
Перемещение — это вектор, соединяющий начальное положение тела с его конечным положением за данный промежуток времени.
Важно!
В процессе движения путь может только увеличиваться, а перемещение как увеличиваться, так и уменьшаться, например, когда тело поворачивает обратно.
При прямолинейном движении в одном направлении путь равен модулю перемещения, а при криволинейном — путь больше перемещения.
Перемещение на замкнутой траектории равно нулю.
Основная задача механики — определить положение тела в пространстве в любой момент времени.
Содержание
- Механическое движение и его виды
- Относительность механического движения
- Правило сложения перемещений
- Правило сложения скоростей
- Относительная скорость
- Скорость
- Ускорение
- Равномерное движение
- График скорости (проекции скорости)
- График перемещения (проекции перемещения)
- Прямолинейное равноускоренное движение
- Свободное падение (ускорение свободного падения)
- Движение тела по вертикали
- Движение тела, брошенного горизонтально
- Движение тела, брошенного под углом к горизонту (баллистическое движение)
- Движение по окружности с постоянной по модулю скоростью
- Основные формулы по теме «Кинематика»
Механическое движение и его виды
Механическое движение — это изменение положения тела в пространстве относительно других тел с течением времени.
Механическое движение может быть:
1. по характеру движения
- поступательным — это движение, при котором все точки тела движутся одинаково и любая прямая, мысленно проведенная в теле, остается параллельна сама себе;
- вращательным — это движение, при котором все точки твердого тела движутся по окружностям, расположенным в параллельных плоскостях;
- колебательным — это движение, которое повторяется в двух взаимно противоположных направлениях;
2. по виду траектории
- прямолинейным — это движение, траектория которого прямая линия;
- криволинейным — это движение, траектория которого кривая линия;
3. по скорости
- равномерным — движение, при котором скорость тела с течением времени не изменяется;
- неравномерным — это движение, при котором скорость тела с течением времени изменяется;
4. по ускорению
- равноускоренным — это движение, при котором скорость тела увеличивается с течением времени на одну и ту же величину;
- равнозамедленным — это движение, при котором скорость тела уменьшается с течением времени на одну и ту же величину.
Относительность механического движения
Относительность движения — это зависимость характеристик механического движения от выбора системы отсчета.
Правило сложения перемещений
Перемещение тела относительно неподвижной системы отсчета равно векторной сумме перемещения тела относительно подвижной системы отсчета и перемещения подвижной системы отсчета относительно неподвижной системы отсчета:
где ( S ) — перемещение тела относительно неподвижной системы отсчета;
( S_1 ) — перемещение тела относительно подвижной системы отсчета;
( S_2 ) — перемещение подвижной системы отсчета относительно неподвижной системы отсчета.
Правило сложения скоростей
Скорость тела относительно неподвижной системы отсчета равна векторной сумме скорости тела относительно подвижной системы отсчета и скорости подвижной системы отсчета относительно неподвижной системы отсчета:
где ( v ) — скорость тела относительно неподвижной системы отсчета;
( v_1 ) — скорость тела относительно подвижной системы отсчета;
( v_2 ) — скорость подвижной системы отсчета относительно неподвижной системы отсчета.
Относительная скорость
Важно! Чтобы определить скорость одного тела относительно другого, надо мысленно остановить то тело, которое мы принимаем за тело отсчета, а к скорости оставшегося тела прибавить скорость остановленного, изменив направление его скорости на противоположное.
Пусть ( v_1 ) — скорость первого тела, а ( v_2 ) — скорость второго тела.
Определим скорость первого тела относительно второго ( v_{12} ):
Определим скорость второго тела относительно первого ( v_{21} ):
Следует помнить, что траектория движения тела и пройденный путь тоже относительны.
Если скорости направлены перпендикулярно друг к другу, то относительная скорость рассчитывается по теореме Пифагора:
Если скорости направлены под углом ( alpha ) друг к другу, то относительная скорость рассчитывается по теореме косинусов:
Скорость
Скорость — это векторная величина, характеризующая изменение перемещения данного тела относительно тела отсчета с течением времени.
Обозначение — ( v ), единицы измерения — м/с (км/ч).
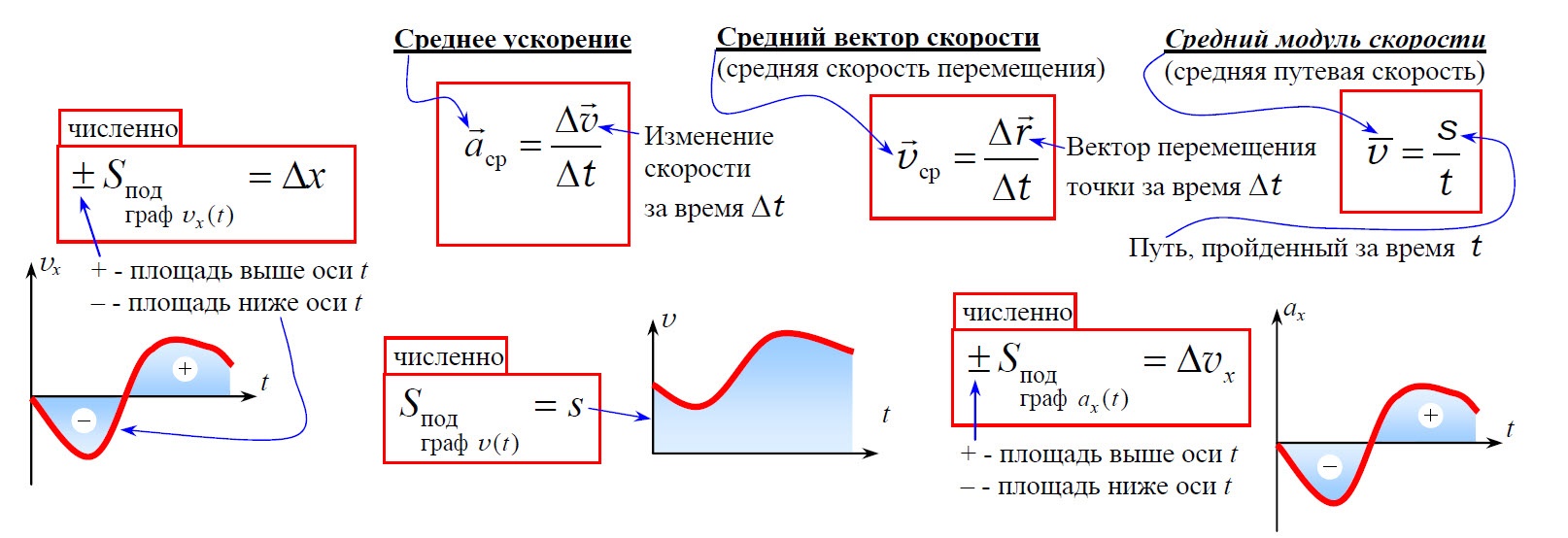
Средняя скорость — это векторная величина, равная отношению всего перемещения к промежутку времени, за которое это перемещение произошло:
Средняя путевая скорость — это скалярная величина, равная отношению всего пути, пройденного телом, к промежутку времени, за которое этот путь пройден:
Важно! Чтобы определить среднюю скорость на всем участке пути, надо время разделить на отдельные промежутки и все время представить в виде суммы этих промежутков.
Чтобы определить среднюю скорость за все время движения, надо путь разделить на отдельные участки и весь путь представить как сумму этих участков.
Мгновенная скорость — это скорость тела в данный момент времени или в данной точке траектории.
Мгновенная скорость направлена по касательной к траектории движения.
Ускорение
Ускорение – это векторная физическая величина, характеризующая быстроту изменения скорости.
Обозначение — ( a ), единица измерения — м/с2.
В векторном виде:
где ( v ) – конечная скорость; ( v_0 ) – начальная скорость;
( t ) – промежуток времени, за который произошло изменение скорости.
В проекциях на ось ОХ:
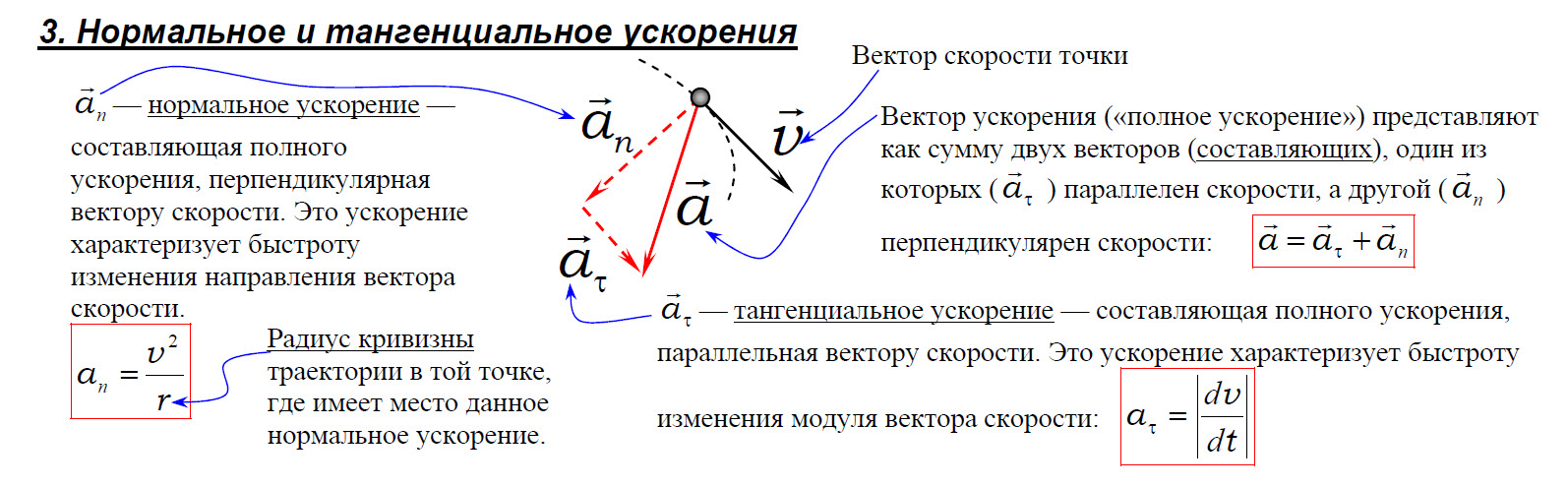
где ( a_n ) – нормальное ускорение, ( a_{tau} ) – тангенциальное ускорение.
Тангенциальное ускорение сонаправлено с вектором линейной скорости, а значит, направлено вдоль касательной к кривой:
Нормальное ускорение перпендикулярно направлению вектора линейной скорости, а значит, и касательной к кривой:
Ускорение характеризует быстроту изменения скорости, а скорость – векторная величина, которая имеет модуль (числовое значение) и направление.
Важно!
Тангенциальное ускорение характеризует быстроту изменения модуля скорости. Нормальное ускорение характеризует быстроту изменения направления скорости.
Если ( a_{tau} ) ≠ 0, ( a_n ) = 0, то тело движется по прямой;
если ( a_{tau} ) = 0, ( a_n ) = 0, ( v ) ≠ 0, то тело движется равномерно по прямой;
если ( a_{tau} ) = 0, ( a_n ) ≠ 0, тело движется равномерно по кривой;
если ( a_{tau} ) = 0, ( a_n ) = const, то тело движется равномерно по окружности;
если ( a_{tau} ) ≠ 0, ( a_n ) ≠ 0, то тело движется неравномерно по окружности.
Равномерное движение
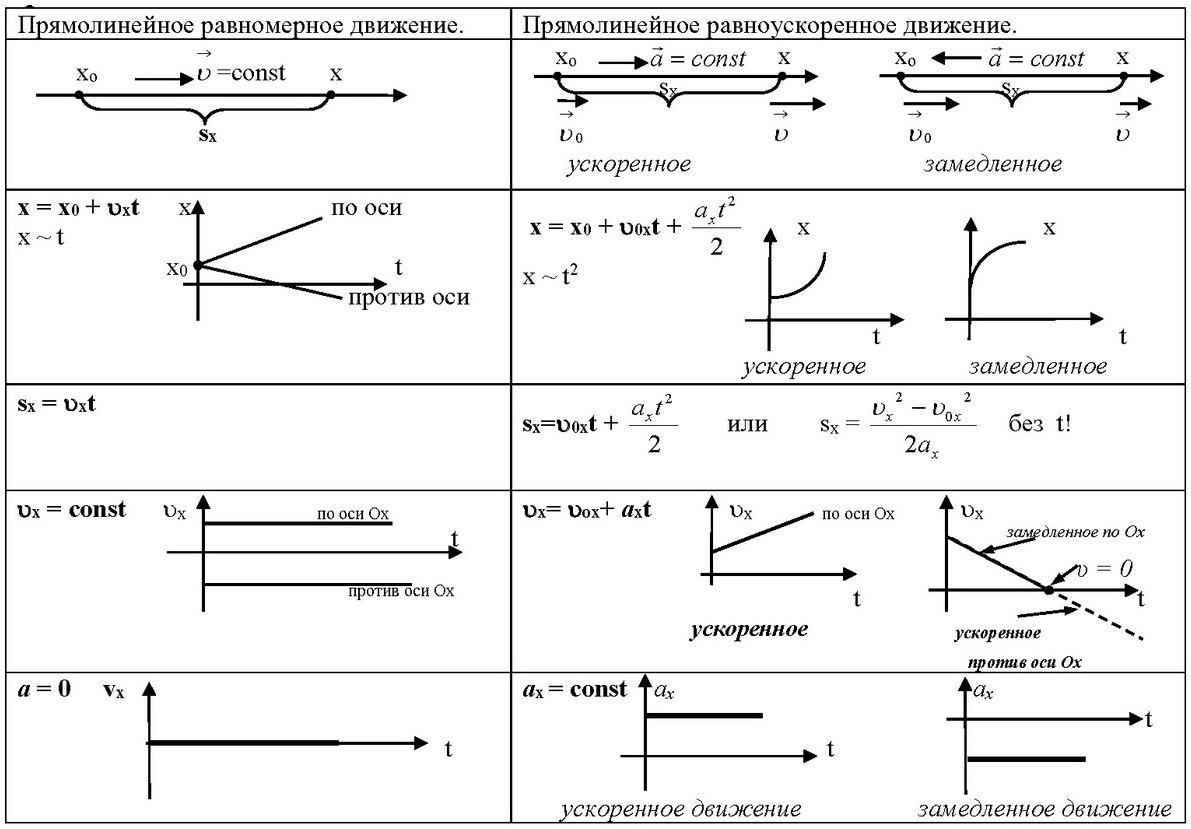
Равномерное движение – это движение, при котором тело за любые равные промежутки времени совершает равные перемещения.
Скорость при равномерном движении – величина, равная отношению перемещения к промежутку времени, за которое это перемещение произошло:
Проекция вектора скорости на ось ОХ:
Проекция вектора скорости на координатную ось равна быстроте изменения данной координаты:
График скорости (проекции скорости)
График скорости (проекции скорости) представляет собой зависимость скорости от времени:
График скорости при равномерном движении – прямая, параллельная оси времени.
График 1 лежит над осью ( t ), тело движется по направлению оси ОХ.
Графики 2 и 3 лежат под осью ( t ), тело движется против оси ОХ.
Перемещение при равномерном движении – это величина, равная произведению скорости на время:
Проекция вектора перемещения на ось ОХ:
График перемещения (проекции перемещения)
График перемещения (проекции перемещения) представляет собой зависимость перемещения от времени:
График перемещения при равномерном движении – прямая, выходящая из начала координат.
График 1 лежит над осью ( t ), тело движется по направлению оси ОХ.
Графики 2 и 3 лежат под осью ( t ), тело движется против оси ОХ.
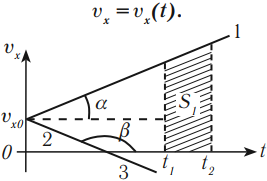
По графику зависимости скорости от времени можно определить перемещение, пройденное телом за время ( t ). Для этого необходимо определить площадь фигуры под графиком (заштрихованной фигуры).
Координата тела при равномерном движении рассчитывается по формуле:
График координаты представляет собой зависимость координаты от времени: ( x=x(t) ).
График координаты при равномерном движении – прямая.
График 1 направлен вверх, тело движется по направлению оси ОХ:
График 2 параллелен оси ОХ, тело покоится.
График 3 направлен вниз, тело движется против оси ОХ:
Прямолинейное равноускоренное движение
Прямолинейное равноускоренное движение – это движение по прямой, при котором тело движется с постоянным ускорением:
При движении с ускорением скорость может как увеличиваться, так и уменьшаться.
Скорость тела при равноускоренном движении рассчитывается по формуле:
При разгоне (в проекциях на ось ОХ):
При торможении (в проекциях на ось ОХ):
График ускорения (проекции ускорения) при равноускоренном движении представляет собой зависимость ускорения от времени:
График ускорения при равноускоренном движении – прямая, параллельная оси времени.
График 1 лежит над осью t, тело разгоняется, ( a_x ) > 0.
График 2 лежит под осью t, тело тормозит, ( a_x ) < 0.
График скорости (проекции скорости) представляет собой зависимость скорости от времени:
График скорости при равноускоренном движении – прямая.
График 1 направлен вверх, тело движется равноускоренно в положительном направлении оси ОХ, ( v_{0x} ) > 0, ( a_x ) > 0.
График 2 направлен вниз, тело движется равнозамедленно в положительном направлении оси ОХ, ( v_{0x} ) > 0, ( a_x ) < 0,
График 3 направлен вниз, тело движется равноускоренно против оси ОХ, ( v_{0x} ) < 0, ( a_x ) < 0. По графику зависимости скорости от времени можно определить перемещение, пройденное телом за промежуток времени ( t_2-t_1 ). Для этого необходимо определить площадь фигуры под графиком (заштрихованной фигуры).
Перемещение при равноускоренном движении рассчитывается по формулам:
Перемещение в ( n )-ую секунду при равноускоренном движении рассчитывается по формуле:
Координата тела при равноускоренном движении рассчитывается по формуле:
Свободное падение (ускорение свободного падения)
Свободное падение – это движение тела в безвоздушном пространстве под действием только силы тяжести.
Все тела при свободном падении независимо от массы падают с одинаковым ускорением, называемым ускорением свободного падения.
Ускорение свободного падения всегда направлено к центру Земли (вертикально вниз).
Обозначение – ( g ), единицы измерения – м/с2.
Важно! ( g ) = 9,8 м/с2, но при решении задач считается, что ( g ) = 10 м/с2.
Движение тела по вертикали
Тело падает вниз, вектор скорости направлен в одну сторону с вектором ускорения свободного падения:
Если тело падает вниз без начальной скорости, то ( v_0 ) = 0.
Время падения рассчитывается по формуле:
Тело брошено вверх:
Если брошенное вверх тело достигло максимальной высоты, то ( v ) = 0.
Время подъема рассчитывается по формуле:
Движение тела, брошенного горизонтально
Движение тела, брошенного горизонтально, можно представить как суперпозицию двух движений:
- равномерного движения по горизонтали со скоростью ( v_0=v_{0x} );
- равноускоренного движения по вертикали с ускорением свободного падения ( g ) и без начальной скорости ( v_{0y}=0 ).
Уравнение скорости:
Уравнение координаты:
Скорость тела в любой момент времени:
Дальность полета:
Угол между вектором скорости и осью ОХ:
Движение тела, брошенного под углом к горизонту (баллистическое движение)
Движение тела, брошенного под углом к горизонту, можно представить как суперпозицию двух движений:
- равномерного движения по горизонтали;
- равноускоренного движения по вертикали с ускорением свободного падения.
Уравнение скорости:
Уравнение координаты:
Скорость тела в любой момент времени:
Угол между вектором скорости и осью ОХ:
Время подъема на максимальную высоту:
Максимальная высота подъема:
Время полета:
Максимальная дальность полета:
Важно!
При движении вверх вертикальная составляющая скорости будет уменьшаться, т. е. тело вдоль вертикальной оси движется равнозамедленно.
При движении вниз вертикальная составляющая скорости будет увеличиваться, т. е. тело вдоль вертикальной оси движется равноускоренно.
Скорость ( v_0 ), с которой тело брошено с Земли, будет равна скорости, с которой оно упадет на Землю. Угол ( alpha ), под которым тело брошено, будет равен углу, под которым оно упадет.
При решении задач на движение тела, брошенного под углом к горизонту, важно помнить, что в точке максимального подъема проекция скорости на ось ОУ равна нулю:
Это облегчает решение задач:
Движение по окружности с постоянной по модулю скоростью
Движение по окружности с постоянной по модулю скоростью – простейший вид криволинейного движения.
Траектория движения – окружность. Вектор скорости направлен по касательной к окружности.
Модуль скорости тела с течением времени не изменяется, а ее направление при движении по окружности в каждой точке изменяется, поэтому движение по окружности – это движение с ускорением.
Ускорение, которое изменяет направление скорости, называется центростремительным.
Центростремительное ускорение направлено по радиусу окружности к ее центру.
Центростремительное ускорение – это ускорение, характеризующее быстроту изменения направления вектора линейной скорости.
Обозначение – ( a_{цс} ), единицы измерения – м/с2.
Движение тела по окружности с постоянной по модулю скоростью является периодическим движением, т. е. его координата повторяется через равные промежутки времени.
Период – это время, за которое тело совершает один полный оборот.
Обозначение – ( T ), единицы измерения – с.
где ( N ) – количество оборотов, ( t ) – время, за которое эти обороты совершены.
Частота вращения – это число оборотов за единицу времени.
Обозначение – ( nu ), единицы измерения – с–1 (Гц).
Период и частота – взаимно обратные величины:
Линейная скорость – это скорость, с которой тело движется по окружности.
Обозначение – ( v ), единицы измерения – м/с.
Линейная скорость направлена по касательной к окружности:
Угловая скорость – это физическая величина, равная отношению угла поворота к времени, за которое поворот произошел.
Обозначение – ( omega ), единицы измерения – рад/с .
Направление угловой скорости можно определить по правилу правого винта (буравчика).
Если вращательное движение винта совпадает с направлением движения тела по окружности, то поступательное движение винта совпадает с направлением угловой скорости.
Связь различных величин, характеризующих движение по окружности с постоянной по модулю скоростью:
Важно!
При равномерном движении тела по окружности точки, лежащие на радиусе, движутся с одинаковой угловой скоростью, т. к. радиус за одинаковое время поворачивается на одинаковый угол. А вот линейная скорость разных точек радиуса различна в зависимости от того, насколько близко или далеко от центра они располагаются:
Если рассматривать равномерное движение двух сцепленных тел, то в этом случае одинаковыми будут линейные скорости, а угловые скорости тел будут различны в зависимости от радиуса тела:
Когда колесо катится равномерно по дороге, двигаясь относительно нее с линейной скоростью ( v_1 ), и все точки обода колеса движутся относительно его центра с такой же линейной скоростью ( v_1 ), то относительно дороги мгновенная скорость разных точек колеса различна.
Мгновенная скорость нижней точки ( (m) ) равна нулю, мгновенная скорость в верхней точке ( (n) ) равна удвоенной скорости ( v_1 ), мгновенная скорость точки ( (p) ), лежащей на горизонтальном радиусе, рассчитывается по теореме Пифагора, а мгновенная скорость в любой другой точке ( (c) ) – по теореме косинусов.
Основные формулы по теме «Кинематика»
Кинематика
3 (59.53%) 127 votes
КИНЕМАТИКА.
Теория и формулы (кратко и сжато)
[button title=»Кинематика – раздел физики, изучающий способы математического описания движения без выяснения его причин.» color=»blue» size=»2″ full_width=»1″]
Механическое движение – изменение положения тела относительно других тел с течением времени. Способы описания: словесный, табличный, графический, формулами.
Материальная точка – тело, собственными размерами которого в данных условиях можно пренебречь.
Траектория – линия, которую описывает материальная точка при своём движении в пространстве. По виду траектории все движения делятся на прямолинейные и криволинейные.
Система отсчёта – часы и система координат, связанные с условно выбираемым телом отсчёта (наблюдателем).
Относительность движения – различие скорости, направления и траектории движения в различных системах отсчёта.
Перемещение – вектор, проведённый из начального положения материальной точки в её конечное положение.
Типы движений
1. Равномерное движение
1.1. Равномерное прямолинейное движение
Равномерное движение – движение тела, при котором за равные интервалы времени оно преодолевает равные части пути.
Скорость равномерного движения равна отношению пройденного пути к интервалу времени, за который этот путь пройден.
Скорость равномерного прямолинейного движения равна отношению перемещения к интервалу времени его совершения.
Уравнение равно-прямолинейного движения x = xo + υoxt показывает, что координата линейно зависит от времени.
Мгновенная скорость равна отношению перемещения к бесконечно малому интервалу времени, за который оно произошло.
1.2 Равномерное движение по окружности (равномерное вращение)
Равномерное движение по окружности — это движение, при котором материальная точка за равные промежутки времени проходит равные по длине дуги окружности.
Равномерное движение тела по окружности — это частный и наиболее простой случай криволинейного движения. Хотя при таком движении модуль скорости остается постоянным, это движение с ускорением, которое является следствием изменения направления вектора скорости.
2. Движение с постоянным ускорением
Равноускоренное движение – движение, при котором мгновенная скорость за любые равные интервалы времени меняется одинаково.
Мгновенное ускорение равно отношению изменения мгновенной скорости тела к бесконечно малому интервалу времени, за который это изменение произошло.
Ускорение равноускоренного движения равно отношению изменения мгновенной скорости тела к интервалу времени, за который это изменение произошло.
Уравнение равноускоренного движения y = yo + υoyt + ½ayt² показывает, что координата квадратично зависит от времени. Уравнение υy = υoy + ayt показывает, что скорость линейно зависит от времени.
Центростремительное ускорение – ускорение, всегда направленное к центру окружности при равномерном движении по ней материальной точки. Модуль центростремительного ускорения равен отношению квадрата модуля скорости равномерного движения по окружности к её радиусу.
3. Гармоническое движение
Виды движений
Прямолинейное движение
Криволинейное движение
Частные случаи равноускоренного движения под действием силы тяжести
Частные случаи решения задач
Дополнительные материалы по кинематике
Кинематика. Таблица кратко.
Это конспект по физике «Кинематика. Теория и формулы для ЕГЭ» + шпаргалка.
Еще конспекты для 10-11 классов:
Физика. Кинематика
Равноускоренное движение по прямой и под углом к горизонту
Как определить положение тела в пространстве? И для чего нужны координаты?
Школьный курс физики начинается с раздела кинематика. Именно она закладывает фундамент для дальнейшего изучения, все остальные разделы так или иначе будут соприкасаться с этим разделом.
Что же такое кинематика? Это раздел физики, который изучает движение некоторого тела в пространстве. При это мы НЕ рассматриваем, что вызывает это движение, что является его причиной. У нас просто есть какое-то двигающееся тело и мы пытаемся его изучить. А на вопрос почему происходит движение, кинематика нам ответа не дает, это мы будем изучать в следующих разделах физики.
Начнем с простого вопроса – что такое «тело»? Это может быть все, что угодно – машина, самолет, мячик, капля воды, планета и т.д., то есть любой движущийся объект. Любое тело в школьной физике мы будем представлять в виде материальной точки.
Определение. Материальная точка – это тело, размерами которого мы можем пренебречь в данной задаче.
Мы просто договариваемся, что любой объект, будь то ракета или песчинка с пляжа, мы представляем в виде точки. Это необходимо для того, чтобы размеры тела не оказывали влияния на наши задачи. Так, например, автобус, двигающийся из Москвы в Санкт-Петербург, можно считать материальной точкой. Его размеры очень малы по сравнению с расстоянием между этими городами. Но движение пассажиров при выходе из автобуса уже нельзя считать материальной точкой, потому что пассажиры относительно автобуса не такие уж и маленькие. Такое школьное допущение (а в физике допущений будет много) упростит нам жизнь. При более глубоком изучении физики вы будете учитывать все эти допущения, в том числе и размеры тела, но в школе вам это, как правило, не нужно.
Задача кинематики – предсказать или описать при помощи законов физики, как этот объект будет двигаться в будущем, например, через час, если ничего не изменится.
Зачем нам это? Очень просто: если мы знаем, по каким законам двигается машина, мы легко сможем предсказать будущее и узнать, где она будет через какое-то время и с какой скоростью будет двигаться. Естественно, мы можем точно так же предсказывать движение брошенного камня и любых других объектов. Например, зная начальную скорость камня и как вы его кинули, можно предсказать, как далеко или высоко он улетит, или через сколько времени и с какой скоростью он упадет на землю.
Траектория, путь и перемещение. Что это такое и чем они отличаются?
Перед тем, как писать формулы, познакомимся еще с несколькими определениями, которые нам понадобятся в дальнейшем. Представим, что человек идет из пункта (А) в пункт (В) (см Рис.1.).
Рис.1. Траектория (зеленая линия). Путь(длина зеленой линии). Перемещение(фиолетовая стрелка)
- Траектория – линия, вдоль которой движется тело. На рис.1 показана зеленой линией.
- Путь – длина траектории. Обычно обозначается буквой (S).
- Перемещение – вектор, соединяющий начальную и конечную точки (фиолетовая линия). О том, что такое вектор, мы поговорим чуть позже. А на нашем рисунке перемещение — это длина отрезка (АВ), кроме длины перемещение еще показывает куда движется тело из начальной точки (А) в конечную (В).
Разберемся подробнее на примере. Если вы ходите по комнате с шагомером туда-сюда и вернетесь в итоге в исходную точку, то ваше перемещение будет равно 0, а путь будет расстоянием, которое вы находили, его покажет шагомер.
Что такое координаты и зачем они нужны?
Все это звучит здорово, но как нам определить положение тела в пространстве? Для этого люди придумали очень удобную штуку, которая называется координатная плоскость. С этим понятием вы должны были сталкиваться в курсе алгебры – построение графиков в осях (х) и (y). Помните, у вас были функции типа (y=x^2-3) и нужно было построить график этой функции по точкам? Вы брали какие-то значения (x) подставляли в (y=x^2-3) и получали значение (y). Потом отмечали получившуюся точку на координатной плоскости. Именно эта плоскость нас и будет интересовать.
Координаты используются людьми повсюду. Например, вся поверхность Земли расчерчена линиями, которые называются долгота и широта. Этих линий очень много, но указав пересечение некоторой долготы (37) с какой-то широтой (55), я укажу вполне конкретную точку на земной поверхности – это примерное расположение города Москва (37;55). Именно такой способ используется для определения положения любого объекта на Земле в географических картах и навигаторах – город, озеро, здание, машина, человек и т.д.
Для начала давайте рассмотрим одномерное движение – это такое движение, при котором машина может двигаться только вперед по дороге или назад, никуда свернуть она не может. (Рис.2.). Наложим на нашу дорогу ось Х, направленную вправо, как на рисунке. Теперь вся наша дорога размечена координатами. И мы можем определить положение машины, просто сказав ее координату. Начало координат мы можем выбрать как угодно, пусть оно будет в точке О. Тогда на рисунке наша машина находится в начальной координате (x_0=3). Из этой точки она может поехать влево (координата будет уменьшаться) или вправо (координата будет увеличиваться).
Расстояние можно измерять в различных единицах измерения: километры, метры, сантиметры, миллиметры и т.д. Пусть все координаты у нас измеряются в метрах, тогда можно сказать, что на рисунке машина находится на расстоянии 3 метра от точки О.
Итак, мы научились определять положение тела в пространстве при помощи координат.
Что такое скорость?
На интуитивном уровне это понятно. Но давайте попробуем вникнуть поглубже. В чем всегда измеряется скорость? В автомобиле это обычно километры в час (км/ч), измеряется при помощи спидометра. То есть спидометр машины показывает, сколько километров проедет машина за один час, если не будет менять скорость. Точно так же скорость можно измерять в метрах в секунду (м/с), километрах в секунду (км/с) и т.д. Значит, если я умножу скорость на количество часов, которые едет машина с этой скоростью, то получу расстояние, пройденное машиной за это время. Можно записать в виде известной формулы движения с постоянной скоростью:
$$S=V*t;$$
Итак, при движении с постоянной скоростью (V), можно посчитать расстояние (S), которое проходит тело за время (t).
Теперь давайте предположим, что машина двигается с постоянной скоростью 1 (м/с) влево из начальной точки с координатой (x_0=3(м)). Это означает, что машина за 1 секунду сдвинется на (S=V*t=1*1=1(м)) метр влево, то есть окажется в точке с координатой (2) (м). Через 2 секунды она пройдет расстояние (S=V*t=1*2=2(м)) и попадет в координату (1)(м), а через 6 секунд на (S=V*t=1*6=6(м)) и окажется в координате (-3)(м).
Скорость кроме величины еще имеет направление – в нашем случае это означает, что если машина едет вправо (туда же, куда направлена ось (х)), то скорость будет положительна, а если влево (в противоположную сторону направлению оси (х)), то скорость будет отрицательна.
Все, что имеет величину и направление, называется вектором. То есть скорость ни что иное, как вектор. Вектор – это ключевое понятие физики. Мы часто будем сталкиваться с величинами, у которых кроме числа есть еще и направление – ускорение, сила.
Немного отвлечемся, и обсудим, что такое вектор.
Вектор – это математический объект, у которого есть величина и направление.
В геометрии вектор – это направленный отрезок. Он имеет величину, равную длине отрезка, и направление.
Например, в случае двигающегося автомобиля принято показывать его направление движения стрелкой, а длина этой стрелки обычно указывает на величину скорости по модулю. Модуль, напомню, все отрицательные величины превращает в положительные. Чем больше длина стрелки, тем больше скорость машины. (См.Рис.3.)
В случае 1 стрелка у красной машины указывает нам на то, что автомобиль двигается вправо. Стрелка подписана сверху (vec{|V_1|}=90(км/ч)). Эта запись означает, что величина скорости красной машины по модулю равна (90(км/ч)).
Если я напишу вектор скорости красной машины без модуля, то он будет выглядеть вот так:
$$ vec{V_1}=+90(км/ч);$$
Знак плюс указывает на то, что скорость машины сонаправлена с выбранной нами осью (х).
В случае 2 синяя машина двигается влево. Ее вектор скорости запишется так:
$$vec{V_2}=-45(км/ч);$$
Знак минус указывает на то, что машина едет в противоположную сторону оси (х).
Как видите, по одной только записи вектора можно сразу сказать, куда едет машина и с какой скоростью – это очень удобно. Знак указывает на направление, а число – на величину.
Обратите внимание, что у красной машины вектор скорости длиннее, чем у синей, это означает, что красная едет быстрее. Не глядя на числа, мы можем с уверенностью сказать это, посмотрев на рисунок. Так принято обозначать. Это тоже удобно.
Равномерное движение
Любое движение с постоянной скоростью называется равномерным движением. Все, что мы рассматривали выше – это примеры равномерного движения.
Теперь мы готовы составить первые уравнения, описывающие равномерное движение. В кинематике нас будет интересовать уравнение, которое описывает положение тела в пространстве в зависимости от времени (изменение координаты тела со временем). Оно выглядит так:
$$ x(t)=x_0+V*t;$$
(x_0) – это начальная координата тела, где оно находилось в момент времени (t=0). Например, на рис.2. начальная координата автомобиля (x_0=3(м)).
(V) – это скорость, с которой двигается тело.
(t) – это время, которое прошло с момента начала движения.
(x(t)=x_{конечная}) – это конечная координата, то есть координата, где окажется тело через время (t). Я написал (x(t)), чтобы показать, что координата тела зависит от времени, ведь в разные моменты времени двигающееся тело находится в разных точках.
Разберем на примере, как работает это уравнение.
Пример 1
Автомобиль начал движение из координаты (x_0=-3(м)) со скоростью (V=5(м/с)) вправо. Где будет автомобиль через 3 секунды? Через какое время автомобиль окажется в точке с координатой (x=12(м))?
Решение: Первым делом всегда рисуем рисунок, он поможет правильно расставить знаки в уравнениях и лучше представить задачу. Чтобы ответить на поставленные вопросы, воспользуемся уравнением для координаты при равномерном движении (x(t)=x_0+V*t.)
Подставим известные величины:
$$x(t)=-3+5*t;$$
Обратите внимание, что скорость входит в уравнение со знаком (+), так как автомобиль едет по условию вправо, а это сонаправленно с осью (х). Если бы он ехал влево, то уравнение выглядело бы так: $$x(t)=-3-5t.$$
Получили уравнение, которое полностью задает движение автомобиля.
Действительно, если в это уравнение подставить некоторое время вместо (t), то можно узнать координату, где находится автомобиль в различные моменты времени.
Например, если (t=0), момент начала движения:
$$x(t=0)=-3+5*0=-3(м);$$
Логично, что в начале автомобиль находился в координате (x_0=-3). Чтобы узнать, где он будет через секунду, подставим (t=1(c)):
$$ x(t=1)=-3+5*1=-3+5=2(м);$$
Отрицательное время подставлять нет смысла, так как время не может быть отрицательным. А координата и скорость могут.
Теперь вспоминаем про задачу. Нам нужно узнать, где будет машина через 3 секунды. Просто подставляем в уравнение (t=3(с)):
$$ x(t=3)=-3+5*3=-3+15=12(м);$$
А как понять, через сколько по времени машина окажется в координате (x(t)=12(м))? Подставим:
$$12=-3+5*t;$$
Осталось решить простое линейное уравнение:
$$t=3(c).$$
Ответ: ( x(t=3)=12(м);) и (t=3(c)).
Равноускоренное движение
Если скорость не меняется, то все понятно. А что делать если скорость непостоянна?
В школе рассматривается случай, когда скорость у тела изменяется (увеличивается или уменьшается) равномерно, то есть за каждую следующую секунду скорость увеличивается/уменьшается на одну и ту же величину. Такое движение называют равноускоренным или равнозамедленным соответственно.
Пример такого движения. Представьте, что лыжник скатывается с горки из состояния покоя, при этом его скорость постоянно увеличивается, например, на 2 м/с ежесекундно. То есть:
$$V(t=0)=0(м/с);$$
$$V(t=1)=V(t=0)+2=0+2=2(м/с);$$
$$V(t=2)=V(t=1)+2=2+2=4(м/с);$$
$$V(t=3)=V(t=2)+2=4+2=6(м/с);$$
$$V(t=4)=V(t=3)+2=6+2=8(м/с);$$
Величина, на которую ежесекундно увеличивается/уменьшается скорость, называется ускорением и обозначается буквой (a).
Ускорение измеряется в (frac{м}{с^2}).
Разумеется, в жизни бывают случаи, когда скорость изменяется неравномерно. Но в школьном курсе такие задачи крайне редкие, и мы их рассматривать не будем.
Как выглядит уравнение, описывающие равноускоренное движение?
$$x(t)=x_0+V_0*t+frac{a*t^2}{2};$$
По сравнению с равномерным движением, у нас добавилось еще одно слагаемое (frac{a*t^2}{2}), которое отвечает за ускоренность/замедленность движения.
Так как скорость теперь переменная величина, для нее тоже можно записать уравнение:
$$V(t)=V_0+at;$$
- (x_0) – начальная координата тела;
- (V_0) – начальная скорость тела; скорость, с которой тело начало движение;
- (x(t)) – конечная координата;
- (V(t)) – конечная скорость;
- (a) – ускорение;
- (t) – время.
Уравнения для координаты и для скорости при равноускоренном движении являются основными уравнениями всей школьной кинематики. Если в них хорошо разобраться, то больше никаких формул учить не нужно. Все выводится из них. Я рекомендую пользоваться только этими двумя уравнениями и не забивать себе голову ничем посторонним.
Внимание! Вообще говоря, ускорение — это векторная величина, так же, как и скорость. Мы это обсуждали в начале темы. И помним, что если вектор сонаправлен с выбранным нами направлением оси координат, то ускорение положительно, а если нет, то отрицательно.
Если же вектора скорости и ускорения направлены в одну сторону, то тело ускоряется. А если в разные, то тормозит.
Посмотрите на рисунки:
В случае а) скорость сонаправлена с осью х, значит она будет положительна. Ускорение тоже сонаправлено с осью х, значит оно положительно. А раз вектора скорости и ускорения направлены в одну сторону, то это значит, что тело ускоряется.
Случай б): скорость положительна, ускорение отрицательно. Раз вектор скорости и вектор ускорения направлены в разные стороны, значит тело замедляется.
Случай в): скорость и ускорение отрицательны, но сонаправлены – тело ускоряется.
Случай г): скорость отрицательна, ускорение положительно – тело замедляется.
Со знаками разобрались, теперь давайте разберем пример.
Пример 2
Лыжник скатывается с горки с нулевой начальной скоростью ((V_0=0(м/с))). Через 5 секунд после начала движения его скорость была (V(t=5(c))=15(м/с)). Определите с каким ускорением движется лыжник и какое расстояние он проедет за 10 секунд?
Решение:
Рисуем рисунок, чтобы представить, что происходит, и правильно расставить знаки. Ось х выбираем, как угодно. Я направил вниз.
Как мы уже обсуждали выше, у нас есть всего два уравнения – для координаты и для скорости, которые полностью описывают любое движение:
$$x(t)=x_0+V_0*t+frac{a*t^2}{2};$$
$$V(t)=V_0+at;$$
Так как нам даны начальная и конечная скорости, то разумно воспользоваться уравнением для скорости. Не забываем про знаки скорости и ускорения – оба вектора сонаправлены с выбранной мною осью х, а значит, и скорость, и ускорение будут в уравнениях положительны.
$$V(t)=V_0+at;$$
$$15=0+a*5;$$
$$a=frac{15}{5}=3frac{м}{с^2};$$
Зная ускорение, с которым движется лыжник, мы можем найти, где будет лыжник через 10 секунд, используя уравнение для координаты:
$$x(t=10)=x_0+V_0*t+frac{a*t^2}{2}=0+0*10+frac{3*10^2}{2}=150(м);$$
Таким образом, мы получили, что лыжник за 10 секунд успеет проехать (150) метров, если будет двигаться с постоянным ускорением (a=3(frac{м}{с^2})).
Работа с графиками в кинематике
В ЕГЭ по физике кинематика часто встречается в самом первом задании и, как правило, там задача с графиками. Графики помогают нам визуально описывать поведение одной некоторой величины в зависимости от другой. В школе вы должны были часто строить графики зависимостей (y) от (x). В кинематике же обычно строят графики зависимости координаты или скорости от времени. Давайте построим пару таких графиков и обсудим, как их читать.
Главное, нужно понять, что перед вами не траектория и не картинка, на которой изображено, как движется тело. Это зависимость одной физической величины от другой. На наших рисунках изображены графики зависимостей координаты и скорости от времени некоторого объекта (пусть это будет велосипедист) при различных видах движения. Например, на графике ((в)) НЕ показано движение некоторого объекта в гору, а просто координата по мере движения увеличивается.
- На графике ((а)) показана зависимость координаты велосипедиста от времени. В моменты времени (t_1) и (t_2) велосипедист находится в одной и той же координате, а значит, он стоит на месте. То есть здесь велосипедист находится в покое.
- На графике ((б)) зависимость скорости от времени. Визуально он очень похож на график ((а)), но смысл совершенно другой. Так как тут показана скорость, мы видим, что в моменты времени (t_1) и (t_2) у велосипедиста была одна и та же скорость (V_0). А раз в различные моменты времени скорость одинаковая, то это равномерное движение или движение с постоянной скоростью. Более того, еще можно сделать вывод, что велосипедист движется вправо (туда, куда направлена ось (х)), потому что скорость положительна.
- В ((в)) линейная зависимость координаты тела от времени (то есть по прямой). Замечаем, что координата с течением времени увеличивается, а это значит, что объект движется вправо. Если бы координата уменьшалась, то движение было бы влево (в противоположную сторону оси (х)). Отметим на графике несколько точек через одинаковый интервал времени. В момент времени (t_1) велосипедист был в координате (x_1), а в момент (t_2) в (x_2). За время (Delta t=t_2-t_1) он прошел расстояние (Delta x=x_2-x_1). И за каждый следующий промежуток времени (Delta t) он будет проходит одинаковое расстояние (Delta x). Это означает, что он двигается с одной и той же скоростью – равномерное движение.
- График под пунктом ((г)) показывает нам линейный рост скорости от времени. Если посмотреть, какая скорость будет у велосипедиста через одинаковые промежутки времени, то мы увидим, что она все время растет на одинаковую величину (Delta V). Если скорость растет, то значит движение ускоренное, а если растет еще и линейно, то равноускоренное. Скорость здесь положительна, значит велосипедист едет вправо (туда, куда направлена ось (х)).
- График ((д)) – это зависимость координаты от времени. Видно, что каждый следующий промежуток времени координата успевает измениться на бОльшую величину – за время (t_4-t_3) он проходит бОльшее расстояние, чем за (t_2-t_1). Значит велосипедист ускоряется. Так как координата по ходу движения уменьшается, значит он двигается влево (противоположную сторону оси (х)).
- И на последнем графике ((е)) показана зависимость скорости от времени. Видим, что скорость с течением времени уменьшается, и каждый следующий промежуток времени скорость меняется быстрее, чем на предыдущем. Так как скорость положительна, велосипедист едет вправо (туда же, куда направлена ось х). Так как скорость уменьшается неравномерно, значит на рисунке показано замедленное движение с переменным ускорением.
Движение в поле тяжести Земли
Теперь рассмотрим движение объектов в поле тяжести нашей планеты Земли. Любое тело, свободно падающее (отпущенное с некоторой высоты без начальной скорости) на Земле, будет двигаться с ускорением свободного падения (g=9.8(м/с^2)). Важно помнить, что (g) всегда направлено к центру Земли.
Внимательно посмотрите на рисунок 8: на нем изображено движение камня, брошенного вертикально вверх с некоторой начальной скоростью (V_0). Сначала он будет двигаться равнозамедленно, пока не достигнет наивысшей точки подъема (H), там остановится (скорость (V=0)), и начнет падать обратно, постепенно набирая скорость, пока не упадет обратно к вам в руку со скоростью (V_к). Для того, чтобы лучше разобраться, представьте, что вы подбросили вверх камень – он будет двигаться именно так, как мы обсудили. Таким образом, задачи на движение в поле тяжести Земли ничем не отличаются от задач равноускоренного / равнозамедленного движения по дороге, только на этот раз нам всегда известно ускорение — (g=9.8 (м/с^2)).
Давайте составим уравнения, описывающие это движение. Как всегда, их будет два – для скорости и для координаты:
$$y(t)=y_0+V_0*t-frac{g*t^2}{2};$$
$$V(t)=V_0-gt;$$
Что изменилось?
- Во-первых, координата теперь не (x), а (y) – тело двигается вдоль вертикальной оси, а ее принято обозначать за (Y).
- Вместо ускорения (a) мы теперь пишем (g) – ускорение свободного падения, оно нам известно.
Разбираемся со знаками: начальная скорость (V_0) направлена вверх (сонаправленно с осью (Y)). Ускорение во время всего движения направленно вниз к центру Земли (в противоположную сторону (Y)). Получаем, что в системе координат, выбранной на рисунке, начальная скорость будет с плюсом, а ускорение с минусом. Систему координат вы можете выбрать и другую, но тогда знаки будут меняться в соответствии с правилами расстановки знаков.
Обратите внимание!Не нужно писать отдельно уравнения для движения вверх и вниз. Уравнения сами учитывают, что тело после подъема полетит вниз.
Решим несколько задач и обсудим еще пару важных нюансов.
Пример 3
Пусть камень брошен вертикально вверх с начальной скоростью (V_0=10(м/с)). Найдите максимальную высоту подъема и время полета.
Решение
Для решения воспользуемся старым рисунком (рис.8).
Любая задача начинается с написания уравнений в общем виде:
$$y(t)=y_0+V_0*t-frac{g*t^2}{2};$$
$$V(t)=V_0-gt;$$
Выберем за начальное положение тела внизу, на Земле. А за конечное – наивысшую точку. Координата камня в наивысшей точке подъема будет — (y(t)=H), а скорость будет равна (V(t)=0 ) (смотрите на рисунок 8).
Важно! Скорость в наивысшей точке подъема будет равна 0 (камень останавливается), мы часто будем это использовать при решении подобных задач.
Начальная координата (y_0=0).
Начальная скорость (V_0=10(м/c)) из условия.
Получим уравнения:
$$H=10*t-frac{9.8*t^2}{2};$$
$$0=10-9.8*t;$$
Из уравнения для скорости можно найти время полета от Земли до наивысшей точки:
$$t=10/9.8=1.02 /,(с)$$
Подставим в первое уравнение:
$$H=10*1.02-frac{9.8*1.02^2}{2}=5.1 (м);$$
Обращаю ваше внимание, что (t) – время полета от Земли до наивысшей точки. А по условию задачи нам нужно найти время всего полета. Для этого нужно время подъема умножить на два.
Важно! Время подъема всегда равно времени падения.
$$T=2*t=1.02*2=2.04 c.$$
Ответ: (T=2.04 /,(с).)
Пример 4
Рассмотрим падение камня с некоторой высоты (H) вертикально вниз с начальной скоростью (V_0). Как тогда будут выглядеть уравнения, описывающие движение камня? (см. Рис.9.)
За конечное положение выберем Землю (y(t)=0), за начальное — высоту (y_0=H).
$$0=H-V_0*t-frac{g*t^2}{2};$$
$$-V_к=-V_0-gt;$$
Знаки расставлены с учетом направления осей координат.
Многие часто полагают, что при броске камня вниз, его конечная скорость у земли будет равна 0, ведь камень останавливается. Но это не так. К сожалению, уравнения кинематики не учитывают воздействие земли на камень, поэтому, говоря «конечная скорость», мы подразумеваем скорость за мгновение до удара о землю, и она, очевидно, не будет равна нулю.
Основные моменты
- В поле тяжести Земли вертикально брошенное тело всегда движется с ускорением свободного падения (g=9.8(м/с^2)).
- Если тело бросили с земли и оно упало обратно на землю, то время падения равно времени подъема.
- Скорость в верхней точке подъема всегда равно нулю.
Рассмотрим, как выглядят графики зависимостей координаты и скорости от времени при бросании камня.
Бросок тела вертикально вверх
Чтобы хорошо разобраться, рекомендую представить полет камня.
Скорость.При движении вверх скорость камня линейно уменьшается, он тормозит с ускорением (g), пока не остановится в верхней точке. После этого камень сразу начинает падать вниз, скорость увеличивается также с ускорением (g). Если же его бросили с земли, и он упал обратно на землю, то начальная скорость броска будет равна конечной скорости за мгновение до удара о землю. (Рис. 10 (б))
Координата. На рисунке 10 (а) изображено, как меняется координата (y(t)) в зависимости от времени полета. Обратите внимание на форму графика – это парабола. Не попадайтесь в визуальную ловушку, перед вами НЕ линия вдоль которой движется камень, в просто зависимость координаты от времени. Видно, что в начале полета тело успевает пройти за единицу времени большее расстояние, чем ближе к середине полета – координата растет сначала быстро, а потом все медленнее и медленнее, и останавливается в наивысшей точке подъема. Это связано с тем, что скорость в начале полета больше. Затем тело начинает падать, постепенно набирая скорость, и координата начинает изменяться все быстрее и быстрее, пока тело не упадет обратно на землю. (Рис. 10 (а))
Аналогичные рассуждения для броска камня вниз с нулевой начальной скоростью. (См. Рис.11)
Рис.10. Бросок камня вертикально вверх
Рис.11. Бросок тела вертикально вниз с нулевой начальной скоростью
Движение тела под углом к горизонту
До этого мы рассматривали одномерные задачи, где движение происходило вдоль одной прямой. В школьном курсе физики подавляющее большинство задач двумерны.
Рассмотрим классическую двумерную задачу кинематики – бросок камня под углом к горизонту в поле тяжести Земли. Представьте, что вы играете в игру, кто дальше кинет камень. Траектория камня будет похожа на параболу, зеленая линия. (См. Рис. 12) Именно такое движение мы и постараемся описать при помощи математики. Для этого нам понадобится двумерная система координат (XoY). Ось (X) будет отвечать за дальность полета, ось (Y) – за высоту. Точка (O) – точка начала движения. (V_0) – начальная скорость, скорость, которую мы придали камню в момент броска. Точка (А) – точка наивысшего подъема.
Рис.12. Движение под углом к горизонту
Для того, чтобы описать такое сложное двумерное движение, разобьем его на два – отдельно горизонтальное, и отдельно вертикальное движения. Мы можем представить, что наш камень в некоторый момент времени летит с вертикальной скоростью (V_y) и ускорением (a_y) вдоль оси (Y), и с горизонтальными скоростью (V_x) и ускорением (a_x) вдоль оси (X). Вместе эти два движения, если их наложить друг на друга, дают сложное двумерное движение по зеленой параболе с скоростью (V) и ускорением (a).
Скорость тела при двумерном движении в любой момент времени направлена по касательной к траектории. На рис.12. она показана красными стрелками в точках (О, А) и (В).
Рассуждая таким образом, мы можем записать уравнения для координаты и скорости по вертикали и потом по горизонтали – всего 4 уравнения, каждое из которых отвечает за свою ось.
$$y(t)=y_0+V_{0y}*t+frac{a_{y}*t^2}{2};$$
$$V_{y}(t)=V_{0y}+a_{y}*t;$$
$$x(t)=x_0+V_{0x}*t+frac{a_{x}*t^2}{2};$$
$$V_{x}(t)=V_{0x}+a_{x}*t;$$
Возникает справедливый вопрос, откуда нам взять все горизонтальные и вертикальные скорости. Есть начальная скорость (V_0), одновременно направленная по обеим осям. Нам нужно как-то рассмотреть эту скорость, как совокупность двух отдельных скоростей – горизонтальной и вертикальной. Вот для этого нам понадобится некоторый математический прием – проекции.
Проекция вектора
Пусть у нас есть некоторый вектор (vec{a}). Напоминаю, что вектор – это направленный отрезок. У него есть начало – т.А, и конец – т.В. (см.Рис.13). Опустим перпендикуляры из точек А и В на ось (Х). Получим соответственно точки (A_x) и (B_x), который называются проекциями точек (A) и (В) на ось (Х). Получившийся отрезок ({A}_{x} {B}_{x}) будет называться проекцией вектора (vec{a}) на ось (Х). Для краткости записи обозначим ({A}_{x} {B}_{x}=a_x) Аналогичным образом получим проекцию (vec{a}) на ось (Y): ({A}_{y} {B}_{y}=a_y).
Посчитаем чему равны (a_x) и (a_y), если нам известен угол и длина вектора (vec{a}). Достроим наш вектор до прямоугольного треугольника с гипотенузой (vec{a}) и катетами (a_x) и (a_y) (На рис.13. показаны зеленым).
Напоминаю, что синус угла в прямоугольном треугольнике равен отношению противолежащего катета к гипотенузе, а косинус – прилежащего катета к гипотенузе:
$$ sin{alpha}=frac{a_y}{a};$$
$$cos{alpha}=frac{a_x}{a};$$
Из этих формул можно выразить (a_x) и (a_y):
$$a_x=a*sin{alpha};$$
$$a_y=a*cos{alpha}.$$
Таким образом, зная длину вектора и угол, мы можем легко найти его проекции. Запомните это.
Вернемся к нашей задаче. Мы остановились на том, что нужно найти горизонтальную и вертикальную составляющие начальной скорости и ускорения. Оказывается, проекции начальной скорости (V_0) на оси (X) и (Y) и будут искомыми начальными скоростями по горизонтали и вертикали. (См. Рис. 12). Оранжевым показаны проекции (V_{0x})- начальная горизонтальная скорость, и (V_{0y})-вертикальная. Заметим, что (BB_x=V_{0y}) и (AB_x=V_{0x}). (См. Рис.14.). Из треугольника (ABB_x) получаем:
Рис.14. Проекция скорости на оси х и y
$$sin{alpha}=frac{BB_x}{AB}=frac{V_{0y}}{V_0};$$
$$cos{alpha}=frac{AB_x}{AB}=frac{V_{0x}}{V_0}.$$
Отсюда
$$V_{0y}=V_0*cos{alpha};$$
$$V_{0x}=V_0*sin{alpha}.$$
Зная угол к горизонту (alpha), под которым бросили тело, и его начальную скорость, мы можем по формулам выше найти начальные скорости для горизонтального и вертикального движений.
Разберемся теперь с каким ускорением движется тело по вертикали и горизонтали. Если вы бросаете камень на Земле, то у него будет вертикальное постоянное ускорение, направленное к центру Земли – ускорение свободного падения (g=9,8(м/с^2)). (См.Рис.12).
По горизонтали ускорение, оказывается, будет равно нулю. Другими словами, по горизонтали камень будет лететь равномерно, с постоянной скоростью. Это связано с тем, что в горизонтальном направлении на тело во время полета не действует никаких сил, то есть ничто не может изменить его скорость. А по вертикали действует сила притяжения Земли, которая вызывает ускорение свободного падения.
Можно просто запомнить, что по вертикали ускорение всегда (g), а по горизонтали ускорение 0.
Используем все наши рассуждения для записи системы уравнений, описывающих движение под углом к горизонту:
$$y(t)=y_0+V_{0y}*t+frac{a_{y}*t^2}{2};$$
$$V_{y}(t)=V_{0y}+a_{y}*t;$$
$$x(t)=x_0+V_{0x}*t+frac{a_{x}*t^2}{2};$$
$$V_{x}(t)=V_{0x}+a_{x}*t;$$
Подставим (V_{0x}=V_0*sin{alpha},, V_{0y}=V_0*cos{alpha},, a_x=0,,a_y=g):
$$y(t)=y_0+V_0*sin{alpha}*t-frac{g*t^2}{2};$$
$$V_{y}(t)= V_0*sin{alpha}-g*t;$$
$$x(t)=x_0+ V_0*cos{alpha}*t;$$
$$V_{x}(t)= V_0*cos{alpha}.$$
Знания и понимания этих четырех уравнений достаточно, чтобы решить любую школьную задачу по кинематике. Часто в школах дают большое количество формул, связывающих расстояние, скорость и ускорение и т.п. Если вы разобрались, как были получены уравнения выше, то в этих формулах нет необходимости. Они легко выводятся.
Основные моменты движения тела, брошенного под углом к горизонту:
- Сложное двумерное движение разбиваем на два: горизонтальное и вертикальное.
- Ускорение по вертикали равно ускорению свободного падения и всегда направлено вниз, к центру Земли. Ускорение по горизонтали в отсутствии сопротивления воздуха равно 0. По горизонтали движение равномерное.
- Скорость полета тела всегда направлена по касательной к траектории полета. Скорость по горизонтали и вертикали можно найти соответственно из формул:
$$V_x=V*cos{alpha};$$
$$V_y=V*sin{alpha};$$ - Дальностью полета называют расстояние по горизонтали между точкой броска и точкой падения камня на землю. На рис.12. дальность показана буквой (S).
- Время подъема равно времени падения. При условии, что тело бросили с Земли и оно упало обратно на Землю.
- Скорость по вертикали в наивысшей точке подъема равна 0. Этот факт часто используют для нахождения времени подъема до наивысшей точки из уравнения для скорости по оси (y):
$$0=V_{0y}-gt.$$
Разберем несколько задач на движение под углом к горизонту.
Пример 5
Камень бросили под углом (alpha=30^о) к горизонту с начальной скоростью (V_0=20(м/с)). Найти дальность его полета. И максимальную высоту подъема.
Бросок камня под углом к горизонту
Решение
Первым делом выпишем все уравнения в общем виде:
$$y(t)=y_0+V_0*sin{alpha}*t-frac{g*t^2}{2};$$
$$V_{y}(t)= V_0*sin{alpha}-g*t;$$
$$x(t)=x_0+ V_0*cos{alpha}*t;$$
$$V_{x}(t)= V_0*cos{alpha}.$$
Начальная скорость направлена вверх и вправо, поэтому в уравнениях она будет со знаком плюс. Ускорение свободного падения направлено вниз – ставим минус.
Выбираем начальное и конечное положение тела, для которого будем записывать уравнение. Логично, что начальная точка – это момент броска с координатами (0;0), а за конечную выберем т.А ((S/2;H)) – наивысшую точку подъема, так как мы знаем, что скорость там по оси (y): (V_y=0).
Подставим координаты и известные величины в систему уравнений:
$$H=20*sin{30}*t-frac{9.8*t^2}{2};$$
$$0= 20*sin{30}-9.8*t;$$
$$S= 20*cos{30}*t;$$
$$V_{x}= 20*cos{30}.$$
Из уравнения для скорости по (y) (2-е уравнение) можно найти (t) – время подъема тела до наивысшей точки.
$$t=frac{20*sin{30}}{9.8}=1.02 (c);$$
Чтобы найти максимальную высоту подъема, подставим найденное время в первое уравнение для координаты (y). Камень будет в наивысшей точке через половину времени полета, потому что время подъема равно времени падения:
$$H=20*sin{30}*1.02-frac{9.8*1.02^2}{2}=5.1(м);$$
Полное время полета:
$$T=2*t=2.04 (c);$$
Найдем дальность, используя уравнения для координаты (x):
$$S= 20*cos{30}*2.04=35.3(м);$$
Мы решили задачу. Рассчитали высоту (H) и дальность полета камня (S), если бросить его под углом в (30^0) и с начальной скоростью (V_0=20(м/с)). Весь полет займет чуть больше 2-х секунд.
Ответ:(S=35.3(м)) и (H=5.1(м)) и (T=2.04(c)).
Пример 6
Камень бросили с балкона с высоты (y_0=20(м)), придав ему начальную скорость (V_0=10(м/с)) и под углом к горизонту (60^0).Найти дальность и максимальную высоту полета.
Бросок камня под углом к горизонту с некоторой высоты
Решение:
Запишем уравнения в общем виде:
$$y(t)=y_0+V_0*sin{alpha}*t-frac{g*t^2}{2};$$
$$V_{y}(t)= V_0*sin{alpha}-g*t;$$
$$x(t)=x_0+ V_0*cos{alpha}*t;$$
$$V_{x}(t)= V_0*cos{alpha}.$$
Подставим все данные в уравнения для координат, согласно условию задачи. За начальную точку выберем точку броска (x_0=0, . y_0=H_0), а за конечную точку падения (x(t)=S, . y(t)=0):
$$0=H_0+V_0*sin{alpha}*t-frac{g*t^2}{2};$$
$$S= V_0*cos{alpha}*t;$$
С учетом данных в условии задачи
$$0=20+10*sin{60^0}*t-frac{g*t^2}{2};$$
$$S= 10*cos{60^o}*t;$$
Выразим время всего полета
$$20+5sqrt{3}*t-4.9*t^2=0;$$
Решаем через дискриминант квадратное уравнение и находим время всего полета
$$t=3.04(с);$$
Чтобы найти дальность полета, подставим найденное время в уравнение для координаты (х)
$$S= V_0*cos{alpha}*t;$$
$$S= 10*cos{60^0}*3.04=15.2(м);$$
Обращаю внимание, что в данной задаче время подъема не равно времени падения, так как задача несимметричная – камень бросают с балкона, а падает он на землю.
Для нахождения максимальной высоты подъема воспользуемся тем, что скорость по (Y) в верхней точке траектории равна (0), и найдем время полета до этой точки:
$$V_{y}(t)= V_0*sin{alpha}-g*t;$$
$$0= 10*sin{60^0}-g*t;$$
$$t=0.88(c);$$
Подставим найденное время в уравнение для координаты (у):
$$y(t)=y_0+V_0*sin{alpha}*t-frac{g*t^2}{2};$$
$$H=20+10*sin{60^0}*0.88-frac{9.8*0.88^2}{2}=28.65-3.79=24.86(м).$$
Ответ: (S=15.2(м)) и (H=24.86(м)).
Пример 7
Тело бросили ГОРИЗОНТАЛЬНО с балкона высотой 20 метров ((H_0=20м)) с начальной скоростью (V_0=10м/с). Найти под каким углом к горизонту будет направлена скорость тела через (t=0.5 с), время всего полета и дальность.
Рис.15. Бросок тела с некоторой высоты горизонтально
Как обычно, начинаем решение задачи с написания всех уравнений в общем виде:
$$y(t)=y_0+V_{0Y}*t-frac{g*t^2}{2};$$
$$V_{y}(t)= V_{0Y}-g*t;$$
$$x(t)=x_0+ V_{0X}*t;$$
$$V_{x}(t)= V_{0X}.$$
Найдем время всего полета и дальность. Начальная точка – это точка броска с координатами ((0;H_0)), конечная точка – падение на Землю ((L;0)).
Обратите внимание, что начальная скорость тела горизонтальна, а значит у нас нет вертикальной составляющей начальной скорости – мы не сообщаем телу начальную скорость по (Y). Поэтому (V_{0y}=0), а (V_{0x}=V_0).
Уравнение по (Y) принимает вид:
$$0=H_0-frac{g*t^2}{2};$$
$$0=20-frac{9.8*t^2}{2};$$
Находим время всего полета
$$t=sqrt{frac{2*20}{9.8}}=2,02(c);$$
Чтобы найти дальность, подставим найденное время в уравнение для координаты (х)
$$L=V_0*t=10*2.02=20.2(м);$$
И осталось ответить на последний вопрос – под каким углом к горизонту будет направлена скорость через (t=0,5(c)). Предположим, что тело в этот момент будет находиться в точке (А) (См.Рис.15). Скорость тела в любой момент времени направлена по касательной к траектории — (V_A).
Для решения этой задачи нам понадобится найти проекции (V_A) на оси (X) и (Y), на рисунке они показаны оранжевым цветом — (V_{AX};. V_{AY}).
Так как движение по горизонтали равномерное, то скорость по (X) в любой момент времени будет постоянна и равна начальной скорости (V_0).
Для нахождения (V_{AY}) запишем уравнение для скорости по (Y)
$$V_{y}(t)= V_{0Y}-g*t;$$
$$V_{0Y}=0;$$
$$V_{y}(t=0.5c)=-g*t;$$
$$V_{y}(t=0.5c)=-9.8*0.5=-4.9м/с;$$
Скорость получилась отрицательная, потому что она направлена вниз – в противоположную сторону оси (Y).
Рис.16. Проекции скорости в произвольной точки траектории
Зная проекции скорости (V_{AX}) и (V_{AY}) мы можем найти угол, под которым направлена скорость. Посмотрите на рис.16. Так как (ABCD) прямоугольник, то (AB=CD=V_{AX}). Тогда из треугольника (ADC) можно найти тангенс (alpha)
$$tg{alpha}=frac{V_{AY}}{V_{AX}}=frac{4.9}{10}=0.5;$$
$$alpha=27^0.$$
Ответ: (t=2.02(c);, L=20.2(м);, alpha=27^0.)