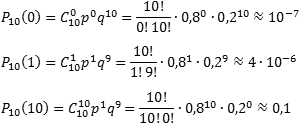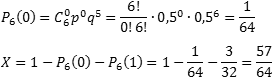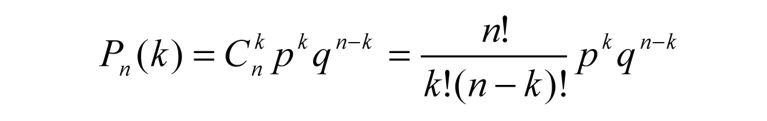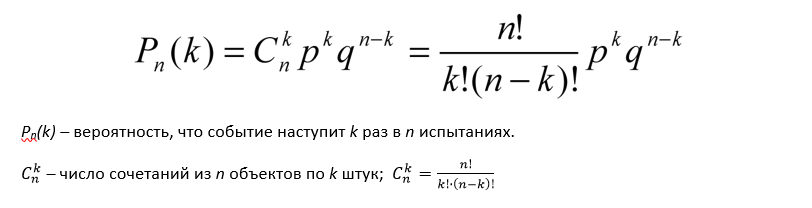« Методика решения сложных задач по теории вероятности с помощью
формулы Бернулли при подготовки к ЕГЭ».
Выполнила:
учитель математики
МКОУ СШ №2 г.Котельниково Волгоградской области
Пирожик Галина
Кирилловна
Цель работы:
·
научиться вычислять вероятности
событий с помощью формулы Бернулли
В результате выполнения практической
работы студент должен:
знать:
·
формулу Бернулли;
уметь:
·
вычислять вероятности событий с помощью формулы Бернулли.
В 2022 году в варианты ЕГЭ по математике профильного
уровня добавились новые задачи по теории вероятностей. По сравнению с теми,
которые раньше были в варианте, это повышенный уровень сложности и требует
применение более глубоких знаний по этой теме. При
решении вероятностных задач часто приходится сталкиваться с ситуациями, в
которых одно и тоже испытание повторяется многократно и исход каждого испытания
независим от исходов других. Такой эксперимент еще называется схемой
повторных независимых испытаний или схемой Бернулли.
Примеры
повторных испытаний:
1)
многократное извлечение из урны одного шара при условии, что вынутый шар после
регистрации его цвета кладется обратно в урну;
2)
повторение одним стрелком выстрелов по одной и той же мишени при условии, что
вероятность удачного попадания при каждом выстреле принимается одинаковой.
3)
бросание симметричной монеты n раз.
Схема Бернулли —
это когда производится n однотипных
независимых опытов, в каждом из которых может появиться интересующее нас
событие A, причем известна вероятность
этого события P(A)
= p. Требуется определить вероятность того, что при проведении n испытаний событие A появится
ровно k раз.
Поскольку
речь идет о испытаниях, и в каждом опыте вероятность события A одинакова,
то возможны лишь два исхода:
1. A — появление события A с
вероятностью p;
2. «не А» — событие А не появилось, что происходит с
вероятностью q = 1 − p.
Важнейшее
условие, без которого схема Бернулли теряет смысл — это постоянство. Сколько бы
опытов мы ни проводили, нас интересует одно и то же событие A,
которое возникает с одной и той же вероятностью p.
Если же условия постоянны, можно точно определить вероятность
того, что событие A произойдет ровно k раз
из n возможных. Сформулируем этот факт в виде теоремы:
Теорема Бернулли.
Пусть вероятность появления события A в каждом опыте постоянна
и равна р. Тогда вероятность того, что в n независимых
испытаниях событие A появится ровно k раз,
рассчитывается по формуле:
где Cnk — число
сочетаний, q = 1 − p.
Эта
формула так и называется: формула Бернулли.
Для
решения по формуле Бернулли надо вспомнить:
1)
определение факториала.
Факториал числа n (n!)— это произведение натуральных
чисел от 1 до n.
n!=1⋅2⋅3⋅…⋅(n−2)⋅(n−1)⋅n
Примеры для вычисления факториала числа:
1)
3! = 1*2*3 = 6 2) 4! = 1*2*3*4 = 24 3) 5! = 1*2*3*4*5 = 120 4)6!
= 1*2*3*4*5*6 = 720
Запоминаем
0! =
1 1! = 1
Свойство факториала n!=(n—1)!⋅n
1) 4! = (4-1)!*4= 3!*4; 2) 5! =(5-1)!*5=4!*5
2) Число сочетаний.
Число сочетаний из n по k элементов (обозначается ) очень
важное понятие в комбинаторике. Оно
показывает сколько существует вариантов выбора k элементов из множества n
элементов.
Число сочетаний вычисляется по формуле:
Примеры
для решени:
1)
2)
Разберем задачи на применение формулы для вычисления простых задач, решаемых по
формуле Бернулли
Задача1. Монету бросают 6
раз. Выпадение орла и решки равновероятно. Найти вероятность того, что орел
выпадет три раза.
Решение:
Событие A, когда выпадает
орел, вероятность этого события равна p = 0,5. Событию A противопоставляется
событие «не A», когда выпадает решка, что случается с
вероятностью q = 1 − 0,5 = 0,5. Нужно определить вероятность
того, что орел выпадет k раз.
Таким
образом, имеем: n = 6; p = 0,5; q = 0,5.
Определим
вероятность того, что орел выпал три раза, т.е. k = 3:
Ответ:
0,3125
Задача2. Монету бросают 6
раз. Выпадение орла и решки равновероятно. Найти вероятность того, что орел
выпадет не менее двух раз.
Решение:
Основная загвоздка — во фразе «не менее».
Получается, что нас устроит любое k,
кроме 0 и 1,
надо
найти значение суммы X = P6(2) + P6(3)
+ … + P6(6).
Заметим,
что эта сумма также равна (1 − P6(0) − P6(1)),
т.е. достаточно из всех возможных вариантов «вырезать» те, когда орел выпал 1
раз (k = 1) или не выпал вообще (k = 0).
Поскольку P6(1) нам уже известно, осталось найти P6(0):
Ответ:0,890625
Задача 3. Монету
бросают 2 раза. Найти вероятность того, что «решка» выпадает хотя бы раз.
Решение:
Решка выпадет хотя бы раз (т. е. или раз из двух, или два из
двух)
p=0,5 – вероятность того,
что выпадет герба,
q=0,5 – вероятность того, что выпадет
решка.
Ответ: 0,75.
Задача 4. (ЕГЭ 2022) Симметричную монету бросают 10 раз. Во сколько
раз вероятность события «выпадет ровно 5 орлов» больше вероятности события
«выпадет ровно 4 орла»?
Решение:
Воспользуемся формулой Бернулли. Найдем вероятность события А,
состоящего в том, что при десяти бросаниях выпадет ровно 5 орлов:
Аналогично найдем вероятность события B, состоящего в том, что при
десяти бросаниях выпадет ровно 4 орла:
Количество вариантов, при которых выпадет ровно 5 орлов, равно
Количество вариантов, при которых выпадет ровно 4 орла, равно
Тогда
Ответ: 1,2
Задача 5. (ЕГЭ 2022) Стрелок стреляет по пяти одинаковым
мишеням. На каждую мишень дается не более двух выстрелов, и известно, что
вероятность поразить мишень каждым отдельным выстрелом равна 0,6. Во сколько
раз вероятность события «стрелок поразит ровно 5 мишеней» больше вероятности
события «стрелок поразит ровно 4 мишени»?
Решение:
Стрелок
поражает мишень с первого раза 0,6 а со второго выстрела 1-0,6=0,4;
Вероятность
поразить мишень равна 0,6+0,4∙0,6=0,84, не поразить 1-0,84=0,16
Вероятность
поразить 5 мишеней из 5 равна
Вероятность
поразить 4 мишени из 5 находим по формуле Бернулли:
=Р2
Ответ: 1,05
Задачи
для самостоятельной работы:
1. Симметричную монету бросают 11 раз. Во сколько раз вероятность события
«выпадет ровно 5 орлов» больше вероятности события «выпадет ровно 4 орла»?
Ответ: 1,4
2. Симметричную монету бросают 12 раз. Во сколько раз вероятность события
«выпадет ровно 4 орла» меньше вероятности события «выпадет ровно 5 орлов»?
Ответ: 1,6
3.Симметричную монету бросают 8 раз. Во сколько раз
вероятность события «выпало ровно 4 орла» больше вероятности события «выпадет
ровно 3~орла»?
Ответ: 1,25
4. Стрелок стреляет по пяти одинаковым мишеням.
На каждую мишень дается не более двух выстрелов, и известно, что вероятность
поразить мишень каждым выстрелом равна 0,5. Во сколько раз вероятность события
«стрелок поразит ровно 3 мишени» больше вероятности события «стрелок поразит
ровно 2 мишени»?
Ответ: 3.
10 июня 2022
В закладки
Обсудить
Жалоба
Формула Бернулли. Примеры решения задач по теории вероятностей
Задачи, которые решаются по схеме Бернулли, чрезвычайно разнообразны: от простеньких (типа «найдите вероятность, что стрелок попадет 1 раз из 10») до весьма суровых (например, задачи на проценты или игральные карты).
formula-bernuli.docx
formula-bernuli.pdf
Схема Бернулли. Примеры решения задач
5 июля 2011
Не будем долго размышлять о высоком — начнем сразу с определения.
Схема Бернулли — это когда производится n однотипных независимых опытов, в каждом из которых может появиться интересующее нас событие A, причем известна вероятность этого события P(A) = p. Требуется определить вероятность того, что при проведении n испытаний событие A появится ровно k раз.
Задачи, которые решаются по схеме Бернулли, чрезвычайно разнообразны: от простеньких (типа «найдите вероятность, что стрелок попадет 1 раз из 10») до весьма суровых (например, задачи на проценты или игральные карты). В реальности эта схема часто применяется для решения задач, связанных с контролем качества продукции и надежности различных механизмов, все характеристики которых должны быть известны до начала работы.
Вернемся к определению. Поскольку речь идет о независимых испытаниях, и в каждом опыте вероятность события A одинакова, возможны лишь два исхода:
- A — появление события A с вероятностью p;
- «не А» — событие А не появилось, что происходит с вероятностью q = 1 − p.
Важнейшее условие, без которого схема Бернулли теряет смысл — это постоянство. Сколько бы опытов мы ни проводили, нас интересует одно и то же событие A, которое возникает с одной и той же вероятностью p.
Между прочим, далеко не все задачи в теории вероятностей сводятся к постоянным условиям. Об этом вам расскажет любой грамотный репетитор по высшей математике. Даже такое нехитрое дело, как вынимание разноцветных шаров из ящика, не является опытом с постоянными условиями. Вынули очередной шар — соотношение цветов в ящике изменилось. Следовательно, изменились и вероятности.
Если же условия постоянны, можно точно определить вероятность того, что событие A произойдет ровно k раз из n возможных. Сформулируем этот факт в виде теоремы:
Теорема Бернулли. Пусть вероятность появления события A в каждом опыте постоянна и равна р. Тогда вероятность того, что в n независимых испытаниях событие A появится ровно k раз, рассчитывается по формуле:
где Cnk — число сочетаний, q = 1 − p.
Эта формула так и называется: формула Бернулли. Интересно заметить, что задачи, приведенные ниже, вполне решаются без использования этой формулы. Например, можно применить формулы сложения вероятностей. Однако объем вычислений будет просто нереальным.
Задача. Вероятность выпуска бракованного изделия на станке равна 0,2. Определить вероятность того, что в партии из десяти выпущенных на данном станке деталей ровно k будут без брака. Решить задачу для k = 0, 1, 10.
По условию, нас интересует событие A выпуска изделий без брака, которое случается каждый раз с вероятностью p = 1 − 0,2 = 0,8. Нужно определить вероятность того, что это событие произойдет k раз. Событию A противопоставляется событие «не A», т.е. выпуск бракованного изделия.
Таким образом, имеем: n = 10; p = 0,8; q = 0,2.
Итак, находим вероятность того, что в партии все детали бракованные (k = 0), что только одна деталь без брака (k = 1), и что бракованных деталей нет вообще (k = 10):
Задача. Монету бросают 6 раз. Выпадение герба и решки равновероятно. Найти вероятность того, что:
- герб выпадет три раза;
- герб выпадет один раз;
- герб выпадет не менее двух раз.
Итак, нас интересует событие A, когда выпадает герб. Вероятность этого события равна p = 0,5. Событию A противопоставляется событие «не A», когда выпадает решка, что случается с вероятностью q = 1 − 0,5 = 0,5. Нужно определить вероятность того, что герб выпадет k раз.
Таким образом, имеем: n = 6; p = 0,5; q = 0,5.
Определим вероятность того, что герб выпал три раза, т.е. k = 3:
Теперь определим вероятность того, что герб выпал только один раз, т.е. k = 1:
Осталось определить, с какой вероятностью герб выпадет не менее двух раз. Основная загвоздка — во фразе «не менее». Получается, что нас устроит любое k, кроме 0 и 1, т.е. надо найти значение суммы X = P6(2) + P6(3) + … + P6(6).
Заметим, что эта сумма также равна (1 − P6(0) − P6(1)), т.е. достаточно из всех возможных вариантов «вырезать» те, когда герб выпал 1 раз (k = 1) или не выпал вообще (k = 0). Поскольку P6(1) нам уже известно, осталось найти P6(0):
Задача. Вероятность того, что телевизор имеет скрытые дефекты, равна 0,2. На склад поступило 20 телевизоров. Какое событие вероятнее: что в этой партии имеется два телевизора со скрытыми дефектами или три?
Интересующее событие A — наличие скрытого дефекта. Всего телевизоров n = 20, вероятность скрытого дефекта p = 0,2. Соответственно, вероятность получить телевизор без скрытого дефекта равна q = 1 − 0,2 = 0,8.
Получаем стартовые условия для схемы Бернулли: n = 20; p = 0,2; q = 0,8.
Найдем вероятность получить два «дефектных» телевизора (k = 2) и три (k = 3):
[begin{array}{l}{P_{20}}left( 2 right) = C_{20}^2{p^2}{q^{18}} = frac{{20!}}{{2!18!}} cdot {0,2^2} cdot {0,8^{18}} approx 0,137\{P_{20}}left( 3 right) = C_{20}^3{p^3}{q^{17}} = frac{{20!}}{{3!17!}} cdot {0,2^3} cdot {0,8^{17}} approx 0,41end{array}]
Очевидно, P20(3) > P20(2), т.е. вероятность получить три телевизора со скрытыми дефектами больше вероятности получить только два таких телевизора. Причем, разница неслабая.
Небольшое замечание по поводу факториалов. Многие испытывают смутное ощущение дискомфорта, когда видят запись «0!» (читается «ноль факториал»). Так вот, 0! = 1 по определению.
P. S. А самая большая вероятность в последней задаче — это получить четыре телевизора со скрытыми дефектами. Подсчитайте сами — и убедитесь.
Смотрите также:
- Локальная теорема Муавра — Лапласа
- Формула полной вероятности
- Тест к уроку «Сложение и вычитание дробей» (легкий)
- Сводный тест по задачам B12 (2 вариант)
- Как решать задачи про летающие камни?
- Задача C1: тригонометрические уравнения и формула двойного угла
Задачи на вероятность егэ 2022 профиль математика
Привет! На связи методический отдел федеральной сети курсов ЕГЭ и ОГЭ Lancman School («Ланцман скул»). Сегодня мы расскажем о том, как готовиться в 2021-2022 учебном году к ЕГЭ по профильной математике. В конце статьи вас ждёт бонус: вебинар по теории вероятности. Наш преподаватель Дмитрий Корабейников расскажет, как решать задания ЕГЭ по профильной математике 2022 года при помощи формулы Бернулли.
Хочешь БЕСПЛАТНО разобрать С опытным преподавателем Все детали новых усложнённых вариантов ЕГЭ по профильной математике 2022 года — приходи на пробное занятие в Lancman School. Мы 13 лет готовим к ЕГЭ на высокие баллы и знаем об экзаменах и поступлении в хорошие вузы буквально всё. Решишь продолжить готовиться к ЕГЭ вместе с нами весь год — дадим скидку после бесплатного пробного занятия. Любой вопрос смело пиши сюда.
Если ты живешь не в Москве, но хочешь заниматься с лучшими столичными репетиторами и сдать ЕГЭ на 80+ баллов, то регистрируйся на наши онлайн-курсы. В этом году мы включили в договор пункт, гарантирующий поступление на бюджет в любой вуз страны. Если ученик будет соблюдать все обговоренные условия, он обязательно поступит. В противном случае мы вернём деньги. Первое пробное занятие БЕСПЛАТНО.
В банке заданий ФИПИ появилось несколько новых задач по теории вероятностей. Часть из них крайне сложно решить без формулы, которую мало кто из одиннадцатиклассников знает. Это формула Бернулли. Выглядит она, конечно, страшновато:
Сейчас мы разберемся, что в ней значат все буквы и символы. А после решим задачу из банка ФИПИ с помощью этой формулы.
Pn(k) – вероятность, что событие наступит k раз в n испытаниях.
Например, человек открывает 7 (n = 7) коробок. В каждой коробке с какой-то вероятностью p может оказаться приз. И по формуле Бернулли можно найти вероятность, например, того, что приз окажется в 3 (k = 3) коробках из 7.
Таких сочетаний получилось 6 шт. Это мы сосчитали вручную. Так делать не всегда удобно: сочетаний может оказаться слишком много.
Наверняка не все знают, как считается так называемый факториал числа: n!
Нужно перемножить это число и все натуральные числа, идущие от 1 до этого числа. Поэтому, например,
Дальше нужно разобраться, что значат буквы p и q.
P и q – взаимообратные вероятности исхода какого-то события. Т. е. p + q = 1. Известный и понятный пример: шансы, что при броске монеты выпадет орел (p) или решка (q). Шанс выпадения орла p = 0,5. Шанс того, что орел не выпадет (а выпадет решка) q = 0,5. Всё сходится: p + q = 1.
Или такая ситуация: в коробке 7 красных карандашей и 3 синих. Обозначим вероятность случайно вытащить красный карандаш за p, а вытащить синий карандаш за q.
В этой ситуации p = 0,7 и q = 0,3; p + q = 1.
Со всеми обозначениями разобрались, давайте теперь решим реальную задачу. Это №10 из профильного ЕГЭ по математике 2022.
Симметричную монету бросают 10 раз. Во сколько раз вероятность события «выпадет ровно 5 орлов» больше вероятности события «выпадет ровно 4 орла»?
Здесь вероятность выпадения орла p = 0,5. Тогда вероятность того, что орел не выпадет (а выпадет решка): q = 1 — p = 0,5.
Всего 10 бросков, т. е. будем рассматривать сочетания из 10 объектов: n = 10.
Далее нам предстоит сравнить два случая:
1) «выпадет ровно 5 орлов», т. е. из n = 10 объектов мы выбираем сочетания по 5, k = 5;
2) «выпадет ровно 4 орла», т. е. из n = 10 объектов мы выбираем сочетания по 4, k = 4.
Хочешь БЕСПЛАТНО разобрать С опытным преподавателем Все детали новых усложнённых вариантов ЕГЭ по профильной математике 2022 года — приходи на пробное занятие в Lancman School. Мы 13 лет готовим к ЕГЭ на высокие баллы и знаем об экзаменах и поступлении в хорошие вузы буквально всё. Решишь продолжить готовиться к ЕГЭ вместе с нами весь год — дадим скидку после бесплатного пробного занятия. Любой вопрос смело пиши сюда. Если ты живешь не в Москве, но хочешь заниматься с лучшими столичными репетиторами и сдать ЕГЭ на 80+ баллов, то регистрируйся на наши онлайн-курсы. В этом году мы включили в договор пункт, гарантирующий поступление на бюджет в любой вуз страны. Если ученик будет соблюдать все обговоренные условия, он обязательно поступит. В противном случае мы вернём деньги. Первое пробное занятие БЕСПЛАТНО.
Всего 10 бросков, т.
Ege. lancmanschool. ru
14.09.2020 13:21:31
2020-09-14 13:21:31
Источники:
Https://ege. lancmanschool. ru/matematika/ege-2022-po-matematike-zadachi-na-teoriyu-veroyatnosti-i-formula-bernu/
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } Задачи на вероятность егэ 2022 профиль математика
Задачи на вероятность егэ 2022 профиль математика
Задачи на вероятность егэ 2022 профиль математика
Задание 10 № 509352
Какова вероятность того, что случайно выбранный телефонный номер оканчивается двумя чётными цифрами?
Вероятность того, что на одном из требуемых мест окажется чётное число равна 0,5. Следовательно, вероятность того, что на двух местах одновременно окажутся два чётных числа равна 0,5 · 0,5 = 0,25.
00,22,44,66, 88. т. е. m=5, но n==100, тогда ведь вероятность равна 0, 05. или нет?
Вы не учли, что может закончиться и на 24 — тоже заканчивается на 2 четные.
Почему вероятность того, что на одном из требуемых мест окажется четное число равна 0,5? Там может оказаться одна из 10 цифр от 1 до 9, из них 4 четные, получается вероятность 0,4
Цифр всего 10: 0,1,2,3,4,5,6,7,8,9. 0 — по определению является четным числом, поскольку при делении на 2, мы получаем целое число — 0:2=0. Таким образом, четных цифр — 5 из 10.
Скажите, а с каких пор 0- четное число? На протяжении всей школьной программы нас учили: «0- ни четное, ни нечетное число.»
Решение не правильное, либо вопрос в задаче не соответствует данному решению.
Какова вероятность того, что случайно выбранный телефонный номер оканчивается двумя чётными цифрами?
Всем известно что половина наших чисел чётная, а половина нет.
Ряд чисел на которые мог бы кончаться номер:
00,01,02,03,04,05,06,07,08,09,10,11,12,13,14,15,16,17,18,19. Наглядно видно, что это половина чисел. А по вашему ответу — 25%, получилось бы что большинство должно быть нечетными.
Если бы шла речь о случайном выпадении цифр, независимом, а не о списке готовых чисел, то да. Подобные задачи насилуют мозг людей, и саму теорию вероятности.
Даже в Вашем списке условию задачи удовлетворяют только 5 пар (00, 02, 04, 06, 08) из 20 (00,01,02,03,04,05,06,07,08,09,10,11,12,13,14,15,16,17,18,19).
Что и составляет 25%
Задание 10 № 319355
Если шахматист А. играет белыми фигурами, то он выигрывает у шахматиста Б. с вероятностью 0,52. Если А. играет черными, то А. выигрывает у Б. с вероятностью 0,3. Шахматисты А. и Б. играют две партии, причём во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза.
Возможность выиграть первую и вторую партию не зависят друг от друга. Вероятность произведения независимых событий равна произведению их вероятностей: 0,52 · 0,3 = 0,156.
Задание 10 № 320212
На рисунке изображён лабиринт. Паук заползает в лабиринт в точке «Вход». Развернуться и ползти назад паук не может, поэтому на каждом разветвлении паук выбирает один из путей, по которому ещё не полз. Считая, что выбор дальнейшего пути чисто случайный, определите, с какой вероятностью паук придёт к выходу
На каждой из четырех отмеченных развилок паук с вероятностью 0,5 может выбрать или путь, ведущий к выходу D, или другой путь. Это независимые события, вероятность их произведения (события, состоящего в том, что паук дойдет до выхода D) равна произведению вероятностей этих событий. Поэтому вероятность прийти к выходу D равна (0,5) 4 = 0,0625.
Примечание Решу ЕГЭ.
Как и обычно в таких задачах, мы определили, с какой вероятностью паук выползет из лабиринта через выход D (а не просто доползет до этого выхода и остановится или, например, проследует дальше к выходу А). Отметим, что вопрос следовало бы сформулировать однозначно. Мы уже связались с разработчиками ЕГЭ и сообщили им об этом.
Задание 10 № 509352
Задание 10 № 319355
Примечание Решу ЕГЭ.
Ege. sdamgia. ru
18.09.2019 20:47:24
2019-09-18 20:47:24
Источники:
Https://ege. sdamgia. ru/test? theme=185
Задание 2 ЕГЭ 2022 по математике профиль вероятность с ответами | ЕГЭ ОГЭ СТАТГРАД ВПР 100 баллов » /> » /> .keyword { color: red; } Задачи на вероятность егэ 2022 профиль математика
Задание 2 ЕГЭ 2022 по математике профиль вероятность с ответами
Задание 2 ЕГЭ 2022 по математике профиль вероятность с ответами
8)В чемпионате по гимнастике участвуют 60 спортсменок: 17 из США, 28 из Мексики, остальные — из Канады. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Канады.
Правильный ответ: 0,25
9)При производстве в среднем на каждые 2982 исправных насоса приходится 18 неисправных. Найдите вероятность того, что случайно выбранный насос окажется неисправным.
Правильный ответ: 0,006
10)Фабрика выпускает сумки. В среднем 8 сумок из 100 имеют скрытые дефекты. Найдите вероятность того, что купленная сумка окажется без дефектов.
Правильный ответ: 0,92
11)В соревнованиях по толканию ядра участвуют 3 спортсмена из Македонии, 8 спортсменов из Сербии, 3 спортсмена из Хорватии и 6 — из Словении. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, который выступает последним, окажется из Сербии.
Правильный ответ: 0,4
12)Научная конференция проводится в 4 дня. Всего запланировано 50 докладов — первые два дня по 11 докладов, остальные распределены поровну между третьим и четвертым днями. Порядок докладов определяется жеребьѐвкой. Какова вероятность, что доклад профессора М. окажется запланированным на последний день конференции?
Правильный ответ: 0,28
13)Конкурс исполнителей проводится в 3 дня. Всего заявлено 40 выступлений — по одному от каждой страны. В первый день 10 выступлений, остальные распределены поровну между оставшимися днями. Порядок выступлений определяется жеребьѐвкой. Какова вероятность, что выступление представителя России состоится в третий день конкурса?
Правильный ответ: 0,375
14)На семинар приехали 3 ученых из Болгарии, 4 из Австрии и 5 из Финляндии. Порядок докладов определяется жеребьѐвкой. Найдите вероятность того, что восьмым окажется доклад ученого из Болгарии.
Правильный ответ: 0,25
15)Перед началом первого тура чемпионата по настольному теннису участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 26 спортсменов, среди которых 13 участников из России, в том числе Владимир Егоров. Найдите вероятность того, что в первом туре Владимир Егоров будет играть с каким-либо спортсменом из России?
Правильный ответ: 0,48
16)В сборнике билетов по химии всего 50 билетов, в 20 из них встречается вопрос по углеводородам. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по углеводородам.
Правильный ответ: 0,4
17)В сборнике билетов по математике всего 60 билетов, в 9 из них встречается вопрос по производной. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по производной.
Правильный ответ: 0,85
18)На чемпионате по прыжкам в воду выступают 25 спортсменов, среди них 3 прыгуна из Украины и 8 прыгунов из Бразилии. Порядок выступлений определяется жеребьѐвкой. Найдите вероятность того, что двенадцатым будет выступать прыгун из Бразилии.
Правильный ответ: 0,32
19)Вася, Петя, Коля и Лѐша бросили жребий — кому начинать игру. Найдите вероятность того, что начинать игру должен будет Петя.
Правильный ответ: 0,25
20)В чемпионате мира участвуют 16 команд. С помощью жребия их нужно разделить на четыре группы по четыре команды в каждой. В ящике вперемешку лежат карточки с номерами групп: 1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4. Капитаны команд тянут по одной карточке. Какова вероятность того, что команда России окажется во второй группе?
Правильный ответ: 0,25
21)На клавиатуре телефона 10 цифр, от 0 до 9. Какова вероятность того, что случайно нажатая цифра будет чётной?
Правильный ответ: 0,5
22)Какова вероятность того, что случайно выбранное натуральное число от 10 до 19 делится на три?
Правильный ответ: 0,3
23)В группе туристов 5 человек. С помощью жребия они выбирают двух человек, которые должны идти в село за продуктами. Турист А. хотел бы сходить в магазин, но он подчиняется жребию. Какова вероятность того, что А. пойдѐт в магазин?
Правильный ответ: 0,4
24)Игральный кубик бросают дважды. Сколько элементарных исходов опыта благоприятствуют событию «А = сумма очков равна 5»?
Правильный ответ: 4
25)В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что наступит исход ОР (в первый раз выпадает орѐл, во второй — решка).
Правильный ответ: 0,25
26)На рок-фестивале выступают группы — по одной от каждой из заявленных стран. Порядок выступления определяется жребием. Какова вероятность того, что группа из Дании будет выступать после группы из Швеции и после группы из Норвегии? Результат округлите до сотых.
Правильный ответ: 0,33
27)В некотором городе из 5000 появившихся на свет младенцев 2512 мальчиков. Найдите частоту рождения девочек в этом городе. Результат округлите до тысячных.
Правильный ответ: 0,498
28)На борту самолѐта 12 мест рядом с запасными выходами и 18 мест за перегородками, разделяющими салоны. Остальные места неудобны для пассажира высокого роста. Пассажир В. высокого роста. Найдите вероятность того, что на регистрации при случайном выборе места пассажиру В. достанется удобное место, если всего в самолѐте 300 мест.
Правильный ответ: 0,1
29)На олимпиаде в вузе участников рассаживают по трѐм аудиториям. В первых двух по 120 человек, оставшихся проводят в запасную аудиторию в другом корпусе. При подсчѐте выяснилось, что всего было 250 участников. Найдите вероятность того, что случайно выбранный участник писал олимпиаду в запасной аудитории.
Правильный ответ: 0,04
30)В классе 26 человек, среди них два близнеца — Андрей и Сергей. Класс случайным образом делят на две группы по 13 человек в каждой. Найдите вероятность того, что Андрей и Сергей окажутся в одной группе.
Правильный ответ: 0,48
31)В фирме такси в наличии 50 легковых автомобилей; 27 из них чѐрные с жѐлтыми надписями на бортах, остальные — жѐлтые с чѐрными надписями. Найдите вероятность того, что на случайный вызов приедет машина жѐлтого цвета с чѐрными надписями.
Правильный ответ: 0,46
32)В группе туристов 30 человек. Их вертолѐтом в несколько приѐмов забрасывают в труднодоступный район по 6 человек за рейс. Порядок, в котором вертолѐт перевозит туристов, случаен. Найдите вероятность того, что турист П. полетит первым рейсом вертолѐта.
Правильный ответ: 0,2
33)Вероятность того, что новый DVD-проигрыватель в течение года поступит в гарантийный ремонт, равна 0,045. В некотором городе из 1000 проданных DVD-проигрывателей в течение года в гарантийную мастерскую поступила 51 штука. На сколько отличается частота события «гарантийный ремонт» от его вероятности в этом городе?
Правильный ответ: 0,006
34)При изготовлении подшипников диаметром 67 мм вероятность того, что диаметр будет отличаться от заданного меньше, чем на 0,01 мм, равна 0,965. Найдите вероятность того, что случайный подшипник будет иметь диаметр меньше чем 66,99 мм или больше чем 67,01 мм.
Правильный ответ: 0,035
35)Вероятность того, что в случайный момент времени температура тела здорового человека окажется ниже чем 36,8 0С, равна 0,81. Найдите вероятность того, что в случайный момент времени у здорового человека температура окажется 36,8 0С или выше.
Правильный ответ: 0,19
36)В кармане у Миши было четыре конфеты — «Грильяж», «Белочка», «Коровка» и «Ласточка», а так же ключи от квартиры. Вынимая ключи, Миша случайно выронил из кармана одну конфету. Найдите вероятность того, что потерялась конфета «Грильяж».
Правильный ответ: 0,25
37)Механические часы с двенадцатичасовым циферблатом в какой-то момент сломались и перестали ходить. Найдите вероятность того, что часовая стрелка застыла, достигнув отметки 10, но не дойдя до отметки 1 час.
Правильный ответ: 0,25
38)За круглый стол на 9 стульев в случайном порядке рассаживаются 7 мальчиков и 2 девочки. Найдите вероятность того, что обе девочки будут сидеть рядом.
Правильный ответ: 0,25
39)В среднем из 1000 садовых насосов, поступивших в продажу, 5 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает.
Правильный ответ: 0,995
40)Фабрика выпускает сумки. В среднем на 92 качественных сумки приходится 8 сумок, имеющих скрытые дефекты. Найдите вероятность того, что выбранная в магазине сумка окажется с дефектами.
Правильный ответ: 0,08
41)Какова вероятность того, что две последние цифры телефонного номера различные?
Правильный ответ: 0,9
42)Какова вероятность того, что номера двух случайно выбранных паспортов оканчиваются одной и той же цифрой?
Правильный ответ: 0,1
43)В группе из девяти человек есть две подруги Даша и Диана. Группу случайным образом делят на три одинаковые по численности подгруппы. Найдите вероятность, что Даша и Диана окажутся в одной подгруппе.
Правильный ответ 0,1.
100ballnik. com
30.06.2019 15:10:29
2019-06-30 15:10:29
Источники:
Https://100ballnik. com/%D0%B7%D0%B0%D0%B4%D0%B0%D0%BD%D0%B8%D0%B5-2-%D0%B5%D0%B3%D1%8D-2022-%D0%BF%D0%BE-%D0%BC%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D0%BA%D0%B5-%D0%BF%D1%80%D0%BE%D1%84%D0%B8%D0%BB%D1%8C-%D0%B2%D0%B5/
Привет! На связи методический отдел федеральной сети курсов ЕГЭ и ОГЭ Lancman School («Ланцман скул»). Сегодня мы расскажем о том, как готовиться в 2021-2022 учебном году к ЕГЭ по профильной математике. В конце статьи вас ждёт бонус: вебинар по теории вероятности. Наш преподаватель Дмитрий Корабейников расскажет, как решать задания ЕГЭ по профильной математике 2022 года при помощи формулы Бернулли.
Хочешь БЕСПЛАТНО разобрать с опытным преподавателем все детали новых усложнённых вариантов ЕГЭ по профильной математике 2022 года — приходи на пробное занятие в Lancman School. Мы 13 лет готовим к ЕГЭ на высокие баллы и знаем об экзаменах и поступлении в хорошие вузы буквально всё. Решишь продолжить готовиться к ЕГЭ вместе с нами весь год — дадим скидку после бесплатного пробного занятия. Любой вопрос смело пиши сюда.
Если ты живешь не в Москве, но хочешь заниматься с лучшими столичными репетиторами и сдать ЕГЭ на 80+ баллов, то регистрируйся на наши онлайн-курсы. В этом году мы включили в договор пункт, гарантирующий поступление на бюджет в любой вуз страны. Если ученик будет соблюдать все обговоренные условия, он обязательно поступит. В противном случае мы вернём деньги. Первое пробное занятие БЕСПЛАТНО.
В банке заданий ФИПИ появилось несколько новых задач по теории вероятностей. Часть из них крайне сложно решить без формулы, которую мало кто из одиннадцатиклассников знает. Это формула Бернулли. Выглядит она, конечно, страшновато:
Сейчас мы разберемся, что в ней значат все буквы и символы. А после решим задачу из банка ФИПИ с помощью этой формулы.
Pn(k) – вероятность, что событие наступит k раз в n испытаниях.
Например, человек открывает 7 (n = 7) коробок. В каждой коробке с какой-то вероятностью p может оказаться приз. И по формуле Бернулли можно найти вероятность, например, того, что приз окажется в 3 (k = 3) коробках из 7.
Таких сочетаний получилось 6 шт. Это мы сосчитали вручную. Так делать не всегда удобно: сочетаний может оказаться слишком много.
Наверняка не все знают, как считается так называемый факториал числа: n!
Нужно перемножить это число и все натуральные числа, идущие от 1 до этого числа. Поэтому, например,
Дальше нужно разобраться, что значат буквы p и q.
p и q – взаимообратные вероятности исхода какого-то события. Т.е. p + q = 1. Известный и понятный пример: шансы, что при броске монеты выпадет орел (p) или решка (q). Шанс выпадения орла p = 0,5. Шанс того, что орел не выпадет (а выпадет решка) q = 0,5. Всё сходится: p + q = 1.
Или такая ситуация: в коробке 7 красных карандашей и 3 синих. Обозначим вероятность случайно вытащить красный карандаш за p, а вытащить синий карандаш за q.
В этой ситуации p = 0,7 и q = 0,3; p + q = 1.
Со всеми обозначениями разобрались, давайте теперь решим реальную задачу. Это №10 из профильного ЕГЭ по математике 2022.
Симметричную монету бросают 10 раз. Во сколько раз вероятность события «выпадет ровно 5 орлов» больше вероятности события «выпадет ровно 4 орла»?
Здесь вероятность выпадения орла p = 0,5. Тогда вероятность того, что орел не выпадет (а выпадет решка): q = 1 — p = 0,5.
Всего 10 бросков, т.е. будем рассматривать сочетания из 10 объектов: n = 10.
Далее нам предстоит сравнить два случая:
1) «выпадет ровно 5 орлов», т.е. из n = 10 объектов мы выбираем сочетания по 5, k = 5;
2) «выпадет ровно 4 орла», т.е. из n = 10 объектов мы выбираем сочетания по 4, k = 4.
Попробуйте решить пару подобных задач самостоятельно, и такие новые задачи по теорверу вас больше не смутят. Но сперва выучите формулу Бернулли:
Обожка поста: pixabay.com
Схема повторных независимых испытаний.
Формула Бернулли
- Краткая теория
- Примеры решения задач
- Задачи контрольных и самостоятельных работ
Краткая теория
Схема Бернулли
Теория вероятностей имеет дело с такими экспериментами, которые
можно повторять (по крайней мере теоретически)
неограниченное число раз. Пусть некоторый эксперимент повторяется
раз, причем результаты каждого повторения не
зависят от исходов предыдущих повторений. Такие серии повторений называют
независимыми испытаниями. Частным случаем таких испытаний являются независимые
испытания Бернулли, которые характеризуются двумя условиями:
1) результатом каждого испытания является один из двух возможных
исходов, называемых соответственно
«успехом» или «неудачей».
2) вероятность «успеха», в
каждом последующем испытании не зависит от результатов предыдущих испытаний и
остается постоянной.
Схему испытаний Бернулли
называют также
биномиальной схемой,
а соответствующие вероятности –
биномиальными, что связано с использованием биномиальных коэффициентов
.
Теорема Бернулли
Если производится серия из
независимых
испытаний Бернулли, в каждом из которых «успех» появляется с вероятностью
, то вероятность того, что «успех» в
испытаниях
появится ровно
раз,
выражается формулой:
где
– вероятность
«неудачи».
– число сочетаний
элементов по
(см.
основные формулы комбинаторики)
Эта формула называется
формулой Бернулли.
Формула Бернулли позволяет
избавиться от большого числа вычислений — сложения и умножения вероятностей —
при достаточно большом количестве испытаний.
Если число испытаний n велико, то пользуются:
- локальной формулой Муавра — Лапласа
- интегральной формулой Муавра — Лапласа
- формулой Пуассона
Примеры решения задач
Пример 1
Всхожесть
семян некоторого растения составляет 70%. Какова вероятность того, что из 10
посеянных семян взойдут: 8, по крайней мере 8; не менее 8?
Если не находите примера, аналогичного вашему, если сами не успеваете выполнить работу, если впереди экзамен по предмету и нужна помощь — свяжитесь со мной:
ВКонтакте
WhatsApp
Telegram
Я буду работать с вами, над вашей проблемой, пока она не решится.
Решение
Воспользуемся
формулой Бернулли:
В нашем
случае
Пусть
событие
– из 10 семян взойдут 8:
Пусть
событие
– взойдет по крайней мере 8 (это значит 8, 9
или 10)
Пусть
событие
– взойдет не менее 8 (это значит 8,9 или 10)
Ответ: P(A)=0.2335;P(B)=0.3828; P(C)=0.3828
Пример 2
В
результате обследования были выделены семьи, имеющие по четыре ребенка. Считая
вероятности появления мальчика и девочки в семье равными, определить
вероятности появления в ней:
а) одного
мальчика;
б) двух мальчиков.
Решение
Вероятность
появления мальчика или девочки равна
. Вероятность появления
мальчика в семье, имеющей четырех детей, находится по формуле Бернулли:
В нашем
случае:
б)
Вероятность появления в семье двух мальчиков:
Ответ: а)
; б)
.
Пример 3
Два
равносильных противника играют в шахматы. Что вероятнее а) выиграть одну партию
из двух или две партии из четырех? б) выиграть не менее двух партий из четырех
или не менее трех партий из пяти? Ничьи во внимание не принимаются.
Решение
Если не находите примера, аналогичного вашему, если сами не успеваете выполнить работу, если впереди экзамен по предмету и нужна помощь — свяжитесь со мной:
ВКонтакте
WhatsApp
Telegram
Я буду работать с вами, над вашей проблемой, пока она не решится.
Играют
равносильные шахматисты, поэтому вероятность выигрыша
, следовательно вероятность проигрыша
тоже равна 1/2. Так как во всех партиях вероятность выигрыша постоянна и
безразлично, в какой последовательности будут выиграны партии, то применима
формула Бернулли:
а) Вероятность
выиграть 1 партию из двух:
Вероятность
выиграть 2 партии из четырех:
Вероятнее
выиграть одну партию из 2-х.
б) Вероятность
выиграть не менее 2-х партий из 4:
Вероятность
выиграть не менее 3-х партий из 5:
Вероятнее
выиграть не менее 2-х партий из 4.
Ответ: а) Вероятнее выиграть одну партию из
2-х; б) Вероятнее выиграть не менее 2-х партий из 4.
Задачи контрольных и самостоятельных работ
Задача 1
Всхожесть
семян данного сорта имеет вероятность 0.7. Оценить вероятность того, что из 9 семян
взойдет не менее 4 семян.
Задача 2
Найти
вероятность того, что в n независимых испытаниях
событие A появится ровно k раз, зная, что в каждом
испытании вероятность появления события равна p.
.
Задача 3
а) Найти
вероятность того, что событие А появится не менее трех раз в четырех
независимых испытаниях, если вероятность появления события А в одном испытании
равна 0,4. б) событие В появится в
случае, если событие А наступит не менее четырех раз. Найти вероятность
наступления события В, если будет произведено пять независимых испытаний, в
каждом из которых вероятность появления события А равна 0,8.
Задача 4
В ралли участвует
10 однотипных машин. Вероятность выхода из строя за период соревнований каждой
из них 1/20.
Найти
вероятность того, что к финишу придут не менее 8 машин.
Если не находите примера, аналогичного вашему, если сами не успеваете выполнить работу, если впереди экзамен по предмету и нужна помощь — свяжитесь со мной:
ВКонтакте
WhatsApp
Telegram
Я буду работать с вами, над вашей проблемой, пока она не решится.
Задача 5
Баскетболист
бросает мяч 4 раза. Вероятность попадания при каждом броске равна 0,7. Найти
вероятность того, что он попадет в корзину: а) три раза; б) менее 3 раз; б)
более трех раз.
Задача 6
В семье
пятеро детей. Считая, что вероятность рождения мальчика равна 0.4, найти
вероятность того, что среди этих детей есть не менее двух девочек.
Задача 7
В
микрорайоне пять машин технической службы. Для бесперебойной работы необходимо,
чтобы не меньше трех машин были в исправном состоянии. Считая верояность
исправного состояния для всех машин одинаковой и равной 0,75, найти вероятность
бесперебойной работы технической службы в микрорайоне.
Задача 8
В среднем
каждый десятый договор страховой компании завершается выплатой по страховому
случаю. Компания заключила пять договоров. Найти вероятность того, что
страховой случай наступит: а) один раз; б) хотя бы один раз.
Задача 9
В
мастерской работают 6 моторов. Для каждого мотора вероятность перегрева к
обеленному перерыву равна 0,8. Найти вероятность того, что к обеденному
перерыву перегреются 4 мотора.
Задача 10
Пусть
вероятность того, что телевизор потребует ремонта в течение гарантийного срока,
равна 0,2. Найти вероятность того, что в течение гарантийного срока из 6
телевизоров: а) не более одного потребует ремонта; б) хотя бы один не потребует
ремонта.
Если не находите примера, аналогичного вашему, если сами не успеваете выполнить работу, если впереди экзамен по предмету и нужна помощь — свяжитесь со мной:
ВКонтакте
WhatsApp
Telegram
Я буду работать с вами, над вашей проблемой, пока она не решится.
Задача 11
Контрольное
задание состоит из 5 вопросов, на каждый из которых дается 4 варианта ответа,
причем один из них правильный, а остальные неправильные. Найдите вероятность
того, что учащийся, не знающий ни одного вопроса, дает: а) 3 правильных ответа;
б) не менее 3-х правильных ответов (предполагается, что учащийся выбирает
ответы наудачу).
Задача 12
Стрелок
попадает в мишень с вероятностью 0,6. Производится серия из 4 выстрелов.
а) Какова
вероятность того, что число промахов будет равно числу попаданий?
б) Найти
вероятность хотя бы одного промаха.
Задание 13
Дана
вероятность p=0.5 появления события A в серии из
независимых испытаний. Найти вероятность того,
что в этих испытаниях событие
появится:
а) ровно
раза
б) не
менее
раз
в) не
менее
раза и не более
раза.
Задача 14
Применяемый
метод лечения в 80% случаев приводит к выздоровлению. Найти вероятность того,
что из четырех больных поправятся:
а) трое;
б) хотя
бы один;
в) найти
наивероятнейшее количество поправившихся больных и соответствующую этому
событию вероятность.
- Краткая теория
- Примеры решения задач
- Задачи контрольных и самостоятельных работ