Формула брахмагупты на егэ - Помощь в подготовке к экзаменам и поступлению

24
Сен 2014

Категория: Планиметрия

Формула Брахмагупты

2014-09-24
2016-09-21

Наверняка вы помните формулу площади треугольника через три известные стороны и – формулу Герона:

где – полупериметр.

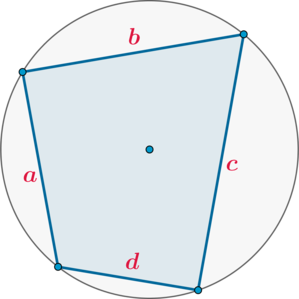
Так вот есть очень похожая формула для площади четырехугольника – формула Брахмагупты. Но вот если формула Герона работает для произвольного треугольника (около него всегда можно описать окружность), то формула Брахмагупты – только для вписанного в окружность четырехугольника.

Итак, вот формула площади вписанного в окружность четырехугольника со сторонами и :

где – полупериметр.

Доказательство:

Пусть нам дан вписанный четырехугольник со сторонами , , и .

Обозначим угол при вершине за . Тогда, так как сумма противоположных углов вписанного четырехугольника равна $180^{circ}$ , то $angle C=180^{circ}-alpha$ .

$S_{ABCD}=S_{ABD}+S_{BCD}=frac{1}{2}ad sinalpha+frac{1}{2}bcsin (180^{circ}-alpha)=$

$=frac{1}{2}sin alpha (ad+bc).$

Откуда

$S_{ABCD}^2=frac{1}{4}sin^2alpha (ad+bc)^2=frac{1}{4}(1-cos^2alpha) (ad+bc)^2$ (*)

Теперь дважды применим теорему Косинусов – сначала к треугольнику , затем к треугольнику , помня о том, что $cos (180^{circ}-alpha)=-cos alpha$ :

Откуда

$cos alpha=frac{a^2+d^2-b^2-c^2}{2(ad+bc)}.$

Вернемся к (*):

$S_{ABCD}^2=frac{1}{4}(1-cos^2alpha) (ad+bc)^2=frac{1}{4}(1-(frac{a^2+d^2-b^2-c^2}{2(ad+bc)})^2)(ad+bc)^2=$

$=frac{1}{4}(1-frac{a^2+d^2-b^2-c^2}{2(ad+bc)})(1+frac{a^2+d^2-b^2-c^2}{2(ad+bc)})(ad+bc)^2=$

$=frac{(2ad+2bc-a^2-d^2+b^2+c^2)(2ad+2bc+a^2+d^2-b^2-c^2)(ad+bc)^2}{16(ad+bc)^2}=$

$=frac{((b+c)^2-(a-d)^2)((a+d)^2-(b-c)^2)}{16}=$

$=frac{((b+c)-(a-d))((b+c)+(a-d))((a+d)-(b-c))((a+d)+(b-c))}{16}=$

$=frac{(2p-2a)(2p-2d)(2p-2b)(2p-2c)}{16}=(p-a)(p-b)(p-c)(p-d)}.$

Наконец,

$S_{ABCD}=sqrt{(p-a)(p-b)(p-c)(p-d)}.$

Что и требовалось доказать.

Применение формулы Брахмагупты можно посмотреть, например, в этой задаче или здесь.

Автор: egeMax |

комментария 2

Источник

5 февраля 2018

В закладки

Обсудить

Жалоба

Какие геометрические факты можно использовать на ЕГЭ без доказательства?

Начнём с того, что для ЕГЭ не нужны сколько-нибудь редкие теоремы, особенно где-нибудь на шпаргалке.

Нужно уметь применять всем знакомые факты, видеть рисунок и решать больше задач. Но вопрос из заголовка задают очень часто, и ответить на него нужно. Естественно, все сотни признаков и свойств, что есть в вашем школьном учебнике можно использовать. Но как насчет более редких фактов: что можно применять без доказательства, а что нет? Точный ответ: любые факты из школьных учебников, рекомендованных минобром на 2017-2018 год.

Ну а вот заветный список того, что мне все-таки удалось обнаружить в соответствующих учебниках:

→ Теорема Менелая (Атанасян. Геометрия 7-9 классы)
→ Теорема Чевы (Атанасян. Геометрия 7-9 классы)
→ Теорема Птолемея (Мерзляк. Геометрия 8 класс)
→ Прямая Эйлера (Мерзляк. Геометрия 8 класс)
→ Теорема об окружности Эйлера (Бутузов. Геометрия 8 класс)
→ Формула медианы треугольника (Шарыгин. Геометрия 7-9 классы)
→ Формула биссектрисы треугольника (Шарыгин. Геометрия 7-9 классы)
→ Теорема о четырех замечательных точках трапеции (Шарыгин. Геометрия 7-9 классы)

Формулу радиуса вневписанной окружности используйте. Каноническое уравнение эллипса — да пожалуйста! Ключевые формулы метода координат для задачи №14, опять же, есть

Но если здесь есть коллеги по цеху, которые могут уточнить еще несколько популярных вопросов насчет непопулярной теории — черкните, буду признателен! Вот интересующие факты: формула Брахмагупты, теорема Стюарта, формула Эйлера для расстояния между центрами вписанной и описанной окружностями треугольника, понятие определителя квадратной матрицы.

Ну и еще раз в заключение. Вероятность того, что задача ЕГЭ не решается без экзотики, равна нулю (такие события называются невозможными). Вероятность того, что вам вообще попадется конфигурация, для которой актуальна, например, теорема о девяти точках окружности, приблизительно равна 0,015. Вероятность того, что школьник в целом знает что-то «запрещенное», приблизительно равна, не кидайтесь камнями, 0,000037.

Источник: vk.com/wildmathing

Источник

Содержание

Введение……………………………………………………………………………2

Глава 1.

1 Различные формулы площадей многоугольников…………………….….3

2 Вывод формул площадей многоугольников………………………………..3

2. 1 Площадь выпуклого четырехугольника……………………………3

2. 2 Площадь ромба…………………………………………………………4

2.3 Площадь трапеции (2 формулы)………………………………………4

2. 4 Площадь дельтоида……………………………………………………..6

2.5 Площадь произвольного треугольника. Формула Герона………….7

2.6 Площадь вписанного четырехугольника. Формула
Брахмагупты.10

2.7 Площадь произвольного четырёхугольника…………………………11

2.8 Универсальная формула……………………………………………….14

2.9 Формула Пика……………………………………………………………15

Глава 2.

Опорные задачи (задачи 1-10)..……………………………………………….16

Глава 3.

Применение опорных задач при решении заданий ЕГЭ(задачи 1-6)….…17

Глава 4.

Решение заданий ЕГЭ с применением формулы Брахмагупты

(задачи 1-2)………………………………………………………………………18

Заключение………………………………………………………………………….19

Литература…………………………………………………………………………20

Введение

Тема «Площади многоугольников»
является неотъемлемой частью школьного курса математики. Ведь исторически само
возникновение геометрии связано с потребностью измерения земельных участков различной
формы. Вместе с тем эта тема в школе раскрыта далеко не полностью.

Школьная программа предусматривает вычисление площадей
лишь двух видов выпуклых четырёхугольников: параллелограмма и трапеции. Для
четырёхугольника, не являющегося параллелограммом или трапецией, формула
нахождения его площади не выводится. В то же время применение такой формулы для
решения ряда задач было бы удобным. Имеется в виду формула вычисления площади
произвольного выпуклого четырёхугольника, которую можно назвать аналогом
формулы Герона, учитывая их некоторое внешнее свойство.

Целью данной работы является поиск дополнительных формул
и изучение опорных задач по теме площади фигур и их применение при решении
заданий ЕГЭ.

В соответствии с поставленной целью в данном исследовании
решались следующие задачи:

1.
обобщить известные формулы для
вычисления площадей четырёхугольников;

2.
найти и доказать другие формулы
для вычисления площадей четырёхугольников в курсе планиметрии;

3.
изучить применение этих формул
при решении задач;

4.
рассмотреть опорные задачи по
теме площади фигур;

5.
показать применение опорных
задач по данной теме при решении заданий ЕГЭ.

Глава 1.

1.1 Формулы для площадей
четырехугольников (приложение 1)

1.2 Вывод
формул площадей некоторых многоугольников

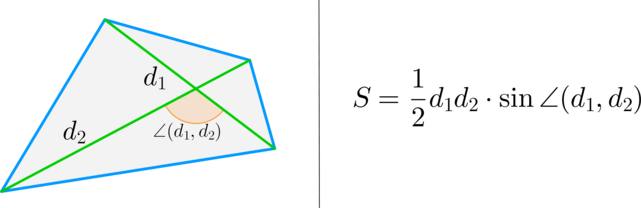
1. Площадь выпуклого четырехугольника.

Площадь выпуклого четырёхугольника можно найти по формуле ,
где d₁ и d₂ – диагонали четырёхугольника, а φ – любой из четырёх углов между ними (рис.
1).

Рис. 1

Доказательство.
В соответствии с рисунком 1 справедливо равенство:

что и
требовалось доказать.

2. Площадь ромба.

Площадь ромба можно
найти по формуле ,

где r – радиус вписанной в ромб окружности, а φ – любой из четырёх углов ромба (рис.2).
Рис.
2

Доказательство. Поскольку
каждая из диагоналей ромба
является биссектрисой угла,
а каждая точка биссектрисы угла
равноудалена от сторон угла, то точка пересечения диагоналей ромба равноудалена
от всех сторон ромба и является центром вписанной в ромб окружности.
Отсюда следует, в частности, что высота ромба в 2
раза больше радиуса вписанной окружности (рис.4). Поэтому

что и
требовалось доказать.

3. Площадь трапеции (2 формулы)

а) Площадь трапеции можно
найти по формуле ,

где a и b –
основания, а c и d – боковые стороны
трапеции (рис.3).

Рис. 3

Доказательство.
Воспользовавшись теоремой Пифагора,
составим следующую систему уравнений с
неизвестными x, y, h (рис. 3):

Следовательно,

что и
требовалось доказать.

б) Площадь трапеции
равна произведению одной из боковых сторон на длину перпендикуляра, опущенного
на неё из середины другой боковой стороны.

Доказательство. Пусть ABCD – данная трапеция (), – середина
стороны – перпендикуляр,
опущенный из точки на
прямую . (рис. 4)
Рис. 4

Проведём через точку K прямую,
параллельную прямой АВ. Пусть М и Р –
точки её пересечения с прямыми ВС и AD.
Параллелограмм АВМР равновелик данной трапеции, так как
пятиугольник АВСКР является для них общим, а треугольник СМК равен
треугольнику KPD, т. е. трапеция и параллелограмм составлены из
одинаковых частей. Поскольку площадь параллелограмма равна произведению его
основания АВ на высоту КН, утверждение доказано.

Замечание. Последний абзац решения можно записать и так: , (по
построению),(по стороне и двум
прилежащим углам), поэтому

следовательно, .

4. Площадь дельтоида.

Площадь дельтоида, можно
найти по формуле: S = (a + b) r,

где a и b – неравные
стороны дельтоида, а r – радиус вписанной в дельтоид окружности (рис.5).

Рис. 5

Доказательство.
Докажем сначала, что в каждый дельтоид можно вписать
окружность. Для этого заметим, что треугольники ABD и BCD равны
в силу признака равенства треугольников «По
трём сторонам» (рис. 5). Отсюда
вытекает, что диагональ BD является биссектрисой углов B и D, а биссектрисы
углов A и C пересекаются в некоторой
точке O, лежащей на диагонали BD. Точка O и
является центром вписанной в дельтоид окружности. Если r –
радиус вписанной в дельтоид окружности, то

что и требовалось
доказать.

5. Площадь произвольного треугольника. Формула Герона.

Площадь произвольного треугольника можно
найти по формуле Герона:

где
a , b , c – длины сторон треугольника, а
p – полупериметр треугольника, т.е. .

Доказательство. Выведем формулу Герона для площади треугольника следующими двумя
способами.

1)В первом используем теорему
косинусов:, где a, b, c –
длины сторон треугольника, γ – угол, противолежащий
стороне с. Находим . Значит,

Замечая, что , , ,

, где — полупериметр
треугольника, получаем: .

Так как , то площадь
треугольника

2) Формулу Герона можно
вывести, опираясь только на теорему Пифагора и не используя теорему косинусов.

Рассмотрим произвольный
треугольник АВС (рис. 6) со сторонами a,b,c.

Рис. 6

В нём всегда найдётся высота,
основание которой лежит на стороне треугольника, а не на её продолжении.
Искомая площадь треугольника АВС:

, следовательно, для её определения достаточно вычислить . По теореме
Пифагора: , . Кроме того, .Решаем
полученную систему трёх уравнений с тремя неизвестными , :

(1)

Вычитая из первого уравнения
системы (1) второе, имеем:

Теперь из первого уравнения
системы (1) находим :

6. Площадь вписанного
четырехугольника. Формула Брахмагупты.

Площадь четырёхугольника, вписанного в
окружность, можно найти по формуле
Брахмагупты:

, где a , b , c , d – длины
сторон четырёхугольника, а p – полупериметр,
т.е.

Доказательство.

Рис.7

Если угол   D   четырёхугольника
  ABCD   обозначить буквой   φ
(рис.7), то, поскольку сумма противоположных углов вписанного
четырёхугольника равна   π
,   угол   B   будет равен   π –
φ .   По этой причине

Следовательно,

Применяя теорему косинусов к
треугольнику ACD , получаем:

AC ² = a² + b² –
2bc cos φ .

Применяя теорему косинусов к треугольнику ABC , получаем:

AC ² = c² + d ² –
2cd cos (π – φ) = c² + d ² +
2cd cos φ .

Следовательно,

Поэтому

Таким образом,,
что и требовалось доказать.

7. Площадь произвольного четырёхугольника

Площадь произвольного выпуклого
четырёхугольника (рис. 1.13) можно выразить через его стороны а, b, c,
d и сумму пары
противоположных углов:

где р –
полупериметр четырёхугольника.

Доказательство. Пусть в четырёхугольнике ABCD АВ = а, ВС
= b,

CD = c, DA = d; ÐABC = β, ÐADC = δ (рис.

Рис. 8

Из :в силу
теоремы косинусов

Из : в силу теоремы
косинусов .

Приравнивая правые части этих выражений, получим:,

или . (1)

Найдём площадь
четырёхугольника ABCD как сумму площадей треугольников ABC и ADC:
,

Откуда (2)

В равенствах (1) и (2) обе части возведём в квадрат, а затем
почленно сложим. Выполним равносильные преобразования, получим

,что и требовалось доказать.

Теорема имеет ряд следствий.

Следствие 1. Площадь произвольного
четырёхугольника, вписанного в окружность, вычисляется по формуле (как было
сказано выше) Брахмагупты:

Доказательство сразу следует
из теоремы, рассмотренной выше, с учётом того, что сумма противолежащих углов
вписанного в окружность четырёхугольника равна 180⁰, т. е., . Поэтому

Следствие 2. Площадь произвольного
четырёхугольника, описанного около окружности, вычисляется по формуле:

Доказательство. Так как у
описанного четырёхугольника суммы противолежащих сторон равны, т. е. ,

То , , , .

Имеем:

Следствие 3. Площадь
четырёхугольника, вписанного в окружность и описанного около окружности, может
быть вычислена по формуле:

Доказательство. Так как и в силу
следствия 1

то

8. Универсальная
формула

Существует универсальная
формула, известная в математике под названием формулы Симпсона, с помощью
которой можно вычислять площади плоских фигур: параллелограмма, трапеции и
треугольника.

Она имеет вид: ,

где  — длина
нижнего основания,  — длина
среднего основания,  — длина
верхнего основания, h – высота фигуры.

Применяя формулу, имеем:

а)для параллелограмма (квадрата, прямоугольника) (рис. 9, а)

б)для трапеции (рис 9, б)

в)для треугольника (рис 9, в)

а)
б) в)

Рис. 9

9. Формула Пика

S = I + B/2 – 1 ,

где
площадь многоугольника обозначена через  ;
количество точек с целочисленными координатами, лежащих строго внутри
многоугольника — через  ;
количество точек с целочисленными координатами, лежащих на сторонах
многоугольника — через  .

Эту формулу называют «формула
Пика» — по имени математика, открывшего её в 1899 году.

Пример.

В = 15 (обозначены красным) I = 34 (обозначены синим)

Простые
треугольники. Площадь любого треугольника,
нарисованного на клетчатой бумаге, легко посчитать, представив её как сумму или
разность площадей прямоугольных треугольников и прямоугольников, стороны
которых идут по линиям сетки, проходящим через вершины нарисованного
треугольника. Проделав это, например, для треугольников, изображённых на
рисунке 9.1, можно убедиться, что площадь получается всегда равной
«полученному» числу – числу вида , где — целое.

Рис. 10

Назовём треугольник простым,
если ни внутри него, ни на его сторонах нет узлов сетки, за исключением вершин.
Все простые треугольники на рис. 1.34 имеют площадь . Мы увидим, что
это не случайно.

Рис. 11

Глава 2.

Опорные задачи

В элементарной математике, самыми трудными считаются
геометрические задачи. При решении геометрических задач, как правило,
алгоритмов нет, и выбирать наиболее подходящую к данному случаю теорему не
просто. Поэтому, желательно в каждой теме выработать какие-то общие положения,
которые полезно знать всякому решающему геометрическиезадачи.
Одним из алгоритмов решения многих геометрических задач является метод
площадей, т.е. решение задач с использованием свойств площадей
(приложение 2).
Решение опорных задач 1-10 (приложение 3).

Глава 3.

Применение опорных задач при решении заданий ЕГЭ.

(приложение 4)
Задача 1. В трапеции ABCD биссектриса угла A пересекает боковую
сторону BC в точке E. Найдите площадь треугольника ABE, если площадь трапеции
равна S, AB=a, AD=b, CD=c (c

Задача
2. Окружность вписана в равнобедренную
трапецию, основания которой равны 18 и 50. Прямая, проходящая через центр
окружности и вершину трапеции, отсекает от трапеции треугольник. Найдите
отношение площади этого треугольника к площади трапеции.

Задача
3. В
прямоугольнике ABCD со сторонами AB=4 и BC=10 на стороне AD расположены точки L
и N таким образом, что DM=4, при этом P — точка пересечения прямых BN и CM.
Площадь треугольника MNP равна 1. Найдите длину отрезка, соединяющего точки L и
N.

Задача
4. Окружность радиуса вписана
в прямой угол. Вторая окружность также вписана в этот угол и пересекается с
первой в точках M и N. Известно, что расстояние между центрами окружностей
равно 8. Найдите MN.

Задача
5. На диагонали параллелограмма взяли
точку, отличную от её середины. Из неё на все стороны параллелограмма
(или их продолжения) опустили перпендикуляры.

а)
Докажите, что четырёхугольник, образованный основаниями этих перпендикуляров,
является трапецией.

б)
Найдите площадь полученной трапеции, если площадь параллелограмма
равна 24, а один из его углов равен 45°.

Задача
6. Две
окружности касаются внешним образом в точке K. Прямая AB касается
первой окружности в точке A, а второй — в точке B.
Прямая BK пересекает первую окружность в точке D,
прямая AK пересекает вторую окружность в точке C.

а)
Докажите, что прямые AD и BC параллельны.

б)
Найдите площадь треугольника AKB, если известно, что радиусы
окружностей равны 4 и 1.

Глава 4.

Решение заданий ЕГЭ с применением формулы Брахмагупты.

(приложение 5)

Задача
1 . (Задание №16 ,тренировочный вариант
№163 А. Ларина).

Четырёхугольник
ABCD со взаимно перпендикулярными диагоналями AC и BD вписан в окружность. а)
Докажите, что квадрат диаметра окружности равен сумме квадратов противоположных
сторон четырёхугольника. б) Найдите площадь четырёхугольника ABCD, если
известно,

что

Задача
2 . (Задание №16 ,тренировочный вариант №
84 А. Ларина).

Вокруг
выпуклого четырёхугольника со сторонами a, b, c, d описана окружность.

а)
Докажите, что отношение длин его диагоналей выражается как .

б)
Найдите площадь четырёхугольника, если a = 2, b=8, c=12, d=4.

Заключение.

Изучив литературу и ознакомившись с геометрическим материалом, описывающим
понятия, законы и теоремы связанные с площадями плоских фигур, я поняла, что
умение решать задачи на нахождение площадей фигур важно и очень интересно.
Навыки, полученные в результате работы над данной темой, могу быть применены
при дальнейшем изучении геометрии .

При выполнении данной работы
я познакомилась с новыми для меня формулами площадей многоугольников, формулой
Пика, формулой Симпсона и др.

Особое внимание было уделено
выводам формул площадей многоугольников, не рассматриваемых в школьном курсе
математики. Основная сложность изучения материалам состоит в том, что не
существует единого универсального метода в нахождении площади n-угольника.
Были разобраны опорные задачи по теме площади фигур, их применение, основные
способы решения заданий №16 ЕГЭ с применением формул площадей n-угольников.

Результаты исследования позволяют сделать следующий вывод: основная сложность
изучения материалам состоит в том, что не существует единого универсального
метода в нахождении площади n-угольника.

Я
надеюсь, что мое исследование может послужить неплохим справочным материалом
при решении заданий ЕГЭ С4 с применением формул площадей.

Литература

1. Атанасян
Л. С. Геометрия 7-9. учебник для общеобразовательных учреждений.- М.:
Просвещение, 2018.

2. Гордин
Р.К. Теоремы и задачи школьной геометрии.-М.: МЦНМО, 2018.

3. Гордин
Р.К. Геометрия. Планиметрия. 7-9 классы.-М.: МЦНМО, 2019.

4. Гордин
Р.К. ЕГЭ-2018 Математика.Геометрия. Планиметрия.Задача 16 ( профильный
уровень).-М.: МЦНМО, 2019.

5. Сайт
А. Ларина.

Приложение
1.

Формулы для
площадей четырехугольников

Четырехугольник	Рисунок	Формула площади	Обозначения
Прямоугольник		S = ab	a и b – смежные стороны
		d – диагональ, φ – любой из четырёх углов между диагоналями
	S = 2R² sin φ Получается из верхней формулы подстановкой d=2R	R – радиус описанной окружности, φ – любой из четырёх углов между диагоналями
Параллелограмм		S = a h_a	a – сторона, h_a – высота, опущенная на эту сторону
	S = absin φ	a и b – смежные стороны, φ – угол между ними
		d₁, d₂ – диагонали, φ – любой из четырёх углов между ними
Квадрат		S = a²	a – сторона квадрата
	S = 4r²	r – радиус вписанной окружности
		d – диагональ квадрата
	S = 2R² Получается из верхней формулы подстановкой d = 2R	R – радиус описанной окружности
Ромб		S = a h_a	a – сторона, h_a – высота, опущенная на эту сторону
	S = a² sin φ	a – сторона, φ – любой из четырёх углов ромба
		d₁, d₂ – диагонали
	S = 2ar	a – сторона, r – радиус вписанной окружности
		r – радиус вписанной окружности, φ – любой из четырёх углов ромба
Трапеция			a и b – основания, h – высота
	S = m h	m – средняя линия, h – высота
		d₁, d₂ – диагонали, φ – любой из четырёх углов между ними
		a и b – основания, c и d – боковые стороны
Дельтоид		S = ab sin φ	a и b – неравные стороны, φ – угол между ними
		a и b – неравные стороны, φ₁ – угол между сторонами, равными a , φ₂ – угол между сторонами, равными b.
	S = (a + b) r	a и b – неравные стороны, r – радиус вписанной окружности
		d₁, d₂ – диагонали
Произвольный выпуклый четырёхугольник			d₁, d₂ – диагонали, φ – любой из четырёх углов между ними
Вписанный четырёхугольник		,	a, b, c, d – длины сторон четырёхугольника, p – полупе-риметр, Формулу называют «Формула Брахмагупты»

Приложение 2.

Свойства площадей .

С–1. Если вершину треугольника
передвигать по прямой, параллельной основанию, то площадь при этом не
изменится.

С–2. Если два треугольника
имеют одинаковые высоты, то отношение их площадей равно отношению длин
оснований (сторон, на которые опущены эти высоты).

С–3. Если два треугольника
имеют общий угол, то их площади относятся как произведение сторон, заключающих
этот угол.

С–4. Отношение площадей
подобных треугольников равно квадрату коэффициента подобия.

С–5. Медиана треугольника
делит его на 2 равновеликие части.

С–6. Медианы треугольника
делят его на три равновеликие части.

С–7. Средняя линия
треугольника площади отсекает от
него треугольник площади .

С–8. Медианы треугольника
делят его на 6 равновеликих частей

С –
1
С – 2

С –
3 С – 4

С – 5 С
– 6

С –
7 С – 8

Приложение 3.
Решение опорных задач

Задача 1. Дано —
трапеция, и —
диагонали. Пересекающиеся диагонали разбивают трапецию на 4 треугольника с
вершиной в точке О. и AOD — треугольники, которые
прилегают к основаниям и треугольники и —
треугольники, которые прилегают к боковым сторонам. Обозначим ,,, ,.

Найдите связь между площадями треугольников.

Рис. 2.2

Выразим площадь трапеции
через и , т. е. через
площади треугольников, прилегающих к основаниям трапеции.

Так как , то надо
выразить и через и .

=, т. к.
треугольники и имеют одинаковые
площади, а если от равных отнять площадь , то получим
равные площади и .

Выразим через и . , .

Докажем, что и . (2.1)

(2.2) Перемножив (2.1) и (2.2), получим

Задача 2. Площадь треугольника, прилегающего к боковой стороне трапеции
есть среднее геометрическое между площадями треугольников, прилегающих к
основаниям трапеции.

Как можно ещё вывести
соотношения ?

; ;

; .

Найдем площадь трапеции (рис.
2.3)

Рис. 2.3

или .

Таким соотношением связана
площадь трапеции с площадями треугольников, прилегающих к её основаниям. Итак,
для трапеции

Задача 3. А какое соотношение между можно
вывести для четырёхугольника (рис. 2.4)?

Рис. 2.4

;

т. е. произведения площадей треугольников, прилегающих к
противоположным сторонам четырёхугольника равны.

Задача 4. (обратная).

Дано: выпуклый
четырёхугольник

Докажите, что этот
четырёхугольник есть трапеция.

Доказательство.

С другой стороны, ,
следовательно , но , (рис. 2.4),
следовательно ,
следовательно , следовательно ,
следовательно и , т. е. , а это
означает, что , т. е.
четырёхугольник — трапеция.

Задача 5. Через некоторую точку, взятую внутри треугольника проведены 3
прямые, соответственно параллельные сторонам треугольника. Эти прямые разделяют
треугольник на 6 частей, из которых три треугольника с площадями . Найдите
площадь треугольника.

Рис. 2.5

Дано: . . . . , , .

Найдите .

Решение.1) ~ ,
следовательно (площади
подобных треугольников относятся как квадрат коэффициента подобия).

2) ; ; ; .

, отсюда .

Задача 6. Пусть
две прямые пересекаются в точке А. В и В₁ –
любые две точки на одной прямой, а С и С₁ –
на другой. Докажите, что

Решение. Углы при вершине А треугольников АВС и АВ₁С₁ либо
равны, либо дополняют друг друга до 180⁰ , то есть в любом
случае синусы этих углов равны. Используя формулу площади треугольника,

имеем .
Задача 7. На сторонах АВ и АС треугольника АВС взяты
точки В₁ и С₁ так,
что , . Докажите, что

Решение следует
непосредственно из предыдущего примера.
Задача 8. Докажите, что длину биссектрисы треугольника АВС можно вычислить по
формуле , где , , , А – угол ВАС.
Решение. Учитывая свойство 3 площади, имеем или . Заменив в левой части равенства и сократив обе его части на , получим , откуда .

Рассмотрим
еще одну полезную задачу.

Задача 9. Пусть О – точка пересечения диагоналей
четырехугольника ABCD. Тогда имеет место равенство

Решение. Пусть

и высоты треугольников ABD и CBD,
проведенные к стороне BD. Очевидно, что . .

Задача 10. В треугольнике АВС на
сторонах АВ, ВС и СА взяты соответственно
точки К, М и Р так, что АК:КВ=2:3,
ВМ:МС=3:4, СР:АР=4:5. В каком отношении отрезок ВР делится
отрезком КМ?

Решение. Пусть ВР и КМ пересекаются
в точке О (рис. 14) и

. Так как , , то . Так как , , то . Так как , , то . Следовательно, и .

Приложение 4.

Применение опорных задач при решении заданий ЕГЭ
Задача 1. В трапеции ABCD биссектриса угла A пересекает
боковую сторону BC в точке E. Найдите площадь треугольника ABE, если площадь
трапеции равна S, AB=a, AD=b, CD=c (c
Решение.

1)
Из формулы находим
высоту трапеции .
Тогда .

2)
Пусть AF — биссектриса угла A. Треугольник ADF— равнобедренный . Тогда CF=b-c.

3)
Треугольник ABE и FCE подобны . Тогда , .

4)
Треугольники ABE и ABC имеют общую высоту, поэтому и .

(рис.12)

Ответ: .
Задача 2.

Окружность вписана
в равнобедренную трапецию, основания которой равны 18 и 50. Прямая, проходящая
через центр окружности и вершину трапеции, отсекает от трапеции треугольник.
Найдите отношение площади этого треугольника к площади трапеции.
Решение1.Пусть окружность радиуса R с центром O, вписанная в
равнобедренную трапецию ABCD с основаниями BC=18 и AD=50, касается боковой
стороны AB в точке М, а оснований AD и BC – в точках К и L соответственно.
Тогда

BM=BL=BC=9,
AM=AK=AD=25,

AB=AM+BM=25+9=34.

2.Отрезок ОМ –
высота прямоугольного треугольника АОВ, проведенная из вершины прямого угла
АОВ, поэтому R=OM===15.

3.Пусть прямая, о
которой говорится в условии задачи, проходит через вершину В и пересекает
основание AD трапеции в точке Р (рис.13). Центр окружности, вписанной в угол,
лежит на биссектрисе угла, поэтому APB=CBP=ABP,
значит, треугольник ABP – равнобедренный, AP=AB=34.

(рис.13)
Следовательно,

S_ΔABP=2S_ΔOAB=2∙AB∙OM=2∙∙34∙15=510.

4.Если S – площадь
трапеции ABCD, а h – ее высота, то h=2R=30,

S = (AD+BC)h=(18+50)∙30=1020.

Следовательно, S_ΔABP/S
= 510/1020=.

5.Поскольку
трапеция равнобедренная, для прямой, проходящую через вершину С, получим тот же
результат.

(рис.14)

6.Пусть теперь указанная прямая проходит через вершину А (рис.14), пересекает
боковую сторону CD в точке Q, а продолжение основания BC – в точке Е.
Треугольник АВЕ – равнобедренный (АЕВ=DAE=BAE),
поэтому

BE=AB=34,
CE=BE-BC=AB-BC=34-18=16.

7.Треугольник
AQD подобен треугольнику
EQC с коэффициентом ,
значит,
если
QH – высота треугольника
AQD, то QH=h=∙30=,
S_Δ_AQD=AD∙QH=∙50∙=.

Следовательно, S_ΔAQD/S==.

Тот
же результат для прямой, проходящей через вершину D.
Ответ: или .
Задача 3.

В
прямоугольнике ABCD со сторонами AB=4 и BC=10 на стороне AD расположены точки L
и N таким образом, что DM=4, при этом P — точка пересечения прямых BN и CM.
Площадь треугольника MNP равна 1. Найдите длину отрезка, соединяющего точки L и
N.
Решение. Пусть высота треугольника делит основание x на два отрезка x1
со стороны угла α и x2 со стороны угла β. Тогда если h — высота треугольника,
то x1=h∙ctgα, x2=h∙ctgβ значит x=x1+x2=h(ctgα + ctgβ) и, следовательно, h=.
Подставив в формулу для площади получим S=.

В зависимости от
порядка расположения точек L и N на AD есть 2 случая:
Случай первый. S_MNP= ,
где ctgα=,
ctgβ=1
Тогда 2+x-10=0x=2.

(рис.15)

Случай второй.
S_MNP= ,
где ctgα=,
ctgβ=1.

Тогда
2-x-10=0x=2,5.
(рис.16)
Ответ: 2 или 2,5.
Задача 4

Окружность
радиуса вписана
в прямой угол. Вторая окружность также вписана в этот угол и пересекается с
первой в точках M и N. Известно, что расстояние между центрами окружностей
равно 8. Найдите MN.
Решение.

1.Пусть
O₁ — центр окружности радиуса ,
O₂ — второй окружности, A — вершина прямого угла, тогда O₁A=

(рис.17)
(рис.18)

Возможны два
случая:

Первый случай:
точка O₁ лежит между точками A и O₂ (рис.17),
тогда O₂A=O₁A+O₁O₂=20, откуда
радиус второй окружности O₂M=10.
В треугольнике O₁MO₂ имеем: O₁O₂=8,
O₁M=,
O₂M=10 .
Поскольку общая хорда MN окружностей перпендикулярна линии центров O₁O₂ и
делится ею пополам, высота MN треугольника O₁MO₂ равна
половине MN.
Полупериметр треугольника O₁MO₂ равен p=4+8 ,
тогда для площади треугольника имеем:

S_O1MO2==8,

откуда
MN==2;
MN=MH=4.
Второй случай:
точка O₂ лежит между точками A и O₁ (рис.18),
тогда O₂A=O₁A-O₁O₂=4, откуда радиус
второй окружности O₂M=2.
В треугольнике O₁MO₂ имеем O₁O₂=8,
O₁M=6,
O₂M=2.
Аналогично первому случаю, высота MN треугольника O₁MO₂ равна
половине MN.

В треугольнике O₁MO₂ полупериметр:
p==4+4
S_O₁_MO₂==8,
откуда MN==2;
MN=MH=4.
Ответ: 4 или
4.
Задача 5

На
диагонали параллелограмма взяли точку, отличную от её середины. Из
неё на все стороны параллелограмма (или их продолжения) опустили
перпендикуляры.а) Докажите, что четырёхугольник, образованный основаниями
этих перпендикуляров, является трапецией.б) Найдите площадь полученной
трапеции, если площадь параллелограмма равна 24, а один из его углов
равен 45°.

(рис.19)
Решение.
а) Возьмём на диагонали AC параллелограмма ABCD точку O (не
посередине) и проведём через неё перпендикуляры NL и KM к
сторонам параллелограмма (см. рис.). Прямоугольные треугольники CKO и AMO подобны.

Точно так же подобны
треугольники CNO и ALO:
OK:OM = OC:OA = ON:OL.

Отсюда следует
подобие треугольников ONK и OLM. Тогда накрестлежащие
углы OML и OKN равны, а поэтому прямые NK и ML параллельны.
Следовательно, четырёхугольник KLMN — параллелограмм
или трапеция.

Докажем, что это
трапеция. Если KLMN — параллелограмм, то ON = OL.

В этом случае OC = OA,
то есть O – середина AC. Противоречие. Значит, KLMN —
трапеция.

б) Обозначим площадь
параллелограмма S , а его острый угол — α . Угол
между диагоналями NL и KM трапеции KLMN равен
углу между перпендикулярными диагоналям прямыми BC и CD,
то есть этот угол равен α .

Поэтому площадь
трапеции равна:

Подставляя =
45° и S = 24, получаем, что площадь трапеции равна

Ответ: 6.
Задача 6

Две
окружности касаются внешним образом в точке K. Прямая AB касается
первой окружности в точке A, а второй — в точке B.
Прямая BK пересекает первую окружность в точке D,
прямая AK пересекает вторую окружность в точке C.

а)
Докажите, что прямые AD и BC параллельны.

б)
Найдите площадь треугольника AKB, если известно, что радиусы
окружностей равны 4 и 1.

(рис. 20)
Решение.
а) Обозначим центры окружностей O₁ и O₂ соответственно.
Пусть общая касательная, проведённая к окружностям в точке K,
пересекает AB в точке M. По свойству касательных,
проведённых из одной точки, AM = KM и KM = BM.
Треугольник AKB, у которого медиана равна половине стороны,
к которой она проведена, прямоугольный. Вписанный угол AKD прямой,
поэтому он опирается на диаметр AD. Значит, AD AB.
Аналогично, получаем, что BC AB.
Следовательно, прямые AD и BC параллельны.

б) Пусть, для определённости,
первая окружность имеет радиус 4, а вторая — радиус 1.
Треугольники BKC и AKD подобны, . Пусть S_BKC = S,
тогда S_AKD = 16S. У треугольников AKD и AKB общая
высота, следовательно ,то
есть S_AKB = 4S. Аналогично, S_CKD = 4S.
Площадь трапеции ABCD равна 25S.

Вычислим площадь
трапеции ABCD. Проведём к AD перпендикуляр O₂H,
равный высоте трапеции, и найдём его из прямоугольного треугольника O₂HO₁:

Тогда

Следовательно, 25S = 20, откуда S = 0,8
и S_AKB = 4S = 3,2.
Ответ: 3,2.

Приложение 5.

Решение заданий ЕГЭ с применением формулы Брахмагупты.

Задача
1 .Задание №16 (тренировочный вариант №163
А. Ларина).

что

Решение:

а) Пусть радиус
данной окружности — R, AB = a, BC = b, CD = c, AD = d. Пусть ∠
BAC = α.

Треугольник ABC
вписан в окружность, значит (по теореме синусов)

(1)

Но и треугольник
ABD вписан в окружность, значит (2)

Тогда из (1) и (2):
; ; (3)

Подставив
последнее равенство (3) в (1), получим: .

Возведя в квадрат,
получим: или .

Аналогично,
применяя теорему синусов для треугольников ABD и CAD,

где ∠
BDA = β, ∠CAD = 90° — β, получим .

Так как , .

То есть, квадрат
диаметра окружности равен сумме квадратов противоположных сторон
четырёхугольника.

б) Опираясь на
пункт (а) задачи, имеем тогда

Откуда
.

Для нахождения площади S
четырёхугольника ABCD воспользуемся формулой Брахмагупты
,

где p —
полупериметр четырёхугольника, вписанного в окружность.

Итак,

Ответ: б)

Задача
2 .Задание №16 (тренировочный вариант № 84
А. Ларина).

Вокруг
выпуклого четырёхугольника со сторонами a, b, c, d описана окружность.

а)
Докажите, что отношение длин его диагоналей выражается как .

б)
Найдите площадь четырёхугольника, если a = 2, b=8, c=12, d=4.

Решение:

а) Пусть нам дан
выпуклый четырёхугольник ABCD,

в
нём
AB = a, BC = b, CD = c, AC = d.

Имеем:

где α — угол
четырёхугольника при вершине A.

(Мы использовали
тот факт, что противоположные углы вписанного четырёхугольника в сумме дают
180°)

Тогда

Аналогично, , где β — угол при
вершине B.

Тогда очевидно равенство:
(1),

Но ведь при этом
по теореме синусов как для треугольника ABD, вписанного в окружность, так и для
треугольника ABC, вписанного в ту же окружность справедливо и
, где R — радиус
окружности, в которую вписан четырёхугольник.

Стало быть, из (1)
получаем

Откуда

б) Для нахождения
площади вписанного четырёхугольника

(со сторонами a,
b, c, d) воспользуемся формулой Брахмагупты:

,
где p — полупериметр.

Согласно условию
задачи

Тогда .

Ответ: .

Источник

Каталог заданий.
2. Площадь четырёхугольника через четыре стороны и два противоположных угла, формула Брахмагупты

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Найдите площадь вписанного четырёхугольника со сторонами 4, 5, 7, 8.

Найдите площадь вписанного четырёхугольника со сторонами 2, 1, 4, 6.

Вокруг выпуклого четырёхугольника со сторонами а, b, c, d описана окружность.

а)  Докажите, что отношение его диагоналей равно

б)  Найдите площадь четырёхугольника, если

Пройти тестирование по этим заданиям

Источник

Площади четырехугольников

В данном разделе рассматриваются только выпуклые фигуры, и считается известной формула:

которая позволяет найти площадь прямоугольника прямоугольника с основанием a и высотой b.

Формулы для площадей четырехугольников

a и b – смежные стороны

d – диагональ,
φ – любой из четырёх углов между диагоналями

Получается из верхней формулы подстановкой d=2R

R – радиус описанной окружности,
φ – любой из четырёх углов между диагоналями

a – сторона,
h_a – высота, опущенная на эту сторону

a и b – смежные стороны,
φ – угол между ними

φ – любой из четырёх углов между ними

a – сторона квадрата

Получается из верхней формулы подстановкой d = 2R

a – сторона,
h_a – высота, опущенная на эту сторону

a – сторона,
φ – любой из четырёх углов ромба

r – радиус вписанной окружности,
φ – любой из четырёх углов ромба

a и b – основания,
h – высота

φ – любой из четырёх углов между ними

a и b – основания,
c и d – боковые стороны

a и b – неравные стороны,
φ – угол между ними

a и b – неравные стороны,
φ₁ – угол между сторонами, равными a ,
φ₂ – угол между сторонами, равными b .

a и b – неравные стороны,
r – радиус вписанной окружности

φ – любой из четырёх углов между ними

a, b, c, d – длины сторон четырёхугольника,
p – полупериметр,

Формулу называют «Формула Брахмагупты»

Четырехугольник	Рисунок	Формула площади	Обозначения
Прямоугольник		S = ab


Параллелограмм


Квадрат		S = a 2
	S = 4r 2


Ромб




Трапеция
	S = m h


Дельтоид		S = ab sin φ



Произвольный выпуклый четырёхугольник
Вписанный четырёхугольник

где
a и b – смежные стороны

где
d – диагональ,
φ – любой из четырёх углов между диагоналями

где
R – радиус описанной окружности,
φ – любой из четырёх углов между диагоналями

Формула получается из верхней формулы подстановкой d = 2R

где
a – сторона,
h_a – высота, опущенная на эту сторону

где
a и b – смежные стороны,
φ – угол между ними

φ – любой из четырёх углов между ними

Получается из верхней формулы подстановкой d = 2R

где
a – сторона,
h_a – высота, опущенная на эту сторону

где
a – сторона,
φ – любой из четырёх углов ромба

где
r – радиус вписанной окружности,
φ – любой из четырёх углов ромба

где
a и b – основания,
h – высота

φ – любой из четырёх углов между ними

где
a и b – основания,
c и d – боковые стороны

где
a и b – неравные стороны,
φ – угол между ними

где
a и b – неравные стороны,
r – радиус вписанной окружности

φ – любой из четырёх углов между ними

где
a, b, c, d – длины сторон четырёхугольника,
p – полупериметр

Формулу называют «Формула Брахмагупты»

Прямоугольник



Параллелограмм



Квадрат
	S = a 2 где a – сторона квадрата
	S = 4r 2


Ромб





Трапеция




Дельтоид

	где a и b – неравные стороны, φ₁ – угол между сторонами, равными a , φ₂ – угол между сторонами, равными b .


Произвольный выпуклый четырёхугольник

Вписанный четырёхугольник

Прямоугольник

где
a и b – смежные стороны

где
d – диагональ,
φ – любой из четырёх углов между диагоналями

где
R – радиус описанной окружности,
φ – любой из четырёх углов между диагоналями

Формула получается из верхней формулы подстановкой d = 2R

Параллелограмм

где
a – сторона,
h_a – высота, опущенная на эту сторону

где
a и b – смежные стороны,
φ – угол между ними

φ – любой из четырёх углов между ними

Квадрат

где
a – сторона квадрата

Получается из верхней формулы подстановкой d = 2R

Ромб

где
a – сторона,
h_a – высота, опущенная на эту сторону

где
a – сторона,
φ – любой из четырёх углов ромба

где
r – радиус вписанной окружности,
φ – любой из четырёх углов ромба

Трапеция

где
a и b – основания,
h – высота

φ – любой из четырёх углов между ними

где
a и b – основания,
c и d – боковые стороны ,

Дельтоид

где
a и b – неравные стороны,
φ – угол между ними

где
a и b – неравные стороны,
φ₁ – угол между сторонами, равными a ,
φ₂ – угол между сторонами, равными b .

где
a и b – неравные стороны,
r – радиус вписанной окружности

Произвольный выпуклый четырёхугольник

φ – любой из четырёх углов между ними

Вписанный четырёхугольник

где
a, b, c, d – длины сторон четырёхугольника,
p – полупериметр

Формулу называют «Формула Брахмагупты»

Вывод формул для площадей четырехугольников

Утверждение 1 . Площадь выпуклого четырёхугольника можно найти по формуле

Доказательство . В соответствии с рисунком 1 справедливо равенство:

что и требовалось доказать.

Утверждение 2 . Площадь параллелограмма параллелограмма можно найти по формуле

где a – сторона параллелограмма, а h_a – высота высота высота , опущенная на эту сторону (рис. 2).

Доказательство . Поскольку прямоугольный треугольник DFC равен прямоугольному треугольнику AEB (рис.26), то четырёхугольник AEFB – прямоугольник. Поэтому

что и требовалось доказать.

Утверждение 3 .Площадь параллелограмма параллелограмма можно найти по формуле

где a и b – смежные стороны параллелограмма, а φ – угол между ними (рис. 3).

то, в силу утверждения 2, справедлива формула

что и требовалось доказать.

Утверждение 4 . Площадь ромба ромба можно найти по формуле

где r – радиус вписанной в ромб окружности, а φ – любой из четырёх углов ромба (рис.4).

что и требовалось доказать.

Утверждение 5 . Площадь трапеции можно найти по формуле

где a и b – основания трапеции, а h – высота высота высота (рис.5).

Доказательство . Проведём прямую BE через вершину B трапеции и середину E боковой стороны CD . Точку пересечения прямых AD и BE обозначим буквой F (рис. 5). Поскольку треугольник BCE равен треугольнику EDF (по стороне и прилежащим к ней углам), то площадь трапеции ABCD равна площади треугольника ABF . Поэтому

что и требовалось доказать.

Утверждение 6 . Площадь трапеции трапеции можно найти по формуле

где a и b – основания, а c и d – боковые стороны трапеции ,

(рис.6).

Доказательство . Воспользовавшись теоремой Пифагора, составим следующую систему уравнений с неизвестными x, y, h (рис. 6):

что и требовалось доказать.

Утверждение 7 . Площадь дельтоида, дельтоида, можно найти по формуле:

где a и b – неравные стороны дельтоида, а r – радиус вписанной в дельтоид окружности (рис.7).

Доказательство . Докажем сначала, что в каждый дельтоид можно вписать окружность. Для этого заметим, что треугольники ABD и BCD равны в силу признака равенства треугольников «По трём сторонам» (рис. 7). Отсюда вытекает, что диагональ BD является биссектрисой углов B и D , а биссектрисы углов A и C пересекаются в некоторой точке O , лежащей на диагонали BD . Точка O и является центром вписанной в дельтоид окружности.

Если r – радиус вписанной в дельтоид окружности, то

Геометрия. Применение формул. Задача 5 Базового ЕГЭ по математике

Чтобы уверенно решать задачи по геометрии — даже такие простые — необходимо выучить основные понятия и формулы.

Это формулы площадей фигур — треугольника (5 формул), параллелограмма, ромба, прямоугольника, произвольного четырехугольника, а также круга. Формулы для длины окружности, длины дуги и площади сектора. Для средней линии треугольника и средней линии трапеции.

Надо знать, что такое центральный и вписанный угол. Знать основные тригонометрические соотношения. В общем, учите основы планиметрии.

Больше полезных формул — в нашем ЕГЭ-Справочнике.

В этой статье — основные типы заданий №5 Базового ЕГЭ по математике. Задачи взяты из Банка заданий ФИПИ.

Вычисление длин отрезков, величин углов и площадей фигур по формулам

1. На клетчатой бумаге с размером клетки изображена трапеция. Найдите длину средней линии этой трапеции.

Средняя линия трапеции равна полусумме её оснований:

2. Найдите величину угла ABC. Ответ дайте в градусах.

Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу. Соединим точки А и С с центром окружности и проведем диаметры через точки А и С. Видим, что величина центрального угла АОС равна Тогда

3. Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на

Проведем из точки В перпендикуляр к прямой ОА. Из прямоугольного треугольника ОВС по теореме Пифагора:

Осталось умножить найденное значение синуса на

4. Найдите площадь ромба, изображенного на клетчатой бумаге с размером клетки Ответ дайте в квадратных сантиметрах.

Самый простой способ — воспользоваться формулой площади ромба, выраженной через его диагонали:

, где и — диагонали.

Получим:

5. Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки Ответ дайте в квадратных сантиметрах.

Площадь трапеции равна произведению полусуммы оснований на высоту:

Основания нашей трапеции равны 4 и 8, а высота равна боковой стороне (поскольку трапеция прямоугольная), то есть 3 см. Площадь трапеции

Нахождение площадей многоугольников сложной формы

А что делать, если надо найти не площадь трапеции или треугольника, а площадь какой-либо сложной фигуры? Есть универсальные способы! Покажем их на примерах из банка заданий ФИПИ и на авторских задачах.

6. Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.

Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным . Высоты этих треугольников равны и . Тогда площадь четырёхугольника равна сумме площадей двух треугольников: .

7. В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.

Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной и трёх прямоугольных треугольников. Видите их на рисунке? Получаем: .

Многие репетиторы рекомендуют в таких задачах пользоваться формулой Пика. В ней нет необходимости, однако эта формула довольно интересна.

Согласно формуле Пика, площадь многоугольника равна В+Г/2-1

где В — количество узлов внутри многоугольника, а Г — количество узлов на границе многоугольника.

Узлами здесь названы точки, в которых пересекаются линии нашей клетчатой бумаги.

Посмотрим, как решается задача 7 с помощью формулы Пика:

Синим на рисунке отмечены узлы внутри треугольника. Зеленым — узлы на границе.

Аккуратно посчитав те и другие, получим, что В = 9, Г = 5, и площадь фигуры равна S = 9 + 5/2 — 1 = 10,5.

Выбирайте — какой способ вам больше нравится.

8. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки

Такой четырехугольник получится, если от квадрата размером отрезать 2 прямоугольника и 4 треугольника. Найдите их на рисунке.

Площадь каждого из больших треугольников равна

Площадь каждого из маленьких треугольников равна

Тогда площадь четырехугольника

9. Авторская задача. Найдите площадь закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки

На рисунке изображен ромб с вырезанным из него квадратом.

Площадь ромба равна половине произведения его диагоналей.

Площадь вырезанного квадрата равна 4.

Площадь фигуры равна 36 — 4 = 32.

Площадь круга, длина окружности, площадь части круга

Длина дуги во столько раз меньше длины окружности, во сколько раз ее градусная мера меньше, чем полный круг, то есть 360 градусов.

Площадь сектора во столько раз меньше площади всего круга, во сколько раз его градусная мера меньше, чем полный круг, то есть 360 градусов.

10. Иногда в задании надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга.Найдите площадь сектора круга радиуса , длина дуги которого равна .

На этом рисунке мы видим часть круга. Площадь всего круга равна , так как . Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна (так как ), а длина дуги данного сектора равна , следовательно, длина дуги в раз меньше, чем длина всей окружности. Угол, на который опирается эта дуга, также в раз меньше, чем полный круг (то есть градусов). Значит, и площадь сектора будет в раз меньше, чем площадь всего круга.

11. На клетчатой бумаге нарисован круг площадью 2,8. Найдите площадь закрашенного сектора.

На рисунке изображен сектор, то есть часть круга. Но какая же это часть? Это четверть круга и еще круга, то есть круга.

Значит, нам надо умножить площадь круга на . Получим:

12. На клетчатой бумаге изображены два круга. Площадь внутреннего круга равна 9. Найдите площадь закрашенной фигуры.

Площадь фигуры равна разности площадей двух кругов, один из которых расположен внутри другого. По условию, площадь внутреннего круга равна 9. Радиус внешнего круга относится к радиусу внутреннего как 4 к 3. Площадь круга равна , то есть пропорциональна квадрату радиуса. Значит, площадь внешнего круга в раза больше площади внутреннего и равна 16. Тогда площадь фигуры равна 16 — 9 = 7.

Задачи на координатной плоскости

13. Найдите площадь четырехугольника, вершины которого имеют координаты (4;2), (8;4), (6;8), (2;6).

Заметим, что этот четырехугольник — квадрат. Сторона квадрата a является гипотенузой прямоугольного треугольника с катетами, равными 2 и 4. Тогда

14. Найдите площадь четырехугольника, вершины которого имеют координаты

На рисунке изображен параллелограмм (четырехугольник, имеющий две пары параллельных сторон). Площадь параллелограмма равна произведению основания на высоту. Основание равно 2, высота 8, площадь равна 16.

Как найти площадь четырехугольника из егэ

Задание 3. Найдите площадь четырёхугольника, изображённого на клетчатой бумаге с размером клетки 1 см х 1 см (см. рисунок). Ответ дайте в квадратных сантиметрах.

1-й способ. Площадь четырехугольника вычислим как разность между площадью прямоугольника, охватывающий четырехугольник и площадями четырех треугольников и одного прямоугольника (см. рисунок ниже).

Площади треугольников равны

Площадь прямоугольника (малого) равна

Таким образом, суммарная вычитаемая площадь составляет

Площадь большого прямоугольника равна

Следовательно, площадь четырехугольника равна

2-й способ. Для вычисления площади сложной фигуры, изображенной на клетчатой бумаге, можно воспользоваться формулой Пика:

где M – число точек на гранях фигуры (на сторонах и вершинах – синие точки на рисунке); N – число точек внутри фигуры (красные точки на рисунке). Причем точки выбираются только на пересечении линий (см. рисунок ниже).

Из рисунка видно, что M = 10, а N = 12. Имеем площадь:

источники:

http://ege-study.ru/ru/ege/materialy/matematika/zadanie-3-zadachi-na-kletchatoj-bumage-ili-koordinatnoj-ploskosti/

http://self-edu.ru/ege2016_36.php?id=27_3

Источник

Факт 1.
(bullet) Площадь выпуклого четырехугольника равна половине произведения диагоналей на синус угла между ними.

Факт 2.
(bullet) Формула Брахмагупты:
если около четырехугольника можно описать окружность, то его площадь равна [{large{S=sqrt{(p-a)(p-b)(p-c)(p-d)}}}]

где (a,b,c,d) – его стороны, (p) – полупериметр.

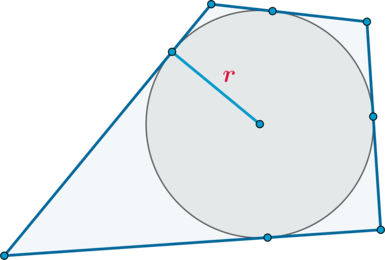
Факт 3.
(bullet) Если в четырехугольник можно вписать окружность, то его площадь равна [{large{S=pcdot r}}]

где (p) – полупериметр, (r) – радиус вписанной окружности.

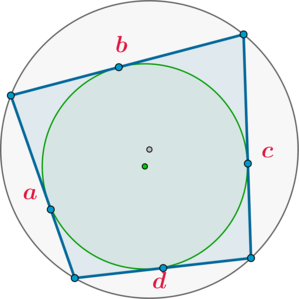
Факт 4.
(bullet) Если в четырехугольник можно вписать окружность, а также около него можно описать окружность, то его площадь равна [{large{S=sqrt{abcd}}}]

где (a,b,c,d) – его стороны.

Источник

In geometry, Brahmagupta‘s formula finds the area of any quadrilateral given the lengths of the sides and some of their angles. In its most common form, it yields the area of quadrilaterals that can be inscribed in a circle.

Basic form[]

In its basic and easiest-to-remember form, Brahmagupta’s formula gives the area of a cyclic quadrilateral whose sides have lengths a, b, c, d as

{displaystyle {sqrt {(s-a)(s-b)(s-c)(s-d)}}}

where s, the semiperimeter, is

${displaystyle s={frac {a+b+c+d}{2}}cdot }$

This formula generalizes Heron’s formula for the area of a triangle.

The assertion that the area of the quadrilateral is given by Brahmagupta’s formula is equivalent to the assertion that it is equal to

${displaystyle {sqrt {{frac {(a^{2}+b^{2}+c^{2}+d^{2})^{2}}{16}}+{frac {abcd}{2}}-{frac {a^{4}+b^{4}+c^{4}+d^{4}}{8}}}}cdot }$

Brahmagupta’s formula may be seen as a formula in the half-lengths of the sides, but it also gives the area as a formula in the altitudes from the center to the sides, although if the quadrilateral does not contain the center, the altitude to the longest side must be taken as negative.

Proof of Brahmagupta’s formula[]

File:Brahmaguptas formula.svg

Diagram for reference

Area of the cyclic quadrilateral = Area of + Area of

${displaystyle ={frac {1}{2}}pqsin A+{frac {1}{2}}rssin C.}$

But since is a cyclic quadrilateral, ${displaystyle angle DAB=180^{circ }-angle DCB.}$ Hence Therefore

${displaystyle {mbox{Area}}={frac {1}{2}}pqsin A+{frac {1}{2}}rssin A}$

${displaystyle ({mbox{Area}})^{2}={frac {1}{4}}sin ^{2}A(pq+rs)^{2}}$

${displaystyle 4({mbox{Area}})^{2}=(1-cos ^{2}A)(pq+rs)^{2},}$

${displaystyle 4({mbox{Area}})^{2}=(pq+rs)^{2}-cos^{2}A(pq+rs)^{2}.,}$

Applying law of cosines for and and equating the expressions for side we have

${displaystyle p^{2}+q^{2}-2pqcos A=r^{2}+s^{2}-2rscos C.,}$

Substituting (since angles and are supplementary) and rearranging, we have

${displaystyle 2cos A(pq+rs)=p^{2}+q^{2}-r^{2}-s^{2}.,}$

Substituting this in the equation for area,

${displaystyle 4({mbox{Area}})^{2}=(pq+rs)^{2}-{frac {1}{4}}(p^{2}+q^{2}-r^{2}-s^{2})^{2}}$

${displaystyle 16({mbox{Area}})^{2}=4(pq+rs)^{2}-(p^{2}+q^{2}-r^{2}-s^{2})^{2},,}$

which is of the form ${displaystyle a^{2}-b^{2}}$ and hence can be written in the form as

${displaystyle (2(pq+rs)+p^{2}+q^{2}-r^{2}-s^{2})(2(pq+rs)-p^{2}-q^{2}+r^{2}+s^{2}),}$

${displaystyle =((p+q)^{2}-(r-s)^{2})((r+s)^{2}-(p-q)^{2}),}$

{displaystyle =(p+q+r-s)(p+q+s-r)(p+r+s-q)(q+r+s-p).,}

Introducing ${displaystyle S={frac {p+q+r+s}{2}},}$

${displaystyle 16({mbox{Area}})^{2}=16(S-p)(S-q)(S-r)(S-s).,}$

Taking square root, we get

{displaystyle {mbox{Area}}={sqrt {(S-p)(S-q)(S-r)(S-s)}}.}

Extension to non-cyclic quadrilaterals[]

In the case of non-cyclic quadrilaterals, Brahmagupta’s formula can be extended by considering the measures of two opposite angles of the quadrilateral:

${displaystyle {sqrt {(s-a)(s-b)(s-c)(s-d)-abcdcos ^{2}theta }}}$

where θ is half the sum of two opposite angles. (The pair is irrelevant: if the other two angles are taken, half their sum is the supplement of θ. Since cos(180° − θ) = −cosθ, we have cos²(180° − θ) = cos²θ.) It follows from this fact that the area of a cyclic quadrilateral is the maximum possible area for any quadrilateral with the given side lengths.

This more general formula is sometimes known as Bretschneider’s formula, but according to MathWorld is apparently due to Coolidge in this form, Bretschneider’s expression having been

{displaystyle {sqrt {(s-a)(s-b)(s-c)(s-d)-textstyle {1 over 4}(ac+bd+pq)(ac+bd-pq)}},}

where p and q are the lengths of the diagonals of the quadrilateral.

It is a property of cyclic quadrilaterals (and ultimately of inscribed angles) that opposite angles of a quadrilateral sum to 180°. Consequently, in the case of an inscribed quadrilateral, θ = 90°, whence the term

${displaystyle abcdcos ^{2}theta =abcdcos ^{2}left(90^{circ }right)=abcdcdot 0=0,,}$

giving the basic form of Brahmagupta’s formula.

[]

Heron’s formula for the area of a triangle is the special case obtained by taking d = 0.

The relationship between the general and extended form of Brahmagupta’s formula is similar to how the law of cosines extends the Pythagorean theorem.

External links[]

MathWorld: Brahmagupta’s formula

Template:Planetmath

ar:معادلة براهماغوبتا
fr:Formule de Brahmagupta
ko:브라마굽타의 공식
it:Formula di Brahmagupta
ja:ブラーマグプタの公式
km:រូបមន្តប្រាម៉ាហ្គឹបតា
ru:Формула Брахмагупты
sr:Формула Брамагупте
fi:Brahmaguptan kaava
zh:婆羅摩笈多公式

Источник