На уроке рассматривается решение 11 задания ЕГЭ по информатике о нахождении информационного объема сообщения
Содержание:
- Объяснение заданий 11 ЕГЭ по информатике
- Измерение информационного объема при работе с текстом
- Измерение информационного объема при работе с различными системами
- Решение заданий 11 ЕГЭ по информатике
- Кодирование сообщений (работа с текстом)
- Работа с различными системами
- Компьютерные системы и автомобильные номера
11-е задание: «Информационный объем сообщения»
Уровень сложности
— повышенный,
Требуется использование специализированного программного обеспечения
— нет,
Максимальный балл
— 1,
Примерное время выполнения
— 3 минуты.
Проверяемые элементы содержания: Умение подсчитывать информационный объём сообщения
До ЕГЭ 2021 года — это было задание № 13 ЕГЭ
Типичные ошибки и рекомендации по их предотвращению:
«Необходимо учитывать, что в заданиях этой линии для кодирования слов обычно отводится одинаковое и минимально возможное целое число байт, а для кодирования символов – одинаковое и минимально возможное целое количество бит»
ФГБНУ «Федеральный институт педагогических измерений»
Для выполнения заданий рекомендуется посмотреть теоретический материал темы 8.
Измерение информационного объема
при работе с текстом
- С помощью K бит можно закодировать Q = 2K различных символов:
- Q — мощность алфавита
- K — количество бит для хранения одного символа из Q вариантов символов
- 2 — равна двум, если двоичная система счисления (данные хранятся в двоичном виде)
- Чтобы найти информационный объем сообщения I, нужно умножить количество символов N на число бит для хранения одного символа K:
- I — информационный объем сообщения,
- N — длина сообщения (количество символов),
- K — количество бит для хранения одного символа.
- В этих двух формулах используется одна и та же переменная:
Q = 2K
* также приняты другие обозначения: N = 2i
I = N * K
Q = 2K I = N * K
Рассмотрим пример с использованием одновременно двух формул:
Пример:
Объем сообщения – 7,5 Кбайт. Известно, что данное сообщение содержит 7680 символов. Какова мощность алфавита?
✍ Решение:
- Воспользуемся формулой:
- Найдем количество бит, необходимое для хранения 1 символа (сначала переведем значение в биты):
- Далее воспользуемся формулой:
- 8 бит на символ позволяют закодировать:
I = N*K;
I — объем сообщения = 7,5 Кбайт;
N — количество символов = 7680;
K — количество бит на 1 символ
I = 7,5 Кбайт = 7,5 * 213 бит
[ K= frac {7,5 * 2^{13}}{7680} = frac {7,5 * 2^{13}}{15 * 2^9} = frac {7,5 * 16}{15} = 8 ]
т.е. K = 8 бит на 1 символ
Q = 2K
K — количество бит для хранения одного символа из Q вариантов символов (= 
Q — количество вариантов символов
28 = 256 различных символов
256 символов — это и есть мощность
Ответ:
256
Измерение информационного объема
при работе с различными системами
- С помощью K бит можно закодировать Q = 2K различных (номеров) объектов некоторой системы:
- Q — общее количество объектов в некоторой системе, данные о которых хранятся в компьютере или передаются в сообщении,
- K — количество бит для хранения одного объекта из общего количества Q,
- 2 — двоичная система счисления (данные хранятся в двоичном виде).
- Чтобы найти информационный объем сообщения I, нужно умножить количество объектов в сообщении — N — на число бит K для хранения одного объекта:
- I — информационный объем сообщения,
- N — количество объектов в сообщении
- K — количество бит для хранения одного объекта системы.
Q = 2K
* также приняты другие обозначения: N = 2i
I = N * K
Пример:
На производстве работает автоматическая система информирования склада о необходимости доставки в цех определенных групп расходных материалов. Система устроена так, что по каналу связи на склад передается условный номер расходных материалов (при этом используется одинаковое, но минимально возможное количество бит в двоичном представлении этого числа). Известно, что был послан запрос на доставку 9 групп материалов из 19 используемых на производстве. Определите объем посланного сообщения (Ответ дайте в битах)
✍ Решение:
- Воспользуемся формулой:
- для хранения номера одной группы потребуется бит:
Q = 2K
K — количество бит для хранения одного номера группы материалов
Q — общее количество номеров для различных групп расходных материалов = 19
25 > 19 => 5 бит
I = N*K;
I — объем сообщения = ? бит;
N — количество передаваемых номеров групп (= 9);
K — количество бит на 1 номер (= 5)
I = 9 * 5 = 45 бит
Ответ: 45
Решение заданий 11 ЕГЭ по информатике
Плейлист видеоразборов задания на YouTube:
Задание демонстрационного варианта 2022 года ФИПИ
Кодирование сообщений (работа с текстом)
✍ Решение:
- Воспользуемся формулой:
I = N * K
I - объем сообщения N - количество символов K - количество бит на 1 символ
I = 7,5 Кбайт = 7,5 * 213 бит
[ K = frac {7,5 * 2^{13}}{7680} = frac {7,5 * 2^{13}}{15 * 2^9} = frac {7,5 * 16}{15} = 8 ]
28 = 256 различных символов
(по формуле Q = 2N)
Результат: 256
Видеоразбор задания представлен после очередной задачи.
11_2:
Мощность алфавита равна 256. Сколько Кбайт памяти потребуется для сохранения 160 страниц текста, содержащего в среднем 192 символа на каждой странице?
Типовые задания для тренировки
✍ Решение:
- Найдем общее количество символов на всех страницах (для удобства будем использовать степени двойки):
160 * 192 = 15 * 211
256 = 2n -> n = 8 бит на 1 символ
[ I = {15 * 2^{11}} * 2^3 бит = frac {15 * 2^{14}}{2^{13}} Кбайт = 30 Кбайт ]
I = 30 Кбайт
Результат: 30
Смотрите подробный разбор заданий на кодирование текста:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
11_3:
Два текста содержат одинаковое количество символов. Первый текст составлен в алфавите мощностью 16 символов, а второй текст – в алфавите из 256 символов.
Во сколько раз количество информации во втором тексте больше, чем в первом?
✍ Решение:
- Необходима формула Q = 2n
- Вычислим требуемое количество бит на хранение одного символа для обоих текстов:
1. 16 = 2n -> n = 4 2. 256 = 2n -> n = 8
Результат: 2
Работа с различными системами
11_4:
Кабельная сеть проводит голосование среди зрителей о том, какой из четырех фильмов они хотели бы посмотреть вечером. Кабельной сетью пользуются 2000 человек. В голосовании участвовало 1200 человек.
Каков объем информации (в байтах), записанный автоматизированной системой голосования?
✍ Решение:
- Так как номера четырех фильмов хранятся в компьютерной системе, то можно найти количество бит, необходимое для хранения номера фильма:
Q = 2k -> 4 = 2k -> k = 2 бита
1200 * 2 = 2400 бит = 2400/8 байт = 300 байт
Результат: 300
Пример решения данного задания ЕГЭ доступно в видеоуроке:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
11_5:
Репетиционный экзамен в школе сдают 105 человек. Каждому из них выделяют специальный номер, идентифицирующий его в автоматической системе проверки ответов. При регистрации участника для записи его номера система использует минимально возможное количество бит, одинаковое для каждого участника.
Каков объем информации в битах, записанный устройством после регистрации 60 участников?
✍ Решение:
Результат: 420
Пример решения данного задания ЕГЭ доступно в видеоуроке:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
11_6:
В базе данных хранятся записи, содержащие информацию о датах. Каждая запись содержит три поля: год (число от 1 до 2100), номер месяца (число от 1 до 12) и номер дня в месяце (число от 1 до 31). Каждое поле записывается отдельно от других полей с помощью минимально возможного числа бит.
Определите минимальное количество бит, необходимых для кодирования одной записи.
✍ Решение:
- Необходима формула Q = 2n.
- Вычислим требуемое количество бит на хранение каждого пункта всей записи:
1. 2100 вариантов: 2100 ~ 212 -> n = 12 бит 2. 12 вариантов: 12 ~ 24 -> n = 4 бит 3. 31 вариант: 31 ~ 25 -> n = 5 бит
12 + 4 + 5 = 21
Результат: 21
11_7:
Репетиционный экзамен сдают 9 потоков по 100 человек в каждом. Каждому из них выделяют специальный код, состоящий из номера потока и номера в потоке. При кодировании этих номеров участников проверяющая система использует минимально возможное количество бит, одинаковое для каждого участника, отдельно для номера потока и номера в потоке. При этом для записи кода используется минимально возможное и одинаково целое количество байтов.
Каков объем информации в байтах, записанный устройством после регистрации 80 участников?
В ответе укажите только число.
✍ Решение:
- Код состоит из двух составляющих: 1. номер потока (в битах) и 2. номер по порядку (в битах). Найдем количество бит, необходимое для их хранения:
1. N = 2i -> 9 = 2i -> i = 4 бит (23 < 9 < 24) 2. N = 2i -> 100 = 2i -> i = 7 бит (26 < 100 < 27)
11/ 8 ~ 2 байта (одного байта недостаточно, 8 < 11)
2 * 80 = 160 байт
Результат: 160
Видеоразбор задания:
📹 YouTube здесь
Компьютерные системы и автомобильные номера
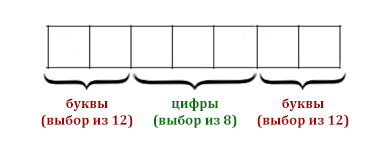
11_8:
Автомобильный номер состоит из нескольких букв (количество букв одинаковое во всех номерах), за которыми следуют три цифры. При этом используются 10 цифр и только 5 букв: Н, О, М, Е и Р. Нужно иметь не менее 100 тысяч различных номеров.
Какое наименьшее количество букв должно быть в автомобильном номере?
✍ Решение:
- Необходима формула Q = mn.
Q - количество вариантов m - мощность алфавита n - длина
5 ... 5 10 10 10 = 5x * 103
100000 <= 5x * 103
x = 3:
53 * 1000 = 125000 (125000 > 100000)
Результат: 3
Предлагаем посмотреть видеоразбор задания:
📹 YouTube здесь
11_9: 11 (13) задание. Демоверсия ЕГЭ 2018 информатика:
При регистрации в компьютерной системе каждому пользователю выдаётся пароль, состоящий из 10 символов. В качестве символов используют прописные буквы латинского алфавита, т.е. 26 различных символов. В базе данных для хранения каждого пароля отведено одинаковое и минимально возможное целое число байт. При этом используют посимвольное кодирование паролей, все символы кодируют одинаковым и минимально возможным количеством бит.
Определите объём памяти (в байтах), необходимый для хранения данных о 50 пользователях.
В ответе запишите только целое число – количество байт.
✍ Решение:
- Основной формулой для решения данной задачи является:
- Чтобы найти количество бит, необходимое для хранения одного пароля, для начала нужно найти количество бит, необходимых для хранения 1 символа в пароле. По формуле получаем:
Q = 2N
где Q — количество вариантов символов, которые можно закодировать с помощью N бит.
26 = 2N -> N ~ 5 бит
10 * 5 = 50 бит всего на пароль
50 бит / 8 ~ 7 байт (берем ближайшее число большее 50 и кратное 8: 56/8 = 7)
7 байт * 50 (пользователей) = 350 байт
Результат: 350
Подробное решение 11 (13) задания демоверсии ЕГЭ 2018 года смотрите на видео:
📹 YouTube здесь
11_10:
В некоторой стране автомобильный номер состоит из 7 символов. Каждый символ может быть одной из 18 различных букв или десятичной цифрой.
Каждый такой номер в компьютерной программе записывается минимально возможным и одинаковым целым количеством байт, при этом используют посимвольное кодирование и каждый символ кодируется одинаковым и минимально возможным количеством бит.
Определите объем памяти в байтах, отводимый этой программой для записи 50 номеров.
В ответе укажите только число.
✍ Решение:
- Так как в номере может быть использована либо одна буква из 18, либо одна цифра из 10, то всего в качестве одного символа в номере может быть использован один из 28 символов:
18 + 10 = 28
28 = 2i => i = 5
I = 7 * 5 = 35 бит
35 / 8 ~ 5 байт
I = 50 * 5 = 250 байт на хранение 50 номеров
Результат: 250
Видеоразбор:
📹 YouTube здесь
11_14:
При регистрации в компьютерной системе каждому пользователю выдаётся идентификатор, состоящий из 10 символов, первый и последний из которых — одна из 18 букв, а остальные — цифры (допускается использование 10 десятичных цифр). Каждый такой идентификатор в компьютерной программе записывается минимально возможным и одинаковым целым количеством байт (при этом используют посимвольное кодирование; все цифры кодируются одинаковым и минимально возможным количеством бит, все буквы также кодируются одинаковым и минимально возможным количеством бит).
Определите объём памяти, отводимый этой программой для записи 25 паролей. (Ответ дайте в байтах.)
✍ Решение:
- Идентификатор пароля по заданию состоит из букв и цифр, необходимо рассмотреть отдельно эти составляющие.
- Поскольку в пароле может присутствовать 18 букв, то подсчитаем, сколько бит необходимо для хранения 1-й буквы:
С помощью n бит можно закодировать 2n различных вариантов, Иначе говоря 18 = 2n, -> n = 5 бит (т.к. 4 мало, 24=16, 25 = 32)
10 = 2n, -> n = 4 бита (т.к. 3 мало, 23=8, 24 = 16)
В битах: 5 4 4 4 4 4 4 4 4 5 или: 5 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 5 = 5 * 2 + 4 * 8 = 42 бита
48 = 6·8 бит (6 байт).
6·25 = 150 байт
Ответ:150
Доступно видеорешение:
📹 YouTube здесь
11_11:
При регистрации в компьютерной системе каждому пользователю выдается пароль, состоящий из 15 символов и содержащий только символы из 12-символьного набора A, B, C, D, E, F, G, H, I, K, L, M, N. В базе данных для хранения сведений о каждом пользователе отведено одинаковое и минимально возможное целое число байт. При этом используют посимвольное кодирование паролей, все символы кодируют одинаковым и минимально возможным количеством бит. Кроме собственно пароля, для каждого пользователя в системе хранятся дополнительные сведения, для чего отведено 12 байт на одного пользователя.
Определите объем памяти (в байтах), необходимый для хранения сведений о 30 пользователях.
В ответе запишите только целое число — количество байт.
Типовые задания для тренировки
✍ Решение:
Результат: 600
Пример решения данного задания ЕГЭ доступно в видеоуроке:
📹 YouTube здесь
11_12:
При регистрации в компьютерной системе каждому пользователю выдается пароль, состоящий из 7 символов и содержащий только символы из 33-символьного алфавита. В базе данных для хранения сведений о каждом пользователе отведено одинаковое и минимально возможное целое число байт. При этом используют посимвольное кодирование паролей, все символы кодируют одинаковым и минимально возможным количеством бит. Кроме собственного пароля, для каждого пользователя в системе хранятся дополнительные сведения, для чего выделено целое число байт; это число одно и то же для всех пользователей.
Для хранения сведений о 60 пользователях потребовалось 900 байт.
Сколько байт выделено для хранения дополнительных сведений об одном пользователе?
В ответ запишите только целое число — количество байт.
Типовые задания для тренировки
✍ Решение:
- Сначала определимся с паролем. По формуле Q = MN получаем:
33 = 2N -> N = 6 бит на 1 символ
-> 7*6 = 42 бит всего на пароль
48/8 = 6 42 бит ~ 6 байт
900 байт / 60 (пользователей) = 15 байт на каждого пользователя
15 байт (на хранение всей информации) - 6 байт (на хранение пароля) = 9 байт на дополнительные сведения
Результат: 9
Пошаговое решение данного 11 задания ЕГЭ по информатике также доступно в видеоуроке:
📹 YouTube здесь
11_13:
При регистрации в компьютерной системе каждому пользователю выдаётся пароль, состоящий из 9 символов. В качестве символов используют прописные и строчные буквы латинского алфавита (в нём 26 символов), а также десятичные цифры. В базе данных для хранения сведений о каждом пользователе отведено одинаковое и минимально возможное целое число байт. При этом используют посимвольное кодирование паролей, все символы кодируют одинаковым и минимально возможным количеством бит. Кроме собственно пароля, для каждого пользователя в системе хранятся дополнительные сведения, для чего выделено 18 байт на одного пользователя. В компьютерной системе выделено 1 Кб для хранения сведений о пользователях.
О каком наибольшем количестве пользователей может быть сохранена информация в системе? В ответе запишите только целое число – количество пользователей.
✍ Решение:
- Так как используются как прописные, так и строчные буквы, то получим всего вариантов символов для кодирования:
26 + 26 + 10 = 62
Q = 2n получим количество бит, требуемое для кодирования 1 символа пароля:Q = 2n -> 62 = 2n -> n = 6
6 * 9 = 54
54 / 8 = 7 байт
18 + 7 = 25 байт
1 Кб = 1024 байт
1024 / 25 = 40,96
Результат: 40
Смотрите видео с решением задания:
📹 YouTube здесь
Урок посвящён 11 заданию из ЕГЭ по информатике нового формата 2022. Проанализируем основные примеры и научимся решать это задание!
В 11 задании из ЕГЭ по информатике часто даются задачи на умение работать с количеством информации.
Приступим к делу! Раньше это задание было под номером тринадцать.
Задача (Демонстрационный вариант ЕГЭ по информатике, 2018)
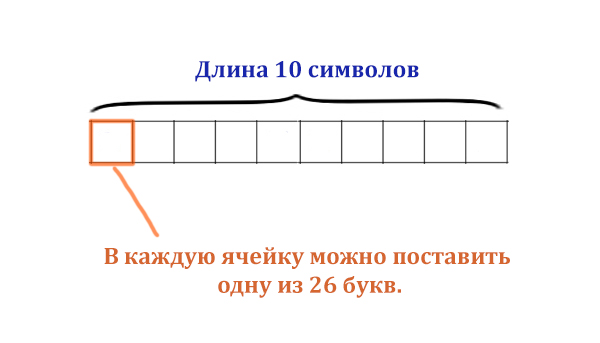
При регистрации в компьютерной системе каждому пользователю выдаётся пароль, состоящий из 10 символов. В качестве символов используют прописные буквы латинского алфавита, т.е. 26 различных символов. В базе данных для хранения каждого пароля отведено одинаковое и минимально возможное целое число байт. При этом используют посимвольное кодирование паролей, все символы кодируют одинаковым и минимально возможным количеством бит. Определите объём памяти (в байтах), необходимый для хранения данных о 50 пользователях. В ответе запишите только целое число – количество байт.
Решение:
У каждого пользователя есть пароль, состоящий из 10 символов. Это значит, длина пароля 10 символов!
И в каждую ячейку мы может выбрать символ из 26 букв!
Здесь важно различать длину пароля и количество символов из которых пользователь выбирает для каждой ячейки пароля.
Теперь нужно определить: сколько бит занимает одна ячейка (1 символ пароля!).
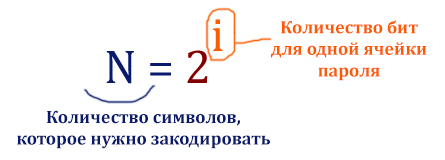
Когда речь идёт о количестве бит, применяем формулу, которую мы использовали в 7 задании из ЕГЭ по информатике. Там мы кодировали цвета для одного пикселя, а здесь нужно закодировать 26 букв для одного поля пароля.
Применяем:
N = 2i = 26
Целого числа нету для i (количества бит), чтобы равенство было верным. Значит берём столько количество бит, сколько точно будет достаточно, чтобы закодировать 26 букв (символов).
N = 25 > 26
Получаем одна ячейка (одно поле) пароля занимаем 5 бит! А в пароле их 10! Значит, весь пароль будет занимать:
Vпароля = 5 бит * 10 символов = 50 бит (в одном пароле!)
В условии сказано: для хранения каждого пароля отведено одинаковое и минимально возможное целое число байт. Это означает, что мы не может выделять память по одному биту. Память выделяется блоками по 8 бит (по одному байту).
Если взять 7 блоков по 8 бит (1 байту), то нам хватит этого на один пароль.
7 блоков (байт) * 8 бит = 56 бит > 50 бит
Таким образом, на 1 пароль потребуется 7 байт!
Тогда на 50 пользователей потребуется:
50 пользователей * 7 байт = 350 байт (для 50 пользователей).
Ответ: 350
Разберём задачу, которая была на реальном экзамене в Москве
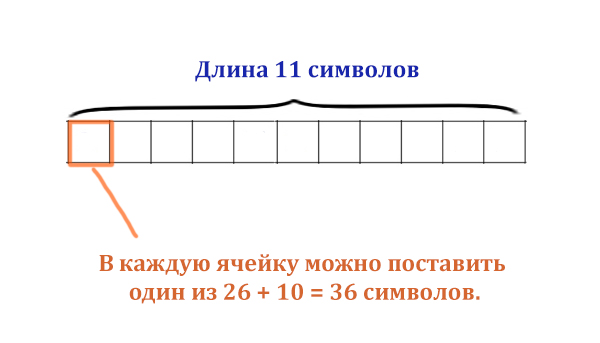
Задача (ЕГЭ по информатике, 2020, Москва)
При регистрации в компьютерной системе каждому пользователю выдаётся
пароль, состоящий из 11 символов. В качестве символов используют 26
прописных букв из латинского алфавита и десять цифр. В базе
данных для хранения каждого пароля отведено одинаковое и минимально
возможное целое число байт. При этом используют посимвольное
кодирование паролей, все символы кодируют одинаковым
и минимально возможным количеством бит.
Кроме собственно пароля для каждого пользователя в системе хранятся дополнительные сведения.
Для кодирования данных о 30 сотрудниках было выделено 750 байт. Сколько памяти(в байтах) выделено для хранения дополнительных сведений об одном пользователе. В ответ запишите только целое число — количество байт.
Решение:
Здесь длина пароля составляет 11 символов!
Найдём сколько бит занимает одна ячейка пароля.
N = 2i = 36
N = 26 = 64 > 36
Значит, 6 бит — минимальное количество бит, которое нужно, чтобы была возможность разместить любой из 36 символов в одной ячейке пароля.
Найдём сколько бит нужно на весь пароль.
Vпароля = 6 бит * 11 символов = 66 бит (в одном пароле!)
Теперь найдём, а сколько байт нужно на 1 пароль:
9 * 8 бит = 72 бит > 66 бит
Следовательно, 9 байт достаточно, чтобы покрыть 66 бит на 1 пароль.
Сказано, что для 30 сотрудников выделено 750 байт. Подсчитаем, сколько байт будет выделено на одного сотрудника.
Vпользователя = 750 байт / 30 = 25 байт (приходится на одного пользователя)
Мы выяснили, что на пароль из этих 25 байт потребуется 9 байт. Тогда на дополнительную информацию о каждом пользователе потребуется:
Vдоп. о 1 пол. = 25 байт — 9 байт = 16 байт
Это и будет ответ.
Ответ: 16
Ещё один важный пример из запасов тренировочных задач ЕГЭ по информатике.
Задача (Номера спортсменов)
В велокроссе участвуют 48 спортсменов. Специальное устройство регистрирует прохождение каждым из участников промежуточного финиша, записывая его номер с использованием минимально возможного количества бит, одинакового для каждого спортсмена. Какой объём памяти будет использован устройством, когда все спортсмены прошли промежуточный финиш? (Ответ дайте в байтах.)
Решение:
Узнаем сколько бит потребуется выделить на каждого спортсмена, чтобы была возможность записать любой номер от 1 до 48.
В этой задаче сказано: записывая его номер с использованием минимально возможного количества бит, одинакового для каждого спортсмена . Это означает что у нас есть 48 различных позиций (номеров), которые нужно закодировать с помощью определённого количества бит. В предыдущей задаче, у нас было 62 различные позиции (символа), которые нужно было закодировать с помощью определённого количества бит. Мы там использовали формулу N = 2i.
Поэтому будем опять применять формулу N = 2i.
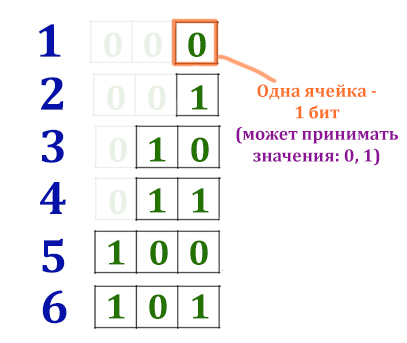
На рисунке показано, как может происходить кодирование чисел. Например, для двух номеров потребуется 1 бит (21 = 2), для четырёх номеров потребуется два бита (22 = 4). Нам нужно закодировать 48 чисел! Причём для каждого участника отведено одинаковое количество бит!
Можно сказать, что здесь работает формула, которую рассматривали в 8 задании. Всего нужно составить 48 различных комбинаций (закодировать 48 номеров). В каждой ячейке можно писать либо 0, либо 1 (Свойство бита информации). Какова должна быть длина «слова» (количество бит) ?
N = 2i = 26 бит = 64 > 48
Получается 6 бит потребуется для того, чтобы была возможность записать любой номер от 1 до 48 для каждого спортсмена. Если взять пять бит, то мы будем иметь возможность записать номера только от 1 до 25 = 32 для каждого спортсмена (этого не хватает).
Т.к. все участники пересекли финиш, а на каждого участника выделено по 6 бит, то получается:
6 бит * 48 = 288 бит = 36 байт
Ответ: 36
Задача (Автомобильный номер)
В некоторой стране автомобильный номер состоит из 7 символов: сначала 2 буквы, затем 3 цифры, затем ещё 2 буквы. При этом буквы могут быть выбраны только из 12 строчных букв местного алфавита. Среди цифр не используются цифры 6 и 9. Автоматизированная система хранит номера автомобилей следующим образом. Используется посимвольное кодирование. В памяти системы для кодирования каждого символа используется минимально возможное и одинаковое целое количество бит (для букв и цифр отдельно). А для номера используется минимально возможное целое количество байт. Какое количество информации (в байтах) требуется для хранения номеров 160 автомобилей ?
Решение:
Найдём сколько бит потребуется для кодирования 4-х букв.
N = 2i = 24 бита = 16 > 12
4 бита хватит для кодирования 12 букв. Всего таких ячейки 4! Поэтому в одном номере на все буквы уйдёт 4 * 4 бита = 16 бит.
Найдём сколько бит потребуется на кодирование 3 ячеек, где находятся цифры.
N = 2i = 23 бита = 8
Для кодирования одной ячейки, где находится цифра, потребуется 3 бита.
Все цифры в одном номере будут закодированы 3 бита * 3 = 9 битами.
Всего на один номер уйдёт 16 бит + 9 бит = 25 бит.
Найдём сколько байт потребуется для кодирования одного номера.
4 * 8 бит (1 байт) = 32 бита > 25 бит
4-х байт достаточно, чтобы закодировать 25 бит. Если взять 3 байта, то 3 * 8 бит (1 байт) = 24 бита. Этого будет не достаточно.
Найдём количество байт, которое нужно для кодирования 160 автомобилей
160 автомобилей * 4 байта = 640 байт
Это и будет ответ.
Ответ: 640
Задача (Закрепление формулы)
Метеорологическая станция ведет наблюдение за влажностью воздуха. Результатом одного наблюдения является целое число от 0 до 100%, записываемое при помощи минимально возможного количества бит. Станция сделала 800 измерений. Определите информационный объем результатов наблюдений. (Ответ дайте в байтах.)
Решение:
Здесь, нужно закодировать сто одно число (от 0 до 100). Ситуация похоже на ту, где мы кодировали номера спортсменов.
N = 2i = 27 бит = 128 > 101
Получается, что 7 бит потребуется, чтобы полностью закодировать 101 число.
Всего было сделано 800 таких измерений
800 * 7 бит = 5600 бит = 700 байт
Ответ: 700
На этом всё! Удачи при решении 11 задания на ЕГЭ по информатике!
Автор материалов — Лада Борисовна Есакова.
Рекурсия — это способ определения объектов (понятий), при котором определение объекта строится, опираясь на само понятие объекта.
Для того, чтобы задать рекурсию, необходимо описать:
— условие остановки рекурсии (базовый случай);
— рекуррентную формулу.
В программировании если процедура вызывает сама себя, то, по сути, это приводит к повторному выполнению содержащихся в ней инструкций, что аналогично работе цикла. Рекурсия позволяет заменить цикл и в некоторых сложных задачах делает решение более понятным, хотя часто менее эффективным.
Некоторые языки программирования не содержат циклических конструкций вовсе, предоставляя программистам организовывать повторения с помощью рекурсии (например, Пролог, где рекурсия — основной прием программирования).
Классическим примером рекурсивного алгоритма является описание вычисления факториала:
где F(n-1)=(n-1)!
Рекурсивные алгоритмы вычисления одной функции
Пример 1.
Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими рекуррентными соотношениями:
F(n) = 1 при n = 1;
F(n) = F(n − 1) · n при n ≥ 2.
Чему равно значение функции F(6)?
В ответе запишите только натуральное число.
Решение:
Последовательно найдём значения функции от базового случая F(1) до искомого значения F(6):
F(1) = 1
F(2) = 2
F(3) = 6
F(4) = 24
F(5) = 120
F(6) = 720
Ответ:720
Рекурсивные алгоритмы вычисления нескольких функций
Пример 2.
Алгоритм вычисления значений функций F(n) и G(n), где n – натуральное число, задан следующими соотношениями:
F(1) = 1; G(1) = 1;
F(n) = F(n–1) – G(n–1),
G(n) = F(n–1) + 2*G(n–1), при n >=2
Чему равно значение величины F(5)/G(5)? В ответе запишите только целое число.
Решение:
Последовательно найдём значения функций от базового случая F(1), G(1) до искомых значений F(5), G(5):
F(1) = 1; G(1) = 1;
F(2) = F(1) – G(1) = 1 – 1 = 0;
G(2) = F(1) + 2*G(1) = 1+2 = 3;
F(3) = F(2) – G(2) = 0 – 3 = -3;
G(3) = F(2) + 2*G(2) = 0+6 = 6;
F(4) = F(3) – G(3) = -3 – 6 = -9 ;
G(4) = F(3) + 2*G(3) = -3+12 = 9;
F(5) = F(4) – G(4) = -9 – 9 = -18;
G(5) = F(4) + 2*G(4) = -9+18 = 9.
F(5)/G(5) = -18/9 = -2
Ответ:-2
Рекурсивные алгоритмы выполнения процедур
Пример 3.
Ниже на пяти языках программирования записан рекурсивный алгоритм F.
|
Бейсик |
Python |
| SUB F(n)
PRINT n IF n < 5 THEN F(n + 1) F(n + 3) END IF END SUB |
def F(n):
print(n) if n < 5: F(n + 1) F(n + 3) |
|
Паскаль |
Алгоритмический язык |
| procedure F(n: integer);
begin writeln(n); if n < 5 then begin F(n + 1); F(n + 3) end end |
алг F(цел n)
нач вывод n, нс если n < 5 то F(n + 1) F(n + 3) все кон |
|
Си |
|
| void F(int n)
{ printf(«%dn», n); if (n < 5) { F(n + 1); F(n + 3); } } |
Чему равна сумма всех чисел, напечатанных на экране при выполнении вызова F(1)?
Решение:
Выпишем последовательно все действия, которые выполнят запускаемые процедуры:
F(1) выполнит следующие действия: Вывод числа 1, F(2), F(4)
F(2) выполнит следующие действия: Вывод числа 2, F(3), F(5)
F(4) выполнит следующие действия: Вывод числа 4, F(5), F(7)
F(3) выполнит следующие действия: Вывод числа 3, F(4), F(6)
F(5) выполнит следующие действия: Вывод числа 5
F(5) выполнит следующие действия: Вывод числа 5
F(7) выполнит следующие действия: Вывод числа 7
F(4) выполнит следующие действия: Вывод числа 4, F(5), F(7)
F(6) выполнит следующие действия: Вывод числа 6
F(5) выполнит следующие действия: Вывод числа 5
F(7) выполнит следующие действия: Вывод числа 7
Просуммируем все числа, выведенные на экран: 1+2+4+3+5+5+7+4+6+5+7 = 49
Ответ: 49
Пример 4.
Ниже на пяти языках программирования записаны две рекурсивные функции (процедуры): F и G.
Сколько символов «звёздочка» будет напечатано на экране при выполнении вызова F(11)?
Решение:
Выпишем последовательно все действия, которые выполнят запускаемые процедуры:
F(11) G(10) * F(7) G(6) * F(3) G(2) * F(-1)
Всего на экране будет напечатано 3 «звездочки».
Ответ: 3
Пример 7.36.
Дан рекурсивный алгоритм:
procedure F(n: integer);
begin
writeln(‘*’);
if n > 0 then begin
F(n-3);
F(n-2);
F(n div 2);
F(n div 2);
end
end;
Сколько символов «звездочка» будет напечатано на экране при выполнении вызова F(6)?
Решение:
Для наглядности изобразим схему работы алгоритма в виде дерева:
Причем, распишем до конца каждое значение F(n) только один раз. Например, расписав один раз F(1), мы видим, что она напечатает в результате 5 звездочек. Т.е. F(1) = 5.
Проанализировав дерево, видим, что
F(0) = 1
F(2) = 3 + 2*F(1) = 13
F(3) = 1 + F(0) + 3*F(1) = 1 + 1 + 15 = 17
F(4) = 1 + F(1) + 3*F(2) = 1 + 5 + 3*13 = 45
F(6) = 1 + 3*F(3) + F(4) = 1 + 3*17 + 45 = 46 + 51 = 97
Ответ: 97
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Задача №11. Использование рекурсивных алгоритмов.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
09.03.2023
- Взрослым: Skillbox, Geekbrains, Хекслет, Eduson, XYZ, Яндекс.
- 8-11 класс: Умскул, Лектариум, Годограф, Знанио.
- До 7 класса: Алгоритмика, Кодланд, Реботика.
- Английский: Инглекс, Puzzle, Novakid.
Формулы для заданий ЕГЭ по информатике
Кодирование текстовой информации
I = n * i
- n — количество символов
- i — количество бит на 1 символ (кодировка)
Формула для нахождения количества цветов в используемой палитре
i = log2N
- N — количество цветов
- i — глубина цвета
Формула объема памяти для хранения растрового изображения
I = M * N * i
- I — объем памяти, требуемый для хранения изображения
- M — ширина изображения в пикселях
- N — высота изображения в пикселях
- i — глубина кодирования цвета или разрешение
Или
I = N * i битов
- N – количество пикселей (M * N)
- i – глубина кодирования цвета (разрядность кодирования)
Для указания объема выделенной памяти встречаются разные обозначения (V или I).
Формула объема звукового файла
I = β * ƒ * t * S
- I — объем
- β — глубина кодирования
- ƒ — частота дискретизации
- t — время
- S — количество каналов (S=1 для моно, S=2 для стерео, S=4 для квадро)
Формула объема переданной информации
I = V * t
- I — объем информации
- v — пропускная способность канала связи (измеряется в битах в секунду и пр.)
- t — время передачи
Формула скорости передачи данных
V = I / t
- I — объем информации
- v — пропускная способность канала связи (измеряется в битах в секунду и пр.)
- t — время передачи
Формулы преобразования
- 1 Мбайт = 220 байт = 223 бит,
- 1 Кбайт = 210 байт = 213 бит
- Взрослым: Skillbox, Geekbrains, Хекслет, Eduson, XYZ, Яндекс.
- 8-11 класс: Умскул, Лектариум, Годограф, Знанио.
- До 7 класса: Алгоритмика, Кодланд, Реботика.
- Английский: Инглекс, Puzzle, Novakid.
В решение заданий демо-версии используется язык программирования Python.
|
Задание 1. Анализ информационных моделей На рисунке схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о протяжённости каждой из этих дорог (в километрах). Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите, какова сумма протяжённостей дорог из пункта D в пункт В и из пункта F в пункт A. В ответе запишите целое число. |
На графе расставим веса вершин. Далее 2 и 7 вершины ведут нас к 5, значит А это 5, оставшаяся «тройка» это вершина Е под номером 6. Сумма дорог BD + AF = 53 + 5 = 58 Ответ: 58 |
||||||||||||||||||
|
Задание 2. Построение таблиц истинности логических выражений Миша заполнял таблицу истинности логической функции F F= ¬(y → x) v (z→ w) v ¬z , но успел заполнить лишь фрагмент из трёх различных её строк, даже не указав, какому столбцу таблицы соответствует каждая из переменных w, x, y, z. Определите, какому столбцу таблицы соответствует каждая из переменных w, x, y, z. В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала буква, соответствующая первому столбцу; затем буква, соответствующая второму столбцу, и т.д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно. Пример. Функция задана выражением ¬x v y, зависящим от двух переменных, а фрагмент таблицы имеет следующий вид. В этом случае первому столбцу соответствует переменная y, а второму столбцу – переменная x. В ответе следует написать yx. |
¬(y → x) v (z→ w) v ¬z=0. Следовательно y → x =1, z→ w=0, z=1. Значит третий столбец z. z→ w=0, значит w=0, и это может быть только 4 столбец. y → x =1, следовательно из второй строки мы видим, что первый столбец может быть только у, а второй х.
Решение на Python Ответ: YXZW |
||||||||||||||||||
Задание 3. Базы данных. Файловая система В прикрепленном файле приведён фрагмент базы данных «Продукты» о поставках товаров в магазины районов города. База данных состоит из трёх таблиц. Таблица «Движение товаров» содержит записи о поставках товаров в На рисунке приведена схема указанной базы данных. Используя информацию из приведённой базы данных, определите общий вес |
На третьем листе книги применим фильтр по району и получим ID четырех магазинов. На втором листе применим фильтр по товару и получим ID товара. На первом листе применим фильтры по ID товара и ID магазинов и типу операции. Все даты попадают в интервал от 1 до 8 июня. Получим: Поступило в продажу 710 упаковок. В упаковке 0,5 кг. Получим 355 кг. Ответ: 355 |
||||||||||||||||||
|
Задание 4. Кодирование и декодирование информации По каналу связи передаются сообщения, содержащие только буквы из набора: А, З, К, Н, Ч. Для передачи используется двоичный код,удовлетворяющий прямому условию Фано, согласно которому никакое кодовое слово не является началом другого кодового слова. Это условие обеспечивает возможность однозначной расшифровки закодированных сообщений. Кодовые слова для некоторых букв известны: Н – 1111, З – 110. Для трёх оставшихся букв А, К и Ч кодовые слова неизвестны. Какое количество двоичных знаков потребуется для кодирования слова КАЗАЧКА, если известно, что оно закодировано минимально возможным количеством двоичных знаков? |
Ответ: 14 |
||||||||||||||||||
|
Задание 5. Анализ и построение алгоритмов для исполнителей На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему 1. Строится двоичная запись числа N. Полученная таким образом запись является двоичной записью искомого числа R.Например, для исходного числа 610 = 1102 результатом является число |
Минимальное R, большее 40, это 41. ИЛИ программное решение Ответ: 16
|
||||||||||||||||||
|
Задание 6. Определение результатов работы простейших алгоритмов Исполнитель Черепаха действует на плоскости с декартовой системой координат. Черепахе был дан для исполнения следующий алгоритм: Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует 5 команд: Поднять хвост, означающая переход к перемещению без рисования; Опустить хвост, означающая переход в режим рисования; Вперёд n (где n– целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова; Назад n (где n– целое число), вызывающая передвижение в противоположном голове направлении; Направо m (где m – целое число), вызывающая изменение направления движения на m градусов по часовой стрелке, Налево m (где m– целое число), вызывающая изменение направления движения на m градусов против часовой стрелки. Запись Повтори k [Команда1 Команда2 … КомандаS] означает, что последовательность из S команд повторится k раз. Черепахе был дан для исполнения следующий алгоритм: Определите, сколько точек с целочисленными координатами будут находиться внутри пересечения фигур, ограниченных заданными алгоритмом линиями, включая точки на границах этого пересечения. |
Сначала нужно построить фигуру. Далее мы находим уравнения прямых, которыми ограничена фигура и решаем ИЛИ Ответ: 1 задание — 38, 2 задание — 128 |
||||||||||||||||||
|
Задание 7. Кодирование и декодирование информации. Передача информации Музыкальный фрагмент был записан в формате моно, оцифрован и сохранён в виде файла без использования сжатия данных. Размер полученного файла – 28 Мбайт. Затем тот же музыкальный фрагмент был записан повторно в формате стерео (двухканальная запись) и оцифрован с разрешением в 3,5 раза выше и частотой дискретизации в 2 раза меньше, чем в первый раз. Сжатие данных не производилось. Укажите размер полученного при повторной записи файла в Мбайт. В ответе запишите только целое число, единицу измерения писать не нужно. |
I = ν ⋅ i ⋅ t ⋅ k, где ν — частота дискретизации (Гц), i — разрешение (бит), t — время (с), k — количество дорожек (1 -моно, 2- стерео, 4 — квадро) I1 = ν ⋅ i ⋅ t I2 = 3,5 · 28 = 98 Ответ: 98 |
||||||||||||||||||
|
Задание 8. Перебор слов и системы счисления Определите количество пятизначных чисел, записанных в восьмеричной системе счисления, в записи которых только одна цифра 6, при этом никакая нечётная цифра не стоит рядом с цифрой 6. |
* * * * * — пятизначное число. 6 * * * * — вариантов 3 ⋅ 7 ⋅ 7 ⋅ 7 = 1029 Ответ: 2961 |
||||||||||||||||||
Задание 9. Работа с таблицами Файл с данными Откройте файл электронной таблицы, содержащей в каждой строке шесть натуральных чисел. Определите количество строк таблицы, содержащих числа, для которых выполнены оба условия: |
Для решения этой задачи понадобится 10 вспомогательных столбцов. Сначала мы посчитаем количество повторяющихся чисел в каждой строке. Затем сумму каждой строки диапазона H:M. Если повторений нет, то эта сумма равна 6. Далее мы найдем среднее арифметическое неповторяющихся значений. Затем найдем сумму повторяющихся значений. Затем проверим соблюдение двух условий. И подсчитаем количество строк, в которых соблюдаются оба условия. Ответ: 2241 |
||||||||||||||||||
Задание 10. Поиск символов в текстовом редакторе Файл с данными Текст произведения Льва Николаевича Толстого «Севастопольские рассказы» представлен в виде файлов различных форматов. Откройте один из файлов и определите, сколько раз встречается в тексте отдельное слово «теперь» со строчной буквы. Другие формы этого слова учитывать не следует. |
В текстовом редакторе используем инструмент найти (по умолчанию он не учитывает регистр, в расширенном поиске есть кнопка больше, где можно проверить настройки). Ищем слово целиком. Ставим галочку учитывать регистр. Слово теперь со строчной буквы встречается 45 раз. Ответ: 45 |
||||||||||||||||||
|
Задание 11. Вычисление количества информации При регистрации в компьютерной системе каждому объекту присваивается идентификатор, состоящий из 250 символов и содержащий только десятичные цифры и символы из 1650-символьного специального алфавита. В базе данных для хранения каждого идентификатора отведено одинаковое и минимально возможное целое число байт. При этом используется посимвольное кодирование идентификаторов, все символы кодируются одинаковым и минимально возможным количеством бит. Определите объём памяти (в Кбайт), необходимый для хранения 65 536 идентификаторов. В ответе запишите только целое число – количество Кбайт. |
I = K · i, N = 2 i ID : ****….**** – всего 250 различных символов в наборе N = 10 + 1650 = 1660, 1024<1660<2048, 2048 = 211, значит для кодирования одного символа нужно 11 бит. IID = 250 · 11 = 2750 бит = 343,75 байт ≈ 344 байт – отводится на идентификатор целое число байт I65536 = 65536 ⋅ 344 = 22544384 байта = 22016 Кбайт– всего Ответ: 22016 |
||||||||||||||||||
|
Задание 12. Выполнение алгоритмов для исполнителей Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки цифр. А) заменить (v, w). Эта команда заменяет в строке первое слева вхождение цепочки v на цепочку w. Б) нашлось (v). Эта команда проверяет, встречается ли цепочка v в строке исполнителя Редактор. Если она встречается, то команда возвращает логическое значение «истина», в противном случае возвращает значение «ложь». Строка исполнителя при этом не изменяется. Цикл выполняется, пока условие истинно. В конструкции ЕСЛИ условие выполняется команда 1 (если условие истинно). В конструкции ЕСЛИ условие выполняется команда 1 (если условие истинно) или команда 2 (если условие ложно). Дана программа для Редактора: |
def pr(n): #функция определяет простое ли число for n in range(100): #перебираем n if ‘>2’ in s: if ‘>0’ in s: sum_s = 0 Ответ: 5 |
||||||||||||||||||
|
Задание 13. Поиск путей в графе На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К, Л. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. |
Начнем подсчет из вершины Е налево через В и возвращаемся в Е через Л. Ответ: 21 |
||||||||||||||||||
|
Задание 14. Кодирование чисел. Системы счисления Операнды арифметического выражения записаны в системе счисления с основанием 15. |
for x in range(15): if n%14 == 0: Ответ: 8767 |
||||||||||||||||||
|
Задание 15. Преобразование логических выражений На числовой прямой даны два отрезка: D = [17; 58] и C = [29; 80]. Укажите наименьшую возможную длину такого отрезка A, для которого логическое выражение |
def deli(n,m): for A in range(1,1000): if Ok: Ответ: 94 |
||||||||||||||||||
|
Задание 16. Рекурсивные алгоритмы Алгоритм вычисления значения функции F(n), где n – натуральное число, |
F(2023) = 2023! = 2023 ⋅ 2022! F(2023)/F(2020) = (2023 ⋅ 2022 ⋅ 2021 ⋅ 2020!)/2020! = 2023 ⋅ 2022 ⋅ 2021 = = 8266912626 Ответ: 8266912626 |
||||||||||||||||||
Задание 17. Проверка на делимость Файл с данными В файле содержится последовательность целых чисел. Элементы последовательности могут принимать целые значения от –10 000 до 10 000 включительно. Определите количество пар последовательности, в которых |
f= open(’17.txt’) k = 0 for i in p: for i in range(1,len(p)): #Осторожно, скобки! print(k,PP) Ответ: 180 190360573 |
||||||||||||||||||
Задание 18. Робот-сборщик монет Файл с данными Квадрат разлинован на N×N клеток (1 < N < 17). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вниз. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вниз — в соседнюю нижнюю. При попытке выхода за границу квадрата Робот разрушается. Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от 1 до 100. Посетив клетку, Робот забирает монету с собой; это также относится к начальной и конечной клетке маршрута Робота. Откройте файл. Определите максимальную и минимальную денежную сумму, которую может собрать Робот, пройдя из левой верхней клетки в правую нижнюю. В ответ запишите два числа друг за другом без разделительных знаков — сначала максимальную сумму, затем минимальную. Исходные данные представляют собой электронную таблицу размером N×N, каждая ячейка которой соответствует клетке квадрата.Пример входных данных:
Для указанных входных данных ответом должна быть пара чисел 41 и 22. |
Сначала скопируем таблицу рядом, начиная со столбца АА, можно уменьшить ширину столбца до 4-5. Ячейка АА1=А1. Ячейка АВ1 = АА1+В1, протягиваем ее до АТ1. Ячейка АА2 = АА1 + А2, протягиваем ее до АА20. Далее ячейка АВ2 = В2+МАКС(АА2;АВ1), протягиваем ее на весь оставшийся диапазон, копируем только значения, не трогая стен. Справа от стен формулы повторяют крайний левый рял, столбец АА, снизу от стен формулы копируют верхнюю строку 1. Далее делаем замену всех формул МАКС на МИН. Ответ: 1099 1026 |
||||||||||||||||||
|
Задание 19. Выигрышная стратегия. Задание 1 Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один камень или увеличить количество камней в куче в два раза. Для того чтобы делать ходы, у каждого игрока есть неограниченное количество камней. Игра завершается в тот момент, когда количество камней в куче становится не менее 129. Победителем считается игрок, сделавший последний ход, т.е. первым получивший кучу из 129 или больше камней. В начальный момент в куче было S камней, 1 ≤ S ≤ 128. Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Укажите такое значение S, при котором Петя не может выиграть за один ход, но при любом ходе Пети Ваня может выиграть своим первым ходом. |
При значениях S < 64 у Пети есть возможность сделать такой ход, что Ваня не сможет выиграть своим первым ходом. При значении S = 64 Петя своим первым ходом может получить 65 или 128 камней в куче. Во всех случаях Ваня увеличивает количество камней в куче в два раза и выигрывает своим первым ходом. Ответ: 64 |
||||||||||||||||||
|
Задание 20. Выигрышная стратегия. Задание 2 Для игры, описанной в задании 19, найдите два таких значения S, при которых у Пети есть выигрышная стратегия, причем одновременно выполняются два условия:
Найденные значения запишите в порядке возрастания. |
Значение S должно быть меньше 64, поскольку иначе Ваня сможет выиграть своим первым ходом. Ответ: 32 63 |
||||||||||||||||||
|
Задание 21. Выигрышная стратегия. Задание 3 Для игры, описанной в задании 19, найдите значение S, при котором одновременно выполняются два условия:
Если найдено несколько значений S, в ответе запишите минимальное из них. |
Ответ: 62 |
||||||||||||||||||
|
Задание 22. Многопроцессорные системы В файле содержится информация о совокупности N вычислительных процессов, которые могут выполняться параллельно или последовательно. Будем говорить, что процесс B зависит от процесса A, если для выполнения процесса B необходимы результаты выполнения процесса A. В этом случае процессы могут выполняться только последовательно. Определите минимальное время, через которое завершится выполнение всей совокупности процессов, при условии, что все независимые друг от друга процессы могут выполняться параллельно. |
В независимых процессах время считается от 0, Ответ: 17 |
||||||||||||||||||
|
Задание 23. Анализ программы с циклами и условными операторами Исполнитель преобразует число на экране. |
def f(x, y): print (f(1,10) * f(10, 35)) Ответ: 98 |
||||||||||||||||||
Задание 24. Анализ программы с циклами и условными операторами Файл с данными Текстовый файл состоит из символов A, C, D, F и O. Определите максимальное количество идущих подряд пар символов вида согласная + гласная |
f=open(’24.txt’) PP = [‘CA’, ‘CO’, ‘DA’, ‘DO’, ‘FA’, ‘FO’] for i in range(1, len(p), 2): Ответ: 95 |
||||||||||||||||||
|
Задание 25. Анализ программы с циклами и условными операторами Назовём маской числа последовательность цифр, в которой также могут Например, маске 123*4?5 соответствуют числа 123405 и 12300405. Среди натуральных чисел, не превышающих 1010, найдите все числа, соответствующие маске 1?2139*4, делящиеся на 2023 без остатка. |
Самый простой способ использовать библиотеку fnmatch. или так полным перебором: y = {»,’0′,’00’,’000′} for x in range (1000): Ответ: 162139404 80148 |
||||||||||||||||||
Задание 26. Анализ программы с циклами и условными операторами В магазине для упаковки подарков есть N кубических коробок. Самой интересной считается упаковка подарка по принципу матрёшки – подарок упаковывается в одну из коробок, та в свою очередь в другую коробку и т.д. |
|||||||||||||||||||
Задание 27. Анализ программы с циклами и условными операторами У медицинской компании есть N пунктов приёма биоматериалов на анализ. Все пункты расположены вдоль автомагистрали и имеют номера, соответствующие расстоянию от нулевой отметки до конкретного пункта. Известно количество пробирок, которое ежедневно принимают в каждом из пунктов. Пробирки перевозят в специальных транспортировочных контейнерах вместимостью не более 36 штук. Каждый транспортировочный контейнер упаковывается в пункте приёма и вскрывается только в лаборатории. Файл А Дано два входных файла (файл A и файл B), каждый из которых в первой строке содержит число N (1 ≤ N ≤ 10 000 000) – количество пунктов приёма биоматериалов. В каждой из следующих N строк находится два числа: номер пункта и количество пробирок в этом пункте (все числа натуральные, количество пробирок в каждом пункте не превышает 1000). Пункты перечислены в порядке их расположения вдоль дороги, начиная от нулевой отметки. Типовой пример имеет иллюстративный характер. Для выполнения задания используйте данные из прилагаемых файлов. |
Ответ: 51063 5634689219329 |
7 января 2022
В закладки
Обсудить
Жалоба
Умение подсчитывать информационный объём сообщения.
Большая подборка с разборами всех прототипов, которые есть на текущий день.
→ кодирование паролей,
→ номера и танки,
→ задачи на определенные конфигурации строк.
11inf.pdf
Источник: vk.com/inform_web
№1. Алгоритм вычисления значения функции
F(n), где n – натуральное число, задан следующими соотношениями:
F(1) = 1
F(2) = 3
F(n) = F(n–1) * n + F(n–2) * (n – 1) , при n >2
Чему равно значение функции F(5)?
В ответе запишите только натуральное число.
Пояснение.
Последовательно находим:
F(3) = F(2) * 3 + F(1) * 2 = 11,
F(4) = F(3) * 4 + F(2) * 3 = 53,
F(5) = F(4) * 5 + F(3) * 4 = 309.
№2. Алгоритм вычисления значения функции
F(n), где n – натуральное число, задан следующими соотношениями:
F(1) = 1
F(2) = 3
F(n) = F(n−1) * F(n−2) + (n−2), при n > 2
Чему равно значение функции F(5)?
В ответе запишите только натуральное число.
Пояснение.
Последовательно находим:
F(3) = F(2) * F(1) + 1 = 4,
F(4) = F(3) * F(2) + 2 = 14,
F(5) = F(4) * F(3) + 3 = 59.
№3. Алгоритм вычисления значения функции
F(n), где n – натуральное число, задан следующими соотношениями:
F(1) = 1
F(2) = 2
F(n) = 2 * F(n–1) + (n – 2) * F(n–2), при n >2
Чему равно значение функции F(6)?
В ответе запишите только натуральное число.
Пояснение.
Последовательно находим:
F(3) = 2 * F(2) + (3 – 2) * F(1) = 5,
F(4) = 2 * F(3) + (4 – 2) * F(2) = 14,
F(5) = 2 * F(4) + (5 – 2) * F(3) = 43,
F(6) = 2 * F(5) + (6 – 2) * F(4) = 142.
№4. Последовательность чисел Фибоначчи
задается рекуррентным соотношением:
F(1) = 1
F(2) = 1
F(n) = F(n–2) + F(n–1), при n >2, где n – натуральное
число.
Чему равно восьмое число в последовательности Фибоначчи?
В ответе запишите только натуральное число.
Пояснение.
Последовательно находим:
F(3) = F(1) + F(2) = 2,
F(4) = F(2)
+ F(3) = 3,
F(5) = F(3)
+ F(4) = 5,
F(6) = F(4)
+ F(5) = 8,
F(7) = F(5)
+ F(6) = 13,
F(8) = F(6) + F(7) = 21.
Восьмое число в последовательности Фибоначчи равно
21.
№5. Последовательность чисел Фибоначчи
задается рекуррентным соотношением:
F(1) = 1
F(2) = 1
F(n) = F(n–2) + F(n–1), при n >2, где n – натуральное
число.
Чему равно девятое число в последовательности Фибоначчи?
В ответе запишите только натуральное число.
Пояснение.
Последовательно находим:
F(3) = F(1) + F(2) = 2,
F(4) = F(2)
+ F(3) = 3,
F(5) = F(3)
+ F(4) = 5,
F(6) = F(4)
+ F(5) = 8,
F(7) = F(5)
+ F(6) = 13,
F(8) = F(6) + F(7) = 21,
F(9) = F(7) + F(8) = 34.
Девятое число в последовательности Фибоначчи
равно 34.
№6. Последовательность чисел трибоначчи
задается рекуррентным соотношением:
F(1) = 0
F(2) = 1
F(3) = 1
F(n) = F(n–3) + F(n–2) + F(n–1), при n >3, где n – натуральное
число.
Чему равно девятое число в последовательности трибоначчи?
В ответе запишите только натуральное число.
Пояснение.
Последовательно находим:
F(4) = F(1) + F(2) + F(3) = 2,
F(5) = F(2)
+ F(3) + F(4) = 4,
F(6) = F(3)
+ F(4) + F(5) = 7,
F(7) = F(4)
+ F(5) + F(6) = 13,
F(8) = F(5) + F(6) + F(7) = 24,
F(9) = F(6) + F(7) + F(8) = 44.
Девятое число в последовательности трибоначчи
равно 44.
№7. Последовательность чисел трибоначчи
задается рекуррентным соотношением:
F(1) = 0
F(2) = 1
F(3) = 1
F(n) = F(n–3) + F(n–2) + F(n–1), при n >3, где n – натуральное
число.
Чему равно одиннадцатое число в последовательности
трибоначчи?
В ответе запишите только натуральное число.
Пояснение.
Последовательно находим:
F(4) = F(1) + F(2) + F(3) = 2,
F(5) = F(2)
+ F(3) + F(4) = 4,
F(6) = F(3)
+ F(4) + F(5) = 7,
F(7) = F(4)
+ F(5) + F(6) = 13,
F(8) = F(5)
+ F(6) + F(7) = 24,
F(9) = F(6)
+ F(7) + F(8) = 44,
F(10) =
F(7) + F(8) + F(9) = 81,
F(11) = F(8) + F(9) + F(10) = 149.
Одиннадцатое число в последовательности трибоначчи
равно 149.
№8. Последовательность чисел Люка задается
рекуррентным соотношением:
F(1) = 2
F(2) = 1
F(n) = F(n–2) + F(n–1), при n >2, где n – натуральное
число.
Чему равно восьмое число в последовательности Люка?
В ответе запишите только натуральное число.
Пояснение.
Последовательно находим:
F(3) = F(1) + F(2) = 3,
F(4) = F(2)
+ F(3) = 4,
F(5) = F(3)
+ F(4) = 7,
F(6) = F(4)
+ F(5) = 11,
F(7) = F(5)
+ F(6) = 18,
F(8) = F(6) + F(7) = 29.
Восьмое число в последовательности Люка равно 29.
№9. Последовательность чисел Люка задается
рекуррентным соотношением:
F(1) = 2
F(2) = 1
F(n) = F(n–2) + F(n–1), при n >2, где n – натуральное
число.
Чему равно десятое число в последовательности Люка?
В ответе запишите только натуральное число.
Пояснение.
Последовательно находим:
F(3) = F(1) + F(2) = 3,
F(4) = F(2)
+ F(3) = 4,
F(5) = F(3)
+ F(4) = 7,
F(6) = F(4)
+ F(5) = 11,
F(7) = F(5)
+ F(6) = 18,
F(8) = F(6) + F(7) = 29,
F(9) = F(7) + F(8) = 47,
F(10) = F(8) + F(9) = 76.
Десятое число в последовательности Люка равно 76.
№10. Последовательность чисел Падована
задается рекуррентным соотношением:
F(1) = 1
F(2) = 1
F(3) = 1
F(n) = F(n–3) + F(n–2), при n >3, где n – натуральное
число.
Чему равно десятое число в последовательности Падована?
В ответе запишите только натуральное число.
Пояснение.
Последовательно находим:
F(4) = F(1) + F(2) = 2,
F(5) = F(2)
+ F(3) = 2,
F(6) = F(3)
+ F(4) = 3,
F(7) = F(4)
+ F(5) = 4,
F(8) = F(5)
+ F(6) = 5,
F(9) = F(6) + F(7) = 7,
F(10) = F(7) + F(8) = 9.
Десятое число в последовательности Падована равно
9.
Вызов рекурсивных процедур
№1. Ниже на пяти языках программирования
записан рекурсивный алгоритм F.
|
Бейсик |
Python |
|
SUB F(n) PRINT n IF n < 5 THEN F(n + 1) F(n + 3) END IF END SUB |
def F(n): print(n) if n < 5: F(n + 1) F(n + 3) |
|
Паскаль |
Алгоритмический язык |
|
procedure F(n: integer); begin writeln(n); if n < 5 then begin F(n + 1); F(n + 3) end end |
алг F(цел n) нач вывод n, нс если n < 5 то F(n + 1) F(n + 3) все кон |
|
Си |
|
|
void F(int n) { printf(«%dn», if (n < 5) { F(n + 1); F(n + 3); } } |
Чему равна сумма всех чисел, напечатанных на экране при
выполнении вызова F(1)?
Пояснение.
Первым действием процедура F(1) выведет число 1.
Далее процедура F(1) вызовет процедуру F(n + 1), в результате
выполнения которой на экране появится число n + 1 = 2. Процедура
F(2) вызовет процедуру F(3), которая выведет на экран число 3 и вызовет
процедуру F(4), которая выведет на экран число 4 и вызовет F(5), которая
выведет на экран число 5.
После этого управление вернётся к процедуре F(4), которая
начнёт выполнять следующий шаг своего алгоритма, т. е. обратиться
к процедуре F(n + 3) = F(7). Процедура F(7) выведет на экран число 7.
Далее управление вернётся к процедуре F(3). Рассуждая аналогично приходим
к выводу, что процедура F(3) дополнительно выведет на экран число 6,
процедура F(2) — 5.
Последним действием процедуры F(1) будет вызов процедуры
F(n + 3) = F(4), которая выведет на экран числа 4, 5, 7.
Таким образом, на экране будут числа 1, 2, 3, 4, 5, 7, 6,
5, 4, 5, 7. Их сумма равна 49.
Ответ: 49.
№2. Ниже на пяти языках программирования
записан рекурсивный алгоритм F.
|
Бейсик |
Python |
|
SUB F(n) IF n > 2 THEN F = F(n — ELSE F = 1 END IF END SUB |
def F(n): if n > return else: return 1 |
|
Паскаль |
Алгоритмический язык |
|
procedure begin if n > F := F(n else F := 1; end; |
алг цел F(цел n) нач если n > 2 то знач := F(n — 1)+F(n — 2) иначе знач := 1 все кон |
|
Си |
|
|
int F(int n) { if (n > 2) return F(n-1) + F(n-2); else return 1; } |
Чему будет равно значение, вычисленное алгоритмом
при выполнении вызова F(5)?
Пояснение.
Значение, вычисленное алгоритмом при вызове F(5)
равно:
F(5)= F(4) + F(3) = F(3) + F(2) + F(2) + F(1) = F(2) + F(1)
+1 + 1 + 1 = 5.
Ответ: 5.
№3. Ниже на пяти языках программирования
записан рекурсивный алгоритм F.
|
Бейсик |
Python |
|
SUB F(n) IF n > 2 THEN F = F(n — ELSE F = 1 END IF END SUB |
def F(n): if n > return else: return 1 |
|
Паскаль |
Алгоритмический язык |
|
procedure begin if n > F := F(n else F := 1; end; |
алг цел F(цел n) нач если n > 2 то знач := F(n — 1)+F(n — 2) иначе знач := 1 все кон |
|
Си |
|
|
int F(int n) { if (n > 2) return F(n-1) + F(n-2); else return 1; } |
Чему будет равно значение, вычисленное алгоритмом
при выполнении вызова F(6)?
Пояснение.
Значение, вычисленное алгоритмом при вызове F(6)
равно:
F(6)= F(5)
+ F(4) = F(4) + F(3) + F(3) + F(2) = F(3) + F(2) + 2(F(2) + F(1)) + 1 =
= F(2) + F(1) + 1 + 2 · 2 + 1= 8.
Ответ: 8.
№4. Ниже на пяти языках программирования
записан рекурсивный алгоритм F.
|
Бейсик |
Python |
|
SUB F(n) PRINT n IF n > 0 THEN F(n — 1) F(n — 3) END IF END SUB |
def F(n): print(n) if n > 0: F(n — 1) F(n — 3) |
|
Паскаль |
Алгоритмический язык |
|
procedure begin writeln(n); if n > begin F(n — 1); F(n — 3) end end |
алг F(цел n) нач вывод n, нс если n > 0 то F(n — 1) F(n — 3) все кон |
|
Си |
|
|
void F(int n) { printf(«%dn», if (n > 0) { F(n — 1); F(n — 3); } } |
Чему равна сумма всех чисел, напечатанных на экране при
выполнении вызова F(5)?
Пояснение.
Первым действием процедура F(5) выведет число 5 и вызовет
процедуры F(4) и F(2).
Далее процедура F(2) выведет на экран число 2 и вызовет
процедуры F(1) и F(−1). Процедура F(1) выведет на экран число 1 и вызовет
процедуры F(0) и F(−2). Функция F(0) выведет на экран число 0. Функции
F(−1) и F(−2) выведут на экран числа −1 и −2.
Процедура F(4) выведет число 4 и вызовет процедуры
F(3) и F(1). Процедура F(1) выведет на экран цифры 1, 0 и −2. Процедура
F(3) выведет число 3 и вызовет процедуры F(2) и F(0). Процедура F(2)
выведет на экран цифры 2, 1, −2, −1 и 0, а процедура F(0) выведет число
0.
В итоге на экране появятся числа 5, 4, 3, 2, 1, 0, −2,
−1, 0, 1, 0, −2, 2, 1, 0, −2, −1.
Сумма чисел будет равна 11.
Ответ: 11.
№5. Ниже на пяти языках программирования
записан рекурсивный алгоритм F.
|
Бейсик |
Python |
|
SUB F(n) PRINT n IF n > 1 THEN F(n — 1) F(n — 3) END IF END SUB |
def F(n): print(n) if n > 1: F(n — 1) F(n — 3) |
|
Паскаль |
Алгоритмический язык |
|
procedure begin writeln(n); if n > begin F(n — 1); F(n — 3) end end |
алг F(цел n) нач вывод n, нс если n > 1 то F(n — 1) F(n — 3) все кон |
|
Си |
|
|
void F(int n) { printf(«%dn», if (n > 1) { F(n — 1); F(n — 3); } } |
Чему равна сумма всех чисел, напечатанных на экране при
выполнении вызова F(6)?
Пояснение.
На первом шаге процедура F(6) выведет число 6 и вызовет
процедуры F(5) и F(3).
На втором шаге процедуры F(5) и F(3) выведут числа 5 и
3 и вызовут процедуры F(4), F(2), F(2) и F(0).
На третьем шаге будут выведены числа 4, 2, 2 и 0; вызваны
процедуры F(3), F(1), F(1), F(−1), F(1), F(−1).
На четвёртом шаге будут выведены числа 3, 1, 1, −1, 1,
−1; вызваны процедуры F(2) и F(0).
На пятом шаге будут выведены числа 2, 0 и вызваны процедуры
F(1), F(−1).
На шестом шаге будут выведены числа 1 и −1.
Найдём сумму выведенных чисел:
6 + 5 + 3 + 4 + 2 + 2+ 0 + 3 + 1 + 1 + (−1) + 1 + (−1) + 2 +
0 + 1 + (−1) = 28.
Ответ: 28.
№6. Ниже на пяти языках программирования
записан рекурсивный алгоритм F.
|
Бейсик |
Python |
|
FUNCTION F(n) IF n > 2 THEN F = F(n — ELSE F = n END IF END FUNCTION |
def F(n): if n > return else: return n |
|
Паскаль |
Алгоритмический язык |
|
function begin if n > F := F(n else F := n; end; |
алг цел F(цел n) нач если n > 2 то знач := F(n — 1)+F(n — 2) иначе знач := n все кон |
|
Си |
|
|
int F(int n) { if (n > 2) return F(n-1) + F(n-2); else return n; } |
Чему будет равно значение, вычисленное алгоритмом
при выполнении вызова F(5)?
Пояснение.
Значение, вычисленное алгоритмом при вызове F(5)
равно:
F(5)= F(4) + F(3) = F(3) + F(2) + F(2) + F(1) = F(2) + F(1)
+2 + 2 + 1 = 8.
Ответ: 8.
Алгоритмы опирающиеся на одно предидущеезначение
№1. Алгоритм вычисления значения функции
F(n), где n – натуральное число, задан следующими соотношениями:
F(1) = 1
F(n) =
F(n–1) * n, при n >1
Чему равно значение функции F(5)? В ответе запишите
только натуральное число.
Пояснение.
Последовательно находим: F(2) = F(1) * 2 = 2, F(3) =
F(2) * 3 = 6, F(4) = F(3) * 4 = 24, F(5) = F(4) * 5 = 120.
Примечание
Использование функции позволяет вычислить так называемый
факториал числа n — произведение натуральных чисел от 1 до n.
Тем самым, F(5) = 1 * 2 * 3 * 4 * 5 = 120.
№2. Алгоритм вычисления значения функции
F(n), где n – натуральное число, задан следующими соотношениями:
F(1) = 3
F(n) =
F(n–1) * (n–1), при n
>1
Чему равно значение функции F(6)?
В ответе запишите только натуральное число.
Пояснение.
Последовательно находим:
F(2) = F(1) * 1 = 3,
F(3) = F(2) * 2 = 6,
F(4) = F(3) * 3 = 18,
F(5) = F(4) * 4 = 72,
F(6) = F(5) * 5 = 360.
№3. Алгоритм вычисления значения функции
F(n), где n – натуральное число, задан следующими соотношениями:
F(1) = 1
F(n) =
5*F(n–1) + 3*n, при n
>1
Чему равно значение функции F(4)?
В ответе запишите только натуральное число.
Пояснение.
Последовательно находим:
F(2) = 5 * F(1) + 3 * 2 = 11,
F(3) = 5 * F(2) + 3 * 3 = 64,
F(4) = 5 * F(3) + 3 * 4 = 332.
№4. Алгоритм вычисления значения функции
F(n), где n – натуральное число, задан следующими соотношениями:
F(1) = 1
F(n) = F(n–1) * F(n–1) − F(n–1) * n + 2 * n, при n >1
Чему равно значение функции F(4)?
В ответе запишите только натуральное число.
Пояснение.
Последовательно находим:
F(2) = F(1) * F(1) − F(1) * 2 + 2 * 2 = 3,
F(3) = F(2) * F(2) − F(2) * 3 + 2 * 3 = 6,
F(4) = F(3) * F(3) − F(3) * 4 + 2 * 4 = 20.
№5. Алгоритм вычисления значения функции
F(n) и G(n), где n – натуральное число, задан следующими соотношениями:
F(1) = 0
F(n) =
F(n–1) + n, при n >1
G(1) = 1
G(n) =
G(n–1) * n, при n >1
Чему равно значение функции F(5) + G(5)?
В ответе запишите только натуральное число.
Пояснение.
Последовательно находим:
F(2) = F(1) + 2 = 2,
F(3) = F(2)
+ 3 = 5,
F(4) = F(3)
+ 4 = 9,
F(5) = F(4)
+ 5 = 14,
G(2) = G(1)
* 2 = 2,
G(3) = G(2)
* 3 = 6,
G(4) = G(3) * 4 = 24,
G(5) = G(4) * 5 = 120.
Затем находим F(5) + G(5)=14 + 120=134.
№6. Алгоритм вычисления значения функции
F(n) и G(n), где n – натуральное число, задан следующими соотношениями:
F(1) = 1
F(n) = 2 *
G(n–1) + 5 * n, при n
>1
G(1) = 1
G(n) =
F(n–1) + 2 * n, при n
>1
Чему равно значение функции F(4) + G(4)?
В ответе запишите только натуральное число.
Пояснение.
Последовательно находим:
F(2) = 2 * G(1) + 5 * 2 = 12,
G(2) = F(1)
+ 2 * 2 = 5,
F(3) = 2 *
G(2) + 5 * 3 = 25,
G(3) = F(2)
+ 2 * 3 = 18,
F(4) = 2 *
G(3) + 5 * 4 = 56,
G(4) = F(3)
+ 2 * 4 = 33.
Затем находим F(4) + G(4)=56 + 33=89.
№7. Алгоритм вычисления значения функции
F(n). где n — натуральное число, задан следующими соотношениями:
F(1) = 1;
F(n) =
F(n-1) * (n+1), при n
>1.
Чему равно значение функции F(4)? В ответе запишите
только натуральное число.
Пояснение.
Последовательно находим:
F(2) = F(1) * 3 = 3,
F(3) = F(2) * 4 = 12,
F(4) = F(3) * 5 = 60.
Ответ: 60.
№8. Алгоритм вычисления значения функции
F(n). где n — натуральное число, задан следующими соотношениями:
F(1) = 1;
F(n) =
F(n-1) * (n+1), при n
>1.
Чему равно значение функции F(5)? В ответе запишите
только натуральное число.
Пояснение.
Последовательно находим:
F(2) = F(1) * 3 = 3,
F(3) = F(2) * 4 = 12,
F(4) = F(3) * 5 = 60
F(5) = F(4) * 6 = 360.
Ответ: 360.
№9. Алгоритм вычисления значения функции
F(n). где n — натуральное число, задан следующими соотношениями:
F(1)= 1; F(2)=1;
F(n) = F(n-2) * n при n >2.
Чему равно значение функции F(7)? В ответе запишите
только натуральное число.
Пояснение.
Последовательно находим:
F(3) =3F(1)
= 3, F(4) = 4F(2) = 4, F(5) = 5F(3) = 15, F(6) = 6F(4) = 24, F(7) = 7F(5) =
105.
№10. Алгоритм вычисления значения функции
F(n), где n — натуральное число, задан следующими соотношениями:
F(1) = 1; F(2) = 1;
F(n) = F(n — 2) * (n — 1), при n > 2.
Чему равно значение функции F(7)? В ответе запишите
только натуральное число.
Пояснение.
Последовательно находим:
F(3) = F(1) * 2 = 2,
F(4) = F(2) * 3 = 3,
F(5) = F(3) * 4 = 8,
F(6) = F(4) * 5 = 15,
F(7) = F(5) * 6 = 48.