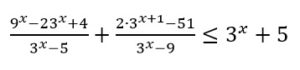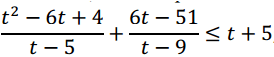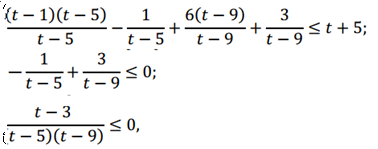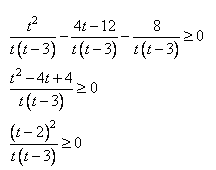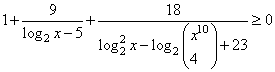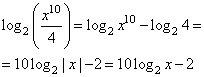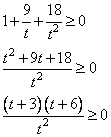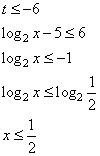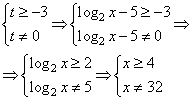Формула для 15 задания егэ математика профиль - Помощь в подготовке к экзаменам и поступлению

Задание 15 Профильного ЕГЭ по математике — «экономическая» задача. Как вы уже поняли, речь пойдет о деньгах. О кредитах и вкладах. О ситуациях, где нужно узнать, при каких значениях переменной будет максимальна прибыль или минимальны издержки. С 2022 года задание 15 оценивается на ЕГЭ в 2 первичных балла.

В этой статье:

Как научиться решать «экономические» задачи. С чего начать.

Две схемы решения задач на кредиты и как их распознать.

Комбинированные задачи.

В чем основная сложность «экономической» задачи.

Задания на оптимальный выбор. В том числе — с применением производной.

Если материал покажется вам сложным — вернитесь к теме «Задачи на проценты» из первой части ЕГЭ по математике.

Надеемся, что вы уже сейчас сможете ответить на такие вопросы:

Что принимается за 100%?
Величина х увеличилась на p%. Как это записать?
Величина y дважды уменьшилась на р%. Как это записать?

Ответы на вопросы, а также подготовительные задачи — в статье «Задача 17 Профильного ЕГЭ по математике. Кредиты и вклады. Начисление процентов». Повторите эту тему.

Запомним, что есть всего две схемы решения задач на кредиты

Первая схема: кредит погашается равными платежами. Или известна информация о платежах. Подробно здесь.

Вторая схема: равномерно уменьшается сумма долга. Или дана информация об изменении суммы долга. Подробно здесь.

В задачах первого типа обычно применяется формула для суммы геометрической прогрессии. В задачах второго типа — формула суммы арифметической прогрессии.

Посмотрите, чем эти схемы отличаются друг от друга. На какие ключевые слова в условии надо обратить внимание.

Потому что первое, что надо сделать, когда решаете «экономическую» задачу на кредиты или вклады, — определить, к какому типу она относится.

Давайте потренируемся.

1. 31 декабря 2014 года Аристарх взял в банке 6 902 000 рублей в кредит под 12,5% годовых. Схема выплаты кредита следующая — 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 12,5%), затем Аристарх переводит в банк X рублей. Какой должна быть сумма X, чтобы Аристарх выплатил долг четырьмя равными платежами (то есть за четыре года)?

Конечно, это задача первого типа. Есть информация о платежах. В условии сказано, что Аристарх выплатит долг четырьмя равными платежами.

Введем обозначения:

S=6902 тыс. рублей — сумма долга. Расчеты будем вести в тысячах рублей.

— процент банка,

$k=1+frac{{ p}}{100}=1+frac{125}{1000}=1+frac{1}{8}=frac{9}{8}$ — коэффициент, показывающий, во сколько раз увеличилась сумма долга после начисления процентов,

— сумма ежегодного платежа.

Составим схему погашения кредита. Заметим, что здесь 4 раза (то есть в течение 4 лет) повторяются одни и те же действия:

— сумма долга увеличивается в раз;

— Аристарх вносит на счет сумму в счет погашения кредита, и сумма долга уменьшается на .

Вот что получается:

Раскроем скобки:

$S{{ k}}^4-{ X}left({{ k}}^3+{{ k}}^2+{ k}+1right)=0.$

Что у нас в скобках? Да, это геометрическая прогрессия, и ее проще записать как

$1+{{ k}+{{ k}}^2+{ k}}^3$ . В этой прогрессии первый член равен 1, а каждый следующий в k раз больше предыдущего, то есть знаменатель прогрессии равен k.

Применим формулу суммы геометрической прогрессии:

${{ Sk}}^4={ X}cdot frac{{{ k}}^4-1}{{ k}-1}=0.$ И выразим из этой формулы .

${ X}=frac{{ S}cdot {{ k}}^4left({ k}-1right)}{{{ k}}^4-1}.$ Что же, можно подставить численные данные. Стараемся, чтобы наши вычисления были максимально простыми. Поменьше столбиков! Например, коэффициент k лучше записать не в виде десятичной дроби 1,125 — а в виде обыкновенной дроби $frac{9}{8}$ , Иначе у вас будет 12 знаков после запятой!

И конечно, не спешить возводить эту дробь в четвертую степень или умножать на S = 6902000 рублей.

${ X}=frac{{ S}cdot {{ k}}^4left({ k}-1right)}{{{ k}}^4-1}=frac{{ S}cdot 9^4left(frac{9}{8}-1right)}{8^4cdot left(frac{9^4}{8^4}-1right)}=frac{{ S}cdot 9^4}{8cdot left(9^4-8^4right)}=frac{{ S}cdot 9^4}{8cdot left(9^2-8^2right)left(9^2+8^2right)}=frac{{ S}cdot 9^4}{8cdot left(9+8right)left(9^2+8^2right)}=$

$=frac{6902cdot {81}^2}{8cdot 17cdot 145}=frac{406cdot {81}^2}{8cdot 145}=frac{203cdot {81}^2}{4cdot 145}=frac{29cdot 7cdot {81}^2}{4cdot 29cdot 5} = 2296,35$ тыс.руб.

Ответ: 2296350 рублей.

Вот следующая задача.

2. Жанна взяла в банке в кредит 1,8 млн рублей на срок 24 месяца. По договору Жанна должна возвращать банку часть денег в конце каждого месяца. Каждый месяц общая сумма долга возрастает на 1 %, а затем уменьшается на сумму, уплаченную Жанной банку в конце месяца. Суммы, выплачиваемые Жанной, подбираются так, чтобы сумма долга уменьшалась равномерно, то есть на одну и ту же величину каждый месяц. Какую сумму Жанна вернёт банку в течение первого года кредитования?

В этой задаче сумма долга уменьшается равномерно — задача второго типа.

Пусть S — первоначальная сумма долга, S = 1800 тысяч рублей.

Нарисуем схему начисления процентов и выплат. И заметим некоторые закономерности.

Как обычно, ${ k}=1+frac{{ p}}{100}.$

Сумма долга уменьшается равномерно. Можно сказать — равными ступеньками. И каждая ступенька равна $frac{1}{24}{ S}.$ После первой выплаты сумма долга равна $frac{23}{24}{ S},$ после второй $frac{22}{24}{ S}.$

Тогда первая выплата ${{ X}}_1={ kS}-frac{23}{24}{ S},$ вторая выплата ${{ X}}_2={ k}cdot frac{23}{24}{ S}-frac{22}{24}{ S}$ ,

dots

Последняя в году выплата ${{ X}}_{12}={ k}cdot frac{13}{24}{ S}-frac{12}{24}{ S}.$

Сумма всех выплат в течение первого года:

${ X}={{ X}}_1+{{ X}}_2+dots +{{ X}}_{12}={ kS}left(1+frac{23}{24}+dots frac{13}{24}right)-{ S}left(frac{23}{24}+frac{22}{24}+dots +frac{12}{24}right).$

В первой «скобке» — сумма 12 членов арифметической прогрессии, в которой ${{ a}}_1=frac{13}{24};{{ a}}_{{ n}}=frac{24}{24}=1.$ Обозначим эту сумму ${{ S}}_1.$

${{ S}}_1=frac{{{ a}}_1+{{ a}}_{12}}{2}cdot 12=frac{13+24}{2cdot 24}cdot 12=frac{37}{4}.$

Во второй скобке — также сумма 12 членов арифметической прогрессии, в которой ${{ b}}_1=frac{12}{24};{{ b}}_{{ n}}=frac{23}{24}.$ Эту сумму обозначим ${{ S}}_{2.}$

${{ S}}_2=frac{{{ b}}_1+{{ b}}_{12}}{2}cdot 12=frac{12+23}{2cdot 24}cdot 12=frac{35}{4}.$

Общая сумма выплат за год:

$small X= S left({ kS}_1-{{ S}}_2right)=frac{1800}{4}left({ 1,01}cdot 37-35right)=$
$=frac{1800cdot { 2,37}}{4}={ 2,37}cdot 450= 1066,5$ тыс. рублей.

Ответ: 1066500 рублей.

Еще одна задача — комбинированная. Здесь мы рисуем такую же схему выплаты кредита, как в задачах второго типа.

3. В июле 2016 года планируется взять кредит в банке на пять лет в размере S тыс. рублей. Условия его возврата таковы:

− каждый январь долг возрастает на 25% по сравнению с концом предыдущего года;

− с февраля по июнь каждого года необходимо выплатить часть долга;

− в июле 2017, 2018 и 2019 долг остаётся равным S тыс. рублей;

− выплаты в 2020 и 2021 годах равны по 625 тыс. рублей;

− к июлю 2021 долг будет выплачен полностью.

Найдите общую сумму выплат за пять лет.

Введем переменные: ${ k}=1+frac{25}{100}=frac{5}{4},Y=625$ тысяч рублей. Рисуем схему погашения кредита:

Общая сумма выплат: Кроме того, долг был полностью погашен последней выплатой .

Это значит, что и тогда

${ S}=frac{left({ k}+1right){ Y}}{{{ k}}^2}{ X}=3cdot frac{left({ k}+1right){ Y}}{{{ k}}^2}left({ k}-1right)+2{ Y}=3{ y}left(frac{{{ k}}^2-1}{{{ k}}^2}right)+2{ Y}=$
$={ Y}left(5-frac{3}{{{ k}}^2}right)=625left(5-frac{3cdot 16}{25}right)=frac{625cdot 77}{25}=77cdot 25=1925$ тысяч рублей.

Ответ: 1925 тыс. рублей.

Но не только задачи на кредиты и вклады могут встретиться в задании 15 Профильного ЕГЭ по математике. Есть еще задачи на оптимальный выбор. Например, нужно найти максимальную прибыль (при соблюдении каких-либо дополнительных условий), или минимальные затраты. Сначала в такой задаче нужно понять, как одна из величин зависит от другой (или других). Другими словами, нужна та функция, наибольшее или наименьшее значение которой мы ищем. А затем — найти это наибольшее или наименьшее значение. Иногда — с помощью производной. А если повезет и функция получится линейная или квадратичная — можно просто воспользоваться свойствами этих функций.

4. Консервный завод выпускает фруктовые компоты в двух видах тары—стеклянной и жестяной. Производственные мощности завода позволяют выпускать в день 90 центнеров компотов в стеклянной таре или 80 центнеров в жестяной таре. Для выполнения условий ассортиментности, которые предъявляются торговыми сетями, продукции в каждом из видов тары должно быть выпущено не менее 20 центнеров. В таблице приведены себестоимость и отпускная цена завода за 1 центнер продукции для обоих видов тары.

Вид тары	Себестоимость, 1 центнера	Отпускная цена, 1 центнера
стеклянная	1500 руб	2100 руб
жестяная	1100 руб	1750 руб

Предполагая, что вся продукция завода находит спрос (реализуется без остатка), найдите максимально возможную прибыль завода за один день (прибылью называется разница между отпускной стоимостью всей продукции и её себестоимостью).

По условию, завод не может выпускать компот только в стеклянных банках или только в жестяных — должны быть и те, и другие.

Пусть x — доля мощностей завода, занятых под поизводство компотов в стеклянных банках, а y — доля мощностей, занятых под производство компотов в жестяных банках, Тогда x+y=1. (Например, х=0,3 и у = 0,7 — то есть 30% производства — это компот в стеклянных банках, а 70% — компот в жестяных банках).

Если бы завод выпускал только компот в стеклянных банках, их бы получилось 90 центнеров в сутки. Однако выпускаются и те, и другие, и компотов в стеклянных банках производится 90x центнеров, а в жестяных банках — 80y центнеров в сутки.

Составим таблицу.

Вид тары	Доля в общем количестве	Производится в сутки	Прибыль за 1 центнер
стеклянная			2100 — 1500 = 600 руб
жестяная			1750 — 1100 = 650 руб

Общая прибыль завода за сутки равна

По условию, и , то есть $xge frac{2}{9}$ и $yge frac{1}{4}.$

Нужно найти наибольшее значение выражения при выполнении следующих условий:

$left{begin{matrix} x+y=1\ {{2}over{9}}leq x textless 1, \ {1over4}leq y textless 1 end{matrix}right. Leftrightarrow left{begin{matrix} y=1-x\ {2over9}leq x leq {3over4} end{matrix}right. .$

Подставим y=1-x в выражение для прибыли завода за сутки. Получим, что она равна Это линейная функция от x. Она монотонно возрастает и свое наибольшее значение принимает при $x=frac{3}{4}.$ Тогда $y=frac{1}{4}$ и максимально возможная прибыль завода за день равна

$2000cdot left(27cdot frac{3}{4}+26cdot frac{1}{4}right)=2000cdot frac{107}{4}=53500$ руб.

Ответ: 53500 руб.

Больше задач по финансовой математике на нахождение наибольших и наименьших значений функций и применение производной — здесь:

Задача 15 Профильного ЕГЭ по математике. Исследование функций и производная

Вот такая она, задача с экономическим содержанием. Мы рассказали о ней самое главное. Если готов осваивать ее самостоятельно — желаем удачи. А если не все будет сразу получаться — приходи к нам в ЕГЭ-Студию на интенсивы, курсы или Онлайн-курс.

Если вам понравился наш материал — записывайтесь на курсы подготовки к ЕГЭ по математике онлайн

Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Задание 15. Финансовая математика u0026#8212; профильный ЕГЭ по математике» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
09.03.2023

Источник

Основные схемы решения задач №15 по Ященко
36 вариантов.

Вариант 1

Решение

S-сумма долга, п=8 (срок),
S/n-уменьшение
долга, R1
-% первый, R2-процент второй

Год	Долг	Остаток	Платеж
0/25	—	S	—
1/26	R1*S		R1*S —
2/27	*R1		*R1 —
3/28	*R1		*R1-
4/29	*R1		*R1-
5/30	*R2		*R2-
6/31	*R2		*R2-
7/32	*R2		*R2-
8/33	*R2	0	*R2 -0

После заполнения таблицы строим математическую
модель

R1*S
— +*R1
— +*R1—+*R1—+*R2—+*R2—+*R2—+*R2
-0 = 1125

Очевидно, здесь спрятана арифметическая
прогрессия, теперь все запишем для простаты вычислений, выполним сложение по цветам

Получаем

R1**(8+7+6+5)+R2**(4+3+2+1)-*(7+6+5+4+3+2+1)=1125

То что выделено это прогрессия,
воспользуемся формулой суммы арифметической прогрессии

Получаем следующий результат

R1**26+ R2**10-*28=1125 умножим обе
части на 8

R1*S*26+R2*S*10-S*28=9000

S(1,2*26+1,18*10-28)=9000

15*S=9000

S=9000/15

S=600 тыс. рублей

Вариант 2 (аналогичная задача, выполните
самостоятельно, для закрепления навыка решения задачи)

Вариант 3

Для решения таких задач необходимо
составить две таблицы для вклада А и вклада Б

год	сумма	Сумма +%
1	S	1.2*S
2	1.2*S	1.21.2S
3	1.21.12S	1.21.21.2*S

Это и есть итоговое уравнение для вклада А
(выделено цветом)

Год	Сумма	Сумма +%
1	S	1.12*S
2	1.12*S	1.121.12S
3	1.121.12S	1.121.12S*()

Это есть итоговое уравнение для вклада Б

Возвращаемся к условию задачи: при каком
условии Б менее выгоден, чем А

Б
< A

1.12*1.12*S*() < 1.2*1.2*1.2*S

Решаем это уравнение

1,2544* S*() < 1.728*S
сокращаем на S

1,2544* () < 1.728

() <1.728/1.2544

() <1.377551 умножаем
на 100

100 + n<137.7551
вычитаем 100

n<37.7551

ближайшее целое число меньшее 37.7551 –
это 37

следовательно ответ 37.

Вариант 4(аналогичен варианту 3 выполните
самостоятельно по предложенной схеме).

Вариант 5

Для решения данной задачи потребуется таже
таблица, что и в варианте 1(2)

S=300, срок п=6, поэтому
осуществляем деление на 6, R2
((на самом деле находим n –
неизвестная величина), R2
– это сумма (1+n/100)), R1=1.2

Год	Долг	Остаток	Платеж
0/25	—	S	—
1/26	R1*S		R1*S —
2/27	*R1		*R1 —
3/28	*R1		*R1-
4/29	*R2		*R1-
5/30	*R2		*R2-
6/31	*R2	0	*R2-

Цветом отмечаю разделение процентов по
годам, чтобы не было путаницы

R1*S — +*R1 — +*R1-+*R1-+*R2-+*R2-=498

Опять можно заметить арифметическую
прогрессию и выполнить все действия аналогично первой задаче

R1**(6+5+4)+ R2**(3+2+1)- *(5+4+3+2+1)=498

2.5*R1+R2*1-2.5=498/300

2.5*1.2+R2-2.5=1.66

R2=1.66-0.5

R2=1.16

R2==1.16 умножим обе части
на 100

n=16 %

ответ 16

Вариант 6 решается аналогично, выполните самостоятельно.

Вариант 7

Данную задачу удобно решать через вершину
параболы, а затем подставить полученные данные и спокойно решить поставленную
задачу.

p*x—q
= p*x-2 —5*x-10
= сгруппируем подобные =

-2+x*(p-5)-10
-графиком является парабола, находим х как вершину параболы.

=
теперь подставляем вместо х значение
полученное выше

p>=29

Ответ: 29

Вариант 8 (задание аналогичное, выполните
самостоятельно)

Вариант 9

Задача данного варианта решается
аналогично задаче варианта №1, единственное сумма столбца ПЛАТЕЖИ это и есть
общая сумма выплат, т.е составляете таблицу и находите сумму всех членов данной
таблицы. Помните, что % меняется, и соответственно надо будет таблицу разделить
на две части используя соответствующий %.

Вариант10
(выполняете самостоятельно, опираясь на решении в варианте 1).

Вариант 11

Для решения данной задачи составляем
таблицу и обязательно учитываем условие, что долг 23,24,25 годов остается
равным 1050 тыс. рублей

Обозначим через S = 1050
тыс. рублей начальную сумму долга. Каждый январь следующего года сумма долга
увеличивается на 10% (100+10=110%, в долях это 1,1), то есть, становится равной
1,1S тыс. рублей. В следующие три года (2023, 2024 и 2025) выплаты делаются
так, что долг остается равным S = 1050 тыс. руб, то есть:

2023: ;

2024: ;

2025: .

Получаем равные выплаты в
размере

тыс. рублей

Затем, в 2026 и 2027
годах делаются равные выплаты k тыс. руб. так, что долг полностью гасится:

Здесь виден аннуитет

Год	Сумма	Сумма +%	Платеж
2026	S	1.1S	1.1*S-k
2027	1.1*S-k	(1.1S-k)1.1	(1.1S-k)1.1-k

И после этого платежа
сумма долга станет равной 0

Таким образом, последний
платеж будет равен 605 тыс. р., зная первый платеж легко найти ответ к задаче. Получаем
разницу между первой и последней выплатами:

605 000 – 105 000 = 500 000 рублей

Ответ: 500 000

Вариант 12

Обозначим через S = 220
тыс. рублей начальную сумму долга. Каждый январь следующего года сумма долга
увеличивается на r %, то есть, становится равной тыс. рублей. Обозначим
через .
В следующие три года (2023, 2024 и 2025) выплаты делаются так, что долг остается
равным S = 220 тыс. руб, то есть, выплаты равны:

откуда

Затем, в 2026 и 2027
годах делаются равные выплаты k тыс. руб. так, что долг полностью гасится:

откуда

По условию задания сумма
всех выплат равна 420 тыс. рублей, то есть:

Найдем t. Умножим обе
части уравнения на 1+t, получим:

Подставим вместо S = 220,
получим:

Имеем один положительный
корень, следовательно

Ответ: 20

Источник

Главная
Теория ЕГЭ
Математика — теория ЕГЭ
Задание 15 ЕГЭ 2021 по математике, теория

08.10.2018

Необходимая теория для успешного освоения и решения заданий №15 по математике профильного уровня на ЕГЭ в 2021 году.

Представлена вся теория и алгоритм решения различных заданий такого типа.

Тренировочные кимы ЕГЭ по математике
Практика — примеры для решения каждого типа заданий

Обсудить решение конкретных заданий вы можете в комментариях ниже.

Смотреть в PDF:

Или прямо сейчас: cкачать в pdf файле.

Сохранить ссылку:

Комментарии (0)
Добавить комментарий

Добавить комментарий

Комментарии без регистрации. Несодержательные сообщения удаляются.

Имя (обязательное)

E-Mail

Подписаться на уведомления о новых комментариях

Отправить

Источник

Неравенства

В задании №15 профильного уровня ЕГЭ по математике необходимо решить неравенство. Чаще всего неравенство связано с логарифмами или степенными выражениями. Для успешного выполнения необходимо хорошо оперировать данными выражениями.

Разбор типовых вариантов заданий №15 ЕГЭ по математике профильного уровня

Первый вариант задания (демонстрационный вариант 2018)

[su_note note_color=”#defae6″]

Решите неравенство:

[/su_note]

Алгоритм решения:

Вводим подстановку.
Записываем выражение неравенства в ином виде.
Решаем неравенство.
Возвращаемся к подстановке.
Записываем ответ.

Решение:

1. Вводим замену t = 3^x . Тогда исходное неравенство примет вид:

2. Преобразуем его:

3. Отсюда получаем решение t ≤ 3; 5 < t < 9.

4. Возвратимся к переменной х.

При t ≤ 3 получим: 3^x ≤ 3 , следовательно x ≤ 1

При 5 < t < 9 получим: 5 < 3x < 9, следовательно log₃5 < x < 2.

5. Решение исходного неравенства: x ≤ 1 и log₃5 < x < 2.

Ответ: (-∞;1] (log₃5;2)

Второй вариант задания (из Ященко, №1)

[su_note note_color=”#defae6″]

Решите неравенство .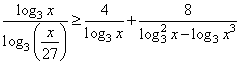

[/su_note]

Алгоритм решения задания:

Вводим замену.
Записываем неравенство в новом виде.
Решаем неравенство.
Возвращаемся к переменной х.
Записываем ответ.

Решение:

1. Вводим замену t = 3^x.

2. Тогда неравенство примет вид:

3. Решаем его:

Отсюда t < 0; t = 2; t> 3.

4. Возвращаемся к переменной х.

При t < 0 получаем:

откуда 0 < x < 1.

При t = 2 получаем:

откуда x = 9.

При t > 3 получаем:

откуда x > 27.

5. Решения исходного неравенства:

Ответ: .

Третий вариант (Ященко, № 5)

[su_note note_color=”#defae6″]

Решите неравенство

[/su_note]

Алгоритм решения:

Находим ОДЗ выражения в неравенстве.
Преобразуем неравенство к иному виду.
Вводим замену и решаем новое неравенство.
Возвращаемся к переменной х.
Записываем ответ.

Решение:

1. Запишем ОДЗ: .

log₂х-5≠0, log₂х≠5, х≠32

2. Преобразуем неравенство:

или

Получаем новое неравенство:

Вводим замену , тогда неравенство принимает новый вид. И его легко решить:

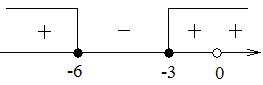
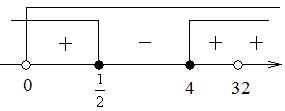
Размещаем полученные решения на числовую ось:

Возвращаемся к переменной х. Рассмотрим два случая:

Ответ:

Даниил Романович | Просмотров: 8.5k

Источник

Результат поиска:

Главная
Новости
ЕГЭ
- ЕГЭ Профиль 2023
- ЕГЭ Профиль 2022
- ЕГЭ Профиль 2016-2021
- Варианты профильного ЕГЭ
- ЕГЭ База 2023
- ЕГЭ База 2022
- ЕГЭ База 2016-2021
ОГЭ
- ОГЭ 2019
- ОГЭ 2023
ГВЭ
- ГВЭ 11 класс
ВПР
- ВПР 4 класс
- ВПР 5 класс
- ВПР 6 класс
- ВПР 7 класс
- ВПР 8 класс
Алгебра
- Алгебра 7-9
- Алгебра 10-11
Геометрия
- Геометрия 7-9
- Геометрия 10-11
YouTube
Прочее
- Class100
- Разработки
- Обо мне
- Репетитор

Результат поиска:

ЕГЭ Профиль №15. Показательные неравенства

ЕГЭ Профиль №15. Показательные неравенстваadmin2018-12-04T22:47:35+03:00

Скачать ЕГЭ Профиль №15. Показательные неравенства в формате pdf.

Нашли ошибку в заданиях? Оставьте, пожалуйста, отзыв.

15 заданием профильного ЕГЭ по математике является неравенство. Одним, из наиболее часто встречаемых неравенств, которое может оказаться в 15 задание, является показательное неравенство. Большая часть показательных неравенств предлагаемых на реальных экзаменах решается с помощью замен, методом интервалов или разложением на множители. Прежде чем решать показательные неравенства необходимо знать свойства показательной функции и уметь решать показательные уравнения (см. задание 13 профильного ЕГЭ «Показательные уравнения»). В данном разделе представлены показательные неравенства (всего 109) разбитые на два уровня сложности. Уровень А — это простейшие показательные неравенства, которые являются подготовительными для решения реальных показательных неравенств предлагаемых на ЕГЭ по профильной математике. Уровень В — состоит из неравенств, которые предлагали на реальных ЕГЭ и в диагностических работах прошлых лет.

Вставить формулу как

Блок

Строка

Дополнительные настройки

Цвет формулы

Цвет текста

#333333

ID формулы

Классы формулы

Используйте LaTeX для набора формулы

Предпросмотр

({})

Формула не набрана

Вставить

Источник