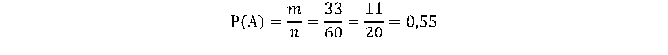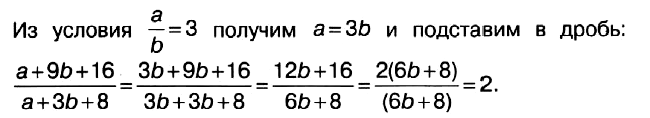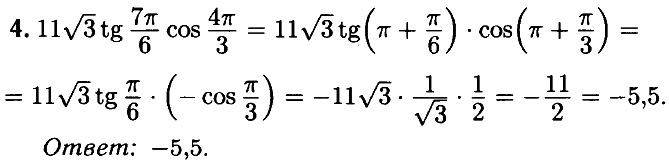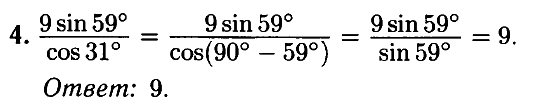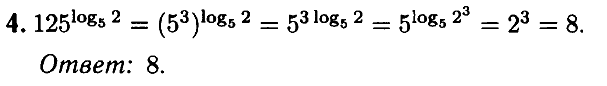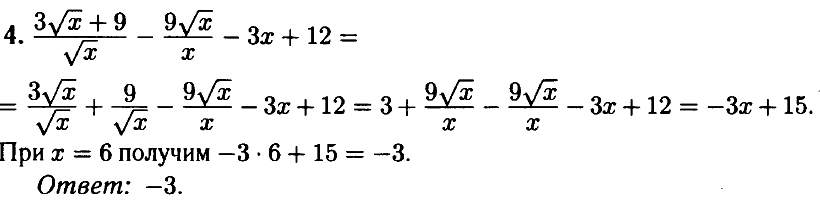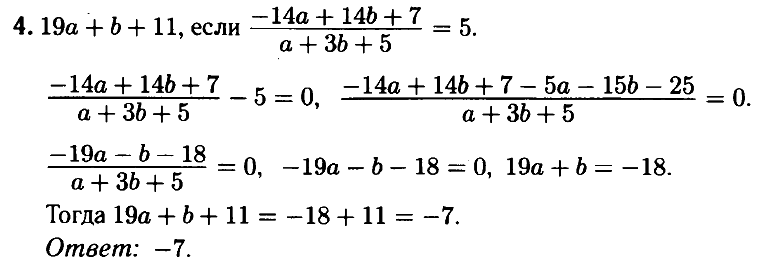17 декабря 2015
В закладки
Обсудить
Жалоба
Всё о теории вероятности в кратком виде.
arhiv.rar
Задание четыре егэ математика профиль
Банковская задача (дифференцированные платежи)
На занятии решены задачи на кредиты с дифференцированными платежами из прошедших тренировочных работ и досрочных ЕГЭ.
Понятие о базах данных
База данных обеспечивает хранение информации и представляет собой поименованную совокупность данных, организованных по определенным правилам, включающим общие принципы описания, хранения и манипулирования данными.
Шпаргалка к заданию №4 ЕГЭ по математике
На занятии решены задачи на кредиты с дифференцированными платежами из прошедших тренировочных работ и досрочных ЕГЭ.
Шпаргалка к заданию 4 ЕГЭ по математике.
4ege. ru
27.10.2017 4:56:49
2017-10-27 04:56:49
Источники:
Http://4ege. ru/matematika/52364-shpargalka-k-zadaniyu-4-ege-po-matematike. html
Задание 4 ЕГЭ математика (профильный уровень) » /> » /> .keyword { color: red; } Задание четыре егэ математика профиль
Задание 4 ЕГЭ математика (профильный уровень)
Задание 4 ЕГЭ математика (профильный уровень)
В четвертом задании предстоит вычислить вероятность события. Вычисления довольно простые, достаточно знать определение вероятности и простейшие способы ее вычисления. Также надо уметь работать с обыкновенными дробями, переводить обыкновенные дроби в десятичные, округлять десятичные дроби, составлять и решать линейные уравнения.
Тип задания: с кратким ответом
Уровень сложности: базовый
Количество баллов: 1
Примерное время на выполнение: 2 минуты
Вероятность всегда выражается дробью, в знаменателе которой стоит общее число исходов, а в числителе – число исходов, удовлетворяющих условию. Чаще всего задача сводится именно к вычислению числа исходов (примеры 1-2). Иногда к сложению или умножению вероятностей отдельных событий (примеры 3-6), и очень редко к нескольким действиям (примеры 7-8).
Знать определения и правила надо. Но при решении задач на вероятность важнее иметь хороший практический навык. Это позволит на экзамене не углубляться в простом задании в сложные математические законы и сэкономить время и собственные нервы. На самом деле трудных задач в четвертом задании нет вообще.
Пример №1.
Для призов участникам технического конкурса в магазине приобрели 30 раскрасок, из которых 10 с танками, 11 с самолетами, а остальные с космическими кораблями. Призы определяются жеребьевкой. Дима хочет получить раскраску с космическими кораблями. Какова вероятность, что его желание исполнится?
Решение: Сначала определим число раскрасок с космическими кораблями: 30-10-11=9
Теперь можем вычислить вероятность: 9/30=0,3
Пример №2
В упаковке лежат блокноты с цветными обложками: 12 с красной, 7 с синей, 9 с черной, 8 с желтой и 14 с белой. Из упаковки вынимают 1 блокнот. Найдите вероятность того, что обложка этого блокнота желтая.
Решение: Всего блокнотов: 12+7+9+8+14=50
Вероятность того, что попадется блокнот с желтой обложкой: 8/50=0,16
Пример №3
В киоске продаются уцененные авторучки. Вероятность неисправности авторучки составляет 0,09. Найдите вероятность того, что приобретенная наугад авторучка исправна.
Решение: Сумма вероятностей купить исправную или неисправную авторучку равна единице. Чтобы определить вероятность покупки хорошей ручки надо из единицы вычесть вероятность покупки неисправной ручки: 1-0,09=0,91
Пример №4
Два кубика бросают одновременно. Найти вероятность выбросить 9 очков.
Решение: Подберем пары чисел от 1 до 6, которые в сумме дают 9
3+6
4+5
5+4
6+3
Понятно, что на первом кубике может выпасть 4 из 6 возможных чисел. Вероятность составляет: 4/6=2/3
При бросании второго кубика должно выпасть 1 число из 6, вероятность этого события 1/6.
Тогда вероятность того, что сумма очков составит 9, равна произведению вероятностей: 2/3*1/6=2/18=1/9=0,11
Эту задачу можно решить с помощью таблицы, где в верхней строке указано число на перовом кубике, в левом столбце – число на втором, а в ячейках – их сумма. (Такую таблицу можно за минуту набросать на черновике)
Из таблицы видно, что из 36 возможных исходов, 9 очков выпадает в 4-х случаях. Т. е. вероятность составляет 4/36=1/9=0,11
Пример №5
Дима хорошо подготовился к олимпиаде по физике. С вероятностью 0,98 он станет призером и с вероятностью 0,84 – победителем олимпиады. С какой вероятностью Дима станет призером, но не станет победителем олимпиады по физике?
Решение: Победитель одновременно является и призером олимпиады. Поэтому вероятность стать призером (0,98) можно представить в виде суммы вероятности стать победителем (0,84) и вероятности стать просто призером (Х).
Х+0,84=0,98
Х=0,98-0,84
Х=0,14
Пример №6
В дежурном отряде 7 мальчиков и 14 девочек. Дежурство распределяется по жребию. На центральные ворота лагеря нужны двое дежурных. Найти вероятность, что дежурить на воротах будут двое мальчиков.
Решение: Первым дежурным окажется мальчик с вероятностью: 7/21=1/3
Второй дежурный выбирается из 20 оставшихся детей, из которых мальчиков осталось только 6: 6/20=3/10
Вероятность, что на воротах будут дежурить два мальчика: 1/3*3/10=0,1
Пример №7
В сквере имеется сеть дорожек, ведущих к смотровым площадкам. Водопад можно наблюдать с площадок F и G. Турист отправляется из точки А. На каждой развилке он выбирает произвольное направление (кроме направления назад). С какой вероятностью турист сможет увидеть водопад?
Решение: Так как водопад виден с двух площадок, то для решения задачи нужно сложить вероятность того, что турист попадет на площадку F, и вероятность того, что он попадет на площадку G
Для площадки F: 1/2*1/3=1/6
Для площадки G: 1/2*1/2=1/4
Для двух площадок: 1/6+1/4=4/24+6/24=10/24=0,42
Пример №8
К зачету надо выучить 10 вопросов. Саша выучил 2, а остальные только прочитал. Если Саше попадется выученный билет, то он сдаст зачет с вероятностью 0,9. Если Саше попадется вопрос, который он только прочитал, то вероятность сдать зачет 0,3. Вопросы на зачете распределяются случайным образом. Найти вероятность того, что Саша сдаст зачет.
Решение: Из 10 билетов выучены 2, не выучены 8. Вероятность получить выученный вопрос 2/10, вероятность получить не выученный вопрос 8/10.
Вероятность сдать зачет по выученному билету: 2/10*0,9=0,18
Вероятность сдать по невыученному билету: 8/10*0,3=0,24
Итоговая вероятность: 0,18+0,24=0,42
Несколько советов по решению 2 задания
Сложнее всего определить, когда вероятности двух событий надо перемножать, а когда складывать. Попадаются задачи, когда надо сделать и то, и другое. Если вы нашли вероятности отдельных событий, но не можете определиться, что с ними делать дальше – доверьтесь интуиции.
Если вы понимаете что вероятность двух событий больше, чем вероятность каждого в отдельности – складывайте. (Например, вероятность выбросить решку на одной из двух монет очевидно больше, чем выбросить решку на одной монете.)
Если вероятность двух событий меньше, чем каждого в отдельности – перемножайте. (Например, вероятность выбросить решку на обеих монетах меньше, чем вероятность выбросить решку на одной из них.)
Понятно, что интуиция – подход ненаучный. Но на ЕГЭ в задании с кратким ответом лучше дать какой-нибудь ответ, чем не дать никакого.
Однако не забывайте, что профильный ЕГЭ по математике является не только выпускным, но и вступительным испытанием. Большинство школьных задач на вероятность можно решить путем логических рассуждений. Это создает иллюзию легкости теории вероятности и математической статистики. Но на самом деле это одна из самых передовых и востребованных областей математики, и в ВУЗе вы ощутите её сложность в полной мере.
Чаще всего задача сводится именно к вычислению числа исходов примеры 1-2.
Uroknadom. ru
04.01.2020 1:25:29
2020-01-04 01:25:29
Источники:
Http://uroknadom. ru/blog/zadaniye-4-ege-matematika/
Задание №4 ЕГЭ по математике профильного уровня ⋆ СПАДИЛО » /> » /> .keyword { color: red; } Задание четыре егэ математика профиль
Задание №4 ЕГЭ по математике профильного уровня
Задание №4 ЕГЭ по математике профильного уровня
В задании №4 профильного уровня ЕГЭ по математике необходимо решить простую задачу по теории вероятностей. Задача совсем простая, достаточно поделить одно число на другое, ну или перед этим вычесть из одного числа другое. Задание интуитивно понятно, и решить его можно даже не зная основных формул комбинаторики. Разберем несколько примеров.
Разбор типовых вариантов заданий №4 ЕГЭ по математике профильного уровня
Первый вариант задания (демонстрационный вариант 2018)
В сборнике билетов по биологии всего 25 билетов. Только в двух билетах встречается вопрос о грибах. На экзамене школьнику достаётся один случайно выбранный билет из этого сборника. Найдите вероятность того, что в этом билете будет вопрос о грибах.
Алгоритм решения:
Обозначаем событие А. Определяем число всех событий. Находим число благоприятствующих исходов. Подсчитываем вероятность. Записываем ответ.
Решение:
1. Пусть А –событие, при котором ученику попадает билет с вопросом о грибах. 2. Всего билетов 25, значит всех событий n=25. 3. Благоприятствующих исходов m=2, т. к. только 2 билета содержат вопрос о грибах. 4. Вероятность события А равна Р(А) = m/n=2/25 = 0,08. Ответ: 0,08.
Второй вариант задания (из Ященко, №1)
В среднем из 600 садовых насосов, поступивших в продажу, 3 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает.
Алгоритм решения:
Обозначим событие «купленный контрольный насос не подтекает» буквой А. Найдем число всех событий. Найдем число благоприятствующих событий. Определим вероятность события А. Запишем ответ.
Решение:
1. Пусть событие А: выбранный случайным образом насос не протекает. 2. Число всех событий n=600. 3. Число благоприятствующих исходов равно m=600-3=597. Тогда вероятность того, что выбранный насос не подтекает, определяется так: m/n = 597/600 = 0,995 Ответ: 0,995
Третий вариант задания (из Ященко, №7)
В фирме такси в наличии 60 легковых автомобилей; 27 из них чёрного цвета с жёлтыми надписями на боках, остальные — жёлтого цвета с чёрными надписями. Найдите вероятность того, что на случайный вызов приедет машина жёлтого цвета с чёрными надписями.
Алгоритм решения:
Обозначим событие «на вызов придет желтая машина» буквой А. Найдем число всех возможных событий. Найдем число благоприятствующих событий. Вычислим вероятность события А. Запишем ответ.
Решение:
1. Пусть событие А: на вызов придет желтое такси. 2. Число всех событий n=60. 3. Число благоприятствующих исходов равно m=60-27= 33. Тогда вероятность того, что выбранное для поездки будет желтым, определяется так: Ответ: 0,55.
Четвертый вариант задания (из Ященко, №21)
На фабрике керамической посуды 20% произведённых тарелок имеют дефект. При контроле качества продукции выявляется 70% дефектных тарелок. Остальные тарелки поступают в продажу. Найдите вероятность того, что случайно выбранная при покупке тарелка не имеет дефектов. Ответ округлите до сотых.
Алгоритм решения:
Обозначим х число всех тарелок, произведенных на фабрике. Найдем число дефектных тарелок. Найдем число всех изымаемых при проверке тарелок. Определим вероятность события А: куплена качественная тарелка. Запишем ответ.
Решение:
1. Пусть на фабрике изготовлено х тарелок.
2. Бракованных тарелок на фабрике изготовлено 20%. Это всего 0,2x штук. Тогда в торговую сеть поступает 0,8х качественных тарелок.
3. При проверке качества изымается 70% бракованных тарелок, значит, из них 30% поступает в продажу. Получается, на прилавок идет 0,2x · 0,3 = 0,06x бракованных.
Всего в торговую сеть поступает 0,8x + 0,06x = 0,86x тарелок.
4. Пусть событие А: купленная тарелка качественная. Тогда число благоприятствующих событий m=N(A) = 0,8x. Всего число исходов n = 0,86x.
5. Вероятность события А определяем формулой вероятности: P(A) = m/n = 0,8x/0,86x = 0,9302325… ≈ 0,93
1. Пусть событие А: на вызов придет желтое такси. 2. Число всех событий n=60. 3. Число благоприятствующих исходов равно m=60-27= 33. Тогда вероятность того, что выбранное для поездки будет желтым, определяется так: Ответ: 0,55.
Задание №4 ЕГЭ по математике профильного уровня
В задании №4 профильного уровня ЕГЭ по математике необходимо решить простую задачу по теории вероятностей. Задача совсем простая, достаточно поделить одно число на другое, ну или перед этим вычесть из одного числа другое. Задание интуитивно понятно, и решить его можно даже не зная основных формул комбинаторики. Разберем несколько примеров.
В сборнике билетов по биологии всего 25 билетов. Только в двух билетах встречается вопрос о грибах. На экзамене школьнику достаётся один случайно выбранный билет из этого сборника. Найдите вероятность того, что в этом билете будет вопрос о грибах.
Алгоритм решения:
Обозначаем событие А. Определяем число всех событий. Находим число благоприятствующих исходов. Подсчитываем вероятность. Записываем ответ.
Решение:
1. Пусть А –событие, при котором ученику попадает билет с вопросом о грибах. 2. Всего билетов 25, значит всех событий n=25. 3. Благоприятствующих исходов m=2, т. к. только 2 билета содержат вопрос о грибах. 4. Вероятность события А равна Р(А) = m/n=2/25 = 0,08. Ответ: 0,08.
Третий вариант задания из Ященко, 7.
Spadilo. ru
07.01.2019 8:51:22
2019-01-07 08:51:22
Источники:
Http://spadilo. ru/zadanie-4-ege-po-matematike-profilnyj/
ЕГЭ по математике Профиль. Задание 4: Уметь выполнять вычисления и преобразования. Материалы для подготовки к итоговой аттестации. Алгоритм выполнения задания. Примеры с объяснением выбора правильного ответа. Анализ типичных ошибок.
Вернуться к Оглавлению раздела «Анализ заданий ЕГЭ по математике».
ЕГЭ Профиль. Задание № 4
АЛГОРИТМ ВЫПОЛНЕНИЯ
Задание № 4 проверяет умение производить вычисления и преобразования рациональных, иррациональных, степенных, логарифмических и тригонометрических выражений. Задание состоит из числового или алгебраического выражения, значение которого необходимо найти, применяя математические преобразования. Ответом является целое число или конечная десятичная дробь.
План выполнения:
- Внимательно прочитайте условие задачи.
- Выполните преобразования.
- Найдите числовое значение выражения.
- Запишите полученное число в поле ответа КИМ и бланк ответов № 1.
Вычисление значений рациональных выражений
Задачи этого типа заключаются в вычислении значений рациональных, то есть дробных выражений. При подготовке необходимо повторить правила действий с дробями, формулы сокращённого умножения.
Задача № 4 (1). Найдите значение выражения
Решение:
Ответ: 1.
Задача № 4 (2). Найдите (a + 9b + 16)/(a + 3b + 8), если a/b = 3.
Решение:
Ответ: 2.
Вычисление значений иррациональных выражений
Задачи этого типа заключаются в вычислении значений иррациональных (содержащих корни) выражений. При подготовке следует повторить правила вычисления корней, свойства корней.
Задача № 4 (3). Найдите значение выражения (3√5 • 6√5) : √5.
Решение:
Ответ: 1.
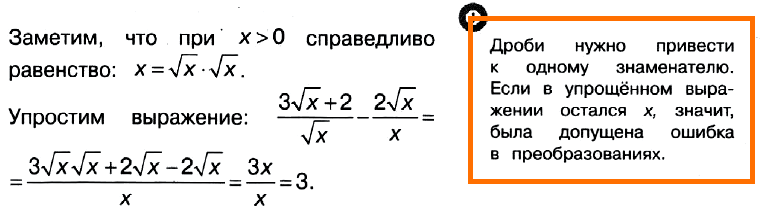
Задача № 4 (4). Найдите значение выражения (3√x + 2)/√x – 2√x/x при х > 0.
Решение:
Ответ: 3.
Вычисление значений степенных выражений
Задачи этого типа заключаются в вычислении значений степенных выражений. При подготовке нужно повторить правила действий со степенями, правило возведения числа в степень.
Задача № 4 (5). Найдите значение выражения 21,5 • 80,5.
Решение:
Ответ: 8.
Задача № 4 (6). Найдите значение выражения (3 – 140,25)(3 + 140,25) : (9 + (70,5 – 21/2)2).
Решение:
Ответ: 27.
Вычисление значений логарифмических выражений
Задачи этого типа заключаются в вычислении значений логарифмических выражений. При подготовке нужно повторить понятие логарифма, основные свойства логарифмов.
Задача № 4 (7). Вычислите log1/2 4√2.
Решение:
Ответ: –0,25.
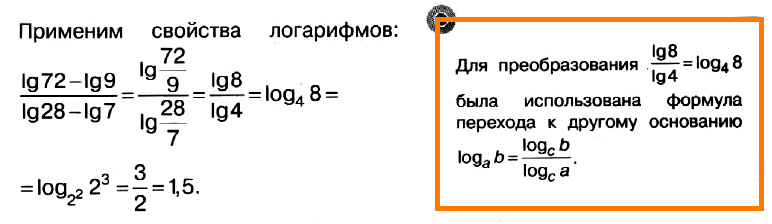
Задача № 4 (8). Найдите значение выражения (lg 72 – lg 9) : (lg 28 – lg 7).
Решение:
Ответ: 1,5.
Вычисление значений тригонометрических выражений
Задачи этого типа заключаются в вычислении значений тригонометрических выражений. При подготовке необходимо повторить основное тригонометрическое тождество, знаки синуса, косинуса, тангенса, формулы приведения, формулы синуса и косинуса двойного аргумента, понятие периодичности тригонометрических функций и табличные значения тригонометрических функций основных углов.
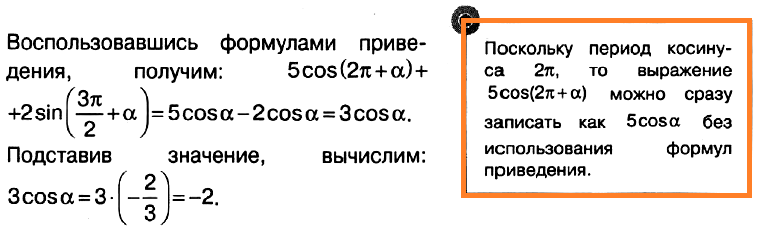
Задача № 4 (9). Найдите значение выражения 5 cos (2π + α) + 2 sin (3π/2 + α), если cos α = –2/3.
Решение:
Ответ: –2.
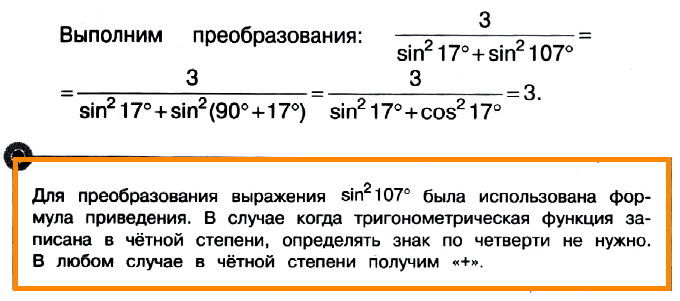
Задача № 4 (10). Найдите значение выражения 3/(sin2 17° + sin2 107°).
Решение:
Ответ: 3.
Тренировочные задания с самопроверкой
№ 4.1. Найдите значение выражения 11√3 • tg (7π/6) • cos (4π/3).
Открыть ОТВЕТ
№ 4.2. Найдите значение выражения (9 sin 59°) / (cos 31°).
Открыть ОТВЕТ
№ 4.3. Найдите значение выражения
Открыть ОТВЕТ
№ 4.4. Найдите значение выражения (3√x + 9)/√x – (9√x)/x – 3x + 12 при х = 6.
Открыть ОТВЕТ
№ 4.5. Найдите значение выражения 19а + b + 11, если (–14a + 14b + 7) : (a + 3b + 5) = 5.
Открыть ОТВЕТ
Вы смотрели: ЕГЭ по математике Профиль. Задание 4: Уметь выполнять вычисления и преобразования. Материалы для подготовки к итоговой аттестации. Алгоритм выполнения задания. Примеры с объяснением выбора правильного ответа. Анализ типичных ошибок.
Вернуться к Оглавлению раздела «Анализ заданий ЕГЭ по математике».
Просмотров:
15 047
4 задание ЕГЭ по математике профильного уровня посвящено теории вероятности. Здесь понадобится не только основная формула P = m / n, но и умение работать с деревом вариантов (вероятностей).
4 задание ЕГЭ по математике профиль 2023 года: разбор теории вероятности
В задаче 1 есть две фабрики. Первая выпускает 45% стекол для автомобильных фар, а вторая — 55%. У первой — 3% бракованных деталей, у второй — 1%. Нужно найти вероятность того, что купленное в магазине стекло будет бракованным. Учитель, старший эксперт по математике и член проверочной комиссии Михаил Попов расскажет как находить решение 4 задания ЕГЭ по математике.
Как вы поняли, при знании основ теории вероятности и внимательности, четвертая задача не представляет особой трудности. Главное — концентрация и аккуратность при расчетах. Удачи в подготовке!
Рассылка с лучшими статьями. Раз в неделю для самых занятных
Для тех, кто ценит свое время. Выбирайте интересную вам тему и подписывайтесь, чтобы ничего не пропустить. Это бесплатно!

В четвертом задании предстоит вычислить вероятность события. Вычисления довольно простые, достаточно знать определение вероятности и простейшие способы ее вычисления. Также надо уметь работать с обыкновенными дробями, переводить обыкновенные дроби в десятичные, округлять десятичные дроби, составлять и решать линейные уравнения.
Тип задания: с кратким ответом
Уровень сложности: базовый
Количество баллов: 1
Примерное время на выполнение: 2 минуты
Вероятность всегда выражается дробью, в знаменателе которой стоит общее число исходов, а в числителе – число исходов, удовлетворяющих условию. Чаще всего задача сводится именно к вычислению числа исходов (примеры 1-2). Иногда к сложению или умножению вероятностей отдельных событий (примеры 3-6), и очень редко к нескольким действиям (примеры 7-8).
Знать определения и правила надо. Но при решении задач на вероятность важнее иметь хороший практический навык. Это позволит на экзамене не углубляться в простом задании в сложные математические законы и сэкономить время и собственные нервы. На самом деле трудных задач в четвертом задании нет вообще.
Пример №1.
Для призов участникам технического конкурса в магазине приобрели 30 раскрасок, из которых 10 с танками, 11 с самолетами, а остальные с космическими кораблями. Призы определяются жеребьевкой. Дима хочет получить раскраску с космическими кораблями. Какова вероятность, что его желание исполнится?
Решение: Сначала определим число раскрасок с космическими кораблями: 30-10-11=9
Теперь можем вычислить вероятность: 9/30=0,3
Ответ: 0,3.
Пример №2
В упаковке лежат блокноты с цветными обложками: 12 с красной, 7 с синей, 9 с черной, 8 с желтой и 14 с белой. Из упаковки вынимают 1 блокнот. Найдите вероятность того, что обложка этого блокнота желтая.
Решение: Всего блокнотов: 12+7+9+8+14=50
Вероятность того, что попадется блокнот с желтой обложкой: 8/50=0,16
Ответ: 0,16.
Пример №3
В киоске продаются уцененные авторучки. Вероятность неисправности авторучки составляет 0,09. Найдите вероятность того, что приобретенная наугад авторучка исправна.
Решение: Сумма вероятностей купить исправную или неисправную авторучку равна единице. Чтобы определить вероятность покупки хорошей ручки надо из единицы вычесть вероятность покупки неисправной ручки: 1-0,09=0,91
Ответ: 0,91.
Пример №4
Два кубика бросают одновременно. Найти вероятность выбросить 9 очков.
Решение: Подберем пары чисел от 1 до 6, которые в сумме дают 9
3+6
4+5
5+4
6+3
Понятно, что на первом кубике может выпасть 4 из 6 возможных чисел. Вероятность составляет: 4/6=2/3
При бросании второго кубика должно выпасть 1 число из 6, вероятность этого события 1/6.
Тогда вероятность того, что сумма очков составит 9, равна произведению вероятностей: 2/3*1/6=2/18=1/9=0,11
Ответ: 0,11.
Эту задачу можно решить с помощью таблицы, где в верхней строке указано число на перовом кубике, в левом столбце – число на втором, а в ячейках – их сумма. (Такую таблицу можно за минуту набросать на черновике)
Из таблицы видно, что из 36 возможных исходов, 9 очков выпадает в 4-х случаях. Т.е. вероятность составляет 4/36=1/9=0,11
Ответ: 0,11.
Пример №5
Дима хорошо подготовился к олимпиаде по физике. С вероятностью 0,98 он станет призером и с вероятностью 0,84 – победителем олимпиады. С какой вероятностью Дима станет призером, но не станет победителем олимпиады по физике?
Решение: Победитель одновременно является и призером олимпиады. Поэтому вероятность стать призером (0,98) можно представить в виде суммы вероятности стать победителем (0,84) и вероятности стать просто призером (Х).
Х+0,84=0,98
Х=0,98-0,84
Х=0,14
Ответ: 0,14.
Пример №6
В дежурном отряде 7 мальчиков и 14 девочек. Дежурство распределяется по жребию. На центральные ворота лагеря нужны двое дежурных. Найти вероятность, что дежурить на воротах будут двое мальчиков.
Решение: Первым дежурным окажется мальчик с вероятностью: 7/21=1/3
Второй дежурный выбирается из 20 оставшихся детей, из которых мальчиков осталось только 6: 6/20=3/10
Вероятность, что на воротах будут дежурить два мальчика: 1/3*3/10=0,1
Ответ: 0,1.
Пример №7
В сквере имеется сеть дорожек, ведущих к смотровым площадкам. Водопад можно наблюдать с площадок F и G. Турист отправляется из точки А. На каждой развилке он выбирает произвольное направление (кроме направления назад). С какой вероятностью турист сможет увидеть водопад?
Решение: Так как водопад виден с двух площадок, то для решения задачи нужно сложить вероятность того, что турист попадет на площадку F, и вероятность того, что он попадет на площадку G
Для площадки F: 1/2*1/3=1/6
Для площадки G: 1/2*1/2=1/4
Для двух площадок: 1/6+1/4=4/24+6/24=10/24=0,42
Ответ: 0,42.
Пример №8
К зачету надо выучить 10 вопросов. Саша выучил 2, а остальные только прочитал. Если Саше попадется выученный билет, то он сдаст зачет с вероятностью 0,9. Если Саше попадется вопрос, который он только прочитал, то вероятность сдать зачет 0,3. Вопросы на зачете распределяются случайным образом. Найти вероятность того, что Саша сдаст зачет.
Решение: Из 10 билетов выучены 2, не выучены 8. Вероятность получить выученный вопрос 2/10, вероятность получить не выученный вопрос 8/10.
Вероятность сдать зачет по выученному билету: 2/10*0,9=0,18
Вероятность сдать по невыученному билету: 8/10*0,3=0,24
Итоговая вероятность: 0,18+0,24=0,42
Ответ: 0,42.
Несколько советов по решению 2 задания
Сложнее всего определить, когда вероятности двух событий надо перемножать, а когда складывать. Попадаются задачи, когда надо сделать и то, и другое. Если вы нашли вероятности отдельных событий, но не можете определиться, что с ними делать дальше – доверьтесь интуиции.
Если вы понимаете что вероятность двух событий больше, чем вероятность каждого в отдельности – складывайте. (Например, вероятность выбросить решку на одной из двух монет очевидно больше, чем выбросить решку на одной монете.)
Если вероятность двух событий меньше, чем каждого в отдельности – перемножайте. (Например, вероятность выбросить решку на обеих монетах меньше, чем вероятность выбросить решку на одной из них.)
Понятно, что интуиция – подход ненаучный. Но на ЕГЭ в задании с кратким ответом лучше дать какой-нибудь ответ, чем не дать никакого.
Однако не забывайте, что профильный ЕГЭ по математике является не только выпускным, но и вступительным испытанием. Большинство школьных задач на вероятность можно решить путем логических рассуждений. Это создает иллюзию легкости теории вероятности и математической статистики. Но на самом деле это одна из самых передовых и востребованных областей математики, и в ВУЗе вы ощутите её сложность в полной мере.
Рекомендуем также ознакомиться с разбором 1, 2 и 3 задания.
Начала теории вероятностей
В задании №4 профильного уровня ЕГЭ по математике необходимо решить простую задачу по теории вероятностей. Задача совсем простая, достаточно поделить одно число на другое, ну или перед этим вычесть из одного числа другое. Задание интуитивно понятно, и решить его можно даже не зная основных формул комбинаторики. Разберем несколько примеров.
Разбор типовых вариантов заданий №4 ЕГЭ по математике профильного уровня
Первый вариант задания (демонстрационный вариант 2018)
[su_note note_color=”#defae6″]
В сборнике билетов по биологии всего 25 билетов. Только в двух билетах встречается вопрос о грибах. На экзамене школьнику достаётся один случайно выбранный билет из этого сборника. Найдите вероятность того, что в этом билете будет вопрос о грибах.
[/su_note]
Алгоритм решения:
- Обозначаем событие А.
- Определяем число всех событий.
- Находим число благоприятствующих исходов.
- Подсчитываем вероятность.
- Записываем ответ.
Решение:
1. Пусть А –событие, при котором ученику попадает билет с вопросом о грибах.
2. Всего билетов 25, значит всех событий n=25.
3. Благоприятствующих исходов m=2, т.к. только 2 билета содержат вопрос о грибах.
4. Вероятность события А равна Р(А) = m/n=2/25 = 0,08.
Ответ: 0,08.
Второй вариант задания (из Ященко, №1)
[su_note note_color=”#defae6″]
В среднем из 600 садовых насосов, поступивших в продажу, 3 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает.
[/su_note]
Алгоритм решения:
- Обозначим событие «купленный контрольный насос не подтекает» буквой А.
- Найдем число всех событий.
- Найдем число благоприятствующих событий.
- Определим вероятность события А.
- Запишем ответ.
Решение:
1. Пусть событие А: выбранный случайным образом насос не протекает.
2. Число всех событий n=600.
3. Число благоприятствующих исходов равно m=600-3=597. Тогда вероятность того, что выбранный насос не подтекает, определяется так:
m/n = 597/600 = 0,995
Ответ: 0,995
Третий вариант задания (из Ященко, №7)
[su_note note_color=”#defae6″]
В фирме такси в наличии 60 легковых автомобилей; 27 из них чёрного цвета с жёлтыми надписями на боках, остальные — жёлтого цвета с чёрными надписями. Найдите вероятность того, что на случайный вызов приедет машина жёлтого цвета с чёрными надписями.
[/su_note]
Алгоритм решения:
- Обозначим событие «на вызов придет желтая машина» буквой А.
- Найдем число всех возможных событий.
- Найдем число благоприятствующих событий.
- Вычислим вероятность события А.
- Запишем ответ.
Решение:
1. Пусть событие А: на вызов придет желтое такси.
2. Число всех событий n=60.
3. Число благоприятствующих исходов равно m=60-27= 33. Тогда вероятность того, что выбранное для поездки будет желтым, определяется так:
Ответ: 0,55.
Четвертый вариант задания (из Ященко, №21)
[su_note note_color=”#defae6″]
На фабрике керамической посуды 20% произведённых тарелок имеют дефект. При контроле качества продукции выявляется 70% дефектных тарелок. Остальные тарелки поступают в продажу. Найдите вероятность того, что случайно выбранная при покупке тарелка не имеет дефектов. Ответ округлите до сотых.
[/su_note]
Алгоритм решения:
- Обозначим х число всех тарелок, произведенных на фабрике.
- Найдем число дефектных тарелок.
- Найдем число всех изымаемых при проверке тарелок.
- Определим вероятность события А: куплена качественная тарелка.
- Запишем ответ.
Решение:
1. Пусть на фабрике изготовлено х тарелок.
2. Бракованных тарелок на фабрике изготовлено 20%. Это всего 0,2x штук. Тогда в торговую сеть поступает 0,8х качественных тарелок.
3. При проверке качества изымается 70% бракованных тарелок, значит, из них 30% поступает в продажу. Получается, на прилавок идет 0,2x · 0,3 = 0,06x бракованных.
Всего в торговую сеть поступает 0,8x + 0,06x = 0,86x тарелок.
4. Пусть событие А: купленная тарелка качественная. Тогда число благоприятствующих событий m=N(A) = 0,8x. Всего число исходов n = 0,86x.
5. Вероятность события А определяем формулой вероятности: P(A) = m/n = 0,8x/0,86x = 0,9302325… ≈ 0,93
Ответ: 0,93.
Даниил Романович | Просмотров: 8.6k
ЕГЭ Профиль №4. Вычисление значений тригонометрических выражений
Скачать файл в формате pdf.
ЕГЭ Профиль №4. Вычисление значений тригонометрических выражений
| Задача 1. Найдите значение выражения (frac{{50sin {{179}^ circ } cdot cos {{179}^ circ }}}{{sin {{358}^ circ }}})
Ответ
ОТВЕТ: 25. |
| Задача 2. Найдите значение выражения (8sin frac{{5{\pi }}}{{12}} cdot cos frac{{5{\pi }}}{{12}})
Ответ
ОТВЕТ: 2. |
| Задача 3. Найдите значение выражения (frac{{24left( {{{sin }^2}{{17}^ circ } — {{cos }^2}{{17}^ circ }} right)}}{{cos {{34}^ circ }}})
Ответ
ОТВЕТ: — 24. |
| Задача 4. Найдите значение выражения (sqrt 3 {cos ^2}frac{{5{pi }}}{{12}} — sqrt 3 {sin ^2}frac{{5pi }}{{12}})
Ответ
ОТВЕТ: — 1,5. |
| Задача 5. Найдите значение выражения (sqrt {12} {cos ^2}frac{{5{pi }}}{{12}} — sqrt 3 )
Ответ
ОТВЕТ: — 1,5. |
| Задача 6. Найдите значение выражения (sqrt 3 — sqrt {12} {sin ^2}frac{{5{pi }}}{{12}})
Ответ
ОТВЕТ: — 1,5. |
| Задача 7. Найдите ( — 47cos 2alpha ), если (cos alpha = — 0,4)
Ответ
ОТВЕТ: 31,96. |
| Задача 8. Найдите значение выражения (frac{{5cos {{29}^ circ }}}{{sin {{61}^ circ }}})
Ответ
ОТВЕТ: 5. |
| Задача 9. Найдите значение выражения (36sqrt 3 {text{tg}}frac{{\pi }}{3}sin frac{{\pi }}{6})
Ответ
ОТВЕТ: 54. |
| Задача 10. Найдите значение выражения (4sqrt 2 cos frac{{\pi }}{4}cos frac{{7{\pi }}}{3})
Ответ
ОТВЕТ: 2. |
| Задача 11. Найдите значение выражения (frac{8}{{sin left( { — frac{{27{\pi }}}{4}} right)cos left( {frac{{31{\pi }}}{4}} right)}})
Ответ
ОТВЕТ: — 16. |
| Задача 12. Найдите значение выражения (33sqrt 2 cos left( {{{495}^ circ }} right))
Ответ
ОТВЕТ: — 33. |
| Задача 13. Найдите значение выражения (2sqrt 3 {text{tg}}left( { — {{300}^ circ }} right))
Ответ
ОТВЕТ: 6. |
| Задача 14. Найдите значение выражения ( — 18sqrt 2 sin left( { — {{135}^ circ }} right))
Ответ
ОТВЕТ: 18. |
| Задача 15. Найдите значение выражения (24sqrt 2 cos left( { — frac{{\pi }}{3}} right)sin left( { — frac{{\pi }}{4}} right))
Ответ
ОТВЕТ: — 12. |
| Задача 16. Найдите значение выражения (frac{{14sin {{19}^ circ }}}{{sin {{341}^ circ }}})
Ответ
ОТВЕТ: — 14. |
| Задача 17. Найдите значение выражения (frac{{36cos {{93}^ circ }}}{{cos {{87}^ circ }}})
Ответ
ОТВЕТ: — 36. |
| Задача 18. Найдите значение выражения (frac{{ — 37{text{tg6}}{{text{3}}^ circ }}}{{{text{tg11}}{{text{7}}^ circ }}})
Ответ
ОТВЕТ: 37. |
| Задача 19. Найдите значение выражения (frac{{14sin {{409}^ circ }}}{{sin {{49}^ circ }}})
Ответ
ОТВЕТ: 14. |
| Задача 20. Найдите значение выражения (5{text{tg1}}{{text{7}}^ circ } cdot {text{tg10}}{{text{7}}^ circ })
Ответ
ОТВЕТ: — 5. |
| Задача 21. Найдите значение выражения ( — 6{text{tg3}}{{text{1}}^ circ } cdot {text{tg5}}{{text{9}}^ circ })
Ответ
ОТВЕТ: — 6. |
| Задача 22. Найдите значение выражения (frac{{ — 12}}{{{{sin }^2}{{131}^ circ } + {{sin }^2}{{221}^ circ }}})
Ответ
ОТВЕТ: — 12. |
| Задача 23. Найдите значение выражения (frac{{27}}{{{{cos }^2}{{116}^ circ } + {{cos }^2}{{206}^ circ }}})
Ответ
ОТВЕТ: 27. |
| Задача 24. Найдите значение выражения (frac{{ — 5}}{{{{sin }^2}{{16}^ circ } + {{cos }^2}{{196}^ circ }}})
Ответ
ОТВЕТ: — 5. |
| Задача 25. Найдите значение выражения (frac{{ — 14sin {{84}^ circ }}}{{sin {{42}^ circ } cdot sin {{48}^ circ }}})
Ответ
ОТВЕТ: — 28. |
| Задача 26. Найдите значение выражения (frac{{5sin {{74}^ circ }}}{{cos {{37}^ circ } cdot cos {{53}^ circ }}})
Ответ
ОТВЕТ: 10. |
| Задача 27. Найдите значение выражения (20sin {135^ circ } cdot cos {45^ circ })
Ответ
ОТВЕТ: 10. |
| Задача 28. Найдите ({text{tg}}alpha ), если (cos alpha = frac{1}{{sqrt {10} }}) и (a in left( {frac{{3{\pi }}}{2};;2{\pi }} right))
Ответ
ОТВЕТ: — 3. |
| Задача 29. Найдите ({text{tg}}alpha ), если (sin alpha = — frac{5}{{sqrt {26} }}) и (alpha in left( {{\pi };;frac{{3{\pi }}}{2}} right))
Ответ
ОТВЕТ: 5. |
| Задача 30. Найдите (3cos alpha ), если (sin alpha = — frac{{2sqrt 2 }}{3}) и (alpha in left( {frac{{3{\pi }}}{2};;2{\pi }} right))
Ответ
ОТВЕТ: 1. |
| Задача 31. Найдите (7sin alpha ), если (cos alpha = frac{{3sqrt 5 }}{7}) и (alpha in left( {1,5{\pi };;2{\pi }} right))
Ответ
ОТВЕТ: — 2. |
| Задача 32. Найдите (24cos 2alpha ), если (sin alpha = — 0,2)
Ответ
ОТВЕТ: 22,08. |
| Задача 33. Найдите (frac{{10sin 6alpha }}{{3cos 3alpha }}), если (sin 3alpha = 0,6)
Ответ
ОТВЕТ: 4. |
| Задача 34. Найдите значение выражения (frac{{3cos left( {{\pi } — beta } right) + sin left( {frac{{\pi }}{2} + beta } right)}}{{cos left( {beta + 3{\pi }} right)}})
Ответ
ОТВЕТ: 2. |
| Задача 35. Найдите значение выражения (frac{{2sin left( {alpha — 7{\pi }} right) + cos left( {frac{{3{\pi }}}{2} + alpha } right)}}{{sin left( {a + {\pi }} right)}})
Ответ
ОТВЕТ: 1. |
| Задача 36. Найдите значение выражения (5{text{tg}}left( {5{\pi } — gamma } right) — {text{tg}}left( { — gamma } right)), если ({text{tg}}gamma {text{ = 7}})
Ответ
ОТВЕТ: — 28. |
| Задача 37. Найдите (sin left( {frac{{7{\pi }}}{2} — alpha } right)), если (sin alpha = 0,8) и (a in left( {frac{{\pi }}{2};;{\pi }} right))
Ответ
ОТВЕТ: 0,6. |
| Задача 38. Найдите (26cos left( {frac{{3{\pi }}}{2} + alpha } right)), если (cos alpha = frac{{12}}{{13}}) и (alpha in left( {frac{{3{\pi }}}{2};;2{\pi}} right))
Ответ
ОТВЕТ: — 10. |
| Задача 39. Найдите ({text{tg}}left( {alpha + frac{{5{\pi }}}{2}} right)), если ({text{tg}}alpha {text{ = 0}}{text{,4}})
Ответ
ОТВЕТ: — 2,5. |
| Задача 40. Найдите ({text{t}}{{text{g}}^2}alpha ), если (4{sin ^2}alpha + 9{cos ^2}alpha = 6)
Ответ
ОТВЕТ: 1,5. |
| Задача 41. Найдите (frac{{3cos alpha — 4sin alpha }}{{2sin alpha — 5cos alpha }}), если ({text{tg}}alpha {text{ = 3}})
Ответ
ОТВЕТ: — 9. |
| Задача 42. Найдите (frac{{10cos alpha + 4sin alpha + 15}}{{2sin alpha + 5cos alpha + 3}}), если ({text{tg}}alpha {text{ = }} — {text{2}}{text{,5}})
Ответ
ОТВЕТ: 5. |
| Задача 43. Найдите ({text{tg}}alpha ), если (frac{{6sin alpha — 2cos alpha }}{{4sin alpha — 4cos alpha }} = — 1)
Ответ
ОТВЕТ: 0,6. |
| Задача 44. Найдите ({text{tg}}alpha ), если (frac{{3sin alpha — 5cos alpha + 2}}{{sin alpha + 3cos alpha + 6}} = frac{1}{3})
Ответ
ОТВЕТ: 2,25. |
| Задача 45. Найдите значение выражения (7cos left( {{\pi } + beta } right) — 2sin left( {frac{{\pi }}{2} + beta } right)), если (cos beta = — frac{1}{3})
Ответ
ОТВЕТ: 3. |
| Задача 46. Найдите значение выражения (5sin left( {alpha — 7{\pi }} right) — 11cos left( {frac{{3{\pi }}}{2} + alpha } right)), если (sin alpha = — 0,25)
Ответ
ОТВЕТ: 4. |
| Задача 47. Найдите (3cos 2alpha ), если (cos alpha = frac{1}{2})
Ответ
ОТВЕТ: — 1,5. |