Формула двойного аргумента егэ - Помощь в подготовке к экзаменам и поступлению

в условии
в решении
в тексте к заданию
в атрибутах

Категория:

Атрибут:

Всего: 429 1–20 | 21–40 | 41–60 | 61–80 …

Добавить в вариант

а)  Решите уравнение

б)  Найдите все корни этого уравнения, принадлежащие промежутку

Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко. 2015 г.

а) Решите уравнение

б)  Укажите корни этого уравнения, принадлежащие отрезку

Источник: ЕГЭ по математике 01.06.2018. Основная волна. Дальний Восток. (C часть)., Задания 13 (С1) ЕГЭ 2018

а)  Решите уравнение

б)  Укажите корни уравнения, принадлежащие отрезку

а)  Решите уравнение $дробь: числитель: синус 2x, знаменатель: косинус левая круглая скобка dfrac Пи 2 плюс x правая круглая скобка конец дроби = корень из 3.$

б)  Укажите корни этого уравнения, принадлежащие отрезку

Источник: ЕГЭ по математике 2015. Досрочная волна, резервная волна (часть С)

а)  Решите уравнение

б)  Укажите корни этого уравнения, принадлежащие отрезку

а)  Решите уравнение

б)  Найдите все корни этого уравнения, принадлежащие отрезку

Источник: Основная волна ЕГЭ по математике 29.05.2019. Дальний восток, Задания 13 (С1) ЕГЭ 2019

а)  Решите уравнение

б)  Найдите все корни этого уравнения, принадлежащие отрезку

Источник: Резервная волна ЕГЭ по математике 24.06.2019. Вариант 992, Задания 13 (С1) ЕГЭ 2019

а)  Решите уравнение

б)  Укажите корни этого уравнения, принадлежащие отрезку

Источник: А. Ларин. Тренировочный вариант № 299.

а)  Решите уравнение

б)  Укажите корни этого уравнения, принадлежащие отрезку

Источник: А. Ларин. Тренировочный вариант № 313. (Часть C)

Дано уравнение

а)  Решите уравнение;

б)  Укажите корни уравнения, принадлежащие отрезку

Дано уравнение

а)  Решите уравнение.

б)  Найдите корни этого уравнения, принадлежащие отрезку

Источник: А. Ларин: Тренировочный вариант № 198.

а)  Решите уравнение

б)  Укажите корни этого уравнения, принадлежащие отрезку

Источник: А. Ларин: Тренировочный вариант № 251.

а)  Решите уравнение

б)  Укажите корни этого уравнения, принадлежащие отрезку

Источник: А. Ларин. Тренировочный вариант № 266.

а)  Решите уравнение

б)  Укажите корни этого уравнения, принадлежащие отрезку

Источник: А. Ларин. Тренировочный вариант № 378.

а)  Решите уравнение

б)  Укажите корни этого уравнения, принадлежащие отрезку

Источник: ЕГЭ по математике 02.06.2022. Основная волна. Санкт-Петербург. Вариант 319, Задания 12 ЕГЭ–2022

а)  Решите уравнение

б)  Укажите корни этого уравнения, принадлежащие отрезку

Источник: ЕГЭ по математике 02.06.2022. Основная волна. Санкт-Петербург. Вариант 321, Задания 12 ЕГЭ–2022

Решите систему уравнений:

а)  Решите уравнение

б)  Укажите корни этого уравнения, принадлежащие отрезку

Источник: ЕГЭ по математике — 2015. Досрочная волна, Запад.

а)  Решите уравнение

б)  Укажите корни этого уравнения, принадлежащие отрезку

Дано уравнение

а)  Решите уравнение.

б)  Укажите корни этого уравнения, принадлежащие отрезку

Источник: А. Ларин: Тренировочный вариант № 167.

Всего: 429 1–20 | 21–40 | 41–60 | 61–80 …

Источник

Преподаватель который помогает студентам и школьникам в учёбе.

Формулы двойного аргумента с примерами решения

Содержание:

Преобразования тригонометрических выражений можно упростить, если рассмотреть частные случаи общих формул. Рассмотрим формулу синуса суммы

Формула синуса двойного аргумента

Получили формулу синуса двойного аргумента:

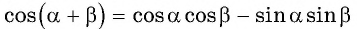
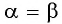
Выведем формулу косинуса двойного аргумента. Используем формулу косинуса суммы для случая и получим:

Формула косинуса двойного аргумента

Формула косинуса двойного аргумента:

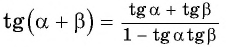
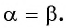
Для вывода формулы тангенса двойного аргумента рассмотрим формулу тангенса суммы при В этом случае имеем:

Формула тангенса двойного аргумента

Получили формулу тангенса двойного аргумента:

Пример №1

Упростите выражение:

Решение:

Применим формулы двойного аргумента:

Пример №2

Вычислите:

Решение:

Применим формулы двойного аргумента «справа налево»:

Пример №3

Найдите значение выражения 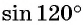двумя способами.

Решение:

Первый способ. Применим формулы приведения:

Второй способ. Применим формулу синуса двойного аргумента:

Пример №4

Представьте данный угол в виде

Решение:

Пример №5

Преобразуйте каждое из выражений с помощью формул двойного угла:

Решение:

Представим угол в каждом из выражений в виде 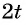и применим формулу двойного аргумента:

Пример №6

Упростите выражение:

Решение:

Применим формулы двойного аргумента и получим:

Пример №7

Найдите значение выражения:

Решение:

Пример №8

Вычислите

Решение:

Применим формулу тангенса двойного аргумента и получим:

Пример №9

Вычислите:

Решение:

б) По формулам приведения

Пример №10

Вычислите 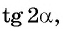если

Решение:

Так как или Поскольку

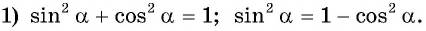
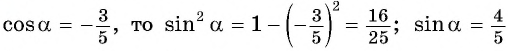
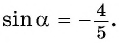
Ответ: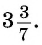

Заказать решение задач по высшей математике

Пример №11

Решите уравнение

Решение:

Используем формулу синуса двойного аргумента:

Ответ:

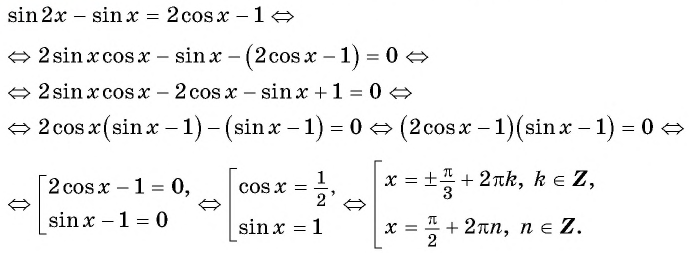
Пример №12

Решите уравнение

Решение:

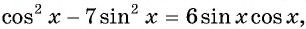
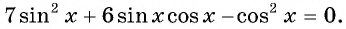
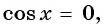
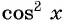
Воспользуемся формулой синуса двойного угла и получим или Так как значения переменной, при которых не являются корнями данного уравнения, то разделим обе части уравнения на и получим

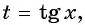
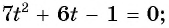
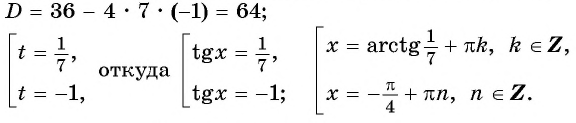
Пусть тогда уравнение примет вид Ответ:

Пример №13

Докажите тождество

Решение:

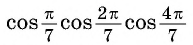
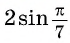
Умножим и разделим выражение на и применим формулу синуса двойного аргумента:

Формулы преобразования суммы и разности синусов (косинусов) в произведение
Корень n-й степени из числа и его свойства
Свойства и график функции y=ⁿ√x (n>1, n∈N)
Иррациональные уравнения
Тригонометрические уравнения
Тригонометрические неравенства
Формулы приведения
Синус, косинус, тангенс суммы и разности

Источник

Самостоятельная работа «Формулы двойного аргумента в заданиях егэ»

Формулы двойного аргумента в задания егэ

Формулы двойного аргумента в заданиях егэ

Вариант 1

Вычислите:

4) 2cos

Найдите: если

Упростите выражения:

1) 0,5 sin 2 ctg 

2) ) 4 sin  cos  cos 2

Решите уравнение

Вариант 2

4) 2cos

Найдите: если

Упростите выражения:

1) 2 sin2  + cos 2

2) sin2 3x – cos2 3x

Решите уравнение

Вариант 3

4) 2cos

Найдите: если

Упростите выражения:

1) sin 2t ctg t – 1

Решите уравнение

Вариант 4

4) 2cos

Найдите: если

Упростите выражения:

1) 1 + cos 2

Решите уравнение

Опубликовано 18.02.18 в 15:07

Размер файла: 18.55 Кбайт

Источник

Проверочная работа «Формулы двойного аргумента в задания егэ»

Формулы двойного аргумента в задания егэ

Формулы двойного аргумента в заданиях егэ

Вариант 1

Вычислите:

1)  































4) 2cos











Найдите:  если

  





   

Упростите выражения:

1) 0,5 sin 2 ctg 

2) ) 4 sin  cos  cos 2

Решите уравнение

 



  

Вариант 2

1)  































4) 2cos











Найдите:  если

  





   

Упростите выражения:

1) 2 sin

 + cos 2

2) sin

3x – cos

Решите уравнение

  





 

Вариант 3

1)  































4) 2cos











Найдите:  если

  





   





Упростите выражения:

1) sin 2t ctg t – 1

Решите уравнение

   







Вариант 4

1)  































4) 2cos











Найдите:  если

 











   

Упростите выражения:

1) 1 + cos 2

Решите уравнение

    





 

Источник

Инфоурок

›

Алгебра

›Другие методич. материалы›Формулы двойного аргумента в заданиях егэ

Формулы двойного аргумента в заданиях егэ

Скачать материал

Сейчас обучается 898 человек из 81 региона

Сейчас обучается 27 человек из 12 регионов

Сейчас обучается 25 человек из 13 регионов

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 156 999 материалов в базе

Выберите категорию:
Выберите учебник и тему

Выберите класс:
Тип материала:
- Все материалы
- Статьи
- Научные работы
- Видеоуроки
- Презентации
- Конспекты
- Тесты
- Рабочие программы
- Другие методич. материалы

Найти материалы

Материал подходит для УМК

«Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа (базовый и углублённый уровни) (в 2 частях)», Ч.1.: Мордкович А.Г., Семенов П.В.; Ч.2.: Мордкович А.Г. и др., под ред. Мордковича А.Г.

Тема

§ 21. Формулы двойного аргумента

Больше материалов по этой теме

Другие материалы

Рабочая программа по алгебре и началом анализа 11 класс

Учебник: «Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа (базовый и углублённый уровни) (в 2 частях)», Ч.1.: Мордкович А.Г., Семенов П.В.; Ч.2.: Мордкович А.Г. и др., под ред. Мордковича А.Г.

25.08.2018
389
0

Рабочая программа по алгебре и началом анализа 10 класс

Учебник: «Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа (базовый и углублённый уровни) (в 2 частях)», Ч.1.: Мордкович А.Г., Семенов П.В.; Ч.2.: Мордкович А.Г. и др., под ред. Мордковича А.Г.

25.08.2018
652
1

Тест по алгебре на тему: Логарифмы.Свойства логарифмов

Учебник: «Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа (базовый и углублённый уровни) (в 2 частях)», Ч.1.: Мордкович А.Г., Семенов П.В.; Ч.2.: Мордкович А.Г. и др., под ред. Мордковича А.Г.
Тема: § 43. Свойства логарифмов

25.08.2018
358
2

Рабочая программа элективного курса по математике 10 класс

Учебник: «Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа (базовый и углублённый уровни) (в 2 частях)», Ч.1.: Мордкович А.Г., Семенов П.В.; Ч.2.: Мордкович А.Г. и др., под ред. Мордковича А.Г.
Тема: Глава 1. Числовые функции

Рейтинг:
4 из 5

24.08.2018
2723
145

Рабочая программа по математике 10 класс

Учебник: «Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа (базовый и углублённый уровни) (в 2 частях)», Ч.1.: Мордкович А.Г., Семенов П.В.; Ч.2.: Мордкович А.Г. и др., под ред. Мордковича А.Г.
Тема: Глава 1. Числовые функции

24.08.2018
663
0

Презентация по математике на тему «Комплексные числа» (10 класс)

Учебник: «Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа (базовый и углублённый уровни) (в 2 частях)», Ч.1.: Мордкович А.Г., Семенов П.В.; Ч.2.: Мордкович А.Г. и др., под ред. Мордковича А.Г.
Тема: § 50. Статистическая обработка данных

24.08.2018
357
0

Контрольная работа на тему «Применение производной к исследованию функций» (10 класс)

Учебник: «Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа (базовый и углублённый уровни) (в 2 частях)», Ч.1.: Мордкович А.Г., Семенов П.В.; Ч.2.: Мордкович А.Г. и др., под ред. Мордковича А.Г.
Тема: § 30. Применение производной для исследования функций на монотонность и экстремумы

Рейтинг:
5 из 5

23.08.2018
6510
156

Набор заданий по теме » Физический смысл производной» (10 класс)

Учебник: «Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа (базовый и углублённый уровни) (в 2 частях)», Ч.1.: Мордкович А.Г., Семенов П.В.; Ч.2.: Мордкович А.Г. и др., под ред. Мордковича А.Г.
Тема: § 27. Определение производной

23.08.2018
656
7

Вам будут интересны эти курсы:

Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»
Курс повышения квалификации «Основы туризма и гостеприимства»
Курс повышения квалификации «Методика написания учебной и научно-исследовательской работы в школе (доклад, реферат, эссе, статья) в процессе реализации метапредметных задач ФГОС ОО»
Курс повышения квалификации «Экономика предприятия: оценка эффективности деятельности»
Курс повышения квалификации «Экономика: инструменты контроллинга»
Курс повышения квалификации «Правовое регулирование рекламной и PR-деятельности»
Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
Курс повышения квалификации «Организация маркетинга в туризме»
Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
Курс профессиональной переподготовки «Организация процесса страхования (перестрахования)»
Курс профессиональной переподготовки «Организация и управление процессом по предоставлению услуг по кредитному брокериджу»

Настоящий материал опубликован пользователем Курикалова Ирина Викторовна. Инфоурок является
информационным посредником и предоставляет пользователям возможность размещать на сайте
методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них
сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с
сайта, Вы можете оставить жалобу на материал.

Удалить материал
- На сайте: 6 лет и 4 месяца
- Подписчики: 1
- Всего просмотров: 38779
- Всего материалов:
  
  26

Источник

Примеры:

(2 sin⁡15^° cos⁡15^°=sin⁡(2·15^°)=sin⁡30^° =frac{1}{2})
(cos⁡6α=cos^2⁡3α-sin^2⁡3α)
(sin⁡α=2 sin⁡frac{α}{2}cos⁡frac{α}{2})
(2 cos^2⁡frac{π}{12}-1=cos⁡frac{2π}{12}=cos⁡frac{π}{6}=frac{sqrt{3}}{2})

Примеры решения задач из ЕГЭ на формулы двойного угла

Пример (ЕГЭ). Найдите значение выражения (frac{12 sin⁡11^° cdot, cos⁡11^°}{sin ⁡22^° }).
Решение. (frac{12 sin⁡11^° cdot, cos⁡11^°}{sin⁡22^°})(=)(frac{12 sin⁡11^° cdot,cos⁡11^°}{2 sin⁡11^° cdot, cos⁡11^° })(=)(frac{12}{2})(=6).

Пример (ЕГЭ).

Пример (ЕГЭ). Найдите значение выражения (sqrt{3}cos^2frac{5π}{12}-sqrt{3}sin^2frac{5π}{12}).
Решение. (sqrt{3}cos^2frac{5π}{12}-sqrt{3}sin^2frac{5π}{12}=sqrt{3}(cos^2frac{5π}{12}-sin^2frac{5π}{12})=sqrt{3}cos(2cdotfrac{5π}{12})=sqrt{3}cosfrac{5π}{6})

Вычислим (cos⁡frac{5π}{6}) с помощью тригонометрического круга. Сначала найдем (frac{5π}{6}) на круге:

(frac{5π}{6}=frac{6π-π}{6}=π-frac{π}{6})

Теперь видно, что (cos⁡frac{5π}{6}=-frac{sqrt{3}}{2})
(sqrt{3}cos⁡ frac{5π}{6}=sqrt{3}cdot(-frac{sqrt{3}}{2})=-frac{3}{2}=-1,5).

Пример (ЕГЭ).

Пример (ЕГЭ). Найдите значение выражения (frac{24(sin^2 17^°- cos^2⁡ 17^°)}{cos⁡34^°}).
Решение. (frac{24(sin^2 17^°- cos^2⁡ 17^°)}{cos⁡34^°})(=)(frac{-24(cos^2⁡ 17^°- sin^2 17^° )}{cos⁡34^°})(=)(frac{-24 cos⁡2cdot 17^°}{cos⁡34^° }) (=)(frac{-24 cos⁡34^° }{cos⁡34^° })(=-24).

Пример (ЕГЭ).

Пример (ЕГЭ). Найдите значение выражения (5sinfrac{11π}{12}cos⁡frac{11π}{12}).
Решение. (5 sinfrac{⁡11π}{12}cos⁡frac{11π}{12}=frac{5}{2}cdot2sin⁡frac{11π}{12}cos⁡frac{11π}{12}=frac{5}{2}sinfrac{⁡2cdot 11π}{12}=frac{5}{2} sin⁡frac{11π}{6}=frac{5}{2}sin⁡frac{12π-π}{6}=frac{5}{2}sin⁡(frac{12π}{6}-frac{π}{6})=)
(=frac{5}{2}sin⁡(2π-frac{π}{6})=frac{5}{2}sin⁡(-frac{π}{6})=-frac{5}{2}sin⁡frac{π}{6}=-frac{5}{2}cdot frac{1}{2}=-frac{5}{4}=-1,25).

Пример. (Задание из ЕГЭ) Найдите значение выражения (frac{5sin⁡98^°}{sin⁡49^° sin⁡ 41^°}).

Решение:

(frac{5sin⁡98^°}{sin⁡49^° sin⁡ 41^°})		Все аргументы разные и что с этим делать не понятно. Однако присмотревшись, замечаем, что (98^°)ровно в два раза больше (49^°). То есть, имеет смысл разложить синус в числителе по формуле двойного угла.
(frac{10sin⁡49^°cos49^°}{sin⁡49^° sin⁡ 41^°})		Одинаковые синусы можно сократить.
(frac{10cos49^°}{sin⁡ 41^°})		Теперь обратите внимание на то, что (49^°=90^°-41^°). Поэтому мы можем заменить (49^°) на (90^°-41^°).
(frac{10cos(90^°-41^°)}{sin⁡ 41^°})		Теперь применим к косинусу формулу приведения: ((90^°-41^°)) – это первая четверть, косинус в ней положителен. Значит, знак будет плюс; (90^°)- находится на «вертикали» — функция меняется на кофункцию. (cos⁡ (90^°-41^°)=sin⁡41^°)
(=frac{10 sin⁡41^° }{sin⁡41^°})( =10)

Ответ: (10).

Пример. (Задание из ЕГЭ) Найдите значение выражения (sqrt{12}cos^2⁡frac{5π}{12}-sqrt{3}).

Решение:

(sqrt{12}cos^2⁡frac{5π}{12}-sqrt{3}=)		С первого взгляда не очевидно, что тут надо делать. Возможно, со второго тоже. И здесь нас выручит золотое правило решения задач по математике: «не знаешь, что делать — делай, что можешь». А тут точно можно преобразовать (sqrt{12}). (sqrt{12}=sqrt{4cdot 3}=2sqrt{3}).
(=2sqrt{3}cos^2⁡frac{5π}{12}-sqrt{3}=)		Теперь можно вынести (sqrt{3}) за скобки.
(=sqrt{3}(2 cos^2⁡frac{5π}{12}-1)=)		Вот теперь видно, что перед нами формула косинуса двойного угла.
(=sqrt{3}cos(2cdotfrac{5π}{12})=)		Сокращаем (2) и (12).
(=sqrt{3}cos(frac{5π}{6})=)		Разложим (frac{5π}{6}): (frac{5π}{6}=frac{6π-π}{6}=frac{6π}{6}-frac{π}{6}=π-frac{π}{6})
(=sqrt{3}cos(π-frac{π}{6})=)		Теперь применим к косинусу формулу приведения: ((π-frac{π}{6})) – это вторая четверть, косинус в ней отрицателен. Значит, знак будет минус; (π) — находится на «горизонтали» — функция не меняется на кофункцию. (cos⁡(π-frac{π}{6})=-cos frac{π}{6})
(=-sqrt{3}cos⁡frac{π}{6}=-sqrt{3}cdotfrac{sqrt{3}}{2}=) (=-frac{3}{2}=-1,5.)

Ответ: (-1,5).

Смотрите также:
Формулы тригонометрии с примерами

Источник

Формулы двойного аргумента в задания егэ

Формулы двойного аргумента в заданиях егэ

Вариант 1

Вычислите:

4) 2cos

Найдите: если

Упростите выражения:

1) 0,5 sin 2 ctg 

2)) 4 sin  cos  cos 2

Решите уравнение

Вариант 2

4) 2cos

Найдите: если

Упростите выражения:

1) 2 sin² + cos 2

2)sin² 3x – cos² 3x

Решите уравнение

Вариант 3

4) 2cos

Найдите: если

Упростите выражения:

1) sin 2tctgt – 1

Решите уравнение

Вариант 4

4) 2cos

Найдите: если

Упростите выражения:

1) 1 + cos 2

Решите уравнение

Источник

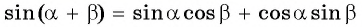
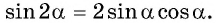
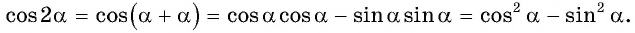
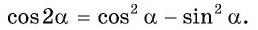
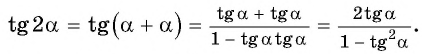
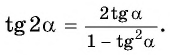
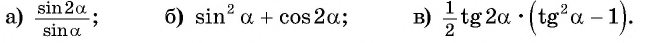
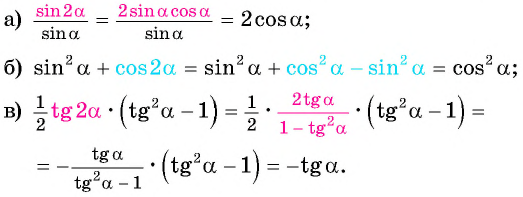
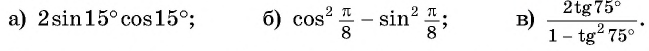
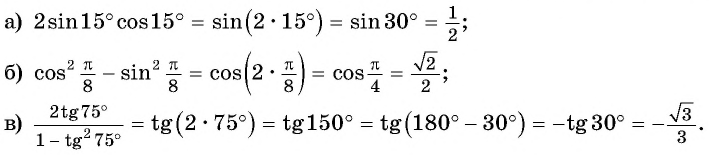
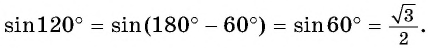
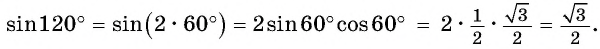
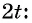
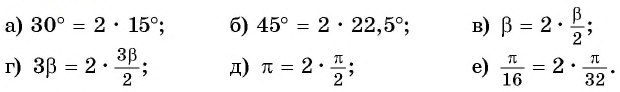
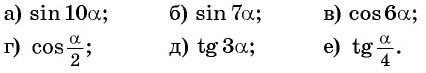
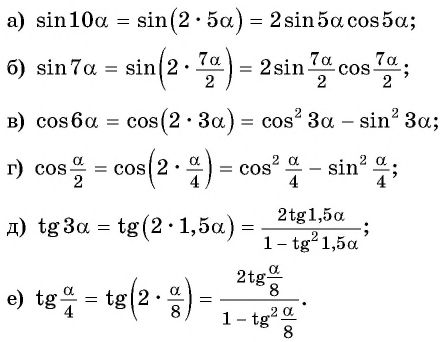
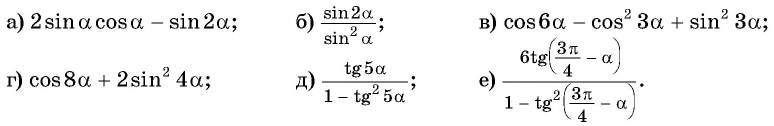
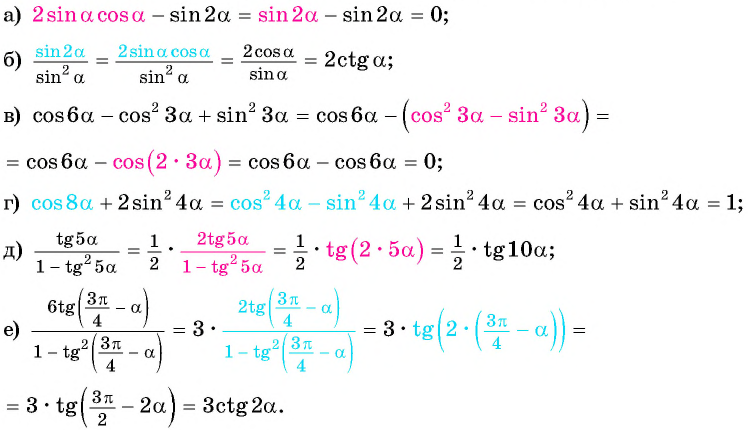
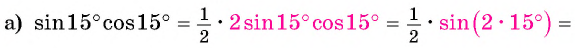
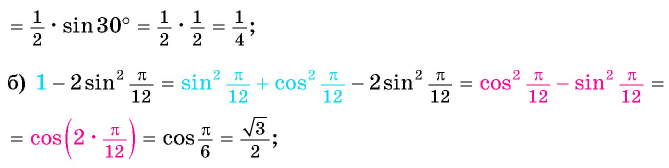
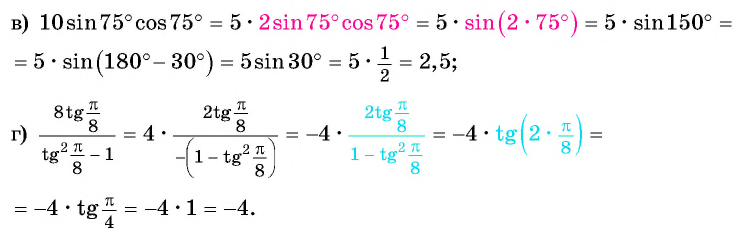
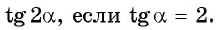
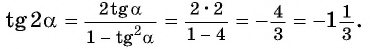
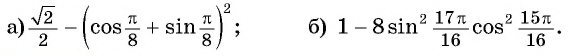
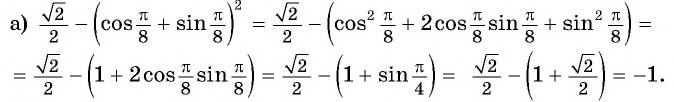
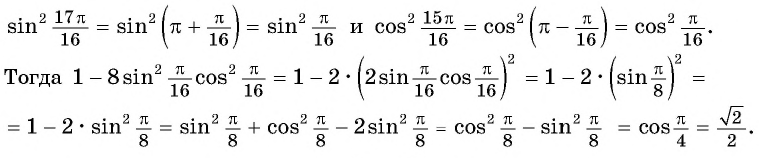
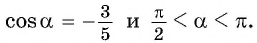
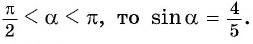
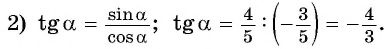
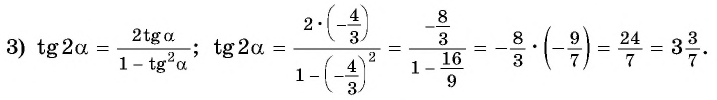
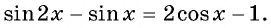
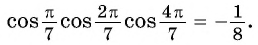
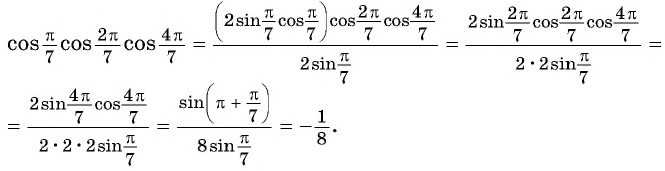
Формулы двойного аргумента с примерами решения

Формула синуса двойного аргумента

Формула косинуса двойного аргумента

Формула тангенса двойного аргумента

Пример №1

Пример №2

Пример №3

Пример №4

Пример №5

Пример №6

Пример №7

Пример №8

Пример №9

Пример №10

Пример №11

Пример №12

Пример №13

Самостоятельная работа «Формулы двойного аргумента в заданиях егэ»

Проверочная работа «Формулы двойного аргумента в задания егэ»

Формулы двойного аргумента в заданиях егэ

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

Материал подходит для УМК

Тема

Другие материалы

Вам будут интересны эти курсы:

Примеры решения задач из ЕГЭ на формулы двойного угла