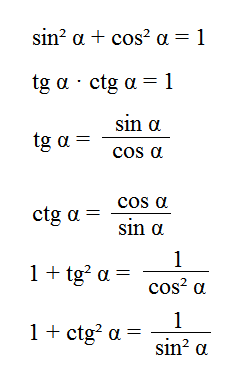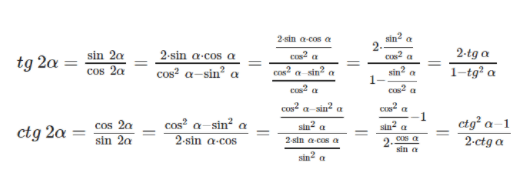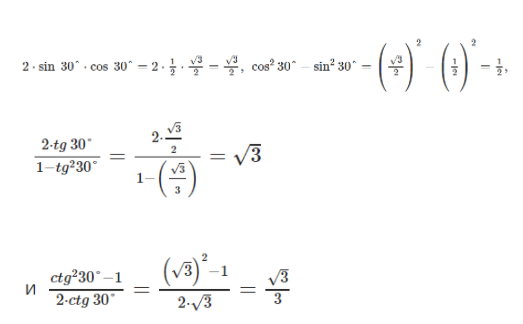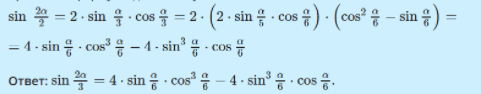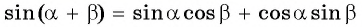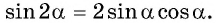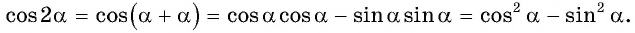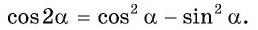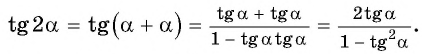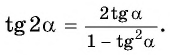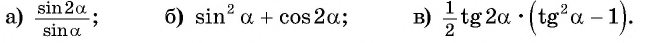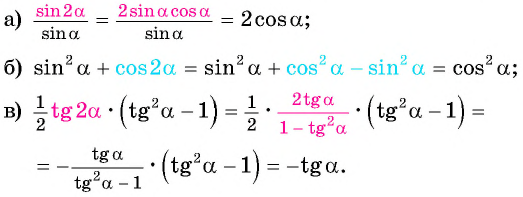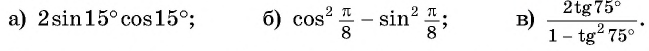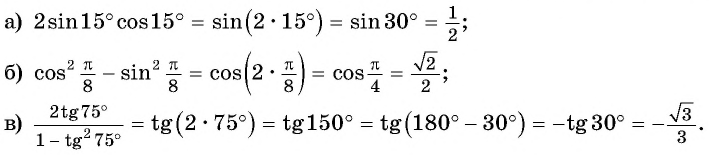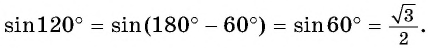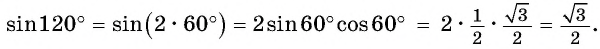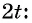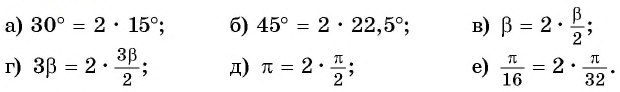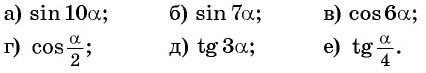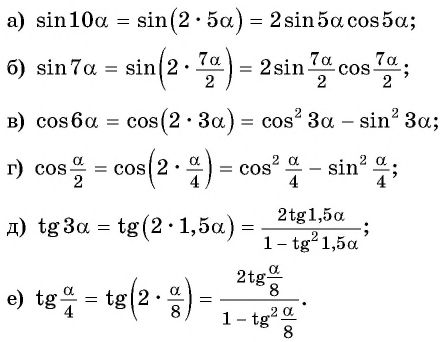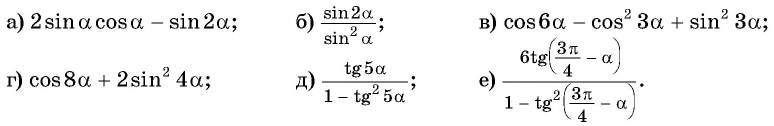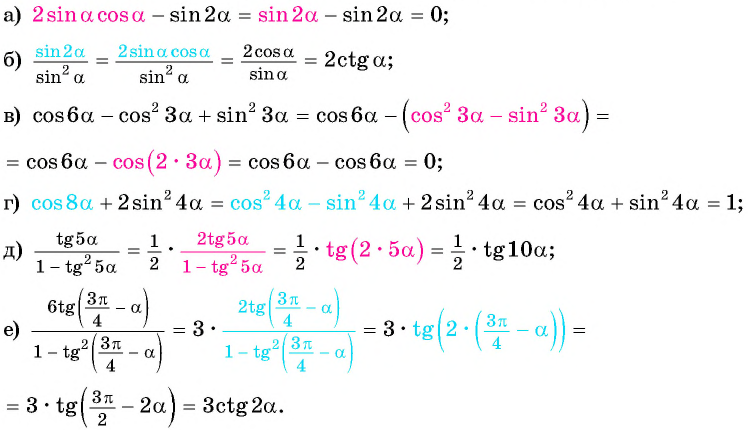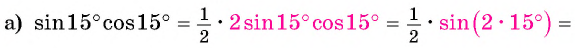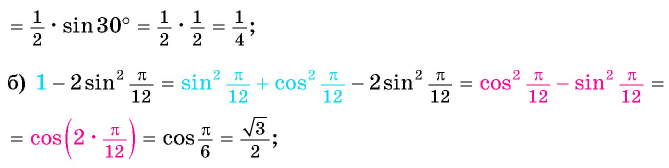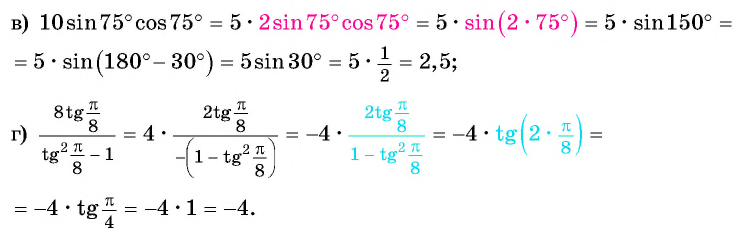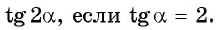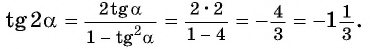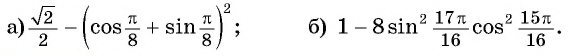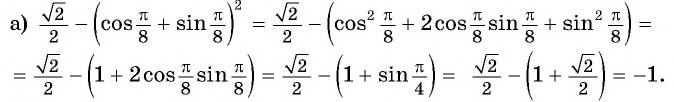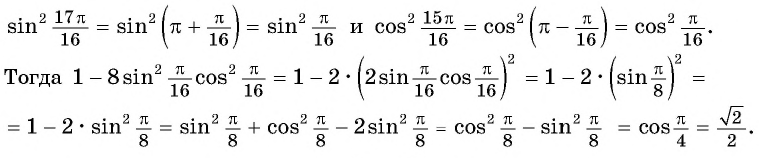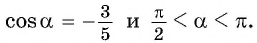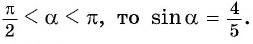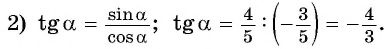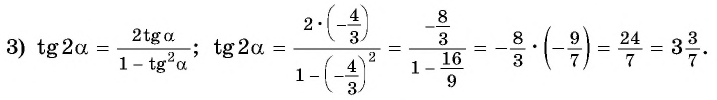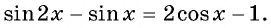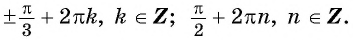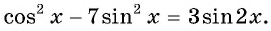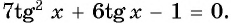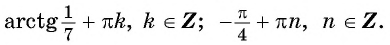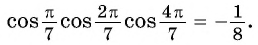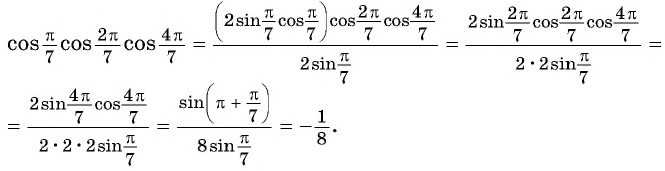в условии
в решении
в тексте к заданию
в атрибутах
Категория:
Атрибут:
Всего: 429 1–20 | 21–40 | 41–60 | 61–80 …
Добавить в вариант
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие промежутку
Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко. 2015 г.
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
Источник: ЕГЭ по математике 01.06.2018. Основная волна. Дальний Восток. (C часть)., Задания 13 (С1) ЕГЭ 2018
а) Решите уравнение
б) Укажите корни уравнения, принадлежащие отрезку
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
Источник: ЕГЭ по математике 2015. Досрочная волна, резервная волна (часть С)
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Источник: Основная волна ЕГЭ по математике 29.05.2019. Дальний восток, Задания 13 (С1) ЕГЭ 2019
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Источник: Резервная волна ЕГЭ по математике 24.06.2019. Вариант 992, Задания 13 (С1) ЕГЭ 2019
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
Источник: А. Ларин. Тренировочный вариант № 299.
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
Источник: А. Ларин. Тренировочный вариант № 313. (Часть C)
Дано уравнение
а) Решите уравнение;
б) Укажите корни уравнения, принадлежащие отрезку
Дано уравнение
а) Решите уравнение.
б) Найдите корни этого уравнения, принадлежащие отрезку
Источник: А. Ларин: Тренировочный вариант № 198.
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
Источник: А. Ларин: Тренировочный вариант № 251.
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
Источник: А. Ларин. Тренировочный вариант № 266.
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
Источник: А. Ларин. Тренировочный вариант № 378.
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
Источник: ЕГЭ по математике 02.06.2022. Основная волна. Санкт-Петербург. Вариант 319, Задания 12 ЕГЭ–2022
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
Источник: ЕГЭ по математике 02.06.2022. Основная волна. Санкт-Петербург. Вариант 321, Задания 12 ЕГЭ–2022
Решите систему уравнений:
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
Источник: ЕГЭ по математике — 2015. Досрочная волна, Запад.
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
Дано уравнение
а) Решите уравнение.
б) Укажите корни этого уравнения, принадлежащие отрезку
Источник: А. Ларин: Тренировочный вариант № 167.
Всего: 429 1–20 | 21–40 | 41–60 | 61–80 …
Примеры:
(2 sin15^° cos15^°=sin(2·15^°)=sin30^° =frac{1}{2})
(cos6α=cos^23α-sin^23α)
(sinα=2 sinfrac{α}{2}cosfrac{α}{2})
(2 cos^2frac{π}{12}-1=cosfrac{2π}{12}=cosfrac{π}{6}=frac{sqrt{3}}{2})
Примеры решения задач из ЕГЭ на формулы двойного угла
Пример (ЕГЭ). Найдите значение выражения (frac{12 sin11^° cdot, cos11^°}{sin 22^° }).
Решение. (frac{12 sin11^° cdot, cos11^°}{sin22^°})(=)(frac{12 sin11^° cdot,cos11^°}{2 sin11^° cdot, cos11^° })(=)(frac{12}{2})(=6).
Пример (ЕГЭ).

Пример (ЕГЭ). Найдите значение выражения (sqrt{3}cos^2frac{5π}{12}-sqrt{3}sin^2frac{5π}{12}).
Решение. (sqrt{3}cos^2frac{5π}{12}-sqrt{3}sin^2frac{5π}{12}=sqrt{3}(cos^2frac{5π}{12}-sin^2frac{5π}{12})=sqrt{3}cos(2cdotfrac{5π}{12})=sqrt{3}cosfrac{5π}{6})
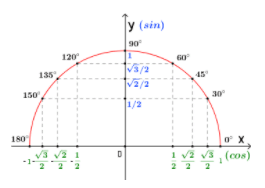
Вычислим (cosfrac{5π}{6}) с помощью тригонометрического круга. Сначала найдем (frac{5π}{6}) на круге:
(frac{5π}{6}=frac{6π-π}{6}=π-frac{π}{6})

Теперь видно, что (cosfrac{5π}{6}=-frac{sqrt{3}}{2})
(sqrt{3}cos frac{5π}{6}=sqrt{3}cdot(-frac{sqrt{3}}{2})=-frac{3}{2}=-1,5).
Пример (ЕГЭ).

Пример (ЕГЭ). Найдите значение выражения (frac{24(sin^2 17^°- cos^2 17^°)}{cos34^°}).
Решение. (frac{24(sin^2 17^°- cos^2 17^°)}{cos34^°})(=)(frac{-24(cos^2 17^°- sin^2 17^° )}{cos34^°})(=)(frac{-24 cos2cdot 17^°}{cos34^° }) (=)(frac{-24 cos34^° }{cos34^° })(=-24).
Пример (ЕГЭ).

Пример (ЕГЭ). Найдите значение выражения (5sinfrac{11π}{12}cosfrac{11π}{12}).
Решение. (5 sinfrac{11π}{12}cosfrac{11π}{12}=frac{5}{2}cdot2sinfrac{11π}{12}cosfrac{11π}{12}=frac{5}{2}sinfrac{2cdot 11π}{12}=frac{5}{2} sinfrac{11π}{6}=frac{5}{2}sinfrac{12π-π}{6}=frac{5}{2}sin(frac{12π}{6}-frac{π}{6})=)
(=frac{5}{2}sin(2π-frac{π}{6})=frac{5}{2}sin(-frac{π}{6})=-frac{5}{2}sinfrac{π}{6}=-frac{5}{2}cdot frac{1}{2}=-frac{5}{4}=-1,25).
Пример. (Задание из ЕГЭ) Найдите значение выражения (frac{5sin98^°}{sin49^° sin 41^°}).
Решение:
|
(frac{5sin98^°}{sin49^° sin 41^°}) |
Все аргументы разные и что с этим делать не понятно. Однако присмотревшись, замечаем, что (98^°)ровно в два раза больше (49^°). То есть, имеет смысл разложить синус в числителе по формуле двойного угла. |
|
|
(frac{10sin49^°cos49^°}{sin49^° sin 41^°}) |
Одинаковые синусы можно сократить. |
|
|
(frac{10cos49^°}{sin 41^°}) |
Теперь обратите внимание на то, что (49^°=90^°-41^°). |
|
|
(frac{10cos(90^°-41^°)}{sin 41^°}) |
Теперь применим к косинусу формулу приведения:
|
|
|
(=frac{10 sin41^° }{sin41^°})( =10) |
Ответ: (10).
Пример. (Задание из ЕГЭ) Найдите значение выражения (sqrt{12}cos^2frac{5π}{12}-sqrt{3}).
Решение:
|
(sqrt{12}cos^2frac{5π}{12}-sqrt{3}=) |
С первого взгляда не очевидно, что тут надо делать. Возможно, со второго тоже. И здесь нас выручит золотое правило решения задач по математике: «не знаешь, что делать — делай, что можешь». А тут точно можно преобразовать (sqrt{12}). |
|
|
(=2sqrt{3}cos^2frac{5π}{12}-sqrt{3}=) |
Теперь можно вынести (sqrt{3}) за скобки. |
|
|
(=sqrt{3}(2 cos^2frac{5π}{12}-1)=) |
Вот теперь видно, что перед нами формула косинуса двойного угла. |
|
|
(=sqrt{3}cos(2cdotfrac{5π}{12})=) |
Сокращаем (2) и (12). |
|
|
(=sqrt{3}cos(frac{5π}{6})=) |
Разложим (frac{5π}{6}): (frac{5π}{6}=frac{6π-π}{6}=frac{6π}{6}-frac{π}{6}=π-frac{π}{6}) |
|
|
(=sqrt{3}cos(π-frac{π}{6})=) |
Теперь применим к косинусу формулу приведения:
(cos(π-frac{π}{6})=-cos frac{π}{6}) |
|
|
(=-sqrt{3}cosfrac{π}{6}=-sqrt{3}cdotfrac{sqrt{3}}{2}=) |
Ответ: (-1,5).
Смотрите также:
Формулы тригонометрии с примерами
Инфоурок
›
Математика
›Презентации›Презентация по математике «Формулы двойного угла на ЕГЭ»
Презентация по математике «Формулы двойного угла на ЕГЭ»
Скачать материал

Скачать материал


- Сейчас обучается 898 человек из 81 региона


- Сейчас обучается 27 человек из 12 регионов


- Сейчас обучается 25 человек из 13 регионов


Описание презентации по отдельным слайдам:
-
1 слайд
Формулы двойного угла на ЕГЭ
-
2 слайд
1) sin2t=2sintcost
формулы двойного угла
-
3 слайд
№1.Найдите , если
2
-0,12 -
4 слайд
№4.Найдите значение выражения
-10, 5
-4 -
5 слайд
№5.Найдите значение выражения
Ответ:-6
№6.Найдите значение выражения .
-0,25 -
6 слайд
ответы
1.2
2.-0, 12
3.-10, 5
4.-4
5.-6
6.-0,5 -
-
8 слайд
На дом:
Mathege.ru
№64423
№64553
№65561
№282535
№282615
№282525
Краткое описание документа:
Данная презентация (не требует сложного программного обеспечения)составлена из номеров открытого банка заданий ЕГЭ по математике.Учитель может использовать данную презентацию на уроке для контроля знаний (если убрать анимации — ответы к каждому заданию), для самоподготовки к уроку,а ученик — для самостоятельного закрепления темы «Формулы двойной угла», используя все формулы для синуса и косинуса двойного угла через синус и косинус, через синус и через косинус, как того требует единый государственный экзамен.Также можно использовать и для объяснения материала и показа какие именно задания могут быть на экзамене по данной теме в первой части
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 156 999 материалов в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Другие материалы
- 13.01.2015
- 1678
- 0
- 13.01.2015
- 2267
- 4
- 13.01.2015
- 1596
- 4
- 13.01.2015
- 988
- 1
- 13.01.2015
- 4006
- 12
-
Настоящий материал опубликован пользователем Волкова Нина Владимировна. Инфоурок является
информационным посредником и предоставляет пользователям возможность размещать на сайте
методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них
сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайтЕсли Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с
сайта, Вы можете оставить жалобу на материал.Удалить материал
-
- На сайте: 8 лет и 2 месяца
- Подписчики: 0
- Всего просмотров: 49811
-
Всего материалов:
15
Задания для занятия по подготовке к ЕГЭ. Формулы двойного угла встречаются в заданиях В11 (тождественные преобразования), очень часто в уравнениях С1. Можно использовать в 10 и 11 классе. У меня не самые сильные ученики.
Просмотр содержимого документа
«задания на занятие «Формулы двойного угла в заданиях ЕГЭ»»
10 класс
-
Найдите 25cos2α, если sinα=−0,7.
-
Найдите значение выражения
-
Найдите значение выражения .
-
Найдите значение выражения
.
-
Найдите значение выражения
.
-
Найдите значение выражения
.
-
Найдите значение выражения
.
-
Найдите значение выражения
.
C1 а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
Решение.
а) Преобразуем исходное уравнение:

Получим числа:
Ответ: а)
б)
Задания Открытого банка ЕГЭ по математике.
Скачать:
Предварительный просмотр:
ЕГЭ (ПУ-9) Формулы двойного угла. Тренировочные задания.
1. Вычислите: а) ; б);
в) ; г)
;
д) ; е);
ЕГЭ (ПУ-9) Формулы двойного угла. Тренировочные задания.
1. Вычислите: а) ; б);
в) ; г)
;
д) ; е);
ЕГЭ (ПУ-9) Формулы двойного угла. Тренировочные задания.
1. Вычислите: а) ; б);
в) ; г)
;
д) ; е);
ЕГЭ (ПУ-9) Формулы двойного угла. Тренировочные задания.
1. Вычислите: а) ; б);
в) ; г)
;
д) ; е);
ЕГЭ (ПУ-9) Формулы двойного угла. Тренировочные задания.
1. Вычислите: а) ; б);
в) ; г)
;
д) ; е);
ЕГЭ (ПУ-9) Формулы двойного угла. Тренировочные задания.
1. Вычислите: а) ; б);
в) ; г)
;
д) ; е);
ЕГЭ (ПУ-9) Формулы двойного угла. Тренировочные задания.
1. Вычислите: а) ; б);
в) ; г)
;
д) ; е);
ж) ; з)
и) Найдите , если
.
к) Найдите , если
.
л) Найдите , если
.
ж) ; з)
и) Найдите , если
.
к) Найдите , если
.
л) Найдите , если
.
ж) ; з)
и) Найдите , если
.
к) Найдите , если
.
л) Найдите , если
.
ж) ; з)
и) Найдите , если
.
к) Найдите , если
.
л) Найдите , если
.
ж) ; з)
и) Найдите , если
.
к) Найдите , если
.
л) Найдите , если
.
ж) ; з)
и) Найдите , если
.
к) Найдите , если
.
л) Найдите , если
.
ж) ; з)
и) Найдите , если
.
к) Найдите , если
.
л) Найдите , если
.
По теме: методические разработки, презентации и конспекты
Урок «Формулы двойного угла»
Урок по теме «Формулы двойного угла».Цели урока:· формирование представлений о формулах двойного угла синуса, косинуса;· ф…
«Формулы двойного угла»
В рабочей программе тема “Формулы двойного угла” входит в раздел 1 “Алгебра и начала анализа” предмета “Математика”. В этой теме изучаются, систематизируются знания студентов об основных формулах триг…
Конспект урока в 10 классе «Формулы двойного угла»
Формирование навыков применения формул двойного углапри выполнении заданий, создание условий, в которых обучающиесямогли самостоятельно планировать и анализировать свои собственные действия, реально о…
- Мне нравится
cos2a, sin2a. Формулы двойного угла. Примеры на ЕГЭ
Примеры решения задач из ЕГЭ на формулы двойного угла
Вычислим (cosfrac<5π><6>) с помощью тригонометрического круга. Сначала найдем (frac<5π><6>) на круге:
Все аргументы разные и что с этим делать не понятно. Однако присмотревшись, замечаем, что (98^°)ровно в два раза больше (49^°). То есть, имеет смысл разложить синус в числителе по формуле двойного угла.
Одинаковые синусы можно сократить.
Теперь обратите внимание на то, что (49^°=90^°-41^°).
Поэтому мы можем заменить (49^°) на (90^°-41^°).
((90^°-41^°)) – это первая четверть, косинус в ней положителен. Значит, знак будет плюс;
(90^°)- находится на «вертикали» — функция меняется на кофункцию. (cos (90^°-41^°)=sin41^°)
Пример. (Задание из ЕГЭ) Найдите значение выражения (sqrt<12>cos^2frac<5π><12>-sqrt<3>).
С первого взгляда не очевидно, что тут надо делать. Возможно, со второго тоже. И здесь нас выручит золотое правило решения задач по математике: «не знаешь, что делать — делай, что можешь». А тут точно можно преобразовать (sqrt<12>).
(sqrt<12>=sqrt<4cdot 3>=2sqrt<3>).
Теперь можно вынести (sqrt<3>) за скобки.
Вот теперь видно, что перед нами формула косинуса двойного угла.
Сокращаем (2) и (12).
Теперь применим к косинусу формулу приведения:
((π-frac<π><6>)) – это вторая четверть, косинус в ней отрицателен. Значит, знак будет минус;
(π) — находится на «горизонтали» — функция не меняется на кофункцию.
Формулы двойного угла в тригонометрии
Формулы двойного угла служат для выражения синусов, косинусов, тангенсов, котангенсов угла со значением 2 α , используя тригонометрические функции угла α . Данная статья познакомит со всеми формулами двойного угла с доказательствами. Будут рассмотрены примеры применения формул. В заключительной части будут показаны формулы тройного, четверного углов.
Список формул двойного угла
Для преобразования формул двойного угла следует помнить о том, что углы в тригонометрии имеют вид n α записи, где n является натуральным числом, значение выражение записывается без скобок. Таким образом, считается, что запись sin n α имеет то же значение, что и sin ( n α ) . При обозначении sin n α имеем аналогичную запись ( sin α ) n . Использование записи применимо для всех тригонометрических функций со степенями n .
Ниже приведены формулы двойного угла:
sin 2 α = 2 · sin α · cos α cos 2 α = cos 2 α — sin 2 α , cos 2 α = 1 — 2 · sin 2 α , cos 2 α = 2 · cos 2 α — 1 t g 2 α = 2 · t g α 1 — t g 2 α c t g 2 α — c t g 2 α — 1 2 · c t g α
Отметим, что данные формулы sin и cos применимы с любым значением угла α . Формула тангенса двойного угла справедлива при любом значении α , где t g 2 α имеет смысл, то есть α ≠ π 4 + π 2 · z , z является любым целым числом. Котангенс двойного угла существует при любом α , где c t g 2 α определен на α ≠ π 2 · z .
Косинус двойного угла имеет тройную запись двойного угла. Все они являются применимыми.
Доказательство формул двойного угла
Доказательство формул берет начало из формул сложения. Применим формулы синуса суммы:
sin ( α + β ) = sin α · cos β + cos α · sin β и косинуса суммы cos ( α + β ) = cos α · cos β — sin α · sin β . Предположим, что β = α , тогда получим, что
sin ( α + α ) = sin α · cos α + cos α · sin α = 2 · sin α · cos α и cos ( α + α ) = cos α · cos α — sin α · sin α = cos 2 α — sin 2 α
Таким образом доказываются формулы синуса и косинуса двойного угла sin 2 α = 2 · sin α · cos α и cos 2 α = cos 2 α — sin 2 α .
Остальные формулы cos 2 α = 1 — 2 · sin 2 α и cos 2 α = 2 · cos 2 α — 1 приводят к виду cos 2 α = cos 2 α = cos 2 α — sin 2 α , при замене 1 на сумму квадратов по основному тождеству sin 2 α + cos 2 α = 1 . Получаем, что sin 2 α + cos 2 α = 1 . Так 1 — 2 · sin 2 α = sin 2 α + cos 2 α — 2 · sin 2 α = cos 2 α — sin 2 α и 2 · cos 2 α — 1 = 2 · cos 2 α — ( sin 2 α + cos 2 α ) = cos 2 α — sin 2 α .
Для доказательства формул двойного угла тангенса и котангенса применим равенства t g 2 α = sin 2 α cos 2 α и c t g 2 α = cos 2 α sin 2 α . После преобразования получим, что t g 2 α = sin 2 α cos 2 α = 2 · sin α · cos α cos 2 α — sin 2 α и c t g 2 α = cos 2 α sin 2 α = cos 2 α — sin 2 α 2 · sin α · cos α . Разделим выражение на cos 2 α , где cos 2 α ≠ 0 с любым значением α , когда t g α определен. Другое выражение поделим на sin 2 α , где sin 2 α ≠ 0 с любыми значениями α , когда c t g 2 α имеет смысл. Чтобы доказать формулу двойного угла для тангенса и котангенса, подставим и получим:
t g 2 α = sin 2 α cos 2 α = 2 · sin α · cos α cos 2 α — sin 2 α = 2 · sin α · cos α cos 2 α cos 2 α — sin 2 α cos 2 α = 2 · sin 2 α cos 2 α 1 — sin 2 α cos 2 α = 2 · t g α 1 — t g 2 α c t g 2 α = cos 2 α sin 2 α = cos 2 α — sin 2 α 2 · sin α · cos = cos 2 α — sin 2 α sin 2 α 2 · sin α · cos α sin 2 α = cos 2 α sin 2 α — 1 2 · cos α sin α = c t g 2 α — 1 2 · c t g α
Примеры использования формул двойного угла
Данный пункт показывает несколько примеров решения с формулами двойного угла. Конкретные примеры помогут глубже понять изучаемый материал. Чтобы убедиться в справедливости формул 2 α для α = 30 ° , применим значения тригонометрических функций для этих углов. Если α = 30 ° , тогда 2 α = 60 ° . Проверим значения sin 60 ° = 2 · sin 30 ° · cos 30 ° , cos 60 ° = cos 2 30 ° — sin 2 30 ° .
Подставив значения, получим t g 60 ° = 2 · t g 30 ° 1 — t g 2 30 ° и c t g 60 ° = c t g 2 30 ° — 1 2 · c t g 30 ° . .
Известно, что sin 30 ° = 1 2 , cos 30 ° = 3 2 , t g 30 ° = 3 3 , c t g 30 ° = 3 и
sin 60 ° = 3 2 , cos 60 ° = 1 2 , t g 60 ° = 3 , c t g 60 ° = 3 3 , тогда отсюда видим, что
2 · sin 30 ° · cos 30 ° = 2 · 1 2 · 3 2 = 3 2 , cos 2 30 ° — sin 2 30 ° = ( 3 2 ) 2 — ( 1 2 ) 2 = 1 2 , 2 · t g 30 ° 1 — t g 2 30 ° = 2 · 3 2 1 — ( 3 3 ) = 3
и c t g 2 30 ° — 1 2 · c t g 30 ° = ( 3 ) 2 — 1 2 · 3 = 3 3
Проведя вычисления, можно сделать вывод, что справедливость для α = 30 ° подтверждена.
Основное использование тригонометрических формул двойного угла – это преобразования тригонометрических выражений. Рассмотрим пример применения двойного угла, года имеем угол, отличный от 2 α . В примере допускается применение формулы двойного угла 3 π 5 . Тогда его необходимо преобразовать, в результате чего получим α = 3 π 5 : 2 = 3 π 10 . Отсюда следует, что формула двойного угла для косинуса будет иметь вид cos 3 π 5 = cos 2 3 π 10 — sin 2 3 π 10 .
Представить sin 2 α 3 через тригонометрические функции, при α 6 .
Заметим, что из условия имеем 2 α 3 = 4 · α 6 . Тогда использовав 2 раза формулу двойного угла, выразим sin 2 α 3 через тригонометрические функции угла α 6 . Применяя формулу двойного угла, получим sin 2 α 3 = 2 · sin α 3 · cos α 3 . После чего к функциям sin α 3 и cos α 3 применим формулы двойного угла: sin 2 α 2 = 2 · sin α 3 · cos α 3 = 2 · ( 2 · sin α 5 · cos α 6 ) · ( cos 2 α 6 — sin α 6 ) = = 4 · sin α 6 · cos 3 α 6 — 4 · sin 3 α 6 · cos α 6
Ответ: sin 2 α 3 = 4 · sin α 6 · cos 3 α 6 — 4 · sin 3 α 6 · cos α 6 .
Формулы тройного, четверного и т.д. угла
Таким же образом выводятся формулы тройного, четверного и т.д. углов. Формулы тройного угла можно вывести из формул сложения двойного угла.
sin 3 α = sin ( 2 α + α ) = sin 2 α · cos α + cos 2 α · sin α = 2 · sin α · cos α · cos α + ( cos 2 α — sin 2 α ) · sin α = = 3 · sin α · cos 2 α — sin 3 α
При замене cos 2 α на 1 — sin 2 α из формулы sin 3 α = 3 · sin α · cos 2 α — sin 3 α , она будет иметь вид sin 3 α = 3 · sin α — 4 · sin 3 α .
Так же приводится формула косинуса тройного угла:
cos 3 α = cos ( 2 α + α ) = cos 2 α · cos α — sin 2 α · sin α = = ( cos 2 α — sin 2 α ) · cos α — 2 · sin α · cos α · sin α = cos 3 α — 3 · sin 2 α · cos α
При замене sin 2 α на 1 — cos 2 α получим формулу вида cos 3 α = — 3 · cos α + 4 · cos 3 α .
При помощи полученных формул преобразуем формулу тройного угла для тангенса и котангенса тройного угла:
t g 3 α = sin 3 α cos 3 α = 3 · sin α · cos 2 α — sin 3 α cos 3 α — 3 · sin 2 α · cos α = 3 · sin α · cos 2 α — sin 3 α cos 3 α cos 3 α — 3 · sin 2 α · cos α cos 3 α = = 3 · sin α cos α — sin 3 α cos 3 α 1 — 3 · sin 2 α cos 2 α = 3 · t g α — t g 3 α 1 — 3 · t g 2 α ; c t g 3 α = cos 3 α sin 3 α = cos 3 α — 3 · sin 2 α · cos α 3 · sin α · cos 2 α — sin 3 α = cos 3 α — 3 · sin 2 α · cos α sin 3 α 3 · sin α · cos 2 α — sin 3 α sin 3 α = = cos 3 α sin 3 α — 3 · cos α sin α 3 · cos 2 α sin 2 α — 1 = c t g 3 α — 3 · c t g α 3 · c t g 2 α — 1
Чтобы выводить формулы четвертой степени, имеет смысл представить 4 α как 2 · 2 α , тогда имеет место использование формулы двойного угла два раза. Для выводы формулы 5 степени, представляем 5 α в виде 3 α + 2 α , что позволит применить формулы тройного и двойного углов для ее преобразования. Таким же образом делаются преобразования разных степеней тригонометрических функций. Их применение достаточно редкое в тригонометрии.
Формулы двойного угла
Время чтения: 20 минут
Основные понятия. Тригонометрия довольно древняя наука, и ее первые упоминания связаны с необходимостью в практичной жизни, в земледелии, астрономии и строительстве. Впервые именно астрономы вывели такие понятия как отношение сторон треугольника. А официальные названия функций стали появляться позже, например, синус, который получил свое название первым, получил свое название от греческих математиков уже в третьем веке до н.э.. а косинус является относительно молодым, и был выведен как дополнение к синусу. История тригонометрии обширна и интересна, из древней науки о треугольниках она перешла в известную нам науку о тригонометрических функциях. Для того чтобы разобраться в формулах двойного угла, необходимо вспомнить основные понятия тригонометрии. Начнём:
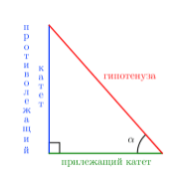
Тригонометрические функции:
- Синус угла — отношение катета напротив угла к гипотенузе:
- Косинус — деление прилежащей стороны треугольника на гипотенузу;
- Тангенс — отношение синуса к косинусу или катета напротив угла к прилежащему;
- Котангенс — деление косинуса на синус, или стороны прилежащей к углу на противолежащую.
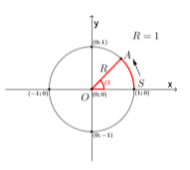
Тригонометрическая окружность — это окружность нанесённая на систему координат, имеющая радиус равный единице и центр в начале координат.
При помощи такой окружность можно наглядно разобраться в тригонометрических формулах и значениях. Например, найти числовые значения функций тригонометрии на системе координат, такие как:
Данные примеры будут использоваться далее по тексту. Мы можем посмотреть их значение на окружности на рисунке ниже.
Основное тождество в тригонометрии, звучит так:
- Синус в квадрате угла плюс косинус в квадрате угла равны единице;
- Произведение тангенса и котангенса угла равно единице;
- Тангенс угла равен, делению, синуса этого угла на косинус, а котангенс наоборот косинуса на синус.
Данные тождества также будут применены для выведения формул двойного, тройного и т.д. углов.
Формулы двойного угла в тригонометрии
Формулы двойного угла тригонометрических функций, необходимы для того чтобы выразить их, при этом угол должен иметь значение 2а, а также используя ТФ этого угла. Для отражения её на графике используют координаты с окружностью.
Список формул двойного угла
Прежде чем преступить к образованию формул двойного угла тригонометрии, давайте вспомним, что в тригонометрии углы принято писать в виде na, в такой записи п — обозначение натурального числа, а а — угол альфа. Обычно такая запись в тригонометрии используется без скобок, значит sin an, это тоже самое что sin (an). А также если рассмотреть запись sin n a, то она тоже имеет аналогичную запись вида (sin а) n . такое правило записи касается всех тригонометрических функций со степенями.
Рассмотрим какие же формулы двойного угла существуют на примерах.
Синус двойного угла формула:
sin 2 α = 2 * sin α * cos α;
Формула косинуса двойного угла:
cos 2 α = cos 2 α — sin 2 α, cos 2α = 1 − 2 * sin 2 α , cos 2α = 2 * cos 2 α−1;
Тангенс двойного угла формула:
Стоит не забывать, что выше приведённые формулы sin и cos, можно применять для любого значения угла. А вот если рассмотреть, формулы для тангенса, то при любых альфа где, tg 2a , имеет смысл, то есть при [a neq frac<pi><4>+frac<pi> <2>cdot z], где z любое целое число. Что же касается формулы двойного угла котангенса, то при любом a, где ctg 2α определён на α ≠ 2 * z .
Как мы видим косинус с таким видом угла, наделён тремя вариантами записи формул, все они равноправны, а это значит, что результат их применения будет абсолютно одинаковым.
Доказательство формул двойного угла
Для того чтобы, формулы двойного угла были доказаны, вернёмся к истокам, формулам сложения. Сначала рассмотрим формулу синуса суммы, которая выглядит следующим образом:
Если считать что a = b, тогда выходит:
И также для косинуса:
Таким способом мы доказали формулы синуса и косинуса двойного угла.
Формулы которые остались: cos 2α = 1 − 2 * sin 2 α , cos 2α = 2 * cos 2 α−1, выразили в таком виде благодаря приведению вместо единицы тождества суммы квадратов, cos 2 α +sin 2 α = 1. Поэтому вышло следующее:
Формулы приведения двойного угла: 1 − 2 * sin 2 α = cos 2 α +sin 2 α — 2 * sin 2 α = cos2α — sin2α.
И так же с третьих примеров формулы двойного угла.
2 * cos 2 α−1 = 2 * cos 2 α -( cos 2 α +sin 2 α ) = cos 2 α — sin 2 α.
Для того, чтобы выполнить доказательство формул для тангенса и котангенса двойного угла тоже применяется равенство следующего вида:
Сделав замену на данные равенства получим следующие выражения:
Представленные выше выражения мы разделим на cos 2 α, при котором cos 2 α ≠ 0, а альфа имеет любое значение, когда тангенс угла альфа определён. Со вторым представленным выражением мы также произведём деление, только на sin 2 α, и он так же не равен нулю, и альфа имеет любое значение, при котором котангенс имеет смысл.
Получим следующие формулы:
Нет времени решать самому?
Наши эксперты помогут!
Как использовать формулы двойного угла
Рассмотрим, как применяются формулы двойного угла в решении на примерах. Такие примеры помогут закрепить и понять материалы рассмотренный ранее.
Чтобы проверить справедлива ли формула двойного угла для при значении угла альфа в тридцать градусов, необходимо применить функции тригонометрии для этих углов. Если α = 30°, тогда 2α = 60°.
Проверим: sin60° = 2 * sin30° * cos30°cos60° = cos230° — sin230°.
Следующим шагом, подставим эти значения в :
Так как мы знаем, что синус тридцати градусов равен одной второй, косинус этого угла, равен корню из трёх, который поделен на два, тангенс заданного угла это корень из трёх на три, котангенс корень из трёх.
Получается, что синус двойного угла, то есть шестидесяти градусов, равен корню из трёх, который поделен на два; косинус — одной второй; тангенс корню из трёх; а котангенс корню из трёх делённому на три.
Получаем следующие выражения:
Сделав все операции по вычислению, можно прийти к выводу, что справедливость для угла альфа тридцати градусов, подтверждена.
Теперь мы понимаем, что применение формул тригонометрии двойного угла, это видоизменение тригонометрических выражений. Стоит также рассмотреть пример применения формул двойного угла, в случае, когда угол не равен 2a. К примеру возьмём значение [frac<5 pi><6>]. Имея такое значение, для решения задания, его необходимо преобразовать, поэтому получаем следующее:
[a=frac<5 pi><6>: 2=frac<5 pi><12>], применив данное выражение формула двойного угла для косинуса получит следующий вид:
Пример:
Необходимо, через тригонометрические функции представить [sin frac<2 a> <3>text < при >frac<6>].
Решение:
Формулы тройного угла и более углов
Так как зачастую в тригонометрии возникает необходимость вычисления не только двойного угла, но и больше, например тройного, четверного и тд. Стоит рассмотреть примеры их вычисления. Выведение их формул аналогично с выведением формул двойного угла, но для этого будем применять формулы сложения (суммы) двойного угла.
Пример:
sin 3α = sin ( 2 α + α ) = sin 2α * cos α + cos 2 α * sin α = 2 * sin α ⋅ cos α * cos α + ( cos 2 α — sin 2 α ) * sin α =
=3 * sin α * cos 2 α — sin 3 α
Заменим cos 2 α, на выражение 1 — sin 2 α, и теперь получившаяся ранее формула тройного угла sin 3α =3 * sin α * cos 2 α — sin 3 α, примет следующий вид: sin 3α = 3 * sin α * cos 2 α — sin 3 α = 3 *sin α — 4* sin 3 α
Аналогично поступим и с формулами cos тройного угла:
cos 3α = cos ( 2 α + α ) = cos 2α * cos α − sin 2α *sin α = ( cos 2 α — sin 2 α ) * cos α − 2* sin α * cos α * sin α =
= cos 3 α − 3* sin 2 α * cos α
Заменяем sin 2 α на выражение разности единицы и косинуса, 1 — cos 2 α, выходит следующая формула : cos 3α =
= -3 * cos α + 4* cos 3 α
Так как теперь у нас есть формулы тройного угла синуса и косинуса, мы можем вывести формулы тройного угла для тангенса и котангенса, подставив полученные выражения в первичные формулы:
К примеру, чтобы привести формулу угла четыре альфа, для удобства лучше 4а представить, как 2 * 2а, и в результате мы получим, что для выведения формулы для 4а, нужно использовать две формулы двойного угла.
А для выведения формулы угла пятой степени, 5а, необходимо выполнить 5а как сумму тройного и двойного угла, то есть 2а+3а.
В результате мы получим выражение из суммы двух формул двойного и тройного угла. Стоит отметить, что такое же правило будет действовать если необходимо вывести формулу половинного угла.
Область применения
Для того чтобы найти значение тригонометрических функций, берётся окружность на оси координат, у которой радиус равен единице, а диаметры у неё находятся в перпендикулярном положении.
Для такого вычисления нам понадобится отложить от точки, которая принадлежит окружности различные дуги, любой длины. Соответственно если мы отложим их против часовой стрелки они примут положительное значение, а если по часовой, то отрицательное.
Допустим конец дуги имеет некую длину s, в таком случае проекция радиуса в любом выбранном значении диаметра станет значением косинуса данной дуги. Выбранная длина s, или радианная мера угла, будет считаться числом аргумента. А если этот самый аргумент, это тригонометрическая функция угла, то мы знаем, что значение может быть и в градусах.
Мы знаем, что острый угол имеет значения больше нуля, но меньше п2. В таком случае тригонометрическая функция рассматривается как катет делённый на гипотенузу. Такие названия сторон связаны с прямоугольным треугольником, в котором величина угла равна 90 градусов.
Чтобы решить задачи с функциями тригонометрии, используют теорему Пифагора. Такая теорема основана на свойствах того самого прямоугольного треугольника, в котором квадрат гипотенузы равен сумму квадратов катетов.
Так как дуга делит окружность на несколько частей, то мы можем увидеть, что углы лежащие в первой четверти больше нуля. А во второй синус меньше, а косинус больше нуля, а в третьей все функции будут меньше нуля, то есть отрицательными, четвёртая имеет значения противоположные второй. Не стоит забывать, что для построения окружности вам понадобится циркуль.
Как мы видим формулы двойного угла, не так трудно вывести, для этого необходимо знать основные тригонометрические тождества и разобраться в единичной окружности на оси координат. Также необходимо отметить, что формулы двойного угла, как и другие формулы тригонометрии используются в разных сферах жизни:
- В астрономии, учёные с помощью формул вычисляют положение небесных тел, а также расстояние до них;
- Для различного вида навигации, к примеру, морской и воздушной;
- В медицине и биологии, при построении биоритма живых организмов, а также тригонометрия служит основой работы некоторой медицинской техники;
- Архитекторам она важна при создании планов строений;
- но и это не всё, тригонометрия важна и для экономики, в производстве и создании электроники, в различных аналитических вычислениях, акустических построениях и многом другом.
источники:
http://zaochnik.com/spravochnik/matematika/trigonometrija/formuly-dvojnogo-ugla-v-trigonometrii/
http://www.napishem.ru/spravochnik/matematika/formuly-dvoynogo-ugla.html
Преподаватель который помогает студентам и школьникам в учёбе.
Формулы двойного аргумента с примерами решения
Содержание:
Преобразования тригонометрических выражений можно упростить, если рассмотреть частные случаи общих формул. Рассмотрим формулу синуса суммы
Формула синуса двойного аргумента
Получили формулу синуса двойного аргумента:
Выведем формулу косинуса двойного аргумента. Используем формулу косинуса суммы 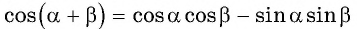
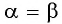
Формула косинуса двойного аргумента
Формула косинуса двойного аргумента:
Для вывода формулы тангенса двойного аргумента рассмотрим формулу тангенса суммы 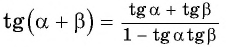
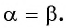
Формула тангенса двойного аргумента
Получили формулу тангенса двойного аргумента:
Пример №1
Упростите выражение:
Решение:
Применим формулы двойного аргумента:
Пример №2
Вычислите:
Решение:
Применим формулы двойного аргумента «справа налево»:
Пример №3
Найдите значение выражения 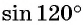
Решение:
Первый способ. Применим формулы приведения:
Второй способ. Применим формулу синуса двойного аргумента:
Пример №4
Представьте данный угол в виде
Решение:
Пример №5
Преобразуйте каждое из выражений с помощью формул двойного угла:
Решение:
Представим угол в каждом из выражений в виде 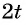
Пример №6
Упростите выражение:
Решение:
Применим формулы двойного аргумента и получим:
Пример №7
Найдите значение выражения:
Решение:
Пример №8
Вычислите
Решение:
Применим формулу тангенса двойного аргумента и получим:
Пример №9
Вычислите:
Решение:
б) По формулам приведения
Пример №10
Вычислите 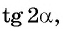
Решение:
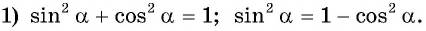
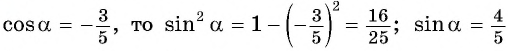
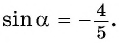
Ответ: 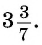
- Заказать решение задач по высшей математике
Пример №11
Решите уравнение
Решение:
Используем формулу синуса двойного аргумента:
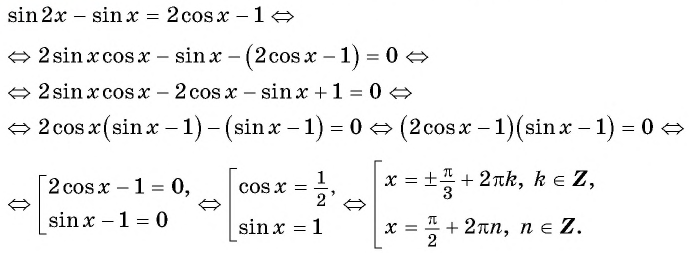
Пример №12
Решите уравнение
Решение:
Воспользуемся формулой синуса двойного угла и получим 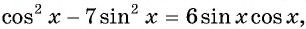
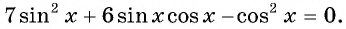
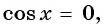
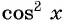
Пусть 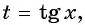
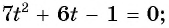
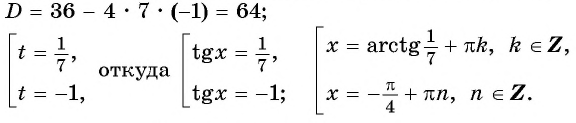
Пример №13
Докажите тождество
Решение:
Умножим и разделим выражение 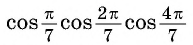
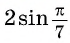
- Формулы преобразования суммы и разности синусов (косинусов) в произведение
- Корень n-й степени из числа и его свойства
- Свойства и график функции y=ⁿ√x (n>1, n∈N)
- Иррациональные уравнения
- Тригонометрические уравнения
- Тригонометрические неравенства
- Формулы приведения
- Синус, косинус, тангенс суммы и разности