Формула концентрации математика егэ - Помощь в подготовке к экзаменам и поступлению

Задачи ЕГЭ на сплавы, смеси, растворы.

Задачи на сплавы, смеси, растворы встречаются и в математике, и в химии. У химиков сложнее – там вещества еще и взаимодействуют, превращаясь во что-то новое. А в задачах по математике мы просто смешиваем растворы различной концентрации. Покажем правила решения на примере задач на растворы. Для сплавов и смесей – действуем аналогично.

. В сосуд, содержащий литров -процентного водного раствора некоторого вещества, добавили литров воды. Сколько процентов составляет концентрация получившегося раствора?

В решении подобных задач помогает картинка. Изобразим сосуд с раствором схематично — так, как будто вещество и вода в нем не перемешаны между собой, а отделены друг от друга, как в коктейле. И подпишем, сколько литров содержат сосуды и сколько в них процентов вещества. Концентрацию получившегося раствора обозначим .

Первый сосуд содержал литра вещества. Во втором сосуде была только вода. Значит, в третьем сосуде столько же литров вещества, сколько и в первом:

$0,12 cdot 5=genfrac{}{}{}{0}{displaystyle x}{displaystyle 100} cdot 12$
x=5 .

. Смешали некоторое количество -процентного раствора некоторого вещества с таким же количеством -процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?

Пусть масса первого раствора равна . Масса второго — тоже . В результате получили раствор массой . Рисуем картинку.

Получаем:

Ответ: .

. Виноград содержит 90% влаги, а изюм — . Сколько килограммов винограда требуется для получения килограммов изюма?

Внимание! Если вам встретилась задача «о продуктах», то есть такая, где из винограда получается изюм, из абрикосов урюк, из хлеба сухари или из молока творог — знайте, что на самом деле это задача на растворы. Виноград мы тоже можем условно изобразить как раствор. В нем есть вода и «сухое вещество». У «сухого вещества» сложный химический состав, а по его вкусу, цвету и запаху мы могли бы понять, что это именно виноград, а не картошка. Изюм получается, когда из винограда испаряется вода. При этом количество «сухого вещества» остается постоянным. В винограде содержалось 90% воды, значит, «сухого вещества» было 10% . В изюме воды и 95% «сухого вещества». Пусть из кг винограда получилось кг изюма. Тогда

10% от x=95% от

Составим уравнение:

и найдем .

Ответ: 190 .

. Имеется два сплава. Первый сплав содержит 10% никеля, второй — 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава меньше массы второго?

Пусть масса первого сплава равна x, а масса второго равна y. В результате получили сплав массой x+y=200 .

Запишем простую систему уравнений:

$left{begin{matrix}x+y=200\ 0,1x+0,3y=0,25 cdot200end{matrix}right.$

Первое уравнение — масса получившегося сплава, второе — масса никеля.

Решая, получим, что .

Ответ: 100 .

. Смешав -процентный и -процентный растворы кислоты и добавив кг чистой воды, получили -процентный раствор кислоты. Если бы вместо кг воды добавили кг -процентного раствора той же кислоты, то получили бы -процентный раствор кислоты. Сколько килограммов -процентного раствора использовали для получения смеси?

Пусть масса первого раствора , масса второго равна . Масса получившегося раствора равна x+y+10 . Запишем два уравнения, для количества кислоты.

$left{begin{matrix}0,3x + 0,6y = 0,36 left(x + y + 10right)\ 0,3x + 0,6y + 0,5 cdot 10 = 0,41 left(x + y + 10right)end{matrix}right.$

Решаем получившуюся систему. Сразу умножим обе части уравнений на 100 , поскольку с целыми коэффициентами удобнее работать, чем с дробными. Раскроем скобки.

$left{begin{matrix}30x + 60y = 36x + 36y + 360\ 30x + 60y + 500 = 41x + 41y + 410end{matrix}right.$

$left{begin{matrix}4y - x = 60\ 11x - 19y = 90end{matrix}right.$

Ответ: .

Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Задачи ЕГЭ на сплавы, смеси, растворы.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена:
09.03.2023

Источник

11. Сюжетные текстовые задачи

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Задачи на растворы, смеси и сплавы

(blacktriangleright) Концентрация вещества в растворе (сплаве) – это процент содержания этого вещества в растворе (сплаве): [text{концентрация вещества}=dfrac{text{масса вещества}}{text{масса раствора}}cdot 100%]

(blacktriangleright) Заметим, что в задачах из данной подтемы зачастую удобно составлять уравнения относительно кислоты или активного вещества.

Задание
1

#846

Уровень задания: Равен ЕГЭ

Сергей смешал раствор, содержащий (20%) кислоты и раствор, содержащий (40%) той же кислоты. В итоге у него получился раствор, содержащий (32,5%) кислоты, причём объём полученного раствора (4) литра. Сколько литров раствора, содержащего (20%) кислоты, использовал Сергей при смешивании?

Пусть (x) литров раствора, содержащего (20%) кислоты использовал Сергей при смешивании, тогда

(4 — x) литров раствора, содержащего (40%) кислоты использовал Сергей при смешивании,

(dfrac{20}{100}x) – объём кислоты в растворе, содержащем (20%) кислоты, (dfrac{40}{100}(4 — x)) – объём кислоты в растворе, содержащем (40%) кислоты.

Так как в итоге кислоты оказалось (dfrac{32,5}{100} cdot 4 = 1,3) литра, то:

[dfrac{20}{100}x + dfrac{40}{100}(4 — x) = 1,3,] откуда находим (x = 1,5).

Ответ: 1,5

Задание
2

#844

Уровень задания: Равен ЕГЭ

Один газ в сосуде А содержал (21%) кислорода, второй газ в сосуде В содержал (5%) кислорода. Масса первого газа в сосуде А была больше массы второго газа в сосуде В на 300 г. Перегородку между сосудами убрали так, что газы перемешались и получившийся третий газ теперь содержит (14,6%) кислорода. Найдите массу третьего газа. Ответ дайте в граммах.

Пусть (x) грамм – масса второго газа, тогда

(x + 300) грамм – масса первого газа,

(dfrac{21}{100}(x + 300)) грамм – масса кислорода в первом газе,

(dfrac{5}{100}x) грамм – масса кислорода во втором газе,

тогда масса кислорода в третьем газе составляет (dfrac{14,6}{100}(2x + 300)) грамм.

Так как третий газ возник в результате смешивания первого и второго, то:

[dfrac{21}{100}(x + 300) + dfrac{5}{100}x = dfrac{14,6}{100}(2x + 300),] откуда находим (x = 600). Таким образом, масса третьего газа равна (600 + 600 + 300 = 1500) грамм.

Ответ: 1500

Задание
3

#843

Уровень задания: Равен ЕГЭ

Иван случайно смешал молоко жирностью (2,5%) и молоко жирностью (6%). В итоге у него получилось 5 литров молока жирностью (4,6%). Сколько литров молока жирностью (2,5%) было у Ивана до смешивания?

Пусть (x) литров молока жирностью (2,5%) было у Ивана, тогда

(5 — x) литров молока жирностью (6%) было у Ивана,

(dfrac{2,5}{100}x) – объём жира в молоке жирностью (2,5%), (dfrac{6}{100}(5 — x)) – объём жира в молоке жирностью (6%).

Так как в итоге жира оказалось (dfrac{4,6}{100} cdot 5 = 0,23) литра, то:

(dfrac{2,5}{100}x + dfrac{6}{100}(5 — x) = 0,23), откуда находим (x = 2).

Ответ: 2

Задание
4

#841

Уровень задания: Равен ЕГЭ

В сосуде А содержится 3 литра 17-процентного водного раствора вещества Х. Из сосуда В в сосуд А перелили 7 литров 19-процентного водного раствора вещества Х. Сколько процентов составляет концентрация полученного в сосуде А раствора?

Концентрация в процентах – это отношение объёма вещества к объёму смеси, умноженное на 100(%). До переливания в сосуде А было (3 cdot 0,17 = 0,51) литра вещества Х, в сосуде В было (7 cdot 0,19 = 1,33) литра вещества Х.

После переливания объём вещества Х в сосуде А стал (0,51 + 1,33 = 1,84) литра, а объём всего раствора (3 + 7 = 10) литров. Тогда концентрация в процентах составила [dfrac{1,84}{10} cdot 100% = 18,4%.]

Ответ: 18,4

Задание
5

#2133

Уровень задания: Равен ЕГЭ

Во сколько раз больше должен быть объём (5)-процентного раствора кислоты, чем объём (10)-процентного раствора той же кислоты, чтобы при смешивании получить (7)-процентный раствор?

Пусть объём (5)-процентного раствора кислоты равен (x) литров, а объём (10)-процентного раствора равен (y) литров, тогда требуется найти значение величины (dfrac{x}{y}) при условии [0,05x + 0,1y = 0,07(x + y)
qquadLeftrightarrowqquad
dfrac{x}{y} = dfrac{3}{2} = 1,5,,] таким образом, ответ: (1,5).

Ответ: 1,5

Задание
6

#2134

Уровень задания: Равен ЕГЭ

Во сколько раз больше должен быть объём (20)-процентного раствора кислоты, чем объём (14)-процентного раствора той же кислоты, чтобы при смешивании получить (18)-процентный раствор?

Пусть объём (20)-процентного раствора кислоты равен (x) литров, а объём (14)-процентного раствора равен (y) литров, тогда требуется найти значение величины (dfrac{x}{y}) при условии [0,2x + 0,14y = 0,18(x + y)
qquadLeftrightarrowqquad
dfrac{x}{y} = 2,,] таким образом, ответ: (2).

Ответ: 2

Задание
7

#2629

Уровень задания: Равен ЕГЭ

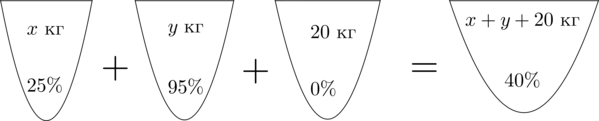
Смешав (25)-процентный и (95)-процентный растворы кислоты и добавив (20) кг чистой воды, получили (40)-процентный раствор кислоты. Если бы вместо (20) кг воды добавили (20) кг (30)-процентного раствора той же кислоты, то получили бы (50)-процентный раствор кислоты. Сколько килограммов (25)-процентного раствора использовали для получения смеси?

Заметим, что вода – это раствор, не содержащий кислоту, то есть содержащий (0%) кислоты.
Пусть (x) кг – масса раствора с (25)-процентным содержанием кислоты, (y) кг – масса раствора с (95)-процентным содержанием кислоты. Составим схему, описывающую получение (40)-процентного раствора:

Заметим, что количество кислоты во всех трех растворах равно количеству кислоты в получившемся растворе. Найдем количество кислоты в первом растворе.
Если раствор весит (x) кг, а в нем (25%) кислоты, то в килограммах в нем (dfrac{25}{100}cdot x) кислоты.

Таким же образом можно посчитать количество кислоты в остальных растворах. Получим первое уравнение:

[dfrac{25}{100}cdot x+dfrac{95}{100}cdot y+
dfrac{0}{100}cdot 20=dfrac{40}{100}cdot (x+y+20)]

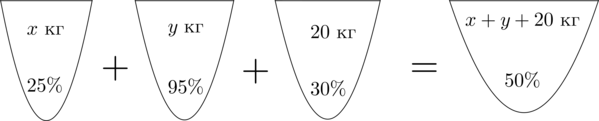
Аналогично составим схему, описывающую получение (50)-процентного раствора:

Значит, уравнение, описывающее эту ситуацию, будет выглядеть так:

[dfrac{25}{100}cdot x+dfrac{95}{100}cdot y+
dfrac{30}{100}cdot 20=dfrac{50}{100}cdot (x+y+20)]

Таким образом, решив систему из полученных двух уравнений, найдем (x). Для этого можно умножить оба уравнения на (100), чтобы сделать их проще на вид:

[begin{cases}
25x+95y+0=40(x+y+20)\
25x+95y+30cdot 20=50(x+y+20)
end{cases}]

Вычтем из второго уравнения первое и получим новую систему:

[begin{aligned} &begin{cases}
25x+95y=40(x+y+20)\
30cdot 20=10(x+y+20)
end{cases} quad Rightarrow quad begin{cases}
5x+19y=8(x+y+20)\
y=40-x end{cases} quad Rightarrow \[2ex] Rightarrow quad
&begin{cases}
3x-11(40-x)+160=0\
y=40-x end{cases} quad Rightarrow quad begin{cases}
x=20\y=20end{cases} end{aligned}]

Таким образом, раствора с (25%) кислоты было (20) кг.

Ответ: 20

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Источник

Возможно, вам нужно заглянут сюда – “Простейшие задачи на проценты”

Задача 1. В сосуд, содержащий литров -процентного водного раствора некоторого вещества, добавили литров воды. Сколько процентов составляет концентрация получившегося раствора?

Решение: + показать

Задача 2. Смешали некоторое количество -процентного раствора некоторого вещества с таким же количеством -процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?

Решение: + показать

Задача 3. Имеется два сплава. Первый сплав содержит % никеля, второй — % никеля. Из этих двух сплавов получили третий сплав массой кг, содержащий % никеля. На сколько килограммов масса первого сплава меньше массы второго?

Решение: + показать

Задача 4. Смешав 54-процентный и 61-процентный растворы кислоты и добавив 10 кг чистой воды, получили 46-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 56-процентный раствор кислоты. Сколько килограммов 54-процентного раствора использовали для получения смеси?

Решение: + показать

Задача 5. Имеются два сосуда. Первый содержит кг, а второй — кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий % кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий % кислоты. Сколько килограммов кислоты содержится в первом сосуде?

Решение: + показать

Задача 6. Виноград содержит % влаги, а изюм — %. Сколько килограммов винограда требуется для получения килограммов изюма?

Решение: + показать

Задача 7. В 2008 году в городском квартале проживало человек. В 2009 году, в результате строительства новых домов, число жителей выросло на %, а в 2010 году — на % по сравнению с 2009 годом. Сколько человек стало проживать в квартале в 2010 году?

Решение: + показать

Задача 8. Цена холодильника в магазине ежегодно уменьшается на одно и то же число процентов от предыдущей цены. Определите, на сколько процентов каждый год уменьшалась цена холодильника, если, выставленный на продажу за рублей, через два года был продан за рублей.

Решение: + показать

Задача 9. В понедельник акции компании подорожали на некоторое количество процентов, а во вторник подешевели на то же самое количество процентов. В результате они стали стоить на % дешевле, чем при открытии торгов в понедельник. На сколько процентов подорожали акции компании в понедельник?

Решение: + показать

Задача 10. Шесть рубашек дешевле куртки на %. На сколько процентов девять рубашек дороже куртки? Видео*

Решение: + показать

Задача 11. Семья состоит из мужа, жены и их дочери студентки. Если бы зарплата мужа увеличилась вдвое, общий доход семьи вырос бы на %. Если бы стипендия дочери уменьшилась вдвое, общий доход семьи сократился бы на %. Сколько процентов от общего дохода семьи составляет зарплата жены?

Решение: + показать

Задача 12. Дима, Андрей, Гриша и Коля учредили компанию с уставным капиталом рублей. Дима внес % уставного капитала, Андрей — рублей, Гриша — уставного капитала, а оставшуюся часть капитала внес Коля. Учредители договорились делить ежегодную прибыль пропорционально внесенному в уставной капитал вкладу. Какая сумма от прибыли рублей причитается Коле? Ответ дайте в рублях.

Решение: + показать

Задача 13. Клиент А. сделал вклад в банке в размере рублей. Проценты по вкладу начисляются раз в год и прибавляются к текущей сумме вклада. Ровно через год на тех же условиях такой же вклад в том же банке сделал Б. Ещё ровно через год клиенты А. и Б. закрыли вклады и забрали все накопившиеся деньги. При этом клиент А. получил на рубля больше клиента Б. Какой процент годовых начислял банк по этим вкладам?

Решение: + показать

Вы можете пройти Тест по задачам на проценты, сплавы, смеси

Источник

15 ноября 2017

В закладки

Обсудить

Жалоба

Решение задач на концентрации

В школьном курсе математики мало внимания уделяется задачам на смеси, сплавы, концентрации растворов. Эти задачи включены в варианты ЕГЭ по предмету и вызывают большие затруднения у выпускников.

Теория и практический материал.

mkoc.docx

Источник