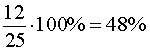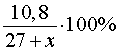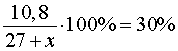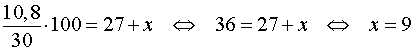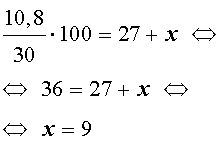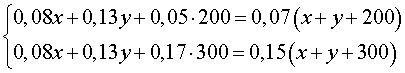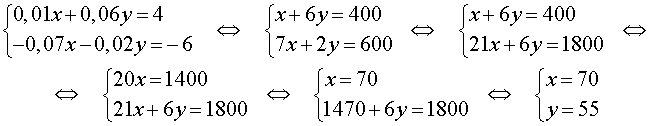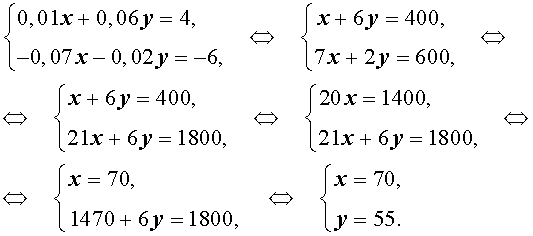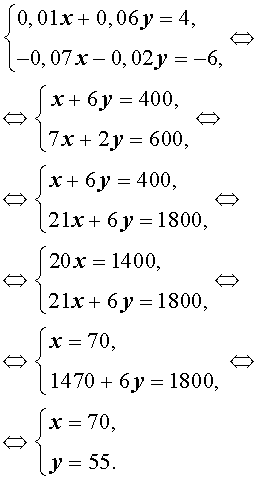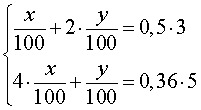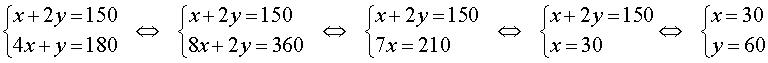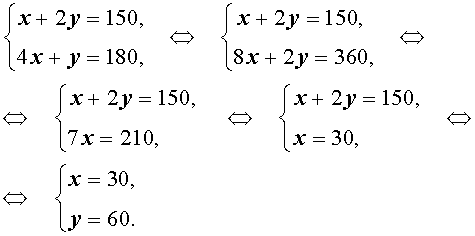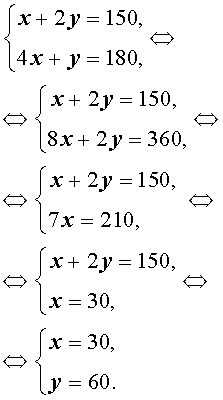Задачи ЕГЭ на сплавы, смеси, растворы.
Задачи на сплавы, смеси, растворы встречаются и в математике, и в химии. У химиков сложнее – там вещества еще и взаимодействуют, превращаясь во что-то новое. А в задачах по математике мы просто смешиваем растворы различной концентрации. Покажем правила решения на примере задач на растворы. Для сплавов и смесей – действуем аналогично.
. В сосуд, содержащий
литров
-процентного водного раствора некоторого вещества, добавили
литров воды. Сколько процентов составляет концентрация получившегося раствора?
В решении подобных задач помогает картинка. Изобразим сосуд с раствором схематично — так, как будто вещество и вода в нем не перемешаны между собой, а отделены друг от друга, как в коктейле. И подпишем, сколько литров содержат сосуды и сколько в них процентов вещества. Концентрацию получившегося раствора обозначим .
Первый сосуд содержал литра вещества. Во втором сосуде была только вода. Значит, в третьем сосуде столько же литров вещества, сколько и в первом:
.
. Смешали некоторое количество
-процентного раствора некоторого вещества с таким же количеством
-процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?
Пусть масса первого раствора равна . Масса второго — тоже
. В результате получили раствор массой
. Рисуем картинку.
Получаем:
Ответ: .
. Виноград содержит
влаги, а изюм —
. Сколько килограммов винограда требуется для получения
килограммов изюма?
Внимание! Если вам встретилась задача «о продуктах», то есть такая, где из винограда получается изюм, из абрикосов урюк, из хлеба сухари или из молока творог — знайте, что на самом деле это задача на растворы. Виноград мы тоже можем условно изобразить как раствор. В нем есть вода и «сухое вещество». У «сухого вещества» сложный химический состав, а по его вкусу, цвету и запаху мы могли бы понять, что это именно виноград, а не картошка. Изюм получается, когда из винограда испаряется вода. При этом количество «сухого вещества» остается постоянным. В винограде содержалось воды, значит, «сухого вещества» было
. В изюме
воды и
«сухого вещества». Пусть из
кг винограда получилось
кг изюма. Тогда
от
от
Составим уравнение:
и найдем .
Ответ: .
. Имеется два сплава. Первый сплав содержит
никеля, второй —
никеля. Из этих двух сплавов получили третий сплав массой
кг, содержащий
никеля. На сколько килограммов масса первого сплава меньше массы второго?
Пусть масса первого сплава равна x, а масса второго равна y. В результате получили сплав массой .
Запишем простую систему уравнений:
Первое уравнение — масса получившегося сплава, второе — масса никеля.
Решая, получим, что .
Ответ: .
. Смешав
-процентный и
-процентный растворы кислоты и добавив
кг чистой воды, получили
-процентный раствор кислоты. Если бы вместо
кг воды добавили
кг
-процентного раствора той же кислоты, то получили бы
-процентный раствор кислоты. Сколько килограммов
-процентного раствора использовали для получения смеси?
Пусть масса первого раствора , масса второго равна
. Масса получившегося раствора равна
. Запишем два уравнения, для количества кислоты.
Решаем получившуюся систему. Сразу умножим обе части уравнений на , поскольку с целыми коэффициентами удобнее работать, чем с дробными. Раскроем скобки.
Ответ: .
Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Задачи ЕГЭ на сплавы, смеси, растворы.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
09.03.2023
08
Янв 2012
08 Задание (2022)ТЕКСТОВЫЕ ЗАДАЧИ

Смешали некоторое количество 15-процентного раствора некоторого вещества с таким же количеством 19-процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?
Решение.
В задачах на сплавы и растворы используется одна единственная формула:
%, где
P — процентное содержание чистого вещества в сплаве или растворе,
m — масса чистого вещества
M — масса сплава или раствора.
Задачи на сплавы и растворы удобно решать с помощью таблицы. Порядок заполнения таблицы такой:
1. Сначала решаем, какую величину мы примем за неизвестное, и заполняем тот столбец таблицы, в котором речь идет об этой величине.
2. Заполняем тот столбец, параметры которого даны.
3. Параметры третьего столбца выражаем через параметры первых двух.
Поясню алгоритм решения задачи на сплавы и растворы на примере данной задачи.
1. Поскольку в условии масса первого раствора не указана, примем ее за х. Масса второго раствора равна массе первого и тоже равна х. После того, как растворы смешали, мы получила раствор, масса которого равна 2х.
Начнем заполнять таблицу:
2. В условии задачи дано процентное содержание вещества в каждом растворе. Внесем эти условия в соответствующий столбец таблицы:
3. Параметры второго столбца, то есть массу чистого вещества выразим через параметры первых двух. Для этого воспользуемся формулой:
:

массе вещества:
разделить
на массу раствора: ,
и умножить на 100%
Получим:
%
%
Ответ: 17%.
Вероятно, Ваш браузер не поддерживается. Чтобы использовать тренажёр «Час ЕГЭ», попробуйте скачать
Firefox

В ряде заданий ЕГЭ по математике встречаются задачи на смешивание растворов. Эти задания могут вызывать затруднения, поскольку математики склонны считать концентрацию растворов разделом химии. На самом деле, эти задания решаются чисто математическим способом, с помощью линейного уравнения.
Преимущества этого способа для ЕГЭ по химии: легко восстановить в памяти (в отличие от метода креста), решает задачу одним уравнением.
В основе метода лежит определение:
масса компонента
массовая доля = ––––––––––––––––– (1)
масса целого
mв-ва
т. е. ω = ––––––––
m
где ω — массовая доля растворенного вещества,
mв-ва — масса растворенного вещества,
m — масса раствора.
Следовательно, масса растворенного вещества равна произведению массы раствора на массовую долю растворенного вещества:
mв-ва = m • ω (2).
При сливании растворов складываются как массы растворов:
m1 + m2 = m3 (3)
так и массы растворенных веществ:
mв-ва1 + mв-ва2 = mв-ва3
Подставляя вместо массы растворенных веществ произведение (2), получаем:
m1 • ω1 + m2 • ω2 = m3 • ω3
Заменяя неизвестную массу на выражение (3), получаем:
m1 • ω1 + m2 • ω2= (m1 + m2) • ω3 (4), или
m1 • ω1 + (m3 − m1) • ω2 = m3 • ω3 (5)
Пример:
Определите массы 10%-ного и 50%-ного (по массе) растворов, необходимые для получения 200 г 20%-ного раствора.
Решение:
ω1 = 10 %, ω2 = 50 %, ω3 = 20 %, m3 = 200 г, m2 = 200 − m1
Составляем уравнение (5):
m1 • 10 + (200 − m1) • 50 = 200 • 20
40 • m1 = 6000
m1 = 150 (г),
m2 = 200 − m1 = 200 − 150 = 50 (г)
Ответ: 150 г, 50 г.
Пример 2:
Определите массы 25%-ного (по массе) раствора и воды, необходимые для получения 200 г 10%-ного раствора.
Решение:
ω1 = 25 %, ω2 = 0 %, ω3 = 10 %, m3 = 200 г
Составляем уравнение (5):
m1 • 25 + m2 • 0 = 200 • 10
25 • m1 = 2000
m1 = 80 (г),
m2 = 200 − m1 = 200 − 80 = 120 (г)
Ответ: 80 г, 120 г.
Концентрация (процентное содержание) вещества
Рассмотрим смесь (сплав, раствор) из нескольких веществ.
Определение 1. Концентрацией (процентной концентрацией, процентным содержанием) вещества A в смеси (сплаве, растворе) называют число процентов pA , выраженное формулой
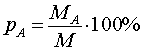 |
(1) |
где MA – масса вещества A в смеси (сплаве, растворе), а M – масса всей смеси (сплава, раствора).
Часто в задачах на растворы указаны не массы входящих в них веществ, а их объёмы. В этом случае вместо формулы (1) для концентрации (процентной концентрации, процентного содержания) вещества A в растворе используется формула
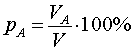 |
(2) |
где VA , – объём вещества А в растворе, а V – объем всего раствора.
Определение 2. Формулу (1) называют формулой для массовой концентрации вещества A в смеси (сплаве, растворе), а формулу (2) – формулой для объёмной концентрации вещества A в растворе.
При решении задач считается, что при слиянии нескольких растворов (сплавов) масса и объем полученной смеси равны сумме масс и объемов смешиваемых компонентов соответственно.
Приёмы, используемые при решении задач на массовые концентрации смесей (сплавов, растворов), а также при решении задач на объёмные концентрации растворов, являются общими, что мы и увидим при решении следующих типовых задач
Примеры решения задач на смеси, сплавы и растворы
Задача 1. Смешали 16 литров 30% раствора кислоты в воде с 9 литрами 80% раствора кислоты в воде. Найти концентрацию полученного раствора кислоты в воде.
Решение. В 16 литрах 30% раствора кислоты в воде содержится
литров кислоты. В 9 литрах 80% раствора кислоты в воде содержится
литров кислоты. Поэтому в смеси этих растворов содержится
4,8 + 7,2 = 12
литров кислоты. Поскольку полученный в результате смешивания раствор имеет объем
16 + 9 = 25
литров, то концентрация кислоты в этом растворе равна
Ответ. 48% .
Задача 2. Имеется 27 килограммов смеси цемента с песком с 40% содержанием цемента. Сколько килограммов песка нужно добавить в эту смесь, чтобы процентное содержание цемента в ней стало 30% ?
Решение. Обозначим буквой x количество килограммов песка, которые нужно добавить в смесь. Поскольку в 27 килограммах смеси с 40% содержанием цемента содержится
килограммов цемента, а после добавления x килограммов песка масса смеси станет равной
27 + x
килограммов, то после добавления песка процентное содержание цемента в получившейся смеси будет составлять
По условию задачи
Следовательно,
Ответ. 9 килограммов.
Задача 3. Смешав 8% и 13% растворы соли и добавив 200 миллилитров 5% раствора соли, получили 7% раствор соли. Если бы вместо 200 миллилитров 5% раствора соли добавили 300 миллилитров 17% раствора соли, то получили бы 15% раствор соли. Сколько миллилитров 8% и 13% растворов соли использовали для получения раствора?
Решение. Обозначив буквой x массу 8% раствора соли, а буквой y – массу 13% раствора соли, рассмотрим рисунки 1 и 2.
| x мл | |
| + | y мл |
| + | 200 мл |
| = | (x + y + 200) мл |
Рис. 1
На рисунке 1 изображена структура раствора, полученного при смешении x миллилитров 8% раствора соли, y миллилитров 13% раствора соли и 200 миллилитров 9% раствора соли. Объем этого раствора равен (x + y + 200) миллилитров.
| x мл | |
| + | y мл |
| + | 300 мл |
| = | (x + y + 300) мл |
Рис.2
На рисунке 2 изображена структура раствора, полученного при смешении x миллилитров 8% раствора соли, y миллилитров 13% раствора соли и 300 миллилитров 17% раствора соли. Объем этого раствора равен (x + y + 300) миллилитров.
Записывая баланс соли в растворе, структура которого изображена на рисунке 1, а также баланс соли в растворе, структура которого изображена на рисунке 2, получим систему из двух уравнений с двумя неизвестными x и y :
Раскрывая скобки и приводя подобные члены, получаем
Ответ. Смешали 70 мл 8% раствора и 55 мл 13% раствора.
Задача 4. Имеются два сплава меди с цинком. Если сплавить 1 килограмм первого сплава с 2 килограммами второго сплава, то получится сплав с 50% содержанием меди. Если же сплавить 4 килограмма первого сплава с 1 килограммом второго сплава, то получится сплав с 36% содержанием меди. Найти процентное содержание меди в первом и во втором сплавах.
Решение. Обозначим x % и y % — процентные содержания меди в первом и во втором сплавах соответственно и рассмотрим рисунки 3 и 4.
| 1 кг | 2 кг | |||
| Медь x % |
Цинк | + | Медь y % |
Цинк |
Рис. 3
На рисунке 3 изображена структура сплава, состоящего из 1 килограмма первого сплава и 2 килограммов второго сплава. Масса этого сплава – 3 килограмма.
| 4 кг | 1 кг | |||
| Медь x % |
Цинк | + | Медь y % |
Цинк |
Рис.4
На рисунке 4 изображена структура сплава, состоящего из 4 килограммов первого сплава и 1 килограмма второго сплава. Масса этого сплава – 5 килограммов.
Записывая баланс меди в сплаве, структура которого изображена на рисунке 3, а также баланс меди в сплаве, структура которого изображена на рисунке 4, получим систему из двух уравнений с двумя неизвестными x и y :
Далее получаем
Ответ. В первом сплаве содержание меди 30% , во втором сплаве содержание меди 60% .
Желающие ознакомиться с примерами решения различных задач по теме «Проценты» и применением процентов в экономике и финансовой математике могут посмотреть раздел нашего справочника «Проценты. Решение задач на проценты», «Простые и сложные проценты. Предоставление кредитов на основе процентной ставки», а также наши учебные пособия «Задачи на проценты» и «Финансовая математика».
Приемы, используемые для решения задач на выполнение работ, представлены в разделе нашего справочника «Задачи на выполнение работ».
С примерами решения задач на движение можно ознакомиться в разделе нашего справочника «Задачи на движение».
С методами решения систем уравнений можно ознакомиться в разделах нашего справочника «Системы линейных уравнений», «Системы с нелинейными уравнениями» и в нашем учебном пособии «Системы уравнений».
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
С демонстрационными вариантами ЕГЭ и ОГЭ, опубликованными на официальном информационном портале Единого Государственного Экзамена, можно ознакомиться на специальной страничке нашего сайта.
Для того, чтобы решать задачи на растворы и концентрацию, необходимо чётко понимать, что
называется концентрацией раствора.
Запомните!
Концентрация раствора — это часть, которую составляет масса растворённого вещества от
массы всего раствора.
- 9%-я концентрация раствора соли — это 9 грамм соли в
100 граммах раствора.
Разбор примера
Килограмм соли растворили в 9 л воды. Чему равна концентрация полученного раствора?
(Масса 1 л воды составляет 1 кг)
Используя определение концентрации данное выше, решим задачу следующим образом.
- 1 кг — масса растворённого вещества (соли)
- 9 кг — масса воды в растворе (не путать с общей массой раствора)
- 9 + 1 = 10 кг — общая масса раствора.
Ответ: 10% — концентрация раствора.
Разбор примера
Теперь решим обратную задачу.
Сколько соли получится при выпаривании 375 граммов 12%-го раствора?
Чтобы найти массу выпаренной соли из раствора, умножим общую массу раствора на процент концентрации.
Не забудем предварительно перевести процент в десятичную дробь.
Ответ: 45 г соли.
Сложная задача на растворы
В растворе 40% соли. Если добавить 120 г соли,
то процентное содержание соли станет равным 70.
Сколько грамм соли было первоначально в растворе?
Для составления пропорции обозначим за «x» первоначальную массу соли в растворе, а
за «y» массу
воды в растворе. Так как концентрация соли в исходном растворе 40%, то соответственно вода составляет
100% − 40%= 60%
Изобразим графически условия задачи.
Составим пропорцию, связывающую эти величины до добавления соли.
Для решения задачи нам надо определить какая из неизвестных («x» или «y») остаётся неизменной
после добавления соли.
Этой величиной является масса воды в растворе «y».
Выразим её, учитывая изменения в растворе после добавления соли.
- (x + 120) г — масса соли в новом растворе
- (100% − 70% = 30% — процентное содержание воды в новом растворе.
Составим пропорцию аналогично предыдущей, но с учётом изменений произошедших
после добавления соли.
Так как масса воды осталось неизменной после добавления соли, приравняем её значения до и
после добавления соли и решим уравнение.
Ответ: 48 г — масса соли в первоначальном растворе.
Теоретическая часть
Растворы занимают промежуточное место между химическими соединениями и механическими смесями. Однородность растворов делает их схожими с химическими соединениями, также на химическое взаимодействие между компонентами растворов указывает выделение теплоты при растворении некоторых веществ.
Еще одним доказательством того, что компоненты растворахимически взаимодействуют друг с другом, служит тот факт, что многие вещества выделяются из водных растворов в виде кристаллов, содержащих кристаллизованную воду – гидратов; причем на каждую молекулу растворенного вещества приходится определенное число молекул воды. Как правило, гидраты
– нестойкие соединения, во многих случаях они разлагаются уже при выпаривании растворов. Но иногда гидраты так прочны, что при выделении растворенного вещества из раствора вода входит в состав его кристаллов. Вещества, в состав которых входят молекулы воды называются кристаллогидратами, а содержащаяся в них вода — кристаллизационной. Состав кристаллогидратов принято изображать формулами, показывающими, какое количество кристаллизованной воды содержит кристаллогидрат. Например, кристаллогидрат сульфата натрия, содержащий на один моль сульфата натрия десять молей воды выражается формулой
Na2SO4 · 10 H2O.
В нашей жизни получили широкое распространение тривиальные названия веществ. Ниже приведены наиболее часто встречающиеся формулы кристаллогидратов, их тривиальные названия и названия по систематической номенклатуре, рекомендованной ИЮПАК.
|
Кристаллогидрат |
Тривиальное название |
Название |
|
|
по систематической номенклатуре |
|||
|
2CaSO4 · H2O |
Алебастр, жженый гипс |
Гидрат сульфата кальция |
|
|
MgSO4 · 7 H2O |
Английская соль, горькая соль |
Гептагидрат сульфата магния |
|
|
4Al2O3 · H2O |
Алюмогель |
Гидрат оксида алюминия |
|
|
Na2B4O7·10H2O |
Бура |
Декагидрат тетрабората натрия |
|
|
ZnSO4 · 7 H2O |
Белыйкупорос, цинковыйкупорос |
Гептагидрат сульфата цинка |
|
|
Na2SO4 · 10 H2O |
Глауберова соль |
Декагидрат сульфата натрия |
|
|
FeSO4 · 7 H2O |
Железный купорос, зеленый |
Гептагидрат сульфата железа (II) |
|
|
купорос |
|||
|
K4[Fe(CN)6] · 3 H2O |
Желтая кровяная соль |
Тригидратгексацианоферрата(II) калия |
|
|
Na2CO3 · 10 H2O |
Кристаллическая сода |
Декагидрат карбоната натрия |
|
|
CuSO4 · 5 H2O |
Медный купорос, синий купорос, |
Пентагидрат сульфата меди (II) |
|
|
синий камень |
|||
|
Ca(NO3)2 · 4 H2O |
Норвежская селитра |
Тетрагидрат нитрата кальция |
|
|
[Sn(OH2)Cl2] · H2O |
Оловянная соль |
Гидрат дихлородиакваолова (II) |
|
|
CaНРO4 · 2 H2O |
Преципитат |
Дигидрат гидрофосфата кальция |
|
|
SiO2 · n H2O |
Силикагель |
Полигидрат оксида кремния |
4

Растворы отличаются от химических соединений тем, что состав взаимодействующих веществ может изменяться в широких пределах. В свойствах раствора можно обнаружить многие свойства компонентов его составляющих, что характерно для механических соединений.
Исходя из всего вышесказанного, можно дать следующее определение раствора. Раствор — однородная многокомпонентная система, состоящая из растворителя,
растворённых веществ и продуктов их взаимодействия, относительные количества которых могут изменяться в широких пределах.
Существует несколько способов классификации растворов.
•По агрегатному состоянию
Раствор
|
Жидкий |
Газообразный |
Твёрдый |
|
(морская вода) |
(воздух) |
(многие сплавы металлов) |
В химической практике наиболее важны растворы, приготовленные на основе жидкого растворителя. Именно жидкие однородные смеси в химии называют просто растворами. Наиболее широко применяемым неорганическим растворителем является вода. Растворы с другими растворителями называются неводными.
•По размеру частиц растворенного вещества
Раствор
|
Истинный |
Коллоидный |
|
|
(размер частиц менее 1·10−9 м) |
(размер частиц 1·10−9 м — 5·10−7 м) |
|
|
Растворенное |
вещество диспергировано до |
Частицы в таких растворах можно обнару- |
|
атомного или молекулярного уровня, частицы |
жить при помощи ультрамикроскопа |
|
|
растворенного вещества не видимы ни визу- |
||
|
ально, ни под микроскопом, свободно пере- |
||
|
двигаются в среде растворителя. Истинные |
||
|
растворы – |
термодинамически устойчивые |
системы, неограниченно стабильные во времени.
5

•С точки зрения термодинамики
Раствор
|
Идеальный |
Неидеальный (реальный) |
Внутренняя энергия каждого компонента не зависит от концентрации. Компоненты раствора смешиваются, как идеальные газы; предполагается, что сил взаимодействия между частицами нет, и вещества смешиваются без выделения или поглощениятеплоты.
Растворы, не удовлетворяющие условиям идеальных растворов, относят к реальным. Чем меньше концентрация раствора, тем ближе он к идеальному раствору.
•Основываясь на величине электрической проводимости
Раствор
|
Электролитический |
Неэлектролитический |
|
(проводитэлектрический ток) |
(электрический ток не проводит) |
•Возможна классификация раствора по количеству растворенного в нем вещества.
Раствор
|
Насыщенный |
Ненасыщенный |
Перенасыщенный |
|
|
Раствор, который находится в ди- |
Раствор, |
содержа- |
Раствор, в котором при данной тем- |
|
намическом равновесии с избыт- |
щий меньше вещест- |
пературе находится в растворенном |
|
|
ком растворённого вещества, то |
ва, чем |
необходимо |
состоянии больше вещества, чем в его |
|
есть молекулярные или ионные |
для насыщения. |
насыщенном растворе при тех же |
|
|
частицы, распределённые в жидком |
Пример: если помес- |
условиях. |
|
|
растворе, присутствуют в нём в |
тить в 100 г воды |
Пример: При нагревании смеси соли с |
|
|
таком количестве, что при данных |
при 20 ºC менее 36 г |
водой до 100 ○C произойдёт растворе- |
|
|
условиях не происходит дальней- |
NaCl. |
ние 39,8 г NaCl в 100 г воды. Если те- |
|
|
шего растворения вещества. Насы- |
перь удалить из раствора нераство- |
||
|
щенный раствор является стабиль- |
рившуюся соль, а раствор осторожно |
||
|
ной системой, т.е. может сущест- |
охладить до 20 ºC, избыточное коли- |
||
|
вовать при данной температуре без |
чество соли не всегда выпадает в |
||
|
изменениясколькоугоднодолго. |
осадок. В этом случае мы имеем дело |
||
|
Пример: если поместить 50 г NaCl |
с перенасыщенным раствором. Такие |
||
|
в 100 г H2O, то при 20 ºC раство- |
растворы очень неустойчивы. Поме- |
||
|
рится только 36 г соли. |
шивание, встряхивание, добавление |
||
|
крупинок соли может вызвать крис- |
|||
|
таллизацию избытка соли и переход в |
|||
|
насыщенноеустойчивоесостояние. |
6
Любой раствор состоит из растворителя и растворенного вещества. В случае растворов газов или твердых веществ в жидкостях растворителем обычно считается жидкость, а растворенным веществом – растворенный газ или твердое вещество, независимо от их относительного количественного содержания. Когда компоненты обладают ограниченной смешиваемостью, то растворителем является тот, прибавление которого к раствору возможно в неограниченном количестве без нарушения гомогенности.
Если компоненты обладают неограниченной растворимостью, то можно выделить два случая. При значительном различии содержания компонентов растворителем считается вещество, присутствующее в относительно большем количестве. Понятия растворитель и растворенное вещество теряют смысл, когда речь идет о смесях с примерно равными или близкими концентрациями компонентов.
Содержание растворенного вещества в растворе может быть выражено либо безразмерными единицами – долями или процентами, либо величинами размерными – концентрациями.
Концентрацией раствора называют содержание растворенного вещества в единице объема или массы раствора или растворителя. Растворы, содержащие растворенное вещество в количестве, соизмеримом с количеством растворителя, называют концентрированными. Растворы с малой концентрацией растворенного вещества, называют разбавленными. Граница между концентрированными и разбавленными растворами условна.
В химии используют более десятка способов выражения концентрации. Ниже в таблице 1 приведены наиболее часто употребляемые на практике способы выражения содержания растворенного вещества в растворе.
7

Таблица 1 — Способы выражения состава раствора
Название Обозначение
|
Массовая доля растворенного |
||
|
вещества В – отношение массы |
ωВ |
|
|
растворенного вещества mВ к |
||
|
массе раствора mр-ра |
||
|
Молярная доля растворенного |
||
|
вещества В – отношение количес- |
||
|
тва этого вещества nВ к суммар- |
χВ |
|
|
ному количеству всех веществ |
||
|
ΣnВi, входящих в состав раствора, |
||
|
включая растворитель nS |
||
|
Молярная концентрация (мо- |
||
|
лярность) – отношение коли- |
||
|
чества растворенного вещества |
cВ |
|
|
В [nВ = mВ/MВ] к объему |
||
|
раствора Vр-ра |
||
|
Молярная концентрация экви- |
||
|
валента (нормальность) – отно- |
||
|
шение эквивалентного количества |
сэк (1/Z В) |
|
|
вещества В [n(1/Z В) = mВ/M(1/Z В)] |
||
|
к объему раствора Vр-ра |
||
|
Моляльная концентрация (мо- |
||
|
ляльность) – отношение коли- |
||
|
чества растворенного вещества В |
cm (В) |
|
|
[nВ = mВ/MВ] к массе раство- |
||
|
рителя mS |
||
|
Титр (массовая концентрация) |
||
|
раствора вещества В – это кон- |
||
|
центрация стандартного раство- |
ТВ |
|
|
ра, равная массе вещества В |
||
|
(mВ), содержащегося в 1 см3 (мл) |
Математическое выражение
ω =
mB
mр-ра или
mB
ω = 
mр-ра
χB = nB
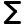
|
сB = |
nB |
= |
mB |
|
|
V |
M |
V |
||
|
р-ра |
B |
р-ра |
|
сэк (1/Z B) = |
nэк (1/Z B) |
= |
mB |
|
|
Vр-ра |
Vр-ра |
|||
|
Mэк (1/Z B) |
|
сm (B) = |
nB |
= |
mB |
|
MB mS |
|||
|
mS |
mB
TB = Vр-ра
8
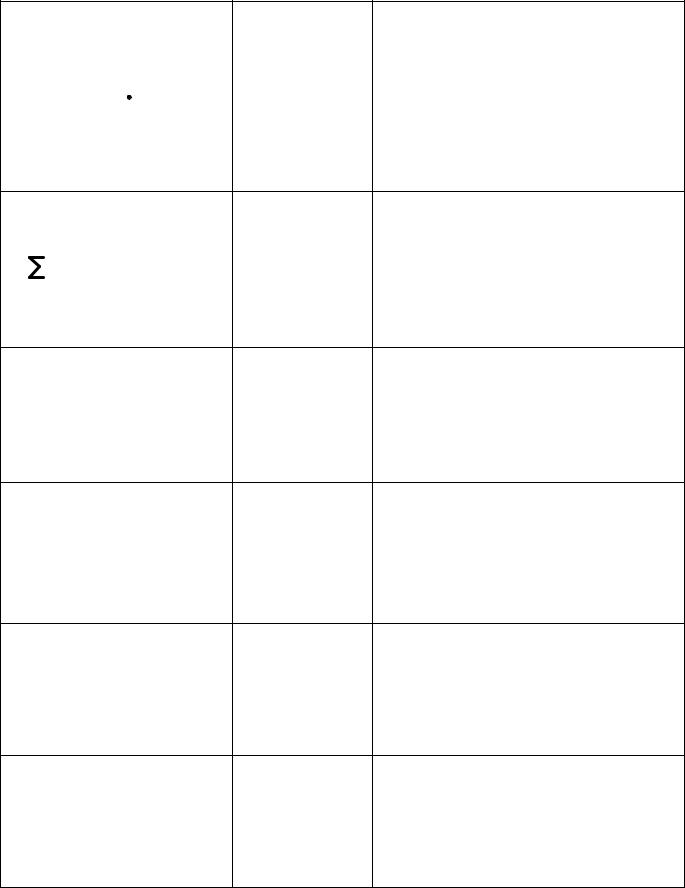
|
Пояснение |
Размерность |
Пример |
||||
|
mр-ра = ρ |
Vр-ра |
, |
безразмерная |
В 100 г воды растворено 82 |
г NaCl. |
|
|
величина |
Массовая доля хлорида натрия в |
|||||
|
где ρ – плотность раствора, |
растворе: |
|||||
|
(%) |
||||||
|
Vр-ра – объем раствора |
ω = 82 г / (100 г + 82 г) = 0,45 |
или 45 % |
||||
безразмерная
nB i = nВ 1 + nB 2 + … . величина
(%)
|
Молярная концентрация КOH в водном |
||
|
где MВ – молярная масса |
моль/дм3 |
растворе, равная 1 моль/дм3, означает, |
|
вещества В |
моль/л |
что в 1 дм3 такого раствора содержится |
|
1 моль КOH |
|
где M(1/Z В) – молярная масса |
Молярная |
концентрация эквивалента |
||
|
моль/дм |
3 |
КOH в |
водном растворе, |
равная |
|
эквивалента вещества В |
1 моль/дм3, означает, что в |
1 дм3 |
||
|
(см. стр. 10) |
моль/л |
раствора содержится 1 моль эквивален- |
||
|
тного количества КOH |
Моляльная концентрация КOH в водном моль/кг растворе, равная 1 моль/кг, означает, что
в1 кгводырастворен1 мольКOH
г/см3 г/мл
9

Общая формула для вычисления молярной массы эквивалента вещества В
|
Mэк (1/Z B) = |
MB |
|||||||||||||||||
|
Z |
, |
|||||||||||||||||
|
где 1/Z – фактор эквивалентности, Z – эквивалентное число вещества В |
||||||||||||||||||
|
1) для кислоты: |
Z — основность кислоты |
|||||||||||||||||
|
Пример: |
||||||||||||||||||
|
Mэк (1/2 H2SO4) = |
2 |
MH + MS + 4 |
MO |
= |
98 |
= 49 г/моль |
||||||||||||
|
2 |
2 |
|||||||||||||||||
|
2) для основания: |
Z — кислотность основания |
|||||||||||||||||
|
Пример: |
||||||||||||||||||
|
Mэк (1/1 NaOH) |
= |
MNa + MO + MH |
40 |
= 40 г/моль |
||||||||||||||
|
= |
||||||||||||||||||
|
1 |
1 |
|||||||||||||||||
|
3) для соли: |
Z = Число атомов металла · Валентность металла |
|||||||||||||||||
|
Пример: |
162 |
|||||||||||||||||
|
Mэк (1/3 FeCl3) = |
MFe + 3 MCl |
= |
= 54 г/моль |
|||||||||||||||
|
1 |
3 |
3 |
||||||||||||||||
Таблица 2 — Соотношение между различными способами выражения состава растворов
|
ωВ |
сВ |
cэк (1/Z В) |
ТВ |
||||||||||||||||||||||
|
Массовая доля |
1000 ρ |
1000 ρ |
Z |
ρ |
|||||||||||||||||||||
|
ωВ |
ωВ |
ωВ |
|||||||||||||||||||||||
|
ωВ |
MB |
||||||||||||||||||||||||
|
MB |
|||||||||||||||||||||||||
|
Молярная |
MB |
cB |
Z |
cB |
MB |
cB |
|||||||||||||||||||
|
концентрация |
|||||||||||||||||||||||||
|
1000 |
ρ |
1000 |
|||||||||||||||||||||||
|
сВ |
|||||||||||||||||||||||||
|
Молярная |
MB сэк (1/Z B) |
сэк (1/Z B) |
MB |
сэк (1/Z B) |
|||||||||||||||||||||
|
концентрация |
|||||||||||||||||||||||||
|
эквивалента |
|||||||||||||||||||||||||
|
1000 |
Z ρ |
Z |
1000 |
Z |
|||||||||||||||||||||
|
cэк (1/Z В) |
|||||||||||||||||||||||||
|
Титр |
TB |
1000 TB |
1000 |
Z TB |
|||||||||||||||||||||
|
ТВ |
ρ |
MB |
MB |
||||||||||||||||||||||
10

Алгоритмы решения задач
Задача 1. Сколько граммов воды и кристаллогидрата сульфата натрия Na2SO4 · 10 H2O необходимо взять, чтобы получить раствор массой 71 г, с массовой долей сульфата натрия
20 %?
Дано:
ωNa2SO4 = 20 % mр-ра = 71 г
mNa2SO4·10 H2O — ? mH2O — ?
Решение:
1. Вычислим массу Na2SO4, необходимую для приготовления 71 г раствора с массовой долей соли 20,00 %, воспользовавшись формулой:
mNa2SO4
ωNa2SO4 = 
mр-ра
Следовательно,
|
mNa2SO4 |
= |
mр-ра ωNa2SO4 |
= |
71 г |
20 % |
= 14,2 г |
|
100 % |
100 % |
2. Поскольку данный раствор готовят из кристаллогидрата Na2SO4 · 10 H2O, то необходимо вычислить его массу, используя следующую пропорцию:
|
mNa2SO4·10 H2O |
— |
mNa2SO4 |
|||||||
|
х г |
14,2 г |
||||||||
|
МNa2SO4·10 H2O |
— |
МNa2SO4 |
|||||||
|
322 г/моль |
142 г/моль, |
||||||||
|
где |
МNa2SO4 = 2·МNa + МS + 4·МО = 2·23 + 32 + 4·16 = 142 г/моль |
||||||||
|
МNa2SO4·10 H2O = МNa2SO4 + 10·МH2O = 142 + 10·18 = 322 г/моль |
|||||||||
|
Тогда, |
mNa2SO4 MNa2SO4 |
||||||||
|
10 H2O |
14,2 г |
322 г/моль |
|||||||
|
mNa2SO4 10 H2O |
= |
= |
= 32,2 г |
||||||
|
MNa2SO4 |
|||||||||
|
142 г/моль |
. |
||||||||
3. Вычислим массу воды:
mH2O = mр-ра – mNa2SO4·10 H2O = 71 г – 32,2 г = 38,8 г Ответ: mNa2SO4·10 H2O = 32,2 г, mH2O = 38,8 г.
Задача 2. Определить массу раствора соли с массовой долей 20,00 %, которую нужно прибавить к 150 г воды для получения раствора соли с массовой долей 15,00 %.
Дано:
ω1 соли = 20 % ω2 соли = 15 %
mH2O = 150 г
m1 р-ра — ?
Решение (I Вариант):
1. Для приготовления раствора с массовой долей соли 15 % из формулы:
mсоли
ω2 соли = m2 р-ра 
выразим массу соли, поскольку она не изменяется при переходе
17

от одного раствора к другому
m2 р-ра 
mсоли =
100 %
2. Подставим полученное выражение в формулу массовой доли исходного раствора (с массовой долей 20,00 %)
mсоли
ω1 соли = m1 р-ра 
Тогда
|
ω |
= |
m2 р-ра |
ω2 соли |
100 % = |
m2 р-ра ω2 соли |
|
1 соли |
m1 р-ра |
100 % |
m1 р-ра |
||
Известно, что второй раствор получили из первого разбавлением водой, т. е.:
m2 р-ра = m1 р-ра + mH2O
Следовательно,
(m1 р-ра + mH2O) 
ω1 соли =
m1 р-ра
3. Из полученной формулы выразим и рассчитаем m1 р-ра
|
m1 р-ра = |
mH2O ω2 соли |
= |
150 г |
15 % |
= 450 г |
|
ω1 соли — ω2 соли |
|||||
|
20 % — 15 % |
Ответ m1 р-ра = 450 г.
Для решения задач на смешение растворов, содержащих различные массовые доли одного и того же вещества очень удобно также использовать «метод креста».
Решение (II Вариант, «метод креста»):
|
20 |
1. Необходимо схематично изобразить квадрат. В верхнем левом |
|
|
углу квадрата записываем наибольшую массовую долю соли в |
||
|
15 |
растворе (20 %), в левом нижнем наименьшую (эту массовую долю |
|
|
обычно принимают за 0 %). В центр квадрата помещаем вторую |
||
|
известную концентрацию (15 %). |
||
|
2. Заполнение правой части квадрата идет по диагоналям от уже |
известных концентраций. Из 20 вычитаем 15, получаем цифру 5, ее записываем в правом нижнем углу. Теперь из 15 вычитаем 0, получаем значение 15, которое помещаем в
правую верхнюю часть квадрата.
3. Полученные числа в правой части квадрата показывают, в каком массовом отношении необходимо смешать исходный раствор соли с массовой долей 20 % и воду. Поэтому записываем следующее соотношение:
,
18

|
m1 р-ра |
15 |
3 |
|||
|
= |
= |
||||
|
m |
5 |
||||
|
Н2О |
1 |
где mH2O = 150 г по условию задачи
Следовательно,
|
mH2O 3 |
150 г |
3 |
= 450 г |
|
|
m1 р-ра = |
= |
|||
|
1 |
1 |
Ответ m1 р-ра = 450 г.
Задача 3. Вычислите молярную концентрацию, молярную концентрацию эквивалента и моляльную концентрацию раствора фосфорной кислоты с массовой долей 6 % (значение плотности раствора найдите в приложении).
Дано:
ωH3PO4 = 6%
сH3PO4 — ?
cэк (1/Z H3PO4) — ?
сm (H3PO4) — ?
Решение:
1. Молярную концентрацию определяем по формуле :
|
сH3PO4 = |
mH3PO4 |
|||
|
MH3PO4 |
Vр-ра |
, |
моль/дм |
3 |
Согласно условию задачи в 100 г раствора содержится 6 г H3PO4. Тогда 6 г H3PO4 содержится в объеме раствора:
|
mр-ра |
100 г |
|||||||
|
Vр-ра = |
= |
= 97 см3 = 97 10-3 дм3 |
||||||
|
ρ |
||||||||
|
1,031 г/см3 |
||||||||
|
Значение плотности фосфорной кислоты ρ(H3PO4) нашли по таблице приложения. |
||||||||
|
Следовательно, |
6 г |
|||||||
|
сH3PO4 = |
= 0,63 моль/дм3 |
|||||||
|
98 г/моль 97 10-3 дм3 |
||||||||
|
, |
||||||||
|
где |
МH3PO4 = 3·МН + МР + 4·МО = 3·1 + 31 + 4·16 = 98 г/моль |
2. Молярную концентрацию эквивалента растворенного вещества определяем по формуле:
|
сэк (1/Z H3PO4) = |
mH3PO4 |
|||||||
|
M |
V |
р-ра , |
||||||
|
эк (1/3 H3PO4) |
моль/дм3 |
|||||||
|
Mэк (1/3 H3PO4) = |
MH3PO4 |
= |
98 г/моль |
= 32,67 г/моль |
||||
|
3 |
3 |
|||||||
Тогда,
Можно воспользоваться формулой перевода (см. табл. 2)
19
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
2
В понедельник акции компании подорожали на некоторое количество процентов, а во вторник подешевели на то же самое количество процентов. В результате они стали стоить на дешевле, чем при открытии торгов в понедельник. На сколько процентов подорожали акции компании в понедельник?
Источник: Яндекс: Тренировочная работа ЕГЭ по математике. Вариант 1.
3
Четыре одинаковые рубашки дешевле куртки на 8%. На сколько процентов пять таких же рубашек дороже куртки?
4
Семья состоит из мужа, жены и их дочери студентки. Если бы зарплата мужа увеличилась вдвое, общий доход семьи вырос бы на 67%. Если бы стипендия дочери уменьшилась втрое, общий доход семьи сократился бы на 4%. Сколько процентов от общего дохода семьи составляет зарплата жены?
5
Цена холодильника в магазине ежегодно уменьшается на одно и то же число процентов от предыдущей цены. Определите, на сколько процентов каждый год уменьшалась цена холодильника, если, выставленный на продажу за 20 000 рублей, через два года был продан за 15 842 рублей.
Пройти тестирование по этим заданиям
11. Сюжетные текстовые задачи
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Задачи на растворы, смеси и сплавы
(blacktriangleright) Концентрация вещества в растворе (сплаве) – это процент содержания этого вещества в растворе (сплаве): [text{концентрация вещества}=dfrac{text{масса вещества}}{text{масса раствора}}cdot 100%]
(blacktriangleright) Заметим, что в задачах из данной подтемы зачастую удобно составлять уравнения относительно кислоты или активного вещества.
Задание
1
#846
Уровень задания: Равен ЕГЭ
Сергей смешал раствор, содержащий (20%) кислоты и раствор, содержащий (40%) той же кислоты. В итоге у него получился раствор, содержащий (32,5%) кислоты, причём объём полученного раствора (4) литра. Сколько литров раствора, содержащего (20%) кислоты, использовал Сергей при смешивании?
Пусть (x) литров раствора, содержащего (20%) кислоты использовал Сергей при смешивании, тогда
(4 — x) литров раствора, содержащего (40%) кислоты использовал Сергей при смешивании,
(dfrac{20}{100}x) – объём кислоты в растворе, содержащем (20%) кислоты, (dfrac{40}{100}(4 — x)) – объём кислоты в растворе, содержащем (40%) кислоты.
Так как в итоге кислоты оказалось (dfrac{32,5}{100} cdot 4 = 1,3) литра, то:
[dfrac{20}{100}x + dfrac{40}{100}(4 — x) = 1,3,] откуда находим (x = 1,5).
Ответ: 1,5
Задание
2
#844
Уровень задания: Равен ЕГЭ
Один газ в сосуде А содержал (21%) кислорода, второй газ в сосуде В содержал (5%) кислорода. Масса первого газа в сосуде А была больше массы второго газа в сосуде В на 300 г. Перегородку между сосудами убрали так, что газы перемешались и получившийся третий газ теперь содержит (14,6%) кислорода. Найдите массу третьего газа. Ответ дайте в граммах.
Пусть (x) грамм – масса второго газа, тогда
(x + 300) грамм – масса первого газа,
(dfrac{21}{100}(x + 300)) грамм – масса кислорода в первом газе,
(dfrac{5}{100}x) грамм – масса кислорода во втором газе,
тогда масса кислорода в третьем газе составляет (dfrac{14,6}{100}(2x + 300)) грамм.
Так как третий газ возник в результате смешивания первого и второго, то:
[dfrac{21}{100}(x + 300) + dfrac{5}{100}x = dfrac{14,6}{100}(2x + 300),] откуда находим (x = 600). Таким образом, масса третьего газа равна (600 + 600 + 300 = 1500) грамм.
Ответ: 1500
Задание
3
#843
Уровень задания: Равен ЕГЭ
Иван случайно смешал молоко жирностью (2,5%) и молоко жирностью (6%). В итоге у него получилось 5 литров молока жирностью (4,6%). Сколько литров молока жирностью (2,5%) было у Ивана до смешивания?
Пусть (x) литров молока жирностью (2,5%) было у Ивана, тогда
(5 — x) литров молока жирностью (6%) было у Ивана,
(dfrac{2,5}{100}x) – объём жира в молоке жирностью (2,5%), (dfrac{6}{100}(5 — x)) – объём жира в молоке жирностью (6%).
Так как в итоге жира оказалось (dfrac{4,6}{100} cdot 5 = 0,23) литра, то:
(dfrac{2,5}{100}x + dfrac{6}{100}(5 — x) = 0,23), откуда находим (x = 2).
Ответ: 2
Задание
4
#841
Уровень задания: Равен ЕГЭ
В сосуде А содержится 3 литра 17-процентного водного раствора вещества Х. Из сосуда В в сосуд А перелили 7 литров 19-процентного водного раствора вещества Х. Сколько процентов составляет концентрация полученного в сосуде А раствора?
Концентрация в процентах – это отношение объёма вещества к объёму смеси, умноженное на 100(%). До переливания в сосуде А было (3 cdot 0,17 = 0,51) литра вещества Х, в сосуде В было (7 cdot 0,19 = 1,33) литра вещества Х.
После переливания объём вещества Х в сосуде А стал (0,51 + 1,33 = 1,84) литра, а объём всего раствора (3 + 7 = 10) литров. Тогда концентрация в процентах составила [dfrac{1,84}{10} cdot 100% = 18,4%.]
Ответ: 18,4
Задание
5
#2133
Уровень задания: Равен ЕГЭ
Во сколько раз больше должен быть объём (5)-процентного раствора кислоты, чем объём (10)-процентного раствора той же кислоты, чтобы при смешивании получить (7)-процентный раствор?
Пусть объём (5)-процентного раствора кислоты равен (x) литров, а объём (10)-процентного раствора равен (y) литров, тогда требуется найти значение величины (dfrac{x}{y}) при условии [0,05x + 0,1y = 0,07(x + y)
qquadLeftrightarrowqquad
dfrac{x}{y} = dfrac{3}{2} = 1,5,,] таким образом, ответ: (1,5).
Ответ: 1,5
Задание
6
#2134
Уровень задания: Равен ЕГЭ
Во сколько раз больше должен быть объём (20)-процентного раствора кислоты, чем объём (14)-процентного раствора той же кислоты, чтобы при смешивании получить (18)-процентный раствор?
Пусть объём (20)-процентного раствора кислоты равен (x) литров, а объём (14)-процентного раствора равен (y) литров, тогда требуется найти значение величины (dfrac{x}{y}) при условии [0,2x + 0,14y = 0,18(x + y)
qquadLeftrightarrowqquad
dfrac{x}{y} = 2,,] таким образом, ответ: (2).
Ответ: 2
Задание
7
#2629
Уровень задания: Равен ЕГЭ
Смешав (25)-процентный и (95)-процентный растворы кислоты и добавив (20) кг чистой воды, получили (40)-процентный раствор кислоты. Если бы вместо (20) кг воды добавили (20) кг (30)-процентного раствора той же кислоты, то получили бы (50)-процентный раствор кислоты. Сколько килограммов (25)-процентного раствора использовали для получения смеси?
Заметим, что вода – это раствор, не содержащий кислоту, то есть содержащий (0%) кислоты.
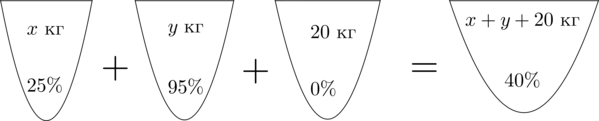
Пусть (x) кг – масса раствора с (25)-процентным содержанием кислоты, (y) кг – масса раствора с (95)-процентным содержанием кислоты. Составим схему, описывающую получение (40)-процентного раствора:
Заметим, что количество кислоты во всех трех растворах равно количеству кислоты в получившемся растворе. Найдем количество кислоты в первом растворе.
Если раствор весит (x) кг, а в нем (25%) кислоты, то в килограммах в нем (dfrac{25}{100}cdot x) кислоты.
Таким же образом можно посчитать количество кислоты в остальных растворах. Получим первое уравнение:
[dfrac{25}{100}cdot x+dfrac{95}{100}cdot y+
dfrac{0}{100}cdot 20=dfrac{40}{100}cdot (x+y+20)]
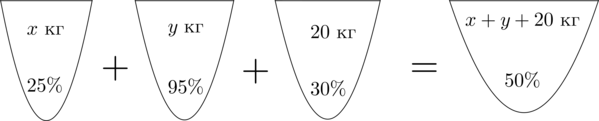
Аналогично составим схему, описывающую получение (50)-процентного раствора:
Значит, уравнение, описывающее эту ситуацию, будет выглядеть так:
[dfrac{25}{100}cdot x+dfrac{95}{100}cdot y+
dfrac{30}{100}cdot 20=dfrac{50}{100}cdot (x+y+20)]
Таким образом, решив систему из полученных двух уравнений, найдем (x). Для этого можно умножить оба уравнения на (100), чтобы сделать их проще на вид:
[begin{cases}
25x+95y+0=40(x+y+20)\
25x+95y+30cdot 20=50(x+y+20)
end{cases}]
Вычтем из второго уравнения первое и получим новую систему:
[begin{aligned} &begin{cases}
25x+95y=40(x+y+20)\
30cdot 20=10(x+y+20)
end{cases} quad Rightarrow quad begin{cases}
5x+19y=8(x+y+20)\
y=40-x end{cases} quad Rightarrow \[2ex] Rightarrow quad
&begin{cases}
3x-11(40-x)+160=0\
y=40-x end{cases} quad Rightarrow quad begin{cases}
x=20\y=20end{cases} end{aligned}]
Таким образом, раствора с (25%) кислоты было (20) кг.
Ответ: 20

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Задачи на смеси и сплавы – подробнее
Концентрация какого-то вещества в растворе – это отношение массы или объема этого вещества к массе или объему всего раствора.
То же самое относится и к сплавам: содержание одного из металлов в сплаве – это отношение массы этого металла к массе всего сплава.
Обычно концентрация измеряется в процентах.
Что такое процент?
Напомню, что это сотая доля числа. То есть, если массу или объем разделить на ( displaystyle 100), получим ( displaystyle 1%) этой массы или объема.
Чтобы вычислить концентрацию в процентах, достаточно полученное число умножить на ( displaystyle 100%).
Почему?
Сейчас покажу: пусть масса всего раствора равна ( displaystyle M), а масса растворенного вещества (например, соли или кислоты) – ( displaystyle m). Тогда один процент от массы раствора равен ( displaystyle frac{M}{100}).
Как узнать, сколько таких процентов содержится в числе ( displaystyle m)?
Просто: поделить число ( displaystyle m) на этот один процент: ( displaystyle frac{m}{frac{M}{100}}=frac{m}{M}cdot 100), но ведь ( displaystyle frac{m}{M}) – это концентрация.
Вот и получается, что ее надо умножить на ( displaystyle 100), чтобы узнать, сколько процентов вещества содержится в растворе.
Более подробно о процентах – в темах “Дроби, и действия с дробями”и “Проценты”.
Поехали дальше.
Масса раствора, смеси или сплава равна сумма масс всех составляющих.
Логично, правда?
Например, если в растворе массой ( displaystyle 10) кг содержится ( displaystyle 3) кг соли, то сколько в нем воды? Правильно, ( displaystyle 7)кг.
И еще одна очевидность:
При смешивании нескольких растворов (или смесей, или сплавов), масса нового раствора становится равной сумме масс всех смешанных растворов.
А масса растворенного вещества в итоге равна сумме масс этого же вещества в каждом растворе отдельно.
Например: в первом растворе массой ( displaystyle 10) кг содержится ( displaystyle 3) кг кислоты, а во втором растворе массой ( displaystyle 14) кг – ( displaystyle 5) кг кислоты.
Когда мы их смешаем, чему будет равна масса нового раствора?
( displaystyle 10+14=24) кг.
А сколько в новом растворе будет кислоты? ( displaystyle 3+5=8) кг.
Перейдем к задачам.
Бонус: Вебинары из нашего курса подготовки к ЕГЭ по математике
ЕГЭ №11. Задачи на растворы, смеси и сплавы (и на проценты)
В этом видео мы научимся решать текстовые задачи на проценты, а так же на растворы, смеси и сплавы – на все, что содержит разные вещества в каком-то соотношении.
Задачи на смеси и сплавы очень часто попадаются на ОГЭ (№23) и профильном ЕГЭ (под номером 12).
Мы научимся очень простому способу сводить эти задачи к обычному линейному уравнению или к системе из двух таких уравнений.
Также мы научимся решать сложные задачи на проценты – в основном они на банковские вклады и кредиты и прочие финансовые штуки.
Это, в том числе, даст нам очень большой задел для “ экономической” задачи №17 (которая стоит аж 3 первичных балла).
ЕГЭ №17 Экономическая задача. Вклады
Экономические задачи в основном довольно простые, но дают аж 3 первичных балла!
Но это не совсем 3 балла нахаляву. Эти задачи требуют очень подробного и чёткого описания решения.
По сути, мы составляем математическую модель какой-то жизненной ситуации (например, связанной с банковскими вкладами или кредитами), и важно научиться ничего не пропускать при описании этой модели: описывать словами все введённые обозначения, обосновывать уравнения, которые мы записываем, и всё в таком духе.
Если не написать эти объяснения, вы гарантированно получите 0 баллов даже за правильно найденный ответ!
На этом уроке мы узнаем, как работают вклады, научимся решать и, главное, правильно оформлять решение таких задач.