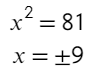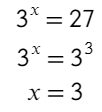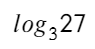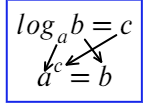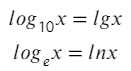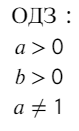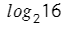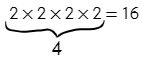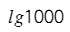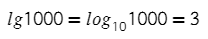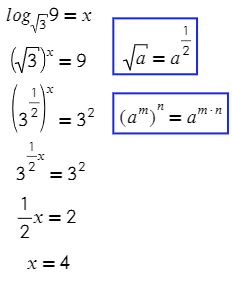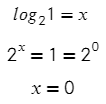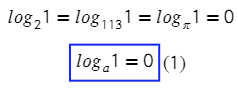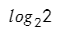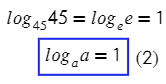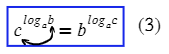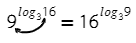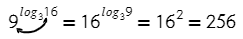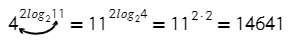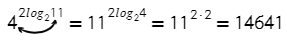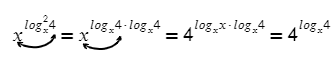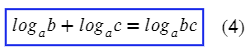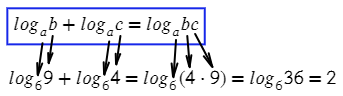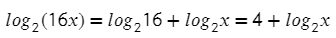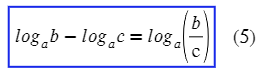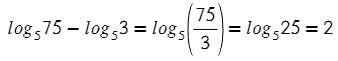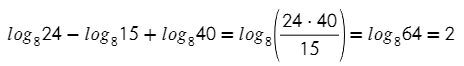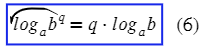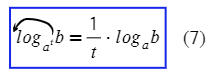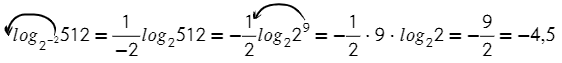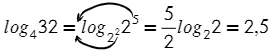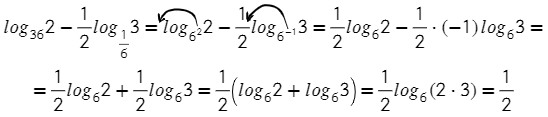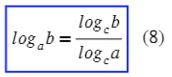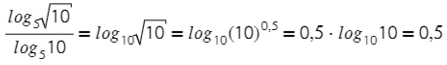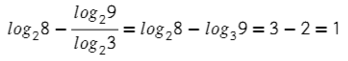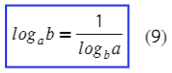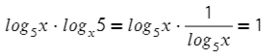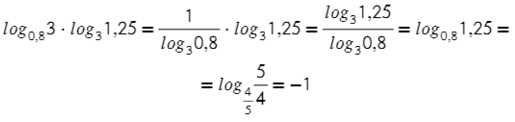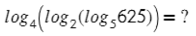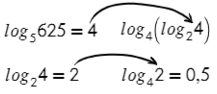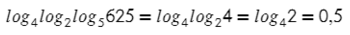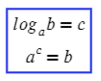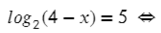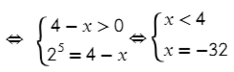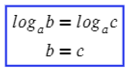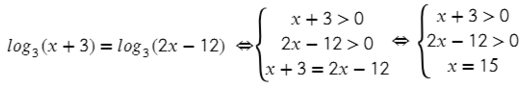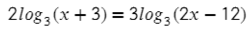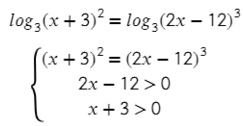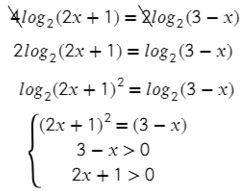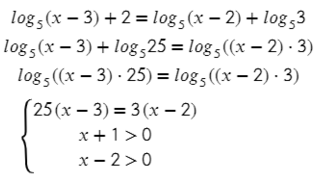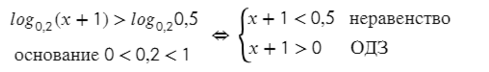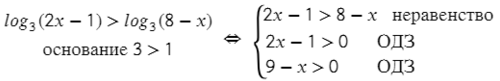Формула логарифма егэ

18
Фев 2013

Категория: Справочные материалы

Логарифм. Определение. Свойства логарифмов

2013-02-18
2021-06-18

Факт 1.
(bullet) Логарифм по основанию (a) от (b) – это число (t), которое показывает, в какую степень нужно возвести (a), чтобы получить (b).
Ограничения: числа (a) и (b) такие, что (a>0, ane 1, b>0).
[Large{{color{blue}{log_a{b}=tquadLeftrightarrowquad
a^t=b }}}]
Т.к. мы имеем право возводить в любую степень, то (tin
mathbb{R}).
Таким образом, верно основное логарифмическое тождество [{Large{a^{log_ab}=b}}]
(bullet) Справедливы следующие формулы: [{large{begin{array}{|ll|l|}
hline qquad qquad qquad qquad {small{text{Формулы}}}
&& qquad qquad{small{text{Ограничения}}}\
&&\
hline textbf{(1)} log_a1=0&&a>0, ane 1\
&&\
textbf{(2)} log_aa=1 &&a>0, ane 1\
&&\
textbf{(3)} log_{a}{b^m}=mlog_a|b|&(m —
{small{text{четн.}}})&a>0, ane 1, bne 0\
&&\
textbf{(4)}log_{a}{b^m}=mlog_ab& (m —
{small{text{нечетн.}}})&a>0, ane 1, b>0\
&&\
textbf{(5)} log_{a^n}{b}=frac 1nlog_{|a|}b&(n —
{small{text{четн.}}})&ane 0, ane 1, b>0\
&&\
textbf{(6)}log_{a^n}b=frac1nlog_ab&(n —
{small{text{нечетн.}}})&a>0, ane 1, b>0\
&&\
textbf{(7)} log_a{bc}=log_a|b|+log_a|c|&&a>0, ane 1, bcne 0\
&&\
textbf{(8)}
log_a{dfrac bc}=log_a|b|-log_a|c|&&a>0, ane 1,bcne 0 \
&&\
textbf{(9)}
a^{log_ab}=b &&a>0, ane 1, b>0\
&&\
textbf{(10)}c^{log_ab}=b^{log_ac}&&a>0, ane 1, b>0, c>0\
&&\
textbf{(11)} log_abcdot log_bc=log_ac && a>0, ane 1,b>0, bne 1, c>0\
&&\
textbf{(11′}) log_bc=dfrac{log_ac}{log_ab}&&a>0, ane 1,b>0, bne 1, c>0\
&&\
&&\
{small{text{ЧАСТНЫЕ СЛУЧАИ:}}}&& \
textbf{(12)} log_abcdot log_ba=1 && a>0, ane 1, b>0, bne 1\
&&\
textbf{(12′}) log_ab=dfrac1{log_ba}&&a>0, ane 1, b>0, bne 1\
&&\ hline
end{array}}}]

Заметим, что при выполнении ограничений данные формулы верны в обе стороны!

Что такое логарифм

Свойства логарифма

Логарифмические уравнения

Логарифмические неравенства

---

Сейчас речь пойдет о трех страшных буквах: l o g.
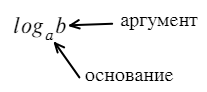
Существовать в нашем бытии они просто так не могут. Обязательно должен быть какой-нибудь индекс — число снизу (основание логарифма) и число после букв (аргумент логарифма). 

Прежде, чем мы перейдем к тому, что такое логарифм, решим парочку подводящих примеров. 

Чтобы справиться с этим примером, мы проговариваем в голове: какое число нужно дважды (т.к. корень квадратный) умножить само на себя, чтобы получить 81. 

А этот пример можно решить по алгоритму (решения показательных уравнений), а можно так же провести разговор с самим собой (главное не вслух, я считаю это нормально, но кого-то вы можете напугать разговором с самим собой): сколько раз нужно число 3 умножить само на себя, чтобы получить 27. Постепенным перемножением мы дойдем до ответа.

Тогда, если дело касается логарифма:

можно сказать так: в какую степень нужно возвести 3 (число снизу — основание логарифма), чтобы получить 27 (число слева — аргумент логарифма). Не напоминает выше стоящий пример?

На самом деле в этом и заключается основная формула (определение логарифма):

Логарифм говорит нам (кому-то кричит): логарифм числа «b» по основанию «a» равняется числу «c». Тогда без логарифма это можно сформулировать так: чтобы получить число «b», требуется число «a» возвести в степень «c». Логарифм — это действие, обратное возведению в степень.

У отца log есть два родных сына: ln и lg. Так же, как сыновья отличаются возрастом (мы говорим о максимальной точности), так и эти логарифмы отличаются основанием (числовым индексом снизу).

Данные логарифмы придумали для упрощения записи. На самом деле в прикладной математики именно логарифмы по такому основанию встречаются чаще всех остальных. А мы все в глубине души народ ленивый, так что почему бы себе жизнь не упростить?

Что нужно запомнить: ln — это обычный логарифм только по основанию e ( e — это число Эйлера, e = 2,7182…, мой номер телефона, кстати, — это последние 11 цифр числа Эйлера, так что буду ждать звонка).

А lg — это обычный логарифм по основанию 10 (10ая система — это система счисления, в которой мы живем, столько пальцев на руках у среднего человека. В общем 10 — это как 9, только на 1 больше).

Как мы не можем существовать без еды, воды, интернета…  Так и логарифм не представляет свое существование без ОДЗ.

Всегда, когда существует логарифм, должно быть:

«Почему это так?» — это первый вопрос, который я предоставляю тебе. Советую начать с того, что логарифм — это обратное действие от возведения в степень.

А теперь  разберем теорию на практике:

В какую степень нужно возвести два (число в основании), чтобы получить шестнадцать (аргумент логарифма). 

Два нужно четыре раза умножить само на себя, чтобы получить 16.

Ответ: 4.

lg — это логарифм по основанию 10. 10 нужно 3 раза умножить само на себя, чтобы получить 1000.

А теперь посложнее, перейдем по определнию к показательному уравнению :

Следующий пример поможет нам узнать первую формулу логарифмов: 

Преобразуем выражение по определению логарифма и получим показательное уравнение. Единица — это же любое значение в нулевой степени?

Тогда можно сделать вывод, что при любом основании и аргументе логарифма, равном 1, все эти логарифмы будут равны нулю.

Нетрудно тогда понять, что есть еще одно следствие:

В какую степень нужно возвести 2, чтобы получить 2? Напряжем все свои извилины и получим — один!

Дальше будут формулы, которые я позволю себе не выводить, чтобы не испугать неискушенных в математике читателей.

Хотя мой вам совет: отследить, откуда эта формула появилась. У логарифмов самое главное помнить, что логарифм — это действие, обратное возведению в степень.

Основное логарифмическое тождество:

В какую степень нужно возвести 3, чтобы получить 9? Значит, логарифм в показателе степени равен двум.

Это единственная формула, где логарифм в показатели степени. Видишь логарифм в степени? Тебе поможет только эта формула.

Еще примерчик, двойка перед логарифмом никак не влияет, формула все так же работает: 

А вот квадрат в логарифме тоже быть может, только лучше сначала разложить:

Дальше с этим ничего сделать не сможем.

Дальнейшие формулы тоже уникальны, это тебе не косинус двойного угла.

Видим сложение логарифмов, выпускаем эту формулы:

А вот примерчик, чтобы порадовать тебя этой формулой, только наоборот:

Видим разность логарифмов, выпускаем эту формулы:

А теперь сразу сумма и разность. По отдельности логарифмы не найти, но вместе они и мы сила:

Теперь посмотрим на степени у аргмента логарифма:

Пример:

А в основании тоже можно? Нужно!

Минус два — это степень у основания:

А все вместе можно? Конечно, логарифмы — это такая свобода: 

А здесь нужно будет соединить две формулы: 1) вынесение степени из основания и 2) разность логарифмов

С основными формулами разобрались, теперь для решения более сложных уравнений/выражений.

Формула перехода к новому основанию: 

Обрати внимание, чем она отличается от разности логарифмов (4). Тут мы делим один логарифм на другой, а там деление происходит под логарифмом.

Тут все просто, разве что стоит вспомнить, что квадратный корень — это степень одна вторая.

Тут первым действием воспользуемся изучаемой формулой, а дальше каждый логарифм в виде числа, потихонечку−полегонечку.

Последняя формула, меняем местами аргумент и основание логарифма:

Используется тоже нечасто, но если ее не знаешь, то никак не выкрутишься через другие формулы.

Простенький примерчик:

Закрепим обе формулы. Используем формулу (9), после (8), а так же не забудь порадовать десятичные дроби — переведи их в обыкновенные, а они порадуют тебя. Теперь посмотрим еще на пару примеров:  

Логарифм в логарифме, что может быть прекраснее? Только решенный логарифм в логарифме.

Начинаем с внутреннего:

И постепенно раскрываем каждый последующий:

После того, как с формулами разобрались, (а их всего 9! Согласись, несложно выучить?), перейдем к уравнениям.

Все логарифмические уравнения решаем по одному из двух алгоритмов.

Первый появляется из определения логарифма:

Только не забываем про ОДЗ:

Второй вариант, когда логарифм с одним основанием равен логарифму с точно таким же основнанием: 

Не забываем про ОДЗ, тогда получится: 

Подставив в ОДЗ x = 15, видим, что все выполняется!

Обязательно только логарифм (без всяких множителей и т.п.) с одним основанием должен быть равен другому логарифму с таким же основанием:

Здесь перед логарифмами стоят разные множители, поэтому прежде всего нужно их внести в логарифм (6 формула), а после убрать логарифмы:

Если стоят одинаковые множители, их можно сократить сразу или сократить на общий множитель:

Бывает, что с одной стороны уравнения есть сумма логарифмов (4) или обычное число, сокращать их сразу нельзя! Только после того, как приведем и левую, и правую часть к одному логарифму:

Что же касается неравенств, убирать логарифмы можно так же, как и в уравнениях, только здесь нужно внимательно смотреть на значение оснований. Если основание логарифма лежит в диапазоне 0 < a < 1 (также как в показательных неравенствах), то после зачеркивания логарифмов знак меняется на противоположный:

Если же основание а > 1, то убираем логарифмы без смены знака и дорешиваем обычное неравенство:

Вывод:

1. Л О Г — это не три страшные буквы, а обратное действие возведению в степень. 
2.  Хоть формул и целых девять, но они никак не пересекаются. Решая пример и ориентируясь в формулах, ты будешь однозначно выбирать необходимую формулу. 
3. Видишь логарифм — ищи ОДЗ и решай его в первую очередь!
4. Решение уравнений происходит по одному из двух вариантов и больше никак.
5. В неравенствах главное — помнить об основании логарифма, когда зачеркиваем логарифмы.

Будь в курсе новых статеек, видео и легкого математического юмора.