Формула пика егэ математика

Грибановский муниципальный район

Воронежской области

Муниципальные педагогические чтения «Киселёвские чтения – 11»

«Формула Пика для нахождения площади многоугольника»

                                                       Подготовила: Табакова Ольга Николаевна

 учитель МКОУ Верхнекарачанской СОШ

2021 г.

«Геометрия есть знание величин,

фигур и их границ,

а также отношений между ними

и производимых над ними операций,

разнообразных положений и движений»

Диа́дох Прокл

В 21 веке, некоторым детям, порой сложно запомнить огромное количество информации, поступающей каждый день в школе, и даже вызубренные формулы по математике, которые используются для нахождения площади различных фигур, будь то треугольник, параллелограмм или трапеция, часто забываются.

Задание, нахождение площади многоугольника, нарисованного на клетчатой бумаге очень интересное, увлекательное. Казалось бы, что увлекательного можно найти на клетчатой плоскости, то есть, на бесконечном листке бумаги, расчерченном на одинаковые квадратики? Оказывается, задачи, связанные с бумагой в клеточку, достаточно разнообразны.  Мы знаем разные способы выполнения таких заданий: способ достраивания, способ разбиения и др. Одним из таких способов является формула Пика для нахождения площади многоугольника.

Актуальность данной темы заключается в том, чтобы помочь выпускникам 9-ых и 11-х классов подготовиться к сдаче ОГЭ и ЕГЭ по математике.

Немного истории:

 Георг Александр Пик

(10. 09. 1859 – 13. 07. 1942)

Георг Александр Пик – австрийский математик. Родился Георг Пик в еврейской семье Он был одарённым ребёнком, его обучал отец, возглавлявший частный институт. До одиннадцати лет Георг получал образование дома (с ним занимался отец), а затем поступил сразу в четвёртый класс гимназии. В шестнадцать лет Пик сдал выпускные экзамены и поступил в университет в Вене. Уже в следующем году Пик опубликовал свою первую работу по математике. После окончания университета в 1879 году он получил право преподавать математику и физику. В 1880 году Пик защитил докторскую диссертацию, а в 1881 году получил место ассистента на кафедре физики Пражского университета. В 1888 году он был назначен экстраординарным профессором математики, затем в 1892 году в Немецком университете в Праге был назначен ординарным профессором (полным профессором).

Круг математических интересов Пика был чрезвычайно широк. В частности, им написаны работы в области функционального анализа и дифференциальной геометрии, эллиптических и абелевых функций, теории дифференциальных уравнений и комплексного анализа, всего более 50 тем. С его именем связаны матрица Пика, интерполяция Пика — Неванлинны, лемма Шварца — Пика.

Широкую известность получила открытая им в 1899 году теорема Пика для расчёта площади многоугольника. Эта теорема оставалась незамеченной в течение некоторого времени, однако в 1949 году польский математик Гуго Штейнгауз включил теорему в свой знаменитый «Математический калейдоскоп». С этого времени теорема Пика стала широко известна.

Теорема привлекла довольно большое внимание и начала вызывать восхищение своей простотой и элегантностью.

В Германии эта теорема включена в школьные учебники.

Когда нацисты вошли в Австрию 12 марта 1938 года, он вернулся Прагу. В марте 1939 года нацисты вторглись в Чехословакию. 13 июля 1942 года Пик был депортирован в созданный нацистами в северной Чехии лагерь Терезиенштадт, где умер две недели спустя в возрасте 82 лет.

Формула Пика.

, где

S- площадь многоугольника

В-количество узлов сетки, лежащих внутри многоугольника;

Г-количество узлов сетки, лежащих на границе многоугольника.

Основное условие для применения формулы Пика: у многоугольника, изображённого на клетчатой бумаге (решётке), должны быть только целочисленные вершины, то есть они обязательно должны находиться в узлах решётки. ( узел –это пересечение клеток ).

 В -7 узлов

Г- 8 узлов

     

Формула Пика универсальна, по ней можно вычислить площадь любого многоулольника на клетчатой бумаге.

В-15 узлов

Г-4 узла

Свавним различные способы вычисления площади многоугольника на клетчатой бумаге:

Задача 1. Найти площадь четырехугольника

	Метод достраивания
	Формула Пика В- 32 Г- 4

Задача 2.

	Метод разбиения на треугольники
	Формула Пика В- 28 Г-18

Сравнивая, полученные результаты, видно, что ответ получается одинаковый. Найти площадь фигуры по формуле Пика, оказалось быстрее и легче, ведь вычислений было меньше. 

Таким образом, видно, что формула Пика имеет ряд преимуществ перед другими способами вычисления площадей многоугольников на клетчатой бумаге:

• для вычисления площади многоугольника, нужно знать всего одну формулу:

• формула Пика проста для запоминания;
• формула Пика  очень удобна  и проста в применении;
• многоугольник, площадь которого необходимо вычислить может быть любой, даже самой причудливой.

Вывод: вычисление площадей сложных фигур с помощью формулы Пика легче, чем вычисление методом достраивания и разбивания фигур на части, так как требуется меньше вычислений, а, следовательно, меньше времени.

Формула Пика — это настоящее спасение для тех учеников, которые так и не смогли выучить все формулы для вычисления площадей фигур, для тех, кто так и не уяснил до конца, как выполнить разбиение фигуры или дополнительное построение, чтобы подобраться к вычислению её площади «через знакомых».

С другой стороны, для тех, кто площадь многоугольника, изображённого на клетчатой бумаге, умеет находить с помощью вышеперечисленных приёмов, формула Пика послужит дополнительным инструментом, с помощью которого можно будет решить задачу ещё и этим способом (и тем самым проверить правильность своего предыдущего решения, сверив полученные ответы).

Чтобы уверенно решать задачи по геометрии — даже такие простые — необходимо выучить основные понятия и формулы.

Это формулы площадей фигур — треугольника (5 формул), параллелограмма, ромба, прямоугольника, произвольного четырехугольника, а также круга. Формулы для длины окружности, длины дуги и площади сектора. Для средней линии треугольника и средней линии трапеции.

Надо знать, что такое центральный и вписанный угол. Знать основные тригонометрические соотношения. В общем, учите основы планиметрии.

Больше полезных формул — в нашем ЕГЭ-Справочнике.

Смотри также материал: Как быстро выучить формулы

В этой статье — основные типы заданий №1 Базового ЕГЭ по математике. Задачи взяты из Банка заданий ФИПИ.

Вычисление длин отрезков, величин углов и площадей фигур по формулам 

1. На клетчатой бумаге с размером клетки  изображена трапеция. Найдите длину средней линии этой трапеции.

Средняя линия трапеции равна полусумме её оснований: 

Ответ: 3.

2. Найдите величину угла ABC. Ответ дайте в градусах.

Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу. Соединим точки А и С с центром окружности и проведем диаметры через точки А и С. Видим, что величина центрального угла АОС равна Тогда

Ответ: 45.

3. Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на

Решение:

Проведем из точки В перпендикуляр к прямой ОА. Из прямоугольного треугольника ОВС по теореме Пифагора:

Осталось умножить найденное значение синуса на

Ответ: 1.

4. Найдите площадь ромба, изображенного на клетчатой бумаге с размером клетки  Ответ дайте в квадратных сантиметрах.

Самый простой способ — воспользоваться формулой площади ромба, выраженной через его диагонали:

 , где и — диагонали.

Получим: 

Ответ: 12.

5. Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки  Ответ дайте в квадратных сантиметрах.

Площадь трапеции равна произведению полусуммы оснований на высоту:

Основания нашей трапеции равны 4 и 8, а высота равна боковой стороне (поскольку трапеция прямоугольная), то есть 3 см. Площадь трапеции

Ответ: 18.

Нахождение площадей многоугольников сложной формы

А что делать, если надо найти не площадь трапеции или треугольника, а площадь какой-либо сложной фигуры? Есть универсальные способы! Покажем их на примерах из банка заданий ФИПИ и на авторских задачах.

6. Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.

Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным . Высоты этих треугольников равны и . Тогда площадь четырёхугольника равна сумме площадей двух треугольников: .

Ответ: .

7. В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.

Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной и трёх прямоугольных треугольников. Видите их на рисунке? Получаем: .

Ответ: .

Многие репетиторы рекомендуют в таких задачах пользоваться формулой Пика. В ней нет необходимости, однако эта формула довольно интересна.

Согласно формуле Пика, площадь многоугольника равна В+Г/2-1

где В — количество узлов внутри многоугольника, а Г — количество узлов на границе многоугольника.

Узлами здесь названы точки, в которых пересекаются линии нашей клетчатой бумаги.

Посмотрим, как решается задача 7 с помощью формулы Пика:

Синим на рисунке отмечены узлы внутри треугольника. Зеленым — узлы на границе.

Аккуратно посчитав те и другие, получим, что В = 9, Г = 5, и площадь фигуры равна S = 9 + 5/2 — 1 = 10,5.

Выбирайте — какой способ вам больше нравится.

8. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки  

Такой четырехугольник получится, если от квадрата размером отрезать 2 прямоугольника и 4 треугольника. Найдите их на рисунке.

Площадь каждого из больших треугольников равна

Площадь каждого из маленьких треугольников равна

Тогда площадь четырехугольника

9. Авторская задача.  Найдите площадь закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки 

Решение:

На рисунке изображен ромб с вырезанным из него квадратом.

Площадь ромба равна половине произведения его диагоналей.

Площадь вырезанного квадрата равна 4.

Площадь фигуры равна 36 — 4 = 32.

Ответ: 32.

Площадь круга, длина окружности, площадь части круга 

Длина дуги во столько раз меньше длины окружности, во сколько раз ее градусная мера меньше, чем полный круг, то есть 360 градусов.

Площадь сектора во столько раз меньше площади всего круга, во сколько раз его градусная мера меньше, чем полный круг, то есть 360 градусов.

10. Иногда в задании надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга.Найдите площадь сектора круга радиуса , длина дуги которого равна .

На этом рисунке мы видим часть круга. Площадь всего круга равна , так как . Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна (так как ), а длина дуги данного сектора равна , следовательно, длина дуги в раз меньше, чем длина всей окружности. Угол, на который опирается эта дуга, также в  раз меньше, чем полный круг (то есть градусов). Значит, и площадь сектора будет в  раз меньше, чем площадь всего круга.

Ответ: .

11. На клетчатой бумаге нарисован круг площадью 2,8. Найдите площадь закрашенного сектора.

На рисунке изображен сектор, то есть часть круга. Но какая же это часть? Это четверть круга и еще круга, то есть круга.

Значит, нам надо умножить площадь круга на . Получим:

Ответ: 1,05.

12. На клетчатой бумаге изображены два круга. Площадь внутреннего круга равна 9. Найдите площадь закрашенной фигуры.

Площадь фигуры равна разности площадей двух кругов, один из которых расположен внутри другого. По условию, площадь внутреннего круга равна 9. Радиус внешнего круга относится к радиусу внутреннего как 4 к 3. Площадь круга равна , то есть пропорциональна квадрату радиуса. Значит, площадь внешнего круга в раза больше площади внутреннего и равна 16. Тогда площадь фигуры равна 16 — 9 = 7.

Ответ: 7.

Задачи на координатной плоскости 

13. Найдите площадь четырехугольника, вершины которого имеют координаты (4;2), (8;4), (6;8), (2;6).

Заметим, что этот четырехугольник — квадрат. Сторона квадрата a является гипотенузой прямоугольного треугольника с катетами, равными 2 и 4. Тогда

Ответ: 20

14. Найдите площадь четырехугольника, вершины которого имеют координаты

На рисунке изображен параллелограмм (четырехугольник, имеющий две пары параллельных сторон). Площадь параллелограмма равна произведению основания на высоту. Основание равно 2, высота 8, площадь равна 16.

Ответ: 16.

Почему бы просто не считать клеточки?

Возможно, вы читаете всё это и думаете: зачем все эти сложности? Формулы запоминать. Дорисовывать. Тут ведь сразу видно, сколько клеточек в фигуре.

Вот, например, трапеция:

Посчитаем клеточки: их всего 46, верно?

Но стоп, там же некоторые из них только наполовину внутри фигуры. Отметим их – всего таких 10. Итого, 36 полных (красные точки) и 10 половинчатых, вместе ( 36+frac{10}{2} = 41)

Вроде бы всё верно. Но, если присмотреться, можно заметить ещё маленькие треугольнички, которые попали внутрь. А также, что «синие» клеточки слева на самом деле разрезаны не ровно пополам – какие-то чуть больше, какие-то меньше…

Как всё это учитывать?

Попробуем рассуждать так: заметно, что тот маленький розовый треугольник дополняет серый кусок клетки.

А жёлтые сколько занимают? Постарайтесь ответить сами.

Если всё сделать правильно, то увидите, что жёлтые кусочки можно сложить вместе в одну целую клетку.

Итак, 2 жёлтых куска = 1 клетка.

Розовый треугольник + серый кусок = 1 клетка. Всего у нас две таких пары (розовый+серый) – это 2 полных клетки. 

Всё остальное как было: 36 полных клеток и 6 половинок у правой стороны – это ( 36+frac{6}{2}=39) клетки.

Итого клеток: ( 1 + 2 + 39 = 42).

Проверим результат по формуле площади трапеции: нижнее основание 11, верхнее основание 3, высота 6. Полусумма оснований равна 7, умножаем на высоту – получилось 42. Всё совпало.

Но! Настолько ли проще был наш способ подсчёта клеточек? Не сказал бы. А если там будет несколько косых линий, то вообще можно замучиться собирать этот паззл (искать, какие кусочки друг друга дополняют).

Вычислите площадь простых фигур тремя способами

Стороны клеток равны 1. Вычислите самостоятельно площадь фигуры всеми тремя способами. Сравните результаты.

Вычислите площадь произвольных фигур по формуле Пика

Вычислите самостоятельно площади фигур с помощью формулы Пика:

Посчитайте площадь корабля и котика по формуле Пика

Посчитайте самостоятельно для тренировки и чтобы запомнить формулу Пика!

Фигуры с отверстиями – посчитайте площади двумя способами

Ну и напоследок фигуры с “дырками”. Как думаешь, здесь придётся вычислять сначала площадь целой фигуры, а потом площадь дырки?

Или достаточно просто посчитать точки внутри закрашенной области и на её границах (в том числе, на границе с дыркой)?

Проверим на простом примере: это квадрат ( 4times 4), и в нём вырезан прямоугольник ( 1times 2), значит, его площадь ( 16-2=14).

А теперь по точкам. На границах (включая внутренние) ( Г = 22). Внутри ( В = 3). Тогда площадь по формуле Пика

Сосчитай сам и проверь.

Что получилось?

У меня снова на 1 меньше.

Так может быть просто формулу немного «подкрутить»? Нет!

Очень и очень не рекомендую вам запоминать несколько похожих формул для похожих случаев, потому что придёт время, и вы обязательно перепутаете формулу.

Даже если вы уверены, что не перепутаете, оно всё равно того не стоит. В общем, наилучший вариант – это запомнить одну формулу. А если попалась фигура с дыркой, вычислить всю фигуру, а потом дырку. И вычесть.

Площадь поверхности пирамиды

Для пирамиды тоже действует общее правило:

Площадь полной поверхности пирамиды – это сумма площадей всех граней.( displaystyle {{S}_{полн. пов. }}={{S}_{боков.пов. }}+{{S}_{основания }})

Теперь давай посчитаем площадь поверхности самых популярных пирамид.

Площадь поверхности правильной треугольной пирамиды

Пусть сторона основания равна ( displaystyle a), а боковое ребро равно ( displaystyle b). Нужно найти ( displaystyle {{S}_{осн}}) и ( displaystyle {{S}_{ASB}}).

И тогда

( displaystyle {{S}_{осн}}) – это площадь правильного треугольника ( displaystyle ABC).

И еще вспомним, как искать эту площадь.

Используем формулу площади:

( displaystyle S=frac{1}{2}abcdot sin gamma ).

У нас «( displaystyle a)» – это ( displaystyle a), а «( displaystyle b)» – это тоже ( displaystyle a), а ( displaystyle sin gamma =sin 60{}^circ =frac{sqrt{3}}{2}).

Значит, ( displaystyle {{S}_{ABC}}=frac{1}{2}{{a}^{2}}frac{sqrt{3}}{2}=frac{{{a}^{2}}sqrt{3}}{4}).

Теперь найдем ( displaystyle {{S}_{Delta ASB}}).

Пользуясь основной формулой площади и теоремой Пифагора, находим

( displaystyle S={{a}^{2}}sqrt{3}).

Авторы: Куровская Юлия, Шагаева
Диана.

Руководители:

• Могутова Татьяна Михайловна
• Дерюшкина Оксана Валерьевна

Девиз проекта:

“Если вы хотите научиться плавать, то
смело входите в воду.
а если хотите научиться решать задачи, то решайте
их”.
Д. Пойя.

Выбор темы проекта не случаен. Способы
нахождения площади многоугольника
нарисованного на “клеточках” очень интересная
тема.

Мы знаем разные способы выполнения таких
заданий: способ сложения, способ вычитания и др.

Нас очень заинтересовала эта тема, мы изучили
много литературы и к нашей огромной радости
нашли еще один способ, способ не известный по
школьной программе, но способ замечательный!
Вычисление площади, используя формулу,
выведенную австрийским ученым – математиком
Георгом Пиком.

Мы решили изучить формулу Пика, при помощи
которой выполнять задания на нахождении площади
очень легко!

Решили поделиться нашим открытием с
одноклассниками, учащимися других школ, создать
электронную презентацию.

Цель исследования

1. Изучение формулы Пика.

2. Расширение знаний о многообразии задач на
клетчатой бумаге, о приёмах и методах решения
этих задач.

Задачи:

1. Отобрать материал для исследования, выбрать
главную, интересную, понятную информацию

2. Проанализировать и систематизировать
полученную информацию

3. Создать электронную презентацию работы для
представления собранного материала
одноклассникам

4. Сделать выводы по результатам работы.

5. Подобрать наиболее интересные, наглядные
примеры.

Методы исследования:

1. Моделирование

2. Построение

3. Анализ и классификация информации

4. Сравнение, обобщение

5. Изучение литературных и Интернет-ресурсов

Георг Пик – австрийский ученый – математик.
Пик поступил в университет в Вене в 1875 году. Свою
первую работу опубликовал в возрасте 17 лет. Круг
его математических интересов был чрезвычайно
широк. 67 его работ посвящены многим разделам
математики, таким как: линейная алгебра,
интегральное исчисление, геометрия,
функциональный анализ, теория потенциала.

Широко известная Теорема появилась в сборнике
работ Пика в 1899 году.

Теорема привлекла довольно большое внимание и
начала вызывать восхищение своей простотой и
элегантностью.

Формула Пика, формула вычисления площади
многоугольника, изображенного на бумаге в
клетку, полезна при решении заданий ЕГЭ и ОГЭ.
Именно, поэтому, она нас очень заинтересовала.

Формула Пика  — классический результат
комбинаторной геометрии и геометрии чисел.

По теореме Пика площадь многоугольника равна:

Г : 2 + В – 1

где

Г – число узлов решетки на границе
многоугольника

В – число узлов решетки внутри многоугольника.

Первым делом мы поставили задачу: изучить,
что такое узлы решетки и как правильно вычислять
их количество. Оказалось, это очень просто.
Приведем несколько примеров.

Пусть дан произвольный треугольник. Узлы на
границе изображены оранжевым цветом, узлы внутри
изображены синим цветом. Найти узлы и подсчитать
их количество очень легко.

В данном случае Г= 15, В = 35

Пример №2 Узлов на границе 18, т.е. Г = 18,
узлов внутри 20, В = 20.

И еще один пример. Дан произвольный
многоугольник. Считаем узлы на границе. Их 14.
Узлом внутри многоугольника 43. Г = 14, В = 43.

С первой задачей мы справились!

Второй этап нашей работы: вычисление площадей
многоугольников.

Рассмотрим несколько примеров.

Пример №1.

Г = 14, В = 43, S = + 43 – 1 = 49

Пример №2.

Г = 11, В = 5, S = + 5 – 1 = 9,5

Пример №3.

Г = 15, В = 22, S = + 22 – 1 = 28,5

Пример №4.

Г = 8, В = 16, S = + 16 – 1 = 19

Пример №5

Г = 10, В = 30, S = + 30 – 1 = 34

На рассмотрение пяти примеров мы затратили
всего 1-2 минуты. Вычислять площадь по формуле
Пика не только быстро, но и очень легко!

Но перед нами встал очень серьезный вопрос:

Можно ли доверять теореме Пика?

Получаются ли одинаковые результаты при
вычислении площадей разными способами?

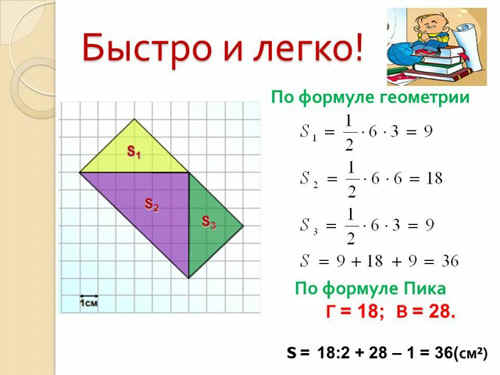
Найдем площади многоугольников по формуле Пика
и обычным способом, применяя формулы геометрии и
способы достроения или разбиения на части. Вот
какие результаты мы получили:

Пример №1.

Вычислим площадь многоугольника по формуле
Пика:

Подсчитаем количество узлов на границе и
внутри. Г = 3, В = 6.

Вычислим площадь: S = 6 + — 1 = 6,5

Достроим многоугольник до прямоугольника.
Площадь прямоугольника равна: 3 * 5 = 15, S? = = 3, S? = = 3 , S = = 2,5

S = 15-3-3-2,5 = 6,5

Результат одинаковый.

Пример №2.

Вычислим площадь по формуле Пика.

Г = 4, В = 9, S = 9 + — 1 = 10

Достроим до прямоугольника.

Площадь прямоугольника равна: 5 * 4 = 20, S₁ = 2 *
1 = 2, S₂ = = 3,

S = = 2 ,
S = = 1,5, S
= = 2,5

Площадь прямоугольника равна

S = 20 – 2 – 3 – 2 – 1,5 – 2,5 = 10

Мы снова получили одинаковые результаты.

Рассмотрим еще один пример.

Пример №3

Вычислим площадь по формуле Пика.

Г = 5, В = 6, S = 6 + — 1 = 7,5

Вычислим площадь, используя способ достроения.

Площадь прямоугольника равна 5·4 = 20

S₁ = 2 * 1 = 2, S₂ = = 1, S₃ = 2 * 1 = 2, S₄ = = 1, S₅
= = 1, S₆
= = 2,5

S₇ = = 3

S = 20 – 2 -1– 2 – 1 – 1 – 2,5 – 3 = 7,5

Результат одинаковый.

В презентации мы рассмотрели три примера, но на
самом деле мы рассмотрели очень много самых
разных примеров. Результат всегда был один и тот
же: Вычисление площади по формуле Пика и другими
способами дает одинаковый результат.

Вывод: формуле Пика можно доверять! Она дает
точный результат.

Мы довольны!

И еще один вопрос встал перед нами: какой способ
вычисления наиболее рациональный, наиболее
удобный для использования?

Чтобы ответить на этот вопрос, достаточно
использовать всю предыдущую работу. Но
рассмотрим еще три примера, которые окончательно
позволят получить ответ на наш вопрос.

Пример №2

Пример №3

При помощи формулы Пика легко вычислить
площадь многоугольника даже самой причудливой
формы. Рассмотрим пример:

Г=16, В=4

S=16:2+4-1=11

Вывод однозначный: наиболее рациональный
способ вычисления площади многоугольника,
изображенного на бумаге в клетку: формула Пика!

Предлагаем каждому из вас вычислить площадь
многоугольника, используя формулу Пика:

— вычислите количество узлов на границе. Они
изображены желтым цветом.

— вычислите количество узлов внутри, красный
цвет.

— Подставьте в формулу, назовите результат. Вы
за одну минуту вычислили площадь.

Итак, формула Пика имеет ряд преимуществ перед
другими способами вычисления площадей
многоугольников на клетчатой бумаге:

Для вычисления площади многоугольника, нужно
знать всего одну формулу:

S = Г:2 + В — 1.

Формула Пика очень проста для запоминания.

Формула Пика очень удобна и проста в
применении.

Многоугольник, площадь которого необходимо
вычислить, может быть любой, даже самой
причудливой формы.

Применяя формулу Пика легко выполнять задание
ЕГЭ и ОГЭ.

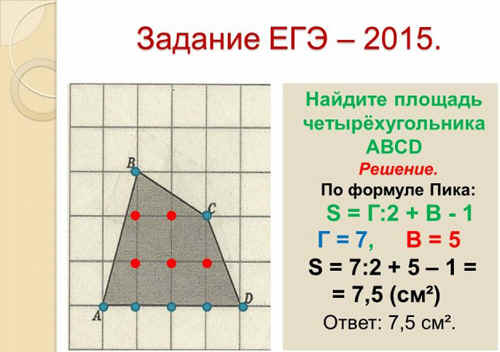
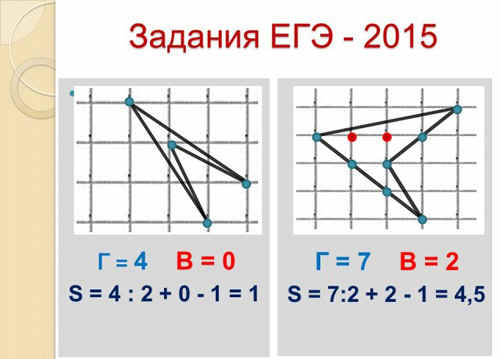
Приведем несколько примеров вычисления
площади из вариантов ЕГЭ – 2015.

Мы решили научить пользоваться формулой Пика
учащихся 9 – 11 классов нашей школы. Провели
фестиваль “Формула Пика”.

Все учащиеся с большим интересом познакомились
с презентацией, научились пользоваться формулой
Пика.

За 30 минут практической работы учащиеся
выполнили большое количество заданий. Каждый
учащийся получил памятку “Формула Пика”.

Мы помогли им в подготовке к ЕГЭ и ОГЭ!

Спустя месяц работы, мы провели опрос учащихся
9–11 классом.

Задали следующие вопросы:

Вопрос №1:

Формула Пика – это рациональный способ
вычисления площади многоугольника?

“Да” — 100% учащихся.

Вопрос №2:

Вы пользуетесь формулой Пика?

“Да” – 100% учащихся

Наша работа не прошла даром! Мы довольны!

Презентацию нашего проекта мы разместили в
сети Интернет. Много просмотров и скачиваний
нашей работы.

Мы оформили альбом “Формула Пика”. Им
постоянно, особенно первое время, пользовались
учащиеся нашей школы.

Результаты работы над проектом:

В процессе работы над проектом изучили
справочную, научно-популярную литературу по теме
исследования.

• Изучили теорему Пика, научились находить
  площади фигур, изображенных на бумаге в клетку
  просто и рационально.
• Расширили свои знания о решении задач на
  клетчатой бумаге, определили для себя
  классификацию исследуемых задач, убедились в их
  многообразии.
• Провели для учащихся 9–11 фестиваль “Формула
  Пика”, научили их находить площадь, использую
  эту формулу. Подобрали много интересных
  примеров.
• Создали электронную презентацию в помощь своим
  ровесникам.
• Оформили альбом “Формула Пика”, который
  постоянно используют учащиеся школы.

Предлагает вам выполнить два задания, чтобы вы
убедились в рациональности нашей работы.

Спасибо за внимания!

Формула Пика

• Авторы
• Руководители
• Файлы работы
• Наградные документы

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

АННОТАЦИЯ

Название проекта: «Формула Пика»

Автор и исполнитель проекта: Горбунов Фёдор Александрович

Научный руководитель: Смирнова Анна Геннадьевна

Цель проекта: создать интерактивный плакат, демонстрирующий применение теоремы Пика.

Задачи проекта:

Изучить биографию Г. Пика, доказательство теоремы Пика.

Изучить и научиться применять формулы нахождения площадей основных геометрических фигур.

Сравнить уровень сложности решения задач на нахождение площадей фигур на квадратной решётке с помощью традиционных формул и теоремы Пика.

Найти и решить задачи из ОГЭ и ЕГЭ с помощью формулы Пика.

Найти и решить задачи на нахождения площадей фигур из других источников более сложного содержания.

Создать плакат.

Показать применение формулы Пика 9 классам и другим ученикам школы.

Краткое описание проекта:

Подготовительный этап:

Повторил тему: «Площадь прямоугольника, квадрата, прямоугольного треугольника». Изучил биографию Георга Пика. Изучил формулу Пика, её доказательство и применение. Изучил формулы площадей основных геометрических фигур. Решил задачи на нахождение фигур на квадратной решётке.

Поисковый (аналитический) этап:

С помощью сайтов «РЕШУ ОГЭ» и «СДАМ ГИА» создал банк задач на нахождение площадей фигур на квадратной решётке. Решил эти задачи с помощью теоремы Пика. Сравнил решение, предложенное на сайте, со своим. Сделал выводы. Решил более сложные задачи. Создал электронную версию плаката по применению теоремы Пика. Напечатал плакат. Выступил перед учащимися 9, 11 классов.

Выводы: Формула Пика позволяет решать задачи на нахождение площадей фигур на квадратной решётке и затрачивать на их решение гораздо меньше времени, чем с помощью других формул и приёмов. Формулу Пика можно использовать для проверки ответа, полученного другим способом. Формула может помочь на ОГЭ ребятам, забывшим формы площадей геометрических фигур.

ВВЕДЕНИЕ

К 6 классу мы научились находить площади прямоугольника и квадрата, в одном из учебников 5 класса мне встретилась формула для нахождения площади прямоугольного треугольника. Этого мне показалось мало, ведь я давно интересуюсь геометрией и знаю множество геометрических фигур. В учебнике геометрии я нашёл формулы для вычисления различных многоугольников. Некоторые из них я смог применить на практике. Не все формулы мне понятны, не говоря уже об их доказательствах. Но желание найти площадь геометрических фигур, решить задачи, используя знания, которыми я обладаю, подтолкнули меня к отысканию другого, возможно универсального способа. От учителя математики я узнал о формуле Пика. Меня заинтересовал этот способ нахождения площадей.

Я решил узнать больше о теореме Пика, её авторе и научиться решать задачи.

Оказалось, что эта тема весьма актуальна, ведь многие задачи, входящие в ОГЭ и ЕГЭ по математике можно решить, используя формулу Пика, и это решение зачастую будет более простым, чем с применением формул. Мне этот факт особенно понравился. Я решил поделиться этим «лайфхаком» с ребятами, которые готовятся к экзамену. Возможно, кому-то из них пригодится это знание. Итак, я поставил перед собой цель: «создать интерактивный плакат, демонстрирующий применение теоремы Пика». Для достижения поставленной цели мне необходимо решить ряд задач:

Изучить биографию Г. Пика, теорему Пика и её доказательство.

Изучить формулы площадей основных многоугольников, свойства площадей.

Сравнить уровень сложности решения задач на нахождение площадей фигур на квадратной решётке с помощью традиционных формул и теоремы Пика.

Решить задачи из ОГЭ и ЕГЭ с помощью теоремы Пика.

Создать интерактивный плакат.

Показать применение формулы Пика 9, 11 классам и не только.

Итогом моей работы является интерактивный плакат.

ОСНОВНАЯ ЧАСТЬ

ТЕОРЕТИЧЕСКИЙ АНАЛИЗ

Георг Александр Пик (1859–1942)

Родился Георг Пик в еврейской семье. Мать его — Йозефа Шляйзингер (Josefa Schleisinger), отец — Адольф Йозеф Пик (Adolf Josef Pick) — возглавлял частный институт. До одиннадцати лет Георг получал образование дома (с ним занимался отец), затем он пошел в четвертый класс гимназии (Leopoldstaedter Communal Gymnasium). В 1875 г. он сдал выпускные экзамены и мог поступать в университет.

Пик поступил в университет в Вене в 1875 году. Уже в следующем году он опубликовал свою первую работу по математике, ему было всего лишь семнадцать лет. Он изучал математику и физику, окончил в 1879 г. университет, получив возможность преподавать оба эти предмета. В 1877 году из Дрезденской Высшей технической школы (Technische Hochschule) переехал Лео Кёнигсбергерг, который занял кафедру в венском университете. Он стал руководителем Пика, и 16 апреля 1880 г. Пик защитил докторскую диссертацию “О классе абелевых интегралов” (Über Eine Klasse abelscher Integrale). Вторым экзаменатором на защите был Эмиль Вейра.

После получения докторской степени Пик был назначен помощником Эрнста Маха в пражском университете Карла-Фердинанда. Мах переехал из Гарца, где он был профессором математики, в Прагу в 1867 году, чтобы занять там кафедру физики. Он, как и Пик, учился в университете в Вене и, к тому времени как Пик стал его помощником, считался одним из ведущих европейских ученых. Пик теперь хотел читать лекции в Праге, и для того чтобы получить на это право, он должен был написать специальную работу (habilitation thesis). Он это сделал достаточно быстро, написав Über die Integration hyperelliptischer Differentiale durch Logarithmen, после чего в 1881 году получил право читать лекции в Праге.

За исключением академического 1884-85 года, который Пик провел в Лейпцигском университете, учась у Кляйна, он оставался в Праге до конца своей карьеры. В 1888 г. он был назначен экстраординарным профессором математики, затем — ординарным профессором (полным профессором) в 1892 году в немецком университете в Праге. Круг его математических интересов был чрезвычайно широк, и 67 его работ посвящены многим темам, таким как линейная алгебра, теория инвариантов, интегральное исчисление, теория потенциала, функциональный анализ и геометрия. Тем не менее, более половины его работ связаны с функциями комплексного переменного, дифференциальными уравнениями и дифференциальной геометрией. Такие термины как матрица Пика, интерполяция Пика — Неванлинны, и лемма Шварца — Пика используются иногда и сегодня. Он больше всего известен, однако, своей теоремой Пика, которая появилась в его восьмистраничной работе 1899 года Geometrisches zur Zahlenlehre, опубликованной в Праге в Sitzungber, Lotos, Naturwissen Zeitschrift.

В немецком университете в Праге Пик стал деканом философского факультета в 1900-01 гг. Он руководил докторскими диссертациями около 20 студентов, наиболее известен из которых Чарльз Левнер, работавший под руководством Пика и получивший докторскую степень за результаты по геометрической теории функций в 1917 г. Существует еще один аспект жизни Пика, который заслуживает внимания. В 1910 г. он был в комитете, созданном Немецким университетом Праги для рассмотрения вопроса о принятии Эйнштейна в университет. Пик был движущей силой этого назначения, и Эйнштейн был принят на кафедру математической физики в Немецком университете в Праге в 1911 г. Он занимал этот пост до 1913 г., и все эти годы он и Пик были близкими друзьями. Мало того что они имели общие научные интересы, но они также оба страстно увлекались музыкой. Пик, который играл в квартете, ввел Эйнштейна в научное и музыкальное общества Праги. На самом деле, в квартет Пика входили четыре профессора университета, в том числе Камилло Кернер, профессор машиностроения.

После того как Пик вышел в отставку в 1927 г., он получил звание почетного профессора и вернулся в Вену, город, в котором он родился. Тем не менее, в 1938 г. он вернулся в Прагу после аншлюса 12 марта, когда немецкие войска вошли в Австрию. В конце сентября 1938 г. правительство Праги попросили отдать Германии все районы Чехии и Моравии, население которых на 50 или более процентов составляли немцы. Лидеры Чехословакии ушли в отставку, но не согласились на это, однако те, кто пришел им на смену, отдали эти регионы Германии. Гитлеровская армия вторглась в Прагу 14 марта 1939 г., и Гитлер оставил здесь своего представителя для того, чтобы управлять страной. Пик был избран членом Чешской академии наук и искусств, но после того как нацисты пришли в Прагу, он был исключен из академии. Нацисты создали лагерь Терезиенштадт в Северной Богемии 24 ноября 1941 г. для размещения престарелых, привилегированных и знаменитых евреев. Из около 144 000 евреев, отправленных в Терезиенштадт, около четверти там умерло, и около 60% были направлены в Освенцим и другие лагеря смерти. Пика отправили в Терезиенштадт 13 июля 1942 г., и он умер там две недели спустя в возрасте 82 лет.

Теорема Пика:

Пусть L — число целочисленных точек внутри многоугольника, B- количество целочисленных точек на его границе, S — его площадь. Тогда справедлива формула Пика: S=L+B/2-1

Для многоугольника на рисунке L=23(желтые точки), B=7(синие точки), значит S=23+3,5-1=25,5 клеток

Доказательство:

Рассмотрим прямоугольник со сторонами, лежащими на линиях решетки. Пусть длины его сторон равны X и Y . Имеем в этом случае:

L=(X-1)(Y-1)

B=2X+2Y

S=XY-X-Y+1+X+Y-1=XY

Рассмотрим прямоугольный треугольник с катетами, II осям координат

Такой треугольник получается при разрезании прямоугольника по диагонали

Пусть на диагонали лежит С точек.

L=((X-1)(Y-1)-C+2)/2

B=X+Y+C-1

S=0,5XY-0,5X-0,5Y+0,5-0,5C+1+0,5X+0,5Y+0,5C-0,5-1

S=0,5XY-0,5X-0,5Y+0,5-0,5C+1+0,5X+0,5Y+0,5C-0,5-1

S=0,5XY

Произвольный треугольник можно получить, отрезав от прямоугольника прямоугольные треугольники и, возможно, прямоугольник.
Поскольку и для прямоугольника, и для треугольника формула Пика верна, мы получаем, что она будет справедлива и для произвольного треугольника.

Доказательство для многоугольника

Пусть многоугольник M и треугольник T имеют общую сторону. Предположим, что для M формула Пика справедлива, докажем, что она будет верна и для многоугольника, полученного из M добавлением T. Так как M и T имеют общую сторону, то все целочисленные точки, лежащие на этой стороне, кроме двух вершин, становятся внутренними точками нового многоугольника. Вершины же будут граничными точками. Обозначим число общих точек через c и получим

LMT=LM+LT+(c-2) — число внутренних целочисленных точек нового многоугольника,

BMT=BM+BT-2(c-2)-2 — число граничных точек нового многоугольника.

Из этих равенств получаем

LM+LP=LMT-(c-2),BM+BP=BMT+2(c-2)+2 .

Так как мы предположили, что теорема верна для M и для T по отдельности, то

SMT=SM+ST=(LM+BM/2-1)+(LT+BT/2-1)=

=(LM+LT)+(BM+BT)/2-2=

= LMT-(c-2)+(BMT+2(c-2)+2)/2-2=

=LMT+BMT/2-1 .

Тем самым, формула Пика доказана.

формулы площадей основных фигур.
h a
a b
a b
a h b
h a

Сравнение способов дополнения фигуры до прямоугольника и формулы Пика

дополнение фигуры	формула Пика
S1 11 S1 11 S1 11 S 11 S1 11 S1=2×3:2×4=3×4=12(см2) S2=4×6=24(см2) S=24-12=12(см2) S=12cм2	S=11+4:2-1=12(см2)
S 11 S3 11 S1 11 S1 11 S2 11 S1=2x3x2:2=6×2:2=12:2=6 S2=3×3:2=4,5 S3=2×2:2=2 S=5×5-(6+4, 5+2)=25-12,5=12,5	S=10+7:2-1=12,5
S 11 S1 11 S2 11 S1=4×1:2=2 S2=4×4:2=8 S=4×6-(8+2)=24-10=14	S=9+12:2-1=14

Сравнение способов разбиения фигуры на геометрические фигуры, формулы площадей которых известны и формулы Пика

разбиение фигуры	формула Пика
S1 11 S3 S2 S1=1×1=1(см2) S2=1×2:2=1(см2) S3=1×2:2=1(см2) S=1+1+1=3	S=8:2-1=3(см2)
S3 S4 S2 S1 S1=(1+2):2×1=1,5S2=3×1:2=1,5 S3=1×1:2=0,5S4=1×2:2=1 S=1,5+1,5+0,5+1=4,5	S=2+7:2-1=4,5(cм2)
S 11 S1 11 S2 11 S1=4×1:2=2 S2=4×4:2=8 S=4×6-(8+2)=24-10=14	S=9+12:2-1=14

ПРОДУКТ ПРОЕКТА

Продуктом проекта стал плакат, который размещён в рекреации около кабинетов математики

ЭЛЕКТРОННАЯ ВЕРСИЯ ПЛАКАТА

(Электронную версию плаката см. приложение 2.)

Этапы создания плаката по теме: «Теорема Пика».

этап	действия	пр-ие
биография Г.А. Пика	сбор информации из различных источников; краткое изложение биографии, размещение файла на Яндекс Диске; создание QR кода
теорема Пика	сбор информации из различных источников, выбор наиболее понятного доказательства; размещения теоремы и доказательства на Яндекс Диске;
сравнение решений	разбор и решения наиболее показательного примера, иллюстрирующего целесообразность применения формулы Пика при нахождении площади фигуры на квадратной решётке; создание таблицы сравнения двух способов;	пр. 3
примеры	решение примеров на нахождение площади из ОГЭ и ЕГЭ выбор нескольких задач для плаката; размещение задач на плакате; размещения решения задач и на Яндекс Диске; создание QR кодов	пр. 1 пр. 4
фон, графика	выбор фона плаката, удовлетворительного разрешения; редактирование графики, текста, размещения информации, цвета и т. д.
печать плаката	изготовление-печать плаката в школьной типографии

ЗАКЛЮЧЕНИЕ

В процессе работы над проектом, я убедился в универсальности и простоте формулы Пика для нахождения площадей различных геометрических фигур. Оказалось, что задач на нахождение площадей фигур на квадратной решётке очень много в вариантах ОГЭ и ЕГЭ, было интересно их решить, являясь учеником 6 класса. Формула Пика облегчает и ускоряет нахождение площади многоугольников. Но и она имеет свои недостатки:

1. Чертёж должен быть очень четким (для подсчета узлов);

2. Формула применяется лишь в том случае, если многоугольник изображен на клетчатой бумаге;

3. Формула не имеет аналогов в пространстве.

Знания, которые я получил при работе над проектом, ещё больше подтолкнули меня к изучению интереснейшей науки — геометрия, я с нетерпением жду 7 класса. Наиболее трудоёмкой частью моей работы стал оформление решения задач и создание электронной версии плаката. Выяснилось, что формулы, графики, геометрические фигуры и математические термины на компьютере набираются достаточно долго и тяжело. Но я рад, что получил и этот опыт. Уверен, что мой плакат и выступление на научно-практической конференции школы помогут ребятам лучше подготовиться к экзаменам. Считаю задачи, поставленные перед собой вначале работы выполненными, цель достигнута. При работе над проектом, мне встретились другие задачи на квадратной решётке. На клетчатом листе можно играть, используя клетки, отгадывать кроссворды, судоку. Я планирую продолжить работать над этой темой и преумножить свои знания. Возможно, эта тема станет темой моей будущей проектной или исследовательской работы.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

Журнал «Квант» [Бумажный ресурс] // Материал №12, 1974 год.

Журнал «Квант» [Бумажный ресурс] //№4, 1977;

Рисс Е.А. Математика на клетчатой бумаге. – Библиотека «Кенгуру», выпуск №8, Санкт-Петербург, «Левша», 2009;

Геометрия на клетчатой бумаге. [Бумажный ресурс] // Материал – Смирнов В.А., Смирнова И.М., Москва, Издательство МЦНМО, 2009.

http://festival.1september.ru

http://www.mathege.ru

Сайт «Решу ОГЭ» [Электронный ресурс] // Материал https://math-oge.sdamgia.ru/

Сайт «Сдам ГИА» [Электронный ресурс] // Материал https://sdamgia.ru/

ПРИЛОЖЕНИЯ

Приложение 1:

Задачи из ОГЭ и ЕГЭ на нахождение площади многоугольника.

(решение проведено с помощью теоремы Пика)

На клетчатой бумаге с размером клетки 1см × 1см изображена трапеция. Найдите её площадь. Ответ дайте в квадратных сантиметрах.

S=7+8:2-1=10

Найдите площадь трапеции, изображенной на рисунке.

S=32+18:2-1=40

3. На клетчатой бумаге с размером клетки 1х1см изображена трапеция. Найдите ее площадь.

S=5+12:2-1=10

4. На клетчатой бумаге с размером клетки 1х1 изображен параллелограмм. Найдите его площадь.

S=10+18:2-1=18

5. На клетчатой бумаге с размером клетки 1х1 изображен параллелограмм. Найдите его площадь.

S=15+12:2-1=20

6. На клетчатой бумаге с размером клетки 1х1 изображён параллелограмм. Найдите его площадь.

S=4+14:2-1=10

7. На клетчатой бумаге с размером клетки 1х1 изображён параллелограмм. Найдите его площадь.

S=7+16:2-1=14

8.На клет­ча­той бу­ма­ге с раз­ме­ром клет­ки 1×1 изоб­ра­же­на фигура. Най­ди­те её площадь.

S=3+18:2-1=11

9.На клет­ча­той бу­ма­ге с раз­ме­ром клет­ки 1×1 изоб­ра­же­на фигура. Най­ди­те её площадь.

S=0+22:2-1=10

10.На клетчатой бумаге с размером клетки 1х1 изображена фигура. Найдите её площадь.

S=7+20:2-1=16

11.На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите её площадь.

S=36+14:2-1=42

12.На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите её площадь.

S=11+16:2-1=18

13.На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите её площадь.

S=24+10:2-1=28

14.На клетчатой бумаге с размером клетки 1х1 изображена фигура. Найдите её площадь.

S=5+8:2-1=8

15.На клетчатой бумаге с размером клетки 1х1 изображена фигура. Найдите её площадь.

S=19+4:2-1=20

16.На клетчатой бумаге с размером клетки 1х1 изображена фигура. Найдите её площадь.

S=11+4:2-1=12

17.На клетчатой бумаге с размером клетки 1х1 изображена фигура. Найдите её площадь.

S=31+12:2-1=36

18.На клетчатой бумаге с размером клетки 1х1 изображена фигура. Найдите её площадь.

S=13+8:2-1=16

19.На клетчатой бумаге с размером клетки 1х1 изображена фигура. Найдите её площадь.

S=36+14:2-1=42

20.На клетчатой бумаге с размером клетки 1х1 изображена фигура. Найдите её площадь.

S=8+10:2-1=12

Приложение 2:

Приложение 3:

Найти площадь четырёхугольника, если длина стороны одной клетки равна 1 см	По формулам геометрии	По формуле Пика
	= = = = =1²=1 =7²=49 S=49-3,5-7-2-2,5-1=3	S=L+B:2-1 B=4 L=31 S=31+4:2-1=3

Приложение 4:

№1. Найдите площадь многоугольника, если

длина стороны одной клетки равна 1см.

Решение №1.

7 2

Решение: S=2+7:2-1=4,5

№2. Найдите площадь многоугольника, если

длина стороны одной клетки равна 1см.

Решение №2.

6 3

Решение: S=3+6:2-1=5(

№3. Найдите площадь многоугольника, если

длина стороны одной клетки равна 1см.

Решение №3.

16 9

S=9+16:2-1=16)

№4. Найдите площадь многоугольника, если

длина стороны одной клетки равна 1см.

Решение №4.

16 19

S=19+16:2-1=26

Просмотров работы: 535