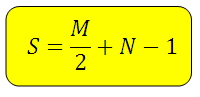Формула площади по клеткам егэ - Помощь в подготовке к экзаменам и поступлению

Чтобы уверенно решать задачи по геометрии — даже такие простые — необходимо выучить основные понятия и формулы.

Это формулы площадей фигур — треугольника (5 формул), параллелограмма, ромба, прямоугольника, произвольного четырехугольника, а также круга. Формулы для длины окружности, длины дуги и площади сектора. Для средней линии треугольника и средней линии трапеции.

Надо знать, что такое центральный и вписанный угол. Знать основные тригонометрические соотношения. В общем, учите основы планиметрии.

Больше полезных формул — в нашем ЕГЭ-Справочнике.

Смотри также материал: Как быстро выучить формулы

В этой статье — основные типы заданий №1 Базового ЕГЭ по математике. Задачи взяты из Банка заданий ФИПИ.

Вычисление длин отрезков, величин углов и площадей фигур по формулам

1. На клетчатой бумаге с размером клетки изображена трапеция. Найдите длину средней линии этой трапеции.

Средняя линия трапеции равна полусумме её оснований: $frac{AD+BC}{2}=frac{4+2}{2}=3.$

Ответ: 3.

2. Найдите величину угла ABC. Ответ дайте в градусах.

Величина вписанного угла alpha равна половине величины центрального угла, опирающегося на ту же дугу. Соединим точки А и С с центром окружности и проведем диаметры через точки А и С. Видим, что величина центрального угла АОС равна ${90}^{circ}.$ Тогда $angle alpha =frac{{90}^{circ}}{2}={45}^{circ}.$

Ответ: 45.

3. Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на $frac{sqrt{5}}{2}.$

Решение:

Проведем из точки В перпендикуляр к прямой ОА. Из прямоугольного треугольника ОВС по теореме Пифагора:

${sin alpha }={sin angle AOB}=frac{4}{2sqrt{5}}=frac{2}{sqrt{5}}.$ Осталось умножить найденное значение синуса на $frac{sqrt{5}}{2}.$

$frac{2}{sqrt{5}}cdot frac{sqrt{5}}{2}=1$

Ответ: 1.

4. Найдите площадь ромба, изображенного на клетчатой бумаге с размером клетки Ответ дайте в квадратных сантиметрах.

Самый простой способ — воспользоваться формулой площади ромба, выраженной через его диагонали:

, где d_1 и d_2 — диагонали.

Получим:

Ответ: 12.

5. Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки Ответ дайте в квадратных сантиметрах.

Площадь трапеции равна произведению полусуммы оснований на высоту:

Основания нашей трапеции равны 4 и 8, а высота равна боковой стороне (поскольку трапеция прямоугольная), то есть 3 см. Площадь трапеции

Ответ: 18.

Нахождение площадей многоугольников сложной формы

А что делать, если надо найти не площадь трапеции или треугольника, а площадь какой-либо сложной фигуры? Есть универсальные способы! Покажем их на примерах из банка заданий ФИПИ и на авторских задачах.

6. Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.

Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным . Высоты этих треугольников равны и . Тогда площадь четырёхугольника равна сумме площадей двух треугольников: .

Ответ: 12,5 .

7. В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.

Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной и трёх прямоугольных треугольников. Видите их на рисунке? Получаем: .

Ответ: 10,5 .

Многие репетиторы рекомендуют в таких задачах пользоваться формулой Пика. В ней нет необходимости, однако эта формула довольно интересна.

Согласно формуле Пика, площадь многоугольника равна В+Г/2-1

где В — количество узлов внутри многоугольника, а Г — количество узлов на границе многоугольника.

Узлами здесь названы точки, в которых пересекаются линии нашей клетчатой бумаги.

Посмотрим, как решается задача 7 с помощью формулы Пика:

Синим на рисунке отмечены узлы внутри треугольника. Зеленым — узлы на границе.

Аккуратно посчитав те и другие, получим, что В = 9, Г = 5, и площадь фигуры равна S = 9 + 5/2 — 1 = 10,5.

Выбирайте — какой способ вам больше нравится.

8. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки

Такой четырехугольник получится, если от квадрата размером отрезать 2 прямоугольника и 4 треугольника. Найдите их на рисунке.

Площадь каждого из больших треугольников равна $frac{1}{2}cdot 3cdot 2=3.$

Площадь каждого из маленьких треугольников равна $frac{1}{2}cdot 1cdot 2=1.$

Тогда площадь четырехугольника

9. Авторская задача. Найдите площадь закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки

Решение:

На рисунке изображен ромб с вырезанным из него квадратом.

Площадь ромба равна половине произведения его диагоналей.

Площадь вырезанного квадрата равна 4.

Площадь фигуры равна 36 — 4 = 32.

Ответ: 32.

Площадь круга, длина окружности, площадь части круга

Длина дуги во столько раз меньше длины окружности, во сколько раз ее градусная мера меньше, чем полный круг, то есть 360 градусов.

Площадь сектора во столько раз меньше площади всего круга, во сколько раз его градусная мера меньше, чем полный круг, то есть 360 градусов.

10. Иногда в задании надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга.Найдите площадь сектора круга радиуса , длина дуги которого равна .

На этом рисунке мы видим часть круга. Площадь всего круга равна , так как R=1 . Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна (так как R=1 ), а длина дуги данного сектора равна , следовательно, длина дуги в раз меньше, чем длина всей окружности. Угол, на который опирается эта дуга, также в раз меньше, чем полный круг (то есть 360 градусов). Значит, и площадь сектора будет в раз меньше, чем площадь всего круга.

Ответ: .

11. На клетчатой бумаге нарисован круг площадью 2,8. Найдите площадь закрашенного сектора.

На рисунке изображен сектор, то есть часть круга. Но какая же это часть? Это четверть круга и еще $frac{1}{8}$ круга, то есть $frac{3}{8}$ круга.

Значит, нам надо умножить площадь круга на $frac{3}{8}$ . Получим:

$frac{3}{8}cdot 2,8 =1,05$

Ответ: 1,05.

12. На клетчатой бумаге изображены два круга. Площадь внутреннего круга равна 9. Найдите площадь закрашенной фигуры.

Площадь фигуры равна разности площадей двух кругов, один из которых расположен внутри другого. По условию, площадь внутреннего круга равна 9. Радиус внешнего круга относится к радиусу внутреннего как 4 к 3. Площадь круга равна pi R^2 , то есть пропорциональна квадрату радиуса. Значит, площадь внешнего круга в ${frac{4}{3}}^2 = frac{16}{9}$ раза больше площади внутреннего и равна 16. Тогда площадь фигуры равна 16 — 9 = 7.

Ответ: 7.

Задачи на координатной плоскости

13. Найдите площадь четырехугольника, вершины которого имеют координаты (4;2), (8;4), (6;8), (2;6).

Заметим, что этот четырехугольник — квадрат. Сторона квадрата a является гипотенузой прямоугольного треугольника с катетами, равными 2 и 4. Тогда

Ответ: 20

14. Найдите площадь четырехугольника, вершины которого имеют координаты

На рисунке изображен параллелограмм (четырехугольник, имеющий две пары параллельных сторон). Площадь параллелограмма равна произведению основания на высоту. Основание равно 2, высота 8, площадь равна 16.

Ответ: 16.

Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Геометрия. Применение формул. Задача 1 Базового ЕГЭ по математике» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена:
09.03.2023

Источник

Почему бы просто не считать клеточки?

Возможно, вы читаете всё это и думаете: зачем все эти сложности? Формулы запоминать. Дорисовывать. Тут ведь сразу видно, сколько клеточек в фигуре.

Вот, например, трапеция:

Посчитаем клеточки: их всего 46, верно?

Но стоп, там же некоторые из них только наполовину внутри фигуры. Отметим их – всего таких 10. Итого, 36 полных (красные точки) и 10 половинчатых, вместе ( 36+frac{10}{2} = 41)

trapetsiya ploshad po polnym i nepolnym kletochkam

Вроде бы всё верно. Но, если присмотреться, можно заметить ещё маленькие треугольнички, которые попали внутрь. А также, что «синие» клеточки слева на самом деле разрезаны не ровно пополам – какие-то чуть больше, какие-то меньше…

Как всё это учитывать?

Попробуем рассуждать так: заметно, что тот маленький розовый треугольник дополняет серый кусок клетки.

А жёлтые сколько занимают? Постарайтесь ответить сами.

Если всё сделать правильно, то увидите, что жёлтые кусочки можно сложить вместе в одну целую клетку.

Итак, 2 жёлтых куска = 1 клетка.

Розовый треугольник + серый кусок = 1 клетка. Всего у нас две таких пары (розовый+серый) – это 2 полных клетки.

Всё остальное как было: 36 полных клеток и 6 половинок у правой стороны – это ( 36+frac{6}{2}=39) клетки.

Итого клеток: ( 1 + 2 + 39 = 42).

Проверим результат по формуле площади трапеции: нижнее основание 11, верхнее основание 3, высота 6. Полусумма оснований равна 7, умножаем на высоту – получилось 42. Всё совпало.

Но! Настолько ли проще был наш способ подсчёта клеточек? Не сказал бы. А если там будет несколько косых линий, то вообще можно замучиться собирать этот паззл (искать, какие кусочки друг друга дополняют).

Вычислите площадь простых фигур тремя способами

Стороны клеток равны 1. Вычислите самостоятельно площадь фигуры всеми тремя способами. Сравните результаты.

Вычислите площадь произвольных фигур по формуле Пика

Вычислите самостоятельно площади фигур с помощью формулы Пика:

Посчитайте площадь корабля и котика по формуле Пика

Посчитайте самостоятельно для тренировки и чтобы запомнить формулу Пика!

ploshad teorema pika po kletochkam zadacha 8

ploshad teorema pika po kletochkam zadacha 9

Фигуры с отверстиями – посчитайте площади двумя способами

Ну и напоследок фигуры с “дырками”. Как думаешь, здесь придётся вычислять сначала площадь целой фигуры, а потом площадь дырки?

Или достаточно просто посчитать точки внутри закрашенной области и на её границах (в том числе, на границе с дыркой)?

Проверим на простом примере: это квадрат ( 4times 4), и в нём вырезан прямоугольник ( 1times 2), значит, его площадь ( 16-2=14).

А теперь по точкам. На границах (включая внутренние) ( Г = 22). Внутри ( В = 3). Тогда площадь по формуле Пика

( S = frac{22}{2} + 3 -1 = 13.)

Хм, близко, но не совпало. Может, я где-то ошибся? Давай ещё одну фигуру, для верности.

Сосчитай сам и проверь.

Что получилось?

У меня снова на 1 меньше.

Так может быть просто формулу немного «подкрутить»? Нет!

Очень и очень не рекомендую вам запоминать несколько похожих формул для похожих случаев, потому что придёт время, и вы обязательно перепутаете формулу.

Даже если вы уверены, что не перепутаете, оно всё равно того не стоит. В общем, наилучший вариант – это запомнить одну формулу. А если попалась фигура с дыркой, вычислить всю фигуру, а потом дырку. И вычесть.

Площадь поверхности пирамиды

Для пирамиды тоже действует общее правило:

Площадь полной поверхности пирамиды – это сумма площадей всех граней.( displaystyle {{S}_{полн. пов. }}={{S}_{боков.пов. }}+{{S}_{основания }})

Теперь давай посчитаем площадь поверхности самых популярных пирамид.

Площадь поверхности правильной треугольной пирамиды

Пусть сторона основания равна ( displaystyle a), а боковое ребро равно ( displaystyle b). Нужно найти ( displaystyle {{S}_{осн}}) и ( displaystyle {{S}_{ASB}}).

И тогда

( displaystyle {{S}_{полн. пов. }}=3{{text{S}}_{ASB}}+{{text{S}}_{text{осн}.}})

Вспомним теперь, что

( displaystyle {{S}_{осн}}) – это площадь правильного треугольника ( displaystyle ABC).

И еще вспомним, как искать эту площадь.

Используем формулу площади:

( displaystyle S=frac{1}{2}abcdot sin gamma ).

У нас «( displaystyle a)» – это ( displaystyle a), а «( displaystyle b)» – это тоже ( displaystyle a), а ( displaystyle sin gamma =sin 60{}^circ =frac{sqrt{3}}{2}).

Значит, ( displaystyle {{S}_{ABC}}=frac{1}{2}{{a}^{2}}frac{sqrt{3}}{2}=frac{{{a}^{2}}sqrt{3}}{4}).

Теперь найдем ( displaystyle {{S}_{Delta ASB}}).

Пользуясь основной формулой площади и теоремой Пифагора, находим

( displaystyle {{S}_{Delta ASB}} = frac{1}{2}asqrt{b^2-frac{a^2}{4}})

Внимание: если у тебя правильный тетраэдр (т.е. ( displaystyle b=a)), то формула получается такой:

( displaystyle S={{a}^{2}}sqrt{3}).

Источник

Формула Пика

Формула Пика. Рассказ о формуле, при помощи которой можно находить площадь фигуры построенной на листе в клетку (треугольник, квадрат, трапеция, прямоугольник, многоугольник). Это формула Пика.

Она секретной не является. Информация о ней в интернете имеется, но многим материал статьи будет крайне полезен. Об этой формуле обычно рассказывается применительно к нахождению площади треугольника. На примере треугольника мы её и рассмотрим.

В задачах, которые будут на ЕГЭ есть целая группа заданий, в которых дан многоугольник построенный на листе в клетку и стоит вопрос о нахождении площади. Масштаб клетки это один квадратный сантиметр.

ФОРМУЛА ПИКА

Площадь искомой фигуры можно найти по формуле:

М – количество узлов на границе треугольника (на сторонах и вершинах)

N – количество узлов внутри треугольника

*Под «узлами» имеется ввиду пересечение линий.

Найдём площадь треугольника:

M = 15 (обозначены красным)

N = 34 (обозначены синим)

Ещё пример. Найдём площадь параллелограмма:

M = 18 (обозначены красным)

N = 20 (обозначены синим)

Найдём площадь трапеции:

M = 24 (обозначены красным)

N = 25 (обозначены синим)

Найдём площадь многоугольника:

M = 14 (обозначены красным)

N = 43 (обозначены синим)

Понятно, что находить площадь трапеции, параллелограмма, треугольника проще и быстрее по соответствующим формулам площадей этих фигур. Но знайте, что можно это делать и таким образом.

А вот когда дан многоугольник, у которого пять и более углов эта формула работает хорошо.

Теперь взгляните на следующие фигуры:

Это типовые фигуры, в заданиях стоит вопрос о нахождении их площади. Такие или подобные им будут на ЕГЭ. При помощи формулы Пика такие задачи решаются за минуту. Например, н айдём площадь фигуры:

M = 11 (обозначены красным)

N = 5 (обозначены синим)

Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см. Ответ дайте в квадратных сантиметрах.

Конечно, можно и эти «микрофигурки» дробить на более простые фигуры (треугольники, трапеции). Способ решения выбирать вам.

Найдём площадь фигуры:

Опишем около неё прямоугольник:

Из площади прямоугольника (в данном случае это квадрат) вычтем площади полученных простых фигур:

В будущем будем рассматривать задания на нахождение площади, связанные с окружностями построенными на листе в клетку, не пропустите! На этом всё. Успехов вам!

Геометрия. Применение формул. Задача 5 Базового ЕГЭ по математике

Больше полезных формул — в нашем ЕГЭ-Справочнике.

В этой статье — основные типы заданий №5 Базового ЕГЭ по математике. Задачи взяты из Банка заданий ФИПИ.

Вычисление длин отрезков, величин углов и площадей фигур по формулам

1. На клетчатой бумаге с размером клетки изображена трапеция. Найдите длину средней линии этой трапеции.

Средняя линия трапеции равна полусумме её оснований:

2. Найдите величину угла ABC. Ответ дайте в градусах.

Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу. Соединим точки А и С с центром окружности и проведем диаметры через точки А и С. Видим, что величина центрального угла АОС равна Тогда

3. Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на

Проведем из точки В перпендикуляр к прямой ОА. Из прямоугольного треугольника ОВС по теореме Пифагора:

Осталось умножить найденное значение синуса на

Самый простой способ — воспользоваться формулой площади ромба, выраженной через его диагонали:

, где и — диагонали.

Получим:

Площадь трапеции равна произведению полусуммы оснований на высоту:

Нахождение площадей многоугольников сложной формы

7. В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.

Согласно формуле Пика, площадь многоугольника равна В+Г/2-1

где В — количество узлов внутри многоугольника, а Г — количество узлов на границе многоугольника.

Узлами здесь названы точки, в которых пересекаются линии нашей клетчатой бумаги.

Посмотрим, как решается задача 7 с помощью формулы Пика:

Синим на рисунке отмечены узлы внутри треугольника. Зеленым — узлы на границе.

Аккуратно посчитав те и другие, получим, что В = 9, Г = 5, и площадь фигуры равна S = 9 + 5/2 — 1 = 10,5.

Выбирайте — какой способ вам больше нравится.

8. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки

Площадь каждого из больших треугольников равна

Площадь каждого из маленьких треугольников равна

Тогда площадь четырехугольника

На рисунке изображен ромб с вырезанным из него квадратом.

Площадь ромба равна половине произведения его диагоналей.

Площадь вырезанного квадрата равна 4.

Площадь фигуры равна 36 — 4 = 32.

Площадь круга, длина окружности, площадь части круга

На этом рисунке мы видим часть круга. Площадь всего круга равна , так как . Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна (так как ), а длина дуги данного сектора равна , следовательно, длина дуги в раз меньше, чем длина всей окружности. Угол, на который опирается эта дуга, также в раз меньше, чем полный круг (то есть градусов). Значит, и площадь сектора будет в раз меньше, чем площадь всего круга.

11. На клетчатой бумаге нарисован круг площадью 2,8. Найдите площадь закрашенного сектора.

На рисунке изображен сектор, то есть часть круга. Но какая же это часть? Это четверть круга и еще круга, то есть круга.

Значит, нам надо умножить площадь круга на . Получим:

Площадь фигуры равна разности площадей двух кругов, один из которых расположен внутри другого. По условию, площадь внутреннего круга равна 9. Радиус внешнего круга относится к радиусу внутреннего как 4 к 3. Площадь круга равна , то есть пропорциональна квадрату радиуса. Значит, площадь внешнего круга в раза больше площади внутреннего и равна 16. Тогда площадь фигуры равна 16 — 9 = 7.

Задачи на координатной плоскости

13. Найдите площадь четырехугольника, вершины которого имеют координаты (4;2), (8;4), (6;8), (2;6).

14. Найдите площадь четырехугольника, вершины которого имеют координаты

Площади фигур, нарисованных на клетчатой бумаге

Рассмотрим несколько задач на вычисление площади фигуры, если фигура нарисована на бумаге в клетку.

Клетку считаем размером 1×1 ед.

Попробуйте решить сами предложенные задачи!

Могу сказать следующее – ответ будет выражаться целым числом 🙂 .

Надо сказать, что кто знаком с такого рода задачками, обычно выдает ответ в считанные секунды… Другие же озадачиваются зачастую тем, а что же делать с площадью круга. Куда ж спрятать …

Итак, ищем площадь «ракеты».

Задача 1.

Найдите площадь фигуры, изображенной на рисунке, считая стороны квадратных клеток равными 1.

Я буду кратка… Никаких слов.

Смотрите и все увидите сами:

Следующая задача предлагалась А. Лариным в одном из Тренировочных вариантов.

Задача 2.

Найдите площадь фигуры, изображенной на рисунке, считая стороны квадратных клеток равными 1.

Ну уж если вы справились с «кувшином», то и с «плачущим сердцем» разберетесь также легко, уверена!

Задача 3.

Найдите суммарную площадь фигур, изображенных на рисунке, считая стороны квадратных клеток равными 1.

Ну а вам я, желаю, конечно, чтоб ваше сердце только б пело, радостно пело!

Чтобы не потерять страничку, вы можете сохранить ее у себя:

источники:

http://ege-study.ru/ru/ege/materialy/matematika/zadanie-3-zadachi-na-kletchatoj-bumage-ili-koordinatnoj-ploskosti/

http://egemaximum.ru/ploshhadi-figur-narisovannyx-na-kletchatoj-bumage/

Источник

В этой статье мы разберем, как находить площадь сектора, нарисованного на бумаге в клеточку. Это задание В5 для подготовки к ЕГЭ по математике.

1. Найдите (в см²) площадь закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). В ответе запишите S/{pi} .

Сначала найдем радиус круга. Считаем клеточки, и получаем, что радиус равен 4.

Тогда площадь круга равна ${pi}r^2=4^2{pi}=16{pi}$

Заштрихованная фигура — это половина круга, и ее площадь равна

В ответе записываем S/{pi} .

Ответ: 8

2. Найдите (в см²) площадь закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). В ответе запишите S/{pi} .

Сначала найдем радиус круга. Считаем клеточки, и получаем, что радиус равен 3.

Тогда площадь круга равна ${pi}r^2=3^2{pi}=9{pi}$

Найдем, какую часть заштрихованная фигура составляет от круга.

Мы видим, что заштрихованная фигура — это половина круга и еще одна четверть от половины, то есть одна восьмая.

Таким образом, площадь заштрихованной фигуры составляет 5/8 от площади круга.

В ответе записываем S/{pi} .

Ответ: 5,625

3. Найдите (в см²) площадь закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). В ответе запишите S/{pi} .

Сначала найдем радиус круга. Считаем клеточки, и получаем, что радиус равен 4.

Тогда площадь круга равна ${pi}r^2=4^2{pi}=16{pi}$

Найдем, какую часть круга составляет незакрашенный сектор. Если мы незакрашенный центральный угол повернем на угол 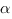alpha , то увидим, что его величина равна $90^{circ}$ :

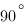
Сектор 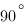$90^{circ}$ — это 1/4 часть круга. Следовательно, закрашенный сектор — это 3/4 круга. И его площадь равна

В ответе записываем S/{pi} .

Ответ: 12

Вероятно, Ваш браузер не поддерживается. Попробуйте скачать

Firefox

И.В. Фельдман, репетитор по математике.

Найди верный ответ на вопрос ✅ «Как рассчитать площадь по клеточкам? …» по предмету 📙 Физика, а если ответа нет или никто не дал верного ответа, то воспользуйся поиском и попробуй найти ответ среди похожих вопросов.

Искать другие ответы

татьяна наумова

Ученик

(236),
закрыт

10 лет назад

не нужно учить формулы площади треугольника,трапеции и т.д. мне сказали что там подсчитывается число целых клеток и не полных, как то умножается….ПОМОГИТЕ ПОЖАЛУЙСТА

~~* Человек-Солнце *~~

Высший разум

(379525)

10 лет назад

Для решения заданий такого типа, в которых необходимо найти площадь фигур расположенных на клетчатой бумаге с размером клетки 1см*1см, удобно использовать формулу

S=Q+W/2-1, где Q- количество вершин клеточек внутри фигуры, W количество пересечений контура фигуры с вершинами клеточек. Формула проста и легко запоминается. Сэкономит Ваше время на экзамене.

Разберем на примере:

Q=7, W=8 S=7+8/2-1=10 Ответ: 10 кв. см.

Найдите правильный ответ на вопрос ✅ «Как рассчитать площадь по клеточкам? …» по предмету 📘 Физика, а если вы сомневаетесь в правильности ответов или ответ отсутствует, то попробуйте воспользоваться умным поиском на сайте и найти ответы на похожие вопросы.

Смотреть другие ответы

Гость:

площадь одной клетки 5мм*5мм= 25 мм^2
считай число полных клеток и умножь на 25 , получишь площадь в мм^2

Пожаловаться

Гость:

1)Считаешь все клетки, которые целиком находятся внутри фигуры 2)
Считаешь клетки, через которые находятся на границе, то есть входят в фигуру не целиком 3) Складываешь 4)Всё!

Пожаловаться

Источник

Грибановский муниципальный район

Воронежской области

Муниципальные педагогические чтения «Киселёвские чтения – 11»

«Формула Пика для нахождения площади многоугольника»

Подготовила: Табакова Ольга Николаевна

учитель МКОУ Верхнекарачанской СОШ

2021 г.

«Геометрия есть знание величин,

фигур и их границ,

а также отношений между ними

и производимых над ними операций,

разнообразных положений и движений»

Диа́дох Прокл

В 21 веке, некоторым детям, порой сложно запомнить огромное количество информации, поступающей каждый день в школе, и даже вызубренные формулы по математике, которые используются для нахождения площади различных фигур, будь то треугольник, параллелограмм или трапеция, часто забываются.

Задание, нахождение площади многоугольника, нарисованного на клетчатой бумаге очень интересное, увлекательное. Казалось бы, что увлекательного можно найти на клетчатой плоскости, то есть, на бесконечном листке бумаги, расчерченном на одинаковые квадратики? Оказывается, задачи, связанные с бумагой в клеточку, достаточно разнообразны. Мы знаем разные способы выполнения таких заданий: способ достраивания, способ разбиения и др. Одним из таких способов является формула Пика для нахождения площади многоугольника.

Актуальность данной темы заключается в том, чтобы помочь выпускникам 9-ых и 11-х классов подготовиться к сдаче ОГЭ и ЕГЭ по математике.

Немного истории:

Георг Александр Пик

(10. 09. 1859 – 13. 07. 1942)

Георг Александр Пик – австрийский математик. Родился Георг Пик в еврейской семье Он был одарённым ребёнком, его обучал отец, возглавлявший частный институт. До одиннадцати лет Георг получал образование дома (с ним занимался отец), а затем поступил сразу в четвёртый класс гимназии. В шестнадцать лет Пик сдал выпускные экзамены и поступил в университет в Вене. Уже в следующем году Пик опубликовал свою первую работу по математике. После окончания университета в 1879 году он получил право преподавать математику и физику. В 1880 году Пик защитил докторскую диссертацию, а в 1881 году получил место ассистента на кафедре физики Пражского университета. В 1888 году он был назначен экстраординарным профессором математики, затем в 1892 году в Немецком университете в Праге был назначен ординарным профессором (полным профессором).

Круг математических интересов Пика был чрезвычайно широк. В частности, им написаны работы в области функционального анализа и дифференциальной геометрии, эллиптических и абелевых функций, теории дифференциальных уравнений и комплексного анализа, всего более 50 тем. С его именем связаны матрица Пика, интерполяция Пика — Неванлинны, лемма Шварца — Пика.

Широкую известность получила открытая им в 1899 году теорема Пика для расчёта площади многоугольника. Эта теорема оставалась незамеченной в течение некоторого времени, однако в 1949 году польский математик Гуго Штейнгауз включил теорему в свой знаменитый «Математический калейдоскоп». С этого времени теорема Пика стала широко известна.

Теорема привлекла довольно большое внимание и начала вызывать восхищение своей простотой и элегантностью.

В Германии эта теорема включена в школьные учебники.

Когда нацисты вошли в Австрию 12 марта 1938 года, он вернулся Прагу. В марте 1939 года нацисты вторглись в Чехословакию. 13 июля 1942 года Пик был депортирован в созданный нацистами в северной Чехии лагерь Терезиенштадт, где умер две недели спустя в возрасте 82 лет.

Формула Пика.

, где

S- площадь многоугольника

В-количество узлов сетки, лежащих внутри многоугольника;

Г-количество узлов сетки, лежащих на границе многоугольника.

Основное условие для применения формулы Пика: у многоугольника, изображённого на клетчатой бумаге (решётке), должны быть только целочисленные вершины, то есть они обязательно должны находиться в узлах решётки. ( узел –это пересечение клеток ).

В -7 узлов

Г- 8 узлов

Формула Пика универсальна, по ней можно вычислить площадь любого многоулольника на клетчатой бумаге.

В-15 узлов

Г-4 узла

Свавним различные способы вычисления площади многоугольника на клетчатой бумаге:

Задача 1. Найти площадь четырехугольника

Метод достраивания

Формула Пика

В- 32

Г- 4

Задача 2.

Метод разбиения на треугольники

Формула Пика

В- 28

Г-18

Сравнивая, полученные результаты, видно, что ответ получается одинаковый. Найти площадь фигуры по формуле Пика, оказалось быстрее и легче, ведь вычислений было меньше.

Таким образом, видно, что формула Пика имеет ряд преимуществ перед другими способами вычисления площадей многоугольников на клетчатой бумаге:

для вычисления площади многоугольника, нужно знать всего одну формулу:

формула Пика проста для запоминания;
формула Пика очень удобна и проста в применении;
многоугольник, площадь которого необходимо вычислить может быть любой, даже самой причудливой.

Вывод: вычисление площадей сложных фигур с помощью формулы Пика легче, чем вычисление методом достраивания и разбивания фигур на части, так как требуется меньше вычислений, а, следовательно, меньше времени.

Формула Пика — это настоящее спасение для тех учеников, которые так и не смогли выучить все формулы для вычисления площадей фигур, для тех, кто так и не уяснил до конца, как выполнить разбиение фигуры или дополнительное построение, чтобы подобраться к вычислению её площади «через знакомых».

С другой стороны, для тех, кто площадь многоугольника, изображённого на клетчатой бумаге, умеет находить с помощью вышеперечисленных приёмов, формула Пика послужит дополнительным инструментом, с помощью которого можно будет решить задачу ещё и этим способом (и тем самым проверить правильность своего предыдущего решения, сверив полученные ответы).

Источник

Каждому из нас нередко приходилось считать площадь решётчатого многоугольника (изображённого, например, на клетчатой бумаге). В основном, это делают ещё по известным со школы формулам. Но в этом случае для каждой фигуры приходится помнить выражение её площади.
Не легче ли использовать одну формулу для всех многоугольников?
— Сказка? — Нет, теорема Пика!

• Названа она в честь Георга Пика (нет, не оружия или покемона), доказавшего её в 1899 году.

Формулировка звучит так:
S = В + Г / 2 − 1, где S — площадь многоугольника, В — количество целочисленных точек внутри многоугольника, а Г — количество целочисленных точек на границе многоугольника.
• Важное замечание: формула справедлива только для многоугольников, у которых вершины расположены в узлах решетки.

Например, для многоугольника на рисунке, В=7 (красные точки), Г=8 (зелёные точки), поэтому S = 7 + 8/2 — 1 = 10 квадратных единиц.

Докажем теорему Пика:
• Рассмотрим прямоугольник со сторонами, лежащими на линиях решетки. Пусть длины его сторон равны a и b. Имеем в этом случае В = (a-1)(b-1), Г = 2a+2b и, по формуле Пика, S = (a-1)(b-1)+a+b-1 = ab .
• Рассмотрим теперь прямоугольный треугольник с катетами, лежащими на осях координат. Такой треугольник получается из прямоугольника со сторонами a и b, рассмотренного в предыдущем случае, разрезанием его по диагонали. Пусть на диагонали лежат c целочисленных точек. Тогда для этого случая В = ((a-1)(b-1)-c+2)/2, Г = (2a+2b)/2+c-1 и получаем, что S = ab/2.
• Теперь рассмотрим произвольный треугольник. Его можно получить, отрезав от прямоугольника несколько прямоугольных треугольников (см. рисунок). Поскольку и для прямоугольника, и для прямоугольного треугольника формула Пика верна, мы получаем, что она будет справедлива и для произвольного треугольника.

• Остается сделать последний шаг: перейти от треугольников к многоугольникам. Любой многоугольник можно триангулировать, т.е. разбить на треугольники (например, диагоналями). Отсюда по индукции следует, что формула Пика верна для любого многоугольника. чтд

К сожалению, эта столь простая и красивая формула плохо обобщается на высшие размерности.
Наглядно показал это Рив, предложив в 1957 г. рассмотреть тетраэдр (называемый теперь тетраэдром Рива) со следующими вершинами:
A(0,0,0), B(1,0,0), C(0,1,0), D(1,1,k)
Тогда этот тетраэдр ABCD при любых k не содержит внутри ни одной точки с целочисленными координатами, а на его границе — лежат только четыре точки A, B, C, D. Таким образом, объём и площадь поверхности этого тетраэдра могут быть разными, в то время как число точек внутри и на границе — неизменны; следовательно, формула Пика не допускает обобщений даже на трёхмерный случай.
Тем не менее, некоторое подобное обобщение на пространства большей размерности всё же имеется, — это многочлены Эрхарта, но они весьма сложны, и зависят не только от числа точек внутри и на границе фигуры.

Специально для ЖЖ матфака, Сергей Романов.

Источник