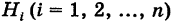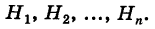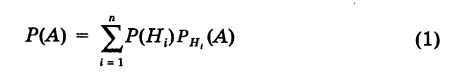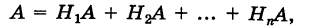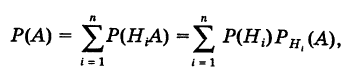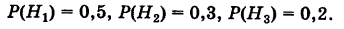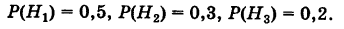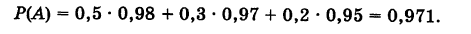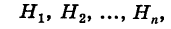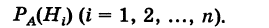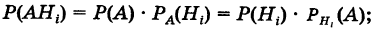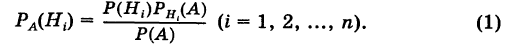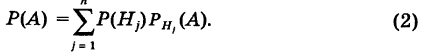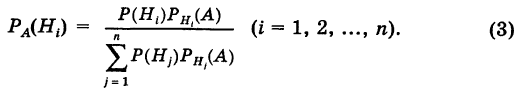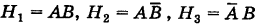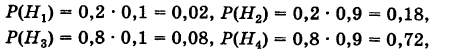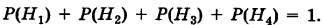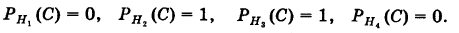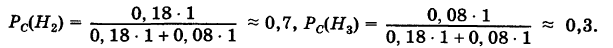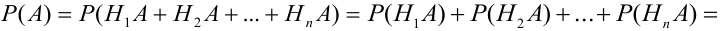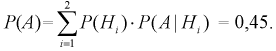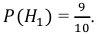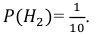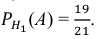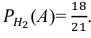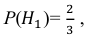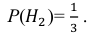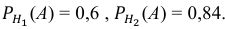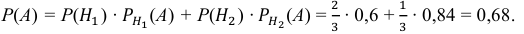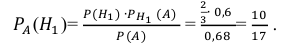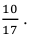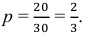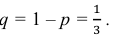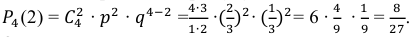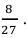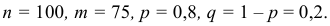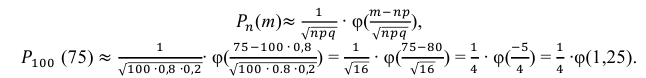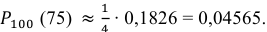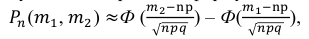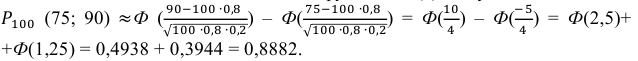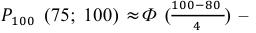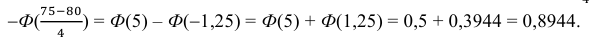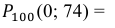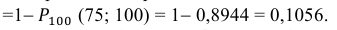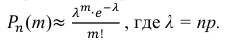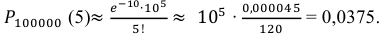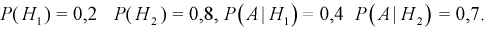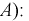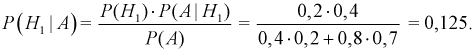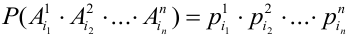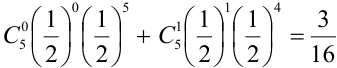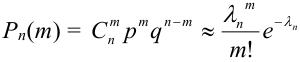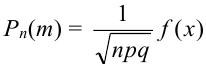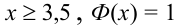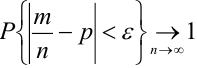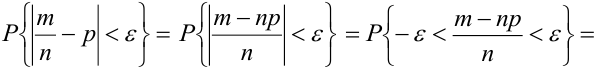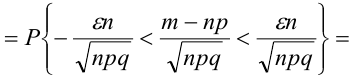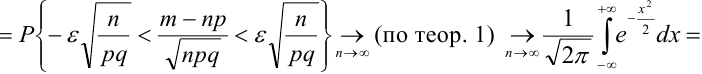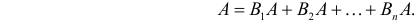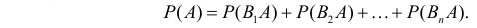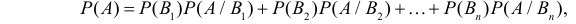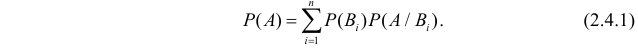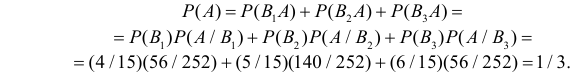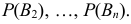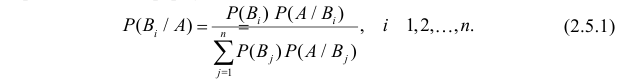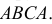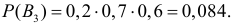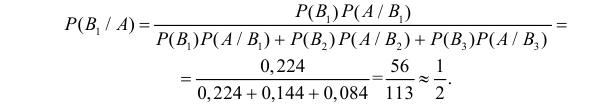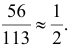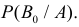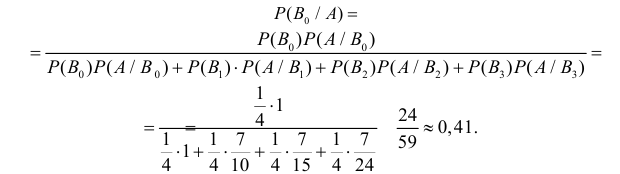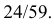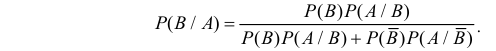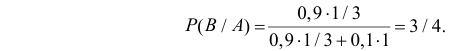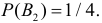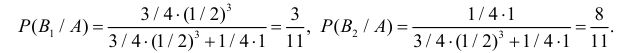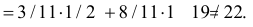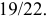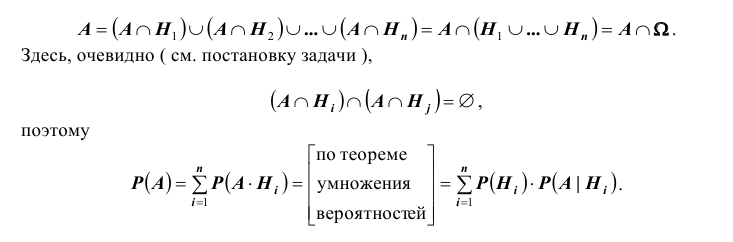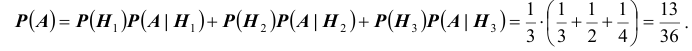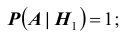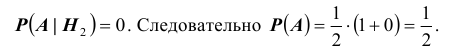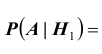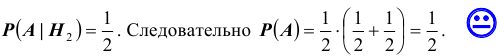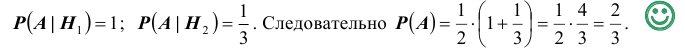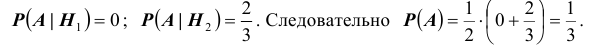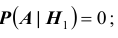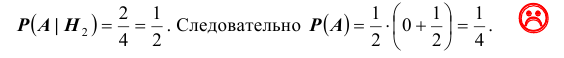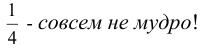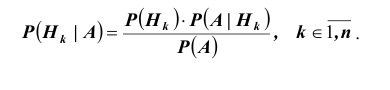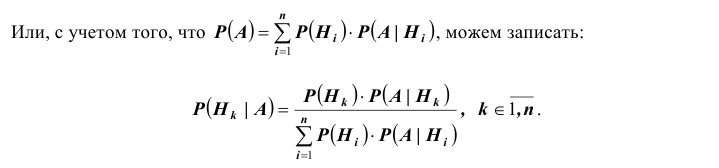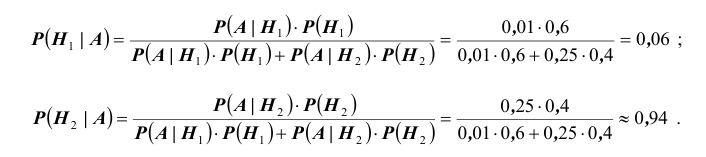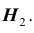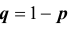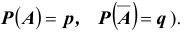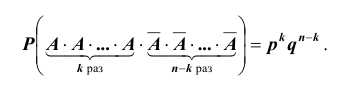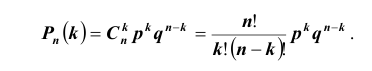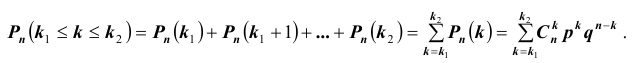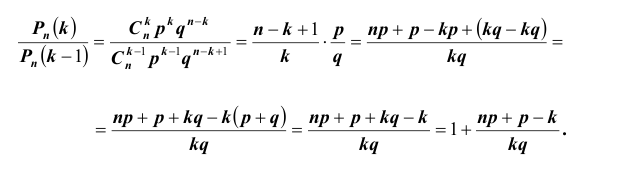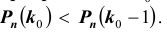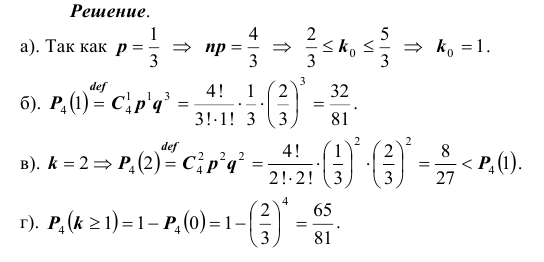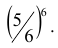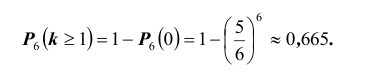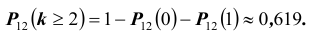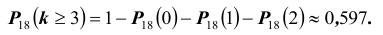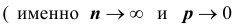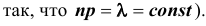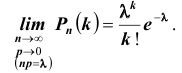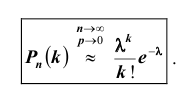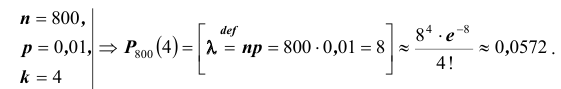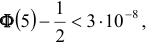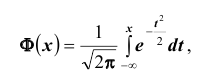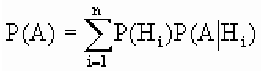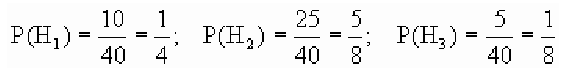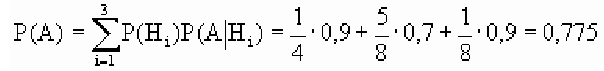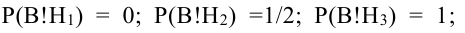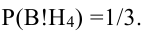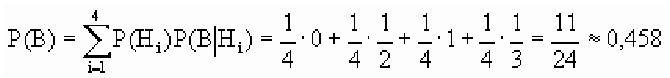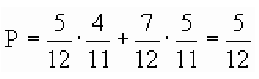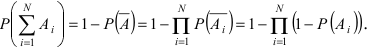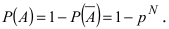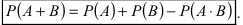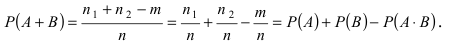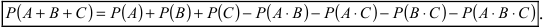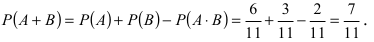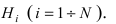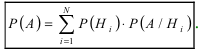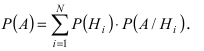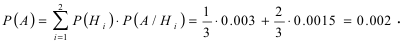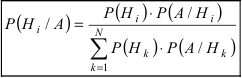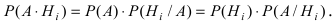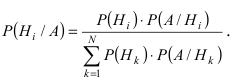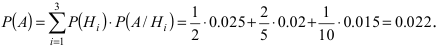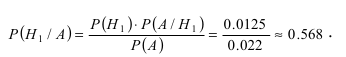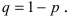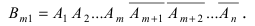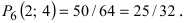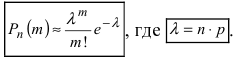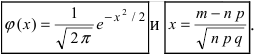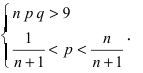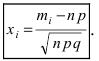Применение
формулы полной вероятности в решении задач ЕГЭ по математике.
Красноперова
Ирина Михайловна (kras.i.m@yandex.ru),
учитель математики МБОУ «Гимназия №1» г. Агрыз РТ
Пусть
событие А может наступить при условии появления одного из событий , которые образуют полную группу попарно
несовместных событий, то есть
зависимые события
.
несовместные
события
События
называют гипотезами, так как неизвестно,
какое из этих событий произойдет в конкретном испытании. Тогда вероятность
события А находят по формуле полной вероятности:
Примечание.
Сумма вероятностей гипотез равна единице:
Пример
1. На сборку телевизоров поступают микросхемы от двух
поставщиков, причем 70% микросхем от первого поставщика, 30% – от второго. Брак
микросхем первого поставщика составляет 2%, второго – 3%. Какова вероятность,
что взятая наудачу микросхема окажется бракованной?
Решение.
Обозначим
– взятая наудачу микросхема изготовлена
первым поставщиком,
– взятая наудачу микросхема изготовлена
вторым поставщиком,
А – взятая наудачу
микросхема дефектная.
Тогда
.
По
условию имеем
Сделаем
проверку: (верно).
Из
условия задачи следует, что
;
.
Тогда
по формуле полной вероятности
.
Пример
2. По самолету производится 3 выстрела с
вероятностями попадания 0,5; 0,6; 0,8. Для вывода самолета из строя заведомо
достаточно трех попаданий; при одном попадании самолет выходит из строя с
вероятностью 0,3; при двух попаданиях – с вероятностью 0,6. Найти вероятность
того, что в результате трех выстрелов самолет будет сбит.
Решение.
Введем событие В – в результате трех выстрелов самолет сбит. Гипотезы:
– в результате трех выстрелов не
произошло ни одного попадания;
– в результате трех выстрелов произошло
одно попадание;
– в результате трех выстрелов произошло
два попадания;
– в результате трех выстрелов произошло
три попадания.
Тогда
,
.
Найдем
вероятности гипотез:
,
,
,
,
Условные
вероятности появления события В:
;
;
;
.
В
итоге имеем
.
Пример
3. Две фабрики выпускают
одинаковые стекла для автомобильных фар. Первая фабрика выпускает
35% этих стекол, вторая – 65%. Первая фабрика выпускает 3% бракованных стекол, а вторая – 5%. Найдите вероятность того, что случайно
купленное в магазине стекло окажется бракованным.
Решение: Введем событие А- купленное в
магазине стекло бракованное.
Гипотезы:
– взятое наудачу стекло изготовлено
первой фабрикой.
– взятое наудачу стекло изготовлено
второй фабрикой.
Тогда
.
По
условию имеем
Сделаем
проверку: (верно).
Из
условия задачи следует, что
;
.
Тогда
по формуле полной вероятности
.
Пример
4. Ковбой
Джон попадает в муху на стене с вероятностью 0,9, если стреляет из пристреленного
револьвера. Если Джон стреляет из непристреленного револьвера, то
он попадает в муху с вероятностью 0,4. На столе лежит 10 револьверов,
из них только 2 пристреленные. Ковбой Джон видит на стене муху, наудачу
хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность
того, что Джон промахнётся.
Решение: Введем событие А-ковбой Джон
промахнется.
Гипотезы:
– взятый наудачу револьвер пристреленный.
– взятый наудачу револьвер
непристреленный.
Тогда
.
По
условию задачи имеется 10 револьверов и 2 из них пристреленных. Тогда по
классическому определению вероятности:
Аналогично
Сделаем
проверку: (верно).
Из
условия задачи следует, что
;
.
(как противоположные события)
Тогда
по формуле полной вероятности
.
Пример
5. Агрофирма
закупает куриные яйца в двух домашних хозяйствах. 40% яиц из первого
хозяйства — яйца высшей категории, а из второго хозяйства —
20% яиц высшей категории. Всего высшую категорию получает 35% яиц.
Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется
из первого хозяйства.
Решение: Введем событие А- купленное у агрофирмы
яйцо высшей категории.
Гипотезы:
– купленное яйцо из первого хозяйства.
– купленное яйцо из второго хозяйства.
Тогда
.
Из
текста задачи видим, что вероятность того, что купленное яйцо из 1-го или 2-го
хозяйства, не дана. Тогда введем неизвестную переменную .
Получаем:
Сделаем
проверку:
Из
условия задачи следует, что
;
.
Тогда
по формуле полной вероятности
.
Задание 3. Теория вероятностей на ЕГЭ по математике.
Мы начнем с простых задач и основных понятий теории вероятностей.
Случайным называется событие, которое нельзя точно предсказать заранее. Оно может либо произойти, либо нет.
Вы выиграли в лотерею — случайное событие. Пригласили друзей отпраздновать выигрыш, а они по дороге к вам застряли в лифте — тоже случайное событие. Правда, мастер оказался поблизости и освободил всю компанию через десять минут — и это тоже можно считать счастливой случайностью…
Наша жизнь полна случайных событий. О каждом из них можно сказать, что оно произойдет с некоторой вероятностью. Скорее всего, вы интуитивно знакомы с этим понятием. Теперь мы дадим математическое определение вероятности.
Начнем с самого простого примера. Вы бросаете монетку. Орел или решка?
Такое действие, которое может привести к одному из нескольких результатов, в теории вероятностей называют испытанием.
Орел и решка — два возможных исхода испытания.
Орел выпадет в одном случае из двух возможных. Говорят, что вероятность того, что монетка упадет орлом, равна .
Бросим игральную кость. У кубика шесть граней, поэтому возможных исходов тоже шесть.
Например, вы загадали, что выпадет три очка. Это один исход из шести возможных. В теории вероятностей он будет называться благоприятным исходом.
Вероятность выпадения тройки равна (один благоприятный исход из шести возможных).
Вероятность четверки — тоже .
А вот вероятность появления семерки равна нулю. Ведь грани с семью точками на кубике нет.
Вероятность события равна отношению числа благоприятных исходов к общему числу исходов.
Очевидно, что вероятность не может быть больше единицы.
Вот другой пример. В пакете яблок, из них
— красные, остальные — зеленые. Ни формой, ни размером яблоки не отличаются. Вы запускаете в пакет руку и наугад вынимаете яблоко. Вероятность вытащить красное яблоко равна
, а зеленое —
.
Вероятность достать красное или зеленое яблоко равна .
БЕСПЛАТНЫЙ МИНИ-КУРС ПО ТЕОРВЕРУ
Определение вероятности. Простые задачи из вариантов ЕГЭ.
Разберем задачи по теории вероятностей, входящие в сборники для подготовки к ЕГЭ.
В фирме такси в данный момент свободно
машин:
красных,
желтых и
зеленых. По вызову выехала одна из машин, случайно оказавшихся ближе всего к заказчице. Найдите вероятность того, что к ней приедет желтое такси.
Всего имеется машин, то есть к заказчице приедет одна из пятнадцати. Желтых — девять, и значит, вероятность приезда именно желтой машины равна
, то есть
.
В сборнике билетов по биологии всего
билетов, в двух из них встречается вопрос о грибах. На экзамене школьнику достаётся один случайно выбранный билет. Найдите вероятность того, что в этом билете не будет вопроса о грибах.
Очевидно, вероятность вытащить билет без вопроса о грибах равна , то есть
.
Родительский комитет закупил
пазлов для подарков детям на окончание учебного года, из них
с картинами известных художников и
с изображениями животных. Подарки распределяются случайным образом. Найдите вероятность того, что Вовочке достанется пазл с животным.
Задача решается аналогично.
Ответ: .
В чемпионате по гимнастике участвуют
спортсменок:
— из России,
— из США, остальные — из Китая. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая последней, окажется из Китая.
Давайте представим, что все спортсменки одновременно подошли к шляпе и вытянули из нее бумажки с номерами. Кому-то из них достанется двадцатый номер. Вероятность того, что его вытянет китайская спортсменка, равен (поскольку из Китая —
спортсменок). Ответ:
.
Ученика попросили назвать число от
до
. Какова вероятность того, что он назовет число кратное пяти?
Каждое пятое число из данного множества делится на . Значит, вероятность равна
.
Брошена игральная кость. Найдите вероятность того, что выпадет нечетное число очков.
— нечетные числа;
— четные. Вероятность нечетного числа очков равна
.
Ответ: .
Монета брошена три раза. Какова вероятность двух «орлов» и одной «решки»?
Заметим, что задачу можно сформулировать по-другому: бросили три монеты одновременно. На решение это не повлияет.
Как вы думаете, сколько здесь возможных исходов?
Бросаем монету. У этого действия два возможных исхода: орел и решка.
Две монеты — уже четыре исхода:
| орел | орел |
| орел | решка |
| решка | орел |
| решка | решка |
Три монеты? Правильно, исходов, так как
.
Вот они:
| орел | орел | орел |
| орел | орел | решка |
| орел | решка | орел |
| решка | орел | орел |
| орел | решка | решка |
| решка | орел | решка |
| решка | решка | орел |
| решка | решка | решка |
Два орла и одна решка выпадают в трех случаях из восьми.
Ответ: .
В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет
очков. Результат округлите до сотых.
Бросаем первую кость — шесть исходов. И для каждого из них возможны еще шесть — когда мы бросаем вторую кость.
Получаем, что у данного действия — бросания двух игральных костей — всего возможных исходов, так как
.
А теперь — благоприятные исходы:
Вероятность выпадения восьми очков равна .
Стрелок попадает в цель с вероятностью
. Найдите вероятность того, что он попадёт в цель четыре выстрела подряд.
Если вероятность попадания равна — следовательно, вероятность промаха
. Рассуждаем так же, как и в предыдущей задаче. Вероятность двух попадания подряд равна
. А вероятность четырех попаданий подряд равна
.
Лень разбираться самому?
Присоединяйся к мини-курсу по теории вероятностей
ПОДРОБНЕЕ
Вероятность: логика перебора.
В кармане у Пети было
монеты по
рублей и
монеты по
рублей. Петя не глядя переложил какие-то
монеты в другой карман. Найдите вероятность того, что пятирублевые монеты лежат теперь в разных карманах.
Мы знаем, что вероятность события равна отношению числа благоприятных исходов к общему числу исходов. Но как посчитать все эти исходы?
Можно, конечно, обозначить пятирублевые монеты цифрами , а десятирублевые цифрами
— а затем посчитать, сколькими способами можно выбрать три элемента из набора
.
Однако есть более простое решение:
Кодируем монеты числами: ,
(это пятирублёвые),
(это десятирублёвые). Условие задачи можно теперь сформулировать так:
Есть шесть фишек с номерами от до
. Сколькими способами можно разложить их по двум карманам поровну, так чтобы фишки с номерами
и
не оказались вместе?
Давайте запишем, что у нас в первом кармане.
Для этого составим все возможные комбинации из набора . Набор из трёх фишек будет трёхзначным числом. Очевидно, что в наших условиях
и
— это один и тот же набор фишек. Чтобы ничего не пропустить и не повториться, располагаем соответствующие трехзначные числа по возрастанию:
…
А дальше? Мы же говорили, что располагаем числа по возрастанию. Значит, следующее — , а затем:
.
Все! Мы перебрали все возможные комбинации, начинающиеся на . Продолжаем:
.
Всего возможных исходов.
У нас есть условие — фишки с номерами и
не должны оказаться вместе. Это значит, например, что комбинация
нам не подходит — она означает, что фишки
и
обе оказались не в первом, а во втором кармане. Благоприятные для нас исходы — такие, где есть либо только
, либо только
. Вот они:
134, 135, 136, 145, 146, 156, 234, 235, 236, 245, 246, 256 – всего благоприятных исходов.
Тогда искомая вероятность равна .
Ответ: .
Сумма событий, произведение событий и их комбинации
Вероятность того, что новый электрический чайник прослужит больше года, равна 0,93. Вероятность того, что он прослужит больше двух лет, равна 0,87. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.
Проработав год, чайник может либо сломаться на второй год, либо благополучно служить и после 2 лет работы.
Пусть – вероятность того, что чайник прослужил больше года.
– вероятность того, что он сломается на второй год,
– вероятность того, что он прослужит больше двух лет.
Очевидно,
Тогда
Ответ: 0,06.
События, взаимоисключающие друг друга в рамках данной задачи, называются несовместными. Появление одного из несовместных событий исключает появление других.
Сумма двух событий – термин, означающий, что произошло или первое событие, или второе, или оба сразу.
Вероятность суммы несовместных событий равна сумме их вероятностей.
В нашей задаче события «чайник сломался на второй год работы» и «чайник работает больше двух лет» — несовместные. Чайник или сломался, или остается в рабочем состоянии.
На рисунке изображён лабиринт. Паук заползает в лабиринт в точке «Вход». Развернуться и ползти назад паук не может. На каждом разветвлении паук выбирает путь, по которому ещё не полз. Считая выбор дальнейшего пути случайным, определите, с какой вероятностью паук выйдет через выход А.
Пронумеруем развилки, на которых паук может случайным образом свернуть в ту или другую сторону.
Он может либо выйти в выход D, и вероятность этого события равна Либо уйти дальше в лабиринт. На второй развилке он может либо свернуть в тупик, либо выйти в выход В (с вероятностью
На каждой развилке вероятность свернуть в ту или другую сторону равна
а поскольку развилок пять, вероятность выбраться через выход А равна
то есть 0,03125.
События А и В называют независимыми, если вероятность появления события А не меняет вероятности появления события В.
В нашей задаче так и есть: неразумный паук сворачивает налево или направо случайным образом, независимо от того, что он делал до этого.
Для нескольких независимых событий вероятность того, что все они произойдут, равна произведению вероятностей.
(А) Два грузовика, работая совместно, вывозят снег с улицы Нижняя Подгорная, причем первый грузовик должен сделать три рейса с грузом снега, а второй — два. Вероятность застрять с грузом снега при подъеме в горку равна 0,2 для первого грузовика и 0,25 — для второго. С какой вероятностью грузовики вывезут снег с улицы Нижняя Подгорная, ни разу не застряв на горке?
Вероятность для первого грузовика благополучно одолеть горку Для второго
Поскольку первый грузовик должен сделать 3 рейса, а второй – два, грузовики ни разу не застрянут на горке с вероятностью
Агрофирма закупает куриные яйца в двух домашних хозяйствах. 40% яиц из первого хозяйства — яйца высшей категории, а из второго хозяйства — 20% яиц высшей категории. Всего высшую категорию получает 35% яиц. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.
Нарисуем все возможные исходы ситуации. Покупатель пришел в магазин, который принадлежит агрофирме, и купил яйцо. Надо найти вероятность того, что это яйцо из первого хозяйства.
Яйца могут быть только или из первого домашнего хозяйства, или из второго, причем эти два события несовместны. Других яиц в этот магазин не поступает.
Пусть вероятность того, что купленное яйцо из первого хозяйства, равна . Тогда вероятность того, что яйцо из второго хозяйства (противоположного события), равна
.
Яйца могут быть высшей категории и не высшей.
В первом хозяйстве 40% яиц имеют высшую категорию, а 60% — не высшую. Это значит, что случайно выбранное яйцо из первого хозяйства с вероятностью 40% будет высшей категории.
Во втором хозяйстве 20% яиц высшей категории, а 80% — не высшей.
Пусть случайно выбранное в магазине яйцо — из первого хозяйства и высшей категории. Вероятность этого события равна произведению вероятностей:
Вероятность того, что яйцо из второго хозяйства и высшей категории, равна
Если мы сложим эти две вероятности, мы получим вероятность того, что яйцо имеет высшую категорию. По условию, высшую категорию имеют 35% яиц, значит, эта вероятность равна 0,35.
Мы получили уравнение:
Решаем это уравнение и находим, что – вероятность того, что яйцо, купленное у этой агрофирмы, оказалось из первого хозяйства.
Всем пациентам с подозрением на гепатит делают анализ крови. Если анализ выявляет гепатит, то результат анализа называется положительным. У больных гепатитом пациентов анализ даёт положительный результат с вероятностью 0,9. Если пациент не болен гепатитом, то анализ может дать ложный положительный результат с вероятностью 0,01. Известно, что 5% пациентов, поступающих с подозрением на гепатит, действительно больны гепатитом. Найдите вероятность того, что результат анализа у пациента, поступившего в клинику с подозрением на гепатит, будет положительным.
С чем пришел пациент в клинику? – С подозрением на гепатит. Возможно, он действительно болен гепатитом, а возможно, у его плохого самочувствия другая причина. Может быть, он просто съел что-нибудь. Вероятность того, что он болен гепатитом, равна 0,05 (то есть 5%). Вероятность того, что он здоров, равна 0,95 (то есть 95%).
Пациенту делают анализ. Покажем на схеме все возможные исходы:
Если он болен гепатитом, анализ дает положительный результат с вероятностью 0,9. То есть анализ покажет: «есть гепатит».
Заметим, что анализ не во всех случаях выявляет гепатит у того, кто действительно им болен. С вероятностью 0,1 анализ не распознает гепатит у больного.
Более того. Анализ может ошибочно дать положительный результат у того, кто не болеет гепатитом. Вероятность такого ложного положительного результата 0,01. Тогда с вероятностью 0,99 анализ даст отрицательный результат, если человек здоров.
Найдем вероятность того, что результат анализа у пациента, поступившего в клинику с подозрением на гепатит, будет положительным.
Благоприятные для этой ситуации исходы: человек болен, и анализ положительный (вероятность одновременного наступления этих двух событий равна ), или человек здоров, и анализ ложный положительный (вероятность одновременного наступления этих двух событий равна
). Так как события «человек болен» и «человек не болен» несовместны, то вероятность того, что результат анализа будет положительным, равна
Ответ: 0,0545.
Чтобы поступить в институт на специальность «Лингвистика», абитуриент З. должен набрать на ЕГЭ не менее 70 баллов по каждому из трёх предметов — математика, русский язык и иностранный язык. Чтобы поступить на специальность «Коммерция», нужно набрать не менее 70 баллов по каждому из трёх предметов — математика, русский язык и обществознание.
Вероятность того, что абитуриент З. получит не менее 70 баллов по математике, равна 0,6, по русскому языку — 0,8, по иностранному языку — 0,7 и по обществознанию — 0,5.
Найдите вероятность того, что З. сможет поступить хотя бы на одну из двух упомянутых специальностей.
Заметим, что в задаче не спрашивается, будет ли абитуриент по фамилии З. учиться и лингвистике, и коммерции сразу и получать два диплома. Здесь надо найти вероятность того, что З. сможет поступить хотя бы на одну из двух данных специальностей – то есть наберет необходимое количество баллов.
Для того чтобы поступить хотя бы на одну из двух специальностей, З. должен набрать не менее 70 баллов по математике. И по русскому. И еще – обществознание или иностранный.
Вероятность набрать 70 баллов по математике для него равна 0,6.
Вероятность набрать баллы по математике и русскому равна
Разберемся с иностранным и обществознанием. Нам подходят варианты, когда абитуриент набрал баллы по обществознанию, по иностранному или по обоим. Не подходит вариант, когда ни по языку, ни по «обществу» он не набрал баллов. Значит, вероятность сдать обществознание или иностранный не ниже чем на 70 баллов равна
В результате вероятность сдать математику, русский и обществознание или иностранный равна Это ответ.
Чтобы полностью освоить тему, смотрите видеокурс по теории вероятностей. Это бесплатно.
Еще задачи ЕГЭ по теме «Теория вероятностей».
Смотрите также: парадокс Монти Холла.
Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Задание 3. Теория вероятностей на ЕГЭ по математике.» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
09.03.2023
События, которые происходят реально или в нашем воображении, можно разделить на 3 группы. Это достоверные события, которые обязательно произойдут, невозможные события и случайные события. Теория вероятностей изучает случайные события, т.е. события, которые могут произойти или не произойти. В данной статье будет представлена в кратком виде теория вероятности формулы и примеры решения задач по теории вероятности, которые будут в 4 задании ЕГЭ по математике (профильный уровень).
Зачем нужна теория вероятности
Исторически потребность исследования этих проблем возникла в XVII веке в связи с развитием и профессионализацией азартных игр и появлением казино. Это было реальное явление, которое требовало своего изучения и исследования.
Игра в карты, кости, рулетку создавала ситуации, когда могло произойти любое из конечного числа равновозможных событий. Возникла необходимость дать числовые оценки возможности наступления того или иного события.
В XX веке выяснилось, что эта, казалось бы, легкомысленная наука играет важную роль в познании фундаментальных процессов, протекающих в микромире. Была создана современная теория вероятностей.
Основные понятия теории вероятности
Объектом изучения теории вероятностей являются события и их вероятности. Если событие является сложным, то его можно разбить на простые составляющие, вероятности которых найти несложно.
Суммой событий А и В называется событие С, заключающееся в том, что произошло либо событие А, либо событие В, либо события А и В одновременно.
Произведением событий А и В называется событие С, заключающееся в том, что произошло и событие А и событие В.
События А и В называется несовместными, если они не могут произойти одновременно.
Событие А называется невозможным, если оно не может произойти. Такое событие обозначается символом
.
Событие А называется достоверным, если оно обязательно произойдет. Такое событие обозначается символом
.
Пусть каждому событию А поставлено в соответствие число P{А). Это число P(А) называется вероятностью события А, если при таком соответствии выполнены следующие условия.
- Вероятность принимает значения на отрезке от 0 до 1, т.е.
.
- Вероятность невозможного события равна 0, т.е.
.
- Вероятность достоверного события равна 1, т.e.
.
- Если события A и В несовместные, то вероятность их суммы равна сумме их вероятностей, т.е.
.
Важным частным случаем является ситуация, когда имеется равновероятных элементарных исходов, и произвольные
из этих исходов образуют события А. В этом случае вероятность можно ввести по формуле
. Вероятность, введенная таким образом, называется классической вероятностью. Можно доказать, что в этом случае свойства 1-4 выполнены.
Задачи по теории вероятностей, которые встречаются на ЕГЭ по математике, в основном связаны с классической вероятностью. Такие задачи могут быть очень простыми. Особенно простыми являются задачи по теории вероятностей в демонстрационных вариантах. Легко вычислить число благоприятных исходов , прямо в условии написано число всех исходов
.
Ответ получаем по формуле .
Пример задачи из ЕГЭ по математике по определению вероятности
На столе лежат 20 пирожков – 5 с капустой, 7 с яблоками и 8 с рисом. Марина хочет взять пирожок. Какова вероятность, что она возьмет пирожок с рисом?
Решение.
Всего равновероятных элементарных исходов 20, то есть Марина может взять любой из 20 пирожков. Но нам нужно оценить вероятность того, что Марина возьмет пирожок с рисом, то есть , где А – это выбор пирожка с рисом. Значит у нас количество благоприятных исходов (выборов пирожков с рисом) всего 8. Тогда вероятность будет определяться по формуле:
Ответ: 0,4
Независимые, противоположные и произвольные события
Однако в открытом банке заданий стали встречаться и более сложные задания. Поэтому обратим внимание читателя и на другие вопросы, изучаемые в теории вероятностей.
События А и В называется независимыми, если вероятность каждого из них не зависит от того, произошло ли другое событие.
Событие B состоит в том, что событие А не произошло, т.е. событие B является противоположным к событию А. Вероятность противоположного события равна единице минус вероятность прямого события,т.е. .
Теоремы сложения и умножения вероятностей, формулы
Для произвольных событий А и В вероятность суммы этих событий равна сумме их вероятностей без вероятности их совместного события, т.е.
.
Для независимых событий А и В вероятность произведения этих событий равна произведению их вероятностей, т.е. в этом случае
.
Последние 2 утверждения называются теоремами сложения и умножения вероятностей.
Не всегда подсчет числа исходов является столь простым. В ряде случаев необходимо использовать формулы комбинаторики. При этом наиболее важным является подсчет числа событий, удовлетворяющих определенным условиям. Иногда такого рода подсчеты могут становиться самостоятельными заданиями.
Сколькими способами можно усадить 6 учеников на 6 свободных мест? Первый ученик займет любое из 6 мест. Каждому из этих вариантов соответствует 5 способов занять место второму ученику. Для третьего ученика остается 4 свободных места, для четвертого — 3, для пятого — 2, шестой займет единственное оставшееся место. Чтобы найти число всех вариантов, надо найти произведение , которое обозначается символом 6! и читается “шесть факториал”.
В общем случае ответ на этот вопрос дает формула для числа перестановок из п элементов В нашем случае
.
Рассмотрим теперь другой случай с нашими учениками. Сколькими способами можно усадить 2 учеников на 6 свободных мест? Первый ученик займет любое из 6 мест. Каждому из этих вариантов соответствует 5 способов занять место второму ученику. Чтобы найти число всех вариантов, надо найти произведение .
В общем случае ответ на этот вопрос дает формула для числа размещений из n элементов по k элементам
В нашем случае .
И последний случай из этой серии. Сколькими способами можно выбрать трех учеников из 6? Первого ученика можно выбрать 6 способами, второго — 5 способами, третьего — четырьмя. Но среди этих вариантов 6 раз встречается одна и та же тройка учеников. Чтобы найти число всех вариантов, надо вычислить величину: . В общем случае ответ на этот вопрос дает формула для числа сочетаний из
элементов по
элементам:
В нашем случае .
Примеры решения задач из ЕГЭ по математике на определение вероятности
Задача 1. Из сборника под ред. Ященко.
На тарелке 30 пирожков: 3 с мясом, 18 с капустой и 9 с вишней. Саша наугад выбирает один пирожок. Найдите вероятность того, что он окажется с вишней.
Решение:
.
Ответ: 0,3.
Задача 2. Из сборника под ред. Ященко.
В каждой партии из 1000 лампочек в среднем 20 бракованных. Найдите вероятность того, что наугад взятая лампочка из партии будет исправной.
Решение: Количество исправных лампочек 1000-20=980. Тогда вероятность того, что взятая наугад лампочка из партии будет исправной:
Ответ: 0,98.
Задача 3.
Вероятность того, что на тестировании по математике учащийся У. верно решит больше 9 задач, равна 0,67. Вероятность того, что У. верно решит больше 8 задач, равна 0,73. Найдите вероятность того, что У. верно решит ровно 9 задач.
Решение:
Если мы вообразим числовую прямую и на ней отметим точки 8 и 9, то мы увидим, что условие “У. верно решит ровно 9 задач” входит в условие “У. верно решит больше 8 задач”, но не относится к условию “У. верно решит больше 9 задач”.
Однако, условие “У. верно решит больше 9 задач” содержится в условии “У. верно решит больше 8 задач”. Таким образом, если мы обозначим события: “У. верно решит ровно 9 задач” – через А, “У. верно решит больше 8 задач” – через B, “У. верно решит больше 9 задач” через С. То решение будет выглядеть следующим образом:
.
Ответ: 0,06.
Задача 4.
На экзамене по геометрии школьник отвечает на один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос по теме «Тригонометрия», равна 0,2. Вероятность того, что это вопрос по теме «Внешние углы», равна 0,15. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
Решение.
Давайте подумаем какие у нас даны события. Нам даны два несовместных события. То есть либо вопрос будет относиться к теме “Тригонометрия”, либо к теме “Внешние углы”. По теореме вероятности вероятность несовместных событий равна сумме вероятностей каждого события, мы должны найти сумму вероятностей этих событий, то есть:
Ответ: 0,35.
Задача 5.
Помещение освещается фонарём с тремя лампами. Вероятность перегорания одной лампы в течение года равна 0,29. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит.
Решение:
Рассмотрим возможные события. У нас есть три лампочки, каждая из которых может перегореть или не перегореть независимо от любой другой лампочки. Это независимые события.
Тогда укажем варианты таких событий. Примем обозначения: – лампочка горит,
– лампочка перегорела. И сразу рядом подсчитаем вероятность события. Например, вероятность события, в котором произошли три независимых события “лампочка перегорела”, “лампочка горит”, “лампочка горит”:
, где вероятность события “лампочка горит” подсчитывается как вероятность события, противоположного событию “лампочка не горит”, а именно:
.
Заметим, что благоприятных нам несовместных событий всего 7. Вероятность таких событий равна сумме вероятностей каждого из событий: .
Ответ: 0,975608.
Еще одну задачку вы можете посмотреть на рисунке:
Таким образом, мы с вами поняли, что такое теория вероятности формулы и примеры решения задач по которой вам могут встретиться в варианте ЕГЭ.
Содержание:
Формула полной вероятности:
Пусть событие А может произойти в результате появления одного и только одного события
События этой группы обычно называются гипотезами.
Теорема: Вероятность события А равна сумме парных произведений вероятностей всех гипотез, образующих полную группу, на соответствующие условные вероятности данного события А, т. е.
(формула полной вероятности), причем здесь
Доказательство. Так как
причем, ввиду несовместности событий 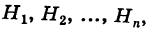
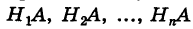
что и требовалось доказать.
Пример:
В магазин для продажи поступает продукция трех фабрик, относительные доли которых есть: I — 50%, II — 30%, III — 20%. Для продукции фабрик брак соответственно составляет: I — 2%, II — 3%, III — 5%. Какова вероятность того, что изделие этой продукции, случайно приобретенное в магазине, окажется доброкачественным (событие А)?
Решение:
Здесь возможны следующие три гипотезы: 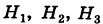
Соответствующие условные вероятности события А равны
По формуле полной вероятности имеем
Формула Бейеса:
Пример:
Имеется полная группа несовместных гипотез
вероятности которых 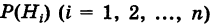
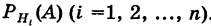
Например, очевидно, следует отбросить гипотезы, отрицающие появление события А. Вообще, проблема состоит в том, что, имея новую информацию, мы должны переоценить вероятности наших гипотез.
Иными словами, нам нужно определить условные вероятности
На основании теоремы умножения вероятностей имеем
отсюда
Для нахождения вероятности Р(А) можно использовать формулу полной вероятности
Отсюда имеем формулу вероятностей гипотез после опыта (<формулу Бейеса)
Пример:
Вероятность поражения самолета при одиночном выстреле для 1-го ракетного расчета (событие А) равна 0,2, а для 2-го (событие В) — 0,1. Каждое из орудий производит по одному выстрелу, причем зарегистрировано одно попадание в самолет (событие С). Какова вероятность, что удачный выстрел принадлежит первому расчету?
Решение:
До опыта возможны четыре гипотезы: 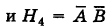
Вероятности их, при независимом действии расчетов, соответственно равны
причем
Условные вероятности для наблюдаемого события С при данных гипотезах будут
Следовательно, гипотезы 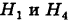
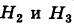
Таким образом, с вероятностью приблизительно 0,7 можно утверждать, что удачный выстрел принадлежит 1-му расчету,
Формула полной вероятности
Пусть событие А еще не произошло, но вскоре должно произойти. Событие А может протекать в различных условиях, относительно характера которых сделано 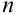
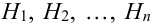
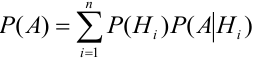
Доказательство.
По условию теоремы гипотезы 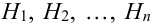
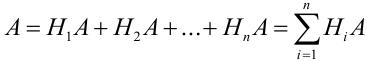
Т.к. гипотезы несовместны, то и комбинации 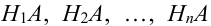
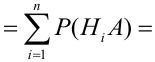
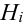
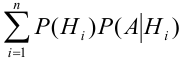
Пример:
Имеется пять урн:
2 урны состава 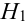
1 урна состава 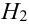
2 урны состава 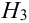
Наудачу выбирается урна, и из нее наудачу выбирается шар. Чему равна вероятность события А = {будет вынут белый шар}?
Решение.
Событие А еще не произошло. Шар может быть вынут из урн разных составов, следовательно, в алгебре событий событие А запишется в виде: 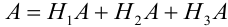
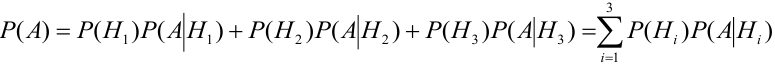
Найдем отдельно вероятности событий:
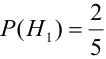
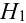
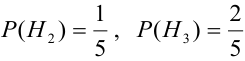
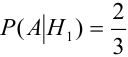
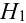
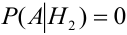
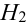
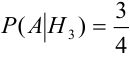
Подставим найденные вероятности в формулу (*): 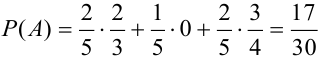
Формула полной вероятности и решение задач
Пример:
В двух одинаковых коробках имеется по 100 резисторов. В 1-й — 60 резисторов по 100 КОм, во 2-й 30 — резисторов по 100 КОм. Определить вероятность того, что взятый наугад из какой-либо коробки резистор будет 100 КОм.
Решение:
Пусть событие 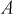
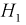
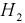
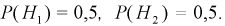
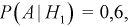
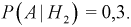
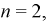
Пример №1
В первой коробке находится 20 деталей, из них 18 стандартных, во второй коробке – 10 деталей, из них 9 стандартных. Из второй коробки наудачу взята одна деталь и переложена в первую коробку.
Какова вероятность того, что деталь, наудачу извлечённая после этого из первой коробки, окажется стандартной?
Решение. Обозначим события:
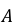
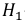
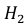
Событие А может наступить при условии наступления одного из событий 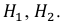
Вероятность того, что из второй коробки извлечена нестандартная деталь
Условная вероятность того, что из первой коробки извлечена стандартная деталь, при условии, что из второй коробки в первую была переложена стандартная деталь,
Условная вероятность того, что из первой коробки извлечена стандартная деталь, при условии, что из второй коробки в первую была переложена нестандартная деталь,
Искомая вероятность того, что из первой коробки будет извлечена стандартная деталь, по формуле полной вероятности равна:
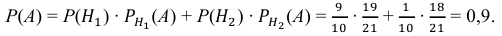
Ответ: 0,9.
Пример №2
Два станка производят одинаковые детали, которые поступают на общий конвейер. Производительность первого станка в два раза больше производительности второго станка. Первый производит 60 % деталей высшего сорта, а второй – 84 %. Наудачу взятая с конвейера деталь оказалась высшего сорта. Какова вероятность того, что эта деталь произведена на первом станке?
Решение. Обозначим события:
А – деталь, взятая с конвейера, оказалась высшего сорта.
Это событие наступит с одним из двух событий (гипотез):
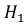
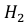
Поскольку производительность первого станка в два раза больше производительности второго станка, вероятности гипотез равны:
Условные вероятности события А даны:
По формуле полной вероятности находим:
По формуле Байеса найдём условную вероятность того, что взятая наудачу деталь высшего сорта произведена на первом станке:
Ответ:
Пример №3
В ящике 20 белых и 10 чёрных шаров. Поочерёдно извлекают 4 шара, причём каждый извлечённый шар возвращают в ящик перед извлечением следующего. Какова вероятность того, что среди четырёх извлечённых шаров окажется два белых?
Решение. Вероятность извлечения белого шара одна и та же во всех четырёх испытаниях, так как каждый извлечённый шар возвращается в ящик:
Тогда вероятность извлечения чёрного шара во всех четырёх испытаниях равна
Используя формулу Бернулли, находим вероятность того, что из четырёх извлечённых шаров два шара будут белыми:
Ответ:
Пример №4
Вероятность поражения мишени при одном выстреле равна 0,8. Какова вероятность того, что при 100 выстрелах мишень будет поражена 75 раз?
Решение. По условию задачи
Так как n – достаточно большое число, воспользуемся локальной формулой Лапласа:
В таблице значений функции 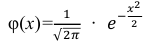
0,1826.
Следовательно,
Ответ: 0,04565.
Пример №5
Вероятность поражения мишени при одном выстреле равна 0,8. Какова вероятность того, что при 100 выстрелах мишень будет поражена
а) не менее 75 раз и не более 90 раз?
б) не менее 75 раз?
в) не более 74 раз?
Решение.
Воспользуемся интегральной формулой Лапласа:
где 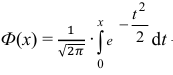
а) По условию задачи 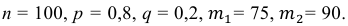
б) Требование того, чтобы событие наступило не менее 75 раз, означает следующее: число появлений события может быть равно либо 75, либо 76, … , либо 100.
Тогда следует принять 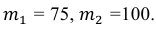
в) Событие «мишень поражена не более 74 раз» и событие «мишень поражена не менее 75 раз» являются противоположными. Поэтому сумма их вероятностей равна 1. Следовательно, искомая вероятность
Ответ: а) 0,8882; б) 0,8944; в) 0,1056.
Пример №6
Учебник издан тиражом 100000 экземпляров.
Вероятность того, что один учебник сброшюрован неправильно, равна 0,0001. Какова вероятность того, что тираж содержит 5 бракованных книг?
Решение. По условию задачи n = 100000, p = 0,0001.
События «из n книг ровно m книг сброшюрованы неправильно», где m = 0,1,2, … ,100000, являются независимыми. Так как число n велико, а вероятность p мала, вероятность 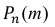
В рассматриваемой задаче 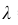
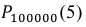
Ответ: 0,0375.
Формула Байеса (Бейеса)
Пусть событие А произошло, причем А могло протекать в различных условиях, относительно характера которых было сделано 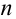
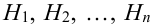
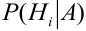
Решение:
По условию теоремы гипотезы 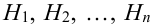
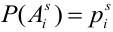
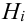
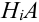
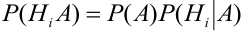
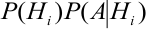
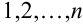
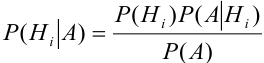
Выразим Р(А) с помощью формулы полной вероятности:
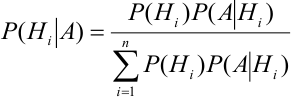
Пример №7
Имеется пять урн:
2 урны состава 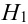
2 урны состава 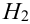
1 урна состава 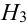
Из одной наудачу выбранной урны взят шар. Он оказался белым (событие А). Чему равна после опыта вероятность события, что шар вынут из урны третьего состава.
Решение.
Событие А произошло. Шар мог быть вынут из урн разных составов, следовательно, в алгебре событий событие А запишется в виде: 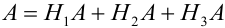
Найдем вероятности событий:
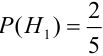
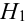
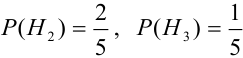
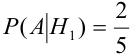
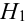
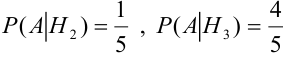
По формуле Байеса найдем условную вероятность 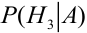
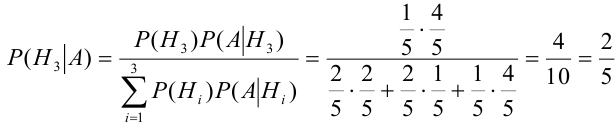
Пример №8
Вероятность дождливого дня в городе равна 0,2. Известно, что вероятность выиграть футбольный матч команде этого города в дождливый день равна 0,4, а в сухой — 0,7. Известно, что команда выиграла матч. Определить, что в этот день шел дождь.
Решение:
Событие 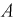
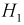
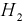
Чтобы ответить на вопрос, пересмотрим вероятность 1-й гипотезы с учетом результата опыта-появилось событие 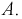
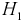
Из полученного результата видим, что с учетом события 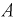
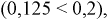
Независимые испытания
Под испытанием станем понимать осуществление определенного комплекса условий, в результате которого может произойти то или иное элементарное событие пространства 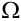
Определение 26. Если производятся испытания, при которых вероятность появления события А в каждом испытании не зависит от исходов других испытаний, то такие испытания называются независимыми относительно события А.
В каждом испытании вероятность появления события А одинакова.
Ряд задач связан с экспериментом, в котором проводятся последовательные независимые испытания, и наблюдается результат совместного осуществления тех или иных исходов каждого испытания.
Рассматривается последовательность п независимых испытаний, под которой будем понимать дискретное новое пространство 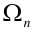
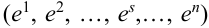
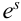

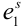
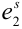
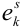
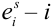



Пример №9
Пусть испытание состоит в подбрасывании игральной кости. Пространство элементарных событий 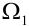
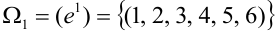
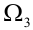
Обычно исходы обозначали большими заглавными буквами. Переобозначим! Пусть происходит 



Обозначим событие 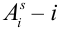



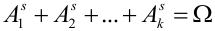
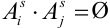
Обозначим вероятность 
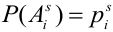
Пусть при первом испытании произошло событие под номером 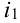
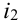

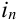

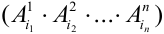
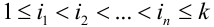
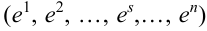
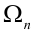
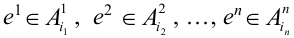
Испытания — независимые, следовательно, по теореме 4, имеет место равенство:
В случае, когда вероятности событий 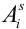
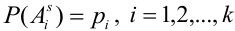
В силу несовместности и единственной возможности исходов, очевидно, что 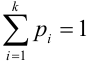
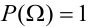
Теорема. Если данные 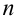
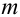
Теорема. Для того, чтобы 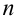
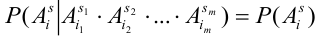
для любой группы чисел 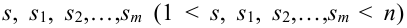
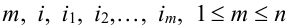
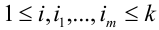
Формулы Бернулли
Пусть проводятся последовательные независимые испытания, и наблюдается результат совместного осуществления тех или иных исходов каждого испытания.
Схема независимых испытаний является математической моделью серии испытаний, повторяющихся при неизменных условиях. Такая схема называется полиномиальной.
Простейшим классом повторяющихся независимых испытаний является последовательность независимых испытаний с двумя исходами (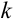
Определение 27. Независимые испытания при двух исходах называются испытаниями Бернулли.
Пример №10
Определить вероятность того, что в результате проведения 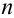

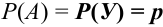
Решение.
Искомую вероятность обозначим 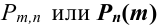
Событие А в данных испытаниях может появиться ровно 
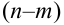
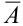
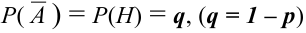
Сначала найдем вероятность того, что события У наступают при определенных 

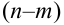
По условию данные события — независимые, следовательно, по теореме 4 для произведения независимых событий можем записать, что
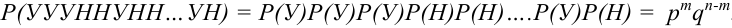
Число успехов и неудач задано. Можно менять только их расположения в цепочках, которое однозначно определяется выбором из 

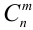
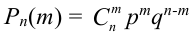
В данной задаче мы доказали теорему Бернулли.
Теорема Бернулли. Если 


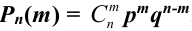
Следствие. 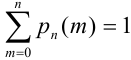

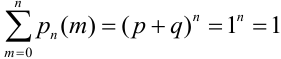
Пример №11
Пусть монета брошена 5 раз. Требуется найти вероятность того, что выпало ровно 3 орла.
Решение.
В каждом из 5 независимых испытаниях (
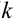
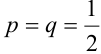

По формуле Бернулли 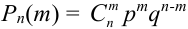
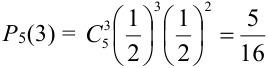
Замечания.
Замечание 1. Вероятность 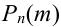
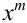
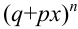
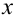
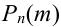
Замечание 2. Рассмотрим схему испытаний с произвольным количеством исходов. Пусть каждое из 
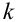
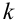
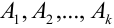
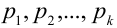

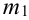
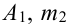
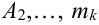
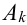

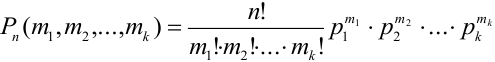
Эта совокупность вероятностей является коэффициентом при 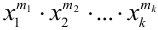
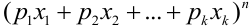
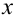
Например. При 

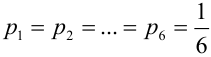
Если различать только «6» и «не 6», то получим схему Бернулли с двумя исходами (
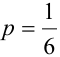
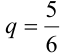
Замечание 3. При вычислении вероятности события, состоящего в том, что число успехов m лежит, например, между а и b, приходится находить числовые значения сумм вероятностей вида: 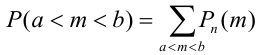
Например, вероятность того, что событие наступит а) менее 



a) 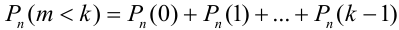
b) 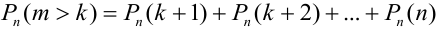
c) 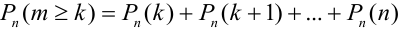
d) 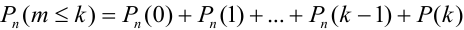
В некоторых случаях удобнее перейти к противоположному событию, например, 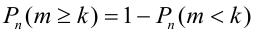
Пример №12
Пусть монета брошена 5 раз. Требуется найти вероятность того, что 1) менее двух раз выпал орел, 2) не менее двух раз выпал орел.
Решение.
Два исхода (
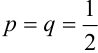
1) Орел выпал менее двух раз, значит, не выпал или выпал раз.
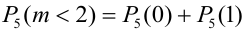
2) Орел выпал не менее двух раз, т.е. выпал два раза или три или четыре или пять:
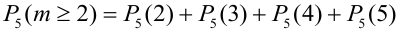
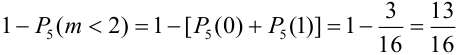
Замечание 4. В примере на формулу Бернулли вычисления проводятся очень легко, однако часто приходится вычислять вероятности при очень больших значениях n и m, например, при n = 1000, m = 500. Также затруднения при вычислении возникают при малых значениях р или q.
В этих случаях удается заменить формулу Бернулли какой-нибудь приближенной асимптотической формулой. Существуют три предельные теоремы, содержащие такие формулы.
Предельные теоремы в схеме Бернулли
Теорема Пуассона (асимптотическая формула для случая малых значений р)
Если вероятность наступления некоторого события А в n независимых испытаниях постоянна и равна р, причем 

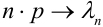
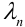
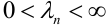
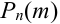

Замечания.
1. Часто формула Пуассона записывается в виде равенства, но надо помнить при этом, что оно верно при 
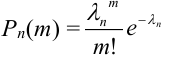
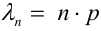
2. Формулой пользуются при больших n и малых р. Например, при n > 100, 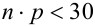
3. Теорема имеет место и в том случае, когда вероятность события А в каждом испытании равна нулю. В этом случае 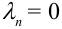
4. Существуют таблицы значений данной вероятности (стр. 410, 411 в задачнике Ефимова -Демидовича).
Пример №13
Вероятность попадания в цель при каждом выстреле равна 0,001. Найти вероятность попадания в цель двумя и более пулями, если число выстрелов равно 5000.
Решение.
Считаем каждый выстрел за испытание и попадание в цель за событие. Количество испытаний n = 5000 (велико), р = 0,001 (мало). По формуле Бернулли считать сложно. Поэтому применим формулу Пуассона.
Найдем среднее число попаданий: 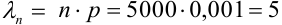
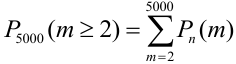
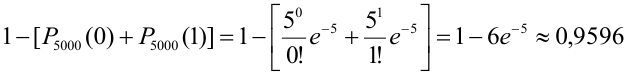
По точной формуле (формуле Бернулли) 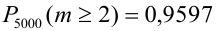
Локальная предельная теорема Муавра — Лапласа (асимптотическая формула для случая больших значений n и m)
Если вероятность наступления некоторого события А в n независимых испытаниях постоянна и равна р, (0 < р < 1), то вероятность 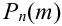

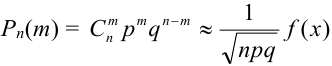
где 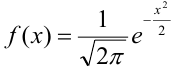
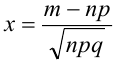
Замечания.
1. Часто формула Пуассона записывается в виде равенства, но надо помнить при этом, что оно верно при 
2. Формулой пользуются при больших n и m. Например, при п > 100, 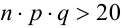
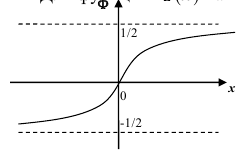
3. Из того, что 
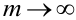
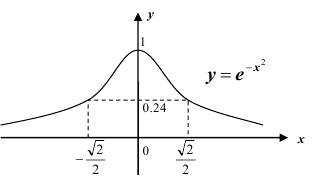
4. Существуют таблицы значений функции 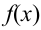
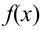
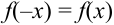
Пример №14
Найти вероятность того, что событие А наступит ровно 70 раз в 243 испытаниях, если вероятность появления этого события в каждом испытании равна 0,25.
Решение.
Количество испытаний n = 243, количество успехов m = 70, вероятность успеха р = 0,25, вероятность неудачи q = 1 — 0,25 = 0,75.
По формуле Бернулли считать сложно. Так как n и m велики, поэтому применим формулу Муавра — Лапласа.
Найдем сначала х и 
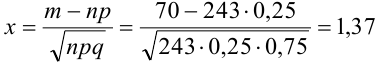
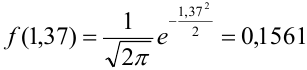
Можно было не считать значение 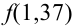
Подставим найденное значение 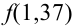
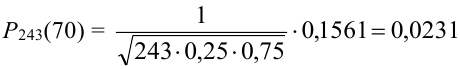
Предельная интегральная теорема Муавра — Лапласа (асимптотическая формула для случая, когда число успехов m лежит в некоторых пределах)
Теорема 1. Если m — число наступлений события А в n независимых испытаниях, в каждом из которых вероятность этого события равна р (0 < р < 1), то равномерно относительно а и b 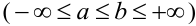
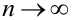
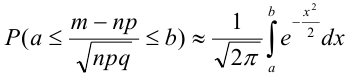
В некоторых источниках 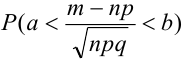
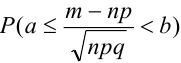
Ранее вывели, что 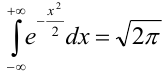
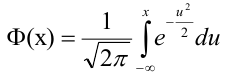
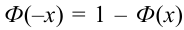
Либо, функция Лапласа может быть в виде: 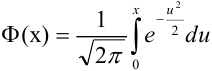
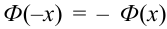
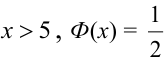
Теорема 2. (Теорема Муавра-Лапласа) Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р (0 < р < 1), событие А наступит не менее 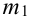
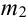
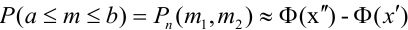
где Ф(х) — функция Лапласа, значения 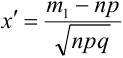
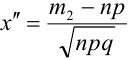
Теорема 3. (Закон больших чисел или теорема Бернулли).
При неограниченном увеличении числа однородных независимых опытов частота события будет сколь угодно мало отличаться от вероятности события в отдельном опыте.
Иначе, вероятность того, что отклонение относительной частоты наступления события 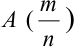
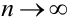
Доказательство.
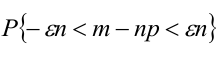
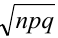
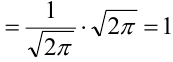
Пример №15
Вероятность появления события А в каждом из 100 независимых испытаний постоянна и равна 0,8. Найти вероятность того, что событие появиться не менее 75 раз и не более 90 раз.
Решение.
Количество испытаний n = 100, вероятность успеха р = 0,8, вероятность неудачи q = 1 — 0,8 = 0,2 , 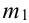
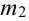
Найдем 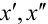
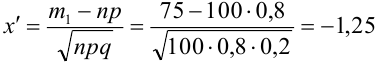
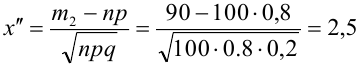
По теореме 2:
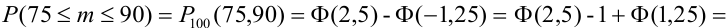
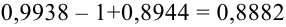
Наивероятнейшее число появления события в независимых испытаниях
Определение 28. Число 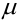
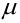
Наивероятнейшее число 
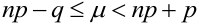
причем 1) если (np — q) -дробное, то существует одно 

Пример №16
Испытывается каждый из 15 элементов некоторого устройства. Вероятность того, что элемент выдержит испытание, равна 0,9. Найти наивероятнейшее число элементов, которые выдержат испытание и вероятность этого числа.
Решение.
Количество испытаний n = 15, вероятность успеха р = 0,9, вероятность неудачи q = 0,1.
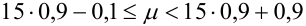
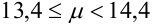
Т.к. 

Всё о формуле полной вероятности
Пусть событие 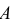
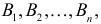
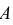
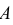
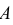
В силу несовместимости событий можно записать
Используя теорему умножения вероятностей, получаем формулу
которая и называется формулой полной вероятности.
Обычно ее записывают кратко:
Пример №17
Имеется две коробки деталей, в каждой из которых по 10 деталей. В первой коробке среди деталей две низкого сорта, а во второй четыре низкосортных детали. Из первой коробки для нужд производства взяли наугад половину деталей, а оставшиеся высыпали во вторую коробку. Через некоторое время из второй коробки взяли наугад деталь. Какова вероятность того, что это деталь низкого сорта?
Решение. Обозначим через A событие, состоящее в выборе из второй коробки детали низкого сорта. Возможность этого выбора зависит от того, какие именно детали были добавлены во вторую коробку. На этот счет можно выдвинуть следующие предположения: B1 – во вторую коробку добавили пять годных деталей; B2 – добавили одну деталь низкого сорта и четыре доброкачественные; B3 – добавили две детали низкого сорта и три доброкачественные. Пять деталей во вторую коробку можно переложить 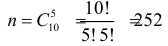
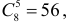
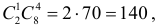
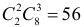
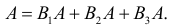

Ответ. 1/ 3.
Всё о Формуле Байеса
Пусть событие A может наступить только при появлении одного из несовместных событий 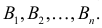

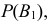
Проделан опыт, в результате которого событие A произошло. Тогда вероятности событий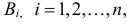
Формулы Байеса позволяют переоценивать вероятности гипотез (событий 
Пример №18
По каналу связи передается одна из последовательностей букв 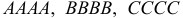
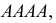
Решение. Для краткости записи формулы обозначим 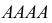
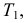
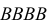
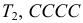
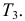
Ответ. 8/9.
Пример №19
Три стрелка производят по одному выстрелу в одну и ту же мишень. Вероятности попадания в мишень при одном выстреле для этих стрелков соответственно равны 0,8; 0,7; 0,6. Какова вероятность того, что третий стрелок промахнулся, если в мишени оказалось две пробоины?
Решение. Обозначим через А событие, состоящее в появлении двух пробоин в мишени. В отношении двух пробоин могут быть три предположения: В1 – попали первый и второй стрелки, а третий не попал, вероятность чего равна 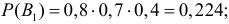
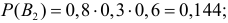
Заметим, что 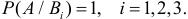
Ответ.
Пример №20
В партии из 10 изделий с равными шансами может оказаться от нуля до трех бракованных. Наугад взяли и проверили три изделия. Они оказались годными. Какова вероятность того, что остальные изделия в партии тоже годные?
Решение. Насчет содержания в партии бракованных изделий по условиям задачи может быть четыре предположения 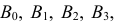
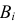
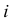
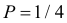
Заметим, что 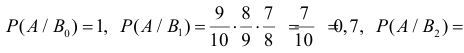
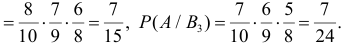
Ответ.
Пример №21
Вероятность того, событие B произойдет в течение часа, равна 0,9. Оказалось, что в течение первых 40 мин. событие B не произошло. Какова вероятность того, что это событие появится в оставшиеся 20 мин. времени?
Решение. В отношении события 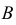
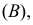
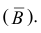
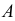
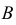
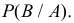
В задаче по умолчанию предполагается, что событие 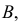
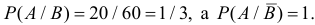
Ответ. 3/4.
Пример №22
В кошельке лежат четыре монеты. Три монеты обычных, а у четвертой на той и другой стороне изображен герб. Наугад взяли монету и подбросили три раза. Все три раза выпал герб. Какова вероятность того, что и при четвертом подбрасывании выпадет герб?
Решение. Обозначим через B1 – выбор монеты с одним гербом, через B2 – выбор монеты с двумя гербами. Априорные вероятности этих событий равны: 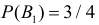
Обозначим через A – выпадение трех гербов подряд. Апостериорные вероятности по формулам Байеса равны:
Тогда по формуле полной вероятности (2.4.1):
P(выпадения герба в четвертый раз)
Ответ.
Подробное объяснение формулы полной вероятности
Постановка задачи: Пусть 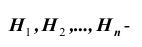
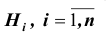


Требуется найти вероятность события A.
Выведем формулу решения этой задачи. Имеем
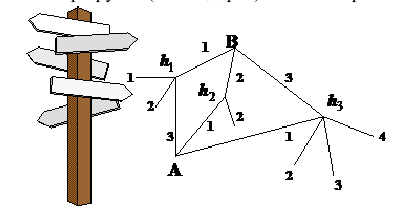
маршрутов (схема дорог). Какова вероятность того, что он попадет в пункт А ?
Решение. Как видим из схемы дорог, путь туриста обязательно проходит через один из пунктов 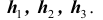
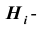
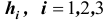
Заметим, что события (гипотезы)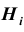
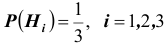
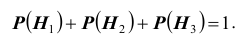
видеть (см. схему), что 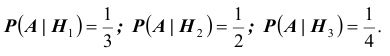
Пример №23 (о мудреце и властелине).
Властелин, разгневавшись на мудреца, приказал отрубить ему голову. Но затем, смягчившись, дал мудрецу возможность попытаться спастись. Итак, властелин взял 2 белых и 2 черных шара и предложил мудрецу распределить их по своему усмотрению по двум одинаковым урнам. После чего, палач сначала наугад выберет одну из урн, а затем также наугад, не глядя, вытащит из неё один шар. Мудрец будет помилован, если вытянутый шар оказался белым. Какую стратегию распределения шаров по урнам должен
выбрать мудрец, чтобы быть помилованным? Какова максимальная вероятность спастись мудрецу? Какая стратегия наименее выгодна для него?
Решение. Выдвинем гипотезы (предположения) 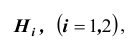
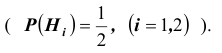
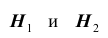
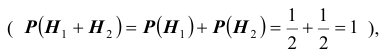
палачом вытянут белый шар. Далее, рассмотрим следующие варианты распределения мудрецом шаров по
урнам:
1). В первой урне 2 белых, а во второй 2 черных шара. Тогда
2 Хотим заметить, что далеко не всегда властелины были глупыми людьми, не знающими математики. Так, например, Наполеон был немного математиком, интересовался, в частности, геометрией. Он вёл дискуссии с Лагранжем и Лапласом, когда ещё не был правителем Франции.
Как-то в одной из таких дискуссий Лаплас резко оборвал Бонапарта: «Менее всего мы хотим от Вас, генерал, урока геометрии». В дальнейшем Лаплас стал его главным военным инженером. Наполеону приписывают теорему: «Если на сторонах произвольного треугольника во внешнюю сторону построены равносторонние треугольники, то их центры образуют равносторонний треугольник» — это так называемый вешний треугольник Наполеона.Так же ему приписывают один из знаменитых палиндромов (читается в обе стороны одинаково): «ABLE WAS I ERE I SAW ELBA» — я был силён, пока не увидел Эльбу.
2). В первой и во второй урнах по 1 белому и 1 черному шару. Тогда
3). В первой урне 1 белый, а во второй 1 белый и 2 черных шара. Тогда
4). В первой урне 1 черный, а во второй 2 белых и 1 черный шары. Тогда
5). Первая урна оказалась пустой, т.е. все шары во второй урне. Тогда
Как видим, наиболее предпочтительной является 3-я стратегия, ей соответствует вероятность быть помилованным равная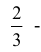
Вероятность гипотез. Формула Байеса
Постановка задачи: Пусть 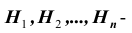
и пусть событие A может произойти лишь совместно с каким — либо одним из этих событий (гипотез) — ситуация аналогичная той, которая была ранее. И пусть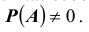
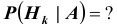
По теореме об умножении вероятностей
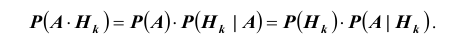
Полученная формула называется формулой Байеса (Бейеса) для переоценки гипотез. Другими словами: вероятность 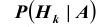
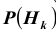
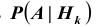
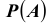
Пример №24
При обследовании больного имеется подозрение (т.е. делаются предположения или, что то же самое, выдвигаются гипотезы)
на одно из двух заболеваний 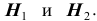
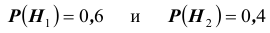
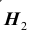
Решение. Во — первых, очевидно, что события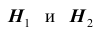
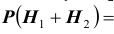
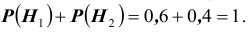
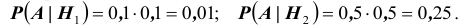
Как видим, при данных результатах обследования следует предполагать болезнь
Повторение испытаний
Формула Бернулли (схема повторения опытов)
Опыты называются независимыми , если вероятность того или иного исхода каждого опыта не зависит от того, какие исходы имели другие опыты. Независимые опыты могут проводиться как в одинаковых условиях, так и в различных. В первом случае вероятность появления какого — либо события A во всех опытах одна и та же, во втором случае — она меняется от опыта к опыту. Ниже мы воспользуемся понятием сложного события, понимая под ним совмещение нескольких отдельных событий, которые называют простыми. Итак, пусть производится n независимых опытов в одинаковых условиях, в каждом из которых некоторое событие A может произойти с одной и той же вероятностью 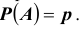
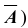
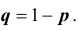
Итак, еще раз: схемой Бернулли называется последовательность n независимых испытаний, проводимых при одних и тех же условиях, в каждом из которых событие A либо происходит с постоянной вероятностью p , не зависящей от номера испытания, либо не происходит с вероятностью
Ставятся задачи:
Задача №1. Найти вероятность 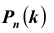
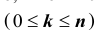
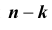
Задача № 2. Найти вероятность 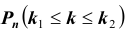
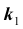
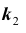
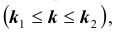
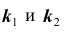
Задача № 3. Найти наивероятнейшее число 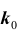
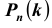
Решение №1.
Вероятность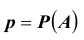
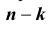
Таких несовместных событий столько, сколько сочетаний из n элементов по k элементов в каждом. Поэтому по теореме о вероятности суммы несовместных событий получим формулу, называемую формулой Бернулли:
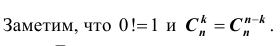
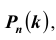
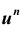
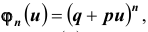
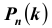
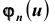
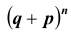
которую называют биномиальным законом распределения вероятностей события A в n испытаниях схемы Бернулли.
Заметим, что вероятность хотя бы одного появления события A в n испытаниях схемы Бернулли равна: 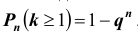
следующим вопросом: честное ли пари вам предлагают, если вы выиграете в том случае, когда при 24-х кратном бросании двух игральных костей хотя бы один раз одновременно появятся две шестёрки? Ответ дайте в конце пары.
(РЕШЕНИЕ. Вероятность одновременного выпадения двух шестерок при одном подбрасывании равна 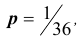
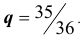
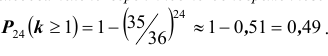
Другие примеры на применение формулы Бернулли, рассмотрим немного позднее, а именно после того, как решим задачи № 2 и № 3
Решение № 2.
Нетрудно показать, что вероятность 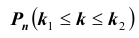
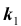
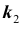
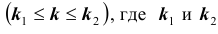
Решение № 3
Важной является задача № 3 о наивероятнейшем числе 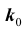
Рассмотрим отношение:
Из полученного следует, что:
1) если 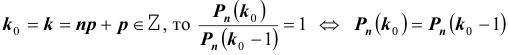
два максимума;
2) если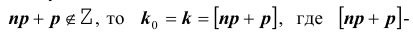
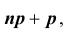
Пример №25
При некоторых условиях стрельбы вероятность p попадания в цель при одном выстреле равна
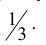
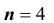
- а). Каково наивероятнейшее число попаданий в цель?
- б). Какова его вероятность?
- в). Какова вероятность двух попаданий?
- г). Какова вероятность хотя бы одного попадания?
Пример №26
Некто Сэмюэль Пепайс обратился к Исааку Ньютону с вопросом: какое из событий наиболее вероятно —
- появление по крайней мере одной «шестерки» при подбрасывании 6-ти игральных костей;
- хотя бы двух «шестерок» при подбрасывании 12-ти;
- хотя бы трех «шестерок» при подбрасывании 18-ти?
Решение.
Вероятность q непоявления «шестерки» при одном подбрасывании, как известно, равна 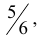
5 . Таким образом, вероятность появления по крайней мере одной «шестерки» при подбрасывании 6-ти игральных костей может быть найдена по формуле:
Событие «хотя бы две» противоположно событию «либо ни разу, либо один раз», т.е.
Событие «хотя бы три» противоположно событию «либо ни разу, либо один раз, либо два раза», т.е.
Таким образом, как видим, предпочтительнее первая стратегия – таким и был ответ Ньютона.
Замечу, что при больших значениях числа n испытаний в схеме Бернулли формула для подсчета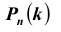
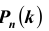
ТЕОРЕМА Пуассона 3. Пусть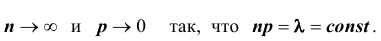
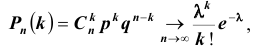
Доказательство
Что и требовалось доказать.
При доказательстве можно воспользоваться приближенной формулой Стирлинга.
Следствие: при указанных выше условиях, т.е. при 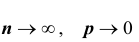
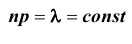
Пример №27
Телефонная станция обслуживает 800 абонентов. Для каждого абонента вероятность того, что в течении часа он позвонит на станцию равна p =0,01. Найти вероятность того, что четыре абонента позвонят на станцию в течении часа.
Решение
Теорема Муавра — Лапласа (локальная)
Остановлюсь еще на двух предельных теоремах в схеме Бернулли — локальной теореме Муавра — Лапласа (её доказательство получим как частный случай закона больших чисел — предельной теоремы Ляпунова, доказательство которой нам ещё предстоит провести) и интегральной теореме Муавра — Лапласа. Итак:
причем, во-первых, погрешность этой формулы есть величина порядка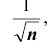
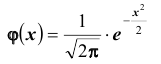
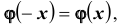
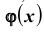
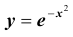
интегральная приближенная формула Лапласа ( при больших
Для функции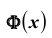
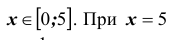
равносильно условию 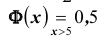
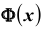
Замечание: если функция Лапласа записана в виде 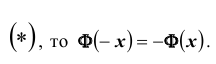
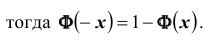
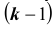
Формула полной вероятности и сложные задачи
В данном разделе мы рассмотрим более сложные задачи, имеющие большое практическое значение. Эти задачи встречается на практике в случае, если имеются несколько возможных сценариев развития событий (несколько вероятных гипотез). Известны как величины вероятности реализации каждого из сценариев, так и вероятность наступления интересующего нас события для любого из этих сценариев, а нас интересует, какова полная (совокупная) вероятность наступления интересующего нас события.
Предположим, что в результате опыта может произойти одно из n несовместных событий (гипотез) 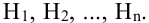
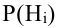
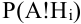
Пример №28
Из 40 деталей 10 изготовлены в первом цехе, 25 — во втором, а остальные — в третьем. Первый и третий цехи дают продукцию отличного качества с вероятностью 0,9, второй цех — с вероятностью 0,7. Какова вероятность того, что взятая наудачу деталь будет отличного качества?
Решение:
Обозначим событие А = {выбрана деталь отличного качества}, Hi= {выбранная деталь изготовлена в i цехе}, i = 1, 2, 3. Тогда
По условию задачи 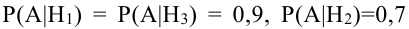
Пример №29
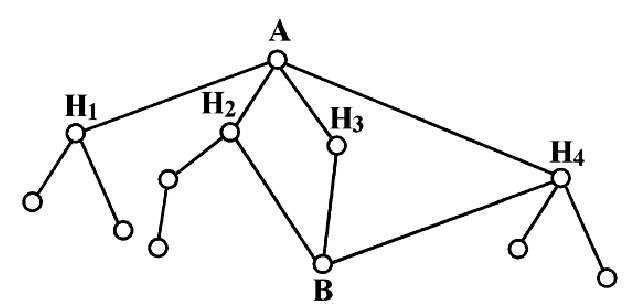
На рисунке изображена схема дорог. Найти вероятность того, что турист, вышедший из пункта А, попадет в пункт В, если на развилке он наугад выбирает любую дорогу (кроме обратной).
Решение:
Обозначим Нi = {приход туриста в пункт Hi}, i = 1, 2, 3, 4. Поскольку, выйдя из пункта А, он выбирает любую дорогу наугад, то 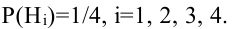
Исходя из схемы дорог, определяем, что
Таким образом, по формуле полной вероятности
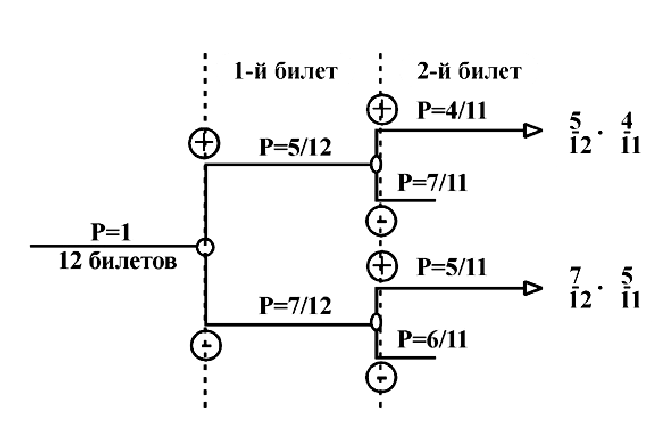
Пример №30
Из двенадцати лотерейных билетов пять выигрышных. Билеты вытягиваются по одному без возвращения. Какова вероятность того, что во второй раз вытянут выигрышный билет?
Решение:
Как обычно, вдоль каждой ветви «дерева вероятностей» значения вероятностей перемножаются, а затем значения на концах нужных веток между собой складываются. В результате получаем ответ:
Случайные события независимые в совокупности
Следует различать попарно независимые случайные события и случайные события независимые в совокупности.
Определение: События называются попарно независимыми событиями, если любые два из них независимы.
Определение: События 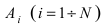
Замечание: Из определений видно, что из попарной независимости еще не следует, что эти события независимы в совокупности. Это означает, что условие независимости в совокупности является более сильным, чем условие попарной независимости случайных событий.
Теорема: Вероятность наступления хотя бы одного из событий 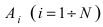
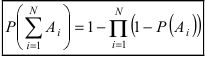
Доказательство: Обозначим через А событие, состоящее в том, что наступит хотя бы одно из событий 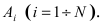
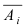
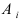
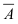
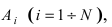
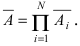
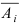
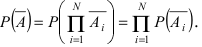
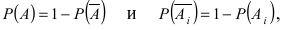
Пример №31
Пусть прибор содержит N последовательно соединенных блоков. Определить вероятность того, что цепь будет разорвана, если вероятность работы каждого блока равна р и она не зависит от работы других блоков.
Решение:
Пусть А — событие, которое состоит в том, что данная цепь разорвана. Это событие происходит, если выходит из строя хотя бы один из блоков, так как блоки включены последовательно. Противоположное событие состоит в том, что все блоки работают, т.е. 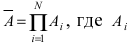
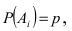
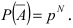
Теорема сложения вероятностей для совместных событий
Если случайные события одновременно появляются в условиях опыта, то имеет место следующая теорема.
Теорема: Вероятность суммы двух совместных событий равна сумме вероятностей этих событий минус вероятность их произведения:
Доказательство: Пусть в результате опыта возможно n равно возможных, несовместных, элементарных исходов. При этом в 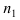
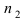
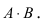
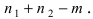
Замечание: Методом математической индукции вышеприведенная теорема может быть обобщена на любое число совместных событий, например, в случае 3 совместных событий А, В и С теорема принимает вид:
Пример №32
Найти вероятность того, что взятое наугад число из чисел от 10 до 20 делится или на 2, или на 3.
Решение:
Всего равновозможных, элементарных исходов 11 (числа от 10 включительно до 20 включительно). В 6 случаях (10, 12, 14, 16, 18, 20) число кратно 2; в 3 случаях (12, 15, 18) число кратно 3; в 2 случаях (12, 18) число кратно и 2, и 3. Пусть событие А состоит в том, что наугад взятое число кратно 2, а событие В состоит в том, что наугад взятое число кратно 3. Сложное событие С состоит в том, что наугад взятое число делится или на 2, или на 3, т.е. С = А + В. Следовательно, вероятность этого события равна:
Все вышерассмотренные теоремы объединяются в теории вероятностей общим названием “основные теоремы теории вероятностей”.
Формула полной вероятности и события
Формула полной вероятности является следствием основных теорем теории вероятностей: теорем сложения и умножения вероятностей событий.
Пусть некоторое случайное событие А наступает с одним и только с одним из несовместных событий
Определение: События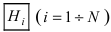
Теорема: Формула полной вероятности определяет вероятность случайного
события л, как сумму произведений вероятности каждой гипотезы 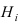
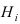
Доказательство: Событие А наступает с одним и только с одним из несовместных событий 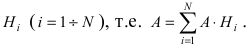
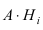
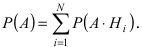
Пример №33
Пусть на сборку поступают детали с двух автоматических станков. Первый станок дает в среднем 0.3 % брака, а второй — 0.15 % брака. Производительность второго станка в два раза выше, чем первого станка. Найти вероятность того, что наугад взятая деталь окажется бракованной.
Решение:
Пусть событие А состоит в том, что наугад взятая деталь окажется бракованной. Тогда гипотеза 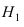
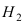
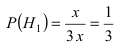
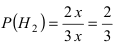
Вероятности события А при условии реализации первой и второй гипотез равны: 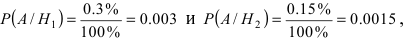
Формула вероятностей гипотез (формула Байеса)
Ниже будет получена формула, которая является следствием основных теорем теории вероятностей и формулы полной вероятности. Эта формула применяется для решения задач следующего типа. Пусть проводится эксперимент, в результате которого может появиться или не появиться событие л, которое наступает с одним и только с одним из несовместных событий 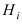
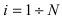
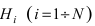
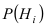
Теорема: Вероятность гипотезы 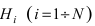
Доказательство: Событие А наступает с одним и только с одним из несовместных событий 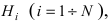
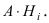
Следовательно, 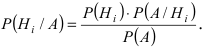
Пример №34
Однотипные пластмассовые детали изготавливаются на 3 прессах. Первый пресс выпускает 50 % всех деталей, второй — 40 %, третий — 10 % . При этом с первого пресса сходит в среднем 0.025 нестандартных деталей, со второго — 0.02 и с третьего — 0.015. Все детали поступают на сборку. Взятая наудачу деталь оказалась нестандартной. Какова вероятность того, что она изготовлена на первом прессе.
Решение:
Событие А состоит в том, что наудачу взятая деталь изготовлена на первом прессе. Гипотеза 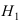
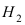
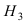
По условию задачи 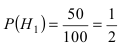
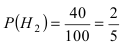
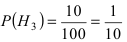
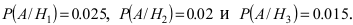
Используя формулу Байеса, получим
Независимые испытания и формула Бернулли
Пусть испытания повторяются n раз, причем событие А появляется в каждом опыте с одной и той же вероятностью р или не появляется с одной и той же вероятностью
Определение: Испытания называются независимыми, если вероятность события А не зависит от того, какие события появились в предыдущих опытах, или появятся в последующих экспериментах.
Пример:
Независимы ли следующие испытания: а) многократное бросание кубика; б) извлечение карты из колоды без ее возвращения в колоду (выяснить самостоятельно).
Формула Бернулли
Теорема: Пусть проводится серия из n независимых испытаний, в каждом из которых событие А появляется с постоянной вероятностью 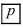
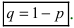
Доказательство: Пусть 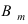
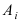
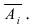
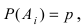
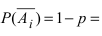
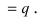
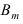
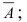
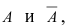
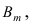
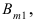
Воспользуемся теоремой умножения вероятностей для независимых событий, получим: 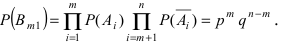
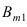
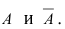
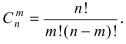
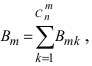
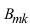
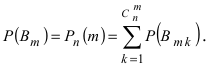
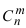
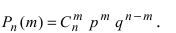

Пример №35
Монета подбрасывается 6 раз. Определить вероятность того, что герб выпадет а) 5 раз; б) от 2 до 4 раз.
Решение:
Вероятность выпадения герба не изменяется от опыта к опыту и равна 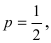
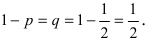
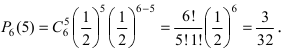
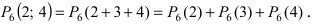
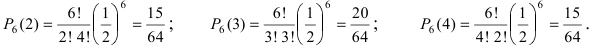
При больших значениях чисел m и n применение формулы Бернулли затруднительно, так как вычисление коэффициентов 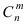
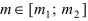
Формула Пуассона
Если при проведении серии испытаний по схеме Бернулли вероятность появления события А мала (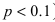
Формулы Муавра-Лапласа
Если при проведении серии испытаний по схеме Бернулли вероятность появления события А р>0.1, то при больших значениях чисел m и n применяют дифференциальную формулу Муавра-Лапласа: 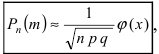
Замечание: В общем случае дифференциальная формула Муавра-Лапласа применяется при выполнении неравенств
Если при проведении серии испытаний по схеме Бернулли числа m и n принимают большие значения, причем число m принимает значения от 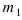
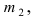
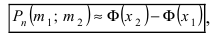
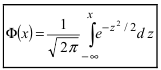
- Повторные независимые испытания
- Простейший (пуассоновский) поток событий
- Случайные величины
- Числовые характеристики случайных величин
- Комбинаторика — правила, формулы и примеры
- Классическое определение вероятности
- Геометрические вероятности
- Теоремы сложения и умножения вероятностей