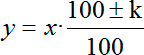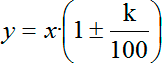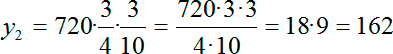Формула сложных процентов егэ

«Хороший учитель обязан понимать, что никакую задачу нельзя исчерпать до конца. Этот взгляд он должен прививать и своим ученикам».
Д. Пойа.

Введение.

Особое внимание я уделяю текстовым задачам на проценты, которые часто встречаются в практике вступительных экзаменов в экономические вузы, но недостаточно полно рассматриваются в школе. Умение выполнять процентные вычисления, − безусловно, одна из самых необходимых математических компетенций. Однако не только те, кто уже давно окончили школу, робеют при виде процентов. Даже на ЕГЭ решаемость задач на проценты не превышает 20 % . Это говорит о том, что такого типа задачи следует решать не только в младших классах, где изучается эта тема, но и на протяжении всех лет обучения в школе.

1. При решении задач на проценты используются основные формулы:

1% числа а равен а.

р% от числа а равно  а.

Если известно, что некоторое число а составляет р% от х, то х можно найти из пропорции

а   − р%

х   − 100%,

откуда х= а.

Пусть имеются числа a, b, причем а<b. Тогда

Число b больше числа а на100%.

Число а меньше числаbна100%.

2. Формула сложных процентов.

Если на вклад положена сумма а денежных единиц, банк начисляет р% годовых, то через n лет сумма на вкладе составит

aден.ед.

3. Задачи на проценты.

Задача 1.

Умных людей на 45 % меньше, чем красивых, 36% умных обладают красивой внешностью. Каков процент умных людей среди красивых?

Решение: пусть х − количество красивых людей, тогда количество умных людей:

х − 0,45х = 0,55х.

Среди умных 36% составляют красивые люди, следовательно, количество умных и одновременно красивых людей:

0,36 ·0,55х= 0,198х.

Составим пропорцию:

х −  100%

0,198х −  а%.

Отсюда получим:

а = 19,8%.

Ответ: 19,8%

Учащиеся с интересом решают текстовые задачи на проценты, которые ближе к реальной жизни. Особый «прикол» представляет собой подача задач не из задачника, а прямо с газетной полосы. Тут уж не возникает мыслей о ненужности математики. А «процентная журналистика» в связи с разразившимся экономическим кризисом на страницах газет буквально процветает.

Задача 2.

Цены на путевки уже подросли: например, туры во Францию − на 20%. Можно ли сказать, на сколько процентов раньше тур во Францию был дешевле?

Решение: пусть х − старая цена, а n − новая цена.

1) Составим первую пропорцию:

х −  100%

n − 120%,

Получим n=1,2х.

2) Составим вторую пропорцию:

1,2х − 100%

х − (100-а%)

(100-а) 1,2х = 100х

Решив уравнение, получим: а ≈17%.

Ответ:17%.

4. Использование формулы сложных процентов.

Задача 3.

На банковский счет было положено 10 тыс. руб. После того, как деньги пролежали один год, со счета сняли 1 тыс. руб. Еще через год на счету стало 11 тыс. руб. Определите, какой процент годовых начисляет банк.

Решение: пусть банк начисляет р% годовых.

1) Сумма в 10000 рублей, положенная на банковский под р% годовых, через год возрастет до величины

10000+

2) Когда со счета снимут 1000 руб., там останется 9000+100р руб.

3) Еще через год последняя величина за счет начисления процентов возрастет до величины

9000+100р+

По условию эта величина равна 11000:

Решив это уравнение получим: =10, =−200 − отрицательный корень не подходит.

Ответ:10%

Задача 4. (ЕГЭ-2015)

Банк под определенный процент принял некоторую сумму. Через год четверть накопленной суммы была снята со счета. Но банк увеличил процент годовых на 40%. К концу следующего года накоплена сумма в 1,44 раза превысила первоначальный вклад. Каков процент новых годовых?

Решение: от суммы вклада ситуация не изменится. Положим в банк 4 рубля (делится на 4). Через год сумма на счету увеличится ровно в p раз и станет равной (4p) рублей.

Поделим её на 4 части, унесём домой (p) рублей, оставим в банке (3p) рублей.

Известно, что к концу следующего года в банке оказалось 4·1,44 = 5,76 рублей. Итак, число (3p) превратилось в число (5,76). Во сколько раз оно увеличилось?

 

Таким образом, найден второй повышающий коэффициент k банка.

Интересно, что произведение обоих коэффициентов равно 1,92:

 

Из условия следует, что второй коэффициент на 0,4 больше первого.

 

 

Избавившись от запятых, сделаем замену t = 10р:

 

Из такого уравнения получить 12 совсем просто.

Итак, p = 1,2, k = 1,6.

В 1,2 раза увеличилась сумма вклада первый раз, в 1,6 раз — во второй раз.

Было 100%, стало 160%. Новый процент годовых равен 160%-100% = 60%.

Ответ: 60%.

Задача 5. (ЕГЭ-2015)

В банк помещена сумма 3900 тысяч рублей под 50% годовых. В конце каждого из первых четырех лет хранения после вычисления процентов вкладчик дополнительно вносил на счет одну и ту же фиксированную сумму. К концу пятого года после начисления процентов оказалось, что 

размер вклада увеличился по сравнению с первоначальным на 725%. 

Какую сумму вкладчик ежегодно добавлял к вкладу?

Решение: пусть х рублей – вкладчик ежегодно добавлял ко вкладу.

50% годовых означает, что каждый год сумма на счету вкладчика увеличивается в 1,5 раза. Если вкладчик ничего бы не добавлял к первоначальной сумме, то через год на его счету было бы 3900·1,5, через два года — 3900·1,52 и так далее.

 Посчитаем, какой доход принесли все четыре добавки.

х∙1,5⁴ + х∙1,5³ + х∙1,5² +х∙1,5

Для этого вынесем х за скобку и вычислим сумму геометрической прогрессии, в которой b = 1,5 и q = 1,5.

Известно, что размер вклада увеличился по сравнению с первоначальным на 725%. 

Это значит, что он стал составлять 825% от начального, т.е. увеличился в 8,25 раз.

Сумма всех слагаемых последнего столбика в 8,25 раз больше, чем 3900 тыс.руб.

Ответ: 210 тысяч рублей.

5. Литература.

1. С.Я. Криволапов. Пособие по математике для абитуриентов. М., 2004.
2. Математика в школе. №6, 2009.
3. Типовые варианты ЕГЭ-2015.

Применение банковских формул простых и сложных процентов при решении задач ЕГЭ экономического содержания

• Авторы
• Руководители
• Файлы работы
• Наградные документы

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

ВВЕДЕНИЕ

В сентябре 2020 года мне исполнилось 14 лет, и я получил свой первый паспорт гражданина РФ. К этому возрасту у меня скопилась определенная сумма денег, которую я запланировал положить в банк под проценты с целью получения прибыли.

Понимая, что это дело важное и ответственное, что к нему нужно подходить основательно, я решил «подковаться» и изучить уроки финансовой грамотности на цифровом образовательном ресурсе «ЯКласс». В разделе «Как сберечь деньги с помощью депозитов» рассказывается о формулах простых и сложных процентов. Используя эти формулы, мною просчитана доходность разных вкладов в ведущих банках России. В результате я определился, в какой банк вложить свои деньги и какой вклад открыть.

Чуть позже мне попалась интересная задача, решенная с применением формулы сложных процентов. Изящество и гениальность приведенного решения поразили меня, ведь не зная этой формулы, пришлось бы выполнить огромное количество вычислений, занявшее много времени. Я узнал у своего учителя математики, что эти формулы не изучаются в школьном курсе математики. А пообщавшись с учащимися 10-11 классов, выяснил, что решение задач экономического содержания при подготовке к ЕГЭ по математике вызывают у многих из них затруднения, потому что приходится выполнять многочисленные вычислительные операции.

Все это обусловило проблему данного исследования, которая заключается в поиске оптимальных приемов и способов решения задач на проценты с учетом приобретенных мной новых знаний.

Главная цель исследования: научиться решать задачи экономического содержания,используя финансовые формулы простых и сложных процентов, найти для себя такие приемы и выработать такие практические навыки решения задач на проценты, которые в будущем помогут мне успешно подготовиться к сдаче ЕГЭ, в частности, раздела финансовой математики.

Гипотеза: используя формулы простых и сложных процентов, можно решать задачи экономического содержания легко и просто!

Задачи:

Познакомиться с основами финансовой грамотности, банковской системой и банковскими операциями с целью получения знаний, способствующих сохранению и преумножению вложенного мной капитала;

Изучить формулы простых и сложных процентов, с их помощью провести анализ вкладов, предлагаемых ведущими банками России, на предмет сохранения и получения максимальной прибыли;

Выработать алгоритм решения задач экономического содержания с применением банковских формул и продемонстрировать его учащимся моей школы;

Наглядно показать, как работать с этим алгоритмом при решении задач экономического содержания, определить способы и приемы их решения;

Подобрать тренировочные задания для отработки изученных приемов с целью приобретения практических навыков.

Предмет исследования: задачи экономического содержания (на проценты) в заданиях ЕГЭ.

Объект исследования: методы и приемы решения задач экономического содержания.

Методы исследования: математический; изучение, анализ и обобщение первичной информации; систематизация, классификация и обобщение.

ГЛАВА 1. Литературный обзор источников информации

Прежде чем приступить к практической части своей работы, мне необходимо было получить теоретические знания.

Для этого на цифровом образовательном интернет-ресурсе «ЯКласс» мною изучен курс «Основы финансовой грамотности» для учащихся 7‑9 классов [9]. Большая часть уроков курса опирается на учебное пособие доктора экономических наук Игоря Липсица и магистра экономики Ольги Рязановой «Финансовая грамотность» серии «Учимся разумному финансовому поведению». Из этого курса я узнал, что такое банковская система, виды финансовых организаций и банковских услуг, выяснил, в чем польза и риск банковских карт, познакомился с их разновидностями, понял, что такое налоги, почему их нужно платить [3]. Кроме того, я узнал, какие финансовые риски существуют, что такое финансовая пирамида и какие виртуальные ловушки подстерегают нас в настоящее время. Также я выяснил, что такое кредит, какие виды кредитования бывают, чем опасны микрокредиты. Особенно меня заинтересовала глава курса «Как сберечь деньги с помощью депозитов», ведь намерение открыть вклад в банке с целью сохранения и преумножения накопленного мной капитала и стало толчком к данному исследованию. Именно в этой главе я впервые узнал о формулах простых и сложных процентов [9].

На следующем этапе работы мною изучены первые три главы учебного пособия кандидата технических наук, заведующего кафедрой Высшей математики Московского финансово-промышленного университета «Синергия» Равгата Хамидуллина «Финансовая математика» [7]. В первой главе пособия я познакомился с основными терминами финансовой математики: понятиями процента, арифметической и геометрической прогрессии и их применением в простейших финансовых задачах. Вторая глава пособия посвящена простым процентам и формулам, по которым они начисляются. Третья глава посвящена формулам сложных процентов. Интересно то, что автор закон сложного процента выводит на основе простого. В конце второй и третьей главы приведено большое количество примеров финансовых и жизненных задач, иллюстрирующих обоснованность применения формул простых и сложных процентов, а также даются контрольные вопросы и задания для закрепления изученного материала.

Второй блок литературы, использованный мной в исследовательской работе, составляют реальные задачи экономического содержания. В частности мне очень помогла учебно-методическая разработка автора-создателя образовательного портала РЕШУ ЕГЭ Д.Д. Гущина «Встречи с финансовой математикой». Книга учит строить математические модели экономических ситуаций, исследовать эти модели, получать и понимать полученные выводы. [1] Также мною изучены и использованы в работе задачи из сборников для подготовки к профильному уровню математики под редакцией Ивана Ященко 2015, 2020 и 2021 годов [4], [5], [6].

Вывод: тщательно подобранные литературные источники помогли мне приобрести новые знания в области финансовой грамотности, изучить основные финансовые термины и формулы, рассмотреть примеры решения задач с применением этих формул, и теперь я готов приступить к практической части своего исследования.

ГЛАВА 2. Основные термины и формулы

Банковский вклад – это денежные средства, размещённые в банке на определённый срок или бессрочно и под определённый процент.

Вкладчик – лицо, помещающее денежные средства на вклад, стремясь сохранить и приумножить свои накопления.

Основные характеристики банковских вкладов:

— срок вклада – это период, в течение которого деньги будут храниться на депозитном счете в банке;

— сумма вклада – это деньги, переданные банку с целью получения дохода в виде процентов, полученных в ходе финансовых операций с вкладом;

— процентная ставка – прибыль в виде процентов, которую выплачивает банк вкладчику за пользование его деньгами.

Современную жизнь нельзя представить без понятия «процент». Оно является базовым понятием финансовой математики.

Процент – это одна сотая часть какой-либо величины, числа. Обозначается процент символом «%». Одна сотая доля числа Х называется одним процентом от числа X: 1% = 0,01X.

При рассмотрении вариантов вложения средств на вклад необходимо рассчитать доход, который будет получен по окончании срока действия вклада. Для этого существуют две финансовые формулы. Рассмотрим каждую из них.

Формула простых процентов:

или (1), где

– первоначальная сумма вклада,

– сумма вклада вместе с прибылью, начисленной по процентам,

– процентная ставка по вкладу,

– количество начислений в заданный срок (кварталов, лет и др.).

Формула простых процентов применяется в том случае, если прибыль по вкладу начисляется на первоначальную сумму вклада в течение всего срока действия договора. При этом сумма накопленных процентов по вкладу прибавляется к нему только по истечении срока его действия или вообще поступает на отдельный счёт. Схема вклада выглядит так:

Формула сложных процентов:

(2), при постоянной процентной ставке

 (3), при различной процентной ставке

Формула сложных процентов применяется в том случае, если сумма начисленных процентов каждый раз поступает не на отдельный счёт, а на счёт вклада. Так, после каждого начисления процентов сумма вклада увеличивается, и в новом периоде процент начисляется на новую (увеличенную) сумму. Такой процесс называется капитализацией вклада. Схема вклада выглядит так:

Выводы:

Вклад, рассчитанный по формуле простых процентов, подходит тем, кто хочет в течение всего срока вклада снимать со счета начисленные проценты и использовать по своему усмотрению, но доходность такого вклада ниже, чем при капитализации вклада (по формуле сложных процентов);

Прибыль при капитализации вклада нельзя снять до окончания срока договора по вкладу, а в случае необходимости это сделать, банк пересчитает прибыль по меньшей процентной ставке;

Прежде чем принять решение по вложению средств по одному из двух видов вклада, нужно оценить конкретную финансовую и жизненную ситуацию, учитывая цели и сроки вклада.

ГЛАВА 3. Практическая часть

Анализ вкладов в ведущих банках России

Чтобы выбрать банк для вложения своих накоплений, я обратился за информацией к независимому интернет-холдингу BANKI.RU [8]. В разделе «Рейтинг банков» представлен рейтинг финансовых организаций по ключевым показателям деятельности, рассчитанным с использованием отчетности этих организаций и опубликованным на сайте Центрального Банка России. Самыми надежными банками оказались: ПАО Сбербанк, ПАО Банк ВТБ, АО ГазпромБанк, АО Альфа-Банк, так как они занимают четыре верхние строчки рейтинговой таблицы.

Подбирая вклад в этих банках, я учитывал следующие условия:

— минимальная сумма вклада не более 50000 рублей (т.к. у меня была именно эта сумма денег);

— срок вклада не менее 3 лет (т.к. в ближайшие три года эти деньги мне точно не понадобятся);

— без пополнения и снятия в течение всего срока вклада, чтобы можно было выбрать между снятием процентов или их капитализацией (т.к. при возможности пополнения или снятия далеко не все банки предлагают варианты вклада со снятием/капитализацией процентов).

Результаты своих расчетов я представил в виде таблицы 1 «Накопительные вклады в крупных банках России на 1 ноября 2020 г.», указав наименование банка, сумму и срок вклада, процентную ставку при снятии и капитализации процентов, полный расчет и доходность по истечении срока договора.

В графе «Расчет» верхняя строка посчитана по формуле (1) – простых процентов, а нижняя строка по формуле (2) – сложных процентов с постоянным приростом. Расчет суммы прироста производил со знаком «+», так как цель вклада в банк – сохранение и преумножение дохода, поэтому вклад уменьшиться не должен.

Таблица 1

Накопительные вклады в крупных банках России на 1 ноября 2020 г.

№ п/п	Банк	Сумма вклада, руб.	Срок, лет	Название вклада	% ставка снятие/ капита-лизация, %	Расчет формула простых %/ формула сложных %, руб.	Доход, в руб.
	ПАО Сбербанк	50 тысяч	3	«Сохраняй Онлайн»	2,8	50000 (1+0,028 3)=54200	4200
2,8	50000 (1+0,028)3=54318	4318
	ПАО Банк ВТБ	Накопительный счет «Копилка»	4,1	50000 (1+0,041 3)=56150	6150
4,1	50000 (1+0,041)3=56405	6405
	АО Газпром- Банк	«Газпромбанк – на жизнь»	3,4	50000 (1+0,034 3)=55100	5100
3,57	50000 (1+0,0357)3=55548	5548
	АО Альфа- Банк	«Накопительный Альфа-Счет»	4,0	50000 (1+0,04 3)=56000	6000
4,24	50000 (1+0,0424)3=56633	6633

Вывод: наиболее доходным является вклад «Накопительный Альфа‑Счет» в Альфа-Банке под процентную годовую ставку 4,24% сроком на 3 года с капитализацией процентов. Он оказался самым подходящим для меня, так как до окончания школы и поступления в ВУЗ у меня есть более трех лет, а я нахожусь на полном обеспечении своих родителей, так что эти деньги в ближайшее время мне не понадобятся. Кроме того я выяснил, что закрыть этот счет самостоятельно я могу только после того, как мне исполнится 18 лет, а это значит, что, чтобы не терять проценты, вклад можно открыть сразу на 4 года.

Применение формул простых и сложных процентов

при решении задач экономического содержания

Я решил сам придумать задачу с экономическим содержанием и решить ее при помощи формулы сложных процентов (2).

Авторская задача

Первый банк в России был открыт 13 мая 1754 года в Петербурге по Указу императрицы Елизаветы Петровны. Представим, что бедный крестьянин положил под 10% годовых с капитализацией вклада 1 копейку (медную денгу). Рассчитайте, сколько бы денег было у него на счету 13 мая 2020 года.

Средняя стоимость операции для ребёнка с врождённым пороком сердца в России составляет 200000 рублей. Скольким детям можно провести такую операцию на накопленные крестьянином деньги?

Решение:

Дано: S₀ = 0,01 руб, i= 10% = 0,1, n = 2020 – 1754 = 266 (лет)

Найти: S

— формула сложных процентов при постоянном приросте.

1). Найдем, какая сумма будет у крестьянина на счету через 266 лет:

≈ 1024363870(руб.)

2). Найдем, скольким детям можно провести операцию:

Ответ: 1024363870 рублей, 5121 ребёнку.

Примечание: в 266-ую степень я возвел с помощью калькулятора, так как тема логарифмов изучается в старших классах. Ведь моей целью было понять – применима ли эта формула в математике при решении задач экономического содержания.

Разобрав большое количество задач на проценты, проанализировав приемы и пути их решения, я заметил общую закономерность и составил для себя алгоритм решения таких задач, которую успешно стал применять.

А лгоритм решения задач экономического содержания

На практике этот алгоритм я применяю так.

Задача 1 (Ю.В. Лепехин, 1996 г., № 785) [2]

Цех в целом увеличил за год выпуск продукции на 34%, причем 20% рабочих увеличили выпуск продукции на 50%. На сколько процентов увеличили выпуск продукции остальные рабочие цеха?

Решение: 1. Представляю краткую запись в виде таблицы с применением формулы (1) простых процентов, так как действие происходит однократно:

	Количество рабочих	Производительность каждого	Производительность общая
1 группа	0,2х	у(1+0,5)	0,2х 1,5у
2 группа	0,8х	у(1+0,01 )	0,8ху(1+0,01 )
Всего	х	у	ху(1 0,34)

2. Записываю уравнение и выражаю неизвестное – i,решаю его:

0,3ху+0,8ху(1+0,01 )=1,34ху | ÷ ху

0,3+0,8+0,008=1,34

0,008 =0,24

=30

Ответ: остальные рабочие увеличили выпуск продукции на 30%.

Надо заметить, что часто в задаче приходится применять сразу несколько формул. Чтобы понять, какие именно, задачу надо разбить на части, а потом к каждой части задать вопросы из данного алгоритма. Умело скомбинированные формулы помогают красиво выстроить решение задачи, а вычисления становятся простыми и понятными.

Задача 2 (Под ред. Ященко И.В. ЕГЭ-2020, стр. 158) [5]

По вкладу «А» банк в конце каждого года планирует увеличивать на 20% сумму, имеющуюся на вкладе в начале года, а по вкладу «Б» — увеличивать эту сумму на 11% в первый год и на одинаковое целое число i процентов и за второй, и за третий годы. Найдите наименьшее значение i, при котором за три года хранения вклад «Б» окажется выгоднее вклада «А» при одинаковых суммах первоначальных взносов.

Решение: 1. Представляю краткую запись в виде таблицы:

	S0	n	i1	i2	i3
Вклад «А»	S0	3	20%
Вклад «Б»	S0	3	11%	i %

2. Записываю сумму вклада через 3 года для вклада «А» и вклада «Б»:

Вклад «А»: — по формуле (2) при постоянном приросте

Вклад «Б»: — комбинацияформул (2) и (3) при постоянном и различном приросте

3. Составляю неравенство и решаю его:

Ответ: вклад «Б» выгоднее вклада «А» приi= 25%.

Задача 3 (Ю.В. Лепехин, 1996 г., № 786) [2]

Цену товара сначала повысили на 50%, потом еще повысили на после чего цену снизили на 50% и, наконец, повысили на 25%. В результате установилась цена 255 рублей. Чему равна первоначальная цена товара?

Решение: 1.Записываю условие задачи:

Дано: S = 255 руб. n = 4, i₁= 50% = 0,5 i₂= 6,25% = 0,0625

i₃= 50% = 0,5i₄= 25% = 0,25

Найти: S₀

Примечание: если в задаче говорится о повышении процентов (производительности труда, концентрации раствора, стоимости товара, ставки по вкладу или кредиту), то внутри скобки в формуле ставится «+», а, если о снижении, то ставится «–».

2. Применив формулу (3) сложных процентов с различным приростом, записываю уравнение, выражаю S₀и произвожу вычисления:

S₀(1 + 0,5)(1 + 0,0625)(1 – 0,5)(1 + 0,25) = 255

1,5 1,06250,5 1,25S₀= 255

S₀ = 256

Ответ: первоначальная стоимость товара составляла 256 рублей.

Задача 4 (Гущин Д.Д., 2016 г., стр. 32, № 7) [1]

Молодой семье на покупку квартиры банк выдает кредит под 20% годовых. Схема выплаты кредита следующая: ровно через год после выдачи кредита банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 20%), затем эта семья в течение следующего года переводит в банк определенную (фиксированную) сумму ежегодного платежа. Семья Ивановых планирует погашать кредит равными платежами в течение 3 лет. Какую сумму может предоставить им банк, если ежегодно Ивановы имеют возможность выплачивать по кредиту 810000 рублей?

Решение:

1.Записываю условие задачи:

Дано: i= 20% = 0,2 S_пл= 810000 руб. Найти: S₀= х

Найти: S₀

Представляю краткую запись в виде таблицы с применением формулы (1) простых процентов, так как остаток долга на конец каждого года буду считать отдельно:

	Долг после начисления %, руб.	Сумма платежа (S0), руб.	Долг после внесения платежа, руб.
1 год	1,2х	S0	1,2х — Sпл
2 год	1,2(1,2х — Sпл)	1,2² х — 1,2Sпл — Sпл
3 год	1,2(1,2² х — 1,2Sпл — Sпл)	1,23х — 1,2²Sпл — 1,2Sпл — Sпл

2. Так как долг после внесения третьего платежа полностью погашен, то можно составить уравнение:

1,2³х — 1,2²S_пл — 1,2S_пл — S_пл = 0

1,2³х — S_пл(1,2² + 1,2 + 1) = 0

1,2³х = S_пл(1,2² + 1,2 + 1)

х =

х =

х = 1706250

Ответ: банк может предоставить кредит в размере 1706250 рублей.

В Приложении 1 к исследовательской работе мною подобраны тренировочные задания для отработки приемов решения задач на проценты: от простых к более сложным. При их выполнении очень хорошо помогает данный алгоритм.

Вывод: использование алгоритма решения задач экономического содержания с применением финансовых формул простых и сложных процентов позволяет мне лучше понять текст задачи, упрощает ее решение, так как не приходится выполнять сложных вычислений, а значит, существенно сокращается время на выполнение задания.

ЗАКЛЮЧЕНИЕ

Подводя общий итог своей работы, я пришел к выводу, что моя гипотеза подтвердилась полностью: используя формулы простых и сложных процентов, можно решать задачи экономического содержания легко и просто!

Свое исследование по данной теме я проводил более девяти месяцев, за это время мне удалось не только повысить уровень своих знаний в области финансовой грамотности, но и заложить предпосылки для успешной сдачи ЕГЭ по математике в будущем, научившись решать самые сложные экономические задачи. В этом и заключается практическая значимость моей работы.

Созданный мной алгоритм я продемонстрировал учащимся нашей школы, ребята заинтересовались им. Поэтому у меня появилась идея записать видеоразборы нескольких задач на проценты из сборников для подготовки к ЕГЭ в качестве дополнительной помощи и для лучшего понимании решения задач экономического содержания с помощью «волшебных» финансовых формул. Познакомиться с ними можно на моем YouTube-канале, пройдя по одной из этих ссылок:

Ну и, конечно, я хочу выразить благодарность тем людям, которые эти формулы придумали, несмотря на то, что мне не удалось узнать их имен.

Источники информации:

1. Гущин Д.Д. Встречи с финансовой математикой. Учебно-методическая разработка. – С-П: Издательский дом «Учительская газета» — 2016, 34 с.

2. Лепехин Ю. В. Почти просто! Задачи по алгебре и началам анализа. — Волгоград: Перемена. — 1996 г.

3. Липсиц И.В., Рязанова О.И. Финансовая грамотность. Материалы для учащихся. 8-9 классы. Серия: Учимся разумному финансовому поведению. – М.: ВИТА-ПРЕСС, 2016 г. – 352 с.

4. Под ред. Ященко И.В. ЕГЭ. 4000 задач с ответами по математике. Базовый и профильный уровни. Все задания. «Закрытый сегмент». – М.: «Экзамен», 2015 г. – 688 с.

5. Под ред. Ященко И.В. ЕГЭ 2020. Математика. Профильный уровень. 50 вариантов. Типовые варианты экзаменационных заданий от разработчиков ЕГЭ. Серия «ЕГЭ. 50 вариантов. Тесты от разработчиков». – М.: «Экзамен», МЦНМО, 2020 г. – 231 с.

6. Под ред. Ященко И.В. ЕГЭ 2021. Математика. Профильный уровень. 50 вариантов. Типовые варианты экзаменационных заданий от разработчиков ЕГЭ. Серия «ЕГЭ. 50 вариантов. Тесты от разработчиков». – М.: «Экзамен», МЦНМО, 2021 г. – 231 с.

7. Хамидуллин Р.Я. Финансовая математика. Учебное пособие. – М.: Издательский дом, 2019 г. – 220 с.

8. Независимый интернет-холдинг BANKI.RU – Режим доступа: https://www.banki.ru/banks/ratings/

9. Образовательный интернет-ресурс «ЯКласс» — Режим доступа: https://dnevnik.ru/ad/promo/yaklass?utm_source=dnevnik&utm_medium=appcentet&utm_content=appcenter#%2Fp%2Fosnovy-finansovoj-gramotnosti%2F7-9-klass

Приложение 1

Задача 1 (Под ред. Ященко И.В. ЕГЭ-2015, стр. 19) [4]

Цена на электрический чайник была повышена на 19% и составила 1785 рублей. Сколько рублей стоил чайник до повышения цены?

Подсказка: (известно S и i, найти S₀, применяем формулу (1))

Ответ: 1500 рублей.

Задача 2 (Под ред. Ященко И.В. ЕГЭ-2015, стр. 24) [4]

Пирожок в кулинарии стоит 12 рублей. При покупке более 30 пирожков продавец делает скидку 5% от стоимости всей покупки. Покупатель купил 40 пирожков. Сколько рублей он заплатил за покупку?

Подсказка: (известно S₀ и i, найти S, применяем формулу (1))

Ответ: 456 рублей.

Задача 3 (Под ред. Ященко И.В. ЕГЭ-2015, стр. 20) [4]

Клиент взял в банке кредит 24000 рублей на год под 9% годовых. Он должен погашать кредит, внося в банк ежемесячно одинаковую сумму денег, с тем, чтобы через год выплатить сумму, взятую в кредит, вместе с процентами. Сколько рублей он должен вносить в банк ежемесячно?

Подсказка: (известно S₀ и i, найти сначала S, применяем формулу (1))

Ответ: 2180 рублей.

Задача 4 (ЯКласс, олимпиада по фин. грамотности, 8 класс, 2 тур) [9]

Плата за квартиру, в которой проживает семья Саши на протяжении двух лет, повышалась на один и тот же процент. Определи, на какой процент повышалась стоимость квартплаты каждый год, если её первоначальная величина равнялась 4000 рублей, а через 2 года уже составила 4840 рублей.

Подсказка: (известно S₀, S и n, найти i, применяем формулу (2))

Ответ: на 10 процентов.

Задача 5 (ЯКласс, олимпиада по фин. грамотности, 8 класс, 2 тур) [9]

Сашин папа купил новую машину за 489700 руб. Предположим, машина будет обесцениваться (амортизироваться) на 18% в год. Определи в таком случае стоимость автомобиля спустя 6 лет. Ответ округлите до целого числа.

Подсказка: (известно S₀, iи n, найтиS, применяем формулу (2))

Ответ: 148872 рубля.

Задача 6 (Гущин Д.Д., 2016 г., стр. 29, № 11) [1]

Цена холодильника в магазине ежегодно уменьшается на одно и то же число процентов от предыдущей цены. Определите, на сколько процентов каждый год уменьшалась цена холодильника, если, выставленный на продажу за 20000 рублей, через два года был продан за 15842 рубля.

Подсказка: (известно S₀, S и n, найти i, применяем формулу (2))

Ответ: на 11 процентов.

Задача 7 (Ю.В. Лепехин, 1996 г., № 822) [2]

Цена товара повысилась на р%, затем снизилась на 50%, потом повысилась в 2 раза и, наконец, снизилась на р%. В результате цена составила 93,75% начальной стоимости. Чему равен р?

Подсказка: (известно S₀, S и n, найти i, применяем формулу (3))

Ответ: 25 процентов.

Задача 8 (Под ред. Ященко И.В. ЕГЭ-2021, стр. 32) [6]

31 декабря 2016 года Сергей взял в банке 2648000 рублей в кредит под 10% годовых. Схема выплаты кредита следующая – 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 10%), затем Сергей переводит в банк x рублей. Какой должна быть сумма x, чтобы Сергей выплатил долг тремя равными платежами (то есть за три года)?

Подсказка: (известно S_0, i и n, найти S_{платежа}, рассчитываем для каждого года отдельно и последовательно, применяя формулу (1))

Ответ: 1064800 рублей.

Задача 9 (Под ред. Ященко И.В. ЕГЭ-2021, стр. 147) [6]

По вкладу «А» банк в конце каждого года планирует увеличивать на 10% сумму, имеющуюся на вкладе в начале года, а по вкладу «Б» — увеличивать эту сумму на 9% в первый год и на одинаковое целое число i процентов и за второй, и за третий годы. Найдите наименьшее целое значение i, при котором за три года хранения вклад «Б» окажется выгоднее вклада «А» при одинаковых суммах первоначальных взносов.

Подсказка: (известно S₀и n, S_1<S₂, найти i, для вклада «А» применяем формулу (2), для вклада «Б» комбинируем формулу (2) и (3), составляем неравенство и выражаемi)

Ответ: 12 процентов.

Задача 10(Гущин Д.Д., 2016 г., стр. 32, № 7) [1]

Молодой семье на покупку квартиры банк выдает кредит под 20% годовых. Схема выплаты кредита следующая: ровно через год после выдачи кредита банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 20%), затем эта семья в течение следующего года переводит в банк определенную (фиксированную) сумму ежегодного платежа. Семья Ивановых планирует погашать кредит равными платежами в течение 5 лет. Какую сумму может предоставить им банк, если ежегодно Ивановы имеют возможность выплачивать по кредиту 810000 рублей? Ответ округлите до целого числа (в меньшую сторону).

Подсказка: (известноS_{платежа}, i и n, найти S₀, рассчитываем для каждого года отдельно и последовательно, применяя формулу (1))

Ответ: 2422395 рублей.

Просмотров работы: 593

«Простые и сложные проценты»

Подборка прототипов задания №19 ЕГЭ по математике 2015 года профильного уровня.

Актуальность темы.

Понимание процентов и умение производить процентные расчеты в настоящее время необходимы каждому человеку: прикладное значение этой темы очень велико и затрагивает финансовую, демографическую, экологическую, социологическую и другие стороны нашей жизни.

Материал актуален для всех, у кого в этом году есть 11 классы.

Когда Ященко, имеющий к составлению КИМов по математике непосредственное отношение, приезжал к нам на семинар в октябре, он сказал, что все прототипы задания 19 будут выложены в открытом банке, так как задание новое.

Задание, решаемое для моего не очень сильного класса, и натаскать на него можно, было бы на чём.

Немного теории…

“Проценты”.

Задание1

а) Что называется процентом? (Процентом называется одна сотая часть какого-либо числа)

б) Как обозначается 1%? (1%? = 0,01)

в) Как называется 1% от центнера? (кг.) Метра? (см.) Гектара? (ар или сотый)

г) Что называется 1% процентом данного числа а? (Процентом данного числа а называется число 0,01•а, т.е. 1% (а) = 0,01*а ) 

д) Как определить р% от данного числа а? (найти число 0,01•р•а, т.е. р% = 0,01*р*а )

е) Как перевести десятичную дробь в проценты? (умножить на 100). А как проценты в десятичную дробь? (разделить на сто, т.е. умножить на 0,01)

ж) Как найти часть от числа в процентах? (Чтобы найти часть в от числа х в процентах, нужно эту часть разделить на число и умножить на 100, т.е. а(%)=(в/х)*100)

д) Как находится число по его проценту ? (Если известно, что а% числа х равно в, то х можно найти по формуле х = (в/а)*100)

Задание 2

Представьте данные десятичные дроби в процентах:

 а)1; 0,5; 0,763; 1,7; 256.

б) Представьте проценты десятичными дробями: 2%; 12%; 12,5%; 0,1%; 200%. 

Задание 3

Найдите % от числа:

в) 0,1% от числа 1200? (1,2)

г) 15% от числа 2? (0,30)

Задание 4

Найдите число по его проценту:

д) Сколько центнеров весит мешок сахарного песка, если 13% составляет 6,5 кг.? (50 кг.= 0,5 ц.)

в) Сколько процентов от 10 составляет 9?

Ответы: а) 9%, б) 0,09%, в) 90%; г) 900%?

Простые и сложные проценты.

Эти термины чаще всего встречаются в банковских делах, в финансовых задачах. 

Банки привлекают средства (вклады) за определенные процентные ставки. В зависимости от процентной ставки вычисляется доход.

На практике применяются два подхода к оценке процентного дохода – простые и сложные проценты.

При применении простых процентов доход рассчитывается от первоначальной суммы вложенных средств не зависимо от срока вложения. В финансовых операциях простые проценты используются преимущественно при краткосрочных финансовых сделках.

Пусть некоторая величина подвержена поэтапному изменению. При этом каждый раз ее изменение составляет определенное число процентов от значения, которое эта величина имела на начальном этапе. Так вычисляются простые проценты. 

При применении сложных процентов накопленная сумма процентов добавляется во вклад по окончании очередного периода начислений. При этом каждый раз ее изменение составляет определенное число процентов от значения, которое эта величина имела на предыдущем этапе. В этом случае имеем дело со “сложными процентами” (т.е. используются начисления “процентов на проценты”)

Первоначальная сумма и полученные проценты в совокупности называются накопленной (наращенной) суммой.

Так, если банковская ставка равна 10%, а первоначальная сумма 100 руб., то накопленная сумма за пять лет при применении простых и сложных процентов будет иметь вид:

Таблица 1. Накопленная сумма с использованием простых и сложных процентов.

	На начало	1-й год	2-й год	3-й год	4-й год	5-й год
Простые проценты	100	110	120	130	140	150
Сложные проценты	100	110	121	133	146	161

Формулы простых и сложных процентов.

I. Пусть некоторая величина A увеличивается n раз (n год) и каждый раз на р%.

Вводим обозначения: A0 – первоначальное значение величины A;

р – постоянное количество процентов;

a процентная ставка; a=р/100 = 0,01*р

An – накопленная сумма за n раз (к концу n-го года) — по формуле простых процентов;

Sn — накопленная сумма за n раз (к концу n-го года) — по формуле сложных процентов.

Тогда ее значение A1 для простых процентов после первого увеличения (к концу первого года) вычисляется по формуле: A1 = A0 + A0 * (0,01р) = A0 (1 + (0,01р) = A0 (1 + p)

В конце второго этапа A2= A1 + A0 * (0,01р) = A0 (1 + a) + A0 * a = A0 (1 + 2a).

В конце третьего этапа A3= A2 + A0 * (0,01р) = A0 (1 + 2a) + A0 * a = A0 (1 + 3a).

Тогда для простых процентов сумма по годам равна:

An = A0 (1 + 0.01р*n) или An = A0 (1 + ?* n) (1)

Для сложных процентов это выглядит иначе:

Пусть некоторая величина S0 увеличивается n раз (n год) и каждый раз на р%.

Тогда ее значение S1 для сложных процентов после первого увеличения (к концу первого года) вычисляется по формуле:

S1 = S0 + S0 (0,01р) = S0 * (1 + 0,01р) = S0 * (1 + ?).

В конце второго этапа S2= S1 + S1 (0,01р) = S1 * (1 + 0,01р) = S0 (1 + ????р)2 = S0 (1 + ?)2.

В конце третьего этапа S3= S2 + S2 (0,01р) = S2 * (1 +0,01р) = S0(1 +0,01р)2*(1 +0,01р)=S0(1 +0,01р)3 = S0 (1 + a)3.

Тогда для сложных процентов сумма по годам равна:

Sn = S0 (1 + 0,01р)n  или Sn = S0 (1 + a)n (2)

Пример 1.

В банке открыт срочный депозит на сумму 50 тыс. руб. по 12% на 3 года. Рассчитать накопленную сумму если проценты:

а) простые; б) сложные.

Решение 1.

По формуле простых процентов

Sn=(1+3*0.12)*50 000 = 68000 руб. (отв. 68000 руб.)

По формуле простых процентов

Sn=(1+0.12)3*50 000 = 70246 руб. (отв. 70246 руб.)

Формула сложных процентов связывает четыре величины: начальный вклад, накопленную сумму (будущую стоимость вклада), годовую процентную ставку и время в годах. Поэтому, зная три величины, всегда можно найти четвертую:

Sn = S0 * (1+0,01р)n

Для определения количество процентов р необходимо:

р = 100 * ((Sn / S0 )1/n – 1) (2.1)

Операция нахождения первоначального вклада S0, если известно что через n лет он должен составить сумму Sn, называется дисконтированием:

S0 = Sn * (1 + 0,01р) –n (2.2)

Сколько лет вклад S0 должен пролежать в банке под р % годовых, чтобы достигнуть величины Sn.

n = (lnSn – lnS0) / (ln(1 + 0,01р) (2.3)

В банковской практике проценты могут начисляться чаще чем 1 раз в год. При этом банковская ставка обычно устанавливается в пересчете на год. Формула сложных процентов будет иметь вид:

Sn = (1 + ?/t )n•t S0 (3)

где t – число реинвестиций процентов в году.

Пример 2.

В банке открыт срочный депозит на сумму 50 тыс. руб. по 12% на 3 года. Рассчитать начисленную сумму если проценты начисляются ежеквартально.

Решение 2.

n = 3

t = 4 (в году – 4 квартала)

По формуле сложных процентов

S3 = (1+0.12/4)3*4*50000 = 1.0312*50000 = 71288 руб. Отв. 71288 руб.

Как следует из примеров 1 и 2, накопленная сумма будет возрастать тем быстрее, чем чаще начисляются проценты.

Приведем обобщение формулы (2), когда прирост величины S на каждом этапе свой. Пусть Sо, первоначальное значение величины S, в конце первого этапа испытывает изменение на р1%, в конце второго на р2%, а в конце третьего этапа на р3% и т.д. В конце n-го этапа значение величины S определяется формулой

Sn = S0 (1 + 0,01р1 )(1 + 0,01р2 )…(1 + 0,01рn ) (4)

Пример 3.

Торговая база закупила партию товара у изготовителя и поставила ее в магазин по оптовой цене, которая на 30% больше цены изготовителя. Магазин установил розничную цену на товар 20% выше оптовой. При распродаже магазин снизил эту цену на 10%. На сколько рублей больше заплатил покупатель по сравнению с ценой изготовителя, если на распродаже он приобрел товар за 140 руб. 40 коп.

Решение 3.

Пусть первоначальная цена составляет S руб., тогда по формуле (4) имеем:

S0 (1 + 0,01*30)(1 + 0,01*20)***(1 – 0,01*10) = 140,4

S0*1,3*1,2*0,9 = S0*1,404 = 140,4

S0 = 140,4: 1,404 = 100 (руб.)

Находим разность последней и первоначальной цены

140,4 – 100 = 40,4 Отв. 40,4 руб.

Примеры задач с решениями

Вариант 1

Задача 1. Владелец автозаправки повысил цену на бензин на 10%. Заметив, что количество клиентов резко сократилось, он понизил цену на 10 %. Как после этого изменилась начальная цена на бензин? (повысилась или понизилась и на сколько % -ов?)

Решение: Пусть S0 – начальная цена, S2 – конечная цена, х — искомое число процентов изменения, где х = (1 — S2/S0 )*100% (*)

Тогда по формуле Sn = S0 (1 + 0,01р1 )(1 + 0,01р2 )***(1 + 0,01рn ) (4), получим

S2 = S0 (1 + 0,01*10 )(1 — 0,01*10) = S0*1,1*0,9 = 0,99*S0.

S2 = 0,99*S0; 0,99 = 99%, значение S2 составляет 99% первоначальной стоимости, значит ниже на 100% — 99% = 1%.

Или по формуле (*) получаем: х = (1 – 0,99 )*100% = 1%.

Ответ: понизилась на 1%.

Задача 2. В течении года предприятие дважды увеличивало выпуск продукции на одно и то же число процентов. Найдите это число, если известно, что в начале года предприятие ежемесячно выпускало 600 изделий, а в конце года стал выпускать ежемесячно 726 изделий.

Решение: Пусть S0 – начальная цена, S2 – конечная цена, р – постоянное количество процентов.

По формуле (2.1) получаем: р = 100 * ((726 / 600 )1/2 – 1) = 10%.

Ответ: 10%

Задача 3. Цена на компьютерную технику были повышены на 44%. После этого в результате двух последовательных одинаковых процентных снижений цена на компьютеры оказалась на 19% меньше первоначальной. На сколько процентов каждый раз понижали цену?

Решение: По формуле (4), составляем уравнение

S3 = S0 (1 + 0,01*44)(1 — 0,01р )(1 — 0,01р) = S0 *1,44*(1 — 0,01р )2 = S0 * (1-0,01*19). Решая уравнение, получаем 2 корня: 175 и 25, где 175 не подходит условию задачи. Поэтому р = 25%.

Ответ: 25%

Задача 4. Для определения оптимального режима повышения цен фирма решила с 1 января повышать цену на один и тот же товар в двух магазинах двумя способами. В одном магазине – в начале каждого месяца (начиная с февраля) на 2%, в другом – через каждые два месяца, в начале третьего (начиная с марта) на одно и то же число процентов, причем такое, чтобы через полгода (1 июля) цены снова стали одинаковыми. На сколько процентов надо повышать цену товара через каждые два месяца, во втором магазине?

Решение: Пусть S0 – начальная цена, р – постоянное количество процентов.

Тогда через 6 месяцев (после шести повышений на 2%) в первом магазине цена на товар станет равна S0 (1 + 0,01*2)6, а во втором магазине (после трех повышений на р%) цена товара будет равна S0 (1 + 0,01р)3. Получаем уравнение S0 (1 + 0,01*2)6 = S0 (1 + 0,01р)3. Решая его, получаем

(1 + 0,01*2)2 = (1 + 0,01р); 1,022= (1 + 0,01р); р = 4,04

Ответ: 4,04%

Вариант 2.

Задача 1. Автомобиль ехал по магистрали с определенной скоростью. Выезжая на проселочную дорогу, он снизил скорость на 20%, а затем на участке крутого подъема он уменьшил скорость на 30%. На сколько процентов эта новая скорость ниже первоначальной?

Решение: Пусть V0 – начальная скорость, V – новая скорость, которая получается после двух разных изменений, р – искомое количество процента.

Тогда по формуле (4), составляем уравнение V0(1 — 0,01*20)(1 — 0,01*30) = V0(1 — 0,01р). Решая его получаем V0*0,8*0,7 = V0(1 — 0,01р); р = 44

Ответ: 44%

Задача 2. Предположим, что в комнатной температуре за день вода испаряется на 3%. Сколько литров воды останется через 2 дня от 100 литров? А сколько воды испарится?

Решение: n=2; р=3%; S0= 100л. Тогда по формуле (2), получаем

S2 = S0 (1 — 0,01р )2 = 100*(1-0,01*3)2 = 100*0,972 = 94,09; S0 – S2= 100 — 94,09 = 5,91

Ответ: 94,09л.; 5,91л.

Задача 3. Вклад, положенный в банк 2 года назад, достиг 11449 рублей. Каков был первоначальный вклад при 7% годовых? Какова прибыль?

Решение: n=2; р=7%; S2= 11449; S0= ?

В формулу (2.2) S0 = Sn * (1 + 0,01р) –n подставляем данные значения, получаем:

S0 = 11449* (1 + 0,01*7) –2 = 11449/ (1,07)2=11449/ 1,1449 = 10000.

11449 – 10000 = 1449

Ответ: 10000 руб.; 1449 руб.

Задача 4. Сберкасса начисляет ежегодно 3% от суммы вклада. Через сколько лет сумма удвоится?

Решение: р=3%; S0 – начальная сумма; n=?

Составим уравнение: 2*S0 = S0 (1 + 0,01р )n; 2*S0 = S0 (1 + 0,03)n; 2 = 1,03n n=log1,032; n ?23.

Самостоятельная работа

1-уровень. После реконструкции завод увеличил выпуск продукции на 10%, а после замены оборудования еще на 30%. На сколько процентов увеличился первоначальный выпуск продукции?

(Ответ: на 43%)

2-уровень. Число 50 трижды увеличили на одно и то же число процентов, а потом уменьшили на это же число процентов. В результате получили число 69,12. На сколько процентов увеличивали, а потом уменьшали данное число?

(Ответ: на 20%)

3-уровень. Банк начисляет ежегодно 7% от суммы вклада. Найдите наименьшее число лет, за которое вклад вырастает более чем на 20%.

(Ответ: 3 года)

№1. Сберегательный банк начисляет по вкладам ежегодно 5,5% годовых. Вкладчик внес в банк 150 тысяч рублей. Какой станет сумма вклада через 2 года?

(Ответ: 166953,75 руб.)

№3. Банк предлагает два варианта депозита

1) под 120% с начислением процентов в конце года;

2) под 100% с начислением процентов в конце каждого квартала.

Определить более выгодный вариант размещения депозитов на один год.

Решение.

Более выгодным считается тот вариант, при котором наращенная за год сумма будет больше. Для оценки вариантов начальную сумму примем равную 100 руб.

По первому варианту накопленная сумма будет равна (1+1,2)*100 руб. = 220 руб.

По второму варианту проценты начисляются ежеквартально. По окончании первого квартала накопленная сумма равна (1+1,0/4)*100 руб. = 125 руб.

По окончании 2-го квартала (1+1,0/4)2*100 руб. = 156 руб.

За год накопленная сумма равна (1+1,0/4)4*100 руб. = 244 руб.

Как следует из расчетов второй вариант значительно выгоднее (244 > 220). Правда, только при условии применения сложных процентов.

Подборка прототипов задания №19 ЕГЭ по математике 2015 года профильного уровня.

19. 31 декабря 2012 года Екатерина взяла в банке 850000 рублей в кредит под 15% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 15%), затем Екатерина переводит в банк определенную сумму ежегодного платежа. Какой должна быть сумма ежегодного платежа, чтобы Екатерина выплатила долг тремя равными ежегодными платежами?

19. Молодой семье на покупку квартиры банк выдает кредит под 20 % годовых.

Схема выплаты кредита следующая: ровно через год после выдачи кредита банк

начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 20%),

затем эта семья в течение следующего года переводит в банк определенную

(фиксированную) сумму ежегодного платежа. Семья Ивановых планирует погашать

кредит равными платежами в течение 4 лет. Какую сумму может предоставить им

банк, если ежегодно Ивановы имеют возможность выплачивать по кредиту 810 000

рублей?

19. В 8-литровой колбе находится смесь азота и кислорода, содержащая 32% кислорода. Из колбы выпустили некоторое количество смеси и добавили столько же азота; затем снова выпустили такое же, как и в первый раз, количество новой смеси и добавили столько же азота. В итоге процентное содержание кислорода в смеси составило 12,5%. Сколько литров смеси выпускали каждый раз?

19. В банк был положен вклад под банковский процент 10%. Через год хозяин вклада снял со счета 2000 рублей, а еще через год снова внес 2000 рублей. Однако, вследствие этих действий через три года со времени первоначального вложения вклада он получил сумму меньше запланированной (если бы не было промежуточных операций со вкладом). На сколько рублей меньше запланированной суммы получил в итоге вкладчик?

19. В первый рабочий день месяца с заводского конвейера сошло некоторое число тракторов. Каждый следующий рабочий день их выпуск возрастал на 3 трактора ежедневно, и месячный план 55 тракторов был выполнен досрочно, причем за целое число дней. После этого ежедневно выпускалось 11 тракторов. Определите, сколько тракторов было выпущено в первый рабочий день, и на сколько процентов был перевыполнен месячный план, если известно, что в месяце было 26 рабочих дней, а плановая работа длилась не менее 3 и не более 10 дней.

19. 8 марта Леня Голубков взял в банке 53 680 рублей в кредит на 4 года под 20% годовых, чтобы купить своей жене Рите новую шубу. Схема выплаты кредита следующая: утром 8 марта следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 20%), а вечером того же дня Леня переводит в банк определенную сумму ежегодного платежа (все четыре года эта сумма одинакова). Какую сумму сверх взятых 53 680 рублей должен будет выплатить банку Леня Голубков за эти четыре года?

19. Семён Кузнецов планировал вложить все свои сбережения на сберегательный счёт в банк «Навроде» под 500%, рассчитывая через год забрать А рублей. Однако крах банка «Навроде» изменил его планы, предотвратив необдуманный поступок. В результате часть денег г-н Кузнецов положил в банк «Первый Муниципальный», а остальные – в банку из-под макарон. Через год «Первый Муниципальный» повысил процент выплат в два с половиной раза, и г-н Кузнецов решил оставить вклад ещё на год. В итоге размер суммы, полученной в «Первом Муниципальном», составил А рублей. Определите, какой процент за первый год начислил банк «Первый Муниципальный», если в банку из-под макарон Семён «вложил» А рублей.

19. Банк планирует вложить на 1 год 30% имеющихся у него средств клиентов в акции золотодобывающего комбината, а остальные 70% – в строительство торгового комплекса. В зависимости от обстоятельств первый проект может принести банку прибыль в размере от 32% до 37% годовых, а второй проект – от 22% до 27% годовых. В конце года банк обязан вернуть деньги клиентам и выплатить им проценты по заранее установленной ставке, уровень которой должен находиться в пределах от 10% до 20% годовых. Определите, какую наименьшую и наибольшую чистую прибыль в процентах годовых от суммарных вложений в покупку акций и строительство торгового комплекса может при этом получить банк.

23 ноября 2013

Сегодня мы разберем всего одну задачу, но решение у нее будет довольно длинным. Это задача B2 на сложные проценты — такая вполне может встретиться на настоящем ЕГЭ по математике, поэтому уметь решать ее совершенно необходимо.

В этом уроке мы начинаем изучать сложные задачи на проценты и решать их будем с помощью метода коэффициентов. Поясню суть этого метода. Для начала давайте вспомним формулу простого процента.

Что такое метод коэффициентов?

Пусть х — начальное значение нашей величины, k — проценты, на которые увеличивается или уменьшается наша величина, а y — итоговое значение величины, полученное после уменьшения или увеличения величины х на k%. Тогда все три величины связаны следующей формулой:

Плюс и или минус перед k ставится в зависимости от того, уменьшается или увеличивается исходная величина х. А теперь давайте раскроем дробь, получим следующее выражение:

Вот именно от этого множителя 1 ± k/100 и произошло название метода коэффициентов. Смотрите: если исходная величина х увеличивается, скажем, на 10%, то для того, чтобы получить итоговое значение величины, нужно умножить х на величину (1 + 10%), т. е. согласно наше формуле 1+ 0,1 = 1,1. Аналогично, если бы исходная величина х уменьшалась, скажем, на 30%, то для получения итогового значения нам нужно провести следующие операции:

1 − 30% = 1 − 0,3 = 0,7

Задача B2 на сложные проценты

Давайте посмотрим, как эта теория работает на практике. Итак, задача:

Задача B2. В школе 720 учеников, из них 25% — ученики начальной школы. Среди учеников средней и старшей школы 30% изучают немецкий язык. Сколько учеников в школе изучают немецкий язык, если в начальной школе немецкий язык не изучается?

Как решать такую задачу? В первую очередь, чтобы найти количество учеников, изучающих немецкий язык, нужно из общего количества, т.е. 720 учеников, вычесть 25%, которые точно не изучают немецкий язык, потому что по условию задачи ученики начальных классов его не изучают точно. Другими словами, х = 720. Из этой величины с помощью метода коэффициентов получаем величину y₁:

y₁ = 720 · (1 − 0,25) = 720 · 0,75

Идем дальше. По условию из учеников средней и старшей школы, т. е. из того количества, которое мы только что нашли, только 30% изучают немецкий язык. Теперь давайте посчитаем второе значение — y₂. Нам нужно найти 30% от полученного числа:

y₂ = 720 · 0,75 · 0,3

Давайте переведем все десятичные дроби в обычные и посчитаем:

Вот мы и нашли 30% от тех учеников, которые учатся в средней или старшей школе. Именно столько людей изучают немецкий язык. Все, задача решена. Ответ — 162.

Замечание по поводу сложных процентов

Единственный вопрос, который может возникнуть у учеников, относится вот к этому моменту:

1 − 30% = 1 − 0,3 = 0,7

Почему здесь при уменьшении на 30% мы вычитаем из единицы 0,3, а при решении задачи просто умножаем на 0,3? Все дело в условии задачи. Там написано, что среди учеников средней и старшей школы 30% изучают немецкий язык, т. е. нужно уменьшать не на 30%, а на 70%, чтобы получить 30%. Давайте посмотрим:

1 − 70% = 1 − 0,7 = 0,3

Таким образом, коэффициент 0,3 участвует в умножении совершенно обосновано.

Если нужно вычесть 30%, умножаем исходное число на 1 − 0,3 = 0,7. Если нужно добавить 30%, умножаем на 1 + 0,3 = 1,3. А если нужно просто найти 30% от исходного числа, умножаем на 0,3. Вот и все, что нужно знать о процентах.

Можно объяснить метод коэффициентов и несколько иначе. Если какая-то величина х, например, уменьшается на 20%, то новое значение этой величины равно:

y = х · (1 – 0,2)

А вот если нам дана некая величина х, от которой нужно найти 30% или 20%, то нам нужно просто умножить эту величину х на 0,3 или на 0,2, т. е. на проценты, деленные на 100.

Вот и вся суть метода коэффициентов. Надеюсь, этот урок будет полезен тем, кто учится решать сложные задачи на проценты и готовится к ЕГЭ по математике. А у меня на этом все. С вами был Павел Бердов. До новых встреч!

Смотрите также:

1. Задача B2: Сложный процент и стандартная формула
2. Сложные задачи на проценты
3. Тест к уроку «Сложные выражения с дробями» (легкий)
4. Метод коэффициентов, часть 1
5. Задача B5: площадь фигур с вершиной в начале координат
6. Сфера, вписанная в куб

Вклады и кредиты

Задание № 17 КИМ ЕГЭ по математике профильного уровня

Текстовая задача с экономическим содержанием – относительно новый вид заданий, появившихся в КИМ ЕГЭ профильного уровня, хотя задачи «на проценты» в вариантах вступительных экзаменов в вузы встречались в «доегэшную пору» достаточно часто, особенно если речь шла об экономических специальностях.

Решение таких задач связано со знанием некоторых специфических математических моделей из области экономики, умением переводить сформулированные в виде текста условия в уравнения и неравенства и пониманием того, как решения полученных уравнений и неравенств соотносятся с тем, что написано в условии задачи, – то есть какой смысл имеют полученные результаты.

         С чего начать подготовку к решению экономической задачи? Прежде всего, стоит вспомнить основные правила решения текстовых задач вообще (они пригодятся и для решения более простой текстовой задачи № 11 варианта КИМ).

Решение любой текстовой задачи складывается из нескольких основных моментов:

• чтение условия задачи; читайте его до тех пор, покуда сможете, не подглядывая в текст, объяснять суть описанного в задаче процесса (без конкретных числовых данных, конечно, – зазубривать ничего не нужно);

•    выбор переменных; для каждого типа задач существуют рекомендации, какие величины лучше всего обозначать как переменные (и это не всегда те величины, о которых идет речь в вопросе задачи); переменных при решении текстовой задачи нужно вводить столько, сколько их нужно для того, чтобы просто и логично составить уравнения и неравенства (не бойтесь, если переменных оказалось слишком много – например, больше, чем число уравнений: если вы все делаете правильно, то «лишние» переменные взаимно уничтожатся или сократятся; еще один вариант – в процессе решения надо будет найти не сами переменные по отдельности, а какую-либо их комбинацию);

• составление уравнений и неравенств, формализация того, что необходимо найти в процессе решения задачи; при составлении уравнений обращайте внимание на единицы измерения – они должны быть одинаковыми для всех одноименных величин;

• решение полученного уравнения, неравенства или системы;

• исследование полученного результата и нахождение ответа на вопрос задачи.

Рекомендую вам «держать в голове» эти основные шаги решения текстовой задачи.

На следующем этапе нужно выяснить, насколько хорошо учащиеся владеют таким понятием как «процент». Начать надо с темы «Вычисление “простых” процентов». Для этого можно порешать задачи на проценты прототипа 11 ЕГЭ.

Далее переходим к изучению «Сложных процентов».

Пропускать данный раздел нельзя, т.к. в дальнейшем формулы сложных процентов мы будем использовать при решении задач с аннуитетными платежами.

Сложные проценты — эффект часто встречающийся в экономике и финансах, когда проценты прибыли в конце каждого периода прибавляются к основной сумме и полученная величина в дальнейшем становится исходной для начисления новых процентов.

Формула вычисления сложных процентов:

(начисление процентов к исходной сумме)

или (списание процентов)

Где S— размер первоначального вклада;

– размер вклада через n лет;
r — процентная ставка за расчетный период (день, месяц, год, …);
n — количество расчетных периодов.

Вывод формулы вычисления сложных процентов выполнить несложно и лучше вместе с учениками вывести данное соотношение.

Решение экономической задачи целесообразно начинать:

1) с анализа данных в задаче и структурирования их в виде таблицы; ( самое важное!)

2) с представления решения задачи в виде понятного, а значит простого алгоритма действий. Алгоритм – запоминаем!

Выполнив первые 2 пункта, вы и построите математическую модель.

Далее решение сводится к исследованию этой модели и получению результата.

И, помните, что каждый тип задачи вы разбираете вместе с учениками, а потом они самостоятельно решают парные задачи каждого типа!

1. Задачи на «сложные» проценты.

1-1. Вкладчик внес в банк 500000 рублей под 20% годовых. В конце каждого года из первых трех лет после начисления процентов он дополнительно вносил одну и ту же сумму. К концу четвёртого года его вклад стал равным 1364400 рублей. Какую сумму в рублях дополнительно вносил вкладчик в течение каждого из первых трех лет?

Решение.

S– вклад, S= 500 000 рублей,

r=20% — процент годовых по вкладу,

– «накапливающий» множитель, m=1,2

Можно использовать формулы:

Парная задача

1-2. Вкладчик внёс в банк 500000 рублей под 20% годовых. В конце каждого из первых трёх лет после начисления процентов он снимал одну и ту же сумму. К концу четвертого года его вклад стал равным 927600 рублей. Какую сумму вкладчик снимал в течение каждого из первых трёх лет?

Ответ: 25000 рублей.

2. Задачи на кредиты (платеж равными взносами), аннуитетные платежи.

Аннуитетный платёж отличает специфика расчёта и выплат – равные части в течение всего срока кредитования, состоящие из кредитного процента и суммы основного долга. Современные банки практикуют преимущественно аннуитетные платежи при кредитовании, ввиду высокой прибыли по процентам.

2. В июле 2020 года планируется взять кредит на некоторую сумму. Условия возврата таковы:

– в январе каждого года долг увеличивается на 20% по сравнению с предыдущим годом;

– с февраля по июнь нужно выплатить часть долга одним платежом.

Определите, какую сумму взяли в кредит, если известно, что кредит был выплачен четырьмя равными платежами (то есть за четыре года) и общая сумма выплат составила 311040 рублей.

Решение.

S–сумма кредита, Sk-общая сумма выплат,

r=20% — процент годовых по вкладу,

– «накапливающий» множитель, m=1,2

x рублей- ежегодная выплата,

Sk=4x;

Кредит был погашен за 4 года, значит:

Ответ: 201 300 рублей.

3. Задачи на кредиты (уменьшение долга каждый год или месяц на одну и ту же величину), дифференцированные платежи.

Основные характеристики дифференцированного платежа

 1. Долг уменьшается равномерно (убывающая арифметическая прогрессия);

2. Платежи уменьшаются равномерно (убывающая арифметическая прогрессия);

3. Дифференцированный платеж равен , где S – сумма (тело) кредита, n – количество выплат, r – процентная ставка;

4. Первый платеж самый большой;

5. Последний платеж самый маленький. 

При расчете дифференцированного платежа общая сумма основного долга делится на равные части пропорционально сроку кредитования. Ежемесячно в течение всего срока погашения кредита заемщик выплачивает банку часть основного долга плюс начисленные на его остаток проценты.

3. 15–го января планируется взять кредит в банке на 24 месяцев. Условия его возврата таковы:

– 1–го числа каждого месяца долг возрастает на 1% по сравнению с концом предыдущего месяца;

– со 2–го по 14–е число каждого месяца необходимо выплатить часть долга;

– 15–го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15–е число предыдущего месяца. Известно, что в течение второго года кредитования нужно вернуть банку 958.5тыс. рублей. Какую сумму нужно выплатить банку за первые 12 месяцев?

Решение.

S–сумма кредита,

r=1% — ежемесячный процент по вкладу,

n=24 – срок кредитования

Выплаты за 2 год

Выплаты за 1 год

Ответ:1 066 500 рублей.

4. Задачи на вклады (выплата долга в соответствии с данной таблицей или разные платежи каждый год).

4. 15 января планируется взять кредит в банке на сумму 1 млн рублей на 6 месяцев. Условия его возврата таковы:

– 1-го числа каждого месяца долг возрастает на целое число r процентов по сравнению с концом предыдущего месяца, где r – целое число;

– со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

– 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей:

Найдите наибольшее значение r, при котором общая сумма выплат будет составлять менее 1.2 млн. рублей.

Решение.

r% — ежемесячный процент по вкладу,

– «накапливающий» множитель,

Общая сумма выплат равна

Sk= m-0.6+0.6m-0.4+0.4m-0.3+0.3m-0.2+0.2m-0.1+0.1m=2.6m-1.6;

2.6m<1.2; m<

Ответ: 7%.

Разобранными в данной работе примерами, конечно, не исчерпываются все возможные вариации задач о вкладах и кредитах.

Сложность таких задач в том, что здесь нет готовых методов решения, каждая задача уникальна и требует своего подхода. Поэтому посоветовать можно только одно: чтобы научиться решать такие задачи, надо их решать.

Использованная литература 

1. ЕГЭ 2020. Математика. Профильный уровень. 36 типовых вариантов заданий.  

М.: 2020. — 168 с.

2. ЕГЭ. Математика. Задача с экономическим содержанием. 220 задач в формате ЕГЭ с ответами.  

4-е изд., перераб. и доп. — М.: 2018. — 128 с.

3. ЕГЭ. Математика. Задание 17. Экономическая задача. Гуев. Т. 

4. ЕГЭ 2018. Математика. Задачи с экономическим содержанием. Задача 17 (профильный уровень) Шестаков С.А.  

М.: 2018. — 208 с.