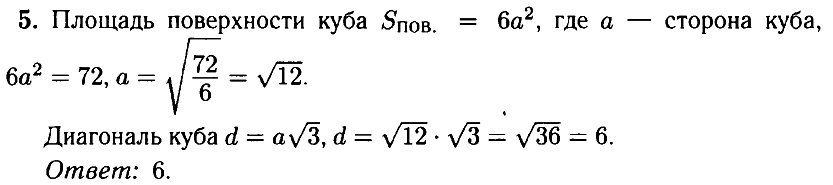Параллельность в пространстве
- Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не имеют общих точек.
- Если две прямые на плоскости перпендикулярны к третьей прямой, то они параллельны.
- Если две прямые в трехмерном пространстве перпендикулярны к одной плоскости, то они параллельны.
- Если прямая a, не лежащая в плоскости $α$, параллельна некоторой прямой $b$, которая лежит в плоскости $α$, то прямая a параллельна плоскости $α$.
- Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым, лежащим в другой плоскости, то такие плоскости параллельны.
Перпендикулярность в пространстве
- Две прямые называются перпендикулярными, если угол между ними равен $90°$.
- Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в этой плоскости.
- Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то заданные плоскости перпендикулярны.
- Теорема о трех перпендикулярах: если прямая, проведенная на плоскости через основание наклонной, перпендикулярна ее проекции, то она перпендикулярна и самой наклонной.
- Если из одной точки проведены к плоскости перпендикуляр и наклонные, то:
- Перпендикуляр короче наклонных.
- Равные наклонные имеют равные проекции на плоскости.
- Большей наклонной соответствует большая проекция на плоскости.
Скрещивающиеся прямые
- Если одна из двух прямых лежит на плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещиваются.
- Через две скрещивающиеся прямые проходит единственная пара параллельных плоскостей.
- Расстояние между скрещивающимися прямыми – это расстояние от некоторой точки одной из скрещивающихся прямых до плоскости, проходящей через другую прямую параллельно первой прямой.
- Угол между скрещивающимися прямыми – это острый угол между двумя пересекающимися прямыми, которые соответственно параллельны заданным скрещивающимся прямым.
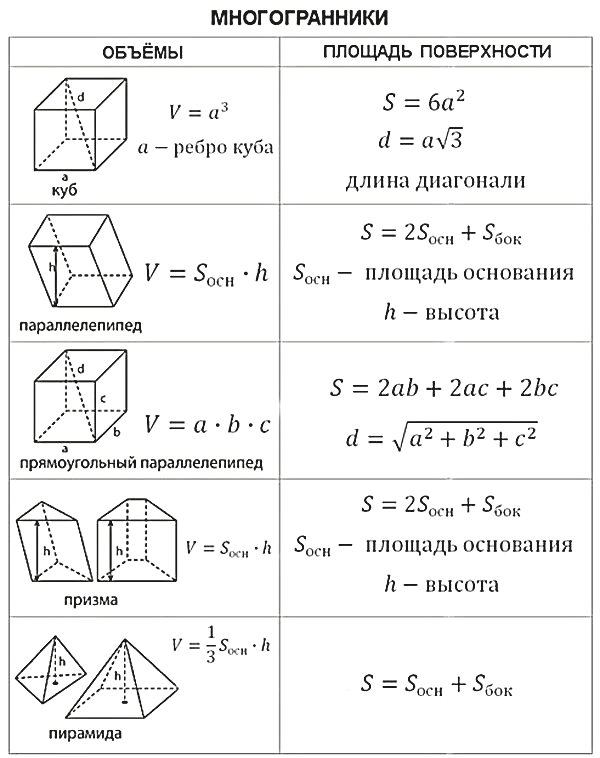
Многогранники
Введем общие обозначения
$P_{осн}$ — периметр основания;
$S_{осн}$ — площадь основания;
$S_{бок}$ — площадь боковой поверхности;
$S_{п.п}$ — площадь полной поверхности;
$V$ — объем фигуры.
| Название | Определение и свойства фигуры | Обозначения и формулы объема, площади |
| Прямоугольный параллелепипед | 1. Все двугранные углы прямоугольного параллелепипеда – прямые. 2. Противоположные грани попарно равны и параллельны. 3. Диагонали прямоугольного параллелепипеда равны. 4. Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений (длины, ширины, высоты). $B_1D^2=AD^2+DC^2+C_1C^2$ |
$V=a·b·c$, где $a, b$ и $с$ – длина, ширина и высота. $S_{бок}=P_{осн}·c=2(a+b)·c$ $S_{п.п}=2(ab+bc+ac)$. |
| Куб | 1. Противоположные грани попарно параллельны. 2. Все двугранные углы куба – прямые. 3. Диагональ куба в $√3$ раз больше его ребра. $B_1 D=АВ√3$ |
Пусть $а$ — длина ребра куба, $d$ — диагональ куба, тогда справедливы формулы: $V=a^3={d^3}/{3√3}$. $S_{п.п}=6а^2=2d^2$ $R={a√3}/{2}$, где $R$ — радиус сферы, описанной около куба. $r={a}/{2}$, где $r$ — радиус сферы, вписанной в куб. |
| Призма |
Призма – это многогранник, состоящий из двух равных многоугольников, расположенных в параллельных плоскостях, и $n$-го количества параллелограммов.
|
$S_{бок}=P_{осн}·h$ $S_{п.п}=S_{бок}+2S_{осн}$ $V=S_{осн}·h$ |
| Пирамида |
|
Формулы вычисления объема и площади поверхности правильной пирамиды. $h_a$ — высота боковой грани (апофема) $S_{бок}={P_{осн}·h_a}/{2}$ $S_{п.п}=S_{бок}+S_{осн}$ $V={1}/{3} S_{осн}·h$ |
| Усеченная пирамида |
|
$V={h(F+f+√{Ff})}/{3}$ Где $F,f$ — площади оснований; $h$ — высота (расстояние между основаниями); Для правильной ус. пирамиды $S_{бок}={(P+p)·a}/{2}$, где $P$ и $p$ – периметры оснований; $а$ – апофема. |
| Цилиндр |
|
$S_{бок.пов.}=2πR·h$ $S_{полной.пов.}=2πR(R+h)$ $V=πR^2·h$ |
| Конус |
|
$S_{бок.пов.}=πR·l$ $S_{полной.пов.}=πR^2+πR·l=πR(R+l)$ $V={πR^2·h}/{3}$ |
| Усеченный конус |
|
$S_{бок}=πl(R+r)$ $S_{п.п.}=π(R^2+r^2+l(R+r))$ $V={πH(R^2+r^2+Rr)}/{3}$ Где $R$ и $r$ – радиусы оснований; $Н$ — высота усеченного конуса. |
| Сфера, шар |
|
$S_{п.п}=4π·R^2=π·d^2$, где $R$ — радиус сферы, $d$ — диаметр сферы $V={4π·R^3}/{3}={π·d^3}/{6}$, где $R$ — радиус шара, $d$ — диаметр шара. |
Тетраэдр
Радиус описанной сферы тетраэдра.
Вокруг тетраэдра можно описать сферу, радиус которой находим по формуле, где $R$ — радиус описанной сферы, $a$ — ребро тетраэдра.
$R={a√6}/{4}$
Радиус вписанной в тетраэдр сферы.
В тетраэдр можно вписать сферу, радиус вписанной сферы находим по формуле, приведенной ниже.
Где $r$ — радиус вписанной в тетраэдр сферы,
$a$ — ребро тетраэдра.
$r={a√6}/{12}$
Составные многогранники
Задачи на нахождение объема составного многогранника:
- Разделить составной многогранник на несколько параллелепипедов.
- Найти объем каждого параллелепипеда.
- Сложить объемы.
Задачи на нахождение площади поверхности составного многогранника.
— Если можно составной многогранник представить в виде прямой призмы, то находим площадь поверхности по формуле:
$S_{полн.пов.}=P_{осн}·h+2S_{осн}$
Чтобы найти площадь основания призмы, надо разделить его на прямоугольники и найти площадь каждого.
— Если составной многогранник нельзя представить в виде призмы, то площадь полной поверхности можно найти как сумму площадей всех граней, ограничивающих поверхность.
Пример:
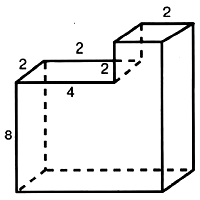
Найдите площадь поверхности многогранника, изображённого на рисунке (все двугранные углы прямые).
Представим данный многогранник как прямую призму с высотой равной $12$.
$S_{полн.пов.}=P_{осн}·h+2S_{осн}$
$P_{осн}=8+6+6+2+2+4=28$
Чтобы найти площадь основания, разделим его на два прямоугольника и найдем площадь каждого:
$S_1=6·6=36$
$S_2=2·4=8$
$S_осн=36+8=44$
Далее подставим все данные в формулу и найдем площадь поверхности многогранника
$S_{полн.пов.}=28·12+2·44=336+88=424$
Ответ: $424$
— Если составной многогранник нельзя представить в виде призмы, то площадь полной поверхности можно найти как сумму площадей всех граней, ограничивающих поверхность.
Задачи на нахождение расстояния между точками составного многогранника.
В данных задачах приведены составные многогранники, у которых двугранные углы прямые. Надо соединить расстояние между заданными точками и достроить его до прямоугольного треугольника. Далее остается воспользоваться теоремой Пифагора для нахождения нужной стороны.
Теорема Пифагора
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
$АС^2+ВС^2=АВ^2$
Задачи на нахождение угла или значения одной из тригонометрических функций обозначенного в условии угла составного многогранника.
Так как в данных задачах приведены составные многогранники, у которых все двугранные углы прямые, то достроим угол до прямоугольного треугольника и найдем его значение по тригонометрическим значениям.
Соотношение между сторонами и углами в прямоугольном треугольнике:
В прямоугольном треугольнике $АВС$, с прямым углом $С$:
Для острого угла $В: АС$ — противолежащий катет; $ВС$ — прилежащий катет.
Для острого угла $А: ВС$ — противолежащий катет; $АС$ — прилежащий катет.
- Синусом ($sin$) острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
- Косинусом ($cos$) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
- Тангенсом ($tg$) острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету.
Значения тригонометрических функций некоторых углов:
| $α$ | $30$ | $45$ | $60$ |
| $sinα$ | ${1}/{2}$ | ${√2}/{2}$ | ${√3}/{2}$ |
| $cosα$ | ${√3}/{2}$ | ${√2}/{2}$ | ${1}/{2}$ |
| $tgα$ | ${√3}/{3}$ | $1$ | $√3$ |
| $ctgα$ | $√3$ | $1$ | ${√3}/{3}$ |
Связь между сторонами правильного n-угольника и радиусами описанной и вписанной окружностей
$АВ=a_n$ — сторона правильного многоугольника
$R$ — радиус описанной окружности
$r$ — радиус вписанной окружности
$n$ — количество сторон и углов
$a_n=2·R·sin{180°}/{n}$;
$r=R·cos{180°}/{n}$;
$a_n=2·r·tg{180°}/{n}$.
Формула нахождения градусной меры угла в правильном многоугольнике:
$α={(n-2)·180°}/{n}$
Формулы площадей треугольников и многоугольников, которые могут находиться в основании многогранников
В основании лежит треугольник
1. $S={a·h_a}/{2}$, где $h_a$ — высота, проведенная к стороне а
2. $S={a·b·sinα}/{2}$, где $a, b$ — соседние стороны, $α$ — угол между этими соседними сторонами.
3. $S=p·r$, где $r$ — радиус вписанной окружности
4. $S={a·b·c}/{4R}$, где $R$ — радиус описанной окружности
5. Для прямоугольного треугольника $S={a·b}/{2}$, где $а$ и $b$ — катеты прямоугольного треугольника.
В основании лежит четырехугольник
Прямоугольник
$S=a·b$, где $а$ и $b$ — смежные стороны.
Ромб
$S={d_1·d_2}/{2}$, где $d_1$ и $d_2$ — диагонали ромба
$S=a^2·sinα$, где $а$ — длина стороны ромба, а $α$ — угол между соседними сторонами.
Трапеция
$S={(a+b)·h}/{2}$, где $а$ и $b$ — основания трапеции, $h$ — высота трапеции.
Площади правильных многоугольников:
1. Для равностороннего треугольника $S={a^{2}√3}/{4}$, где $а$ — длина стороны.
2. Квадрат
$S=a^2$, где $а$ — сторона квадрата.
3. Правильный шестиугольник
Шестиугольник разделим на шесть правильных треугольников и найдем площадь как:
$S=6·S_{треугольника}={6·a^{2}√3}/{4}={3·a^{2}√3}/{2}$, где $а$ — сторона правильного шестиугольника.
Задание 2 Профильного ЕГЭ по математике – это основы стереометрии. Это задачи на вычисление объемов и площадей поверхности многогранников и тел вращения.
Ничего сложного здесь нет. Все эти задачи доступны даже десятикласснику. И даже гуманитарию.
Как решать задания по стереометрии из первой части Профильного ЕГЭ?
Повторим формулы для вычисления объемов и площадей поверхности многогранников (призмы, пирамиды… ) и тел вращения (цилиндра, конуса и шара)
Проверим себя – умеем ли мы рисовать чертежи?
Посмотрим, как решаются простые задачи по стереометрии и задачи с секретами.
Запоминаем один из главных лайфхаков решения задач по стереометрии:
Отношение объемов подобных тел равно кубу коэффициента подобия.
Если все линейные размеры объемного тела увеличить в k раз, то его площадь увеличится в раз, а объем в
раз.
И решаем задачи. У нас все получится!
1. Во сколько раз увеличится площадь поверхности и объем куба, если его ребро увеличить в два раза?
Отношение площадей поверхности подобных тел равно квадрату коэффициента подобия, а отношение объемов – кубу коэффициента подобия. При увеличении ребра в 2 раза площадь поверхности увеличится в 4 раза, а объем – в 8 раз.
2. Площадь основания конуса равна 18. Плоскость, параллельная плоскости основания конуса, делит его высоту на отрезки длиной 3 и 6, считая от вершины. Найдите площадь сечения конуса этой плоскостью.
Плоскость, параллельная основанию, отсекает от конуса меньший конус, все линейные размеры которого в 3 раза меньше, чем у большого. Поэтому площадь сечения в 9 раз меньше площади основания. Она равна 2.
3. Объем пирамиды равен 10. Через середину высоты параллельно основанию пирамиды проведено сечение, которое является основанием меньшей пирамиды с той же вершиной. Найдите объем меньшей пирамиды.
Меньшая пирамида подобна большой, коэффициент подобия Отношение объемов подобных тел равно кубу коэффициента подобия. Поэтому объем меньшей пирамиды в 8 раз меньше объема исходной пирамиды. Он равен
4. Объём правильной четырёхугольной пирамиды SABCD равен 116. Точка E — середина ребра SB. Найдите объём треугольной пирамиды EABC.
Площадь основания пирамиды ЕАВС в 2 раза меньше, чем у пирамиды ABCDS. Высота пирамиды ЕАВС равна половине высоты пирамиды ABCDS. Значит, объем пирамиды ЕАВС в 4 раза меньше объема пирамиды ABCDS. Он равен
5. В правильной четырехугольной пирамиде SABCD точка E – середина ребра AB, боковое ребро SC равно 4, длина отрезка SE равна Найти объем пирамиды SABCD .
Найдем сторону основания пирамиды. По теореме Пифагора, для треугольника SAE получаем, что Соответственно, сторона основания пирамиды равна
Если обозначить центр основания за H, то высоту пирамиды найдем по теореме Пифагора, для треугольника SHE – она равна 2.
Применяя формулу для объема пирамиды , получаем ответ: 16.
Многие задания №2 Профильного ЕГЭ по математике можно считать подготовительными – для того, чтобы научиться решать задачу 14 из второй части ЕГЭ.
Для решения некоторых из них стоит выучить основные определения и теоремы стереометрии. В общем, то, что входит в программу по стереометрии.
6. Стороны основания треугольной пирамиды равны 15, 16 и 17. Боковые ребра наклонены к плоскости основания под углами 45°. Найдите объем пирамиды.
Пусть точка О – проекция точки S на плоскость основания пирамиды. Прямоугольные треугольники АОS, ВОS, СОS равны (по общему катету ОS и острому углу). Значит, АО = ВО = СО. Точка О, равноудаленная от вершин основания, – это центр окружности, описанной вокруг треугольника АВС. Тогда АО = ВО = СО = OS = R, где R – радиус этой окружности.
Радиус описанной окружности найдем по формуле
Площадь найдем по формуле Герона:
, где
– полупериметр.
Заметим, что если боковые ребра пирамиды наклонены к плоскости основания под одинаковым углом, то вершина проецируется в центр основания.
7. В правильной треугольной призме , все ребра которой равны 3, найдите угол между прямыми
и
. Ответ дайте в градусах.
Угол между скрещивающимися прямыми равен углу между параллельными им прямыми, лежащими в одной плоскости. Поскольку и
параллельны, найдем угол между
и
. Он равен 45 градусов, так как грань – квадрат.
Ответ: 45.
Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Профильный ЕГЭ по математике. Задание №2. Стереометрия» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
09.03.2023
Формулы стереометрии. Общий обзор!
Формулы стереометрии. В этой статье общий обзор формул для решения задач по стереометрии. Нужно сказать, что задачи по стереометрии довольно разнообразны, но они несложны. Это задания на нахождение геометрических величин: длин, углов, площадей, объёмов.
Рассматриваются: куб, прямоугольный параллелепипед, призма, пирамида, составной многогранник, цилиндр, конус, шар. Печалит тот факт, что некоторые выпускники на самом экзамене за такие задачи даже не берутся., хотя более 80% таких задач решаются элементарно, практически устно.
Остальные требуют небольших усилий, наличия знаний и специальных приёмов. В будущих статьях мы с вами будем рассматривать все эти задачи, не пропустите!
Для решения необходимо знать формулы площадей поверхности и объёмов параллелепипеда, пирамиды, призмы, цилиндра, конуса и шара. Ещё раз подчеркну, что сложных задач нет, все они решаются в 2-3 действия (максимум). Важно «увидеть» какую формулу необходимо применить, только и всего.
Все необходимые формулы представлены ниже:
Конечно, кроме указанных формул необходимо знать теорему Пифагора, определения тригонометрических функций, понятие средней линии треугольника и ещё немного теоретических фактов, о которых мы поговорим в следующей статье.
С уважением, Александр.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Категория: Формулы Теория | ЕГЭ-№2Формулы
НЕ ОТКЛАДЫВАЙ! Заговори на английском!
ДОЛОЙ обидные ошибки на ЕГЭ!!
Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!
Замучили боль и скованность в мышцах спины?
*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.
- ЕГЭ по математике профиль
Задание 5 профильного уровня ЕГЭ, а также задач 4 и 7 базового уровня ЕГЭ представляет собой несложное показательное, логарифмическое, дробно-рациональное или иррациональное уравнение базового уровня, которое в одно-два действия сводится к линейному или квадратному уравнению, или тригонометрическое уравнение.
Если уравнение сводится к квадратному, то в условии задаётся дополнительное ограничение для отбора корня. В случае логарифмического или иррационального уравнения один из корней может быть отброшен как посторонний без дополнительного ограничения.
→ скачать конспект (простейшие уравнения)
Автор: Алькаева Л. Р.
Практический материал:
→ задание 5 из банка ФИПИ
→ задание 5 — тригонометрические уравнения
→ задание 5 — логарифмические уравнения
→ задание 5 — показательные уравнения
→ задание 5 — иррациональные уравнения
→ задание 5 — линейные, дробно-рациональные, квадратные уравнения
При решении уравнений встретятся ловушки и «подводные камни». Список тем, которые нужно повторить:
— Квадратные уравнения
— Арифметический квадратный корень
— Корни и степени
— Показательная функция
— Показательные уравнения
— Логарифмическая функция
— Логарифмические уравнения
— Тригонометрический круг
— Формулы приведения
— Формулы тригонометрии
— Простейшие тригонометрические уравнения
Связанные страницы:
ЕГЭ по математике Профиль. Задание 5: Уметь выполнять действия с геометрическими фигурами, координатами и векторами. Материалы для подготовки к итоговой аттестации. Алгоритм выполнения задания. Примеры с объяснением выбора правильного ответа. Анализ типичных ошибок.
Вернуться к Оглавлению раздела «Анализ заданий ЕГЭ по математике».
ЕГЭ Профиль. Задание № 5
АЛГОРИТМ ВЫПОЛНЕНИЯ
Задание № 5 рассчитано на умение решать простейшие стереометрические задачи на нахождение геометрических величин (длин, углов, площадей, объёмов), использовать при выполнении знание свойств основных пространственных тел, применять планиметрические факты и методы.
Задание состоит из текстовой задачи и рисунка. Рассматриваются простые пространственные тела: куб, прямоугольный параллелепипед, правильная пирамида, правильная призма. Ответом является конечная десятичная дробь или целое число.
План выполнения:
- Внимательно прочитайте задачу.
- При необходимости выполните на черновике чертёж и дополнительные построения.
- Сделайте на черновике необходимые вычисления.
- Запишите полученное число в поле ответа КИМ и бланк ответов № 1.
Задачи на Прямоугольный параллепипед
Для решения подобных задач необходимо повторить свойства куба и прямоугольного параллелепипеда, формулы для вычисления площади поверхности, объёма этих тел.
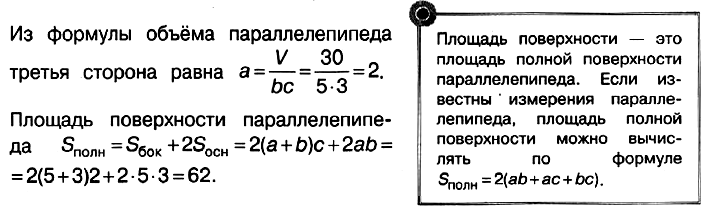
Задача № 5 (1). Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 3 и 5. Объём параллелепипеда равен 30. Найдите площадь его поверхности.
Решение:
Ответ: 62.
Задачи на Составные многогранники
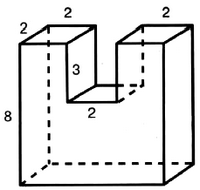
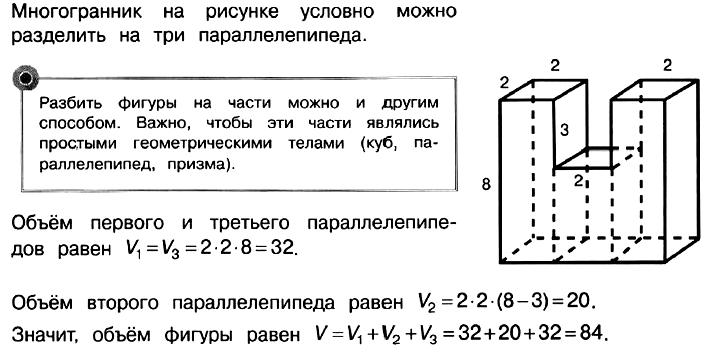
Задача № 5 (2). Найдите объём многогранника, изображённого на рисунке. Все двугранные углы многогранника прямые.
Решение:
Ответ: 84.
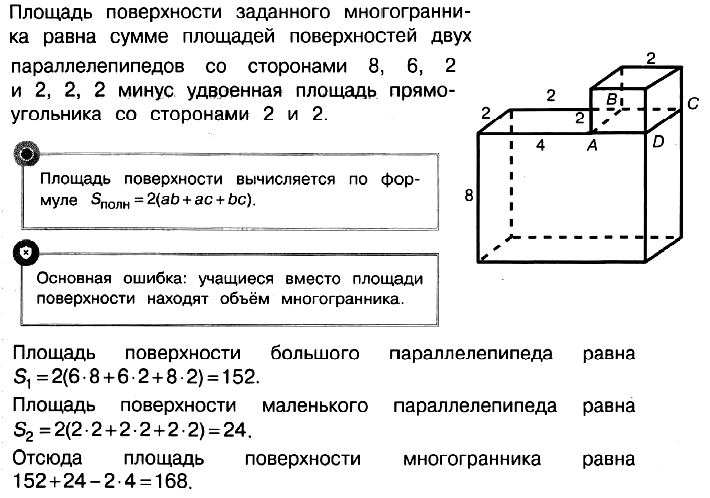
Задача № 5 (3). Найдите площадь поверхности многогранника, изображённого на рисунке. Все двугранные углы многогранника прямые.
Решение:
Ответ: 168.
Задачи на Призмы
Для решения задач этого типа необходимо повторить свойства призмы, формулы для вычисления площади поверхности и объёма призмы.
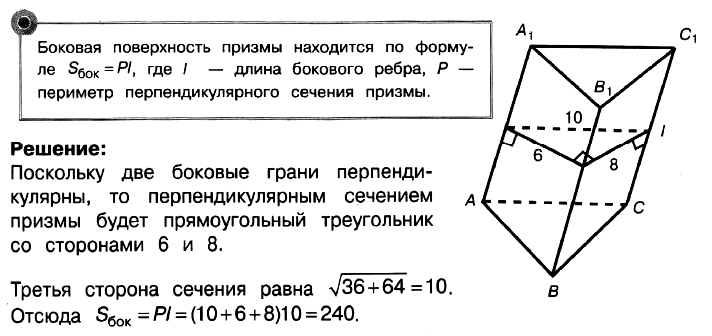
Задача № 5 (4). В треугольной призме две боковые грани перпендикулярны. Их общее ребро равно 10 и отстоит от других боковых рёбер на 6 и 8. Найдите площадь боковой поверхности этой призмы.
Решение:
Ответ: 240.
Задачи на Пирамиды
При подготовке нужно повторить основные свойства пирамиды, формулы для вычисления площади поверхности и объёма пирамиды.
Задача № 5 (5). Основание пирамиды — треугольник, у которого длины двух сторон равны 2 и 6, а угол между этими сторонами составляет 30°. Вычислите объём пирамиды, если её высота равна 3.
Решение:
Ответ: 3.
Задачи на Цилиндры
Для решения задач этого типа необходимо повторить формулы вычисления площади круга, длины окружности, площади поверхности цилиндра, объёма цилиндра.
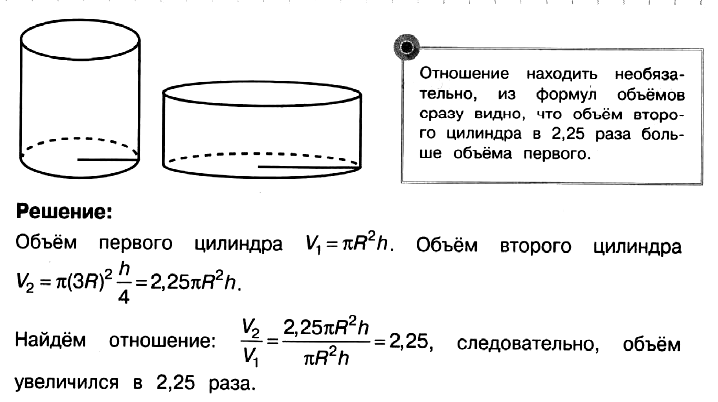
Задача № 5 (6). Радиус основания цилиндра увеличили в 3 раза, а его высоту уменьшили в 4 раза. Во сколько раз увеличится объём цилиндра?
Решение:
Ответ: 2,25.
Задачи на Конусы
При подготовке необходимо повторить свойства конуса, формулы для вычисления площади поверхности и объёма конуса, площади круга и длины окружности.
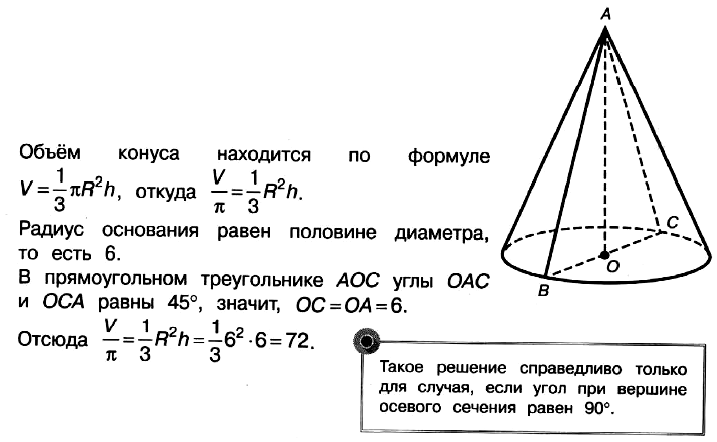
Задача № 5 (7). Диаметр основания конуса равен 12, угол при вершине осевого сечения равен 90°. Вычислите объём конуса, делённый на π.
Решение:
Ответ: 72.
Задачи на Шары
Для решения задач этого типа необходимо повторить формулы для вычисления площади круга, длины окружности, площади поверхности шара, объёма шара.
Задача № 5 (8). Площадь сечения шара плоскостью равна 36π см2. Найдите радиус шара, если плоскость находится на расстоянии 8 см от центра шара.
Решение:
Ответ: 10.
Задачи на Комбинации многогранников
и тел вращения
Задача № 5 (9). В основании прямой призмы лежит прямоугольный треугольник с катетами 3 и 4. Боковые рёбра призмы равны 4/π. Найдите объём цилиндра, описанного около этой призмы.
Решение:
Ответ: 25.
Задача № 5 (10). Шар вписан в цилиндр. Площадь полной поверхности цилиндра равна 15. Найдите площадь поверхности шара.
Решение:
Ответ: 10.
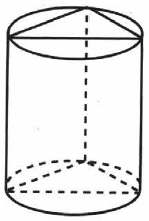
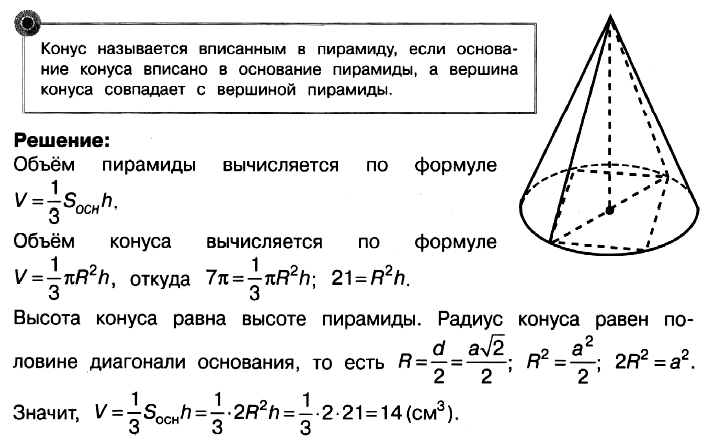
Задача № 5 (11). Объём конуса равен 7π см3. Найдите объём правильной четырёхугольной пирамиды, вписанной в конус.
Решение:
Ответ: 14.
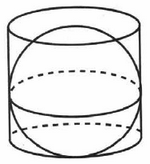
Задача № 5 (12). Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объём шара равен 20. Найдите объём конуса.
Решение:
Ответ: 5.
Тренировочные задания с самопроверкой
№ 5.1. Площадь поверхности куба равна 72 (см. рис.). Найдите его диагональ.
Открыть ОТВЕТ
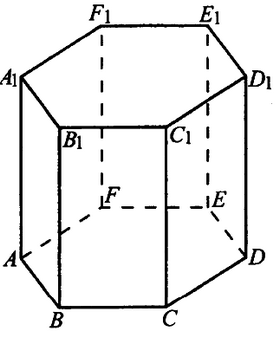
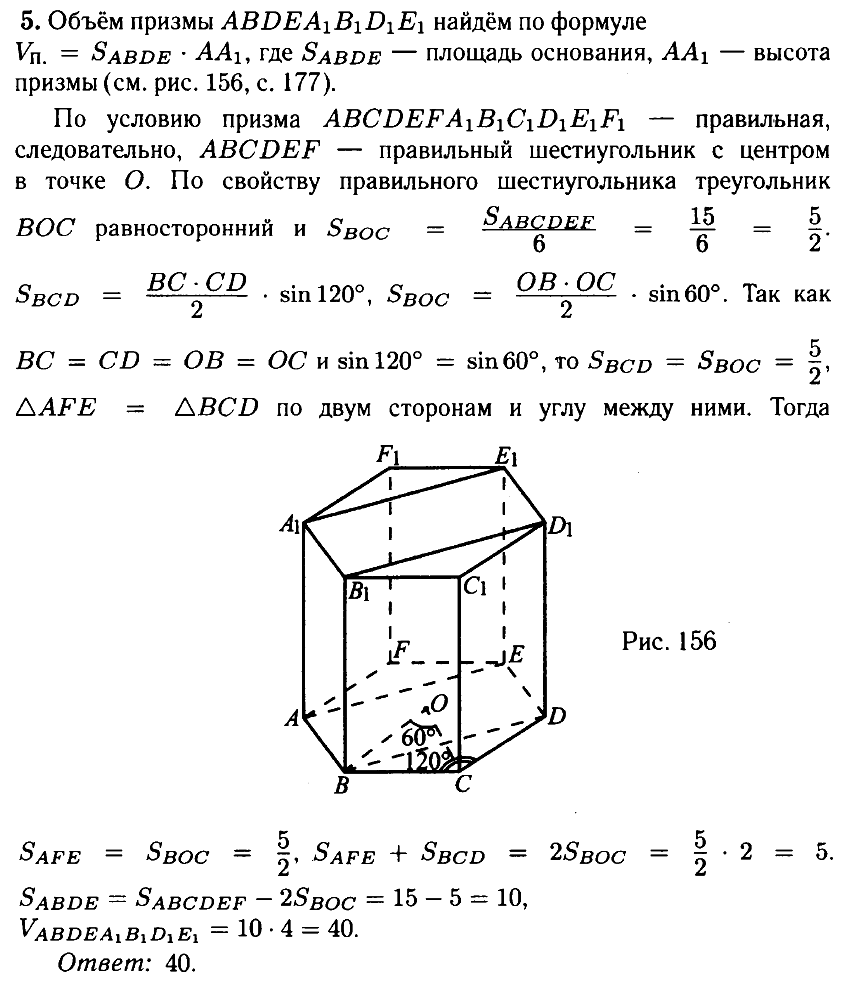
№ 5.2. Найдите объём многогранника, вершинами которого являются точки А, В, D, Е, А1, В1, D1, E1 правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1 (см. рис.). Площадь основания призмы равна 15, а боковое ребро равно 4.
Открыть ОТВЕТ
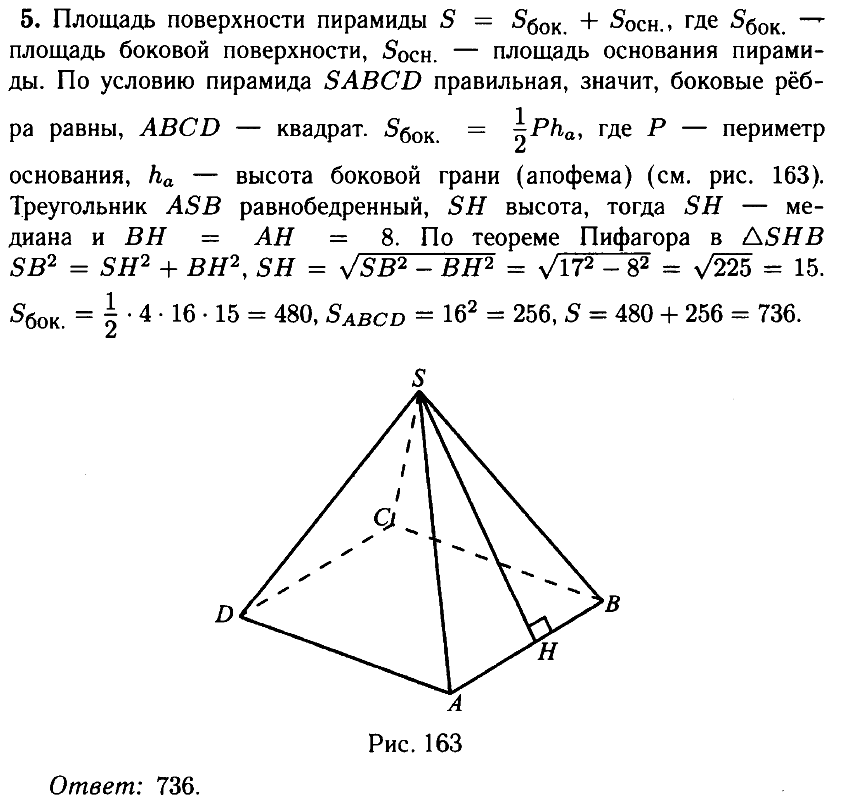
№ 5.3. Стороны основания правильной четырёхугольной пирамиды равны 16, боковые рёбра равны 17 (см. рис.). Найдите площадь поверхности этой пирамиды.
Открыть ОТВЕТ
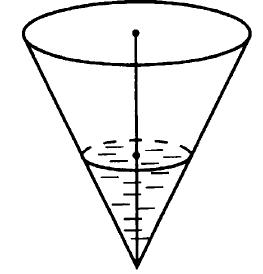
№ 5.4. В сосуде, имеющем форму конуса, уровень жидкости достигает 1/2 высоты (см. рис.). Объём жидкости равен 60 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?
Открыть ОТВЕТ
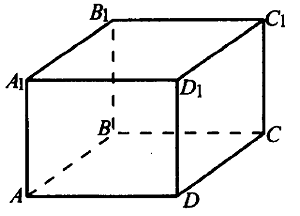
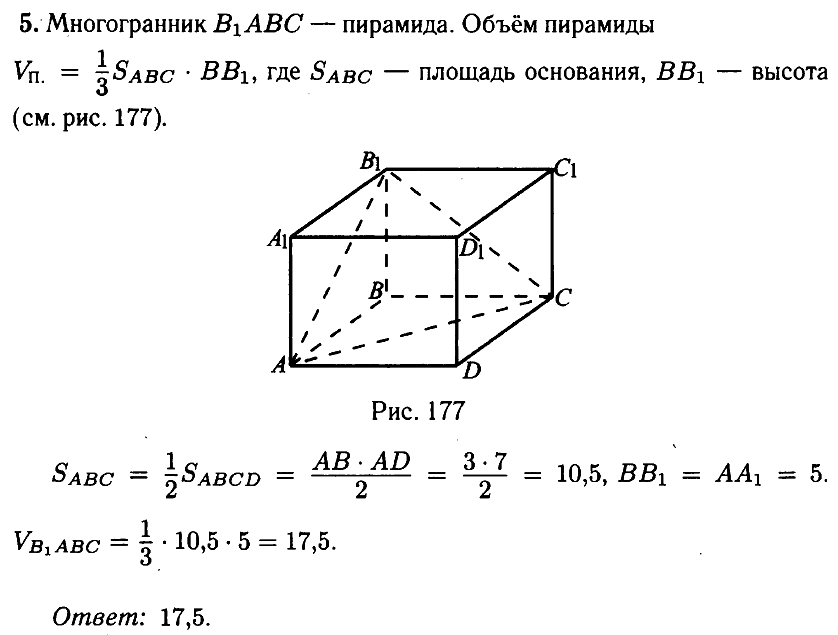
№ 5.5. Найдите объём многогранника, вершинами которого являются точки А, В, С, В прямоугольного параллелепипеда ABCDA1B1C1D1, у которого АВ = 3, AD = 7, АА1 = 5 (см. рис.).
Открыть ОТВЕТ
Вы смотрели: ЕГЭ по математике Профиль. Задание 5: Уметь выполнять действия с геометрическими фигурами, координатами и векторами. Материалы для подготовки к итоговой аттестации. Алгоритм выполнения задания. Примеры с объяснением выбора правильного ответа. Анализ типичных ошибок.
Вернуться к Оглавлению раздела «Анализ заданий ЕГЭ по математике».
Просмотров:
13 775
Площадь поверхности – это суммарная площадь всех поверхностей, которые составляют объемную фигуру.
Призма
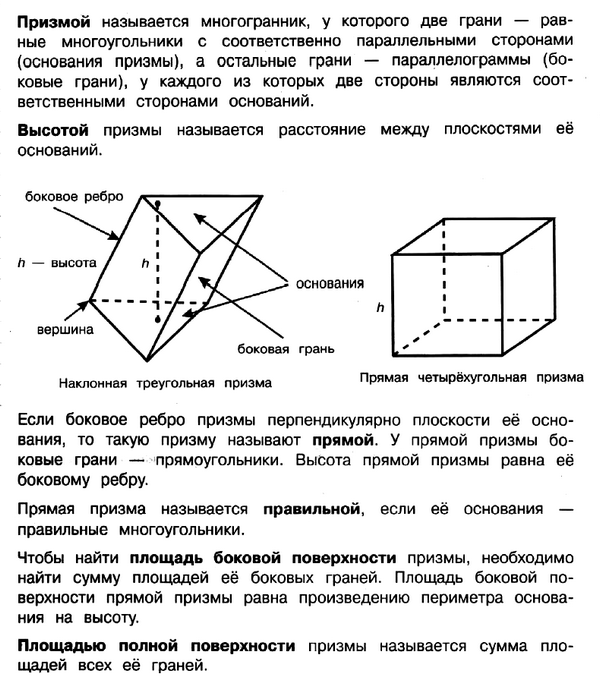
1. Призма — это многогранник, у которого две грани (основания) — равные (n)-угольники, лежащие в параллельных плоскостях, остальные (n) граней (боковые) — параллелограммы. Призмы подразделяются на треугольные, четырехугольные, пятиугольные и т. д. в зависимости от количества сторон основания.
Высотой призмы называется перпендикуляр, опущенный из точки верхнего основания на плоскость нижнего.
2. Призма, у которой боковое ребро перпендикулярно основанию, называется прямой. Ее боковые грани — прямоугольники, и высота равна боковому ребру.
Прямая призма, в основании которой лежит правильный многоугольник, называется правильной. Ее боковые грани, равные прямоугольники.

3. Площадь боковой поверхности призмы равна сумме площадей ее боковых граней: (S_{бок}= S_1+ S_2+…+ S_n).
Площадь поверхности призмы равна сумме площади боковой поверхности и двух площадей оснований: (S_{полн} = S_{бок}+ 2S_{осн}).
4. Объем произвольной призмы равен произведению площади основания на высоту: (V_{призмы}=S_{осн}cdot h).
Параллелепипед
5. Параллелепипедом называется призма, в основании которой лежит параллелограмм. Противоположные боковые грани параллелепипеда равны.
Прямой параллелепипед — это параллелепипед, у которого боковое ребро перпендикулярно основанию.
Прямоугольный параллелепипед — это прямой параллелепипед, у которого в основании лежит прямоугольник.
Диагональ прямоугольного параллелепипеда выражается через его измерения (ширину, длину и высоту) формулой (d^2=a^2+b^2+c^2).
Куб — параллелепипед, у которого все грани квадраты. Диагональ куба с ребром (a): (d=asqrt{3}).


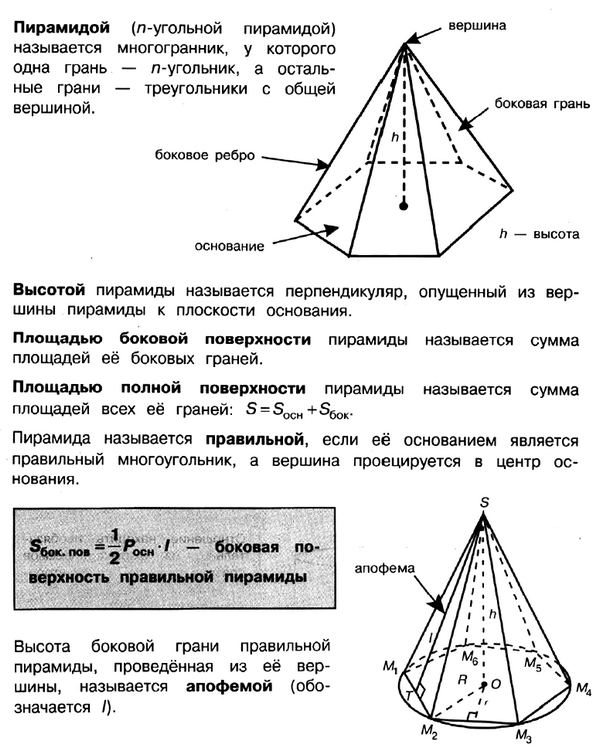
Пирамида
6. Пирамидой называется многогранник, у которого одна грань (основание) — (n)—угольник, а остальные (n) граней (боковые) — треугольники с общей вершиной. Пирамиды подразделяются на треугольные, четырехугольные, пятиугольные и т. д. в зависимости от количества сторон основания.
Тетраэдер – другое название треугольной пирамиды.
Высотой пирамиды называется перпендикуляр, опущенный из вершины пирамиды на основание.
7. Пирамида называется правильной, если ее боковые ребра равны, а в основании лежит правильный многоугольник.
Основание высоты правильной пирамиды совпадает с центром ее основания, углы наклона боковых ребер к основанию равны, двугранные углы при основании равны, все боковые грани — равные равнобедренные треугольники.
Апофема – высота боковой грани правильной пирамиды, проведенная из её вершины к ребру основания.
8. Площадь боковой поверхности пирамиды равна сумме площадей ее боковых граней: (S_{бок}= S_1+ S_2+…+ S_n).
Площадь полной поверхности пирамиды равна сумме площади боковой поверхности и площади основания: (S_{полн} = S_{бок}+ S_{осн}).

9. Объем произвольной пирамиды равен произведению одной трети площади основания на высоту: (V=frac{1}{3} S_{осн}cdot h).

Сфера и шар
10. Сфера — это множество всех точек пространства, равноудаленных от данной точки, называемой центром сферы.
Радиусом сферы называется отрезок, соединяющий центр сферы с точкой на сфере, или длина этого отрезка.
Хордой сферы называется отрезок, соединяющий две точки на сфере.
Диаметр сферы — это хорда, которая проходит через центр сферы. Диаметр сферы равен двум радиусам сферы.
11. Площадь сферы находится по формуле: (S_{сф}=4πR^2).
12. Шаром называется часть пространства, ограниченная сферой, вместе с самой сферой и ее центром. Данная сфера называется поверхностью шара.
Сечение шара с радиусом (R) плоскостью, проходящей через центр шара, называется большим кругом шара. Радиус, хорда, диаметр шара те же, что и его сферы.
13. Объем шара находится по формуле (V_{шара}=frac{4}{3} πR^2).

Цилиндр
14. Цилиндром называется тело, полученное при вращении прямоугольника вокруг прямой, проходящей через одну из его сторон.
Прямая вращения называется осью цилиндра.
Сечение цилиндра плоскостью, проходящей через ось цилиндра, называется осевым сечением.Осевое сечение цилиндра — прямоугольник со сторонами (2r) и (l), где (r) — радиус основания цилиндра, (l) — его образующая.
Образующая цилиндра — отрезок (обозначается (l) или (L)), перпендикулярный основаниям цилиндра и соединяющий точку окружности верхнего основания с точкой окружности нижнего основания.
Высотой цилиндра называется расстояние между плоскостями оснований (обозначается (h) или (H)).
15. Площадь боковой поверхности цилиндра: (S_{бок}=2πrh); (S_{полн} = S_{бок}+ 2S_{осн}=2πrh+2πr^2).
16. Объем цилиндра (V_{цил}=S_{осн} h=πr^2 h).

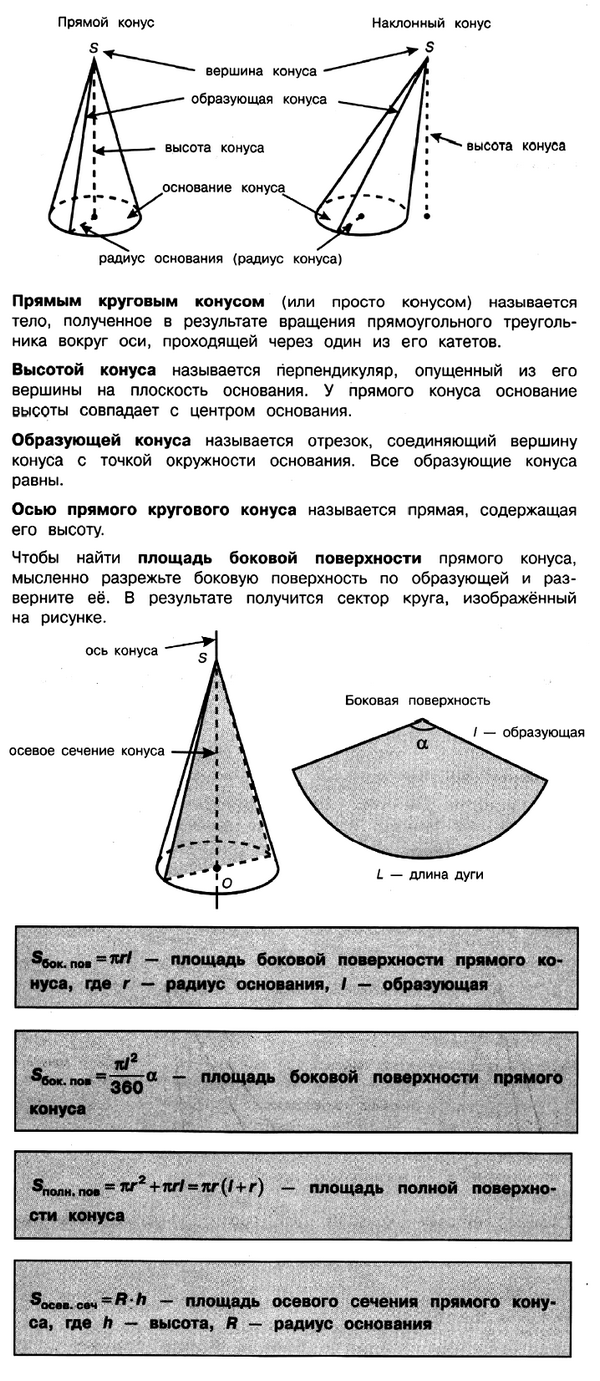
Конус
17. Конусом называется тело, полученное при вращении прямоугольного треугольника вокруг прямой, проходящей через один из его катетов.
Прямая вращения называется осью конуса.
Сечение конуса, проходящее через ось, называется осевым сечением. Осевое сечение конуса — равнобедренный треугольник со стороной основания (2r) боковой стороной (l), где (r) — радиус основания конуса, (l) — его образующая.
Вершина осевого сечения является вершиной конуса.
Образующая конуса (обозначается (l) или (L)) — отрезок, соединяющий вершину конуса и точку окружности основания.
Высотой конуса называется расстояние от вершины конуса до плоскости основания (обозначается (h) или (H)). Высота конуса равна высоте осевого сечения, опущенной на основание.
18. Площадь боковой поверхности конуса: (S_{бок кон}=πrl), (S_{кон}=S_{бок}+S_{осн}=πrl+2πr^2).
19. Объем конуса: (V_{кон}=frac{1}{3}S_{осн}h=frac{1}{3}πr^2 h).